1. INTRODUCTION
Investigations of the role of hollow atoms in the spectra produced from dense plasmas has been the focus of many theoretical and experimental efforts in the last 20 years. Hollow atoms are exotic multiexcited atoms where most of the electrons of the atom or ion are in the outermost shells (Briand et al., Reference Briand, De Billy, Charles, Essabaa, Geller, Desclaux, Bliman and Rastori1990). In the context of this study, hollow atoms will refer specifically only to ions with a one-electron vacancy in each of the K and L shells. These ions then can de-excite by an electron decay from the L shell into the vacant K shell; this has been labeled in the literature KLL – LLL′ transitions, involving 1s −12l −1 (l = s,p) vacancies, i.e., one-electron removed from the K-shell and one electron removed from the L-shell.
The importance of the emission from such transitions was first recognized by the Rhodes group (McPherson et al., Reference Mcpherson, Luk, Thompson, Borisov, Shirayev, Chen, Boyer and Rhodes1994a; Reference Mcpherson, Luk, Thompson, Borisov, Shirayev, Chen, Boyer and Rhodes1994b; Boyer & Rhodes, Reference Boyer and Rhodes1994; Borisov et al., Reference Borisov, Mcpherson, Boyer and Rhodes1996) who investigated the possibility of using such a source as a media for X-ray lasers. Emission from hollow atoms have also been used as a diagnostic for studies of warm dense matter. Experimentally, the formation of hollow atoms has been achieved through neutralization of highly charged ions within solids (Briand et al., Reference Briand, De Billy, Charles, Essabaa, Geller, Desclaux, Bliman and Rastori1990, Reference Briand, Giardino, Borsoni, Froment, Eddrief, Sebenne, Bardin, Schneider, Jin, Khemliche and Prior1996; Gauthier et al., Reference Gauthier, Geindre, Audebert, Rousse, Dos Santos, Grillon, Antonetti and Mancini1995; Aglitsky et al., Reference Aglitsky, Lehecka, Deniz, Hardgrove, Seely, Brown, Feldman, Pawley, Gerber, Bodner, Obenschain, Lehmberg, Mclean, Pronko, Sethian, Stamper, Schmitt, Sullivan, Holland and Laming1996; Suto & Kagawa, Reference Suto and Kagawa1998; Moribayshi et al., Reference Moribayashi, Suto, Zhidkov, Sasaki and Kagawa2001; Rosmej et al., Reference Rosmej, Funk, Geissel, Hoffmann, Tauschwitz, Faenov, Pikuz, Skobelev, Flora, Bollanti, Di Lazzaro, Letardi, Grilli, Palladino, Reale, Tomassetti, Scafati, Reale, Auguste, D'Oliveira, Hulin, Monot, Maksimchuk, Pikuz, Umstadter, Nantel, Bock, Dornik, Stetter, Stöwe, Yakushev, Kulisch and Shilkin2000), through collisions in cluster targets (McPherson et al., Reference Mcpherson, Thompson, Borisov, Boyer and Rhodes1994a, 1999b), and even in gaseous targets (Rosmej et al., Reference Rosmej, Faenov, Pikuz, Magunov, Skobelev, Auguste, D'Oliveira, Hulin, Monot, Andreev, Chegotov and Veisman1999). More recently, hollow atom spectra have been explored from heavy atom targets (Diamant et al., Reference Diamant, Huotari, Hämäläinen, Kao and Deutsch2000a, Reference Diamant, Huotari, Hämäläinen, Kao and Deutsch2000b, Reference Diamant, Huotari, Hämäläinen, Sharon, Kao and Deutsch2001; Shigeoka et al., Reference Shigeoka, Oohashi, Tochio, Ito, Mukoyama, Vlaicu and Fukushima2004) using synchrotron radiation. Transient hollow ion atomic radiation field kinetics have been explored (Rosmej & Lee Reference Rosmej and Lee2007), which shows that short pulse intense narrow-band X-ray sources (for example, future X-ray free electron lasers) enable the rise of hollow ion population densities in dense plasmas higher than without pumping. Other important experimental studies of hollow ion formation have also been carried out at GSI (Rosmej et al., Reference Rosmej, Hoffmann, Suess, Geissel, Rosmej, Faenov, Pikuz, Auguste, D'Oliveira, Hulin, Monot, Hansen and Verbookhaven2001). Laser-plasma interactions probing production of multicharged accelerated ions or warm dense matter have also been studied extensively (see for example, Cao et al., Reference Cao, Uschmann, Zamponi, Kampfer, Fuhrmann, Forster, Holl, Redmer, Toleikis, Tschentscher and Glenzer2007; Batani et al., Reference Batani, Dezulian, Redaelli, Benocci, Stabile, Canova, Desai, Lucchini, Krousky, Masek, Pfeifer, Skala, Dudzak, Rus, Ullschmied, Malka, Faure, Koenig, Limpouch, Nazarov, Pepler, Nagai, Norimatsu and Nishimura2007; Nickles et al., Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Sandner, Schreiber, Hilscher, Jahnke, Andreev and Tikhonchuk2007; Faenov et al., Reference Faenov, Magunov, Pikuz, Skobelev, Gasilov, Stagira, Calegari, Nisoli, de Silvestri, Poletto, Villoresi and Andreev2007; Kado et al., Reference Kado, Daido, Fukumi, Li, Orimo, Hayashi, Nishiuchi, Sagisaka, Ogura, Mori, Nakamura, Noda, Iwashita, Shirai, Tongu, Takeuchi, Yamazaki, Itoh, Souda, Nemoto, Oishi, Nayuki, Kiriyama, Kanazawa, Aoyama, Akahane, Inoue, Tsuji, Nakai, Yamamoto, Kotaki, Kondo, Bulanov, Esirkepov, Utsumi, Nagashima, Kimura and Yamakawa2006). Experiments at JAEA (Fukuda et al., Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Kishimoto, Yamakawa, Faenov, Magunov, Pikuz, Skobelev, Abdallah, Csanak, Boldarev and Gasilov2004) have probed Ar clusters for hollow atom production, and other studies have been done on laser absorption mechanisms in clusters (Kanapathipillai, Reference Kanapathipillai2006).
One of the principal difficulties for experimental measurements of emission from such systems is the low intensities of lines from these transitions, as well as the complicated spectra that results due to overlaps with spectra from transitions in other ions in the plasma. For example, in Xe spectra (McPherson et al., Reference Mcpherson, Thompson, Borisov, Boyer and Rhodes1994a), many transitions belonging to usual M-shell satellites overlap strongly with the hollow atom spectra for near Ne-like ions. The many thousands of transitions in such a spectral range make it almost impossible to separate the lines, and to estimate the influence of the hollow atom spectra on the line intensities. A simpler situation may arise if one considers hollow atom spectra near K α lines (e.g., KL–LL transitions (involving one electron removed from either the K or L shells; (1s2s)−1 or (1s2p)−1 vacancies) (Gauthier et al., Reference Gauthier, Geindre, Audebert, Rousse, Dos Santos, Grillon, Antonetti and Mancini1995). Fewer lines exist in such a region and it can be possible to distinguish and investigate the mechanism for their production (Gauthier et al., Reference Gauthier, Geindre, Audebert, Rousse, Dos Santos, Grillon, Antonetti and Mancini1995). The most “clean” spectral range may be the wavelength range between the Ly and Heα lines of highly-charged ions (Faenov et al., Reference Faenov, Magunov Pikuz, Skobelev, Pikuz, Urnov, Abdallah, Clark, Cohen, Jonson, Kyrala, Wilke, Maksimchuk, Umstadter, Nantel, Doron, Behar, Mandelbaum, Schwob, Dubau, Rosmej and Osterheld1999; Abdallah et al., Reference Abdallah, Skobelev, Faenov, Magunov, Pikuz, Flora, Bollanti, DI LAZZARO, Letardi, Burattini, Grilli, Reale, Palladino, Tomassetti, Scafati and Reale2000; Rosmej & Lee, Reference Rosmej and Lee2007) (where the hollow atom transitions (arising from L-shell ions) are from states where the initial K shell is completely vacant (1s)−2). In these cases, hollow atom spectra from Li-, Be-, and other L-shell lines are well separated from, not only each other, but from the usual dielectronic satellites from such ions.
Although high brightness X-ray sources, intense fast electron- and ion-beams can be used to efficiently produce hollow atoms, the mechanisms and kinetics of hollow atom production are far from clear. Theoretically, the calculation of spectra from such exotic species are complicated by the requirement that transitions from all configurations (including all multiply-excited configurations) that can contribute in the spectral range must be included in any kinetics model. This can easily result in a very large system of rate equations, which may need to be solved at a sufficient level of detail to accurately compute line positions, as well as including the effects of configuration-interaction between the electronic configurations in question.
In the experimental work described here, an investigation was made of the spectra between the Ly- and Heα lines, and near the K α lines of ions produced from an ultrashort-pulse laser-driven Ar cluster target. Unfortunately, no hollow atom spectra from L-shell ions, in the wavelength range between the Ly- and Heα lines, were observed. However, spectra with high resolution was observed between the Heα and K α lines and detailed comparisons of these line intensities with theoretical calculations has been made. The theoretical calculations were made using the Los Alamos plasma kinetics code ATOMIC (Abdallah et al., Reference Abdallah, Batani, Desai, Lucchini, Faenov, Pikuz, Magunov and Narayanan2007; Magee et al., Reference Magee, Abdallah, Colgan, Hakel, Kilcrease, Mazevet, Sherrill, Fontes, Zhang, Cohen, Mazevet and Kilcrease2004), with the time-dependent rate equations solved until the system has reached steady-state. Configurations including double-electron excitations from the K- and L-shells were included for all Ar ions from neutral through N-like. A recently described mixed-unresolved-transition-array (MUTA) model (Mazevet & Abdallah, Reference Mazevet and Abdallah2006) was used to compute the spectra from configuration-average ion populations. Various electron temperatures and ion densities were considered in our investigations. It is our aim in this study to show that spectra from hollow atom configurations can be identified in kinetics modeling, and that evidence for this is found in supporting experimental measurements.
2. METHOD
2.1. Experimental Techniques
The Ar cluster experiments were performed with the Japan Atomic Energy Agency (JAEA) (Kyoto, Japan) Ti:sapphire laser system based on the technique of chirped pulse amplification, which was designed to generate 20 fs pulses and is capable of producing a focused intensity up to 1020 W/cm2 (Yamakawa et al., Reference Yamakawa, Aoyama, Matsuoka, Kase, Akahane and Takuma1998; Kado et al., Reference Kado, Daido, Fukumi, Li, Orimo, Hayashi, Nishiuchi, Sagisaka, Ogura, Mori, Nakamura, Noda, Iwashita, Shirai, Tongu, Takeuchi, Yamazaki, Itoh, Souda, Nemoto, Oishi, Nayuki, Kiriyama, Kanazawa, Aoyama, Akahane, Inoue, Tsuji, Nakai, Yamamoto, Kotaki, Kondo, Bulanov, Esirkepov, Utsumi, Nagashima, Kimura and Yamakawa2006; Akahane et al., Reference Akahane, Ma, Fukuda, Aoyama, Kiriyama, Sheldakova, Kudryashov and Yamakawa2006). In this study the amplified pulses were compressed to 30 fs by a vacuum pulse compressor yielding a maximum pulse energy of 360 mJ (Fukuda et al., Reference Fukuda, Yamakawa, Akahane, Aoyama, Inoue, Ueda, Abdallah, Csanak, Faenov, Magunov, Pikuz, Skobelev, Boldarev and Gasilov2003; Abdallah et al., Reference Abdallah, Csanak, Fukuda, Akahane, Aoyama, Inoue, Ueda, Yamakawa, Faenov, Magunov, Pikuz and Skobelev2003; Sherrill et al., Reference Sherrill, Abdallah, Csanak, Dodd, Fukuda, Akahane, Aoyama, Inoue, Ueda, Yamakawa, Faenov, Magunov, Pikuz and Skobelev2006). Two types of experiments were performed. In the first set of experiments, only one double Pockels cell was used after the regenerative amplifier, which allowed us to reduce the laser prepulse by up to 5 × 10−4 compared with the main laser pulse. In addition, experiments were performed where after the regenerative amplifier, the laser pulse is passed through two double Pockels cells, which allows the possibility of reducing the laser prepulse even further. The final contrast ratio between the prepulse and main laser pulse, which precedes it by 10 ns, was better than 4.6 × 10−6: 1. In a vacuum target chamber, the pulses were focused using a f/3 Au-coated off-axis parabolic mirror. The measured spot size was 11 μm at 1/e2, which was 1.1 times as large as that of the diffraction limit. Approximately 64% of the laser energy was contained in the 11 μm Gaussian spot. These specific experiments were carried out with various laser energies (49 – 115 mJ), and in a wide range of laser pulse durations from 30 up to 1000 fs, which corresponds to laser intensities of about 6 × 1016–2 × 1018 W/cm2.
A cluster-gas target was produced by expanding 60-bar Ar gas into a vacuum using a pulsed valve connected with a special nozzle consisting of three truncated cones with different apex angles. The nozzle has the capability to produce Ar clusters with an average diameter of around 1.5 μm (Fukuda et al., Reference Fukuda, Yamakawa, Akahane, Aoyama, Inoue, Ueda, Abdallah, Csanak, Faenov, Magunov, Pikuz, Skobelev, Boldarev and Gasilov2003, Bodlarev et al., Reference Boldarev, Gasilov, Faenov, Fukuda and Yamakawa2006). As mentioned previously, in the present experiments, the laser pulse contrast varied from 5 × 10−4 up to 4.6 × 10−6. To minimize the tendency of the laser prepulse to destroy the clusters, we purposely used in our experiments very big clusters, since the rate of cluster decay is primarily determined by the number of atoms in the cluster (Ditmire et al., Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996). In such cases, the micron-sized clusters can significantly reduce the cluster's sensitivity to the laser prepulse, preclude low-density preplasma formation, and thus guarantee the direct interaction between the high-density cluster and the main fs pulse. The existence of a dense core region of the clusters was confirmed via analysis of the X-ray emissions from the Ar clusters in separate experiments (Fukuda et al., Reference Fukuda, Yamakawa, Akahane, Aoyama, Inoue, Ueda, Abdallah, Csanak, Faenov, Magunov, Pikuz, Skobelev, Boldarev and Gasilov2001, 2003, Skobelev et al., Reference Skobelev, Faenov, Magunov, Pikuz, Boldarev, Gasilov, Abdallah, Junkel-Vives, Auguste, Dobosz, D'oliveira, Hulin, Monot, Blasco, Dorchies, Caillaud, Bonte, Stenz, Salin, Loboda, Litvinenko, Popova, Baidin and Sharkov2002). It was demonstrated in these studies that, if the laser prepulse was too big, clusters were destroyed, no frozen part of cluster remained, and no X-rays were observed. So, although the prepulse intensity was strong enough to ionize the Ar atoms in the clusters in our experiments, the ionization and the expansion occur at the cluster peripheral region, and the cluster core can be treated as frozen at all prepulse intensities of about 1011 – 1014 W/cm2. Indeed, in the case of higher prepulses, the remaining part of the frozen cluster was smaller compared with a higher laser contrast.
The position and timing of the nozzle were precisely adjusted so that the X-ray signal is maximized. As a result, the laser pulse under optimal conditions for X-ray production was focused onto the edge of the gas jet, i.e., 1.5 mm downstream of the gas flow from the nozzle outlet. The spatially resolved X-ray spectra were measured using focusing spectrometers with spatial resolution (Fukuda et al., Reference Fukuda, Yamakawa, Akahane, Aoyama, Inoue, Ueda, Abdallah, Csanak, Faenov, Magunov, Pikuz, Skobelev, Boldarev and Gasilov2003; 2004; Faenov et al., Reference Faenov, Pikuz, Erko, Bryunetkin, Dyakin, Ivanenkov, Mingaleev, Pikuz, Romanova and Shelkovenko1994; Reference Faenov, Skobelev, Magunov, Pikuz, Abdallah, Junkel-Vives, Blasco, Dorchies, Stenz, Salin, Auguste, Dobosz, Monot, D' Oliveira, Hulin, Boldarev and Gasilov2001). This spectrometer is equipped with a spherically bent mica crystal (R = 150 mm) and a vacuum compatible X-ray charge coupled device camera (DX420-BN, ANDOR). The spherically bent mica crystal was placed at a distance of 381.2 mm from the plasma source and was centered at 4.05 Å, which corresponds to a Bragg angle of 35.7° for fourth order reflection of the crystal. This instrument recorded He-like spectra of Ar including the associated satellite lines. In Figure 1, typical X-ray spectra in the spectral range between the resonance Heα line of Ar XVII and Kα line of Ar are presented, for five cases with various laser parameters as listed in Table 1.
From the traces in Figure 1 and the parameters listed in Table 1, it is evident that large differences exist in the spectral features obtained when better or worse laser contrast (as previously discussed, in the case of better contrast a larger part of the frozen (solid) cluster remains when main laser pulse interacts with it) is employed. Generally in the case of better laser contrast, the low Z (F-, O-, N-like …) isoelectronic sequence satellites practically disappear and high Z (Li-, Be-like ) satellites remain at the same intensity. The clearest example of this is in comparing spectra obtained with the same 150 fs laser pulse duration for both contrasts (see Fig. 1 cases 2 and 5, which correspond to the laser parameters in rows 2 and 5 in Table 1). Even stronger features in the difference of the satellite intensities could be seen in the case of further decreasing the laser prepulse intensities (for example, in Fig. 1 cases 3 and 5, which correspond to the laser parameters in rows 3 and 5 in Table 1). Also we emphasize that our measurements with clusters demonstrate that at any laser contrast and laser pulse duration the intensity of neutral Kα lines are very small compared with the intensity of satellite lines, which is in contrast to the experimental observations made when fs laser pulses interact with solid targets (see for example, Gauthier et al., Reference Gauthier, Geindre, Audebert, Rousse, Dos Santos, Grillon, Antonetti and Mancini1995). This strong difference in neutral Kα line intensities for fs laser interaction with cluster and solid targets is related to the fact that in the case of clusters, due to the relatively small size of each cluster the laser prepulse heats atoms inside the cluster and ionizes some electrons. Then, when the main laser pulse interacts with the cluster, there are almost no neutral atoms inside the cluster and hot electrons, which are generated by the main laser pulse, interact not with neutral atoms (which is necessary to generation of neutral Kα lines), but with warm dense slightly ionized targets. In the case of fs laser interaction with solid targets, the laser prepulse also ionizes some atoms in the laser focus, but most of the atoms remain neutral inside the solid target. Then, when the main pulse interacts with the solid and generates hot electrons a lot of neutral atoms exist and strong Kα emission is found. In addition, from trace 3 in Figure 1, we see that in the case of experiments with the best laser contrast in the spectra of Ar, we observe strong structure around 4.17 Å and practically no other lines up to the wavelengths 4.1 Å. Such behavior of observed spectra is quite unusual, because usually lines belong to F-, O-, and N- ions should have practically the same intensities in such a spectral range (see traces 1, 4, and 5). It is our hypothesis that the observed features are connected with the strong influence of transitions from hollow atom ion stages. We now turn to our theoretical calculations which explore this idea.
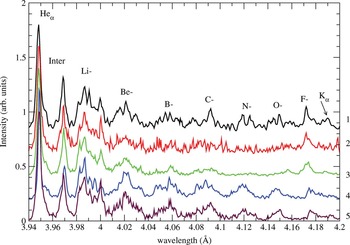
Fig. 1. Experimental spectra obtained for all five sets of conditions as described in Table 1 and in the text.
Table 1. Laser pulse parameters in the various experiments performed

2.2. Theoretical Techniques
The atomic data used in this model were generated from the Los Alamos suite of computer codes developed over many years to calculate atomic structure and atomic scattering quantities. The CATS code (Abdallah et al., Reference Abdallah, Clark and Cowan1988), which is an adaptation of Cowan's atomic structure codes (Cowan, Reference Cowan1981), was used to calculate wavefunctions, energy levels, oscillator strengths, and plane-wave Born collision strengths for ionization stages of Ar from neutral through N-like. To facilitate calculation of atomic populations, ionization stages for C-like through to the bare ion included only ground-state configurations. CATS was used to generate data in the configuration-average approximation. Electron-impact ionization, photoionization, and autoionization cross sections were calculated using the multi-purpose ionization GIPPER code (Archer et al., Reference Archer, Clark, Fontes and Zhang2002). The latter two processes were calculated explicitly with distorted-wave continuum functions while the electron-impact ionization calculations used scaled hydrogenic cross sections that were designed to reproduce distorted-wave calculations. Collisional de-excitation, three-body, radiative, and dielectronic recombination rates were obtained from detailed balance.
The atomic model used for this Ar study included a limited number (around 30) of configurations per ion stage. The most relevant configurations for this study were configurations where two electrons are excited from the K and L shells into the n = 3 (M) shell, for example, 1s 1 2s 1 2p 6 3s 2 3p 6 3d 2 for neutral Ar. Such configurations can easily describe a large number of fine-structure levels, which can make a full calculation at the fine-structure level prohibitive. The MUTA approach, which retains the strongest lines within a given transition array (Mazevet & Abdallah, Reference Mazevet and Abdallah2006), was employed to allow a reasonable calculation while retaining the accurate spectral description required for this study. A consistent set of configurations for neutral Ar through N-like were generated including all such two-electron excitations into the n = 3 shell. The model was limited to n = 3 to allow timely calculations.
The solution of the rate equations for the Ar system was carried out using the Los Alamos code ATOMIC, which has been described previously (Magee et al., Reference Magee, Abdallah, Colgan, Hakel, Kilcrease, Mazevet, Sherrill, Fontes, Zhang, Cohen, Mazevet and Kilcrease2004). The MUTA capability allows us to obtain ionic populations at the configuration-average level (thus significantly reducing the computational time required for the atomic wavefunctions) while retaining the ability to provide a spectral description comparable in accuracy to a detailed (fine-structure) approach, where all lines are included explicitly in the calculation. This development was crucial since it enabled us to include configurations where two electrons were excited from the K and L shells within a calculation that could be completed in a timely manner. The time-dependent rate equations were solved until the transient plasma had reached a steady-state. Studies were made of the behavior of the emitted spectra as a function of the electron temperature, and atom density, for Maxwellian electron distributions, and for electron distributions containing some small fraction of hot electrons.
In an effort to more clearly discern the source of the many emission lines seen in the transient plasma several smaller models were also constructed. These involved removing the F- and O-like configurations from the calculation, removing the hollow-atom configurations from the calculation, and finally removing both the configurations associated with F- and O-like, and the hollow atoms from a calculation. This allowed us to identify the source of many of the strong lines observed in our calculations.
3. RESULTS AND DISCUSSION
In Figure 2, we show emission spectra from our calculations performed for an electron temperature of 100 eV and an atom density of 1022 cm3. The black solid lines show the results from a full calculation including all configurations described in the previous section. Calculations are shown for three times as the plasma evolves; at 60%, 80%, and 100% of the final time of 10−12 s. Strong emission peaks are observed in the wavelength region near 4.17 Å and also around 4.14 Å. In an effort to determine whether these peaks arise from transitions in the hollow atom configurations, or from transitions in the F- or O-like ions, all of which are in this wavelength region, we performed some further calculations in which various types of configurations were removed. The red dashed line shows similar calculations with no transitions within the F- and O-like ion stages included. The green dot-dashed line shows calculations in which transitions from hollow atoms have been removed, and the fourth, blue dotted line, shows calculations in which both of these types of transitions have been removed.

Fig. 2. ATOMIC calculations of the Ar spectra for all four models as described in the text, for an electron temperature of 100 eV, and for an atom density of 1022/cm3. All four models are shown for three times in the evolution of the plasma; at 60%, 80%, and 100% of the final time of 10−12s.
From this study, several conclusions can be drawn. The emission in the region around 4.17 Å is mostly from neutral to Ne-like ions, except for the two most intense lines which are from the 1s2s 2 2p 6 – 1s 2 2s 2 2p 5 transition in F-like argon. The difference between the red dot-dashed line and the blue dotted line at a wavelength just above 4.17 Å (as shown in the inset) indicates a peak due to a hollow atom transition. The close proximity of this transition to the F- and O-like peaks shows how difficult it can be to unambiguously identify the source of the emission peaks in such regions. Figure 2c also indicates that the strong peaks near 4.14 Å are due to transitions within the F- and O-like ions, as seen also in the experimental measurements of Figure 1.
The spectra at earlier times also tell us that strong emission peaks around 4.17 Å can arise from hollow atom transitions, since the black solid line and red dashed line in Figure 2a are so similar. However, as the plasma evolves, the average ionization stage of the plasma increases, and so the relative strength of these lines decreases, so that the hollow atom transitions make relatively little contribution to the emission spectra seen at the final time.
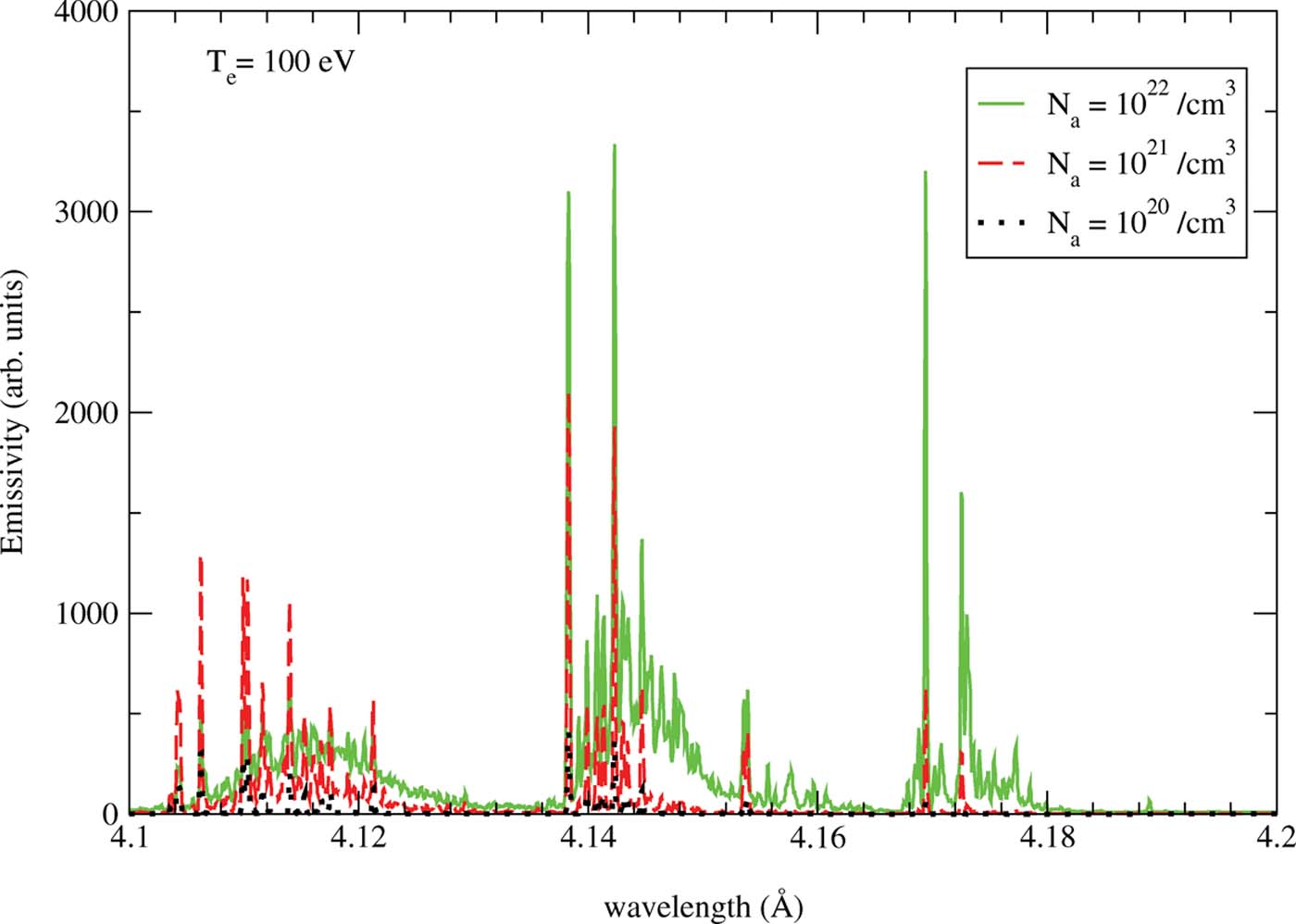
In Figure 3, we examine the dependence of our spectra from the most complete ATOMIC model on the atom density of the plasma, for an electron temperature of 100 eV. To properly contrast the calculations at different atom densities, we have divided each emissivity by the atom density and by the time of propagation. It is immediately obvious that, at the lowest atom density, (1020 atoms/cm3), relatively little emission is observed. As the density is increased more initial states are accessible, and so more possible emission lines are found. At the highest density (1022 atoms/cm3), emission due to the hollow atom transitions are observed, as discussed previously. In Figure 4, we present the average ionization stage of the plasma for the three calculations shown in Figure 3. In each case, the plasma starts out neutral and evolves to a steady state over time. The lower density calculations take longer to reach steady-state as shown. However, at the final time in each case, the average ionization stages are quite similar (around 10), even though the spectra presented in Figure 3 are quite different. This reflects the greater emissivity from the initial states, which are more readily populated when the densities are larger.
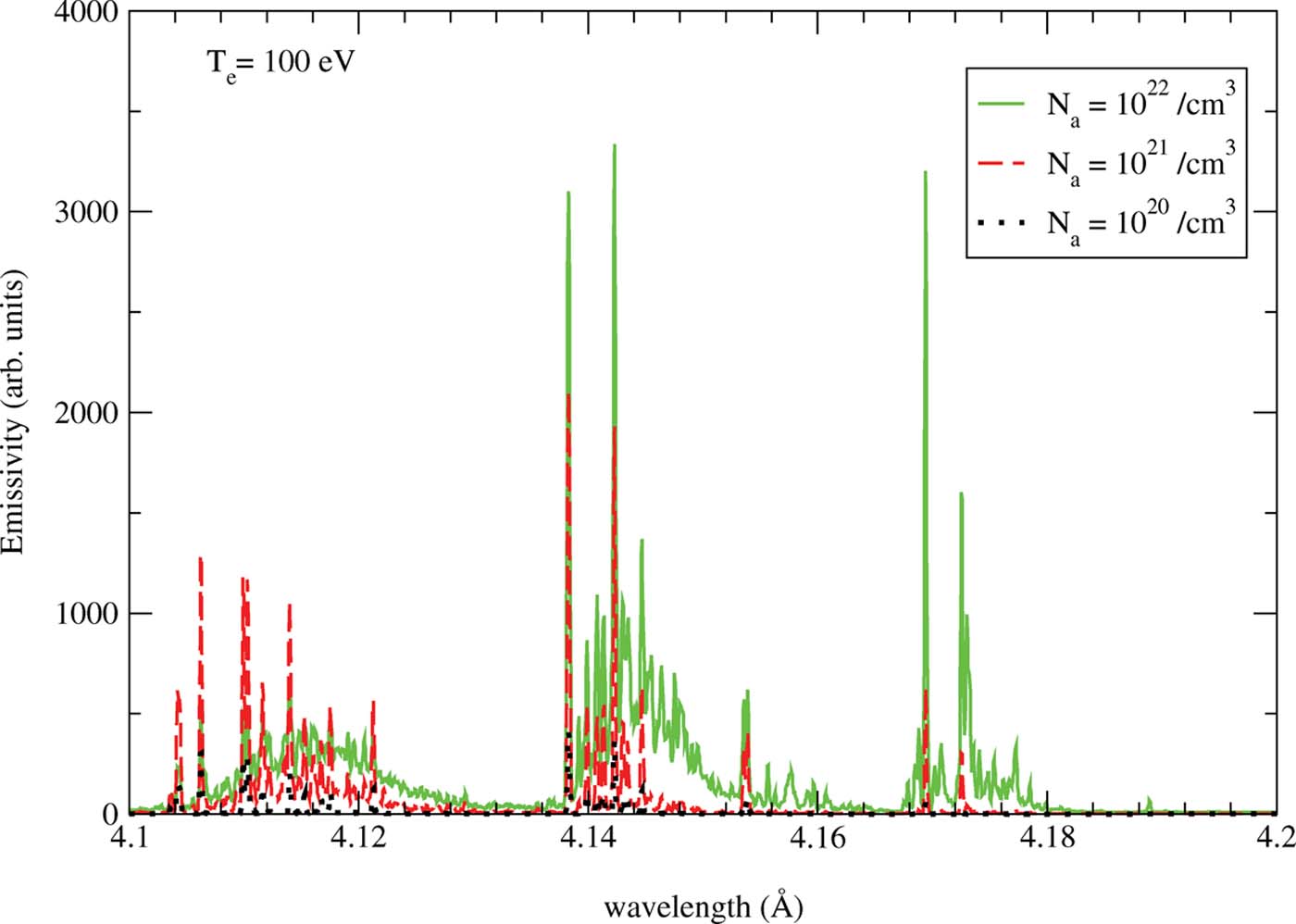
Fig. 3. ATOMIC calculations of the Ar spectra using the full model at an electron temperature of 100 eV for three atom densities as indicated. The spectra is shown at the final time of the plasma evolution, when each case has reached steady-state. To properly compare these spectra, each curve has been divided by the atom density and the final time of propagation.

Fig. 4. Average ionization stage as a function of time for the three cases shown in Figure 3. The lower density calculations were propagated to longer times to reach a steady-state distribution, as indicated.
We also can examine whether the presence of “hot” electrons in the plasma (which can be a common occurrence in laser-produced plasmas) can significantly alter the emission spectra. In Figure 5, we again show calculations using our full model, for an electron temperature of 50 eV, and an atom density of 1022/cm3. Three calculations are presented; one with no hot electrons; one with 1% of the electrons at a temperature of 5 keV; and one with 3% of the electrons at a temperature of 5 keV. Addition of the hot electrons results in significantly more emission in the wavelength region around 4.14 Å. Again, this corresponds to emission from the F- and O-like ion stages. The spectra are fairly sensitive to even small amounts of hot electrons in this wavelength region. Small changes to the ionization state of the plasma lead to noticeable spectral changes. In addition, the strong peaks near 4.17 Å due to F-like emission, discussed above, are also enhanced. We can also contrast the calculations where all the electrons are at 50 eV with the calculations shown in Figure 3, where the electrons are at a temperature of 100 eV. The lower temperature calculations show almost no emission around 4.14 Å from the F- and O-like ions, which reflects the lower average ionization stage at this temperature.

Fig. 5. ATOMIC calculations of the Ar spectra using the full model at an electron temperature of 50 eV at an atom density of 1022/cm3. Three calculations are shown; one with a Maxwellian electron distribution (black solid line), one including 1% hot electrons at 5 keV (dashed red line), and a calculation including 3% hot electrons at 5 keV (dot-dashed light green line).
Finally, in Figure 6, we are in a position to compare our theoretical calculations with the experimental measurements, obtained when the laser prepulse was smallest and the remaining part of the cluster was most dense and closest to the initial conditions. In this case, we choose to compare Case 3 of the experimental data presented in Figure 1, with calculations made at an electron temperature of 50 eV and an atom density of 1022/cm3. We show calculations where 3% of the electrons are at a temperature of 5 keV. These conditions were chosen since the ratio between the two peaks at 4.15 and 4.17 Å were closest to the experimental measurements of Case 3, in which we have hypothesized that the spectra are due to hollow atom transitions. In our calculations at an electron temperature of 100 eV, we also find peaks at the lower wavelengths, and calculations at 50 eV with no hot electrons find no peak around 4.15 Å.

Fig. 6. Comparison of theory and experiment. Our ATOMIC calculations are at an electron temperature of 50 eV, atom density of 1022/cm3, and includes 3% hot electrons at 5 keV. We show results from the full model (red solid lines) and from our calculations in which configurations containing hollow atoms are removed from the calculation (light green dashed line). The experimental measurement is the case 3 as described in the text (black lines with dots).
The agreement between the calculations and the measurements is quite good. Both theory and experiment find intense emission lines at 4.17 Å, which arise from 1s 2 2s 2 2p 52P 1.5 – 1s 1 2s 2 2p 62S 0.5 and 1s 2 2s 2 2p 52P 0.5 – 1s 1 2s 2 2p 62S 0.5 transitions in the F-like ion stage, as well as transitions between hollow atom configurations and Kα transitions in neutral to Ne-like argon. The smaller peak is calculated to be at 4.15 Å, whereas the measured peak is found to be nearer 4.16 Å. This smaller peak is largely due to usual satellite transitions in the F-like ion stages. A portion of the emission around 4.17 Å arises from transitions in hollow atom configurations, as can be seen in the inset, where calculations without the hollow atom configurations are shown as the green dashed line. A strong hollow atom emission peak is observed around 4.173 Å, and several other smaller peaks due to hollow atom emission are found between 4.17 and 4.18 Å. We also see that theory predicts a smaller Kα peak at 4.19 Å compared with the measurement. It is possible that these relatively small disagreements may be due to our use of configuration-average kinetics, or neglect of high n-state configurations, which may lead to slight inaccuracies in the population distribution. However, overall the agreement between theory and experiment is quite satisfactory. It is also important to point out that it is necessary to include hot electrons in the theoretical model to produce the spectra arising from the hollow atom configurations at this bulk electron temperature. Also, the presence of the hollow atoms adds only around 2% to the line emission from the plasma, indicating that the relative emissivity from these excited configurations is still quite small. Finally, we note that the main aim of this study is to demonstrate that spectra arising from hollow atom configurations can be identified in theoretical kinetics modeling, which we have done so here. This conclusion is qualitatively backed up by the comparison with experimental measurements as presented in Figure 6.
4. CONCLUSIONS
A study has been made of the role of hollow atoms in the spectra arising from an Ar cluster exposed to an ultrashort-pulse-laser. The effects of hollow atoms on the observed emission spectra was found to be difficult to isolate, due to the close proximity of strong lines from transitions within the F- and O-like ion stages of Ar, as well as the nearby Kα lines. Detailed theoretical calculations made using the ATOMIC plasma kinetics code, which include configurations with two electrons excited from the K and L shells, have allowed exploration of these emission lines. The sensitivity of the emission spectra to the electron temperature, the atom number density, and the presence of hot electrons has been explored. It is found that the closest agreement with the experimental measurements come from a calculation where the electron temperature is 50 eV, with 3% of these electrons at 5 keV, and an atom density of 1022/cm3. The dominant features in the spectra still arise from transitions in the F- and O-like ions, but some spectra solely due to hollow atom transitions are also identified. From this experimental study and theoretical modeling of the measured X-ray spectra of Ar, we could see that the population of hollow atoms are increased in the case of laser interaction with dense cold targets, compared with the cases when the same laser interacts with less dense preplasma. Analogous behavior of hollow atom production was previously observed for fs laser interaction with solid matter (see for example, Gauthier et al., Reference Gauthier, Geindre, Audebert, Rousse, Dos Santos, Grillon, Antonetti and Mancini1995; Rosmej et al., Reference Rosmej, Funk, Geissel, Hoffmann, Tauschwitz, Faenov, Pikuz, Skobelev, Flora, Bollanti, Di Lazzaro, Letardi, Grilli, Palladino, Reale, Tomassetti, Scafati, Reale, Auguste, D'Oliveira, Hulin, Monot, Maksimchuk, Pikuz, Umstadter, Nantel, Bock, Dornik, Stetter, Stöwe, Yakushev, Kulisch and Shilkin2000, Faenov et al., Reference Faenov, Magunov Pikuz, Skobelev, Pikuz, Urnov, Abdallah, Clark, Cohen, Jonson, Kyrala, Wilke, Maksimchuk, Umstadter, Nantel, Doron, Behar, Mandelbaum, Schwob, Dubau, Rosmej and Osterheld1999). Further improvement of hollow atom generation by fs laser interaction with larger (around 1 μm) clusters could be reached by using recently developed (Lévy et al., Reference Lévy, Ceccotti, D'Oliveira, Réau, Perdrix, Quéré, Monot, Bougeard, Lagadec, Martin, Geindre and Audebert2007; Kiriyama et al., Reference Kiriyama, Mori, Nakai, Yamamoto, Tanoue, Akutsu, Shimomura, Kondo, Kanazawa, Daido, Kimura and Miyanaga2007) laser systems with a very high (up to 109) contrast. In such cases, the main laser pulse will interact with an initial (almost) solid cold part of the cluster, which should cause the hollow atom production to intensify.
It should be noted that the Ar plasma with Te = 50 eV, with an average ionization of 6, and and ion density Ni = 1022 cm−3 is weakly coupled. For these plasma parameters the electron-electron coupling factor Γee = 0.11 and the electron-ion coupling factor Γie = 0.37. Generally speaking, strongly-coupled plasmas can modify the probabilities for various collisional processes, for example, the three-body recombination rates. As has been shown by Biberman et al (Reference Biberman, Vorobev and Yakubov1987), for a strongly-coupled plasma, the three-body recombination rate can be decreased by a factor of Γie5/2 compared with the rate for an isolated atom. In our experiments Γie < 1 and this effect will not be large. So, our use of the isolated-atom approximation for the description of the collisional processes within the plasma is justified. However, the interaction of super contract femtosecond laser pulses with condensed media (see for example, Rosmej et al., Reference Rosmej, Faenov, Pikuz, Magunov, Skobelev, Auguste, D'Oliveira, Hulin, Monot, Andreev, Chegotov and Veisman1999; Faenov et al., Reference Faenov, Magunov Pikuz, Skobelev, Pikuz, Urnov, Abdallah, Clark, Cohen, Jonson, Kyrala, Wilke, Maksimchuk, Umstadter, Nantel, Doron, Behar, Mandelbaum, Schwob, Dubau, Rosmej and Osterheld1999; Riley et al., Reference Riley, Weaver, Mcsherry, Dunne, Neely, Notley and Nardi2002) may lead to the creation of an even more dense and, consequently, more strongly-coupled plasma. In these cases the influence of plasma effects on the elementary atomic processes should be taken into account.
ACKNOWLEDGMENTS
This work was performed under the auspices of the US Department of Energy through the Los Alamos National Laboratory. A portion of this work was performed with the support of the Russian Foundation for Basic Researches (Projects No. 06-02-16174 06-02-72005-MNTIA) and by the RAS Presidium Program of basic researches No. 9.