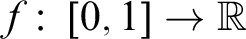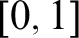1 Introduction
A main topic of reverse mathematics is to determine the axiomatic strength of theorems from classical analysis. For instance, the base system
$\mathsf {RCA}_{0}$
proves the intermediate value theorem. Over
$\mathsf {RCA}_{0}$
, the fact that every continuous real function on
$[0,1]$
is uniformly continuous is equivalent to the system
$\mathsf {WKL}_0$
, while the Bolzano–Weierstrass theorem (every bounded sequence of reals has a convergent subsequence) is equivalent to the stronger system
$\mathsf {ACA}_0$
(see [Reference Simpson11, Theorems II.6.6, IV.2.3, and III.3.2], respectively).
Our purpose is to determine the strength of two important, interrelated theorems from analysis. Interpreting these theorems over
$\mathsf {RCA}_{0}$
necessitates to develop some theory of representations of functions and of Martin–Löf randomness over this weak base system.
1.1 The axiomatic strength of Jordan’s decomposition theorem
Jordan’s theorem, dating from 1879, states that every function
$f \colon [0,1] \to \mathbb {R}$
of bounded variation can be written as
$g-h$
where g and h are nondecreasing functions (see e.g., [Reference Carothers2] for background on real analysis). One calls the pair
$g,h$
a Jordan decomposition of f. In the setting of real analysis, the proof that a Jordan decomposition exists is simple: let
$g(x)$
be the variation of f from
$0$
to x, and let
$h= g-f$
. However, even if f is computable in the usual sense of computable analysis, the function g is not necessarily computable: the variation of f, which equals
$g(1)$
, can be any non-negative left-c.e. real by Rettinger and Zheng [Reference Zheng and Rettinger16, Theorem 3.3.(ii)]. They also give in Theorem 5.3 an example of a computable function of bounded variation without any computable Jordan decomposition. Since the computable sets form a model of
$\mathsf {RCA}_{0}$
, it follows that Jordan’s theorem cannot be proved in
$\mathsf {RCA}_{0}$
.
Our first main topic is to determine the strength of Jordan’s theorem. It turns out that its strength depends on which functions we admit in a decomposition. The version where all functions involved are continuous is equivalent to
$\mathsf {ACA}_0$
. The version where the non-decreasing functions
$g,h$
in the decomposition can be discontinuous is equivalent to
$\mathsf {WKL}_{0}$
. For the second version, we need to develop a theory of representing such functions
$g, h$
in models of
$\mathsf {RCA}_{0}$
. In Definition 4.1 we introduce rational presentations of functions, which broadly speaking provide information about all possible inequalities
$g(p)< q$
and
$g(p)>q$
for rationals
$p,q$
, while leaving open equalities.
Greenberg et al. [Reference Greenberg, Miller and Nies5, Theorem 1.4 and Section 2.3], going back to unpublished work with Slaman, built a computable function of bounded variation such that any continuous Jordan decomposition computes the halting problem, and every Jordan decomposition allowing discontinuity computes a completion of Peano arithmetic. To prove some of our results above, we adapt their methods to the setting of reverse mathematics. This will require considerable additional effort.
1.2 The axiomatic strength of Lebesgue’s theorem on a.e. differentiability
Lebesgue [Reference Lebesgue7] proved that every nondecreasing function f is almost everywhere differentiable. By Jordan’s theorem, it follows that the same conclusion holds for functions of bounded variation. See e.g., [Reference Carothers2, Theorem 20.6 and Corollary 20.7].
Our second main topic is the strength of this theorem and of its corollary. We show that with reasonable interpretations of “almost everywhere” and “differentiable” that work over
$\mathsf {RCA}_{0}$
, both are equivalent to weak weak König’s Lemma
${\textsf {WWKL}}_{0}$
introduced by Simpson and Yu [Reference Yu and Simpson15], which roughly speaking states that every tree of positive measure has a path. Showing this requires recasting a fair amount of the methods of Brattka et al. [Reference Brattka, Miller and Nies1] over
$\mathsf {RCA}_{0}$
. In one important place they used
$\Sigma ^0_2$
-bounding (in the form of the infinitary pigeon hole principle), which is not allowed in
$\mathsf {RCA}_{0}$
. So we have to circumvent this. To get around the fact that a computable function of bounded variation may not have a computable Jordan decomposition, they use a set computing a completion of Peano arithmetic, and relativize randomness to it. Since such sets are unavailable within
$\mathsf {RCA}_{0}$
, in Lemma 6.5 we will instead recast this idea using an argument of Simpson and Yokoyama [Reference Simpson and Yokoyama12]. They extend a model of
${\textsf {WWKL}}_{0}$
to a model of
${\textsf {WKL}}_{0}$
in a restrictive way, in that for each of the new sets A, some set in the given model is random relative to A. This is one of the few examples from earlier years where methods stemming from the algorithmic theory of randomness have been reviewed with the mindset of reverse mathematics.
It is interesting that of our two topics, proving Jordan decomposability requires the stronger systems, even though differentiation appears to be a more complex operation than taking a Jordan decomposition. In fact when we say that f is differentiable at z we cannot assert that the limit of slopes around z exists in the model of
$\mathsf {RCA}_0$
, as this would be equivalent to
$\mathsf {ACA}_0$
when considering suitable functions. To get around this we work with the concept of pseudo-differentiability going back to Demuth [Reference Demuth3]: f is pseudo-differentiable at z if the slopes get closer and closer to each other as one zooms in on z (similar to the case of Cauchy sequences). If f is continuous at z and pseudo-differentiable at z, then f is differentiable at z (but the value of the derivative at z may still not exist in the model).
We mention that Shafer and the first author [Reference Nies and Shafer9] have recently looked at further connections between reverse mathematics and randomness. They consider randomness notions for infinite bit sequences. For instance, they study the reverse mathematical content of a well-known result: the characterization of two-randomness of a bit sequence Z via the plain Kolmogorov complexity of initial segments
$Z\upharpoonright n$
.
2 Preliminaries
2.1 Effectively uniformly continuous functions
We make the following definitions within
$\mathsf {RCA}_0$
, borrowing terminology from computable analysis. An effectively uniformly continuous function
$f:[0,1] \to \mathbb {R}$
is presented by a Cauchy name: a sequence
$(f_s)_{s \in \mathbb {N}}$
of rational polynomials (or, alternatively, polygonal functions with rational breakpoints) such that
$||f_s - f_r||_\infty \le 2^{-s}$
for all
$r> s$
. The sequence
$(f_s)_{s\in \mathbb {N}}$
is intended to describe
$f = \lim _{s \to \infty } f_s$
. Within
$\mathsf {RCA}_{0}$
this definition is equivalent to the definition of continuous functions with a modulus of uniform continuity given in [Reference Simpson11, Definition IV.2.1]. Note that a uniformly continuous function may not have a modulus of uniform continuity within
$\mathsf {RCA}_{0}$
. In contrast, within
$\mathsf {RCA}_{0}$
a continuous function with a Cauchy name always has a modulus of uniform continuity, and vice versa.
2.2 Functions of bounded variation
Suppose that
$\Pi = \{t_0, \dots , t_n\}$
is a partition of an interval
$[a,b]$
, i.e.,
$a=t_{0}<t_{1},\dots ,t_n=b$
(abbreviated by
$\Pi \lhd [a,b]$
). We let
$$ \begin{align*} V(f, \Pi) = \sum_{i=0}^{n-1} |f(t_{i+1}) - f(t_i)|. \end{align*} $$
We say that a continuous function
$f:[0,1]\to \mathbb {R}$
is of bounded variation if there is
$k \in \mathbb {N}$
such that
$V(f, \Pi ) \le k$
for every partition
$\Pi $
of
$[0,1]$
. We define bounded variation in this way in order to avoid declaring that the supremum exists. We write
$\mathbf {v}_{f}(t)=\sup _{\Pi \lhd [0,t]}V(f,\Pi )$
, and
$\mathbf {v}_{f}=\mathbf {v}_{f}(1)$
in case the sup exists. For a given rational number
$q\in \mathbb {Q}$
, we will use the assertion “
$\mathbf {v}_{f}(t)\le q$
” in the sense above. It can be expressed by a
$\Pi ^{0}_{1}$
formula independent of the sup exists.
3 Jordan decomposition for effectively uniformly continuous BV functions
Jordan’s theorem states that for every function f of bounded variation there is a pair of non-decreasing functions
$g,h$
, called a Jordan decomposition, such that
$f= g-h$
. For functions
$f, g : [0,1] \to \mathbb {R}$
, write
$$ \begin{align*} f \le_{\textsf{slope}} g \text{ iff } \forall x \forall y [x < y \to f(y) - f(x) \le g(y) - g(x)]; \end{align*} $$
i.e., the slopes of g are at least as big as the slopes of f. Finding a Jordan decomposition of f is equivalent to finding a non-decreasing function g such that
$f \le _{\textsf {slope}} g$
: If
$f= g-h$
for non-decreasing functions
$g,h$
, then
$f \le _{\textsf {slope}} g$
. Conversely, if
$f \le _{\textsf {slope}} g$
for a non-decreasing function g, then
$h= g-f$
is nondecreasing and
$f = g - h$
.
We consider a strong version of the Jordan decomposition theorem: the principle
$\textsf {Jordan}_{\mathtt {cont}}$
, which states that for every continuous function f of bounded variation, there exist non-decreasing effectively uniformly continuous functions
$g,h:[0,1] \to \mathbb {R}$
such that
$f=g-h$
. Equivalently, there is a non-decreasing effectively uniformly continuous function
$g:[0,1] \to \mathbb {R}$
such that
$f \le _{\textsf {slope}} g$
.
Theorem 3.1. The following are equivalent over
$\mathsf {RCA}_{0}$
.
-
1.
$\mathsf {ACA}_0$
. -
2.
$\textsf {Jordan}_{\mathtt {cont}}$
. -
3. For every effectively uniformly continuous function f of bounded variation, there exist non-decreasing continuous functions
$g,h:[0,1] \to \mathbb {R}$
such that
$f=g-h$
.
Proof To show 1
$\Rightarrow $
2, given a continuous function f of bounded variation, we construct a code for a continuous function
$\mathbf {v}_f$
. Note that within
$\mathsf {ACA}_0$
,
$\mathbf {v}_{f}(t)$
always exists, and one can describe the function
$t\mapsto \mathbf {v}_{f}(t)$
by an arithmetical formula. Thus, one can easily construct a code for
$\mathbf {v}_{f}$
by arithmetical comprehension. Then
$g=\mathbf {v}_{f}$
is the desired function.
2
$\Rightarrow $
3 is trivial. To show 3
$\Rightarrow $
1, let
$$ \begin{align*} q_n = 1 - 2^{-n - 1} \text{, and } q_{n,s} = q_n - 2^{-n - s - 1}. \end{align*} $$
$\mathsf {ACA}_0$
is equivalent to the following: if
$h : \mathbb {N} \to \mathbb {N}$
is an injective function, then the range of h exists [Reference Simpson11, Lemma III.1.3]. The plan is to encode the range of h into the variation of an effectively uniformly continuous function f.
For
$v \in \mathbb R^+$
and
$r \in \mathbb N$
, we let
$\textrm {M}_A(v, r)$
denote a “sawtooth” function on the interval A with r many teeth of height v. Given an injective function h, for each
$s \in \mathbb {N}$
, define a continuous function
$f_s$
as follows. On each interval of the form
$I_k = [q_{h(k), k}, q_{h(k), k+1}]$
put
$$ \begin{align*} f_s = \begin{cases} \textrm{M}_{I_k}(2^{-k}, 2^{k - h(k)}) & \text{if } s\ge k> h(k), \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
Let
$f_s = 0$
elsewhere. Note that on
$I_{k}$
,
$f_{s}=f_{t}$
if
$t>s\ge k$
or
$k>t>s$
, and
$\|f_{s}-f_{t}\|_{\infty }\le 2^{-s}$
if
$t\ge k>s$
. Thus, the sequence
$(f_s)_{s \in \mathbb {N}}$
defines an effectively uniformly continuous function
$f = \lim _{s \to \infty }f_s$
. We show that f is of bounded variation with bound
$1$
. Note that we only need to examine the variation of f on the disjoint intervals
$[q_{h(k),k}, q_{h(k),k+1}]$
since
$f= 0$
elsewhere.
Let
$m \in \mathbb {N}$
. For
$k \in \{0, \dots , m\}$
, let
$\Pi _k$
partition
$I_k$
. We estimate the variation of f on the interval
$\bigcup _{k \le m} I_k$
. Without loss of generality we may assume that each partition contains the midpoints and endpoints of the sawteeth defined on
$I_k$
.Footnote
1
This allows us to easily compute the variation of f as the piece-wise combination of non-decreasing functions. For all
$s \ge m$
one has
$$ \begin{align*} \sum \limits_{k = 0}^m V(f, \Pi_k) = \sum \limits_{k = 0}^m V(f_s, \Pi_k) \le \sum \limits_{k = 0}^m 2^{-h(k) + 1} < 1, \end{align*} $$
which establishes the desired bound.
By
$\textsf {Jordan}_{\mathtt {cont}}$
, take
$g:[0,1] \to \mathbb {R}$
non-decreasing and continuous such that
$f \le _{\textsf {slope}} g$
. Given that the range of h is encoded in the variation of f, we will use the (easily computable) variation of g on the interval
$[q_{n, k}, q_{n, k+1}]$
to bound to possible pre-images of n under h.
Define a
$\Delta ^{0}_{1}$
definable function
$\gamma :\mathbb {N} \to \mathbb {N}$
such that
$g(q_n) - g(q_{n, \gamma (n)}) < 2^{-n}$
as follows. There is a
$\Sigma ^0_0$
formula
$\theta (n, m, k)$
such that
$$ \begin{align*} \exists m \, \theta(n, m, k) \leftrightarrow g(q_n) - g(q_{n,k}) < 2^{-n}. \end{align*} $$
Since g is continuous and
$\lim _{s \to \infty } q_{n,s} = q_n$
one has
$\forall n \exists k \exists m \, \theta (n, m, k).$
As this sentence is
$\Pi ^0_2$
, given any instance of the variable n one can effectively obtain a witness
$\langle m, k \rangle $
for the
$\Sigma ^0_1$
formula
$\exists k \exists m \theta (n, m, k)$
(see, e.g., [Reference Simpson11, Theorem II.3.5]). Thus we may put
$\gamma (n) = k$
, where
$\langle m, k \rangle $
is least such that
$\theta (n,m,k)$
holds.
Now if
$h(k) = n<k$
then by the monotonicity of g,
$$ \begin{align*} g(q_n) - g(q_{n,k}) \ge g(q_{n,k+1}) - g(q_{n, k}). \end{align*} $$
Let
$\Pi $
be a partition of
$[q_{n,k}, q_{n,k+1}]$
containing the endpoints and midpoints of each sawtooth defined on that interval. Then since
$g - f \le g$
and the variation of an increasing function is the difference of its values at its endpoints one has
$$ \begin{align*} 2^{-n + 1} = V(f, \Pi) & = V(g - (g - f), \Pi) \le V(g, \Pi) + V(g - f, \Pi) \le 2(g(q_{n,k+1}) - g(q_{n,k})). \end{align*} $$
Thus
$g(q_n) - g(q_{n,k}) \ge 2^{-n}$
, and then
$k < \gamma (n)$
. Hence
$$ \begin{align*} n \in \text{rng}(h) \leftrightarrow \exists k < \max\{\gamma(n),n+1\} [h(k) = n], \end{align*} $$
so the range of h exists by
$\Delta ^0_1$
comprehension. ⊣
4 Jordan decomposition for BV functions of rational domain
In the foregoing section, we required that a Jordan decomposition consist of effectively uniformly continuous functions. Then the Jordan decomposition theorem has the same axiomatic strength as
$\mathsf {ACA}_0$
. To see this, we encoded the range of an injective function h into the variation of a function f of bounded variation. A Jordan decomposition of f into uniformly continuous functions allowed us to recover enough information to decide whether some number was the image of another under the injective function h.
We now relax the requirement on the Jordan decomposition by only stipulating that the decomposition is given by functions which are defined on the rationals. Such functions can be represented by finite strings that cumulatively describe the behaviour of the function at each rational. We will see that such simple objects do not allow the encoding of sets of high complexity.
Greenberg et al. [Reference Greenberg, Miller and Nies5] proved that there is a computable function f on
$[0,1]$
of bounded variation such that every Jordan decomposition of f in this weak sense is PA-complete. One direction of our argument, 4
$\Rightarrow $
1 of Theorem 4.10, is based on their proof; extra effort is required to make it work over
$\mathsf {RCA}_0$
as a base theory.
4.1 Rational presentations of functions
Let
$[0,1]_{\mathbb {Q}} := [0,1]\cap \mathbb {Q}$
. We present a function
$g : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
by a set
$Z\subseteq [0,1]_{\mathbb {Q}}\times \mathbb {Q}$
in the following way. We require that
$(p,q)\in Z$
if
$g(p) < q$
, and
$(p,q)\notin Z$
if
$g(p)> q$
. We leave open whether
$(p,q)\in Z$
in case that
$g(p)=q$
. The formal definition follows.
Definition 4.1. A set
$Z\subseteq [0,1]_{\mathbb {Q}}\times \mathbb {Q}$
is called a rational presentation if
-
(i) for any
$p\in [0,1]_{\mathbb {Q}}$
, there exist
$q,q'\in \mathbb {Q}$
such that
$(p,q)\in Z$
and
$(p,q')\notin Z$
and -
(ii) for any
$p\in [0,1]_{\mathbb {Q}}$
and for any
$q,q'\in \mathbb {Q}$
with
$q < q'$
,
$(p,q)\in Z$
implies
$(p,q')\in Z$
.
A rational presentation Z determines a function
$g_{Z}: [0,1]_{\mathbb {Q}} \to \mathbb {R}$
via
$$ \begin{align*} g_{Z}(p) = \inf \{q \in \mathbb{Q} : (p,q)\in Z\}. \end{align*} $$
We say that Z is a rational presentation of
$g_Z$
(and also of any function on
$[0,1]$
extending
$g_Z$
).
One can determine
$g_{Z}(p)$
within
$\mathsf {RCA}_{0}$
since for any
$n\in \mathbb {N}$
, one can effectively find
$q,q'\in \mathbb {Q}$
such that
$(p,q)\in Z$
,
$(p,q')\notin Z$
, and
$|q-q'|\le 2^{-n}$
. Even though a rational presentation of a function is not unique if the function has some rational value, we sometimes identify Z with
$g_{Z}$
.
For given
$x,y,z\in \mathbb {Q}$
and a rationally presented function
$g_{Z}:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
, the assertion “
$g_{Z}(x)-g_{Z}(y)\le b$
” is expressed by a
$\Pi ^{0}_{1}$
formula with free variables
$Z, x,y,b$
:
$$ \begin{align*} \forall p_{0},p_{1},q_{0},q_{1}\in\mathbb{Q} \, [p_{0}=x \wedge p_{1}=y \wedge (p_{0},q_{0})\notin Z\wedge (p_{1},q_{1})\in Z\ \to \ q_{0}-q_{1}\le b]. \end{align*} $$
Similarly, “
$g_{Z}(x)-g_{Z}(y)\ge b$
” can be expressed by a
$\Pi ^{0}_{1}$
formula, and “
$g_{Z}(x)-g_{Z}(y)< z$
” and “
$g_{Z}(x)-g_{Z}(y)> z$
” by
$\Sigma ^{0}_{1}$
formulas. Thus, the assertion “
$\mathbf {v}_{g_{Z}}(x)\le z$
” is also expressed by a
$\Pi ^{0}_{1}$
formula. (Here, we only consider partitions with rational end points.) We say that
$g_{Z}$
is of bounded variation if
$\mathbf {v}_{g_{Z}}(1)\le k$
for some
$k\in \mathbb {N}$
.
A function
$f:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
can be canonically encoded by a function
$f:[0,1]_{\mathbb {Q}}\times \mathbb {N}\to \mathbb {Q}$
such that
$|f(p,n)-f(p,n+k)|\le 2^{-n}$
for each
$p\in [0,1]_{\mathbb {Q}}$
and
$n,k\in \mathbb {N}$
. Rational presentations are essentially sufficient for presenting all real-valued functions on
$[0,1]_{\mathbb {Q}}$
: as we show next, within
$\mathsf {RCA}_{0}$
any function
$f:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
has a rational presentation up to a vertical shift.
Lemma 4.2 (
$\mathsf {RCA}_{0}$
)
For every function
$f:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
, there exists a real
$a\in \mathbb {R}$
such that
$f(p)+a \not \in \mathbb {Q}$
for any
$p\in [0,1]_{\mathbb {Q}}$
.
Proof Let
$\{p_{i}\}_{i\in \mathbb {N}}$
be an enumeration of
$[0,1]_{\mathbb {Q}}$
. We recursively define a sequence of rationals
$\{a_{i}\}_{i\in \mathbb {N}}$
as follows. Let
$a_{0}=0$
.
For given
$a_{i}\in \mathbb {Q}$
we let
$a_{i+1}\in \mathbb {Q}$
such that
$|a_{i}-a_{i+1}|<4^{-i}$
and
$|f(p_{i})-a_{i+1}|>4^{-i}/2 $
. One can always pick such
$a_{i+1}$
effectively since the required condition on
$a_{i+1}$
given
$a_i$
is
$\Sigma ^{0}_{1}$
. (Here we use the well-known fact that a dependent choice function for a
$\Sigma ^{0}_{1}$
binary predicate of numbers is available within
$\mathsf {RCA}_{0}$
. See, e.g., the argument in the proof of [Reference Simpson11, Theorem II.5.8], or [Reference Yokoyama14, Theorem 2.1].) Put
$a=\lim _{n\to \infty }a_{i}$
and note that
$|a - a_{i+1}| \le 4^{-i}/3$
. Therefore
$|f(p_{i})-a|> 4^{-i}/2 - 4^{-i}/3>0$
. ⊣
Proposition 4.3.
-
(i)
$\mathsf {WKL}_0$
proves that every function
$f:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
has a rational presentation. -
(ii)
$\mathsf {RCA}_{0}$
proves that every function
$f:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
has a rational presentation up to a vertical shift. That is, there exists a rational presentation Z and a real
$r\in \mathbb {R}$
such that
$f+r=g_{Z}$
.
Proof (i) Consider the
$\Sigma ^{0}_{1}$
-definable sets
$\mathcal {A}=\{(p,q)\in [0,1]_{\mathbb {Q}}\times \mathbb {Q}: f(p)< q\}$
and
$\mathcal {B}=\{(p,q)\in [0,1]_{\mathbb {Q}}\times \mathbb {Q}: f(p)> q\}$
. To obtain a rational presentation for f, it suffices to find a set
$Z\subseteq [0,1]_{\mathbb {Q}}\times \mathbb {Q}$
such that
$\mathcal {A}\subseteq Z\subseteq [0,1]_{\mathbb {Q}}\times \mathbb {Q}\setminus \mathcal {B}$
. Such a set Z is obtained by an instance of
$\Sigma ^{0}_{1}$
-separation, an axiom scheme which follows from
$\mathsf {WKL}_0$
over
$\mathsf {RCA}_{0}$
[Reference Simpson11, Lemma IV.4.4].
(ii) We may assume that f avoids rational numbers after passing to a vertical shift of f via Lemma 4.2. Then both
$\mathcal {A}$
and
$\mathcal {B}$
are
$\Delta ^{0}_{1}$
. ⊣
Corollary 4.4.
-
(i)
$\mathsf {WKL}_0$
proves that the restriction to
$[0,1]_{\mathbb {Q}}$
of any continuous function
$f:[0,1]\to \mathbb {R}$
has a rational presentation. -
(ii)
$\mathsf {RCA}_{0}$
proves that the restriction to
$[0,1]_{\mathbb {Q}}$
of any continuous function
$f:[0,1]\to \mathbb {R}$
has a rational presentation on
$[0,1]_{\mathbb {Q}}$
up to a vertical shift.
Proof Within
$\mathsf {RCA}_{0}$
, one can effectively find the value of a continuous function. Thus, the restriction to
$[0,1]_{\mathbb {Q}}$
of a continuous function
$f:[0,1]\to \mathbb {R}$
has a canonical encoding. ⊣
Taking a vertical shift is essential in the above discussion: an effectively uniformly continuous function itself might not have a rational presentation within
$\mathsf {RCA}_{0}$
. To see this apply the next fact to a recursively inseparable pair.
Proposition 4.5. Given a disjoint pair
$A,B$
of c.e. sets, there is a computable non-decreasing function
$f \colon [0,1] \to \mathbb {R}$
such that every rational presentation computes a set X such that
$A \subseteq X \subseteq \mathbb {N} \setminus B$
.
Sketch of proof
We define a uniformly computable sequence of reals
$(r_e) $
such that
$r_e$
is very close to
$2^{-e}$
; say
$|r_e - 2^{-e}| \le 2^{-2e}$
. The function f is then obtained by linear interpolation between the values
$f(2^{-e})= r_e$
; in particular
$f(0)=0$
and f is computable in the usual sense of computable analysis.
We define
$r_e$
using a Cauchy name, as follows. Initially we let
$r_e = 2^{-e}$
. If stage s is least such that
$s\ge 2e$
and
$e \in A_s$
we subtract
$2^{-s}$
to
$r_e$
and leave
$r_e$
at this value. If stage s is least such that
$s\ge 2e$
and
$e \in B_s$
we add
$2^{-s}$
from
$r_e$
and leave
$r_e$
at this value.
If Z is a rational presentation of f, let
$X = \{e \colon \, (2^{-e},2^{-e}) \in Z\}$
. If
$e \in A$
then
$f(2^{-e})< 2^{-e}$
and hence
$e \in X$
. If
$e \in B$
then
$f(2^{-e})> 2^{-e}$
and hence
$e \not \in X$
. ⊣
Proposition 4.6. The assertion “every effectively uniformly continuous function
$f:[0,1]\to \mathbb {R}$
has a rational presentation” implies
$\mathsf {WKL}_0$
over
$\mathsf {RCA}_{0}$
.
Proof It is routine to transfer the computability theoretic proof above into an argument that the given assertion implies
$\Sigma ^0_1$
separation over
$\mathsf {RCA}_{0}$
. By [Reference Simpson11, Lemma IV.4.4] the scheme of
$\Sigma ^0_1$
separation is equivalent to
${\textsf {WKL}}_{0}$
over
$\mathsf {RCA}_{0}$
. ⊣
The above discussions recast the problem of converting Cauchy representations and Dedekind cuts for reals studied by Hirst [Reference Hirst6]. Proposition 4.6 can be viewed as a strengthening of [Reference Hirst6, Theorem 7].
4.2 Jordan decomposition by rationally presented functions
We modify the
$\le _{\textsf {slope}}$
notation for functions of rational domain. For
$f, g : \subseteq [0,1] \to \mathbb {R}$
we let
$$ \begin{align*} f \le^*_{\textsf{slope}} g \text{ iff } \forall x, y \in [0,1]_{\mathbb{Q}} [x < y \to (f(y) - f(x) \le g(y) - g(x))]. \end{align*} $$
We will use the following “folklore” fact for the next theorem.
Lemma 4.7 (
$\mathsf {WKL}_0$
)
Every
$\Pi ^{0}_{1}$
definable infinite tree
$T\subseteq 2^{<\mathbb {N}}$
has a path.
Proof Suppose that
$\tau \in T\leftrightarrow \forall n \, \theta (n,\tau )$
. By
$\Delta ^{0}_{1}$
comprehension, there exists a tree
$$ \begin{align*} \bar{T}=\{\tau: \forall n\le |\tau|\forall \sigma\preceq\tau \, \theta(n,\sigma)\}. \end{align*} $$
Then,
$T\subseteq \bar {T}$
, and any path of
$\bar {T}$
is a path of T by the definition of T. By
$\mathsf {WKL}_0$
,
$\bar {T}$
has a path, thus T has a path. ⊣
Theorem 4.8 (
$\mathsf {WKL}_0$
)
For every rationally presented function
$f : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
of bounded variation, there is a rationally presented non-decreasing function
$g : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
such that
$f \le ^*_{\textsf {slope}} g$
.
Proof Let
$M\in \mathbb {N}$
such that
$\mathbf {v}_{f}\le M$
. We fix an effective listing
$( p_n, q_n )_{n \in \mathbb {N}}$
of all elements of
$[0,1]_{\mathbb {Q}}\times \mathbb {Q}$
, and identify
$Z:\mathbb {N}\to \{0,1\}$
as
$\{(p_{n},q_{n}):Z(n)=1\}\subseteq [0,1]_{\mathbb {Q}}\times \mathbb {Q}$
. We construct a binary tree T such that any path Z through T encodes a non-decreasing function
$g :[0,1]_{\mathbb {Q}} \to \mathbb {R}$
with
$f \le ^*_{\textsf {slope}} g$
. To do so, we ensure that the following conditions hold:
$\mathcal {R}_0:$
for any
$r\in \mathbb {N}$
,
$0\le g(p_r) \le M$
;
$\mathcal {R}_1:$
for any
$r,s\in \mathbb {N}$
, if
$p_s \le p_r$
,
$q_s \ge q_r$
, and
$g(p_s)> q_s$
then
$g(p_r)> q_r$
; and
$\mathcal {R}_2:$
for any
$r,s\in \mathbb {N}$
, if
$p_s \le p_r$
then
$f(p_r) - f(p_s) \le g(p_r) - g(p_s)$
.
Here,
$\mathcal {R}_1$
guarantees that any g encoded by a path
$Z_g$
through T is non-decreasing, and
$\mathcal {R}_2$
guarantees the slope condition. Formally, we will consider a
$\Pi ^{0}_{1}$
definable tree T to be the set of all
$\tau \in 2^{<\mathbb {N}}$
such that
$$ \begin{align*} \text{(r0)}& \ \forall r < |\tau| \Big[(q_{r}\le 0\to \tau(r) = 0) \wedge (q_{r}\ge M\to \tau(r) = 1)\Big], \\ \text{(r1)}& \ \forall r, s < |\tau| \Big[(p_r \le p_s \land q_r \ge q_s \land \tau(r) = 0) \to \tau(s) = 0\Big], \\ \text{(r2)}& \ \forall r, s < |\tau| \Big[ (p_r \le p_s \land \tau(r) = 0 \land \tau (s) = 1) \to | f(p_s) - f(p_r) | \le q_{s}-q_{r}\Big]. \end{align*} $$
To see that T is infinite, notice that since f is of bounded variation, the string
$Z_{v_{f}}|_k$
defined as
$s\in Z_{v_{f}}|_k$
iff
$\mathbf {v}_{f}(p_{s})<q_{s}$
and
$s<k$
, which is available from bounded
$\Sigma ^{0}_{1}$
comprehension (see [Reference Simpson11, Theorem II.3.10]), is an element of T for every
$k \in \mathbb {N}$
. Thus by Lemma 4.7, T has a path Z. By (r0) and (r1) (for the case
$p_{r}=p_{s}$
), Z encodes a rational presentation. Let g be the unique function
$ [0,1]_{\mathbb {Q}} \to \mathbb {R}$
defined as
$g=g_{Z}$
.
Claim 4.8.1. The function g is non-decreasing.
Proof Take
$x, y \in [0,1]_{\mathbb {Q}}$
with
$x < y$
. Let
$q \in \mathbb {Q}$
. It suffices to show that if
$g(x)> q$
then
$g(y)> q$
. There are
$r, s \in \mathbb {N}$
such that
$p_s = y$
,
$q_s = q$
,
$p_r = x$
, and
$q_r = q$
. If
$g(p_r)> q_r$
then
$Z(r)=0$
, and then by clause (r1),
$Z(s)=0$
, which means
$g(p_s)> q_s$
.
$\diamondsuit $
Claim 4.8.2.
$f \le ^*_{\textsf {slope}} g$
.
Proof Let
$x, y \in [0,1]_{\mathbb {Q}}$
such that
$x < y$
. It is enough to show that for any
$q\in \mathbb {Q}$
such that
$g(y)-g(x)<q$
,
$|f(y)-f(x)|<q$
. By the definition of g, one can find
$r,s\in \mathbb {N}$
such that
$x=p_{r}$
,
$y=p_{s}$
,
$g(p_{r})>q_{r}$
,
$g(p_{s})<q_{s}$
and
$q_{s}-q_{r}<q$
. Then, by (r2) we have
$|f(y)-f(x)|=|f(p_{s})-f(p_{r})|\le q_{s}-q_{r}<q$
.
$\diamondsuit $
Thus, this
$g=g_{Z}$
is the desired function.⊣
It is a well-known fact that every
$\Pi ^{0}_{1}$
-class with only finitely many members has a computable member. Greenberg et al. used this fact to build a computable function f on
$[0,1]$
of bounded variation such that any Jordan decomposition of f is PA-complete; see [Reference Greenberg, Miller and Nies5, Section 2.3 and in particular Proposition 2.9]. A natural formalization within
$\mathsf {RCA}_{0}$
of this fact is as follows: if an infinite tree T has only boundedly many incomparable nodes that are extendible, then T has a path that is computable relative to T. Simpson and Yokoyama [Reference Simpson and Yokoyama13] showed that this formalization already requires
$\Sigma ^{0}_{2}$
-induction. Instead, we will use the following lemma.
Lemma 4.9 (
$\mathsf {RCA}_{0}$
)
Let
$T\subseteq 2^{<\mathbb {N}}$
be an infinite tree. If there is a bound on the cardinality of an arbitrary prefix-free subset of T, then T has a path.
Proof Take
$K\in \mathbb {N}$
so that
$|P|<K$
for any prefix-free set
$P\subseteq T$
. By
$\Sigma ^0_1$
induction, take
$$ \begin{align} k = \max\{i\le K : \text{there is a prefix-free set } P \subseteq T \text{ with } |P| = i\}. \end{align} $$
Let
$P_k \subseteq T$
witness (1). Let
$\sigma = \max P_k$
, where the max is taken with respect to the usual integer encoding of binary strings. Let
$\ell = \max \{|\tau | : \tau \in P_k\}$
. Any
$\tau \in T$
with
$|\tau |> \ell $
must extend an element of
$P_k$
, and can have at most one successor. By the pigeonhole principle (which is available from
$\Sigma ^{0}_{1}$
induction), there exists
$\tau \in P_{k}$
with infinitely many extensions in T. Since each extension of
$\tau $
of length exceeding
$\ell $
has exactly one successor, we can effectively find a path through
$ T$
extending
$\tau $
.⊣
We now establish the main theorem of this section.
Theorem 4.10. The following are equivalent over
$\mathsf {RCA}_{0}$
.
-
1.
$\mathsf {WKL}_0$
. -
2.
$\textsf {Jordan}_{\mathbb {Q}}$
: for every rationally presented function f of bounded variation, there is a rationally presented non-decreasing function
$g : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
such that
${f \le ^*_{\textsf {slope}} g}$
. -
3. For every continuous function f of bounded variation, there is a rationally presented non-decreasing function
$g : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
such that
$f \le ^*_{\textsf {slope}} g$
. -
4. For every effectively uniformly continuous function f of bounded variation which has a rational presentation, there is a rationally presented non-decreasing function
$g : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
such that
$f \le ^*_{\textsf {slope}} g$
.
Proof 1
$\Rightarrow $
2 is Theorem 4.8, 2
$\Rightarrow $
3 is a direct consequence of Corollary 4.4(ii), and 3
$\Rightarrow $
4 is trivial. We show 4
$\Rightarrow $
1. We reason within
$\mathsf {RCA}_0$
. Let
$T \subseteq 2^{<\mathbb {N}}$
be an infinite binary tree. Assume for a contradiction that T has no path. Let
$\widetilde {T} = \{\tau \in 2^{<\mathbb {N}} : \tau \not \in T \land \tau |_{(|\tau | - 1)} \in T\}$
. Without loss of generality we may assume that
$\widetilde {T}$
is infinite. Consider the
$\Sigma ^{0}_{1}$
definable set
$$ \begin{align*} \textrm{Nonext}(T):=\{\tau \in T : \tau \text{ has only finitely many extensions in } T\}. \end{align*} $$
Then, by [Reference Simpson11, Lemma II.3.7], there exists a one-to-one function
$h:\mathbb {N}\to \mathbb {N}$
such that
$\text {rng}(h)=\textrm{Nonext}(T)$
. (Here, we identify a binary string with its usual integer encoding.)
Let
$(\widetilde {\sigma }_k)_{k\in \mathbb {N}}$
be an enumeration of
$\widetilde {T}$
such that
$|\widetilde {\sigma }_i| \le |\widetilde {\sigma }_{i+1}|$
. Note that for any
$k, \ell \in \mathbb {N}$
,
$$ \begin{align} |\widetilde \sigma_k | \le \ell \rightarrow k \le 2^\ell. \end{align} $$
For all
$\sigma \in 2^{<\mathbb {N}}$
put
$I_\sigma = [0.\sigma , 0.\sigma + 2^{-|\sigma |}]$
. For each
$s \in \mathbb {N}$
define a polygonal function
$f_s :[0,1] \to \mathbb {R}$
as follows. On the interval
$I_{\widetilde {\sigma }_k}$
set
$$ \begin{align} f_s = \begin{cases} \textrm{M}_{I_{\widetilde{\sigma}_k}}(2^{-k}, 2^{k - h(k)}) & \text{if } s\ge k> h(k), \\ 0 & \text{otherwise.} \end{cases} \end{align} $$
Let
$f_s = 0$
elsewhere. Then
$(f_s)_{s\in \mathbb {N}}$
defines an effectively uniformly continuous function
$f = \lim _{s}f_s$
. By Corollary 4.4(ii), one may replace f with a vertical shift and then assume that f has a rational presentation.
We show that f is of bounded variation. As in the proof of Theorem 3.1, we only need to consider the variation of f on the disjoint intervals
$I_{\widetilde {\sigma }_k}$
. Let
$m \in \mathbb {N}$
, and for each
$k \le m$
let
$\Pi _k$
be a partition of
$I_{\widetilde {\sigma }_k}$
containing the midpoints and endpoints of each sawtooth defined on that interval. For all
$s \ge m$
one has
$$ \begin{align*} \sum \limits_{k = 0}^m V(f, \Pi_k) = \sum \limits_{k = 0}^m V(f_s, \Pi_k) \le \sum \limits_{k = 0}^m 2^{-h(k) + 1} < 1, \end{align*} $$
as required.
By our hypothesis in (5), there exists a rationally presented non-decreasing function
$g :[0,1]_{\mathbb {Q}} \to \mathbb {R}$
such that
$f \le ^*_{\textsf {slope}} g$
. Let
$\Delta : \mathbb {N} \to \mathbb {R}$
be the function given by
$\Delta (k) = \max \{g(0.\sigma + 2^{-|\sigma |}) - g(0.\sigma ) : \sigma \in T \land |\sigma | = k\}.$
Note that
$\Delta $
is non-increasing.
There are two cases to consider. If
$\lim _{n \to \infty } \Delta (n) = 0$
, then g behaves like a continuous function. This provides a decomposition of f that allows us to use an argument similar to the one in Theorem 3.1 to prove the existence of
$\text {rng}(h)$
. One can then find a path through T by avoiding this set.
Otherwise, there is a jump-type discontinuity of g. The intervals around this point correspond to strings which form an infinite subtree
$\widehat T$
of T. One can bound the size of any prefix-free subset of
$\widehat T$
using the size of this jump, and thus effectively find a path through
$\widehat T$
.
We now analyse the two cases in detail.
Case 1.
$\lim _{n\to \infty }\Delta (n) = 0$
. Take
$\gamma : \mathbb {N} \to \mathbb {N}$
such that
$\Delta (\gamma (n)) < 2^{-n}$
. Such
$\gamma $
exists by
$\Delta ^{0}_{1}$
comprehension since “
$\Delta (k)<2^{-n}$
” can be described by a
$\Sigma ^{0}_{1}$
formula. If
$h(k) = n<k$
then by (3),
$$ \begin{align*} g(0.\widetilde{\sigma}_k + 2^{-|\widetilde{\sigma}_k|}) - g(0.\widetilde{\sigma}_k) \ge V(\textrm{M}_{I_{\widetilde{\sigma}_k}}(2^{-k}, 2^{k - h(k)}), \Pi_k)= 2^{-h(k)+1}\ge 2^{-n}. \end{align*} $$
Hence
$|\widetilde {\sigma }_k| \le \gamma (n)$
, and then by (2)
$k \le 2^{\gamma (n)}$
. This gives
$$ \begin{align*} n \in \text{rng}(h) \leftrightarrow \exists k \le \max\{2^{\gamma(n)},n\}[h(k) = n], \end{align*} $$
so
$\text {rng}(h)=\textrm{Nonext}(T)$
exists by
$\Delta ^0_1$
comprehension. Thus
$\textrm{Ext}(T)=T \setminus \textrm{Nonext}(T)$
exists. Now, one can construct a path of T by an easy primitive recursion: starting from the empty string, one can choose the left most immediate extension of a given string in
$\textrm{Ext}(T)$
.
Case 2. There exists
$M \in \mathbb {N}$
such that
$\forall m \exists n [n> m \land \Delta (n) > 2^{-M}]$
Then there are infinitely many strings
$\sigma \in T$
such that
$$ \begin{align*} g(0.\sigma + 2^{-|\sigma|}) - g(0.\sigma)>2^{-M}. \end{align*} $$
Without loss of generality, we may take
$K\in \mathbb {N}$
such that
$0\le g(0)<g(1)\le K$
. Let
$L=\{i/2^{M+2}: 0\le i\le K2^{M+2}\}$
. Given a rational presentation Z of g, for
$x,y,z\in \mathbb {Q}$
, we write
$g(y)-g(x)\ge _{L}z$
if there exist
$r,s\in \mathbb {N}$
such that
$x=p_{r}$
,
$y=p_{s}$
,
$q_{r},q_{s}\in L$
,
$Z(r)= {1}$
(which implies that
$g(p_{r})<q_{r}$
),
$Z(s)={0}$
(which implies that
$g(p_{s})>q_{s}$
) and
$q_{s}-q_{r}\ge z$
. Since L is finite,
$g(y)-g(x)\ge _{L}z$
is actually
$\Delta ^{0}_{1}$
statement as we only need to check finitely many r and s. Note that if
$g(y)-g(x)>2^{-M}$
, then
$g(y)-g(x)\ge _{L}2^{-M-2}$
since there are at least two points in
$L\cap (g(x),g(y))$
.
The tree
$\widehat T\subseteq T$
defined by
$\widehat T=\{\sigma \in T: g(0.\sigma + 2^{-|\sigma |}) - g(0.\sigma ) \ge _{L}2^{-M-2}\}$
. is an infinite subtree of T. (The case assumption guarantees that
$\widehat T$
is infinite, and
$\widehat T$
is closed under prefixes because g is non-decreasing.) We verify the cardinality of any prefix-free subset of
$\widehat T$
is bounded. For any prefix-free
$P \subseteq \widehat T$
, we have
$$ \begin{align*} |P|2^{-M-2} \le \sum \limits_{\sigma \in P} g(0.\sigma + 2^{-|\sigma|}) - g(0.\sigma) \le g(1) - g(0) \le K. \end{align*} $$
Thus,
$|P|\le K2^{M+2}$
. Hence by Lemma 4.9,
$\widehat T$
has a path, and thus T has a path. ⊣
We thank Paul Shafer for providing helpful comments on a previous version of this proof.
5 Martin–Löf randomness within
$\mathsf {RCA}_{0}$
To study Martin–Löf random reals within
$\mathsf {RCA}_{0}$
, we need to define a notion of uniform measure for open sets. A set of binary strings
$S\subseteq 2^{<\mathbb {N}}$
is a code of an open set
$U\subseteq 2^{\mathbb {N}}$
if
$Z\in U\leftrightarrow \exists \sigma \in S \, [Z\succ \sigma ]$
. We write
$[[S]]$
for the open set coded by S. (Note that a
$\Sigma ^{0}_{1}$
-definable set may be used to code an open set, but one can easily find an (existing) set which codes the same open set by
$\Delta ^{0}_{1}$
-comprehension.) Given such a code
$S\subseteq 2^{<\mathbb {N}}$
, let
$T_{S}:=\{\sigma \in 2^{<\mathbb {N}}: \forall n<|\sigma |(\sigma {\upharpoonright } n\notin S)\}$
. Note that
$T_{S}$
forms a tree, which we view as a code of the complement of U. We first define the measure for a code S of an open set, and also of its complementary code
$T=T_{S}$
:
$$ \begin{align*} \mu(S):=1-\mu(T)=1-\lim_{n\to\infty}\frac{|\{\sigma\in T: |\sigma=n\}|}{2^{n}}. \end{align*} $$
Note that if S is prefix free, then
$\mu (S)=\sum _{\sigma \in S}2^{-|\sigma |}$
. The existence of the limit is not guaranteed within
$\mathsf {RCA}_{0}$
, but one can still make assertions such as
$\mu (S)\le a$
or
$\mu (T_{S})\ge a$
, which can be expressed by
$\Pi ^{0}_{1}$
-formulas.
$Z\in 2^{\mathbb {N}}$
is said to be Martin–Löf random relative to X if for any X-computable sequence of codes for open sets
$\langle S_{n}: n\in \mathbb {N} \rangle $
such that
$\mu (S_{n})\le 2^{-n}$
, there exists
$n\in \mathbb {N}$
such that
$Z\notin [[S_{n}]]$
. The assertion “for any X there exists a Martin–Löf random real relative to X” is equivalent to
$\textrm{WWKL}$
by Simpson and Yu [Reference Yu and Simpson15]. We always identify a real
$z\in [0,1] $
that is not a dyadic rational with its unique binary expansion viewed as an element of
$2^{\mathbb {N}}$
.
Besides the fact that the measure of an open set may not exist as a real in the model, there is another problem when developing measure theory within
$\mathsf {RCA}_{0}$
. There might exist two codes for open sets
$S_{1}$
and
$S_{2}$
such that
$\forall x\in 2^{\mathbb {N}}(x\in [[S_{1}]]\leftrightarrow x\in [[S_{2}]])$
but
$\mu (S_{1})\neq \mu (S_{2})$
. Thus the value of
$\mu $
depends on codes. We define the measure for an open set
$U\subseteq 2^{\mathbb {N}}$
as
$$ \begin{align*} \bar{\mu}(U):=\sup\{\mu(S)\mid U=[[S]]\}. \end{align*} $$
This definition agrees with the internal measure of open sets defined in [Reference Yu and Simpson15, p. 174]. Within
$\mathsf {WWKL}_0$
,
$[[S_{1}]]=[[S_{2}]]$
implies
$\mu (S_{1})=\mu (S_{2})$
, thus
$\mu $
and
$\bar \mu $
coincide. Fortunately, the definition of Martin–Löf randomness will not be affected even if the two don’t coincide. We take any of the two equivalent conditions below as a definition in the context of
$\mathsf {RCA}_{0}$
that Z is not Martin–Löf random relative to X.
Proposition 5.1 (
$\mathsf {RCA}_{0}$
)
The following are equivalent for
$Z,X\in 2^{\mathbb {N}}$
.
-
1. There exists an X-computable sequence
$\langle S_{i}\mid i\in \mathbb {N} \rangle $
of codes of open sets such that
$\mu (S_{i})\le 2^{-i}$
and
$Z\in \bigcap _{i\in \mathbb {N}}[[S_{i}]]$
. -
2. There exists an X-computable sequence
$\langle S_{i}\mid i\in \mathbb {N} \rangle $
of codes of open sets such that
$\bar \mu ([[S_{i}]])\le 2^{-i}$
and
$Z\in \bigcap _{i\in \mathbb {N}}[[S_{i}]]$
.
Proof 2
$\Rightarrow $
1 is trivial. To show 1
$\Rightarrow $
2, let
$\langle S_{i}\mid i\in \mathbb {N} \rangle $
be an X-computable sequence of codes for open sets such that
$\mu (S_{i})\le 2^{-i}$
and
$Z\in \bigcap _{i\in \mathbb {N}}[[S_{i}]]$
. If Z is of the form
$\sigma ^{\frown }0^{\mathbb {N}}$
, put
$S^{\prime }_{i}:=\{\sigma ^{\frown }0^{i}\}$
. We have
$\bar \mu ([[S^{\prime }_{i}]])\le 2^{-i}$
and
$Z\in \bigcap _{i\in \mathbb {N}}[[S^{\prime }_{i}]]$
. Otherwise, put
$$ \begin{align*} S^{\prime}_{i}:=\{\sigma^{\frown}0^{k}{{\hspace{-0.0001pt}}}^{\frown} {1}: \sigma\in S_{i}, k\in \mathbb{N}\}. \end{align*} $$
Then
$T_{S_{i}'}=\{\tau \in 2^{<\mathbb {N}}\mid \tau =\sigma ^{\frown }0^{k}$
for some
$\sigma \in T_{i}$
and
$k\in \mathbb {N}\}$
. Since
$T_{S_{i}'}\supseteq T_{S_{i}}$
we have
$\mu (T_{S_{i}'})\le \mu (T_{S_{i}})$
. We still have
$Z\in \bigcap _{i\in \mathbb {N}}[[S_{i}']]$
by the case assumption on Z. On the other hand, for any
$\widehat S\subseteq 2^{<\mathbb {N}}$
, if
$ \forall x\in 2^{\mathbb {N}}(x\in [[\widehat S]]\to x\in [[S_{i}']]) $
then
$T_{\widehat S}\supseteq T_{S_{i}'}$
because
$\sigma \in T_{S_{i}'}\to \sigma ^{\frown }0^{\mathbb {N}}\in [T_{\widehat S}]$
. Thus,
$\bar \mu ([[S_{i}']])\le \mu (S_{i}')\le 2^{-i}$
.⊣
6 Differentiability of functions of bounded variation in
${\textsf {WWKL}}_{0}$
Lebesgue’s theorem states that functions on
$[0,1]$
of bounded variation are a.e. differentiable. The main result of this section, Theorem 6.8, shows that several versions of this result are equivalent to
${\textsf {WWKL}}_{0}$
over
$\mathsf {RCA}_{0}$
. For a function f and distinct reals
$a,b $
in the domain of f, we denote the slope by
$$ \begin{align*} S_f(a, b)= \frac{f(b)- f(a)}{b-a}. \end{align*} $$
Definition 6.1 (Section 2.3 of [Reference Brattka, Miller and Nies1], going back to Demuth, within
$\mathsf {RCA}_{0}$
)
Let
$f : \subseteq [0,1] \to \mathbb {R}$
be a function with domain containing
$[0,1]_{\mathbb {Q}}$
(f may be a continuous function or a rationally presented function). For a given
$h>0$
, the h-derivative of f at
$x\in [0,1]$
is the set of reals defined by
$$ \begin{align*} D_{h} f(x) = \{S_f(a, b) : a,b \in [0,1]_{\mathbb{Q}} \ \land \ a \le x \le b \ \land \ 0 < b - a < h \}. \end{align*} $$
The function f is pseudo-differentiable at
$z \in (0,1)$
if
$\lim _{h \to 0^+} \textrm{diam}(D_{h} f(z))=0$
, or more formally, for any
$\varepsilon>0$
, there exist
$c,d\in \mathbb {Q}$
and
$h>0$
such that
$d-c<\varepsilon $
and
$D_{h} f(z)\subseteq [c,d]$
.
The upper and lower pseudo-derivatives of f are defined by
and
. Then, the assertion
$\lim _{h \to 0^+} \textrm{diam}(D_{h} f(z))=0$
formally means that
without referring to the limits themselves. The point is that we don’t have to require that
$f(z)$
be defined; for instance we could be interested in a function f only defined on rationals. In this way we can include in our equivalences with
${\textsf {WWKL}}_{0}$
in Theorem 6.8 a statement about functions with rational presentations. It follows from [Reference Brattka, Miller and Nies1, Lemma 2.5] that if f is defined and continuous at z, then the pseudo-derivative at z exists iff the usual derivative exists, and they agree.
Note that the real
may fail to exist in a model of
$\mathsf {RCA}_{0}$
even if
and
are equal. We will avoid mentioning the values
or
and just consider inequality, as we already did in the case for bounded variation.
6.1 Pseudo-differentiability of non-decreasing functions within
$\textsf {RCA}_0$
Lemma 6.2 (a version of part of [Reference Brattka, Miller and Nies1, Theorem 4.3])
Let
$f:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
be a rationally presented non-decreasing function, and let
$z\in [0,1]$
be Martin–Löf random relative to f. Then f is pseudo-differentiable at z.
Proof Without loss of generality, we may suppose that
$0\le f(0)\le f(1)\le 1$
. Assume that f is not pseudo-differentiable at z. If z is rational, then z is not Martin–Löf random, so assume that z is irrational. We will consider the following two cases.
Case 1.
. Thus, for any
$m\in \mathbb {N}$
, there exists
$a_{0}<z<b_{0}$
such that for any
$a,b\in \mathbb {Q}$
,
$a_{0}<a<z<b<b_{0}\to S_{f}(a,b)>2^{m}$
. For a given
$\sigma \in 2^{<\mathbb {N}}$
, we let
$l_{\sigma }=0.\sigma $
and
$r_{\sigma }=0.\sigma +2^{-|\sigma |}$
. Let
$\varphi (m,\sigma )$
be a
$\Pi ^{0}_{1}$
-formula saying that
$S_{f}(l_{\sigma },r_{\sigma })\le 2^{m}$
. Write
$\varphi (m,\sigma )\equiv \forall s \theta (s,m,\sigma )$
for a
$\Sigma ^{0}_{0}$
-formula
$\theta $
, and put
$$ \begin{align*} T_{m}:=\{\sigma\in 2^{<\mathbb{N}}: \forall \tau\preceq \sigma \forall s<|\sigma|\theta(s,m,\tau)\}. \end{align*} $$
Since
$f(1)-f(0)\le 1$
, for each
$m\in \mathbb {N}$
and
$k\in \mathbb {N}$
, there are at most
$2^{k}$
strings of length
$m+k$
which are not in
$T_{m}$
. Thus,
$\mu (T_{m})\ge 1-2^{m}$
, and hence
$\langle 2^{\mathbb {N}}\setminus [T_{m}]: m\in \mathbb {N} \rangle $
forms a Martin–Löf test. By the assumption,
$z\notin [T_{m}]$
for any
$m\in \mathbb {N}$
. Thus z is not Martin–Löf random relative to f.
Case 2.
and
. We will follow the proof of (iii)
$\to $
(ii) of [Reference Brattka, Miller and Nies1, Theorem 4.3] halfway within
$\mathsf {RCA}_{0}$
.
Since f is non-decreasing and
, the limit
$\lim _{y \to z} f(y)$
exists by nested interval completeness [Reference Simpson11, Theorem II.4.8] which holds in
$\mathsf {RCA}_{0}$
. So we may assume that
$f(z)$
exists and f is continuous at z; this will be needed in the following argument when we apply a version of [Reference Brattka, Miller and Nies1, Lemma 2.5] formalized within
$\mathsf {RCA}_{0}$
.
For given
$p,q\in \mathbb {Q}$
, an interval A is said to be a
$(p,q)$
-interval if it is of the form
$A=(pi2^{-n}+q,p(i+1)2^{-n}+q)$
for some
$n\in \mathbb {N}$
and
$i\in \mathbb {Z}$
. For a finite set
$L\subseteq \mathbb {Q}^{2}$
, an interval is said to be L-interval if it is a
$(p,q)$
-interval for some
$(p,q)\in L$
. One can formalise within
$\mathsf {RCA}_{0}$
the proofs of Lemmas 2.5 and 4.1, and most of the proof of Lemma 4.4 of [Reference Brattka, Miller and Nies1]. To see this, note that these arguments only rely on elementary arithmetic, which can be formalised within
$\mathsf {RCA}_{0}$
. Hence we have the following.
Claim 6.2.1. There exist rationals
$\beta>\gamma >0$
and a finite set
$L\subseteq \mathbb {Q}^{2}$
such that
$$ \begin{align*} \gamma &> \lim_{h\to 0} \inf \{S_{f}(A): A\text{ is an } L\text{-interval}\wedge |A|\le h\wedge z\in A\},\\ \beta & < \lim_{h\to 0} \sup \{S_{f}(A): A\text{ is an } L\text{-interval}\wedge |A|\le h\wedge z\in A\}. \end{align*} $$
In the final step of the proof of [Reference Brattka, Miller and Nies1, Lemma 4.4] for both inequalities there, one picks
$(p,q)$
and
$(r,s)$
from L which by themselves witness the two inequalities above, respectively; that is, we only need to look at
$(p,q)$
intervals for the first, and at
$(r,s)$
-intervals for the second. However, this is impossible within
$\mathsf {RCA}_{0}$
since it requires an essential use of the infinite pigeonhole principle (also known as
$\textrm{RT}^{1}$
) which is equivalent to
$\textrm{B}\Sigma ^0_2$
. Thus, we need to take a detour around this part of the proof.
We fix
$\beta ,\gamma $
and
$L\subseteq \mathbb {Q}^{2}$
as in Claim 6.2.1. An n-depth alternation L-sequence is a length
$2n+1$
decreasing sequence of L-intervals
$[0,1]\supseteq A_{0}\supseteq A_{1}\supseteq \dots \supseteq A_{2n}$
such that
$S_{f}(A_{2i})<\gamma $
for any
$i\le n$
,
$S_{f}(A_{2i+1})>\beta $
for any
$i<n$
. For
$(p,q),(r,s)\in L$
, an n-depth alternation
$(p,q)$
;
$(r,s)$
-sequence is an n-depth alternation L-sequence such that
$A_{2i}$
is a
$(p,q)$
-interval for any
$i\le n$
and
$A_{2i+1}$
is an
$(r,s)$
-interval for any
$i<n$
. The last interval of an n-depth alternation
$(p,q)$
;
$(r,s)$
-sequence is called an n-depth
$(p,q)$
;
$(r,s)$
-interval. By Claim 6.2.1, for any
$n\in \mathbb {N}$
, there exists an n-depth alternation L-sequence such that
$z\in A_{2n}$
. Furthermore, by the finite pigeon hole principle, every
$n|L|^{2}$
-depth alternation L-sequence contains an n-depth alternation
$(p,q)$
;
$(r,s)$
-subsequence for some
$(p,q),(r,s)\in L$
. Thus, we have the following claim.
Claim 6.2.2. For any
$n\in \mathbb {N}$
there exist
$(p,q),(r,s)\in L$
and an n-depth
$(p,q)$
;
$(r,s)$
-interval A such that
$z\in A$
.
Note that we cannot fix
$(p,q),(r,s)\in L$
for all
$n\in \mathbb {N}$
in this claim since it would require
$\textrm{B}\Sigma ^0_2$
again.
Next, we will calculate the size of n-depth
$(p,q)$
;
$(r,s)$
-intervals. Fix
$(p,q),(r,s)\in L$
and let
$\{A^{s}\}_{s<u}$
be a finite collection of n-depth
$(p,q)$
;
$(r,s)$
-intervals. Take an n-depth alternation
$(p,q)$
;
$(r,s)$
-sequence
$A^{s}_{0}\supseteq \dots \supseteq A^{s}_{2n}=A^{s}$
for each
$s<u$
, and let
. For a finite union of intervals
which is described by a finite disjoint union as
, put
and
. Since any two
$(p,q)$
-intervals (or
$(r,s)$
-intervals) are disjoint, or one includes the other, we have that
for any
$i\le n$
and
for any
$i<n$
. Thus, for any
$i<n$
,
Hence,
Now, put
$$ \begin{align*} U_{n}^{(p,q);(r,s)} &:= \bigcup \{ A: A\text{ is an } n \text{-depth }(p,q);(r,s)\text{-interval}\},\\ U_{n}&:=\bigcup_{(p,q),(r,s)\in L}U_{n}^{(p,q);(r,s)}. \end{align*} $$
Note that one can enumerate all n-depth
$(p,q)$
;
$(r,s)$
-intervals f-computably. By
$(4)$
,
$\bar \mu (U_{n}^{(p,q);(r,s)})\le (\gamma /\beta )^{n}$
. Thus,
$\bar \mu (U_{n})\le (\gamma /\beta )^{n}|L|^{2}$
. By Claim 6.2.2,
$z\in \bigcap _{n\in \mathbb {N}}U_{n}$
. Thus z is not Martin–Löf random relative to f.
Remark 6.3. By a careful formalization of the notion of test for computable randomness within
$\mathsf {RCA}_{0}$
, one can reformulate the above proof to obtain the following assertion within
$\mathsf {RCA}_{0}$
: for any rationally presented non-decreasing function
$f:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
, there exists a computable test relative to f such that f is pseudo-differentiable at
$z\in [0,1]$
if z passes the test. On the other hand, one can easily see within
$\mathsf {RCA}_{0}$
that for any computable test relative to X, there exists a real computable from X which can pass it. Thus, within
$\mathsf {RCA}_{0}$
, every rationally presented non-decreasing function is pseudo-differentiable at some point. However, as we will see in Theorem 6.8, this does not imply that every rational presented non-decreasing function is pseudo-differentiable almost surely (as defined below).
6.2 A.e. pseudo-differentiability of functions of bounded variation
We introduce a notion of a.e. differentiability in a form that is appropriate within
$\mathsf {RCA}_{0}$
. In that setting, any open set
$U\subseteq [0,1]$
can be identified with an open set in
$2^{\mathbb {N}}$
via the canonical surjection
$\pi :2^{\mathbb {N}}\to [0,1]$
defined by
$\pi (Z)=\sum _{n\in Z}2^{-n}$
. We define the measure for open sets in
$[0,1]$
by
$\bar \mu (U)=\bar \mu (\pi ^{-1}(U))$
. This
$\bar \mu $
coincides with the Lebesgue measure on
$[0,1]$
as in [Reference Yu and Simpson15, p. 174].
Definition 6.4. A function
$f : \subseteq [0,1] \to \mathbb {R}$
with domain containing
$[0,1]_{\mathbb {Q}}$
is pseudo-differentiable almost surely if
$\bar \mu (U)= 1$
for any open set
$U\subseteq [0,1]$
containing every point of pseudo-differentiability of f.
For the main results of this section we need two preliminaries. The first one is a model-theoretic generalization of the fact that any Martin–Löf random real is Martin–Löf random relative to some
$\textrm{PA}$
-degree by Downey et al. [Reference Downey, Hirschfeldt, Miller and Nies4, Proposition 7.4] and Reimann and Slaman [Reference Reimann and Slaman10, Lemma 4.5].
Lemma 6.5 (Simpson/Yokoyama [Reference Simpson and Yokoyama12])
For any countable model
$(\mathcal {M}, \mathcal {S}) \models {\mathsf {WWKL}_0}$
there is
$\widehat {\mathcal {S}} \supseteq {\mathcal {S}}$
satisfying
-
1.
$(\mathcal {M}, \widehat {\mathcal {S}}) \models {\mathsf {WKL}_0}$
and -
2. for any
$A \in \widehat {\mathcal {S}}$
there is
$Z \in {\mathcal {S}}$
such that Z is Martin–Löf random relative to A.
The following is related to a well known result of Ku
$\check {\text {c}}$
era; also see [Reference Nies8, Proposition 3.2.24]. We say that W is a tail of a set
$Z \subseteq \mathbb {N}$
if there is n such that
$W(i) = Z(n+i)$
for each i.
Lemma 6.6 (
$\mathsf {RCA}_{0}$
)
Let
$U\subseteq [0,1]$
be an open set such that
$\bar \mu (U)<1$
, and let
$S\subseteq 2^{<\mathbb {N}}$
be a code for an open set such that
$[[S]]=\pi ^{-1}(U)$
. Let
$Z\in 2^{\mathbb {N}}$
be Martin–Löf random relative to S. There exists a tail W of Z such that
$0.W=\pi (Z)\in [0,1]\setminus U$
.
Proof Choose
$q\in \mathbb {Q}$
such that
$ \mu (S)\le \bar \mu (U) \le q<1$
. Then,
$\mu (T_{S})\ge 1-q$
. Let
$\widetilde {T} = \{\tau \in 2^{<\mathbb {N}} : \tau \not \in T_{S} \land \tau |_{(|\tau | - 1)} \in T_{S}\}$
. Put
$$ \begin{align*} T^{n}:=\{\sigma_{0}^{\frown}\dots^{\frown}\sigma_{k}: k< n\wedge [ \forall i< k\, \sigma_{i}\in \widetilde{T}]\wedge \sigma_{k}\in T_{S}\}. \end{align*} $$
Then, we have
$\mu (T^{n})\ge 1-q^{n}$
. Thus, for large enough
$l\in \mathbb {N}$
,
$\langle 2^{\mathbb {N}}\setminus [T^{ln}]: n\in \mathbb {N} \rangle $
forms a Martin–Löf test relative to S, and hence
$Z\in [T^{ln}]$
for some
$n\in \mathbb {N}$
. By
$\Sigma ^{0}_{1}$
-induction, take
$$ \begin{align*} m=\max\{m': \exists c\le ln\, \exists \langle \sigma_{i}\in\widetilde{T}: i<c \rangle(Z|_{m'}=\sigma_{0}^{\frown}\dots^{\frown}\sigma_{c-1})\}. \end{align*} $$
Then, the tail W of Z defined by
$W(i)=Z(i+m)$
is in
$[T_{S}]$
, whence
$0.W\in [0,1]\setminus U$
.⊣
Theorem 6.7 (
${\textsf {WWKL}}_{0}$
)
Every rationally presented function of bounded variation is pseudo-differentiable at some point, and is actually pseudo-differentiable almost surely.
Proof We show that the result holds in any countable model
$(\mathcal {M}, \mathcal {S})$
of
${\textsf {WWKL}}_{0}$
. Let
$f : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
be a rationally presented function of bounded variation in
$(\mathcal {M}, \mathcal {S})$
, and let
$U\subseteq [0,1]$
be an open set such that
$\bar \mu (U) < 1$
. We will show that there exists a real
$z\in [0,1]\setminus U$
such that f is pseudo-differentiable at z. Let
$(\mathcal {M}, \widehat {\mathcal {S}}) \models {\textsf {WKL}}_{0}$
be the model given by Lemma 6.5. By Theorem 4.10,
$$ \begin{align*} (\mathcal{M}, \widehat{\mathcal{S}}) \models \textsf{Jordan}_{\mathbb{Q}}. \end{align*} $$
Hence
$\widehat {\mathcal {S}}$
contains a non-decreasing function
$g : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
such that
$f \le ^*_{\textsf {slope}} g$
.
Within
$(\mathcal {M}, \widehat {\mathcal {S}})$
, define
$h : [0,1]_{\mathbb {Q}} \to \mathbb {R}$
by
$h(x) = g(x) - f(x)$
. By Lemma 6.5 again, there is a real
$z \in [0,1]$
such that
$z \in \mathcal {S}$
and
$z \in \mathsf {MLR}^{g \oplus h\oplus \mathcal {U}}$
. By Lemma 6.6, we may assume that
$z\in [0,1]\setminus U$
. The functions g and h are pseudo-differentiable at z in
$(\mathcal {M}, \widehat {\mathcal {S}})$
by Lemma 6.2. Therefore f is pseudo-differentiable at z in
$(\mathcal {M}, \widehat {\mathcal {S}})$
, and hence in
$(\mathcal {M}, \mathcal {S})$
.⊣
A continuous function
$f:[0,1]\to \mathbb {R}$
is said to be absolutely continuous if for any
$\varepsilon>0$
there exists
$\delta>0$
such that for any
$0\le a_{0}\le \dots \le a_{n}\le 1$
with
$a_{n}-a_{0}<\delta $
,
$\sum _{i<n}|f(a_{i+1})-f(a_{i})|<\varepsilon $
. Note that every absolutely continuous function is of bounded variation within
$\mathsf {RCA}_{0}$
.
Theorem 6.8. The following are equivalent over
$\mathsf {RCA}_0$
.
-
1.
$\mathsf {WWKL}_0$
. -
2. Every rationally presented function of bounded variation is pseudo-differentiable almost surely.
-
3. Every rationally presented non-decreasing function is pseudo-differentiable almost surely.
-
4. Every continuous function of bounded variation is pseudo-differentiable almost surely.
-
5. Every effectively uniformly continuous and absolutely continuous function which has a rational presentation is pseudo-differentiable at some point.
Proof 1
$\Rightarrow $
2 is Theorem 6.7, 2
$\Rightarrow $
3 is trivial, 2
$\Rightarrow $
4 is straightforward from Corollary 4.4. For 4
$\Rightarrow $
5, within
$\mathsf {RCA}_{0}$
, we have
$\bar \mu (\emptyset )=0$
, since if
$[[S]]=\emptyset $
, then S is empty, so
$\mu (S)=0$
. Thus, if an open set
$U\subseteq [0,1]$
has positive measure, then U is not empty. It remains to show
$\neg $
1
$\Rightarrow \neg $
3 and
$\neg $
1
$\Rightarrow \neg $
5.
We show
$\neg $
1
$\Rightarrow \neg $
3. Assuming
$\neg $
1 we first construct an open set
$U\subseteq [0,1]$
such that
$\bar {\mu }(U)<1$
and
$[0,1]\setminus U$
only contains rationals. The idea is similar to the one in the proof of Proposition 5.1: If
$\textrm{WWKL}$
fails, there is a tree T with no paths such that
$\mu (T)\ge \varepsilon $
where
$\varepsilon>0$
. Put
$T'=\{\tau \in 2^{<\mathbb {N}}\mid \tau =\sigma ^{\frown }0^{k}$
for some
$\sigma \in T$
and
$k<|\tau |\}$
,
$\widetilde T=\{\tau \in 2^{<\mathbb {N}}\mid \tau \notin T'$
and
$\tau |_{|\tau |-1}\in T'\}$
, and
$U=\bigcup _{\tau \in \widetilde T}(0.\tau ,0.\tau +2^{-|\tau |})\subseteq [0,1]$
.
As in the proof of Proposition 5.1, we have
$\bar \mu (2^{\mathbb {N}}\setminus [T'])\le 1-\mu (T)<1$
, and any path of
$T'$
is rational. Thus
$\bar \mu (U)\le \bar \mu (2^{\mathbb {N}}\setminus [T'])<1$
and
$[0,1]\setminus U$
only contains rationals.
Next we construct a rationally presented non-decreasing function which is not pseudo-differentiable at any rational. Let
$\{q_{i}\}_{i\in \mathbb {N}}$
be an enumeration of
$[0,1]_{\mathbb {Q}}$
. Define a function
$f:[0,1]_{\mathbb {Q}}\to \mathbb {R}$
by
$f(p)=\sum _{q_{i}<p}2^{-i}$
. Clearly, f is non-decreasing and not pseudo-differentiable at any rational. By Proposition 4.3, some vertical shift of f has a rational presentation. Thus we have
$\neg $
3.
Finally, we show
$\neg $
1
$\Rightarrow \neg $
5. This implication is related to [Reference Brattka, Miller and Nies1, Theorem 6.7] (originally due to Demuth) in the setting of reverse mathematics. If
$\textrm{WWKL}$
fails, there is a tree T with no path such that
$\mu (T)\ge \varepsilon $
where
$\varepsilon>0$
. We construct a sequence of trees
$\langle T_{n}: n\in \mathbb {N} \rangle $
such that no
$T_{n}$
has a path and
$\mu (T_{n})\ge 1-2^{-4n}$
. Let the
$T^{i}$
be defined as in the proof of Lemma 6.6 where
$q = 1- \varepsilon $
. No
$T^{i}$
has a path, and
$\mu (T^{i})\ge 1-(1-\varepsilon )^{i}$
. Thus, one can effectively choose
$i_{0}<i_{1}<\dots $
so that
$\mu (T^{i_{n}})\ge 1-2^{-4n}$
. Now let
$T_n = T^{i_n}$
.
Let
$\widetilde {T}_{n} = \{\tau \in 2^{<\mathbb {N}} : \tau \not \in T_{n} \ \land \ \tau |_{|\tau | - 1} \in T_{n}\}$
. As before put
$I_{\sigma }:=[0.\sigma ,0.\sigma +2^{-|\sigma |}]$
. Since
$T_{n}$
has no path we have
$[0,1]=\bigcup _{\sigma \in \widetilde {T}_{n}}I_{\sigma }$
for any n. Since
$\mu (T_{n})\ge 1-2^{-4n}$
we have
$\sum _{\sigma \in \widetilde {T}_{n}}|I_{\sigma }|\le 2^{-4n}$
. Note that if
$\sigma \in \widetilde {T}_{n}$
and
$m<n$
, there exists
$\tau \in \widetilde {T}_{m}$
such that
$\tau \preceq \sigma $
. Note also that
$|\sigma |\ge n$
for any
$\sigma \in \widetilde {T}_{n}$
.
For
$v \in \mathbb R^+$
and
$r \in \mathbb N$
, recall
$\textrm {M}_A(v, r)$
denotes a sawtooth function on the interval A with r many teeth of height v. For each
$n,s \in \mathbb {N}$
define a polygonal function
$f_{n,s} :[0,1] \to \mathbb {R}$
as follows. For
$\sigma \in \widetilde {T}_{n}$
, on the interval
$I_{\sigma}$
, set
$$ \begin{align*} f_{n,s} = \begin{cases} \textrm{M}_{I_{\sigma}}(2^{-2n-|\sigma|}, 2^{5n}) & \text{if } |\sigma|\le s, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
Then
$(f_{n,s})_{s\in \mathbb {N}}$
defines an effectively uniformly continuous function
$f_{n}$
. For these functions
$f_{n}$
one can check the following properties.
-
(i) If
$\sigma \in \widetilde {T}_{n}$
,
$x\in I_{\sigma }$
and
$m\ge n$
, then
$0\le f_{m}(x)\le 2^{-2m-|\sigma |}$
. In particular,
$|f_{n}|\le 2^{-2n}$
. -
(ii) For any
$0\le x<y\le 1$
and for any
$n\in \mathbb {N}$
,
$|f_{n}(x)-f_{n}(y)|/|x-y|\le 2^{3n+1}$
. -
(iii)
$\mathbf {v}_{f_{n}}\le 2^{-n+1}$
.
(i) and (ii) follow from the definition. To see (iii),
$$ \begin{align*} \mathbf{v}_{f_{n}}=\sum_{\sigma\in \widetilde{T}_{n}}\mathbf{v}_{\textrm{M}_{I_{\sigma}}(2^{-2n-|\sigma|}, 2^{5n})}=\sum_{\sigma\in \widetilde{T}_{n}}2^{3n-|\sigma|+1}\le 2^{3n+1}2^{-4n}=2^{-n+1}. \end{align*} $$
Define an effectively uniformly continuous function f by
$f=\sum _{n\in \mathbb {N}}f_{n}$
. Then, f is of bounded variation since
$\mathbf {v}_{f}=\sum _{n\in \mathbb {N}} \mathbf {v}_{f_{n}}\le 2$
. Actually, f is absolutely continuous. One can see this as follows. For any
$x\in [0,1]$
and
$\varepsilon>0$
, take large enough
$n\in \mathbb {N}$
so that
$\sum _{j>n}\mathbf {v}_{f_{j}}<\varepsilon /2$
. Since each
$f_{i}$
,
$i\le n$
, is absolutely continuous by (ii), one can find
$\delta>0$
so that
$\sum _{i\le n}(f_{i}(x)-f_{i}(y))<\varepsilon /2$
for any y such that
$|x-y|<\delta $
.
By Corollary 4.4(ii), after replacing f with a vertical shift we may assume that f has a rational presentation.
We will see that this f is not pseudo-differentiable at any point. Let
$x\in [0,1]$
,
$\delta>0$
and
$K\in \mathbb {N}$
. We will find
$a\le x\le b$
so that
$b-a<\delta $
and
$|S_{f}(a,b)|>K$
. Take
$n\in \mathbb {N}$
large enough so that
$2^{3n-1}>K$
and
$|I_{\sigma }|<\delta $
for any
$\sigma \in \widetilde {T}_{n}$
. Since
$T_{n}$
has no path, there exists
$\sigma \in \widetilde {T}_{n}$
such that
$x\in I_{\sigma }$
. Let
$a\le x\le b$
so that
$a,b$
are nearest to x yielding extreme values of the saw-tooth function
$\textrm {M}_{I_{\sigma }}(2^{-2n-|\sigma |}, 2^{5n})$
. Then,
$|f_{n}(b)-f_{n}(a)|=2^{-2n-|\sigma |}$
and
$b-a=2^{-5n-1-|\sigma |}$
. By (i),
$|f_{j}(b)-f_{j}(a)|\le 2^{-2j-|\sigma |}$
for any
$j>n$
, and by (ii),
$|f_{i}(b)-f_{i}(a)|/|b-a|\le 2^{3i+1}$
for any
$i<n$
. Thus,
$$ \begin{align*} \frac{|f(b)-f(a)|}{|b-a|}&\ge \frac{|f_{n}(b)-f_{n}(a)|}{|b-a|}-\sum_{j>n}\frac{|f_{j}(b)-f_{j}(a)|}{|b-a|}-\sum_{i<n}\frac{|f_{i}(b)-f_{i}(a)|}{|b-a|}\\ &\ge\frac{2^{-2n}-|\sigma|}{2^{-5n-1-|\sigma|}}-\sum_{j>n}\frac{2^{-2j-|\sigma|}}{2^{-5n-1-|\sigma|}}-\sum_{i<n}2^{3i+1}\\ &\ge 2^{3n+1}-2^{3n}-2^{3n-1} = 2^{3n-1}. \end{align*} $$
Hence,
$|S_{f}(a,b)|>K$
.⊣
Remark 6.9. The equivalence of conditions 1 and 3 in the foregoing theorem seems rather strange compared to [Reference Brattka, Miller and Nies1, Theorem 4.3] and our discussion in Remark 6.3 since there is no appearance of Martin–Löf random reals. Note that the existence of computable random reals doesn’t imply
$\textrm{WWKL}$
over
$\mathsf {RCA}_{0}$
. This tricky situation may be understood that it is caused by a bad behavior of the Lebesgue measure within
$\mathsf {RCA}_{0}$
. For example, one cannot say that every open set
$U\subseteq [0,1]$
is of measure
$1$
if
$[0,1]\setminus U$
is countable. In fact, this is equivalent to
$\textrm{WWKL}$
by the argument in the previous proof.
Acknowledgments
Nies’ work is partially supported by the Marsden fund of New Zealand. Yokoyama’s work is partially supported by JSPS KAKENHI (grant numbers 19K03601 and 15H03634) and JSPS Core-to-Core Program (A. Advanced Research Networks).
