2. SYMMETRY OF IRRADIATION AND ENERGY DEPOSITION

Let us recall the assumed conditions of irradiation (Garanin et al., Reference Garanin, Bel'kov and Bondarenko2012; Rozanov et al., Reference Rozanov, Gus'kov, Vergunova, Demchenko, Stepanov, Doskoch, Yakhin, Bel'kov, Bondarenko and Zmitrenko2013, Reference Rozanov, Gus'kov, Vergunova, Demchenko, Stepanov, Doskoch, Yakhin and Zmitrenko2015). As the working wavelength of planned laser facility the wavelength of second harmonic of Nd-laser is chosen which has the value of 0.530 µm. The total energy of the laser pulse is 2 MJ. The irradiation occurs along the sides of the cube, on each of them eight clusters consisting of four beams are located (see Fig. 4a). The radiation intensity distribution in the plane passing through the center of the target and perpendicular to the optical axis of the beam has the form

(1)$$I(r) = {I_0}\exp \left[ { - {{\left( {\displaystyle{r \over a}} \right)}^n}} \right],$$

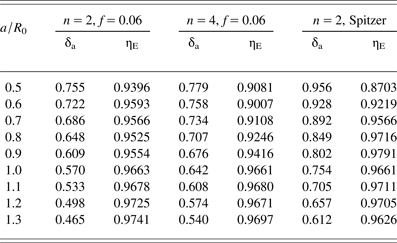
where r is the distance from the optical axis, a, characteristic radius of the beam, and I ₀, intensity on the optical axis. Calculation of the laser energy absorption was conducted using numerical code RAPID (Afanas'ev et al., Reference Afanas'ev, Gamalii, Demchenko and Rozanov1982). Different values of n in Eq. (1) as well as various models of thermal conductivity (Spitzer model and one using the flux limiting parameter f = 0.06) were considered while performing the simulations. Dependencies of the quantities characterizing the absorption of laser energy on specified parameters are shown in Table 1. Here δ_a is the proportion of absorption, η_E = E _t^min/E _t^max, the degree of absorption homogeneity, where E _t is absorbed energy, R ₀, radius of the target at initial time moment (R ₀ = 1595 µm in this work). Note that η_E increases with increasing radius of the beam. Using a model of the limited thermal conductivity for n = 2 and n = 4 in the case of a/R ₀ ≥ 1 η_E takes almost equal values, and using the model of Spitzer conductivity, since a/R ₀ = 0.8 the value η_E is changing slightly. In further calculations we use Gaussian beam (n = 2) and the model with a limited thermal conductivity (f = 0.06) as the most adequately describing the experimental results of the interaction of nanosecond laser pulse with plasma (Volosevich et al., Reference Volosevich, Kosyrev and Levanov1978; Basov et al., Reference Basov, Volosevich, Gamalii, Zakharenkov, Kiselev, Kurdyumov, Levanov, Rozanov, Rupasov, Samarskii, Sklizkov, Sotskii and Shikanov1988; Dolgoleva, Reference Dolgoleva2013).

Fig. 4. (a) Symmetry of the irradiation of the thermonuclear target; (b) time dependence of the incident laser flux power Q _L.

Table 1. Dependencies of the proportion of absorption and the degree of absorbtion homogeneity on the characteristic radius of the beam for different values of n in (1), and different conductivity models

For the considered multi-beam system and parameters n = 2, a/R ₀ = 1, f = 0.06 in Figure 5 the angle distribution of absorbed energy during the laser pulse is shown. On this map one can select the area limited by angles’ ranges 0° ≤ φ ≤ 45° (azimuthal angle) and 0° ≤ θ ≤ 90° (polar angle) which with the help of elementary transformations can be translated to the rest of the o sphere surface. Due to the need for further detailed 1D numerical simulation, we need to allocate some of the most interesting points in the elementary region, namely the points sufficiently different from each other in terms of irradiation conditions. In this study, 18 points were chosen that are marked with white circles in Figure 5. Let us give to them dependencies of function of the angular distribution of the absorbed flux W on time (see Figs. 6a–6c). Function W is normalized so that its average value over the solid angle 4π is 1. Figure 6d shows the dependence of the efficiency of absorption of laser energy δ_abs from time. The dependence of the absorbed laser flux Q _a defined by the expression Q _a(t, φ, θ) = Q _L(t)W(t, φ, θ). This value is used for further 1D numerical calculation. Note that due to the symmetry of the cube according to the values of W(t) for θ = 0° and θ = 90° for φ = 0° are the same. Dependencies also coincide for all φ at θ = 0°.

Fig. 5. Angular distribution of the absorbed energy on account of inverse Bremsstrahlung during the laser pulse (a/R ₀ = 1, n = 2).

Fig. 6. (a)–(c) Time dependence of the function of the angular distribution of the absorbed flux; (d) time dependence of the absorption efficiency.

Another important factor identified by the study of the efficiency of absorption of laser irradiation is the displacement of the surface of characteristic density at which the energy is deposited from the target center due to refraction. In the following 1D calculations this fact was taken into account due to the adjustment of the wavelength of the incident laser irradiation, namely, reducing the effective value of the critical density (ρ_cr ~ λ⁻²).

3. DETAILED 1D SPHERICALLY SYMMETRIC CALCULATIONS AND CONDITIONS FOR INSTABILITIES DEVELOPMENT

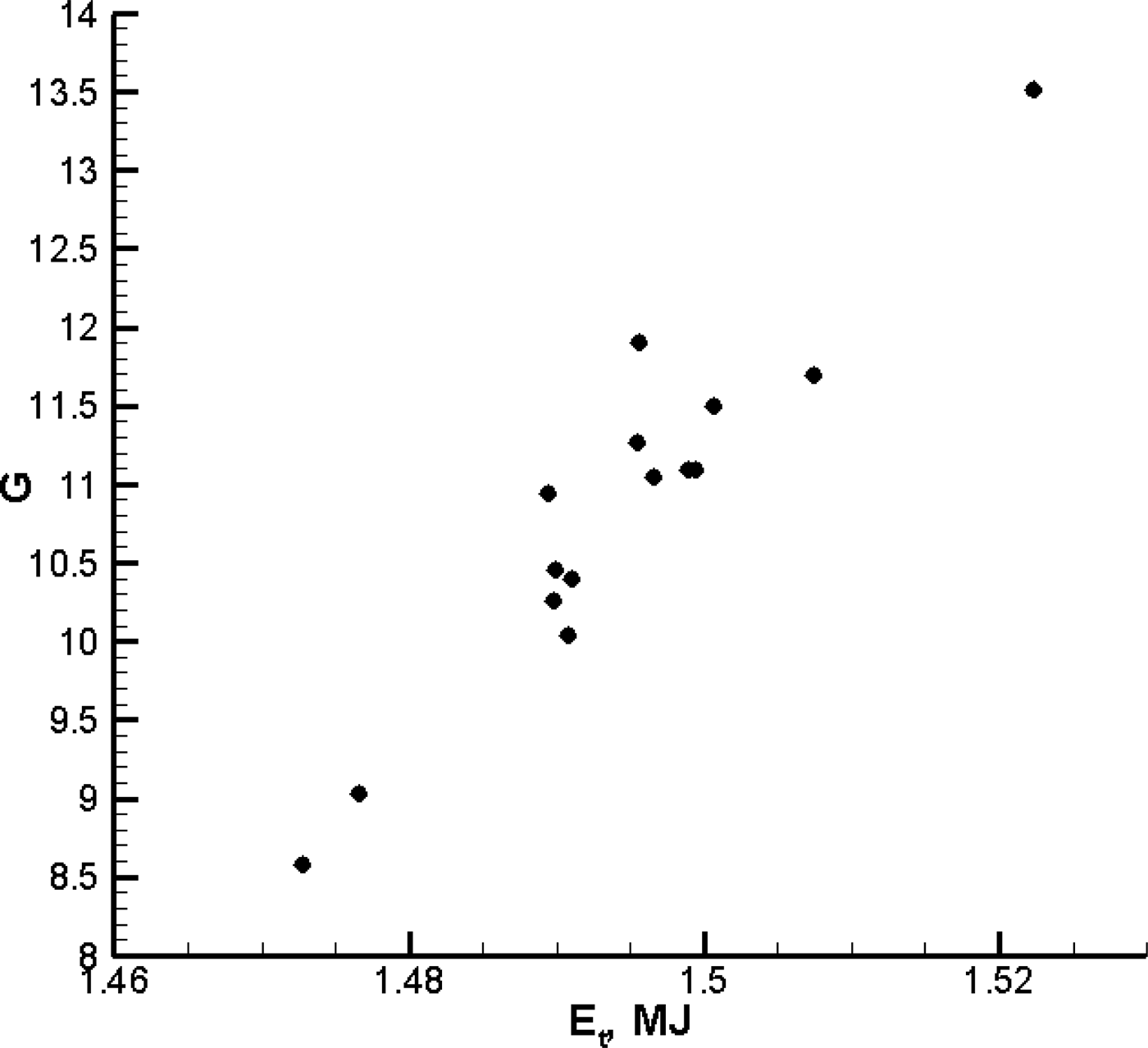
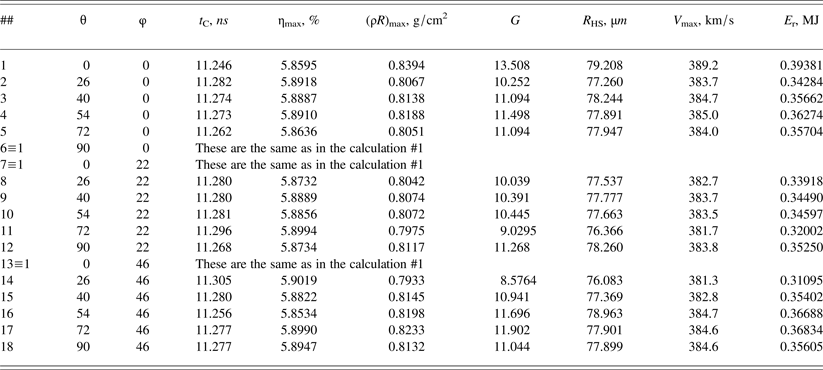
For the 18 points on the sphere chosen in the previous section, characterized by the angles θ = 0, 26, 40, 54, 72, and 90, and φ = 0, 22, and 46, 1D calculations of baseline target compression and burning with the parameters that are discussed in Section 1 were carried out using the DIANA program (Zmitrenko et al., Reference Zmitrenko, Karpov, Fadeev, Shelaputin and Shpatakovskaya1983). For simulations of target compression this Lagrangian numerical code uses one-fluid two-temperature model and also takes into account electron and ion heat transfer, the exchange of energy between ion and electron components, local energy deposition from thermonuclear reactions, burning out of DT-fuel, volume energy losses due to bulk emission, and incident laser flux absorption due to inverse Bremsstrahlung mechanism and resonant one in the vicinity of critical density. The main difference between performed series of calculations in comparison with the previous one (Rozanov et al., Reference Rozanov, Gus'kov, Vergunova, Demchenko, Stepanov, Doskoch, Yakhin and Zmitrenko2015) is that the absorption of the laser radiation is δ-shaped manner on the surface of the target, where the density is about 76% of the critical one which corresponds to the second harmonic Nd-laser radiation. The following Table 2 shows the basic quantities characterizing the compression and burning of the target for each of the calculations. In all calculations, taking into account the variations in the absorption coefficient depending on the position of the point on the sphere, the value of the target thermonuclear gain G varied in the range of 8–14, and the absorbed energy E _t in the range 1.47–1.53 MJ. Below in Figure 7 dependency of the gain on the absorbed energy (i.e., irradiation conditions) is presented which characterizes the spreading values of G in the conducted series of 1D calculations.

Fig. 7. Distribution of the thermonuclear gain G of conducted 1D calculations depending on the absorbed laser energy E _t.

Table 2. Integral characteristics of 1D numerical simulations corresponding to different pairs of angles (θ, φ). Here η _max (%) is the maximal hydro-efficiency, (ρR)_max, the maximal optical thickness of the region occupied by DT, G, the thermonuclear gain, E _r, the radiation energy losses, t _C, the collapse time, R _HS, the radius of the hot-spot defined by ion temperature 7 keV, V _max, the maximal velocity of implosion

Let us analyze the scale of the differences between the calculations due to the inhomogeneity of irradiation of the target using the radius of the outer surface of DT-ice, taken at the time moment t = 10 ns. The values between the points on the sphere, which correspond to 1D calculations are determined by interpolation using cubic splines (Kalitkin, Reference Kalitkin1978). The resulting distribution of radius values is shown in Figure 8. It is seen that the spread of these values is calculated by the formula δ_ψ = 2(ψ_max − ψ_min)/(ψ_max + ψ_min), where ψ≡R _DT/CH is 2%, which indicates a relatively weak influence of irradiation asymmetry on the target compression dynamics. Note that, as expected, the resulting distribution of radii is correlated with absorbed energy map as shown in Figure 3: Points with a smaller radius correspond to large values of absorbed energy.

Fig. 8. Distribution of the radii of DT-ice outer surface at the time moment t = 10 ns.

Such an interpolation procedure may be performed for other values. For example, the dispersion values of the radial velocity at the surface of the DT-ice/ablator are 6 km/s (δ_V ≈ 1.7%), density, 0.61 g/cc (δ_ρ ≈ 4%), pressure, 15.1 Mbar (δ_p ≈ 8%). The data in Table 2 show some impact of the considered irradiation conditions on the parameters characterizing a 1D spherical compression and burning of the target, but they do not lead to the disruption of ignition.

Let us analyze the conditions for the development of instabilities in the calculation example # 1 in Table 2. We shall follow up the values of density, pressure, velocity, temperature, acceleration, and adiabatic curve at a point inside DT-layer, namely, at a distance of 1443 µm from the center at the initial time moment. These dependences are shown in Figure 9. Areas of positive acceleration in Figure 9b correspond to deceleration of inward motion of DT-layer and cause instabilities development. For these conditions of laser energy absorption the collapse of the target occurs approximately at time t = 11.25 ns, followed by the explosion, which is not discussed in this work.

Fig. 9. Time dependencies (а) pressure, density, and radial velocity, (b) acceleration, (c) the parameter α = p/p _F, (d) ion and electron temperature, (e) R-t diagram of inner and outer boundary of the DT-layer.

With the data presented in Figure 9, one can say that at the moment of maximum compression (t = 11.25 ns) radius of the inner surface of DT-layer is $R_{{\rm min}}^{{\rm inner}} \approx 50\;{\rm \mu m}$, and the outer one is approximately $R_{{\rm min}}^{{\rm outer}} \approx 130\;{\rm \mu m}$. Classic increment of Rayleigh–Taylor instability is given by the formula ${\rm \gamma} _0^2 = kA{g_0}$, where A, Atwood number, k, wave vector and can be calculated by referring to Figure 9b. The average value of the deceleration is found to be g ₀ ≡ 〈a〉5.10⁵ cm/μs², the duration of which is about Δt ≈ 0.1 ns. According to the data of the irradiation inhomogeneity one can estimate the most significant for instability development wavenumber of spherical harmonic as l ≈ 8–10. Assuming for estimates A ≈ 1 and $k \approx {l / R}_{{\rm min}}^{{\rm outer}} $ we get γ₀ ≈ 20 ns⁻¹ and growth factor Γ = γ₀Δt ≈ 2. Note that this is a very modest value. Thus, the initial perturbation of the shell with amplitude equal ΔR/2 ≈ 5 µm (see Fig. 8) grows approximately 7.4 times, reaching a value of about 40 µm when the DT-ice shell thickness is about 80 µm (see Figure 9e) at the time moment t = 11.25 ns. This means that there is strong mixing of ablator with the fuel.

Note that the estimations of the instability development were performed using linear theory which is not quite true. Namely, the characteristic wavelength is λ_c ≈ R _min/l ≈ 10 µm that is of the same order as the initial amplitude. As it is known, the development of hydrodynamic instability at the nonlinear stage is significantly slower than at the linear one (Kuchugov et al., Reference Kuchugov, Zmitrenko, Rozanov, Yanilkin, Sin'kova, Statsenko and Chernyshova2012).

Thus it is evident that the development of instability in these irradiation conditions can lead to significant performance degradation of 1D compression. Further studies carried out using 2 and 3D hydrodynamic codes demonstrate influence extent of instabilities on the compression and burning of the target.

4. 2D SIMULATIONS

In the previous section we have shown that the results of the multi-dimensional (i.e., 2D and 3D) modeling will be substantially different from the 1D ones, showing close to the real dynamics of the compression and burning of thermonuclear target. The study of the processes in these cases gives a more complete and clear picture of the occurring physical phenomena. Note that in this case adequate description of the totality of the physical processes that may have not been implemented in (Edwards et al., Reference Edwards, Lindl, Spears, Weber, Atherton, Bleuel, Bradley, Callahan, Cerjan, Clark, Collins, Fair, Fortner, Glenzer, Haan, Hammel, Hamza, Hatchett, Izumi, Jacoby, Jones, Koch, Kozioziemski, Landen, Lerche, MacGowan, MacKinnon, Mapoles, Marinak, Moran, Moses, Munro, Schneider, Sepke, Shaughnessy, Springer, Tommasini, Bernstein, Stoeffl, Betti, Boehly, Sangster, Glebov, McKenty, Regan, Edgell, Knauer, Stoeckl, Harding, Batha, Grim, Herrmann, Kyrala, Wilke, Wilson, Frenje, Petrasso, Moreno, Huang, Chen, Giraldez, Kilkenny, Mauldin, Hein, Hoppe, Nikroo and Leeper2011, Reference Edwards, Patel, Lindl, Atherton, Glenzer, Haan, Kilkenny, Landen, Moses, Nikroo, Petrasso, Sangster, Springer, Batha, Benedetti, Bernstein, Betti, Bleuel, Boehly, Bradley, Caggiano, Callahan, Celliers, Cerjan, Chen, Clark, Collins, Dewald, Divol, Dixit, Doeppner, Edgell, Fair, Farrell, Fortner, Frenje, Gatu Johnson, Giraldez, Glebov, Grim, Hammel, Hamza, Harding, Hatchett, Hein, Herrmann, Hicks, Hinkel, Hoppe, Hsing, Izumi, Jacoby, Jones, Kalantar, Kauffman, Kline, Knauer, Koch, Kozioziemski, Kyrala, LaFortune, Le Pape, Leeper, Lerche, Ma, MacGowan, MacKinnon, Macphee, Mapoles, Marinak, Mauldin, McKenty, Meezan, Michel, Milovich, Moody, Moran, Munro, Olson, Opachich, Pak, Parham, Park, Ralph, Regan, Remington, Rinderknecht, Robey, Rosen, Ross, Salmonson, Sater, Schneider, Seguin, Sepke, Shaughnessy, Smalyuk, Spears, Stoeckl, Stoeffl, Suter, Thomas, Tommasini, Town, Weber, Wegner, Widman, Wilke, Wilson, Yeamans and Zylstra2013; Clark et al., Reference Clark, Hinkel, Eder, Jones, Haan, Hammel, Marinak, Milovich, Robey, Suter and Town2013) plays a decisive role. As a possible illustration we present here the results of 2D calculations made by NUTCY program (Tishkin et al., Reference Tishkin, Nikishin, Popov and Favorskii1995; Lebo & Tishkin, Reference Lebo and Tishkin2006), which takes into account the necessary physics, that is, the local energy deposition from thermonuclear reactions, the electron heat conductivity and asymmetry of target irradiation as well.

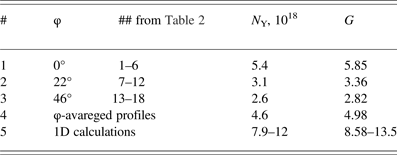
Formation of the initial setting for the 2D calculations was performed according to the (Gus'kov et al., Reference Gus'kov, Demchenko, Zhidkov, Zmitrenko, Litvin, Rozanov, Stepanov, Suslov and Yakhin2010). Using the data obtained from 1D calculations, which correspond to the individual points on the sphere, we have approximated the data between these points to get 2D distribution. The procedure was performed for the profiles of three different angles φ = 0.22 and 46°, as well as for φ-averaged profiles. The calculated neutron yield N _Y and thermonuclear gain G are presented in Table 3. The table shows the degradation of the burning conditions in comparison with 1D spherically symmetrical simulations discussed in Section 3 of this paper. In particular, it should be noted that the observed gain G is approximately two times smaller than the one obtained in 1D calculations.

Table 3. Neutron yield and thermonuclear gain for the series of 2D calculations in comparison with 1D ones

Figure 10 illustrates the density and temperature distributions at the time moment close to the target collapse for #1 and 3 calculations in Table 3 which received the highest and lowest values of the gain coefficient, respectively. A comparison of these two variants gives the following result. In case #3 the temperature drop in the central area is observed because of intense development of instabilities and mixing (as a consequence of more inhomogeneous irradiation), and this results in the decrease of the rate 〈σv〉 _DT of the main thermonuclear reaction (Kozlov, Reference Kozlov1962; Dolgoleva & Zabrodina, Reference Dolgoleva and Zabrodina2014). So, a slight inhomogeneity of irradiation leads to a significant decrease in the gain coefficient. However, the proposed target design remains to be applicable, that is, it is ignited.

Fig. 10. Density and temperature distributions obtained in #1 (a) and #3 (b) calculations from Table 3 at the time moment t = 11.1 ns close to the target collapse.

5. A STEP TO FULL 3D PROCESS DESCRIPTION

3D simulations are one more step to a deeper understanding of the real process of thermonuclear target implosion. Mathematical modeling in this case presents an individual applied problem and is rather resource-intensive. In this paper we would like to give an example of a carried out 3D hydrodynamic calculation of target compression without heat conductivity and thermonuclear burning taken into account which, however, is indicative of the need to account of 3D effects.

Just as it was earlier (Gus'kov et al., Reference Gus'kov, Demchenko, Zhidkov, Zmitrenko, Litvin, Rozanov, Stepanov, Suslov and Yakhin2010), we take as the initial data for 3D simulation the distributions from the 1D calculation at the time moment corresponding to the time when the target shell deceleration starts. For the discussed target this moment precedes the target collapse by 1 ns, and defines the end of the laser pulse. A possibility of spherical target compression modeling with the help of the Euler code NUT-GPU (Kuchugov, Reference Kuchugov2014; Kuchugov et al., Reference Kuchugov, Shuvalov and Kazenov2014) in Cartesian coordinates was discussed in (Rozanov et al., Reference Rozanov, Zmitrenko, Kuchugov, Stepanov, Statsenko, Yanilkin and Yakhin2014). To demonstrate the experimentally realized surface shape, let us consider the model perturbation of DT-shell radial velocity. The perturbation amplitude constitutes 4% of 1D calculation value, that is, $U_{\rm r}^{3{\rm D}} = U_{\rm r}^{1{\rm D}} \left[ {1 + 0.04Y_8^6 ({\rm \theta}, {\rm \phi} )} \right]$, where $Y_{\rm l}^{\rm m} ({\rm \theta}, {\rm \phi} )$ is a spherical harmonic. The simulation area is a cube with a side 0.9 cm, and the target is placed in its center. The cube side contains 640 cells of a computational grid.

In Figure 11 the density isolines with markers (left column) which correspond to DT-gas/DT-ice and DT-ice/ablator (CH) interfaces, and the isolines of radial velocity (right column) at the time moment t = 11.1 ns close to the target collapse are shown. The presented pictures demonstrate a typical Rayleigh–Taylor instability flow. The bubbles of a less dense matter are formed, and they penetrate through a denser matter which is still moving to the center. In the bubble tips the closest convergence of the inner and outer surface of DT-shell is observed, and there is a tendency to its destruction.

Fig. 11. Density and radial velocity isolines in plane cross-sections y = xtg(φ), φ = 0° (the upper line) и φ = 40° (the bottom line) at the time moment t = 11.1 ns. Black and white points correspond to the inner and outer boundaries of DT-layer.

Note again that in the problem of thermonuclear fusion ignition it is absolutely essential that high velocity of the matter (or its part), that is, the kinetic energy, acquired due to external influence should be effectively converted into the internal one. This requires a fairly high degree of spherical symmetry of motion at all stages of implosion. As soon as the symmetry is violated, the conditions of energy conversion are becoming much worse. This is clearly seen in 2D problem (see Section 4) and, especially, in 3D one. The given example of 3D simulation confirms this statement, and shows complicated flow due to simple initial perturbations and at the same time the general symmetry of motion remains quite good. One can easily imagine the situation when not two counter-propagating jets (i.e., high-density areas) will collide, but the jets and the areas between the jets, and this will far more worsen the conditions of kinetic energy conversion into the potential one. Similar ideas have been put forward in a recent paper (Taylor & Chittenden, Reference Taylor and Chittenden2014), and the nature of such situations has been explained by the mode interaction in the real multimode initial perturbations. In future we are planning such 3D simulations in order to define quantitative parameters of thermonuclear target compression.

Fig. 12. Scale of convergence of inner and outer surface of the DT-ice layer in the bubble tips.