1. INTRODUCTION
Short-pulse lasers may be potentially useful as a time and space resolved diagnostic for inertial confinement fusion (lCF) experiment (Hinkel et al., Reference Hinkel, Williams and Berger1995). In the interaction of intense short-pulse laser with a plasma, the electron cloud is instantly and without thermal losses receiving the acceleration in the laser field by direct conversion of nearly 100 percent of laser energy into mechanical motion and accelerate up to 1020 cm/s2 (Hora, Reference Hora2012). When the plasma is heated by relativistic laser beam, it may excite the natural modes of vibration of the plasma, that is, the electron plasma wave and ions waves. This electron plasma wave can have a very high phase velocity (on the order of the velocity of light), and so can produce very energetic electrons when it damps. Such electrons can preheat the fuel in laser fusion applications. During this process, various parametric instabilities (filamentation, stimulated Raman scattering, stimulated Brillouin scattering, etc.) take place and due to this, energy of high power laser beam is not efficiently coupled to the plasma (Kruer, 1996; Purohit et al., Reference Purohit, Chauhan and Sharma2008). Brillouin scattering occurs in the interaction of picosecond laser pulse with a plasma that involves the coupling of large amplitude light wave into a scattered light wave plus an ion acoustic wave (IAW). Previous researches have shown that this scattering leads to an instability with specific growth rate in plasma. Stimulated Brillouin scattering (SBS) plays an important role in laser-plasma interaction as it produces a backscattered light and therefore this process is one of the real threat to the inertial confinement fusion research. The control of the SBS instability remains as one of the key issues for the success of the laser fusion. SBS in a plasma is the decay of an incident (pump) light wave into a frequency downshifted (Stokes) light wave and an ion-acoustic wave (IAW) (Yin et al., Reference Yin, Albright and Bowers2007). In this process, laser light interacts with an ion acoustic wave and is scattered backward. The scattered wave and the laser pump exert a ponderomotive force on the electrons, driving the acoustic wave (Kar et al., Reference Kar, Tripathi and Sawhney2002). SBS is important in the ICF experiments because it scatters the laser beams away from the target, thereby reducing the energy available to drive the compressive heating of the nuclear fuel. Also, in the case of backward SBS, it causes laser's reflection and leads to a net energy loss (Chen et al., 1985; Kruer, Reference Kruer1998; Jaimana et al., Reference Jaiman and Tripathi1998; Bernhardt et al., Reference Bernhardt and Selcher2010). The SBS instability occurs over a wide range of electron density up to the critical layer (Kruer, Reference Kruer1998). For most plasma conditions and laser intensities of interest in linear regime, the SBS growth time is on the order of a picosecond (Baton et al., Reference Baton, Rousseaux, Mounaix, Labaune, Fontaine, Pesme, Renard, Gary, Louis-Jacquet and Baldis1994).
Brillouin instability can be most simply characterized as the resonant decay of an incident photon with frequency ω0 and wave number k 0 into a scattered photon with frequency ωs and wave number k s plus an ion acoustic photon. The frequency and wave number matching conditions then are, (ω0 = ωs + ω) and (k0 = ks + k). Where, ω and k are the frequency and wave number of the ion acoustic wave. Since the frequency of an ion acoustic wave is much less than ω0, it is clear that this instability can occur throughout the underdense plasma. Furthermore, nearly all the energy can be transferred to the scattered light wave.
When laser beam propagates through plasma, the motion of electron will be modified according to the nonlinearity present in the plasma and will give rise to changes in the dispersion of the laser beam and nonlinear current density. Nonlinear interaction of seed IAW with the laser beam leads to its in which IAW gets excited due to nonlinear coupling with high-power laser beam because of ponderomotive nonlinearity (Shrama et al., Reference Sharma, Bhardwaj and Sharma2012).
In collisionless plasmas, the nonlinearity arises through the ponderomotive force-induced redistribution of plasma (Sharma et al., Reference Sharma, Sharma, Chauhan and Ji2010). This nonlinarity is very important in a laser fusion experiment where plasma blocks are generated and accelerated by the nonlinear ponderomotive force, which leads to the heating of the fuel in the fast ignition (Hora, Reference Hora2005; Reference Hora2009).
The SBS instability has been extensively studied in magnetized and unmagnetized plasmas for many years both theoretically and experimentally (Kong et al., Reference Kong, Yoon, Beak, Shin, Lee and Lee2007; Wang et al., Reference Wang, Lu, He, Zheng and Zhao2009; Bernhardt et al., Reference Bernhardt and Selcher2010; Froula et al., Reference Froula, Divol, MacKinnon, Gregori and Glenzer2003). Magnetic fields play an important role in many nonlinear interactions such as excitation of an upper hybrid waves (UHW) to heat the plasma near upper hybrid frequency (Purohit et al., 2009). In first efforts on stimulated Brillouin scattering, Grebogi and Liu (Reference Grebogi and Liu1980), considered propagation of an extraordinary electromagnetic pump wave incident on a magnetized plasma where the static magnetic field was in axial direction. Their results displayed that the magnetic field reduces the threshold for Brillouin backscattering by the lower hybrid wave. Salimullah et al. (Reference Salimullah, Liu and Haines1984), made a theoretical investigation about the stimulated Raman and Brillouin backscattering of laser radiation at the upper hybrid frequency in a laser-produced plasma. They ignored relativistic effects and employed a nonlinear Vlasov equation to obtain the growth rate of Raman and Brillouin backscattering in a plasma produced by CO2 and Nd-glass lasers. Their results show that the Brillouin backward scattering (BBS) growth rate increases with the increasing density of electrons in plasma. They also observed that the growth rate increases with the self-generated magnetic field (on the order of a few megagauss). In another work, Salimullah et al. (Reference Salimullah and Hassan1990) investigated the relativistic effect on the stimulated scattering of large amplitude laser radiation in the presence of the self-generated magnetic field in a laser-produced plasma. They noted that the extreme relativistic effect increases the growth rates of the stimulated scattering. They also noticed that the self-generated magnetic field does not have appreciable effects on these stimulated scatterings. Baton et al. (Reference Baton, Rousseaux, Mounaix, Labaune, Fontaine, Pesme, Renard, Gary, Louis-Jacquet and Baldis1994), developed an experimental study of SBS with a 1 ps laser pulse in a large underdense preformed plasma. They show that the SBS reflectivity increases from 10−4 to 10−1 as the intensity of the interaction beam rises from 5 × 1014 to 5 × 1016 W/cm2. Salimullah et al. (Reference Salimullah, Ferdousi and Majid1994) studied the phenomenon of SBS of a large-amplitude extraordinary electromagnetic wave by the electron acoustic wave in a piezoelectric semiconductor plasma in the presence of an external uniform magnetic field. They solved the Boltzmann equation with a Krook model for the collisional term in the guiding center coordinates for the nonlinear response of the plasma electrons. It was noticed that the threshold power density for the SBS decreases rapidly with the increase of magnetic field. It was reported that the growth rate of the SBS of high-frequency laser radiation is directly proportional to the pump-induced drift velocity of electrons and also it increases with the plasma density and increases rapidly with the increase of the external magnetic field. Shalabi and Al-Khateeb (Reference Shalabi and Al-Khateeb2001), studied Brillouin backscattering instability in inhomogeneous collisional plasma with linear density ramp. They concluded that the presence of collisions leads to a reduction in both the growth rate and the amplification factor, where the threshold intensity for the instability to occur increases. Froula et al. (Reference Froula, Divol, Braun, Cohen, Gregori, Mackinnon, Williams, Baldis, Montgomery and Johnson2003) reported the first direct evidence of detuning of SBS by a velocity gradient, which was achieved by directly measuring the frequency shift of the SBS-driven acoustic wave relative to the local resonant acoustic frequency. It was found that in the expanding part of the plasma, ion-acoustic waves are driven off resonance by the ponderomotive force, which leads to the saturation of the SBS instability. In another experimental study, Froula et al. (Reference Froula, Divol, Braun, Cohen, Gregori, Mackinnon, Williams, Baldis, Montgomery and Johnson2003) investigated the effects of velocity gradients and kinetic effects on the saturation of ion-acoustic waves in a plasma. They found that in a linear regime, SBS is moderated primarily by velocity gradients, while for intensities above this threshold, nonlinear trapping is relevant. Bawaaneh et al. (Reference Bawa'neh2006) have investigated the problem of SBS of an extraordinary light wave from a linear magnetized plasma in nonrelativistic regime. They show that small values of static magnetic field increases the BBS instability growth rate, while high magnetic fields reduce the instability bringing it to zero at a cut-off field where the cut-off field is just above 200 KG. Gao et al. (2011) proposed a new approach to measure SBS threshold based on the output energy characteristic of SBS optical limiting. They found out that the SBS threshold should be estimated according to the medium properties, length, and the wavelength in order to determine the optimum working point of the amplifier. Recently, Sharma et al. (Reference Sharma, Bhardwaj and Sharma2012) have considered the propagation of high power laser beam in the presence of ponderomotive nonlinearity. It is observed that the spitted profile of the laser beam modify the process of excitation ion acoustic wave. This modified profile of the laser beam affects the nonlinear coupling between the laser beam and IAW. In the previous works, nonlinear effects of BBS are presented for lower order computations or simulations. Most of the above mentioned works on Brillouin scattering of the laser beam has not included the relativistic and nonlinear effects simultaneously.
In this present theoretical work, the growth rate of BBS instability is calculated in a plasma by taking into account the relativistic and nonlinearity effects up the third order. It is assumed that plasma is affected by an external static magnetic field perpendicular to the direction of laser pulse propagation. Also, plasma electrons have a significant mass increase from their relativistic quiver velocity in the pump field. In this work, we have considered both weakly relativistic and ponderomotive nonlinearities as well as the nonlinearity due to high orders of external magnetic field. In Section 2, a model is introduced based on the laser plasma interaction. In Section 3, methods and calculations are presented. Section 4 is devoted to results and discussion and finally, conclusion is presented in Section 5. It should be stressed here that the present treatment ignores the effect of self-focusing and nonlocal effects as well, hence is valid when the laser spot size is much bigger than c/ωp.
2. THE METHOD
Here, propagation of an intense short laser pulse is going to be considered in an underdense transversely magnetized plasma in a weakly relativistic regime. In this model, we have assumed a linearly polarized ordinary light wave in the form 
${\bf E}\lpar z\comma \; t\rpar = {\widehat x} E_0 \lpar z\rpar \cos\lpar k_0 z - {\rm \omega}_0 t\rpar $ with angular frequency ω0 that propagates in the +z direction in a transversely magnetized plasma. Interaction region of the laser pulse with plasma is imbedded in an external magnetic field of 
${\bf B} = B_0 {\widehat y}$.
The wave equation governing the propagation of the laser pulse through the plasma medium, the Lorentz force equation for plasma electrons and the continuity equation, respectively have the form of
$$\lpar \nabla ^2 - \displaystyle{1 \over {c^2 }}\displaystyle{{\partial ^2 } \over {\partial t^2 }}\rpar {\bf E} = \displaystyle{{4{\rm \pi} } \over {c^2 }}\displaystyle{{\partial {\bf J}} \over {\partial t}}\comma \;$$
$$\displaystyle{d \over {dt}}\lpar {\rm \gamma} {\bf v}\rpar = - \displaystyle{e \over m}\lpar {\bf E} + {\bf v} \times \lpar {\bf B}+{\bf B}_0 \rpar \rpar \comma \;$$
$$\displaystyle{{\partial n} \over {\partial t}} + \nabla .\lpar n{\bf v}\rpar = 0.$$ Here, J = −ne v is the plasma electron current density in which n is the electron density and v is the velocity of plasma electrons. 
${\bf B} = B{\widehat y}$ is the magnetic field of the laser pulse, and γ is the relativistic factor of electron motion. Using Eq. (1) and Eq. (2), we can find the nonlinear current density of plasma electrons up to the third order in the laser pulse radiation field (Paknezhad & Dorranian, Reference Paknezhad and Dorranian2011),
$$J_{\rm x} = - enca_0 u_0 \lpar {\rm \omega} _0\rpar \sin\lpar k_0 z - {\rm \omega} _0 t\rpar \comma \;$$where u 0 (ω0) = ω02/(ω02 − ωc 2) − N 0a 02, in which coefficient N 0 has the form of
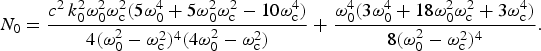$$N_0 = \displaystyle{{c^2\, k_0^2 {\rm \omega} _0^2 {\rm \omega} _{\rm c}^2 \lpar 5{\rm \omega} _0^4+5{\rm \omega} _0^2 {\rm \omega} _{\rm c}^2 - 10{\rm \omega} _{\rm c}^4 \rpar } \over {4\lpar {\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 \rpar ^4 \lpar 4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 \rpar }}+\displaystyle{{{\rm \omega} _0^4 \lpar 3{\rm \omega} _0^4+18{\rm \omega} _0^2 {\rm \omega} _{\rm c}^2+3{\rm \omega} _{\rm c}^4 \rpar } \over {8\lpar {\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 \rpar ^4 }}.$$Here, ωc(=eB/m) is the electron cyclotron frequency and N 0 is the nonlinear coefficient of the pump wave. Now, using E0 = −c −1 ∂A0/∂t (A0 is the vector potential) and by applying Eq. (4) in Eq. (1), we can obtain the nonlinear wave equation for the vector potential of the propagated wave
$$\lpar \displaystyle{{\partial ^2 } \over {\partial t^2 }} - c^2 \nabla ^2 \rpar {\bf A}_0 = - \displaystyle{{4{\rm \pi} ne^2 } \over m}u_0 \lpar {\rm \omega} _0 \rpar {\bf A}_0.$$3. CALCULATIONS
3.1. Perturbational Coupled Equations
To obtain the coupled equation describing the Brillouin instability, we consider the response of an initially uniform plasma driven by a large amplitude light wave. Scattering of the electromagnetic pump wave in the interaction of laser pulse with plasma will generate another electromagnetic wave with frequency close to the pump wave frequency plus an excited plasma wave as perturbations in plasma. Perturbed quantities can be contributed in the form of 
${\bf A} = {\bf A}_0 + {\tilde {\bf A}}$ and 
$n = n_0 + \tilde n$, which leads to the growth of instability in a plasma. So, 
${\tilde {\bf A}}$, the amplitude of perturbation i.e., scattered electromagnetic wave, is another answer of Eq. (6). In this new case, the current density can be written as 
${\tilde {\bf J}} = - \tilde ne{\bf v}_{0 \bot} - n_0 e \mathop {{\tilde {\bf v}}}\nolimits_{\bot}$. Then Eq. (6) can be presented in its new form
$$\bigg( \displaystyle{{\partial ^2 } \over {\partial t^2 }} - c^2 \nabla ^2 \bigg) {\tilde {\bf A}}=- \displaystyle{{4{\rm \pi} n_0 e^2 } \over m}u\lpar \tilde {\rm \omega} \rpar {\tilde {\bf A}} - \displaystyle{{4{\rm \pi} \tilde ne^2 } \over m}u\lpar {\rm \omega} _0 \rpar {\bf A}_0\comma \;$$
where, 
$u\lpar \tilde {\rm \omega} \rpar = \mathop {\tilde {\rm \omega} }\nolimits^2 /\lpar \mathop {\tilde {\rm \omega} }\nolimits^2 - {\rm \omega} _{\rm c}^2 \rpar - Na^2 $. Here, N, the nonlinear coefficient of scattered wave, can be obtained by substituting k0 and ω0 with k and 
$\tilde {\rm \omega} $ in N 0 definition. 
$\tilde {\rm \omega} $, k and a are the angular frequency, wave vector and normalized vector potential of the scattered wave, respectively. Only the fluctuation in electron density appears in Eq. (7), since the ion response to the light frequency field of the light wave is less than the electron response by Zm/M, where Z is the charge state, m is the electron mass, and M is the ion mass. Using the perturbed quantities in the continuity equation and in the equation of motion we have
$$\displaystyle{{\partial \tilde n} \over {\partial t}}+n_0 \nabla .\mathop {{\tilde {\bf v}}}\nolimits_{\rm e} = 0\comma \;$$and
$$\displaystyle{{\partial \mathop {{\tilde {\bf v}}}\nolimits_e } \over {\partial t}} + \mathop {{\tilde {\bf v}}}\nolimits_{\rm e} .\nabla \mathop {{\tilde {\bf v}}}\nolimits_{\rm e} = - \displaystyle{e \over m}\lpar {\bf E}+\displaystyle{{{\bf v}_{\rm e} \times \lpar {\bf B}+{\bf B}_0 \rpar } \over c}\rpar - \displaystyle{{\nabla \tilde p} \over {n_e m_e }}.$$ For the Brillouin instability, the density fluctuation 
$\tilde n$ is the low frequency fluctuation associated with an ion acoustic wave. We describe the electrons as a warm fluid and separate the fluid velocity v e into longitudinal and transverse components. Since, we are considering a low frequency fluctuation, we neglect the electron inertia (
$\partial \mathop {{\tilde {\bf v}}}\nolimits_e /\partial t$ ) and use the isothermal equation of state (p e = nT e), where T e is the electron temperature. So, in the direction of laser pulse propagation, Eq. (9) becomes
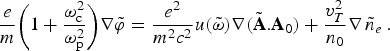$$\displaystyle{e \over m}\bigg( 1+\displaystyle{{{\rm \omega} _{\rm c}^2 } \over {{\rm \omega} _{\rm p}^2 }}\bigg) \nabla \tilde{\rm \varphi} = \displaystyle{{e^2 } \over {m^2 c^2 }}u\lpar \tilde{\rm \omega} \rpar \nabla \lpar {\tilde {\bf A}}.{\bf A}_0 \rpar + \displaystyle{{v_T^2 } \over {n_0 }}\nabla \mathop {\tilde n}\nolimits_e.$$ Where, 
${\tilde \varphi}$ is the electrostatic potential of plasma fluctuations. The first term in the right-hand-side of Eq. (10) arises due to the electrostatic fluctuations of electrons at the upper hybrid frequency, while the second term is due to the ponderomotive force exerted on plasma electrons in the interaction of pump and scattered light wave. To treat the ion response, we describe the ions as a charged fluid with density n i and velocity vi . The perturbed continuity and force equations are,
$$\displaystyle{{\partial \mathop {\tilde n}\nolimits_i } \over {\partial t}} + n_0 \nabla .\mathop {{\tilde {\bf v}}}\nolimits_i = 0\comma \;$$
$$\displaystyle{{\partial \mathop {{\tilde {\bf v}}}\nolimits_i } \over {\partial t}} = - \displaystyle{{Ze} \over M}\nabla \tilde {\rm \varphi}+\displaystyle{e \over {Mc}}\lpar \mathop {{\tilde {\bf v}}}\nolimits_i \times \;{\bf B}_0\rpar.$$Here, we have neglected the ion pressure for simplicity. Taking a time derivative of Eq. (11), a divergence of x and z components Eq. (12) and combining them gives:
$$\displaystyle{{\partial ^2 \mathop {\tilde n}\nolimits_i } \over {\partial t^2 }} = \displaystyle{{n_{0i} Ze} \over M}\nabla ^2 \tilde {\rm \varphi} - \Omega _c^2 \mathop {\tilde n}\nolimits_i.$$ Where, Ωc (= eB 0/Mc) is the ion cyclotron frequency. If we substitute for 
$\tilde {\rm \varphi} $ using Eq. (10), we finally obtain an equation for the low frequency density fluctuation
$$\lsqb \displaystyle{{\partial ^2 } \over {\partial t^2 }}+\Omega _c^2 - c_s^2 \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}\nabla ^2 \rsqb \mathop {\tilde n}\nolimits_e = \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}\displaystyle{{n_0 Ze^2 } \over {mMc^2 }}u\lpar \tilde {\rm \omega} \rpar \nabla ^2 \lpar {\bf A}_0 .{\tilde {\bf A}}\rpar.$$Here, c s = (ZT e/M)1/2 is the ion acoustic velocity. Eq. (14) describes the excitation of an ion acoustic wave by the interaction between the incident and scattered light waves. Eqs. (7) and (14), which are two nonlinear coupled equations for perturbed scattered light wave and perturbed electron density in a magnetized plasma, can be simultaneously solved to investigate the Brillouin instabilities in the laser-plasma interaction.
3.2. Instability Analysis
Brillouin scattering process in the transversely magnetized plasma includes the decay of a large-amplitude electromagnetic pump wave into low-frequency electrostatic ion-acoustic and electrostatic ion cyclotron waves plus two scattered Stokes/anti-Stokes sidebands (Jaiman et al., Reference Jaiman and Tripathi1998; Shukla et al., Reference Shukla and Stenflo2010; Bernhardt et al., Reference Bernhardt and Selcher2010). The laser and sidebands exert a pondermotive force on electrons driving electrostatic waves. The scattered wave and the pump wave provide oscillatory velocities to electrons parallel to the static magnetic field. They also exert a parallel pondermotive force on the electrons driving an ion acoustic wave whose frequency is much less than the pump frequency. The density perturbation associated with the ion acoustic wave couples with the oscillatory velocity due to the pump to produce a nonlinear current, driving the sideband wave (Jaiman et al., Reference Jaiman and Tripathi1998). We assume that both scattered light waves (Stokes/anti-Stokes) have linearly polarization as same as the pump wave. So, the required quantities including the vector potentials of incident electromagnetic wave and scattered light wave as well as density perturbation that can be assumed as
$${\bf A}_0 = \displaystyle{1 \over 2}{\bf A}_0 \lpar z\comma \; t\rpar e^{i {\rm \theta} _0 } + c.c.$$
$${\tilde {\bf A}} = \displaystyle{1 \over 2}{\tilde {\bf A}}\lpar z\comma \; t\rpar e^{i {\rm \theta}_ \pm } + c.c.$$
$$\tilde n = \displaystyle{1 \over 2}\tilde n\lpar z\comma \; t\rpar e^{i{\rm \theta} } + c.c.$$
where, θ0 = k 0z − ω0t, θ± = k ±z − ω±t, and θ = kz − ωt are the phases of electrical pump wave, scattered sidebands (Stokes/anti-Stokes) and perturbation oscillation, respectively. In backward Brillouin scattering for the right-hand plane wave, we have 
${\bf A}_0 .{\tilde {\bf A}} = A_0 \tilde A$ and using Fourier transformation, we can find equations for the amplitudes 
$\tilde A\lpar k_\pm\comma \; {\rm \omega}_\pm \rpar $ by substituting Eqs. (15), (16), and (17) into Eq. (7), looking for e iθ± dependence. So we can deduce the following term
$$\lsqb {\rm \omega} _ \pm ^2 - c^2\, k_ \pm ^2 - u\lpar {\rm \omega} _ \pm \rpar {\rm \omega} _{\rm p}^2 \rsqb \tilde A\lpar k_ \pm\comma \; {\rm \omega} _ \pm \rpar = \displaystyle{{2{\rm \pi} e^2 } \over m}u\lpar {\rm \omega} _0 \rpar A_0 \tilde n\lpar k\comma \; {\rm \omega}\rpar.$$ A similar equation for 
$\tilde n\lpar k\comma \; {\rm \omega} \rpar $ can be derived by seeking e iθ dependence in Eq. (14).
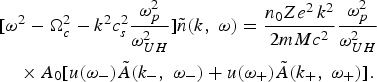$$\eqalign{& \lsqb {\rm \omega} ^2 - \Omega _c^2 - k^2 c_s^2 \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}\rsqb \tilde n\lpar k\comma \; {\rm \omega} \rpar = \displaystyle{{n_0 Ze^2\, k^2 } \over {2mMc^2 }}\displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }} \cr & \quad \times A_0 \lsqb u\lpar {\rm \omega} _ - \rpar \tilde A\lpar k_ -\comma \; {\rm \omega} _ - \rpar +u\lpar {\rm \omega} _+\rpar \tilde A\lpar k_+\comma \; {\rm \omega} _+\rpar \rsqb .}$$ As it can be observed, the first harmonic of the Stokes electromagnetic wave with 
$\tilde A\lpar k_-\comma \; {\rm \omega}_ - \rpar $ amplitude and anti-Stokes electromagnetic wave with 
$\tilde A\lpar k_+\comma \; {\rm \omega} _+\rpar $ amplitude are resulting from the beating of the pump wave and perturbated scattered wave, which are generated in plasma with angular frequency of 
$\tilde {\rm \omega}={\rm \omega} _ \pm = {\rm \omega} _0 \pm {\rm \omega} $ and wave vector of 
$\tilde k=k_ \pm = k_0 \pm k$. By combining Eq. (18) and Eq. (19), the dispersion relation can be found as
$${\rm \omega} ^2 - \Omega _c^2 - k^2 c_s^2 \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }} = \displaystyle{{k^2 v_{{\rm os}}^2 \Omega _{\rm p}^2 } \over {4u\lpar {\rm \omega} _0 \rpar }}\displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}\lsqb \displaystyle{{u\lpar {\rm \omega} _+\rpar } \over {D\lpar k_+\comma \; {\rm \omega} _+\rpar }}+\displaystyle{{u\lpar {\rm \omega} _ - \rpar } \over {D\lpar k_ -+{\rm \omega} _ - \rpar }}\rsqb.$$ Where, 
$\Omega _{\rm p} \lpar\!\! = {\rm \omega} _p \sqrt{\displaystyle{{Zm} \over M}}\rpar $ is the plasma ion frequency. To calculate Eq. (20), the effect of second and higher harmonics generation are neglected. Here, D(k −, ω−) and D(k +, ω+) are the dispersion coefficients of Stokes and anti-Stokes waves, respectively, which can be defined as
$$D\lpar k_ \pm\comma \; {\rm \omega}_ \pm \rpar = {\rm \omega}_ \pm ^2 - c^2\, k_ \pm ^2 - u\lpar {\rm \omega} _\pm \rpar {\rm \omega} _{\rm p}^2.$$Maximum growth clearly occurs for k such that the both scattered light wave and the exited electrostatic wave are resonant mode (ω = Ω, D(k −, ω−) = 0) i.e., when
$$\lpar {\rm \omega} _0 - \Omega \rpar ^2 - c^2 \lpar k - k_0 \rpar ^2 - u\lpar {\rm \omega} _0 - \Omega \rpar {\rm \omega} _{\rm p}^2 = 0.$$ Where,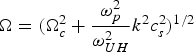 
$\Omega = \lpar \Omega _c^2 + {\displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}}k^2 c_s^2 \rpar ^{1/2}$.
The frequency matching condition for Stokes wave is ω− = ω0 − Ω and the wave number k is determined by Eq. (22). Assuming Ωc≪ω0, we obtain the wave number of the ion acoustic wave in a transversely magnetized plasma
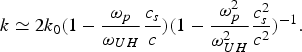$$k \simeq 2k_0 \lpar 1 - \displaystyle{{{\rm \omega} _p } \over {{\rm \omega} _{UH} }}\displaystyle{{c_s } \over c}\rpar \lpar 1 - \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}\displaystyle{{c_s^2 } \over {c^2 }}\rpar ^{ - 1}.$$In Figure 1, the normalized plasma frequency ωp/ω0 is plotted against the normalized wave number k/k 0 according to Eq. (23). As we know, value of the normalized wave number k/k 0 in an unmagnetized plasma is independent of the plasma density (Kruer, Reference Kruer1998). For a example, it is about k/k 0 = 1.96084 when c s/c = 0.02. However, in a magnetized plasma, it depends on the plasma frequency as well as the plasma electron cyclotron frequency. For instance, in a plasma with ωp/ω0 = 0.2, for two electron cyclotron frequencies ωc/ω0 = 0.1 and ωc/ω0 = 0.2, the value of k/k 0 is about 1.9649 and 1.9721, respectively. As it is apparent from Figure 1, increasing the external magnetic field, enhances the maximum value of k/k 0 in a magnetized plasma.
Fig. 1. Normalized plasma frequency versus normalized wave number of the excited plasma wave for two different magnetized plasma (ωc/ω0 = 0.1, ωc/ω0 = 0.2) when c s/c = 0.02 and a 0 = 0.2.
Instability growth rate is readily found from Eq. (20). For Brillouin back scatter, k is on the order of k 0 and so only the downshifted light wave needs be retained (Kruer, Reference Kruer1998),
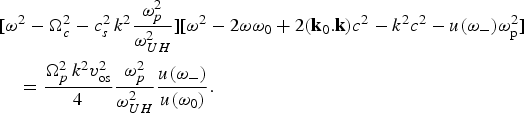$$\eqalign{& \lsqb {\rm \omega} ^2 - \Omega _c^2 - c_s^2\, k^2 \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}\rsqb \lsqb {\rm \omega} ^2 - 2{\rm \omega} {\rm \omega} _0 + 2\lpar {\bf k}_0 .{\bf k}\rpar c^2 - k^2 c^2 - u\lpar {\rm \omega} _ - \rpar {\rm \omega} _{\rm p}^2 \rsqb \cr & \quad = \displaystyle{{\Omega _p^2\, k^2 v_{{\rm os}}^2 } \over 4}\displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}\displaystyle{{u\lpar {\rm \omega} _ - \rpar } \over {u\lpar {\rm \omega} _0 \rpar }}.}$$We consider Brillouin backscatter, which has the largest growth rate. In first, the weak field limit in which ω = Ω + iγ, where γ≪kc s, Eq. (24) becomes
$$\eqalign{& 2i{\rm \gamma} \Omega \lsqb \!- 2i{\rm \omega} _0 {\rm \gamma} - 2{\rm \omega} _0 kc_s+2k_0 kc^2 - k^2 c^2 - u\lpar {\rm \omega} _ - \rpar {\rm \omega} _{\rm p}^2 \rsqb \cr & \quad = \displaystyle{{\Omega _p^2\, k^2 v_{{\rm os}}^2 } \over 4}\displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _{UH}^2 }}\displaystyle{{u\lpar {\rm \omega} _ - \rpar } \over {u\lpar {\rm \omega} _0 \rpar }}.}$$With assuming u(ω−) ≃ u(ω0) and using Eq. (23) we can obtain the growth rate of BBS instability from the real part of Eq. (25)
$${\rm \gamma} = \displaystyle{{k_0 v_{os} \Omega _p } \over {2\sqrt {{\rm \omega} _0 \Omega } }}\displaystyle{{{\rm \omega} _p } \over {{\rm \omega} _{UH} }}\lpar 1 - \displaystyle{{c_s } \over c}\displaystyle{{{\rm \omega} _p } \over {{\rm \omega} _{UH} }}\rpar.$$Eq. (26) can be simplified for different plasmas and conditions. In a underdense plasma, where v os = cu(ω0)a 0, (Paknezhad & Dorranian, Reference Paknezhad and Dorranian2011) so, the growth rate can be presented in a new form
$$\Gamma _{NBBS} = \displaystyle{{a_0 u\lpar {\rm \omega} _0 \rpar {\rm \omega} _0 \Omega _p } \over {2\sqrt {{\rm \omega} _0 \Omega } }}\displaystyle{{{\rm \omega} _p } \over {{\rm \omega} _{UH} }}\lpar 1 - \displaystyle{{c_s } \over c}\displaystyle{{{\rm \omega} _p } \over {{\rm \omega} _{UH} }}\rpar.$$Here, ΓNBBS is the temporal growth rate of nonlinear backward Brillouin instability in a weakly coupled (Γ≪ Ω and a 02 ≪ 1) magnetized plasma. By considering the effect of nonlinearity in the absence of external magnetic field, this growth rate reduces to the growth rate of BBS instability in a weakly coupled relativistic plasma as follow
$$\Gamma _{BBS} = \displaystyle{{a_0 } \over {2\sqrt 2 }}\lpar 1 - \displaystyle{3 \over 8}a_0^2 \rpar \lpar 1 - \displaystyle{{c_s } \over c}\rpar \displaystyle{{{\rm \omega} _0 \Omega _p } \over {\sqrt {{\rm \omega} _0\, k_0 c_s } }}.$$ One can easily see that ignoring the external magnetic field ωc = 0, using the approximation (a 0 ≪ 1, c s ≪ c) and obtaining 
$\Gamma \lpar \!\!={\displaystyle{1 \over {2\sqrt 2 }}}{\displaystyle{{k_0 v_{os} \Omega _p } \over {\sqrt {{\rm \omega} _0\, k_0 c_s } }}}\rpar $ as a nonrelativistic BBS growth rate, our model reduces to a linear unmagnetized regime. So, we recover the standard growth rate of BBS instability in an underdense unmagnetized plasma by neglecting the relativistic nonlinearity. Upon this method, the effect of different plasma parameters is investigated in the growth rate of instability.
4. RESULTS AND DISCUSSION
We can investigate the variations of BBS instability growth rate according to Eq. (23) and Eq. (27). Figure 2 represents influence of the plasma density on the growth rate of BBS in a linear and nonlinear magnetized plasma, when ωc/ω0 = 0.1. Basically, by increasing the plasma density, instability increases. We can also see from this figure that the BBS growth rate in the nonlinear magnetized plasma is a bit higher than that in a linear regime. Because of the nonlinear nature of magnetic force and relativity, the effect of nonlinearity is very important in the case of magnetized plasma in comparison with unmagnetized plasma. Figure 3 shows the variation of the normalized growth rate of BBS as an function of the normalized electron cyclotron frequency. It follows that in an underdense transversely magnetized plasma, the normalized growth rate of instability decreases with the normalized electron cyclotron frequency. This may be due to the fact that in the case of Brillouin scattering in an underdense plasma, ions are not stationary and can response to the external magnetic field. The transverse magnetic filed push plasma ions with plasma electrons at the same direction so that, ions follow electrons in plasma. This effect reduce the plasma fluctuations associated with the ponderomotive force. In this situation, ion cyclotron motions postpone the resonance of plasma oscillations and hence, the growth rate decrease. So, the static transverse magnetic field can reduces the BBS instability. Additionally, as it is obvious from this figure, the growth rate is higher for the high plasma frequency (ωp/ω0 = 0.12) than the low plasma frequency (ωp/ω0 = 0.1). As a matter of fact, increasing the plasma density, give rise the plasma fluctuations cause to quickly resonance of plasma oscillations, satisfying the matching condition lead to more Brillouin backward scattering of laser beam in plasma, that is enhance the possibility of beating the pump wave and scattered light wave and hence the instability increases. Figure 4 shows the variation of the nonlinear BBS instability growth rate ΓNBBS as a function of normalized radiation field amplitude a0 in the interaction of high intensity short laser pulse with an underdense unmagnetized (ωc/ω0 = 0) and two magnetized plasmas (ωc/ω0 = 0.1, ωc/ω0 = 0.2) based on the described model. It is evident from the figure that for both unmagnetized and magnetized plasmas, the growth rate of BBS increases with the normalized radiation field amplitude a 0. As a matter of fact, rising the laser pulse intensity enhance the ponderomotive force that leads to an increasing in the amplitude of the plasma density fluctuations, i.e., increase the BBS instability amplitude. However, the growth rate in the case of magnetized plasma is lower than in unmagnetized case.
Fig. 2. Normalized growth rate of BBS instability versus normalized plasma frequency in a linear and nonlinear magnetized plasma when a 0 = 0.2, c s/c = 0.02 and ωc/ω0 = 0.1.
Fig. 3. Normalized growth rate of nonlinear BBS instability versus normalized plasma electron cyclotron frequency for two different laser field amplitude when c s/c = 0.02 and a 0 = 0.2.
Fig. 4. Normalized growth rate of nonlinear BBS instability versus normalized vector potential in unmagnetized and magnetized plasmas when c s/c = 0.02, ωp/ω0 = 0.1.
5. CONCLUSION
In this Paper, we have investigated the nonlinear Brillouin scattering of an intense short-pulse laser from a transversely magnetized plasma. This study is the new effort to understand the physics involved in governing the nonlinear nature of BBS in a magnetized plasma. Here for a first time, we have obtained a clear expression for the growth rate of Brillouin backward instability in a transversely magnetized plasma by taking in to account the nonlinearity effects up to third order. Results show that increasing the external magnetic field decrease the BBS growth rate. Also, our calculations reveal that relativistic and higher order nonlinearities due to the external magnetic field, give rise the BBS instability. Our results are in a very good agreement with that similar works was mentioned in the introduction (Salimullah et al., Reference Salimullah, Ferdousi and Majid1994; Baton et al., Reference Baton, Rousseaux, Mounaix, Labaune, Fontaine, Pesme, Renard, Gary, Louis-Jacquet and Baldis1994; Paknezhad & Dorranian, Reference Paknezhad and Dorranian2011).
ACKNOWLEDGEMENT
This work is a part of a project entitled “Nonlinear study of Brilouin instability in a magnetized plasma” and is supported by the Islamic Azad University-Shabestar Branch under Contract number 51953890818005.
