A. Alloy compositions and preparation

Four Pb-based alloys were investigated in addition to 99.97% pure Pb and the industry standard alloy used in copper electrowinning (Pb–0.08Ca–1.52Sn); the custom Pb-binary alloys studied were Pb–0.73Mg, Pb–0.05Ag, Pb–0.07Rh, and Pb–1.4Zn. All alloy compositions are given in wt%. For the purpose of this investigation all alloys were studied in their as-cast form, including the industry standard Pb–Ca–Sn. The compositions selected were close to the maximum of solubility of each dopant in pure Pb (and hence the unique alloy loading in each case). The custom alloys were produced via the conventional crucible method. Finely chopped pieces of Pb and powdered alloying elements were heated in a quartz tube that was backfilled with argon (Ar) before sealing. The quartz tube was placed in a muffle furnace and held for extended periods at temperatures suitable for alloying of the respective elements. The alloy compositions were externally confirmed by ICP-AES (Spectrometer Services, Coburg, Australia). To enable the in situ S-XRD experimentation using a novel electrochemical flow cell [such a cell was previously described in Clancy et al. (Reference Clancy, Styles, Bettles, Birbilis, Chen, Zhang, Gu, Kimpton and Webster2015)] a section of each alloy was mounted in epoxy resin before the surfaces were ground to a 1200 grit finish using SiC paper.

B. In situ S-XRD

In situ S-XRD experiments were performed on the powder diffraction beamline at the Australian Synchrotron. Schematics of the flow cell and photographs of the experimental setup have been provided previously (Clancy et al., Reference Clancy, Styles, Bettles, Birbilis, Chen, Zhang, Gu, Kimpton and Webster2015). 1.6 M H₂SO₄ (sulphuric acid) solution was pumped over the alloy at 45 °C, and S-XRD data were collected throughout six galvanostatic – open circuit (GALV-OCP) electrochemical cycles, with individual data sets collected for 1 min using two detector positions, P1 and P2 (the detector contains 0.2° gaps every 5°2θ; data were collected in two detector positions 0.5° apart in order to cover the entire 2θ range). Asymmetric diffraction geometry with an incident beam-to-sample angle (defined hereafter as ω) of 8° was utilised for data collection, over the range 10° ≤ 2θ ≤ 90°. The vertical and horizontal slit widths were 0.2 and 5.0 mm, respectively. The X-ray wavelength was 0.9998 Å and was calibrated using LaB₆ (NIST 660b line position standard) contained in a 0.3 mm diameter glass capillary.

For the purposes of visualisation of the formation and decomposition of phases as the electrochemical experiment progressed, individual P1 and P2 data sets were merged using CONVAS2 (Rowles, Reference Rowles2010) to remove the detector gaps. Merged data sets were stacked to produce a plot of accumulated data with elapsed time plotted vs. 2θ, viewed down the intensity axis. The merged data sets were also used for Rietveld refinement-based quantitative phase analysis (QPA) implemented in TOPAS (Bruker, 2014). A correction to account for sample displacement error in the asymmetric diffraction geometry was incorporated into the refinement model, as was an intensity correction to account for the asymmetric diffraction geometry and also the absorption of the diffracted X-rays in H₂SO₄. Details of the models have been provided previously (Clancy et al., Reference Clancy, Styles, Bettles, Birbilis, Chen, Zhang, Gu, Kimpton and Webster2015). Phase concentration values are relative crystalline wt% calculated via the Hill and Howard (Reference Hill and Howard1987) algorithm. The crystal structure information reported in Goodwin and Whetstone (Reference Goodwin and Whetstone1947), Straumanis (Reference Straumanis1949), Wyckoff (Reference Wyckoff1963) and D'Antonio and Santoro (Reference D'Antonio and Santoro1980) were used for Pb, β-PbO₂, α-PbO₂, and PbSO₄, respectively. An anisotropic crystallite size broadening correction was implemented to account for the observed peak profiles for the β-PbO₂ phase, to improve the quality of fit of the profile calculated using the conventional crystallite size (CS) and microstrain (MS) models. Details of the model, including equations, have been provided previously (Clancy et al., Reference Clancy, Styles, Bettles, Birbilis, Chen, Zhang, Gu, Kimpton and Webster2015), with Lorentzian CS and MS being refineable parameters in the Rietveld analysis.

For the purposes of calculation of the thickness (t) of the PbO₂/PbSO₄ surface layer as a function of time, the decay in intensity (I/I ₀) of the (111) Pb reflection at 20.2°2θ was implemented in (Cullity, Reference Cullity1978).

(1) $$\displaystyle{I \over {I_0}} = e^{ - \mu t(1/\sin \omega + 1\!/\!\sin \beta )}$$

where μ is the X-ray linear absorption coefficient of the PbO₂/PbSO₄ surface layer, ω is 8° and β is the angle of the diffracted beam to the detector (i.e. β = 2θ – ω = 12.2° for the (111) Pb reflection). The relative concentrations of β-PbO₂, α-PbO₂, and PbSO₄ returned from the QPA were used to calculate the value of μ at each data point. This approach assumes crystallographic density of the surface layers, and is treated as a semi-quantitative approach only without accurate knowledge of the actual surface layer density as a function of time.

C. Electrochemical conditions

The working electrode (Pb-based anode alloy) was exposed to a galvanostatic signal via a BioLogic^® SP-150 potentiostat in conjunction with EC-Lab software. The potentiostat was connected to the cell via leads to the working electrode, the Ag/AgCl reference electrode and a Pt counter electrode. The applied current was equal to that used in industrial tank-houses, such that the current density was 300 A m⁻² for each sample. After 40 min of applied galvanostatic current, the OCP was recorded for a 30 min period, during which no applied current was imposed to the system. This experiment was designed to examine the performance of the Pb-based anodes during a tank-house power failure or when the power is switched off. The galvanostatic segment, followed by the OCP segment, which made up one cycle, was repeated a further five times to record the evolution of the electrochemical performance of the Pb-based anode. It is important to note that the reference electrode used for the in situ flow cell study utilised an Ag/AgCl electrode, which has a potential difference of +0.199 V versus the standard hydrogen electrode.

A. Electrochemical characteristics of Pb-alloys

The electrochemical potential versus time plots during the galvanostatic–OCP cycling for (a) Pb–Mg, (b) Pb–Ag, (c) Pb–Rh, (d) Pb–Zn, and (e) pure Pb alloys, are individually compared against the Pb–Ca–Sn alloy (Figure 1). There was a minor disturbance caused by a bubble in the cell for the Pb–Rh alloy. This is evidenced in Figure 1(c) by a spike in the measured potential in the first cycle, but was resolved once the bubble migrated away from the surface of the working electrode surface. During the OCP segments the PbO₂ transforms to PbSO₄ at a potential of ~1.25 V_Ag/AgCl. The rate at which each system undergoes the PbO₂ to PbSO₄ transformation, and to what extent over the 30 min period, varies significantly as can be seen in the results presented in Figure 4.

Figure 1. (Colour online) Potential versus time plots for the (a) Pb–0.73Mg, (b) Pb–0.05Ag, (c) Pb–0.07Rh, and (d) Pb–1.4Zn alloys (red traces), compared with the industry standard Pb-0.08Ca–1.52Sn alloy (black trace). For completeness the results reported by Clancy et al. (Reference Clancy, Styles, Bettles, Birbilis, Chen, Zhang, Gu, Kimpton and Webster2015) for the pure Pb anode are also shown in (e). The GALV and OCP segments of the first electrochemical cycle for the Pb–Mg/Pb–Ca–Sn alloys are labelled in (a).

The systems ranked in descending rate of transformation, were Pb–Ca–Sn, Pb, Pb–Zn, Pb–Mg, Pb–Ag, and Pb–Rh. In other words, the “best” performing alloy overall was considered to be the Pb–Rh alloy, with the Pb–Ag alloy only marginally behind in performance. Such an assessment is also based on the lower overpotential (~1.5 V_Ag/AgCl) achieved in response to the same galvanostatic polarisation conditions as the Pb–Ca–Sn, Pb–Mg, Pb–Zn, and pure Pb alloys (each measuring an overpotential of ~1.7 V_Ag/AgCl). This can have a significant (beneficial) effect in lowering the overall energy requirement of the cell, where the power requirement is i × V, where “i” is a constant fixed galvanostatic current, and “V” (in the context of power requirement) is the overpotential. Herein, the overpotential resulting from Rh and Ag additions is minimised, translating to a lower overall power requirement. Furthermore, the reduced change in the OCP across the six cycles compared with the other alloys is also unique to the Pb–Rh alloy. For example, the potential during the OCP segment of the first cycle for the Pb–Rh alloy reached a minimum value of 0.14 and 0.25 V_Ag/AgCl in the sixth cycle. In comparison, the potential during the OCP segment of the first cycle for the Pb–Ca–Sn alloy reached a minimum value of 0.21, and 0.98 V_Ag/AgCl in the sixth cycle. Based on these measures, the Pb–Mg, and Pb–Zn anodes also exhibit improved electrochemical performance from electrochemical testing, when compared with Pb–Ca–Sn. The stark differences induced by relatively low level alloying additions are indeed significant. It should be noted, however, that properties such as good mechanical strength and creep resistance, which are key factors in pure Pb being an unsuitable anode material for industrial use, must also be taken into account when considering an alloy to replace the industry standard. One feature of the Pb–Rh, and Pb–Ag alloys identified here, however, and which is a factor that would require longer term testing, is the minor increase in potential with each galvanostatic cycle, compared with the insignificant change in the potential galvanostatic region for the other alloys.

B. Surface evolution and phase analysis

Figure 2 reveals the plot of accumulated in situ S-XRD data for the Pb–Mg alloy. The first of the six galvanostatic and OCP segments is labelled. During the galvanostatic segments, the tetragonal β and orthorhombic α polymorphs of PbO₂ both formed, while the orthorhombic form of PbSO₄ formed during the OCP segments. Other than those from the substrate, no reflections from any other phases were observed during the experiment. α-PbO₂ was observed together with the β phase during the galvanostatic segments of the experiments performed for the Pb–Ca–Sn, Pb–Ag, and Pb–Zn alloys; for pure Pb and the Pb–Rh alloy however, β-PbO₂ was the only phase observed during the galvanostatic segments. A shift of the broad PbO₂ reflections to lower 2θ during conversion of this phase to PbSO₄ was observed, which is attributed to substitution of larger Pb²⁺ (ionic radius = 1.33 Å) (Shannon, Reference Shannon1976) cations for Pb⁴⁺ (0.915 Å) in the β-PbO₂ structure during conversion to PbSO₄, forming a non-stoichiometric phase (Butler and Copp, Reference Butler and Copp1956).

Figure 2. (Colour online) A plot of accumulated diffraction data collected for the Pb-0.73Mg alloy during electrochemical cycling, where GALV = galvanostatic and OCP = power interruption regimes. Some of the key Pb, β-PbO₂, α-PbO₂, and PbSO₄ reflections are labelled. The features at ~18.7° and 19.2°2θ, which are present over the duration of the experiment are artefacts from the detector.

Another noteworthy feature of the in situ S-XRD data is that the β-PbO₂ peaks for Pb–Rh, and Pb–Ag (seen specifically for Pb–Ag in Figure 3) are significantly sharper than those observed in the data for the other alloys investigated. This manifests in a higher value for the CS parameter in our anisotropic CS broadening model (Table I). Owing to the nature of the experimental setup and the assumptions in the modelling employed, these values are only an approximate measure of the CS. However, they can provide a qualitative insight into the microstructure of the β-PbO₂ layer on the different alloys, namely the β-PbO₂ crystallites appear larger on the Pb–Ag and Pb–Rh than on the other alloys. The CS value for the Pb–Ag alloy was higher than that for Pb–Rh, which may be the property giving rise to the greater upwards slope of the galvanostatic segment for this alloy, thought to be a potential indicator of a lack of long term stability in the oxide layer.

Figure 3. (Colour online) A plot of accumulated diffraction data collected for the Pb-0.05Ag alloy during electrochemical cycling. The β-PbO₂ peaks are significantly narrower in these data, compared with the Pb–0.73Mg sample (Figure 2), indicating a larger average crystallite size.

Table I. Refined values of the Lorentzian crystallite size (CS, in nm) and micro-strain (MS) parameters for β-PbO₂ in the dataset collected after 237 min i.e. during the fourth galvanostatic segment) for each alloy. The numbers in parentheses are Rietveld errors indicative of error in fit between the experimental and calculated profiles.

C. QPA and thickness evolution

The comprehensive results of Rietveld refinement-based QPA are presented in Figure 4, showing the evolution in relative concentration of the alloy substrate and the β-PbO₂, α-PbO₂, and PbSO₄ surface layers as a function of time. It should be noted that the S-XRD data collection for the Pb–Zn alloy stopped after 248 min because of an unforeseen loss of the X-ray beam, whereas the electrochemistry was allowed to continue until after the sixth cycle was complete. Figure 4(b) shows the QPA results for the Pb–Mg alloy, and general trends observed across Figures 4(a)–4(e) are discussed in relation to these results. Both β- and α-PbO₂ formed immediately on the substrate, and continued to grow during the galvanostatic segment of the first cycle, as indicated by the increase in crystalline phase concentration from 6 wt% (β-PbO₂) and 2 wt% (α-PbO₂) at t = 0 min, to 22 and 9 wt%, respectively at the end of the segment (t = 38 min). The concentration of β-PbO₂ also increased as the number of cycles increased; β-PbO₂ represented 45 wt% at the start of the galvanostatic segment of the second cycle (t = 74 min), compared with 22 wt% at the end of the galvanostatic segment of the first cycle, for example. In addition, whilst at each of the OCP to galvanostatic transitions the PbSO₄ transforms completely, the dissolution of β- and α-PbO₂ at the galvanostatic to OCP transitions is incomplete and the amount of residual PbO₂ increases, reaching 25 wt% (for β-PbO₂) in the final cycle. No α-PbO₂ was detected on the Pb and Pb–Rh surfaces during cycling, whereas the Pb–Mg and Pb–Zn systems showed the most significant amounts which remained quite stable throughout electrochemical exposure. After the six galvanostatic cycles the Pb–Ca–Sn, Pb–Mg, Pb–Zn, and Pb alloys all had combined relative phase concentrations of β-PbO₂ and PbSO₄ that were significantly higher than those of the Pb–Ag and Pb–Rh alloys. Given that the detected Pb is from the underlying substrate, the alloys with these higher phase concentrations (of β-PbO₂ and PbSO₄) are likely to have thicker surface layers than Pb–Ag or Pb–Rh. It is suggested that Rh functions to lessen the rate of the PbO₂ to PbSO₄ transformation, resulting in a preference to retain a thinner, denser layer of β-PbO₂ on the substrate surface.

Figure 4. (Colour online) Results of Rietveld refinement-based quantitative phase analysis, showing the evolution in relative concentration of the alloy substrate and the β-PbO₂, α-PbO₂, and PbSO₄ surface layers during the electrochemical tests for (a) Pb–0.08Ca-1.52Sn, (b) Pb–0.73Mg, (c) Pb–0.05Ag, (d) Pb–0.07Rh, (e) Pb–1.4Zn, and (f) pure Pb [reported by Clancy et al. (Reference Clancy, Styles, Bettles, Birbilis, Chen, Zhang, Gu, Kimpton and Webster2015)]. In (e), at 248 min there was a loss of beam and so X-ray data were not collected beyond this point. The electrochemical cycling, however, was allowed to continue [Figure 1(d)].

The evolution of the thickness of the PbO₂/PbSO₄ surface layers formed on each alloy, calculated from the diffraction data using Eq. (1), is presented in Figure 5. The calculated surface layer thickness was greatest for the pure Pb anode. However, from electrochemical testing it was not the anode with the greatest surface layer thickness that had the poorest electrochemical performance, rather the Pb–Ca–Sn alloy (Figure 1). As such, the surface layer thickness appears not the prime factor in dictating anode performance, where a more detailed interpretation based on the results of the QPA reveals that poor electrochemical performance of the Pb–Ca–Sn alloy was governed chiefly by two factors. The first is that the relative amount of β-PbO₂ did not overtake that of PbSO₄ until the fifth cycle – this occurred earlier for each of the other alloys (during the second cycle for Pb–Ag, Pb–Rh and Pb, during the third cycle for the Pb–Mg and Pb–Zn). As such the difference between the maximum β-PbO₂ and PbSO₄ concentrations during the sixth cycle is only 6 wt% for the Pb–Ca–Sn alloy. In contrast, the difference values for the Pb–Mg, Pb–Ag, Pb–Rh, and pure Pb anodes were 16, 14, 12, and 15 wt%, respectively. Secondly, the amount of retained β-PbO₂ during the OCP segments is lower for the Pb–Ca–Sn alloy than for the other anodes; 12 wt% during the sixth cycle, compared with 25, 20, 18, and 17 wt% for Pb–Mg, Pb–Ag, Pb–Rh, and pure Pb, respectively. It is, however, not completely clear at present if the stability of an anode alloy can be decided based on the dissolution of PbO₂ and subsequent formation of PbSO₄. Other very important variables that can and will affect mass transport across the anodic layer that has formed are the associated porosity, conductivity, and texture limitations. Such factors require dedicated studies, however, the time-resolved measurements of relative phase fractions and surface layer thicknesses presented in this study provide significant new insights.

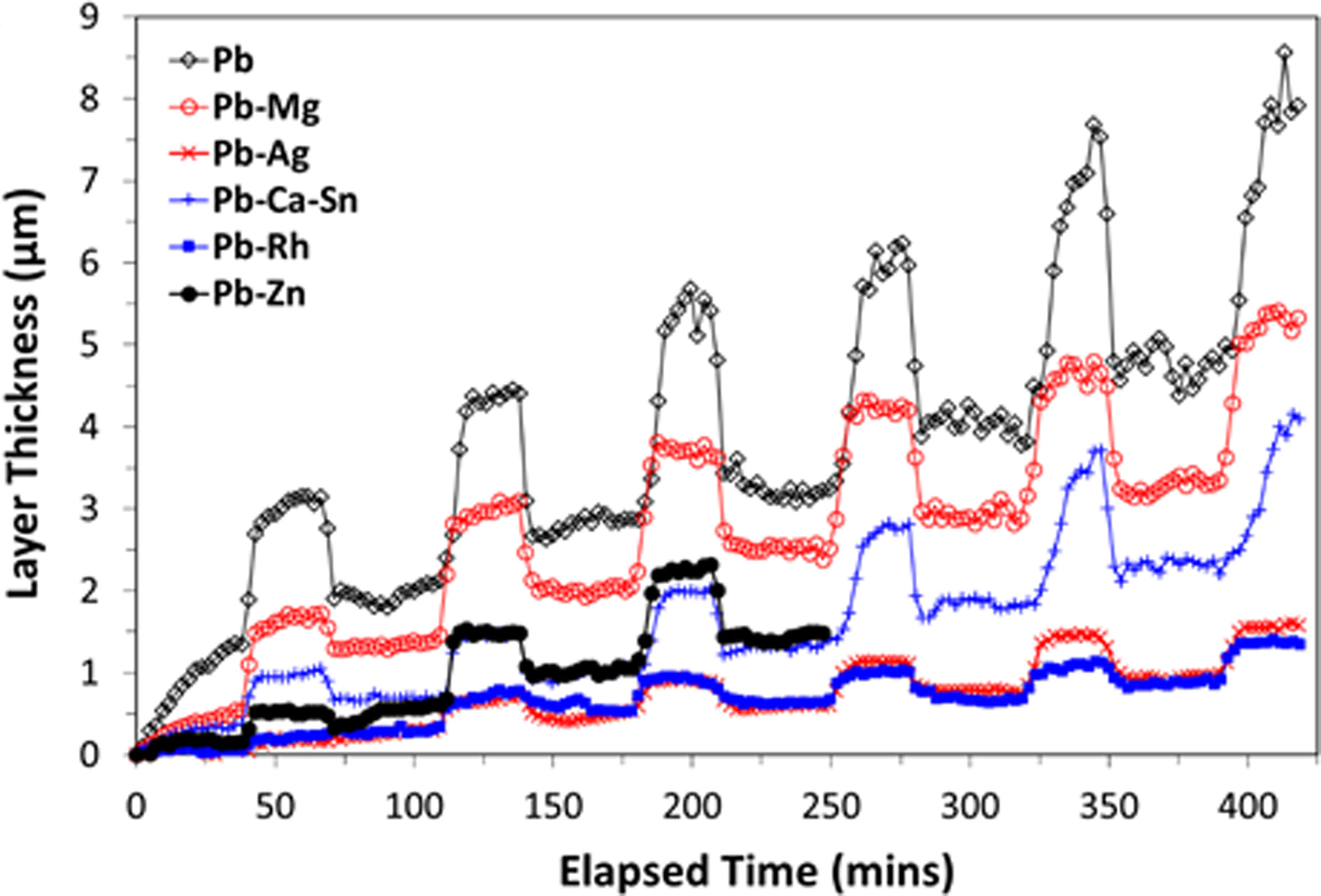
Figure 5. (Colour online) Calculated surface layer thickness as a function of time for each alloy.

Further evidence of the layer thickness not being the sole determining factor in electrochemical behaviour is the comparison between the thickness curves for Pb–Mg and Pb–Zn in Figure 5, which are significantly different. Again, the key factor in determining electrochemical performance appears to be the similar proportions of the PbO₂ and PbSO₄ phases as cycling progressed [Figures 4(b) and 4(e)]. It is also noted that the model used to calculate the layer thickness [Eq. (1)] assumes that the density of the passivation layer is consistent across all of the samples. Variations in the density of this layer from sample to sample could affect the interpretation of the electrochemical performance. Further work is required to investigate the role of porosity within the passivation layers of these alloys. Based on the available data there is not considered to be sufficient evidence to determine whether or not the formation of α-PbO₂ is detrimental to the performance of an alloy material. Formation of the α-PbO₂ phase may be promoted by the presence of dopants with a tendency to form divalent cations, since the Pb–Mg and Pb–Zn alloys resulted in the formation of up to 11 wt% of this phase, with 5 wt% being the next highest amount observed (for the industry standard alloy which happens to contain Ca). Consequently, the influence of so-called “reactive elements” uniquely is also an area worthy of further pursuit.