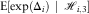2.1. Mixed poisson model for annual claim frequencies

Consider an insurance portfolio comprising n policies observed during several periods. Let N _it be the number of claims reported by policyholder i, i=1,2,…,n, during period t, t=1,2,…,T _i . Compared to classical actuarial studies dealing with annual periods, insurers using telematics data generally work with shorter time periods, like a quarter or a month.

At the beginning of each insurance period, the actuary has at his disposal some information about each policyholder summarised into p features x _itj that may evolve over time. The a priori information x _it =(x _it1,…,x _itp )^Τ is recorded in the data basis under consideration. Resorting to standard regression (or supervised learning) machinery, this information is integrated into the prediction of the annual expected number of claims, or claim frequency. Specifically, define

$$\eqalignno{ x_{{it}} {\equals} & {\rm features}\,{\rm for}\,{\rm policyholder}\,i{\rm ,}\,i{\rm {\equals}1,}\,\ldots{\rm \!\!,}n{\rm ,} \cr& {\rm during}\,{\rm period}\,t{\rm ,}\,t{\rm {\equals}1,2,}\,\ldots\,\!\!\!{\rm ,}T_{i} \cr d_{{it}} {\equals} & {\rm exposure{\hbox-}to{\hbox-}risk,}\,{\rm distance}\,{\rm driven}\,{\rm in}\,{\rm kilometers} \cr \eta _{{it}} {\equals} & \eta (x_{{it}} ) \cr {\equals} & {\rm score}\,{\rm for}\,{\rm policyholder}\,i\,{\rm in}\,{\rm period}\,t \cr \lambda _{{it}} {\equals} & d_{{it}} \exp (\eta _{{it}} ){\equals}\exp \left( {\ln d_{{it}} {\plus}\eta _{{it}} } \right). $$

Adding $$\ln d_{{it}} $$ to the score η _it (i.e. treating this quantity as an offset) means that the insurer’s price list is expressed per kilometer, and varies according to traditional risk features included in the vector x _it . The score η _it can be calibrated by means of any Poisson regression technique, ranging from basic generalised linear models (GLM) to sophisticated machine learning algorithms.

A random effect Δ _i is added to the score η _it to recognise the residual heterogeneity of the portfolio. We refer to Denuit et al. (Reference Denuit, Marechal, Pitrebois and Walhin2007) for more details about this classical construction. In this paper, we assume that the residual effect of all unknown characteristics relating to policyholder i is represented by a random variable Δ _i . The numbers of claims N _i1, N _i2, N _i3,… are then assumed to be independent given Δ _i . The latent unobservable Δ _i characterises the correlation structure of the claim counts N _it for each policyholder i. Specifically, the model is based on the following assumptions:

A1 given Δ _i =δ, the random variables N _it , t=1, 2,…, are independent and conform to the Poisson distribution with mean

$$\lambda _{{it}} \exp (\delta ){\equals}\exp (\ln d_{{it}} {\plus}\eta _{{it}} {\plus}\delta ),$$

which is henceforth denoted as $$N_{{it}} \,\sim\,{\cal P}oi(\lambda _{{it}} \exp (\delta ))$$ . Formally,

$$\eqalignno{ {\rm P}[N_{{i1}} {\equals}k_{1} ,\,\ldots\,N_{{iT_{i} }} {\equals}k_{{T_{i} }} \,\mid\,\Delta _{i} {\equals}\delta ] & {\equals}\prod\limits_{t{\equals}1}^{T_{i} } {\rm P}[N_{{it}} {\equals}k_{t} \,\mid\,\Delta _{i} {\equals}\delta ] \cr & {\equals}\prod\limits_{t{\equals}1}^{T_{i} } \left( {\exp ({\minus}\lambda _{{it}} \exp (\delta )){{(\lambda _{{it}} \exp (\delta ))^{{k_{t} }} } \over {k_{t} \,!\,}}} \right). $$

A2 at the portfolio level, the sequences (Δ _i , N _i1, N _i2,…) are assumed to be independent.

A3 the random effects Δ _i are independent, Normally distributed with zero mean and constant variance $$\sigma _{\Delta }^{2} $$ .

When the canonical log link function is used in the Poisson regression model, as assumed here, assumption A3 amounts to using a Poisson-LogNormal model for claim counts. Contrarily to what is generally assumed in the actuarial literature, where the random effects Δ _i are supposed to be such that $${\rm E}[\exp (\Delta _{i} )]{\equals}1$$ , the statistical literature devoted to mixed models assumes that the random effects Δ _i are centred. Under assumption A3, we then have $${\rm E}[\exp (\Delta _{i} )]{\equals}\exp (\sigma _{\Delta }^{2} \,/\,2)$$ according to the formula giving the mathematical expectation for the LogNormal distribution. Therefore, the latter factor has to be included in the calculation of the a priori expected number of claims (with a linear score η _it , the intercept of the regression model has thus to be modified accordingly). Formally, the a priori expected number of claims is equal to

$${\rm E}[N_{{it}} ]{\equals}{\rm E}\left[ {{\rm E}[N_{{it}} \,\mid\,\Delta _{i} ]} \right]{\equals}\lambda _{{it}} {\rm E}[\exp (\Delta _{i} )]{\equals}\lambda _{{it}} \exp (\sigma _{\Delta }^{2} \,/\,2).$$

2.2. Single behavioural variable, or signal

In order to predict the number of claims N _it filed by policyholder i during period t, let us assume that the insurer has a signal S _it at its disposal about the policyholder’s behaviour behind the wheel during the same period. This unique signal summarises all the information collected by means of telematic devices installed in the vehicle. For commercial purposes, it may be preferable to use a unique signal as premium updating formulas are more compact and easier to understand (in the next section, several signals will be used simultaneously).

To refine risk evaluation, we now combine past claims experience with the available signal. Hence, each contract is represented by the sequence

$$(\Delta _{i} ,\Gamma _{i} ,N_{{i1}} ,S_{{i1}} ,N_{{i2}} ,S_{{i2}} ,N_{{i3}} ,S_{{i3}} ,\,\ldots\,)$$

where

∆ _i accounts for hidden information influencing claim frequencies N _it

Γ _i reects the quality of driving revealed by the observed signal S _it .

It is important to realise here that signals are also influenced by traditional risk factors included in x _it so that we need to account for this effect in model design. Here is a possible model specification in case of a Gaussian signal S _it (notice that even if the initial signal does not obey the Gaussian distribution, it can easily be transformed to meet approximately this condition): we supplement assumptions A1-A3 stated in Section 2.1 with

A4 Given Δ _i , the counts N _i1, N _i2,… are independent and independent of Γ _i , S _i1, S _i2,….

A5 Given Γ _i , the signals S _i1, S _i2,… are independent and independent of Δ _i , N _i1, N _i2,…, and

$$S_{{it}} {\equals}\nu _{{it}} {\plus}\Gamma _{i} {\plus}{\scr E}_{{it}} $$

where ν _it is the signal score based on a priori features x _it , Γ _i is Normally distributed and represents the additional information contained in the signal about claim frequencies, corrected for the effect of the features x _it whereas the Normally distributed error terms $${\scr E}_{{it}} $$ represent the noise comprised in the observed signal S _it which do not reveal anything about claim counts. We also make the following assumptions about the dependence structure of these random variables

1. (a) The random variables $$\Gamma _{i} ,{\scr E}_{{i1}} ,\,{\scr E}_{{i2}} ,\,\ldots\,$$ are mutually independent.

2. (b) The random variables $${\scr E}_{{i1}} ,\,{\scr E}_{{i2}} ,\,\ldots\,$$ are independent from (Δ _i , N _i1, N _i2, N _i3,…).

A6 Given Δ _i and Γ _i , all the observable random variables N _i1, S _i1, N _i2, S _i2,… are independent.

From assumptions A4–A6, we see that only the Γ _i component involved in the signal S _it is relevant to predict claim frequencies: we assume that the pair (Δ _i , Γ _i ) is normally distributed, with zero mean vector and its covariance drives the corrections brought by signals in the evaluation of future expected number of claims.

Continuous signals are certainly appealing as many embarked devices produce real measures. Another approach consists in recording a number of events, or to round a continuous signal in multiples of a natural unit. This makes the mechanism more transparent, at the cost of a negligible loss of accuracy.

If the signal counts a number of events then A4–A6 above are replaced with

A4 Given Δ _i , the claim counts N _i1, N _i2,… are independent and independent of Γ _i , S _i1, S _i2,….

A5 Given Γ _i , the signal counts S _i1, S _i2,… are independent and independent of Θ _i , N _i1, N _i2,…, and

$$S_{{it}} \,\sim\,{\cal P}oi\left( {d_{{it}} \exp (\nu _{{it}} {\plus}\Gamma _{i} )} \right).$$

where ν _it is the signal score based on a priori features x _it and $$\Gamma _{i} $$ is Normally distributed with zero mean and represents the additional information contained in the signal about claim frequencies. The noise present in the observed signal $$S_{{it}} $$ is now represented by the Poisson error structure.

A6 Given $$\Delta _{i} $$ and $$\Gamma _{i} $$ , all the observable random variables $$N_{{i1}} ,S_{{i1}} ,N_{{i2}} ,S_{{i2}} ,\,\ldots\,$$ are independent.

Assumptions A4–A6 are in line with the traditional actuarial approach to experience rating, in that they postulate that the dependence between signal and claim counts is only apparent and results from missing information. If we had a complete knowledge of policyholder’s characteristics, i.e. if we knew $$\Delta _{i} $$ , then the signal would not be needed for pricing. Because of limited knowledge about policyholder’s driving style, the insurer uses the information contained in the signal that reveals the missing elements in expected claim counts. This is why the signal is separated into three components: the effect $$\nu _{{it}} $$ of the available features $$x_{{it}} $$ , the relevant information $$\Gamma _{i} $$ contained in the signal, that may explain expected claim counts beyond the available $${\mib{x}} _{{it}} $$ , and the random noise $${\scr E}_{{it}} $$ . The correlation $$\rho _{{\Delta ,\Gamma }} $$ between $$\Delta _{i} $$ and $$\Gamma _{i} $$ can be exploited to improve the estimation of the expected number of claims by combining observed signal values with past claims history.

Notice that claim counts $$N_{{it}} $$ and signal values $$S_{{it}} $$ are correlated by means of the pair $$(\Delta _{i} ,\Gamma _{i} )$$ of random effects. For a signal consisting in a mixed Poisson count, this is easily seen as follows:

$${\rm C}[N_{{it}} ,S_{{it}} ]{\equals}{\rm C}\left[ {{\rm E}[N_{{it}} \,\mid\,\Delta _{i} ,\Gamma _{i} ],{\rm E}[S_{{it}} \,\mid\,\Delta _{i} ,\Gamma _{i} ]} \right]$$

because the conditional covariance is zero by virtue of A6. Hence,

$${\rm C}[N_{{it}} ,S_{{it}} ]{\equals}d_{{it}}^{2} \exp (\eta _{{it}} {\plus}\nu _{{it}} ){\rm C}\left[ {\exp (\Delta _{i} ),\exp (\Gamma _{i} )} \right].$$

Now, as the pair $$(\Delta _{i} ,\Gamma _{i} )$$ is jointly Normal, with zero mean, variances $$\sigma _{\Delta }^{2} $$ and $$\sigma _{\Gamma }^{2} $$ , and correlation $$\rho _{{\Delta ,\Gamma }} $$ , we get

$${\rm C}\left[ {\exp (\Delta _{i} ),\exp (\Gamma _{i} )} \right]{\equals}{\rm E}\left[ {\exp (\Delta _{i} {\plus}\Gamma _{i} )} \right]{\minus}{\rm E}\left[ {\exp (\Delta _{i} )} \right]{\rm E}\left[ {\exp (\Gamma _{i} )} \right]$$

$$\hskip70pt{\equals}\exp \left( {{{\sigma _{\Delta }^{2} {\plus}\sigma _{\Gamma }^{2} } \over 2}} \right)(\exp \left( {\rho _{{\Delta ,\Gamma }} \sigma _{\Delta } \sigma _{\Gamma } } \right){\minus}1)$$

which is not zero unless $$\rho _{{\Delta ,\Gamma }} {\equals}0$$ , that is, unless $$\Delta _{i} $$ and $$\Gamma _{i} $$ are mutually independent (so that the signal brings no information about the claim counts).

2.3. Multiple signals

Assume that $$q$$ signals, denoted as $$S_{{it}}^{{(j)}} $$ , $$j{\equals}1,2,\,\ldots\,,q$$ , are available in addition to the $$p$$ features comprised in $${\mib{x}} _{{it}} $$ . In case several signals are available, the insurer may either combine them into a single one and proceed as explained above. A natural approach would consist in using a linear combination of the signals for instance, and to work with the unique, composite signal $$\mathop{\sum}\limits_{j{\equals}1}^q \alpha _{j} S_{{it}}^{{(j)}} $$ for appropriate weights $$\alpha _{j} $$ (determined so to maximise the correlation with the observed claim counts $$N_{{it}} $$ ). Another possibility is to extend the model from the preceding section to the multivariate case by assuming a specific dynamics for each signal as explained next.

In case of multivariate Normally-distributed signals, we supplement assumptions A1–A3 with

A4 Given $$\Delta _{i} $$ , claim counts $$N_{{i1}} ,N_{{i2}} ,\,\ldots\,$$ are independent and independent of $$\Gamma _{i}^{{(j)}} ,S_{{i1}}^{{(j)}} ,S_{{i2}}^{{(j)}} ,\,\ldots\,$$ for $$j{\equals}1,2,\,\ldots\,,q$$ .

A5 Given $$\Gamma _{i}^{{(j)}} $$ , the signals $$S_{{i1}}^{{(j)}} ,S_{{i2}}^{{(j)}} ,\,\ldots\,$$ are independent and independent of $$\Delta _{i} ,N_{{i1}} ,N_{{i2}} ,\,\ldots \hskip-1.5pt \hbox{,}\;$$ and admit the representation

$$S_{{it}}^{{(j)}} {\equals}\nu _{{it}}^{{(j)}} {\plus}\Gamma _{i}^{{(j)}} {\plus}{\scr E}_{{it}}^{{(j)}} $$

where $$\nu _{{it}}^{{(j)}} $$ is the score for the $$j$$ th signal based on a priori features $${\mib{x}} _{{it}} $$ , $$\Gamma _{i}^{{(j)}} $$ is Normally distributed with zero mean and represents the additional information contained in the $$j$$ th signal about claim frequencies, corrected for the effect of the features $${\mib{x}} _{{it}} $$ whereas the Normally distributed error terms $${\scr E}_{{it}}^{{(j)}} $$ represent the noise comprised in the observed signal which do not reveal anything about claim counts.

We also make the following assumptions about the dependence structure of these random variables:

• - The random variables $$\Gamma _{i}^{{(j)}} ,{\scr E}_{{i1}}^{{(j)}} ,{\scr E}_{{i2}}^{{(j)}} ,\,\ldots\,$$ are mutually independent.

• - The random variables $${\scr E}_{{i1}}^{{(j)}} ,{\scr E}_{{i2}}^{{(j)}} ,\,\ldots\,$$ , $$j{\equals}1,2,\,\ldots\,$$ are mutually independent.

• - The random variables $${\scr E}_{{i1}}^{{(j)}} ,{\scr E}_{{i2}}^{{(j)}} ,\,\ldots\,$$ are independent from $$(\Delta _{i} ,N_{{i1}} ,N_{{i2}} ,N_{{i3}} ,\,\ldots)$$ .

• - The random vector $$(\Delta _{i} ,\Gamma _{i}^{{(1)}} ,\Gamma _{i}^{{(2)}} ,\,\ldots\,,\Gamma _{i}^{{(q)}} )$$ is multivariate Normally distributed with zero mean vector and variance-covariance matrix Σ.

A6 Given $$(\Delta _{i} ,\;\Gamma _{i}^{{(1)}} ,\;\Gamma _{i}^{{(2)}} ,\,\ldots\hskip-1.5pt \hbox{,}\; \Gamma _{i}^{{(q)}} )$$ , all the observable random variables $$N_{{i1}} ,\;S_{{i1}}^{{(1)}} ,\;S_{{i1}}^{{(2)}} $$ , $$\ldots\,$$ , $$N_{{i2}} ,S_{{i2}}^{{(1)}} ,S_{{i2}}^{{(2)}} ,\,\ldots\,$$ are independent.

The random vectors $$(\Delta _{i} ,\;\Gamma _{i}^{{(1)}} ,\;\Gamma _{i}^{{(2)}} ,\,\ldots\,,\Gamma _{i}^{{(q)}} )$$ are independent and all obey the same Normal distribution. The covariance structure drives the corrections induced by the signals on future expected claim counts. We acknowledge here that the multivariate Normal assumption may appear to be restrictive in some applications because it constrains the dependence structure (prohibiting tail dependence, for instance). Other multivariate distributions, such as Elliptical ones can be useful to model the dependency of the signals, and a copula construction can be employed to this end.

If the signals consist in counts of different events then assumptions A1–A3 are supplemented with

A4 Given $$\Delta _{i} $$ , claim counts $$N_{{i1}} ,\;N_{{i2}} ,\,\ldots$$ are independent and independent of $$\Gamma _{i}^{{(j)}} ,\;S_{{i1}}^{{(j)}} ,\;S_{{i2}}^{{(j)}} ,\,\ldots\,$$ for $$j{\equals}1,2,\,\ldots\hskip-1.5pt \hbox{,}\; q$$ .

A5 Given $$\Gamma _{i}^{{(j)}} $$ , the signal counts $$S_{{i1}}^{{(j)}} ,\;S_{{i2}}^{{(j)}} ,\,\ldots$$ are independent and independent of $$\Delta _{i} ,\;N_{{i1}} ,\;N_{{i2}} ,\,\ldots\hskip-1.5pt \hbox{,}$$ and

$$S_{{it}}^{{(j)}} \,\sim\,{\cal P}oi\left( {d_{{it}} \exp (\nu _{{it}}^{{(j)}} {\plus}\Gamma _{i}^{{(j)}} )} \right)$$

where $$\nu _{{it}}^{{(j)}} $$ is the score for the $$j$$ th signal based on a priori features $${\mib{x}} _{{it}} $$ and $$\Gamma _{i}^{{(j)}} $$ is Normally distributed with zero mean and represents the additional information contained in the $$j$$ th signal about claim frequencies, corrected for the effect of the features $${\mib{x}} _{{it}} $$ . Also, the random vector $$(\Delta _{i} ,\;\Gamma _{i}^{{(1)}} ,\;\Gamma _{i}^{{(2)}} ,\,\ldots\hskip-1.5pt \hbox{,}\;\Gamma _{i}^{{(q)}} )$$ is multivariate Normally distributed with zero mean vector and variance-covariance matrix Σ.

A6 Given $$(\Delta _{i} ,\;\Gamma _{i}^{{(1)}} ,\;\Gamma _{i}^{{(2)}} ,\,\ldots\Gamma _{i}^{{(q)}} )$$ , all the observable random variables $$N_{{i1}} ,\;S_{{i1}}^{{(1)}} ,\;S_{{i1}}^{{(2)}} $$ , $$\,\ldots\hskip-1.5pt \hbox{,}$$ $$N_{{i2}} ,\;S_{{i2}}^{{(1)}} ,\;S_{{i2}}^{{(2)}} ,\,\ldots$$ are independent.

Of course, the insurer could use a blend of continuous and integer signals so that many variants to the models proposed above can be envisaged.

2.4. Credibility updating formulas

In addition to accounting for overdispersion and serial correlation, the random effects

$$(\Delta _{i} ,\Gamma _{i}^{{(1)}} ,\;\Gamma _{i}^{{(2)}} ,\,\ldots\hskip-1.5pt \hbox{,}\;\Gamma _{i}^{{(q)}} )$$

allow for credibility updates. In the classical actuarial approach based on claim counts, only, past numbers of claims enter the credibility formulas in addition to observable features $${\mib{x}} _{{i,T_{i} {\plus}1}} $$ to explain $$N_{{i,T_{i} {\plus}1}} $$ . Formally, the experience used to revise future premiums relates to past claims history

$${\scr H}_{{i,T_{i} }}^{{{\rm claim}}} {\equals}\{ N_{{it}} ,\quad t{\equals}1,\,\ldots\,,T_{i} \} .$$

This information enters the predictive distribution, i.e. the conditional distribution of $$N_{{i,T_{i} {\plus}1}} $$ given $${\scr H}_{{i,T_{i} }}^{{{\rm claim}}} $$ . With experience rating, the a priori expectation

$${\rm E}[N_{{i,T_{i} {\plus}1}} ]{\equals}\lambda _{{i,T_{i} {\plus}1}} {\rm E}[\exp (\Delta _{i} )]$$

is replaced with the a posteriori expectation

$${\rm E}[N_{{i,T_{i} {\plus}1}} \,\mid\,{\scr H}_{{i,T_{i} }}^{{{\rm claim}}} ]{\equals}\lambda _{{i,T_{i} {\plus}1}} {\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,T_{i} }}^{{{\rm claim}}} ].$$

The pricing structure is slow to adapt in personal lines because the $$\lambda _{{it}} $$ are generally small.

With telematics and IoT, the past claims history $${\scr H}_{{i,T_{i} }}^{{{\rm claim}}} $$ can be enriched with behavioural data. This allows the pricing structure to become much more reactive but requires the development of multivariate credibility models. In this case, the policy-specific history $${\scr H}_{{i,T_{i} }} $$ gathers all the a posteriori information

$${\scr H}_{{i,T_{i} }} {\equals}{\scr H}_{{i,T_{i} }}^{{{\rm claim}}} {\cup}{\scr H}_{{i,T_{i} }}^{{{\rm signals}}} {\equals}\{ N_{{it}} ,S_{{it}}^{{(1)}} ,\,\ldots\,,S_{{it}}^{{(q)}} ,\quad t{\equals}1,\,\ldots\,,T_{i} \} .$$

The multivariate mixed/credibility model describes the joint dynamics of $$N_{{it}} ,S_{{it}}^{{(1)}} ,\,\ldots\,,S_{{it}}^{{(q)}} $$ , given a priori features $${\mib{x}} _{{it}} $$ . The predictive distribution now corresponds to the conditional distribution of $$N_{{i,T_{i} {\plus}1}} $$ given $${\scr H}_{{i,T_{i} }} $$ . The a priori expectation is replaced with an a posteriori one

$${\rm E}[N_{{i,T_{i} {\plus}1}} \,\mid\,{\scr H}_{{i,T_{i} }} ]{\equals}\lambda _{{i,T_{i} {\plus}1}} {\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,T_{i} }} ].$$

The factor $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,T_{i} }} ]\,/\,{\rm E}[\exp (\Delta _{i} )]$$ is the credibility correction, i.e. the ratio between the a posteriori and the a priori expected numbers of claims.

3.1. Presentation of the data set

In order to illustrate the approach proposed in Section 2, we perform a case study based on real driving data recorded by GPS, collected by a Spanish insurance company within the framework of a new form of insurance cover. Under such policies, motor insurance premiums are determined by taking into account not only the traditional risk factors but also the number of kilometers driven in a given period of time as well as information on the number of kilometers driven at night, the number of kilometers driven in an urban area, and the number of kilometers driven at excess speed. The information available is a panel that describes yearly records on the number of claims and the driving patterns for each driver measured thanks to telemetry.

Excess speed, night-time driving and urban driving are considered to be signals of the type of driving habits or skills. We treat these signals as entire numbers, by rounding excess speed, night-time driving and urban driving in natural units of 500 km. Specifically, the three signals at our disposal are as follows:

\hskip-147pt$$S_{{it}}^{{(1)}} {\equals}{\rm distance}\,{\rm travelled}\,{\rm in}\,{\rm the}\,{\rm night}\,{\rm (in}\,{\rm multiples}\,{\rm of}\,{\rm 500}\,{\rm kilometers)}$$

$$\hskip-118pt S_{{it}}^{{(2)}} {\equals}{\rm distance}\,{\rm driven}\,{\rm above}\,{\rm the}\,{\rm speed}\,{\rm limit}\,{\rm (in}\,{\rm multiples}\,{\rm of}\,{\rm 500}\,{\rm kilometers)}$$

$$\hskip-133pt S_{{it}}^{{(3)}} {\equals}{\rm distance}\,{\rm travelled}\,{\rm in}\,{\rm urban}\,{\rm zones}\,{\rm (inmultiples}\,{\rm of}\,{\rm 500}\,{\rm kilometers)}{\rm .}$$

The joint dynamics of the number of claims $$N_{{it}} $$ filed by policyholder $$i$$ during period $$t$$ and the three signals $$S_{{it}}^{{(j)}} $$ , $$j{\equals}1,2,3$$ , will be exploited to predict the future number of claims. To this end, we use the modelling approach proposed in Section 2.3.

Notice that these are not compositional data in the sense of Verbelen et al. (Reference Verbelen, Antonio and Claeskens2018). Such data model percent exposure and they have to cope with the restriction that percentages need to add up to 100% at the policyholder level. Here, the sum of the distances used as signals does not necessarily match the total distance travelled. Data on the total distance driven per year (in kilometers) is considered as an exposure to risk and as such enters our models as an offset. To avoid large dispersion, distance driven is expressed in hundreds of kilometers.

Let us briefly comment on the choice of these three signals. Night-time driving is usually associated to more accidents than day-time, especially at young ages (see, for instance, Williams, Reference Williams1985), and the first signal captures this effect. As pointed out by Bolderdijk et al. (Reference Bolderdijk, Knockaert, Steg and Verhoef2011), vehicle speed is commonly considered as the major determinant of crash risk for young adults. Specifically, these authors demonstrated that reducing the amount of time spent above the speed limit, holds the potential of dramatically reducing accidents. This is exactly the information captured by the second signal, time being here measured by the actual distance driven above the speed limits (integrating the total distance travelled by means of offset). Notice that the signal excess speed records the number of kilometers travelled at a speed in excess of the posted limit. However we do not have enough information to include the amount of excess, so we cannot distinguish between a driver who drives 10% faster or 20% than the posted limit. Finally, we note that urban areas are often congested and crash risk is higher there than in sub-urban or rural zones, because of heavy traffic. The third signal records the distance travelled in the accident-prone urban areas.

3.2. Descriptive statistics

The sample is made up of $$n{\equals}2,494$$ insured drivers followed over the three calendar years 2009–2011. All policyholders have been observed for three years (so that $$T_{i} {\equals}3$$ for all $$i$$ ). The mean age of all drivers in the sample in 2009 is 25.17 years (standard deviation 2.44). In the participating insurance company, the policies that involve collecting telematics information are only offered to young drivers (the maximum age in the sample being 30 years). Our sample comprised 51.60% of male drivers and 48.40% of female drivers.

In Table 1, we present descriptive statistics for telematics data observed in the sample for each year. It is worth stressing that distance driven dropped the last year. However, since we have distance driven as an offset in our model, we predict the expected number of claims per mileage, and therefore this is automatically corrected in the analysis.

Table 1 Sample statistics for raw telematic information by year ( $$n{\equals}2,494$$ ).

Our yearly responses are the number of claims, and then the number of count units of excess speed, night-time driving and urban driving (rounded in 500 s km). Our measure of exposure-to-risk is the distance driven measured as a continuous variable in 100 s km. Figure 1 shows four histograms of the raw telematics data in 2009. This helps to figure out the sample distribution of the total distance travelled as well as of the three signals entering the analysis.

Figure 1 Histograms of telematic information recorded in 2009 ( $$n{\equals}2,494$$ ).

Table 2 presents the counts information for the 3 years and the four counts once the signals of speed, night-time and urban are transformed in discrete counts in units of 500 s km. We can see there that the majority of claim counts as well as night-time and speed signals concentrate in low-frequency cells, whereas the counts of the signal urban are located in a higher frequency level. The information in Table 2 indicates that 2,004 drivers did not claim any accident in 2009 (2,038 and 2,091 in 2010 and 2011, respectively). In 2009, one policyholder claimed as much as six accidents, while the maximum number of claims was four in 2010 and 2011. A few policyholders recorded high levels of speed limit excess in 2009 and even a bit more in 2010.

Table 2 Counts of claims and driving signals (expressed in 500 s km) in 2009, 2010 and 2011.

3.3. Association between signals and claim counts

We focus specifically on the three signals $$S_{{it}}^{{(j)}} $$ because we expect a clear association between claims and excess speed, night-time driving and urban driving. We treat total driving distance as a total exposure offset. There is an extensive literature on how all these factors are associated to claiming. Ayuso et al. (Reference Ayuso, Guillen and Pérez-Marín2016, Reference Ayuso, Guillen and Nielsen2018) showed that information on speed excess, night-time driving and urban driving improves the prediction of the number of claims, compared to classical models not using telematics information. Guillen et al. (Reference Guillen, Nielsen, Ayuso and Pérez-Marín2018) provide an extended overview on how accumulated distance driven shows evidence that drivers improve their skills, a phenomenon that is known as the “learning effect.”

All this previous knowledge is the reason why we focus specifically on variables that reflect the driving habits, such as excess speed, night driving and urban driving, and for which we expect a clear association with the number of claims as well as distance driven. Let us now investigate the strength of this association on our data set. Figure 2 shows a correlation between the distance and the three raw indicators (speed, night-time, urban) in 2009–2011. Just by illustration in Figure 3, we also show the correlation between distance driven in the three observed years. As expected, distance driven correlates with the signals and between consecutive years. Notice that no correction has been made for standard risk factors at this stage so that the correlation may only be apparent, being generated by the confounding effects of the standard risk factors comprised in $${\mib{x}} _{{it}} $$ . The multivariate credibility model will precisely avoid this possible pitfall.

Figure 2 Correlation matrix of telematic information recorded in 2009–2011 ( $$n{\equals}2,494$$ ).

Figure 3 Correlation matrix of distance driven in 2009–2011 ( $$n{\equals}2,494$$ ).

3.4. Fitted models

Here, we assume that the joint dynamics of $$(N_{{it}} ,S_{{it}}^{{(1)}} ,S_{{it}}^{{(2)}} ,S_{{it}}^{{(3)}} )$$ , $$t{\equals}1,2,\,\ldots\,$$ , is described by the multivariate mixed Poisson model described in Section 2.3. Such mixed Poisson models are particular cases of Generalised Linear Mixed-effects Models (or GLMM). The glmer function included in the R package lme4 can be used to fit a GLMM which incorporates both fixed-effects parameters and random effects in a linear predictor, via maximum likelihood. The multivariate Poisson-LogNormal model for claim and signal counts considered in the present section was fitted using the glmer function which performs Poisson regression with structured random effects.

The expression for the likelihood of a mixed-effects model involves an integral over all the random effects. In our case, the likelihood associated to the observations $$(n_{{it}} ,s_{{it}}^{{(1)}} ,s_{{it}}^{{(2)}} ,s_{{it}}^{{(3)}} )$$ , $$t{\equals}1,2,3$$ , writes

$$\hskip -82pt{\scr L}{\equals}\prod\limits_{i{\equals}1}^n {\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty \prod\limits_{t{\equals}1}^3 \left{\vscale 115% \scale 131% \Bigg(} {\exp \left( {{\minus}d_{{it}} \exp (\eta _{{it}} {\plus}\delta )} \right){{\left( {d_{{it}} \exp (\eta _{{it}} {\plus}\delta )} \right)^{{n_{{it}} }} } \over {n_{{it}} \,!\,}}} \right.$$

$$\quad \left. {\prod\limits_{j{\equals}1}^3 \left( {\exp \left( {{\minus}d_{{it}} \exp (\nu _{{it}}^{{(j)}} {\plus}\gamma _{j} )} \right){{\left( {d_{{it}} \exp (\nu _{{it}}^{{(j)}} {\plus}\gamma _{j} )} \right)^{{s_{{it}}^{{(j)}} }} } \over {s_{{it}}^{{(j)}} }}} \right)} \right)f_{{\sum }} (\delta ,\gamma _{1} ,\gamma _{2} ,\gamma _{3} )d\delta d\gamma _{1} d\gamma _{2} d\gamma _{3} $$

where $$f_{\Sigma } $$ is the joint probability density function of the random vector $$(\Delta _{i} ,\Gamma _{i}^{{(1)}} ,\Gamma _{i}^{{(2)}} ,\Gamma _{i}^{{(3)}} )$$ , corresponding to the assumed multivariate Normal distribution with zero mean vector and variance-covariance matrix Σ. For a GLMM, the integral must be approximated with the help of quadrature formulas. Let us mention that to achieve convergence, some care is needed and appropriate control parameters must be selected in relation with the nonlinear optimiser. To ensure numerical stability of the optimisation algorithms, policyholder’s age has been rescaled (divided by 100). Gender is coded as 1 for male drivers and as 0 for female drivers. Also, different units have been tested for the three signals (in 100 and 1,000 km, without affecting the results).

Both fixed effects and random effects are specified via the model formula. The multivariate model considers claim counts and the three signals simultaneously. We fit the multivariate model at once following the approach proposed by Faraway (Reference Faraway2016, Section 9.3). The idea is to define count and signal identifiers by means of a categorical feature signalName with four levels, N, S1, S2 and S3, say, treated as fixed effects and to introduce an interaction between the signals and the other fixed effects, as well as corresponding four-dimensional policyholder-specific random effects. In order to get four correlated random effects between claim counts and the three signals, we need to specify the random effect structure as (-1+signalName|id) where id denotes the policy identifier (allowing the actuary to track the same contract over time) entering model formula.

To illustrate the relevance of the approach proposed in this paper, we compare the multivariate credibility model described above, including past claims history as well as the three signals, with a classical credibility model, based on claim counts only. More precisely, we fit univariate mixed Poisson models for panel data, separately for each signal and the number of claims. The results for the univariate models can be considered as those obtained by replacing the covariance matrix Σ with a diagonal one, with marginal variances along the main diagonal. In the univariate modelling, the four responses $$N_{{it}} $$ , $$S_{{it}}^{{(1)}} $$ , $$S_{{it}}^{{(2)}} $$ and $$S_{{it}}^{{(3)}} $$ are thus considered to be mutually independent (but serial dependence for fixed $$i$$ is taken into account in all four cases). In the univariate approach (i.e. considering claim counts, or each signal, in isolation), the random effects are included by means of the component (1|id) entering model formula. In this case, only past claim experience is used to update the expected number of claims in future years.

Table 3 presents the results of the univariate and the multivariate counts models (estimated with the 3-year panel 2009–2011). The difference between the univariate approach and the multivariate approach is that the former only considers one of the signals at a time and it completely ignores the association between them. However, the reason to introduce a multivariate framework is that, for instance a claim in 2009 can influence the driver in such a way that he or she drives more carefully in 2010 in terms of excess speed and even in the total distance. This phenomenon had been noted before (see Guillen and Pérez-Marín, Reference Guillen and Pérez-Marín2018) but it had not been studied in the way it is done here.

Table 3 Model results for panel data on claims and driving count signals, 2009–2011.

$$^{{{\asterisk}{\asterisk}{\asterisk}}} p\,\lt\,0.001$$ , $$^{{{\asterisk}{\asterisk}}} p\,\lt\,0.01$$ , $$^{{\asterisk}} p\,\lt\,0.05$$ .

We see that age has an overall effect that is negative, meaning that the older the driver the less claims are expected. Here we chose a linear effect because the interval of ages is small for this sample of young drivers and we could not find a non-linear association. We also tried interactions between age and gender, but again we could not find significant cross-effects.

The joint dynamics of the number of claims $$N_{{it}} $$ filed by policyholder $$i$$ during period $$t$$ and the three signals $$S_{{it}}^{{(1)}} $$ , $$S_{{it}}^{{(2)}} $$ and $$S_{{it}}^{{(3)}} $$ is as follows. In the multivariate modelling, the correlation structure and the serial dependence are both taken into account for the four responses $$N_{{it}} $$ , $$S_{{it}}^{{(1)}} $$ , $$S_{{it}}^{{(2)}} $$ , and $$S_{{it}}^{{(3)}} $$ : precisely, given centred, multivariate Normally-distributed random effects $$(\Delta _{i} ,\Gamma _{i}^{{(1)}} ,\Gamma _{i}^{{(2)}} ,\Gamma _{i}^{{(3)}} )$$ , the responses are Poisson distributed with respective conditional means

$${\rm E}[N_{{it}} \,\mid\,\Delta _{i} ]{\equals}d_{{it}} \exp \left( {{\minus}5.08{\minus}5.21{\rm age}_{i} {\minus}0.11{\rm I}[{\rm gender}_{i} {\equals}{\rm male}]{\plus}\Delta _{i} } \right)$$

$$\hskip-30pt {\rm E}[S_{{it}}^{{(1)}} \,\mid\,\Gamma _{i}^{{(1)}} ]{\equals}d_{{it}} \exp (({\minus}5.08{\plus}0.76){\plus}({\minus}5.21{\plus}3.84){\rm age}_{i} $$

$$\qquad \qquad \qquad \qquad {\plus}({\minus}0.11{\plus}0.49){\rm I}[{\rm gender}_{i} {\equals}{\rm male}]{\plus}\Gamma _{i}^{{(1)}} )$$

$$\hskip-30pt {\rm E}[S_{{it}}^{{(2)}} \,\mid\,\Gamma _{i}^{{(2)}} ]{\equals}d_{{it}} \exp (({\minus}5.08{\plus}1.78){\plus}({\minus}5.21{\plus}0.76){\rm age}_{i} $$

$$\qquad \qquad \qquad \qquad {\plus}({\minus}0.11{\plus}0.34){\rm I}[{\rm gender}_{i} {\equals}{\rm male}]{\plus}\Gamma _{i}^{{(2)}} )$$

$$\hskip-30pt {\rm E}[S_{{it}}^{{(3)}} \,\mid\,\Gamma _{i}^{{(3)}} ]{\equals}d_{{it}} \exp (({\minus}5.08{\plus}2.47){\plus}({\minus}5.21{\plus}3.02){\rm age}_{i} $$

$$\qquad \qquad \qquad \qquad {\plus}({\minus}0.11{\plus}0.14){\rm I}[{\rm gender}_{i} {\equals}{\rm male}]{\plus}\Gamma _{i}^{{(3)}} ).$$

The estimated fixed effects are coherent between the multivariate and univariate models so that the estimated scores $$\widehat{\eta }_{{it}} $$ and $$\widehat{\nu }_{{it}}^{{(j)}} $$ are very similar in both cases. The main advantage of the multivariate model is to estimate the covariance matrix Σ of the random vector $$(\Delta _{i} ,\Gamma _{i}^{{(1)}} ,\Gamma _{i}^{{(2)}} ,\Gamma _{i}^{{(3)}} )$$ which connects claim counts $$N_{{it}} $$ to corresponding signals $$(S_{{it}}^{{(1)}} ,S_{{it}}^{{(2)}} ,S_{{it}}^{{(3)}} )$$ .

The estimated covariance matrix $$\widehat{\Sigma }$$ is as follows. The marginal standard deviations are estimated to

$$\widehat{\sigma }_{\Delta } {\equals}0.836$$

$$\widehat{\sigma }_{{\Gamma ,1}} {\equals}0.521$$

$$\widehat{\sigma }_{{\Gamma ,2}} {\equals}0.753$$

$$\widehat{\sigma }_{{\Gamma ,3}} {\equals}0.438.$$

The estimated correlation coefficients are given by

$$\widehat{\rho }_{{\Delta ,\Gamma ,1}} {\equals}0.019$$

$$\widehat{\rho }_{{\Delta ,\Gamma ,2}} {\equals}{\minus}0.204$$

$$\widehat{\rho }_{{\Delta ,\Gamma ,3}} {\equals}0.602$$

$$\widehat{\rho }_{{\Gamma ,1,2}} {\equals}0.026$$

$$\widehat{\rho }_{{\Gamma ,1,3}} {\equals}0.058$$

$$\widehat{\rho }_{{\Gamma ,2,3}} {\equals}{\minus}0.484.$$

We see that signal 1 (night-time driving) brings little information about claim counts in our data basis. The effects of signals 2 and 3 clearly dominate with respective correlations of about 20% and 60%, exhibiting opposite signs. Signal 3 (urban driving) appears to be the most informative, and negatively correlated to signal 2 (excess speed). This can be explained by traffic congestion, reducing speed in urban areas. On our data set, the estimated correlation between $$\Delta _{i} $$ and $$\Gamma _{i}^{{(2)}} $$ appears to be negative. This can be attributed to the way excess speed has been recorded in the data basis, without distinctions between small and large violations of the posted speed limit.

3.5. A posteriori corrections

The multivariate model does not outperform the classical, univariate one on aggregate. This is easily seen from Table 3, by noticing that the estimated fixed effects are very similar for the claim count component of the multivariate model and the univariate model for claim counts, only. In fact, a simple Poisson GLM with an intercept would produce predicted numbers of claims close to the observed ones (provided the portfolio experience is stationary) both at the portfolio level and within sub-portfolios. This comes from the marginal totals constraints imposed by the likelihood equations. The added value of the multivariate model proposed in this paper consists in refined individual premium corrections, as explained next.

The credibility approach consists in predicting the number of claims for next year using the conditional distribution of the response given past experience. Here, past experience gathers the observed numbers of claims filed in the past for the univariate model. In the multivariate case, it also includes the history of the three signals. Approximations for the predictions can be obtained using large-sample results such as formula (3.21) on page 151 of Wood (Reference Wood2017) giving the a posteriori, or predictive distribution of the estimated regression coefficients and random effects (used in the ranef function of glmer that extracts the conditional modes of the random effects from the fitted model). Here, we prefer to implement exact formulas for a posteriori expectations in the proposed credibility model.

The expected number of claims $$N_{{i,T_{i} {\plus}1}} $$ to be filed by policyholder $$i$$ in year $$T_{i} {\plus}1$$ given past numbers of claims $$N_{{it}} {\equals}k_{{it}} $$ , $$t{\equals}1,2,\,\ldots\,,T_{i} $$ , and past values of signals $$S_{{it}}^{{(j)}} {\equals}l_{{it}}^{{(j)}} $$ , $$t{\equals}1,2,\,\ldots\,,T_{i} $$ , $$j{\equals}1,2,3$$ , can be obtained as follows. As random effects are static, past experience is more conveniently summarised into the statistics

$$k_{i} {\equals}\mathop{\sum}\limits_{t{\equals}1}^{T_{i} } k_{{it}} {\rm\; and\;}l_{i}^{{(j)}} {\equals}\mathop{\sum}\limits_{t{\equals}1}^{T_{i} } l_{{it}}^{{(j)}} .$$

Also, we define

$$\lambda _{i} {\equals}\mathop{\sum}\limits_{t{\equals}1}^{T_{i} } \lambda _{{it}} {\equals}\mathop{\sum}\limits_{t{\equals}1}^{T_{i} } \exp (\ln d_{{it}} {\plus}\eta _{{it}} ){\rm \;and\;}\mu _{i}^{{(j)}} {\equals}\mathop{\sum}\limits_{t{\equals}1}^{T_{i} } \exp (\ln d_{{it}} {\plus}\eta _{{it}}^{{(j)}} ).$$

Then,

$${\rm E}[N_{{i,T_{i} {\plus}1}} \,\mid\,N_{{i1}} {\equals}k_{{it}} ,S_{{it}}^{{(j)}} {\equals}l_{{it}}^{{(j)}} ,t{\equals}1,2,\,\ldots\,,T_{i} ,j{\equals}1,2,3]$$

$$\hskip26pt {\equals}{\rm E}[N_{{i,T_{i} {\plus}1}} \,\mid\,N_{{i1}} {\plus}\,\ldots\,{\plus}N_{{iT_{i} }} {\equals}k_{i} ,S_{{i1}}^{{(j)}} {\plus}\,\ldots\,{\plus}S_{{iT_{i} }}^{{(j)}} {\equals}l_{i}^{{(j)}} ,j{\equals}1,2,3]$$

$$\eqalignno { & \hskip-46pt {\equals}d_{{i,T_{i} {\plus}1}} \exp (\eta _{{i,T_{i} {\plus}1}} ){\rm E}[\exp (\Delta _{i} )\,\mid\,N_{{i1}} {\plus}\,\ldots\, \cr &\hskip-20pt{\plus}N_{{iT_{i} }} {\equals}k_{i} ,S_{{i1}}^{{(j)}} {\plus}\,\ldots\,{\plus}S_{{iT_{i} }}^{{(j)}} {\equals}l_{i}^{{(j)}} ,j{\equals}1,2,3]$$

$$\hskip-149pt{\equals}d_{{i,T_{i} {\plus}1}} \exp (\eta _{{i,T_{i} {\plus}1}} ){A \over B}$$

where

$$A{\equals}(k_{i} {\plus}1){\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty \exp \left( {{\minus}\lambda _{i} \exp (\delta )} \right)\left( {\exp (\delta )} \right)^{{k_{i} {\plus}1}} $$

$$\hskip130pt\prod\limits_{j{\equals}1}^3 \left(\exp \left( {{\minus}\mu _{i}^{{(j)}} \exp (\gamma _{j} )} \right)\left( {\exp (\gamma _{j} )} \right)^{{l_{i}^{{(j)}} }} \right)f_{{\bf \sum}} (\delta ,\gamma _{1} ,\gamma _{2} ,\gamma _{3} )d\delta d\gamma _{1} d\gamma _{2} d\gamma _{3} $$

$$\hskip-40pt B{\equals}{\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty {\int}_{{\minus}\infty}^\infty \exp \left( {{\minus}\lambda _{i} \exp (\delta )} \right)\left( {\exp (\delta )} \right)^{{k_{i} }} $$

$$\quad \prod\limits_{j{\equals}1}^3 \left(\exp \left( {{\minus}\mu _{i}^{{(j)}} \exp (\gamma _{j} )} \right)\left( {\exp (\gamma _{j} )} \right)^{{l_{i}^{{(j)}} }} \right)f_{{\bf \sum}} (\delta ,\gamma _{1} ,\gamma _{2} ,\gamma _{3} )d\delta d\gamma _{1} d\gamma _{2} d\gamma _{3} .$$

The updating coefficient is thus given by $$A\,/\,B$$ . The integrals involved in $$A$$ and $$B$$ can be computed numerically with quadrature formulas as implemented in the R package MultiGHQuad.

In the univariate case, we simply get the ratio of two Mellin transforms:

$${\rm E}[N_{{i,T_{i} {\plus}1}} \,\mid\,N_{{i1}} {\equals}k_{{it}} ,t{\equals}1,2,\,\ldots\,,T_{i} ]{\equals}{\rm E}[N_{{i,T_{i} {\plus}1}} \,\mid\,N_{{i1}} {\plus}\,\ldots\,{\plus}N_{{iT_{i} }} {\equals}k_{i} ]$$

$$\hskip53pt{\equals}d_{{i,T_{i} {\plus}1}} \exp (\eta _{{i,T_{i} {\plus}1}} ){\rm E}[\exp (\Delta _{i} )\,\mid\,N_{{i1}} {\plus}\,\ldots\,{\plus}N_{{iT_{i} }} {\equals}k_{i} ]$$

$$\hskip-76pt {\equals}d_{{i,T_{i} {\plus}1}} \exp (\eta _{{i,T_{i} {\plus}1}} ){C \over D}$$

where

$$\hskip33pt C{\equals}(k_{i} {\plus}1){\int}_{{\minus}\infty}^\infty \exp \left( {{\minus}\lambda _{i} \exp (\delta )} \right)\left( {\exp (\delta )} \right)^{{k_{i} {\plus}1}} f_{{\sigma _{\Delta }^{2} }} (\delta )d\delta $$

$$\hskip-8ptD{\equals}{\int}_{{\minus}\infty}^\infty \exp \left( {{\minus}\lambda _{i} \exp (\delta )} \right)\left( {\exp (\delta )} \right)^{{k_{i} }} f_{{\sigma _{\Delta }^{2} }} (\delta )d\delta $$

where $$f_{{\sigma _{\Delta }^{2} }} $$ is the probability density function of the Normal distribution with zero mean and variance $$\sigma _{\Delta }^{2} $$ .

Let us now demonstrate the added value of the multivariate model by computing individual premium corrections. The boxplots of the values of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}} ]$$ based on the multivariate model involving the three signals and of the values of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}}^{{{\rm claim}}} ]$$ based on the univariate model (i.e. the classical credibility construction based on the Poisson-LogNormal model for claim counts) are displayed in Figure 4. Apart from the common increasing trend according to the number of claims $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} $$ filed during the observation period, we see that there is more dispersion in the $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}} ]$$ values compared to the $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}}^{{{\rm claim}}} ]$$ values, because of the variety in the signal.

Figure 4 Boxplots of the values of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}} ]$$ based on the multivariate model (left panel) and of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}}^{{{\rm claim}}} ]$$ (right panel) obtained from the univariate model, according to the total number of claims $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} $$ filed during the observation period.

Let us now compare the values of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}} ]$$ based on the multivariate model involving the three signals to the values of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}}^{{{\rm claim}}} ]$$ obtained from the univariate model for claim counts, only, according to the total number of claims $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} $$ filed during the observation period. The numerical values are displayed in Figure 5. For claim-free policyholders, we see that the univariate model always grants a discount whereas its multivariate counterpart may impose a penalty, depending on the experience with signals. When a single claim is reported, both univariate and multivariate models may still award a discount or induce a penalty. For the univariate model, it depends on the a priori features of the driver (a priori riskier drivers are less penalised when a claim is reported to the company). For the multivariate model, it depends on the a priori features as well as on the experience recorded on signals. When two claims are reported, the univariate model always imposes a penalty whereas its multivariate counterpart may still award a discount, based on favourable experience related to signals. When three claims (or more) are reported, both the univariate and multivariate models impose a penalty, but its extent also depends on the signals in the multivariate case.

Figure 5 Values of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}} ]$$ based on the multivariate model and of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}}^{{{\rm claim}}} ]$$ obtained from the univariate model, according to the total number of claims filed during the observation period: $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}0$$ (top left), $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}1$$ (top right), $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}2$$ (bottom left), and $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}3$$ (bottom right).

Let us now consider a male policyholder with average age and driving the average annual distance. Also, we fix the signals 1 and 2 at their average value, but we let the third signal vary from 0 to its maximal value given the assumed total mileage. Based on the number of claims reported during the three years, we compute the a posteriori corrections to assess the impact of the signal. The results are displayed in Figure 6. For a policyholder without claim ( $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}0$$ ), we see that having a better driving style (small value of the signal) increases the discount compared to the classical credibility correction based on past claims, only (represented by the horizontal line on the graph). For a policyholder having reported a single claim, ( $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}1$$ ), we see that depending on the value of the signal, the premium may increase or decrease (whereas it moderately increases using the classical credibility formula). Hence, the signal can compensate for the effect of a single claim. When two or three claims are reported, the policyholder suffers a penalty whatever the value of the signal, but the latter can attenuate the penalty compared to the classical credibility model based on past claim experience, only.

Figure 6 Values of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}} ]$$ for an hypothetical male, mean-aged driver in function of the distance travelled in urban areas, based on the multivariate model and of $${\rm E}[\exp (\Delta _{i} )\,\mid\,{\scr H}_{{i,3}}^{{{\rm claim}}} ]$$ obtained from the univariate model, according to the total number of claims filed during the observation period: $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}0$$ (top left), $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}1$$ (top right), $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}2$$ (bottom left), and $$N_{{i1}} {\plus}N_{{i2}} {\plus}N_{{i3}} {\equals}3$$ (bottom right).