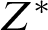1 Symétrons
Nous rappelons qu'un espace symétrique est une structure dans le langage d'une fonction binaire
$s(x,y)$
satisfaisant aux équations suivantesFootnote
1
:
-
1.
$s(x,x) = x,$
-
2.
$s(s(x,y),y) = x,$
-
3.
$s(s(x,z),s(y,z)) = s(s(x,y),z).$
Ou, quand la fonction est notée comme une loi binaire
$s(x,y) = x*y$
:
-
1.
$x*x = x,$
-
2.
$(x*y) * y = x,$
-
3.
$(x*z) * (y*z) = (x*y) * z.$
A y fixé, la fonction unaire
$s(x,y)$
est appelée symétrie de centre y,
$s(x,y)$
étant le symétrique de x par rapport à y; nous noterons également
$s_y(x)$
cette symétrie de centre y.
Les deux premières équations signifient que chaque symétrie est une application involutive qui fixe son centre, et la dernière que chaque symétrie est un automorphisme de la structure; elle équivaut, en posant
$u = s(x,z) $
, à l'équation
$s(u,s(y,z)) = s(s(s(u,z),y),z)$
, qui signifie que la symétrie
$s_z$
conjugue la symétrie de centre y et la symétrie de centre
$s_z(y)$
.
Par exemple l'application
$s(x,y) = x$
définit un espace symétrique sur n'importe quel ensemble, pour lequel chaque symétrie est l'application-identité. Plus substantiellement, n'importe quel groupe est un espace symétrique pour l'opération
$s(x,y) = y.x^{-1}.y$
.
Pour une raison que nous éclaircirons plus tard, les sous-structures d'un espace symétrique S, c'est-à-dire ses sous-ensembles clos pour l'opération
$s(x,y)$
, sont qualifiées de sous-ensembles convexes de S.
Les permutations de S qui sont produits de deux symétries sont appelées transvexions primaires, et leur ensemble est noté
$T_1(S); T_n(S)$
note l'ensemble des produits de
$2^{n}$
symétries, et la réunion des
$T_n(S)$
est le groupe
$T(S)$
des transvexions de S, formé des produits d’un nombre pair de symétries; le groupe engendré par les symétries est
$ST(S) = T(S) \cup s_{u}.T(S)$
pour n'importe quelle symétrie
$s_{u}$
, les produits d'un nombre impair de symétries étant appelés réflexions de S.
Chaque
$T_{n}(S)$
est normal dans
$ST(S)$
.
Nous dirons que
$T(S)$
est borné si
$T(S) = T_{n}(S)$
pour n assez grand; ce terme est préférable à définissable, car les
$T_{n}(S)$
ne sont pas en général inclus naturellement dans un même ensemble définissable.
Les symétries de l'espace symétrique S forment elles-mêmes un espace symétrique
$\varSigma (S)$
quand on interprète
$s(\sigma ,\tau )$
par la conjugaison
$\tau .\sigma .\tau $
de
$\sigma $
par
$\tau $
, à l'intérieur du groupe des permutations de S; si à un point y de S on associe la symétrie de centre y, on obtient un homomorphisme de S sur
$\varSigma (S)$
.
Un espace symétrique est dit injectif si chacune de ses symétries n'a qu'un seul point fixe, c'est-à-dire s'il satisfait à l'axiome universel:
$s(x,y) = x \Rightarrow x = y$
; il est alors isomorphe à l'espace symétrique de ses symétries.
Un espace symétrique injectif (même réduit à un point!) correspond donc à la donnée, dans un groupe, d'un ensemble d'involutions clos par conjugaison et ne commutant pas deux-à-deux; il convient de remarquer que deux tels ensembles d'involutions peuvent définir des espaces symétriques isomorphes sans engendrer des groupes isomorphes: si
$\varSigma $
est l'un d'entre eux, engendrant un groupe G,
$ST(\varSigma )$
est le quotient de G par son centreFootnote
2
. Ce n'est pas a priori une structure bien exigeante car, étant donnés deux points, il peut y avoir plusieurs, ou aucune, symétries qui les échangent.
Un espace symétrique est dit surjectif si, pour chaque couple de points x et y, il existe une symétrie qui les échangeFootnote 3 .
L'espace symétrique d'un groupe G est injectif si et seulement si G ne contient pas d'involutions, c'est-à-dire pas de points d'ordre deux différents de l'élément neutre; en effet, a.i est un point fixe de la symétrie
$a.x^{-1}.a$
si et seulement si
$i^{2} = 1$
. Il est surjectif si et seulement si tout point de G est un carré; en effet
$a.x^{-1}.a = y$
si et seulement si
$(a.x^{-1})^{2} = y.x^{-1}$
.
Plaçons-nous maintenant dans l'espace
$\varSigma (G)$
des symétries du groupe G. Les symétries
$a.x^{-1}.a$
et
$b.x^{-1}.b$
sont égales, c'est-à-dire
$a.x^{-1}.a = b.x^{-1}.b$
pour tout x, soit encore
$b^{-1}.a = x^{-1}.b.a^{-1}.x$
pour tout x, si et seulement si
$i = b.a^{-1}$
est central (car il n'a qu'un seul conjugué) et
$i^{2} = 1$
(poser
$x = a$
). On voit de même qu'elles commutent si et seulement si
$i^{4} = 1$
et
$i^{2}$
est central;
$\varSigma (G)$
est donc injectif si et seulement si la deuxième condition implique la première, c'est-à-dire si le quotient
$G_{1}$
de G par le groupe des involutions centrales de G n'a pas d'involutions;
$\varSigma (G)$
est alors isomorphe à
$\varSigma (G_{1})$
, et à l'espace symétrique de
$G_{1}$
.
Si S est un espace symétrique injectif, pour chacun de ses points u nous notons
$S_{u}$
le translaté
$s_{u}.\varSigma = \varSigma .s_{u}$
de
$\varSigma $
par la symétrie
$s_{u} $
; il est formé des transvexions primaires de la forme
$s_{u}.s_{v}$
, où de façon équivalente
$s_{w}.s_{u} = s_{u}.(s_{u}.s_{w}.s_{u})$
;
$S_{u}$
est une partie convexe du groupe T(S), sur laquelle l'application
$y.x^{-1}.y$
définit un espace symétrique isomorphe à S, par l'application qui à v associe
$s_{u}.s_{v}$
, puisque
$s_{u}.s_{v}.(s_{u}.s_{w})^{-1}.s_{u}.s_{v} = s_{u}.(s_{v}.s_{w}.s_{v})$
; elle engendre T(S), tout point de
$T_{1}(S)$
étant produit de deux points de
$S_{u}$
, puisque
$s_{v}.s_{w} = s_{u}.s_{u}.s_{v}.s_{u}.s_{u}.s_{w} = (s_{u}.s_{u}.s_{v}.s_{u}).(s_{u}.s_{w})$
. Dans
$\varSigma $
, qui se compose d'involutions, les symétries sont des conjugaisons; mais ce qui est transporté par translation, c'est la symétrie, pas la conjugaison!
On voit donc qu'un espace symétrique injectif est isomorphe à celui défini par une partie convexe et génératrice de son groupe de transvexions.
Remarque 1. Les groupes ST(S),
$ST(\varSigma )$
et
$ST(S_{u})$
sont isomorphes, mais pas identiques puisqu'ils n'agissent pas sur le même ensemble. Si
$t = s_{1}.\ldots .s_{n}$
est un produit de n symétries de S, chacune agit par conjugaison sur Σ, sur lequel l'action de t est
$t.\sigma .t^{-1}$
.
Son action sur
$S_{u} = s_{u}.\varSigma = \varSigma .s_{u}$
comme composé de symétries est
$s_{u}ts_{u}.s_{u}\sigma .t^{-1}$
, ou, si on préfère l'autre côté,
$t.\tau s_{u}.s_{u}t^{-1}s_{u}$
; en particulier, quand t est la symétrie s, c'est
$s_{u}ss_{u}.s_{u}\sigma .s = s_{u}s.(s_{u}\sigma )^{-1}.s_{u}s$
. Si t commute avec
$s_{u}$
, il agit par conjugaison sur
$S_{u}$
; c'est ainsi que
$s_{u}$
inverse
$S_{u}$
.
Nous appellerons symétron un espace symétrique pour lequel, étant donnés x et y, il existe un unique z tel que
$s(x,z) = y$
; nous qualifions ce point z de milieu de x et de y. Un symétron est à la fois injectif et surjectif.
Un simple comptage montre qu'un espace symétrique surjectif fini est en fait un symétron, et le Lemme 1(vii) qui suit affirme qu'il en est de même d'un espace symétrique injectif fini.
Les symétries du groupe G forment un symétron si et seulement si chaque point de G a une unique racine carrée; nous dirons qu'un tel groupe est médial. Nous dirons aussi qu'un groupe est sous-médial si la racine carrée y est unique à condition d'exister, c'est-à-dire si
$x^{2} = y^{2}$
implique
$x = y$
.
En résumé, la donnée d'un symétron équivaut à celle, dans un groupe, d'un ensemble Σ d'involutions vérifiant les deux conditions suivantes:
-
(i) pour tous a et b dans
$\varSigma $
, a.b.a est dans
$\varSigma $
; -
(ii) pour tous a et b dans Σ, il existe un unique c dans Σ tel que
$c.a.c = b$
.
Elle équivaut également à la donnée d'une partie convexe X d'un groupe telle que, pour tous a et b dans X, il existe un unique c dans X tel que
$c.a^{-1}.c = b$
.
Il est avantageux de décrire les symétrons dans le langage des deux fonctions binaires
$m(x,y)$
et
$s(x,y)$
(milieu et symétrie); bien sûr, chacune permet de définir l'autre (en effet, z est le symétrique de x par rapport à y si et seulement si y est le milieu de x et de z), mais il faut faire ainsi si nous voulons une classe équationelle, et la stabilité par sous-structure. Dans ce langage, un symétron est une structure satisfaisant aux quatre équations suivantes:
-
2.
$s(s(x,y),y) = x$
; -
3.
$s(s(x,z),s(y,z)) = s(s(x,y),z)$
; -
4.
$s(x,m(x,y)) = y$
; -
5.
$m(x,s(x,y)) = y$
.
En effet, comme les équations 4 et 5 signifient que, à x fixé, milieu et symétrie sont des fonctions unaires inverses l'une de l'autre, il ne reste à vérifier que que chaque symétrie fixe son centre, c'est-à-dire que
$x = s(x,x) = m(x,x)$
; cela vient de ce que, comme
$x = s(s(x,x),x) = s(s(x,x),s(x,x)), x\ \text{et}\ s(x,x)$
sont tous les deux le milieu de x et de
$s(x,x)$
. On remarque que 2 peut être remplacée par 2'.
$m(x,y) = m(y,x)$
, et 3 par 3'.
$s(m(x,y),z) = m(s(x,z),s(y,z))$
.
Dans le langage du milieu, les axiomes de symétron sont les suivants:
$m(x,x) = x; m(x,y) = m(y,x)$
; pour tous x et z il existe un unique y tel que
$m(x,y) = z$
; quant à la l'équation 3, elle est remplacée par l'Axiome du losange: si
$z = m(x,u) = m(y,v)$
, alors
$m(m(x,y),m(u,v)) = z$
.
Si X est un sous-ensemble du symétron S, son symétriseur
$Sym(X)$
est l'ensemble de ses centres de symétrie, c'est-à-dire l'ensemble des u tels que
$s_u(X) = X$
; X est convexe s'il est inclus dans son symétriseur;
$Sym(X)$
est lui-même convexe, puisque la symétrie de centre
$s_u(v)$
est
$s_u.s_v.s_u$
. On remarque que, si X n'est pas vide,
$Sym(X)$
s'injecte dans X; en effet, fixant a dans X, à chaque y de
$Sym(X)$
nous associons
$x = s_y(a)$
; comme y est le milieu de x et de a, il s'agit bien d'une injection.
Lemme 1. Dans un espace symétrique injectif S:
-
(i) Deux symétries ne commutent que si elles sont égales.
-
(ii) Une transvexion ou une réflexion fixe le point u si et seulement si elle commute avec
$s_u$
, et alors elle normalise
$S_u$
. -
(iii) Il n'y a pas de transvexions primaires involutives (autres que l'identité).
-
(iv) Toute puissance d'une transvexion primaire est une transvexion primaire; plus précisément, si t est dans
$S_u$
,
$t^n$
aussi. -
(v) Le centre de
$T(S)$
est formé des transvexions qui sont inversées par conjugaison par chaque symétrie; il ne contient pas d'involutions. -
(vi) S est un symétron si et seulement si, pour chaque u, chaque point de
$S_u$
a une unique racine carrée dans
$S_u$
. -
(vii) Si S est oméga-stable ou si
$T_1(S)$
est périodique, S est un symétron; de plus chaque point de
$T_1(S)$
a alors une unique racine carrée dans
$T_1(S)$
, qui est son unique racine carrée dans
$T(S)$
si ce dernier n'a pas d'involutions.
-
(i) Elles ont même point fixe.
-
(ii) La conjuguée de
$s_u$
par cette application est une symétrie, qui fixe u. Nous avons remarqué que son action sur
$S_u$
se fait alors par conjugaison. -
(iii) Si
$(s_u.s_v)^2$
vaut l'identité,
$s_u$
et
$s_v$
commutent, et sont égales. -
(iv)
$(s_{u}.s_{v})^{n} = s_{u}.s_{v}.(s_{u}.s_{v})^{n-1}$
; or
$s_{v}.(s_{u}.s_{v})^{n-1}$
, étant exprimé par un mot symétrique de longueur impaire, est une symétrie. -
(v) Soient t une transvexion centrale et
$s_{u}$
une symétrie; posons
$t' = s_{u}.t.s_{u}$
; comme t commute avec
$s_{v}.s_{u}$
, chaque symétrie
$s_{v}$
échange t et t'; les symétries induisent donc un même automorphisme involutif
$\sigma$
sur le centre de
$T(S)$
;
$t.\sigma (t)$
est fixé par
$\sigma$
, commute avec tous les
$s_{u}$
, et vaut donc l'identité, si bien que
$\sigma (t) = t^{-1}$
. Réciproquement, si la transvexion t est inversée par chaque symétrie, elle commute avec chaque transvexion, et si de plus
$t = t^{-1}$
elle fixe chaque point de S et vaut l'identité. -
(vi)
$s_{v} = s_{w}.s_{u}.s_{w}$
si et seulement si
$s_{u}.s_{v} = s_{u}.(s_{w}.s_{u}.s_{w}) = (s_{u}.s_{w})^{2}$
. -
(vii) Nous considérons
$a = s_{u}.s_{v}$
et l'ensemble C des points de
$S_{u}$
qui commutent avec tous les points de
$S_{u}$
qui commutent avec a; C est un ensemble convexe commutatif définissable qui contient a et 1; si x et y sont dans C,
$x^{2}.y^{-1} = y^{-1}.x^{2}$
est aussi dans C, si bien que ce dernier est clos par élévation au carré et passage à l'inverse.
Nous observons aussi que l'élévation au carré est injective de C dans C; en effet, si
$y^{2} = z^{2}$
où y et z sont dans C, comme ils commutent
$y.z^{-1}$
est d'ordre 2, et appartient à
$T_{1}(S)$
qui ne contient pas d'involutions.
Dans le cas périodique, si x est dans C ses puissances
$2^{n}$
-ièmes forment un ensemble fini inclus dans C; comme l'élévation au carré est une injection de cet ensemble dans lui-même, elle est bijective et x a une racine carrée dans C; par conséquent C est un groupe.
Dans le cas oméga-stable, comme l'élévation au carré est injective, tout point générique de C (c-à-d dont le type est de rang de Morley maximal) est le carré d'un point de C, et son carré est aussi générique. Si x est générique sur y, c-à-d si
$RM(x/y) = RM(C)$
,
$x^{4}.y^{-1}$
est générique, et c'est le carré d'un point z de C; il en est de même de
$y = (x^{2}.z^{-1})^{2}$
; on en conclut pareillement que C est un groupe (commutatif et médial).
Par conséquent a possède une racine carrée b dans C; si b' est une racine carrée de a dans
$S_{u}$
, b et b' commutent, si bien que
$b^{-1}.b'$
est d'ordre deux; comme c'est un point de
$T_{1}(S)$
,
$b = b'$
.
Supposons que a ait aussi une racine carrée c dans
$S_{v}$
, ce qui implique que a est dans
$S_{u} \cap S_{v}$
; comme a appartient à un groupe commutatif C inclus dans
$S_{u}$
, et à un autre C' inclus dans
$S_{v}$
, et que
$C \cap C'$
est définissable dans le cas oméga-stable, ce dernier est 2-divisible, et l'unique racine carrée b de a dans
$S_{u}$
est aussi son unique racine carrée c dans
$S_{v}$
.
Comme
$T_{1}(S)$
est normal, tout point de ST(S) qui commute avec un point a de
$T_{1}(S)$
commute aussi avec son unique racine carrée b située dans
$T_{1}(S)$
, et les autres racines carrées de a sont de la forme b.i, où i est une involution qui commute avec a.⊣
Remarque 2. Ce lemme met en évidence le fait fondamental sur lequel s'appuient toutes les démonstrations qui suivent: dans un symétron oméga-stable, deux points sont toujours inclus dans un sous-symétron définissable isomorphe aux symétries d'un groupe commutatif médial.
Lemme 2. Dans un symétron S:
-
(i) Une réflexion ou transvexion involutive a au moins un point fixe, et si elle n'en a qu'un seul c'est une symétrie.
-
(ii) Si une transvexion primaire a un point fixe, elle vaut l'identité.
-
(iii) Etant donné trois points u, x et y de S, il existe un unique v dans S tel que
$s_{u}.s_{v}(x) = y$
. -
(iv) Les transvexions primaires sont les commutateurs des symétries; T(S) est le groupe dérivé de ST(S).
-
(v) Le centre de T(S) est l'intersection des
$S_{u}$
; il est médial quand S est oméga-stable ou quand
$T_{1}(S)$
est périodique.
-
(i) Soit t involutif dans ST(S); pour chaque x de S, t échange x et t(x), et fixe leur milieu u; si u est son unique point fixe, t est égale à
$s_{u}$
. -
(ii) Supposons que
$s_{u}.s_{v}$
fixe x, dont nous notons y l'image par
$s_{v}$
; ces deux symétries échangent x et y, ont toutes deux pour centre le milieu de x et de y, et sont donc égales. -
(iii) Cela signifie que
$s_{v}.s_{u}(y) = x$
, soit encore que
$v$
est le milieu de
$s_{u}(y)$
et de x. -
(iv)
$s_{u}.s_{v} = s_{u}.(s_{w}.s_{u}.s_{w}) = [s_{u}.s_{w}]$
, où w est le milieu de u et de
$v$
. -
(v) Soient t une transvexion centrale et u un point de S; comme
$s_{u}$
inverse t,
$s_{u}.t$
est une involution; si
$v$
est un de ses points fixes,
$s_{v}.s_{u}.t = s_{u}.t.s_{v}$
, soit encore, en faisant commuter t et
$s_{v}.s_{u}$
,
$s_{v}.s_{u}.s_{v} = t^{-1}.s_{u}.t$
, si bien que
$v$
est le milieu de u et du centre
$t^{-1}(u)$
de la symétrie
$t^{-1}.s_{u}.t$
; l'involution
$s_{u}.t$
, n'ayant qu'un seul point fixe, est donc une symétrie, ce qui signifie que t est dans
$S_{u}$
. Réciproquement, si t est dans chaque
$S_{u}$
, il est inversé par toutes les
$s_{u}$
.
Le dernier point est conséquence du Lemme 1(vii). ⊣
Corollaire 3. Dans un symétron S:
-
(i) S'il n'y a pas de transvexions involutives, les seules involutions de ST(S) sont les symétries, et
$S_{u}$
est l'ensemble des transvexions inversées par
$s_{u}$
. -
(ii) Si T(S) est sous-médial, chaque réflexion a au plus un point fixe.
-
(iii) Si T(S) est médial, chaque réflexion a exactement un point fixe.
-
(iv) Si chaque réflexion a au plus un point fixe, il n'y a pas de transvexions involutives, et même chaque transvexion a les mêmes points fixes que son carré.
-
(i) D’après le Lemme 2(i), si r est une réflexion involutive,
$s_{u}.r$
est une transvexion involutive pour un certain u, et vaut l'identité par hypothèse; si
$s_{u}$
inverse t, c’est que
$s_{u}.t$
est une involution. -
(ii) Si la réflexion r fixe u et
$v$
, elle commute avec
$s_{u}$
et
$s_{v}$
, si bien que, dans T(S),
$s_{u}.r$
comme
$s_{v}.r$
sont l’unique racine carrée de
$r^{2}$
. -
(iii) Si r est une réflexion,
$r^{2}$
a une unique racine carrée dans T(S); comme elle commute avec r, elle est de la forme
$s_{u}.r$
. -
(iv) Si la transvexion t échange x et t(x), de milieu u, ce sont des points fixes de la réflexion
$t.s_{u}$
, qui sont donc égaux. ⊣
Lemme préparatoire. Soient G un groupe commutatif sans involutions et X une partie de G contenant l'élément neutre; on suppose que G est périodique, ou bien qu'il est oméga-stable et que X est définissable. Alors, si X est convexe, ou bien s'il est clos par prise de milieu, c'est un sous-groupe de G.
Démonstration. Si X est convexe, on reprend la démonstration du Lemme 1(vii). Si X est clos par milieu, il faut montrer que X est clos par somme.
On note G additivement. Si a est dans X, a/2 l'est aussi, car c'est le milieu de 0 et de a. Dans le cas périodique, l'intersection de X et du groupe (fini) engendré par a est clos pour l'injection x/2, donc aussi pour son inverse, si bien que 2a est dans X. Si a et b sont dans X, ce dernier contient également le double de leur milieu, qui est
$a+b$
.
Dans le cas oméga-stable, comme la division par 2 est injective, et que les types génériques (c'est-à-dire de rang de Morley maximal) de X sont en nombre fini, si x est un point générique de X (pris dans une extension élémentaire de G), 2x l'est aussi. Si x est générique sur a,
$(x+a)/2$
, ayant même rang de Morley que x, est un point générique de X, ainsi que son double
$x+a$
. Comme à x fixé la relation
$z = x + y$
établit une bijection entre le type de z et celui de y, si z et y sont génériques indépendants, z - y est générique. De plus tout générique est de cette forme, et si x est générique dans X,
$-x$
l'est aussi. Soient alors a et b deux points de X et x générique sur
$\{a,b\}; a - x$
et
$b + x$
le sont aussi, et le milieu de leurs doubles, qui vaut
$a+b$
, est dans X. ⊣
Exemple 1. Les points de
$\mathbf{Z}\times \mathbf{Z}$
dont l'une des coordonnées est paire forment un ensemble convexe qui n'est pas un groupe. Voir la démonstration du Théorème 5 de Poizat Reference Poizat2018.
Théorème 4. On considère une partie non vide X du symétron S, et on suppose soit que
$T_{1}(S)$
est périodique, soit que S est oméga-stable et que X est définissable (si S est fini, chacune des deux hypothèses est vérifiée).
-
(i) Si X est convexe, il est clos par prise de milieu, et égal à son symétriseur.
-
(ii) Si X est clos par prise de milieu, il est convexe.
Démonstration. (i) & (ii) On considère u et
$v$
dans X; dans le premier cas, il faut voir que X contient le milieu de u et de
$v$
, et dans le deuxième qu'il contient le symétrique de u par rapport à
$v$
. On remplace S par
$\varSigma $
, puis on translate par
$s_{u}$
, et on note Y l'ensemble des
$s_{u}.s_{w}$
, où
$w$
parcourt X; posant
$a = s_{u}.s_{v}$
, il faut voir dans le premier cas que le milieu de 1 et de a, c'est-à-dire l'unique racine carrée de a contenue dans
$S_{u}$
, est dans Y, et dans le second cas que
$a^{2}$
est dans Y.
Nous avons vu, dans la démonstration du Lemme 1(vii), que les points de
$S_{u}$
commutant avec tous les points de
$S_{u}$
qui commutent avec a forment un groupe commutatif médial C, qui est définissable dans le second cas. En posant
$Z = C\cap Y$
on est ramené au lemme préparatoire.
Si X convexe il est inclus dans
$Sym(X)$
; s'il est non vide et clos par prise de milieu,
$Sym(X)$
est inclus dans X, chacun de ses points étant au milieu de deux points de X. ⊣
Nous avons remarqué qu'un symétron peut être vu comme une structure dans le langage de la fonction-milieu
$m(x,y)$
, ou bien dans celui de la fonction-symétrie
$s(x,y) = s_{y}(x)$
, qui sont interdéfinissables; dans les cas favorables considérés dans le Théorème 4, la notion de sous-structure ne dépend pas de ce choix de langage. Mais, dans le cas général, pour obtenir un symétron induit sur une sous-structure X de S, nous devons supposer que X est à la fois convexe et clos par prise de milieu: nous dirons dans ce cas qu'il est un sous-symétron de S; T(X) est alors une section de T(S).
Pour un symétron oméga-stable, nous obtenons la condition de chaîne descendante sur les convexes définissables; en effet, si X est strictement inclus dans Y, nous prenons a dans
$Y-X$
; comme X est close par prise de milieu, la symétrie
$s_{a}(x)$
définit une injection définissable de X dans
$Y-X$
, si bien que le rang de Morley de X est strictement inférieur à celui de Y, ou sinon le degré de Morley de X est strictement inférieur à celui de Y.
2 L'exemple primordial: les groupes de rang de Morley fini sans involutions
Soit G un groupe. Les transvexions de son espace symétrique sont des translations, applications de la forme
$a.x.b$
; on remarque que
$a.x.b = a'.x.b'$
pour tout x si et seulement
$a' = c.a$
et
$b' = c^{-1}.b$
pour un c central dans G. L'ensemble
$T_{1}(G)$
est formé des translations qui s'écrivent
$ab.x.ba$
. De même les réflexions sont des inversions, applications de la forme
$a.x^{-1}.b$
.
Un calcul rapide montre qu'inversions et translations sont des automorphismes de l'espace symétrique de G, dont elles permutent les parties convexes.
Nous appelons convexe diagonal le sous-ensemble du groupe
$G\times G$
formé des points
$(a,a^{-1})$
inversés par l'échange des coordonnées. Quand G est médial et que u représente le passage à l'inverse (qui est la symétrie centrée sur l'élément neutre),
$S_{u}$
est formé des translations qui s'écrivent
$a.x.a$
; en posant
$x = 1$
on voit que cette écriture est unique, si bien que l'isomorphisme entre
$S_{u}$
et le symétron de G l'identifie au convexe diagonal (via l'homomorphisme de
$G\times G$
sur le groupe des translations qui à
$(a,b)$
associe
$a.x.b^{-1}$
)Footnote
4
.
Lemme 5.
(i) Le groupe
$ST(G)$
est formé des
$a.x^{$\pm $1}.b$
, où a et b sont congrus modulo le dérivé
$G'$
de G.
(ii) Si G est engendré par son dérivé et par les carrés de ses éléments centraux, il est égal à celui des inversions-translations, étant formé de tous les
$a.x^{$\pm $1}.b$
.
(iii) Si G est égal à son dérivé et a un centre trivial, ce groupe est isomorphe au produit semi-direct de
$G\times G$
par l'échange des coordonnées.
(iv) Si le dérivé
$G'$
de G est définissable,
$T(G)$
est un sous-groupe définissable du groupe des translations de G; si tout élément de
$G'$
est produit d'un nombre fixé de commutateurs,
$T(G)$
est borné. Les réciproques sont vraies quand le centre de G est trivial.
(v) Plus généralement, si le centre
$Z(G)$
de G est 2-divisible,
$T(G)$
est définissable si et seulement si le dérivé de
$G/Z(G)$
est définissable;
$T(G)$
est borné si et seulement si tout élément du dérivé de
$G/Z(G)$
est produit d'un nombre fixé de commutateurs.
(vi) Le groupe
$T(X)$
des transvexions d'une partie convexe définissable X d'un groupe de rang de Morley fini G est borné (et définissable!). Il est médial si G n'a pas d'involutions.
(vii) Dans un groupe de rang de Morley fini, chaque élément du dérivé est produit d'un nombre borné de commutateurs.
Démonstration. (i) Un produit de symétries s'écrit
$a_{1}.a_{2}. \ldots .a_{n}.x^{\pm 1}.a_{n}. \ldots .a_{2}.a_{1}$
. Pour la réciproque,
$a.b.a^{-1}b^{-1}.x.a^{-1}b^{-1}.b.a = [a,b].x$
, si bien que
$ab.x^{$\pm $1}.ca$
est un produit de symétries si b et c sont dans
$G'$
.
(ii) Si
$a = \alpha ^{2}\gamma $
et
$b = \beta ^{2} \delta $
, où
$\alpha $
et
$\beta $
sont centraux tandis que
$\gamma $
et
$\delta $
sont dans le dérivé,
$a.x^{\pm 1}.b = (\alpha \beta ).\gamma .x^{\pm 1}.\delta .(\alpha \beta )$
.
(iii) Dans ces conditions,
$a.x.b = a'.x.b'$
seulement si
$a = a'$
et
$b = b'$
; on associe alors au point
$(a,b)$
de
$G\times G$
la translation
$a.x.b^{-1}$
.
(iv) D'après (i), les transvexions de
$T(G)$
sont les translations qui s'écrivent ga.x.a, où g est dans
$G'$
, si bien que
$T(G)$
est définissable si
$G'$
l'est. Pour l'aspect borné des choses, nous avons vu lors de la démonstration de (i) qu'une translation par un commutateur est produit de trois translations de la forme
$\alpha .x.\alpha $
, si bien que, si g est produit de n commutateurs, la translation ga.x.a est produit de
$3n + 1$
ou
$3n + 2$
symétries suivant la parité de n.
Si le centre de G est trivial, l'écriture de ces translations est unique, et g.x est dans
$T(X)$
si et seulement si g est dans
$G'$
; si elle est produit de
$n+1$
symétries, g est de la forme
$g = a_{1}. \ldots .a_{n}.a_{n+1}$
où
$a_{n+1}.a_{n}. \ldots .a_{1} = 1$
, c'est-à-dire que
$g = a_{1}. \ldots . a_{n}.a_{1}^{-1}. \ldots .a_{n}^{-1}$
; en faisant commuter
$a_{n}^{-1}$
et
$a_{1}^{-1}. \ldots .a_{n-1}^{-1}$
, on montre alors par récurrence sur n que g est produit de n commutateurs.
(v) On remarque que si c est central et g est dans
$G'$
, gca.x.a est dans
$T(G)$
, étant égal à
$g\gamma a.x.\gamma a$
où γ est une racine carrée centrale de c; comme
$G'.Z(G)$
est l'image réciproque du dérivé de
$G/Z(G)$
, les hypothèses signifient qu'il est définissable, ou bien engendré modulo
$Z(G)$
par des produits bornés de commutateurs, et on conclut comme en (iv).
(vi) Après translation on peut supposer que X contient l'élément neutre; les couples
$(a,a^{-1})$
, où a parcourt X, forment une partie convexe définissable du groupe
$G\times G$
contenant (1,1), qui, d'après la Proposition 13 de Poizat Reference Poizat2018, engendre de façon bornée un sous-groupe
$\Gamma $
définissable; vu comme ensemble d'applications de G dans G, le groupe engendré par les symétries centrées en X est formé des
$\alpha .x^{\pm 1}.\beta $
avec
$(\alpha ,\beta ^{-1})$
dans
$\Gamma $
; pour obtenir les transvexions de X, on quotiente les
$\alpha .x.\beta $
par celles d'entre elles qui valent l'identité sur X. Le dernier point vient de ce que
$T(X)$
est une section définissable de
$G\times G$
.
(vii) On reprend les démonstrations précédentes en se plaçant non pas dans le groupe des translations de G, mais dans le groupe
$G\times G$
, et en considérant le groupe engendré par le convexe diagonal. ⊣
Remarques 3. (i) Le Lemme 5(vii) est un résultat bien connu de Zil'ber; on le montre habituellement (Poizat 1987, p. 89; Borovik & Nesin Reference Borovik and Nesin1994, p. 87–88) en s'appuyant sur le fait qu'un groupe qui n'a qu'un nombre fini de commutateurs a un dérivé fini (Rosenlicht Reference Rosenlicht1961); la démonstration offerte ici repose sur le fait plus simple qu'un ensemble convexe fini, contenant l'élément neutre, engendre un groupe fini. La philosophie de l'histoire, c'est que, pour tout groupe G,
$G'$
et le groupe engendré par le convexe diagonal sont définissables l'un à partir de l'autre.
(ii) Dans un groupe de rang de Morley fini (ou même seulement stable), s'il n'y a qu'un nombre fini de commutateurs, chaque point n'a qu'un nombre fini de conjugués et centralise la composante (centralisateur-)connexe du groupe. Or il est facile de voir que si le centre du groupe G est d'indice fini dans G, le groupe dérivé de G est fini. En effet, dans le groupe
$G\times \tilde{G}/Z$
, où Z est formé des
$(\gamma ,\gamma )$
, avec
$\gamma $
central dans G, le convexe diagonal C des
$(a,a)$
a une image finie, engendrant un groupe fini; il existe donc
$g_{1}, \ldots, g_{n}$
dans
$G'$
et
$a_{1}, \ldots, a_{n}$
dans G tel que tout point du groupe engendré par C soit de la forme
$(g_{1}.a_{1}.\gamma ,a_{1}.\gamma )$
ou … ou
$(g_{n}.a_{n}.\gamma ,a_{n}.\gamma )$
;
$(h,1)$
ne peut être dans ce groupe que si h est l'un des
$g_{i}$
.
Un groupe G médial, ou même seulement sous-médial, ne contient pas d'involutions, puisque 1 y est l'unique racine carrée de 1; réciproquement les groupes sans involutions périodiques, et en particulier finis, ou oméga-stables sont médiaux (en effet, dans ces groupes chaque point a une racine carrée de même centralisateur; voir Poizat Reference Poizat2018); c'est donc le cas des groupes périodiques simples construits dans Olshanskii Reference Ol’shanskii1982. Nous verrons que la structure de ses symétries, c'est-à-dire la loi binaire
$y.x^{-1}.y$
, ne détermine pas nécessairement G, même à isomorphie près.
Si le groupe médial G est commutatif, l'inversion
$a.x^{-1}.b$
est la symétrie
$c.x^{-1}.c$
, où c est la racine carrée de ab; chaque translation est alors produit de deux symétries.
Remarque 4. Dans le langage des groupes et de la racine carrée, les groupes médiaux forment une variété, définie par les équations:
$(x^{1/2})^{2} = x$
,
$(x^{2})^{1/2} = x$
,
$(y.x.y^{-1})^{1/2} = y.x^{1/2}.y^{-1}$
; en effet la deuxième équation impose qu'il n'y a pas d'involutions, et la troisième que x et
$x^{1/2}$
ont même centraliseur.
Exemple 2. Comme nous l'avons annoncé, si Σ est un symétron contenu dans un groupe et formé d'involutions, le groupe ST(Σ) est le quotient du groupe engendré par Σ par son centre, qui n'est pas nécessairement trivial. L'exemple le plus simple est un Σ constitué d'une seule involution.
Plus généralement, considérons un groupe G médial, et le produit semi-direct de
$G\times G$
par l'échange ε des coordonnées. Les conjuguées de ε s'écrivent
$(z,z^{-1}).\varepsilon $
; elles forment un symétron Σ, qui est isomorphe à celui des symétries du groupe G. Les produits d'un nombre pair de points de Σ engendrent le même groupe que le convexe diagonal, formé des points
$(a,a^{-1}.d)$
, où d est dans
$G'$
. Si G ≠ 1, le centralisateur de Σ dans le groupe qu'il engendre est formé des (a,a), où
$a^{2}$
est dans
$G'$
.
Exemple 3. Il ne faut pas confondre isomorphisme de groupe et isomorphisme de symétron, car deux sous-ensembles convexes d'un groupe, même médial, peuvent être des symétrons isomorphes sans engendrer des groupes isomorphes.
Pour construire un exemple, prenons un groupe médial G ayant un sous-groupe Γ également médial; l'ensemble Σ des symétries de G ayant leur centre dans Γ est un sous-symétron de l'ensemble S des symétries de G, et si c est un commutateur de Γ la conjugaison
$c.x.c^{-1}$
est produit d'un nombre pair de points de Σ, et commute avec tout élément de Σ si en outre c est central dans Σ. Il est facile de trouver des exemples algébriques, et même finis, de cette situation où c n'est pas central dans G, de sorte que cette conjugaison ne soit pas l'identité. Le groupe ST(Σ), étant défini par l'action de Σ sur Σ, est égal au quotient du groupe engendré par Σ dans ST(S) par son centre, et ces deux groupes ne sont pas les mêmes.
Le groupe T(S) est médial, et engendré par la copie
$S_{1}$
de S, obtenue en le translatant par la symétrie de centre 1: elle est composée des transvexions de la forme a.x.a; si
$\varSigma _{1}$
est la copie de Σ obtenue par la même translation, le groupe engendré par
$\varSigma _{1}$
dans T(S) n'est pas isomorphe à celui qu'engendre son image isomorphe (en tant que symétron!) dans
$T(\varSigma _{1})$
.
Exemple 4. Le produit semi-direct du groupe additif des entiers par lui-même, dont la loi de groupe est
$(x,u).(y,v) = (x + (-1)^{u}.y, u + v)$
, n'a pas d'involutions, mais n'est pas sous-médial; c'est un groupe superstable.
Lemme 6. Dans un groupe médial G:
-
(i) Chaque centralisateur est clos par extraction de racine carrée; le quotient de G par son centre est médial.
-
(ii) Aucun point ≠ 1 n'est conjugué de son inverse.
-
(iii) Le groupe de toutes les translations est médial; chaque translation a les mêmes points fixes que son carré; si X est une partie convexe non-vide de G, le groupe
$T(X)$
est sous-médial (en particulier si
$X = G$
). -
(iv) Une inversion a un unique point fixe. Si X est une partie convexe de G, les réflexions de ST(X) ont au plus un point fixe.
Démonstration. (i) Si x conjugue y et z, il doit aussi conjuguer leurs uniques racines carrées
$y^{1/2}$
et
$z^{1/2}$
; par conséquent, si x commute avec y, il commute avec
$y^{1/2}$
.
Supposons que
$x^{2} = y^{2}.z$
, où z est central; comme
$z^{1/2}$
est aussi central,
$x^{2} = (y.z^{1/2})^{2}$
, et
$x = y.z^{1/2}$
.
(ii)
$(xa)^{2} = a^{2}$
si et seulement si a conjugue x et son inverse; en fait, cette condition signifie que G est sous-médial.
(iii) La translation
$a^{1/2}.x.b^{1/2}$
est racine carrée de la translation a.x.b, et il faut voir que c'est son unique racine carrée; supposons que
$a^{2}.x.b^{2} = $\alpha $^{2}.x.$\beta $^{2}$
pour tout x; alors
$a^{2} = c.$\alpha $^{2}$
et
$b^{2} = c^{-1}.$\beta $^{2}$
où c est central; d'après (i),
$c^{1/2}$
est aussi central; comme les racines carrées sont uniques,
$a = c^{1/2}.\alpha $
,
$b = c^{-1/2}. \beta $
, et
$a.x.b = \alpha .x.\beta $
pour tout x.
Si
$a^{2}.x.b^{2} = x$
, x conjugue
$b^{-2}$
et
$a^{2}$
, ainsi que leurs uniques racines carrées respectives
$b^{-1}$
et a.
Quitte à la translater, on peut supposer que X contient 1. Une translation
$\alpha .x.\beta $
vaut alors l'identité sur X si et seulement si
$\alpha = \beta ^{-1}$
et centralise X. Si donc les carrés des deux translations a.x.b et a'.x.b', produits d'un nombre pair de symétries centrées en X, ont même action sur X, il existe c centralisant X tel que
$a^{2} = a'^{2}.c$
et
$b^{2} = c^{-1}.b'^{2}$
; comme c centralise aussi a, b, a' et b', qui sont produits d'éléments de X,
$a^{2} = (a'.c^{1/2})^{2}$
et
$b^{2} = (b'.c^{1/2})^{2}$
; comme G est médial,
$a = a'.c^{1/2}$
et
$b = b'.c^{1/2}$
, si bien que a.x.b et a'.x.b' ont même action sur X.
(iv)
$a.x^{-1}.b = x$
signifie que x est le milieu de a et de b. Si
$a.x^{-1}.b$
est involutive,
$ab^{-1}.x.a^{-1}b$
vaut l'identité, ce qui implique que
$c = ab^{-1}$
est central, et que
$a.x^{-1}.b$
est la symétrie de centre
$b.c^{1/2}$
.
Si i est produit d'un nombre impair de symétries centrées en X, elle a un unique point fixe u, et sa restriction à X a zéro ou un point fixe suivant que u est dans X ou pas. ⊣
Remarque 5. Si G est périodique sans involutions, il en est de même de ses sections; si G est oméga-stable sans involutions, il en est de même de ses sections définissables. Si X est une partie convexe non vide de G, définissable dans le deuxième cas, elle est close par prise de milieu d'après le Théorème 4, et toute inversion produit de symétries ayant leur centre dans Xa son point fixe dans X: c'est une conséquence du Corollaire 3(iii) et du Lemme 6.
3 Symétrons abéliens
Nous commençons par vérifier que, si le centre du groupe G est médial, le centre du groupe des transvexions T(G) du symétron associé est formé des a.x.a, où a parcourt le deuxième centre de G.
En effet, deux transvexions sont de la forme a.x.a.g et
$\alpha .x.\alpha .\gamma $
avec g et γ dans G'; elles commutent si et seulement si, pour tout x,
$\alpha .a.x.a.g.\alpha .\gamma = a.\alpha .x.\alpha .\gamma .a.g$
, soit encore
$x^{-1}.\alpha ^{-1}.a^{-1}.\alpha .a.x = \alpha .\gamma .a.g.\alpha ^{-1}.a^{-1}$
, ce qui implique que le commutateur
$[\alpha ,a]$
, n'ayant qu'un seul conjugué, est central; si pour a et g donnés cela se produit pour tout α et γ, a est dans le deuxième centre, et par conséquent commute avec les commutateurs; comme
$\alpha .a = a.\alpha .\beta $
pour un β central, l'égalité se transforme en
$a.\alpha .\beta .x.g.a.\alpha .\gamma = a.\alpha .x.a.\alpha .\beta .\gamma .g$
, et finalement en
$g.a.\alpha .\gamma = a.\alpha .\gamma .g$
, ce qui signifie que g est central; finalement
$a.x.a.g = a.g^{1/2}.x.a.g^{1/2}$
a bien la forme indiquée. Réciproquement, si a est dans le deuxième centre, a.x.a commute avec toutes les
$\alpha .x.\alpha .\gamma $
.
Par conséquent T(G) est commutatif si et seulement si G est nilpotent de classe 2; si G est 2-nilpotent et médial, T(G) est isomorphe au groupe G*, défini sur le même ensemble que G, mais dont la multiplication est
$a_{*}b = a.b.[b,a]^{1/2}$
: on voit sans peine que G* est un groupe commutatif médial qui a les mêmes symétries que G, c'est-à-dire que
$a_{*}b^{-1}_{*}a = a.b^{-1}.a$
.
Nous observons que si le groupe T(S) des transvexions d'un symétron S est 2-nilpotent avec un centre médial (voir le Lemme 2(v)), alors il est commutatif; en effet, dans ce cas T(T(S)) est alors commutatif.
Tout cela est un prélude à la caractérisation des symétrons dont le groupe de transvexions est commutatif, que nous appelons symétrons abéliens:
Théorème 7. Pour un symétron S, les choses suivantes sont équivalentes:
-
(i) Tout produit de trois symétries est une symétrie (soit encore les symétries forment une cossette, ensemble fermé sous l'opération ternaire
$x.y^{-1}.z$
, dans le groupe qu'elles engendrent). -
(ii) Tout produit de trois symétries est une involution.
-
(iii)
$T_{1}(S)$
est un groupe (égal à T(S)). -
(iv)
$T_{1}(S)$
est une partie convexe de T(S). -
(v) Pour un, ou pour chaque u de S, S u est un groupe.
-
(vi) Pour un, ou pour chaque u de S, S u est commutatif.
-
(vii) Pour un, ou pour chaque u de S,
$T_{1}(S) = S_{u}$
.
Et quand c'est le cas,
$T(S) = T_{1}(S)$
est un groupe commutatif médial; S est isomorphe à l'ensemble des symétries de T(S), et ST(S) est isomorphe au produit de T(S) par le passage à l'inverse.
Démonstration. Ce qui se passe pour un u se passe pour chacun d'eux, puisque les s u sont conjuguées.
(v) signifie que, pour tous u, v, w il existe t tel que
$s_{u}.s_{v}.s_{u}.s_{w} = s_{u}.s_{t}$
, ce qui est équivalent à (i); (vi) signifie que, pour tous u, v et w,
$s_{u}.s_{v}.s_{u}.s_{w} = s_{u}.s_{w}.s_{u}.s_{v}$
, ce qui est équivalent à (ii).
(i) implique (ii), qui implique (vi), qui implique que T(S) est commutatif, soit encore, puisque S
u agit transitivement, que
$T(S) = S_{u} = T_{1}(S)$
, c'est-à-dire (v) et (vii); si (vii) est vérifié, pour chaque u, v et w il existe t tel que
$s_{v}.s_{w} = s_{u}.s_{t}$
, et (i) est vérifié.
Reste à voir que (iv) implique (iii): soient a, b, c, d dans S, et m le milieu de a et de b;
$s_{a}.s_{b}.s_{c}.s_{d} = s_{a}.s_{m}.s_{a}.s_{m}.s_{c}.s_{d} = s_{a}.s_{m}.(s_{a}.s_{m}.s_{c}.s_{d}.s_{m}.s_{a}).s_{a}.s_{m}$
; comme
$T_{1}(S)$
est clos par conjugaison, il est clos par symétrie si et seulement s'il est clos par produit.
Par ailleurs nous savons que dans S u il y a existence et unicité de la racine carrée. ⊣
Lemme 8. Un symétron engendré par deux points est abélien.
Démonstration. Si S est engendré par u et v, S
u est engendré par 1 et
$a = s_{u}.s_{v}$
; comme S
u est clos par puissances et extraction d'unique racine carrée, le groupe engendré par les racines
$2^{n}$
.ièmes de a est commutatif et médial, et en fait égal à
$S_{u}$
. ⊣
On voit donc que le symétron libre à deux générateurs est celui des symétries du groupe additif des rationnels de la forme
$m/2^{n}$
, et qu'un symétron fini engendré par deux points est celui des symétries d'un groupe cyclique d'ordre impair.
Question 1. Est-ce qu'un symétron minimal, c'est-à-dire un symétron infini dont tous les sous-ensembles définissables propres sont finis ou cofinis, est abélien? Quid d'un symétron fortement minimal?
La raison pour laquelle les sous-symétrons ont été qualifiés de convexes dans Poizat Reference Poizat2018 est que ce sont les sous-ensembles dans lesquels deux points quelconques sont reliés par un sous-symétron abélien. C'est pour une raison semblable que les symétrons ont été qualifiés de dyadiques par Lawson & Lim Reference Lawson and Lim2004, car ce sont les espaces symétriques dans lesquels deux points quelconques sont reliés par une image du symétron libre à deux générateurs. Voir la Remarque 2, sur laquelle se fonde notre analyse locale des symétrons oméga-stables.
Nous concluons la section par des exemples de symétrons abéliens ou pas.
Exemple 5. Considérons la multiplication des matrices triangulaires unitaires d'ordre trois, à coefficients dans un corps:
$$ \begin{align*} m(a,b;c) = \left[\begin{array}{@{}ccc@{}} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 & 1 \end{array}\right], \end{align*} $$
$$ \begin{align*} & m(a,b;c).m(\alpha ,\beta ;\gamma ) = m(a+ \alpha ,b+ \beta ;c+ \gamma +a.\beta ),\\ & m(a,b;c)^{2} = m(2a,2b;2c+a.b), \\ & m(a,b;c)^{-1} = m(-a,-b;-c+a.b), \\ & [m(a,b;c), m(\alpha , \beta ; \gamma )] = m(0,0, a.\beta - \alpha .b). \end{align*} $$
Ce groupe est 2-nilpotent; son centre est formé des m(0,0;c), qui sont tous des commutateurs; il est médial sauf si 2 est la caractéristique du corps.
Ces formules de multiplication font sens dès que a, b et c parcourent des groupes commutatifs A, B et C respectivement, et qu'on dispose d'une application bilinéaire φ de A×B dans C pour interpréter le produit
$a.b = \varphi (a,b)$
, dont la bilinéarité suffit à montrer l'associativité du produit des matrices.
Le groupe ainsi défini est médial si et seulement si A, B et C le sont, et l'application bilinéaire φ la plus libre possible est le produit tensoriel de A et de B en tant que Z[1/2]-modules. Pour simplifier l'exposé, nous prendrons pour A et B des espaces vectoriels sur un corps k de caractéristique ≠2, par exemple
$k = F_{3}$
, et pour C leur produit tensoriel sur k. Nous notons
$U_{3}(A,B)$
le groupe 2-nilpotent médial ainsi obtenu.
Ses commutateurs correspondent aux points de C qui sont sommes de (un ou!) deux tenseurs purs, de la forme
$x\otimes y + u\otimes v$
; si A et B sont de dimension infinie, son dérivé n'est pas borné, car
$e_{1}\otimes f_{1} + \dotsb + e_{n}\otimes f_{n}$
n'est pas somme de moins de n tenseurs purs quand
$\{e_{1}, \ldots, e_{n}\}$
d'une part et
$\{f_{1}, \ldots, f_{n}\}$
d'autre part sont linéairement indépendants (cet exercice d'algèbre linéaire est laissé au lecteur). On remarque qu'il est ω-stable, de rang
$\omega +2$
, le générique de C étant réalisé dans une extension élémentaire de ce dernier par les points hors de A⊗B; il est localement fini quand le corps k est fini.
Comme il est 2-nilpotent son symétron est abélien et donc borné; on obtient un symétron non borné en incrémentant la dimension, c'est-à-dire en introduisant le groupe
$U_{4}(A,B,C)$
des matrices diagonales unitaires d'ordre 4 ayant A, B et C sur la deuxième diagonale, A ⊗ B et B ⊗ C sur la troisième et A ⊗ B ⊗ C dans le coin.
Exemple 6. Nous considérons deux groupes commutatifs A et B, le premier noté multiplicativement et le second additivement, avec une action de A sur B; le produit semi-direct de A par B est le groupe R défini sur B × A par la loi:
$(b,a).(\beta ,\alpha ) = (b+a. \beta ,a. \alpha )$
; il est isomorphe au groupe des transformations affines de B de la forme a.t + b. Cela donne:
$(b,a)^{2} = (b+a.b,a^{2})$
;
$(b,a)^{-1} = (-a^{-1}.b,a^{-1})$
;
$[(a,b).(\alpha ,\beta )] = (b+a.\beta -\alpha .b -\beta ,1)$
.
Il s'agit d'un groupe 2-résoluble, le groupe (B,1), que nous identifions à B, étant normal; nous identifions de même A à (0,A).
Ce groupe est médial si A l'est, et si, pour chacun de ses points a, l'homomorphisme y + a.y est une bijection de B dans B; cela implique que B est aussi médial, et c'est automatiquement vérifié quand A et B sont périodiques sans involutions.
(b,a) est central quand a fixe tous les points de B et b est fixé par tous les points de A; nous supposerons désormais que le centre est trivial, c'est-à-dire qu'un a≠1 n'agit pas identiquement, et qu'un b≠0 n'est pas fixé par A.
Les commutateurs sont les points de B qui sont sommes de un ou deux éléments de la forme b - a.b.
Si nous prenons pour B le groupe additif d'un corps K de caractéristique ≠2 et pour A un de ses sous-groupes multiplicatifs médiaux non trivial, on obtient un groupe médial sans centre, dont tout point du dérivé (B,1) est un commutateur; d'après BHMW Reference Baudisch, Hils, Martin-Pizarro and Wagner2009 il peut être de rang de Morley trois. Toute transvexion du symétron S de R est produit de quatre symétries.
Supposons maintenant que le corps K possède un automorphisme involutif σ qui inverse chaque point de A. Le convexe S des points inversés par l'automorphisme de R induit par σ est clos par prise de milieu: c'est un sous-symétron de R, et un calcul simple d’algèbre linéaire montre qu’il engendre R. Par conséquent les transvexions de S sont les applications de la forme
$a.x.\sigma (a^{-1})$
avec a dans R, et le groupe T(S) est isomorphe à R.
Comme exemple d'application, on considère
$K = F_{25}$
, qui est engendré par une racine cubique de l'unité j; son automorphisme σ échange j et
$j^{2}$
. On prend pour A le groupe
$\{1, j, j^{2}\}$
, qui est d'ailleurs la seule possibilité; S a quinze points, et son groupe de transvexions R en a septante-cinq; S n'est pas isomorphe au symétron d'un groupe médial, car tous les groupes d'ordre quinze sont commutatifsFootnote
5
.
Pour trouver un exemple de dérivé non borné, nous prenons pour A un espace vectoriel de dimension infinie sur le corps
$k = F_{3}$
(mais n'importe quel corps fini de caractéristique ≠2 conviendrait) et pour B l'espace vectoriel
$k ^{A}$
des applications de A dans k qui sont nulles sauf en un nombre fini de points; sa base canonique est en bijection avec A, qui agit sur B par translation des coordonnées.
On obtient ainsi un groupe 2-résoluble d'exposant 9, qui est localement fini et donc localement nilpotent; son centre est trivial, car un point de B centralisé par A doit avoir toutes ses coordonnées égales, si bien qu'il est nul. C'est donc un groupe instable, avec des chaînes infinies de centralisateurs; comme les centralisateurs du groupe sont définissables dans son symétron (
$s_{1}.s_{u}$
commute avec
$s_{1}.s_{v}$
si et seulement si u et v commutent, puisque le centre de R est trivial), ce dernier est également instable.
Reste au lecteur à s'atteler à un exercice de combinatoire: les points du dérivé de notre groupe sont ceux dont la somme des coordonnés est nulle, et la fonction caractéristique de 3.n points de A linéairement indépendants n'est pas somme de moins de n commutateurs. Le dérivé n'est pas borné, non plus que son symétron, puisque son centre est trivial.
4 Symétrons finis et localement finis
Si le symétron S est fini, son nombre d'éléments n est impair, puisque les symétries n'ont qu'un seul point fixe; si t est chaque transvexion primaire,
$t^{m}$
aussi, et elle vaut l'identité dès qu'elle a un point fixe: cela veut dire que tous ses cycles ont même nombre d'éléments, qui est un diviseur de n.
Quand n = p est un nombre premier, chaque translation primaire t ≠ 1 est d'ordre p; si
$t = s_{u}.s_{v}$
, les
$t^{m}$
parcourent
$S_{u}$
, et chaque
$s_{w}$
est de la forme
$s_{u}.t^{m}$
; comme
$s_{u}$
inverse t par conjugaison, chaque point de ST(S) est de la forme
$t^{m}$
ou
$s_{u}.t^{m}$
. On voit que S est isomorphe au symétron des symétries du groupe cyclique d'ordre p; plus généralement, le symétron du groupe cyclique d'ordre n est caractérisé par le fait qu'il a une transvexion primaire d'ordre n.
En fait, comme il a été remarqué dans KNN Reference Kano, Nagao and Nobusawa1976, la structure des symétrons finis est totalement élucidée par le résultat suivant, qui s'appuie sur un grand théorème de la théorie des groupes finis: chacun est isomorphe au symétries d'une partie convexe d'un groupe fini sans involutions.
Théorème 9. Un symétron fini n'a pas de transvexions involutives.
Démonstration. Soit s une symétrie du symétron fini S; dans ST(S), elle ne commute avec aucune de ses conjuguées si ce n'est elle-même, si bien que le
$Z*$
-Theorem de Glauberman Reference Glauberman1966 affirme qu'elle est centrale modulo le plus grand sous-groupe normal d'ordre impair de ST(S); comme ST(S) est engendré par les conjuguées de s, ce sous-groupe est T(S). ⊣
Nous dirons qu'un symétron est localement fini si chacune de ses parties finies est contenue dans un sous-symétron fini.
-
(i) Un symétron est localement fini si et seulement si son groupe de transvexions est localement fini.
-
(ii) Un symétron localement fini n'a pas de transvexions involutives (son groupe de transvexions est donc médial, et localement résoluble).
-
(iii) Un groupe médial est localement fini en tant que groupe si et seulement s'il l'est en tant que symétron.
Démonstration. (i) Supposons S localement fini; des symétries
$s_{1}, \ldots, s_{n}$
sont contenues dans une partie convexe finie F de Σ; comme un produit d'éléments de F, s'il ne vaut pas l'identité, peut s'écrire comme un produit d'éléments de F distincts, F engendre un groupe fini; ST(S), et son sous-groupe T(S), sont donc localement finis.
Supposons T(S) localement fini; comme il est d'indice un ou deux dans ST(S), ce dernier est aussi localement fini. Des symétries
$s_{1}, \ldots s_{n}$
engendrent donc un groupe fini G; l'ensemble des symétries contenues dans G est clos par conjugaison, c'est-à-dire par symétrie, et d'après le Théorème 4 est clos par prise de milieu: c'est un sous-symétron de S, qui est bien localement fini.
(ii) Soit t une transvexion telle que
$t^{2} = Id$
, engendrée par les symétries
$s_{1}, \ldots, s_{n}$
, et soit s une symétrie quelconque; les centres des symétries
$s_{1}, \ldots, s_{n}$
et s engendrent un symétron fini, qui, d'après le Théorème 9, n'a pas de transvexions involutives. La restriction de t à ce dernier vaut l'identité, et t fixe le centre de s; comme cela a lieu pour tout s, t vaut l'identité. La dernière assertion est conséquence du Théorème de Feit et Thompson.
(iii) Si le groupe G est localement fini, le groupe des transvexions de son symétron, qui est une section de
$G\times G$
, est localement fini. Si le symétron de G est localement fini, chaque translation a.x.a, qui est produit de deux symétries, est d'ordre fini; mais, comme il n'y a pas d'involutions dans G,
$a^{n}.x.a^{n}$
ne peut valoir l'identité que si
$a^{n} = 1$
, si bien que G est périodique. Si g est dans le dérivé G' de G, la translation g.x est un produit de symétries, si bien que G' est localement fini; comme par ailleurs G/G' est localement fini, G est localement fini. ⊣
Théorème 11. (i) Toute structure définissable dans un corps algébriquement clos satisfait les énoncés vrais dans chaque structure localement finie (elle est “pseudo-localement-finie”).
(ii) Soient G un groupe algébrique simple (sur un corps K algébriquement clos), et …
$\sigma _{i}$
, … une famille d'automorphismes de G; si la structure (
$G, \ldots \sigma _{i}, \ldots $
) a un rang de Morley fini, elle est pseudo-localement-finie.
(iii) Un groupe de rang de Morley fini dont la composante connexe est un groupe algébrique simple est pseudo-localement-fini.
(iv) Le groupe des transvexions d'un symétron algébrique, c'est-à-dire définissable dans un corps algébriquement clos, est sous-médial, et chacune de ses inversions a un unique point fixe.
Démonstration. (i) Un énoncé très semblable est montré dans Poizat Reference Poizat2001. Par élimination des imaginaires, on peut supposer que la structure est définie sur une partie constructible, c'est-à-dire combinaison booléenne d'ensembles définis par des équations polynomiales, de
$K^{n}$
; ses relations et ses fonctions sont également constructibles. Pour elle, la satisfaction d'un énoncé φ se traduit par la satisfaction par les coefficients des polynômes mis en jeu d'une formule φ
$(\bar{a})$
du langage des corps. Comme le corps K algébriquement clos satisfait à (∃
$\bar{x}$
)φ
$(\bar{x})$
, cet énoncé est également vrai, pour un certain nombre premier p, dans la clôture algébrique L des corps finis de caractéristique p. Soient donc
$\bar{b}$
dans L satisfaisant à φ
$(\bar{b})$
, et k un sous-corps fini de L contenant
$\bar{b}$
; comme tout point hors de k peut être déplacé par un k-automorphisme de L, les fonctions de la structure associée à
$\bar{b}$
ne peuvent faire sortir de k, et cette dernière est localement finie.
(ii) Soit σ un automorphisme de G, qu'on suppose infini; la version modèle-théorique du Théorème de Borel-Tits (Poizat Reference Poizat1988, Poizat Reference Poizat1987 p.149–153), reposant sur la notion d'internalité de Hrushovski, permet d'obtenir un automorphisme θ du corps K tel que (G,σ) soit définissable dans (K,θ), et tel que (K,θ) ait une copie définissable dans (G, σ).
Si (G,σ) est de rang de Morley fini, (K,θ) l'est aussi; en caractéristique nulle le corps des invariants de θ est algébriquement clos, et θ vaut l'identité; en caractéristique p, l'application de Frobenius est un automorphisme pour (K,θ), et Wagner Reference Wagner2001 affirme que le modèle premier de la théorie de cette structure est porté par la clôture algébrique du corps premier; on conclut comme en (i), et le même argument est valable s'il y a plusieurs automorphismes.
(iii) Si on choisit un représentant ρ(x) dans G de chaque x de G/G°, le groupe G est définissable à partir des automorphismes de G° induit par les ρ(x) et des constantes
$c_{x,y} = \rho (x). \rho (y). \rho (x.y)^{-1}$
.
(iv) est conséquence de (i), du théorème précédent et du Lemme 5. ⊣
Remarque 6. L'intérêt de la démonstration des points (ii) et (iii) vient de ce qu'elle ne demande aucune inspection de la structure du groupe algébrique simple G; il faut seulement savoir que ses borels ne sont pas nilpotents, ce qui permet de définir dans G, par la méthode de Zil'ber, une copie du corps de base K, et par ailleurs montre économiquement que G contient, pour tout nombre premier p, des éléments d'ordre p; c'est une information qu'on obtient en remarquant qu'un mauvais groupe n'est pas pseudo-localement-fini.
Malheureusement, si on considère, dans une situation de rang de Morley fini, un groupe H définissable d'automorphismes du groupe algébrique simple G, il faut une description plus fine des propriétés algébriques de G pour mettre en évidence un groupe d'automorphismes du corps K, qui ne peut qu'être trivial même en caractéristique p; le groupe du Théorème 11(iii) est en fait un groupe algébrique. C'est également nécessaire pour montrer que H° est composé d'automorphismes intérieurs, ce que nous utiliserons dans la Section 8; voir ABC Reference Altinel, Borovik and Cherlin2008, p. 134–135.
5 Symétrons oméga-stables et types génériques
Pour la démonstration du Théorème 4, nous avons choisi une méthode plus directe que celle du Théorème 12 de Poizat Reference Poizat2018; cela nous permet d'expliciter plus simplement le lien entre un symétron oméga-stable S et ses types génériques.
Si p est un 1-type complet sur S, et si a est un point de S, nous notons
$s_{a}(p)$
le type sur S des
$s_{a}(x)$
où x réalise p. Si q est un autre type, l'ensemble
$Sym(p \leftrightarrow q)$
des a de S tels que
$s_{a}(p) = q$
, qui est aussi celui des a de S tels que
$s_{a}(q) = p$
, est définissable puique les types le sont, et c'est un sous-symétron de S: en effet, si a et b sont dans
$Sym(p\leftrightarrow q)$
, x réalise p sur
$\{a, b\}$
et y est le symétrique de x par rapport à b,
$s_{a}(b)$
est le milieu de
$s_{a}(x)$
et de
$s_{a}(y)$
. En particulier
$Sym(p) = Sym(p\leftrightarrow p)$
est un convexe définissable; il en est de même, si
$p_{1}, \ldots, p_{n}$
est un ensemble fini de types, de l'ensemble
$Sym(p_{1}, \ldots, p_{n})$
des a de S qui les permutent par symétrie.
Théorème 12. Dans un symétron oméga-stable, toute partie convexe définissable non vide est le symétriseur de ses types génériques (c'est-à-dire de rang de Morley maximum); elle se décompose de manière unique en un nombre fini, qui est impair, de sous-ensembles définissables convexes disjoints de degré de Morley un, que nous appelons ses composantes connexes.
Démonstration. Notre ensemble convexe X est contenu dans le symétriseur
$Sym(p_{1}, \ldots p_{n})$
de ses types génériques; par ailleurs, si a est dans ce dernier, il est au milieu de deux réalisations de types génériques, si bien qu'il y a égalité.
Notons
$X_{i}$
l'ensemble des points a de X tels que
$s_{a}(p_{1}) = p_{i}$
, ce qui équivaut à
$s_{a}(p_{i}) = p_{1}$
; les
$X_{i}$
forment une partition de X en sous-ensembles convexes. Chacun ne peut contenir qu'un seul type générique: en effet, si a est générique dans
$X_{i}$
et x est une réalisation de
$p_{1}$
générique sur a,
$y = s_{a}(x)$
est une réalisation de
$p_{i}$
générique sur a, et comme a est le milieu de x et de y, a et y se correspondent par une bijection définissable avec x comme paramètre; x et y sont donc génériques et indépendants, et le type de a est déterminé. Il faut donc que chaque
$X_{i}$
contienne un type générique.
Si q est le type générique de
$X_{i}$
, ce dernier est le symétriseur de q, et si p est un autre générique, il n'est pas possible que q soit au milieu de deux réalisations de p, si bien que les génériques ≠ q sont appariés deux par deux sous l'action de la symétrie par q; le nombre n est donc impair.
Si
$X = Y_{1} \cup Y_{2} \cup \dotsb \cup Y_{m}$
est une autre partition de X en ensembles convexes de degré de Morley un, et si
$RM(Y_{k}) = RM(X)$
,
$Y_{k}$
est le symétriseur de son générique, et c'est donc l'un des
$X_{i}$
; comme il n'y a rien en dehors de la réunion des
$X_{i}$
, c'est la même partition, à permutation près. ⊣
On voit qu'on obtient une structure de symétron sur les types génériques de S; en effet, si x et y sont génériques et indépendants et
$z = s_{x}(y)$
, les trois points x, y et z sont deux à deux génériques et indépendants, et les types de x et de y déterminent celui de z; de même, si x et z sont génériques et indépendants et y est le milieu de x et de z, les trois points x, y et z sont deux à deux génériques et indépendants, et les types de x et de z déterminent celui de y.
Théorème 13. Si X est une partie définissable du symétron oméga-stable S, elle est générique (c'est-à-dire RM(X) = RM(S)) si et seulement si S est recouvert par un nombre fini de translatées de X par des points de
$T_{1}(S)$
.
Démonstration. Si X vérifie le critère, elle est générique car ses translatées ont même rang de Morley. Supposons réciproquement X générique; soit x une réalisation d'un de ses types génériques p; soient q un autre type générique, y une réalisation de q indépendante de x, et z le milieu de x et de y, qui vérifie s(x,z) = y; comme x et z d'une part, y et z d'autre part, sont indépendants, s(p,z) = q, et comme cette propriété s'exprime grâce aux définitions des types p et q, on trouve a dans S tel que s(p,a) = q. En conséquence, une réunion Y des translatées de X par un nombre fini de symétries contient tous les types génériques de S.
Soit maintenant x une réalisation d'un type r quelconque, et y générique sur x; s(x,y) est générique, et donc satisfait Y; par conséquent il existe a dans S tel que s(r,a) satisfasse Y. Autrement dit tout type peut être envoyé par symétrie dans Y; par compacité, cela signifie qu'un nombre fini de symétrisées de Y recouvrent S. ⊣
Exemple 7. Considérons un groupe G de rang de Morley fini, et p et q deux types au-dessus de G. Alors, si Sym(p,q) n’est pas vide, RM(p) = RM(q) ≥ RM(Sym(p↔q)); en effet, si
$a.p^{-1}.a = q$
, p et q ont même rang, et a est au milieu d’une réalisation de p et d’une réalisation de q.
Soient X un ensemble définissable de rang n, x et y deux réalisations indépendantes de types p et q de rang maximum dans X; si le plus petit ensemble convexe définissable contenant x et y est inclus (ou même seulement génériquement inclus) dans X, alors
$RM(Sym(p\leftrightarrow q)) = n$
; en effet, le milieu z de x et de y est dans X, et comme 2.n = RM(x, y) = RM(x, y, z) = RM(x, z) = RM(y, z), RM(x/z) = RM(y/z) = RM(z) = n et z est dans
$Sym(p\leftrightarrow q)$
Footnote
6
.
Cette remarque permet d’obtenir rapidement, et sans calculs, la partie délicate de la démonstration par contradiction de Frecon Reference Frecon2018. Soit G un mauvais groupe de rang trois, et X l’ensemble des x pour lesquels il existe y tel que [x,y] = a, où a est un paramètre générique; on voit facilement que RM(X) = 2, et que par tout x de X passe une famille de rang un de cossettes modulo des centralisateurs contenues dans X; il existe donc y générique sur x tel que x et y soient contenus dans une de ces cossettes, ce qui produit un convexe définissable de rang deux; à partir de ce dernier on fabrique aisément un automorphisme involutif définissable de G, ce qui est impossible (voir Poizat Reference Poizat2018). La même démonstration vaut pour Wagner Reference Wagner and Kikuchi2017.
6 Génération elliptique
Nous disons qu'un sous-goupe H d'un groupe G est elliptiquement engendré par une partie X de G si chaque point de H est produit de n éléments de
${X} \cup X^{-1}$
pour un entier n fixé (nous n'exigeons pas que H soit tous le groupe engendré par X).
Nous avons fait allusion, dans notre Lemme 5, à la Proposition 13 de Poizat Reference Poizat2018, qui s'appuie sur une version particulièrement commode du Théorème des Indécomposables de Zil'ber, précisément parce qu'elle ne mentionne pas d'indécomposables, et qui peut être démontrée en adaptant au cas des groupes le Théorème 14 qui suit: si X est une partie définissable du groupe de rang de Morley fini G, il existe un plus grand sous-groupe e(X) définissable, connexe et elliptiquement engendré par X; de plus X normalise e(X), et le quotient X/e(X) est fini.
Question 2. Un groupe infini de rang de Morley fini peut-il être finiment engendré? Soit encore: une partie définissable d'un groupe de rang de Morley peut-elle engendrer un groupe définissable de manière non elliptique? (Comme ce n'est pas possible pour un groupe abélien ou algébrique, une réponse positive contredirait la Conjecture d'Algébricité).
Dans le cadre d'un symétron S, nous dirons que X engendre elliptiquement le sous-symétron S' si chaque point de S' s'obtient à partir de X par symétries et prises de milieu en moins de n étapes, pour un n fixé. Voici ce que devient le Théorème de Zilber dans ce contexte:
Théorème 14. Dans un symétron S de rang de Morley fini:
(i) Deux sous-symétrons définissables connexes non disjoints engendrent un sous-symétron définissable connexe, et ce de façon elliptique.
(ii) Une famille arbitraire de sous-symétrons définissables connexes deux-à-deux non disjoints engendre un sous-symétron définissable connexe, qui est en fait elliptiquement engendré par un nombre fini d'entre eux.
(iii) Si X est un sous-ensemble définissable de S, la relation “x et y appartiennent à un même convexe connexe définissable elliptiquement engendré par X” est une relation d'équivalence sur le symétron engendré par X, qui n'a qu'un nombre fini de classes sur X.
(iv) Dans un groupe de rang de Morley fini sans torsion, toute partie définissable convexe C est connexe, et il existe une partie finie F de C tel que ce dernier soit le plus petit ensemble définissable convexe contenant F.
Démonstration. (i) Soint A et B nos deux convexes, et a un de leurs points communs; on considère un type p de rang maximal obtenu à partir de points x satisfaisant à la formule définissant A ∪ B par symétries et prises de milieu;
$s_{A}(p)$
ne contient qu'un nombre fini de types
$p_{1}, \ldots, p_{m}$
de même rang que p, si bien qu'on obtient une partition de A en un nombre fini
$A_{1} \cup \dotsb \cup A_{m}$
de sous-symétrons définissable S' formé, où
$A_{i} = Sym(p\leftrightarrow p_{i}) \cap A$
: étant connexe, A est en fait l'un d'entre eux. On voit donc que A est inclus dans le symétron définissable S' formé des u tels que
$s_{u}(p) = s_{a}(p)$
; il en est de même de B; comme chaque point de S' est au milieu d'une réalisation de p et d'une réalisation de
$s_{a}(p)$
, S' est elliptiquement engendré par A ∪ B. Par ailleurs, A comme B sont inclus dans la même composante connexe de S', si bien que S' est connexe, et que c'est le symétron engendré par A et B.
(ii) C'est le convexe de rang maximal engendré par un nombre fini d'entre eux.
(iii) Si a est dans le symétron engendré par X, un convexe définissable connexe elliptiquement engendré par X, contenant a, et de rang de Morley maximum, est maximum d'après (i); en conséquence la relation E de l'énoncé est bien transitive.
On considère un type p de rang maximal engendré par X;
$s_{X}(p)$
est un ensemble fini
$p_{1}, \ldots, p_{m}$
, et X est partitionné par les
$X_{ij} = S_{ij} \cap X$
, où
$S_{ij}$
parcourt l'ensemble des composantes connexes des
$Sym(p\leftrightarrow p_{i})$
; deux points dans un même
$X_{ij}$
sont équivalents.
(iv) C'est vrai si C est vide; sinon, une translation ramène au cas ou il contient l'élément neutre; pour chaque x de C, le convexe définissable minimal
$C_{x}$
contenant x et 1 est un groupe abélien divisible, donc connexe, et C est le convexe engendré par un nombre fini de
$C_{x}$
. ⊣
Remarque 7. Si C est une classe de E, c'est-à-dire un sous-symétron définissable connexe elliptiquement engendré par X, et a est un point de S(X), s(X,a) est aussi une classe de E. Si C et C' sont deux classes de E, les milieux d'un point de C et d'un point de C' forment donc le convexe
$Sym(C\leftrightarrow C')$
des centres des symétries qui échangent C et C'; par conséquent toutes les classes de E ont même rang de Morley, si bien que
$Sym(C\leftrightarrow C')$
est une classe modulo E; il en suit que, si a et b sont congrus modulo E, s(C,a) = s(C,b). La conclusion est que symétrie et milieu passent au quotient modulo E, et que S(X)/E est un symétron. On voit que S(X) est elliptiquement engendré par X si et seulement si S(X)/E est fini.
Question 3. Un symétron infini de rang de Morley fini peut-il être finiment engendré?
8 Une démonstration hypothétique
Traduit dans notre langage, le Théorème 1 de Glauberman Reference Glauberman1966 affirme que si, dans un groupe, S est un symétron fini formé d'involutions, c'est-à-dire un ensemble d'involutions clos par conjugaison et ne commutant pas deux-à-deux, les produits des paires d'éléments de S engendrent un groupe sans involutions; c'est un peu plus fort que de dire que S n'a pas de transvexions involutives, car T(S) est le quotient de ce groupe par le centralisateur de S. La question de l'extension de ce résultat au contexte de rang de Morley fini est posée dans Borovik-Nesin Reference Borovik and Nesin1994 p. 355, mais il est remarquable que ce théorème ne soit pas mentionné dans ABC Reference Altinel, Borovik and Cherlin2008.
Si on ajoute au cocktail le Théorème de Feit et Thompson, on obtient un corollaire indifférent à l'existence d'un centre: le groupe ST(S) est résoluble; c'est sous cette forme édulcorée (qui néanmoins s'oppose à l'existence de groupes finis simples sans involutions) que nous allons tout d'abord généraliser le Théorème de Glauberman sous l'hypothèse de la Conjecture d'Algébricité, c'est-à-dire en admettant que tout groupe simple de rang de Morley fini est un groupe algébrique (sur un corps algébriquement clos).
Nous commençons par quelques préliminaires, en considérant un groupe de rang de Morley fini ayant une partie définissable S close par conjugaison et formée d'involutions ne commutant pas deux-à-deux. Le groupe G engendré par S est définissable; en effet, si
$G^{\circ}$
est le plus grand sous-groupe définissable connexe elliptiquement engendré par S, G/S est fini et clos par conjugaison, et engendre un groupe fini puisque dans un produit d'éléments de G/S on peut éliminer les répétitions. Notons H° le plus grand sous-groupe définissable connexe engendré par les paires d'éléments de S; comme S.S est normalisé par S, H° aussi, et S/H° est fini, si bien que
$H^{\circ} = G^{\circ}$
, que le groupe engendré par S.S est définissable et a même composante connexe que celui engendré par S.
Nous devons aussi reprendre brièvement la description bien connue des sous-groupes diédraux d'un groupe oméga-stable, qui reproduit ce qui se passe dans un groupe périodique (voir Borovik-Poizat Reference Borovik and Poizat1990, Borovik-Nesin Reference Borovik and Nesin1994 p. 173); cela contribuera d'ailleurs à éclairer les démonstrations des premières sections de cet article, basées sur le fait que deux symétries d'un symétron oméga-stable sont toujours contenues dans une cossette définissable. Soient i et j deux éléments de S distincts; nous notons d(i, j) le plus petit sous-groupe définissable contenant i et j, et d(i.j) le plus petit sous-groupe définissable contenant leur produit i.j; du simple fait que i et j sont des involutions, d(i.j) est le produit d'un groupe cyclique d'ordre
$2^{\textrm n}$
et d'un groupe commutatif
$D_{ij}$
divisible par 2; comme i inverse d(i.j) par conjugaison, ses conjugués dans d(i, j) sont les points de la forme
$i.\alpha^{\textrm 2}$
, où α est dans d(i.j), si bien que si d(i.j) contenait une involution k, i.k serait conjugué de i ou bien de j, ce que contredit la condition de non-commutativité. Dans notre contexte, cette condition équivaut donc au fait que, pour tous i et j dans S, d(i.j) ne contient pas d'involutions; cela a pour conséquence que, si H est un sous-groupe définissable propre normal dans G, S/H est aussi un symétron formé d'involutions; on remarque aussi que i et j sont uniquement conjuguées dans d(i, j), ce qui est conforme à notre Lemme 1(vii).
Théorème 15. Sous l'hypothèse de la Conjecture d'Algébricité, dans un groupe de rang de Morley fini, un sous-ensemble définissable composé d'involutions formant un symétron engendre un groupe résoluble.
Démonstration. Soit S notre symétron, et G le groupe qu'il engendre; comme
$G/G^{\circ}$
est résoluble d'après le Théorème de Glauberman, il suffit de montrer que
$G^{\circ}$
l'est.
Notons
$R^{\circ}$
son plus grand sous-groupe définissable résoluble connexe normal, et R l'ensemble des éléments centraux modulo
$R^{\circ}$
; R est normalisé par
$G^{\circ}$
, et aussi par S, et le quotient
$G^{\circ}/R$
est semi-simple: s'il n'est pas trivial ses groupes normaux minimaux
$N_{\textrm 1}, \ldots, N_{\textrm n}$
sont définissables et simples, et le groupe qu'ils engendrent est de la forme
$N_{\textrm 1}\times \dotsb \times N_{\textrm n}$
.
Si un point s de S échange deux
$N_{\textrm i}$
, après un quotient on obtient un sous-groupe de la forme N × N sur lequel s agit par échange des coordonnées, si bien que
$s.(a,a^{\textrm -1}) = (1,a).s.(1,a^{\textrm -1})$
est conjugué de s, et ne peut commuter avec s que si a = 1; il est donc nécessaire que N n'ait pas d'involutions, ce qui est impossible pour un groupe algébrique simple.
Par conséquent S les normalise tous, et au prix d'un quotient on est ramené au cas où il n'y en n'a qu'un, soit N, qui par hypothèse est algébrique; d'après la Remarque 6, chaque point de
$G^{\circ}$
agit par automorphisme intérieur sur N, dont le centralisateur est trivial, si bien que
$G^{\circ} = N$
, et que G est un groupe algébrique; comme G est pseudo-localement-fini,
$G^{\circ}$
, qui est engendré par S.S, ne contient pas d'involutions, autre impossibilité. ⊣
Remarque 8. On peut voir que la Conjecture d'Algébricité équivaut au fait suivant: si G est un groupe de rang de Morley fini, il existe un sous-groupe normal résoluble définissable R de G tel que G/R soit pseudo-localement-fini; la direction réciproque est donnée par le Théorème de Simon Thomas, qui repose sur la classification des groupes simples finis (voir Poizat Reference Poizat2001).
Ce théorème implique, sous la Conjecture d'Algébricité, que le groupe des transvexions d'un symétron S borné de rang de Morley fini est résoluble; comme T(S) est le dérivé de ST(S), cela interdit à une symétrie d'être une transvexion, sauf si S est réduit à un point.
Sa démonstration est très peu satisfaisante; c'est comme si, dans le cas fini, on s'appuyait sur la classification pour montrer le Théorème de Glauberman! Une réponse positive à la question qui suit montrerait que le seul obstacle au Théorème 15 serait l'existence de groupes simples sans involutions.
Question 4. ABC Reference Altinel, Borovik and Cherlin2008 contient-il suffisamment de matériaux pour éliminer inconditionnellement les groupes simples avec involutions qui apparaissent dans la démonstration du Théorème 15?
Le dernier théorème de la section est inconditionnel, son corrolaire conditionnel étant que la Conjecture d'Algébricité implique qu'un symétron borné de rang de Morley fini n'a pas de transvexions involutives, qu'il est isomorphe au symétron d'une partie définissable convexe d'un groupe de rang de Morley fini sans involutions.
Théorème 16. Si le groupe des transvexions d'un symétron borné de rang de Morley fini est résoluble, il ne contient pas d'involutions.
Démonstration. On remplace notre symétron S par une partie définissable convexe Σ d'un groupe de rang de Morley fini, composée d'involutions et formant un symétron définissablement isomorphe à S. Soit G le groupe engendré par Σ; comme ST(S) est isomorphe au quotient de G par son centre, G est un groupe définissable résoluble; s'il est fini, on emploie le Théorème de Glauberman; sinon le dérivé N de
$G^{\circ}$
en est un sous-groupe propre définissable et connexe; il n'est pas possible que Σ soit inclus dans
$G^{\circ}$
, car sinon
$G^{\circ}/N$
serait réduit à deux points.
Dans un premier temps, on suppose que S est connexe; comme l'intersection de Σ avec une cossette modulo
$G^{\circ}$
est convexe, tous les points de Σ sont dans la même classe modulo
$G^{\circ}$
,
$G/G^{\circ}$
est d'ordre 2,
$G^{\circ} = G'$
. Quand on quotiente par N, on obtient un symétron abélien, si bien que
$G^{\circ}/N$
n'a pas d'involutions; tous les 2-éléments de
$G^{\circ}$
sont dans N, et comme ce dernier est nilpotent, il n'a qu'un seul 2-sylow
${T}$
(voir Poizat & Wagner Reference Poizat and Wagner2000). Chaque point i de Σ est contenu dans un 2-sylow
${T}_{i}$
de G, qui ne peut en contenir un deuxième j puisque i.j n'est pas un 2-élément; i est donc central dans
${T}_{i}$
, qui est le groupe engendré par T et i. On voit donc que Σ centralise
${T}$
, qui est central dans G, et que G'/Z(G) n'a pas d'involutions.
Ensuite on décompose Σ en ses composantes connexes
$\varSigma_{\textrm 1}, \ldots, \varSigma_{\textrm d}$
; la composante connexe
$H_{\textrm i}$
du groupe engendré par
$\varSigma_{\textrm i}$
n'a qu'un seul 2-sylow; comme G permute les
$\varSigma_{\textrm i}$
par conjugaison,
$G^{\circ}$
normalise chaque
$H_{\textrm i}$
, si bien que le groupe H qu'ils engendrent n'a lui aussi qu'un seul 2-sylow; comme H est connexe et
$\varSigma /H$
est fini, H égal à
$G^{\circ}$
; pour une raison semblable à celle évoquée ci-dessus, son unique 2-sylow est central dans G.
Il ne reste plus qu'à invoquer encore une fois le Théorème de Glauberman qui déclare qu'il n'y a pas d'involutions dans le dérivé de
$G/G^{\circ}$
. ⊣
9 Symétrons quotients
Comme les symétrons forment une variété (dans le langage de la symétrie et du milieu), l'image d'un symétron par un homomorphisme f est un symétron f(S); l'équivalence f(x) = f(y) est alors appelée congruence (de symétron).
Par exemple, si G est un groupe médial et H est un sous-groupe normal de G, l'équivalence modulo H est une congruence de symétron à condition que G/H soit médial.
On voit qu'une classe C de la congruence E est un sous-symétron de S; elle détermine E, puisque les autres classes de E s'obtiennent par symétries à partir de C.
Comme les points de ST(S) sont définis par des termes, le groupe ST(S/E) est une image du groupe ST(S), par un homomorphisme surjectif dont le noyau Ker(E) détermine lui aussi la congruence, ainsi d'ailleurs que
$\mathrm{Ker}(E)\cap T_{\textrm 1}(S)$
; nous appellerons T-noyau l'intersection de T(S) avec le noyau.
Si N est un sous-groupe normal de ST(S), par passage au quotient on obtient une structure d'espace symétrique (surjectif) sur S/N; la condition pour que ce quotient soit injectif est qu'aucun élément de
$T_{\textrm 1}(S)$
ne devienne une involution modulo N (c'est-à-dire que, si
$t^{\textrm 2}$
est dans
$N\cap T_{\textrm 1}(S)$
, t y est aussi); pour que ce soit un symétron, il faut en outre que tout point t de
$T_{\textrm 1}(S)$
qui commute modulo N avec une symétrie soit dans N (c'est-à-dire que, si
$[t,s_{\textrm u}]$
est dans N, t y est aussi); cela suffit car, si dans le quotient
$s_{\textrm w}$
conjugue
$s_{\textrm u}$
et
$s_{\textrm v}$
,
$s_{\textrm w}.s_{\textrm m(u,v)}$
commute modulo N avec
$s_{\textrm u}$
.
Si
$T_{\textrm 1}(S)$
est périodique, ou bien si S est oméga-stable et
$N\cap T_{\textrm 1}(S)$
est définissable, ces deux conditions sont toujours réalisées; en effet, dans le premier cas le groupe engendré par le produit
$s_{\textrm u}.s_{\textrm v}$
de deux symétries est cyclique d'ordre impair, et dans le deuxième cas ce produit est contenu dans un sous-groupe définissable médial de
$T_{\textrm 1}(S)$
, si bien que dans le quotient
$s_{\textrm u}$
et
$s_{\textrm v}$
sont égales ou ne commutent pas; ce quotient est donc un espace symétrique injectif, et un symétron d'après le Lemme 1.
On observe que les groupes qui définissent la même congruence que N sont ceux qui sont compris entre le groupe engendré par
$N\cap T_{\textrm 1}(S)$
et le noyau.
Lemme 17. Si S est un sous-symétron définissable d'un groupe médial de rang de Morley fini G et E est une congruence définissable de S, le groupe des transvexions de S/E est médial.
Démonstration. Dans ce contexte, un groupe définissable est médial dès qu'il n'a pas d'involutions. On sait par le Lemme 5 que le groupe T des transvexions de S est une section définissable de
$G\times G$
, et qu'il respecte l'équivalence E; le groupe des transvexions de S/E est isomorphe à
$T/T_{\textrm E}$
, où
$T_{\textrm E}$
est le groupe des transvexions de S qui fixent chaque classe de E; comme c'est une section définissable du groupe médial T, il n'a pas d'involutions. ⊣
Si S est un symétron oméga-stable, sa partition en composantes connexes est une congruence, dont le noyau est formé des points qui fixent chaque type générique de S. Sous les hypothèses du Lemme 15, on peut se passer du Théorème de Glauberman pour montrer que le groupe des transvexions de ce symétron fini n'a pas d'involutions.
Plus généralement, l'équivalence décrite dans le Théorème 14(iii) est une congruence de symétron.
Question 5. Cette équivalence E est-elle toujours la trace sur S(X) d'une congruence définissable entre éléments du plus petit sous-symétron définissable contenant X?
Exemple 8. La relation d'équivalence dont les classes sont les orbites du centre C du groupe des transvexions du symétron S est une congruence de symétron. En effet, si
$s_{\textrm u}.s_{\textrm v}.s_{\textrm u} = s_{\textrm w}.t$
, où t est centrale, comme les symétries inversent les points de C,
$t^{\textrm 1/4}.s_{\textrm u}.t^{\textrm -1/4}.s_{\textrm v}.t^{\textrm 1/4}.s_{\textrm u}.t^{\textrm -1/4} = s_{\textrm w}$
, si bien que
$t^{\textrm 1/4}.s_{\textrm u}.t^{\textrm -1/4}$
est le milieu de
$s_{\textrm v}$
et de
$s_{\textrm w}$
, et qu'il y a unicité du milieu modulo C. Cependant, T(S/C), étant le quotient de T(S) par les transvexions qui fixent modulo C chaque symétrie, n'est pas en général égal à T(S)/C. On vérifie sans peine que le T-noyau est compris entre C et le deuxième centre de T(S), et qu'il contient strictement C quand S est le symétron d'un groupe médial 3-nilpotent non 2-nilpotent.
10 Quelques axiomes
Nous récapitulons en conclusion un certain nombre de conditions qui éliminent les transvexions involutives; il semble que la plus forte - la médialité du groupe des transvexions - ne puisse s'exprimer au premier ordre, car on ne voit pas comment affirmer l'existence d'une racine carrée d'un point de
$T_{\textrm n}$
sans préciser dans quel
$T_{\textrm m}$
elle se trouve. Par contre, les suivantes correspondent à la satisfaction d'une infinité d'axiomes du premier ordre (un axiome par longueur possible des mots). On exclut de la discussion les symétrons réduits à un point.
-
A. Transvexions et réflexions sont disjointes, c'est-à-dire qu'une symétrie ne peut être une transvexion, qu'une réflexion ne peut être égale à l'identité.
-
B. Les réflexions ou transvexions involutives sont les symétries.
-
C. Pas de transvexions involutives.
-
D. Chaque transvexion a les même points fixes que son carré.
-
E. Deux transvexions de même carré sont égales.
-
F. Chaque réflexion a au plus un point fixe.
-
G. Chaque réflexion a exactement un point fixe.
Il est clair que G implique F, que D implique C, et que C implique A; par ailleurs, nous avons vu dans le Corollaire 8 que E implique F et D, et que C implique B.
Cette cascade d'axiomes pose la question de leur indépendance, et de leur indépendance dans des contextes particuliers. Nous remarquons qu'ils sont tous vérifiés dans le cas d'une partie définissable convexe d'un groupe de rang de Morley fini sans involutions.
Nous soupçonnons l'existence de symétrons de rang de Morley fini, et même de symétrons définissables dans un corps algébriquement clos, ayant un groupe de transvexions non borné, bien que nous n'en connaissions pas d'exemples. Pour ces éventuels symétrons de rang de Morley fini non bornés, se posera la question de l'égalité des rangs de Morley, de Cantor et de Lascar (ce n'est pas le cas pour les symétrons bornés, qui ne sont que des groupes dans un langage augmenté; voir le Lemme 5(vi) et la préface de Poizat Reference Poizat1987).
