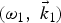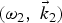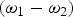1. INTRODUCTION
The terahertz (THz) radiation generation has attracted a widespread interest in the scientific community due to potential applications of these waves in medical and biological imaging, remote sensing, material characterization, explosive detection, and outer space communication (Pickwell et al., Reference Pickwell and Wallace2006; Zhong et al., Reference Zhong, Redo-Sanchez and Zhang2006; Beard et al., Reference Beard, Turner and Schmuttenmar2002; Shen et al., Reference Shen, Lo, Taday, Cole, Tribe and Kemp2005). Conventional methods using semiconductors and electro-optic crystals were not efficient enough to achieve high energy pulses of terahertz radiation. Since then, various routes are proposed to generate strong electromagnetic wave in terahertz range by employing high power laser plasma interaction. Plasma as a nonlinear media for terahertz generation has an added advantage of not having damage limit. Hamster et al. (Reference Hamster, Sullivan, Gordon, White and Falcone1993) observed a high power terahertz radiation from a plasma short pulse produced by laser, employing 1 TW, 100 fs laser beam focused on gas and solid targets. They also observed terahertz radiation in a laser induced plasma channel where ponderomotive force drives radiations (Hamster et al., Reference Hamster, Sullivan, Gordon and Falcone1994). Antonsen et al. (Reference Antonsen, Palastra and Milchberg2007) examined the ponderomotive force driven THz radiation generation in a plasma with space periodic axial density variation.
Gildenberg et al. (Reference Gildenburg and Vvedenskii2007) proposed a novel scheme of employing a femtosecond laser pulse on a low density gas jet target. In this model, the laser quickly tunnel ionizes the gas in the axial region. Electrons born inside the pulse retain finite transverse momentum after the passage of the pulse and set in oscillations of the electron plasma cylinder with respect to the ion cylinder, producing THz radiation at the frequency of oscillation 
${\rm \omega}_p /\sqrt 2 $, where ωp is the plasma frequency of the cylinder. Liu et al. (Reference Liu and Tripathi2009) derived a scheme for producing tunable teraheartz radiation using a short pulse laser to tunnel ionize a gas jet immersed in a magnetic field. Tripathi et al. (Reference Tripathi, Bhasin, Uma and Tripathi2010) proposed that a two-dimensional amplitude modulated laser propagating in a ripple-density plasma can resonantly excite THz radiation at the modulation frequency 
$\Omega={\rm \omega}_p /\sqrt 2$. Du et al. (Reference Dua, Chena, Shenga and Zhanga2011) investigated the THz radiation generation from two color laser pulse interaction with gas targets using Ammosov-Delone-Krainov ionization model. Hu et al. (Reference Hu, Shen, Lei, Li and Xu2010) proposed a scheme to improve the intensity of THz radiation, which is emitted from a single laser filament through transition-Cherenkov radiation mechanism.
Pathak et al. (Reference Pathak, Dahiya and Tripathi2009) employed the free electron laser concept in a rippled density plasma and looked for the possibility of radiation generation in the THz range. A weakly relativistic electron beam propagating through a rippled underdense plasma couples with a seed terahertz signal to produce a space charge beam mode. This beam mode beats with density ripple and generates a coherent electromagnetic wave in the THz frequency range in forward direction. For an electron beam with 5 MW power, they proposed ~40 kW at 1 THz frequency. Tripathi et al. (Reference Tripathi and Liu1990) proposed a mechanism for short wavelength electromagnetic wave generation in a periodic dielectric material. When a moderately energetic electron beam passes through a periodic dielectric along with a copropagating electromagnetic wave, the latter gets amplified. Kumar et al. (Reference Kumar, Kumar and Tripathi2010) have studied the excitation of THz plasmons Eigen mode by a relativistic sheet electron beam propagating through a parallel plane guiding semiconductor system. They achieved a growth rate of 5.93 × 108 rad/s at a frequency of 0.51 THz of surface plasmons for a beam current of 168 A.
The presence of magnetic field may strongly influence the nonlinear interaction of short pulse high intensity lasers with plasma, because magnetized plasma may support various new modes depending upon the orientation of magnetic field with respect to the incident laser. Verma et al. (Reference Verma and Sharma2011) obtained the mode structure of right circularly polarized nonlinear laser Eigen mode in a self created plasma channel in the presence of an axial magnetic field, and observed that the presence of magnetic field modifies the Eigen frequency of the fundamental laser Eigen modes in stimulated Raman scattering. Paknezhad et al. (Reference Paknezhad and Dorranian2011) studied the nonlinear effects in the interaction of high power short laser pulse with plasma up to third-order nonlinearity in the presence of external magnetic field. They show an increase in the growth rate of Raman backward instability due to cyclotronic motion of plasma electrons in the external magnetic field. Ghorbanalilu et al. (Reference Ghorbanalilu2012) studied the conversion of a fraction of a laser beam to its second and third harmonics into a transversely magnetized plasma. The harmonic radiation cut-off when magnetic field increases to saturation strength. Verma et al. (Reference Verma and Sharma2009) shown the effect of the azimuthal magnetic field to generate laser second harmonic in a rippled density plasma and found that, as magnetic field increases, generation of second harmonic becomes faster. In a similar fashion, the amplitude and energy conversion efficiency of terahertz radiation generation may also be enhanced by utilizing cyclotron resonance condition for maximum energy transfer in magnetized plasma.
In the present paper, we study terahertz generation by beating of two extra-ordinary lasers in rippled density magnetized plasma. The static magnetic field 
$\vec B_s$ is perpendicular to the direction of laser propagation, while the ripple wave vector is parallel to the laser wave vector (Fig. 1). Due to the presence of a static magnetic field in the direction of the laser propagation, there are components of nonlinear ponderomotive force in the direction of the lasers and perpendicular to it. In the presence of corrugation in the plasma density (space-periodic plasma density structure), the ponderomotive force gives rise to an oscillatory current that oscillates at beating frequency of lasers, which produces terahertz radiation. The density ripple of suitable wave number turns the process to be a resonant one.
Fig. 1. (Color online) Schematic of beat excitation of terahertz radiation in the presence of transverse static magnetic field 
$\vec B_s$.
The organization of this paper is as follows: the model equations for THz radiation generation by beating of two extra-ordinary lasers are derived in Section 2. In the same section, amplitude and efficiency of THz radiation generation are also calculated. Section 3 is devoted for discussion.
2. TERAHERTZ RADIATION GENERATION DUE TO LASER BEATING
Consider a laser produced rippled plasma of density 
$n_0=$
$n_0^0+n_q $, 
$n_q=n_{q_0 } e^{iqx}$ with static magnetic field 
$B_s \hat z$, where 
$n_{q_0 }$ is the amplitude of ripple, and q is the periodicity of the density ripple, structure. These plasma density ripples can be produced using various techniques involving transmission ring grating and patterned mask, where the control of ripple parameters might be possible by changing groove period, groove structure and duty cycle in such a grating, and by adjusting the period and the size of mask (Kuo et al., Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007; Malik & Nishida, Reference Malik, Malik and Nishida2011; Malik & Stroth, Reference Malik, Malik and Stroth2011; Bhasin et al., Reference Bhasin and Tripathi2009; Layer et al., Reference Layer, York, Antonsen, Varma, Chen, Leng and Milchberg2007; Malik et al., Reference Malik, Malik and Stroth2012). Two x-mode lasers co-propagate through it along the 
$\hat x$-direction with electric field:
$$\vec E_j=\left({\hat y - \displaystyle{{{\rm \epsilon}_{\,jxy} } \over {{\rm \epsilon}_{\,jxx} }}\hat x} \right)A_{0j} e^{ - i\lpar {\rm \omega}_j t - k_j x\rpar }\comma \; \eqno \lpar 1\rpar$$where
$$k_j=\displaystyle{{{\rm \omega}_j } \over c}\left({1 - \displaystyle{{{\rm \omega}_p^2 } \over {{\rm \omega}_j^2 }}\displaystyle{{{\rm \omega}_j^2 - {\rm \omega}_p^2 } \over {{\rm \omega}_j^2 - {\rm \omega}_p^2 - {\rm \omega}_c^2 }}} \right)^{1/2}\comma \; \quad j=1\comma \; 2.$$ Here, 
${\rm \omega}_p=\sqrt {n_0 e^2 /{\rm \epsilon}_0\, m}$ and 
${\rm \omega}_c=eB_s /m$ are the electron plasma frequency and electron cyclotron frequency, respectively; −e and m are electronic charge and mass, respectively; and 
${\rm \varepsilon}_{\,jxx}=\lsqb 1 - \lpar {\rm \omega}_p^2 /{\rm \omega}_j^2 - {\rm \omega}_c^2 \rpar \rsqb $ and 
${\rm \epsilon}_{\,jxy}=- i$
$\lsqb {\rm \omega}_c {\rm \omega}_p^2 /{\rm \omega}_j \lpar {\rm \omega}_j^2 - {\rm \omega}_c^2 \rpar \rsqb $ are components of the dielectric tensor 
${\rm \varepsilon}_j.$ Lasers impart oscillatory velocities to plasma electrons, given by
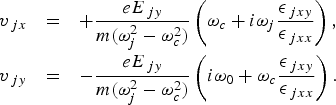$$\matrix{ {v_{\,jx} } \hfill &=\hfill & {+\displaystyle{{eE_{\,jy} } \over {m\lpar {\rm \omega}_j^2 - {\rm \omega}_c^2 \rpar }}\left({{\rm \omega}_c+i{\rm \omega}_j \displaystyle{{{\rm \epsilon}_{\,jxy} } \over {{\rm \epsilon}_{\,jxx} }}} \right)\comma \; } \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {v_{\,jy} } \hfill &=\hfill & { - \displaystyle{{eE_{\,jy} } \over {m\lpar {\rm \omega}_j^2 - {\rm \omega}_c^2 \rpar }}\left({i{\rm \omega}_0+{\rm \omega}_c \displaystyle{{{\rm \epsilon}_{\,jxy} } \over {{\rm \epsilon}_{\,jxx} }}} \right).} \hfill \cr }\eqno \lpar 2\rpar$$ Lasers beat together and exert a ponderomotive force F p on plasma electrons at frequency 
${\rm \omega}={\rm \omega}_1 - {\rm \omega}_2$ and wave vector 
$\vec k=\vec k_1 - \vec k_2$.
Given by,
$$\vec F_p=-e(\vec v \times \vec B) - m (\vec v\cdot\nabla \vec v)\eqno \lpar 3\rpar$$
Substituting values of 
$\vec v_1$ and 
$\vec v_2$ in Eq. (3), we obtain the x and y components of the ponderomotive force, as follows:
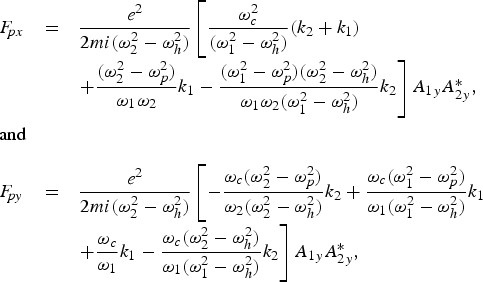$$\matrix{ {F\!\!_{px} } \hfill &=\hfill & {\displaystyle{{e^2 } \over {2mi\lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar }}\left[{\displaystyle{{{\rm \omega}_c^2 } \over {\lpar {\rm \omega}_1^2 - {\rm \omega}_h^2 \rpar }}\lpar k_2+k_1 \rpar } \right.} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {\left. {+\displaystyle{{\lpar {\rm \omega}_2^2 - {\rm \omega}_p^2 \rpar } \over {{\rm \omega}_1 {\rm \omega}_2 }}k_1 - \displaystyle{{\lpar {\rm \omega}_1^2 - {\rm \omega}_p^2 \rpar \lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar } \over {{\rm \omega}_1 {\rm \omega}_2 \lpar {\rm \omega}_1^2 - {\rm \omega}_h^2 \rpar }}k_2 } \right]A_{1y} A_{2y}^{\ast} }\comma \; \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {\rm and} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {F\!\!_{py} } \hfill &=\hfill & {\displaystyle{{e^2 } \over {2mi\lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar }}\left[{ - \displaystyle{{{\rm \omega}_c \lpar {\rm \omega}_2^2 - {\rm \omega}_p^2 \rpar } \over {{\rm \omega}_2 \lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar }}k_2+\displaystyle{{{\rm \omega}_c \lpar {\rm \omega}_1^2 - {\rm \omega}_p^2 \rpar } \over {{\rm \omega}_1 \lpar {\rm \omega}_1^2 - {\rm \omega}_h^2 \rpar }}k_1 } \right.} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {\left. {+\displaystyle{{{\rm \omega}_c } \over {{\rm \omega}_1 }}k_1 - \displaystyle{{{\rm \omega}_c \lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar } \over {{\rm \omega}_1 \lpar {\rm \omega}_1^2 - {\rm \omega}_h^2 \rpar }}k_2 } \right]A_{1y} A_{2y}^{\ast}}\comma \; \hfill \cr } \eqno \lpar 4\rpar$$
where, 
${\rm \omega}_h^2={\rm \omega}_p^2+{\rm \omega}_c^2$. The ponderomotive force drives space charge oscillation at 
${\rm \omega}={\rm \omega}_1 - {\rm \omega}_2$ and wave number (
$\vec k = \vec k_1 - \vec k_2 $). Let the space charge potential of this mode be φ. The oscillatory velocity of electrons in the presence of static magnetic field due to space charge oscillations along with ponderomotive force is given by
$$\matrix{ {v_x } \hfill &=\hfill & {\displaystyle{{\rm \omega} \over {m\lpar {\rm \omega} ^2 - {\rm \omega}_c^2 \rpar }}\lsqb \!- ek{\rm \phi}+\displaystyle{{{\rm \omega}_c } \over {\rm \omega} }F\!\!_{\,py}+iF\!\!_{\,px} \rsqb \comma \; } \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {\rm and} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {v_y } \hfill &=\hfill & {\displaystyle{{\rm \omega} \over {m\lpar {\rm \omega} ^2 - {\rm \omega}_c^2 \rpar }}\lsqb \!\!- iek\displaystyle{{{\rm \omega}_c } \over {\rm \omega} }{\rm \phi}+iF\!\!_{\,py} - \displaystyle{{{\rm \omega}_c } \over {\rm \omega} }F\!\!_{\,px} \rsqb .} \hfill \cr } \eqno \lpar 5\rpar$$ The nonlinear velocity given by Eq. (5) along with continuity equations produce density perturbation given by 
$n=n^L+n^{NL}$, where
$$n^L=\displaystyle{1 \over {4{\rm \pi} e}}k^2 {\rm \chi} {\rm \phi}\comma \; \eqno \lpar 6\rpar$$and
$$\matrix{ {n^{NL} } \hfill &=\hfill & {\displaystyle{{in_0\, k} \over {m\lpar {\rm \omega} ^2 - {\rm \omega}_c^2 \rpar }}F\!\!_{\,px} }\comma \; \hfill \cr } \eqno \lpar 7\rpar$$ where 
${\rm \chi}=- {\rm \omega}_p^2 /\lpar {\rm \omega} ^2 - {\rm \omega}_c^2 \rpar $. Linear density perturbation 
$\lpar n^L \rpar $ is induced self consistently by space charge field and nonlinear density perturbation 
$\lpar n^{NL} \rpar $ is the consequence of ponderomotive force. Here, density perturbation is assumed to be small as compared to the density ripple. Using the density perturbation 
$n=n^L+n^{NL}$ in the Poisson's equation 
$\nabla ^2 {\rm \phi}=4{\rm \pi} ne$, we obtain
$${\rm \varepsilon} {\rm \phi}=- \displaystyle{{4{\rm \pi} e} \over {k^2 }}n^{NL}\comma \; \eqno \lpar 8\rpar$$
where, 
${\rm \epsilon}=1+{\rm \chi} $. One can rearrange Eq. (8) as follows:
$${\rm \phi}=- \displaystyle{{4{\rm \pi} n_0 e} \over {mk\lpar {\rm \omega} ^2 - {\rm \omega}_h^2 \rpar }}\left[{iF\!\!_{\,px}+\displaystyle{{{\rm \omega}_c } \over {\rm \omega} }F\!\!_{\,py} } \right]. \eqno \lpar 9\rpar$$Substituting this value of φ in Eq. (5), we obtain
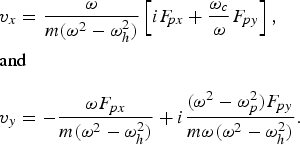$$\matrix{ {v_x } = {\displaystyle{{\rm \omega} \over {m\lpar {\rm \omega} ^2 - {\rm \omega}_h^2 \rpar }}\left[{iF\!\!_{px}+\displaystyle{{{\rm \omega}_c } \over {\rm \omega} }F\!\!_{\,py} } \right]\comma \; } \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {\rm and} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {v_y } = { - \displaystyle{{{\rm \omega} F\!\!_{\,px} } \over {m\lpar {\rm \omega} ^2 - {\rm \omega}_h^2 \rpar }}+i\displaystyle{{\lpar {\rm \omega} ^2 - {\rm \omega}_p^2 \rpar F\!\!_{\,py} } \over {m{\rm \omega} \lpar {\rm \omega} ^2 - {\rm \omega}_h^2 \rpar }}.} \hfill \cr } \eqno \lpar 10\rpar$$ Oscillations at 
$\lpar {\rm \omega}\comma \; \vec k_1 - \vec k_2 \rpar $ in the presence of density ripple 
$n_{q_0 } e^{iqx}$ excite nonlinear current at 
$\lpar {\rm \omega}\comma \; \vec k_1 - \vec k_2+q\rpar $, which can be written as
$$\vec J^{NL}=- \displaystyle{1 \over 2}n_{q_0 } e\vec v_{\rm \omega} e^{iqx}\comma \eqno \lpar 11\rpar$$ where, 
$\vec v_{\rm \omega}$ is given by Eq. (10). It can be observed from Eq. (11) that 
$J^{NL}$ varies as 
$\sim \!\!e^{ - i\lpar {\rm \omega} t - kx\rpar } $, where, 
$k=k_1 - k_2+q$, and it is responsible for terahertz radiation generation. It is clear that, wave number q of density ripple is responsible for providing extra momentum in x-direction to achieve the resonance condition. The resonance condition can be tuned by varying plasma density and magnetic field 
$\lpar B_s \rpar $. For strong THz radiation, plasma density ripples should be periodic, otherwise 
$k\lpar \!\!=k_1 - k_2+q\rpar $ will exhibit non-periodic behavior; resonance condition can not be achieved and maximum energy transfer will not take place and consequently a weak field THz radiation will be generated. The wave equation governing the propagation of terahertz wave can be written as
$$-\nabla ^2 \vec E+\nabla .\lpar \nabla .\vec E\rpar =\displaystyle{{4{\rm \pi} i{\rm \omega} } \over {c^2 }}\vec J+\displaystyle{{{\rm \omega} ^2 } \over {c^2 }}\lpar {\rm \epsilon} .\vec E\rpar \comma \; \eqno \lpar 12\rpar$$
where, 
${\rm \epsilon}$ is the plasma permittivity tensor at 
${\rm \omega} $. Taking fast phase variations in the electric field profile of terahertz radiation as 
$\vec E=\vec A\lpar x\rpar e^{ - i\lpar {\rm \omega} t - kx\rpar } $, the wave equation governing the propagation of terahertz waves can be splitted into x and y components and rearranged as follows:
$$A_x=- \displaystyle{{4{\rm \pi} i} \over {{\rm \omega} {\rm \epsilon}_{xx} }}J_x^{NL} - \displaystyle{{{\rm \epsilon}_{xy} } \over {{\rm \epsilon}_{xx} }}A_y\comma \; \eqno \lpar 13\rpar$$and
$$\matrix{ {\left[{2ik\displaystyle{{\partial A_y \lpar x\rpar } \over {\partial x}}+\displaystyle{{{\rm \omega} ^2 } \over {c^2 }}{\rm \epsilon}_{yy} A_y \lpar x\rpar - k^2 A_y \lpar x\rpar } \right]e^{ - i\lpar {\rm \omega} t - kx\rpar } } \hfill \cr {} \hfill \cr \quad {=- \displaystyle{{4{\rm \pi} {\rm \omega} } \over {c^2 }}J_y^{NL} - \displaystyle{{{\rm \omega} ^2 } \over {c^2 }}{\rm \epsilon}_{yx} A_x }. \hfill \cr } \eqno \lpar 14\rpar$$Substituting the value of A x from Eq. (13) into Eq. (14), we obtain
$$\eqalign{& \matrix{ {2ik\displaystyle{{\partial A_y \lpar x\rpar } \over {\partial x}} e^{ - i\lpar {\rm \omega} t - kx\rpar } } {+\left[{\displaystyle{{{\rm \omega} ^2 } \over {c^2 }}\left({{\rm \epsilon}_{yy}+\displaystyle{{{\rm \epsilon}_{xy} {\rm \epsilon}_{yx} } \over {{\rm \epsilon}_{xx} }}} \right)- k^2 } \right]} \quad {A_y \lpar x\rpar e^{ - i\lpar {\rm \omega} t - kx\rpar } }} \cr {} \hfill &\quad\quad\quad\quad\quad\quad\quad\quad {=- \displaystyle{{4{\rm \pi} i{\rm \omega} } \over {c^2 }}J_y^{NL}+\displaystyle{{4{\rm \pi} i{\rm \omega} } \over {c^2 }}\displaystyle{{{\rm \epsilon}_{yx} } \over {{\rm \epsilon}_{xx} }}J_x^{NL}}.}$$From Eq. (15), it can be observed that terahertz radiation generation demands to satisfy the following dispersion relation for exact phase matching condition in rippled magnetized plasma:
$$\displaystyle{{k^2 c^2 } \over {{\rm \omega} ^2 }}={\rm \epsilon}_{yy}+\displaystyle{{{\rm \epsilon}_{xy} {\rm \epsilon}_{yx} } \over {{\rm \epsilon}_{xx} }}. \eqno \lpar 16\rpar$$This expression is the dispersion relation of x-mode terahertz radiation, which gives the following phase matching condition
$$q=\displaystyle{{\rm \omega} \over c}\left\vert {\left({{\rm \epsilon}_{yy}+\displaystyle{{{\rm \epsilon}_{xy} {\rm \epsilon}_{yx} } \over {{\rm \epsilon}_{xx} }}} \right)^{1/2} - 1} \right\vert. \eqno \lpar 17\rpar$$ This phase matching condition provides the estimate of periodicity of rippled structure and suggests that the maximum energy transfer from beating lasers to THz radiation will take place at resonance 
${\rm \omega} \simeq {\rm \omega}_h$. In Figure 2a, we have plotted normalized periodicity of rippled structure (cq/ωp) as a function of normalized THz wave frequency (ω/ωp) and normalized cyclotron frequency, when ωp/2π = 1 THz and ω1 = 2 × 1014 rad/s (CO2 laser). Periodicity of ripples q decreases with THz wave frequency, but increases with betatron frequency. The periodicity q attains maximum value as ω tends to ωh. So, we can conclude that for the efficient energy transfer at resonance 
${\rm \omega} \simeq {\rm \omega}_h $, the wavelength of density ripples 
$\lpar {\rm \lambda}_r=2{\rm \pi} /q\rpar $ should be small corresponding to larger value of q i.e., sharp ripples at closer distances should be constructed for strong THz radiation. The excited THz radiation can propagate through the plasma as extra-ordinary electromagnetic wave only if its frquency lies in the two propagating regimes of extra ordinary wave in a plasma given by (1) 
${\rm \omega}_L\lt {\rm \omega}\lt {\rm \omega}_h$ and (2) 
${\rm \omega}\gt {\rm \omega}_R $ where 
${\rm \omega}_L={1 \over 2}\Big[{ - {\rm \omega}_c+\sqrt {{\rm \omega}_c^2+4{\rm \omega}_p^2 }} \Big]$ and 
${\rm \omega}_R={1 \over 2}\big[{{\rm \omega}_c+} \sqrt {{\rm \omega}_c^2+4{\rm \omega}_p^2 }\big]$. In the present scheme ωc/ωp = 0.0 − 0.6 and correspoding to this, variation of ωL/ωp, ωR/ωp, and ωh/ωp is shown in Figure 2b. Regions I and III are non-propagating regions and regions II and IV are propagating regions for the present scheme. It is clear from Figure 2b that, the frequency of THz radiation in the present sceme ω/ωp = 1.6 − 3.0 lies in propagating regime IV. Thus excited THz radiation can easily move out of the plasma by propagating through it as extra-ordinary electromagnetic wave.
Fig. 2. (Color online) Plot of various parameters of THz radiation generation scheme by beat wave process. (a) Plot of the normalized ripple factor as a function of the nomalized frequency and normalized cyclotron frquency. (b) Sketch of the normalized frequency of THz radiation as a function of normalized cyclotron frquency. Lower, Middle and Upper lines are corresponding to ωL/ωp, ωh/ωp and ωR/ωp, respectively.
Substituting the phase matching condition in Eq. (15), we obtain the amplitude of THz radiation
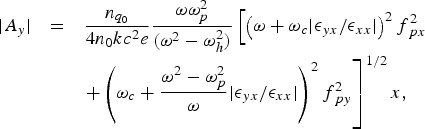$$\matrix{ {\vert A_y \vert } \hfill &=\hfill & {\displaystyle{{n_{q_0 } } \over {4n_0 kc^2 e}}\displaystyle{{{\rm \omega} {\rm \omega}_p^2 } \over {\lpar {\rm \omega} ^2 - {\rm \omega}_h^2 \rpar }}\left[{\left({{\rm \omega}+{\rm \omega}_c \vert {\rm \epsilon}_{yx} /{\rm \epsilon}_{xx} \vert } \right)^2 f_{\,px}^2 } \right.} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {\left. {+\left({{\rm \omega}_c+\displaystyle{{{\rm \omega} ^2 - {\rm \omega}_p^2 } \over {\rm \omega} }\vert {\rm \epsilon}_{yx} /{\rm \epsilon}_{xx} \vert } \right)^2 f_{\,py}^2 } \right]^{1/2} x}\comma \; \hfill \cr } \eqno \lpar 18\rpar$$
where, 
$f_{\,px}=iF\!\!_{\,px}$ and 
$f_{\,py}=iF\!\!_{\,py} $. The normalized amplitude of terahertz radiation can be written as follows:
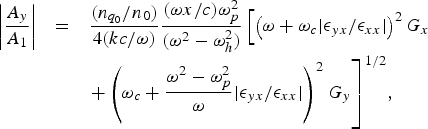$$\matrix{ {\left\vert {\displaystyle{{A_y } \over {A_1 }}} \right\vert } \hfill &=\hfill & {\displaystyle{{\lpar n_{q_0 } /n_0 \rpar } \over {4\lpar kc/{\rm \omega} \rpar }}\displaystyle{{\lpar {\rm \omega} x/c\rpar {\rm \omega}_p^2 } \over {\lpar {\rm \omega} ^2 - {\rm \omega}_h^2 \rpar }}\left[{\left({{\rm \omega}+{\rm \omega}_c \vert {\rm \epsilon}_{yx} /{\rm \epsilon}_{xx} \vert } \right)^2 G_x } \right.} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {\left. {+\left({{\rm \omega}_c+\displaystyle{{{\rm \omega} ^2 - {\rm \omega}_p^2 } \over {\rm \omega} }\vert {\rm \epsilon}_{yx} /{\rm \epsilon}_{xx} \vert } \right)^2 G_y } \right]^{1/2} }\comma \; \hfill \cr } \eqno \lpar 19\rpar$$where
$$\matrix{ {G\!_{\,px} } \hfill &=\hfill & {\displaystyle{{{\rm \omega}_2^2 \left\vert {v_2 } \right\vert ^2 } \over {4\lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar }}\,\left[{\displaystyle{{{\rm \omega}_c^2 } \over {\lpar {\rm \omega}_1^2 - {\rm \omega}_h^2 \rpar }}\lpar k_2+k_1 \rpar } \right.} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {\left. {+\displaystyle{{\lpar {\rm \omega}_2^2 - {\rm \omega}_p^2 \rpar } \over {{\rm \omega}_1 {\rm \omega}_2 }}k_1 - \displaystyle{{\lpar {\rm \omega}_1^2 - {\rm \omega}_p^2 \rpar \lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar } \over {{\rm \omega}_1 {\rm \omega}_2 \lpar {\rm \omega}_1^2 - {\rm \omega}_h^2 \rpar }}k_2 } \right]^2 }\comma \; \hfill \cr }$$and
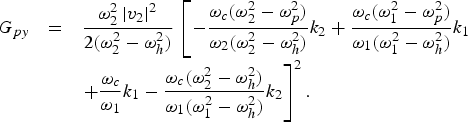$$\matrix{ {G\!_{\,py} } \hfill &=\hfill & {\displaystyle{{{\rm \omega}_2^2 \left\vert {v_2 } \right\vert ^2 } \over {2\lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar }}\,\left[{ - \displaystyle{{{\rm \omega}_c \lpar {\rm \omega}_2^2 - {\rm \omega}_p^2 \rpar } \over {{\rm \omega}_2 \lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar }}k_2+\displaystyle{{{\rm \omega}_c \lpar {\rm \omega}_1^2 - {\rm \omega}_p^2 \rpar } \over {{\rm \omega}_1 \lpar {\rm \omega}_1^2 - {\rm \omega}_h^2 \rpar }}k_1 } \right.} \hfill \cr {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {\left. {+\displaystyle{{{\rm \omega}_c } \over {{\rm \omega}_1 }}k_1 - \displaystyle{{{\rm \omega}_c \lpar {\rm \omega}_2^2 - {\rm \omega}_h^2 \rpar } \over {{\rm \omega}_1 \lpar {\rm \omega}_1^2 - {\rm \omega}_h^2 \rpar }}k_2 } \right]^2.} \hfill \cr }$$ This equation reveals that the normalized terahertz amplitude is directly proportional to the normalized amplitude of density ripples 
$n_{q_0 } /n_0 $, thus THz field increases on increasing ripple amplitude. Its explanation lies in Eq. (11); higher the ripple amplitude, greater the number of electrons involving in the generation of oscillatory nonlinear current. Higher number of charge carriers result into higher nonlinear current 
$\lpar \vec J^{NL} \rpar $, which leads to more efficient THz radiation. Similar type of observations are made by Antonsen et al. (Reference Antonsen, Palastra and Milchberg2007) who proposed that the phase matching requirements for efficient energy transfer from laser pulse to THz can be matched in a parabolic plasma channel (in radius) by z sequence of delta-function peaks with period d and strength 
$\Delta $, in axial distance.
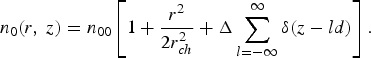$$n_0 \lpar r\comma \; z\rpar =n_{00} \left[{1+\displaystyle{{r^2 } \over {2r_{ch}^2 }}+\Delta \sum\limits_{l=- \infty }^\infty {\rm \delta} \lpar z - ld\rpar } \right].$$Here, delta function type axial coagulated plasma density acts as ripples. This inhomogeneity couples with the density perturbation provided by ponderomotive force and gives rise to a nonlinear current responsible for THz generation.
It can be observed from Figure 3 that enhancement in THz wave amplitude is more pronounced, when THz frequency ω approaches the resonance condition 
${\rm \omega} \simeq 1.3{\rm \omega}_p \lpar \!\simeq {\rm \omega}_h \rpar $, and it can be attributed to the factor 
$\lpar {\rm \omega} ^2 - {\rm \omega}_h^2 \rpar $, present in denominator of Eq. (19). This factor is introduced in the potential ϕ of space charge mode of plasma due to the presence of perpendicular magnetic field. In the presence of magnetic field, the potential of space charge mode will achieve its peak value at 
${\rm \omega} \simeq {\rm \omega}_h$ and energy transfer in beat wave process will be maximal. This maximally developed space charge mode along with density ripple give rise to strong nonlinear current responsible for maximum THz amplitude. The amplitude of THz wave decreases as one moves away from the resonance condition 
${\rm \omega} \simeq {\rm \omega}_h $. For (approximately) 
${\rm \omega} \lt 1.3 {\rm \omega}_p\comma \; k^2 \lt 0$, so, the generation of THz does not take place. The amplitude 
$A_y$ increases with the normalized distance (
$xc/{\rm \omega} $) along propagation direction. THz wave attains maximum value for broader range of normalized frequency 
${\rm \omega} /{\rm \omega}_p$ with the increase of 
$xc/{\rm \omega}$ values. In Figure 3b, we analyze simultaneous effects of electron plasma density and applied magnetic field on the amplitude of THz radiation. It can be observed that, a particular amplitude of THz radiation can be obtained in two ways: (1) either choosing higher value of magnetic field in a low density plasma or (2) choosing lower value of magnetic field at relatively higher density of plasma. This result is corresponding to resonant excitation of THz radiation. At resonance, 
${\rm \omega} ^2 \sim {\rm \omega}_h^2 \approx {\rm \omega}_c^2+{\rm \omega}_p^2 $, which gives us approximation condition for resonance as 
$\left({{\rm \omega}_p^2 /{\rm \omega} ^2 } \right)+\left({{\rm \omega}_c^2 /{\rm \omega} ^2 } \right)={\rm constant}$. Thus, maximum amplitude is obtained when above condition is satisfied.
Fig. 3. (Color online) Diagram of THz amplitude radiation as a function of different parameters. (a) THz radiation field vs normalized frequency of beat and transverse distance when 
$n_{q_0 }/n_0=0.2$ and 
${\rm \omega}_c /{\rm \omega}_p=0.6$. (b) Sketch of THz radiation field vs normalized frequency of beat and the cyclotron frequency when 
$n_{q_0 } /n_0=0.2$.
The efficiency of the THz radiation generation can be examined by calculating the ratio of the energies of THz radiation and the incident laser (pump). According to Rothwell et al. (Reference Rothwell and Cloud2009), average electromagnetic energy per unit volume stored in electric and magnetic fields is given by
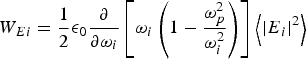$$W_{Ei}=\displaystyle{1 \over 2}{\rm \epsilon}_0 \displaystyle{\partial \over {\partial {\rm \omega}_i }}\left[{{\rm \omega}_i \left({1 - \displaystyle{{{\rm \omega}_p^2 } \over {{\rm \omega}_i^2 }}} \right)} \right]\left\langle {\left\vert {E_i } \right\vert ^2 } \right\rangle \eqno \lpar 20\rpar$$and
$$W_{Bi}=\displaystyle{{\left\langle {\left\vert {B_i } \right\vert ^2 } \right\rangle } \over {2{\rm \mu}_0 }} \;{\rm where} \;\left\langle {B_i } \right\rangle=\displaystyle{{k\left\langle {E_i } \right\rangle } \over {{\rm \omega}_i }}.$$Using these expressions, we obtain the efficiency of the THz radiation as follows:
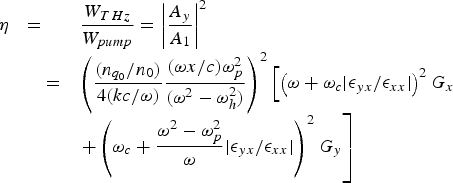$$\eqalign{& \matrix{ {\rm \eta} \hfill &=\hfill & {\displaystyle{{W_{THz} } \over {W\!\!_{\,pump} }}=\left\vert {\displaystyle{{A_y } \over {A_1 }}} \right\vert ^2 } \hfill \cr & \quad =\hfill & {\left({\displaystyle{{\lpar n_{q_0 } /n_0 \rpar } \over {4\lpar kc/{\rm \omega} \rpar }}\displaystyle{{\lpar {\rm \omega} x/c\rpar {\rm \omega}_p^2 } \over {\lpar {\rm \omega} ^2 - {\rm \omega}_h^2 \rpar }}} \right)^2 \left[{\left({{\rm \omega}+{\rm \omega}_c \vert {\rm \epsilon}_{yx} /{\rm \epsilon}_{xx} \vert } \right)^2 G_x } \right.} \cr & \quad & {\left. {+\left({{\rm \omega}_c+\displaystyle{{{\rm \omega} ^2 - {\rm \omega}_p^2 } \over {\rm \omega} }\vert {\rm \epsilon}_{yx} /{\rm \epsilon}_{xx} \vert } \right)^2 G_y } \right]} \hfill \cr }}\eqno \lpar 21\rpar$$In Figure 4, we have plotted the efficiency of THz radiation generation as a function of normalized beat frequency, normalized magnetic field, and normalized density ripple. Maximum efficiency is achieved at resonance condition and decreases sharply as one moves away from the resonance condition (Fig. 4a). The maximum efficiency at resonance increases with the ripple amplitude because number of electrons involved in the generation of oscillatory nonlinear current (leading to THz radiation generation) increases on increasing ripple amplitude (Fig. 4b).
Fig. 4. (Color online) Diagram of the efficiency of THz as a function of different parameters. (a) Figure of efficiency of THz radiation vs normalized frequency and applied magnetic field when normalized distance X = 10. (b) Sketch of efficiency of THz radiation vs normalized frequency and normalized riple density amplitude when normalized distance X = 10 and applied magnetic field ωc = 0.6.
All the dimensionless parameters are chosen for CO2 laser (λ = 1.06 × 10−5 m), having frequency ω1 = 2 × 1014 rad/sec and intensity I L = 2 × 1015 Wcm−2. We have chosen the electron plasma frequency ωp = 2π × 1012 Hz, which is corresponding to the electron plasma density 
$n_0^0=1.78 \times 10^{19} {\rm m}^{-3}$. Density ripple amplitude 
$n_{q_0}$ is 
$3.53 \times 10^{18} {\rm m}^{-3}$ for 
$n_{q_0} /n_0^0=$
$0.2$. The value of applied magnetic field B S lies in a range of 36 − 215 kG corresponding to ωc/ωp = 0.1 − 0.6. Such magnetic fields can be generated by typical electric circuit having current carrying coil with magnetic core.
3. DISCUSSION
A magnetized rippled density plasma can resonantly excite terahertz waves by the beating of two x-mode lasers of frequencies in upper hybrid range when the periodicity of ripples satisfies the required phase matching conditions. The required ripple wave number for terahertz radiation generation increases as the magnetic field increases and decreases as the terahertz frequency increases. Thus, THz radiation frequency can be easily tuned by varying plasma density and applied magnetic field. The terahertz radiation amplitude scales directly to the density rippled amplitude and at the same time, THz efficiency is maximized as frequency (
${\rm \omega} $) approaches to resonance frequency (
$ \approx \!\!{\rm \omega}_h $).
In this model, magnetic field plays two roles. It controls the phase velocity and group velocity of beating lasers on one side and the polarization of generated THz wave on the other. In case of Gaussian lasers, it will also affect the self focusing of laser beam as well as the geometry of THz wave (Sharma et al., Reference Sharma, Monika, Sharma, Chauhan and Jia2010). It may be mentioned that two long laser pluses are not necessary for THz generation. Instead, one could employ a single laser pulse of duration comparable to the inverse of the frequency of THz. Bhasin et al. (Reference Bhasin and Tripathi2009) have considered a scheme of resonant THz radiation generation by the optical rectification of a picosecond laser pulse in a rippled density magnetized plasma. The terahertz power scales as the square of density ripple amplitude and rises with magnetic field strength (similar to present scheme). But, the power conversion efficiency of this scheme is one order less as compared to present scheme.
The efficiency of the present scheme is much better than those of other investigators. For example, Sheng et al. (Reference Wu, Sheng and Zhang2008) reported theoretical as well as numerical simulation of powerful THz emission using inhomogeneous plasma density. In their model, the maximum energy conversion efficiency at peak intensity 5.48 × 1012 W/cm2 is 0.0005, which is much lower than present model. Malik et al. (Reference Malik, Malik and Stroth2012) have reported the conversion efficiency ~0.002 by beating of two spatial-Gaussian lasers; whereas in our case, the conversion efficiency is ~0.015 where we use two x-mode lasers. Kim et al. (Reference Kim, Taylor, Glownia and Rodriguez2008) proposed a model for the generation of THz radiation by irradiating different gases with a symmetry-broken laser field composed of the fundamental and second harmonic laser pulses. In that model, the energy conversion efficiency was ~10−5, which is two order lesser as compared to present model. Hamester et al. (1993) also obtained the efficiency ~10−5 with a single laser that is Gaussian in space and time which is two order lesser as compared to the conversion efficiency of present scheme.
