A) Transmitter module

Consider a traveling wave incident on the input port of the power divider. Owing to impedance mismatch and inevitable inconsistency of the channels, signals arriving at input ports of the Lange coupler are as follows:

(1a)$$\hbox{Port}\,\, \roundone \colon \ u_1 = - {j \over \sqrt{2L_0}} a \sqrt{G_0} \Delta_1 \exp \,\, \lpar j \varphi_0\rpar \comma\;$$

(1b)$$\hbox{Port}\,\, \roundtwo \colon\ u_2 = - {j \over \sqrt{2L_0}} a\sqrt{G_0} \Delta_2 \exp \,\, [ j\lpar \varphi_0 + \Delta \varphi\rpar \rsqb .$$

Here, L ₀ and G ₀ indicate the power loss of the transmission and the average gain of the power amplifiers, respectively. Δ₁ and Δ₂ describe the amplitude fluctuation, ideally Δ₁ = Δ₂ = 1. The differential phase is indicated as Δφ. Consequently, the outputs of the Lange coupler are

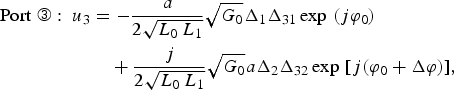(2a)$$\eqalign{\hbox{Port}\,\, \roundthree \colon \ u_3 &= - \displaystyle{a \over 2\sqrt{L_0\, L_1}} \sqrt{G_0} \Delta_1 \Delta_{31} \exp \,\, \lpar j\varphi_0\rpar \cr &\quad + \displaystyle{j \over 2\sqrt{L_0\, L_1}} \sqrt{G_0} a\Delta_2 \Delta_{32} \exp \,\, [ j\lpar \varphi_0 + \Delta \varphi\rpar \rsqb \comma \; }$$

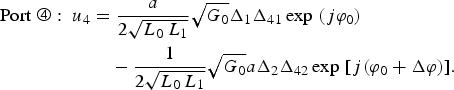(2b)$$\eqalign{\hbox{Port}\,\, \roundfour \colon \ u_4 & = \displaystyle{a \over 2\sqrt{L_0\, L_1}} \sqrt{G_0} \Delta_1 \Delta_{41} \exp \,\, \lpar j\varphi_0 \rpar \cr &\quad - \displaystyle{1 \over 2\sqrt{L_0\, L_1}} \sqrt{G_0} a\Delta_2 \Delta_{42} \exp \,\, [ j\lpar \varphi_0 + \Delta \varphi\rpar \rsqb .}$$

Compared with the work given in [Reference van der Bent, de Boer, van Dijk, van der Graaf, de Hek and van Vliet3], (2a) and (2b) give the general expressions including inconsistency of the amplitude and phase between two channels. L ₁ indicates the power loss of the Lange coupler, and Δ_ij is the fluctuation coefficient of transmission from port j to port i, ideally,

(3)$$\Delta_{31} = \Delta_{41} = \Delta_{32} = \Delta_{42} = 1.$$

We assume that the characteristics of the dual channels are consistent, that is Δ₁ = Δ₂ = 1, the dual outputs of the Lange coupler are obtained from (2a) and (2b) as

(4a)$$u_3 = - \displaystyle{a \over 2 \sqrt{L_0\, L_1}} \sqrt{G_0 } \sqrt{2[ 1 + \sin \lpar \Delta \varphi\rpar \rsqb } \exp \,\, [ j\lpar \varphi _0+\varphi _H \rpar \rsqb \comma$$

(4b)$$u_4 = - \displaystyle{a \over 2\sqrt{L_0\, L_1}} \sqrt{G_0} \sqrt{2[ 1 - \sin \,\, \lpar \Delta \varphi\rpar \rsqb } \exp \,\, [ j\lpar \varphi_0 + \varphi_V\rpar \rsqb \comma$$

which implies

(5a)$$\tan \varphi_H = \displaystyle{\cos\,\, \lpar \Delta \varphi\rpar \over 1 + \sin\,\, \lpar \Delta \varphi\rpar }\comma$$

(5b)$$\tan \varphi_E = \displaystyle{1 - \sin\,\, \lpar \Delta \varphi\rpar \over \cos\,\, \lpar \Delta \varphi\rpar}.$$

In fact, tan φ _H = tan φ _E, that is |φ _H − φ _V| = 0, π. Equations (4a)–(5b) give two outputs of the Lange coupler neglecting the amplitude inconsistency. It is obvious that the outputs of the Lange coupler are in phase or have opposite phase, in spite of the phase shifter settings. This guarantees linear polarization when the transmitter module is used in combination with the antenna element. It is assumed that the horizontally and vertically polarized field patterns of the antenna element are all isotropic. Then, the combined radiated field of the antenna element can be obtained as

(6a)$$u_c = \displaystyle{a \over \sqrt{L_0\, L_1}} \sqrt{G_0 } \exp \,\, [ j\lpar \varphi_0 + \varphi_H\rpar \rsqb \hat{p}\comma$$

(6b)$$\hat{p} = \displaystyle{\sqrt 2 \over 2} \left[ \hat{h} \sqrt {1 + \sin\,\, \lpar \Delta \varphi \rpar } \pm \hat{v} \sqrt{1 - \sin \,\, \lpar \Delta \varphi\rpar }\right] \comma$$

where $\hat{p}$ is the unit vector of variable linear polarization. It is concluded from (6a) and (6b) that arbitrary linear polarization can be obtained from differential phase setting Δφ, which is illustrated in Table 1. Beam steering can be obtained from phase setting φ ₀ of every antenna element.

Table 1. Relationship between differential phase Δφ and polarization orientation α based on the assumption of consistency of two channels.

If there is amplitude inconsistency between the channels at the input ports of the Lange coupler, neglecting the amplitude inconsistency of the Lange coupler, that is

(7)$$\Delta_1 \ne \Delta_2\comma \; \Delta_{31} = \Delta_{41} = \Delta_{32} = \Delta_{42} = 1.$$

Substitute (7) into (2a) and (2b),

(8a)$$\eqalign{\hbox{Port}\,\, \roundthree \colon\ u_3 &= - \displaystyle{a \over 2\sqrt{L_0\, L_1}} \sqrt{G_0} \Delta_1 \exp \,\, \lpar j \varphi_0\rpar \cr &\quad \times \lcub [ \,\, - 1 - \Delta_a \sin\,\, \lpar \Delta \varphi\rpar \rsqb + j \Delta_a \cos\,\, \lpar \Delta \varphi\rpar \rcub \comma \; }$$

(8b)$$\eqalign{\hbox{Port}\,\, \roundfour \colon\ u_4 &= - \displaystyle{a \over 2\sqrt{L_0\, L_1}} \sqrt{G_0} \Delta_1 \exp \,\, \lpar j \varphi_0\rpar \cr & \quad \times \lcub - \Delta_a \cos\,\, \lpar \Delta \varphi\rpar + j[ 1 - \Delta_a \sin\,\, \lpar \Delta \varphi\rpar \rsqb \rcub \comma \; }$$

where Δ_a = Δ₂/Δ₁, measuring the amplitude inconsistency between two channels. The radiated field of the antenna element can be obtained as

(9)$$\eqalign{u_c & = \displaystyle{a \over \sqrt{L_0\, L_1}} \sqrt{G_0} \Delta_1 \exp \,\, \lpar j\varphi_0\rpar \cr &\quad \times [ \hat{h} \sqrt{1 + \Delta_a^2 + 2 \Delta_a \sin \lpar \Delta \varphi\rpar } \exp \,\, \lpar j\varphi_H\rpar \cr & \quad +\hat{v}\sqrt {1+\Delta _a^2 - 2\Delta _a \sin \lpar \Delta \varphi \rpar } \exp \,\, \lpar j\varphi _V \rpar \rsqb }$$

Here,

(10a)$$\tan \varphi_H = \displaystyle{\Delta_a \cos\,\, \lpar \Delta \varphi\rpar \over 1 + \Delta_a \sin\,\, \lpar \Delta \varphi\rpar }\comma$$

(10b)$$\tan \varphi_E = \displaystyle{1 - \Delta_a \sin \,\, \lpar \Delta \varphi\rpar \over \Delta_a \cos \,\, \lpar \Delta \varphi\rpar }.$$

Then, Δ_a ≠ 1 implies |φ _H − φ _V| ≠ 0 and π. Consequently, the amplitude inconsistency results in the phase difference of two outputs between 0 and π in radian. The ratio of output at port V to output at port H is |(1 + Δ_a)/(1 − Δ_a)|, with differential phase Δφ of two phase shifters set to −90°. Compared with Table 1, elliptical polarization instead of pure vertical polarization at Δφ = −90° is achieved, which is caused by the amplitude inconsistency of two channels.

B) Receiver module

The receiver module has similar characteristics as transmitter module, since they are reciprocal in theory. The effects of the amplitude inconsistency between two channels on combined polarization are the same as the transmitter module. Phase inconsistency introduced by components other than phase shifters can be compensated for by phase shifters, not affecting the polarization tracking performance.

The transmission response and the equivalent noise are analyzed. We assume that the incident plane wave has the following polarization given in Fig. 2. Referring to Fig. 1(b), the input signals arriving at the input ports of the Lange coupler are:

(11a)$$\hbox{Port}\,\, \roundthree \colon \ u_3 = a\sqrt{G_{amp}} \cos \alpha\comma$$

(11b)$$\hbox{Port}\,\, \roundfour \colon\ u_4=a\sqrt {G_{amp} } \sin \alpha .$$

Assuming that the two channels are consistent, the signal at the output of the receiver module can be obtained as

(12)$$\eqalign{u_c &= \displaystyle{a \over 2\sqrt{L_T}} \sqrt{G_{amp}} \exp \,\, [ j\lpar 180^{\circ} - \alpha + \varphi_0\rpar \rsqb \cr &\quad + \displaystyle{a \over 2\sqrt{L_T}} \sqrt{G_{amp}} \exp \,\, [ j\lpar 90^{\circ} + \varphi_0 + \Delta \varphi + \alpha\rpar \rsqb \comma \; }$$

where G _amp is the gain of the LNA, and L _T is the average insertion loss in each channel. If the phase factor in (12) satisfies the condition as follows,

(13)$$\Delta \varphi = 90^{\circ} - 2\alpha\comma$$

the combined signal has no polarization mismatch loss. In this case, the maximum combined signal is given as

(14)$$u_c = \displaystyle{a \over \sqrt{L_T}} \sqrt{G_{amp}} \exp \,\, [ j\lpar 180^{\circ} - \alpha + \varphi_0\rpar \rsqb .$$

If the input of LNA 1 is fed with the input signal and noise and the other input of LNA 2 is terminated generating a two port network, the noise factor of the receiver module shown in Fig. 1(b) can be measured. An input signal a is assumed at the input port of LNA1. Thus, the output signal u ₀ can be determined by

(15)$$u_0 = \displaystyle{1 \over 2\sqrt{L_T}} a \sqrt{G_{amp}} \sqrt{2[ 1 + \sin\,\, \lpar \Delta \varphi\rpar \rsqb } \exp \,\, [ j\lpar \varphi_0 + \varphi_H\rpar \rsqb \comma$$

which leads to

(16)$$S_0 = \displaystyle{a^2 \over 2L_T} G_{amp} [ 1 + \sin\,\, \lpar \Delta \varphi\rpar \rsqb .$$

If we neglect the LNAs, the effective noise N _add of the remaining passive network can be obtained using the thermal dynamic equilibrium method,

(17)$$N_{add} = 2\lpar L_T - 1\rpar T_0.$$

In the measurement, the noise factor of Fig. 1(b) is

(18)$$F_{meas} = \displaystyle{S_i / N_i \over S_0 / N_0} = \displaystyle{2 \over 1 + \sin\,\, \lpar \Delta \varphi\rpar } \left(F_{amp} + \displaystyle{L_T - 1 \over G_{amp}} \right).$$

Here, F _amp indicates the noise factor of the LNA. In the measurement with the terminated input port of LNA 2, the two-port measured noise factor varies with phase difference Δφ between the two channels because of (16). If Δφ = 0°, considering the phase introduced by the Lange coupler, the two channels are not in phase. Therefore, the combined signal power is reduced by half shown in (16), and F _meas is approximately twice as much as F _amp, which is verified by the measured results shown in the following Fig. 7. If Δφ = −90°, the phase of the Lange coupler contributes to the in-phase combination of the signal, therefore F _meas approximates F _amp.

A) Performance of the LTCC vertical transition

In microwave modules with LTCC techniques, microwave vertical transmission is used widely to reduce the size of the modules [Reference Bara and Jacob11–Reference Tsai, Cheng, Huang, Hsu and Wu13]. For better bandwidth performance, a vertical transition configuration shown in Fig. 3 is introduced in both transmitter and receiver modules [Reference Zhou, Shi, Dou and Shen14], where the LTCC hard substrate and Rogers RO4050B soft substrate for motherboard are used. As shown in Fig. 3, the structure contains vertical transition from CPW on top of the LTCC module to the internal SL (strip-line), and transition from the internal SL to the CPW on the motherboard.

Fig. 3. The vertical transition in the LTCC-based modules.

From Fig. 4, it is observed that good agreement can be obtained between the simulated and measured results from 2 to 18 GHz. The measured return loss is better than −16 dB up to 18 GHz, and the insertion loss is less than 1.5 dB. Since the measured result contains insertion loss of about 0.6 dB at 18 GHz introduced by the testboard, simulated and measured results of the insertion loss are a little more different.

Fig. 4. Return loss and insertion loss of vertical transition.

B) Measured results of the modules

Based on the schematic circuits shown in Fig. 1 and the vertical transition shown in Fig. 3, we have designed the transmitter and receiver modules for Ku band polarization tracking phased array demonstrator. The developed prototypes are displayed in Fig. 5, where the transmitter module has a size of 12 mm × 11 mm ×3.4 mm, and the receiver has a size of 13 mm × 11 mm ×4 mm. Each module weights about 2.5 g. Various monolithic microwave integrated circuit (MMICs) and control circuits are mounted on top of the LTCC-based modules. The wire bonding technique is used to interconnect microwave transmission lines and MMICs. A lot of logic control lines and power supply lines are buried in the LTCC substrate for high density integration of the modules [Reference Lee and Park15]. In the proposed modules, logic control lines and power supply lines are low frequency circuits, which results in similar design requirements and specifications with the ones of printed circuit board (PCB). Thus, the locations and paths of logic control lines and power supply lines are designed reasonably to meet the requirements of electromagnetic compatibility. The RF ports using vertical transition structure shown in Fig. 3(b) and controlling I/O ports are laid on the bottom of the modules. Many metal filled via holes are fabricated for grounding and electromagnetism shielding of layers. A rectangle Kovar frame is attached to the top of the substrate to protect the circuit. A metal cover with 0.1 mm thickness is hermetically soldered on the frame.

Fig. 5. Photograph of the proposed modules (left: transmitter module, right: receiver module).

When the two phase shifters are set to 0°, the measured gain and output powers of the transmitter module are shown in Fig. 6. The gain of both channels shown in Fig. 1(a) is above 25 dB in the frequency range from 14.0 to14.5 GHz. The output powers of both channels exceed 22 dBm. The amplitude inconsistency of the two channels leads to different gain and different output powers as shown in Fig. 6. The measured gain and noise figure of the receiver module are plotted in Fig. 7, where the receive gain of the two channels shown in Fig. 1(b) is above 29 dB in the frequency range from 12.25 to 12.75 GHz. Similar to the transmitter module, the inconsistency of the two input channels results in slightly different measured gain at Δφ = 0°. The measured noise figure of each channel is between 5.0 and 6.0 dB. The noise figure of one channel is measured using the noise figure analyzer, with the other channel terminated in 50 Ω load. Thus, the noise from the load increases the measured result, which is expressed explicitly in (18). Then, the measured noise figure of the receiver module will be about twice as much as that of the LNA at Δφ = 0°. In fact, the noise figure of the MMIC used for the LNA is about 2.5 dB, just about one half of the measured results. Thus, the correctness of (18) is verified.

Fig. 6. The measured gain and output powers of the transmitter module (Δφ = 0°).

Fig. 7. The measured gain and noise figure of the receiver module (Δφ = 0°).

Figures 8 and 9 give the measured gain of two channels for transmitter and receiver module respectively. Owing to reciprocity, it can be seen that the curve shapes of the two figures are basically the same. The following discussion takes the transmitter module as an example. When differential phase Δφ increases from 0° to −360° with a step of −5.625°, the measured gain of the two channels varied in the range from about −2.5 to 26 dB with different trend, which can be used to control linear polarization of antenna element (Fig. 2). The measured gain of the two ports is almost the same at Δφ = 0°, which contributes to diagonally linear polarization (α = 45°). When Δφ is set as −78.75°, the measured gain of port H and port V is about 2.2 and 25.7 dB respectively, which results in approximately vertical polarization. When Δφ is set as −281.25°, more output at port H results in approximately horizontal polarization. The phase-controlled variation of the gain given in Fig. 8 produces the arbitrary linear polarization of the antenna element.

Fig. 8. The measured gain of the transmitter module with Δφ varying in the range of 360° at 14.25 GHz.

Fig. 9. The measured gain of the receiver module with Δφ varying in the range of 360° at 12.5 GHz.

Based on the assumption of the consistency of dual channels, the accurate vertical polarization will be obtained at Δφ = −90°, as mentioned in Table 1. However, in the experiment, we have obtained maximum gain of 25.7 dB at port V, and minimum gain of 2.2 dB at port H for Δφ = −78.75°. The deviation of Δφ from −90° to −78.75° is due to the phase inconsistency of two channels with phase shifters set to 0°. There is small output instead of 0 at port H, which is caused by the amplitude inconsistency of two channels. Thus, pure vertical polarization cannot be achieved. As mentioned in Table 1, horizontal polarization will be achieved with Δφ set to −270°, since no output exists at port V. However, the experimental results indicate the deviation of Δφ from −270° to −281.25° due to the phase inconsistency. Amplitude inconsistency contributes to small output at port V. Thus, pure horizontal polarization cannot be obtained. The measured results have verified the correctness of the analysis of inconsistency discussed before. As for the receiver module, same effects of inconsistency exist.

C) Measured patterns of the phased array

Based on the LTCC modules shown in Fig. 5, we have developed two small active polarization tracking phased array demonstrators. The proposed modules result in the low profile receive and transmit phased array antennas with a height of 55 and 53.5 mm, respectively. Both of the phased array demonstrators realized the linear polarization with arbitrary orientation. With the differential phase Δφ shown in Fig. 1 electronically set to −90° and −270°, the phased array demonstrators have switched the vertical polarization to the horizontal one automatically. The polarization agile patterns at frequencies of 12.5 and 14.25 GHz are illustrated in Figs 10 and 11. While the beam is steered, the polarization agility is realized simultaneously, which can be used to electronically match the polarization of the phased array on mobile terminal to that of the satellite borne antennas.

Fig. 10. Measured polarization agile patterns of receive phased array antenna at 12.5 GHz.

Fig. 11. Measured polarization agile patterns of transmit phased array antenna at 14.25 GHz.