1 Introduction
Despite being microscopic in nature, the liquid–solid interface can have a strong influence on various macroscale dynamics, such as liquid drop impact on solid surfaces (Yarin Reference Yarin2006), solid-body impact into a liquid pool (Duez et al. Reference Duez, Ybert, Clanet and Bocquet2007) and inertial separation between liquid flow and solid (Duez et al. Reference Duez, Ybert, Clanet and Bocquet2010). Drop impact on a solid surface has been of particular interest for understanding the complex physical phenomena involved, as well as for its consequences in many industrial processes (Josserand & Thoroddsen Reference Josserand and Thoroddsen2016). Despite its huge interest, the effect of surface wettability on droplet impact dynamics remains debated. On the one hand, experiments show its pronounced role on spreading (Bayer & Megaridis Reference Bayer and Megaridis2006; Vadillo et al. Reference Vadillo, Soucemarianadin, Delattre and Roux2009; Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) or bouncing (Richard & Quere Reference Richard and Quere2000) at low impact velocity, whereas others show no influence at larger impact velocities (Clanet et al. Reference Clanet, Beguin, Richard and Quere2004; Tsai et al. Reference Tsai, Hendrix, Dijkstra, Shui and Lohse2011). Local characterisation even points to the crucial effect of a trapped air film during impact (de Ruiter et al. Reference de Ruiter, Lagraauw, van den Ende and Mugele2015). On the other hand, a large number of theoretical, numerical and experimental studies have evidenced that surface friction can play an important role during drop impact at large impact velocity, mainly by considering the two limiting cases of frictionless impact (Clanet et al. Reference Clanet, Beguin, Richard and Quere2004; Tsai et al. Reference Tsai, Pacheco, Pirat, Lefferts and Lohse2009; Lastakowski et al. Reference Lastakowski, Boyer, Biance, Pirat and Ybert2014) and fully frictional impact with a zero velocity condition at the solid substrate (Roisman Reference Roisman2009; Roisman, Berberovic & Tropea Reference Roisman, Berberovic and Tropea2009; Eggers et al. Reference Eggers, Fontelos, Josserand and Zaleski2010; Schroll et al. Reference Schroll, Josserand, Zaleski and Zhang2010; Lagubeau et al. Reference Lagubeau, Fontelos, Josserand, Maurel, Pagneux and Petitjeans2012). In the latter case, drop spreading after impact is governed by the buildup of a viscous boundary layer in the vicinity of the substrate. The case of partial friction, however, has hardly been explored.
With the development of micro- and nanofabrication techniques, it is possible to engineer surfaces with well-controlled topography. Particularly, hydrophobic surfaces with micro- or nanoscale features – so-called superhydrophobic (SHPo) surfaces – are found to promote unique liquid dynamic characteristics due to the reduced liquid–solid contact (Callies & Quéré Reference Callies and Quéré2005). For example, previously unseen phenomena such as crystallographic splashing (Reyssat et al. Reference Reyssat, Richard, Clanet and Quere2010; Tsai et al. Reference Tsai, Hendrix, Dijkstra, Shui and Lohse2011), pancake bouncing (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) and reduced contact time (Bird et al. Reference Bird, Dhiman, Kwon and Varanasi2013) were observed upon impact on such surfaces. On SHPo surfaces, the presence of a stress-free liquid–gas interface not only affects the wetting properties of the droplet but also results in a frictional drag reduction, which is commonly quantified using the effective slip length denoted 
$b$, defined as the ratio of slip velocity to the shear rate at the wall (Choi & Kim Reference Choi and Kim2006; Joseph et al. Reference Joseph, Cottin-Bizonne, Benoit, Ybert, Journet, Tabeling and Bocquet2006; Ybert et al. Reference Ybert, Barentin, Cottin-Bizonne, Joseph and Bocquet2007; Rothstein Reference Rothstein2010). This effect has been ignored for impacts of simple fluid drops, as it has been observed to have no consequences on droplet spreading (Clanet et al. Reference Clanet, Beguin, Richard and Quere2004; Tsai et al. Reference Tsai, Hendrix, Dijkstra, Shui and Lohse2011), although a giant drag reduction has been observed with complex fluids (Luu & Forterre Reference Luu and Forterre2013). Determining how the boundary layer – and the overall impact dynamics – is affected by an intermediate friction is the goal of this study. We focus on a regime at high impact velocities, where the effect of friction on the substrate, quantified by the so-called slip length, is relevant for drop spreading dynamics.
One of the main concerns in conducting quantitative experimental studies on an SHPo surface is that it can sustain a low frictional Cassie–Baxter state as long as the drop interacts with the top region of surface structures without intruding into them (Lee, Choi & Kim Reference Lee, Choi and Kim2008). However, during drop impact, the dynamic pressure in the liquid drop might overcome the resistance upon imbibition provided by surface tension, leading to the so-called Cassie-to-Wenzel transition (Bartolo et al. Reference Bartolo, Eouamrirene, Verneuil, Buguin, Silberzan and Moulinet2006; Reyssat et al. Reference Reyssat, Pein, Marty, Chen and Quere2006). It was proposed that the impalement during impact might be avoided by using SHPo surface with nanometric features (Deng et al. Reference Deng, Varanasi, Hsu, Bhate, Keimel, Stein and Blohm2009; Tsai et al. Reference Tsai, Pacheco, Pirat, Lefferts and Lohse2009), but it would compromise the slip length, as the slip length is proportional to the structural pitch of surface features. This problem can be addressed by employing multiscale superhydrophobic surfaces (Lee & Kim Reference Lee and Kim2011), where microscale features ensure a large slip length, while nanoscale features prevent the detrimental Cassie-to-Wenzel transition.
Figure 1. Scanning electron microscopy images of (a) the textured SHPo surfaces B and (b) the disordered SHPo surface C. (c) Snapshot of an 80 % mixture of water and glycerol drop impact on surface B (
$U=1.5~\text{m}~\text{s}^{-1}$, time interval 2 ms). (d) Top view of a water droplet impact on surface B (
$U=1.5~\text{m}~\text{s}^{-1}$). (e) Snapshots of the impact at maximal spreading for impact on surfaces A (left) and B (right); scale bar corresponds to 1 mm (
$U=2.6~\text{m}~\text{s}^{-1}$, 
$\unicode[STIX]{x1D702}=21~\text{cS}$).
Table 1. The three types of surface used and their characteristics.
2 Experiments
We designed two types of multiscale superhydrophobic surfaces (figure 1a,b and appendix A), denoted B and C, resulting in both cases in similar large static contact angles, but in different friction characteristics and so different slip lengths for water (table 1). A bare smooth silicon wafer was used as a reference (surface A).
Drop impact is captured from the side with a high-speed camera (Photron SA-4) at up to 30 000 frames per second (figure 1c). The liquids used are mixtures of ultra-pure water and glycerol, with a kinematic viscosity 
$\unicode[STIX]{x1D708}$ ranging from 1 cS (pure water) to 630 cS (pure glycerol). Drops of radius 
$R\approx 1~\text{mm}$ are used, with an impact velocity 
$0.1<U<3.5~\text{m}~\text{s}^{-1}$. We introduce as relevant non-dimensional numbers the Weber number 
$We=\unicode[STIX]{x1D70C}RU^{2}/\unicode[STIX]{x1D6FE}$, which gives the relative importance of inertia compared to surface tension, and the Reynolds number, defined here as 
$Re=UR/\unicode[STIX]{x1D708}$. Accordingly, 
$We$ varies between 40 and 1000, and 
$Re$ between 8 and 11 000. The time 
$t=\unicode[STIX]{x1D70F}$ to reach the maximum spreading radius (
$t=0$ when the drop reaches the substrate) is a relevant parameter to probe the dynamics. The 
$U$, 
$R$ and 
$\unicode[STIX]{x1D70F}$ values were detected automatically via image analysis using Python (appendix B). For each set of parameters, three experiments are recorded and 
$\unicode[STIX]{x1D70F}$ is averaged.
To confirm that multiscale surfaces ensure robustness towards the Cassie-to-Wenzel transition, a top view image of an impact on SHPo surface B is reported in figure 1(d). One can observe that the region where the transition might have occurred, characterised by small dark dots on the picture, is very limited. More interestingly, dynamical wetting properties seem to be very similar in the three cases considered. In figures 1(c) and 1(e) left and right, corresponding to spreading on surfaces C, A and B, respectively, a dynamic contact angle can be measured and is approximately 140° ± 10° in both cases, so fully in a hydrophobic regime. We can notice that, in our range of impact parameters, lamella lift-off is never observed.
3 Analysis: scaling laws
The different regimes of drop impact are summarised in figure 2 in the 
$Re$–
$We$ phase diagram. In the frictionless case, two regimes can be identified, depending on 
$We$ values. At low 
$We$, the inertial time scale to reach the pressure-gradient-free regime (
$\unicode[STIX]{x1D70F}_{i}\sim R/U$) is larger than the time scale of capillary recoil (
$\unicode[STIX]{x1D70F}_{c}\sim \sqrt{\unicode[STIX]{x1D70C}R^{3}/\unicode[STIX]{x1D6FE}}$) and a pancake regime is observed as described in Clanet et al. (Reference Clanet, Beguin, Richard and Quere2004), defined by the orange zone of figure 2. At larger 
$We$, the rim dynamic limits the drop spreading and 
$\unicode[STIX]{x1D70F}\sim \unicode[STIX]{x1D70F}_{c}=\unicode[STIX]{x1D70F}_{i}We^{1/2}$ (Eggers et al. Reference Eggers, Fontelos, Josserand and Zaleski2010; Lastakowski et al. Reference Lastakowski, Boyer, Biance, Pirat and Ybert2014), whatever the impact velocity (Biance, Pirat & Ybert Reference Biance, Pirat and Ybert2011). This regime is defined by the yellow region in figure 2. We limit our study here to 
$We>40$, avoiding pancake regimes and coupling between intrusion time scale and spreading (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014).
Figure 2. Schematic of the drop impact regimes in the 
$We$–
$Re$ phase diagram. Grey, yellow and orange areas correspond, respectively, to the viscous, capillary and inertial regimes (see text). In the case of total friction, the limit between the capillary regime and the viscous regime is determined by the dashed line (
$We=8Re^{2/5}$). In the case of partial friction, the capillary regime is extended towards the grey region until the solid line following 
$We=8Re^{2/5}(1+0.024Re^{2/5})$, corresponding to 
$b=59~\unicode[STIX]{x03BC}\text{m}$. Data points correspond to experiments performed on smooth (A) and rough superhydrophobic surface (B). Colour scales correspond to the value of 
$\unicode[STIX]{x1D70F}$(SHPo)/
$\unicode[STIX]{x1D70F}$(smooth).
When friction comes into play, a viscous boundary layer builds up from the substrate. It has been demonstrated numerically (Josserand et al. Reference Josserand, Lemoyne, Troeger and Zaleski2005; Eggers et al. Reference Eggers, Fontelos, Josserand and Zaleski2010) and experimentally (Roisman et al. Reference Roisman, Berberovic and Tropea2009; Lagubeau et al. Reference Lagubeau, Fontelos, Josserand, Maurel, Pagneux and Petitjeans2012; Lastakowski et al. Reference Lastakowski, Boyer, Biance, Pirat and Ybert2014) that the spreading is stopped when the viscous boundary layer meets the upper interface of the thinning lamella. Since pressure-free drop thinning follows 
$h_{t}\sim R^{3}/U^{2}t^{2}$ (Lastakowski et al. Reference Lastakowski, Boyer, Biance, Pirat and Ybert2014), whereas viscous boundary layer development follows 
$h_{BL}\sim \sqrt{\unicode[STIX]{x1D708}t}$, the spreading dynamics is stopped for a critical lamella thickness satisfying
$$\begin{eqnarray}\frac{R^{3}}{U^{2}\unicode[STIX]{x1D70F}_{v}^{2}}\simeq \sqrt{\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}_{v}},\end{eqnarray}$$ thus at a viscous time 
$\unicode[STIX]{x1D70F}_{v}\sim \unicode[STIX]{x1D70F}_{i}Re^{1/5}$. From the comparison of 
$\unicode[STIX]{x1D70F}_{v}$ with 
$\unicode[STIX]{x1D70F}_{c}$, the viscous regime is dominant over the capillary regime if 
$We\gtrsim Re^{2/5}$ (Lagubeau et al. Reference Lagubeau, Fontelos, Josserand, Maurel, Pagneux and Petitjeans2012). This corresponds to the grey region of figure 2.
We now consider the case of a slippery surface. Introducing the slip length 
$b$, the no-slip boundary condition is changed to 
$bu_{z}=u|_{z=0}$, where 
$u$ is the fluid velocity tangential to the surface and the subscript 
$z$ denotes partial differentiation with respect to 
$z$. From the unsteady one-dimensional momentum diffusion equation 
$\unicode[STIX]{x2202}_{t}u=\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{zz}u$, it can be shown that a self-similar solution for 
$u$ can be approximated by 
$u(z,t,b)\simeq U_{f}(z+b)/\sqrt{\unicode[STIX]{x03C0}\unicode[STIX]{x1D708}t}$ in the vicinity of the surface (
$z\sim b$), where 
$U_{f}$ is the fluid velocity far from it (appendix C). Asymptotically, the effect of slippage is to shift by 
${\sim}b$ the viscous boundary layer towards the surface, and 
$\unicode[STIX]{x1D70F}_{s}$, the value of 
$\unicode[STIX]{x1D70F}$ in the slippery case, is thus given by
$$\begin{eqnarray}\frac{R^{3}}{U^{2}\unicode[STIX]{x1D70F}_{s}^{2}}\simeq \sqrt{\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}_{s}}-b.\end{eqnarray}$$Assuming that the slippage has a weak influence on the dynamics, a perturbation of the viscous case readily leads to
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{s}\simeq \unicode[STIX]{x1D70F}_{v}(1+2\unicode[STIX]{x1D6FC}),\quad \text{with }\unicode[STIX]{x1D6FC}=\frac{b}{5\sqrt{\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}_{v}}}=\frac{b}{5R}Re^{2/5}.\end{eqnarray}$$ Comparing 
$\unicode[STIX]{x1D70F}_{s}$ with 
$\unicode[STIX]{x1D70F}_{c}$, a new critical transition line can be defined in the 
$Re$–
$We$ phase space when slippage effects appear. The result is that the critical domain for which the capillary-driven regime is observed is extended in the viscous regime, and is given by 
$We\sim Re^{2/5}(1+4\unicode[STIX]{x1D6FC})$. This is shown in figure 2, where the classical boundary (no-slip) between capillary and viscous regimes is presented by a dotted line, while the new boundary in the presence of a slip length 
$b$ appears as a solid line. We focus then on a new regime that should be caused by a slip-delayed viscous boundary layer development.
Figure 3. Time 
$\unicode[STIX]{x1D70F}$ to reach the maximal radius versus the Reynolds number on smooth (A, open symbols) and on SHPo (B, filled symbols) substrates with 
$\unicode[STIX]{x1D708}=505~\text{cS}$ (triangle), 
$\unicode[STIX]{x1D708}=103~\text{cS}$ (diamond), 
$\unicode[STIX]{x1D708}=40.5~\text{cS}$ (circle), 
$\unicode[STIX]{x1D708}=21~\text{cS}$ (square), 
$\unicode[STIX]{x1D708}=9.4~\text{cS}$ (hexagon), 
$\unicode[STIX]{x1D708}=4.3~\text{cS}$ (star), 
$\unicode[STIX]{x1D708}=2.8~\text{cS}$ (cross) and 
$\unicode[STIX]{x1D708}=1.9~\text{cS}$ (pentagon). Solid lines correspond to 
$\unicode[STIX]{x1D70F}=(R/U)Re^{1/5}$ and the horizontal band corresponds to the interval containing
$\unicode[STIX]{x1D70F}=0.41\sqrt{\unicode[STIX]{x1D70C}R^{3}/\unicode[STIX]{x1D6FE}}$.
Figure 4. Time 
$\unicode[STIX]{x1D70F}$(SHPo) to reach the maximal radius on slippery surfaces normalised by the time 
$\unicode[STIX]{x1D70F}$(smooth) to reach the maximal radius on smooth surface. Blue filled symbols, ordered rough surface B; open red symbols, disordered rough surface C. For ordered rough surfaces, viscosities are 
$\unicode[STIX]{x1D708}=505~\text{cS}$ (triangle), 
$\unicode[STIX]{x1D708}=103~\text{cS}$ (diamond), 
$\unicode[STIX]{x1D708}=40.5~\text{cS}$ (circle) and 
$\unicode[STIX]{x1D708}=21~\text{cS}$ (square). For disordered rough surfaces, viscosity used are 
$\unicode[STIX]{x1D708}\geqslant 250~\text{cS}$ (triangle), 
$\unicode[STIX]{x1D708}=67~\text{cS}$ (cross) and 
$\unicode[STIX]{x1D708}=27~\text{cS}$ (star). The solid line corresponds to adjustment by (3.3) with 
$b=59~\unicode[STIX]{x03BC}\text{m}$.
4 Discussion
We now discuss our experimental results concerning the spreading time reported in figure 3. Deviations between the two cases (impact on smooth and SHPo substrates) are observed whatever the Reynolds number. When the spreading time is larger than the capillary time 
$\unicode[STIX]{x1D70F}_{c}$, indicated in figure 3 by an orange band, spreading on an SHPo surface is shorter than on a smooth substrate, a surprising behaviour but one that is not in our region of interest. On the contrary, when the spreading time is shorter than the capillary time 
$\unicode[STIX]{x1D70F}_{c}$, the spreading time observed for impact on smooth surfaces A is always shorter than the one on slippery SHPo surfaces B. Even though significant, this increase could be attributed to rim shape or contact angle differences in both cases. To disentangle the effects of wetting and slippage, we performed similar experiments on surface C, which remains superhydrophobic but with a larger friction coefficient.
We then report in figure 4 the ratio of the spreading time on SHPo surfaces (B or C) to that on smooth substrate (A) 
$\unicode[STIX]{x1D70F}(\text{SPHo})/\unicode[STIX]{x1D70F}(\text{smooth})$ in identical impact conditions as a function of the Reynolds number. Comparing surfaces only differing in their slippage properties allows one to evidence a small yet clear experimental effect, with surface B showing a delayed spreading that increases with Reynolds number. On the contrary, surface C shows a spreading essentially identical to a classical no-slip wetting surface, with even a slightly shortened spreading, a behaviour we can attribute to either contact-line effects (Laan et al. Reference Laan, de Bruin, Bartolo, Josserand and Bonn2014) or fragmentation (Wachters & Westerling Reference Wachters and Westerling1966). To show a quantitative agreement, a fit of our data with (3.3) is performed, allowing us to define an average slip length 
$b$ of the order of 59 ± 8 μm. This value is fully consistent with the slip length obtained by torque measurements (40–50 μm) for water on the same surfaces (Lee & Kim Reference Lee and Kim2011). However, considering that our analysis is performed for a two-dimensional stationary flow, that the slip length varies with the liquid viscosity and nature (here water–glycerol mixtures instead of water), the applied pressure (Lee & Kim Reference Lee and Kim2011) (here dynamical pressure during impact), as well as a partial transient impalement on the microstructure, the quantitative comparison should be taken cautiously.
To define more generally the range of parameters for which these effects are relevant, we report experimental observations on the 
$Re$–
$We$ diagram defined in figure 2. The colour bar corresponds to the experimental values of the ratio 
$\unicode[STIX]{x1D70F}$(SHPo)/
$\unicode[STIX]{x1D70F}$(smooth). One can indeed observe an increase of this ratio in the viscous regime. A new frontier between the capillary and slippery regimes can be defined by balancing 
$\unicode[STIX]{x1D70F}_{s}$ and 
$\unicode[STIX]{x1D70F}_{c}$ (figure 2).
5 Conclusion
We propose here a semi-analytical analysis that accounts for drag reduction on viscous impact. A phase diagram is built to better identify the physical parameters for which these effects on the overall dynamics are relevant. It shows the consequences of a weak friction on the spreading dynamics, which can be crucial in many situations. To test it, impacts are performed on two types of multiscale SHPo surfaces, which both resist the Cassie–Baxter-to-Wenzel transition and have similar wetting properties but different friction characteristics. Longer spreading is indeed observed for the lower friction.
Taking into account this effect would be particularly relevant for the design of efficient cooling or anti-icing systems built upon such substrates, where increasing heat transfer through extended contact time and on an extended surface is of crucial interest. On a more fundamental prospect, we propose here an experimental demonstration and a simple analysis of the effect of slippage on the buildup of a viscous boundary layer in a non-stationary flow, a complex mathematical problem (Matthews & Hill Reference Matthews and Hill2008; Gie & Kelliher Reference Gie and Kelliher2012), still investigated recently (Fujioka & Wei Reference Fujioka and Wei2018).
Acknowledgements
We thank H. Lastakowski for preliminary experiments. G.M. acknowledges ENS Paris-Saclay for funding. This work was supported by the Basic Research Program (2017R1A2B4008028) through the National Research Foundation of Korea funded by the Ministry of Science and ICT. This work was sponsored by the French National Agency for Research (Freeflow project ref. ANR-11-B504-001-01).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Surface fabrication and characterisation
Surface B is a well-structured surface with multiscale pillars. First, micro-sized cylindrical pillars were obtained using photolithography, followed by deep reactive ion etching on silicon. Pillars are arranged in a square lattice with a fixed structural pitch 
$L$ (centre-to-centre distance of two adjacent pillars) of 50 μm. The top pillar area fractions 
$\unicode[STIX]{x1D719}_{s}=\unicode[STIX]{x03C0}D^{2}/(4L^{2})$, with 
$D$ the pillar diameter, is set to 0.1. Then, over microscale pillars, nanoscale pillars with a structural pitch of 0.5–1 μm and very sharp tips were generated using a self-masking nanofabrication method known as the black silicon method (Sun et al. Reference Sun, Gao, Zhao and Zhang2010; Lee & Kim Reference Lee and Kim2011). The surface is made hydrophobic with a few nanometres thick Teflon layer coating. Using torque measurements, the slip length of water on this surface is found to be approximately 35 ± 5 μm.
Surface C is a randomly textured surface made of CuO obtained by oxidation of a copper sample in a mixture of NaClO2, NaOH and Na3PO4. It is made hydrophobic by silane vapour deposition. Images of the surface are reported in figure 1. The slip length from water Poiseuille flow rate measurements in a microfluidic channel is found to be 8 ± 1 μm. Note that, even if slip length measurement methods are different for the two surfaces, they both involve a relatively low liquid pressure and a laminar flow condition, and they can be reasonably compared (Lee et al. Reference Lee, Laan, de Bruin, Skantzaris, Shahidzadeh, Derome, Carmeliet and Bonn2016).
Static angles on both surfaces were found to be similar and above 160°. Dynamical contact angles during the spreading are also similar in the three cases of smooth substrate (A) and superhydrophobic surfaces (B and C), larger than 160°.
Appendix B. Spreading time detection and accuracy
Typical snapshots of impact recording are reported in figure 1. The droplet contour and position are determined by subtracting the background and thresholding (figure 5). Results are hardly dependent on the choice of the threshold (1 pixel). The contact time origin is automatically determined by looking at the presence of a bright pixel below the drop. The droplet maximum radius is determined by fitting the evolution of the droplet radius versus time and fitting the curve in the vicinity of the maximum by a second-order polynomial. The maximum of the function and the time to reach this maximum correspond then for each experiment at the spreading radius and spreading time, respectively. Finally, the spreading time uncertainty is 0.17 ms.
Figure 5. Analysed images from a video of a spreading droplet of a 70 % glycerol–water mixture on surface C: (a,c) images with subtracted background; (b,d) binary images.
Appendix C. Boundary layer development over a surface with a Navier condition
C.1 Two-dimensional analysis – infinite surface
We consider the motion of a liquid near a solid infinite plane located at 
$z=0$. The liquid and the plate are initially at rest and then the plate is moved at a velocity 
$U_{f}$, in the 
$x$ direction. We investigate the development of a viscous boundary layer in the 
$z$ direction taking into account this effect. The momentum diffusion equation locally reads
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}t}=\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}u_{x}}{\unicode[STIX]{x2202}z^{2}},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D708}$ is the kinematic viscosity of the liquid.
Introducing 
$\unicode[STIX]{x1D709}=z/\sqrt{\unicode[STIX]{x1D708}t}$ and the two constants 
$A$ and 
$B$, the solution of (C 1) is
$$\begin{eqnarray}u_{x}(z,t)=A\int _{0}^{\unicode[STIX]{x1D709}}\text{e}^{-y^{2}/4}\,\text{d}y+B.\end{eqnarray}$$ Boundary conditions are that: (i) the fluid is at rest far from the surface, 
$(\lim u_{x}(x\rightarrow +\infty )=0)$; and (ii) in the vicinity of the surface (
$z=0$), the slip condition is defined by slip length 
$b$, where 
$b(\unicode[STIX]{x2202}u_{x}/\unicode[STIX]{x2202}z)|_{z=0}=u_{x}|_{z=0}-U_{f}$. Then, the velocity profile reads
$$\begin{eqnarray}u_{x}(z,t)=\frac{U_{f}}{{\displaystyle \frac{b}{\sqrt{\unicode[STIX]{x03C0}\unicode[STIX]{x1D708}t}}}+1}\left(1-\text{erf}\left(\frac{z}{\sqrt{4\unicode[STIX]{x1D708}t}}\right)\right),\end{eqnarray}$$ where we recover its usual form for 
$b=0$. The deviation due to slippage is then
$$\begin{eqnarray}\frac{u_{x}(z,t,b)}{u_{x}(z,t,0)}=\frac{1}{{\displaystyle \frac{b}{\sqrt{\unicode[STIX]{x03C0}\unicode[STIX]{x1D708}t}}}+1}.\end{eqnarray}$$ This term is negligible when 
$t\geqslant b^{2}/\unicode[STIX]{x1D708}$. As the boundary layer develops from the substrate, it reaches the altitude 
$z$ after a characteristic time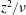 
$z^{2}/\unicode[STIX]{x1D708}$; the effect of slippage will be important if 
$b\geqslant z$. We define the effect of slip on the altitude at which viscous friction is felt versus time. Considering that the viscous friction is felt when 
$u_{x}(z,t)/U_{f}=k$, with 
$k$ between 0 and 1, the time-dependent 
$z$ at which viscous effects are important reads
$$\begin{eqnarray}z(b,t,k)=\sqrt{4\unicode[STIX]{x1D708}t}\,\,\text{erf}^{-1}\left(1-k-\frac{bk}{\sqrt{\unicode[STIX]{x03C0}\unicode[STIX]{x1D708}t}}\right).\end{eqnarray}$$ The effect of slippage can be captured by estimating 
$z(b,t,k\rightarrow 1)-z(0,t,k\rightarrow 1)$. When 
$t\rightarrow \infty$, this value is converging to 
$b$. The boundary layer is shifted up by a length 
$b$.
C.2 Consequences on droplet dynamics upon impact: time scales
We consider a drop impacting on a solid substrate. We distinguish here the three cases of drop impact without friction (i.e. Leidenfrost case), with large friction (smooth solid substrate) and with slippage (superhydrophobic substrate). For each regime, we identify the characteristic time to reach the maximal radius, and these times will be compared to identify which regime is predominant as a function of the Weber
$We=\unicode[STIX]{x1D70C}R^{3}/\unicode[STIX]{x1D6FE}$ and Reynolds 
$Re=UR/\unicode[STIX]{x1D708}$ numbers.
C.2.1 Frictionless case
In this regime, two cases can be determined depending only on the Weber number. A deceleration phase over a time 
$\unicode[STIX]{x1D70F}_{i}\sim R/U$ (Clanet et al. Reference Clanet, Beguin, Richard and Quere2004) is followed by a capillary oscillation over 
$\unicode[STIX]{x1D70F}_{c}\sim \sqrt{\unicode[STIX]{x1D70C}R^{3}/\unicode[STIX]{x1D6FE}}$. If 
$\unicode[STIX]{x1D70F}_{c}$ is smaller than 
$\unicode[STIX]{x1D70F}_{i}$, only the deceleration is observed and we reach a pancake regime, whereas on the contrary a capillary recoil (Roisman et al. Reference Roisman, Berberovic and Tropea2009; Eggers et al. Reference Eggers, Fontelos, Josserand and Zaleski2010; Lastakowski et al. Reference Lastakowski, Boyer, Biance, Pirat and Ybert2014) is observed. The transition is given by 
$\unicode[STIX]{x1D70F}_{c}=\unicode[STIX]{x1D70F}_{i}$, which implies a critical Weber number 
$We_{1}$. In the following analysis, we assume that 
$We$ is always above 
$We_{1}$.
C.2.2 Large friction
In this case, it has been shown that the development of a boundary layer sets the maximal attained radius, i.e. when the droplet thickness is comparable to this developed boundary layer, the droplet stops spreading and thinning. For 
$We$ larger than 
$We_{1}$, this criterion reads (Roisman et al. Reference Roisman, Berberovic and Tropea2009; Eggers et al. Reference Eggers, Fontelos, Josserand and Zaleski2010; Lastakowski et al. Reference Lastakowski, Boyer, Biance, Pirat and Ybert2014)
$$\begin{eqnarray}\frac{R^{3}}{U^{2}(\unicode[STIX]{x1D70F}_{v})^{2}}\simeq k\sqrt{\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F}_{v})}\end{eqnarray}$$ and then the spreading viscous time scales as 
$\unicode[STIX]{x1D70F}_{v}\sim \unicode[STIX]{x1D70F}_{i}Re^{1/5}$. This regime is relevant if this time is shorter than 
$\unicode[STIX]{x1D70F}_{c}$, i.e. 
$We\geqslant Re^{2/5}$.
C.2.3 Slippage
Following previous asymptotic analysis, the characteristic time 
$\unicode[STIX]{x1D70F}_{s}$ to develop the boundary layer over the distance 
$h$ satisfies
$$\begin{eqnarray}\frac{R^{3}}{U^{2}\unicode[STIX]{x1D70F}_{s}^{2}}\simeq k\sqrt{\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}_{s}}-b.\end{eqnarray}$$ Let us now assume that the effect of slippage is small compared to viscous effects. The characteristic viscous slippery time 
$\unicode[STIX]{x1D70F}_{s}$ can then be written as
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D70F}_{v}+t_{s}\end{eqnarray}$$ with 
$t_{s}=o(\unicode[STIX]{x1D70F}_{v})$ the slippage contribution. Equation (C 7) can then be developed as
$$\begin{eqnarray}\displaystyle & \displaystyle -\frac{R^{3}}{U^{2}\unicode[STIX]{x1D70F}_{v}^{2}}\frac{2t_{s}}{\unicode[STIX]{x1D70F}_{v}}\simeq k\sqrt{\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}_{v}}\frac{t_{s}}{2\unicode[STIX]{x1D70F}_{v}}-b, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70F}_{s}\simeq \unicode[STIX]{x1D70F}_{v}\left(1+\frac{2b}{5R}Re^{2/5}\right). & \displaystyle\end{eqnarray}$$ The capillary region is then extended to 
$We\lesssim Re^{2/5}(1+(2b/5R)Re^{2/5})$ (figure 2).
