1. INTRODUCTION
Precise point positioning (PPP) based on global positioning systems boosts many advantages, such as the absence of ground reference station, independence of baseline length and high precision of coordinates (Zumberge et al., Reference Zumberge, Heflin, Jefferson, Watkins and Webb1997), endowing it with wide applications such as satellite geometric orbit determination (Zhang et al., Reference Zhang, Li and Zuo2013) and earthquake monitoring and warning (Wright et al., Reference Wright, Houlié, Hildyard and Iwabuchi2012). At present, static and kinematic PPP of single-system GPS can achieve positioning accuracy at the decimetre and even at the centimetre level. However, its slow convergence time, impeding the achievement of high positioning accuracy, exists as a major drawback. Therefore, integration of multiple global and regional navigation satellite systems (multi-GNSS/RNSS) is a valid measure to improve convergence time.
The original American Global Positioning System (GPS) is being modernised, and has been joined by the Russian Global Navigation Satellite System (GLONASS), the Chinese BeiDou Navigation Satellite System (BDS), the European Galileo Satellite Navigation System (Galileo) and the Japanese Quasi-Zenith Satellite System (QZSS). Hence it has become possible to greatly enhance the positioning stability, reliability and availability of PPP solutions by utilising multiple global and regional navigation satellite systems (multi-GNSS/RNSS), especially in ‘urban canyon’ areas, ravines, etc. (Geng et al., Reference Geng, Teferle, Shi, Meng, Dodson and Liu2009; Laurichesse et al., Reference Laurichesse, Mercier, Berthias, Broca and Cerri2009; Shi and Gao, Reference Shi and Gao2013). Therefore, PPP using multi-GNSS/RNSS is becoming the future developing tendency of GNSS precise positioning.
Research on combined-system PPP was originally conducted on the combined dual system of GPS/GLONASS. The functional model and stochastic model for the integrated GPS/GLONASS PPP were deduced based on the ionosphere-free observation model. As suggested by testing, the combined-system PPP exhibited equal positioning accuracy to the PPP of single-system GPS with an enhanced convergence speed (Cai and Gao, Reference Cai and Gao2012). On the one hand, the positioning accuracy as well as the convergence time of PPP under challenging conditions (i.e. limited GPS satellites) could be improved by the integration of GLONASS and GPS (Martin et al., Reference Martín, Anquela, Capilla and Berné2011). Meanwhile, the PPP of the integrated dual-system GPS/GLONASS could enhance the accuracy of the initial ambiguity solution, resulting in shortening the ambiguity fixed timing for PPP (Jokinen et al., Reference Jokinen, Feng, Schuster, Ochieng, Hide, Moore and Hill2013; Li et al., Reference Li, Ge, Dai, Ren, Fritsche, Wickert and Schuh2015a, Reference Li, Zhang, Ren, Fritsche, Wickert and Schuh2015b).
From 27 December 2012 the Chinese BDS began to service the Asia-Pacific region for positioning, navigation and timing. However, when the PPP of combined GPS/BDS was compared with that of the single GPS, a slight deterioration was observed, possibly because of the multipath possessed by BDS GEO satellites (Zhao et al., Reference Zhao, Guo, Li, Qu, Hu, Shi and Liu2013). The PPP of the combined triple-system GPS/GLONASS/BDS demonstrated better convergence time compared with that of single-system GPS or GLONASS, while no apparent enhancement of positioning accuracy was observed using the processed daily data (Li et al., Reference Li, Ge, Dai, Ren, Fritsche, Wickert and Schuh2015a, Reference Li, Zhang, Ren, Fritsche, Wickert and Schuh2015b; Zhao et al., Reference Zhao, Wang, Liu, Ou and Yu2016). Fortunately, the reliability and availability of PPP from single-system GPS in challenging environments can be enhanced by using the PPP solution of the combined quad-system GPS/GLONASS/BDS/Galileo (Li and Zhang, Reference Li and Zhang2013; Cai et al., Reference Cai, Gao, Pan and Zhu2015; Li et al., Reference Li, Ge, Dai, Ren, Fritsche, Wickert and Schuh2015a, Reference Li, Zhang, Ren, Fritsche, Wickert and Schuh2015b).
Recently, the Quasi-Zenith Satellite System (QZSS) has attracted research attention due to its increasing development and application. Its signal design and orbit characteristics have been introduced (Li and Chen, Reference Li and Chen2016), while its noise, signal–noise ratio (SNR) as well as multipath error were evaluated according to the measurement data of the International GNSS Service (IGS) (Hong et al., Reference Hong, Tu, Zhang, Fan, Zhang and Han2020). The performance of QZSS in the China region has been analysed from three aspects: signal accuracy, availability and kinematic PPP (Lou et al., Reference Lou, Zheng, Gong and Gu2016). Hitherto the dual-system GPS/GLONASS, dual-system GPS/BDS (Yang et al., Reference Yang, Zhao, Li, Feng and Cheng2018), triple-system GPS/GLONASS/BDS (Abdi et al., Reference Abdi, Ardalan, Karimi and Rezvani2017), and quad-system GPS/GLONASS/BDS/Galileo (Li et al., Reference Li, Ge, Dai, Ren, Fritsche, Wickert and Schuh2015a, Reference Li, Zhang, Ren, Fritsche, Wickert and Schuh2015b; Pan et al., Reference Pan, Zhang, Liu, Li and Li2017; Wang et al., Reference Wang, Li, Ge, Neitzel, Wang and Yuan2018) have been the main focus of research. Therefore, in this study, the performance exhibited by the latest penta-system GPS/GLONASS/BDS/Galileo/QZSS PPP is further assessed and the role played by QZSS in the GPS/GLONASS/BDS/Galileo PPP is analysed.
The status quo regarding multi-GNSS/RNSS is first presented in Section 2. Section 3 focuses on expounding the PPP observation model together with the data processing strategy for the penta-system GPS/GLONASS/BDS/Galileo/QZSS. In Section 4, evaluation of the static and kinematic multi-GNSS/RNSS PPP solution is conducted from two perspectives: (1) positioning accuracy and (2) convergence time, based on the data from seven Multi-GNSS Experiment (MGEX) stations. Section 5 is the summary and conclusions.
2. MULTI-GNSS/RNSS STATUS QUO
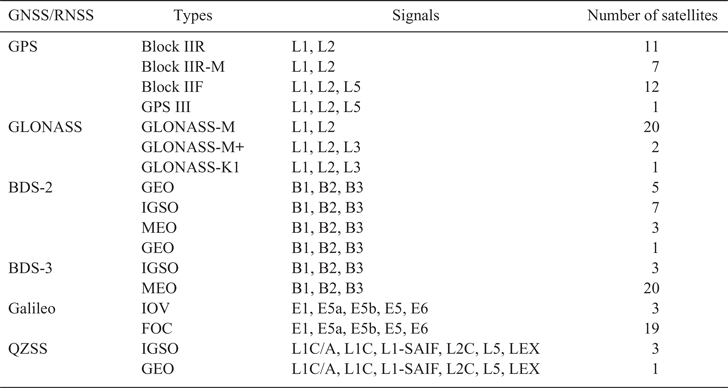
This account of the status quo of GNSS/RNSS is current as of January 2020 (see Table 1). As of January 29, 2020 there are 31 GPS satellites in operation: 11 Block IIR satellites, seven Block IIR-M satellites, 12 Block IIF satellites and one GPS III. The modernised GPS transmits L5 (at 1176·45 MHz), L1 (at 1575·42 MHz) and L2 (at 1227·60 MHz) signals (https://www.glonass-iac.ru/en/GPS/). Meanwhile, a total of 23 GLONASS satellites (20 GLONASS-M satellites, two GLONASS-M+ satellites and one GLONASS-K1 satellite) are now operating in the orbital constellation (https://www.glonass-iac.ru/en/GLONASS/). Since starting in December 2012, BDS has serviced the Asia-Pacific region for regional navigation and positioning, usually called BDS-2. At present, BDS-2 includes five geostationary orbit satellites (GEOs) and seven inclined geosynchronous orbit satellites (IGSOs), together with three medium orbit satellites (MEOs). BDS global services will be available in 2020, called BDS-3. Twenty-four BDS-3 satellites are in operation (http://www.beidou.gov.cn/). BDS transmits three frequency bands (i.e. B1 at 1575·42 MHz, B2 at 1191·795 MHz and B3 at 1268·52 MHz). Galileo has 22 operating satellites: three Galileo-IOV satellites and 19 Galileo-FOC satellites. Galileo transmits four frequency bands (i.e. E1 at 1575·42 MHz, E5a at 1176·450 MHz, E5b at 1207·140 MHz and E6 at 1278·750 MHz). The E5 (1191·795 MHz) signal is also transmitted as a combination of E5a and E5b signals (https://en.wikipedia.org/wiki/List_of_Galileo_satellites). QZSS is a regional satellite navigation system that has one GEO satellite together with three IGSO satellites and transmits six frequency bands (i.e. L1-C/A at 1575·42 MHz, L1C at 1575·42 MHz, L2C at 1227·6 MHz, L5 at 1176·45 MHz, l1-saif at 1575·42 MHz and LEX at 1278·75 MHz). Detailed information on the multi-GNSS/RNSS mentioned above is collected in Table 1 (https://en.wikipedia.org/wiki/Quasi-Zenith_Satellite_System). The 24 h ground track for the six positioning systems' satellites on 16 December 2019 is illustrated in Figure 1.
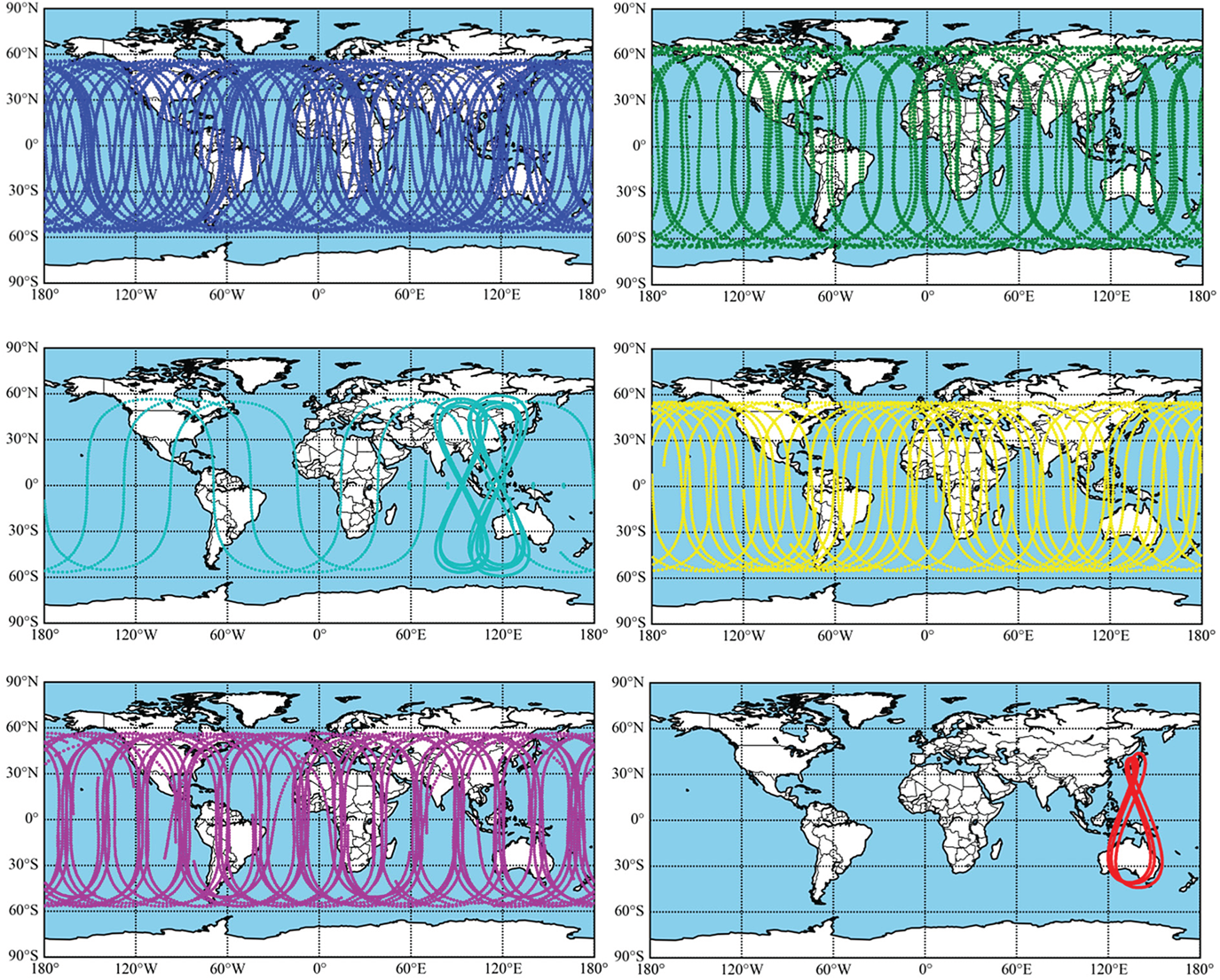
Figure 1. Ground tracks for six satellite navigation systems on 16 December 2019. Blue, green, cyan, yellow, pink and red represent GPS, GLONASS, BDS-2, BDS-3, Galileo and QZSS, respectively.
Table 1. The multi-GNSS/RNSS status quo (29 January 2020).
3. MULTI-GNSS/RNSS PPP MODEL
3.1. GNSS observation model
Below are the observation equations that include P of pseudo-range together with Φ of the carrier phase for PPP (Zhao et al., Reference Zhao, Wang, Liu, Ou and Yu2016; Zhou et al., Reference Zhou, Dong, Li, Li and Schuh2019)
$$\begin{cases} P_{r,i}^{s,Q} =\rho _r^{s,Q} +c\cdot \delta t_r^Q -c\cdot \delta t^{s,Q}+M_{r,d}^{s,Q} \cdot \delta _{r,zhd}\\ \quad \qquad +\,M_{r,w}^{s,Q} \cdot \delta _{r,zwd} +\gamma _i^Q \cdot I_{r,1}^{s,Q} +c\cdot (b_{r,i}^{s,Q} -b_i^{s,Q} )+\varepsilon _{r,i}^{s,Q} \\ \Phi _{r,i}^{s,Q} =\rho _r^{s,Q} +c\cdot \delta t_r^Q -c\cdot \delta t^{s,Q}+M_{r,d}^{s,Q} \cdot \delta _{r,zhd}\\ \qquad \quad +\,M_{r,w}^{s,Q} \cdot \delta _{r,zwd} -\gamma _i^Q \cdot I_{r,1}^{s,Q} +\lambda _i (N_{r,i}^{s,Q} +B_{r,i}^{s,Q} +B_i^{s,Q} )+\xi _{r,i}^{s,Q} \end{cases}$$ In Equation (1), s, i and r are the satellite, the signal frequency and the receiver, respectively; Q is the satellite system, GPS (G), GLONASS (R), BDS (C), Galileo (E) and QZSS (J); 
$\rho _{r}^{s, Q} $ refers to the geometric distance; c denotes the light speed symbol; 
$\delta t_{r}^{Q} $ is the clock error related to the receiver and δ t s, Q is that related to the satellite; 
$M_{r, d}^{s, Q} $ is the dry tropospheric mapping function and 
$M_{r, w}^{s, Q} $ is the wet tropospheric mapping function; 
$\delta _{r, zhd} $ is the dry zenith tropospheric delay and 
$\delta _{r, zwd} $ is the wet zenith tropospheric delay; 
$b_{r, i}^{s, Q} $ and 
$b_{i}^{s, Q} $ refer to the frequency-dependent uncalibrated code delay (UCD) specific to the receiver and the satellite, respectively, and 
$B_{r, i}^{s, Q} $ and 
$B_{i}^{s, Q} $ refer to the frequency-dependent uncalibrated phase delay (UPD); 
$I_{r, 1}^{s, Q} $ represents ionospheric delay on the frequency f 1; 
$\gamma _{i}^{Q} $ means the ionospheric amplification factor, 
$\gamma _{i}^{Q} =( {f_{1}^{s, Q} }/ {f_{i}^{s, Q} }) ^{2}$; 
$N_{r, i}^{s, Q} $ refers to the recorded integer ambiguity parameter; λi refers to the wavelength within different frequencies; 
$\varepsilon _{r, i}^{s, Q} $ and 
$\xi _{r, i}^{s, Q} $ respectively denote the sum of the measurement noises and the sum of the observation multipath errors.
Precise clock error products assist in correcting the clock error of a satellite, which contain the satellite UCD of the ionosphere-free (IF) code observations (Kouba and Héroux, Reference Kouba and Héroux2001; Zhou et al., Reference Zhou, Dong, Li, Li and Schuh2019). Thus, it can be obtained that
$$\delta t_{{\rm IF}_{12} }^{s,Q} =\delta t^{s,Q}+b_{{\rm IF}_{12} }^{s,Q}$$with
$$\begin{cases} b_{{\rm IF}_{12} }^{s,Q} =\alpha _{12}^Q b_1^{s,Q} +\beta _{12}^Q b_2^{s,Q} \\ \alpha _{12}^Q =\dfrac{\gamma _2^Q }{\gamma _2^Q -1},\beta _{12}^Q =-\dfrac{1}{\gamma _2^Q -1} \end{cases}$$
where 
$\delta t_{{\rm IF}_{12} }^{s, Q} $ denotes the precise clock error product; 
$b_{{\rm IF}_{12} }^{s, Q} $ represents the satellite UCD of IF code observation; f s, Q is signal frequency; 
$\alpha _{12}^{Q} , \; \beta _{12}^{Q} $ are frequency-dependent factors. Substituting Equation (2) into Equation (1), the following can be obtained:
$$\left\{ {\begin{array}{@{}l} P_{r,i}^{s,Q} =\rho_r^{s,Q} +c\cdot \delta t_r^Q -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot b_{r,i}^{s,Q} +M_{r,d}^{s,Q} \cdot \delta_{r,zhd} +M_{r,w}^{s,Q} \cdot \delta_{r,zwd}\\ \qquad\quad +\,\gamma_i^Q \cdot (I_{r,1}^{s,Q} -c\cdot \beta_{12}^Q {\rm DCB}_{P_1 P_2 }^{s,Q} )+\varepsilon_{r,i}^{s,Q} \\ \Phi_{r,i}^{s,Q} =\rho_r^{s,Q} +c\cdot \delta t_r^Q -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot b_{{\rm IF}_{12} }^{s,Q} +M_{r,d}^{s,Q} \cdot \delta_{r,zhd} +M_{r,w}^{s,Q} \cdot \delta_{r,zwd}\\ \qquad\quad -\,\gamma_i^Q \cdot I_{r,1}^{s,Q} +\lambda_i (N_{r,i}^{s,Q} +B_{r,i}^{s,Q} +B_i^{s,Q} )+\xi_{r,i}^{s,Q} \end{array}} \right.$$with
$${\rm DCB}_{P_1 P_2 }^{s,Q} =b_1^{s,Q} -b_2^{s,Q}$$
where 
${\rm DCB}_{P_{1} P_{2} }^{s, Q} $ is the frequency-dependent satellite differential code bias (DCB) between the code observations 
$P_{r, 1}^{s, Q} $ and 
$P_{r, 2}^{s, Q} $. In GLONASS the UCD for the receiver is different from other satellite systems like GPS, BDS and Galileo, as well as QZSS, because GLONASS offers frequency division multiple access (FDMA) signals. Therefore, the UCD for the receiver is expressed as (Zhou et al., Reference Zhou, Dong, Li, Jiang, Wickert and Schuh2018):
$$\left\{ {\begin{array}{@{}l} b_{r,i}^{s,Q} =b_{r,i}^Q +\theta_{r,i}^{s,Q} ,Q={\rm R} \\ b_{r,i}^{s,Q} =b_{r,i}^Q ,Q={\rm G},{\rm E},{\rm C},{\rm J} \\ \end{array}} \right.$$
where 
$b_{r, i}^{Q} $ of all satellites in system Q is identical at frequency i; it can be expressed as
$$\label{eq7} b_{r,i}^Q =b_{r,{\rm IF}_{12} }^Q +\gamma _i^Q \beta _{12}^Q {\rm DCB}_{r,P_1 P_2 }^Q$$with
$$\label{eq8} \left\{ {\begin{array}{@{}l} b_{r,{\rm IF}_{12} }^Q =\alpha_{12}^Q b_{r,1}^{s,Q} +\beta_{12}^Q b_{r,2}^{s,Q} \\ {\rm DCB}_{r,P_1 P_2 }^{s,Q} =b_{r,1}^{s,Q} -b_{r,2}^{s,Q} \\ \end{array}} \right.$$
where 
${\rm DCB}_{r, P_{1} P_{2} }^{Q} $ is frequency-dependent receiver DCB between code observations 
$P_{r, 1}^{s, Q} $ and 
$P_{r, 2}^{s, Q} $. It is possible to neglect the pseudo-range inter-frequency bias (IFB) term 
$\theta _{r, i}^{s, Q} $ and the pseudo-range residuals will see their effects due to the much lower weight of the pseudo-range observations relative to the carrier phase observation in PPP processing (Cai and Gao, Reference Cai and Gao2012; Chen et al., Reference Chen, Zhang, Wang, Yang, Dong, Wang, Qu and Wu2015). Substituting Equation (6) into Equation (4), it can be obtained that
$$\begin{align} \label{eq9} \left\{ {\begin{array}{@{}l} P_{r,i}^{s,Q} =\rho_r^{s,Q} +c\cdot \delta \bar {t}_r^Q -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +M_{r,d}^{s,Q} \cdot \delta_{r,zhd} +M_{r,w}^{s,Q} \cdot \delta_{r,zwd} +\gamma_i^Q \cdot \bar {I}_{r,1}^{s,Q} +\varepsilon_{r,i}^{s,Q} \\ \Phi_{r,i}^{s,Q} =\rho_r^{s,Q} +c\cdot \delta \bar {t}_r^Q -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +M_{r,d}^{s,Q} \cdot \delta_{r,zhd} +M_{r,w}^{s,Q} \cdot \delta_{r,zwd} -\gamma_i^Q \cdot \bar {I}_{r,1}^{s,Q} +\bar {N}_{r,i}^{s,Q} +\xi_{r,i}^{s,Q} \end{array}} \right. \end{align}$$with
$$\begin{align}\label{eq10} \left\{ {\begin{array}{@{}l} \delta \bar {t}_r^Q =\delta t_r^Q +b_{r,{\rm IF}_{12} }^Q \\ \bar {I}_{r,1}^{s,Q} =I_{r,1}^{s,Q} +c\beta_{12}^Q ({\rm DCB}_{r,P_1 P_2 }^Q -{\rm DCB}_{P_1 P_2 }^{s,Q} ) \\ \bar {N}_{r,i}^{s,Q} =\lambda_i^{s,Q} (N_{r,i}^{s,Q} +B_{r,i}^{s,Q} -B_j^{s,Q} )+c(b_{{\rm IF}_{12} }^{s,Q} -b_{r,{\rm IF}_{12} }^Q )+c\gamma_i^Q \beta_{12} ({\rm DCB}_{r,P_1 P_2 }^Q -{\rm DCB}_{P_1 P_2 }^{s,Q} ) \end{array}} \right. \end{align}$$The University of Calgary (UofC) model is provided in Equation (11) to analyse the PPP performance of the combined systems (Gao and Shen, Reference Gao and Shen2001). The delay regarding the one-order ionosphere is eliminated using this model, which also produces smaller code observation noise. The function model is expressed as:
$$\left\{\begin{array}{@{}l} L_{r,i}^{s,Q} =\dfrac{P_{r,i}^{s,Q} +\Phi_{r,i}^{s,Q} }{2} \\ \qquad =\rho_r^{s,Q} +c\cdot \delta \bar {t}_r^Q -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +M_{r,d}^{s,Q} \cdot \delta_{r,zhd} +M_{r,w}^{s,Q} \cdot \delta_{r,zwd} +\dfrac{\lambda_i^{s,Q} \bar{N}_{r,i}^{s,Q} }{2}+\varepsilon_L \\ \Phi_{r,{\rm IF}_{12} }^{s,Q} =\dfrac{(f_1^{s,Q} )^2\cdot \Phi_{r,1}^{s,Q} -(f_2^{s,Q} )^2\cdot \Phi_{r,2}^{s,Q} }{(f_1^{s,Q} )^2-(f_2^{s,Q} )^2} \\ \qquad =\rho_r^{s,Q} +c\cdot \delta \bar {t}_r^Q -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +M_{r,d}^{s,Q} \cdot \delta_{r,zhd} +M_{r,w}^{s,Q} \cdot \delta_{r,zwd} +N_{r,{\rm IF}_{12} }^{s,Q} +\varepsilon_{\Phi_{{\rm IF}_{12} } } \end{array}\right.$$
where 
$N_{r, {\rm IF}_{12} }^{s, Q} $ is the ambiguity of the IF observations.
The additional inter-system bias (ISB) parameter shall be estimated in the GPS/ GLONASS/BDS/Galileo/QZSS PPP model; Equation (12) expresses the code observation and phase observation specific to the PPP of the combined GPS/GLONASS/BDS/Galileo/ QZSS:
$$\begin{align}\label{eq12} \left\{ {\begin{array}{@{}l} L_{r,i}^{s{\rm ,G}} =\rho_r^{s,{\rm G}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +M_{r,d}^{s,{\rm G}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm G}} \cdot \delta_{r,zwd} +\dfrac{\lambda_i \bar {N}_{r,i}^{s,{\rm G}} }{2}+\varepsilon_L \\ \Phi_{r,{\rm IF}_{{\rm 12}} }^{s,{\rm G}} =\rho_r^{s,{\rm G}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +M_{r,d}^{s,{\rm G}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm G}} \cdot \delta_{r,zwd} +N_{r,{\rm IF}_{12} }^{s,{\rm G}} +\varepsilon_{\Phi_{{\rm IF}_{12} } } \\ L_{r,i}^{s{\rm ,R}} =\rho_r^{s,{\rm R}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot ISB_r^{\rm R} +M_{r,d}^{s,{\rm R}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm R}} \cdot \delta_{r,zwd} +\dfrac{\lambda_i \bar {N}_{r,i}^{s,{\rm R}} }{2}+\varepsilon_L \\ \Phi_{r,{\rm IF}_{{\rm 12}} }^{s,{\rm R}} =\rho_r^{s,{\rm R}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot ISB_r^{\rm R} +M_{r,d}^{s,{\rm R}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm R}} \cdot \delta_{r,zwd} +N_{r,{\rm IF}_{12} }^{s,{\rm R}} +\varepsilon_{\Phi_{{\rm IF}_{12} } } \\ L_{r,i}^{s{\rm ,C}} =\rho_r^{s,{\rm C}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot ISB_r^{\rm C} +M_{r,d}^{s,{\rm C}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm C}} \cdot \delta_{r,zwd} +\dfrac{\lambda_i \bar {N}_{r,i}^{s,{\rm C}} }{2}+\varepsilon_L \\ \Phi_{r,{\rm IF}_{{\rm 12}} }^{s,{\rm C}} =\rho_r^{s,{\rm C}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot ISB_r^{\rm C} +M_{r,d}^{s,{\rm C}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm C}} \cdot \delta_{r,zwd} +N_{r,{\rm IF}_{12} }^{s,{\rm C}} +\varepsilon_{\Phi_{{\rm IF}_{12} } } \\ L_{r,i}^{s{\rm ,E}} =\rho_r^{s,{\rm E}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot ISB_r^{\rm E} +M_{r,d}^{s,{\rm E}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm E}} \cdot \delta_{r,zwd} \dfrac{\lambda_i \bar {N}_{r,i}^{s,{\rm E}} }{2}+\varepsilon_L \\ \Phi_{r,{\rm IF}_{{\rm 12}} }^{s,{\rm E}} =\rho_r^{s,{\rm E}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot ISB_r^{\rm E} +M_{r,d}^{s,{\rm E}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm E}} \cdot \delta_{r,zwd} +N_{r,{\rm IF}_{12} }^{s,{\rm E}} +\varepsilon_{\Phi_{{\rm IF}_{12} } } \\ L_{r,i}^{s{\rm ,J}} =\rho_r^{s,{\rm J}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot ISB_r^{\rm J} +M_{r,d}^{s,{\rm J}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm J}} \cdot \delta_{r,zwd} \dfrac{\lambda_i \bar {N}_{r,i}^{s,{\rm J}} }{2}+\varepsilon_L \\ \Phi_{r,{\rm IF}_{{\rm 12}} }^{s,{\rm J}} =\rho_r^{s,{\rm J}} +c\cdot \delta \bar {t}_r^{\rm G} -c\cdot \delta t_{{\rm IF}_{12} }^{s,Q} +c\cdot ISB_r^{\rm J} +M_{r,d}^{s,{\rm J}} \cdot \delta_{r,zhd} +M_{r,w}^{s,{\rm J}} \cdot \delta_{r,zwd} +N_{r,{\rm IF}_{12} }^{s,{\rm J}} +\varepsilon_{\Phi_{{\rm IF}_{12} } } \end{array}} \right. \end{align}$$In Equation (12), the clock error of the GPS receiver is regarded as a reference; then, the ISB parameter is defined as follows.
$$\left\{ {\begin{array}{@{}l} ISB_r^{\rm R} =b_{r,{\rm IF}_{12} }^{\rm R} -b_{r,{\rm IF}_{12} }^{\rm G} \\ ISB_r^{\rm C} =b_{r,{\rm IF}_{12} }^{\rm C} -b_{r,{\rm IF}_{12} }^{\rm G} \\ ISB_r^{\rm E} =b_{r,{\rm IF}_{12} }^{\rm E} -b_{r,{\rm IF}_{12} }^{\rm G} \\ ISB_r^{\rm J} =b_{r,{\rm IF}_{12} }^{\rm J} -b_{r,{\rm IF}_{12} }^{\rm G} \end{array}} \right.$$The parameter X of multi-GNSS/RNSS PPP is
$$\textbf{X}=\left[\begin{matrix} \textbf{x} & {\delta \tilde {t}_r^Q } & {ISB_r^Q } & {\delta_{r,zwd} } & {\tilde {N}_{r,1}^{s,Q} } & {\tilde{N}_{r,2}^{s,Q} } \end{matrix}\right]^{\rm T}$$where x denotes the positioning parameter.
3.2. Data processing approach
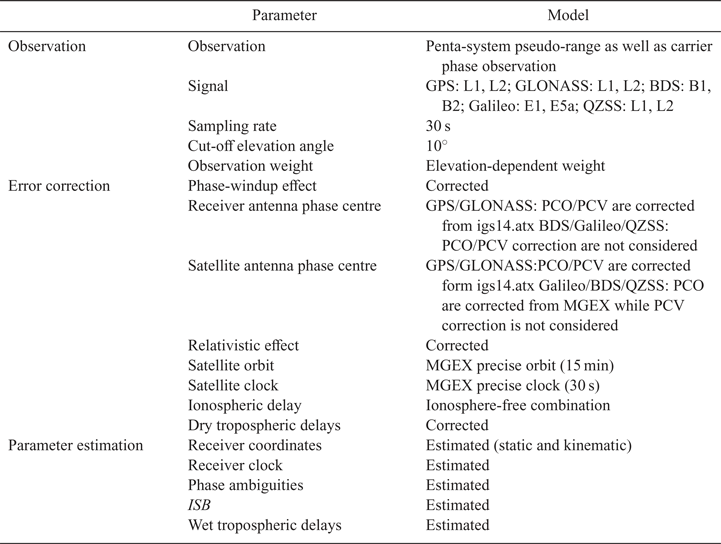
This section has shown how this model estimates the parameters of the receiver position, the wet tropospheric delay, the receiver clock error and the ambiguities, as well as the ISB by using the UofC model combined with extended Kalman filter. The phase centre offset (PCO) together with the phase centre variation (PCV) of GPS and GLONASS are introduced in the ANTEX file released by IGS. The satellite-end PCOs of BDS, Galileo and QZSS are also provided by the ANTEX file. Meanwhile, the study does not consider the PCV at the satellite end or the PCO and PCV at the receiver end because they cannot be found (Wang et al., Reference Wang, Li, Ge, Neitzel, Wang and Yuan2018). Table 2 lists the parameters of the observation and the error correction, as well as the estimation.
Table 2. Processing approach of static and kinematic PPP specific to the multi-GNSS/RNSS.
4. PPP PERFORMANCE IN THE MULTI-GNSS/RNSS
4.1. Data collection
A period of seven days (DOY 350–356, 2019) was adopted for collecting observations from seven MGEX stations, with a sampling rate of 30 s. Each receiver is capable of receiving signals from GPS, BDS, GLONASS, Galileo and QZSS satellites (BDS means BDS-2). Figure 2 displays the distribution of the stations and Table 3 lists information on the stations. Performance evaluation and comparison of static and kinematic PPP solutions were conducted in line with the data processing performed in 13 different GNSS combinations: single system (GPS, GLONASS, BDS and Galileo, abbreviated as G, R, C and E), dual system (combined GPS/GLONASS, GPS/BDS, GPS/Galileo and GPS/QZSS, abbreviated as GR, GC, GE and GJ), and multi-system (combined GPS/GLONASS/BDS, GPS/GLONASS/Galileo, GPS/GLONASS/QZSS, GPS/GLONASS/BDS/Galileo and GPS/GLONASS/BDS/Galileo/QZSS, abbreviated as GRC, GRE, GRJ, GREC and GRECJ).
Figure 2. Distribution of MGEX stations.
Table 3. Receiver information in detail.
4.2. GNSS satellite availability
The measured data obtained from seven stations on 16 December 2019 (DOY 350, 2019) were used to analyse the availability of single-system, dual-system and multi-system satellites. Regarding the PPP data processing, the number of visible satellites together with the satellite geometry distribution decides the PPP convergence time. The average number of visible satellites together with the mean PDOP (position dilution of precision) values for single system and dual-system and multi-system combinations at 10° cut-off elevation angle are illustrated in Figures 3–5. The results are summarised as follows:
(1) As illustrated in Figure 3, BDS has the most visible satellites, except for station ALIC, followed by GPS. From the perspective of PDOP, GPS possesses a smaller and more stable PDOP value relative to BDS because BDS mostly comprises GEO and IGSO in the Asia-Pacific region. Galileo possesses the largest PDOP value mainly because it has about five visible satellites on average at this stage.
(2) As shown in Figure 4, the GPS/BDS combined system has the most visible satellites of the dual-system combinations. The mean PDOP values were improved by 70·7%, 49·9% and 78·2% after adding GPS, respectively, compared with single GLONASS, single BDS and single Galileo. The mean PDOP value was also enhanced by 19·5% after adding QZSS compared with single GPS. Therefore, the dual-system combination contributes to more visible satellites and remarkably lowers the PDOP value.
(3) As demonstrated in Figure 5, the penta-system combination has the most satellites and the smallest PDOP value of the multi-system combinations. The mean PDOP value of the GPS/GLONASS/BDS/Galileo combined system was improved by 20·6% compared with the GPS/GLONASS/BDS combined system. The mean PDOP value was further improved by 5·6% after adding QZSS compared with the quad-system combination. To sum up, the multi-GNSS/RNSS has a better geometry distribution than a single system, contributing to improvement of the navigation and positioning service.
Figure 3. Mean visible satellite number and mean PDOP values for single systems at 10° cut-off elevation angle.
Figure 4. Mean visible satellite number and mean PDOP values for dual systems at 10° cut-off elevation angle.
Figure 5. Mean visible satellite number and mean PDOP values for multi-systems at 10° cut-off elevation angle.
4.3. Static PPP
In this subsection, static PPP is determined using the observation data from 16–22 December 2019 (DOY 350–356, 2019) at the seven MGEX stations. Positioning error is the difference between the positioning solution and the IGS weekly solution. Filtering convergence refers to the positioning errors in the North and East components being less than 10 cm. Filtering is considered as converging at an epoch when the positioning errors during the last 20 epochs are still confined to the limit (Zhao et al., Reference Zhao, Wang, Liu, Ou and Yu2016). The mean convergence times for static PPP for the single-system, dual-system and multi-system data from each station are displayed in Figures 6–8.
Figure 6. Mean convergence time for static PPP of single systems in each station.
Figure 7. Mean convergence time for static PPP of dual systems in each station.
Figure 8. Mean convergence time for static PPP of multi-systems in each station.
As shown in Figure 6, the static PPP of GPS and GLONASS hold the mean convergence times of 19·4 min and 24·6 min, respectively, while for BDS and Galileo systems, the mean convergence times are 64·5 min and 68·6 min, respectively, due to the poorer accuracy of the BDS orbit as well as its clock products, and the smaller number of Galileo satellites, about four to six in a single epoch. From Figure 7 it can be seen that the static PPP of the GPS/GLONASS combined system presents the shortest mean convergence time, just 14·4 min. Moreover, the PPPs of the dual-system GPS/BDS, GPS/Galileo and GPS/QZSS cost 16·1 min, 14·4 and 16·8 min, respectively. Compared with the single GLONASS, single BDS and single Galileo, the mean convergence time of static PPP increased 41·5%, 75·0% and 79·0%, respectively, after adding GPS. Relative to single GPS, its static PPP saw enhanced mean convergence time by 13·4% after adding QZSS. In summary, the dual systems have quicker convergence speeds relative to the single systems. Figure 8 shows that the PPPs of the GPS/GLONASS/BDS, GPS/GLONASS/Galileo and GPS/GLONASS/QZSS combined systems present similar mean convergence times of about 13 min. The GPS/GLONASS/Galileo/BDS/QZSS combined system PPP has the shortest mean convergence time, just 11·5 min, followed by the GPS/GLONASS/Galileo/BDS (12·4 min). Therefore, adding the QZSS system helped further to decrease the convergence time regarding multi-GNSS PPP.
Tables 4–6 list the root mean square (RMS) of static PPP for single systems, dual systems and multi-systems under 10o cut-off elevation angles. As listed in Table 4, the average RMS of the PPP solutions for single GPS and single GLONASS exceeds 1 cm in horizontal directions and 2 cm in the Up direction. Considering the poorer accuracy exhibited by the precise satellite orbit as well as clock products provided for BDS, together with the lower number of Galileo satellites, BDS and Galileo have poor positioning accuracy compared with GPS and GLONASS. According to Table 5, the positioning accuracy exhibited by GPS/GLONASS PPP in the horizontal direction is the same as that of GPS/BDS, GPS/Galileo and GPS/QZSS, while it presents a better positioning accuracy in the vertical direction relative to other dual-system combinations. The positioning accuracy of PPP is obviously improved after adding GPS, compared with single BDS and single Galileo. As suggested from the results given in Table 6, the average RMSs of multi-systems PPP solution are better than 0·8 and 1·7 cm in horizontal directions and Up direction, respectively.
Table 4. Positioning accuracy for single-system PPP following convergence (cm).
Table 5. Positioning accuracy for dual-system PPP following convergence (cm).
Table 6. Positioning accuracy for multi-system PPP following convergence (cm).
The cut-off elevation angles wer set in the range of 10°–40° in every 5° to simulate a harsh environment, aiming to analyse the advantages of the multi-GNSS/RNSS PPP. It is well known that it takes at least about half an hour to obtain positioning accuracy at centimetre level in static mode for ambiguity-float PPP (Zhao et al., Reference Zhao, Wang, Liu, Ou and Yu2016). The 168 h observation data from the seven stations are separated in every 0.5 h to get 2352 group data sets. Hence, the 2,352 group data sets were analysed to evaluate their convergence percentage and convergence time, as well as positioning accuracy with changing cut-off elevation angles. As the cut-off elevation angle rises, both satellites that participate in the calculation and the geometry strength decrease. Moreover, it also affects the PPP solution performance. The convergence percentage and convergence time for single-system, dual-system and multi-system PPP are illustrated in Figures 9–11. It can be observed that, specific to various types of combination, increasing the cut-off elevation angle will lead to a decrease in the convergence percentage and time. Under 35° cut-off elevation angle, the convergence percentages specific to GPS/GLONASS, GPS/BDS and GPS/Galileo decreased 89·0%, 17·6% and 73·0%, respectively, compared with single GLONASS, single BDS and single Galileo. Furthermore, the convergence percentage of GPS/QZSS is improved by 35·9% compared with a single GPS. For the GPS/GLONASS/BDS/Galileo/QZSS combination, PPP exhibits a relatively optimal performance when the cut-off angle is the same due to the rich observation data resulting from more satellites. Specifically, the convergence percentage regarding the GPS/GLONASS/BDS/Galileo/QZSS combined PPP is 80·9% higher relative to other combined systems with the cut-off elevation angle at 35°.
Figure 9. Convergence percentage and convergence time for single-system PPP. (a) Percentage of positioning at centimetre level at 10°–40° cut-off elevation angles, (b) Mean convergence time for obtaining the positioning at centimetre level with changing cut-off elevation angles.
Figure 10. Convergence percentage and convergence time for dual-system PPP. (a) Percentage of positioning at centimetre level at 10°–40° cut-off elevation angles, (b) Mean convergence time for obtaining positioning at centimetre level with changing cut-off elevation angles.
Figure 11. Convergence percentage and convergence time for multi-system PPP. (a) Percentage occupied by the centimetre-level positioning under 10°–40° cut-off elevation angles, (b) Mean convergence time for obtaining centimetre-level positioning with changing cut-off elevation angles.
The percentages of the RMSs of PPP within 0–5 cm are presented in Figures 12–14 to further evaluate the accuracy of PPP solutions for single system, dual system and multi-system. As shown in Figure 12, the percentage for GPS was higher relative to other single systems with the cut-off elevation angle below 35°. In line with Figure 13, GPS/ GLONASS and GPS/Galileo present higher percentages relative to other dual systems when the cut-off elevation angle is changed. At 30°, GPS/GLONASS see increased percentages by 59·0%, 57·4% and 66·1% in North, East and Up directions, respectively, compared with single GPS. The percentages in the North and East directions of the combined systems: GPS/GLONASS/Galileo/BDS/QZSS, GPS/GLONASS/Galileo/ BDS and GPS/GLONASS/Galileo are basically equal and are better the GPS/GLONASS/ BDS and GPS/GLONASS/QZSS combined systems. Meanwhile, the GPS/GLONASS/ Galileo/BDS/QZSS combined system in the Up direction presents a much higher percentage compared with the other combined systems. At 40°, GPS/GLONASS/Galileo/BDS/ QZSS sees strengthened percentage by 4·1%, 3·7% and 28·6% in the North, East and Up directions, respectively, relative to GPS/GLONASS/Galileo/BDS. To sum up, multi-GNSS/RNSS is capable of remarkably strengthening the positioning accuracy with the cut-off elevation angle being high.
Figure 12. Percentage of RMS values of PPP within 0–5 cm for single systems in North, East and Up directions at 10°–40° cut-off elevation angle.
Figure 13. Percentage of RMS values of PPP within 0–5 cm for dual systems in North, East and Up directions at 10°–40° cut-off elevation angle.
Figure 14. Percentage of RMS values of PPP within 0–5 cm for multi-systems in North, East and Up directions at 10°–40° cut-off elevation angle.
4.4. Kinematic PPP
To evaluate the performance exhibited by kinematic PPP, static data is used to simulate the kinematic conditions for solution (Ren et al., Reference Ren, Zhang, Li and Zhang2015). The observed data (DOY 353, 2019) from seven stations were verified to assess the latest performance regarding kinematic PPP in multi-GNSS and analyse the contribution of QZSS to the GPS/GLONASS/BDS/Galileo PPP. The data processing strategy described in Section 2.2 was adopted to investigate kinematic PPP at six stations. Figure 15 displays the RMS values of kinematic PPP solutions at 10° for GPS-only system, GPS/GLONASS/Galileo/BDS and GPS/GLONASS/Galileo/BDS/QZSS.
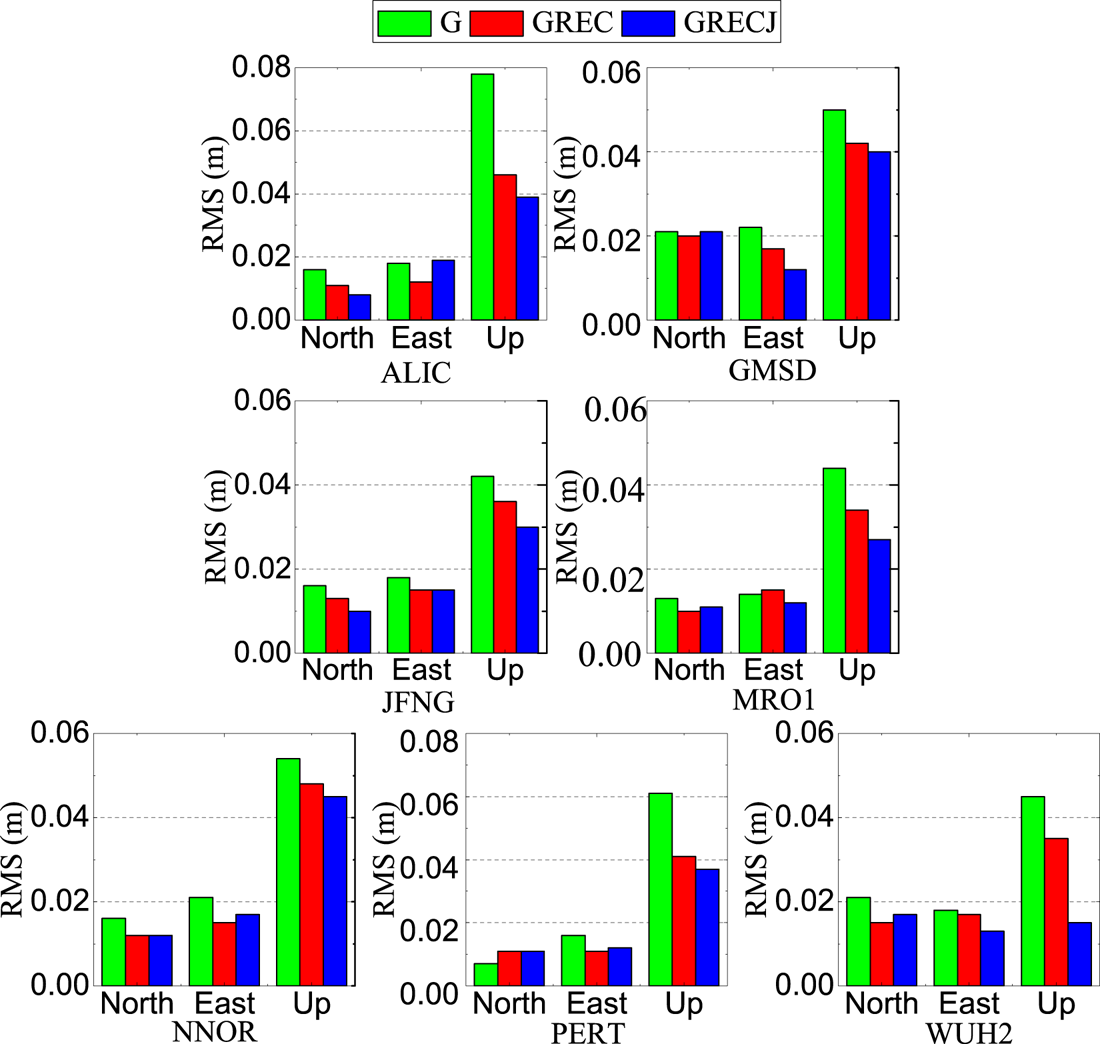
Figure 15. Daily RMS values of kinematic PPP solutions for single GPS, GPS/GLONASS/Galileo/BDS and GPS/GLONASS/Galileo BDS/QZSS.
As observed in Figure 15, the mean RMS of kinematic PPP for single GPS is 0·015 m, 0·018 m and 0·053 m in the the North, East and Up directions, respectively. Meanwhile, the positioning accuracy exhibited by the kinematic PPP of the combined GPS/GLONASS/Galileo/BDS increased 16·4%, 19·7% and 24·6% in the three directions, respectively, compared with the single GPS system. In the three directions, the positioning accuracy of kinematic PPP exhibited by combined GPS/GLONASS/Galileo/BDS was further improved by 2·2%, 2·0% and 17·4%, respectively, after adding the QZSS system. Therefore, the positioning availability and accuracy of the combined GPS/GLONASS/Galileo/BDS undergo enhancement by using QZSS for a single receiver. To sum up, the penta-system combination in particular is capable of enhancing the PPP positioning accuracy. Relative to the single-system PPP solution, the positioning accuracy exhibited for the Up direction is strengthened while that exhibited for horizontal direction is not significantly improved by multi-GNSS/RNSS PPP.
Furthermore, the PPPs for single-system GPS and multi-GNSS/RNSS at various cut-off elevation angles were processed to simulate challenging environments such as ‘urban canyon’ areas. Kinematic PPP solutions obtained from the single-system model, quad-system model and penta-system model at JFNG and GMSD stations were compared at two cut-off elevation angles, as illustrated in Figures 16 and 17. The figures indicate that the influence of cut-off elevation angle on single-system GPS positioning is larger than on multi-GNSS/RNSS because the multi-system GPS/GLONASS/BDS/Galileo and GPS/GLONASS/BDS/Galileo/QZSS combinations can still obtain high accuracy positioning at a cut-off elevation angle of 40°. Moreover, the combined system shows higher stability compared with the single system.
Figure 16. Comparison of PPP results in single GPS and multi-GNSS/RNSS modes under 10° elevation cut-off (left) and 40° elevation cut-off (right) at JFNG station.
Figure 17. Comparison of PPP results in single GPS and multi-GNSS/RNSS modes under 10° elevation cut-off (left) and 40° elevation cut-off (right) at GMSD station.
5. CONCLUSIONS
Multi-GNSS/RNSS not only enriches routine observations but also enhances the geometrical strength of satellites, contributing to improving the positioning performance. Experiments on static as well as kinematic PPP for single systems and combined GNSS/RNSS were performed according to the data obtained from MGEX reference stations, considering positioning accuracy as well as convergence time. The reliability, availability and stability of GPS positioning drops sharply in complicated or bleak situations, such as ‘urban canyon’ areas and steep valleys, because fewer satellites remain visible in these areas. Thus, the penta-system PPP solutions under various cut-off elevation angles were analysed to verify comprehensively the performance of multi-GNSS/RNSS positioning. The main conclusions are as follows:
(1) The penta-system combination had the most satellites as well as the smallest PDOP value of the multi-system combinations. Compared with the GPS/GLONASS/BDS combined system, using GPS/GLONASS/BDS/Galileo the mean PDOP value was improved by 20·6%. Meanwhile, the mean PDOP value was further improved by 5·6% after adding QZSS compared with the quad-system combination. In summary, the multi-GNSS/RNSS had a better geometry distribution than a single system, contributing to improvement of the navigation and positioning service.
(2) Compared with GLONASS, BDS and Galileo as single systems, the mean convergence time of static PPP decreased 41·5%, 75·0% and 79·0% after adding GPS, respectively, and that was enhanced by 13·4% after adding the QZSS compared with single-system GPS. The multi-systems GPS/GLONASS/BDS, GPS/GLONASS/Galileo and GPS/GLONASS/QZSS had basically the same mean PPP convergence time of about 13 min. The GPS/GLONASS/Galileo/BDS/QZSS combined system PPP presented the shortest mean convergence time (11·5 min), followed by GPS/GLONASS/Galileo/BDS in second place (12·4 min). Therefore, adding the QZSS system helped further reduce the convergence time of multi-GNSS PPP.
(3) The convergence percentage regarding the GPS/GLONASS/BDS/Galileo/QZSS combined PPP was 80·9% higher relative to other combined systems at a cut-off angle of 35°. At 40°, the percentages of the RMS in the range of 0 ~ 5 cm specific to GPS/GLONASS/Galileo/BDS/QZSS rose by 4·1%, 3·7% and 28·6% in North, East and Up directions, respectively, compared with GPS/GLONASS/Galileo/BDS. Therefore, multi-GNSS/RNSS is capable of remarkably improving the positioning accuracy with the cut-off elevation angle being high.
(4) Relative to single-system GPS, the kinematic PPP of GPS/GLONASS/Galileo/BDS saw improved positioning accuracy by 16·4%, 19·7% and 24·6% in the North, East and Up directions, respectively. The positioning accuracy exhibited by the kinematic PPP of GPS/GLONASS/Galileo/BDS was further improved by 2·2%, 2·0% and 17·4% in the three directions, respectively, following the addition of the QZSS system. Therefore, the availability as well as accuracy related to GPS/GLONASS/Galileo/BDS positioning were enhanced by using QZSS for a single receiver.
ACKNOWLEDGEMENTS
We thank the anonymous reviewers for their helpful suggestions. This work is supported by the Postgraduate Research & Practice Innovation Program of Jiangsu Province (nos. sjky19_0513 and 2019B60114), the National Natural Science Foundation of China (nos. 41604018 and 41704008), the Fundamental Research Funds for the Central Universities (no. 2019B17514) and the Program for Excellent Talents in University of Anhui Province of China (no. gxyq2017008). We also thank the IGS communities for the provision of GNSS data and products.
