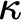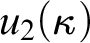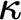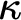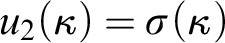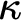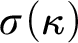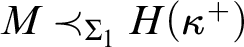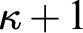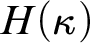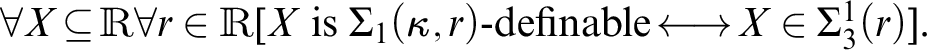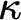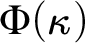1. Introduction
There are a number of properties in the literature that fall in the region of being weaker than measurability, but stronger than
$0^{\#},$
and thus inconsistent with the universe being that of the constructible sets.
Actual cardinals of this nature have been well known and are usually of ancient pedigree: Ramsey cardinals, Rowbottom cardinals, Erdős cardinals, and the like (cf. for example, [Reference Kanamori7]). Some concepts are naturally not going to prove the existence of such large cardinals, again for example, descriptive set theoretical properties which are about
$V_{\omega +1}$
do not establish the existence of such large cardinals but rather may prove the consistency of large cardinal properties in an inner model. Weak generic absoluteness results, perhaps again only about
, may require some property such as closure of sets under
$\#$
’s, or more, throughout the whole universe.
An example of this is afforded by admissible measurability (defined below):
Theorem ([Reference Welch15], Theorem 4, Lemma 1)
Let
$\Psi $
be the statement:
$$\begin{align*}{\forall} D { \,\subseteq\, } \omega_{1}(D \mbox{ is universally Baire } {\,\Longleftrightarrow\,} {\exists} r { \,\subseteq\, } \omega ( D \in L[r] )). \end{align*}$$
If K is the core model then
$\Psi ^{K}$
is (set)-generically absolute if and only if there are arbitrarily large admissibly measurable cardinals in K.
This is a very weak property: weaker than an
$\omega _{1}$
-Erdős, but certainly stronger than “For any set
$X{ \,\subseteq \, } On, X^{\sharp }$
exists” (thus indeed stronger than, say, two step
$\Sigma ^{1}_{3}$
-generic absoluteness—see [Reference Feng, Magidor, Woodin, Judah, Just and Woodin5]). Essentially it is often an assertion about the density of the mouse order in some, or alternatively arbitrarily large,
$H(\kappa )$
. This is also the guiding spirit behind the notions of stable measurability defined here.
In [Reference Lücke8] and [Reference Lücke, Schindler and Schlicht9] the authors study, in essence,
$\Sigma _{1}$
-definable properties of a regular cardinal
$\kappa $
in various forms: whether there is a
$\Pi _{1}(\kappa )$
definition of the club filter on
$\kappa $
for example, or whether
$\Sigma _{1}(\kappa )$
-definable subsets of
$\kappa $
enjoy some kind of homogeneity property, such as that from [Reference Lücke8] defined below at 1.23. The theorems of the abstract involve a strengthening of admissible measurability to stable measurability. This allows us an exact calibration of the strength of Lücke’s
$\boldsymbol {\Sigma }_{1}$
-club property. It also allows minor improvements in the assumptions of certain theorems from [Reference Lücke, Schindler and Schlicht9]. (Here we abbreviate that a relation may be
$\Sigma _{n}(p_{1},\ldots ,p_{n})$
-definable rather than the more formal
$\Sigma _{n}(\{p_{1},\ldots ,p_{n}\})$
; boldface definitions such as
$\boldsymbol {\Sigma }_{1}$
are taken to be those that
$\Sigma _{1}(X)$
for some unspecified set of parameters as usual.)
Stable measurability, whilst being ostensibly about
$\Sigma _{1}$
-definable subsets of
$\kappa $
, and whether an iterable measure can be put on the least stable set, is really something about the bounded subsets of
$\kappa $
. It says something about the strength of the mouse order in
$H(\kappa )$
(the class of sets hereditarily of cardinality less than
$\kappa $
), or relatedly, the size of the least uniform indiscernible above
$\kappa $
for bounded subsets of
$\kappa $
. In the core model K, (at least below
$0^{pistol}$
) it is literally saying that the mouse order has length up to the least
$\Sigma _{1}$
stable ordinal
$\sigma (\kappa )$
as defined in this context. As the
$\boldsymbol {\Sigma }_{1}$
-club property turns out to be equivalent to stable measurability, it too, although phrased in terms of homogeneity properties of simply defined functions on
$\kappa $
, or subsets of
$\kappa $
, is in turn capable of being viewed as being actually about bounded subsets of
$\kappa $
.
Note: By premouse or mouse we mean that in the modern sense: see [Reference Zeman17]. By a Dodd–Jensen mouse (or
$DJ$
-mouse) we mean that of [Reference Dodd3]. We do not need many details of the latter: simply that they are similar to the levels of
$L[\mu ]$
where the levels are defined as in simple relativised constructibility from a predicate
$\mu $
. A
$DJ$
-mouse then is a structure of the form
${\langle } J_{\alpha }^{U},\in , U{\rangle }\models \mbox {``}U \mbox { is a normal measure on } \kappa \mbox {''}$
with wellfounded iterated ultrapowers. Another required feature of a
$DJ$
-mouse M is that there is always a new subset of the measurable cardinal
$\kappa $
definable over M. Consequently there is always also a definable onto map
$f:\kappa {\,\longrightarrow \,} J_{\alpha }^{U}$
. The Dodd–Jensen core model
$K^{DJ}$
can be thought of as an
$L[E]$
hierarchy whose initial segments are all sound mice in the usual fashion, or alternatively as simply the union of the older
$DJ$
-mice. These universes are the same. Whenever the
$K^{DJ}$
model is mentioned, for fixity we shall assume the former, modern, now standard, presentation.
In
$K^{DJ}$
there is a natural method of comparison of
$DJ$
-mice in
$H(\kappa )$
: iterate them all
$\kappa $
times, and the union thus obtained is the “Q-structure at
$\kappa $
”, and is of the form
$Q = Q(\kappa )=(J^{F_\kappa }_{\theta (\kappa )}, \in , F_\kappa )$
for some ordinal
$\theta (\kappa )$
where
$F_\kappa $
is the cub filter on
$\kappa $
, but which is an amenable iterable measure on Q. This is a useful structure to work with even if it does not conform to the modern notion of mouse. With sufficiently many
$\sharp $
’s in
$H(\kappa )$
,
$\theta (\kappa )$
can be (but is not always) the second ‘uniform indiscernible’ for bounded subsets of
$\kappa $
. But if it is then the critical points of the iterates of Q enumerate precisely these uniform indiscernibles.
All of this is in K the core model. However here in this paper we also step out of K and look at generalizations
$\bar{Q}(\kappa )$
(Definition 1.9) and similar characterisations that now generate the uniform indiscernibles in V. Roughly speaking the greater the ordinal height of
$\bar{Q}(\kappa )$
(corresponding to the earlier ordinal height
$\theta (\kappa )$
of
$Q(\kappa )$
in K) the ‘stronger’ the iterability properties instantiated in
$H(\kappa )$
.
If we approach from the other direction and ask if any subsets of
$\kappa $
(rather than bounded subsets of
$\kappa $
) can be put in sufficiently closed iterable structures
$(M,\in , U)$
(think of putting any subset of
$\kappa $
in a transitive
$\kappa $
-sized models
$M= {{\hspace {-0.0001pt}}}^{<\kappa }M$
with a wellfounded ultrapower map
$j:M\rightarrow N$
to get weak compactness) then we get a notion of iterable cardinal. This is of course weaker than measurability, but it is also weaker than Ramseyness ([Reference Sharpe and Welch12], Lemma 5.2) which requires (as Mitchell [Reference Mitchell11], Jensen [Reference Donder, Jensen, Koppelberg, Jensen and Prestel4] showed) not just that
$(M,\in , U)$
be iterable but that additionally U be
$\omega $
-closed.
Several of the theorems of [Reference Lücke8], [Reference Lücke, Schindler and Schlicht9] use as an iterability assumption that
$\kappa $
be an iterable cardinal. We observe here that instead one needs only something weaker: that a
$\Sigma _1$
-substructure N of
$H(\kappa ^+)$
be itself placed in such an iterable
$(M,\in , U)$
. This is the notion of being
$(\Sigma _1)$
-stably measurable. That this is not just some minor improvement resides in the fact that some of the properties turn out to be equiconsistent to stable measurability, or even equivalent in a canonical inner model such as
$K^{DJ}$
.
Theorem 2.6.
$(V=K^{DJ})$
$$\begin{align*}\sigma ( \kappa ) =u_{2} ( \kappa ) {\,\longleftrightarrow\,} \kappa\mbox{ has the } {\boldsymbol{\Sigma}}_{1}\mbox{-club}\mbox{ property }{\,\longleftrightarrow\,} \kappa \mbox{ is stably measurable. }\end{align*}$$
Our theorem in the analogous form to that which began this introduction is spread over the following two statements. We have:
Theorem 3.1. Let
$\Phi (\kappa )$
be the following sentence:
Assume
$\kappa $
is stably measurable. Then
$\Phi (\kappa )$
holds.
In one sense we have an equivalence:
Theorem 3.3. Assume
$V=K^{DJ}$
.
$$\begin{align*}\kappa\mbox{ is stably measurable }{\,\longleftrightarrow\,} \Phi(\kappa) \mbox{ is preserved by small forcings of size } < \kappa.\end{align*}$$
Corollary 3.6. Assume
$V=K^{DJ}$
(or
$V=K^{strong})$
. Then
$\exists \kappa \Phi (\kappa )$
is (set)-generically absolute if and only if there are arbitrarily large stably measurable cardinals.
Our theme in essence is to tease out the implications between the notions of stable measurability, good
$\boldsymbol {\Sigma }_1 (\kappa )$
-wellorders, and the length of the mouse order when working in
$L[E]$
models, or, when in V, the height of the
$\bar {Q}(\kappa )$
-structure which contains all the
$\kappa $
’th iterates of coarse ‘mouse-like’ objects in
$H(\kappa )$
.
In the final section we make some comments on inner model reflection by identifying the least
$L[E]$
models which reflect
$\Pi _{n}$
sentences into their inner models. Such a model is then not ‘pinned down’ by such a sentence (with ordinal parameters allowed). This phenomenon occurs before stable measurability, and can be seen to happen when
$u_{2}(\kappa )<\sigma (\kappa )$
, but the mouse order is sufficiently long to be beyond ‘admissible measurability’.
1.1. Stable measurability
Definition 1.1. We say that N is a
$\kappa $
-model if:
$\operatorname {Trans}(N)$
,
$\kappa \in N$
and
${} ^{<\kappa }N{ \,\subseteq \, } N$
.
Definition 1.2. Let
$\omega < \kappa \in \operatorname {Reg}$
. Then
$\kappa $
is
$\Sigma _{n}$
-stably measurable if, for some transitive
$M \prec _{\Sigma _{n}} H ( \kappa ^{+} )$
with
$M \supseteq H ( \kappa ) \cup \{ \kappa \}$
, there is a
$\kappa $
-model
$N\supseteq M$
and a filter F with
$( N, \in ,F ) \models $
“F is a normal measure on
${\mathcal {P}} ( \kappa )$
” so that
$( N, \in ,F )$
is amenable, and it is iterable, that is, has wellfounded ultrapowers by the measure F and its images. We say that (M and)
$( N, \in ,F )$
“witnesses
$\Sigma _n$
-stable measurability.”
The above is by way of analogy with the notion of admissibly measurable which was coined in [Reference Welch15]. This required only that M be the least transitive admissible set containing
$H ( \kappa ) \cup \{ \kappa \}$
and again with an appropriate filter F with wellfounded ultrapowers. In the above if
$n=1$
we just refer to stable measurability.
Definition 1.3. We say that
$\prec $
is a good
$\Sigma _{1}(p)$
-wellorder of
${\mathcal {P}}(\kappa )$
if
$\prec $
as a binary relation has a
$\Sigma _{1}(p)^{H ( \kappa ^{+} )}$
definition (in some parameter
$p\in H(\kappa ^{+})$
, and so that the set of all initial segments
$\{z \, | \, {\exists } x\in {\mathcal {P}}(\kappa ) \wedge z = \{y\, | \, y \prec x\}\}$
is a
$\Sigma _{1}(p)^{H ( \kappa ^{+} )}$
set.
Note: (i) If there is a good
$\Sigma _{1}^{H ( \kappa ^{+} )}(\{\kappa , p\})$
wellorder of
${\mathcal {P}} ( \kappa )$
, (for some
$p\in H(\kappa )$
) we can define
$\Sigma _{1}$
-Skolem functions in the usual manner and more readily define such an M. In some
$L [ E ]$
models this will be the case, and we shall use below the example of the Dodd–Jensen core model
$K=K^{\operatorname {DJ}}$
.
(ii) For
$\Sigma _1$
-stability
$( n=1 )$
we shall show that we can take N as an M which is itself a
$\Sigma _1$
elementary substructure. If
${\langle {N, \in ,F} \rangle }$
witnesses stable measurability at
$\kappa $
, we should just emphasise that without additional requirements, we cannot assume that it is an iterable premouse of any form of the usual definition(s) of premouse.
(iii) If
$\kappa $
is
$\Sigma _1$
-stably measurable then it is easily seen to be a Mahlo cardinal. (If there is a
$C{ \,\subseteq \, } \kappa $
a cub set of singular cardinals, then there is such in
$M\prec _{\Sigma _{1}}H(\kappa ^{+})$
. Now as M is contained in some iterable N if
$j:N{\,\longrightarrow \,} N'$
is the first ultrapower of N by the N-normal measure, then
$\kappa \in j(C)$
is singular in
$N'$
which leads to a contradiction.)
(iv) Just using the increased elementarity available it is easy to see that for any
$n \geqslant 2$
that
$\Sigma _{n}$
-stable measurability is equivalent to iterability. Hence we shall mostly be interested in
$\Sigma _{1}$
-stable measurability (and drop the “
$\Sigma _{1}\!$
”).
Definition 1.4. We set
$\sigma = \sigma ( \kappa ) = \operatorname {On} \cap M$
to be the least ordinal which is the height of a transitive M with
$M \prec _{\Sigma _{1}} H ( \kappa ^{+} )$
and
$M \supseteq H ( \kappa ) \cup \{ \kappa \}$
.
We shall remark below that our definition of stable measurability will ensure that there is such an M as a least
$\Sigma _{1}$
-substructure of
$( H ( \kappa ^{+} ) , \in )$
containing
$H ( \kappa ) \cup \{ \kappa \} ,$
even in the absence of some canonical wellorder, or canonically chosen skolem functions, for
$H ( \kappa ^{+} )$
.
Definition 1.5. Let
$M_{0}=M_{0}(\kappa ) {=_{\operatorname {df}}} \left \{ A \, | \, A { \,\subseteq \, } \kappa \wedge \{ A \} \right .$
is a
$\Sigma _{1} ( \kappa ,p )$
-singleton set for some
$ p \in H ( \kappa ) \}$
.
In the above we could have written
$\{ A \}$
is to be a
$\Sigma _{1}^{H ( \kappa ^{+} )} ( \kappa ,p )$
-singleton, by Levy-absoluteness.
Definition 1.6.
-
(i) For
$A { \,\subseteq \, } \kappa $
let
$\sigma _{A} {=_{\operatorname {df}}}$
the least
$\sigma> \kappa $
such that
$L_{\sigma } [ A ] \prec _{\Sigma _{1}} H ( \kappa ^{+} )^{L[A]}$
. -
(ii)
$\widetilde M=\widetilde{M}(\kappa ) {=_{\operatorname {df}}} \bigcup _{A \in M_{0}} L_{\sigma _{A}} [ A ]$
. -
(iii)
$ \widetilde{M}^{-}= \widetilde{M}^{-}(\kappa ) {=_{\operatorname {df}}} \bigcup \{ L_{\sigma _{a}} [ a ]\, | \, {a {{ \,\subseteq \, }} \gamma <\kappa ,\, a^{\sharp } \mbox { exists}}\}.$
The last definitions might seem peculiar at first glance, but they are suitable for analysing certain sets when we do not assume a good
${\boldsymbol {\Sigma }_1}(\kappa )$
-wellorder of
${\mathcal {P}}(\kappa )$
.
$\widetilde{M}$
can be thought of as an approximation to a
$\Sigma _{1}$
-substructure of
$H(\kappa ^{+})$
. Add a good
${\boldsymbol {\Sigma }_1}(\kappa )$
-wellorder and it will be (see Lemma 1.8 below). Moreover stable measurability of
$\kappa $
will imply (Lemma 1.15) that
$\widetilde{M} = \widetilde{M}^{-}$
. It is this last equality that prompts the idea that
$\Sigma _{1}$
-stability of
$\widetilde{M}$
is really about the bounded subsets of
$\kappa $
.
Lemma 1.7. Every
$x \in \widetilde{M}$
is coded by some
$B \in M_{0}$
.
Proof. Fix an
$x \in \widetilde{M}$
; there is thus some
$A \in M_{0}$
,
$\alpha < \sigma _{A}$
, with
$x \in L_{\alpha } [ A ]$
. Standard reasoning shows that there are arbitrarily large
$\beta < \sigma _{A}$
with
$J^{A}_{\beta +1} \models $
“
$\kappa $
is the largest cardinal” and so that there is a
$\Sigma ^{J^{A}_{\beta +1}}_{1}( A, \kappa )$
definable function
$f: \kappa {\,\longrightarrow \,} J^{A}_{\beta +1}$
. We may further assume that
$T,$
the
$\Sigma _{1}$
-
$\operatorname {Th} ( J^{A}_{\beta +1} , \in ,A )$
coded as a subset of
$\kappa $
is in fact a
$\Sigma _{1} ( \kappa ,A,q )$
singleton, for some
$q \in H ( \kappa )$
, and hence a
$\Sigma _{1} \left ( \kappa , {\langle } p,q {\rangle } \right )$
-singleton where
$\{ A \} \in \Sigma _{1} ( \kappa ,p )$
. (This is because we can take T as the unique
$\Sigma _{1}$
-Theory of a level in the
$L [ A ]$
hierarchy where some
$\Sigma _{1}$
sentence
$\psi ( q )$
about some
$q \in L_{\kappa } [ A ]$
first becomes true.) But then from the theory T we obtain f and then may define
${\langle {\operatorname {TC} ( \{ x \} ) , \in } \rangle } \cong B_{0} {=_{\operatorname {df}}} \left \{ {\langle {\xi _{0} , \xi _{1}} \rangle } \, | \, f ( \xi _{0} ) \in f ( \xi _{1} ) \in f ( \zeta ) \right \}$
for some
$\zeta < \kappa $
, if
$\{ x \} \in J^{A}_{\beta +1}$
. Coding
$B_{0}$
by Gődel pairing as subset of
$\kappa $
, B, we have
$\{ B \} \in \Sigma _{1} \left ( \kappa , {\langle {p,q, \zeta } \rangle } \right )$
and so
$B \in M_{0}$
as required. Q.E.D
Lemma 1.8. Suppose there is a good
$\Sigma _{1}^{H(\kappa ^{+})}(\kappa ,p)$
wellorder of
${\mathcal {P}}(\kappa )$
for some
$p\in H(\kappa )$
. Then
$\widetilde{M} \prec _{\Sigma _{1}}H(\kappa ^{+})$
.
Proof. Using the good wellorder we have
$\Sigma _{1}$
-skolem functions for
${\langle } H(\kappa ^{+}),\in\! {\rangle }$
which are themselves
${\Sigma _{1}}^{H(\kappa ^{+})}$
. Suppose that we have for each
$\Sigma _{1} \,\exists v_{0}\varphi (v_{0},v_{1})$
a skolem function
$f_{\varphi }$
so that for all
$A\subseteq \kappa $
if there is u so that
$\varphi (u,A)$
then
$H(\kappa ^{+}) \models \varphi (f_{\varphi }(A),A)$
holds. Suppose that
$\exists v_{0}\varphi (v_{0},A)$
holds with
$A\in M_{0}$
. Then we may assume that the witness u is itself a subset of
$\kappa $
which is a
$\Sigma _{1}(\kappa , A)$
singleton. This is because every set in
$H(\kappa ^{+})$
has cardinality there less than or equal to
$\kappa $
; given the good wellorder, we thus have for every u there is a least, in the sense of the wellorder, subset of
$\kappa $
, U say, that codes a u that witnesses
$\varphi (u,A)$
. Then
$\{U\}$
is a
$\Sigma _{1}(\kappa , A, p)$
-singleton, and so
$U \in M_{0}{ \,\subseteq \, } \widetilde{M}$
. Putting this together we have that
$(\exists v_{0}\varphi (v_{0},A))^{\widetilde{M}}$
. Q.E.D
1.2. On
$ \widetilde{Q}$
Definition 1.9. Let
${\widetilde{Q}}(\kappa )$
denote:
$$\begin{align*}\bigcup \{ N_{\kappa}\, | \, N_{\kappa} \mbox{ is the } \kappa\text{'} \mbox{th iterate of some amenable iterable } {\langle {N,\in, U} \rangle}\in H(\kappa)\}. \end{align*}$$
Under the hypothesis of the next lemma we shall have that
$\widetilde{{Q}}$
is rud. closed.
Lemma 1.10. Suppose all bounded subsets of
$\kappa $
have sharps. Then
$\widetilde{M}^{-}(\kappa ) = \widetilde{Q}(\kappa ) $
. Additionally any
$X\in {\mathcal {P}}(\kappa )^{\widetilde{{Q}}}$
either contains or is disjoint from a set cub in
$\kappa $
.
Proof.
$({ \,\subseteq \, })$
: If
$x \in {\widetilde{Q}}$
then for some
$a = {\langle } N,\in U{\rangle } \in H(\kappa )$
,
$x \in N_\kappa $
. But
$N_\kappa \in L_{\sigma _a}[a]$
. So
$x \in {\widetilde{M}^{-}}$
.
$(\supseteq )$
: Let
$x\in L_{\sigma _a}[a]\cap {\mathcal {P}}(\kappa )$
some
$a \in H(\kappa )$
. As
$a^\sharp $
exists, let
$N^a$
be the
$a^\sharp $
mouse. Then
$L_{\kappa '}[a]{ \,\subseteq \, } (N^a )_\kappa $
where
$\kappa '= (\kappa ^+ )^{L[a]}$
. As
$\sigma _a < \kappa '$
,
$x\in (N^a )_\kappa { \,\subseteq \, } {\widetilde{Q}}$
. This shows that any such x will be disjoint from, or contain a tail of the cub set of the sequence of iteration points of
$N^a$
.Q.E.D
Lemma 1.11. Suppose all bounded subsets of
$\kappa $
have sharps. Then (i)
$\widetilde{Q}$
is rudimentary closed; (ii)
${\langle {\widetilde{Q}},F_{\kappa } \rangle } $
is amenable and iterable, with
$F_{\kappa }\cap \widetilde{Q}$
a
$\widetilde{Q}$
-normal ultrafilter.
Proof. (i) As the rudimentary functions have as a generating set a finite set of binary functions [Reference Jensen6], it suffices by the last lemma, since each
$L_{\sigma _{a}}[a]$
is rud. closed (it is an admissible set), to show that if
$X,Y\in \widetilde{Q}$
, that there is c a bounded subset of
$\kappa $
with
$X,Y\in L_{\sigma _{c}}[c]$
. By our supposition any
$a\in H(\kappa )$
is a member of the least a-mouse generating
$a^{\sharp }$
,
$N^{a}$
, and moreover
$L_{\sigma _{a}}[a]\in N^{a}_{\kappa }$
, the
$\kappa $
’th iterate of
$N^{a}$
. But then it is trivial that if
$\{X\}\in N^{a}$
and
$\{Y\}\in N^{b}$
then
$\{X,Y\}\in N^{a\oplus b}\in \widetilde{Q}$
as
$L_{\sigma _{a}}[a] \cup L_{\sigma _{b}}[b]{ \,\subseteq \, } L_{\sigma _{a\oplus b}}[a\oplus b]$
.
For (ii): That
$F_\kappa $
measures
${\mathcal {P}}(\kappa )\cap \widetilde{Q}$
is the last corollary. For amenability just note that any
${\langle {Z_{\nu }\, | \, \nu <\kappa } \rangle } \in L_{\sigma _{a}}[a]$
is again in
${\langle {N^{a}_{\kappa }, F_{\kappa }\cap N^{a}_{\kappa }} \rangle } $
. But the latter structure is amenable, (this is true of any a-mouse) and so
$\{\nu \, | \, Z_{\nu }\in F_{\kappa }\}\in N^{a}_{\kappa }\in \widetilde{Q}$
. Normality of
$F_{\kappa }\cap \widetilde{Q}$
in
$\widetilde{Q}$
is similar, and iterability follows from the countable closure of
$F_{\kappa }$
. Q.E.D
For notation we set
$I^{c}$
, the closed and unbounded class of Silver indiscernibles for
$L [ c ]$
, to be enumerated as
${\langle {\iota _{\alpha }^{c} \, | \, \alpha \in \operatorname {On}} \rangle }$
for c a set of ordinals.
Definition 1.12. Suppose for every bounded subset
$b $
of
$\kappa $
,
$b^{\#} $
exists. Then set
$$\begin{align*}u_{2} ( \kappa ) = \sup \{ \iota^{b}_{\kappa +1} \, |\, b \mbox{ a bounded subset of } \kappa \} .\end{align*}$$
More generally:
$$\begin{align*}{\langle { u_{\iota} ( \kappa )\, | \, 0<\iota \in On} \rangle}\end{align*}$$
enumerates in increasing order
$\bigcap \{ I^{b}\, | \, b \mbox { a bounded subset of } \kappa \}.$
Then this is by way of analogy for the second uniform indiscernible for the reals, but now for bounded subsets of
$\kappa $
. By the same arguments as for reals,
$u_{2} ( \kappa )$
is also
$\sup \{ \kappa ^{+L [ b ]} \, | \, b \in H ( \kappa ) \cap {\mathcal {P}} ( \kappa ) \} $
. Indeed, as is well known, for any successor
$\iota +1$
:
$$\begin{align*}u_{\iota +1}= \sup \{ u_{\iota}^{+L [ b ]} \, | \, b \mbox{ a bounded subset of } \kappa \} = \sup \{ \iota^{b}_{u_{\iota}+1} \, | \, b \mbox{ a bounded subset of } \kappa \} .\end{align*}$$
It is an exercise in the use of sharps to add to this that
$$\begin{align*}u_{2}(\kappa)= \sup \{ \sigma_b \, | \, b \mbox{ a bounded subset of } \kappa \}.\end{align*}$$
The size of
$u_{2}(\kappa )$
with reference to
$\kappa $
, gives, roughly speaking, the length of the mouse order on
$H ( \kappa )$
. Indeed in
$L [ E ]$
models (at least below a strong cardinal) this can be made precise. Thus the next lemma interpreted in for example, the Dodd–Jensen core model
$K^{\operatorname {DJ}}$
, is declaring the length of the mouse order restricted to
$H ( \kappa )$
there, as somewhat long. In fact it will turn out to be maximal for this model.
Lemma 1.13. Suppose that
$H(\kappa )$
is closed under sharps. Then the critical points of the iterated ultrapowers of
${\langle {\widetilde{Q},F_{\kappa }} \rangle } $
are the uniform indiscernibles
${\langle {u_{\iota }(\kappa )\, | \, 0 < \iota \in On} \rangle } .$
Moreover if
${\langle {\widetilde{Q}_{\alpha },F^{\alpha }} \rangle }_{\alpha \in On} $
is the iteration of
${\langle {\widetilde{Q}_{1},F^{1}} \rangle } = {\langle {\widetilde{Q}},F_{\kappa } \rangle } $
, with iteration maps
$j_{\alpha ,\beta }\, (1\leqslant \alpha < \beta \in On)$
, and critical points
$\lambda _{\alpha }(1\leqslant \alpha \in On)$
then
$$ \begin{align} u_{\alpha}(\kappa) &= \lambda_{\alpha.} \end{align} $$
$$ \begin{align} u_{\alpha +1}(\kappa) & = {\widetilde Q}_{\alpha} \cap On. \end{align} $$
Proof. First we note that as
${\langle {{\widetilde Q},F_{\kappa }} \rangle } = {\langle {{\widetilde Q}_{1},F^{1}} \rangle }$
is a rudimentary closed structure, we can prove a Los Theorem for its ultrapowers and the usual result for such a structure that it is a
$\Sigma _{0}$
preserving embedding which is cofinal (that is if
$k:{\langle {{\widetilde Q},F_{\kappa }} \rangle } {\,\longrightarrow \,} Ult ({\widetilde Q},F_\kappa )$
, and if
$\pi :Ult ({\widetilde Q},F_\kappa ){\,\longrightarrow \,} ({\widetilde Q}_{2},F^{2})$
is the transitive collapse map, then taking
$j= j_{1,2}=\pi \circ k$
we have that
$\forall x\in {\widetilde Q}_2\exists y \in {\widetilde Q} ( x{ \,\subseteq \, } j(y))$
). Thus j is in fact
$\Sigma _{1}$
-preserving. Note that by the amenability of
${\langle {{\widetilde Q},F_{\kappa }} \rangle } $
,
${\mathcal {P}}(\kappa )\cap {\widetilde Q} = {\mathcal {P}}(\kappa )\cap {\widetilde Q}_{2}$
. Suppose now
$[f] < [c_{\kappa }]$
in
$Ult ({\widetilde Q},F_\kappa )$
. Thus
$f\in {\widetilde Q}, \, f:\kappa {\,\longrightarrow \,} On \cap {\widetilde Q}$
and by normality, with
$\{\xi \, | \, f(\xi )< \kappa \}\in F_{\kappa }$
. Thus for
$a \in H(\kappa )\cap {\mathcal {P}}(\kappa )$
we shall have
$f\in L_{\sigma _{a}}[a]$
. By Silver indiscernibility
$f(\xi ) = h^{L[a]}(i,a, \vec \gamma , \xi , \vec \gamma ')$
for some
$\vec \gamma , \vec \gamma ' \in [I^{a}]^{{<\omega }}$
with
$\operatorname {max}(\vec \gamma ) \leqslant \xi <\operatorname {min}(\vec \gamma '))$
and
$h^{L[a]}$
a canonical
$\Sigma _{1}$
-skolem function for
$(L[a],\in , a)$
. But going to
$a^{\sharp }$
we shall have
$f(\xi ) = h^{L[a^{\sharp }]}(i',a, \vec \gamma , \xi )$
for some
$i'$
. In particular
$f(\xi )<\gamma ' =g(\xi ){=_{\operatorname {df}}} \operatorname {min} I^{a^{\sharp }}\backslash \operatorname {max}(\vec \gamma , \xi ) +1$
. Let
$\gamma _{0}' {=_{\operatorname {df}}} \operatorname {min} I^{a^{\sharp }}\backslash (\kappa +1)$
. Then
$\gamma _{0}' < On \cap \bar {Q} _{1}$
. But then we have that
$[f] < [g]$
and
$j(f)(\kappa )<j(g)(\kappa )< \gamma _{0}' < On \cap \bar {Q} _{1}$
. This shows that
$j(\kappa ) \leqslant On \cap \bar {Q} _{1}$
. But clearly as well
$j(\kappa ) \geqslant On \cap \bar {Q} _{1}$
.
Thus (recalling that
$\lambda _{1} = \kappa $
and
$ {\widetilde Q}_{1}={\widetilde {Q}} $
):
$$\begin{align*}u_2(\kappa) = \operatorname{sup}\{\iota^{a}_{\lambda_{1}+1}\, | \, a \in H(\kappa)\cap {\mathcal{P}}(\kappa)\} = \operatorname{sup}\{\sigma_{a}\, | \, a \in H(\kappa)\cap {\mathcal{P}}(\kappa)\} = On \cap {\widetilde Q}_{1} .\end{align*}$$
But we have just seen that
$j_{1,2}(\lambda _{1})=\lambda _{2}= On \cap {\widetilde Q}_{1}.$
This establishes (1) for
$\alpha = 2$
, and (2) for
$\alpha = 1$
, and the reader can deduce the cases for larger
$\alpha $
from this. Q.E.D
This then gives a simple expression for the uniform indiscernibles of the bounded subsets of
$\kappa $
: they are the iteration points of
$ {\langle {{\widetilde Q},F_{\kappa }} \rangle } $
as well as (their successor) elements being the ordinal height of the ultrapowers. (The reader will recall that under
$AD$
, in
we have that for reals,
$u_{2}=\aleph _{2}$
and the ultrapower of
${\langle {u_{1},<} \rangle }/ F_{\omega _{1}}$
is
$u_{2}$
.) The following is well known for reals but follows immediately from the above:
Corollary 1.14.
$\operatorname {cf}(u_{\alpha +1}(\kappa )) =\operatorname {cf}(u_{2}(\kappa )) $
.
Proof.
$j_{1,\alpha }$
“
$On \cap {\widetilde {Q}}_{1}$
is cofinal in
$On \cap {\widetilde {Q}}_{\alpha }$
. Q.E.D
The point of the next lemma is that although
${\widetilde M}$
is ostensibly about the collection of
$\Sigma _{1}$
-singleton subsets of
$\kappa $
, with the assumption of stable measurability, considerations about it reduce to the
$\Sigma _{1}$
-stable parts of bounded subsets of
$\kappa $
.
Lemma 1.15. Suppose
$\kappa $
is stably measurable. Then
${\widetilde M}={\widetilde Q}$
.
Proof. We first remark that
$\kappa $
being stably measurable implies all bounded subsets of
$\kappa $
have sharps.
$(\, \supseteq \,)$
is straightforward.
$\left ( { \,\subseteq \, } \right )$
:
${\widetilde M}$
is clearly transitive. Let
$x \in {\widetilde M}$
and by Lemma 1.7 let it be coded by some
$X \in M_{0}$
. Let
${\langle {M, \in ,F} \rangle }$
witness stable measurability. Then for some
$p \in H ( \kappa )$
,
$\{ X \} \in \Sigma _{1}^{M} ( \kappa ,p )$
. Then find some
${\langle {N, \in ,F_{0}} \rangle }\prec {\langle {M, \in ,F} \rangle }$
with
$| N | < \kappa $
,
${\langle {N, \in ,F_{0}} \rangle } \models $
“
$F_{0}$
is a normal measure on
$\bar {\kappa }$
”, and
$X \cap \bar {\kappa } \in N_{0}$
,
$p \in H ( \bar {\kappa } )^{N}$
. By elementarity
$\{ X \cap \bar {\kappa } \}$
is a
$\Sigma ^{{\langle {N, \in } \rangle }}_{1} \{ \bar {\kappa } ,p \}$
singleton by the same definition as
$\{ X \}$
was. As
${\langle {M, \in ,F} \rangle }$
is iterable, so is
${\langle {N, \in ,F_{0}} \rangle }$
and if
$j_{\alpha , \beta } ( 0 \leqslant \alpha \leq \beta \in \operatorname {On} )$
are its (
$\Sigma _{1}$
-preserving) iteration maps, we shall have that
$\{ j_{0, \kappa } ( X \cap \bar {\kappa } ) \}$
satisfies the same definition as that of
$\{ X \}$
in
$N'$
where
$j_{0, \kappa } :N {\,\longrightarrow \,} N'$
. That is:
$j_{0, \kappa } ( X \cap \bar {\kappa } ) =X$
. Note also that
$N' \in {\widetilde Q}={{\widetilde M}}^{-}$
, as
$N' \in L_{\sigma _{N}} [ N ]$
. Thus X and so x are in
$L_{\sigma _{N}} [ N ]$
and we are done. Q.E.D
Lemma 1.16. If
$\kappa $
is stably measurable, then it is witnessed to be so by
$({\widetilde M}, \in ,F )$
where
$( {\widetilde M}, \in )$
is as above; in particular
${\langle } {\widetilde M}, \in\! {\rangle }\prec _{\Sigma _{1}}{\langle } H(\kappa ^{+}),\in\! {\rangle }$
itself and
$F=F_{\kappa } \cap M$
where
$F_{\kappa }$
is the c.u.b. filter on
${\mathcal {P}} ( \kappa). $
Thus
$({\widetilde M}, \in ,F_{\kappa } ) \models $
“
$F_{\kappa }$
is the c.u.b. filter and is a normal measure on
$\kappa $
”.
Proof. We first show that
${\langle } {\widetilde M}, \in\! {\rangle }\prec _{\Sigma _{1}}{\langle } H(\kappa ^{+}),\in\! {\rangle }$
: by assumption there is some
${\langle } M, \in\! {\rangle }\prec _{\Sigma _{1}}{\langle } H(\kappa ^{+}),\in\! {\rangle }$
, some
$\kappa $
-model
$N\supseteq M$
, and some U with
${\langle } N, \in , U{\rangle }$
witnessing stable measurability. Then
${\widetilde M} { \,\subseteq \, } M$
(because
$M_{0}{ \,\subseteq \, } M$
), so suppose that
${\langle } {\widetilde M}, \in\! {\rangle}$
is not a
${\Sigma _{1}}$
substructure of
${\langle } M, \in\! {\rangle }.$
Let
$\varphi (A,\kappa , a)^{M}$
but, for a contradiction,
$\neg \varphi (A,\kappa , a)^{{\widetilde M}}$
, for some
$A{ \,\subseteq \, } \kappa $
,
$A\in {\widetilde M}$
where
$A\in M_{0}$
, and parameter
$a\in H_{\kappa }$
. There is some
$\psi \in \Sigma _{1}$
so that
$\psi (A',\kappa ,b)$
defines uniquely
$A' =A$
as a
$\Sigma _{1}(\kappa ,b)$
singleton. By
$\Sigma _1 $
-elementarity,
$\psi (A',\kappa ,b)$
holds in M and by upwards persistence both it and
$\varphi (A,\kappa , a)$
hold in N too. By the same argument find
${\langle } N',\in , U\cap N' {\rangle } \prec {\langle } N, \in , U{\rangle }$
with
$\operatorname {TC}(\{a\}\cup \{b\}), A \in N'\cap \kappa = \kappa _{0}\in \kappa $
. Let
${\langle } N_{0},\in , V_{0}{\rangle } $
be its transitive collapse with
$V_{0}$
now an
$N_{0}$
-normal measure on
$\kappa _{0}$
. Then iterate
${\langle } N_{0},\in , V_{0}{\rangle } $
to
${\langle } N_{\kappa },\in , V_\kappa {\rangle } $
with some map
$j_{0,\kappa }$
now satisfying
$\varphi ( j_{0, \kappa } ( A \cap {\kappa }_{0} ),\kappa , a)^{N_{\kappa }}$
. But
$N_{\kappa }\in {\widetilde M}$
, and also
$\psi (j_{0, \kappa } ( A \cap {\kappa }_{0} ),\kappa ,b)^{N_{\kappa }}$
. By uniqueness of A’s definition via
$\psi $
and upwards absoluteness of
$\Sigma _{1}$
formulae,
$j_{0, \kappa } ( A \cap {\kappa }_{0} ) = A$
. But then
$\varphi (A,\kappa ,a)^{{\widetilde M}}$
—a contradiction.
We just saw that any
$X \in {\widetilde M} \cap {\mathcal {P}} ( \kappa )$
is of the form
$j_{0, \kappa } ( X \cap {\kappa }_{0} )$
for some iteration map
$j_{0, \kappa } : ( N,F_{0} ) {\,\longrightarrow \,} ( N' ,F' )$
by repeating ultrapowers by an N-normal measure. Thus
$X=j_{0, \kappa } ( X \cap {\kappa }_{0} )$
either contains, or is disjoint from a tail of the critical points of the embeddings
$j_{\alpha , \alpha +1}$
for
$\alpha < \kappa $
. As these critical points form a c.u.b subset of
$\kappa $
, definable from
$N \in H ( \kappa )$
, and which is thus in
${\widetilde M}$
,
$F_\kappa $
is thus a measure on
${\widetilde M}$
. For amenability, let
${\langle } X_{\nu }{\rangle } _{\nu <\kappa } \in {\widetilde M} $
be a sequence of subsets of
$\kappa $
. Let it be coded by some
$X{ \,\subseteq \, } \kappa $
,
$X\in {\widetilde M}$
, and as above have X (and thus
${\langle } X_{\nu }{\rangle } _{\nu <\kappa }$
) in some
$N'$
,
$X=j_{0, \kappa } ( X \cap {\kappa }_{0} )$
etc. as above.
$( N' ,F' )$
is amenable and
$F'$
is generated by the tail filter on the cub in
$\kappa $
set of the critical points. But then
$\{\nu \, | \, X_{\nu }\in F' \} = \{\nu \, | \, X_{\nu }\in F_{\kappa } \}\in N'\in {\widetilde M}$
, and amenability is proven. The proof of
${\widetilde M}$
-normality is similar.
Finally note that
${{\hspace {-0.0001pt}}}^{<\kappa }{\widetilde M}{ \,\subseteq \, } {\widetilde M}$
: suppose
$f:\alpha {\,\longrightarrow \,} {\widetilde M}$
for some
$\alpha <\kappa $
. As
${\widetilde M} = {\widetilde Q}$
, each
$f(\xi )$
is in
$L_{\sigma _{a(\xi )}}$
for some
${a(\xi )}$
a bounded subset of
$\kappa $
. However now code
${\langle } a(\xi ){\rangle }_{\xi <\alpha }$
by some a still a bounded subset of
$\kappa $
. Then
${\rangle }(f)\in L_{\sigma (a)}{ \,\subseteq \, } {\widetilde M}$
. Q.E.D
We thus can, and do, assume that
${\langle } {\widetilde M}, \large {\in } , F_{\kappa } \cap {\widetilde M}{\rangle }$
witnesses stable measurability, if it occurs.
Corollary 1.17.
$\kappa $
stably measurable implies
${\langle } {\widetilde M}, \large {\in }{\rangle }$
is the minimal
$\Sigma _{1}$
-substructure of
${\langle } H(\kappa ^{+}),\in\! {\rangle }$
containing
$\{\kappa \}\cup H(\kappa )$
, and
$\sigma (\kappa )=On\cap {\widetilde M}$
.
Proof. Any such
$\Sigma _{1}$
-substructure of
${\langle } H(\kappa ^{+}),\in\! {\rangle }$
must contain
$\bigcup _{a \in H ( \kappa )} L_{\sigma _{a}} [ a ]$
, which we have just seen equals
${\widetilde M}$
. Q.E.D
Corollary 1.18.
$\kappa $
stably measurable implies that for every
$A { \,\subseteq \, } \kappa $
, with
$ A \in {\widetilde M} $
,
$A^{\#}$
exists, and is in
${\widetilde M}$
.
Proof. Again let
$A= j_{0, \kappa } ( A \cap \bar {\kappa } )$
for some iteration
$j_{0, \kappa } : ( N,F_{0} ) {\,\longrightarrow \,} ( N' ,F' )$
. As
$( N' ,F' ) \in L_{\sigma _{N}} [ N ]$
, so are the next
$\omega $
-many iterates
$j_{\kappa , \kappa + \omega } : ( N' ,F' ) {\,\longrightarrow \,} ( \widetilde{N} ,G )$
(because
$( N' ,F' )\in L_{\sigma _{N}} [ N ]$
and the latter is an admissible set); but these critical points above
$\kappa $
,
${\langle {\kappa _{\kappa +i} \, | \, 0<i< \omega } \rangle }$
are Silver indiscernibles for
$L [ A ]$
and are below
$\sigma _{N}$
. Thus
$A^{\#}$
, either thought of as an A-mouse or coded as a subset of
$\kappa $
, can be constructed in
$L_{\sigma _{N}} [ N ]$
and is thus in
${\widetilde M}$
. Q.E.D
Lemma 1.19.
$\mbox {If there is a good } \Sigma _{1}(\kappa ,p)$
wellorder of
${\mathcal {P}}(\kappa )$
for some
$p\in H(\kappa )$
then:
$$\begin{align*}\kappa \mbox{ is stably measurable } {\,\Longleftrightarrow\,} {\widetilde M} = {{\widetilde M}}^{-}.\end{align*}$$
Proof. The direction
$(\Rightarrow )$
is Lemmata 1.10 and 1.15 and does not require the additional assumption. For
$(\Leftarrow )$
: first suppose that
${\widetilde M} = {{\widetilde M}}^{-}$
; then notice trivially for every
$a{ \,\subseteq \, } \gamma <\kappa $
there is the least a-mouse,
$N^{a}$
, witnessing that
$a^{\sharp }$
exists. And its
$\kappa $
’th iterate
$N_{\kappa }^{a}\in {\widetilde Q}$
(
$= {{\widetilde M}}^{-}$
) and
$\sigma _{a} < \kappa ^{+ L[a]}= On \cap N^{a}_{\kappa }$
. In particular
$L_{\sigma _{a}}[a]\in {\langle {N_{\kappa }^{a},F^{a}} \rangle } $
where
$F^{a}=F_{\kappa }\cap N_{\kappa }^{a}$
. Consequently
${\langle {{\widetilde Q}, F_{\kappa }} \rangle }\models $
“
$F_{\kappa }$
is a normal ultrafilter on
$\kappa $
”. By the existence of the good
$\Sigma _{1}$
-wellorder, Lemma 1.8 states that we have that
${\widetilde M} \prec _{\Sigma _{1}}H(\kappa ^{+})$
and
${\langle {{\widetilde M}, F_{\kappa }} \rangle }$
witnesses stable measurability. Q.E.D
In fact there is more to be said on the sharps in
${\widetilde M}$
.
Lemma 1.20. Let
$\kappa $
be stably measurable. Then
$u_{2} ( \kappa ) = \sigma ( \kappa )$
.
Proof.
$( \leqslant )$
Let
$a \in H ( \kappa )$
be a set of ordinals. Then
$a^{\#}$
(which exists by Corollary 1.18), considered as the least a-mouse
$( \bar {N}^{a} , \in , \bar {U} )$
is in
$H ( \kappa $
) and can be iterated
$\kappa +1$
many times, inside
$L_{\sigma _{\alpha ^{\#}}} [ a^{\#} ] { \,\subseteq \, } {\widetilde M}$
. If these iterations points are
$\{ \lambda _{\alpha } \}_{\alpha \leqslant \kappa +1}$
then as above these are Silver indiscernibles for
$L [ a ]$
and thus
$\lambda _{\kappa +1} = \iota _{\kappa +1}^{a} < \sigma _{\alpha ^{\#}} < \text{On } \cap\ {\widetilde M} = \sigma .$
$( \geqslant )$
Just note that for any
$\gamma < \sigma = \operatorname {On} \cap \, {\widetilde M}$
there is, by Lemma 1.15, some
$a \in H ( \kappa )$
with
$\gamma < \sigma _{a} \leqslant \sigma .$
But
$a^{\#}$
exists and then
$\gamma < \sigma _{a} < \kappa ^{+L [ a ]} < u_{2}$
. Q.E.D
However the converse of the last lemma may fail: suppose (for
$\kappa = \omega _1$
) that
$u_2(\omega _{1}) =\omega _2$
(which it may, by a result of Woodin, if there is a measurable cardinal and
$NS_{\omega _1}$
is saturated); but then also
$\sigma (\omega _1) = \omega _2$
. It is easy to see that
$\kappa $
stably measurable implies that
$\kappa $
is Mahlo (see Note (iii) after Definition 1.3 above). Hence in general
$u_2(\kappa ) = \sigma (\kappa ) \not \!\!\!\!\!\! {\,\longrightarrow \,} \kappa $
is stably measurable. But we may ask for a converse under the assumption that
$\kappa $
is inaccessible.
The following is similar to Lücke 7.1(ii) showing weakly compact cardinals with the
$\boldsymbol {\Sigma }_{1}$
-club property (to be defined below) reflect on a stationary set.
Lemma 1.21. If
$\kappa $
is weakly compact and stably measurable, then the set of cardinals
$\alpha $
below
$\kappa $
which are stably measurable is stationary.
Proof. Let
${\langle } \bar {M}^{\kappa },F_{\kappa }{\rangle }$
witness the stable measurability of
$\kappa $
. Thus
. Let
$C{ \,\subseteq \, } \kappa $
be cub. Choose
$M \prec H(\kappa ^{+})$
with
$|M|=\kappa $
and
and
$ {} ^{<\kappa }M { \,\subseteq \, } M$
with some elementary map
$j:M{\,\longrightarrow \,} N$
, with critical point
$\kappa $
as given by weak compactness. Note that
. In general
$H(\kappa ^{+}))^{M}\subsetneq ( H(\kappa ^{+}))^{N}$
, but
${\mathcal {P}}(\kappa )^{M}{ \,\subseteq \, } N$
(and
$(F_\kappa )^M{ \,\subseteq \, } (F_\kappa )^N$
). As
is an element of
$H(\kappa ^{+}))^{M} $
it is in N. We claim:
Claim:
and thus
witnesses stable measurability of
$\kappa $
in N.
If the claim holds then
$N\models $
But then there is some
$\alpha \in C$
with
witnessing stable measurability, and we are done.
Proof of Claim Let
with
$\varphi (\vec{A})^{N}$
. By upwards absoluteness:
$\varphi (\vec{A})^{H(\kappa ^{+})}$
and then by downwards
$\Sigma _{1}$
-elementarity:
.Q.E.D
The next result says that stable measurability is easily propagated upwards; but is perhaps less surprising when one realises that stable measurability at
$\kappa $
is more about the bounded subsets of
$\kappa $
. [Reference Lücke8], Theorem 7.4 has that a stationary limit of iterable cardinals has the
${\boldsymbol {\Sigma } _{1}}\operatorname {-club}$
property (to be defined below). We have a weaker hypothesis and a stronger conclusion.
Theorem 1.22. If
$\kappa $
is the stationary limit of stably measurable cardinals, then
$\kappa $
is stably measurable.
Proof. Using
$AC$
, choose S a
$\Sigma _{1}$
-satisfaction predicate for
${\langle } H(\kappa ^{+}),\in\! {\rangle }$
. Choose
${\langle {X,\in , S\cap X} \rangle } \prec {\langle {H(\kappa ^{+}),\in , S} \rangle } $
with
$X\cap \kappa \in \kappa $
, and
$H(X\cap \kappa ){ \,\subseteq \, } X$
(note
$\kappa $
is a strong limit), and letting
$\pi : {\langle {X, X\cap S} \rangle } {\,\longrightarrow \,} {\langle {\bar H, \bar S} \rangle } $
be the transitive collapse, let
$\pi (\kappa ) = \bar \kappa $
. By assumption we may additionally assume that
$\bar \kappa $
is stably measurable. Then, let
(the latter since by assumption all bounded subsets of
$\kappa $
will have sharps); the sets of the right hand side here are all contained in
$\bar H$
. Then
and is definable there. By the stable measurability of
$\bar \kappa $
, i.e. using that
, and the inclusion
, and noting that
$\bar S$
codes
$\Sigma _{1}$
-satisfaction over
${\langle {\bar H,\in } \rangle }$
, we have that
Applying
$\pi ^{-1}$
we have
. We then have:
$$\begin{align*}{\langle {H(\kappa^{+}),S} \rangle} \models \, {\widetilde{Q}}(\kappa) \prec_{\Sigma_{1}} V\, \wedge {\langle {{\widetilde{Q}}(\kappa), F_{\kappa}} \rangle}\models\mbox{``} F_{\kappa}\mbox{ is a normal measure on }\kappa\mbox{''.}\end{align*}$$
In other words,
${\langle {{\widetilde {Q}}(\kappa ), F_{\kappa }} \rangle }$
witnesses that
$\kappa $
is stably measurable. Q.E.D
We now relate stable measurability and its analysis above to Lücke’s notion of the
${\boldsymbol {\Sigma } _{1}}$
-club property.
Definition 1.23. (Lücke [Reference Lücke8], Lemma 4.1)
$\kappa $
has the
${\boldsymbol {\Sigma } _{1}}\operatorname {-club}$
property if, for any
$A { \,\subseteq \, } \kappa $
so that
$\{ A \} \in \Sigma ^{{\hspace {-0.0001pt}}}_{1} ( \kappa ,z )$
where
$z \in H ( \kappa )$
, then A contains or is disjoint from a club subset of
$\kappa $
.
(Actually this is not Lücke’s basic definition, but he shows this is equivalent to it.) Note that by ‘
$\Sigma _{1} ( \kappa ,z )$
definable’, we can take this to mean
$\Sigma _{1}^{H ( \kappa ^{_{+}} )} ( \kappa ,z )$
-definable, by Lőwenheim–Skolem and upwards absoluteness arguments.
We introduced in [Reference Sharpe and Welch12] the following notion when discussing variants of Ramseyness.
Definition 1.24.
$\kappa $
is called (
$\omega _{1}$
-)iterable if for any
$A { \,\subseteq \, } \kappa $
there is a transitive set M, and filter U, with
$A \in M$
and
$( M, \in ,U ) \models $
“
$ U$
is a normal measure”; further it is amenable, iterable by U and has wellfounded ultrapowers.
(In [Reference Sharpe and Welch12] this was rather obscurely called the Q property.) It was shown there (op. cit. Lemma 5.2) to be strictly weaker than Ramseyness: that would require additionally that the filters U be
$\omega $
-closed. One can show that an
$\omega _{1}$
-Erdos cardinal is a stationary limit of
$\omega _{1}$
-iterable cardinals (see [Reference Sharpe and Welch12], Lemma 5.2). But notice that iterability is clearly stronger than stable measurability: every subset of
$\kappa $
must be in some iterable structure, not just the
$\Sigma _{1} ( \kappa )$
-singletons. Lücke shows the following:
Theorem 1.25. (Lücke [Reference Lücke8], Corollaries 4.12 and 4.5)
-
(i)
$\kappa $
iterable
${\,\Rightarrow \,} $
the
$\boldsymbol {\Sigma }_{1}$
-club property holds at
$\kappa $
. -
(ii) The
$\boldsymbol {\Sigma }_{1}$
-club property at
exists).
We remark later that the gap above can be closed by showing that the
$\boldsymbol {\Sigma }_{1}$
-club property is equiconsistent with stable measurability. However first we may show outright:
Theorem 1.26.
$\kappa $
has the
$\boldsymbol {\Sigma }_{1}$
-club property, if
$\kappa $
is stably measurable.
Proof. We’ve seen above at Corollary 1.16 that if
$\kappa $
is stably measurable, then it is witnessed to be so by
$({\widetilde M}, \in ,F_{\kappa } \cap {\widetilde M} )$
; but the latter contains
$ M_{0}$
so this suffices.
Q.E.D
The converse can be false:
Lemma 1.27.
$ZFC\not \vdash $
$\kappa $
is strongly inaccessible and has the
$\boldsymbol {\Sigma }_{1}$
-club property
${\,\longrightarrow \,} \kappa $
is stably measurable.
Proof. Lücke points out in [Reference Lücke8], Corollary 7.3, that if
$\kappa $
is a regular limit of measurables, then the
$\boldsymbol {\Sigma }_{1}$
-club property holds. But such a
$\kappa $
need not be Mahlo, and so not stably measurable. Q.E.D
However conversely, we do have (and by the above, some assumption in the next lemma is necessary):
Lemma 1.28. Assume there is a good
${\boldsymbol {\Sigma }_{1}}(\kappa )$
-WO of
${\mathcal {P}}(\kappa )$
. Then
$\kappa $
has the
$\boldsymbol {\Sigma }_{1}$
-club property implies
$\kappa $
is stably measurable.
Proof. That
$\kappa $
has the
$\boldsymbol {\Sigma }_{1}$
-club property ensures, by an application of Lemma 1.7 that
$F_{\kappa }$
measures
${\mathcal {P}}(\kappa )\cap {\widetilde M}$
. The regularity of
$\kappa $
implies the countable closure of
$F_{\kappa }$
which in turn guarantees the iterability of
${\langle {{\widetilde M}, \in , F_{\kappa }} \rangle }$
. That there is a good
${\boldsymbol {\Sigma }_{1}}(\kappa )$
-WO of
${\mathcal {P}}(\kappa )$
will ensure that
${\widetilde M} \prec _{\Sigma _{1}}H(\kappa ^{+})$
. Q.E.D
Putting the argument of the last lemma together with the fact that stably measurable cardinals are Mahlo, one can conclude:
Corollary 1.29. If
$\kappa $
is a regular cardinal which is not Mahlo, but is a limit of measurable cardinals, then there fails to be a good
${\boldsymbol {\Sigma }_1}(\kappa )$
-wellorder of
${\mathcal {P}}(\kappa )$
.
In fact [Reference Lücke and Schlicht10], Corollary 1.4 show this directly for all regular limits of measurables, but only for lightface
$\Sigma _1(\kappa )$
good wellorders.
2. Stable measurability in
$L[E]$
-models
We consider what happens when stable measurability is instantiated in models with fine structure. The outcome is an equivalence between the notions considered.
2.1. When
$K=K^{DJ}$
We let in this subsection
$K=K^{\operatorname {DJ}}$
. We shall show that the stable measurability is downward absolute to K.
We note first:
Lemma 2.1.
$(V=K^{DJ})$
${\widetilde M} \prec _{\Sigma _{1}}H(\kappa ^{+})$
.
Proof. By Lemma 1.8, as in
$K^{DJ}$
we have a good
$\Sigma _{1}^{H(\kappa ^{+})}(\kappa )$
wellorder
$<$
of
${\mathcal {P}}(\kappa )$
.
Q.E.D
We then relate
${\widetilde {Q}} (\kappa )$
to an older notion.
Definition 2.2. (The Q-structure at
$\kappa $
)[Reference Dodd3] In K, let
$Q ( \kappa ) {=_{\operatorname {df}}} {\langle {J^{F_{\kappa }}_{\theta ( \kappa )} , \in ,F_{\kappa }} \rangle }$
be the union of the
$\kappa $
’th iterates of all DJ-mice
$M \in H ( \kappa )$
.
As the measure of each such
$\kappa $
-iterate
$M_{\kappa }$
of such a DJ-mouse
$M \in H ( \kappa )$
, is generated by the tail sequence filter of its closed and unbounded in
$\kappa $
sequence of critical points, the measure on
$ M_{\kappa }$
is just
$F_{\kappa } \cap M_{\kappa }$
, and thus
$M_{\kappa }$
is of the form
${\langle {J^{F_{\kappa }}_{\alpha } , \in ,F_{\kappa }} \rangle }$
.
$Q ( \kappa )$
is the union of all such, and is itself a DJ-mouse. (The reader should be reminded that DJ-mice, whilst amenable, are not acceptable in the modern meaning of the word. Indeed for a DJ-mouse M with critical point
$\kappa $
it need not be the case that
$(H_\kappa )^M\in M$
. Such is the case for example with
$Q(\kappa )$
.) The height of
$Q ( \kappa )$
is thus proportional to the length of the critical mouse order of
$H ( \kappa )$
. (It can be shown (i) that
$\operatorname {if} \eta $
is this order type then
$\theta ( \kappa ) = \kappa \cdot \eta $
, and thus (ii)
$H(\kappa )$
is closed under sharps iff
$\eta $
is a multiple of
$\kappa ^{2}$
.)
Lemma 2.3. In
$K^{DJ}$
: for any cardinal
$\kappa $
,
$\theta (\kappa )\leqslant u_{2}(\kappa )$
.
Still in
$K^{DJ}\!$
, [Reference Welch15], Lemma 3(i) shows that the uniform indiscernibles for bounded subsets of
$\kappa $
(of which thus
$u_{2}(\kappa )$
is the second) are precisely the critical points of the successive ultrapowers of
$Q(\kappa )$
.
$Q(\kappa )$
need not have the all the sets of
${\widetilde {Q}}(\kappa )$
(it may be too short, indeed in this case even if all bounded subsets of
$\kappa $
have sharps, we may have
${\widetilde {Q}}(\kappa )\neq Q(\kappa )$
) but if
$Q(\kappa )$
is admissible then we shall have
$Q(\kappa ) = {\widetilde {Q}} (\kappa )$
. Still assuming
$Q(\kappa )$
is admissible the discussion in [Reference Welch16] showed that
$u_{2}(\kappa )=\theta (\kappa )$
. What we shall see is that if in K,
$\sigma ( \kappa ) =u_{2} ( \kappa )$
, then we shall have also that
$\theta ( \kappa ) = \sigma ( \kappa )$
and moreover that
${\widetilde {Q}}(\kappa )=Q ( \kappa ) = {\langle {J^{F_{\kappa }}_{\theta ( \kappa )} , \in ,F_{\kappa }} \rangle }$
itself witnesses stable measurability in K.
Lemma 2.4. Suppose
$V= K^{DJ}$
and that
$Q(\kappa )$
is admissible. Then
${\widetilde {Q}} (\kappa ) = Q(\kappa )$
.
Proof. It is easy to see that
$(\,\supseteq \,)$
holds, by the previous style of arguments. For
$({ \,\subseteq \, })$
: let
$a \in H(\kappa )\cap {\mathcal {P}}(\kappa )$
. The a is simply an element of a
$DJ$
-mouse
$N\in H(\kappa )$
(as
$K^{DJ}$
is the union of such). However then
$a\in N_{\kappa }$
which is an initial segment of
$Q(\kappa )$
. Now suppose
$x\in {\widetilde {Q}} $
; then
$x \in L_{\sigma _{a}}[a]$
for such an a. (We are using here, that as
$Q(\kappa )$
is admissible,
$On\cap Q(\kappa )$
is a multiple of
$\kappa ^{2}$
and thus
$H(\kappa )$
is certainly closed under
$\sharp $
’s, and thus
${{\widetilde M}}^{-} = {\widetilde {Q}}$
.) Then
$a^{\sharp }$
is in some
$DJ$
-mouse
$M\in H(\kappa )$
. But
$Q(\kappa )\supseteq H(\kappa )$
. Hence
$M,\kappa \in Q(\kappa )$
. By KP then the
$\kappa $
’th iterate of M,
$M_{\kappa }$
is in Q. But
${\mathcal {P}}(\kappa )\cap L[a]{ \,\subseteq \, } M_{\kappa }$
. Thus there is a subset of
$\kappa $
that codes the ordinal
$\sigma _{a}$
, and so also a code for the structure
$L_{\sigma _{a}}[a]$
, in
$M_{\kappa }$
, and so, by KP again, these sets themselves are in Q. This puts
$x\in Q$
. Q.E.D
Theorem 2.5.
-
(i)
$\sigma ( \kappa ) =u_{2} ( \kappa ) {\,\Rightarrow \,} \sigma ( \kappa )^{K} =u_{2} ( \kappa )^{K} $
. If additionally
$\neg 0^{\dagger }$
then
$\sigma ( \kappa ) = \sigma ( \kappa )^{K}$
. -
(ii)
$\kappa $
is stably measurable
$ {\,\Rightarrow \,} ( \kappa $
is stably measurable)
$\!\!\!^{K}$
as witnessed by
$Q ( \kappa ) = {\langle {J^{F_{\kappa }}_{\theta ( \kappa )} , \in ,F_{\kappa }} \rangle }$
.
Proof. For (i): assume
$\sigma ( \kappa ) =u_{2} ( \kappa )$
. First note that if
$0^{\dagger }$
exists, then every uncountable cardinal
$\kappa $
is Ramsey in K, and hence is iterable, hence stably measurable in
$K.$
Then the conclusion follows by Lemma 1.20. So assume
$\neg 0^{\dagger }$
.
(1)
$\sigma ( \kappa )^{K} = \sigma ( \kappa ) =u_{2} ( \kappa ) =u_{2} ( \kappa )^{K} .$
Proof. of (1). By
$\Sigma ^{1}_{3}$
-absoluteness arguments going back to Jensen (see, e.g., [Reference Dodd3] or [Reference Donder, Jensen, Koppelberg, Jensen and Prestel4]) for reals, but applying them for bounded subsets of
$\kappa $
,
$u_{2} ( \kappa ) =u_{2} ( \kappa )^{K}$
. So we are left with showing the following claim:
Claim:
$\sigma ( \kappa )^{K} = \sigma ( \kappa ).$
Proof.
$\sigma ( \kappa )^{K} \leqslant \sigma ( \kappa )$
follows from the wellorder of
${\mathcal {P}} ( \kappa ) \cap K $
being a good
$\Sigma ^{H ( \kappa ^{+} )^{K}}_{1} ( \kappa )$
-definable wellorder which at the same time is a good
$\Sigma ^{H ( \kappa ^{+} )}_{1} ( \kappa )$
wellorder in V; thus if
$\{ A \}$
is a
$\Sigma _{1} ( \kappa ,p )^{K}$
singleton subset of
$\kappa $
, it is also a
$\Sigma _{1} ( \kappa ,p )^{}$
singleton in V. Hence any such
$A \in M_{0}^{K}$
coding a wellorder
$\tau < \sigma ( \kappa )^{{K}}$
is also in
$ M_{0}$
. Clearly then
$\tau $
and so
$\sigma ( \kappa )^{K} \leqslant \sigma ( \kappa )$
.
But
$\sigma ( \kappa )^{K} \geqslant u_{2} ( \kappa )^{K}$
, since the latter is also
$\sup \{ \operatorname {cp} ( N_{\kappa +1} ) \, | \, N_{\kappa +1} $
is the
$\kappa +$
first iterate of a mouse N in
$ H ( \kappa ) \}$
and moreover
$On\cap N_{{\kappa +1}}< \sigma _{N}$
. All such
$N_{\kappa +1}$
are in
if the latter is any
$\Sigma _{1}$
-substructure of
$H ( \kappa ^{+} )^{K}$
containing
$H ( \kappa ) \cup \{ \kappa \}$
. Hence
$\sigma ( \kappa )^{K} \geqslant u_{2} ( \kappa )^{K} = u_{2}(\kappa )=\sigma ( \kappa )$
. □
For (ii) assume that
$\kappa $
is stably measurable.
Claim:
$Q ( \kappa) $
witnesses that
$\kappa $
is stably measurable in K.
Proof. Work in K. Let
${\widetilde M}={\widetilde M ^{K}}$
.
$Q ( \kappa ) { \,\subseteq \, } {\widetilde M}$
since
$Q ( \kappa )$
is the union of the
$\kappa $
’th iterate of DJ-mice
$N \in H ( \kappa )$
and all such iterates are in
${\widetilde M}$
.
$Q ( \kappa ) \supseteq {\widetilde M}$
: By Lemma 1.7 it suffices to show
$M_{0}^{K}{ \,\subseteq \, } Q(\kappa )$
. Let
$A \in M_{0}^{K}$
. By the argument for (1),
$A \in M_{0}$
, and by Corollary 1.18, using stable measurability in V,
$A^{\#}$
exists, and by absoluteness it exists in K.
Hence
$A \in M_{0}^{K} \cap {\mathcal {P}} ( \kappa )\, {\,\Rightarrow \,} \,A^{\#} \in M_{0}^{K}$
. However then there is some DJ-mouse
$N_{A}$
with
$A \in N_{A}$
. Note now the
$<^{\ast }$
-least such mouse
$N_{A}$
projects to
$\kappa $
and so has a code B a subset of
$\kappa $
. But
$\{A\}$
is a
$\Sigma _{1}(\kappa ,p)$
singleton set (some
$p\in H(\kappa )$
), and thus such a code set
$\{B\}$
is also a
$\Sigma _{1}(\kappa ,p)$
singleton set and so it, and thence
$N_{A}$
, is in
${\widetilde M}$
.
Moreover if
${\langle {\lambda _{i} \, | \, i \in \omega } \rangle }$
are the first
$\omega $
iteration points of
$N_{A}$
which are Silver indiscernibles for
$L [ A ]$
, then
$\widetilde{\lambda } = \sup \{ \lambda _{i} \}_{i< \omega } < \sigma (\kappa ) =u_{2} ( \kappa )$
(the latter equality by part (i)). So there is some
$\bar {N} \in H ( \kappa )$
with
$\operatorname {cp} ( \bar {N}_{\kappa +1} )> \widetilde{\lambda }$
. As
$\bar {N}_{\kappa +1}$
is a DJ-mouse, there is some
$f: \kappa {\,\longrightarrow \,} \operatorname {On} \cap \bar {N}_{\kappa +1}$
which collapses
$\widetilde\lambda $
with
$f \in \Sigma _{\omega } ( \bar {N}_{\kappa +1} )$
. In particular
$\widetilde {\lambda }$
is collapsed, so
$\bar {N} \mbox { } ^{\ast }\! \!\geqslant N_{A}$
. However then
$A \in {\mathcal {P}} ( \kappa )^{N_{A}} { \,\subseteq \, } {\mathcal {P}} ( \kappa )^{\bar {N}_{\kappa +1}} { \,\subseteq \, } {\mathcal {P}} ( \kappa )^{Q ( \kappa )}$
. Thus
$Q(\kappa ) = {\widetilde M}$
and
${\langle } Q(\kappa ), F_\kappa {\rangle }$
is iterable, etc. So
$\kappa $
is stably measurable. Q.E.D
Theorem 2.6.
$(V=K^{DJ})$
$$\begin{align*}\sigma ( \kappa ) =u_{2} ( \kappa ) {\,\Longleftrightarrow\,} \kappa\mbox{ has the } {\boldsymbol{\Sigma}_{1}}\operatorname{-club}\mbox{ property }{\,\Longleftrightarrow\,} \kappa \mbox{ is stably measurable. }\end{align*}$$
Proof. Note first that
${\widetilde M} \prec _{\Sigma _{1}}H(\kappa ^{+})$
. This is by Lemma 1.8 as in
$K^{DJ}$
we have a good
$\Sigma _{1}^{H(\kappa ^{+})}(\kappa )$
wellorder of
${\mathcal {P}}(\kappa )$
.
If
$\kappa $
has the
$\boldsymbol {\Sigma }_{1}$
-club property then
${\langle } {\widetilde M}, \in , F_{\kappa }{\rangle } \models $
“F is a normal measure on
$\kappa $
”, and as usual is iterable. Thus
${\langle } {\widetilde M}, \in , F_{\kappa }{\rangle }$
witnesses stable measurability. This in turn implies
$\sigma =u_{2} ( \kappa )$
(by 1.20). We are left with showing
$\sigma =u_{2} ( \kappa )$
implies the
$\boldsymbol {\Sigma }_{1}$
-club property. As we have
${\widetilde M} \prec _{\Sigma _{1}}H(\kappa ^{+})$
, it suffices to show that
$F_{\kappa }$
measures all
${\mathcal {P}}(\kappa )^{{\widetilde M}}$
.
Let
$A \in {\mathcal {P}}(\kappa )^{{\widetilde M}}$
. Then
$A \in {\widetilde M} {\,\Rightarrow \,} \sigma _{A} \leqslant \sigma $
. As we are in K if
$\neg A^{\#}$
, then
$K=L [ A ]$
. (If we define
$K^{L[A]}$
inside
$L [ A ]$
and this is not all of K, then there is some least mouse
$P \notin L [ A ]$
. But then P generates
$A^{\#}$
.) But in this case, as
$H ( \kappa ) =H ( \kappa )^{L [ A ]}$
we should have that if
$o(A)$
is the least ordinal so that
$\mathcal {A=} L_{o(A)} [ A ] \models \operatorname {KP}$
,
$o \geqslant u_{2}$
, as all
$\kappa +$
first iterates of mice
$N \in H ( \kappa )$
are in fact in
$\mathcal {A} $
. But
$\mathcal {A}$
is merely the first A-admissible
$> \kappa $
containing
$H ( \kappa ) \cup \{ \kappa \}$
. Thus
$o(A) < \sigma _{A}$
(as
$\sigma _A$
is a limit of A-admissibles) and the latter is
$\leqslant \sigma = u_{2}$
—a contradiction. Hence
$A^{\#}$
exists. Let
$N_{A}$
be the
$<^{\ast }$
-least mouse with
$A \in N_{A}$
. By the
$\Sigma _{1}$
elementarity of
${\widetilde M}$
, we have
$N_{A}\in {\widetilde M}$
. By the same argument with
$N_{A}$
in place of A we cannot have
$H({\kappa }){ \,\subseteq \, } L_{o(N_A)}[N_{A}] $
the least admissible set containing
$N_{A}$
. Hence there is some
$<^{\ast }$
-least mouse
. Thus
. As
where
is the
$\kappa $
’th iterate of
, either A or
$cA$
contains a tail of the club of critical points
. Q.E.D
Corollary 2.7. In
$K^{DJ}$
, if
$\sigma ( \kappa ) =u_{2} ( \kappa )$
then these two ordinals both equal
$\theta ( \kappa ) $
and if
$<^{\ast }$
is the prewellordering of mice, then
$o.t. \left ( <^{\ast }\! \!{\upharpoonright } H_{\kappa } \right ) = \sigma ( \kappa). $
Remark. In
$K^{DJ}$
it can happen that
$\theta ( \kappa ) < \sigma ( \kappa $
) (for example if
$K=L [ 0^{\#} ]$
) but
$\theta ( \kappa )$
can never be strictly greater than
$\sigma ( \kappa $
) as we always have
$Q ( \kappa ) { \,\subseteq \, } {\widetilde M}_{0}$
. Now just as a corollary to the above we have immediately:
Theorem 2.8. The following are equiconsistent over
$ZFC$
:
-
(i)
${\exists } \kappa ( \kappa \mbox { is stably measurable})$
; -
(ii)
${\exists } \kappa ( \boldsymbol {\Sigma }_{1}$
-club property holds at
$\kappa )$
; -
(iii)
${\exists } \kappa ( \sigma (\kappa ) = u_{2}(\kappa )).$
Philipp Lücke has also pointed out that a further equivalence can now be obtained in
$K^{DJ}$
with a hypothesis that is also used in his paper [Reference Lücke8] at Lemma 3.13 and Theorem 3.14. We derive this as follows.
Lemma 2.9. In
$K^{DJ}$
we have
$\kappa $
is stably measurable iff
$H(\kappa )$
is not
$\boldsymbol {\Sigma }_{1} (\kappa )$
-definable.
Proof. Note that
$H(\kappa ){ \,\subseteq \, } Q(\kappa )$
and is a
$\Sigma _{1}$
-definable class over, but is never an element of, the latter. By definition of
${\widetilde M}$
we always have
$Q(\kappa ){ \,\subseteq \, } {\widetilde M}$
. Hence the equivalences
$On\,\cap \, Q(\kappa ) < \sigma (\kappa )=On\cap {\widetilde M}$
iff
$Q(\kappa )\in {\widetilde M}$
iff
$H(\kappa )\in {\widetilde M}$
iff
$H(\kappa )$
is
$\boldsymbol {\Sigma }_{1} (\kappa )$
-definable are all true for any
$\kappa> \omega $
. However by Theorem 2.6 and Corollary 2.7 we have
$On\,\cap \, Q(\kappa ) = u_{2}(\kappa )=\sigma (\kappa )$
iff
$\kappa $
is stably measurable. Q.E.D
2.2. When
$K=K^{{strong}}$
In this subsection we assume
$V=K$
but
$\neg 0^{pistol}$
. There is thus no mouse M with a measure with a critical point
$\kappa $
and
$\lambda < \kappa $
with
$o^M(\lambda )\geqslant \kappa $
. (Such a mouse engenders a sharp for an inner model with a strong cardinal.) Let us call K built under this hypothesis
$K^{strong}$
.
Lemma 2.10. Suppose the measurable cardinals in K less than
$\kappa $
are bounded by some
$\lambda ^{+} <\kappa $
.
Then there is a good
$\boldsymbol {\Sigma }_1 (\kappa )$
-wellorder of
${\mathcal {P}}(\kappa )$
.
Note the assumption here implies that although the measurable cardinals of K below
$\kappa $
are bounded by some
$\lambda ^{+}$
, but allows some measurable
$\tau \leqslant \lambda $
to be strong up to
$\kappa $
.
Proof. Let
$e =_{\operatorname {df}} E^K{\upharpoonright } \lambda ^{+}$
with
$\lambda $
such a bound. If some
$\tau \leqslant \lambda $
is strong up to
$\kappa $
on the sequence
$E^{K}$
, then, by a use of
$\neg 0^{pistol}$
we may take
$\lambda $
as this
$\tau $
. Then let
$\psi (E,\lambda )$
be the assertion that
$\lambda $
is strong up to
$\kappa $
as witnessed by the sequence E. Otherwise let
$\psi (E,\lambda )$
be “All measurable cardinals on the sequence E have their critical points
$\leqslant \lambda $
”. Then e will serve as a parameter for defining the wellorder on
${\mathcal {P}}(\kappa )$
given by:
We shall set
$ x \vartriangleleft y \mbox { iff } x<_M y$
where
$<_M$
is the usual order of construction of the structure of M, for an M satisfying the following:
“
$E^M{\upharpoonright } \lambda ^{+} = e\wedge M\models KP + \psi (E^{M},\lambda )\, \wedge M \textit { is a sound mouse } \wedge $
$ M\, \textit { is the least level of the} J^{E^M}\textit{-hierarchy that contains } x \textit { and } y \textit { which is a } KP\textit{-model } $
$\wedge \ M \textit {is} \in$
-minimal satisfying these conditions”.
Note that these conditions require that
$\rho ^\omega _M=\kappa $
. That this is a good
$\Sigma _1(\kappa , e)$
-wellorder follows directly from:
Claim: If
$M,N$
are two mice satisfying the above for
$x,y{ \,\subseteq \, } \kappa $
then
$M=N$
.
Proof of Claim by standard comparison considerations, which we shall give in any case. Let
$M=M_0$
and
$N= N_0$
be two such mice; let them be compared to
$M_\theta $
and
$N_\theta $
. We want that the comparison is trivial, i.e.
$M=N$
. Suppose for a contradiction that
$\nu _0$
is the point of least difference between
$E^{M_0}$
and
$E^{N_0}$
. As they both satisfy
$\psi (E,\lambda )$
there are no measurable cardinals in the interval
$(\lambda ^{+},\kappa )$
on either of the
$E^{M_0}$
,
$E^{N_0}$
sequences. Suppose first that
$\psi (E,\lambda )$
asserts only that the measurables are bounded by
$\lambda $
, that is the measurables (and their measures) in
$M,N$
are just those in e. Thus were
$\nu _0<\kappa $
we should have a truncation on one side, wlog, the N-side to create a full measure to form an ultrapower. As there can be no truncation on the M-side by a consequence of the Dodd–Jensen Lemma, the comparison must run for at least
$\theta \geqslant \kappa $
stages finally iterating some measure of order zero in some
$N_\iota $
up to
$\kappa $
. As there are no measures in this interval on the M-side to take ultrapowers with, then there has been no movement on the M-side:
$M_0=M_\kappa $
. However the iteration of the initial truncate
$N^\ast _0$
of
$N_0$
to
$N_\kappa $
is from some stage before
$\kappa $
onwards, a simple iteration (after perhaps finitely many further truncations) that can be defined inside the
$KP$
model
$N_0$
. We may conclude that
$N_\kappa \in N_0$
.
$N_\kappa $
is of the form
$(J^{E^{N_\kappa }}_\alpha , F^{N_\kappa })$
for some filter
$F^{N_\kappa }$
. Now
$M=M_\kappa $
is a simple
$KP$
model, with
$\kappa $
as its largest cardinal. Hence it is a proper initial segment of the
$ZF^-$
-model
$J^{E^{N_\kappa }}_\alpha $
and thus is an element of N. But this contradicts the assumption on the
$\in $
-minimality of N. Consequently any nontrivial comparison must start by using some
$\nu _0>\kappa $
indexing some filter with critical point
$\geqslant \kappa $
. However this is also a contradiction since both
$\rho ^\omega _M=\kappa =\rho ^\omega _N$
, our conditions insure that if
$M\neq N$
then we see by comparison that the code of one as a subset of
$\kappa $
is a member of the other. But that also contradicts the minimality conditions on the appearance of
$x,y$
in the two hierarchies above
$\kappa $
. We conclude that
$M=N$
.
In the case that in
$E^{K}$
that
$\lambda $
is strong up to
$\kappa $
then let M be some initial admissible segment K satisfying the requirements. Suppose N is another mouse satisfying them with
$\lambda $
strong up to
$\kappa ,$
but the extenders on the
$E^{N}$
sequence must agree with those on the
$E^{K}=E^{M}$
sequence below
$\kappa $
. Otherwise in the comparison of M with N if
$\nu _{0} $
is the least index used, this must be because both
$F_{0}{=_{\operatorname {df}}} E^{M}_{\nu _{0}} $
and
$F_{1}{=_{\operatorname {df}}} E^{N}_{\nu _{0}}$
are both nonempty. But we are in K and
${\mathcal {P}}(\lambda )\in M\cap N$
. Thus both
$F_{0},F_{1}$
are
$\omega $
-complete [Reference Zeman17], Lemma 8.2.12); this guarantees that
${\langle } J^{E^{K}}_{\nu _{0}},\in , E^{K},F_{0},F_{1}{\rangle } $
is a bicephalus. And thus
$F_{0}=F_{1}$
(op. cit. Lemma 8.2.9). Thus if any comparison is to be done it must involve an index
$\nu _{0}>\kappa $
indexing an extender with critical point
$>\kappa $
(by
$\neg 0^{pistol}$
). But just as before this contradicts our minimality conditions on
$M,N$
and we conclude that
$M=N$
. Q.E.D
Corollary 2.11.
$(V=K)$
Let
$\kappa $
satisfy the assumption (a) that the measurables below
$\kappa $
are bounded by some
$\lambda ^{+}$
below
$\kappa $
and (b) that there is no measurable
$\gamma <\kappa $
which is strong up to
$\kappa $
. Then
$$\begin{align*}\kappa \text{ has the } \boldsymbol{\Sigma}_{1}\operatorname{-club} \, \text{property} \Longleftrightarrow \kappa \text{ is stably measurable }\Longleftrightarrow \sigma ( \kappa ) =u_{2} ( \kappa ) .\end{align*}$$
Proof. We just repeat as before that
${\mathcal {P}}(\kappa )$
having a good
$\boldsymbol {\Sigma }_1 (\kappa )$
-wellorder (by (a)) together with the
$\boldsymbol {\Sigma }_{1}$
-club property implies that
$({\widetilde M},\in , F_{\kappa })$
witnesses stable measurability. The right-to-left direction of the first equivalence is now straightforward. The left-to-right direction of the second equivalence is Lemma 1.20. That
$\sigma ( \kappa ) =u_{2} ( \kappa ) $
implies that
$\kappa \mbox { has the } \boldsymbol {\Sigma }_{1}$
-club property can be argued now as for
$K^{DJ}$
by (b): there is some
$\delta < \kappa $
where no index of an extender on the
$E^{K}$
-sequence is that of a full measurable, and thus above
$\delta $
the
$E^{K}$
hierarchy consists only of partial filters, and hence is “
$K^{DJ}$
-like” for the corresponding argument in Theorem 2.6 to be run. Q.E.D
As we saw at Lemma 1.27, without an assumption the first equivalence can fail, for example
$\kappa $
a regular limit of measurables, which is not a Mahlo cardinal.
Lemma 2.12. Assume
$\neg 0^{pistol}$
.
$\sigma ( \kappa ) =u_{2} ( \kappa ) {\,\Rightarrow \,} \sigma ( \kappa )=\sigma ( \kappa )^{K} =u_{2} ( \kappa )^{K} $
.
Proof. The assumption implies that bounded subsets of
$\kappa $
are closed under
$\sharp $
’s. By
$\neg 0^{pistol}$
and absoluteness arguments
$u_{2}= u_{2}^{K}$
. Q.E.D
2.3. When
$K=K^{{JS}}$
Let
$V=K^{{JS}}$
be the Jensen-Steel core model built assuming there is no inner model of a Woodin cardinal. Then the comparison argument in Lemma 2.10 goes through with the same effect, for a
$\kappa $
which is not a limit of K-measurables.
3. Two applications
3.1.
$\; \Sigma _{1}$
-stable measurability
There are two further recent theorems that could benefit from the weakening of an assumption from iterability to stable measurability. They are proven in [Reference Lücke, Schindler and Schlicht9] as Theorems 1.9 and 1.8 respectively with the assumption of
$(\omega _{1}$
-)iterability, which we now weaken to stable measurability by adapting their argument. But the proofs are now shorter.
Theorem 3.1. Assume
$\kappa $
is stably measurable. Then the following are equivalent for
:
-
(i) X is
$\Sigma _{1} ( \kappa )$
-definable; -
(ii) X is
$\Sigma ^{1}_{3}$
definable.
Proof. (ii)
${\,\Rightarrow \,}$
(i) is unaltered as in [Reference Lücke, Schindler and Schlicht9]. (i)
${\,\Rightarrow \,}$
(ii): Let
${\langle {{\widetilde M}, \in ,F_{\kappa }} \rangle } $
witnesses stable measurability. Exactly as in [Reference Lücke, Schindler and Schlicht9] define the
$\Sigma ^{1}_{3}$
set:
where
$\varphi ( \kappa ,v_{1} ) \in \Sigma _{1}$
defines X. Then
$Y \supseteq X$
since for any
$y \in X$
we can take a countable elementary substructure
${\langle {N_{0} \rangle } , \in ,U_{0}} \prec {\langle {{\widetilde M}, \in ,F} \rangle } \models \varphi ( \kappa ,y )$
. Then we have a witness to put y into Y. Conversely any witness
${\langle {N_{0} , \in ,U_{0}} \rangle } \models \varphi ( \bar {\kappa } ,x )$
that
$x \in Y$
, iterates to a structure
${\langle {N_{\kappa } , \in ,U_{\kappa }} \rangle } \models \varphi ( \kappa ,x )$
, with
$N_{\kappa } \in {\widetilde {Q}}$
. But
${\widetilde {Q}} = {\widetilde M}$
by Lemmata 1.10 and 1.19. But then by
$\Sigma _{1}$
-upwards absoluteness
$ \varphi ( \bar {\kappa } ,x )$
holds in
${{\widetilde M}}$
and in V.
Q.E.D
For completeness we repeat the following immediate, but nice, Corollary 6.3 from [Reference Lücke, Schindler and Schlicht9] with this improved hypothesis.
Corollary 3.2. Suppose
$\kappa $
is stably measurable. If there is a
$\Sigma _{1}(\kappa )$
wellordering of
then there is such which is
$\Sigma ^{1}_{3}$
.
In K we get a form of equivalence in Theorem 3.1.
Theorem 3.3. Assume
$V=K^{DJ}$
. Let
$\Phi (\kappa )$
be the following sentence:
Then we have:
$$\begin{align*}\kappa\mbox{ is stably measurable }{\,\longleftrightarrow\,} \Phi(\kappa) \mbox{ is preserved by small forcings of size } < \kappa.\end{align*}$$
Proof. By Theorem 3.1
$\kappa $
is stably measurable implies
$\Phi (\kappa )$
, and stable measurability is preserved by small forcing. This proves
$(\rightarrow )$
.
First just note that if
$H(\kappa )$
is not closed under sharps (which implies that
$\kappa $
is not stably measurable) then the right hand side fails: let
$a{ \,\subseteq \, } \gamma < \kappa $
have no sharp; then
$V=L[a]$
as we must have
$K{ \,\subseteq \, } L[a]$
for otherwise
$a^\sharp $
would exist. Let
; then
$V[G]\models V= L[r]$
, where r is a real coding G and a. But now any analytical (in r) set whatsoever is definable over
$L_{\omega _1}[r]$
and thus is
$\Sigma _1(L_\kappa [r],r)$
and then
$\Sigma _1(\kappa ,r)$
. Consequently the right hand side fails.
So now assume that
$H(\kappa )$
is closed under sharps.
-
(1) Any
$ X\in \Sigma ^{1}_{3}(r)$
is
$\Sigma _{1}^{Q(\kappa )}(r)$
. This follows from the fact that there is a Martin-Solovay tree for
$\Pi ^1_2$
is
$\Delta _{1}$
-definable over
$Q(\kappa )$
(cf. [Reference Welch, Drake and Truss13], [Reference Welch14], Section 1). -
(2)
${\widetilde M}\prec _{\Sigma _{1}}H(\kappa ^{+})$
, by Lemma 2.1 and then by definition
$\sigma \leqslant On\cap {\widetilde M}$
.
Suppose
$\kappa $
is not stably measurable. Then
$Q(\kappa )$
cannot witness stable measurability and moreover:
-
(3)
$\theta (\kappa )\leqslant u_{2} < \sigma $
.
But then:
-
(4)
$Q(\kappa )\in {\widetilde M}$
.
Proof. We have that
$\theta (\kappa )= On \cap Q(\kappa ) < \sigma \leqslant On \cap {\widetilde M}$
. But then for some
$z\in H(\kappa )$
,
$\theta (\kappa ) \in \Sigma _1^{{\widetilde M}}(\kappa , z)$
. But then also
$J_{\theta (\kappa )}^{F_\kappa }$
is also
$\Sigma _1^{H(\kappa ^+)}(\kappa , z)$
, and so is in
${{\widetilde M}}$
. Q.E.D
Let G be
-generic over V for some
which collapses
$TC(\{z\})$
, for a z chosen as in (4), to be countable. Then as
${\widetilde M}\prec _{\Sigma _{1}}H(\kappa ^{+})$
, we have
${\widetilde M}[G]\prec _{\Sigma _{1}}H(\kappa ^{+})[G] = (H(\kappa ^{+}))^{V[G]}$
in
$V[G]$
. Let
code z. Then
$Q(\kappa )$
, which is not altered in the passage to
$V[G]$
, is in
$\Sigma _{1}^{{\widetilde M}}(\kappa , r)$
.
Consequently if
is a universal
$\Pi ^1_3$
set, then
$X\in \Pi _{1}^{Q(\kappa )}$
but would then be
$\Sigma _1^{{\widetilde M}}(\kappa , r)$
; but such an X is not
$\Sigma ^1_3(s)$
for any
. So this provides a counterexample to the preservation of
$\Phi (\kappa )$
under small forcing. Q.E.D
Within K we can replace the stable measurability by any of its equivalents from Theorem 2.6 of course. Outside of K even assuming sufficient sharps for
$\Sigma ^{1}_{3}$
-absoluteness we can only show by similar methods results such as the following:
Lemma 3.4.
$(\neg 0^{{\dagger }} \wedge \forall a\in {\mathcal {P}}_{<\kappa } (\kappa )(a^{\#}$
exists
$))$
. Assume there is a good
$\boldsymbol {\Sigma }_1$
-wellorder of
${\mathcal {P}}(\kappa )$
. Then:
$$\begin{align*}u_{2}(\kappa)<\sigma(\kappa) {\,\Rightarrow\,} \Phi(\kappa) \mbox{ fails in a small generic extension}.\end{align*}$$
Proof. Use that if
${\widetilde M}$
is a
$\Sigma _{1}$
-substructure, that
$\theta (\kappa ) \leqslant (u_2)^{K} = u_{2}$
by the correctness of the calculation of
$u_{2}$
inside K due to the assumed absoluteness from
$\neg 0^{\dagger }$
, and thus is
$\Sigma _{1}^{{\widetilde M}}(\kappa , z)$
definable from some
$z\in {\mathcal {P}}_{<\kappa } (\kappa )$
, and thus also
$Q(\kappa )\in {\widetilde M}$
as above. But then the first
$\omega $
iterates of Q are in
${\widetilde M}$
and this is enough to define the Martin-Solovay tree of K on these uniform indiscernibles as an element of
${\widetilde M}$
. (The assumptions of the lemma again ensure the correctness of this tree in V.) But now we get as before
$\Pi ^{1}_{3}$
sets of reals as
$\Sigma _{1}(\kappa , r)$
where r is a real in a small generic extension coding z. Q.E.D
But we don’t have a converse to this.
Theorem 3.5. Assume
$V=K^{strong}$
. Let
$\kappa $
not be a limit of measurable cardinals. Then the conclusion of the last Theorem 3.3 holds.
Proof. The direction
$(\rightarrow )$
is as before, again we seek to prove
$(\leftarrow )$
. Instead of using the Dodd–Jensen
$Q(\kappa )$
we use the generalised
${\widetilde {Q}}(\kappa )$
. If
${\widetilde {Q}}(\kappa )$
is in
${\widetilde M}$
we’ll reason as before that if
${\widetilde M}$
fails to witness stable measurability, that analytical sets are definable over
${\widetilde {Q}}(\kappa )$
because again a Martin-Solovay tree is so definable. We again then have a counterexample to the right handside.
The case that
$H(\kappa )$
is not closed under sharps is a small variant: let
$a{ \,\subseteq \, } \gamma < \kappa $
have no sharp; let
$a'$
code both a and
$K{\upharpoonright } \gamma '$
where
$\gamma ' < \kappa $
is least with
$a\in K{\upharpoonright }\gamma '$
. Then
$V=L[a']$
. Let
; then
$V[G]\models V= L[r]$
, where r is a real coding G and
$a'$
. We can finish as before,
We assume then
$H(\kappa )$
is closed under sharps; we are done if we can show
${\widetilde {Q}}(\kappa ) \in {\widetilde M}$
. Note that by Lemma 2.10 we have a good
$\Sigma _1(\kappa , e)$
wellorder of
${\mathcal {P}}(\kappa )$
and hence
${\widetilde M}\prec _{\Sigma _{1}}H(\kappa ^{+})$
. (Recall that e was the initial segment of the
$E^{K}$
extender sequence
$E^K{\upharpoonright } \lambda ^{+}$
for some
$\lambda < \kappa $
which bounds the measurable cardinals.) By the assumed failure of stable measurability at
$\kappa $
we must have
${\widetilde M} \neq {\widetilde {Q}}(\kappa )$
as otherwise
$({\widetilde M}, F^\kappa )$
would be a witness to this. Let
$A\in M_0$
be such that
$A\in {\widetilde M}{\backslash } {\widetilde {Q}}(\kappa )$
. Without loss of generality we may assume
$A{\upharpoonright } \lambda ^{+}$
codes
$e = E^K{\upharpoonright } \lambda ^{+}$
.
First suppose that
$\neg A^\sharp $
. Then covering lemma arguments show that
$K^{A}{=_{\operatorname {df}}} (K)^{L[A]}$
is a universal weasel, and as we are below
$0^{pistol}$
it is a simple iterate of the true K—that is without truncations in the comparison. However A codes the initial segment of K given by
$E^{K}{\upharpoonright } \lambda ^{+}$
and thus
$E^{K^{A}}{\upharpoonright } \lambda ^{+} =E^{K}{\upharpoonright } \lambda ^{+}$
. Consequently no comparison index is used below
$\kappa $
. Consequently we have that
$K^{A}_\kappa = K_{\kappa }= L_{\kappa }[A]= H(\kappa )$
. But
$L_\kappa [A]\in {\widetilde M}$
. But then
${\widetilde {Q}}(\kappa )$
is definable within the admissible set
${\widetilde M}$
from
$H(\kappa )$
and we’ve achieved our goal.
Thus suppose
$A^\sharp $
exists. If
$L_\kappa [A]= K_\kappa =H(\kappa )$
, then we could reason as we just have done that
${\widetilde {Q}}(\kappa )$
is definable within
${\widetilde M}$
. So there is some
$<^\ast $
-least sound mouse P with
$A\in P$
and
$\rho ^\omega _P=\kappa $
. By the elementarity of
${\widetilde M}$
in
$H(\kappa ^+)$
we have that
$P\in {\widetilde M}$
as it is
$\Sigma _1$
definable from A. Then in comparison of
$P=P_0$
with
$R_0 {=_{\operatorname {df}}} K_ \kappa $
we cannot have that
$R_0$
is truncated below
$\kappa $
and some
$R_0^\ast $
is iterated past P, as in that case A is an element of an iterate of the
$\kappa $
’th iterate of (some final truncate of)
$R_0^\ast $
, and the latter along with A would be in
${\widetilde {Q}}(\kappa )$
. So then, as K has no full measures in the interval
$(\lambda ,\kappa ]$
, the coiteration is trivial below
$\kappa $
, indeed altogether trivial, and
$H(\kappa ) = K{\upharpoonright } \kappa \in P{ \,\subseteq \, } {\widetilde M}$
, and we may finish as before. Q.E.D
Putting together the above we have:
Corollary 3.6. Assume
$V=K^{DJ}$
(or
$V=K^{strong}$
). Then
$\exists \kappa \Phi (\kappa )$
is (set)-generically absolute if and only if there are arbitrarily large stably measurable cardinals in K.
As in Lemma 3.4 we can prove the following with these methods.
Corollary 3.7. Assume
$\neg 0^{pistol} \wedge \forall a\in {\mathcal {P}}_{<\kappa } (\kappa )(a^{\#}$
exists
$))$
. Assume there is a good
$\boldsymbol {\Sigma }_1$
-wellorder of
${\mathcal {P}}(\kappa )$
. Then:
$$\begin{align*}u_{2}(\kappa)<\sigma(\kappa) {\,\Rightarrow\,} \Phi(\kappa) \mbox{ fails in a small generic extension}.\end{align*}$$
The following is a strengthening of [Reference Lücke, Schindler and Schlicht9], Theorem 1.8 where the assumption is that
$\kappa $
is iterable; it is based on their template but now follows easily from the analysis above.
Theorem 3.8. Assume
$\kappa $
is stably measurable. Assume
$X { \,\subseteq \, } {\mathcal {P}} ( \kappa )$
separates
$F_{\kappa }$
from
$\operatorname {NS}_{\kappa }$
, then
$X $
is not
$\Delta ^{H ( \kappa ^{+} )}_{1}$
.
Proof. Let
$\kappa $
be stably measurable as witnessed by
${\langle {{\widetilde M}, \in ,F_{\kappa }} \rangle }$
as usual. For a contradiction let
$\varphi ( v_{0} ,v_{1} ) $
and
$\psi ( v_{0} ,v_{1} ) $
be
$\Sigma _{1}$
and define some
$X \supseteq F_{\kappa }$
and its complement in
${\mathcal {P}} ( \kappa )$
, but with
$X \cap {\rm NS}_{\kappa } = \varnothing$
. Then
$F_{\kappa } \cap {\widetilde M}$
is
$\Delta ^{{\widetilde M}}_{1}$
and the statement that it is an ultrafilter is
$\Pi _{1}^{{\widetilde M}}$
. As
${\widetilde M} \prec _{\Sigma _{1}} H ( \kappa ^{+} )$
, we thus have an
$\widetilde {F } \supseteq F$
, which is a definable
$H ( \kappa ^{+} )$
-ultrafilter. But this is absurd, as [Reference Lücke, Schindler and Schlicht9] says, as then
$\widetilde {F} $
is definable over
$H ( \kappa ^{+} )^{\operatorname {Ult} ( H ( \kappa ^{+} , \widetilde {F} ) )}$
. Q.E.D
4. When
$\sigma> u_{2}$
and canonical models
The following definition can be given a first order formulation as a scheme.
Definition 4.1. Let
$\varphi (v_{0})$
be a formula of the language of set theory with the single free variable
$v_{0}$
. Let M be an inner model of ZFC (thought of as a transitive proper class of sets defined by some class term). We say that M is canonically defined by
$\varphi (\xi )$
(for some parameter
$\xi \in On$
), if
$\varphi (\xi )^{M}$
but for no other inner model
$M'$
do we have
$\varphi (\xi )^{M'}$
.
Clearly then L is such (“
$V=L$
”) but also
$L[\mu ]$
(“
$V=L[\mu ]$
where
$\mu $
is a normal measure on
$\kappa $
”—using the ordinal parameter
$\kappa $
).
$``V=K$
” by itself does not canonically define any inner model, but
$L[0^{\#}]$
or the least inner model where all sets have
$\#$
’s,
$L^{\#}$
, are canonical in this sense. Hence Carl and Schlicht ask: what is the least
$L[E]$
-model which is not canonical? Clearly if an inner model thinks that it is not canonically definable, then it is a model of an inner model reflection principle (see Definition 4.4 below). Then [Reference Barton, Caicedo, Fuchs, Hamkins, Reitz and Schindler2] ask for upper bounds to the existence of a model of inner model reflection, thus essentially the same question.
We identify this model (Corollary 4.8), as an inner model, and it turns out to be an inner model of the full Dodd–Jensen core model below a measurable cardinal. It is a model which is intermediate in consistency strength between admissible measurability and stable measurability. In this model no Q-structure
$Q ( \kappa ) = {\langle {J^{F_{\kappa }}_{\theta ( \kappa )} , \in ,F_{\kappa }} \rangle }$
witnesses stable measurability, but such can be admissible, and moreover can be first order reflecting.
Definition 4.2. A transitive admissible set
$\mathcal {A}$
is first order (or
$\Pi ^{0}_{\omega }$
) reflecting if for any formula
$\varphi (\vec p)$
with parameters
$\vec p \in \mathcal {A}$
such that
$(\varphi (\vec p))^{\mathcal {A}}$
there is a transitive
$u\in \mathcal {A}$
so that
$(\varphi (\vec p))^{u}$
.
We shall adopt a version of this appropriate for Q-structures: for u we just take a proper initial segment of Q. (Note that “
$V=L[F]$
” is in any case
$\Pi _2$
so this is not a restriction.)
Definition 4.3.
$Q(\kappa )$
is
$\Pi ^{0}_{n}$
reflecting if for any
$\Pi ^{0}_{n}\ \varphi (\vec p)$
with parameters
$\vec p \in H(\kappa )$
with
$Q(\kappa )\models \varphi (\vec p)$
there is
$\tau $
with
$\kappa \leqslant \tau < \theta (\kappa )$
with
$J^{F_{\kappa }}_{\tau }\models \varphi (\vec p)$
. It is
$\Pi ^{0}_{\omega }$
reflecting, if it is so for some
$\Pi ^{0}_{n}$
with
$n<\omega $
.
We shall tie this up with a version of:
Definition 4.4 (Inner model reflection)
(i) An inner model M is reflecting for
$\varphi (p)$
, for
$p\in M$
,
$\varphi \in {\mathcal {L}}_{\dot \in , \dot =}$
when, if it is a model of
$\varphi (p)$
, then there is a proper inner model
$M'\subset M$
which is a model of
$\varphi (p)$
.
(ii) An inner model is first order reflecting if it is first order reflecting for all
$\varphi (p)$
. It is
$\Pi _{n}$
-reflecting when it is so for all p and all
$\psi (v_{0})\in \Pi _{n}$
.
Clearly a model which is first order reflecting cannot be canonical in the sense above.
Given a mouse N (in the modern sense) in
$K^{DJ}$
this generates an inner model
$K^{N}$
(which is of the form
$L[E^{K^{N}}]$
for some predicate
$E^{K^{N}}$
). Let
$C_{N}= {\langle } \kappa _\alpha \, | \, \alpha \in On {\rangle }$
be the cub class of the iteration points of N as we iterate by its top active measure. It then generates the inner model
$K^{N}=\bigcup _{\alpha \in On}H_{\kappa _{\alpha }}^{N_{\alpha }}$
. As above we can let
$Q^{N}(\gamma )$
be the union of all the Dodd–Jensen mice in
$H_{\gamma }^{K^{N}}$
iterated to comparability at
$\gamma $
.
Theorem 4.5. Let N be a mouse that generates an inner model
$K^{N}$
which is
$\Pi _{n}$
-reflecting. Then for any
$\kappa \in C_{N}$
,
$Q^{N}(\kappa )$
is
$\Pi ^{0}_{n}$
-reflecting. Conversely if N generates the model
$K^{N}$
so that for some
$\kappa \in C_{N}$
,
$Q^{N}(\kappa )$
is
$\Pi ^{0}_{n}$
-reflecting, then
$K^{N}$
is
$\Pi _{n}$
-reflecting.
Proof. Recall that for any
$\gamma \in \operatorname {Card}^{K^{N}}$
,
$K^{N}_{\gamma }= (H({\gamma }))^{K^{N}}$
. As the elements of
$C_{N}= \{\kappa _{\alpha }\, | \, \alpha \in On\}$
are indiscernible for
$K^{N}$
we shall have that for any
$\alpha $
so that
$\kappa _{\alpha }> \max \operatorname {rk}_{K^{n}}(\vec p)$
:
$$\begin{align*}(1) {\langle {{K^{N}} \rangle},\in}\kern-0.3pt\models\kern-0.3pt \varphi(\vec p)\, &{\,\longleftrightarrow\,} \, {\langle {{K^{N} \rangle}_{\kappa_{\alpha}}},\in}\kern-0.3pt\models\kern-0.3pt\varphi(\vec p)\,\\ &{\,\longleftrightarrow\,} \,{\langle {Q^{N}(\kappa_{\alpha}),\in} \rangle}\kern-0.3pt \models\kern-0.3pt\mbox{ ``}{\langle {H(\kappa_\alpha),\in} \rangle}\kern-0.3pt\models\kern-0.3pt \varphi(\vec p)\mbox{''}.\end{align*}$$
For a
$Q(\kappa )$
-mouse the first projectum
$\rho _{Q}^{1}$
is
$\kappa $
(indeed all projecta are). By the fine structure for such mice, we have that any
$\Pi _{n}^{{\langle } Q(\kappa ),\in\! {\rangle }}$
relation
$R{ \,\subseteq \, } H(\kappa )^{Q(\kappa )}$
is
$\Pi _{n}$
over
${\langle } H(\kappa )^{Q(\kappa )},\in\! {\rangle }$
. (Officially because we use that
$J_{\rho ^{1}_{Q}}^{{A^{1}_{Q}}} = H(\kappa )^{Q(\kappa )}$
, where
$A^{1}_{Q}$
is the first mastercode of
$Q=Q(\kappa )$
. We shall write
$Q^{N}(\kappa )$
for
$Q^{K^N}(\kappa )$
.) Using this with
$\kappa = \kappa _{\alpha }$
in the equivalences at (1), together with
$H(\kappa _\alpha )^{K^{N}} = K^{N}_{\kappa _{\alpha }}= H(\kappa _\alpha )^{Q^{N}(\kappa _\alpha )}$
we have the equivalence of the right hand statement with
$ {\langle {Q^{N}(\kappa _{\alpha }),\in } \rangle } \models \mbox { ``} \varphi (\vec p)\mbox {''}$
.
Now suppose
$K^{N}$
is
$\Pi _{n}$
-reflecting, there is an inner model
$K'\subset K^{N}$
in which
$\varphi (\vec p) + \mbox {``}V=K\mbox {''}$
holds (at least if
$n\geqslant 2$
; if
$n=1$
it reflects to
$L[\vec p]$
). But any such model
$K'$
is actually some
$K^{M}$
for an
$M<^{\ast }N$
(and thus
$M\in K^{N}$
). Now choose
$\alpha $
sufficiently large so that it is greater than
$|M|^{K^{N}}$
and is also in
$C_{M}$
. As M is missing from
$K^{M}$
it is easy to see that
$Q^{M}(\kappa _{\alpha })$
is a proper initial segment of
$Q^{N}(\kappa _{\alpha })$
. However the sequence of equivalences in (1) holds with M replacing N throughout.
Now for the converse suppose
$K^{N}\models \psi (\vec p)$
, and then via (1) above, we have
$Q^{N}(\kappa )\models \psi (\vec p)$
for a
$\psi \in \Pi _{n}$
,
$\kappa \in C_{N}$
, and
$Q^{N}(\kappa )$
,
$\Pi ^{0}_{n}$
-reflecting. We note that
$Q^{N}(\kappa ) = \bigcup \{M_{{\kappa }} \, | \, {M \in Q^{N}(\kappa )},\,\operatorname {On}\, \cap \, M < \kappa , \,M \mbox { a }DJ-\mbox {mouse}\}$
; the latter is described by a
$\Pi ^{0}_{2}$
formula, which may assume then is a conjunct of the formula
$\psi $
. (Another way of putting this is to say that
$\theta ^{{N}}({\kappa })$
is a multiple of
$\kappa $
.) By (1) again we have this is equivalent to
$K^{N}_{\kappa }\models \psi (\vec p)$
. As
$Q^{N}(\kappa )$
is
$\Pi _{n}$
-reflecting, there is some
${\kappa }<\tau < \operatorname {On}\,\cap \, Q^{N} (\kappa )$
with
$J_{\tau }^{F_{\kappa }}\models \psi (\vec p)$
and
$J_{\tau }^{F_{\kappa }} = \bigcup \{M_{{\kappa }} \, | \, {M \in J_{\tau }^{F_{\kappa }} }, \operatorname {On}\, \cap \, M < \kappa , M \mbox { a }DJ-\mbox {mouse}\}$
. Now with this property of
$\tau $
, this ensures that the
$<^{\ast }$
-least mouse
$M\notin H^{J_{\tau }^{F_{\kappa }}}_{\kappa }$
with
$\operatorname {crit}(M)=\kappa $
generates a proper inner model of
$K^{N}, K^{M}$
, with
$Q^{M}_{\kappa }=J_{\tau }^{F_{\kappa }}$
and now, applying (1) once more,
$(\psi (\vec p))^{K^{M}} $
. Q.E.D
Perhaps unsurprisingly, there is a strict hierarchy under
$\subset $
of
$\Pi _{n}$
-reflecting inner models in
$K^{DJ}$
for increasing n.
Corollary 4.6. For
$n> 1$
, if a mouse N generates an inner model
$K^{N}$
which is
$\Pi _{n}$
-reflecting, then for
$\kappa \in C_{N}$
, we have that
$Q^{N}(\kappa )$
is a
$\Pi ^{0}_{n}$
-reflecting admissible set. Furthermore for such
$\kappa $
there is
$M <^{\ast } N$
and a
$U^{M_{\kappa }}$
measure one set of
$\xi < \kappa $
such that
$Q^{M}(\xi )$
is
$\Pi ^{0}_{n-1}$
-reflecting. Hence
$K^{M}$
is a proper inner model of
$K^{N}$
which is
$\Pi _{n-1}$
-reflecting.
Proof. The first sentence is just a restatement of part of the proof above. The statement “
$Q({\kappa })$
is
$\Pi ^{0}_{n-1}$
reflecting” is itself a
$\Pi ^{0}_{n}$
statement over
$Q(\kappa )$
:
$$\begin{align*}\forall \varphi \in \Pi_{n-1}{\forall} x \in H_{\kappa}[\varphi(x){\,\Rightarrow\,} \exists \tau J_{\tau}^{F_{\kappa}}\models \varphi(x)].\end{align*}$$
So by
$\Pi ^{0}_{n}$
-reflection this holds of some
$ J_{\bar \theta }^{F_{\kappa }} = Q^{M}(\kappa ) $
for some
$\kappa < \bar \theta < \theta ^{N}(\kappa )$
, some
$M\in H_{\kappa }^{K^{N}}$
. Q.E.D
We then have the equivalent formulation of
$\Pi ^{0}_{\omega }$
-reflection over a
$Q^{N}(\kappa )$
analogous to that of [Reference Aczel and Richter1], Theorem 1.18.
Lemma 4.7.
(i) If a mouse N generates an inner model
$K^{N}$
which is first order-reflecting, then for
$\kappa \in C_{N}$
, we have that
$Q^{N}(\kappa )$
is a
$\Pi ^{0}_{\omega }$
-reflecting admissible set.
(ii) Let
$\widetilde F_{\kappa } = F_{\kappa }\cap J^{F_{\kappa }}_{\theta (\kappa )}$
. Then:
Such a
$Q^{N}(\kappa )= J^{F_{\kappa }}_{\theta (\kappa )}$
is
$\Pi ^{0}_{\omega }$
-reflecting if and only if
$J^{ F_{\kappa }}_{\theta (\kappa )}\prec _{\Sigma _{1}}J^{\widetilde F_{\kappa }}_{\theta (\kappa )+1}$
.
(By
$J^{\widetilde F_{\kappa }}_{\theta (\kappa )+1}$
we mean the next level in the J-hierarchy, constructing using the rudimentary functions, augmented by the
$\widetilde F_{\kappa }$
-rudimentary function
$F(x,y)=x\cap \widetilde F_{\kappa }$
.)
Proof. (i) is a consequence of the above. For (ii) one may argue in the manner of [Reference Aczel and Richter1], Theorem 1.18, but one has to adapt the reasoning to the appearance of sets in the J-hierarchy, rather than the L-hierarchy. We omit these details. Q.E.D
Corollary 4.8. The least noncanonical
$L[E]$
in the sense above, is that generated by a mouse N for which its
$Q(\kappa )$
-structure is
$\Pi ^{0}_{\omega }$
-reflecting.
Question 1. Under the assumptions of Lemma 1.19, does
$\kappa $
inaccessible and
$ u_{2}(\kappa )=\sigma (\kappa )$
imply that
$\kappa $
is stably measurable?
We conjecture not, but if so, then a non-
$V=K$
version of Theorem 3.3 would be provable.
Question 2. For inaccessible
$\kappa $
does
$u_{2}(\kappa )=\sigma ({\kappa })$
imply the
$\boldsymbol {\Sigma }_{1}$
-club property for
$\kappa $
?
In [Reference Lücke8] there is a small list of large cardinal properties implying this conclusion, some of which imply the antecedent here, so it is natural to try to add this to the list. A positive answer to this fills the last gap in providing a positive answer to the next question.
Question 3. Assume
$\kappa $
is inaccessible and there is a good
$\boldsymbol {\Sigma }_{1}$
-wellorder of
${\mathcal {P}}(\kappa )$
. Then
$$\begin{align*}\sigma ( \kappa ) =u_{2} ( \kappa ) {\,\Longleftrightarrow\,} \kappa\mbox{ has the } \boldsymbol{\Sigma}_{1}\operatorname{-club}\mbox{ property }{\,\Longleftrightarrow\,} \kappa \mbox{ is stably measurable. }\end{align*}$$
Lemma 1.27 shows the assumption is necessary to go from the second property to the last. This then would be the V-version of that in
$K^{DJ}$
of Theorem
2.6
.
