This work is motivated by the forthcoming development of a new accelerator complex at Gesellschaft für Schwerionenforschung (GSI) (Darmstadt, Germany) which will be capable of accelerating relatively dense bunches of positive ions, in arbitrary charge states, to Lorentz factors up to about 30. It will be possible to irradiate the ions with superintense laser pulses produced by the Petawatt High Energy Laser for Heavy Ion Experiments (PHELIX) source, which is currently developed on the same site. This source has a working wavelength of 1053.7 nm and a peak intensity well above 10²¹ W/cm². We suppose here that the laser beam is oriented so as to counterpropagate with respect to the ions beam, which will be feasible at GSI. In their own frame of reference, the ions would then be exposed to a laser field with a wavelength much reduced by the Doppler effect. Our long term interest in the present work is the efficacy, in these conditions, of high order above-threshold ionization and recollisional multiple ionization. For simplicity, we examine here the case of high order harmonic generation. At the single-ion level, this process is similar to the other two in arising from the same mechanism: the active electron is detached from the core through tunneling ionization, then propagates in the continuum like a free electron accelerated by the electromagnetic field, and finally interacts with the core as it comes back to its vicinity. At this point, the electron may recombine radiatively, which leads to the emission of an energetic photon, or are simply scattered, which leads to high order above-threshold ionization, or collide inelastically, which leads to nonsequential multiple ionization. As is well-known, these three-step processes are inhibited at high intensity by the Lorentz force exerted by the magnetic field component of the laser pulse, which tend to push the electron in the direction of propagation of the pulse, away from the core (Dammasch et al., 2001; Klystra et al., 2001; Milošević et al., 2001). The suppression is particularly severe for electrons coming back to the core with a high velocity. However, as we argue here, the combination of high intensities and high frequencies that can be achieved at GSI makes it possible to attenuate this effect.

Our calculations are carried out in the frame of the ion using the non-relativistic, non-dipole strong field approximation (SFA) (Klystra et al., 2001; Chirilă et al., 2002). Within this approach, the instantaneous dipole moment of the ion irradiated by the field can be expressed as

The sum runs over detachment times, t_d, for which the detached electron comes back at the core at time t. The ionization amplitude a_ion(t,t_d), the propagation amplitude a_pr(t,t_d) and the recombination amplitude a_rec*(t,t_d) are obtained as described by Chirilă et al., (2002) and Ivanov et al. (1996), with depletion of the initial state neglected. However, in the present work, we correct the strong field approximation for the Coulomb potential of the core. Namely, we assume that the electron interacts with the core through a pure Coulomb potential, −Z/r. (Atomic units are assumed throughout this paper, unless specified otherwise. Z = (2I_p)^1/2, where I_p is the ionization potential of the initial state.) The ionization amplitude is calculated using the Coulomb correction proposed some time ago by Krainov (1997), and the recombination amplitude by making the impulse approximation (Milošević & Ehlotzky, 1998; Garland et al., 2002). The Coulomb interaction is taken into account in different ways in the ionization amplitude and the recombination amplitude because of the physical difference between the corresponding steps: at the ionization stage, the electron is detached with essentially zero velocity by tunneling through the potential barrier, while at the recombination stage it moves at high velocity. We have tested this procedure by comparing the Coulomb-corrected SFA spectrum of photons emitted by an He⁺ ion with the result of an exact integration of the time-dependent Schrödinger equation (Worthington & Potliege, 2002). Illustrative results are presented in Figure 1. The quantity represented is the squared modulus of the Fourier transform of the dipole acceleration (the second order derivative of the dipole moment with respect to time) for a two-cycle Ti:Sapphire pulse of angular frequency ω = 0.057 a.u., plotted versus the harmonic order, Ω/ω, where Ω is the angular frequency of the emitted photon. The plateau structure that is seen can be readily understood by analyzing the classical trajectories of the detached electrons (Potvliege et al., 2000; Chirilă et al., 2002). The Coulomb correction significantly improves the agreement of the SFA results with the exact ones, bringing the two together to within a factor of 2.

The magnitude squared of the Fourier transform of the dipole acceleration, in atomic units, as a function of the energy of the emitted photon (in units of the laser frequency) for a He+ ion exposed to 2-cycle Ti:Sapphire laser pulse of 800 nm wavelength and 1 × 1016 W/cm−2 peak intensity. The vector potential envelope is a sin2 function. Left panel: comparison between the spectrum obtained by solving the time-dependent Schrödinger equation numerically (1) and the predictions of the strong field approximation (2). Right panel: spectrum obtained within our Coulomb corrected SFA.

An ion moving with speed v collinearly against a laser pulse of angular frequency ω, electric field amplitude F and magnetic field amplitude B is effectively submitted to a laser pulse of angular frequency ω_ion, electric field amplitude F_ion and magnetic field amplitude B_ion given by the relations

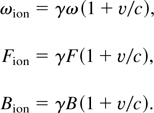
Here γ = (1 − v²/c²)^−1/2 is the Lorentz factor and c denotes the speed of light. The vector potential amplitude A = F/ω is a Lorentz invariant, and so are the ponderomotive energy U_p = F²/(4ω²) and the Keldysh parameter γ_K = ωZ/F. Since the magnitude of the velocity of the detached electron with respect to the parent ion in three-step processes is proportional to U_p^1/2, it is the same whether the ion moves or not. However, if the ion moves at a relativistic velocity (v ≈ c), the frequency is Doppler-boosted by almost a factor 2γ compared to an ion at rest, and the intensity by almost a factor 4γ².

In order to quantify how the relativistic Doppler boost affects recollisional processes, we compare photon emission by two ions exposed to the same field, one still, the other moving relativistically. The laser pulse is modeled as a stationary electromagnetic field whose intensity and wavelength in the laboratory frame are I_L = 10¹⁷ W cm⁻² and λ_L = 1053.7 nm. This intensity is high enough for the magnetic-field induced suppression of recollision to be potentially significant, but not so high as to invalidate our non-relativistic SFA (Chirilă et al., 2002). The ponderomotive energy, U_p, is 10.4 keV, and the maximum energy of photons emitted by the ion is given by approximately I_p + 3U_p. The first ion is the sodium-like Ar⁷⁺ ion (Z = 3.247, I_p = 143 eV), which we assume to be at rest in the lab frame (γ = 1). For the laser parameters chosen here, this ion suffers an ionization loss of about 2.2% per optical cycle. The laser intensity is thus slightly below saturation. The corresponding Keldysh parameter is γ_K = 0.08. The second ion is the hydrogen-like Ne⁹⁺ ion (Z = 10, I_p = 1.36 keV), assumed to move in the lab frame with a Lorentz factor γ = 15. The ionization loss per cycle, in this case, is about 1.0%. (This species was chosen because at γ = 15 it ionizes in the field at about the same rate as Ar⁷⁺ at γ = 1, which facilitates comparison.) The Keldysh parameter is 0.26, sufficiently small that the SFA can still be expected to be adequate. Owing to the Doppler boost in intensity, the Ar⁷⁺ ion would be promptly ionized if moving at γ = 15 against the laser pulse. Indeed, in the ion's frame of reference, the intensity is almost 9 × 10¹⁹ W cm⁻² when γ = 15.

The corresponding harmonic generation spectra are presented in Figure 2. Two sets of results are shown for each ion, namely the results obtained within the dipole approximation (within which the effect of the magnetic field component of the laser field is neglected), and the results obtained with the magnetic field taken into account within our non-dipole SFA. In the case of Ar⁷⁺, the magnetic field reduces the intensity of emission by about three orders of magnitude in the high energy part of the spectrum. This dramatic reduction, and the bending of the plateau, disappearance of intermediate cutoffs and of the oscillations marking the dipole spectrum, are well known non-dipole effects and are readily explained within the semi-classical model (Milošević et al., 2001; Chirilă et al., 2002). The difference between dipole and non-dipole spectra is much less for Ne⁹⁺. In particular, despite the higher intensity, there is no significant decrease in the efficiency of the harmonic emission as compared to the dipole calculation. Striking is the much larger intensity of emission for Ne⁹⁺.

The magnitude squared of the Fourier transform of the dipole acceleration over one cycle, in atomic units, as a function of photon energy for (1) Ne9+ (at γ = 15) and (2) Ar7+ (ions at rest), as obtained within the Coulomb-corrected SFA. For each ion, the upper curve shows the results obtained within the dipole approximation and the lower curve the results obtained without making this approximation. The laser field is stationary and linearly polarized. The intensity is 1 × 1017 W/cm−2 and the wavelength is 1053.7 nm.

The higher emission efficiency of Ne⁹⁺ has a double origin: It is due both to the larger recombination amplitude, which is proportional to Z^5/2, and to the lesser spreading of the electronic wave packet between the time of detachment and the time of recombination. (In the frame of reference of the ion, the difference between these two times is smaller by a factor 30 for γ = 15.) We expect that the adverse effect of wave packet spreading on the efficiency of high-order above−threshold ionization (ATI) and non-sequential double ionization would be similarly reduced by going to relativistic velocities.

The relative weakness of the non-dipole effects in the case of Ne⁹⁺ originates from the dependence of the ionization amplitude a_ion(t,t_d) on the magnetic field and on the ionization potential of the initial state. The largest part of the difference between the value of a_ion(t,t_d) in the dipole approximation and its non-dipole value can be traced to an exponential factor this amplitude is proportional to. In the frame of reference of the ion one has, more precisely (Chirilă et al., 2002; Walser et al., 2000),

where E(t_d) is the electric field at the time of detachment and v_∥ is the velocity in the laser propagation direction an electron must have at time t_d to return to the core at time t. In the dipole approximation, v_∥ = 0. However, with A denoting the vector potential,

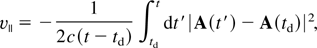
when allowance is made for the acceleration in the propagation direction due to the magnetic field. For the above laser parameters, v_∥ ≈ 2 a.u. for electrons returning with the highest possible kinetic energy (3.17U_p). This value is the same for the two ions—it is independent of I_p and does not vary with the Lorentz factor. Taking E(t_d) equal to the electric field amplitude, we get w(v_∥ = 0) = 1.4 × 10⁻⁶ for Ar⁷⁺ at γ = 1 and w(v_∥ = 0) = 1.9 × 10⁻⁶ for Ne⁹⁺ at γ = 15: in the dipole approximation, the probability for the active electron to be ionized and to return to the core at high velocity is similar for the two ions. However, w(v_∥ = 2) = 3.1 × 10⁻¹⁰ for Ar⁷⁺ at γ = 1 while w(v_∥ = 2) = 8.7 × 10⁻⁷ for Ne⁹⁺ at γ = 15: while the return probability is reduced for both ions once the laser's magnetic field is taken into account, it is much more reduced for Ar⁷⁺ than for Ne⁹⁺. This is simply due to the fact that adding a non-zero v_∥² to 2I_p is a smaller change in the argument of the exponential in the case of Ne⁹⁺, because of the larger ionization potential of this ion and the larger electric field at γ = 15. A possible physical explanation of the lesser sensitivity of Ne⁹⁺ to non-dipole effects is that the initial state has a wider momentum distribution, which makes it less unlikely that the electron is ejected with the required velocity along the laser's propagation direction.

We note, to conclude, that the smaller importance of the non-dipole effects at large Lorentz factors illustrated here for high-order harmonic generation can also be expected for other high-order ATI or nonsequential double ionization, as it originates from the ionization stage of the process and this stage is virtually identical for all three-step processes. We stress that this smaller importance is not a relativistic effect per se. The speed of the ions intervenes only through the Doppler effect, which makes it possible to detach electrons from highly charged ions without imposing a large magnetic drift to these electrons. Clearly, identical results would be obtained by irradiating ions at rest with a laser field of sufficiently high intensity and (which would be problematic in practice) sufficiently high frequency. The photon emission spectra of relativistic ions in the laboratory frame will be presented elsewhere.