INTRODUCTION
The relationship between money growth and the real economy has been studied extensively for several decades. Tobin (1965) was the first to arouse interest in this topic, as his paper focused on how money growth affects capital accumulation. An enormous amount of literature has grown up, containing many important insights, yet no clear conclusion has been reached on how money growth affects the real factors. The real effects of money growth may, in summary, be basically positive as in the money-in-the-production-function approach [Fischer (1974), King and Plosser (1984), and Wang and Yip (1992a)]; negative as in the cash-in-advance (CIA) approach [Stockman (1981, 1985), Wang and Yip (1992b), Palivos and Yip (1995), and Mino (1997)]; or neutral as in the money-in–the-utility-function approach [Sidrauski (1967)].1
It is worthwhile to mention that Feenstra (1986) pointed out the structural equivalence between liquidity constraints on consumption-goods purchases and the inclusion of money balances in the utility function. Koenig (1989) equally demonstrated that liquidity constraints on the purchase of investment goods could be regarded as being equivalent to including real balances in the production function.
Most of the models mentioned above are formulated within the context of the one-sector growth theory. The conventional one-sector model is useful in illustrating the intertemporal effect of inflation, but it ignores its distributional effect. In the two-sector model, as Foley and Sidrauski (1970, 1971) demonstrated, permanent inflation may have a distributional effect, but their analysis is hampered by the non-optimizing nature of the model. Although Huo (1997) used an optimizing framework to illustrate the distributional effects of inflation, his model is a specific-factor model in which capital input is allocated to only one of the two sectors.
The purpose of this paper is to investigate the effects of money growth on real variables by formulating a Heckscher–Ohlin CIA model. The Heckscher–Ohlin model is more flexible in discussing the effects of money growth by allowing a more general production-function structure. Previous CIA studies usually focused on whether investment is subject to a CIA constraint. Stockman (1981) showed that money growth and capital are inversely related when a CIA constraint applies to both consumption and investment, and money is superneutral if investment is not subject to the CIA constraint. Wang and Yip (1992b), Palivos and Yip (1995), and Mino (1997) reached the same conclusion.
No one in the literature has talked about the role that production structure might have in influencing the effects of money growth. The adoption of the Heckscher–Ohlin model allows us to broaden the discussion. Interestingly, Huo (1997) showed a nonsuperneutrality result without the inclusion of investment in the cash-in-advance constraint, which is quite different from previous findings. To retrace the interesting concern and to generalize it further, we generate a CIA constraint that contains only two consumption purchases and allow a fraction between 0 and 1 for the two goods to be purchased by cash.
We first treat labor supply as exogenous; later in this paper, we consider an endogenous labor/leisure choice to examine its negative role. By employing a Heckscher–Ohlin CIA model, we find all possible effects of permanent inflation as shown in the literature in a single model. Whether monetary growth generates a Tobin (i.e., capital accumulation), reversed Tobin (i.e., capital decumulation), or superneutral effect depends on the factor intensity ranking and the relative degree of severity of cash requirements for purchasing the two goods. When the endogenous labor/leisure choice is taken into account, we observe an enhanced negative effect of inflation. Inflation unambiguously increases the steady-state leisure, and higher inflation reduces the steady-state labor supply, consumption purchases, and economic welfare in most cases.
The paper is organized as follows. A CIA model, the first-order conditions, and the steady-state characterizations are illustrated in the next section. In Section 3 the steady-state effects of a change in the monetary growth are examined. Section 4 studies the same issue with an endogenous labor/leisure choice. Section 5 provides brief conclusions for this paper.
MODEL
In this model we consider a competitive two-sector economy in which one sector produces a final good, c1, that is used either for consumption or for adding to the existing capital stock, while the other sector produces a final good, c2, that is used for consumption only. Both sectors produce outputs by employing capital, k, and labor, l, with constant-returns-to-scale technology. Capital does not depreciate.
The production technologies are summarized as follows:
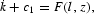
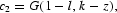
where F and G are constant-returns-to-scale production functions with standard properties. In the expression, we have normalized the total labor endowment to unity, so that l and (1−l) are the shares of labor allocated to the first and the second sectors, respectively. Terms z and (k−z) are the stocks of capital allocated to the first and the second sector, respectively. Let
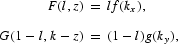
where kx≡z/l is the capital/labor ratio in the first sector and ky≡(k−z)/(1−l) is the ratio in the second sector. The labor productivity functions, f and g, are assumed to be strictly increasing and strictly concave.
Given (1) and (2), it is clear that c1 and
must sell for the same price in a competitive market, but c1 and c2 need not do so. Labor and capital are assumed to be mobile across industries. The structure of production in this paper can be thought of as a generalization of Huo (1997). The economy consists of an aggregation of identical, infinitely lived representative households, each of which maximizes an intertemporal utility function that is separable in c1 and c2:2
Without separability, the comparative static exercises below become rather complicated. A general utility function without separability may have multiple steady states; see Brock (1974, pp. 775–776, appendix), and Obstfeld and Rogoff (1983, p. 677 fn.4).
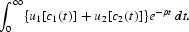
We solve here an optimization problem under competitive equilibrium, in other words, a social planning problem. The planner takes the technology constraints as given and seeks to maximize household utility over consumption plans. This means that the planner tries to maximize (3) subject to (1) and (2), where ρ>0 is a constant subjective rate of time preference. The instantaneous utility functions u1(·) and u2(·) are strictly increasing, strictly concave, continuously differentiable, and satisfy the Inada conditions. The representative household holds either capital (k) or cash (M). Cash is injected into the system through lump-sum transfers (and withdrawn by lump-sum taxes).
The household's budget constraint is
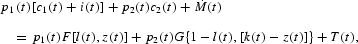
and the capital accumulation constraint is given by
with k(0) and M(0) given. In the expressions, p1(t) and p2(t) are the nominal prices of c1 and c2, respectively, at time t. Term T(t) is the lump-sum nominal transfer from the government at time t. It is assumed that the purchases of c1 and c2 are restricted by a CIA constraint of the following general form:
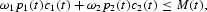
where ω1 and ω2 are, respectively, the fractions of cash needed to purchase c1 and c2, 0[les ]ω1, ω2[les ]1, ω1+ω2≠0∀t, and M(t), the cash balance at time t, is introduced to the system through the above CIA constraint.
Denoting as H the Hamiltonian of the optimization problem, α and β are the costate variables associated with M and k, respectively, λ is the Lagrangian multiplier attached to the CIA constraint, and i is the slack variable. We can therefore write H as
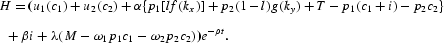
Applying Pontryagin's Maximum Principle, we find that the optimizing program is described by the following first-order conditions:
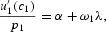
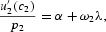
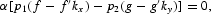
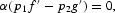
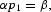
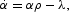
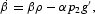
together with two transversality conditions,
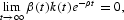
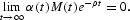
The necessary conditions (7), together with Eqs. (1) and (2), can be used to characterize the solution to (3). A sufficient condition for a solution to (3) to exist is that the Hamiltonian be concave in (l, k), which is met, given the specification of preferences and technologies. Equation (7a) [(7b)] equates the marginal utility of c1(c2) per dollar spent to the sum of the marginal utility of income and the fractions of the purchase of c1(c2) constrained by cash times the marginal utility of cash. Equation (7c) [(7d)] equates the marginal products of capital (labor) in each sector. Equation (7e) equates the marginal benefit of investment per dollar spent to the marginal benefit of income. Equation (7f) [(7g)] describes the dynamic behavior of the marginal benefit of income (investment). Equation (7h) [(7i)] rules out Ponzi-game behavior in trading capital (cash).
We define p=p2/p1 to be the relative price of the two consumption goods. Equations (7c) and (7d) require that the real rates of return on capital and labor be equalized across sectors. Let w≡f(kx)−kxf′(kx) denote the market real wage on labor and r≡f′(kx) denote the market real rental on capital. Equations (7c) and (7d) can be used to solve for the factor intensities in each sector and factor prices as functions of p alone. Totally differentiating (7c) and (7d) and using the definition of factor prices will yield
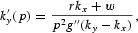
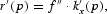
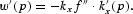
By (8c) and (8d), it can be seen that there is a monotonic relation between the relative costs (prices) of the goods and the relative factor prices, which is the well-known Stolper–Samuelson relation.3
See Krauss and Johnson (1974, Ch. 2).
The relation is a consequence of the assumed difference in factor intensities between commodities, and holds so long as both goods are produced.
4 To avoid problems with corner solutions, each group is assumed to always demand some of both goods, at all relative commodity prices.
The solutions to (8) can be combined with the full employment condition, which requires that lkx(p)+(1−l)ky(p)=k, which implies that
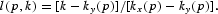
Equation (9) shows that the optimum labor fraction is a function of the relative price and capital stock.
STEADY-STATE ANALYSIS
The equilibrium conditions for the economy require that the goods markets, factor markets, and money market all clear. Equilibrium in the goods market is represented above by (1) and (2), whereas factor market equilibrium requires that both labor and capital be fully employed. The money market equilibrium implies a binding CIA constraint.
To simplify the system of (7), we first substitute (7d) and (7e) into (7g) to obtain
By (7a) and (7b), we next obtain
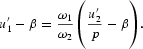
Taking logarithms of both sides of the above equation and differentiating with respect to time results in
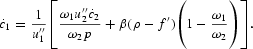
By (7a), (7b), and (7e), we can solve for λ, and then substituting the value of λ into (7f), we obtain
The money market clearing condition implies that the CIA constraint is binding. Taking logarithms of both sides of (6) and differentiating with respect to time,
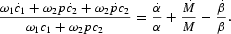
The money supply is assumed to follow a constant rate of growth, μ,
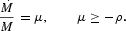
The condition of μ[ges ]−ρ is generally known to ensure the existence of a monetary steady state. Substituting (10), (13), and (15) into (14), we can solve for
. The second-good market-clearing condition implies that we can substitute (2) into (12) to obtain
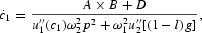
where
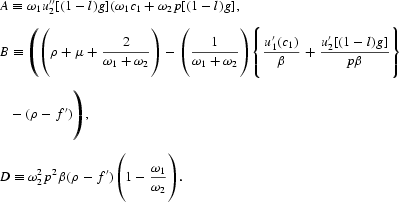
Note that in (16), l≡l(p, k), f≡f[kx(p)], and g≡g[ky(p)]; therefore,
is a function of c1, k, and β. The equilibrium motion of (c1, k, β) is thus completely characterized by (1), (10), and (16).5
Huo (1997) was able to characterize the monotonicity and speed of adjustment in the neighborhood of the steady state by linearizing the single difference equations. This procedure is not feasible for the two-sector model we are considering here.
In the steady state,
. Before the formal comparative analysis, it should be noted that equation (10) implies that the steady-state marginal productivity of capital is tied to the rate of time preference:
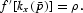
Equation (17) shows that the bar over the variable denotes its steady-state value, implying that the steady-state marginal productivity of capital is tied to the rate of time preference. The steady-state real rate of return on capital is determined by the Modified Golden Rule (without population growth) from the traditional optimal growth theory. Here, we can interpret the relationship between the relative price of commodities and the rate of time preference. On the one hand, we observe a monotonic relation between the relative prices of the goods (p) and the relative factor prices (r, w) in equation (8) as Stolper–Samuelson predicted. On the other hand, r≡f′[kx(p)]=ρ in the steady state, which represents that the rental price of capital is equal to a constant rate of time preference.
It therefore follows that the steady-state relative commodity price is determined by an exogenous rate of time preference, and therefore is irrelevant to the inflation rate. The result is surprising compared to the other two-sector models [Huo (1997), Mino (1997)]. The constancy of the relative commodity price comes from the CIA constraint. In this model, we assume only that the purchases of consumption goods need cash, whereas the purchases of investment and factor inputs (labor and capital) do not. Since cash is not needed to purchase factor inputs, inflation has no influence on the relative factor price. In addition, it is known that there is a monotonic relation between the relative factor price and the relative commodity price; therefore, it is trivial to see that the relative commodity price is also independent of the inflation rate.
We may now conjecture that when investment purchases are also subject to the CIA constraint, the proposition that inflation does not affect the relative commodity price will no longer be valid.6
For example, in the case of p1(c1+i)[les ]M, we find that
. It shows that in the steady state, the relative commodity price (
is not only determined by the exogenous rate of time preference (ρ), but also the rate of inflation (μ).
By exploiting the CIA setting in the Heckscher–Ohlin model, this paper actually provides a mechanism to bring the well-known characteristics (i.e., Stolper–Samuelson relation, golden rule) of a real model to a model with money.
To elucidate the relationship between anticipated inflation and the steady-state capital stock, we rewrite (14) as
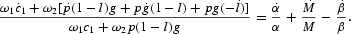
Since
in the steady state and (17) implies that
, it follows that
, and
. We substitute (13) and (15) into (18) to obtain
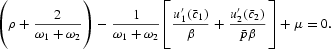
From (7a), (7b), and (7e), we see that in the steady state,
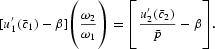
To investigate the effects of permanent anticipated inflation on the steady-state capital stock, we first differentiate (19) and (20). From the goods-markets equilibrium conditions of (1), (2), and (7), it is known that in the steady state,
and
. By applying the relations that
and
, we have
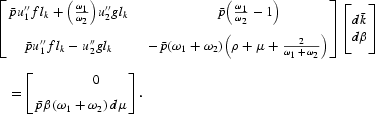
This in turn implies that
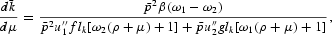
where lk=1/(kx−ky). Since p>0, β>0, f, g>0, u″1, u″2<0, equation (21) shows that the factor intensities (kx and ky) and the fractions of consumption purchases made using cash (ω1 and ω2) determine the effects of inflation on steady-state capital accumulation. The results can be shown as follows:
The results show that factor intensities and the fractions of purchases of consumption goods constrained by CIA determine the effect of permanent anticipated inflation on the steady-state capital stock. Moreover, if a more capital-intensive good is also less (more) cash intensive, then inflation will induce higher (lower) capital accumulation. The reasoning for the results can be illustrated by supposing that the economy is in a steady state initially.
- We first consider the case where the product is relatively capital intensive and less cash intensive [(kx>ky and ω1<ω2) or (kx<ky and ω1>ω2)]. Higher inflation raises the opportunity cost of purchasing a cash-intensive good; this induces the utility-maximizing households to make a new consumption choice on their indifference curves, and results in a substitution of credit good for cash good. Since the less cash-intensive good is relatively more capital-intensive, the increase in the demand for the less cash-intensive good leads to more capital accumulation.
- It is easy to see that, vice versa, higher inflation induces capital decumulation when a sector is labor-intensive and less cash-intensive [(kx<ky and ω1<ω2) or (kx>ky and ω1>ω2)].
- It is also clear that, regardless of the factor intensity, as long as the purchases of the two consumption goods are equally constrained by the CIA (ω1=ω2), then higher inflation equally affects the purchases of the two goods. It does not lead to any distributional effect in the production of the two sectors; therefore, higher inflation has no effect on capital accumulation.
We generally observe reversed Tobin effects when the capital-intensive good is also a cash-intensive good and Tobin effects when the capital-intensive good is a less cash-intensive good. The steady-state effect of inflation on capital accumulation comes solely from the substitution effect between the two consumption goods made by inflation, not from the changes in the relative prices. Although this model does not take capital depreciation into consideration, it is found that adding depreciation to the model will not alter the results if the depreciation is relatively small.7
The discussion about taking into account capital depreciation is available by the author upon request.
CIA MODEL WITH ENDOGENOUS LABOR SUPPLY
The aim of this section is to see through the role of endogenous labor supply in this model. The model is similar to the model in the preceding section except the production technologies are modified as follows:
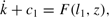
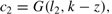
where l1 and l2 are the shares of labor allocated to the first and the second sector, respectively. We next let
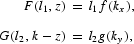
where kx≡z/l1 is the capital/labor ratio in the first sector, and ky≡(k−z)/l2 is the ratio in the second sector.
The economy consists of an aggregation of identical, infinitely lived representative households each of which maximizes an intertemporal utility function that is separable in c1 and c2 and leisure [ell ]:
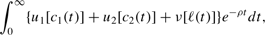
where ρ>0 is a constant subjective rate of time preference. The instantaneous utility functions u1(·), u2(·), and ν(·) are all strictly increasing, strictly concave, continuously differentiable, and satisfy the Inada conditions. We normalize the time endowment to unity, which is l1+l2+[ell ]=1. The Hamiltonian H is
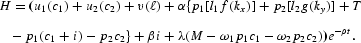
The first-order conditions are the same as in equation (7) except that there is an extra FOC in this section as the following:
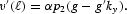
We use the same methodology to simplify the FOC and market-clearing conditions. By applying the relations of
and
, we obtain
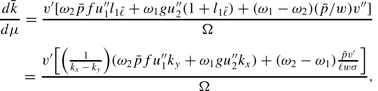
and
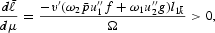
where
.
It is quite trivial that, from (22), inflation leads to higher demand for leisure by reducing the opportunity cost of leisure. Hence, higher inflation reduces the total labor supply with no doubt in the model concerning the endogenous labor/leisure choice. This result is consistent with that of Brock (1974), but different from that of Yip (1991).8
Yip (1991) argued that his conclusion is in great contrast to Brock's (1974). It is due to the introduction of money into the transactions effort technology through time allocation, rather than the inclusion of both money and leisure in the utility function as in Brock, where labor and leisure have to be negatively correlated.
Note that
, and σ=−v′/[ell ]v″,9
σ([ell ]t)≡lims→t−dln([ell ]s/[ell ]t)/dln[v′([ell ]s)/v′([ell ]t)]=−v′([ell ]t)/[ell ]tv″([ell ]t), where s and t are time subscripts.
which represents the elasticity of the intertemporal substitution of leisure. Since
p>0, β>0,
f,
g>0, and
u″
1,
u″
2,
v″<0, equation (21″) shows that aside from the factor intensities (
kx and
ky) and the fractions of consumption purchases made by using cash (ω
1 and ω
2), the elasticity of intertemporal substitution of leisure also plays a role in determining the effects of inflation on steady-state capital accumulation:
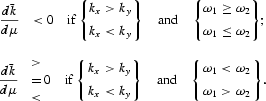
The steady-state effect of inflation comes mainly from factor redistribution in the Heckscher–Ohlin model. Comparing the results with last section's, we definitely find a negative role of endogenous labor supply in the real effects of money growth, which is in accordance with Brock (1974), Stockman (1985), Yip (1991), Gomme (1993), and Mino (1997). A sector that produces a capital-intensive and less cash-intensive good is no longer guaranteed to induce higher capital accumulation for an increase in inflation rate. Here, we should be more careful in presenting the redistribution effect of labor input.
Note that
, and in order for us to clarify the redistribution effect of labor supply by inflation between the two sectors, we obtain
,
in most cases; whereas
only occurs when ω1<ω2 and
; and
only occurs when ω1>ω2 and σ<[(ω2−ω1)v′]/([ell ]wω2fu″1)≡σB. We further obtain the relations that
,
. This shows that inflation affects steady states c1 and c2 in the same direction as it affects l1 and l2, respectively.
For the effects of inflation on capital accumulation, we obtain a reversed Tobin effect in most cases when the endogenous labor/leisure choice is taken into account. The economic reasoning is as follows:
- We first consider the case that a capital-intensive sector is also cash-intensive [(kx>ky and ω1>ω2) or (kx<ky and ω1<ω2)]. The income effect of inflation leads to a decrease in the purchases of both goods. In addition, the higher inflation decreases the demand for the cash-intensive good and therefore leads to less capital accumulation [(dk/dμ)<0] since the cash-intensive good is a capital-intensive good. Total labor supply (l1+l2) decreases because leisure becomes more valuable in a higher inflation period. The share of labor allocated to the cash-intensive sector decreases with certainty. In most cases, the shares of labor allocated to the less cash-intensive sector decrease and therefore the demand for the less cash-intensive goods decreases; only when the elasticity of intertemporal substitution of leisure is extremely small is the chance that the labor ratio and the demand for the goods in this sector can increase. Long-run capital stock definitely decreases with an increase in inflation.
- In the case of ω1=ω2, inflation equally affects the opportunity costs of the two consumption purchases. The income effect of inflation leads to a decrease in the demand for both consumption goods. Inflation also equally affects the shares of factor input allocated to the two sectors, leading to a reduction in both l1 and l2. The decrease in both demand for consumption goods and labor supply of the two sectors causes the demand for capital to decrease, and therefore the long-run capital stock is reduced. We obtain a reversed Tobin effect when ω1=ω2. When comparing this with the superneutral result in the preceding section, the negative role of endogenous labor supply is apparent.
- The steady-state effect of inflation on real economic variables is complex and ambiguous in the case where the capital-intensive good is also a less cash-intensive good [(kx<ky and ω1>ω2) or (kx>ky and ω1<ω2)]. Higher inflation results in a substitution of the less cash-intensive good for the cash-intensive good. The steady-state level of the cash-intensive good and the labor ratio of this sector definitely decrease, but the values in the other sector may decrease or increase, depending upon the magnitude of the elasticity of the intertemporal substitution of leisure. Since the cash-intensive good is labor-intensive and the less cash-intensive good is capital-intensive, the steady-state capital stock decreases unambiguously when the demand for both goods decreases; but it may increase, decrease, or not change when the demand for the less cash-intensive good increases. In contrast to the results in the exogenous labor supply model where inflation unambiguously leads to higher capital accumulation, the concern of the elasticity of intertemporal substitution of leisure plays an important role.
Although, in general, we obtained a Tobin effect (i.e., capital accumulation), a reversed Tobin effect (i.e., capital decumulation), or a zero effect again as in the preceding section, we do find a negative role of endogenous labor supply. This section requires further consideration on the elasticity of the intertemporal substitution of leisure and the redistribution between labor and leisure. Through the redistribution effects in factor inputs, we conclude that inflation has a positive effect on steady-state leisure and has negative effects on other variables (labor supply, consumption goods, and capital accumulation) in most cases.
We can also demonstrate the effect of inflation on economic welfare:
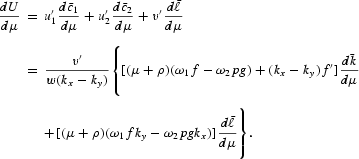
The sign of the above expression is uncertain. For simplicity, we assume that the condition is used to ensure that the existence of a monetary steady state (μ[ges ]−ρ) is binding. Replacing by μ+ρ=0, the above expression can be reduced to
We derive that sign (dU/dμ) = sign (
is negative in most cases and nonnegative in fewer cases. Accordingly, it implies that, in general, an increase in the rate of money growth reduces welfare in the steady state, which is consistent with the results in Bailey (1956), Lucas (1981), Cooley and Hansen (1989, 1991), and Yip (1991).10
In Chuang and Huo (2003), it is shown that when one takes into account the welfare loss on the dynamic adjustment path, higher inflation reduces overall economic welfare with certainty. A similar result is applicable here; that is, when μ=−ρ, money grows exactly according to Friedman's OQM.
Compared to other literature, this paper is more general and comprehensive by combining all situations in one model and being able to explain all situations.
CONCLUSION
This paper provides a framework for a Heckscher–Ohlin CIA model to examine the effects of changes in permanent anticipated inflation on steady-state capital. In this model we introduce a more complete and generalized setting for production technologies and CIA constraints. This paper shows how Stockman's result can be reproduced without imposing a CIA constraint to the purchase of capital.
A special finding is that, in contrast to other two-sector model studies, the distributional effects of permanent inflation do not take place through the changes in the relative commodity price since its steady-state value is tied to the rate of time preference. As mentioned earlier, the special characteristics of this model are that the purchase of factor inputs does need not use cash. Therefore, the relative factor price is not affected by inflation. The Stolper–Samuelson theorem indicates that there is a monotonic relation between the relative commodity price and the relative factor price. Hence, the relative commodity price, being not affected by inflation, can be shown in this model.
The effects of permanent anticipated inflation on the steady-state capital stock might be positive, negative, or neutral, depending on the ranking of factor intensities and the structure of the CIA constraint. Roughly put, inflation is beneficial for capital accumulation when more capital-intensive goods are less cash-intensive, and harmful when more capital-intensive goods are more cash-intensive in the Heckscher–Ohlin model. With an endogenous labor/leisure choice, we observe a “reversed Tobin effect” in most cases. Moreover, higher inflation unambiguously reduces the steady-state labor supply, and reduces consumption purchases and welfare in most cases. The endogenous labor/leisure choice enhances the negative role of inflation on the real variables, which is consistent with the literature.
I am indebted to Teh-Ming Huo for valuable discussion. Special thanks go to Dr. Barnett, the editor, for his thoughtfulness and suggestions. I also want to thank two anonymous referees for helpful comments.
