Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T18:38:31.310Z Has data issue: false hasContentIssue false
  • English
  • Français

Inhibition factor reduces fast ignition threshold for laser fusion using nonlinear force driven block acceleration

Published online by Cambridge University Press:  01 April 2008

M. Ghoranneviss ,
B. Malekynia ,
H. Hora ,
G.H. Miley  and
X. He
M. Ghoranneviss
Affiliation:
Plasma Physics Research Centre, Science and Research Division, Islamic Azad University, Tehran-Poonak, Iran
B. Malekynia
Affiliation:
Plasma Physics Research Centre, Science and Research Division, Islamic Azad University, Tehran-Poonak, Iran
H. Hora*
Affiliation:
Department of Theoretical Physics, University of New South Wales, Sydney, Australia
G.H. Miley
Affiliation:
Department of Nuclear, Plasma and Radiological Engineering, University of Illinois, Urbana, Illinois
X. He
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, China
*
Address correspondence and reprint requests to: Heinrich Hora, Department of Theoretical Physics, University of New South Wales, Sydney 2052, Australia. E-mail: h.hora@unsw.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Fast ignition for fusion energy by using petawatt-picosecond (PW-ps) laser pulses was modified due to an anomaly based on extremely clean suppression of prepulses. The resulting plasma blocks with space charge neutral ion current densities above 1011 Amp/cm2 may be used to ignite deuterium-tritium at densities at or little above solid state density. The difficulty is to produce extremely high energy flux densities of the blocks. Results are reported how the threshold can be reduced by a factor up to fife if the inhibition factor for thermal conductivity due to electric double layers is included in the hydrodynamic analysis.

Keywords

Fast igniterFusion EnergyLaser Driven ICFLaser driven very high ion densitiesPlasma block (piston) ignition of deuterium-tritiumSelf-focusing
Type
Research Article
Information
Laser and Particle Beams , Volume 26 , Issue 1 , March 2008 , pp. 105 - 112
Copyright
Copyright © Cambridge University Press 2008

1. INTRODUCTION

Since laser pulses of petawatt power (PW) in the range of picoseconds (ps) are available, the scheme of fast ignition (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994) is studied extensively as a possible approach to generate fusion energy from the reaction of deuterium and tritium (DT). When studying the interaction of terawatt (TW) to PW laser pulses with solid targets, an anomaly was discovered which differed from all the broad stream experiments (Sauerbrey Reference Sauerbrey1996, Zhang et al., Reference Zhang, He, Chen, Li, Zhang, Wong, Li, Feng, Zhang, Tang and Zhang1998, Badziak et al. Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999) where the suppression of prepulses by a contrast ratio of at least 108 for times of less than few dozens of ps before the arrival of the main pulse was necessary. It was clarified (Hora et al. Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikova, Kraska, Laska, Parys, Perina, Pfeifer and Rohlena2002, Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007) and confirmed by subsequent experiments (Badziak et al. Reference Badziak, Hora, Woryna, Jablonski, Laska, Parys, Rohlena and Wolowski2003, Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2004, Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005) that these conditions avoided relativistic self focusing (Hora, Reference Hora1975) which in all other experiments was involved to result in very high energy ions of high ionisation and extremely intense and hard X-ray emission.

The anomalous interaction resulted in the generation of directed plasma blocks moving against the laser beam or in the beam direction generated by a skin layer interaction driven by the nonlinear (ponderomotive) force (Hora Reference Hora1969, Reference Hora2000) where space charge neutral plasma block were generated with current densities above 1010 Amp/cm2 of highly directed energetic ions. These ion beams increased the efficiency for ion beam fusion by a factor of 1000 (Badziak et al., Reference Badziak, Glowacz, Hora, Jablonski and Wolowski2006). It was evident from the beginning (Hora, Reference Hora2002, Reference Hora2003, Reference Hora2007) that these ion beam pulses may be used for ignition of a fusion flame front in solid state DT. This is similar to the scheme by Nuckolls and Wood. (Reference Nuckolls and Wood2002) where a modification of the fast igniter (Tabak et al. Roth et al., Reference Roth, Brambrink, Audebert, Blazevic, Clarke, Cobble, Geissel, Habs, Hegelich, Karsch, Ledingham, Neelz, Ruhl, Schlegel and Schreiber2005; Hoffmann et al., Reference Hoffmann, Blazevic, Ni, Rosemej, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005) with PW-ps laser pulses generated very intense relativistic electron beams for energy production by ignition of DT that is 12 times the solid state density or less by efficiencies up to 10000 times fusion energy per energy of the laser pulse.

This focuses on the special potential of inertial fusion energy (IFE) with lasers as highlighted by Dean (Reference Dean2008) who especially underlines the interest in a single-shot “ignition campaign by petawatt lasers.” Dean has indeed to acknowledge all directions for generating fusion energy and mentions well the very extensive and expensive research on fusion confinement by magnetic fields B (MCF) as the tokamak with the International Thermonuclear Experimental Reactor (ITER), Z-pinch, reverse field pinch, mirror machines, or the Nuckolls-Rubbia push (Hora, Reference Hora2000) for the IFE line with heavy ion beam fusion. The position of ITER in Cadarach/France has to be compared in view of the fusion gain which will be increased only by a factor of seven against the successful earlier Joint European Toru (JET) experiment in Culham/Etigland (Hora, Reference Hora2007) being a neutral beam fusion scheme. What had been learnt from IFE is the principle of nonlinear physics (Hora, Reference Hora2000) which can change results from right to completely wrong by neglecting only very tiny effects of linear physics. The tokamak scheme was earlier based on linear physics. On top, several new effects of plasmas internal electric fields E, rotation by E × B forces, anomalous resistivity, turbulence, double layers and others have not been taken into account completely for magnetic confinement. In contrast to this position of MCF, Dean (Reference Dean2008) argues that IFE can be based on a very rich knowledge about tbe involved mechanisms, as known e.g., from underground nuclear explosions (Hora, Reference Hora1991).

The Nuckolls-Wood (Nuckolls et al., Reference Nuckolls and Wood2002) petawatt IFE scheme is based in a very detailed way to reach fusion gains of 10,000. However, it is still not a single-shot scheme because the PW laser generating the very intense 5 MeV electron beam, needs the interaction with highly compressed plasma by an other preceding longer laser pulse. The scheme with the PW-ps nonlinear force driven plasma blocks (Hora, Reference Hora2003, Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007) is a single-shot scheme as aimed by Dean (Reference Dean2008) – if successful – may lead to a drastic simplification for an eventually possible iow cost fusion power plant.

The difficulty for the ignition of solid state density DT was shown by Bobin (Reference Bobin, Schwarz and Hora1974) and Chu (Reference Chu1972) from the result that an energy flux density E* is necessarily limited by

(1)
\hbox{E}^{\ast}\gt \hbox{E}_{\rm o}^{\ast} = 4.5\times 10^{8} \hbox{J/cm}^{2}.

The experiments with TW-ps laser pulses (Badziak et al., Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005) well arrived at values of E* in the range of up to 106 J/cm2, but it is essential that the conditions for the results of Chu (Reference Chu1972) have to be re-examined in view of effects which were discovered later. One of these effects is the strong reduction of the thermal conductivity of the electrons by an “inhibition factor” F*. The re-evaluation of the hydrodynamic analysis of Chu (Reference Chu1972) is reported here how the threshold Eo* of Eq. (1) is changed.

2. REDUCTION OF THERMAL CONDUCTIVITY BY INHIBITION FACTORS

The reduction of the thermal conductivity of the electrons by the inhibition factor F* was discovered in an empirical way from the evaluation of experiments of laser fusion. It was the time when the “fast pusher” was the aim to irradiate spherical pellets (micro balloons) filled with DT gas by laser beams and to measure the fusion gain. The fusion gain was always very much lower than theoretically expected. It was first assumed that there is a very strong preheat of the central parts of the compressed fuel due to hot electrons, but it was clarified that the electric double layers – not known before for these cases – fully prevent the penetration of the expected number of hot electrons into the core. The reason for the failure were the generation of shock waves which destroy the ideal adiabatic compression. Only if the adiabatic compression according to the self-similarity model was verified by empirical variation of the experimental parameters, the highest gains were achieved. This was clearly evaluated, see Figure. 6 in Hora et al. (Reference Hora, Azechi, Kitagawa, Mima, Murakami, Nakai, Nishihara, Takabe, Yamanaka, Yamanaka and Yamanaka1998) as a kind of volume burn as a pre-step to volume ignition, while the evaluation of fast pusher experiments indicated the devastating effect of the shock waves as seen in the mentioned Figure from the fast pusher measurements.

It was a merit of re-calculating the hydrodynamic compression at the experiments in comparison with the measurements and to play with an artificially thermal conductivity corrected by an fitting inhibition factor F*. It was observed that the preheating of plasma interior in a laser irradiated pellet was lower to derive a factor F* = 20 than calculated before (Rockett et al. Reference Rockett, Tarvin, Busch, Charatis, Johnson, Schroeder, Shpepard, Simpson, Slater, Sullivan and Bird1983; Yaakobi et al. Reference Yaakobi, Deletterz, Mccrory, Marjoribanks, Richardson, Shvarts, Soures, Verdon, Villeneuve, Boehli, Hutchinson, Letzring, Hora and Miley1984) and it was discovered that the reduction by a factor F* = 100 was necessary for the fit (Deng et al. Reference Deng, Tao and Wang1982). The further evaluation was from the nonlinear (ponderomotive) force produced cavitons with the inverted double layers (Hora et al., Reference Hora, Lalousis and Eliezer1984).

The explanation by electric double layers was the solution. Electric double layers in inhomogeneous plasmas were well known from ionosphere plasmas, but these were ignored in plasma studies based on the fact that plasmas had about metallic electric conductivity, and as known from homogenous metals, any electric field decays in less than a femtosecond. This arrived at such a dogma, that in a book review about Nobel laureate Alfven's “Cosmic Plasmas”, Kulsrud (Reference Kulsrud1983) denounced that “Alfven's electric fields which are intuitively not clear …” The next step about double layers after the extraterrestrial plasmas originated from the detailed theory of the nonlinear (ponderomotive) forces (Hora, Reference Hora1969, Reference Hora2000). In order to get a more detailed description of the mechanisms of the laser interaction in the inhomogeneous plasmas need the establishing of the genuine two fluid model (Lalousis & Hora, Reference Lalousis and Hora1983, 1991: Sections 8.7-8.9 & 10.7; Hora et al., Reference Hora1984.) with separate hydrodynamics of the electrons and that of the ions with coupling by the Poisson equation led immediately to the electric double layers (Eliezer & Hora, Reference Eliezer and Hora1989) in inhomogeneous plasmas showing the internal electric fields and their complicated dynamic development. For simplified conditions of a plasma surface expanding into vacuum (see Fig. 2.2 in Hora, Reference Hora1991) or at a wall confining a plasma, the Debye layer is generated showing a depletion of electrons. The electrons from the plasma interior are electrically reflected at the ions which remain in the double layer whose positive charge results in an electron return current of the electrons back into the plasma, Figure. 1. The potential step given by kT/2 (one dimension!) corresponds to the work function of the plasma similar to that of a metal surface following the generalization of the Richardson equation for the transmission of exceptionally energetic electrons to produce the thermionic emission [Eliezer et al., Reference Eliezer, Ghatak, Hora and Teller2002: Eq. (1.26)]. The thermal conduction is performed by the ions only and in the equation of energy conservation for the electrons one has to take the ionic thermal conductivity

(2)
\hbox{K}_{\rm i} = \hbox{K}_{\rm e} \lpar \hbox{m}_{\rm e}/\hbox{m}_{\rm i}\rpar ^{1/2}\comma

instead of the electron conductivity Ke, determined by the mass me of the electrons and that mi of the ions. Using the average ion mass of a 50:50 DT plasma, the square root in Eq. (2) defines the inhibition factor of F* = 67.5 in agreement with the semi-empirical evaluation. For a wide spread double layer of an inhomogeneous plasma the hydrodynamic evaluation (Lalousis & Hora, Reference Lalousis and Hora1983; Hora et al., Cicchitelli et al., 1984; Hora Reference Hora1991) results in summary at the same potential step to justify the same inhibition in general.

Fig. 1. The positive charge of the double layer between the hot and the cold plasma causes a return current of the electrons to the hot plasma apart from transmission of exceptionally fast electrons such that the heat transport though the double layer is basically due to ions only Cicchitelli et al., Reference Cicchitelli, Elijah, Eliezer, Ghatak, Goldsworthy, Hora and Laousis1984.

Fig. 2. Evaluations of differences between the computation of Chu Reference Chu(1972)—lowest curve—for the function T(t) at E* = 2.9 × 108 J/cm2 with the here reported computations due to the difference of ion and electron temperature needed for the inclusion of the inhibition factor.

3. REPRODUCTION OF HYDRODYNAMICS WITHOUT INHIBITION

In order to see the importance of the inhibition factor, F* in the hydrodynamic equations, first the results of Chu (Reference Chu1972) are going to be reproduced with a minium of changes in the conditions used before, and in the following section the inhibiton factor will be used. It is to be underlined from the preceding section, that the inibition factor was not at all known at the time of Chu's treatment. The hydrodynamic equations are used as close as possible on the same assumptions as used by Chu (Reference Chu1972). The equations of continuity and reactions (D + T → α +  n) may be combined to yield as equations of mass conservation

(3)
{\partial \rho \over \partial t} + {\partial \over \partial x} \lpar \rho u\rpar = 0

and

(4)
{\partial Y \over \partial t} +u {\partial Y \over \partial x}=W

where ρ is the mass density, u is the mass velocity and Y is the fraction of material burned, defined by

Y = \lpar n_\alpha + n_n \rpar / \lpar n_D+n_T + n_\alpha + n_n \rpar .

W is the reaction rate function, given by

W = {1 \over 2} n \lpar 1 - Y\rpar ^2 \langle \sigma \, \nu \rangle .

It is obvious that Eq. (3) is the same as the mass conservation equation, due to the small percentage (~0.35%) of mass transformed into energy. In the equation for Y, the n's are the particle densities, and the subscripts are for the different particle species. In the equation for W, the n stands for the total number density of the ions.

The equation of motion expressing the conservation of momentum is

(5)
\eqalign{{\partial u \over \partial t} + u{\partial u \over \partial x} & =- \rho^{ - 1} {k \over m_i} {\partial \over \partial x} [\rho \lpar T_i + T_e \rpar ]\cr & \quad + \rho^{ - 1} {\partial \over \partial x} \left[\lpar \mu _i + \mu _e \rpar {\partial u \over \partial x} \right]\comma}

in which pressure and viscosity terms are included. μi,e is the viscosity coefficients whose values are taken to be

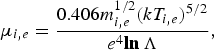
\mu _{i\comma e} = \frac{0.406m_{i\comma e}^{1/2} \lpar kT_{i\comma e} \rpar ^{5/2}}{e^4 {\bf ln} \, \Lambda}\comma \;

where ln Λ is the usual Spitzer logarithm.

The ion and electron temperature equations are expressing the conservation of energy

(6)
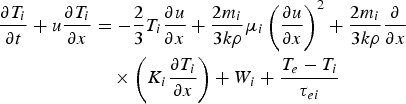
\eqalign{{\partial T_i \over \partial t} + u {\partial T_i \over \partial x} &= - {2 \over 3}T_i {\partial u \over \partial x} + {2m_i \over 3k\rho}\mu _i \left({\partial u \over \partial x}\right)^2 + {2m_i \over 3k\rho}{\partial \over \partial x} \cr & \quad \times \left(K_i {\partial T_i \over \partial x}\right)+ W_i + {T_e - T_i \over \tau _{ei}}}

and

(7)
\eqalign{{\partial T_{e} \over \partial x} + u{\partial T_{e} \over \partial x} &= - {2 \over 3}T_e {\partial u \over \partial x} + {2m_{i} \over 3k\rho}\mu_e \left({\partial u \over \partial x}\right)^2 + {2m_{i} \over 3k\rho} {\partial \over \partial x} \cr & \quad \times \left(K_e {\partial T_{e} \over \partial x}\right)+ W_e + {T_{i} - T_{e} \over \tau_{ei}} - A\rho T_e^{1/2}\comma \; }

where included on the right-hand side are the pressure, viscosity, conductivity, thermonuclear energy generation, equilibration terms, and energy transfer terms W 1 and W 2 following Chu (Reference Chu1972). The last term on the right-hand side of Eq. (7) is the bremsstrahlung term.

For the following reported computations the bremsstrahlung is based on the electron temperature T e working with Eq. (15) of Chu (Reference Chu1972) with the maximum at x = 0, thus,

(8)
W_i+W_e = A\rho T_e ^{1/2} + {8 \over 9} \lpar {k/m_i}\rpar \lpar 1/aT_{e} ^{1/2}\rpar + {2 \over 9} \lpar {T_e } / t \rpar

Eq. (8) is a little different from Eq.(20) of Chu (Reference Chu1972) where T i = T e is assumed, while the following computations with the inhibition factor has to be for general temperatures.

For comparison of the results, the development of the temperature on time t given in Figure 2 of Chu (Reference Chu1972) is used to be compared with the following new output of the ion temperature T i = T instead. The results of Chu's Figure 2 for the special case of an input energy flux density of E* = 2.9 × 108 J/cm2 are compared with the new calculations. It is seen that the results of Chu are up to few percents lower in some ranges of time but basically comparable with the new results.

4. IGNITION THRESHOLD WITH INHIBITION

The problem discussed here is that the thermal conductivity Ke for the electrons in Eq. (6) has to be modified by the inhibition factor F* which initially was discovered after the work of Bobin (Reference Bobin, Schwarz and Hora1974) and Chu (Reference Chu1972) from numerical evaluation of the hydrodynamic properties of laser irradiated plasmas and how to fit with measurements as explained in Section 2.

The following numerical evaluation of the hydrodynamic equations uses practically all of the input parameters as in the work by Chu (Reference Chu1972). A minor modification is that now the electron and ion temperature have to be included separately for the following evaluation with the inhibition factor. This results in a slight difference seen in Fig. 2. which was done for comparison with the results given in Figure 2. of Chu (Reference Chu1972). The new results in Figure 3 are practically identical for the given parameters of input energy flux density apart from some minor differences in the range of less than few percents due to the here used difference of the electron and ion temperature.

Fig. 3. Temperature T (in keV) dependence of the ions on time t in ns at non-ignition cases compared with the threshold ignition temperature for DT at 7.3 keV for cases with irradiation by an energy flux of E* = 2.9 × 1015 erg/cm2 and lower values for comparison with the calculations of Chu (Reference Chu1972) reported in his Figure 2 without the inhibition factor.

What is important for the physics is that the same ignition threshold for an input energy flux of E* = 4.75 × 108 J/cm2 is resulting from the plasma temperature T(t) given by the ion temperature, showing saturation at longer times t in perfect agreement also with Bobin (Reference Bobin, Schwarz and Hora1974). For lower E*, the temperature reached a maximum at about the time of t = 1ns and decreased then indicating absence of ignition. It is interesting that the threshold ignition line is at 7.3 keV. This is interesting since the detailed evaluation of the spark ignition laser fusion of Storm et al. (Reference Storm, Lindl, Campbell, Bernat, Coleman, Emmett, Hogan, Horst, Krupke and Lowdermilk1988) arrived at nearly the same temperature (Hora et al., 1998) for the fusion detonation wave between the volume ignited low density high temperature core and the high density mantle of low temperature.

Using the inhibition factor F* = 67.5 from Eq. (2) results in T(t) dependences for parameters E* as shown in Figure 4. We see that the non-igniting values E* of Figure 3 are now appearing at the lower value E* = 1.08 × 108 J/cm2. The result is that the ignition energy flux density E* was reduced by a factor 4.398 by the inhibition factor compared with the earlier values of Chu (Reference Chu1972) without inhibition which was not known then. This reduction of the ignition threshold is a rather important step in favour of the nonlinear force driven plasma block ignition (Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007) as one of the modifications of fast ignition (Tabak et al., 1984) by ion beams. This improvement may be in favour also for the electron beam ignition of Nuckolls and Wood (Reference Nuckolls and Wood2002).

Fig. 4. Same as Figure 3 with an inhibition factor of F* = 67.76 for a the Debye sheath produced electric double layer in the inhomogeneous DT plasma showing ignition for energy flux densities E* above 1.08 × 108 J/cm2.

5. RETROGRADE PROPERTIES AT EARLY TIMES

It should be noted that T(t) in Figure 4 for times at 0.5 ns or less is slightly higher even for lower E*. Figure 5 shows more details of this kind of retrograde property. This is due to the competitive mechanisms of electronic heating compared with the adiabatic cooling of the ions which may be slower at lower E*. This is well known from volume ignition (Hora et al., 1998) if higher than the optimum energy input is used and a subsequent faster adiabatic expansion and cooling follows with reduction of the thermonuclear fusion gain below the maximum values at the optimum temperature see the parabolas in Figure 13.6 Hora (Reference Hora1991) or in Figure 2 in Ref. Miley et al. (Reference Miley, Hora, Osman, Evans and Toups2005).

Fig. 5. Same as Figure 3 with stretched abscissa to show the retrograde behaviour of curves T(t) between times t up to 0.7 ns. With higher temperature T at lower irradiation energy flux density as parameter.

The more complicate conditions of such a retrograde behaviour was found in the evaluation of the volume ignition gain computation for the hydrogen-boron(11) reaction as it was clarified before (Scheffel et al., Reference Scheffel, Stening, Hora, Hopfl, Martinez-Val, Eliezer, Kasotakis, Pieara and Sarris1997). This is similar also for the inertial confinement fusion reaction at volume ignition of pellets consisting of the pure 3He isotope (Khoda-Bakhsh et al., Reference Khoda-Bakhsh, Soltanian and Amniat-Talab2007). The effect seen in Figure 5 is of too little value that a more detailed evaluation is indicated, but at least it was necessary to mention this final result of the computations presented here, that such a retrograde property can appear in the research of inertial confinement fusion nuclear reactions.

6. DISCUSSION

There are many further questions open, how the results of Chu (Reference Chu1972) have to be modified due to other processes than the inhibition factor, which were not included in the computations. The results reported here are covering only the hydrodynamic description of the properties while it was noted that this cannot cover the complicate mechanisms of the interpenetration between the hot plasma block with highly directed velocities interacting with the cold DT fusion fuel at block ignition. At least the inhibition factor was now evaluated which in continuation of the research of Chu (Reference Chu1972) and Bobin (Reference Bobin, Schwarz and Hora1974) is arriving at a remarkable improvement of the ignition condition. About an attempt to consider the interpenetration phenomena, estimations of further improvements were shown by Hora (Reference Hora1984). The new developments with particle-in-cell (PIC) computations (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Klimo Reference Klimo and Limpouch2006; Patin et al., Limpouch, Reference Patin, Lefebvre, Bourdier and D'humieres2006) may provide a tool for these studies, however the collision and dissipation processes have additionally to be incorporated into these procedures as well as the ionisation mechanisms in the fusion fuel (Eisenbarth et al., Reference Eisenbarth, Rosmei, Shevelko, Blazevic and Hoffmann2007).

ACKNOWLEDGMENT

The authors M. Ghoranneviss and B. Malekynia gratefully acknowledge encouragement for fusion energy research at the Plasma Physics Research Center of I.A.U. by the International Atomic Energy Agency (IAEA) in Vienna/German-Austria based on the Coordinate Research Program C.R.P. Contract No. 13508. The author Heinrich Hora thanks Professor Reza Amrollahi for discussions at the International Centre of Theoretical Physics (ICTP) in Trieste/Italy and for remarks about the results of Bobin (Reference Bobin, Schwarz and Hora1974) at a seminar at the Tehran Polytechnic University Amirkabir, and gratefully acknowledges encouraging guidance by publications of His Eminency Cardinal Graf Schönborn, Vienna.

References

REFERENCES

Badziak, J., Kozlov, A.A., Makowksi, J., Parys, P., Ryc, L., Wolowski, J., Woryna, E. & Vankov, A.B. (1999). Investigation of ion streams emitted from plasma produced with a high-power picosecond laser. Laser Part. Beams 17, 323–329.CrossRefGoogle Scholar
Badziak, J., Hora, H., Woryna, S., Jablonski, S., Laska, L., Parys, P., Rohlena, K. & Wolowski, J. (2003). Experimental evidence of differences of fast ion fluxes from short-pule and long-pulse laser-plasma interaction. Phys. Lett A 312, 452–457.CrossRefGoogle Scholar
Badziak, J., Glowacz, S., Jablonski, S., Parys, P., Wolowski, J. & Hora, H. (2004). Production of ultrahigh-current-density ion beams by short-pulse laser-plasma interaction. App Phys. Lett 85, 3041–3043.CrossRefGoogle Scholar
Badziak, J., Glowacz, S., Jablonski, S., Parys, P., Wolowski, J. & Hora, H. (2005). Generation of picosecond high-density ion fluxes by skin-layer laser-plasma interaction. Laser Part. Beams 23, 143–148.CrossRefGoogle Scholar
Badziak, J., Glowacz, S., Hora, H., Jablonski, S. & Wolowski, J. (2006). Studies of laser driven generation of fast-density plasma blocks for fast ignition. Laser Part. Beams 24, 249–254.CrossRefGoogle Scholar
Bobin, J.L. (1974). Nuclear fusion reactions in fronts propagating in solid DT, In Laser Interaction and Related Plasma Phenomena, Schwarz, H. & Hora, H., eds., Vol. 4B, pp. 465–494, New York: Plenum Press.CrossRefGoogle Scholar
Chu, M.S. (1972). Thermonuclear reaction waves at high densities. Phys. Fluids 15, 413.CrossRefGoogle Scholar
Cicchitelli, L., Elijah, J.S., Eliezer, S., Ghatak, A.K., Goldsworthy, M.P., Hora, H. & Laousis, P. (1984). Pellet fusion gain calculations modified by electric double layers and by spin polarized nuclei. Laser Part. Beams 2, 467–475.CrossRefGoogle Scholar
Dean, S.O. (2008). The Rationale for an Expanding Inertial Fusion Energy Program. J. Fusion Energy 27, No. 4, available from http://springerlink.metropress.com. or IFE_whitepaper.pdf.CrossRefGoogle Scholar
Deng, Xi-Ming, Tao, Wao-Hai & Wang, Run-Wen (1982). Hydrodynamic evaluation of laser irradiated pellets. Plasma Nucl. Fusion China 1, 187.Google Scholar
Eliezer, S. & Hora, H. (1989). Double-layers in laser-produced. Phys. Rept. 172, 339–407.CrossRefGoogle Scholar
Eliezer, S., Ghatak, A.J., Hora, H. & Teller, E. (2002). Fundamentals of Equations of State. Singapore: World Scientific.CrossRefGoogle Scholar
Esirkepov, T., Borghesi, M., Bulanov, S.V., Mourou, G. & Tajima, T. (2004). Highly efficient relativistic-ion generation in the laser-piston regime. Phys. Rev. Lett. 92, 175003/1-4.CrossRefGoogle ScholarPubMed
Eisenbarth, S., Rosmei, O.N., Shevelko, V.P., Blazevic, A. & Hoffmann, D.H.H. (2007). Numerical simulations of the projectile ion charge difference in solid gaseous stopping matter. Laser Pat. Beams 25, 601–612.CrossRefGoogle Scholar
Hoffmann, D.H.H., Blazevic, A., Ni, P., Rosemej, P., Roth, M., Tahir, N.A., Tauschwitz, A., Udrea, S., Varentsov, D., Weyrich, K. & Maron, Y. (2005). Present and future perspectives for high energy density physics with intense heavy ion and laser beams. Laser Part. Beams, 23, 47–53.CrossRefGoogle Scholar
Hora, H. (1969). Nonlinear confining and deconfining forces associated with the interaction of laser radiation with plasma, Phys. Fluids 12, 182–191.CrossRefGoogle Scholar
Hora, H. (1975). Theory of relativistic self-focusing of laser radiation in plasmas, J. Opt. Soc. Am. 65, 882–886.CrossRefGoogle Scholar
Hora, H. (1984). Interpenetration burn for controlled inertial confienement fusion by nonlinear forces. Atomkernenergie 42, 7–10.Google Scholar
Hora, H. (1991). Plasmas at High Temperature and Density. Heidelberg: Springer.Google Scholar
Hora, H. (2000). Laser Plasma Physics: Forces and the Nonlinearity Principle. Bellingham WA: SPIE Press.Google Scholar
Hora, H. (2002). Fusion reactor with petawatt laser. German Patent Disclosure (Offenelgungsschrift) DE 102 08 515 A1 (28 FEB 2002, declassified 5 SEP 2002).Google Scholar
Hora, H. (2003). Skin-depth theory explaining anomalous picosecond-terawatt laser-plamsa interaction. Czech. J. Phys. 53, 199–217.CrossRefGoogle Scholar
Hora, H. (2007). New aspects for fusion energy using inertial confinement Laser Part. Beams 25, 37–45.CrossRefGoogle Scholar
Hora, H., Lalousis, P. & Eliezer, S. (1984). Analysis of the inverted double layers in nonlinear force produced cavitons at laser-plasma interaction, Phys. Rev. Lett. 53, 1650–1652.CrossRefGoogle Scholar
Hora, H, Azechi, H., Kitagawa, Y., Mima, K., Murakami, M., Nakai, S., Nishihara, K., Takabe, H., Yamanaka, C., Yamanaka, M. & Yamanaka, T. (1998). Measured laser fusion gains reproduced by self-similar volume compression and volume igntion for NIF conditions. J. Plasma Phys. 60, 743–760.CrossRefGoogle Scholar
Hora, H., Badziak, J., Boody, F., Höpfl, R., Jungwirth, K., Kralikova, B., Kraska, J., Laska, L., Parys, P., Perina, P., Pfeifer, K. & Rohlena, J. (2002). Effects of picosecond and ns laser pulses for giant ion source. Optics Commun. 207, 333–338.CrossRefGoogle Scholar
Hora, H., Badziak, J., Read, M.N., Li, Y-T, Liang, T-J, Liu, H., Sheng, Z-M., Zhang, J., Osman, F., Miley, G.H., Zhang, W., He, X., Peng, H., Glowacz, S., Jablonski, S., Wolowski, J., Skladanowski, Z., Jungwirth, K., Rohlena, K. & Ullschmied, J. (2007). Fast ignition by laser driven particle beams of very high intensity Phys. Plasmas 14, 072701-1/072701-7.CrossRefGoogle Scholar
Khoda-Bakhsh, R., Soltanian, A., Amniat-Talab, M. (2007). Volume ignition of 3He pellets. Nucl. Instrum. & Methods A 581, 839–843.CrossRefGoogle Scholar
Klimo, O. & Limpouch, J. (2006). Particle simulation of acceleration of quasineutral plasmas blocks by short laser pulses. Laser Part. Beams 24, 107–112.CrossRefGoogle Scholar
Kulsrud, R. (1983). Book Review. Physics Today 34 No. 4, 56 (3rd Col. 7th line).Google Scholar
Lalousis, P. & Hora, H. (1983). First direct electron and ion fluid computation of high electrostatic fields in dense inhomogeneous plasmas with subsequent nonlinear laser interaction, Laser Part. Beams 1, 283–304.CrossRefGoogle Scholar
Miley, G.H., Hora, H., Osman, F., Evans, P. & Toups, P. (2005). Single event laser fusion using ns. MJ laser pulses. Laser Part. Beams 23 (4): 453–460.CrossRefGoogle Scholar
Nuckolls, J.H. & Wood, L. (2002). Future of Inertial Fusion Energy. Preprint UCRL-JC-149860. Livermore, CA: Lawrence Livermore National Laboratory.Google Scholar
Patin, D., Lefebvre, E., Bourdier, A. & D'humieres, E. (2006). Stochastic heating in ultra high intensity laser-plasma interaction:theory and PIC code simulations. Laser Part. Beams 24, 223.CrossRefGoogle Scholar
Rockett, P.C., Tarvin, J.A., Busch, G.A., Charatis, G., Johnson, R.R., Schroeder, R., Shpepard, C.L., Simpson, J.D., Slater, D.C., Sullivan, D. & Bird, C.K. (1883). Fast pusher experiments for laser irradiated fusion pellets. Europhysics Conference Abstracts (Fusion Aachen) 7D, 11.Google Scholar
Roth, M., Brambrink, E., Audebert, B., Blazevic, A., Clarke, R., Cobble, J., Geissel, M., Habs, D., Hegelich, M., Karsch, S., Ledingham, K., Neelz, D., Ruhl, H., Schlegel, T. & Schreiber, J. (2005). Laser accelerated ions and electron transport in ultra-intense laser matter interaction. Laser Part. Beams 23, 95–100.CrossRefGoogle Scholar
Sauerbrey, R. (1996). Acceleration of femtosecond laser produced plasmas, Phys. Plasmas 3, 4712–4716.CrossRefGoogle Scholar
Scheffel, C.H.R., Stening, R.J., Hora, H., Hopfl, R., Martinez-Val, J.M., Eliezer, S., Kasotakis, G., Pieara, M. & Sarris, E. (1997). Analysis of the retrograde hydrogen boron fusion gains at inertial confinement fusion with volume ignition. Laser Part. Beams,15, 565–574.CrossRefGoogle Scholar
Storm, E., Lindl, J.D., Campbell, E.M., Bernat, T.P., Coleman, I.W., Emmett, J.L., Hogan, W.J., Horst, Y.T., Krupke, W.F. & Lowdermilk, W.H. (1988). Progress in Laboratory High-Gain ICF: Progress for the future. LLNL Report 47312. Livermore, CA: LLNL.Google Scholar
Tabak, M., Hammer, J., Glinsky, M.N., Kruer, W.L., Wilks, S.C, Woodworth, J., Campbell, E.M., Perry, M.D. & Mason, R.J. (1994). Ignition and high gain with ultrapowerful lasers, Phys. Plasmas 1, 1626–1634.CrossRefGoogle Scholar
Yaakobi, B., Deletterz, R.L., Mccrory, R.L., Marjoribanks, R.L., Richardson, M.C., Shvarts, D., Soures, J.M, Verdon, C., Villeneuve, D.B., Boehli, T., Hutchinson, R. & Letzring, S. (1984). Thermal transport measurement in 1.05 µm laser irradiation on spherical targets. Laser Interaction and Related Plasma Phenomena, Hora, H. and Miley, G.H. eds., Vol. 6, pp. 731–570, New York: Plenum Press.CrossRefGoogle Scholar
Zhang, P., He, J.T., Chen, D.B., Li, Z.H., Zhang, Y., Wong, L., Li, Z.H., Feng, B.H., Zhang, D.X., Tang, X.W. & Zhang, J. (1998). X-ray emission from ultraintense-ultrashort laser irradiation. Phys. Rev., E57, 3746–3752.Google Scholar
Figure 0

Fig. 1. The positive charge of the double layer between the hot and the cold plasma causes a return current of the electrons to the hot plasma apart from transmission of exceptionally fast electrons such that the heat transport though the double layer is basically due to ions only Cicchitelli et al., 1984.

Figure 1

Fig. 2. Evaluations of differences between the computation of Chu (1972)—lowest curve—for the function T(t) at E* = 2.9 × 108 J/cm2 with the here reported computations due to the difference of ion and electron temperature needed for the inclusion of the inhibition factor.

Figure 2

Fig. 3. Temperature T (in keV) dependence of the ions on time t in ns at non-ignition cases compared with the threshold ignition temperature for DT at 7.3 keV for cases with irradiation by an energy flux of E* = 2.9 × 1015 erg/cm2 and lower values for comparison with the calculations of Chu (1972) reported in his Figure 2 without the inhibition factor.

Figure 3

Fig. 4. Same as Figure 3 with an inhibition factor of F* = 67.76 for a the Debye sheath produced electric double layer in the inhomogeneous DT plasma showing ignition for energy flux densities E* above 1.08 × 108 J/cm2.

Figure 4

Fig. 5. Same as Figure 3 with stretched abscissa to show the retrograde behaviour of curves T(t) between times t up to 0.7 ns. With higher temperature T at lower irradiation energy flux density as parameter.