2.1 Flight trajectory optimisation

The objective of a flight trajectory optimisation process is to identify the optimal flight profile for a particular optimisation problem defined by the aircraft model (flight performance and envelope limitations), initial aircraft load and fuel quantity, initial and final trajectory points data and constraints (crossing time at the initial point, initial and final aircraft geographic locations, altitudes and speeds), navigation constraints, atmospheric conditions and selected optimisation criteria. The optimisation criterion is, in general, the minimisation of a cost function (e.g. minimisation of fuel burn, total cost, flight time, etc.). However, it can also be a maximisation of the cost function (e.g. maximum loitering time, etc.).

An aircraft flight trajectory can be decomposed into two components:

• A lateral flight profile, represented by the projection of the flight trajectory onto the Earth’s surface; and

• A vertical flight profile, defined by the evolution of the aircraft’s flight parameters (e.g. altitude, speed, vertical speed/rate of climb or descent/angle of climb or descent, acceleration/deceleration, load factor, etc.) along the lateral flight profile.

In still air (no wind), International Standard Atmosphere (ISA) conditions and the absence of navigation constraints, the optimal lateral flight profile is the orthodromic route (the shortest route on the sphere/ellipsoid) between the initial and final point of the flight plan under optimisation. The optimal vertical flight profile is specific to the aircraft model, aircraft weight and the cost function selected as optimisation criterion. When real atmospheric conditions are taken into account, i.e. wind and non-standard atmospheric temperature conditions, it may be advantageous to deviate from the orthodromic route, and to perform altitude and speed changes to benefit from more advantageous wind and air temperature conditions.

A flight trajectory optimisation process is conducted by successively evaluating flight trajectory profiles from a set of candidate flight profiles, in each step retaining as solution the ‘best’ flight profile relative to the cost function and criterion set as objective for the optimisation. The optimisation process can be conducted for only one or for both components of the flight profile. In the former case, one of the components of the flight plan (lateral or vertical) is common to all the candidate flight plans while the other component is different for each candidate flight plan. In the latter case, both flight plan components can change.

The methodologies used to generate the set of candidate flight plans and select the flight plan to be evaluated at each step of the optimisation process are heuristic methods, selected depending on the specific optimisation problem, selected cost function, constraints, etc.

For flight plans with navigation constraints (e.g. altitude, time, etc.), the constraints take precedence relative to the flight profile’s optimality. If the constraints are not satisfied, the flight plan is considered non-valid and rejected. Similarly, a flight plan is considered non-valid and is rejected if:

• The flight profile generated based on the flight plan yields aircraft flight parameters that are beyond the aircraft’s flight envelope boundaries; or if

• The flight along the resulted flight profile requires more fuel than is available.

The particular optimisation problem considered in this paper is specific to the cases where:

• The flight plans do not have navigation constraints;

• Both the lateral and vertical components of the flight plan can be modified during the optimisation; and

• The objective is to minimise the total cost for the flight.

The total cost for a flight is calculated as the sum of the fuel cost and the operational costs, which are proportional to the flight time and expressed as fuel quantity (kg of fuel). A detailed presentation of the total cost function, and the elements that contribute to it, can be found in refs. (Reference Robertson39–Reference Dejonge and Syblon41).

The total cost is calculated using the following formula:

(1) \begin{equation}TC = fuel\_burn + CI\; \times \;fligh\_time\; \times \;60\end{equation}

where:

• TC is the total cost, expressed in terms of fuel quantity [kg of fuel];

• fuel_burn is the fuel burned for the flight along the evaluated flight profile [kg of fuel];

• flight_time is the flight time for the flight along the evaluated flight profile [h]; and

• CI, the cost index, is a constant (specific to each airline, aircraft type and route) that converts the flight time into operational costs expressed in terms of fuel quantity [kg of fuel/min].

The CI value adjusts the optimisation to obtain a trade-off between the fuel consumption and the flight time; the larger the CI value, the greater the weight that is attributed to the reduction of the flight time in the optimisation process.

If CI = 0, the optimisation criterion becomes fuel burn minimisation. When the CI value reaches a maximum value (e.g. 999), specific for a platform, the optimisation criterion becomes flight time minimisation.

The flight performance and aircraft dynamics (e.g. fuel burn, flight time, speeds, accelerations, travelled distances, etc.) parameters are calculated by performing an accelerated simulation of the flight along the evaluated flight profile. These calculations are performed using an Aircraft Performance Model (APM) specific to the aircraft type, the atmospheric data along the flight profile (wind and air temperature), the aircraft’s configuration parameters (mass, engine thrust setting, landing gear, flaps and speed brake positions, etc.) and the flight profile’s data (speed, climb/descent angle, bank angle, load factor, etc.).

The method presented in this paper does not take into account any navigation constraints (such as restricted areas or airways, Required Time of Arrival (RTA), etc.), and adopts the TBO/‘free flight’ paradigm; the aircraft is thus free to fly along the trajectory that is best suited for the origin–destination pair, atmospheric conditions, aircraft performance and load.

2.2 Aircraft performance model (APM)

The APM used in this study is the Base of Aircraft Data (BADA) version 4.0⁽⁴²⁾, developed and maintained by Eurocontrol. The APM provides specific aircraft type data (i.e. mathematical models and the related coefficients for the aircraft parameters, valid aircraft flight configurations, flight envelope limitations, etc.), a methodology for calculating the aero propulsive forces acting on the aircraft, the aircraft motion as a result of these forces (equations based on the Total Energy Model (TEM)) and the associated fuel burn. An overview of the BADA APM can be found in refs. (42–Reference Nuic, Poles and Mouillet43), ref (44) (for BADA version 3.7) and ref. (Reference Nuic45) (for BADA version 3.8). Specific information regarding the BADA version 4.0 APM can be obtained from Eurocontrol⁽⁴²⁾ upon request, and is subjected to a licence agreement.

The set of input parameters used in the calculation of the flight performance parameters, and in the aircraft’s evolution along the flight path, their range of valid values and units of measurement, are specific to the APM. As an example, the input parameters can be:

• Aircraft configuration parameters: aircraft mass, centre of gravity position, landing gear position, flaps/slats position, spoilers/speed brakes position, etc.;

• Engine parameters: These parameters are specific to the engine type. For a jet engine, they can be the Thrust Lever Angle (TLA), engine fan speeds, etc.;

• Atmospheric conditions: air temperature and wind; and

• Flight trajectory parameters: altitude, speed, acceleration/deceleration, bank angle, load factor, climb/descent angle, rate of climb/descent, etc.

A flight trajectory is composed of a succession of elementary flight profile types (e.g. constant-speed cruise segment, acceleration/deceleration cruise segment, constant-speed constant-TLA climb/descent, constant-TLA constant-rate-of-climb accelerated climb segment, etc.). Depending on the type of flight profile evaluated, some of the parameters presented above are input parameters while others are output parameters (resulting from the flight performance calculations). For example, for a cruise segment at constant altitude and constant speed, a selected speed (an input parameter) will require a specific engine thrust setting and thus fuel burn rate (an output parameter) to maintain the selected speed and altitude. Conversely, a selected engine thrust setting (an input parameter) will determine the speed and fuel burn rate (output parameters). The flight trajectory performance calculation model, developed using the APM, implements a specific performance calculation function for each elementary flight profile type and set of output parameter(s) of interest.

2.3 Atmospheric data

Atmospheric conditions have an important influence on aircraft flight performance characteristics and dynamics. The air temperature influences the engine performance and, as a result, affects the available thrust, the maximum altitude for a selected speed, the minimum and maximum speeds at a selected altitude, the fuel burn rate, etc. The aircraft speed along the flight trajectory is defined in terms of the Indicated Air Speed (IAS) or MACH number. The aircraft’s aerodynamic characteristics are functions of the True Airspeed (TAS), which is the aircraft’s speed relative to the mass of air. The aircraft’s evolution along the flight trajectory is a function of the ground speed (GS), which is the aircraft’s speed relative to the ground. The TAS value, computed as a function of the active speed value and its type (IAS or MACH), is affected by the air temperature and static pressure values.

For MACH speeds, the TAS is expressed only as a function of the air temperature^{(Reference Botez46)}:

(2) \begin{equation}TAS = M\sqrt {\gamma RT} = M\sqrt {\gamma R{T_0}} \sqrt {\frac{T}{{{T_0}}}} = M{a_0}\sqrt \theta \end{equation}

where:

• M is the Mach number;

• $\gamma $ = 1.4 is the adiabatic index for air;

• R = 287.05J/kg/K is the universal gas constant for dry air;

• T is the air temperature [K];

• T ₀ = 288.15K is the standard air temperature at Sea Level Altitude (SLA), considered as 0ft, in International Standard Atmosphere (ISA) conditions;

• ${a_0} = \sqrt {\gamma R{T_0}} =340.29\;{\rm{m}}/{\rm{s}}$ is the speed of sound at SLA in ISA conditions; and

• $\theta = \;\frac{T}{{{T_0}}}$ is the air temperature ratio relative to the ISA SLA air temperature.

For a flight in the IAS speed mode, in the subsonic regime, when air compressibility effects are neglected, the relationship between the TAS and the IAS is described in ref. (Reference Botez46):

(3) \begin{equation}TAS = {a_0}\sqrt {5\theta \left[ {{{\left( {\frac{{{q_c}}}{{{p_s}}}+1} \right)}^{3.5}} - 1} \right]} \end{equation}

where q _c is the dynamic pressure computed for the IAS speed at the SLA in ISA conditions:

(4) \begin{equation}{q_c} = {p_{s0}}\left\{ {{{\left[ {1+0.2{{\left( {\frac{{IAS}}{{{a_0}}}} \right)}^2}} \right]}^{3.5}} - 1} \right\}\end{equation}

and:

• a₀ is the speed of sound at SLA and in ISA conditions;

• $\theta $ is the air temperature ratio relative to the ISA SLA air temperature;

• p _S is the static air pressure at the flight altitude (pressure altitude);

• p _S0 = 101,325Pa is the static air pressure at SLA (0 ft) in ISA conditions; and

• IAS is the scheduled speed that is converted to TAS.

An aircraft flight trajectory is composed of segments defined by a set of fixed geographic points (waypoints (WPTs)) selected between the departure and destination points. In still air, in the absence of winds, the aircraft’s heading is the segment heading at the aircraft location and the GS is equal to the TAS. In the presence of winds, for the aircraft’s trajectory to follow the segment’s track, the aircraft’s heading must change (a process called ‘crabbing’) so that the GS vector’s direction, resulting as the vectorial summation between the TAS and wind vector, is oriented along the segment’s heading at that location. The GS value and the aircraft’s crabbing angle ( ${\alpha _{CRB}}$ . ) relative to the segment heading are computed using the wind triangle algorithm^{(Reference Botez46)}. Their expressions are:

(5) \begin{equation}\left\{ {\begin{array}{*{20}{l}}{GS}&=&{\left( {{W_V}cos{\alpha _{Segm}} + {W_U}sin{\alpha _{Segm}}} \right) + \sqrt {{{\left( {TAScos{\alpha _{CD}}} \right)}^2} - {{\left( {{W_V}sin{\alpha _{Segm}} - {W_U}cos{\alpha _{Segm}}} \right)}^2}} }\\{{\alpha _{CRB}}}& = &{\frac{{180}}{\pi }arcsin\left( {\frac{{{W_V}\sin {\alpha _{Segm}} - {W_U}\;cos{\alpha _{Segm}}}}{{TAS}}} \right)}\end{array}} \right.\end{equation}

where:

• GS is the ground speed;

• ${\alpha _{CRB}}\;$ is the aircraft’s crabbing angle relative to the segment heading;

• TAS is the true airspeed;

• W _V and W _U are the wind speed components along the geographic north and east axes;

• ${\alpha _{CD}}$ is the aircraft’s climb/descent angle; and

• ${\alpha _{Segm}}$ is the flight trajectory segment’s heading, relative to geographic north, at the aircraft’s location.

Equations (3), (4) and (5) show that the air temperature and the wind affect the TAS and the GS values. This influence, in turn, affects the flight performance (lift, drag, required thrust, etc.) and the flight trajectory/dynamics: the flight times along and/or the lengths (ground distances) of the segments composing the flight profile (climb/descent distances, climb/descent speeds, rate of climb/descent, etc.). For an accurate estimation of the aircraft’s trajectory and flight performance parameters, it is therefore necessary to perform the calculations using atmospheric conditions that are as close as possible to the real conditions encountered during flight.

The atmospheric conditions (i.e. air temperature and wind) are constantly changing, and at each time instance, their values are different, being functions of the geographic location (latitude and longitude) and the altitude of the point where they are measured. The atmospheric data used in flight performance calculations are generated based on prediction data issued by meteorological agencies. Due to the chaotic nature of the atmosphere and to the limitations of the atmosphere models used in the prediction process, atmospheric data predictions issued by the meteorological agencies may differ from the actual atmospheric conditions occurring at the prediction location (latitude, longitude and altitude) and time. The magnitudes of the prediction errors vary as a function of the forecast type (global or regional) and resolution (forecast grid size), the time of year, the time of day (day or night), region, how far ahead in time the prediction is made, etc.^{(Reference Lee, Weygandt, Schwartz and Murphy27,Reference Stohl47–Reference Cole, Green, Jardin, Schwartz and Benjamin50)} .

The atmospheric data used in this study are a Global Deterministic Prediction System (GDPS)⁽⁵¹⁾ forecast issued by Environment Canada in GRIB2^(52,53) data file format. GDPS is a global level forecast, issued twice a day, at 00h and 12h Coordinated Universal Time (UTC), that provides atmospheric data forecasts at the nodes of a 4D grid (latitude, longitude, pressure altitude and time) in the following format:

• On a latitude–longitude map projection, available with two grid resolutions: 0.25° × 0.25°⁽⁵⁴⁾ and 0.6° × 0.6°⁽⁵⁵⁾;

• At a fixed set of 27 isobaric levels (pressure altitudes); and

• The forecasts are made at 3-h intervals, for 240h for the 0.25° × 0.25° grid, and 144h for the 0.6° × 0.6° grid.

Therefore, each atmospheric parameter of interest (air temperature and wind) can be computed as a function f(lat, lon, static air pressure, t) of the location of the point (latitude, longitude and pressure altitude) and the time instant for which they are evaluated.

Graphical illustrations of a GDPS atmospheric data forecast (air temperature and winds) on a 0.6° × 0.6° grid, issued by Environment Canada on 25 February 2019, at 12:00 UTC, for 25 February 2019, at 21:00 UTC, at a pressure altitude of 300hPa (30,065f.), cropped to a geographic area delimited by latitude 10ºN and 75ºN and longitude 130ºW and 30ºE, are presented in Figs 1 and 2.

Figure 1. Example of air temperature forecast data issued by Environment Canada on 25 February 2019 at 12 UTC for 25 February 2019 at 21 UTC, at 300hPa pressure altitude.

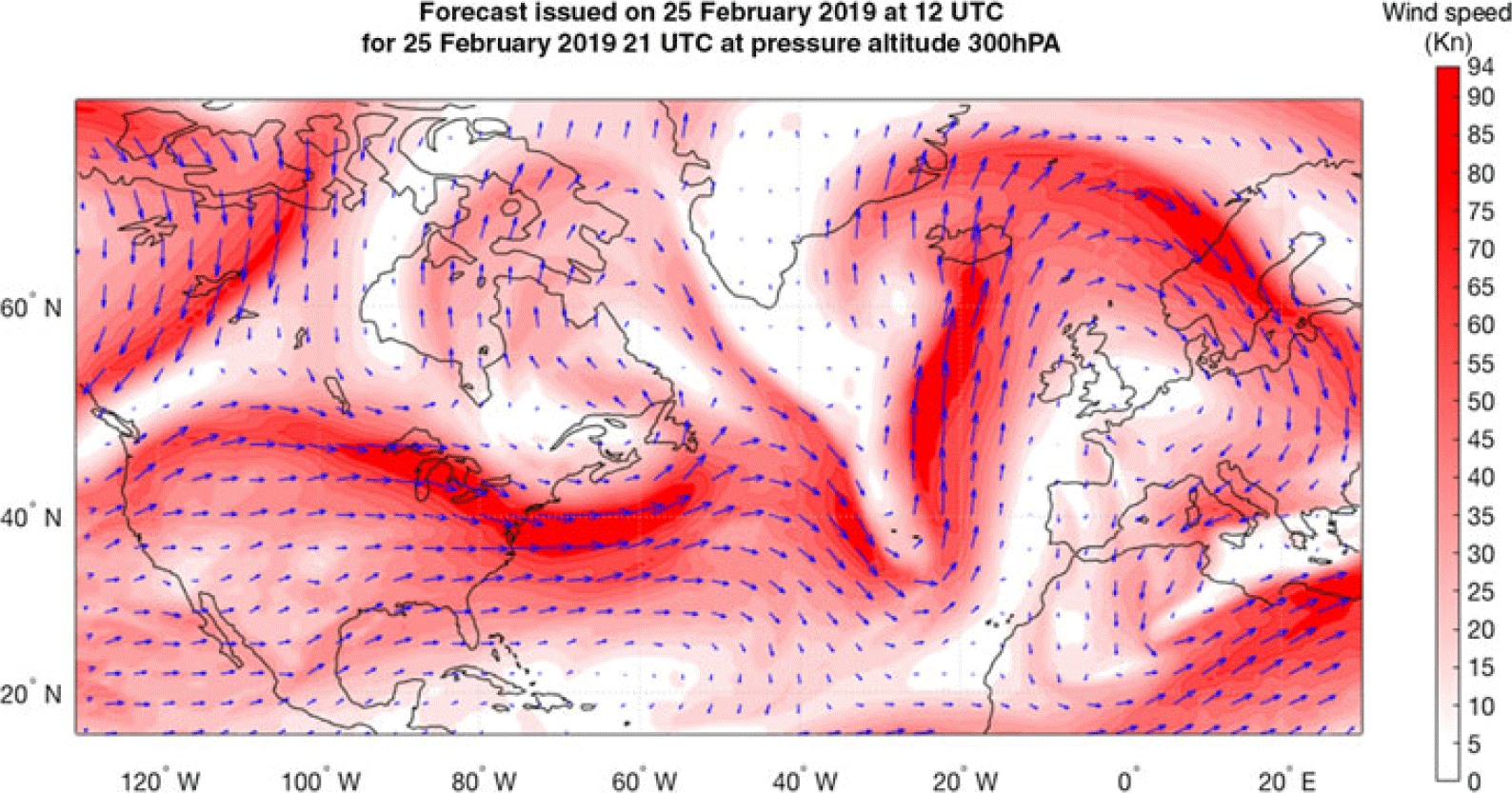
Figure 2. Example of wind forecast data issued by Environment Canada on 25 February 2019 at 12 UTC for 25 February 2019 at 21 UTC, at 300hPa pressure altitude.

The atmospheric parameters at a point other than a node of the forecast’s 4D grid are computed by interpolation. The method selected in this study for atmospheric parameter interpolation is ‘4D linear interpolation’, as predominantly used in flight trajectory optimisation algorithms and flight trajectory performance calculations^{(Reference Stohl47,Reference Schwartz, Benjamin, Green and Jardin48,Reference Stohl, Wotawa, Seibert and Kromp-Kolb56–Reference Wickramasinghe, Harada and Miyazawa61)} . More complex interpolation methods (such as quadratic, bicubic, spline, polynomial, etc.) are potentially more precise but are slower than 4D linear interpolation. These interpolation methods have often been used in the literature^{(Reference Soler, Olivares and Staffetti11,Reference Soler, Olivares and Staffetti12,Reference Soler, Olivares, Staffetti and Bonami62,Reference Fukuda, Shirakawa and Senoguchi63)} , on ground-based platforms, in conjunction with regional atmospheric data forecasts and near-horizon flight profile predictions such as the descent phase of a flight/CDO^{(Reference Jin, Cao and Sun64)}. Regional atmospheric data predictions, such as RDPS⁽⁶⁵⁾ and RUC^{(Reference Schwartz, Benjamin, Green and Jardin48)}, are short-time forecasts issued for a reduced geographic area, but updated at a much higher rate and being more precise.

2.4 Flight trajectory/flight plan

Generally, an aircraft flight trajectory can be very complex, limited only by the aircraft’s performance capabilities (flight envelope limitations), the abilities of the pilot and the required workload (if a manoeuvre is performed in manual mode), or the FMS/autopilot capabilities. Additional constraints are imposed by navigation and safety regulations, and passenger comfort.

In the fields of flight trajectory planning and optimisation, ATM, and FMS, a flight trajectory is defined by a flight plan^{(Reference Altus66,67)} that contains all the information regarding the intended evolution of the aircraft, in a concise and standard format. The flight plan contains all the information necessary to predict the precise space–time evolution of the aircraft. The description of the flight trajectory using a standard format is a result of the necessity to:

• Reduce the complexity of flight profiles;

• Easily construct the flight trajectory in ATM and FMS platforms, based on the submitted/selected flight plan;

• Implement the functionalities required for the calculation of the aircraft flight performance parameters and aircraft flight dynamics, along a selected trajectory, through accelerated simulation, in order to:

  • Compute flight performance parameters (e.g. fuel burn, flight time, etc.);

  • Ensure that the flight parameters (e.g. altitude, speed, etc.) remain within the aircraft’s flight envelope limits;

  • Evaluate the aircraft’s position relative to the flight plan, and follow the planned trajectory (FMS);

  • Evaluate possible conflicts with other aircraft within the same airspace region (ATM); and

  • Validate the flight plan relative to imposed navigation constraints, fuel requirements, etc.

As mentioned in Section 2.1, an aircraft flight trajectory can be decomposed into two components:

• A lateral flight profile, representing the projection of the flight trajectory onto the Earth’s surface; and

• A vertical flight profile, defined by the evolution of the aircraft’s flight parameters along the lateral flight profile.

Accordingly, a flight plan has a lateral and a vertical component, corresponding to the two components of the flight trajectory.

2.4.1 Lateral flight plan description and resulting lateral flight profile

The lateral flight plan defines the segments composing the lateral flight profile:

• The sequence of waypoints (WPTs) that define the lateral flight profile segments overflown by the aircraft (geographic locations defined by pairs of latitude and longitude coordinates); and

• The lateral flight profile segment type(s): loxodromic or orthodromic^{(Reference Lenart68)} (Fig. 3).

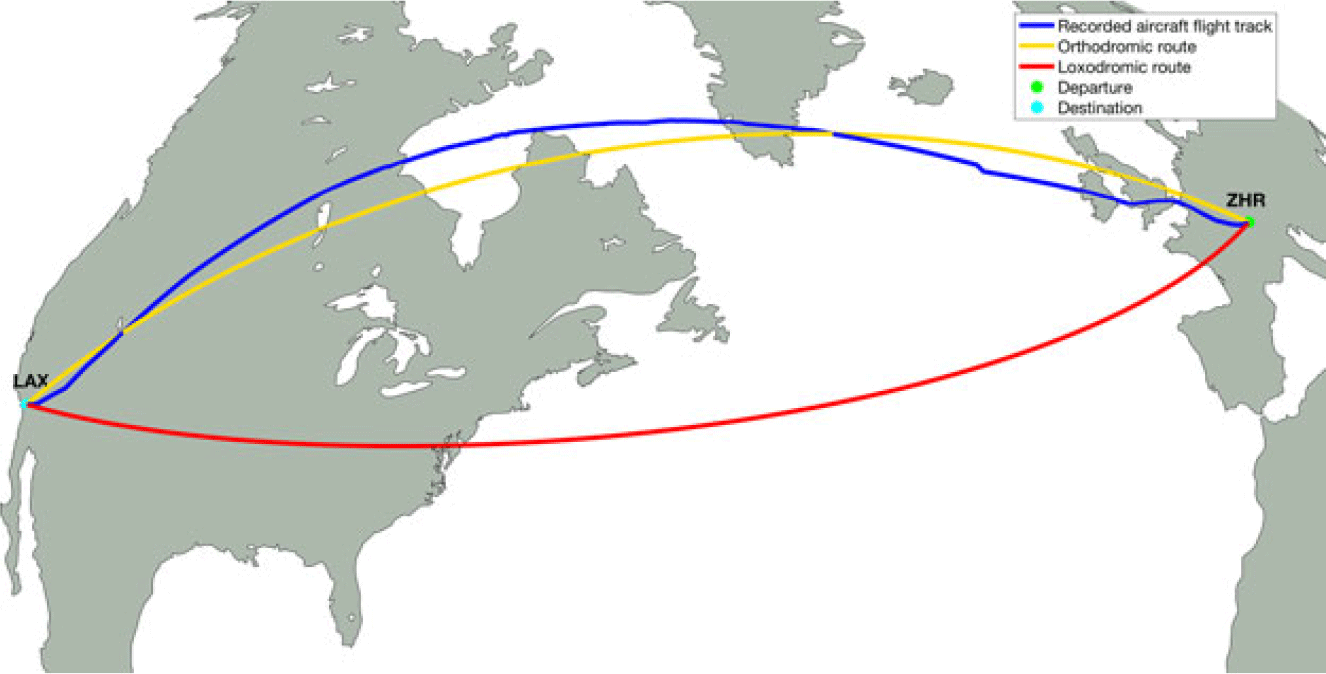
Figure 3. Illustration of orthodromic and loxodromic routes, and a recorded flight track⁽⁶⁹⁾ between Zurich (ZHR) and Los Angeles (LAX).

A loxodromic segment (represented by the red line in Fig. 3) has the property that, at every point on the segment, the departure heading required to advance along the segment is constant. However, a loxodromic segment is not the shortest route between two points on a sphere or ellipsoid.

An orthodromic segment (represented by the yellow line in Fig. 3) is the shortest route between two points on a sphere/ellipsoid (the geodesic or great circle that connects two geographic points). On an orthodromic route, the segment heading is not constant; it varies from the departure WPT (beginning of the segment) to the arrival WPT (end of the segment).

Although the orthodromic route between two geographic locations is the shortest flight distance between two points, aircraft do not necessarily follow accurate orthodromic routes due to air traffic constraints, atmospheric conditions (to avoid strong head winds and/or turbulence), navigation constraints, etc. The blue line in Fig. 3 illustrates the lateral flight profile of a real flight, flight SWR40 between Zurich (ZHR) and Los Angeles (LAX), on 25 February 2019, retrieved from the FlightAware web site⁽⁶⁹⁾.

Two consecutive WPTs from the lateral flight plan define a flight profile segment and, together with the segment type information, determine the segment’s SLA length, and the departure and arrival headings (the angle relative to geographic north) at each point along the segment. Conversely, given the initial WPT of a segment and the segment type, the departure heading from the initial WPT and the SLA for a point of interest, it is possible to compute the geographic coordinates of the point of interest and the arrival heading at this point.

For a loxodromic segment, the calculations of various parameters (SLA length, the segment heading, the coordinates of a point situated at a given SLA distance, etc.) are performed using the rhumb line equations^{(Reference Carlton-Wippern70)} for the Earth model (spherical or ellipsoid). For orthodromic segments, the calculations are performed differently as they are functions of the Earth model used: spherical trigonometry for a spherical earth model, and Vincenty’s formulas^{(Reference Karney71)} for an ellipsoid Earth model.

The segment’s length at the aircraft’s flight altitude is obtained by multiplying the SLA distance by a correction factor calculated as:

(6) \begin{equation}{c_{f\_dist}} = \;\frac{{{R_{earth}}\; + \;{h_{geom}}\; \times \;FT\_TO\_NM}}{{{R_{earth}}}}\end{equation}

where:

• ${c_{f\_dist}}$ is the segment length correction factor with altitude;

• R _earth = 3440.1n.m. is the Earth’s radius;

• h _geom is the aircraft geometric altitude relative to sea level, in ft; and

• FT_TO_NM = 16.457884 × 10⁻⁵n.m./ft is the ft to n.m. conversion factor.

As an example, for a geometric altitude of 36,000ft, ${c_{f\_dist}}$ = 1.0017222.

2.4.2 Vertical flight plan description and resulting vertical flight profile

A vertical flight plan defines, in a succinct form, the aircraft’s altitude–speed evolution along the lateral flight profile, and specifies the locations (WPTs) along the lateral flight plan segments where changes occur in the planned vertical flight profile parameters (e.g. altitudes and speeds), as well as their new values. In this paper, it is assumed that the vertical flight plan defines the locations along the lateral flight plan where the changes are initiated (e.g. at the beginning of an acceleration/deceleration to a new speed, at the beginning of a climb/descent to a new flight altitude, etc.). A vertical flight plan (profile) can be decomposed into seven main phases: take-off, initial climb, climb, cruise, descent, approach and landing. Each flight phase can include one segment or a succession of vertical flight plan segments.

The vertical flight profile, generated by the vertical flight plan, is obtained by applying accelerated flight performance calculations (see Section 2.5). Each flight plan segment is decomposed in a succession of ‘standard’ type segments, i.e. segments in which the control parameters and the mathematical models describing the aircraft’s evolution (the dynamic and the status parameters) do not change (e.g. a constant-altitude constant-speed segment, a constant-altitude acceleration segment, a climb segment at constant speed and constant climb angle, a climb segment at constant speed and rate of climb, etc.).

The set of parameters that define a vertical flight plan segment are specific to the flight segment type. The values of a vertical flight plan segment parameter can be specified:

• Explicitly, provided as input;

• Implicitly, when the parameter value:

  • Is ‘inherited’ and does not change relative to the value it had at the end of the previous vertical flight plan segment; or

  • Results from the flight performance parameter calculation (e.g. the geographic location where a constant-altitude acceleration/deceleration segment ends, the geographic location where a climb segment ends, the altitude and geographic location where an accelerated climb segment ends, etc.).

The climb and descent sections are flown at ‘scheduled speed’, defined as an [IAS, MACH] speed pair. The speed mode switch (between IAS and MACH) takes place at the crossover altitude, defined as the altitude where the TAS computed from the IAS, described by Equation (3), is equal to the TAS computed from the MACH speed, given by Equation (2). The IAS speed is in effect below the crossover altitude, and the MACH speed is above the crossover altitude. The reason for the speed mode change at the crossover altitude is that a climb at constant IAS speed beyond the crossover altitude would result in a MACH speed beyond the maximum MACH operating speed limit (MMO); similarly, a descent at constant MACH below the crossover altitude would result in an IAS speed beyond the maximum operating speed limit (VMO). An example of a climb speed profile is presented in Fig. 4, where the flight plan starts when the aircraft is at an altitude of 10,000ft and speed of 250Kn IAS, and defines a climb segment at [300Kn IAS, 0.80 MACH] to the cruise altitude (33,000ft). Following the accelerated flight performance calculations, the resulting flight profile is composed of three segments:

• An acceleration in climb, from 250Kn to the scheduled speed climb IAS (300Kn), which starts at 10,000ft and ends at an altitude that is a function of the aircraft performance parameters, such as weight, etc.;

• Climb at constant IAS (300Kn) to the crossover altitude (30,594ft); and

• Climb at constant scheduled speed MACH (0.8) to the cruise altitude (33,000ft).

Figure 4. Example of altitude–speed profile for the climb phase of a flight.

It should be noted that the positions along the lateral flight plan segments (lateral flight profile) where the accelerated climb segment and the constant-speed climb segments end are determined during the accelerated flight performance calculations. These positions are not only dependent on the flight plan speeds but also dependent on the aircraft flight performance characteristics, weight and atmospheric conditions.

The structure of a descent altitude–speed profile is similar to that of a climb altitude–speed profile, except that the evolution along the profile is reversed.

The cruise phase is composed of a succession of constant-altitude and climb (step climb) segments flown at MACH speed (constant-speed, acceleration or deceleration segments). Generally, descent segments (step descents) are not employed, as the aircraft performance is better at higher altitudes, and repeated sequences of step climbs and step descents result in an increased number of pressure change cycles on the airframe, thereby increasing maintenance costs.

Figure 5 shows an example of an altitude profile for the climb, cruise and descent phases of a real flight (flight Swiss SWR40, from Zurich to Los Angeles, flown on 25 February 2019), as retrieved from FlightAware⁽⁶⁹⁾. The altitude profile data presented in Fig. 5 have been selected to show the trajectory for altitudes above 10,000ft.

Figure 5. Example of altitude profile for flight SWR40, Zurich to Los Angeles, on 25 February 2019. Data for altitudes above 10,000ft, as retrieved from FlightAware⁽⁶⁹⁾.

Figure 6. Illustration of the TOC, EOC and TOD positions along the altitude flight profile.

The transition between the climb and cruise sections of the flight trajectory occurs at the Top of Climb (TOC), the point where the aircraft reaches the cruise altitude. The transition between the cruise and descent sections of the flight trajectory occurs at a point denoted as the Top of Descent (TOD), where the aircraft initiates the descent. Another important point along the vertical flight profile is the End of Cruise (EOC), situated in the cruise section of the vertical flight profile, at a pre-set sea level distance from the final point of the descent. The EOC is the point along the flight trajectory beyond which the accelerated flight performance calculation function performs the calculations in ‘descent’ mode, which is a methodology specific to the descent phase of the flight. A more detailed presentation regarding the positions of the TOC, EOC and TOD along the lateral flight profile is provided in the next sub-section (2.5). Figure 6 illustrates the TOC, EOC and EOD positions along the altitude flight profile.

2.5 Accelerated flight performance calculation

The aircraft model developed based on the APM provides a set of functions that compute the flight performance parameters and the aircraft dynamics for each ‘standard’ flight profile segment type that can be used to construct a flight trajectory, as well as to evaluate the flight parameters relative to the aircraft’s flight envelope.

The evolution of the aircraft along the selected flight trajectory, the flight performance and the aircraft status parameters are computed iteratively, segment by segment, starting from the initial point, by accelerated simulation:

• The flight trajectory is constructed as a succession of ‘standard’ segments;

• Each segment of the flight trajectory is decomposed into sub-segments (integration steps);

• The parameter along which a segment is decomposed into sub-segments (time, distance, altitude) depends upon the segment’s type;

• The integration step size (sub-segment decomposition step size) is chosen as a result of a tradeoff between the estimated result precision and computation time. Larger step sizes would result in a smaller number of sub-segments and, therefore, faster calculations. However, this would also reduce the accuracy of the results;

• For each sub-segment, the specific parameters are calculated in a point on the sub-segment (situated along the decomposing parameter dimension) using the appropriate evaluation function, aircraft configuration, atmospheric conditions, etc.;

• The performance parameters for the sub-segment are obtained by integration: the parameters returned by the function are multiplied by a factor computed based on the integration step size; and

• The aircraft’s state and configuration parameters, and its position along the lateral flight profile, are updated. The new values become the input data for the trajectory performance calculation on the next sub-segment.

At each step, the aircraft performance parameters, its state, position and dynamics are validated relative to the flight envelope limitations (such as altitude and speed), quantity of fuel on board, flight trajectory, navigation constraints, etc.

The methodology used for constructing the flight trajectory profile and computing the performance parameters is presented in ref. (Reference Schreur72). The flight trajectory construction and the flight performance parameter calculation start from the initial point of the flight plan (initial geographic location and altitude), with the initial aircraft status parameter values (zero fuel weight, fuel quantity, centre-of-gravity position, speed, climb angle, bank angle, etc.), and the time instance when the aircraft crosses the initial point of the flight plan. The climb phase is computed first, followed by the cruise phase. The TOC location, namely the point where the aircraft reaches the cruise altitude, is determined by the climb profile calculation module. The cruise phase calculations stop at a pre-set sea level distance from the final point of the flight plan (EOC), heuristically selected so that it is further away from the destination than the beginning of the descent flight profile (TOD). The aircraft weight and crossing time at the final point of the flight profile (flight plan) are then estimated using a heuristic, and the estimated values are used to construct the descent flight profile. The descent flight profile is constructed in reverse order (backwards integration), from the final point of the descent flight plan to the TOD, at the cruise altitude and speed. At this stage, the geographic location of the TOD and the aircraft crossing time at the TOD are known. Finally, the performance parameters are computed for the last segment of the cruise flight profile, delimited by the EOC and TOD. Validation of the estimated aircraft weight and crossing time at the end of the flight profile is performed by comparing their values obtained at the TOD, viz. the values obtained from the descent profile calculations with the values obtained from the cruise profile calculations. If the aircraft weight and/or the crossing time difference are larger than selected threshold values, considered acceptable, then the estimated values at the end of the descent are corrected (based on the difference obtained for the parameter value) and the process is started again for a new decent profile computation, EOC to TOD profile calculation and comparison between the obtained values. This process stops when both the time difference and the aircraft weight difference are smaller than the selected threshold values. Figure 7 shows a flowchart of the accelerated flight profile calculation process.

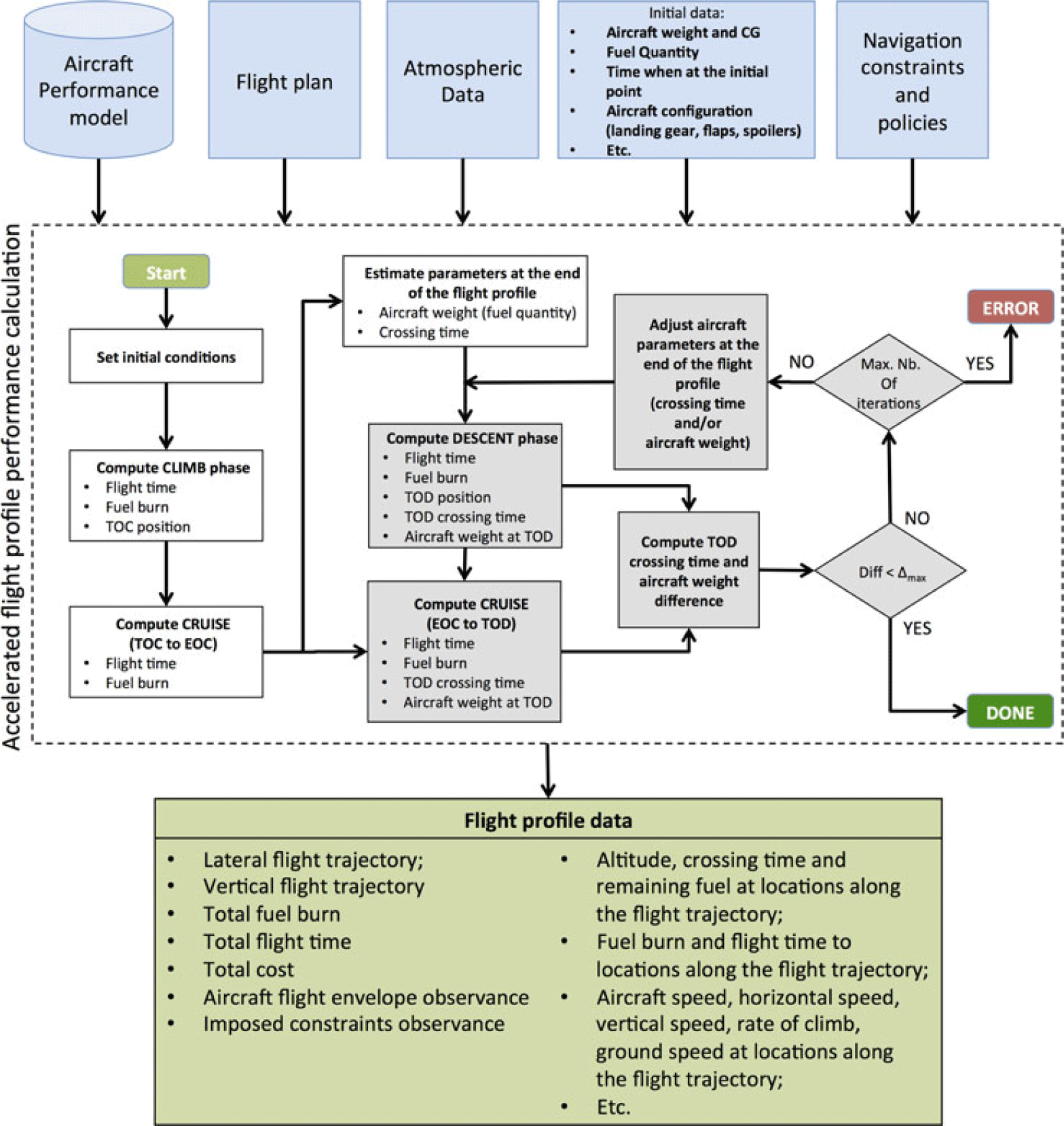
Figure 7. Accelerated flight profile calculation process flowchart.

Navigation constraints (such as altitude, speed, RTA, etc.), assigned at different points along the flight path, are validated by comparison with their corresponding values resulting from the flight performance calculations.

2.6 Optimisation method

The optimisation method presented in this paper is intended for flight trajectory optimisation (Section 2.4) where modifications are made to both the lateral and vertical flight profiles. For a specific optimisation problem, defined by:

• Aircraft model (flight performance data), load (weight) and onboard fuel quantity;

• Geographic locations of the initial and final points of the flight trajectory;

• Aircraft flight altitude and speed at the beginning and at the end of the flight profile under optimisation;

• Navigation policies such as: Climb at Maximum Climb (MCMB) TLA, IDLE descent, climb/descent mode (e.g. vertical speed, climb/descent angle, rate of climb/descent), etc.;

• Selected values for the range of cruise altitudes, and the maximum deviation from the orthodromic route between the beginning and the end of the flight trajectory under optimisation; and

• Optimisation criterion: minimisation of fuel burn, flight time or total cost.

The algorithm implementing the proposed optimisation method identifies the ‘optimal’ flight plan, viz. the combination of lateral (Section 2.4.1) and vertical (Section 2.4.2) flight plans that minimises the selected cost function.

The optimisation problem presented in this paper considers a discrete/combinatorial optimisation with a very large number of candidate solutions, determined by the characteristics of the family of candidate flight plan solutions (Sections 2.6.1 and 2.6.2). Some of the parameters that are used in the calculations (e.g. the atmospheric conditions, aircraft performance model) are defined by piecewise functions. The evolution of the aircraft is described by piecewise functions due to the decomposition into sub-segments in which the mathematical model that describes the evolution of the aircraft and flight parameters do not change (see Section 2.5, which describes the methodology used to compute the flight performance for a flight plan). Moreover, the total cost is expressed by a complex non-linear function due to the relationship between the parameters that determine the total cost (fuel burn, flight time) and the input parameters: aircraft weight, flight plan parameters (altitude and speed flight profile) and atmospheric conditions. The total cost of a flight segment depends not only on its selected parameters but also on the parameters of previous flight profile segments. The aircraft weight, altitude and crossing time at the beginning of a segment result from the fuel burn and flight time on previous segments (and thereby their flight profile characteristics). This fact affects the aircraft’s performance characteristics and the atmospheric conditions encountered on the segment, which affect the fuel burn and flight time and, as a consequence, the segment’s total cost. This optimisation problem might have multiple local minima and many (‘near’-)optimal solutions. For these reasons, the optimisation method described in this paper is based on genetic algorithms.

Due to the random nature of genetic algorithms, the optimality of the solution is not guaranteed; it is expected that the solution will be a ‘near-optimal’ flight plan. Multiple runs of the optimisation algorithm, for an identical optimisation problem, yield different ‘optimal’ solutions.

The proposed optimisation method starts by defining the families (‘templates’) of lateral and vertical flight plans from which the candidate flight plans (the combination of lateral and vertical flight plans) can be selected and evaluated during the optimisation process. Then, a genetic algorithm iteratively selects random new candidate flight plans, from the candidate set or by applying genetic operators (‘crossover’ and ‘mutation’) on pairs of selected candidates, and computes the flight performance parameters (through accelerated simulation), and the cost. The genetic operators are applied in such a way that the resulting flight plans after applying the genetic operators are themselves members of the candidates’ set.

The first sub-section presents the methodology used for constructing the set of candidate lateral flight plans, and the configuration parameters that determine their characteristics. The next sub-section describes the methodology employed for constructing the family of vertical flight plans, and the configuration parameters that determine their characteristics. The last sub-section presents the implementation of the genetic algorithm used in the optimisation.

2.6.1 Lateral flight profile routing grid and candidate lateral flight plan construction

This sub-section presents the methodology used for constructing the set of lateral flight plans that can be selected as components of the flight plans evaluated in the optimisation. The definition of the set of lateral flight plans starts from the assumption that the lateral flight plan is composed by a succession of segments, each of which is delimited by two geographic locations (WPTs) and is one of two possible types: orthodromic or loxodromic. Another assumption made in this study is that the WPTs delimiting the lateral flight plan segments and, therefore, the aircraft’s lateral flight trajectory are restricted to a selected geographic area. It is also assumed that the set of WPTs that delimit the segments of a lateral flight plan are selected from a ‘grid’ (routing grid), in which each segment is delimited by two adjacent WPTs from the grid.

The set of lateral flight plans is, therefore, defined by:

• The geographic area within which the flight plan WPTs can be selected;

• The methodology used to construct the routing grid, which defines the set of WPTs that delimit the flight plan segments;

• The type of the segments (orthodromic or loxodromic) composing the lateral flight plan; and

• The methodology used for selecting, from the routing grid, the set of WPTs that define the succession of segments of the lateral flight profile.

In this study, the lateral flight profile is composed of orthodromic segments. Each segment is characterised by:

• An SLA length;

• The headings required to advance along the segment: at the initial WPT of the segment (departure heading) and at points along the segment; and

• The heading when arriving at the final WPT of the segment.

The segment’s length, the departure and arrival headings and the segment headings at points along the segment are computed using the Vincenty’s formulae^{(Reference Karney71)} and the WGS84 ellipsoid Earth model^{(Reference Janssen73)}.

In this study, the routing grid, and thus the geographic area to which the set of flight plans are restricted, is defined based on the orthodromic route (ORT) between the initial and final WPTs of the trajectory under optimisation. The routing grid is constructed as an ‘orthogonal’ grid. First, a number of equidistant WPTs are generated along the ORT. Then, from each such WPT along the ORT, an orthodrome perpendicular to the ORT is constructed, and new routing grid WPTs are generated along this orthodrome. The new WPTs are equidistant, placed symmetrically, on both sides of the ORT, up to a maximum deviation relative to the ORT. An illustration of the routing grid construction is presented in Fig. 8.

Figure 8. Example of routing grid construction.

The first step in constructing the routing grid is to select the configuration parameters for the grid:

• The maximum distance between the WPTs generated along the ORT;

• The maximum deviation from the ORT; and

• The distance between WPTs on the normal to the ORT.

It is assumed that the aircraft always moves to a new WPT situated at a (routing grid) step along the ORT track, and at a maximum number of grid steps across. The lengths of the segments along and across the orthodromic track, and the number of waypoint steps ‘across’ the ORT, are chosen such that each segment, constructed as presented above using waypoints selected from the grid, represents an integration step (has a maximum length that is below the maximum length of a computation step) for the flight performance estimation function.

These parameters can also be used to refine the optimisation process, as smaller distances produce a finer grid, which can yield profiles that are ‘better’ adapted to the atmospheric conditions, although this would result in a large increase in the number of ‘candidate’ profiles to explore.

Given that, at each step, the aircraft moves to a new WPT situated at one grid step along the ORT and at a selected maximum number of steps across the ORT, the routing grid starts at the initial WPT, with no WPTs across the ORT. Then, at each step along the ORT, the number of WPTs across the ORT increases by the selected maximum number of steps across, up to the maximum number of deviations resulting from the selected maximum deviation from the ORT and the lateral deviation step size. Similarly, at the other end, the number of WPTs across the ORT decreases, at each step along the ORT, by the maximum number of lateral deviation steps, until it reaches the final point of the grid (the final WPT of the flight) with no WPTs across the ORT. Figure 9 presents an illustration of a routing grid.

Figure 9. Example of a routing grid.

The lateral flight plans, generated as candidates in the optimisation, are random routes that traverse the routing grid, where the succession of WPTs must follow the rules set out above. One method for generating the lateral flight plan is to select the set of WPTs successively, one step along the orthodromic route at a time (with each new WPT being situated one step further along the orthodromic route). The domain of valid steps along the normal to the orthodromic route (the range of lateral steps that would end in a grid WPT) is determined, at each step, and the new WPT deviation is selected randomly, from the set of valid deviations. Tests showed that such a method yields zigzag lateral flight plans (e.g. the red flight track in Fig. 10), which result in flight trajectories that are not in accordance with normal operations/navigation.

Figure 10. Example of random lateral flight plan generation using the ‘point by point’ and ‘segment by segment’ methods.

This paper proposes a method to generate better candidate lateral flight plans by generating longer segments (longer steps along the orthodromic route), along which the lateral step value is maintained. For each new segment, the range of valid lateral step values (which can yield a grid WPT for at least one step along the orthodromic route) is determined, and the segment lateral step value is selected randomly from the range of valid values. The maximum number of valid steps along the orthodromic grid route is then calculated for the selected lateral step value: the maximum number of steps needed to reach the limit of the routing grid. The segment’s length (the number of steps along the grid’s orthodromic route) is selected randomly, within the set of valid values. Finally, the set of grid WPTs corresponding to the new segment, generated by advancing one orthodromic step at a time, and the selected lateral step size for the selected number of orthodromic steps are added to the generated lateral flight plan.

2.6.3 Genetic algorithm

Genetic algorithms^{(Reference Schmitt75)} are population-based metaheuristic algorithms, inspired from the evolution theory presented by Darwin, which can be used for solving complex search problems for which the solution space is too large for an exhaustive exploration, in a timely manner, and/or are complex and nonlinear for other search techniques. In a genetic algorithm, the population, composed of a set of individuals (candidate solutions), evolves for a selected maximum number of generations or until a selected termination criterion is satisfied (the global optimum or an acceptable solution is found). Each generation has the same number of individuals, and all the individuals that are generated and evaluated in a genetic algorithm conform to a genetic structure template (‘genotype’): they all have the same number of chromosomes, and each chromosome, situated at a given position in the genetic structure, has the same meaning (represents the same characteristic/parameter for the problem under optimisation). For the initial population, the individuals are generated randomly or according to selected ‘values’ that are deemed to conduct to optimal solutions. At each generation step, the fitness of each of the members of the population is evaluated. Then, the next generation (population) is selected/created through one or a combination of the following genetic operations:

• ‘Elitism’, where the best individuals are copied to the next generation; and

• ‘Crossover’ and ‘mutation’ based on individual(s) selected from the current population.

To increase the population diversity, a number of individuals of a new generation may be generated randomly.

The selection of individuals to be subjected to the crossover and/or mutation operations can be made randomly or as a function of their fitness relative to the set of individuals in the current population. Some of the possible fitness-based selection methods are:

• ‘Tournament’, where two individuals from the population are chosen at random, their fitness values are compared and the best individual is retained;

• ‘Roulette wheel’ (proportional) selection, in which the selection is performed by generating a random number between 0 and 1 and retrieving the individual that falls within the corresponding area of the roulette disk; and

• ‘Stochastic acceptance’^{(Reference Lipowski and Lipowska76)}.

The crossover operation consists of exchanging ‘genetic’ data (‘chromosomes’) between two individuals (‘parents’) selected from the candidate solution population. Firstly, the position along the genome where the crossover will be performed is randomly selected. The new individual (‘child’), a member of the new generation population, is then constructed by concatenating the initial chromosome sequence (up to the crossover position) from one parent and the final sequence from the other parent.

A mutation changes the value of one chromosome, selected at random, to a new value among the range of values for the selected chromosome. This genetic operation can be applied independently, to a randomly selected individual from a population, or additionally to a crossover, to increase the diversity of the individuals from the new generation.

2.6.3.1 Candidate flight plan selection for mutation and crossover operations

The flight plan(s) on which the crossover or mutation operations are to be performed are retrieved using ‘roulette wheel’ selection. The roulette wheel is created based on the list of total cost values for the population. For each element of the roulette wheel list (normalised values with a total sum equal to one), the corresponding roulette wheel value is calculated as the quotient between:

• The cost values for the population element; and

• The sum for the entire population.

A random number between zero and one is used as a ‘pointer’ to the list member (the population member) that will be selected for the genetic operation.

2.6.3.2 Lateral flight plan crossover and mutation

As presented in Section 2.6.1, the lateral flight plan is defined by a succession of segments delimited by the WPTs of the routing grid. For each lateral flight plan segment, the final WPT is situated one step further along the grid’s orthodromic route direction, and up to a maximum number of steps across the orthodromic route, relative to the initial point. Therefore, to obtain a lateral flight plan that maintains this characteristic, the crossover between two lateral flight plans (as well as a mutation of a flight plan) can be only performed at the points of the lateral flight plan segment that are routing grid nodes. The flight plan WPT where the crossover or mutation is performed is identified by its grid position along the orthodromic route direction (N_M). Firstly, the crossover or mutation WPT is selected randomly from the WPTs that define the flight plan, except for the initial and final WPTs (which would not yield any profile changes). Each lateral flight plan P_i can thus be divided into two sections: from the initial point to the crossover location (P_i1), and from the crossover location to the end of the lateral flight plan (P_i2).

The child lateral flight plan (C_LFPL) resulting from the crossover operation of two parent lateral flight plans (P₁ and P₂) will have its initial section (up to the crossover position) identical to that of the first parent (P₁₁). The final section (from the crossover position to the end) will be constructed based on the locations of the flight plan WPT offsets on the routing grid at the crossover position N_M, and on the structure of the final section from the other parent lateral flight plan (P₂₂).

The two parent lateral flight profiles can have different grid offsets at the points following the crossover position, relative to the orthodromic grid route, where the difference can be greater than the maximum step across the orthodromic grid route direction. Therefore, the final section of a child flight plan cannot be obtained by simply copying the final section from the other parent (P₂₂ from P₂). A transition section, which starts at the crossover position, the final WPT of the initial section (P₁₁), and ‘intercepts’ the new section (P₂₂) at a further WPT, must be constructed along the orthodromic route direction, one step at a time. At each step S_j along the orthodromic grid route direction, the offset of the next lateral flight plan WPT, situated at step S_j+1, is selected based on:

• The offset (along the direction normal to the orthodromic grid route) at the current location (S_j); and

• The offset of the target flight plan section (P₂₂) WPT situated at step S_j+1.

This selection ensures the fastest convergence to the target flight plan section after the crossover (P₂₂). An example of a child lateral flight plan resulting after a crossover between two parent flight plans is presented in Fig. 11.

Figure 11. Example of lateral flight plan crossover.

A lateral flight plan mutation consists in modifying the offset (relative to the routing grid’s orthodromic route) of a lateral flight plan segment limit WPT (other than the first or last WPT of the flight plan), randomly selected. The offset change is selected at random from a range of offsets that can be reached from the preceding WPT, with a step size within the imposed maximum range (Section 2.6.1). For the lateral flight plan section following the mutation location, the WPT’s offsets are shifted by a value equal to the difference between the mutated and initial offset at the mutation position, and bounded to the routing grid. An example of lateral flight plan mutation is presented in Fig. 12.

Figure 12. Example of lateral flight plan mutation.

2.6.3.3 Vertical flight plan crossover and mutation

The vertical flight plan crossover operation is performed only on the cruise section of the flight plan, at the locations where step altitude and speed changes are allowed (see Section 2.6.2), so that the resulting child vertical profiles conform to the vertical flight plan template selected for the family of candidate flight plans. Similarly to the flight plan crossover operation, the vertical flight plan operation starts by selecting, at random, the location where the crossover will be performed. Next, the child vertical flight plans are constructed by copying the initial section from one parent and the final section from the other parent (Fig. 13).

Figure 13. Example of altitude vertical flight plan crossover, where no altitude correction is necessary.

Given that step descents are not allowed, the segment altitudes for the final sections of the child flight plans are adjusted, if needed, to values equal to or higher than the altitudes at the final point of the initial section (crossover position), as shown in Fig. 14.

Figure 14. Example of altitude vertical flight plan crossover, where an altitude correction is necessary to avoid a step descent.

For the mutation operation, firstly the section where the mutation is performed (climb, cruise or descent) is selected at random, and then the parameter to be changed:

• The IAS, the MACH or the target climb altitude (the initial cruise altitude) for the climb phase;

• The cruise segment and the altitude or speed for the selected segment – for the cruise phase; or

• The IAS or the MACH for the descent phase.

As mentioned for the crossover operation, if the mutation performs an altitude change for a cruise segment, the new selected altitude must be equal to or higher than the altitude on the previous cruise segment, or than the initial cruise altitude (if the selected segment is the first cruise segment).

2.7 Reference flight profile data (FlightAware)

For each specific flight planning/optimisation problem, the lateral and vertical flight plans are built based on the actual data for the flight: initial and final geographic locations for the flight trajectory limits (departure and destination airports or flight trajectory section limits), navigation constraints, aircraft data (performance data, weight, fuel load) and atmospheric conditions.

In this paper, the set of candidate lateral and vertical flight plans, and the reference flight plan used for evaluating the performance of the optimisation method, were constructed based on the flight track data of a real flight, retrieved from the FlightAware (www.flightaware.com) website. This was done to generate a realistic optimisation problem and to compare the optimal profile performance, identified by the proposed method, with the performance of a flight plan as close as possible to an ‘as-flown’ flight profile.

FlightAware is a company that retrieves real-time aircraft flight data from various sources (ACARS, transponders, ADS-B, radar, etc.) and provides, to various users, a platform to access this information, at different levels of detail as a function of the subscription type. Information about the area covered by the real-time data providers, the types of data and the specific regions covered for each of the specific data types can be found in ref. (77). For aircraft without ADS-B transmitters, the position of the aircraft is determined, under certain circumstances, by multilateration based on transponder data reception⁽⁷⁸⁾. For areas not covered by the data feeders, the real-time aircraft positions are estimated based on the flight plans submitted to the FAA.

The flight track data used in this study were retrieved from FlightAware using guest account privileges. The available flight track information is therefore a list of aircraft data points describing:

• The flown flight track:

  • A set of geographic location overflown by the aircraft;

  • Aircraft flight parameters in the set of overflown geographic locations:

    • The date and time of crossing;

    • Aircraft altitude;

    • Aircraft heading;

    • Ground speed; and

    • Rate of climb/descent.

• The submitted lateral flight plan data (flight route plan) is a list that enumerates:

  • The name of the navigation point that defines a limit of a flight segment;

  • The geographic location of the navigation point;

  • The aircraft departure heading from that location (on the new segment);

  • The distance to the next navigation point (the segment length);

  • The distance remaining to the destination; and

  • The distance flown from the initial point.

The flight track data retrieved from FlightAware via a guest account has important limitations that make it impossible to perform an accelerated simulation along the flight trajectory and compute the performance parameters for the flight (such as fuel burn). The flight track data lack essential information, such as: aircraft configuration (weight and fuel load), atmospheric conditions encountered by the aircraft, unknown moments and locations where the flight profile changes are initiated or end (the data points can be considered ‘random’ data points), etc.

An analysis of the flight track data showed that, for the flight track domains located in geographic areas not covered by the FlightAware data sources, the track data provide estimations of the geographic locations, crossing times and aircraft heading. However, the altitude, ground speed and rate of climb are set to zero.

It was observed that, occasionally, for data points along the flight track, the sequence of crossing times and/or geographic locations are not in the natural order for flight track data (probably due to particular cases of position estimation using multilocation):

• A crossing time that is earlier than the crossing time at the previous location; and

• A sequence of flight track geographic locations that generates a succession of lateral flight track segments with excessive heading changes, which are not consistent with normal flight for passenger aircraft.

Given the facts presented above, the raw flight track data cannot be used as a reference flight profile. The reference flight profile must be created based on the filtered (corrected) flight track data, according to case-specific assumptions and criteria.