1. INTRODUCTION
With the development of laser chirped pulse amplification technique, ultraintense short-pulse lasers with intensity of 1019–1021 W/cm2 have been made available in laboratories. Such ultraintense lasers provide a strong field gradient on the order of 104–106 MV/m, which is much higher than that of conventional accelerators. Thus laser-plasma accelerators have been proposed as a next generation of compact accelerators to produce relativistic electron beams (Karmakar & Pukhov, Reference Karmakar and Pukhov2007; Shi et al., Reference Shi2007; Lifschitz et al., Reference Lifschitz, Faure, Glinec, Malka and Mora2006; Koyama et al., Reference Koyama, Adachi, Miura, Kato, Masuda, Watanabe, Ogata and Tanimoto2006; Yin et al., Reference Yin, Albright, Hegelich and Fernandez2006; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Gupta & Suk, Reference Gupta and Suk2007; Kalashnikov et al., Reference Kalashnikov, Osvay and Sandner2007; Santala et al., Reference Santala, Najmudin, Clark, Tatarakis, Krushelnick, Dangor, Malka, Faure, Allott and Clarke2001; Pukhov & Meyer-ter-Vehn, Reference Pukhov and Meyer-ter-Vehn2002; Schmitz & Kull, Reference Schmitz and Kull2002).
The laser wakefield accelerator (LWFA) utilizes a short pulse laser to excite a plasma wave. The accelerated electrons can be taken from the background plasma as well as from externally injected particles in a LWFA. The acceleration of particles from the background plasma tends to produce a beam with 100% energy spread in the self-modulated laser wakefield accelerator (Schroeder et al., Reference Schroeder, Esarey, Geddes, Toth, Shadwick, Tilborg, Faure and Leemans2003; Ting et al., Reference Ting, Kaganovich, Gordon, Hubbard and Sprangle2005; Fomyts'kyi et al., Reference Fomyts'kyi, Chiu, Downer and Grigsby2005). The effect of laser pulse shape on plasma wave growth has been studied and it was found that the rectangular–triangular pulses are more desirable for laser-plasma accelerators, in contrast to those Gaussian-like pulse and rectangular-Gaussian pulse (Malik et al., Reference Malik, Kumar and Nishida2007).
The spectra of the energetic electrons produced by a laser interaction with underdense plasma have been measured at relativistic intensities. The interaction of the laser field with the nonlinear focusing force of the channel leads to electron acceleration (Mangles et al., Reference Mangles, Walton, Tzoufras, Najmudin, Clarke, Dangor, Evans, Fritzler, Gopal, Hernandez-Gomez, Mori, Rozmus, Tatarakis, Thomas, Tsung, Wei and Krushelnick2005, Reference Mangles, Walton, Najmudin, Dangor, Krushelnick, Malka, Manclossi, Lopes, Carias, Mendes and Dorchies2006). The required relativistic electron beams should be well collimated, quasimonoenergetic, and with small beam divergence in real applications in medicine, biology, and high-energy physics etc. (Nickles et al., Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Sandner, Schreiber, Hilscher, Jahnke, Andreev and Tikhonchuk2007). A high-quality electron beam can be extracted from a channel guided laser wakefield accelerator by carefully choosing the injection energy (Geddes et al., Reference Geddes, Toth, Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Mangles et al., Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick2004; Faure et al., Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004). The uniformly phased particles can be quickly bunched by the accelerator itself and subsequently accelerated to relativistic energy.
When an intense laser propagates in a plasma, quasistatic multi-GG magnetic fields are self-generated (Wagner et al., Reference Wagner, Tatarakis, Gopal, Beg, Clark, Dangor, Evans, Haines, Mangles, Norreys, Wei, Zepf and Krushelnick2004). The magnetic field is generated by several mechanisms. It is generated by a jet of fast electrons in the direction of the laser propagation or by the nonlinear current of the background plasma electrons. During the interaction of the plasma electrons with the circularly polarized laser pulse, electrons absorb not only the laser energy but also the proportional amount of the total angular momentum of the laser pulse, which leads to the electron rotation around the direction of the laser propagation and generation of the axial magnetic field by the azimuthal electron current (Kostyukov et al., Reference Kostyukov, Shvets, Fisch and Rax2002; Haines, Reference Haines2001). The generation of the axial magnetic field in the plasma by a circularly (or elliptically) polarized laser is often referred to as the inverse Faraday effect (IFE). Electron acceleration by a circularly polarized laser pulse in the presence of this self-generated axial magnetic field in a plasma has been studied (Singh, Reference Singh2004). Betatron resonance occurs between the electrons and electric field of the laser pulse for two values of optimum values of magnetic fields—for lower value for underdense plasma and for higher value for overdense plasma. If we take the propagation of the laser along the z-axis, then the generated magnetic field is azimuthal as the laser photons carry momentum in the direction of their propagation regardless of their polarization. The electrons make transverse betatron oscillations in the self-generated magnetic fields. When the betatron frequency coincides with the Doppler shifted frequency, a resonance occurs, leading to an effective energy exchange between the laser and electron, and the electrons are effectively accelerated to relativistic energies with beam collimation effect (Tanimoto et al., Reference Tanimoto, Kato, Miura, Saito, Koyama and Koga2003; Pukhov et al., Reference Pukhov, Sheng and Meyer-ter-Vehn1999; Gahn et al., Reference Gahn, Tsakiris, Pukhov, Meyer-ter-Vehn, Pretzler, Thirolf, Habs and Witte1999).
Electron acceleration by an intense laser in an azimuthal magnetic field in plasma has been studied using relativistic three-dimensional (3D) single particle code. It has been shown that resonance saturates beyond a specific point of time without any frequency and the electrons lose the energy. If we introduce a suitable frequency chirp, resonance can be maintained for a longer duration, and electron energy can be increased. This article is organized as follows: The governing equations are given in the next section. The results and discussion are given in Section 3 and conclusions are drawn in Section 4.
2. GOVERNING EQUATIONS
Analytical expression for the resonance condition has been found in the following description. A plane polarized laser wave has been considered for the sake of simplicity with electric and magnetic fields given by
where k = (ω/c)(1 − ωp2/ω2)1/2, relativistic plasma frequency ωp2 = 4πn 0e 2/m, −e and m are the electronic charge and effective mass, respectively. The laser wave imparts energy to the electrons that carry an electric current in the z-direction, which produces an azimuthal magnetic field experienced by the electrons that follow. The azimuthal magnetic field can be modeled as follows:
![{\bf B}_{\theta} = -\hat{y} B_0 {{\bf r} \over r_0} \exp \left[-{r^2 \over r_0^2}\right]. \eqno \lpar 3\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000372_eqn3.gif?pub-status=live)
Magnetic field generation in intense laser plasma interaction has been investigated (Qiao et al., Reference Qiao, He and Zhu2006). The magnetic field profile given by Eq. (3) is similar to the profile obtained by Qiao et al. (Reference Qiao, He and Zhu2006). The equations governing electron momentum and energy are
![{dP_x \over dt} = -{eE_0 \over \omega} \lpar \omega - kv_z\rpar \cos \lpar \omega t - kz\rpar - ev_z B_0 {x \over r_0} \exp \left[-{r^2 \over r_0^2}\right]\comma \; \eqno \lpar 4\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000372_eqn4.gif?pub-status=live)
Using Eq. (5) with v x = P x/γm 0, Eq. (4) can be written as follows
![\eqalignno{{dv_x \over dt} + {v_z \over \gamma} {eB_0 \over m_0 r_0} x \exp \left[-{r^2 \over r_0^2}\right]&=- {eE_0 \over \gamma m_0} \left(1 - {kv_z \over \omega} - {v_x^2 \over c^2}\right)\cr &\quad\hskip.5pt\times cos \lpar \omega t - kz\rpar \comma \;}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000372_eqn6.gif?pub-status=live)
![\eqalignno{{dx^2 \over dt^2} + \omega_b^2 x \exp \left[-{r^2 \over r_0^2}\right]&=-{eE_0 \over \gamma m_0} \left(1 - {kv_z \over \omega} - {v_x^2 \over c^2}\right)\cr &\quad\hskip.5pt\times \cos \lpar \omega t - kz\rpar \comma \;}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000372_eqn7.gif?pub-status=live)
where ωb2 = ev zB 0 γm 0r 0.
Resonance condition can be written using ωb = ω− kv z,

Using γ2 = 1 + (P x2 + P z2)/m 02c 2,

Using Eq. (9) in Eq. (8), resonance condition can be written as follows,

Figure 1 variation shows (γc/v z)(1 − kv z/ω)2 as a function of relativistic factor γ for k = 0.98 and k = 0.99. The value of (γc/v z)(1 − kv z/ω)2 decreases with γ for low values of γ, however, for highly relativistic regime (γ >> 1), (γc/v z)(1 − kv z/ω)2 increases with γ. The laser frequency must decrease with time to keep resonance condition satisfied.
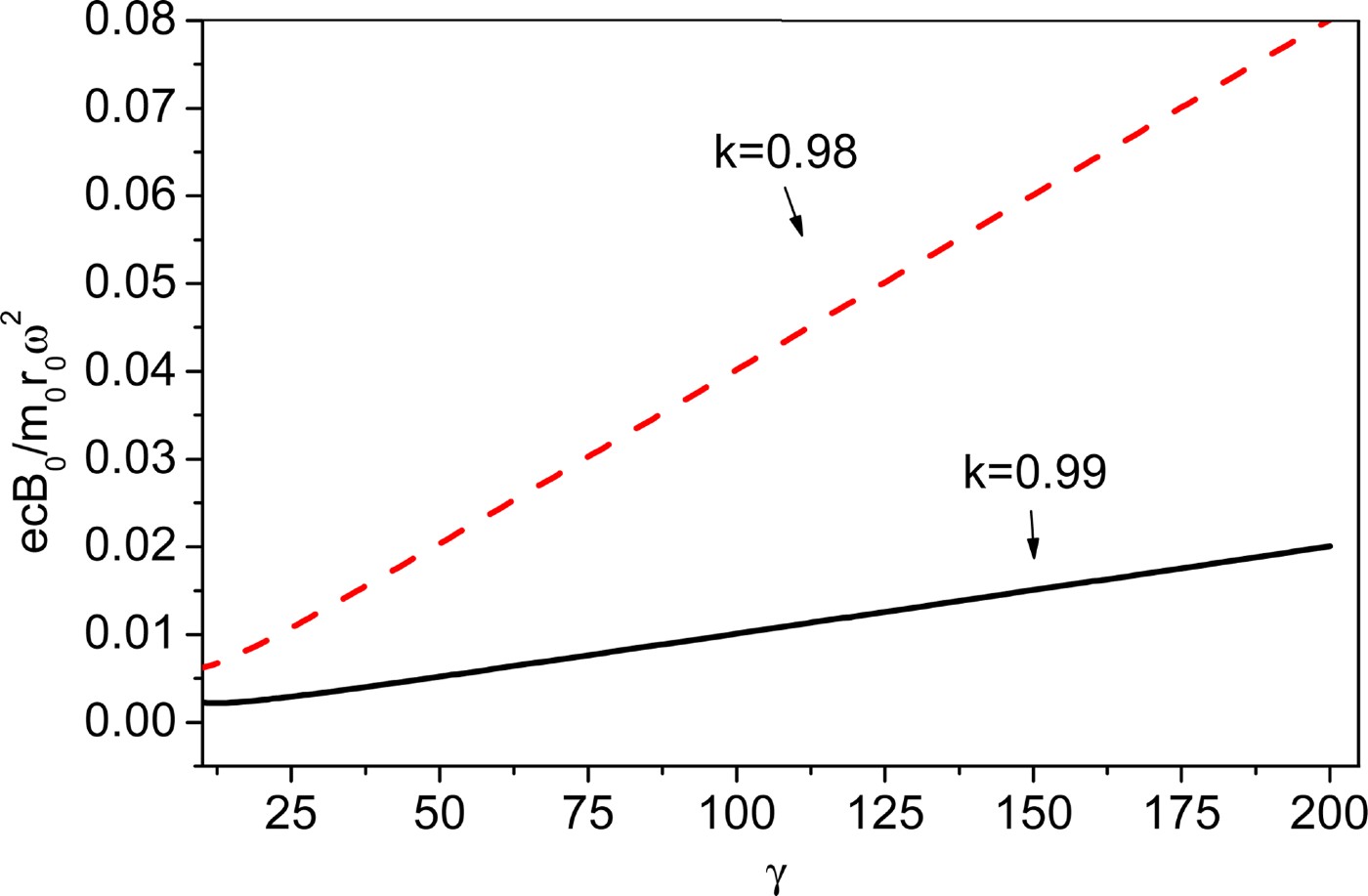
Fig. 1. (Color online) The variation of RHS ((γc/v z)(1 − kv z/ω)2) of the resonance condition given by Eq. (8) as a function of relativistic factor γ for k = 0.98 and k = 0.99.
In the relativistic regime (γ >> 1) and in the underdense plasma; resonance condition can be written as follows,

Again, resonance condition given by Eq. (10) indicates that laser frequency must decrease with time to keep resonance condition satisfied and thus to keep the electrons accelerating. Resonance can be maintained for longer duration if a suitable frequency chirp is introduced. Consider the propagation of a laser pulse with electric field
![\eqalignno{{\bf E}_L &= E_0 \left[\hat{x}\cos \lpar \omega \lpar t\rpar t - k\lpar t\rpar z\rpar + \hat{z} {2x \over k\lpar t\rpar r_0^2} \sin \lpar \omega \lpar t\rpar t - k\lpar t\rpar z\rpar \right]\cr &\quad \times \exp \left[-{\lpar t - \lpar z - z_L\rpar /v_g\rpar \over \tau^2}^2 - {r^2 \over r_0^2}\right]\comma \;}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000372_eqn11.gif?pub-status=live)
where z L is the initial position of the pulse peak, ω(t) = ω/(1 + αt), α is frequency chirp parameter, k(t) = (ω(t)/c)(1 − ωp2/ω(t)2)1/2, group velocity v g = c(1 − ωp2/ω(t)2)1/2, relativistic plasma frequency ωp2 = 4πn 0e 2/m, −e and m are the electronic charge and effective mass, respectively.
The magnetic field related to the electric field of the laser pulse is given by ∇ × E = −∂B/∂t.
![\eqalignno{{\bf B}_L &= E_0 {k\lpar t\rpar c \over \omega} \left[\hat{y}\cos \lpar \omega \lpar t\rpar t - k\lpar t\rpar z\rpar + \hat z {2y \over kr_0^2} \sin \lpar \omega \lpar t\rpar t - k\lpar t\rpar z\rpar \right]\cr &\quad \times \exp \left[-{\lpar t - \lpar z - z_L\rpar /v_g\rpar \over \tau^2}^2 - {r^2 \over r_0^2}\right]\comma \;}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000372_eqn12.gif?pub-status=live)
It has been assumed that a laser pulse having an appropriate frequency chirp survives nonlinear effects and maintains the chirp throughout the interaction process. The laser with frequency chirp up to a few tens percent is possible after propagation of an intense fs laser pulse through a plasma channel or with existing few-cycle systems (Gordon et al., Reference Gordon, Hafizi, Hubbard, Peñano, Sprangle and Ting2003). The reflection of EM pulses from a relativistic ionization fronts is promising to generate larger frequency chirps when the gamma factor of the front changes during the reflection (Dias et al., Reference Dias, Stenz, Lopes, Badiche, Blasco, Santos, Silva, Oliveira, Mysyrowicz, Antonetti and Mendonça1997).
The equations governing electron motion in the presence of electromagnetic fields and azimuthal magnetic field are solved numerically for electron trajectory and energy using fourth-order Runge–Kutta method with adaptive time step for various parameters and initial conditions.
3. RESULTS AND DISCUSSION
Throughout this paper time length, velocity, and frequency chirp parameter α are normalized by 1/ω, c/ω, c and ω. The normalized laser intensity parameter a 0 = eE 0/m 0ωc, and normalized magnetic field intensity parameter b 0 = eB 0/m 0ω has been used. The normalized laser spot size has been taken to be r 0 = 70, the normalized pulse duration τ = 200, and the normalized initial position of pulse peak z L =−400. The initial position of the electron is assumed at origin. In the experiments, the electrons are preaccelerated by the ponderomotive force of the laser or by the plasma wave before the acceleration process by betatron resonance starts. The initial transverse momentum of the electron is taken to be zero and the initial longitudinal momentum is taken to be p z0 as specified in the description of the results. Each figure in the following description has three lines for a 0 = 2 (dotted line), a 0 = 5 (dashed line), and a 0 = 10 (solid line). Only those values of magnetic field are considered for which resonance between the electric field of the laser and the electron occurs. These values are in the same range as given by Qiao et al. (Reference Qiao, He and Zhu2006). Three values of α are related to the different values of laser intensity. Figures (2) to (4) are for k = 0.98 and Figures (5) and (6) are for k = 0.99. The electron momentum and the displacement in the y direction has been found to be negligible, therefore, has not been shown. The results of our numerical simulations are as follows.
Figure 2 show variation of the normalized transverse momentum p x, x-coordinate, and the relativistic factor γ as a function of normalized time t without any frequency chirp (α = 0) for normalized initial electron momentum p z0 = 0.5, and normalized magnetic field intensity parameter b 0 = 5.2. The electrons at the front of the pulse are accelerated by the ponderomotive force of the pulse in the beginning and thereafter acceleration process by betatron resonance between the electric field of the laser and the electron starts. The transverse momentum and x-coordinate of the electron are oscillatory with time. The amplitude of oscillations attains a maximum and then decreases. The electron energy peaks around the same point where amplitude of oscillations is highest. The resonance condition does not hold beyond the point of highest energy gain and the electron loses the gained energy. The peak value of relativistic factor is nearly 120. The electron gains nearly the same energy for the three values of laser intensities. The acceleration gradient is higher for higher laser intensity. The normalized electron momentum in the z-direction is a major contributor to the energy and nearly equals the relativistic factor γ.

Fig. 2. (Color online) The transverse electron momentum p x, x-coordinate and the relativistic factor γ as a function of normalized time t for k = 0.98, P z0 = 0.5, magnetic field intensity parameter b 0 = 5.2 without any frequency chirp α = 0. Different lines are for a 0 = 2 (dotted line), a 0 = 5 (dashed line) and a 0 = 10 (solid line).
Figure 3 shows variation of the transverse electron momentum p x, displacement x, and relativistic factor γ as a function of normalized time t for p z0 = 0.5, b 0 = 2.9, α1 = 3.04 × 10−5, α2 = 5.24 × 10−5, and α3 = 7.2 × 10−5. The transverse momentum and the x-coordinate are oscillatory like Figure 2, however, magnitude of the transverse momentum p x and the amplitude of oscillations does not saturate, and keep on increasing with time. The resonance condition remains satisfied with the introduction of frequency chirp and the electron energy keeps on increasing. It can be seen that electron energy is nearly two times of the energy that without any frequency chirp.

Fig. 3. (Color online) The transverse electron momentum p x, x-coordinate and the relativistic factor γ as a function of normalized time t for k = 0.98, initial electron momentum P z0 = 0.5, magnetic field intensity parameter b 0 = 2.9, with laser frequency chirp parameters α1 = 3.04 × 10−5, α2 = 5.24 × 10−5, and α3 = 7.2 × 10−5. Different lines are for α0 = 2 (dotted line), a 0 = 5 (dashed line), and a 0 = 10 (solid line).
Figure 4a shows variation of the relativistic factor γ as a function of normalized time t for initial electron momentum p z0 = 1, magnetic field parameter b 0 = 3.15 without any frequency chirp (α = 0). A comparison between the results of Figures 3 and 4 shows that the value of magnetic field at which resonance occurs decreases with initial electron energy. An electron with less initial energy reaches close to pulse peak before it starts leaving behind the pulse, hence, interacts with the laser pulse for a longer duration and gains more energy than the electrons with higher initial energy. A higher value of required magnetic field for a low initial electron energy also leads to more effective energy exchange and the electron gains more energy in Figure 3a for the initial electron momentum P z0 = 0.5 than that in Figure 4a for the initial electron momentum P z0 = 1. Figure 4b show variation of the relativistic factor γ as a function of the normalized time t for magnetic field intensity parameter b 0 = 1.5, with frequency chirp parameters α1 = 4.8 × 10−5, α2 = 7.32 × 10−5, and α3 = 1.02 × 10−4. The resonance condition remains satisfied for a longer duration and the energy gained by the electron increases. The maximum energy with frequency chirp in Figure 4b is again nearly two times of the energy gain without any frequency chirp in Figure 4a.

Fig. 4. (Color online) The relativistic factor γ as a function of normalized time t for k = 0.98, initial electron momentum P z0 = 1, (a) magnetic field intensity parameter b 0 = 3.15 without any frequency chirp α = 0, and (b) magnetic field intensity parameter b 0 = 1.5, laser frequency chirp parameters α1 = 4.8 × 10−5, α2 = 7.32 × 10−5, and α3 = 1.02 × 10−4. Different lines are for a 0 = 2 (dotted line), a 0 = 5 (dashed line), and a 0 = 10 (solid line).
Figure 5a shows variation of the relativistic factor γ as a function of the normalized time t for the initial electron momentum P z0 = 0.5, and magnetic field intensity parameter b 0 = 2.58 without any frequency chirp (α = 0). The electron gains more energy than that in Figure 2c. The group velocity of the laser pulse increases with the decrease in plasma density and the duration of interaction of laser pulse and electron increases, which leads to increase in the electron energy. The Doppler shifted frequency also decreases with plasma density, hence, the value of magnetic field required for resonance decreases with the decrease in plasma density. Figure 5b shows variation of the relativistic factor γ for the initial electron momentum P z0 = 0.5, magnetic field intensity parameter b 0 = 1.2, and laser frequency chirp parameters α1 = 1.25 × 10−5, α2 = 2.625 × 10−5, and α3 = 3.65 × 10−5. The maximum energy with frequency chirp in Figure 5b is again nearly two times of the energy gain without any frequency chirp in Figure 5a.

Fig. 5. (Color online) The relativistic factor γ as a function of normalized time t for k = 0.99, initial electron momentum P z0= 0.5, (a) magnetic field intensity parameter b 0 = 2.58 without any frequency chirp α = 0, (b) P z0 = 0.5, magnetic field intensity parameter b 0 = 1.2 and laser frequency chirp parameters α1 = 1.25 × 10−5, α2 = 2.625 × 10−5, and α3 = 3.65 × 10−5. Different lines are for a 0 = 2 (dotted line), a 0 = 5 (dashed line), and a 0 = 10 (solid line).
Figure 6a shows variation of the relativistic factor γ as a function of the normalized time t for the initial electron momentum P z0 = 1 and the magnetic field intensity parameter b 0 = 1.6 without any frequency chirp (α = 0). The electron energy and the value of magnetic field at which resonance occurs both decrease with initial electron energy as in Figure 4. Figure 6b shows electron energy γ for the initial electron momentum P z0 = 1, the magnetic field intensity parameter b 0 = 1, and the laser frequency chirp parameters α1 = 1.58 × 10−5, α2 = 2.54 × 10−5, and α3 = 3.54 × 10−5. The maximum energy with frequency chirp in the present figure is again nearly two times of the energy gain without any frequency chirp in the Figure 6a.

Fig. 6. (Color online) The relativistic factor γ as a function of normalized time t for k = 0.99, initial electron momentum P z0 = 1, (a) magnetic field intensity parameter b 0 = 1.6 without any frequency chirp α = 0, and (b) magnetic field intensity parameter b 0 = 1, laser frequency chirp parameters α1 = 1.58 × 10−5, α2 = 2.54 × 10−5, and α3 = 3.54 × 10−5. Different lines are for a 0 = 2 (dotted line), a 0 = 5 (dashed line), and a 0 = 10 (solid line).
The group velocity of the laser pulse decreases with plasmas density. The pulse is not able to catch up with the accelerated electron at higher plasma density. It leads to reduction in the duration of interaction between the laser pulse and the electron, and the energy gained by the electron decreases.
The particle accelerators are used in different fields, ranging from tabletop narrow band femtosecond X-ray sources, free-electron lasers, material science, medicine and biology to high-energy physics. It has been difficult to use laser accelerators efficiently for practical applications because they produce poor-quality electron beams with large angular spreads. It has already been found by other authors that betatron resonance can produce quasi-monoenergetic beams. The energy of these quasi-monoenergetic beams can further be enhanced by introducing a suitable frequency chirp as shown in the above discussion.
4. CONCLUSIONS
Electron acceleration by a chirped laser pulse in an azimuthal magnetic field in a plasma has been studied. The resonance between electric field of the laser pulse and the electrons can be maintained for a longer period if a suitable frequency chirp is introduced. The energy gained by the electron with frequency chirp is nearly two times of the energy without any frequency chirp. The magnetic field for which the resonance occurs increases with plasma density and decreases with initial electron energy. The duration of interaction gets reduced for higher plasma densities and higher initial electron energy, resulting in decrease in the energy gained by the electron.
ACKNOWLEDGEMENT
This work was supported by Simutech.








