1. Introduction
Small landholders are known to be one of the main drivers of deforestation in the Brazilian Amazon and other tropical areas (Margulis, Reference Margulis2003; Aldrich et al., Reference Aldrich, Walker, Arima, Caldas, Browder and Perz2006; Mullan et al., Reference Mullan, Sills, Pattanayak and Caviglia-Harris2018).Footnote 1 The government often settles these families on public or expropriated lands for purposes of frontier development, or the smallholders squat on land without secure property rights (Lima et al., Reference Lima, Merry, Nepstad, Amacher, Azevedo-Ramos, Lefebvre and Resque2006; Ludewigs et al., Reference Ludewigs, Brondízio and Hetrick2009). Construction of highways and subsidized credit for cattle grazing have increased incentives for smallholder movement into the Amazon (Andersen et al., Reference Andersen, Granger, Reis, Weinhold and Wunder2002; Merry et al., Reference Merry, Amacher and Lima2008; Pacheco, Reference Pacheco2009; Brandão et al., Reference Brandão, Souza, Veríssimo, Pinto and Amaral2013).
According to the National Institute for Colonization and Agrarian Reform (INCRA), between 1994 and 2015, the Brazilian government settled over 17,000 families in the eight states that comprise the ‘Legal Amazon’.Footnote 2 Each smallholder family settles approximately 100 hectares of land on average (Merry et al., Reference Merry, Amacher and Lima2008), and once settled, Aldrich et al. (Reference Aldrich, Walker, Arima, Caldas, Browder and Perz2006) have demonstrated a progression in their behavior from clearing forest for subsistence agriculture, to eventually engaging in cattle ranching as they accumulate wealth (Ludewigs et al., Reference Ludewigs, Brondízio and Hetrick2009); in many cases it has been argued that smallholders are primarily interested in eventual cattle production (Pereira et al., Reference Pereira, Simmons and Walker2016). These landholders often sell timber when they clear land, but they also sell timber from uncleared forest on their lot, eventually transitioning from agriculture to cattle as incomes and resources accumulate. Harvesting of native forests that begins such transitions commonly happens either in partnership with or under pressure from both legal and illegal logging companies, and this forestland is often viewed as having a high opportunity cost vis-à-vis other agricultural opportunities, especially when long-term wealth accumulation effects are considered (Mullan et al., Reference Mullan, Sills, Pattanayak and Caviglia-Harris2018). It has also been argued that cutting of trees is the first step of wealth transformation that begins the eventual adoption of cattle for smallholders (Lima et al., Reference Lima, Merry, Nepstad, Amacher, Azevedo-Ramos, Lefebvre and Resque2006; Merry et al., Reference Merry, Amacher, Macqeen, Guimares dos Santos, Lima and Nepstad2006, Reference Merry, Amacher and Lima2008).
It is therefore not surprising that key government laws and policies have targeted restriction of the percentage of settled plots that can be cleared of forest. The most important of these is the Brazilian Forest Code. Enacted in 1965Footnote 3 and revised in 2012, the Forest Code in general restricts deforestation of private lots in Amazonia to 20 per cent (Nepstad et al., Reference Nepstad, McGrath, Stickler, Alencar, Azevedo, Swette, Bezerra, DiGiano, Shimada, da Motta and Armijo2014; Soares-Filho et al., Reference Soares-Filho, Rajão, Macedo, Carneiro, Costa, Coe, Rodrigues and Alencar2014). Since its inception, Brazil has not enforced the Code consistently. However, that changed with the environmental administration elected to power in 2003, which immediately implemented a new program of frontier policies within the Action Plan for Prevention and Control of the Legal Amazon Deforestation (PPCDAM). Through this program, resources were supposedly committed to better enforcement of the Forest Code in Amazonia, among other actions.Footnote 4 Whether actual increased enforcement has occurred or whether the government has largely used rhetoric is unclear, and its effect on smallholder land clearing remains unknown regardless.
In this paper, we seek to investigate incentives to comply with the Forest Code through better understanding of land clearing under the supposed shift in enforcement. We do this by first developing a dynamic model of land clearing decision for a smallholder who can clear land and sell the harvested timber to make way for agriculture or grazing, and who can also sell wood from uncleared land. The goal of developing this model is to derive a land-clearing path over time that is sensitive to smallholder assessment of Forest Code enforcement. We do this by assuming that the representative smallholder's assessment of the probability of being caught not complying is an unobserved endogenous factor that selects smallholders into compliance or noncompliance. We then use a unique data set of more than 1,000 smallholders sampled in 2003, before implementation of greater Forest Code enforcement under PPCDAM (or, at least, increased rhetoric concerning such enforcement), and then again in 2014 using an endogenous selection model that allows examination of land clearing regimes and a study of the incentives for noncompliance.
Our work contributes to the literature by proposing and then testing a dynamic model to show how land clearing incentives are influenced by unobserved environmental legislation enforcement. As such we are able to identify not only the most important drivers of forest clearance among smallholders selected into complying and not complying, but also to identify the most important characteristics that determine selection of a given smallholder into each of these groups. Because our selection approach is endogenous, it improves upon methods in which land clearing is considered only for observed compliers or noncompliers, or for cases where land clearing is examined for all smallholders together without selection. Our approach allows for the fact that a current complier with the Forest Code may have more in common with current noncompliers, and thus this smallholder is transitioning toward not complying with their land clearing decisions over time.Footnote 5 Our resampling of the same smallholder families more than a decade apart, using an identical survey instrument, allows this novel comparison.
The literature on land clearing has studied incentives for smallholders to clear forest for agricultural uses, with empirical applications based on cross sectional or regional/country data. Barbier and Burgess (Reference Barbier and Burgess2001) classify land clearing studies into two groups: those that seek to empirically identify drivers of deforestation in tropical countries, and those that propose models of economic behavior to explain the incentives behind the land clearing decision itself. Our model contributes to the latter as we build upon the ‘classical’ land clearing model that assumes smallholders maximize household utility based on net benefits they can extract from the land (e.g., see Pfaff et al., Reference Pfaff, Amacher and Sills2013). These types of decisions have been investigated in myriad specific market and institutional settings (Caviglia-Harris and Sills, Reference Caviglia-Harris and Sills2005; Takasaki, Reference Takasaki2007; Bowman et al., Reference Bowman, Amacher and Merry2008; Pfaff et al., Reference Pfaff, Amacher and Sills2013; Mullan et al., Reference Mullan, Sills, Pattanayak and Caviglia-Harris2018). However, there is no previous work we are aware of which accounts for smallholder responses to laws restricting use of their land.Footnote 6
Previous land clearing models therefore ignore the possibility of unobserved selection when investigating drivers of land clearing. Our approach also allows for a more complete analysis of deforestation that incorporates underlying incentives and government enforcement. Additionally, from an economic theory perspective, ours is the first study in which the Forest Code, or a policy of this sort, is considered in a dynamic smallholder land clearing decision model.
2. Household model of land clearing with uncertain enforcement assessment
Let the representative smallholder have an initial forested land endowment at time zero of 
$L_{0}=\bar{L}$, so that land available to clear at time t is 
$L_{t} \le \bar{L}$. The smallholder decides how much land to clear in each period, denoted by a control variable c t, to increase agricultural and grazing production possibilities.Footnote 7 The reduction in the area of land available for clearing at each time period t corresponds to forested area cleared in that period. This time rate of change in land available is given by 
$\dot{L}_{t}=-c_{t}$. At any time t, the land that has been cleared in the past is equal to 
$\int_{0}^{t} c_{t}\,dt$ and future land available to clear equals 
$L_{t} =\bar{L}-\int_{0}^{t} \,c_{t}\,dt$.
Cleared land at time t produces rents from agriculture and grazing given by 
$A_{t} =a\left(\int_{0}^{t} c_{t} \,dt, {\bi p}_{{\bi a}}\right)$, which depend on the total area in production from time t = 0 until the current time period and on a vector of agricultural prices, 
${\bi p}_{{\bi a}}$. To make our focus on land clearing simple, the rent function is separable and concave in new land cleared and land previously cleared (infra-marginal land). That is,
$$A_t\equiv a\left( {\int_0^{t-1} {c_t} dt + c_t,{\bi p}_{\bi a}} \right)\equiv a\left( {\int_0^{t-1} {c_t} dt, {\bi p}_{\bi a} } \right) + a(c_t, {\bi p}_{\bi a}),$$ where 
$((\partial a)/(\partial c_{t} ))\ge 0$ and 
$((\partial ^{2}a)/(\partial ^{2}c_{t} ))\le 0$. Thus, cleared land is a perfect substitute for existing agricultural land in an agricultural production sense.Footnote 8 Other non-land inputs for agricultural and grazing production, such as capital and labor, are assumed to be employed at their optimal levels, such that the choice we are focusing on is how much land to clear in every period t.Footnote 9 Additionally, whenever land is cleared, the small landholder has the option to extract and sell the timber available, in which case the net revenues from timber sales are net of clearing costs and denoted 
$R_t = {\rm {\cal R}}(c_t, {\bi p}_{\rm {\cal R}})$. Thus, net revenues from timber sales are a function of area of land cleared at time t and of a timber price vector, 
${\bi p}_{\rm {\cal R}}$. Because smallholders take prices as given and there are central markets that determine these prices, we write 
$A_{t} =a\left( {\int_{0}^{t} {c_{t} \,dt} \,} \right)$ without loss of generality.
Standing forested land also produces rents from forest uses, such as non-timber forest products (NTFPs) extraction (e.g., seeds, fruits, resins, oils, among others) and game meat. We denote such rents by the function 
$F_t = f\left( {\bar{L}-\int_0^t {c_t dt,{\bi p}_{\bi f}} } \right)\equiv f\lpar {L_t,{\bi p}_{\bi f}} \rpar $. That is, standing forest rents are a function of the area of forest land available for clearing at the beginning of period t and of a NTFP price vector, p f. All forest-related prices are also assumed constant through time for simplicity in the theoretical derivations.
When deciding how much forestland to clear in time period t, the smallholder household weighs expected gains in rents from timber extraction and from agriculture and grazing against the lost revenues from foregoing NTFPs and game meat that are no longer producible on cleared land units. An additional factor in this decision is the Forest Code, defined as a proportion β in rewriting the land clearing equation as Footnote 10
$$\int_0^t {c_t} dt \le \beta \bar{L},$$ where β defines the fraction of the initial forest land endowment that the landholder is allowed to clear in total according to the Forest Code, under the assumption that land is entirely forested upon settlement (t = 0). At any time t, the landholder may or may not be observationally compliant with the law depending on the amount of land they have cleared since t = 0, and once they become noncompliant and in violation of (1), we assume they cannot become compliant at a later point in time, which fits our empirical analysis. Thus, according to (1), a noncompliant household can be thought of as one for which the constraint is binding for all 
$s>t,\int_{0}^{t} {c_{t} dt=\beta \bar{L}} $, while a compliant household is one for which the constraint is not binding. The ‘bindingness’ of this constraint to describe noncompliance is a mathematical construct and would be the same if we were to think about compliance as clearing less than allowed (as a strict inequality) and noncompliance as clearing more than allowed. In other words, the constraint is used only to define notationally what we mean by compliant and noncompliant levels of land clearing under the exogenously given Forest Code requirement, and this is useful below when defining a co-state variable in (6).
In deciding how much land to clear in period t, the household will also consider potential costs from not being compliant with the Forest Code should they cheat and be caught. These potential costs include fines to be paid to the government and costs associated with additional penalties the government could levy related to the extent of the crime. We write the costs of being detected not complying as 
$M_{t} =m\left( {\int_{0}^{t} {c_{t} dt,t} } \right)$, where 
$((dM_{t} )/(dc_{t} ))>0$, with a conventional convexity assumption, 
$((d^2M_t)/(dc_t ^2))>0$. These costs are defined by the government administrative process and are assumed known by the smallholder. While the smallholder does not know the government's actual enforcement effort in each time period, he does have an assessment of this probability of being caught and uses it in his land clearing decisions. The expected costs are defined by this assessment. Herein we call this assessment of the probability the ‘perceived probability’ of being caught and define it by 
$\gamma \in \lsqb {0,1} \rsqb $. For the model of a representative smallholder, we adopt a notation 
$\gamma ({\brOmega })$ to reflect household characteristics 
${\brOmega}$ that can influence the assessment.
Using the definitions above, the representative smallholder household maximizes expected net returns to forest and agricultural land uses,
$$\mathop {\max }\limits_{c_t} \int_0^T E [ {\pi_t\lpar {L_t, c_t, {\bi p}, \gamma ;{\brOmega }} \rpar } ] e^{-rt}dt,$$ where 
${\bi p}$ is a price vector with components 
${\bi p}_{{\bi a}}$, 
${\bi p}_{{\cal R}}$, and 
${\bi p}_{{\bi f}}$. Expected profits at time t are a function of forest land available for clearing L t and the amount of land cleared at each time c t, assuming all non-land productive inputs are employed at their optimal levels on each land use. Expected profits are also a function of 
${\brOmega}$, which determines the landholder's perceived probability of being caught if not compliant with the Forest Code. Decomposing (2) further, under the assumption that the household does not comply with the Forest Code we have:
$$\eqalign{ E[ {\pi_t} ] & \equiv \gamma \lpar {\brOmega } \rpar *\left\{ {{\rm {\cal R}}\lpar {c_t} \rpar + a\left( {\int_0^t {c_t} dt} \right) + f\lpar {L_t} \rpar -m\left( {\int_0^t {c_t} dt} \right)} \right\} \cr & + (1-\gamma ({\brOmega }))*\left\{ {{\rm {\cal R}}\lpar {c_t} \rpar + a\left( {\int_0^t {c_t} dt} \right) + f\lpar {L_t} \rpar } \right\}.} $$The first terms in braces represent expected profits if the smallholder cheats and clears more than allowed and is caught by the government, while the second braced terms represent rents captured when the government does not detect the smallholder's land clearing behavior.Footnote 11 If the smallholder does comply with the Forest Code, then this compliant household would have a different land clearing path through time than one who does not.
In addition to (1), there are three other constraints to the problem in (2). First, the control variable is non-negative, c t ≥ 0. Second, the initial condition for the state variable, land available to clear, is given by the forested land endowment at time zero, 
$L_{t} (t=0)=\bar{L}$. Finally, land available for clearing changes through time according to the following equation of motion:
$$\dot{L}_t = -c_t.$$Using these constraints and definitions to rewrite the smallholder's land clearing problem, the expected present value profits become:
$$\mathop {\max }\limits_{c_t} \int_0^T {\left[ {{\rm {\cal R}}(c_t) + a\left( {\int_0^t {c_t} dt} \right) + f(L_t)-\gamma ({\brOmega }) \times m\left( {\int_0^t {c_t} dt} \right)} \right]} \times e^{-rt}dt.$$We form the Hamiltonian function as:
$$\eqalign{ {\rm {\cal H}} =& \left\{ {{\rm {\cal R}}(c_t) + a\left( {\int_0^t {c_t} dt} \right) + f(L_t)-\gamma ({\brOmega })m\left( {\int_0^t {c_t} dt} \right)} \right\}e^{-rt}-\lambda _tc_t \cr & + \xi _t\left( {\beta \bar{L}-\int_0^t {c_t} dt} \right) + \eta _tc_t,} $$ where the co-state variable λt in (6) is the shadow value of a unit of forested land in (5). The symbols ξt and ηt are the multipliers corresponding to the legal land clearing restriction (1) and non-negativity condition for the control variable c t, respectively. Additionally, we have the initial condition for the state variable, 
$L_{0} =\bar{L}$. The Maximum Principle requires (4) and the following other necessary conditions to hold:
$$\lcub {{R}^{\prime}\lpar . \rpar + {a}^{\prime}\lpar . \rpar -\gamma \lpar {\Omega } \rpar {m}^{\prime}\lpar . \rpar -{f}^{\prime}\lpar . \rpar } \rcub e^{-rt} + \xi _t + \eta _t = \lambda _t$$
$$\displaystyle{{\partial f\lpar {L_t} \rpar } \over {\partial L_t}}e^{-rt} = -\mathop {\lambda _t}\limits^. $$
$$\xi _t\left( {\beta \bar{L}-\int_0^t {c_t} dt} \right) = 0$$
$$\eta _tc_t = 0$$
$$\lambda _T = 0.$$Condition (7) implies land clearing is chosen at each point in time to equate the marginal net timber sale and agricultural rents from an additional land unit cleared net of expected penalty costs if caught cheating and lost non-timber forest rents from cleared land to the shadow value of cleared land captured by λt. Condition (8) implies that the change in this shadow value depends on the marginal forest rent change from land kept uncleared through time. Condition (9) corresponds to the constraint on compliance (with multiplier ξt ≥ 0), whereas (10a) and (10b) are the non-negativity constraint (with multiplier ηt ≥ 0) and the transversality condition, respectively. The latter reflects a free-endpoint optimal control problem, in which by the end of our fixed time horizon, T, the amount of land cleared c T may take on any value such that the value extracted from the land may be maximized during the time horizon in consideration and, as a result, such that the shadow value of the last hectare of land cleared is equal to zero.Footnote 12
To derive a condition for perfect compliance of smallholder land clearing with the Forest Code, we assume for the moment that 
$\beta \bar{L}-\int_{0}^{t} c_{t} dt=0$, which together with ξt > 0 and c t > 0 implyFootnote 13
$$({R}^{\prime}(.) + {a}^{\prime}(.)) < (\gamma {\brOmega }){m}^{\prime}(.) + {f}^{\prime}(.)).$$ Thus, a compliant smallholder at a time t views the expected cost of cheating plus lost NTFP rents (RHS terms) as being greater than the marginal benefits from clearing an additional unit of land for agriculture rents and forest timber sales (LHS terms). Obviously, a noncompliant smallholder would find that at the point in time s where cheating just occurs, and 
$\beta \bar{L}<\int_{0}^{s} {c_{t}dt}$, the LHS of this condition was equal to or greater than expected penalties and lost NTFP rents. Therefore, not only a small landholder's preferences but also their perception of the probability of being caught cheating 
$\gamma ({\brOmega})$ plays an important role in the path of clearing land over time; the latter, through the decision to be compliant with the Forest Code or not.
The necessary conditions can be used to derive a path for land clearing through time. Assuming that c t > 0 so that ηt = 0, and that the smallholder is compliant with the Forest Code so that ξt = 0, we take the time derivative of (7) and substitute this result into equation (8). Restating the condition in terms of the instantaneous rate of change in land clearing, we obtain:
$$\matrix{ {\matrix{ \matrix{\displaystyle{{{\dot{c}}_t} \over {c_t}} = \displaystyle{r \over {c_t}} \left[ {\displaystyle{{{R}^{\prime}\lpar . \rpar + {a}^{\prime}(.)-{f}^{\prime}\lpar . \rpar \displaystyle{{1 + r} \over r}-\gamma \lpar {\Omega } \rpar {m}^{\prime}(.)} \over {{R}^{\prime \prime}(.){\rm +\ }{a}^{\prime \prime}\lpar . \rpar + {f}^{\prime \prime}(.){\rm -\ }\gamma ({\Omega }){m}^{\prime \prime}(.)}}} \right] \hfill \cr \quad \quad -\left[ {\displaystyle{{{a}^{\prime \prime}(.){\rm +\ }{f}^{\prime \prime}\lpar . \rpar -\gamma \lpar {\Omega } \rpar {m}^{\prime \prime}(.)} \over {{R}^{\prime \prime}(.){\rm +\ }{a}^{\prime \prime}\lpar . \rpar + {f}^{\prime \prime}(.){\rm -\ }\gamma ({\Omega }){\rm {m}^{\prime \prime}}(.)}}} \right], \hfill} \hfill \cr } } \hfill \cr } $$which gives an equation for the path of land clearing under perceptions of enforcement of the Forest Code by the government. This is a time autonomous path but has second-order effects for rent functions and for the government penalty function for the extent of cheating; these second-order effects are due to changes in land availability for the smallholder. If we highlight the penalty function by removing second-order rent effects, the land clearing path simplifies toFootnote 14:
$$\displaystyle{{\mathop {c_t}\limits^. } \over {c_t}} = \left\{ {\displaystyle{r \over {c_t}}\left[ {\displaystyle{{{R}^{\prime}\lpar . \rpar + {a}^{\prime}\lpar . \rpar + {f}^{\prime}\lpar . \rpar \left( {\displaystyle{{1-r} \over r}} \right)-\gamma \lpar {\Omega } \rpar {m}^{\prime}\lpar . \rpar } \over {-\gamma \lpar {\Omega } \rpar m^{{\prime}{\prime}}\lpar . \rpar }}} \right]-1} \right\}.$$Equation (12b) tells us that the instantaneous rate of change in land clearing depends on the marginal benefits from land clearing net of the sum of the forgone benefits from a unit of forested land and the perceived cost of being caught cheating.
A key component of (12a) and (12b) is the perception that the smallholder has regarding the probability of being enforced under the Forest Code. Clearly, as the representative smallholder's perception of 
$\gamma ({\brOmega})$ changes, so does the path and rate of change in land clearing; if the smallholder expects a higher probability of getting caught or a steeper fine function over time, then the time rate of land clearing slows. This may be because they believe the government rhetoric concerning more serious punishments and stepped-up efforts to catch noncompliers. We can therefore test this parameter indirectly for its effects on land clearing by testing for a different regime in land clearing over time in our sample for those smallholders who select into a high perceived probability and those with a low probability; we can do this by also including and thus correcting for known drivers in a land clearing regression, so that regime differences are due to the unobserved probability perception. Moreover, given condition (12), we also expect a separation in terms of compliers and noncompliers with respect to their land clearing decision. This too will be tested in the empirical model.
2.1 Non-constant prices and rents
Over a longer period of time, there is the possibility that there could be changes and shifts in prices that define the rent functions in (2)–(6). This changes the level of the optimal path for land clearing derived in (12a)–(12b), but it does not change the basic premise that we find of two regimes defining land clearing in the Forest Code problem. To see this, assume now that expected net rents from land clearing are specifically time dependent, due to both agricultural and forest harvest price shifts through time. In this case we write the Hamiltonian function for clearing land in each time point as:
$$\eqalign{ {\rm {\cal H}} = & \left\{ {{\rm {\cal R}}(c_t,t) + a\left( {\int_0^t {c_t} dt,t} \right) + f(L_t,t)-\gamma \lpar {\brOmega } \rpar m\left( {\int_0^t {c_t} dt,t} \right)} \right\}e^{-rt} \cr & -\lambda _t c_t + \xi _t\left( {\beta \bar{L}-\int_0^t {c_tdt} } \right) + \eta _tc_t.} $$ Although the time dependency in the penalty function 
$m\left( {\int_{0}^{t} {c_{t} dt,t} } \right)$ may seem redundant given that shifts in perceptions about the expected cost through the parameter 
$\gamma ({\brOmega})$,before and after Forest Code implementation, have already been included in (12a) and (12b), a specific time dependence is still possible. Using time shifting rent paths, we follow the procedure earlier in deriving (12a) and arrive at a new land clearing path given by:
$$\eqalign{\displaystyle{{\mathop {c_t}\limits^. } \over {c_t}} =& \displaystyle{{\displaystyle{r \over {c_t}}\left\{ {{\rm {{\cal R}}^{\prime}}\lpar . \rpar \left[ {1-\displaystyle{{R\lpar . \rpar } \over r}} \right] + {a}^{\prime}\lpar . \rpar \left[ {1-\displaystyle{{a\lpar . \rpar } \over r}} \right]-{f}^{\prime}(.)\left[ {1-\displaystyle{{f\lpar . \rpar + 1} \over r}} \right]-\gamma \lpar {\Omega } \rpar {m}^{\prime}(.)\left[ {1-\displaystyle{{m\lpar . \rpar } \over r}} \right]} \right\}} \over {\lcub {{\rm {{\cal R}}^{\prime \prime}}\lpar . \rpar + {a}^{\prime \prime}\lpar . \rpar + {f}^{\prime \prime}(.)-\gamma \lpar {\Omega } \rpar {m}^{\prime \prime}\lpar . \rpar } \rcub }} \cr & -\displaystyle{{\lcub {{a}^{\prime \prime}\lpar . \rpar + f(.){\rm -\ }\gamma \lpar {\Omega } \rpar {m}^{\prime \prime}(.)} \rcub } \over {\lcub {{\rm {{\cal R}}^{\prime \prime}}\lpar . \rpar + {a}^{\prime \prime}\lpar . \rpar + {f}^{\prime \prime}(.)-\gamma \lpar {\Omega } \rpar {m}^{\prime \prime}\lpar . \rpar } \rcub }}.} $$ This is a straightforward and relatively minor modification of (12a). In fact, according to this new path, the interpretations concerning the importance of the perception of the probability of the smallholder being detected not complying with the Forest Code are identical. However, now these perceptions change land clearing through three channels operating on expected penalty costs. First, there are changes in prices, which change 
${\rm {\cal R}}(c_t,t)$ and f(L t, t) through time. Second, there is the effect through the term 
$\gamma \lpar {\brOmega } \rpar {m}^{\prime}(.)$, which is due to the extent of cheating. Finally, there is a new effect that depends simply on time, through the term 
$\gamma ({\brOmega }){m}^{\prime}(.)\lsqb {((\dot{m}(.))/r)} \rsqb $, that may come through shifts in government resource availability, that are not observed by the smallholder but that impact penalty likelihood of enforcement (for example: changes in the local judicial system or in management of Forest Code implementing agencies).
3. Empirical data
We examine our expectations of land clearing regimes using a household survey carried out in 2003 along the Transamazon Highway and implemented again in 2014 using the same sampling procedure detailed in Merry et al. (Reference Merry, Amacher and Lima2008) for six municipalities: Brasil Novo, Uruará, Medicilândia and Placas, and government settlements along the BR163 Highway called PA Moju I & II, about 40 Km south of Santarém and also to the west of Altamira (see figure 1). There were 542 households that remained on their lots in 2014 out of the 1,108 sampled in 2003, for a total of 1,084 observations. A household continued to represent the domicile interviewed in 2003 if the smallholder had not moved during the first and second sampling periods. While unable to study out-migration due to the impossibility of sampling relocated households, the proportion of families who have left their smallholdings is similar to that found by Aldrich et al. (Reference Aldrich, Walker, Arima, Caldas, Browder and Perz2006).
Figure. 1. Location of surveys along the Transamazon and BR163 highways.
There are two notes we should make before proceeding. First, so that monetary values are comparable across periods, all currency dependent (nominal) variables are restated in 2014 Brazilian reais (R$) using published price index data available from Fundação Getúlio Vargas.Footnote 15 Second, although we are essentially asking about cleared land, the questions were asked in multiple ways (e.g., size of the lot, size of agricultural plots, forested area, original size of forest and agricultural plots, area cleared in the previous year) for both time periods. Thus, in comparing the data, we minimized errors in false responses to these questions. More importantly, given the similarity of smallholders in this region in terms of resources and opportunities, we assume such errors to be small or, at least, expected to be consistent across smallholders.
Descriptive statistics and two sample t-tests for relevant variables appear in tables 1 and 2, by year sampled (rounds) and observed compliance status, respectively. Significant differences between rounds are observed for variables related to land clearing such as deforested area, harvested area and herd size, suggesting clearing expansion despite Forest Code enforcement measures enacted in our sampling time span. In fact, as expected, total land cleared is significantly larger for 2014 compared to 2003: mean deforested area increased by 45 per cent. Additionally, there is significantly less hunting on the lots in 2014 than in 2003, reflecting less forested area consistent with the greater land clearing observations in the second survey period. The value of agricultural production across sampling times is not significantly different across sampling periods. This result is consistent with the natural progression of smallholders transitioning from agricultural to grazing mentioned earlier.
Table 1. Descriptive statistics by sample period
Notes: **p < 0.05, ***p < 0.01.
Table 2. Descriptive statistics by Forest Code compliance
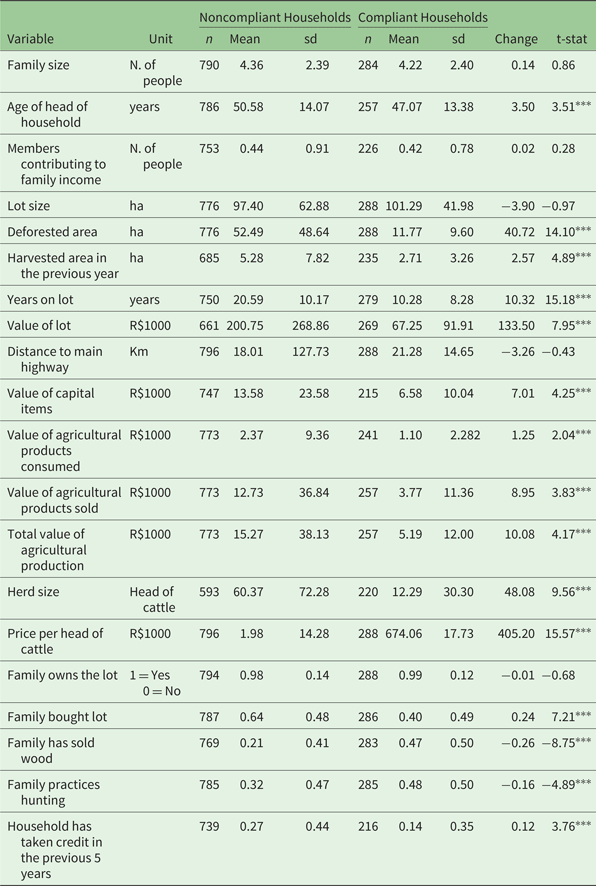
Notes: ***p < 0.01.
The means of variables important to checking consistency across sampling periods for the econometric analysis are not found to be significantly different. Mean lot sizes are not significantly different, which suggests the absence of significant activity as far as purchasing adjacent lands between sample periods is concerned and allows for land clearing behavior comparisons for each household across time. Moreover, distance to the main highway in dirt and gravel roads (either the Transamazon or the BR163, for the case of PA Moju) is also not significantly different, validating that we are sampling the same households (that is, that lot locations have not changed). Ownership status of the lot also appears unchanged over time for each smallholder household, suggesting stability in a landholder's property rights regime. The proportion of households that sold wood also appears fairly stable over time, although our estimates of propensity to sell wood between periods is statistically different, with a higher propensity to sell in the second round of interviews.
Table 2 shows descriptive statistics between observed compliers and noncompliers of the Forest Code. The proportion of smallholders in our sample who were compliant decreased significantly from 35 to 18 per cent in the ten years between data collections based on total area cleared of forest on their lot. On average, Forest Code compliant households cleared 11.55 per cent of forests on their lot, while those not complying cleared on average 53.89 per cent of their lot. We observe significant differences at the 1 per cent level between compliers and noncompliers in the propensity to sell wood and to engage in hunting in the forested part of their lot. Additionally, significant differences appear to exist with compliers having lower values for variables relevant to our analysis, such as harvested area in previous year, value of capital items, total value of agricultural production, and herd size.
The descriptive statistics show that there are indeed observable differences between compliers and noncompliers and also suggest that cattle is important to compliance as well as the use of the forest by the small landholder. One may argue that these differences are to be expected, in that they point to a progression smallholders go through over time and that noncompliance, thus, is inevitable. However, this is not necessarily the case given that the (unobserved) perceived probability of enforcement is from our model another factor influencing the decisions of smallholders to comply with the Forest Code.
4. Econometric estimation
The land clearing paths in (12a)–(12c) reveal that smallholders will clear according to variables important to rents, household characteristics such as wealth, and the perception of how government enforcement of the Forest Code is executed, reflected by the probability variable 
$\gamma ({\brOmega})$. Given 
$\gamma ({\brOmega})$, there is a type of selection between smallholders who have the same rent possibilities but perceive different probabilities of Forest Code enforcement. Differences in the perceived probability of being caught critically influence the likelihood that a household in our sample will comply, as described in (11) and realized through the path derivation for a compliant household in (12a)–(12c).
4.1 Econometric model
An endogenous switching regression model allows investigation of this problem, as we have a situation in which, we assert, an unobserved factor is contributing to the decision to clear land, that is, the perception of being caught violating the Forest Code. This factor is a driver of land clearing in addition to those that have been investigated throughout the literature. Moreover, such a factor also contributes to the probability of whether a household will eventually decide to be compliant or not with the Forest Code; that is, we have a nonrandom self-selection into compliance or noncompliance, which we need to account for in order to avoid selection bias in investigating the existence of this unobserved land clearing driver. The endogenous switching regression method has been shown to be appropriate to correct for selection of this type.Footnote 16 For this reason, several studies have applied this approach, mostly within the labor economics realm, but also in housing demand estimation and program evaluation (Lokshin and Sajaia, Reference Lokshin and Sajaia2004; Dutoit, Reference Dutoit2007). Recently, this method has been used in technology adoption within the economics of development and agricultural economics fields.Footnote 17 Ours is the first paper we are aware of using such a method in the analysis of land clearing behavior by small landholders.Footnote 18
The endogenous switching regression model accounts for the fact that we cannot distinguish between compliant households according to our data that may not comply in the future versus households that have definitely not complied (that is, it allows for unobserved selection bias in this decision). Such an interpretation follows because the only unobserved variable in the land clearing paths in our theoretical model, not corrected for with observational data in the empirical model, is enforcement perception; all other variables that determine land clearing paths are observed and faced exogenously by each price taker smallholder household. Moreover, as discussed earlier, because compliers and noncompliers to the Forest Code likely have different perceptions of the risk of being caught, 
$\gamma ({\brOmega})$, from (12a)–(12c), this parameter generates two different types of observed land clearing path behaviors.
The switching regression model relies on a binary criterion function I i and it used in several articlesFootnote 19:
$$Y_{1ti} = {X}^{\prime}_{1ti}\beta _1 + u_{1i}\quad iffI_i = 1,$$
$$Y_{2ti} = {X}^{\prime}_{2ti}\beta _2 + u_{2i}\quad iffI_i = 0,$$such that
$$I_i = \left\{ {\matrix{ {1\quad iff:W_{{i}^{\prime}}\alpha -\vartheta_i > 0} \hfill \cr {0\quad iff:W_{{i}^{\prime}}\alpha -\vartheta_i \le 0,} \hfill \cr } } \right.$$ where α and βi are coefficients to estimate, and Y 1i and Y 2i correspond to the land area cleared at the moment of the interview for two regimes: Forest Code noncompliance: I i = 1 (clearance of more than 20 per cent of lot size) and Forest Code compliance I i = 0 (clearance within 20 per cent of lot size). Equation (15) is the latent selection equation, representing the net benefits from clearing land. The regression variables on the RHS are weekly exogenous. This model corrects for selection in our data into compliance and noncompliance due to unobserved perceptions about 
$\gamma ({\brOmega})\,$driving behavior (Lokshin and Sajaia, Reference Lokshin and Sajaia2004). We will follow Lokshin and Sajaia (Reference Lokshin and Sajaia2004) in estimating the model and all parameters simultaneously using a full information maximum likelihood (FIML) method. The FIML approach by definition assumes a trivariate normal distribution and possible correlation for the error variables u 1i, u 2i, and ϑi. Thus, FIML estimates are efficient, producing robust and asymptotically consistent coefficient estimates and standard errors, and are more appropriate than estimating the two stage processes described in Maddala (Reference Maddala, Griliches and Intriligator1986).
Using our representative perception assumption concerning the probability of being caught through government enforcement of the Forest Code, 
$\gamma ({\brOmega})$, condition (15) follows from (11), while (13) and (14) follow from the derived optimal land clearing path 
$((\dot{c}_{t})/(c_{t}))$. Noncompliance holds for household i only when the expected benefits from noncompliance are greater than its expected costs (I i = 1). Forest Code compliance, on the other hand, is given by the second equation in (15) and it governs land clearing according to (14), when the smallholder's expected net benefits from noncompliance are negative (I i = 0). Equation (15) therefore represents a latent net benefit of forest clearing.
The latent selection variable I i is endogenous and determines our switching regression rule as it embeds the expected probability of being caught for each smallholder into the observed data on land cleared. The variables X 1i and X 2i are variables on the RHS of the theoretical land clearing paths, 
$((\dot{c}_{t})/(c_{t}))$ in (12a)–(12b), and include prices, production inputs, forest production preferences, and household characteristics. The variables determining the unobserved latent variable, W i, include in addition those that could determine compliance. The endogenous switching regression model allows for some of the variables within W i to be, by definition, the same as those in X 1i and X 2i. Such a model is necessary as it is here when the variance of these variables in determining the latent variable is nonzero, or 
$\sigma _{1v} \ne 0$ and 
$\sigma _{2v} \ne 0$.Footnote 20 The advantage of this model is that it fits our theory closely: we showed that similar variables determine whether a smallholder household will comply or not with the Forest Code and also determine the rate of land clearing for each regime. From our theory and our sampling, we have no a priori expectation that the variable sets will differ in these equations and thus can assume a similar specification for explanatory variables of (13)–(15).
4.2 Econometric model results
We must address several econometric issues in estimating (13)–(15). Exogenous (nonproduction) income is important, yet we have missing observations for this variable in our data for the first round and for the PA Moju area. Thus, we predict those missing observations in advance of estimating the switching regression using a first stage regression of households that report exogenous income. Second, in our sample, and generally in the Transamazon, smallholders may choose to sell wood from forested parts of their lots to logging enterprises that approach them. We expect this decision to represent an endogenous variable in (13)–(15). Ideally, we would use prices for wood sold faced by the smallholder price taker as an exogenous instrument for wood sales. Since that data was not available to us, we estimated the probability that each smallholder would sell wood using a first stage probit regression, a common procedure for endogenous qualitative response variables.Footnote 21
Finally, despite the representative small landholder assumption underlying 
$\gamma ({\brOmega})$ in the theoretical model, we ran a robust version of our switching regression model correcting for heteroskedasticity. If all smallholders are representative ‘enforcement takers’, then they present the same empirical realization of 
$\gamma ({\brOmega})$ and therefore we can write 
$\gamma \equiv \gamma ({\brOmega})$. This is plausible, as smallholders in each region visit and work in the same markets and are price takers in these markets. The information they have is likely similar and individual specific rent differences would be small due to differences in perceptions of γ. Additionally, smallholders face the same local governmental agents, and any shifts in Forest Code enforcement intensity may affect or not smallholder decisions in the same direction. The alternative possibility is that smallholders who comply perceive a different probability than those who do not, or the probability perceived differs in unknown ways across individual smallholders. This is simply a case in the econometric model of heterogeneity across smallholders in the sample, reflected in heteroskedastic variances of land clearing behavior, for which we correct with robust standard error computation. Table 3 presents the results, tests, and selection statistics for three different specifications of equations (13)–(15).
Table 3. Endogenous switching regressions results, model specifications and selection
Notes: t-statistics in parentheses. *p < 0.05, **p < 0.01, ***p < 0.001.
Our estimates are robust in that they are consistent across all specifications. In the first two sections of table 3, the dependent variable is land cleared as of the date of the interview for noncompliers and then for compliers sorted through the endogenous selection estimation and corresponding to the land clearing paths in (12a)–(12c). The third section of the table presents results for the latent criterion function or switching rule, corresponding to the corner solution presented in equation (11) of our theoretical model. It measures the probability a household would be noncompliant based on the net benefits of noncompliance corrected for unobserved selection, and, thus, indicates important explanatory variables driving a smallholder's incentive to comply or not with the Forest Code. All regressions have highly significant χ2 statistics and reject the null hypothesis that there is no switching regime or selection present in the data at a 1 per cent significance level.
Turning first to estimates relative to the land clearing path for those selected into the Forest Code noncomplier group, significant variables at the 1 per cent level are lot size, herd sizeFootnote 22 and, for the last specification, value of capital goods owned by the household. Estimated probability of selling wood is significant at the 1 per cent level for the first two specifications and not significant for the other two. Time of residence in the lot is significant at the 5 per cent level. This way, the results clearly establish lot size, herd size, and wealth in the form of value of capital goods to be strong positive predictors of land cleared for noncompliers. Additionally, probability to sell wood has a protective forest effect as per the first two specifications.
For smallholders selected into the compliers group, the variable that seems to determine positive land clearing in all specifications is lot size, significant at 1 per cent levels. The effect of a unit of lot size over the size of area deforested is much lower than for noncompliers. The estimated probability of selling wood is significant at the 5 per cent level for the first two specifications for this group, but its negative or protective effect is much lower than for noncompliers as well. Number of family members contributing to household income is significant at the 1 per cent level for the last specification, and it is not significant for noncompliers in any specification. Here, we observe that herd size is not significant at any level. The same is true for exogenous income, contrasting with the group of noncompliers. Despite these differences, though, we can say that the signs and, to a smaller extent, the significance of estimated coefficients for both groups are similar, as expected in our theoretical model where we showed that expected net benefits and expected costs of not complying are interconnected with Forest Code compliance. However, the land clearing paths for Forest Code compliers and noncompliers are different and justify our endogenous switching regression empirical approach.
The third section of table 3 shows the estimation of our latent equation or endogenous switching rule. These results demonstrate what variables are important to a smallholder's perceived net benefits of not complying with the Forest Code, correcting for selection due to unobserved variation (that is, perceptions of Forest Code enforcement in our model). These results are, in effect, an endogenous selection-corrected assessment of the main driving variables in predicting incentives to cheat – they are drivers of the perceived net benefits from noncompliance with the Forest Code. Significant determinants here are: lot size (−), land tenure measured as years on the lot (+), cattle herd size (+), distance to a main highway (−), whether the household is located in PA Moju (−). The regional effect of PA Moju makes sense because it is closer to Santarém, a region ‘hub’ where offices of governmental agencies, such as INCRA and IBAMA (central to enforcement of the Forest Code), are located. Moreover, PA Moju has been on the radar of the government for the last 15 years due to a specific relationship between households and local logging companies (see Lima et al., Reference Lima, Merry, Nepstad, Amacher, Azevedo-Ramos, Lefebvre and Resque2006). Thus, we would expect these households to view the net benefits from cheating with any government forest law to be lower, both from the benefits they may get from the government but also from a Code enforcement standpoint.
However, lot size, land tenure time, distance to a main highway and herd size yield the most useful results in our switching rule. The conventional wisdom has been that roads are a major driver of deforestation, as we expect households located closer to highways to face greater market rents. Indeed, we find distance to a main highway to have a negative effect on the decision to transition into noncompliance with the Forest Code. That is, being closer to a main highway means the net benefits from not complying are perceived by the smallholder to be higher, despite higher risk for the household to get caught cheating.
Longer land tenure means an increase in perceived net benefits from not complying according to our results. Perhaps, as times passes by, the smallholder learns that the Forest Code is not enforced as expected. Or, perhaps land clearing in a slash-and-burn fashion, in face of limited knowledge or resources to return to the same agriculture plot in a sequence of years, requires that the smallholder clear new parcels of land every year or perhaps they transition to cattle production as they become wealthier. The latter is most plausible, however, as larger lots (and, thus, more marginal land) mean that the household perceives less net benefit from noncompliance. Indeed, the number of cattle the smallholder has emerges as a significant factor to the perceived net benefits of not complying. This is supportive of the observation that smallholders often transition to cattle production relative to crop production and, as we find, there is increased pressure on land clearing when this happens.
Certain variables that we do not find to be statistically significant in the switching rule also deserve mention. For instance, the value of agricultural production does not appear important given that the regressions are corrected for cattle grazing. This suggests that studies of forest clearing must consider both types of production systems, as they are quite different from the perspective of our results. This may be because we sampled smallholders who have stayed in a location long enough to transition to the more expensive cattle production system.
Collectively, the results allow assessment of whether smallholders are better off from not complying with the Forest Code under the current enforcement regime. In our theory, we showed that the compliance decision comes down to a comparison between expected net rents from complying and not complying with the Forest Code, captured by the corner solution in (11). The fact that the switching regression is significant for noncompliers in the first section of table 3 and that the incentives or net benefits from not complying (the switching rule in the third part of the table) is a highly significant regression makes it clear that a large subset of households choose to not comply and satisfy our corner solution. These households are better off by clearing more than is allowed. We can go further in our interpretation of this welfare effect, as the estimated switching regression rule indicates what types of households will find it better not to comply: those with longer tenure, smaller lot size, larger herd size and greater distance from the main highway. Being in PA Mojú, however, tends to reduce the perceived welfare from not complying with the Forest Code.
5. Conclusions
We proposed a dynamic smallholder land clearing model where smallholders hold an assessment of government enforcement of forest clearing rules that is unobserved but is present given the Brazilian Forest Code, the main law governing land clearing on private lots. By controlling for observed factors that affect land clearing, we find that this unobserved assessment of the risk of being caught does induce selection into those smallholders who comply and those who do not comply, or, rather, those who have different land clearing regimes consistent with the complier and noncomplier groups. This selection is critical not only in determining the path of land clearing over time, but also is a more general means for identifying drivers of land clearing.
We apply an endogenous switching regression model approach consistent with our theoretical model to a unique data set collected from smallholders in the Transamazon and BR163 highways in the state of Pará, Brazil, who were interviewed twice in the time span of a decade. The period immediately after the first sampling involved installment of a new administration with documented rhetoric concerning stricter enforcement of the Forest Code in our sampling region. Our econometric results show that frontiers where land tenures are longer and there are opportunities for smallholders to transition to cattle grazing from agriculture should be a major focus of enforcement of land clearing laws and restrictions. We also find that longer land tenure does not mean protection of forests, but rather induces greater clearing and greater incentives not to comply with the Forest Code. Use of the forest by a smallholder is a protective signal that must be considered and somehow encouraged, that is, those who have a higher estimated probability of selling wood are more likely to comply and clear less forest. Finally, while market access in terms of distance to a main highway matters in the compliance decision, the significance of cattle herd in our model was much higher in all specifications.
Our results seem to suggest that alleged government efforts to enforce the Forest Code in the Transamazon-BR163 highway regions have been ineffective even if they have been real. In addition, our results are a cause for concern in light of other findings, for example, Schons et al. (Reference Schons, Azevedo and Alencar2013), who show that 71 per cent of the credit provided to small landholders in the region between 1999 and 2012 were to those engaged primarily in cattle grazing. It therefore appears that current government development programs have provided incentives for cattle production in the region combined with ineffective enforcement of land clearance laws, rather than actually targeting the incentives to clear forests and most importantly incentives to switch from the compliant into the noncompliant group with respect to the Forest Code. Our results also point to an interesting area of future work, namely, understanding the cattle grazing decision in and of itself. Particularly the drivers of smallholder transitions to cattle grazing as a frontier matures should be a major focus of future work if we are to completely understand the land clearing process.
Our results inform future Forest Code enforcement and land clearing policies. One potential option is intensification of the smallholder production systems in order to increase cattle production efficiency and provide incentives to use less land. Our results show that the perceived costs of cheating are not high enough to surpass the cost of transitioning into more efficient production systems, thus intensification measures will likely not be effective. The same may also be true for the payments for ecosystem services schemes aiming at increasing incentives to keep forestland intact.Footnote 23
Acknowledgements
We thank The Inter-American Development Bank, The Gordon and Betty Moore Foundation and CAPES for funding this work. We also thank Equipe da Conservação da Amazônia (ECAM), Aliança da Terra, Instituto Floresta Tropical (IFT), Instituto de Pesquisa Ambiental da Amazônia (IPAM), Ailton Alves and Diego Pinheiro de Menezes. All remaining errors are our own.
