1. INTRODUCTION
The following appear promising for various applications requiring
propagation across magnetic field to a stand-off target and/or
captured in ambient magnetized plasma: microsecond duration, intense
neutralized ion (IB), and plasma beams (PB) with ion energies in the range
of EIB ∼ 0.1 MeV and EPB ∼
100 eV, and ion current densities of j ∼1 to 30
A/cm2 and j ∼10 to 100 A/cm2
for IB and PB, respectively. Numerous experimental and theoretical
research with IBs and PBs generated in plasma Hall type accelerators
(Morozov, 1974), high current ion accelerators
(Bystritskii & Didenko, 1989), plasma
thrusters (Dailey, 1965), laser produced plasma
flows (Rai et al., 2003), and laser
guided plasma channels (Niemann et al.,
2003), have addressed the mechanisms of beam across B-field
propagation in a vacuum and ambient plasma with respect to beam parameters
(density, energy, temperature, size) (Peter et
al., 1979; Song, 1990).
Qualitatively, the propagation of PBs/IBs across B-field and the
dynamics of B-field penetration into the beams depend on the value of
β, which represents the ratio of the beam specific kinetic energy to
B-field energy density. More specifically, the picture of beam propagation
across B-filed can be roughly divided into three different modes,
summarized as follows:
- Single particle mode which is typical for low density small diameter
beams, where beam diamagnetism is negligible, and the time for external
B-field (ExB) penetration into the beam is in the order of,
Rb/c. Here, Rb is the
radius of the beam, and c is the speed of light. The induced
polarization E-field, limited by the low density and small size of the
beam, is not sufficient to support ExB propagation. As a result, the ions
and electrons are decoupled and follow single particle orbits with their
respective Larmor radii.
- Collective mode which is predicted for moderate to high density
PBs/IBs of either small or large diameter, if the condition
tdif/tb < 1 is fulfilled.
Here, tdif is the time of B-field diffusion into the
beam, and tb is the beam pulse duration. Beam
interaction with the B-field results in the build-up of a polarization
E-field inside the bulk of the beam, due to the formation of thin,
oppositely charged sheathes along the beam outer boundary. This restores a
force-free ExB propagation of the beam as a whole, with a drift velocity
of cE/B equal to the average velocity of the beam (except for
particles in the charged layers, which are being continuously lost and
replenished from within the beam during propagation).
- Diamagnetic mode is typical for intense particle beams with very
high thermal energy density, satisfying the conditions:
nkTeB2/8π > 1 and
tdif/tb >> 1. Here, the
first expression is the ratio of beam thermal energy density to B-field
energy density, and the second expression requires that the B-field
diffusion time into the beam be much longer than the duration of the
pulsed beam. In this mode of propagation, due to the induced current at
the beam surface, the ExB does not penetrate into the beam, and the main
bulk of the beam propagates in a field free environment.
The requisite conditions for the collective mode of propagation across
B-field, compiled from the previous studies which are of interest for the
present study, are listed below:
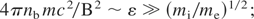
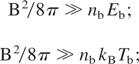
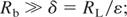
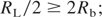
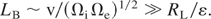
Here, B is the applied B-field; nb is the beam
density; β = v/c is relative beam translational
velocity; nbEb is the specific
translational energy of the beam ions;
nbTb is the specific thermal
energy of the beam; kB is Boltzmann's constant;
Rb is the beam radius; RL is the
Larmor ion radius; (mi/me) is
the ion to electron mass ratio; δ is the polarized sheath thickness;
LB is the length of beam transport and ε is the
beam dielectric constant equal to 1 +
(ωi/ΩL)2, where
ωi and ΩL are the plasma and ion cyclotron
frequencies.
Condition (1) is derived from the requirement that the energy density
of the induced E-field in a beam traversing a B-field cannot be larger
than the translational energy density of the beam, which can be written as
E2/8π << nbmv2/2. Conditions (2a and 2b) account for the
requirement of fast magnetization of the beam, when the ExE pressure is
much larger than the translation energy density of the beam. Condition
(2a) is applicable for the PB with a translational energy of the same
order as its temperature (kBTb
∼ Eb), while condition (2b) is applicable for the
IB, with a thermodynamic pressure a few orders less than its translational
energy (kBTb <<
Eb). In the other limits, where
B2/8π < nbEb and B2/8π <
nbkBTb,
strong diamagnetism during beam propagation can be expected. Condition (3)
defines the magnitude of the polarized sheath thickness; δ, which must
be much smaller than the size of the beam, Rb.
Condition (4) was derived from the requirement that the full induced
electric potential across the beam must be less than the translational
energy of the ions. One-dimensional (1D) analysis (Peter et al., 1979) predicts the splitting of
the beam into several beamlets if condition (4) is not met. Condition (5)
defines the length of the virtual anode formation,
LVA, which can impede the propagation of the beam and
is based on a 1D estimation of LVA ∼
vb/(ΩiΩe)1/2.
Condition (6), which is in fact equivalent to condition (1), requires the
scale length formation of the polarized sheath, δ, to be much less
than the LVA (Wessel et
al., 1990). It is worth noting that, in the real
two-dimensional (2D) geometry of the beam, a considerable decrease in the
axial induced E-field occurs due to its partial shorting, by the
accompanying beam electrons and subsequently the ions are able to
propagate much farther than in the 1D estimation. In reality, the
existence of an adequate neutralizing source of electrons along the
B-field lines in experiments (i.e., conducting walls, ambient plasmas,
etc.) alleviates this concern. The above general conditions can be
combined and rewritten using the relations: Eb =
nbeδ/ε0 and
nb = j/eβc, in more practical forms
providing a range for the desired beam parameters corresponding to the ExB
mode of beam propagation across B-field:
Combining conditions 1 and 2:
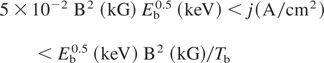
results:
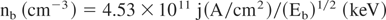
Combining conditions 2 and 5:
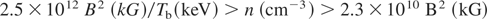
results:
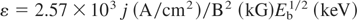
Combining conditions 3 and 4:
results:
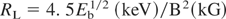
Here, for the sake of simplicity we substituted the symbol of strong
inequality (>>) by (>) with an additional factor of 10. In our
experiments, we studied ion and plasma beams which differed by three
orders of magnitude in energy, two orders in density, and one order in
pulse duration (102 keV, 1011 cm−3,
1 μs, and 0.1 keV, 1013 cm−3, 20 μs,
respectively). Such a wide range of IB and PB parameters provided us with
an opportunity to test the experimental applicability of the above
criteria at higher levels of current density and B-field than was done in
earlier experiments (Song, 1990).
This paper consists of five sections. In section 2, we briefly
characterize the experimental setup including plasma sources for the
generation of IBs and PBs and their respective parameters and diagnostics.
Section 3 is dedicated to experiments on PB cross B-field injection and
results. Section 4 discusses experiments on IB injection and results.
Section 5 is dedicated to analysis and conclusion.
2. EXPERIMENTAL SETUP
The schematic of the experimental setup is given in Figure 1. The system consisted of: (1) A vacuum vessel
with ports located in the middle of the vessel length; (2) Plasma or ion
beam accelerator, connected to the middle port of the vacuum vessel with
beam injection normal to vessel axis 25 cm below vessel median plane; (3)
Two sets of internal plasma guns which generated an ambient plasma column
injected along the B-field; (4) Power drivers for ambient plasma guns; and
(5) External solenoid coil for generating pulsed longitudinal B-field. The
vacuum in the vessel was 4 × 10−6 to
10−5 Torr. The main operational parameters of the
subsystems are given in Table 1.
Operational parameters of the subsystems
Schematic of the experimental setup: (1) Plasma guns power supply, (2)
Set of plasma guns, (3) ExB coil, (4) PA/IA, (5) Coaxial vacuum vessel
walls, (6) Ion beam and (7) Plasma column.
2.1. IB accelerator
The ion accelerator produced a 1.5 to 2 kA, 70 to 120 kV, 0.5 to 1
μs H+ beam < 10 cm in diameter at the entrance port to
the vessel with an average divergence half angle of 3°. The IB
estimated ion temperature was TIB ∼ 200 eV which
was based on the size and shape of ion beamlet autographs on heat
sensitive paper obtained by using multi-aperture pinholes placed at the
exit of the ion accelerator. The average density of IB was in the range of
1011 to 1012 cm−3. It has already
been established by a variety of experiments that high current IB are
almost completely charged neutralized (> 99%) at the exit from the
accelerator, by the accompanying electrons being dragged in the IB by the
self E-field of the IB from surrounding walls. The average velocity of the
neutralizing electrons is of the same order as the ions (Humphries et al., 1976). In fact, such a high
current IB could be considered for as synthesized non-equilibrium plasma
of energetic ions with respect to electrons. The ion accelerator consisted
of a: (1) 120 kV, 1 μs, 1.8 Ohm Marx generator; (2)
magnetically-insulated ballistic-focusing diode (MID) with a magnetic
coils system and a hydrogen puff valve located in the center of the anode;
(3) a plasma source, based on a fast shock coil, which drives an inductive
discharge in the expanding hydrogen flow; (4) a toroidal magnetic lens and
a guiding solenoid for the focusing and transport of the IB to the
entrance port of the vessel. The distance traveled by the IB to the vessel
entrance from the MID was 90 cm and about 155 cm to the opposite wall of
the vessel. For a more detailed description of the design and
characteristics of the IB accelerator and ion beam parameters, we refer
the reader to (Bystritskii & Didenko, 1989;
Anderson et al., 2004).
2.2. PB accelerator
The design of the plasma accelerator was based on the conventional
Marshal gun with modifications based on earlier experiments (Morozov, 1974; Morozov et
al., 2002) in an attempt to increase the plasma flow pulse
duration. In most of the experiments, we used a squirrel cage type,
coaxial, conical electrodes with and without additional radial plasma
cable guns placed at the breach of the accelerating channel. The
simplified schematic of the plasma accelerator is given in Figure 2. The plasma accelerator has an outer 27 cm
long squirrel-cage-type conical electrode which is grounded at its 9.5 cm
diameter base, and has a 3.7 cm diameter near the beam exit. The inner HV
cathode is also a conical squirrel cage, however, is 23 cm long with a 2.5
cm diameter base.
Schematic of the plasma beam accelerator.
The plasma accelerator was driven with a HV pulse (10 μs, 3 to 9
kV, 80 to 140 kA) from a 150 μF capacitor bank and was switched by an
ignitron. The hydrogen was delivered to the breach of the plasma
accelerator by a fast electromagnetic puff valve with an opening time of
< 80 μs and plenum pressure in the range of 100 to 400 kPa. The
plasma accelerator worked in two modes: (1) with trigger-controlled
application of the HV pulse to the cathode which followed the puff valve
initiation to form snow-plow propagation of the formed plasma discharge;
and (2) with DC application of HV to the cathode, resulting in the self
breakdown deflagration mode of propagation (Cheng,
1990).
In the first mode, the gas breakdown in the plasma accelerator takes
place near the breach of the accelerating channel (that is, near the
insulating interface) and could be initiated near the high pressure branch
of the Paschen pd-curve for pd > 10, (beyond minimum). These results in
the snow-plow mode with a fast rising of the current through the plasma
and its acceleration to the end of the cathode under the I × B force
accompanied by a slanting of the current channel due to the Hall effect.
Current slanting limits the initial pulse duration of the axial plasma
acceleration to a few microseconds (the so-called anode current crisis
when the accelerating force Ie × Bφ
becomes radial and pushes the plasma flow from the outer anode to the
axis), and consequently, reduces the final translational energy of the
accelerated plasma (Morozov, 1974).
The typical ion signals of the accelerated plasma flow from the
Faraday cups featured a two peak structure with a very short, a few μs
duration, high amplitude first spike and ion average velocity in the range
of ∼ 15 cm/μs (100 eV). The second peak occurred (a few tens
of μs) after the first peak, and was lower in intensity with a > 20
μs pulse duration and velocity ranging between 106 to
107 cm/s.
To mitigate the influence of the current crisis and to extend the
duration of the accelerated plasma, the plasma accelerator was modified by
adding several (up to 4) cable plasma guns (see Fig.
2) near the insulator interface which fired radially inside the
accelerator. Using this technique, we were able to obtain plasma ion
pulses with durations of 40 to 50 μs, though with lower
reproducibility and average plasma velocity. It is possible this could be
due to the high concentration of carbon ions in the plasma generated by
the cable guns, resulting in fast cooling of the hydrogen plasma flow from
the plasma accelerator. Another possibility may be due to the limited
reproducibility of the gas puff operation relative to the triggering of
the cable guns. The CFC signals still featured a very short, high
amplitude initial spike of a few μs in duration and an average ion
velocity of ∼ 15 cm/μs (100 eV), however, with a less
prominent two pulse structure than was seen without the additional cable
guns.
In the deflagration mode, with the DC-voltage “sitting” on
the inner electrode, the gas breakdown takes place automatically when
reaching the pd-minimum of the Paschen curve at the front of the gas
(Cheng, 1990). This results in the fast
ionization and acceleration of the small front portion of the out flowing
gas resulting in higher plasma velocities. When working in the
deflagration mode, we did not succeed in extending its duration with the
use of additional cable guns. The main experimental part of the data
presented in this paper was taken for the snow plow mode with controlled
triggering of the plasma accelerator.
2.3. Background plasma gun array
The background plasma column was injected along the ExB from opposite
sides of the vacuum vessel and was generated by two circular arrays of 16
TiH plasma guns (PG) of I × B type which were coaxial with the
vessel axis and distributed uniformly along a circumference of 25 cm
radius. The distance between two arrays could be varied from 0.8 to 1.3 m.
The guns were driven in groups of four in parallel, by 20 μF
capacitors charged between 7 to 13 kV with a total current of up to 100 kA
per group producing a 10 μs FWHM pulse. Each capacitor was switched by
a commercial ignitron with a rise time of ∼1 μs. The guns
consisted of a titanium central electrode and outer washer electrode which
were hydrogenated to the level of 1: 1, following the procedure outlined
in Bystritskii et al. (1984). The PG
schematic is given in Figure 3. The central Ti
positive HV electrode was 5 cm long and 6.3 mm in diameter. The grounded
coaxial Ti washer with a conical inner surface was placed at the exit from
the PG forming a circular vacuum gap with the central electrode of 0.3 to
0.4 mm.
Schematic of the coaxial TiH plasma gun. (1) Stainless steel (SS) tube
diameter 16 mm; (2) Polycarbonate insulator; (3) HV (6 to 10 kV) SS
cathode stalk; (4) Ceramic disk; (5) TiH cathode; (6) TiH outer tube; and
(7) Conical TiH washer.
2.4. Diagnostics
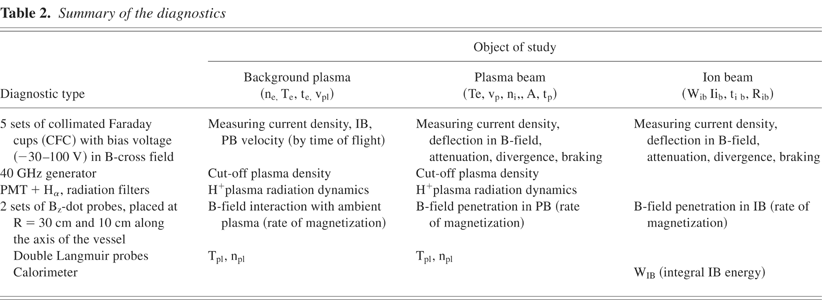
Measurements of the B-fields and the characteristic dynamics of the
ambient plasma, PB, and IB were done with a variety of diagnostics which
are listed in Table 2. Their respective
locations are shown in Figure 4.
Summary of the diagnostics
Schematic diagnostic locations in the vessel (1) Double Langmuir
Probe; (2), (5) Linear vertical CFC arrays; (3) Microwave source and
receiver; (4), (6) Two BZ-dot arrays along the axis of the vessel; (7)
Horizontal 900 bend CFC array; (8) Circular rotatable “shower
head” CFC array; (9) PB/IB accelerator; (10) Transport solenoid;
(11) Cable guns; (12) Horizontal CFC array.
The CFC had apertures of 7 × 10−3 to 4 ×
10−2 cm2, graphite electrodes of 3 mm in
diameter, and were operated at bias voltages of −30 to −50 V
and/or a transverse B-field of a few hundred Gauss. The ambient plasma
density and speed of the plasma flow was recorded by two circular CFC
arrays placed at a radius of 20 cm and opposite to each other in the plane
of the PGs. Two Bz-dot probe arrays with 5 mm coil diameters were
distributed along the axis of the vessel. One Bz-dot array was placed on
the surface of the vessel's inner wall at a radius of ∼ 12 cm,
while the other Bz-dot array was placed on the surface of the
vessel's outer wall at a radius of ∼ 40 cm. The Bz-dot probes in
both arrays were spaced at axial increments of 10 cm. The locations of
these Bz-dot arrays provided us with the opportunity to map the topology
of the B-field in time during PB and IB injection.
The temperature of the background plasma from the PG arrays was
measured in several locations by a standard double Langmuir probe (LP)
with tungsten tips, 1 mm in diameter, 1 cm in length, and 3.5 mm inter tip
distance. The LP was energized, with controlled time delay, by pulse width
duration of 200 ns. The current in the LP was registered by a commercial
Pearson probe. The voltage between the probe tips was corrected for the
inductive drop (LdI/dt) by the scheme shown in Figure 5.
Schematic of the double LP with voltage auto-correction.
3. EXPERIMENT
3.1. Background plasma and B-field
characteristics
In the bulk of experiments with background plasma, the driver bank was
charged between 7 to13 kV. The background plasma ion signal featured a
familiar two pulse structure with the first pulse lasting a few
microseconds and having a velocity ∼ 107 cm/s, and the
second pulse lasting 10 to 20 μs with a velocity of 2 to 5 ×
106 cm/s. 40 GHz microwave (μwave) measurements of
background plasma density at a distance of 10 cm from the location of the
TiH gun arrays, and 20 cm from the plane of the PB/IB injection,
recorded a reliable signal cut-off, corresponding to a plasma density of
n ∼ 3 × 1013 cm−3 (10 to 15
μs) after the background plasma arrays were fired. Each circular
background plasma arrays of 16 guns produced an expanding tubular plasma
layer with a divergence half angle of α ∼ 10° when fired
without B-field and a thickness at the vessel mid-plane of ∼ 20 cm, as
estimated by measurements from CFC array #2. With both background
plasma arrays and axial B-field, the cut-off duration reached 100 μs
and longer, depending on the charging voltage, and B-field strength. After
a few hundred firings, there was a significant drop in the μ-wave
cut-off duration which indicated a depletion of hydrogen in the TiH guns,
and a need to replace the gun electrodes with re-hydrated pieces. The
measurements of the background plasma temperature by the double LP, at the
same position as the μ-wave horn, gave an average
Te in the range of 5 to 10 eV, and average
translational velocity (measured by CFC time-of-flight array) of a few
106 cm/s which could be slightly varied with driver
voltages. The estimated full inventory of background plasma ion flow,
based on this data, gives ∼ 1018 ions. Assuming energy of
∼100 eV is needed on average for the production of one H+
ion, the total energy input required for the background plasma volume
formation is 0.8 kJ of the 8 kJ of total stored energy. Measurements of
the plasma characteristics, when using cable guns as the background plasma
source, gave lower reproducibility in the average data, higher initial
translational velocity (up to 107 cm/s), and faster cooling
(most likely due to carbon ion impurity). The ExB penetration rate in the
background plasma was measured by an array of B-dot probes 10 to 15 μs
after background plasma arrays were fired. This timing matched the plasma
arrival at the mid-plane indicated by CFC arrays and the time needed for
the density to buildup to cut-off level. The PB/IB injection was
organized near this moment of time. The estimate of the classical
conductivity of the background plasma, σ, based on the B-field
penetration time delay τdif =
4πσL2/c2, gave ∼
1013 (in CGS units). Here, L is the thickness of the
plasma layer. This value is two orders lower than the Spitzer value based
on double LP temperature measurements. This discrepancy could be due to
other fast B-field penetration mechanisms such as whistler waves (Armal & Rostoker, 1996) produced by the Hall
effect which help to “carry” the B-field in the plasma. An
additional cause could be related to ion-neutral collisions, (especially
with multi-electron impurities), resulting in the fast cooling of the
plasma. The parameters of the ambient plasma and PB/IB are given in
the Table 3.
Main parameters of the IB and PB
3.2. Plasma Beam propagation experiments
All experimental runs on beam propagation were done with a controlled
triggering of the subsystems via computer. In testing the deflagration
mode, the plasma accelerator fired ∼ 750 μs after the puff valve
was energized, when the H2 pressure reached the required
Paschen minimum for breakdown at the set voltage. In the snow plow mode,
the optimal operation was obtained at a controlled HV application time
delay of ∼ 800 μs after energizing the gas puff valve. Average
jitter between plasma accelerator trigger and its actual firing was < 5
μs. The cause of this jitter was attributed to some mechanical
inconsistency in the puff valve operation.
In the first part of the experiments, the exit of the plasma
accelerator was located at 90 cm from the vessel mid-plane. In the second
part, the exit was located 115 cm away from the mid-plane due to the
addition of a beam expander and a 2.5 cm diameter collimator. The sequence
of the subsystems operation and typical waveforms are illustrated in Figure 6.
The sequence of subsystems operations and respective typical pulse
waveforms: (1) Applied B-field, (2) Background plasma gun current, (3)
Plasma accelerator current, (4) PB current density.
3.2.1. PB propagation in vacuum without B-field
As mentioned before, the typical plasma accelerator beam displayed a
two-peak structure with translational energies in the range of 100 to 120
eV and 30 to 60 eV for the first and second peak, respectively.
Time-of-flight measurements were taken between two positions of CFC
arrays. When operating without the beam expander and additional diaphragm,
linear CFC array #2 in the mid-plane (90 cm from the plasma
accelerator anode) measured PB current densities between 30 to 60
A/cm2. This value dropped between 3 to 6
A/cm2 at 120 cm from the anode (near the opposite vessel
wall). With the expander/collimator in place, the current density in
the mid-plane ranged between 2 to 5 A/cm2 (∼ 115 cm
from the plasma accelerator anode) and dropped below 2
A/cm2 near the opposite vessel wall (∼ 145 cm from the
anode). Based on these numbers and the measured distributions of the IB
current density at various locations, the estimated half angles of
divergence of the PB at the entrance port to the vessel, at the mid-plane
of the vessel, and at the opposite vessel wall were ∼ 10°, ∼
14°, and ∼ 20°, respectively. Typical ion current density
distributions measured by the CFC array #2 at the mid-plane of the
vessel are illustrated in Figure 7a.
(a). PB current density distribution at the vessel mid-plane
in vacuum without B-field. R- (vertical) radial distance of the CFC from
PB injection axis. (b). PB current density distribution at the
vessel mid-plane in ambient plasma w/o B-field. R- (vertical) radial
distance of the CFC from PB injection axis.
3.2.2. PB propagation in the ambient plasma without
B-field
Studies of the PB propagation in background plasma were performed with
the collimated PB only. It was found that the addition of the
expander/collimator deteriorated beam transport efficiency. The
current densities for PB transport in ambient plasma were nearly
identical, if not worse, to the vacuum case (∼ 5 A/cm2
and ∼ 2 A/cm2 at the mid-plane and opposite vessel
wall, respectively). Several tentative causes why the transport efficiency
did not increase with background plasma could be: (a) high initial angular
divergence of the PB at the injection port; (b) ion-ion/neutral
scattering; (c) background plasma-PB instabilities (they have comparable
density); and (d) the influence of the residual self B-fields in the PB
from plasma accelerator current loops. In the case of vacuum propagation,
these current loops may have provided some self-focusing which would be
absent in the case of PB injection into a current neutralizing background
plasma. The typical current density distribution in the vessel mid-plane
across the PB width for propagation in the background plasma can bee seen
in Figure 7b.
3.2.3. PB propagation in vacuum across B-field
The main results can be stated as follows:
- When transported in vacuum across a strong B-field with 0.1 <
β ∼ 1 the PB displayed no visible deflection from its direction of
injection. This agrees well with the ExB mechanism for β ∼ 1 or
strong beam diamagnetism for β ∼ 10.
- The propagation of the PB was characterized by a pronounced loss of
its peripheral layers, accompanied with a large increase of its density
(one order and more to nb ∼ 1014
cm−3) in the surviving central core reaching ∼ 200
A/cm2 at B-fields > 1 kG. The diameter of the remaining
non-deflected central part was ∼ 4 cm for 0.3 kG and < 1.5 cm for B
> 1.2 kG. This is illustrated by ion current density histograms
obtained at the mid-plane with CFC array # 2 at variable B-field
amplitudes in Figure 8a.
- The PB featured strong braking during its propagation and density
build-up. The resulting beam translational energy of the surviving central
core, after its transport to the mid-plane across B-fields > 1 kG,
dropped to 30 to 40 eV from ∼ 100 eV at the entrance port.
- The PB demonstrates preferential expansion along the B-field, as
registered with horizontal CFC arrays.
(a) Typical current density distributions across PB vertical
cross section in vacuum at vessel mid-plane for B-field strengths: 0.3 kG
(left), 0.8 kG (middle), and 1.2 kG (right). R- (vertical) radial distance
of the CFC from PB injection axis. (b) Typical current density
distributions across vertical cross section of PB in magnetized plasma at
the vessel mid-plane for B-field: 0.3 kG (left), 0.8 kG (middle), and 1.0
kG (right). R- (vertical) radial distance of the CFC from PB injection
axis.
3.2.4. PB propagation across B-field in magnetized
plasma
These experiments were done with a variable time delay (10 to 30
μs) between firing the background plasma gun arrays along the B-field
and cross-injection of the collimated PB. The estimated ambient plasma
density measured by μ-wave cut-off was on the level of ∼
1013 cm−3. Compared with PB propagation in the
background plasma without B-field, there was an expected overall drop in
the density of the transported beam, assuming an adequate shorting of the
induced E-field by the background plasma and respective bending of the PB.
This said, the PB did not display any evident bulk deflection
“up,” defined by the direction of the ExB, when measured by
the CFC array # 8 at distances from the entrance port comparable with
RL, (RL = 15 cm at B = 0.1 kG, for
EPB = 100 eV). In some experiments, the distribution
of the current density across the PB could be interpreted as some
deflection (few cm) in the “down” direction. A possible cause
for the absence of a clear deflection could be due to low ambient plasma
density, nBP, with respect to plasma beam density
nb (nBP <
nb). In other words, the ambient plasma was
insufficient to provide reliable shorting of the induced E-field in the
PB. Another possible cause may have been the wide PB splitting into
several beamlets. See Figure 8a for a PB current
density distribution as a function of applied B-field in magnetized
plasma.
3.3. Ion beam propagation experiments
The main part of the experiments with IB was done using an additional
solenoid section of 60 cm length to increase the efficiency of the beam
transport from the MID to the vessel entrance port. We also used two
additional plasma cable guns in the space between the exit of the MID and
entrance to the transport solenoid for local neutralization of the IB. The
effectiveness of this approach is illustrated in Figures 9a and 9b. The IB was injected through the
same port as the PB was attached to, located 25 cm lower than the
equatorial plane of the vessel.
(a) IB current density distribution at the mid-plane in
vacuum and without transverse B-field. R– (vertical) radial distance
of the CFC from the IB injection axis. (b) IB current density
distribution at the mid-plane with background plasma and w/o
transverse B-field. R– (vertical) radial distance of the CFC from
the IB injection axis.
3.3.1. IB propagation in vacuum across B-field
The IB as a whole showed very small, if any, deflection from the axis
of beam injection when propagating across B-fields in the range of 0.1 to
1.5 kG, as was expected according to the picture of ExB propagation. At
the same time, its transport across the B-field was characterized by a
strong attenuation of the IB current density across the beam width,
including its core, in contrast to the case of central core bunching of
the PB when transporting in similar conditions. At injection energy of 60
to 100 keV, the IB current density without B-field was 15 to 20
A/cm2 at the injection port and dropped to ∼ 1.5
A/cm2 at the mid-plane. With B-fields of 0.3, 0.8, and 1.2
kG, current densities at the mid-plane dropped further to ∼1, 0.75,
and ∼0.5 A/cm2, respectively. These CFC measurements
were done with linear CFC array #2 and are shown in Figures 10a to 10c.
(a) IB current density distributions near mid-plane with
transverse B-field. R– (vertical) radial distance of the CFCs from
the IB injection port axis. (b) IB current density distributions
near mid-plane with transverse B-field. R– (horizontal) radial
distance of the CFCs from the IB injection port axis. (c) Current
density distributions of IB in vacuum at vessel mid-plane with transverse
B-field of 0.3 kG (left), 0.8 kG (middle), and 1.2 kG (right). R–
(vertical) radial distance of the CFCs from the IB injection axis.
(d) Current density distributions across vertical cross section
of the IB in magnetized plasma at vessel mid-plane for B-field strengths:
0.3 kG (left), 0.8 kG (middle) and 1.2 kG (right). R- (vertical) radial
distance of the CFC from the IB injection axis.
3.3.2. IB propagation in background plasma across
B-field
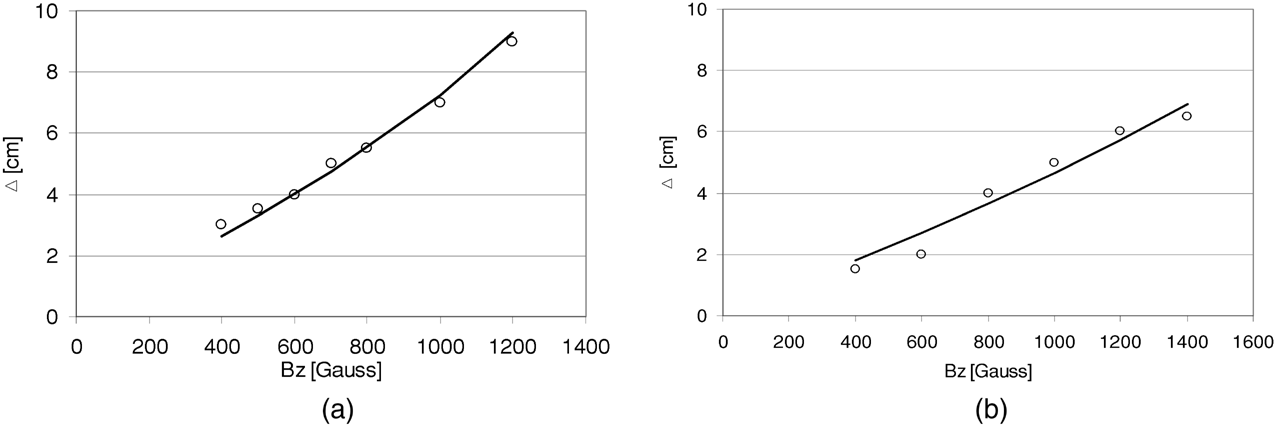
Unlike PB, IB when injected into magnetized plasma, displayed a single
particle type behavior, and followed a classical trajectory defined by the
Lorenz force. Therefore, the IB propagation length, in general, was
limited by the distance of < RL. This type of
propagation is also accompanied by a very strong “bleeding”
off (that is to say, attenuation), across the entire width of the IB. The
IB current density profiles across the beam width for different B-field
values at the mid-plane of the vessel are illustrated in Figure 10d. For a clearer picture of IB bending, which
corresponds to the average velocity of the main portion of the IB, see
Figures 11a and 11b for the ∼ 60 keV and the
∼ 120 keV IB, respectively.
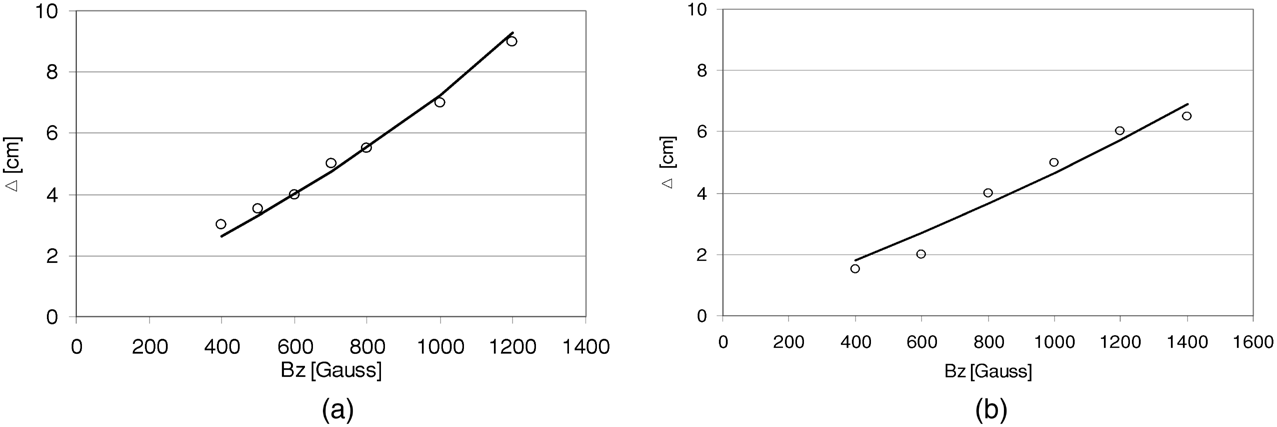
Radial shift of the current density “center of mass” with
respect to the axis of the IB injection as function of the transverse
B-field strength. Circles—experiment, line—calculation for
∼ 60 and ∼ 120 keV IB, respectively.
4. DISCUSSION
Comparison of the experimental beam parameters with calculations based
on criteria 1 through 3 is given in Table 4. As
seen from criterion #3, the transverse size of the experimental PB is
far from the estimated range, which indicates a possible splitting of the
beam into several beamlets. Another feature of PB propagation could be the
formation of the virtual anode (Peter et al.,
1979) as the beam enters the B-field region at the injection port.
If the density nears the estimated limit, following criterion #1, a
resulting partial reflection and/or enhanced expansion of the PB may
occur.
Comparison of the experimental beam parameters with calculated based
on the criterions 1–3
The results that deflection of the IB in magnetized plasma follows a
one particle trajectory and that the efficiency of IB propagation in
ambient plasma does not improve, but worsens compared to cross B-field IB
propagation in vacuum, support the picture of efficient neutralization of
the polarization E-field and enhanced scattering of the IB due to
beam-plasma instabilities. Indeed, in the simplified condition for the
onset of plasma-beam instabilities, vb >
(nBP/nb)1/3〈vb〉,
was easily fulfilled in our experiment (J. Huba, 2000, private
communication). Here, <vb> is the thermal
velocity of the beam ions (1 to 3 × 107 cm/s),
vb is the translational velocity of the beam (3 to 5
× 108 cm/s) and
(nBP/nb)1/3 was
∼ 3 to 4 in this experiment. Respective growth rates and frequencies
of said instability, results in trapping (that is to say, braking) of the
accompanying IB fast electrons, were in the range of (0.1 to
1)ωe or 108 to
109s−1. Here, ωe is the
electron plasma frequency. Another candidate for the “pumping
up” of beam-plasma instabilities in case of “hot” plasma
electrons requires the fulfilling of the condition
〈vBP〉 > vb.>
〈vb〉, which was marginally satisfied in our
experiment.
In general, the cause for the undeflected propagation of the wide PB
in the magnetized plasma was credited to the background plasma density
being insufficient to provide effective shorting of the polarization
E-field. The above conditions for the on-set of fast instabilities, as in
the case of IB propagation, are not fulfilled for the PB. Rather, slow
instabilities of the ion trapping type (such as modified two stream,
and/or ion-ion interactions), were deemed responsible for the enhanced
scattering and broadening of the PB. Additional experiments are needed to
elucidate exactly which mechanisms are dominating in both cases.
5. CONCLUSIONS
Comparing the experimental results with the expected results based on
the criteria formulated in Section 1, we can make the following
conclusions about the main features of the PB and IB behavior when
propagating in vacuum and plasma across a B-field:
- Propagation of the intense PB in vacuum and B-field is described
adequately by collective mode ExB transport for β ∼ 0.1 and by the
diamagnetic mode for β ∼ 1. A less expected phenomena, namely the
dramatic buildup of the PB core density, assumed to be due to the braking
and respective bunching of the PB needs a more detailed study;
- In all cases of PB and IB propagation, cross-B-field transport
results in large losses of the peripheral layers of the beam and
preferential expansion of the beam along B-field lines;
- The presence of resistive background plasma, with an applied ExB,
that has a density on the same order as the density of the PB, in general,
worsens the transport efficiency over a distance of ∼
RL due to scattering and instabilities, resulting in
heating of the background plasma. Thus, a high density PB injected into
resistive plasma could be used for effective heating as an alternative or
an addition to current drive heating;
- Propagation of a large orbit IB in vacuum across a B-field mainly
displayed an ExB collective mode of transport;
- Propagation of a large orbit, intense and “warm” IB with
translational and thermal energies of 100 keV and < 1 keV across a
B-field in vacuum at distances comparable or larger than
RL is feasible, but with low efficiency due to very
large losses of beam peripheral layers;
- Capture of the large orbit IB in neutralizing magnetized plasma is
feasible, but due to large losses, has low efficiency. A cold,
monochromatic IB is crucial to improving transport
efficiency.
ACKNOWLEDGMENTS
The authors would like to acknowledge stimulating discussions with
Drs. S. Dettrick, W. Heidbrink, A Qerushi, F. Wessel, and the technical
help of laboratory staff: S. Armstrong, M. Morehouse, K. Walters, and G.
Strashnoy. This work was supported by The Tri Alpha Energy, Inc. and The
University of California, Irvine.
