2. Wealth accounting and ecological capital

In economics, and in systems of national accounts, ‘capital’ is conventionally defined as reproducible real assets, which includes roads, railways, buildings, private dwellings, factories, machinery, equipment and other human-manufactured fixed assets. Thus, investment in the economy, or gross capital formation, is conventionally measured as outlays or additions to these reproducible assets plus net changes in the level of inventories and valuables. If allowance is made for any capital consumption, or depreciation, then the net changes in reproducible assets represent net investment in the economy.

However, as discussed in the introduction, the economy does not just depend on reproducible assets but also on human and natural capital. Traditionally, investment in human capital, which can be thought of as the education, skills and health per person, are not included in the national accounts. Similarly, additions to and depreciation of natural capital are excluded. In a true wealth accounting framework to estimate the NDP of an economy, both of these omissions need correcting. That is, the three basic assets comprising the overall wealth of an economy are reproducible, human and natural capital.

More formally, assume a closed economy with a constant population that is normalized to one.Footnote ⁴ At time t, let K(t) be a numerical index of the economy's stock of reproducible capital assets, and H(t) be a numerical index of the total quantity of human capital, i.e., the level of health, education and skills per person. Reproducible capital depreciates at the constant rate ω > 0, and assume that E(t) is investment in human capital (e.g., current education, health and training expenditures). Denoting the real GDP of the economy at time t as Y(t) and aggregate consumption of goods and services as C(t), then net accumulation of reproducible capital is

(1)$$\dot {K}=Y \lpar t \rpar -C \lpar t \rpar -\omega K \lpar t \rpar - E \lpar t \rpar \comma \;$$

where $\dot {K}={dK \lpar t \rpar }/ dt$, which is the conventional notation for the time derivative of a variable that will be used throughout the paper.

Following Hamilton and Clemens (Reference Hamilton and Clemens1999), letting h(E(t)) represent the rate at which education, health and training investments are transformed into human capital, then the latter accumulates according to

(2)$$\dot {H}=h \lpar {E \lpar t \rpar } \rpar \comma \; \quad {h}^\prime\gt 0\comma \; \quad {h}^{\prime \prime}\le 0.$$

Along with human and reproducible capital, the aggregate stock of natural capital available at time t is also important to the economy. Clearly, this stock must include those conventional natural resources that are the source of raw material, land and energy inputs to the economy, such as fossil fuels, minerals, metals, forest resources and arable land. If we represent these natural resource stocks as Z(t), and let

(3)$$\dot {Z}=G\lpar {Z\lpar t \rpar } \rpar -R\lpar t\rpar \comma \; \quad {G}''\lt 0$$

where the function G represents the natural growth rate for any renewable resources, which is concave with respect to its stock size, and R(t) is the use of any natural resource inputs by the economy.

But, in addition to Z(t), natural capital should include those ecosystems which, through their natural functioning and habitats, provide important goods and services to the economy. If we are to view ecosystems as economic assets, and measure their economic depreciation in wealth accounting, then we need a way of accounting for the benefits accruing from this form of ‘ecological wealth’ Mäler (Reference Mäler2008). As suggested by Barbier (Reference Barbier2007), these benefits are wide ranging, which in economics would normally be classified under three different categories:

1. (i) ‘goods’ (e.g., products obtained from ecosystems, such as resource harvests, water and genetic material),

2. (ii) ‘services’ (e.g., recreational and tourism benefits or certain ecological regulatory and habitat functions, such as water purification, climate regulation, erosion control and habitat provision), and

3. (iii) cultural benefits (e.g., spiritual and religious beliefs, heritage values).

It is clear that some of these ecosystem goods and services contribute directly to human wellbeing, e.g., through enhancing recreation and other direct enjoyment of the environment, augmenting our current and future natural heritage or by reducing harmful pollution and assimilating waste. But some services, either on their own or combined with human inputs, also contribute indirectly to human welfare by supporting economic production (e.g., raw materials, food and other harvested inputs, and provision of freshwater, watershed protection, coastal habitats for offshore fisheries) or by protecting production activities, property and lives (e.g., flood control, storm protection, managing climate). In other words, ‘ecosystem services are the direct or indirect contributions that ecosystems make to the well-being of human populations’ (EPA, 2009: 12).

However, ecosystems globally are under threat from degradation and loss. Global land use change has been a major cause of the alteration and loss of terrestrial ecosystems, especially in developing economies and tropical regions (Dirzo and Raven, Reference Dirzo and Raven2003; MA, 2005; FAO, 2006; Barbier, Reference Barbier2011). Coastal and marine ecosystems are also some of the most heavily used and threatened natural systems globally, such that 50 per cent of salt marshes, 35 per cent of mangroves, 30 per cent of coral reefs and 29 per cent of seagrasses are either converted or degraded worldwide (Valiela et al. Reference Valiela, Bowen and York2001; MA, 2005; Orth et al., Reference Orth, Carruthers and Dennison2006; UNEP, 2006; FAO, 2007b; Waycott et al., Reference Waycott, Duarte and Carruthers2009). The major reason for this loss is land conversion, such as the transformation of forests and wetlands to crop and grazing land, expansion of aquaculture and agriculture in coastal areas, and the demand for land for urban and commercial development. In national accounting terms, the implication is that the depreciation of an important natural asset – ecosystems – is partly compensated for the appreciation of another asset – more land for economic production and development. As Hartwick (Reference Hartwick1992) has illustrated with the example of agricultural conversion of tropical forests, such changes in the stock of an economy's wealth must be included as capital value adjustments in an accounting framework. In effect, the opportunity cost of holding onto ecosystems as natural capital is the foregone benefit of economic development based on converting ecological landscape (Barbier, Reference Barbier2008, Reference Barbier2011).

In sum, ecosystems affect current economic wellbeing, either directly or indirectly through supporting production and protecting human lives and property. However, this ecological capital is unlikely to be intact, as in most economies ecosystems continue to be converted to land for economic development and production. Let N(t) be the stock of ecological capital at time t and N(0) = N ₀ is the initial stock. If c(t) ≥ 0 represents any ecosystem conversion to developed land at time t, then $N\lpar t \rpar =N_{0} -\vint_{0}^{t} {c\lpar s \rpar ds}$ and $\dot{N}=-c\lpar t\rpar $. It follows that, if D(t) is the area of land use in the development activity and D(0) = D ₀ is the initial developed land area, then $D\lpar t \rpar =D_{0} +\vint_{0}^{t} {c\lpar s \rpar ds}$ and thus the aggregate stock of developed land, D(t), increases at the expense of ecological capital N(t)

(4)$$\dot {D}=c\lpar t \rpar =-\dot {N}.$$

Given equations (1)–(4), the economy's real GDP, denoted as Y(t), can be stated as

(5)$$Y\lpar t \rpar =AF\lpar {K\lpar t \rpar \comma \; H\lpar t \rpar \comma \; R\lpar t\rpar \comma \; D\lpar t \rpar \comma \; N\lpar t \rpar } \rpar \comma \;$$

where F is a non-decreasing and twice differentiable function, A represents Hicks-neutral technology (i.e., total factor productivity), and F = 0 if any of its arguments are zero. Note that the production function of the economy should include ecological capital, N(t), given that many ecosystem services support and protect production activities.Footnote ⁵

Letting V(t) denote intergenerational wellbeing at time t, which takes the form

(6)$$V\lpar t \rpar =\vint_t^\infty {U\lpar {C\lpar \tau\rpar \comma \; N\lpar \tau \rpar } \rpar e^{-\delta \lpar {\tau -t}\rpar }d\tau } =V\lpar {K\lpar t \rpar \comma \; H\lpar t \rpar \comma \; Z\lpar t\rpar \comma \; N\lpar t \rpar \comma \; D\lpar t \rpar } \rpar$$

where δ > 0 is the social rate of discount. Intergenerational welfare depends not only on aggregate consumption but also on the direct benefits of ecosystems, which are represented by the inclusion of N(t) in the function for instantaneous wellbeing, or ‘utility’, U(t). It is assumed that the latter function is twice differentiable and concave with respect to its two arguments. However, both the current and future states of the economy rely on the economy's stock of assets at time t; consequently, intergenerational wellbeing V(t) depends on this aggregate wealth (Arrow et al., Reference Arrow, Dasgupta, Goulder, Mumford and Oleson2012).

As Dasgupta (Reference Dasgupta2009) proves, regardless of whether or not the resource allocation mechanism of the economy is optimal or even efficient, given (1)–(6), for any such mechanism it is possible to define a set of shadow prices at time t for the various assets of the economy

(7)$$v^i\lpar t \rpar ={\partial V\lpar t \rpar } /{\partial i}\lpar t\rpar \comma \; \quad i=K\comma \; H\comma \; Z\comma \; N\comma \; D.$$

Given these shadow prices, the economy's aggregate, or inclusive, wealth W(t) and investment I(t) at time t are, respectively

(8)$$W\lpar t\rpar =v^{K}K\lpar t \rpar +v^{H}H\lpar t \rpar +v^Z{Z}\lpar t\rpar +v^N{N}\lpar t \rpar +v^D{D}\lpar t \rpar$$

and

(9)$$I\lpar t \rpar =v^{K} \dot {K}+v^{H} \dot {H}+v^{Z} \dot {Z}+v^{N} \dot {N}+v^{D}\dot {D}^6.$$

Define U _C as the price consumption in ‘utils’ (utility flow), and U _N as the price of ecosystem goods and services that directly influence wellbeing. Then the aggregate NDP of the economy at time t in ‘utils’ is

(10)$$NDP\lpar t\rpar =U_{C} C\lpar t\rpar +U_{N} N\lpar t\rpar +I\lpar t\rpar .$$

Equation (10) depicts NDP as the sum of investment in the aggregate capital stocks of an economy plus the value of consumption and ecosystem goods and services. Differentiating (6) with respect to time yields

(11)$${dV \lpar t\rpar \over {dt}}=I \lpar t\rpar \comma \;$$

where I(t) is defined by (9). Condition (11) states that investment in the aggregate capital stock of an economy determines changes in intergenerational wellbeing over time, and as a result NDP as defined by (11) is an exact measure of these welfare changes. That is, (10) and (11) yield a condition akin to Proposition 9 in Dasgupta (Reference Dasgupta2009)

(12)$$dV\lpar t\rpar /dt\ge 0 \hbox{ if and only if } NDP\lpar t \rpar \ge U_{C} C\lpar t \rpar +U_{N} N\lpar t \rpar .$$

As long as NDP exceeds the value of consumption and ecosystem goods and services, intergenerational welfare will not decline.

Condition (12) has an important economic interpretation, given that non-declining welfare is the crucial criterion defining sustainable development of an economy.Footnote ⁷ As dV(t)/dt ≥ 0 also implies I(t) ≥ 0, then it follows from (8) that sustainable economic development will occur at time t if the aggregate wealth of the economy W(t) does not decline. Thus, the sustainability criterion that ‘welfare does not decline over time’ essentially ‘requires managing and enhancing a portfolio of economic assets, the total capital stock, such that its aggregate value does not decline over time’, but only if it is recognized that ‘the total stock of the economy available to the economy for producing goods and services, and ultimately well-being, consists not just of human and physical capital but also of natural capital’ (Pearce and Barbier, Reference Pearce and Barbier2000: 20–21).

To understand the importance of measuring explicitly the contributions of natural capital, and especially that of ecological capital, it is necessary to decompose NDP as defined by (9), which can be rewritten (suppressing the time arguments) as

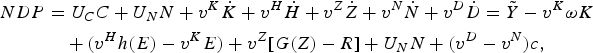(13)$$\eqalign{ NDP &= U_{C} C+U_{N} N+v^{K}\dot {K}+v^{H}\dot {H}+v^{Z}\dot {Z}+v^{N}\dot {N}+v^{D}\dot{D}= \tilde {Y}-v^{K}\omega K \cr & \quad +\lpar v^{H}h\lpar E\rpar -v^{K}E\rpar +v^Z\lsqb G\lpar Z\rpar -R\rsqb +U_{N} N+\lpar {v^D-v^N}\rpar c\comma \; }$$

where $\tilde {Y}=v^{K}\dot {K}+\lpar U_{C} -v^{K}\rpar C.$

In (13), Ỹ(t) − v ^K(t)ωK (t) is conventionally defined NDP, i.e., the GDP of the economy less any depreciation (in value terms) of previously accumulated reproducible capital. This is NDP as currently measured in most national accounts of economies, although of course it is usually valued at market prices rather than in ‘utils’. It is clear from (13) that, if NDP is to serve as a true measure of the changes in an economy's wealth, it must include any change in valuable human and natural capital as well. For instance, v ^Hh(E(t)) − v ^K(t)E(t) is the net gain or loss (in value terms) in human capital, and v ^Z(t)[G(Z(t)) − R(t)] represents the net changes (in value terms) in natural resource stocks.Footnote ⁸ In the case of non-renewable resources, such as fossil fuels and minerals, G(Z) = 0 and so −v ^ZR measures the deduction from NDP of resource depletion. For renewable resources, such as forests and fisheries, NDP must include any depreciation in natural resource stocks if G(Z) < R. The expression U _NN(t) + [v ^D(t) − v ^N(t)]c(t) includes both the benefits to current wellbeing provided by ecosystems, U _NN, and any capital revaluation that occurs as ecosystems are converted by land use change for development, (v ^D − v ^N)c.Footnote ⁹ To interpret the latter term, it is helpful to explore further the shadow value of ecological capital v ^N(t) and developed land v ^D(t), respectively.

By definition, from (10), $v^{N}\lpar t\rpar =\vint_{t}^{\infty} {{\partial U}\over{\partial N}} \lpar \tau \rpar e^{-\delta \lpar {\tau -t} \rpar }d\tau$ and $v^{D}\lpar t\rpar =\vint_{t}^{\infty}{{\partial U}\over{\partial D}} \lpar \tau \rpar e^{-\delta \lpar {\tau -t} \rpar }d\tau $. Making use of $U\lpar {C\comma \; N} \rpar =U\lpar {Y-\dot {K}-\omega K-E\comma \; N} \rpar $, it follows that

(14)$$\eqalign{v^D\lpar t \rpar -v^N\lpar t \rpar &=\vint_t^\infty {e^{-\delta \lpar {\tau -t} \rpar }U_C \lpar \tau \rpar AF_D \lpar \tau\rpar d\tau } -\vint_{t}^{\infty} e^{-\delta \lpar {\tau -t}\rpar }\lsqb U_N \lpar \tau \rpar \cr & \quad +U_C \lpar \tau \rpar AF_N \lpar \tau \rpar \rsqb d\tau .}$$

Thus, v ^D(t) is the present value of any additional production resulting from any increase in land for economic development land, whereas v ^N(t) is the present value of any additional ecosystem benefits due to increases in ecosystem land. That is, v ^D(t) and v ^N(t) are the capitalized values, or prices, of development and ecosystem land, respectively. As ecosystems are converted by land use change for development, (v ^D − v ^N)c is the capital gain (depreciation) in land that occurs if v ^D > v ^N (v ^D < v ^N). As land is a durable and capital good, condition (11) indicates that NDP must be adjusted for any such capital revaluation.

To summarize, although conditions (13) and (14) seem complicated, they help clarify how we should value and include changes in ecological capital in wealth accounting. First, we should adjust the NDP of the economy to include two contributions due to ecological capital:

• • the value of the direct benefits provided by the current stock of ecosystems, U _NN, and

• • any capital revaluation as a result of conversion of ecosystems to other land uses, (v ^D − v ^N)c, with the price of changes in ecological capital, v ^N (t), reflecting the present value of the future direct and indirect benefits of ecosystems.

These adjustments to NDP for ecological capital are similar to those for environmental resource stocks derived by Mäler (Reference Mäler1991). It appears that, although ecosystems generate a wide variety of complex goods and services, the actual rules for determining how the direct and indirect benefits of ecological capital should be accounted for in NDP are no different from those for any stock that affects human welfare either directly or indirectly via supporting or protecting economic production.

As discussed previously, the direct ecosystem benefits might include the value of ecosystems in providing recreational, educational and scientific benefits, their value in terms of natural heritage or bequests to future generations or the value of ecosystems in reducing harmful pollution, assimilating waste and managing climate. In addition, ecological capital protects or supports economic activity, property and human lives. These indirect ecosystem benefits are broad ranging, and include raw materials, food and other harvested inputs used in production, provision of freshwater, watershed protection, coastal habitats for offshore fisheries, flood control, storm protection, climate stabilization and similar services. Finally, in the wealth accounting framework adopted here, the resource allocation mechanism of the economy may not be optimal or even efficient, so it is possible that ecosystem conversion may be taking place even though the capitalized value, or ‘price’, of developed land is actually less than the capitalized value of ecosystems. In which case, NDP should be adjusted for the depreciation in ecological capital that occurs as it is converted to less valuable developed land.

3. Measurement issues

There are two important measurement issues that can arise in allowing for the economic contributions of ecosystem goods and services in wealth accounts. The first issue is that, for a ‘mixed’ ecological landscape containing more than one type of ecosystem – forests, wetlands and rivers, it may be difficult to determine how a particular ecosystem benefit arises from the landscape or to ascribe it to one type of ecosystem. Such a measurement and valuation problem can only be resolved through careful analysis and collaboration among economists, ecologists and other natural scientists to estimate the benefits of specific ecosystem goods and services.Footnote ¹⁰ However, even if this valuation challenge is resolved, a second double counting problem may arise if one assumes that NDP should be adjusted for all the benefits provided by ecological capital.

As the methodology developed in the previous section indicates, the NDP of the economy should be adjusted for the value of the direct benefits provided by the current stock of ecosystems. But NDP should not be adjusted for any indirect benefits of this current stock through its support or protection of production in the economy. The reason for the latter omission is that it may create problems of double counting in the wealth accounts of an economy. Because the indirect benefits of ecological capital arise through its support or protection of current economic production, NDP already accounts for this contribution. This relationship is one reason why it is possible to calculate the ‘value added’ contribution of ecological capital as an intermediate input in production. Just like other intermediate inputs into production, however, this benefit of ecological capital should not be accounted for in NDP to avoid double counting.

The production function method is an important non-market valuation approach to measuring the economic contribution of many ecosystem goods and services that affect human welfare indirectly through their support or protection of production activities, property or human lives (Freeman III, Reference Freeman2003; McConnell and Bocksteal, Reference McConnell, Bockstael, Mäler and Vincent2005; Barbier, Reference Barbier2007). In other words, ecosystem services that arise from the regulatory functions of ecosystems, such as waste management, habitat support, storm protection, flood mitigation or groundwater recharge, often serve as intermediate inputs in economic production activities, which are in turn often marketed. Similarly, goods or products from ecosystems, such as harvested raw materials, water supplies, food, fiber and fuel, may themselves be marketed, or in turn are processed by industries into marketed products. But if these goods and services produced from the current stock of ecosystems serve as intermediate inputs into marketed production, then conventionally defined NDP will most likely already reflect their current contribution. To add to NDP the marginal value contribution to economic production of ecosystem goods and services that are intermediate inputs would result in double counting (Mäler, Reference Mäler1991; Mäler, Reference Mäler2008).

For example, if a coastal marsh or mangrove serves as a nursery or breeding habitat for an offshore commercial fishery, then this habitat will have an influence on the current harvested and marketed output of the fishery. However, the harvested fish will already be included in the conventional NDP of an economy, as it is a marketed product. Similarly, if the wetlands also protect coastal property from storm damages, the value of the latter assets already accounts for the storm protection value of the wetlands. In addition, if the wetlands themselves are a source of currently harvested food, fiber and raw materials, which are in turn sold commercially, then the NDP will already be included in these marketed products. In contrast, if any harvested wetland products are not marketed but support the subsistence needs of harvesting households, then the value of these ecological goods will not appear in conventionally measured NDP. Because they are consumed and not marketed, these products are essentially direct benefits to households. Finally, coastal wetlands may generate many other non-marketed ecosystem services that also directly influence welfare, such as filtering water pollution that affects human health, enhancing enjoyment of coastal areas and recreation and providing cultural benefits. Again, these current values of the wetlands are unlikely to appear in conventional NDP.

In sum, to avoid double counting, the NDP of an economy should not be adjusted by including the value of any goods and services provided currently by ecosystems, if they serve as intermediate inputs in the production of marketed final goods and services. However, if ecosystem goods and services affect current production activities that are not marketed, such as raw materials, food, fiber and water that are consumed directly by households, then the value of these ecological contributions should be assessed and added to NDP. This particular double counting problem does not arise when adjusting NDP to account for any capital revaluation in the economy that occurs when, say, ecosystems are converted to other land uses. In this case, the capitalized value of converted ecosystems must reflect the present value of all foregone future benefits of these ecosystems, whether they influence welfare directly or indirectly through production of marketed final goods and services.

4. A case study: adjusted NNP and mangrove loss in Thailand

The purpose of this section is to provide an example of the wealth accounting adjustments implied by conditions (13) and (14). This example, based on mangrove ecosystem goods and services in Thailand, is illustrative only. As pointed out by Smulders (Reference Smulders2012, 369) the ‘Achilles heel’ in the inclusive wealth method lies in ‘the determination of shadow prices’, and because ‘future shadow values are determined by current capital stocks, the “resource allocation mechanism”, and exogenous factors that capture (changes in) institutions, technologies and preferences … the resulting values are hypothetical’. It is therefore presumptuous to assume that the information is available to calculate explicitly the necessary shadow values for mangroves in Thailand. Nevertheless, conditions such as (11) and (12) are of practical use, as they help clarify how we should adjust the NDP of the Thai economy to include the contributions due to an important form of ecological capital, such as mangrove ecosystems.Footnote ¹¹

Thailand is estimated to have lost around a third of its mangroves since the 1960s, mainly to shrimp farming expansion and other coastal development (FAO, 2007a; Spalding et al., Reference Spalding, Kainuma and Collins2010). During this period, real GDP per capita in Thailand has increased five-fold (World Bank, 2011). A measure of the adjusted NDP, taking into account human and natural capital loss since 1970, can therefore be constructed, relying on the data and methods employed by the World Bank (2011). Based on estimates of four mangrove ecosystem benefits – collected products, habitat–fishery linkages, storm protection and carbon sequestration – the following Thailand case study illustrates the methodology of adjusting NDP additionally for the value of the direct benefits provided by the current stock of ecosystems, and any capital revaluation that occurs as a result of ecosystem conversion to other land uses.

In 1961, Thailand was estimated to have around 368,000 ha of mangroves (see figure 1). Mangrove deforestation proceeded swiftly in the 1970s and 1980s, but since 2000, the area of mangroves seems to have stabilized around 240,000–250,000 ha. The main cause of mangrove loss in Thailand is attributed to conversion to shrimp aquaculture (Aksornkoae and Tokrisna, Reference Aksornkoae, Tokrisna, Barbier and Sathirathai2004). The principal reason for the slowdown in mangrove loss is that many of the suitable sites for establishing shrimp farms in the Gulf of Thailand have been deforested, whereas the mangrove areas on the Andaman Sea (Indian Ocean) coast are too remote and less suitable for shrimp farms (Barbier and Cox, Reference Barbier and Cox2004).

Source: FAO (2007b) and Spalding et al. (Reference Spalding, Kainuma and Collins2010).

Figure 1. Estimated mangrove area, Thailand, 1961–2009

As indicated in equation (13), the NDP of an economy must be adjusted for the benefits to current wellbeing provided by ecosystems, U _NN, and any capital revaluation that occurs as ecosystems are converted by land use change for development, (v ^D − v ^N)c. Mangrove ecosystems in Thailand provide four essential goods and services. These are the role of mangroves as natural ‘barriers’ to periodic damaging coastal storm events, their role as nursery and breeding habitats for offshore fisheries, their ability to store carbon, and the exploitation of mangrove forests by coastal communities for a variety of wood and non-wood products. Estimates of the value of all four benefits exist for Thailand, and they are used as the basis for determining both the current value of these benefits as well as the capital revaluation that results from mangrove conversion.

For example, the value of coastal protection from storms is based on a marginal value per ha of damages avoided (in 1996 US$) of US$1,879; over a 20-year time horizon and a 10 per cent discount rate this yields a net present value (NPV) of US$15,997 per ha (Barbier, Reference Barbier2007). The value of habitat–fishery linkages is based on a net value per ha (in 1996 US$, assuming a price elasticity for fish of −0.5) of mangrove habitat of US$249; over a 20-year time horizon and a 10 per cent discount rate this yields a NPV of US$2,117 per ha (Barbier, Reference Barbier2003). The value of wood and non-wood products is based on net income per ha from mangrove forests to the local community (updated to 1996 US$) of US$101; over a 20-year time horizon and a 10 per cent discount rate this yields a NPV of US$864 per ha (Sathirathai and Barbier, Reference Sathirathai and Barbier2001). Chmura et al., (Reference Chmura, Anisfeld, Cahoon and Lynch2003) estimate permanent carbon sequestration by global mangroves of 2.1 metric tons per ha per year, and World Bank (2011) values unit CO₂ damage at US$20 per ton of carbon (1995 US$), which yields an annual value (in 1995 US$) of US$42 per ha for carbon sequestration. Over a 20-year time horizon and a 10 per cent discount rate this yields a NPV of US$413 per ha. These values are converted to 2000 US$ using the GDP deflator for Thailand (World Bank, 2011). The result is that the current benefits of mangroves in Thailand have a constant 2000 US$ value of US$2,519 per ha, and a capitalized value, v ^N, of US$21,443 per ha.

As the main activity responsible for mangrove conversion in Thailand has been shrimp aquaculture, the capitalized value of this activity is used for v ^D. The NPV per ha for the commercial net returns to shrimp farming over a 20-year time horizon and 10 per cent discount rate is based on Sathirathai and Barbier (Reference Sathirathai and Barbier2001) which, when updated to 1996 US$, amounts to a value of US$9,632 per ha. However, many of the inputs used in shrimp pond operations are subsidized, below border-equivalent prices, thus increasing artificially the private returns to shrimp farming. Without these subsidies, the resulting economic net returns to shrimp farming result in an NPV of US$1,220 per ha. When converted to 2000 US$ using the GDP deflator for Thailand (World Bank, 2011), the capitalized value of mangroves converted to shrimp farms, v ^D, is US$1,351 per ha. Because the capitalized value, or ‘price’, of mangroves converted to shrimp farming is less than the capitalized value of mangroves, or (v ^D − v ^N) < 0, then the NDP of Thailand should be adjusted for this resulting capital depreciation in mangrove land.

However, not all the current benefits of mangroves impact welfare directly, but may do so only through the support or protection of economic activity and property. That is certainly the case for the storm protection benefits of mangroves, which are estimated through an expected damage approach that determines their value in terms of protecting economic property (Barbier, Reference Barbier2007). As this benefit is already accounted for in the current market values of property, to avoid double counting, the NDP of the Thai economy should not be adjusted to include the benefit of storm protection provided by the current stock of mangroves. Similarly, a survey of four Thai villages from two coastal provinces indicates that only 12.4 per cent of the value of collected wood and non-wood products from mangroves and 5.3 per cent of the value of coastal fishery harvests can be attributed to subsistence production (Sarntisart and Sathirathai, Reference Sarntisart, Sathirathai, Barbier and Sathirathai2004).Footnote ¹² Thus, the NDP should be adjusted only for the subsistence contributions of these two benefits of the mangroves in Thailand.

Using these data and assumptions, table 1 depicts the per capita wealth accounting estimates for Thailand's mangroves from 1970 to 2009. Average annual mangrove loss has fallen steadily in every decade since the 1970s (see also figure 1). Nevertheless, because around a third of the mangrove area has been deforested from 1970 to 2009, whereas Thailand's population has nearly doubled over this period, the current per capita benefits of mangroves has halved since the 1970s, from US$0.57 to US$0.28 per person.Footnote ¹³ In the 1970s, when mangrove loss in Thailand was at its highest, mangrove depreciation amounted to US$2.26 per person, whereas by the 2000s it had fallen to only US$0.03 per capita. The result is that the net value of mangroves per capita in Thailand, which is the total value less mangrove depreciation, was actually negative in the 1970s and 1980s, averaging -US$1.69 and -US$0.76 per person, respectively. However, in the 1990s and 2000s, the net value was slightly positive, averaging US$0.11 and US$0.22, respectively.

Table 1. Wealth accounting for mangrove capital, Thailand, 1970–2009

Notes: As storm protection value is based on expected damages to economic property, it is assumed that this benefit is already accounted for in the current market values of property. Current habitat–fishery linkages benefits are based only on the imputed subsistence value, which is based on a survey of four Thai coastal villages and is approximately 5.3% of total household income (Sarntisart and Sathirathai, Reference Sarntisart, Sathirathai, Barbier and Sathirathai2004: tables 6.3 and 6.4). Current wood and non-wood product benefits are based only on the imputed subsistence value, which is based on a survey of four Thai coastal villages and is approximately 12.4% of total household income (Sarntisart and Sathirathai, Reference Sarntisart, Sathirathai, Barbier and Sathirathai2004: tables 6.3 and 6.4).

Table 2 depicts an approximate estimate of adjusted net domestic product (ANDP) per capita for real changes in reproducible, human and natural capital for Thailand over 1970 to 2009. ANDP is GDP less consumption of fixed capital and natural resource depletion, plus education expenditure and net values of mangrove depletion. The latter estimate is based on the net value of mangroves from table 1. Since the 1970s, both consumption of fixed capital and natural resource depreciation have increased significantly in Thailand. The value of expanding human capital, as proxied by education expenditures, has also increased, and because of the slowdown in mangrove loss, the net value of this ecological capital has gone from a negative to a positive contribution to NDP.

Table 2. Wealth accounting, Thailand, 1970–2009

Notes: GDP, gross domestic product; ANDP, adjusted net domestic product, or GDP less consumption of fixed capital and natural resource depletion, plus education expenditure and net value of mangroves (estimated in table 1). Natural resource depletion is the sum of net forest depletion, energy depletion, and mineral depletion. Net forest depletion is unit resource rents × the excess of roundwood harvest over natural growth. Energy depletion is the ratio of the value of the stock of energy resources to the remaining reserve lifetime (capped at 25 years). It covers coal, crude oil and natural gas. Mineral depletion is the ratio of the value of the stock of mineral resources to the remaining reserve lifetime (capped at 25 years). It covers tin, gold, lead, zinc, iron, copper, nickel, silver, bauxite and phosphate.

Source: World-Bank (2011), except for net value of mangroves, which is from table 1.

Overall, the value of mangroves and expanding human capital has not kept pace with reproducible capital depreciation and natural resource depletion in Thailand. As a consequence, ANDP per capita in Thailand has remained consistently below GDP per capita since the 1970s. As shown in figure 2, since 1990 the gap between GDP and ANDP per capita in Thailand has widened significantly.Footnote ¹⁴

Figure 2. GDP and ANDP per capita, Thailand, 1970–2009

To summarize, because many of the benefits provided by the current stock of mangroves in Thailand arise through supporting or protecting marketed production and property, these benefits should already be included in the conventionally measured GDP for Thailand. However, any ANDP measure does need to take into account the current direct benefits provided by mangroves in the form of carbon sequestration, habitat and breeding ground services that support any fishery harvests consumed by coastal households and mangrove products that also comprise subsistence consumption. On the other hand, all future mangrove benefits are lost as a result of mangrove conversion, which has been substantial in Thailand since the 1970s. The considerable mangrove depreciation that occurred in the 1970s and 1980s meant that the net value of mangroves was actually negative in these decades. Although mangrove deforestation and thus its capital depreciation has slowed since then, the net value of mangroves per capita, as an indicator of its contribution to the wealth of Thailand, is still extremely low. Thus, the Thailand mangrove case study not only provides an illustration of the ANDP methodology for ecological capital but also illustrates how significant loss of this capital can influence its net value in wealth accounts.

5. Accounting for the threat of ecological collapse

Many ecological studies identify irreversible landscape conversion as posing a threat of ecosystem collapse (Busing and White, Reference Busing and White1993; Turner et al., Reference Turner, Romme, Gardner, O'Neill and Kratz1993; Peterson et al., Reference Peterson, Allen and Holling1998; Dobson et al., Reference Dobson, Lodge and Alder2006; Lotze et al., Reference Lotze, Lenihan and Bourque2006). That is, the ability of an ecosystem to survive may be linked to its overall landscape size or scale. For example, as (Dobson et al., Reference Dobson, Lodge and Alder2006, 1921) conclude, because ‘species drive ecosystem processes’ in most ecological landscapes, as habitat size declines, ‘we would thus expect to see an initial sequential reduction in economic goods and services as natural systems are degraded, followed by a more rapid sequential collapse of goods and services’. This relationship may be especially pronounced in coastal ecosystems, such as mangroves and salt marsh, as positive interactions among ecological functions, trophic cascades and linkages, and biodiversity appear to be positively correlated with how much of the remaining ecological landscape is left intact (Silliman and Bertness, Reference Silliman and Bertness2002; Peterson et al., Reference Petersen, Kemp and Bartleson2003; Rilov and Schiel, Reference Rilov and Schiel2006; Elliott et al., Reference Elliott, Burdon, Hemingway and Apitz2007; Halpern et al., Reference Halpern, Silliman, Olden, Bruno and Bertness2007). In the case of mangroves, there is also evidence from Thailand that the excess sediments discharged from nearby shrimp ponds reduce the growth rates and increase mortality rates in the remaining mangrove areas, thus threatening ecosystem collapse (Vaiphasa et al., Reference Vaiphasa, de Boer, Skidmore, Panitchart, Vaiphasa, Bamrongrugsa and Santitamnont2007). The implication is that the probability of ecological collapse is likely to increase with a diminishing size, or conversion, of the ecological landscape.

Thus, the resilience or robustness of an ecosystem – its ability to absorb large shocks or sustained disturbances and still maintain internal integrity and functioning – may be an important attribute determining the extent to which landscape conversion and ecosystem degradation affect the risk of ecological collapse.Footnote ¹⁵ As a consequence, one approach to accounting for the resilience property of ecosystems is to measure directly the wealth effects of resilience (Mäler, Reference Mäler2008; Walker et al., Reference Walker, Pearson, Harris, Mäler, Li, Biggs and Baynes2010). Once these wealth effects of ecosystem resilience are estimated, then the NDP of an economy can be adjusted accordingly.

For example, Walker et al. (Reference Walker, Pearson, Harris, Mäler, Li, Biggs and Baynes2010) estimate and value ecosystem resilience for the Goulburn–Broken Catchment (GBC) in southeast Australia. The GBC is prime agricultural land, most of which is used for dairy pasture. However, the agro-ecosystem is threatened by increased soil salinity due to rising water tables from the removal of native vegetation. At the 2 m water table threshold, the system is in danger of flipping to a different regime dominated by degraded and salinized pasture. The authors estimate resilience as the distance from the current water table to the 2 m threshold. Under normal climate conditions, a 0.5 m change in ecosystem resilience is valued at about $23 million, or around 7 per cent of the total wealth of the GBC in 1991. Under drier climatic conditions, resilience is worth US$28 million, or 8.4 per cent of total wealth. As this Australian example indicates, the economic benefits of ecosystem resilience can be considerable. In such highly productive ecosystems supporting economic activity, regime shift can be catastrophic. Or, to put it differently, the value of avoiding regime shift by maintaining or enhancing the resilience of ecosystems can be a sizable component of the total economic wealth generated by these systems.

Here, an alternative approach is suggested for adjusting NDP to account for the threat of ecological collapse. Instead of measuring the wealth contributions of ecosystem resilience, it should also be possible to incorporate the risk of ecosystem collapse due to conversion directly into measures of the economic benefits of ecosystems. The methodology of this approach can be easily demonstrated through modifying the above model of wealth accounting and ecological capital, and then illustrated with the case study of Thailand's mangroves.

Assume as before that ecosystems are represented as a stock of ecological capital, N(t). Consider that this stock is vulnerable to random catastrophic collapse as ecological landscape is converted irreversibly for development. Up until the collapse (if it occurs), ecological capital can still be converted to land for development activity, D(t), as governed by (4), and the remaining intact ecosystems yield indirect and direct benefits. However, if ecological collapse occurs at some time t*, a minimum level of direct ecosystem benefits are derived, which correspond to U(N*).

The expected NPV of intergenerational wellbeing up to the time of collapse t* is therefore

(15)$$J=E\left[{\vint_t^{t\ast } {U\lpar {C\lpar \tau\rpar \comma \; N\lpar \tau\rpar } \rpar e^{-\delta \lpar {\tau -t} \rpar }d\tau +e^{-\delta t\ast }U\lpar {N^\ast } \rpar } } \right].$$

The likelihood of collapse can be characterized by a hazard rate function that specifies the probability that the ecosystem collapses at time t, given that it has survived so far up to that time. Formally, the hazard rate can be defined as

(16)$$\lpar t \rpar ={\lim_{\Delta t\to 0}} \rm{Pr} {\lpar {t\le T \lt t+\Delta t\vert {T\ge t} } \rpar }/{\Delta t}={f\lpar t\rpar \over S\lpar t \rpar }$$

where f(t) is the corresponding density function of the probability distribution of the duration T of ecological capital F(t) = Pr ( T < t). If S(t) is the upper tail of this probability distribution, i.e., S(t) = 1 − F(t) = Pr ( T≥ t), then S(t) is the probability that ecosystems survive to time t. It follows that h(t) = f(t)/S(t) = ( d F/dt)/S(t) = −(d S/dt)/S(t), and thus

(17)$$h\lpar t\rpar = -{\dot{S}\over S} = -{d \ln S\lpar t\rpar \over dt}\comma \; -\ln S\lpar t\rpar =\vint^t_0 h\lpar u\rpar du\comma \; S\lpar t\rpar = \exp \left\{-\vint^t_0 h\lpar u\rpar du\right\}\comma \;$$

with S(0) = 1 and $\dot {S}={dS}/{dt<0}$. The probability that ecological capital continues to survive is decreasing over time.

As shown in the appendix, expression (17) can be used to introduce a new state variable $y\lpar t \rpar =-\ln S\lpar t \rpar =\vint_{0}^{t} {h\lpar u \rpar du}$, then $\dot {y}=h\lpar t\rpar $ and $S\lpar t\rpar =e^{-y\lpar t \rpar }$. If the probability of ecological collapse, and therefore the hazard rate function, depends on ecosystem conversion to developed land, c(t), then the new state equation can be written as

(18)$$\dot{y}=h\lpar t\rpar =\psi \lpar c\lpar t\rpar \rpar \comma \; {\psi ^{\prime}} \gt 0\comma \; {\psi ^{\prime\prime}} \ge 0\comma \; y\lpar 0\rpar =0.$$

It follows that (18) is a new ‘asset’ constraint imposed on intergenerational wellbeing (15), which as shown in the appendix can be rewritten as

(19)$$\tilde {V}\lpar t \rpar =\vint_t^\infty {e^{-\delta \lpar {\tau -t} \rpar -y\lpar {\tau -t} \rpar }\lsqb {U\lpar {C\lpar \tau\rpar \comma \; N\lpar \tau\rpar } \rpar -\delta U\lpar {N^\ast } \rpar } \rsqb d\tau +U\lpar {N^\ast } \rpar }.$$

Once again, it is possible to define a set of shadow prices at time t for the various assets of the economy

(20)$$v^i\lpar t \rpar ={\partial \tilde {V}\lpar t \rpar }/{\partial i\lpar t \rpar \comma \; \quad i=K\comma \; H\comma \; Z\comma \; N}\comma \; D\comma \; y\comma \;$$

where v ^y(t) is the shadow price at time t for the new asset associated with the risk of collapse, y(t).

By employing again the utility prices of U _C and U _N for consumption and direct ecosystem benefits, respectively, and valuing U(N*) as U _NN*, equation (20) can be used to define the aggregate NDP of the economy at time t in ‘utils’

(21)$$\eqalign{NDP & = S\lpar t \rpar \lsqb U_C C+U_N N-\delta U_N N^{\ast }\rsqb +I\lpar t\rpar +v^{y}\dot{y} \cr &=\tilde{Y}-v^{K}\omega K+\lpar v^{H}h\lpar E\rpar -v^{K}E\rpar +v^{Z}\lsqb G\lpar Z\rpar -R\rsqb \cr & \quad +S\lpar t\rpar \lsqb U_{N} N-\delta U_{N} N^{\ast }\rsqb +\lpar v^{D}-v^{N}\rpar \left[c-{{\psi \lpar c\rpar }\over{\psi }\prime }\right]\comma \; \cr \tilde{Y} &= v^{K}\dot{K}+\lpar S\lpar t \rpar U_{C} -v^{K} \rpar C\comma \; }$$

where use is made of the relationship $v^{D}=v^{N}-v^{y}{\psi }'$.

Equation (21) indicates that we should still adjust NDP for the value of the direct benefits provided by the current stock of ecosystems, U _NN, but now, because of the risk of ecological collapse, these benefits should be weighted by the probability of ecological capital surviving, S(t), while also deducting the value at time t of the minimum direct ecosystem benefits after collapse, $S\lpar t \rpar \delta U_{N} N^{\ast} $. As the latter value is deducted from current ecosystem benefits, it is also conditional on the ecosystem surviving up to time t.

In addition, according to equation (21), any capital revaluation as a result of conversion of ecosystems to other land uses, (v ^D − v ^N)c, must be adjusted for the change in the risk of collapse caused by such conversion, $-\lpar {v^{D}-v^{N}} \rpar {{\psi \lpar c \rpar }\over{\psi '}}$. As the relative risk of collapse, ${{\psi \lpar c \rpar }\over{\psi '}}$, rises (falls) with increased (decreased) conversion, the sign of adjustment depends on whether or not the capitalized value of developed land, v ^D, exceeds the capitalized value of the remaining ecological landscape, v ^N. If an increase in land values occurs as a result of ecosystem conversion, v ^D > v ^N, then these values must be adjusted downwards because of the greater risk of collapse, as $-\lpar {v^{D}-v^{N}} \rpar {{\psi \lpar c \rpar }\over{\psi '}}<0$. Although land is gaining value as it is converted from ecological landscape to development activities, the risk of collapse to the remaining ecological landscape detracts from this gain in land values. However, if the value of land depreciates as it is converted from ecosystems to development, v ^D < v ^N, then land values must be corrected upwards because of the increased risk, as $-\lpar {v^{D}-v^{N}} \rpar {{\psi \lpar c \rpar }\over{\psi '}}>0$. The net loss in land values is not as large because the remaining ecological capital may not survive.

The case study of Thailand's mangroves can be employed to illustrate how these adjustments to NDP account for the risk of ecological collapse. Conducting this simulation requires specifying specific functional form for the hazard rate function, h(t), and the corresponding probability density function, f(t). For this analysis, it is assumed that $h\lpar t \rpar =\lpar {c\lpar t \rpar } \rpar ^{\psi}$ and $f\lpar t \rpar =h\lpar t \rpar -2bt$, where ψ and b are parameters. From (16), one therefore obtains a specific expression for the survival probability, $S\lpar t \rpar ={\lpar {c^{\psi} -2bt} \rpar }/{c^{\psi} }$. In addition, it is also assumed that the minimum value of mangrove goods and services after collapse, U _NN*, is 5 per cent of the value of the current direct benefits of mangroves in 1970. As before, the social discount rate, δ, is 10 per cent, v ^N is US$21,443 per ha, and v ^D is US$1,351 per ha. For the purposes of simulation, ψ = 1.5 and b = 2.0, and 1970 is the base year t = 0.

Using these data and assumptions, table 3 depicts the per capita wealth accounting estimates for Thailand's mangroves from 1970 to 2009 that also includes the various influences of the risk of ecological collapse as depicted by equation (17). The results in table 3 can be compared to table 1, which exclude the risk of collapse effects.

Table 3. Wealth accounting for mangrove capital with the risk of ecological collapse, Thailand, 1970–2009

Although mangrove conversion has slowed from the 1970s to the 2000s, the conditional probability of survival, S(t), has declined from nearly 100 per cent to 85.5 per cent. This is expected, given (17) and a positive hazard rate related to mangrove conversion, c, as indicated by (18). The total value of surviving mangroves, S(t)U _NN, depicted in table 3, is therefore lower than the current per capita benefits of mangroves, U _NN, estimated for each decade and shown in table 1. In addition, the periodic value of mangroves after collapse, $S\lpar t \rpar \delta U_{N} N^{\ast} $, must also be subtracted from NDP. In per capita terms, this value was around US$0.07 through the 1990s, and then US$0.06 in the 2000s. Mangrove depreciation, which is the same in tables 1 and 3, must be adjusted for the risk of ecological collapse. As explained previously, as v ^D < v ^N, this must be a positive adjustment.

A comparison of the last columns of tables 1 and 3 indicates the overall effects of the risk of ecological collapse on the net value of mangroves per capita in Thailand. In the 1970s and 1980s, taking into account the risk of collapse reduces the negative net value of mangroves, to −$0.25 and −$0.06 per person, respectively. On the other hand, in the 1990s, the positive net value of mangroves increased slightly due to the risk of collapse, from US$0.11 per capita (table 1) to US$0.18 (table 3), whereas in the 2000s the net value of mangroves per capita was reduced from US$0.25 to US$0.17.