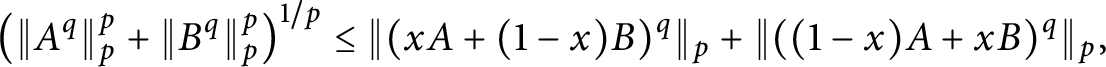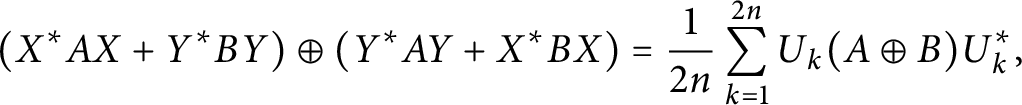1 Elementary scalar inequalities

Extending basic scalar inequalities, for instance, $|a+b|\le |a|+|b|$ , to matrices lies at the very heart of matrix analysis. Here, we are interested in the elementary inequality which supports the Hermite–Hadamard inequality. This classical theorem can be stated as follows.

Proposition 1.1 Let $f(t)$ be a convex function defined on the interval $[a,b]$ . Then,

$$ \begin{align*}f\left(\frac{a+b}{2}\right)\ \le \int_0^1 f((1-x)a+xb)\, {\mathrm{d}}x\le \frac{f(a)+f(b)}{2}. \end{align*} $$

In spite of its simplicity, the Hermite–Hadamard inequality is a powerful tool for deriving a number of important inequalities (see the nice paper [Reference Niculescu and Persson12] and the references therein).

The first inequality immediately follows from the convexity assumption

(1.1) $$ \begin{align} f\left(\frac{a+b}{2}\right) \le \frac{f((1-x)a+xb) +f(xa +(1-x)b)}{2}. \end{align} $$

The second inequality is slightly more subtle; it follows from the sums property

(1.2) $$ \begin{align} f((1-x)a+xb) +f(xa +(1-x)b) \le f(a) + f(b), \end{align} $$

which requires the convexity assumption twice. This is the key for Proposition 1.1, and it has a clear geometric interpretation; (1.2) is equivalent to the increasingness of

$$ \begin{align*}\varphi(t) := f(m+t) +f(m-t), \end{align*} $$

with $m=(a+b)/2$ and $t\in [0,b-m]$ . In fact, if we assume that $f(t)$ is $C^2$ and observe that for $t\in [0,b-m]$ ,

$$ \begin{align*}\varphi'(t)=f'(m+t)-f'(m-t) =\int_{m-t}^{m+t} f''(s) \,{\mathrm{d}}s, \end{align*} $$

we can estimate $\varphi '(t)$ with $f''(s)\ge 0$ .

The extremal property (1.2) of $f(t)$ says that for four points in $[a,b]$ ,

(1.3) $$ \begin{align} p\le s\le t\le q, \ p+q=s+t \Rightarrow f(s)+f(t) \le f(p)+f(q). \end{align} $$

Let us see now what can be said for matrices. Important matrix versions of (1.1) are well known. Let $\mathbb {M}_n$ denote the space of $n\times n$ matrices and $\mathbb {M}_n^{s.a}$ its self-adjoint (Hermitian) part with the usual order $\le $ induced by the positive semidefinite cone $\mathbb {M}_n^+$ . We recall [Reference Bourin and Lee6, Corollary 2.2].

Theorem 1.2 Let $A,B\in \mathbb {M}_n^{s.a}$ with spectra in $[a,b]$ , and let $f(t)$ be a convex function on $[a,b]$ . Then, for some unitaries $U,\,V\in \mathbb {M}_n$ ,

$$ \begin{align*} f\left(\frac{A+B}{2}\right)\le \frac{1}{2}\left\{U\frac{f(A)+f(B)}{2}U^*+V\frac{f(A)+f(B)}{2}V^*\right\}. \end{align*} $$

If furthermore $f(t)$ is monotone, then we can take $U=V$ .

Theorem 1.2 is a major improvement of the classical trace inequality of von Neumann (around 1920),

$$ \begin{align*}{\mathrm{Tr\,}}f\left(\frac{A+B}{2}\right) \le {\mathrm{Tr\,}}\frac{f(A)+f(B)}{2}, \end{align*} $$

which entails the following trivial extension of Proposition 1.1.

Proposition 1.3 Let $f(t)$ be a convex function defined on the interval $[a,b]$ , and let $A,B\in \mathbb {M}_n^{s.a}$ with spectra in $[a,b]$ . Then,

$$ \begin{align*}{\mathrm{Tr\,}}f\left(\frac{A+B}{2}\right)\ \le {\mathrm{Tr\,}}\int_0^1 f((1-x)A+xB)\, {\mathrm{d}}x\le {\mathrm{Tr\,}}\frac{f(A)+f(B)}{2}. \end{align*} $$

What about matrix versions of the equivalent scalar inequalities (1.2) and (1.3)? There is no hope for (1.3): in general, the trace inequality

$$ \begin{align*}{\mathrm{Tr}\,} f(P) + {\mathrm{Tr}\,} f(Q) \le {\mathrm{Tr}\,} f(S) + {\mathrm{Tr\,}} f(T) \end{align*} $$

does not hold for all Hermitian matrices $P,Q,S,T$ with spectra in $[a,b]$ such that

$$ \begin{align*}P\le S\le T \le Q, \quad P+Q=S+T. \end{align*} $$

In the matrix setting, (1.2) and (1.3) are not equivalent. This paper aims to establish two matrix versions of the extremal inequality (1.2). Doing so, we will obtain several new matrix inequalities.

For an operator convex functions $h(t)$ on $[a,b]$ , and $A,B\in \mathbb {M}_n^{s.a}$ with spectra in this interval, the matrix version of (1.2) (as well as Proposition 1.1) obviously holds,

(1.4) $$ \begin{align} h((1-x)A+xB) +h(xA +(1-x)B) \le h(A) + h(B), \end{align} $$

for any $0<x<1$ . Our results hold for much more general convex/concave functions and have applications to eigenvalue inequalities that cannot be derived from (1.4), even in the case of the simplest operator convex/concave function $h(t)=t$ .

We often use a crucial assumption: our functions are defined on the positive half-line, and we deal with positive semidefinite matrices. In the matrix setting, the interval of definition of a function may be quite important; for instance, the class of operator monotone functions on the whole real line reduces to affine functions.

2 The sums property for matrices

For concave functions, the inequality (1.2) is reversed. Here is the matrix version. An isometry $U\in \mathbb {M}_{2n,n}$ means a $2n\times n$ matrix such that $U^*U=I$ , the identity of $\mathbb {M}_n$ .

Theorem 2.1 Let $A, B\in \mathbb {M}_{n}^+$ , let $0<x<1$ , and let $f(t)$ be a monotone concave function on $[0,\infty )$ with $f(0)\ge 0$ . Then, for some isometry matrices $U,V\in \mathbb {M}_{2n,n}$ ,

$$ \begin{align*}f(A)\oplus f(B) \le Uf((1-x)A+xB)U^* + Vf(xA+(1-x)B)V^*. \end{align*} $$

Proof Let $x=\sin ^2 \theta $ , $1-x=\cos ^2\theta $ , consider the unitary Hermitian matrix

$$ \begin{align*}R:=\begin{bmatrix} \sqrt{1-x} I& \sqrt{x}I\\ \sqrt{x}I& -\sqrt{1-x} I \end{bmatrix}, \end{align*} $$

and note the unitary congruence

(2.1) $$ \begin{align} R \begin{bmatrix} A & 0 \\ 0 & B \end{bmatrix}R= \begin{bmatrix} (1-x)A+xB & \star \\ \star & xA+(1-x)B \end{bmatrix}, \end{align} $$

where the stars hold for unspecified entries.

Now, recall the decomposition [Reference Bourin and Lee6, Lemma 3.4]: given any positive semidefinite matrix $\begin {bmatrix} C & X \\ X^* & D \end {bmatrix}$ partitioned in four blocks in $\mathbb {M}_n$ , we have

$$ \begin{align*}\begin{bmatrix} C & X \\ X^* & D \end{bmatrix} = U_0\begin{bmatrix} C & 0 \\ 0 & 0 \end{bmatrix} U_0^*+ V_0 \begin{bmatrix} 0 & 0 \\ 0 & D \end{bmatrix} V_0^*, \end{align*} $$

for some unitary matrices $U_0,V_0\in \mathbb {M}_{2n}$ . Applying this to (2.1), we obtain

(2.2) $$ \begin{align} \begin{bmatrix} A & 0 \\ 0 & B\end{bmatrix} = U_1\begin{bmatrix} (1-x)A+xB & 0 \\ 0 & 0 \end{bmatrix} U_1^*+ V_1 \begin{bmatrix} 0 & 0 \\ 0 & xA+(1-x)B \end{bmatrix} V_1^* , \end{align} $$

for two unitary matrices $U_1,V_1\in \mathbb {M}_{2n}$ .

Next, recall the subadditivity inequality [Reference Bourin and Lee6, Theorem 3.1]: given any pair of positive semidefinite matrices $S,T\in \mathbb {M}_d$ , we have

$$ \begin{align*}f(S+T) \le U_2f(S)U_2^* + V_2f(T)V_2^*, \end{align*} $$

for two unitary matrices $U_2,V_2\in \mathbb {M}_{d}$ . Applying this to (2.2) yields

$$ \begin{align*}\begin{bmatrix} f(A) & 0 \\ 0 & f(B)\end{bmatrix} &\le U\begin{bmatrix} f((1-x)A+xB) & 0 \\ 0 & f(0)I \end{bmatrix} U^*\\ & \quad + V \begin{bmatrix} f(0)I & 0 \\ 0 & f(xA+(1-x)B) \end{bmatrix} V^* , \end{align*} $$

for two unitary matrices $U,V\in \mathbb {M}_{2n}$ . This proves the theorem when $f(0)=0$ .

To derive the general case, we may assume that $f(t)$ is continuous (a concave function on $[0,\infty )$ might be discontinuous at $0$ ). Indeed, it suffices to consider the values of $f(t)$ on a finite set, the union of the spectra of the four matrices A, B, $(1-x)A+xB$ , and $xA+(1-x)B$ . Hence, we may replace $f(t)$ by a piecewise affine monotone concave function $h(t)$ with $h(0)\ge 0$ . Now, because $h(t)$ is continuous, a limit argument allows us to suppose that A and B are invertible. Therefore, letting $\lambda _n^{\downarrow }(Z)$ denote the smallest eigenvalue of $Z\in \mathbb {M}_n^{s.a}$ ,

$$ \begin{align*}r:=\min\{\lambda_n^{\downarrow}(A), \lambda_n^{\downarrow}(B)\}>0. \end{align*} $$

We may then replace $h(t)$ by $h_r(t)$ defined as $h_r(t):=h(t)$ for $t\ge r$ , $h_r(0):=0$ , and $h_r(s):=h(r)\frac {s}{r}$ , for $0\le s\le r$ . The function $h_r(t)$ is monotone concave on $[0,\infty )$ and vanishes at $0$ ; thus, the case $f(0)=0$ entails the general case.▪

Let $\lambda _j^{\downarrow }(Z)$ , $j=1,2,\ldots , n$ , denote the eigenvalues of $Z\in \mathbb {M}_n^{s.a}$ arranged in the nonincreasing order.

Corollary 2.2 Let $A, B\in \mathbb {M}_{n}^+$ , let $0<x<1$ , and let $f(t)$ be a nonnegative concave function on $[0,\infty )$ . Then, for $j=0,1,\ldots , n-1$ ,

$$ \begin{align*}\lambda_{1+2j}^{\downarrow}\left(f(A\oplus B)\right) \le \lambda_{1+j}^{\downarrow}\left(f(xA+(1-x)B) \right) + \lambda_{1+j}^{\downarrow}\left(f((1-x)A+xB)\right), \end{align*} $$

and

$$ \begin{align*}\lambda_{1+j}^{\downarrow}\left\{\left(f(xA+(1-x)B) \right) + \left(f((1-x)A+xB)\right)\right\} \le 2\lambda_{1+j}^{\downarrow}\left(f\left(\frac{A+B}{2}\right) \right). \end{align*} $$

Proof The first inequality is a straightforward consequence of Theorem 2.1 combined with the inequalities of Weyl [Reference Bhatia2, p. 62]: for all $S,T\in \mathbb {M}_d^{s.a}$ and $j,k\in \{0,\ldots , d-1\}$ such that $j+k+1\le d$ ,

$$ \begin{align*}\lambda_{1+j+k}^{\downarrow}(S+T) \le \lambda_{1+j}^{\downarrow}(S) + \lambda_{1+k}^{\downarrow}(T). \end{align*} $$

The second inequality is not new; it follows from Theorem 1.2.▪

Corollary 2.3 Let $A, B\in \mathbb {M}_{n}^+$ , let $0<x<1$ , and let $f(t)$ be nonnegative concave function on $[0,\infty )$ . Then, for all $p\ge 1$ ,

$$ \begin{align*}\left(\|f(A)\|_p^p + \|f(B)\|_p^p\right)^{1/p} \le \|f(xA+(1-x)B)\|_p+ \|f((1-x)A+xB)\|_p. \end{align*} $$

Proof From Theorem 2.1, we have

$$ \begin{align*}\|f(A)\oplus f(B)\|_p \le \|Uf((1-x)A+xB)U^* + Vf(xA+(1-x)B)V^*\|_p. \end{align*} $$

The triangle inequality for $\|\cdot \|_p$ completes the proof.▪

Corollary 2.3 with $f(t)=t^q$ reads as the following trace inequality.

Corollary 2.4 Let $A, B\in \mathbb {M}_{n}^+$ and $0<x<1$ . Then, for all $p\ge 1\ge q\ge 0$ ,

$$ \begin{align*}\left\{{\mathrm{Tr\,}}A^{pq} + \mathrm{Tr\,}B^{pq}\right\}^{1/p} \le \left\{{\mathrm{Tr\,}}(xA+(1-x)B)^{pq}\right\}^{1/p}+ \left\{{\mathrm{Tr\,}}((1-x)A+xB)^{pq}\right\}^{1/p}. \end{align*} $$

Choosing in Corollary 2.4 $q=1$ and $x=1/2$ yields McCarthy’s inequality,

$$ \begin{align*}{\mathrm{Tr\,}}A^{p} +{\mathrm{Tr\,}}B^{p} \le {\mathrm{Tr\,}}(A+B)^{p}.\end{align*} $$

This shows that Theorem 2.1 is already significant with $f(t)=t$ . Our next corollary, for convex functions, is equivalent to Theorem 2.1.

Corollary 2.5 Let $A, B\in \mathbb {M}_{n}^+$ , let $0<x<1$ , and let $g(t)$ be a monotone convex function on $[0,\infty )$ with $g(0)\le 0$ . Then, for some isometry matrices $U,V\in \mathbb {M}_{2n,n}$ ,

$$ \begin{align*}g(A)\oplus g(B) \ge Ug((1-x)A+xB)U^* + Vg(xA+(1-x)B)V^*. \end{align*} $$

Because the Schatten q-quasinorms $\|\cdot \|_q$ , $0<q<1$ , are superadditive functionals on $\mathbb {M}_n^+$ (see [Reference Bourin and Hiai4, Proposition 3.7] for a stronger statement), Corollary 2.5 yields the next one.

Corollary 2.6 Let $A, B\in \mathbb {M}_{n}^+$ , let $0<x<1$ , and let $g(t)$ be a nonnegative convex function on $[0,\infty )$ with $g(0)\le 0$ . Then, for all $0<q<1$ ,

$$ \begin{align*}\left(\|g(A)\|_q^q+ \|g(B)\|_q^q\right)^{1/q} \ge \|g(xA+(1-x)B)\|_q+ \|g((1-x)A+xB)\|_q. \end{align*} $$

From the first inequality of Corollary 2.2, we also get the following statement.

Corollary 2.7 Let $A, B\in \mathbb {M}_{n}^+$ , and let $f(t)$ be a nonnegative concave function on $[0,\infty )$ . Then, for $j=0,1,\ldots , n-1$ ,

$$ \begin{align*}\lambda_{1+2j}^{\downarrow}\left(f(A\oplus B)\right) \le 2\int_{0}^1 \lambda_{1+j}^{\downarrow}\left(f(xA+(1-x)B) \right) \,{\mathrm{d}}x. \end{align*} $$

Up to now, we have dealt with convex combinations $(1-x)A +xB$ with scalar weights. It is natural to search for extensions with matricial weights ( $C^*$ -convex combinations). We may generalize Theorem 2.1 with commuting normal weights.

Theorem 2.8 Let $A, B\in \mathbb {M}_{n}^+$ , and let $f(t)$ be a monotone concave function on $[0,\infty )$ with $f(0)\ge 0$ . If $X,Y\in \mathbb {M}_n$ are normal and satisfy $XY=YX$ and $X^*X+Y^*Y=I$ , then, for some isometry matrices $U,V\in \mathbb {M}_{2n,n}$ ,

$$ \begin{align*}f(A)\oplus f(B) \le Uf(X^*AX+Y^*BY)U^* + Vf(Y^*AY+X^*BX)V^*. \end{align*} $$

Proof The proof is quite similar to that of Theorem 2.1 except that we first observe that the $2n\times 2n$ matrix

$$ \begin{align*}H:=\begin{bmatrix} X & Y \\ Y & -X \end{bmatrix}, \end{align*} $$

is unitary. Indeed, for two normal operators, $XY=YX$ ensures $X^*Y=YX^*$ and a direct computation shows that $H^*H$ is the identity in $\mathbb {M}_{2n}$ . We then use the unitary congruence

(2.3) $$ \begin{align} H^* \begin{bmatrix} A & 0 \\ 0 & B \end{bmatrix}H= \begin{bmatrix} X^*AX+Y^*BY & \star \\ \star & Y^*AY+X^*BX \end{bmatrix}, \end{align} $$

where the stars hold for unspecified entries.▪

Hence, in the first inequality of Corollary 2.2 and in the series of Corollaries 2.3–2.6, we can replace the scalar convex combinations $(1-x)A+B$ and $xA+(1-x)B$ by $C^*$ -convex combinations $X^*AX+Y^*BY$ and $Y^*AY + X^*BX$ with commuting normal weights. Here, we explicitly state the generalization of Corollary 2.5.

Corollary 2.9 Let $A, B\in \mathbb {M}_{n}^+$ , and let $g(t)$ be a monotone convex function on $[0,\infty )$ with $g(0)\le 0$ . If $X,Y\in \mathbb {M}_n$ are normal and satisfy $XY=YX$ and $X^*X+Y^*Y=I$ , then, for some isometry matrices $U,V\in \mathbb {M}_{2n,n}$ ,

$$ \begin{align*}g(A)\oplus g(B) \ge Ug(X^*AX+Y^*BY)U^* + Vg(Y^*AY+X^*BX)V^*. \end{align*} $$

3 Majorization

The results of Section 2 require two essential assumptions: to deal with positive matrices and with subadditive (concave) or superadditive (convex) functions. Thanks to these assumptions, we have obtained operator inequalities for the usual order in the positive cone.

The results of this section will consider Hermitian matrices and general convex or concave functions. We will obtain majorization relations. We also consider $C^*$ -convex combinations more general than those with commuting normal weights.

We recall the notion of majorization. Let $A,B\in \mathbb {M}_n^{s.a}$ . We say that A is weakly majorized by B, and we write $A\prec _{w}B$ , if

$$ \begin{align*}\sum_{j=1}^k\lambda_j^{\downarrow}(A) \le \sum_{j=1}^k\lambda_j^{\downarrow}(B), \end{align*} $$

for all $k=1,2,\ldots , n$ . If furthermore the equality holds for $k=n$ , that is, A and B have the same trace, then we say that A is majorized by B, written $A\prec B$ . See [Reference Bhatia2, Chapter 2], [Reference Hiai9] for a background on majorization. One easily checks that $A\prec _wB$ is equivalent to $A+C\prec B$ for some $C\in \mathbb {M}_n^+$ . We need two fundamental principles:

1. (1) $A\prec B \Rightarrow g(A) \prec _w g(B)$ for all convex functions $g(t)$ .

2. (2) $A\prec _w B \iff {\mathrm {Tr\,}} f(A) \le {\mathrm {Tr\,}} f(B) $ for all nondecreasing convex functions $f(t)$ . Equivalently, $A\prec B \iff {\mathrm {Tr\,}} g(A) \le {\mathrm {Tr\,}} g(B) $ for all convex functions $g(t)$ .

Lemma 3.1 Let $A, B\in \mathbb {M}_{n}^{s.a}$ , and let $g(t)$ be a convex function defined on an interval containing the spectra of A and B. If $X,Y\in \mathbb {M}_n$ satisfy $X^*X+Y^*Y=XX^*+YY^*=I$ , then

$$ \begin{align*}{\mathrm{Tr\,}}\left\{g(X^*AX+Y^*BY)+g(Y^*AY+X^*BX)\right\}\le {\mathrm{Tr\,}} \left\{g(A)+g(B)\right\}. \end{align*} $$

Proof By the famous Hansen–Pedersen trace inequality [Reference Hansen and Pedersen8] (see also [Reference Bourin and Lee6, Corollary 2.4] for a generalization),

$$ \begin{align*} {\mathrm{Tr\,}}&\left\{g(X^*AX+Y^*BY)+g(Y^*AY+X^*BX)\right\} \\ &\le {\mathrm{Tr\,}}\left\{X^*g(A)X+Y^*g(B)Y)+Y^*g(A)Y+X^*g(B)X\right\} \\ &= {\mathrm{Tr\,}}\left\{(g(A) + g(B))(XX^* +YY^*)\right\}= {\mathrm{Tr\,}} \left\{g(A)+g(B)\right\}, \end{align*} $$

where the first equality follows from the cyclicity of the trace. ▪

Theorem 3.2 Let $A, B\in \mathbb {M}_{n}^{s.a}$ and $X,Y\in \mathbb {M}_n$ . If $X^*X+Y^*Y=XX^*+YY^*=I$ , then, for some unitary matrices $\{U_k\}_{k=1}^{2n}$ in $\mathbb {M}_{2n}$ ,

$$ \begin{align*}(X^*AX+Y^*BY)\oplus (Y^*AY+X^*BX) =\frac{1}{2n}\sum_{k=1}^{2n} U_k (A\oplus B)U_k^*. \end{align*} $$

Proof From Lemma 3.1, we have the trace inequality

$$ \begin{align*}{\mathrm{Tr\,}}g\left((X^*AX+Y^*BY)\oplus (Y^*AY+X^*BX) \right)\le {\mathrm{Tr\,}}g(A\oplus B), \end{align*} $$

for all convex functions defined on $(-\infty ,\infty )$ . By a basic principle of majorization, this is equivalent to

(3.1) $$ \begin{align} (X^*AX+Y^*BY)\oplus (Y^*AY+X^*BX) \prec A\oplus B. \end{align} $$

By [Reference Bourin and Lee7, Proposition 2.6], the majorization in $\mathbb {M}_d^{s.a}$ , $S\prec T$ , ensures that (and thus is equivalent to)

$$ \begin{align*}S\le \frac{1}{d} \sum_{j=1}^d V_jTV_j^*, \end{align*} $$

for d unitary matrices $V_j\in \mathbb {M}_d$ . Applying this to (3.1) completes the proof.▪

Remark 3.3 We can prove the majorization (3.1) in a different way by observing that our assumption on X and Y ensures that the map $\Phi $ , defined on $\mathbb {M}_{d}$ (here $d=2n$ ),

$$ \begin{align*}\Phi \left(\begin{bmatrix} A&C \\ D&B\end{bmatrix}\right):=\begin{bmatrix}X^*AX+Y^*BY&0 \\ 0&Y^*AY+X^*BX\end{bmatrix}, \end{align*} $$

is a positive linear map unital and trace preserving. Such maps are also called doubly stochastic. It is a classical result (see Ando’s survey [Reference Ando1, Section 7] and the references therein) that we have

(3.2) $$ \begin{align} \Phi(Z) \prec Z, \end{align} $$

for every doubly stochastic map on $\mathbb {M}_d$ and Hermitian Z. Here, our map is even completely positive (it is a so-called doubly stochastic map, or a unital quantum channel). It is well known in the literature [Reference Ando1, Theorem 7.1] that we have then

$$ \begin{align*}\Phi(Z)=\sum_{j=1}^{m} t_j U_j^* ZU_j, \end{align*} $$

for some convex combination $0<t_j\le 1$ , $\sum _{j=1}^{m} t_j=1$ , and some unitary matrices $U_j$ (these scalars $t_i$ and matrices $U_i$ depend on Z). In 2003, Zhan [Reference Zhan14] noted that we can take $m=d$ . That we can actually take an average,

$$ \begin{align*}\Phi(Z)=\frac{1}{d}\sum_{j=1}^{d} U_j^* ZU_j, \end{align*} $$

follows from the quite recent observation [Reference Bourin and Lee7, Proposition 2.6] mentioned in the proof of Theorem 3.2. For unital quantum channels, one has the Choi–Kraus decomposition (see [Reference Bhatia3, Chapter 3])

$$ \begin{align*}\Phi(A) =\sum_{i=1}^{d^2} K_iAK_i^* , \end{align*} $$

for some weights $K_i\in \mathbb {M}_d$ such that $\sum _{i=1}^{d^2} K_iK_i^*=\sum _{i=1}^{d^2} K_i^*K_i=I$ . So, the proof of Lemma 3.1 shows that, for unital quantum channels, one may derive the fundamental majorization (3.2) from two results for convex functions: the basic principle of majorization and Hansen–Pedersen’s trace inequality.

Theorem 3.2 combined with a variation of Theorem 1.2 [Reference Bourin and Lee6, Corollary 2.4] provides a number of interesting operator inequalities. The next corollary can be regarded as another matrix version of the scalar inequality (1.2). We will give a proof independent of [Reference Bourin and Lee6, Corollary 2.4].

Corollary 3.4 Let $A, B\in \mathbb {M}_n^{s.a}$ , and let $f(t)$ be a convex function defined on an interval containing the spectra of A and B. If $X,Y\in \mathbb {M}_n$ satisfy $X^*X+Y^*Y=XX^*+YY^*=I$ , then, for some unitary matrices $\{U_k\}_{k=1}^{2n}$ in $\mathbb {M}_{2n}$ ,

$$ \begin{align*}f\left(X^*AX+Y^*BY\right)\oplus f\left(Y^*AY+X^*BX \right) \le\frac{1}{2n}\sum_{k=1}^{2n} U_k f\left(A\oplus B\right)U_k^*. \end{align*} $$

In particular, for the absolute value, we note that

$$ \begin{align*}\left|X^*AX+Y^*BY\right|\oplus \left|Y^*AY+X^*BX \right| \le\frac{1}{2n}\sum_{k=1}^{2n} U_k \left|A\oplus B\right|U_k^*. \end{align*} $$

Proof The majorization (3.1) and the basic principle of majorizations show that

$$ \begin{align*}f\left(X^*AX+Y^*BY\right)\oplus f\left(Y^*AY+X^*BX \right) \prec_w f(A\oplus B), \end{align*} $$

for all convex functions defined on an interval containing the spectra of A and B. Thus,

$$ \begin{align*}f\left(X^*AX+Y^*BY\right)\oplus f\left(Y^*AY+X^*BX \right) +C \prec f(A\oplus B), \end{align*} $$

for some positive semidefinite matrix $C\in \mathbb {M}_{2n}^+$ . Hence, as in the previous proof,

$$ \begin{align*}f\left(X^*AX+Y^*BY\right)\oplus f\left(Y^*AY+X^*BX \right) +C \le \frac{1}{2n}\sum_{k=1}^{2n} U_k f\left(A\oplus B\right)U_k^*, \end{align*} $$

for some family of unitary matrices $U_k\in \mathbb {M}_{2n}$ .▪

Corollary 3.5 Let $A, B\in \mathbb {M}_n^+$ . If $X,Y\in \mathbb {M}_n$ satisfy $X^*X+Y^*Y=XX^*+YY^*=I$ , then

$$ \begin{align*}\det(X^*AX+Y^*BY)\det (Y^*AY+X^*BX) \ge \det A\det B. \end{align*} $$

The case $A=B$ and $X,Y$ are two orthogonal projections reads as the classical Fisher’s inequality.

Corollary 3.4 yields inequalities for symmetric norms and antinorms on $\mathbb {M}_{2n}^+$ . Symmetric norms, $\|\cdot \|$ , also called unitarily invariant norms, are classical objects in matrix analysis. We refer to [Reference Bhatia2, Reference Hiai9], [Reference Hiai and Petz10, Chapter 6], and, in the setting of compact operators, [Reference Simon13]. The most famous examples are the Schatten p-norms, $1\le p\le \infty $ , and the Ky Fan k-norms.

Symmetric anti-norms $\|\cdot \|_!$ are the concave counterpart of symmetric norms. Famous examples are the Schatten q-quasi norms, $0<q<1$ , and the Minkowski functional considered in the proof of Corollary 3.5. We refer to [Reference Bourin and Hiai4], [Reference Bourin and Hiai5, Section 4] for much more examples.

We close this section by mentioning Moslehian’s weak majorization which provides a matrix version of the first inequality of Proposition 1.1. We may restate [Reference Moslehian11, Corollary 3.4] as inequalities for symmetric and antisymmetric norms.