Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-11T15:26:06.130Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermonuclear gain and parameters of fast ignition ICF-targets

Published online by Cambridge University Press:  07 June 2005

S. YU. GUS'KOV
S. YU. GUS'KOV
Affiliation:
P.N. Lebedev Physical Institute of the Russian Academy of Sciences, Moscow, Russia
Rights & Permissions [Opens in a new window]

Abstract

The requirements of matching shell ICF target parameters, parameters of compressing, and triggering drivers under direct (fast) ignition are developed. Thin shell target, which represents a shell-ablator with a DT-ice layer, frosted on the inner surface of the shell are considered. Design of a target which ensures the energy supply from the triggering driver to the central part of thermonuclear fuel, in both spherical and cylindrical geometry is developed. Spherical target is furnished with one or two conical channels for the injection of the triggering driver radiation. The ends of the cylindrical target are protected by heavy material walls that have the holes of the radius equal to the final radius of compressed fuel. It was found that the parameters of fast ignition spherical and cylindrical targets, which provide high thermonuclear gain of 500–2000 in the range of the compressing driver energy of 1–10 MJ, may be matched with the drivers parameters at low aspect ratios of the targets, 10–20. The operation of spherical targets at the moderate radius convergence ratio of 15–20, may be provided at the triggering driver energy not higher than 30 kJ. The operation of cylindrical target with spin-oriented DT-fuel at radius convergence ratio of 20–25 may be provided at 150–200 kJ of the triggering driver energy.

Keywords

DriverIgnitionShell targetSpin-oriented fuelThermonuclear gain
Type
Research Article
Information
Laser and Particle Beams , Volume 23 , Issue 2 , June 2005 , pp. 255 - 260
Copyright
2005 Cambridge University Press

1. INTRODUCTION

This work presents a self-similar theory of compression, heating, and burning processes in the inertial fusion spherical, and cylindrical targets under direct (fast) ignition (Basov et al., 1991, 1992; Tabak et al., 1994; Caruso, 1995). The theory was developed for two-layer thin shell target, which represents a shell-ablator with a DT-ice layer frosted onto the inner surface of the shell. Advanced technologies of production of the high gain targets of such a type were developed (see, for example, Borisenko et al., 2003). It is expected that the target design ensures the energy supply from the triggering driver to the central part of thermonuclear fuel of a given mass, and at the same time, allows one to perform a symmetrical radial compression of the target by the compressing driver. In a spherical geometry such a target may be furnished with one or two conical channels for the injection of the triggering driver radiation. A cylindrical target was proposed to be constructed to provide the suppression of the plasma expansion along the direction of target axis. The ends of such a target are protected by the walls which are made of a heavy material and have the holes of the radius equal to the final radius of compressed fuel.

2. THERMONUCLEAR GAIN OF FAST IGNITION TARGET

For effective burning of fast ignition target, the action of compressing and triggering drivers should result in the following plasma parameters. If we assume that the target with DT fuel reaches, for definiteness sake, a central ignition, the product ρb × Rb of the density and size of all the thermonuclear fuel should be sufficiently high, and, at least, exceed the value of 1 g/cm2. Then within the region of primary ignition, the conditions should be provided for the initiation of the thermonuclear burning wave, that is, the plasma temperature must exceed 5 keV, and the parameter ρig × Rig–0.3 g/cm2.

The internal energy of cold compressed fuel Ec and primary ignition region Eig are

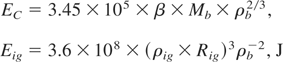
here, Mb and ρb are the mass and density of the compressed fuel, β is the degree of degeneration. According to (1), for the effectively burning fast ignition targets with ρb × Rb >1 g/cm2 and ρb > 100 g/cm3, it is correct that Ec > Eig. The transfer of the compressing driver energy Ecd and the triggering driver energy Eid into the plasma intrinsic energy proceeds with a certain efficiency: Ec = ηcdEcd, Eig = ηidEid. The efficiency of transfer of the compressing driver energy is conditioned by the driver radiation absorption efficiency ηab = Eab /Eid and the efficiency of conversion of the absorbed energy Eab into the intrinsic energy of a thermonuclear plasma. The last value is defined by ηh, the hydrodynamic efficiency of the target compression, and ηt, the efficiency of energy conversion into the intrinsic energy of thermonuclear plasma. ηh = Eh /Eab is the ratio between the kinetic energy of the part of the target moving to the centre and the absorbed energy. ηt = Ep /Eh is the ratio between the intrinsic energy of the thermonuclear plasma and the kinetic energy of the non-evaporated part of shell.

So, for the compressing driver we have ηd = ηabηhηt. The values of the mentioned efficiencies of energy conversion are as follows (Afanas'ev & Gus'kov, 1993): for the first three harmonics of an Nd-laser of the intensity of 1013–1014 W/cm2: ηab = 0.6–0.8; ηh = 0.1–0.4; ηt = 0.5–0.7. So, ηd = 0.05–0.15. Following the predictions of Hatchett et al. (2000), Gus'kov (2001), and Mulser & Bauer (2004), the efficiency of the triggering driver energy conversion can reach ηid = 0.2–0.3.

So, for the fast ignition targets with high gain we have not only Ec > Eig, but Ecd >> Eid, and, hence, the thermonuclear gain is the ratio between fusion energy Ef and energy Ecd

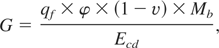
here qf = 3.34 × 1011 J/g is the fusion energy released in one gram of DT fuel; ν, the relative fuel mass losses through input holes; φ, the degree of thermonuclear matter burning in the fusion reactions. According to Andreev et al. (2002) the expression for φ, generalized to the case of a cylindrical target is

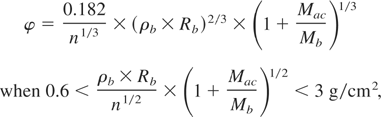
where for a cylindrical and spherical targets n = 2,3, correspondingly, and Mac = μ × Mao is the mass of ablator-shell at the moment of maximal compression, Ma0 is the initial ablator shell mass.

On the base (1), (2) and (3) we get for the gain coefficient

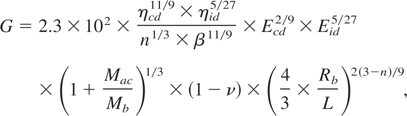
here: L is the length of a cylindrical target; drivers' energy expressed in J here and farther.

One can expect that the design of the input channel in a spherical target may allow to make the fuel mass loses ν insignificant. For cylindrical target when input hole of edge wall has a same radius as compressed fuel radius, Rb, the fuel mass losses may be estimated as

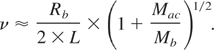
Taking into account the second factor of gain coefficient dependence on cylindrical target length, G ∝ (Rb /L)2/9, the target length corresponding to the maximal gain equals

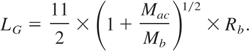
The maximal length of a cylindrical target under point-like ignition is defined from the condition that during the confinement time all fuel will be involved by burning wave

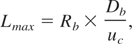
here Db is the velocity of a thermonuclear burning wave and uc is the velocity of target compression toward the centre.

As a result an optimal length of a cylindrical target makes Lopt = min(LG,Lmax). At the low-entropy compression the shell velocity constitutes about uc ∼ (0.5–1)107 cm/s, the velocity of thermonuclear burning wave, Db ∼ (2–3) 108 cm/s; the mass ratio Mac /Mb changes within the range of 3–8, so, Lmax ≈ (20–30) Rb, LG ≈ (10–15) Rb. From this follows that under radius convergence ratio R0 /Rb ≈ 20–40 (R0 is the initial target radius), the optimal length of a cylindrical fast ignition target makes (0.5–0.3) R0. One can expect the gain of such a target will be smaller than spherical target one by not more than 2–2.5 times. According to (1), for ρbRb > 1 g/cm2, ηcd = 0.1, ηcd = 0.3 and Eid = 30–50 kJ the high gain bottom boundary of the compressing driver energy for a spherical target makes 0.5–1 MJ. For a cylindrical target that value in the ratio L/Rb is greater, and for target of optimal length is about 5–10 MJ.

Figure 1 illustrates the dependence of the thermonuclear gain of a spherical fast ignition target on the compressing driver energy at the different triggering driver energies. The efficiencies of drivers energy transfer were taken as ηcd = 0.07 and ηid = 0.3. For comparison, the figure shows also the data on the gain of spherical targets with hydrodynamic “spark ignition,” namely, the direct driven thin shell target from (Rozanov et al., 1995) and “laser greenhouse” target (Gus'kov et al., 2003.). The data show that the thermonuclear gain of fast ignition target exceeds by 5–10 times the gain of hydrodynamically ignited targets

Thermonuclear gain vs. compressing driver energy. The curves I1, I2, I3 attributed to spherical fast ignition target at triggering driver energies 10, 20 and 50 kJ, respectively; curves Ho and Hp–“optimistic” and “pessimistic” predictions for direct driven shell target; point LGH–“laser greenhouse” target.

3. LOW-ENTROPY COMPRESSION OF A SHELL TARGET

Target compression under the action of a laser pulse with a constant intensity Icd and duration τcd is described by a model of ablative-driven acceleration of the shell and the model of adiabatic compression (Afanas'ev & Gus'kov, 1993) at the initial entropy introduced in compressed matter by a shock wave initiated by the ablation pressure. The absorption of laser radiation of relatively low intensity, corresponding to low-entropy compression, due to the bremsstrahlung mechanism.

3.1. Ablation acceleration of the shell

The analytical solution for the shell velocity and mass generalized to the case of the target cylindrical geometry is

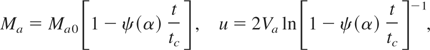
where the time of shell motion to the centre (compression time) tc, final shell velocity uc expressed through the matter velocity at a critical density region Va are

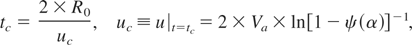
where

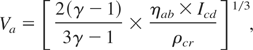
and the function ψ of the dimensionless parameter of the task, the acceleration parameter α, have the form

Here A and z are the atomic number and the mean ion charge of the evaporated matter, correspondingly; γ, adiabatic exponent; λ, the radiation wavelength of the compressing driver in micrometers; Δa and ρa0, the initial thickness and density of the ablator-shell, correspondingly.

From this one can find the hydrodynamic efficiency

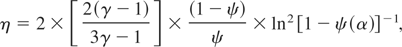
which presents a non-monotonic function of the parameter α, and its maximum for both geometries of the shell makes approximately 0.43. Under the variation of the parameter α, the final velocity and mass of the cylindrical shell changes faster (the velocity grows, and the mass drops) than in the case of a spherical shell. As a consequence, in a cylindrical shell the hydrodynamic efficiency reaches its maximum at αm = 1.8, and shell mass completely evaporates at αev = 3 (the values by 1.5 times smaller than in the case of a spherical shell (αm = 2.7 and αev = 4 .5)). The reason is that the surface area of a cylindrical shell decreases with a decrease in the radius more slowly (S ∝ R), than the surface area of a spherical one (S ∝ R2). So, the average surface area of cylindrical shell turns to be greater than for a spherical one, and it ensures more effective acceleration and evaporation.

3.2. Target compression

The state of compressed target is stipulated by the condition of equal pressure in the ablator-shell and fuel, as well as the condition of transfer of the shell kinetic energy into the intrinsic energy of ablator and fuel. The final fuel density ρb and energy transfer efficiency ηt are

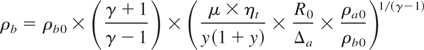
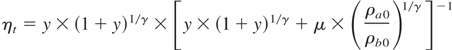
and the radius convergence ratio is

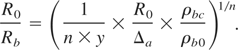
In these expressions, the fraction of the non-evaporated shell mass, μ = [1 − ψ(α)] is defined by the formula (5); y = Δb /Δa. Both the values of ρb and R0 /Rb increase with the growth of an aspect ratio R0 /Δa and the ratio between ablator and fuel masses (the decrease of the y). But that growth of convergence ratio R0 /Rb for the cylindrical target is faster as compared to spherical one. The efficiency ηt slowly decreases with the growth in the ablator and fuel masses ratio. For example, for a plastic shell and DT fuel and under a 4-fold (from 5 to 20) increase in the mass ratio (y decreases from 0.8 to 0.2) the efficiency ηt reduces from 0.6 to 0.4 at μ = 0.4 and from 0.75 to 0.58 at μ = 0.2.

4. THE TARGET AND DRIVERS PARAMETERS AT FAST IGNITION

4.1. The target shell and driver parameters

Matching of these parameters is defined by the following requirements. The laser pulse duration τcd must be equal to the compression time ts. The energy balances for triggering and compressing drivers, according to (1) with taking into account of energy transfer efficiencies and expression (8) should be used. For the targets with moderate aspect ratio R0 /Δa < 50 (acceleration parameter α << 1) it is provided (for γ = 5/3)

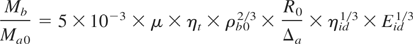
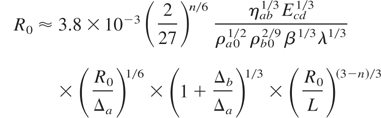
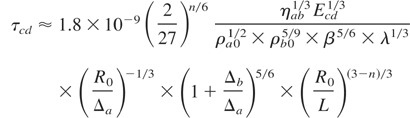
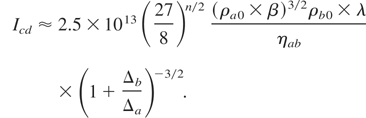
And the final velocity of matched shell is

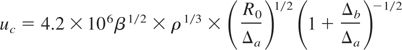
here the values of R0, τcd, Icd, and uc are measured in cm, s, W/cm2, and cm/s, respectively.

The radius of matched target grows as the aspect ratio increases and the compressing driver radiation wavelength decreases. Pulse duration of a matched compressing driver increases as the driver energy increases, and the aspect ratio and the wavelength are decreasing. The compressing driver intensity is independent of the aspect ratio and decreases with the wavelength decreasing.

Table 1 collects, calculated by (8)–(12), data of the matched target and the driver's parameters, as well as compressed thermonuclear plasma parameters and the thermonuclear gain at the compressing driver energy levels of 1 MJ and 10 MJ. The calculations were performed for a plastic shell-ablator (ρa = 1 g/cm3) and Nd-laser third harmonic radiation (λ = 0.35 μm). The only one supposition was made that the absorption efficiency had to be ηab = 0.7. The targets, which could provide the hydrodynamic efficiency of ηh = 0.2 were calculated. According to (7), the aspect ratio had to be of 17 for spherical shell and 14 for cylindrical shell, the part of the evaporated mass being of 0.4. The calculated value of the efficiency of the shell kinetic energy transformation into thermonuclear fuel internal energy for all targets was varied in a narrow range of 0.62–0.66.

Matched target and drivers parameters, as well as compressed thermonuclear plasma parameters and the thermonuclear gain under the compressing driver energy levels of 1 MJ and 10 MJ

A cylindrical target, as compared to a spherical target, has an advantages of a more simple and reliable input of triggering driver radiation into the target (Caruso & Strangio, 2001; Basko et al., 2002). But at the energy Eid ≤ 100 kJ the cylindrical target is operating at the radius convergence ratio R0 /Rb ≈ 40–50, which is 2.5–3 times greater that for the spherical target. This circumstance makes the solution of the problem of compression stability for a cylindrical target much more complicated. A decrease in the radius convergence ratio, for a cylindrical target, to the acceptable values of 20–25 may be possible at increasing energy of the triggering driver. The value of such increasing may be significantly reduced by the use of spin-oriented thermonuclear fuel. The use of spin oriented DT-fuel gives a significant profit spatially in fast ignition concept. Indeed, the fusion reaction rate of spin-oriented D and T nuclei is higher in factor 1.5 in comparison with not oriented ones. It leads to decreasing, of the value of ignition parameter ρigRig, approximately, in the same factor. Since, according (1) Eig × ρb2 ∝ (ρigRig)3 the decreasing factors for triggering driver energy and fuel density can be high enough, respectively, 3.5, and 2. So, the use of spin oriented DT-fuel gives a possibility to decrease within an wide enough range a triggering driver energy or fuel density or both of them (probably, in a different degree). In particular, the calculations show that the fast ignition cylindrical target with spin-oriented DT-fuel may provide the thermonuclear gain of 500–1000 at the radius convergence ratio of 20–25 and the triggering driver energy 150–200 kJ.

4.2. The input channel and edge wall parameters

The functionality of the spherical target input channel consists in guaranteeing the delivery of the triggering driver radiation to the compressed fuel. The channel wall should prevent the propagation of the matter flows into the channel volume under the pressure of the compressed target. The edge walls of cylindrical target must suppress the shell plasma expansion along the direction of target axis.

An important question is the limiting position of the channel apex inside the spherical target. In order to provide central triggering, it seems to be promising to place the channel apex as close to the target centre as possible. However, at the stage of target compression, the part of the channel located on the target centre closer than the compressed fuel boundary, should experience pressure of the matter with a density of several hundreds g/cm3. Such pressures can be suppressed during the time of inertial confinement only by the channel wall with the thickness comparable to the initial radius of the target. So, it seems to be very difficult to locate the end part of the channel in the area of the thermonuclear matter location. Thus, the most practical way to solve this problem is to reduce the location of the channel apex by the final radius of thermonuclear matter, and for all the triggering drivers this assumes, beside the ion beam, the edge initiation of the thermonuclear burning wave. In this case, the design of the channel must ensure the impediment of the matter expansion into the channel at the stage of the shell acceleration. The shock wave velocity in the channel wall is expressed through the shell velocity in the following form

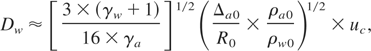
here ρw0 and γw are respectively, the density and the adiabatic exponent of the channel wall matter.

From this the minimal thickness of the channel wall (Δw = Dw × τc) and the energy losses in the channel with relation to the energy of the accelerated shell we get

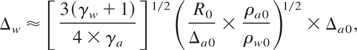
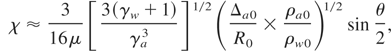
here θ is the cone angle and sinθ/2 ≈ Δw /Δa + Rb. Calculations show that θ lies in the range of 60–80 degrees.

At the limitation of the thermonuclear mass loss by the value of (5–10)% such a design of the channel provides the possibility to have the radius of apex hole equal to 2–3 of the triggering beam radius. The formulas (13) and (14) with the coefficient accuracy up to 1 is just for the edge walls of the cylindrical target. As far as the energy losses in the edge walls are concerned, they are given by expression (15) at sin θ/2 = 1, multiplied by factor of R0 /L. The smaller is the ratio between the densities of the ablator shell and the channel wall, the smaller are the wall thickness and the energy losses. When the wall density essentially exceeds the shell density, for example, by 20, then for the shell with an aspect ratio of 15–20 wall thickness is close to the target shell thickness, 100–300 μm. The energy losses in spherical target channel are 3–5% of shell energy. In cylindrical target with optimal length the energy losses in edge walls is 10–20 % and the mass losses through the holes with radius equal to compressed fuel radius is, approximately, 18%.

5. CONCLUSION

The parameters of fast ignition spherical and cylindrical targets which provide high gain of 500–2000 in the range of compressing driver energy 1–10 MJ may be matched with drivers parameters at low shell aspect ratios, 10–20. Pulse duration and intensity of compressing driver should vary within the ranges of (50–350) ns and (1–2) 1013 W/cm2.

The operation of spherical targets at the moderate radius convergence ratio of 15–20, may be provided at the triggering driver energy not higher than 30 kJ. The cylindrical target operation at the moderate radius convergence ratio would require significantly higher energy of the triggering driver. That energy may be reduced by use a spin-oriented DT-fuel. The operation of cylindrical target with spin-oriented DT-fuel at convergence ratio of 20–25 may be provided at 150–200 kJ of triggering driver energy.

ACKNOWLEDGMENTS

The work was supported by Project # B-0049 of “Basic Optics and Spectroscopy” Educational-Scientific Center and ISTC Project #2155.

Footnotes

This paper was presented at the 28th ECLIM conference in Rome, Italy.

References

REFERENCES

Afanas'ev, Yu.V. & Gus'kov, S.Yu. (1993). Energy transfer to the plasma in laser target. In Nuclear Fusion by Inertial Confinement (Velarde, G., Ed.), pp. 99–118. Ann Arbor: CRC Press.
Andreev, A.A., Gus'kov, S.Yu, Il'in D.V, Levkovskii, A.A., Rozanov, V.B., &Sherman, V.E. (2002). On the possibility of target plasma ignition under the conditions of inertial nuclear fusion. JETP 96, 695–703.Google Scholar
Basko, M.M., Churazov, M.D. & Aksenov, A.G. (2002). Prospects of heavy ion fusion in cylindrical geometry. Laser Part. Beams 20, 411–414.CrossRefGoogle Scholar
Basov, N.G., Gus'kov, S.Yu. & Feoktistov, L.P. (1991). ICF targets with direct heating of the ignitor. Proc. 21st European Conference on Laser Interaction with Matter, Warsaw, Poland, 189–191.
Basov, N.G, Gus'kov, S.Yu. & Feoktistov, L.P. (1992). Thermonuclear gain of ICF targets with direct heating of the ignitor. J. Soviet Laser Res. 13, 396–399.CrossRefGoogle Scholar
Borisenko, N.G., Akunets, A.A., Bushuev, V.S., Dorogotovtsev, V.M. & Merkuliev, Yu.A. (2003). Motivation and fabrication methods for inertial confinement fusion and inertial fusion energy targets. Laser Part. Beams 21, 505–509.Google Scholar
Caruso, A. (1995). Gain of laser compressed DT-fuel ignited by injected triggers. Proc. of I.A.E.A. Technical Committee Meeting on Drivers for Inertial Confinement Fusion, pp. 325–339. Paris, France.
Caruso, A. & Strangio, C. (2001). Studies on nonconventional high-gain target design for ICF. Laser Part. Beams 19, 295–308.CrossRefGoogle Scholar
Gus'kov, S.Yu. (2001). Direct ignition of inertial fusion targets by a laser-plasma ion stream. Quantum Electronics 31, 885–890.CrossRefGoogle Scholar
Gus'kov, S.Yu., Demchenko, N.N., Rozanov, V.B., Stepanov R.V., Zmitrenko, N.V., Caruso, A., &Strangio, C. (2003). Symmetric compression of “laser greenhouse targets” by a few laser beams. Quantum Electronics 33, 95–104.CrossRefGoogle Scholar
Hatchett, S.P., Brown, C.G., Cowan, Th.E., Henry, E.A., Johnson, J.S., Key, M.H., Koch, J.A., Langdon, A.B., Lasinski, B.F., Lee, R.W., Mackinnon, A.J., Pennington, D.M., Perry, M.D., Phillips, Th.W., Roth, M., Sangster, T.C., Singh, M.S., Snavely, R.A., Stoyer, M.A., Wilks, S.C. & Yasuike, K. (2000). Electron, photon, and ion beams from the relativistic interaction of Petawatt laser pulses with solid targets. Phys. Plasmas 7, 2076–2082.CrossRefGoogle Scholar
Mulser, P. & Bauer, D. (2004). Fast ignition of fusion pellets with superintense lasers: Concepts, problems and prospectives. Laser Part. Beams 22, 5–12.CrossRefGoogle Scholar
Rozanov, V.B., Verdon, C.P., Decroisette, M., Gus'kov, S.Yu., Lindl, J., Nakai, S., Nishihara, M. & Velarde, G. (1995). Inertial confinement target physics. In Energy from Inertial Fusion (Hogan, W., Ed.), pp. 1–64. Vienna: INEA
Tabak, M., Hammer, J., Glinsky, M.E., Kruer, W.L., Wilks, S.C., Woodworth, J., Campbell, E.M., Perry, M.D. & Mason, R.J. (1994). Ignition and high gain with ultrapowerful lasers. Phys. Plasmas 1, 1626–1634.CrossRefGoogle Scholar
Figure 0

Thermonuclear gain vs. compressing driver energy. The curves I1, I2, I3 attributed to spherical fast ignition target at triggering driver energies 10, 20 and 50 kJ, respectively; curves Ho and Hp–“optimistic” and “pessimistic” predictions for direct driven shell target; point LGH–“laser greenhouse” target.

Figure 1

Matched target and drivers parameters, as well as compressed thermonuclear plasma parameters and the thermonuclear gain under the compressing driver energy levels of 1 MJ and 10 MJ