Children’s ability to enumerate a finite set of items, rapidly and without the need to count each individual element, is believed to be a basic aspect of numerical cognition, which emerges previously to symbolic numerical representations such as Arabic numerals or number names (Halberda & Feigenson, Reference Halberda and Feigenson2008; Lemer, Dehaene, Spelke, & Cohen, Reference Lemer, Dehaene, Spelke and Cohen2003; Odic, Libertus, Feigenson, & Halberda, Reference Odic, Libertus, Feigenson and Halberda2013; Trick, Enns, & Brodeur, Reference Trick, Enns and Brodeur1996; Xu, Spelke, & Goddard, Reference Xu, Spelke and Goddard2005). Nonetheless, the behavior associated with this ability seems to vary depending on the amount of items present. Subjects can easily estimate the number of objects that conforms a set, however, the precision with which they do so depends on the size of the array or, when comparing two sets of objects, on the ratio between them (Jevons, Reference Jevons1871; Kaufman, Lord, Reese, & Volkmann, Reference Kaufman, Lord, Reese and Volkmann1949; Lipton & Spelke, Reference Lipton and Spelke2004; Trick & Pylyshyn, Reference Trick and Pylyshyn1994). It appears that small numerosities are identified fast, effortless and without error, while determining how many elements constitute a larger set is significantly slower and error prone. This has been confirmed both in adults and children (Atkinson, Campbell, & Francis, Reference Atkinson, Campbell and Francis1976; Gallistel & Gelman, Reference Gallistel, Gelman, Kessen, Ortony and Kraik1991; Mandler & Shebo, Reference Mandler and Shebo1982; Svenson & Sjöberg, Reference Svenson and Sjöberg1978; Trick, Reference Trick2008; Trick et al., Reference Trick, Enns and Brodeur1996).
When analyzing reaction times (RTs) and precision, the subjects’ responses generate a characteristic curve that suggests the existence of two different processes involved in the task. The enumeration of up to 4 items generates approximately constant RTs, after which they increase linearly, from about 250 to 350 ms per additional item in the case of adults (Jevons, Reference Jevons1871; Kaufman et al., Reference Kaufman, Lord, Reese and Volkmann1949; Lipton & Spelke, Reference Lipton and Spelke2004; Trick & Pylyshyn, Reference Trick and Pylyshyn1994) and an average of 1000 ms per additional item in 7 and 8 year-old children (Svenson & Sjöberg, Reference Svenson and Sjöberg1978). Large quantities can be identified by counting each individual item, a method that is slow but reasonably accurate, or by estimating the numerosity of the set, which is faster but is significantly less precise.
Since Kaufman et al. (Reference Kaufman, Lord, Reese and Volkmann1949) first coined the term subitizing to refer to the rapid and accurate apprehension of small numerosities (1 to 4 items), researchers have focused on identifying the cognitive processes that underlie this ability. One hypothesis proposes that subitizing reflects an estimation procedure used for both small and large quantities (Chi & Klahr, Reference Chi and Klahr1975; Dehaene & Changeux, Reference Dehaene and Changeux1993; Gallistel & Gelman, Reference Gallistel, Gelman, Kessen, Ortony and Kraik1991). This theory suggests that the differences observed in RTs and precision are the effect of the variability inherent in the system that sustains the estimation process. As a result, a subject comparing two magnitudes will be faster and more accurate discriminating them the more distant they are. Also, the level of error and the resolution time will increase the greater the size of the set. In accordance with this, the variability characteristic of estimation is low when it comes to 1, 2, 3 or 4 objects, which could explain the subitizing phenomenon. Simultaneously, after 5 elements the estimation process would become too imprecise to generate a reliable answer (Chi & Klahr, Reference Chi and Klahr1975; Dehaene & Changeux, Reference Dehaene and Changeux1993; Gallistel & Gelman, Reference Gallistel, Gelman, Kessen, Ortony and Kraik1991).
However, there is evidence that suggests the existence of two distinct cognitive systems for processing small and large numerosities. On one hand, studies have found that the pattern of discrimination responses, regarding both accuracy and RTs, differs for small and large sets, even when controlling for ratio. For example, the specific response pattern identified as subitizing emerges when enumerating from 1 to 8 items in numerosities 1 to 4, but not in numerosities 10 to 40 when naming quantities from 10 to 80 (Revkin, Piazza, Izard, Cohen, & Dehaene, Reference Revkin, Piazza, Izard, Cohen and Dehaene2008). Also, authors Trick et al. (Reference Trick, Enns and Brodeur1996) studying subjects from 6 to 72 years of age, observed that age affected differently the enumeration of items in the subitizing range than those in the counting or estimation range. The RTs decreased from ages 6 to 22, and then remained stable throughout life with 1 to 4 elements, while from 6 to 9 items RTs tended to increase once again with senior adults, generating a u-shape curve. This distinct pattern might indicate the involvement of different processes.
Moreover, several studies found no correlation between individual differences in subitizing capacity and estimation precision in adults, which suggest the two do not depend on the same cognitive system (Piazza, Fumarola, Chinello, & Melcher, Reference Piazza, Fumarola, Chinello and Melcher2011; Revkin et al., Reference Revkin, Piazza, Izard, Cohen and Dehaene2008). Also, when comparing the performance of high and low discrimination-precision groups in a discrimination task, there was a significant difference between them when the quantities were larger than 4, though not in the subitizing range (Revkin et al., Reference Revkin, Piazza, Izard, Cohen and Dehaene2008). It appears that the subitizing capacity does not rely on the internal representation of magnitude on which the estimation procedure depends.
In accordance with the notion of two independent processes, Trick and Pylyshyn (Reference Trick and Pylyshyn1994) offer an alternative explanation for the phenomenon perceived during the visual enumeration of small quantities. The authors suggest that subitizing takes advantage of a basic mechanism in charge of the simultaneous individuation of multiple objects, not specific for the numerical domain. This process would occur at an early stage of the visual analysis, when the image is segregated into individual elements, before the involvement of more complex attentional processes. It would consist in a limited-capacity visual indexing system, which would be able to tag and track up to 3 or 4 elements in parallel. The theory sustains that a number of mental tokens can bind themselves to specific features and spatial locations, so that each element maintains its identity, creating a map of protruding objects that can later be enumerated. This account differs greatly from the notion that subitizing reflects the recognition of a specific geometrical pattern (Logan & Zbrodoff, Reference Logan and Zbrodoff2003; Mandler & Shebo, Reference Mandler and Shebo1982; Von Glasersfeld, Reference Von Glasersfeld1982). Additionally, the fact that subitizing can be carried out even when the target stimuli are placed among distractors or some of the objects’ features change, is coherent with the notion that spatial location may be key to this process (Trick, Reference Trick2008).
In line with this, the differences found in RTs and precision between the enumeration of small and large quantities can suggest limitations inherent in this specific visual mechanism which would count with a limited amount of tags (Hyde et al., Reference Hyde, Winkler-Rhoades, Lee, Izard, Shapiro and Spelke2011; Trick & Pylyshyn, Reference Trick and Pylyshyn1994).
Even though many authors concur with the multiple individuation theory, nowadays most of them argue that attention is a key function of subitizing. While estimation only requires a rough representation of quantity, exact enumeration depends on the precise delimitation of individual objects, and the later mapping of the set onto a symbolic representation of value, a more complex cognitive process (Mazza & Caramazza, Reference Mazza and Caramazza2015; Railo, Koivisto, Revonsuo, & Hannula, Reference Railo, Koivisto, Revonsuo and Hannula2008; Vetter, Butterworth, & Bahrami, Reference Vetter, Butterworth and Bahrami2008). Also, the fact than RTs increase approximately 40 ms. per additional item from 1 to 4 elements, contradicts the preattentive parallel indexing theory which predicts no RT differences within the subitizing range (Railo et al., Reference Railo, Koivisto, Revonsuo and Hannula2008). Simultaneously, studies have found that modulation of attentional load may interfere with the subitizing range (Mazza & Caramazza, Reference Mazza and Caramazza2015; Pagano, Lombardi, & Mazza, Reference Pagano, Lombardi and Mazza2014; Railo et al., Reference Railo, Koivisto, Revonsuo and Hannula2008).
A number of authors also suggests that the reason why subjects can only subitize up to 4 items is related to visuospatial working memory (VSWM)’s limited capacity, which implies that only a small number of items can be represented actively at the same time. As a limited system for storing and processing information, working memory would prevent an item from being enumerated more than once (Cowan, Reference Cowan2001; Klahr, Reference Klahr and Chase1973; Logie & Baddeley, Reference Logie and Baddeley1987). It is also possible that both abilities rely on a domain-general internal mechanism in charge of discriminating multiple objects in parallel, based on their features and spatial locations, such as the one described by Trick and Pylyshyn (1994; Pagano et al., Reference Pagano, Lombardi and Mazza2014; Piazza et al., Reference Piazza, Fumarola, Chinello and Melcher2011).
To test this hypothesis, Piazza, Fumarola, Chinello, and Melcher (Reference Piazza, Fumarola, Chinello and Melcher2011) studied the relation between visual working memory, subitizing and large number estimation. They design 3 single task experiments, consisting of a dot counting task, a dot comparison task, and a visual working memory task. The latter involves the simultaneous encoding of a number of objects to subsequently compare them to a second set. The authors also design 2 dual-task experiments to analyze the effect of manipulating working memory load in subitizing and estimation: dot counting and visual working memory, and dot comparison and visual working memory. The secondary task consisted in the same type of stimuli as the visual working memory simple-task.
This study found that individual differences in visual working memory positively correlate with differences in subitizing capacity and that manipulation of visual working memory load in adults reduces their subitizing range. The same work observed that measures of visual working memory and subitizing do not correlate with individual differences in numerosity comparison precision or large number estimation. These findings are consistent with the notion that estimation is a core numerical ability, independent of other cognitive processes, while subitizing is based on a limited-capacity visual system not specific for number processing, shared by other cognitive functions.
On the other hand, Shimomura and Kumada (Reference Shimomura and Kumada2011) studied the effect of manipulating working memory load on subitizing and counting, differentiating spatial working memory (encoding positions) from non-spatial visual working memory (encoding items, Baddeley & Logie, Reference Baddeley, Logie and Shah1999; Logie, Reference Logie1995). The authors found that spatial working memory load only affected speed and precision when counting more than 5 elements, whereas subitizing efficiency and range remained unchanged. Even more, the study showed that non-spatial visual memory load had no effect over subitizing or counting efficiency.
The aim of this study was to analyze the possible associations between individual differences in subitizing, estimation and working memory, in 4 and 6 year-old children, to explore if these abilities -subitizing and estimation- have the same relation with VSWM in children as in adults. It was presumed that, being a purely numerical ability, independent of the visual map that allows exact enumeration, no correlations would be found between estimation and subitizing or VSWM.
Method
Participants
The sample consisted of 120 children of both sexes, equally divided into two age groups: 60 4-year-old children (35 females –58,3 %– 25 males) and 60 6-year-old children (29 females –48,3 %– 30 males). The children attended a private school in Ciudad Autónoma de Buenos Aires, Argentina. Parents were asked to sign a written authorization for their children to participate in the study after being informed of the aim of the research and the type of tests that would be used. The information gathered was anonymous and confidential. Children with hearing or speech deficit, neurological or psychiatric disorder, or an IQ lower than 80, were excluded from this work. The IQ was estimated through an abbreviated version of WISC-III (Wechsler, Reference Wechsler1994), using Tellegen and Briggs (Reference Tellegen and Briggs1967) procedure, which has a high correlation with the IQ obtained through the administration of the complete scale IQ (r u = .911; r = .803; Sattler, Reference Sattler1992). The group of 4 year-old children had a mean IQ of 102, with a SD of 11, and the group of 6 year-old children had a a mean IQ of 105, with a SD of 7.
The experiment was performed with a computer, and carried out in a well lit room, free from distracting noises. The children sat in front of the screen at a distance of about 50 cm. They were asked to keep their index fingers over a button box when necessary. Each participant completed four tasks individually. The tasks were administered in a random orden. Manual responses (for the discrimination task and the Corsi block-tapping task) and vocal responses (for the enumeration task) were recorded and monitored through OpenSesame (Mathôt, Schreij, & Theeuwes, Reference Mathôt, Schreij and Theeuwes2012), an open source software for the design of psychological experiments. For the Corsi block-tapping task only correct and incorrect answers were registered. For the other tests both accuracy and RT were taken into consideration.
In the case of vocal responses, for the enumeration task, the recording initiated with the presentation of the stimuli and ended when the administrator pressed a button after the child either issued a response or manifested not knowing the answer. Each individual audio file was then run through the software Audacity 2.1.0. To obtain the RT and to register if the answer was correct or not. This method helped prevent problems associated with voice activated software such as latencies created by the premature onset of the recording by noises not related to the verbal response.
Materials and procedure
Enumeration task
This task was administered to obtain a measure for each subject’s subitizing capacity. It consists in the presentation of an array of high contrast items: one to ten black dots appearing on the computer screen in a white circle with a diameter of 17 cm (see Figure 1A), where the participant has to identify the quantity and express aloud the corresponding number as fast and precise as possible. Each dot has a diameter of 0.7 cm and there is a minimum of 1.5 cm and a maximum of 7 cm between adjacent dots. The distribution of the element in the display is random and it does not form a canonical pattern (such as the distributions found in dices). In the case of the quantity 3 the dots do not form a straight line or an equilateral triangle in either of the displays.

Figure 1. A. Enumeration task: example of stimuli and trial structure. B. Discrimination task: example of stimuli, trial structure, timing and responses.
The stimuli are presented in a random sequence in which every numerosity is displayed twice. The wording of the instructions is as follows: “In the screen you will see a group of dots. You have to say how many dots are there as fast as possible”. The image remains present until the child issues a verbal response. The task comprises 24 trials, which include four training trails administered before the beginning of the experiment itself. If the subjects committed a mistake during the training trails these were re-administered twice. If a participant failed to understand the task the administration was interrupted and the data from any other task was dismissed. The information gathered from the training trials was not used for data analysis, neither were the RTs associated to incorrect responses.
Discrimination task
This task was administered to obtain a measure of each subject’s estimation capacity. It involves the simultaneous presentation of two arrays of dots, one on each side of the screen (see Figure 1B). The items are of high contrast (black dots over a white background). Each dot has a diameter of 3 mm and there is a minimum of 1 cm and a maximum of 3 cm between adjacent dots. There is also a minimum of 1.5 cm separating the dots from the margins of the display and 5 cm between the groups of dots located at the left and right sides of the screen.
On each trial the participant was asked to decide, as quickly as possible, which set is the most numerous, and indicate so by pressing the left or right button of a button box, depending on the array’s location. The wording of the instructions is as follows: "In the screen you will see two groups of dots, one on each side of the screen. You have to decide as fast as possible which side has more dots. If there are more dots on this side (pointing to the left side of the screen) you have to press this button (pointing to the left button). If there are more dots on this side (pointing to the right side of the screen) you have to press this button (pointing to the right button). You have to be quick, because the dots will only be on the screen for a short time". Before starting, the participant is asked to position their right and left index fingers on each of the buttons in order to avoid possible delays due to the time it takes the child to locate the hand correctly over the corresponding key. The stimulus remains on screen for 3000 ms to prevent the participant from counting the dots and if the child does not respond within the time frame this is registered as an errors.
The numerical ratio between the two arrays can be 1.15, 1.5, 2 or 3. The smaller numerosities are 4, 6, 8 and 16 for every ratio (eg., the trials for the ratio 2 are 4 vs 8, 6 vs 12, 8 vs 16 and 16 vs 32), except for ratio 1.15 where the smaller numerosities are 6, 7, 13 and 20. The task consists of 20 trials, which include four training trails administered at the beginning of the test that were not used for data analysis. If the subjects committed a mistake during the training trails these were re-administered twice, after which, if the participant continued to error, the administration was interrupted and the data from any other task was dismissed. The RTs associated with incorrect responses were not used in the analysis.
Corsi block-tapping task
Visuospatial working memory was assessed through a computerized version of the traditional Corsi block-tapping task (Corsi, Reference Corsi1972). In this case, nine white blocks positioned unevenly through the screen, in compliance with the original test, light up one at a time. The participant must observe the specific sequence in which they illuminate, remember it and reproduce it. The task includes two training trails, and six levels with three trials each. The initial level consists of patterns of only two blocks and each subsequent level includes an additional block, reaching up to seven items. The participant must perform the training trials correctly in order to commence the task. The training trials are administered up to two times, after which, if the child continues to error the administration is interrupted and the data collected from any other task is dismissed. Each participant has to remember at least two trials within a level to reach the next one. After two erroneous responses in the same level the administration is concluded.
The test includes two different tasks: a first one where the participant must reproduce the sequence in the exact order in which it was presented, which measures VSWM’s storage capacity, and a second one where the child has to repeat the pattern in a backwards order, which measures, not only storage, but also processing of visuospatial information (see Figures 2A and 2B). Every participant has a VSWM measure for storage and one for processing of information which is the total of correct responses obtained in each modality (forwards and backwards respectively).

Figure 2. A. Corsi blocks tapping test: example of stimuli, trial structure and timing. B. Corsi blocks tapping test - backwards version: example of stimuli, trial structure and timing.
Results
Group analyses
Subitizing and counting
To begin with, the RTs (only those associated with correct answers) and the correct responses obtained with the enumeration task were subjected to a 2 (age groups) x 10 (quantity of dots) mixed design ANOVA. The Bonferroni correction was used as a post-hoc analysis to contrast the differences in RTs between each individual quantity. The same analysis was performed on the number of correct answers (see Table 1).
Table 1. Descriptive statistics of each quantity’s RTs and proportion of correct responses (accuracy)

The analysis showed a significant main effect of the number of dots over the average response time (RT), F(9, 1062) = 720.59, MSE = 734394, p < .001, η2 = .86, as well as over the number of correct responses, F(9, 1062) = 42.15, MSE = .194, p < .001, η2 = .26. Both resolution time and errors increased together with the size of the array. Nevertheless, this growth was statistically significant only from the quantity 4 onward (see Figures 3A and 3B).

Figure 3. A. Mean RTs for Enumeration task. B. Proportion of correct responses for Enumeration task.
Regarding age, 4 year-olds were significantly slower than 6 year-olds when enumerating sets of items F(1, 118) = 252.71, MSE = 3091928, p < .001, η2 = .68. Also, the younger group showed a significant reduction of correct responses when compared with the older group F(1, 118) = 36.84, MSE = .923, p < .001, η2 = .23.
Interactions were found between the factors number of dots*age, both with RT F(9, 1062) = 47.36, MSE = 734394, p < .001, η2 = .29 and correct responses F(9, 1062) = 9.71, MSE = .194, p < .001, η2 = .07.
Analyzing the RTs we observed that the differences in the enumeration of 1, 2 and 3 items were not statically significant, and the same was valid for correct responses (see Table 1). Speed and accuracy did not seem to vary greatly within that small range in any of the age groups. On the contrary, any quantity equal or greater than 4 showed significant differences in both RTs and correct responses when compared to the enumeration of 1 to 3 items, and even when contrasting larger quantities among their selves (p < .001).
Based on this, a subitizing range was estimated for each age group. The slopes for the RT curves for numerosities 1–3 and 5–10 were obtained using the method of least squares (Shimomura & Kumada, Reference Shimomura and Kumada2011; Watson, Maylor, & Bruce, Reference Watson, Maylor and Bruce2005). The data from the quantity 4 was excluded given that it is considered the border between subitizing and counting (Shimomura & Kumada, Reference Shimomura and Kumada2011; Trick & Pylyshyn, Reference Trick and Pylyshyn1994; Watson, Maylor, & Bruce, Reference Watson, Maylor and Bruce2005).
In keepings with previous findings, and based on these results, we established that for this age groups the subitizing range included quantities 1 through 3. Using the confidence intervals at 95% we could observe that, regarding correct responses, there are no significant differences between the 4 year-olds and the 6 year-olds when enumerating a set within the subitizing range. However, for any quantity equal or larger than 4, 4 year-olds were significantly less accurate that the older group. In the case of RTs, there were significant differences between both age groups for each one of the numerosities, except when enumerating 1 item.
To verify the accuracy of the subitizing range estimated above the slopes for the RTs were calculated with a linear regression as a function of the number of dots, for quantities 1 to 3 and 5 to 10 (see Table 2) and then compared using a paired t-test. The numerosity 4 was excluded from this analysis as it is the boundary between subitizing and enumeration of larger quantities.
Table 2. Slopes for enumeration task in subitizing and estimation ranges
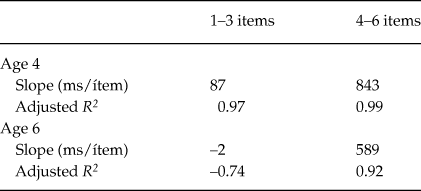
The paired t-tests showed a significant difference in slope between subitizing range and enumeration of more than 4 items t(2) = –5.13, p < .05, d = –7.25.
Estimation
Differences in estimation capacity between 4 and 6 year-old children were obtained by carrying out a paired t-test on each variable: speed (average RT of correct responses) and accuracy (total correct responses). Results showed significant differences between the age groups for estimation accuracy, t(118) = –7.26, SEM = .43, p < .001, d = –1.34 and speed, t(118) = 4.76, SEM = .54.58, p < .001, d = .88.
Visuospatial Working Memory (VSWM)
Differences in VSWM between both age groups were obtained by carrying out a paired t-test on storage and concurrent processing capacity. Results showed significant differences between 4 and 6 year-old children in both storage, t(118) = –14.48, SEM = .31, p < .001, d = –2.67 and concurrent processing, t(118) = –9.37, SEM = .35, p < .001, d = –1.73.
Individual differences analyses
Each participant obtained measures for subitizing range and speed (average RT of correct responses), counting slope, estimation accuracy (correct responses) and speed (average RT of correct responses), storage and concurrent processing of visuo-spatial information in working memory (see Table 3).
Table 3. Descriptive statistics of variables

The RTs pattern in an enumeration task that includes quantities 1 through 10 typically describes a sigmoid-shaped curve that starts with a lower plateau, with a null slope, which eventually bends into a linear section with a steeper slope. Each participant’s subitizing range was estimated by fitting their data (all RTs associated with correct responses) with a sigmoid function of number of dots (Green & Bavelier, Reference Green and Bavelier2003; Piazza et al., Reference Piazza, Fumarola, Chinello and Melcher2011; Revkin et al., Reference Revkin, Piazza, Izard, Cohen and Dehaene2008) and obtaining the bend point of the curve (Sebaugh & McCray, Reference Sebaugh and McCray2003). The data fit was very good (age 4: R 2 = .88; SD = .08; age 6: R 2 = .91, SD = .08) and showed a mean subitizing range of 2.79 with a SD of .66 for 4 year-olds and of 3.11 with a SD of .64 for 6 year-olds. The steeper slope within the curve was associated with a counting process. The slope for each subject’s counting range was calculated.
Correlation analyses were conducted between the variables described above (see Table 4).
Table 4. Correlation between variables

**p < .01; *p < .05.
Subitizing range showed a low association with VSWM’s storage capacity (r = .274; p < .05) and no relation to concurrent processing, while average RTs within the subitizing range were associated with both VSWM’s measures: storage capacity (r = –.398; p < .001) and concurrent processing (r = –.412; p < .001).
The measures obtained for estimation also showed significant correlation with the VSWM’s measures. Accuracy (total correct responses) showed moderated and positive correlations with VSWM’s storage capacity (r = .537; p < .001), and with VSWM’s concurrent processing (r = .447, p < .001). Simultaneously, speed (average RT) showed lower and medium negative associations with VSWM’s storage capacity (r = –.348; p < .001) and with VSWM’s concurrent processing (r = –.258, p = .005). Counting slope also showed significant correlations with VSWM’s storage capacity (r = –.295; p = .001) and concurrent processing (r = –.305; p = .001).
Finally, subitizing range and average RTs showed a low association with estimation accuracy (range: r = .234; p < .05; speed: r = –.398; p < .001). Neither subitizing range nor speed were related to estimation speed (average RTs) or counting slope.
Discussion
Children’s ability to perceive and judge quantities without counting each individual item is believed to be a cornerstone of numerical cognition, a domain specific skill that allows a subject to apprehend rapidly the number of items present in a scene (Halberda & Feigenson, Reference Halberda and Feigenson2008; Lemer et al., Reference Lemer, Dehaene, Spelke and Cohen2003; Odic et al., Reference Odic, Libertus, Feigenson and Halberda2013; Trick et al., Reference Trick, Enns and Brodeur1996; Xu et al., Reference Xu, Spelke and Goddard2005). The precision and velocity with which they do so depends on the size of the array: small quantities can be identified rapidly and without error, whereas the apprehension of larger numerosities requires more effort, tends to be slower and error prone (Atkinson et al., Reference Atkinson, Campbell and Francis1976; Jevons, Reference Jevons1871; Kaufman et al., Reference Kaufman, Lord, Reese and Volkmann1949; Lipton & Spelke, Reference Lipton and Spelke2004; Mandler & Shebo, Reference Mandler and Shebo1982; Trick & Pylyshyn, Reference Trick and Pylyshyn1994). This finding suggests that there might be different processes involved in numeracy: the identification of larger quantities can be achieved through the approximate estimation of the number of items, which is fast but inexact, or the serial process of counting each individual item, which is more precise but slower; while small numerosities (1 to 4 items) can be identify rapidly and without error. The latter ability, subitizing, has been the focus of several studies which tried to identify the mechanism that underlies it (Burr, Turi, & Anobile, Reference Burr, Turi and Anobile2010; Gallistel & Gelman, Reference Gallistel, Gelman, Kessen, Ortony and Kraik1991; Mazza & Caramazza, Reference Mazza and Caramazza2015; Pagano et al., Reference Pagano, Lombardi and Mazza2014).
Trick and Pylyshyn (Reference Trick and Pylyshyn1994) proposed that subitizing relies on a limited-capacity indexing system in charge of individuating, tagging and tracking multiple objects in parallel, depending on their spatial location and visual features. Given the characteristics of this system, a number of authors have discussed its possible association with VSWM, implying working memory and subitizing may rely on a common basic process (Cowan, Reference Cowan2001; Piazza et al., Reference Piazza, Fumarola, Chinello and Melcher2011; Trick, Reference Trick2005). In this regard, a study conducted in adults (Piazza et al., Reference Piazza, Fumarola, Chinello and Melcher2011) found associations between individual differences in subitizing capacity and visual working memory, with no correlation with estimation measures. It also showed that performing a secondary memory task diminishes the subject’s subitizing efficiency and range.
On the other hand, Shimomora and Kumada (Reference Shimomura and Kumada2011) found that the manipulation of spatial working memory load affected the enumeration of large quantities, but not subitizing efficiency or range. Additionally, the authors showed that the manipulation of visual working memory load did not affect subitizing or counting efficiency.
Following previous research, the aim of the present study was to analyze the possible associations between individual differences in subitizing, estimation and working memory, in 4 and 6 year-old children. The subjects had to carry out three independent tasks: enumeration task, discrimination task and Corsi block tapping task, both the forward and backwards version.
The data obtained from the Enumeration task, both RTs and mean correct responses, were analyzed in order to estimate the mean subitizing range for each age group. The results showed that the enumeration of 1, 2 and 3 items was significantly more rapid and accurate than with larger quantities. Moreover, no significant differences were found in precision between ages 4 and 6 when enumerating 1–3 items, whereas with quantities larger than 4 the 6 year-old children were significantly more accurate than the 4 year-olds. Further analyses produced an average subitizing range of 2.79 at age 4 and of 3.11 at age 6. These findings are consistent with a study by Svenson and Sjöberg (Reference Svenson and Sjöberg1978) which calculated an average subitizing range of 3.22 for 7 and 8 year-old children, and a study by Hannula, Räsänen, and Lehtinen (Reference Hannula, Räsänen and Lehtinen2007) which, by using a short and fix presentation time (120 ms) for the stimuli, obtained an average subitizing range of 2.79 for 5 year-olds. This evidence suggests that, while adults may be able to subitize up to 4 items (Atkinson et al., Reference Atkinson, Campbell and Francis1976; Feigenson, Dehaene, & Spelke, Reference Feigenson, Dehaene and Spelke2004; Gallistel & Gelman, Reference Gallistel, Gelman, Kessen, Ortony and Kraik1991; Mandler & Shebo, Reference Mandler and Shebo1982; Revkin et al., Reference Revkin, Piazza, Izard, Cohen and Dehaene2008; Trick, Reference Trick2008; Trick et al., Reference Trick, Enns and Brodeur1996), for ages 4 and 6 the range is smaller.
The measures obtained in the enumeration task, subitizing range, subitizing speed and counting slope, were later studied in relation to estimation and VSWM capacity. Consistent with Piazza et al. (Reference Piazza, Fumarola, Chinello and Melcher2011), subitizing measures showed no association with estimation capacity when comparing correct responses and a poor association when comparing speed, and no correlation with counting slope. This evidence is in keepings with the existence of different processes that underlie the enumeration ability: on one hand, a limited-capacity process for the exact and rapid enumeration of small quantities, and, on the other hand, the processes in charge of identifying larger quantities. Numerical estimation is fast but error prone since it accesses an approximate representation of quantities with an inherent variability that depends on the size of the array. Counting, on the other hand, is a serial process which is more precise but significantly slower. Also, in line with the study conducted by Piazza et al. (Reference Piazza, Fumarola, Chinello and Melcher2011), subitizing measures were associated with VSWM. Subitizing range was only related to the storage of visuo-spatial information, while subitizing speed was associated with both storage and concurrent processing capacity. However, contrary to Piazza’s findings, the present work also showed associations between estimation capacity, both accuracy and speed, and VSWM’s storage and processing.
While the evidence obtained in this study may suggest that at this age numeracy relies on VSWM for subitizing, numerical estimation and counting some of the measures themselves may be influencing the results. Speed of information processing or RTs and working memory have been found to correlate with a general factor, intelligence, which would explain the associations between the numerical variables described above and a domain general ability such as working memory (Injoque-Ricle, Barreyro, Formoso, & Burín, Reference Injoque-Ricle, Barreyro, Formoso and Burin2015; Jensen, Reference Jensen1987; Miller & Vernon, Reference Miller and Vernon1996). Also, VSWM mediates the encoding of visual information, and while it has a limited capacity to store and process information, a better processing speed would allow the subject to incorporate new information faster and with less effort for the memory system (Injoque-Ricle et al., Reference Injoque-Ricle, Barreyro, Formoso and Burin2015; Miller & Vernon, Reference Miller and Vernon1996). Hence, it is possible that the associations observed do not reflect the numerical variables dependence on VSWM or even the existence of a domain general visual indexing system such as the one proposed to explain subitizing’s limited capacity. Moreover, it has been described that changes in working memory due to age are accompanied by changes in processing speed, which could also explain the differences found in RT for these variables between 4 and 6 year-old children (Wilhelm & Oberauer, Reference Wilhelm and Oberauer2006). A future study could control the groups for simple reaction time to observe if the associations found remain significant.
Nevertheless, associations were also found between subitizing range (which did not depend on processing speed, rather than on the slope of the enumeration function) and VSWM’s storage capacity, and between estimation accuracy and both measures of VSWM. Also, if RT contributed greatly to the variability of the scores it would be expected that the abilities measured by RT latencies were all associated with each other. Instead, subitizing measures only correlated with estimation accuracy, but not estimation speed, and none of these variables was associated to counting slope.
Another aspect that should be taken into consideration is that the design of the tasks used to assess the different variables may yield different results to these analyses. Subitizing range can be obtained through an enumeration task with a short time of presentation for each display, which prevents the child from counting the dots (Fischer, Gebhardt, & Hartnegg, Reference Fischer, Gebhardt and Hartnegg2008; Hannula et al., Reference Hannula, Räsänen and Lehtinen2007). This may provide a more exact measure of the numerosity the subject can apprehend almost instantaneously. Hannula et al. (Reference Hannula, Räsänen and Lehtinen2007) study, in particular, did not require a verbal response (i.e., the verbal label associated to each quantity), instead the child had to choose from two subsequent displays which had the same number of items as the one presented previously (for 120 ms). While this design allows the researcher to measure the participants’ subitizing capacity independently from their knowledge of the verbal labels, it also uses VSWM resources to temporarily store the first set of items and then compare it to the two new ones. Large number estimation can also be measured by an enumeration task were the displays are presented briefly to prevent the subject from counting the items, instead of a discrimination task such as the one used in the present study (Piazza et al., Reference Piazza, Fumarola, Chinello and Melcher2011). Having to compare two quantities may require additional resources from the VSWM, which could influence the results obtained through the correlation analysis between these variables. Further studies should be conducted with different tasks to assess estimation capacity in order to corroborate the findings of this work.
The evidence obtained in this study suggests the existence of different enumeration processes, independent from each other, at ages 4 and 6. It also may suggest that at this ages enumeration by subitizing, numerical estimation and counting relies on VSWM. These abilities may grow independent from working memory later on. Further studies regarding the association of enumeration with VSWM and the effect of manipulating VSWM load on the enumeration of small and large quantities in children of various ages are necessary.









