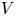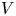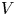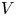1. Introduction
In [Reference SoergelSoe90], Soergel gave a combinatorial description of the category ![]() $\mathcal {O}$ for semisimple Lie algebras. This celebrated work has many applications: another proof of the Kazhdan–Lusztig conjecture (which does not rely on the theory of
$\mathcal {O}$ for semisimple Lie algebras. This celebrated work has many applications: another proof of the Kazhdan–Lusztig conjecture (which does not rely on the theory of ![]() $\mathcal {D}$-modules), Koszul duality of the category
$\mathcal {D}$-modules), Koszul duality of the category ![]() $\mathcal {O}$, etc. Later, Soergel [Reference SoergelSoe07] defined a certain category purely in terms of combinatorics of Coxeter systems, without any representation theory. This category describes the category
$\mathcal {O}$, etc. Later, Soergel [Reference SoergelSoe07] defined a certain category purely in terms of combinatorics of Coxeter systems, without any representation theory. This category describes the category ![]() $\mathcal {O}$. More precisely, this category is equivalent to the category of projective modules in (a deformed version of) the principal block of the category
$\mathcal {O}$. More precisely, this category is equivalent to the category of projective modules in (a deformed version of) the principal block of the category ![]() $\mathcal {O}$ (cf. [Reference SoergelSoe90, Reference FiebigFie06]).
$\mathcal {O}$ (cf. [Reference SoergelSoe90, Reference FiebigFie06]).
Let ![]() $(W,S)$ be a Coxeter system and
$(W,S)$ be a Coxeter system and ![]() $V$ a reflection-faithful representation of
$V$ a reflection-faithful representation of ![]() $W$. Then Soergel attached the category of Soergel bimodules. When
$W$. Then Soergel attached the category of Soergel bimodules. When ![]() $W$ is the Weyl group of a semisimple Lie algebra, we may take
$W$ is the Weyl group of a semisimple Lie algebra, we may take ![]() $V$ to be a Cartan subalgebra, and Soergel's category is the category which describes the category
$V$ to be a Cartan subalgebra, and Soergel's category is the category which describes the category ![]() $\mathcal {O}$.
$\mathcal {O}$.
Fiebig used this category (or, more precisely, the category of sheaves on moment graphs, which is equivalent to the category of Soergel bimodules [Reference FiebigFie08a]) to give an alternative proof of Lusztig's conjecture which says that the irreducible characters of an algebraic group over an algebraically closed field of positive characteristic are given by affine Kazhdan–Lusztig polynomials if the characteristic is large enough. He used the Soergel bimodules attached to an affine Weyl group ![]() $(W,S)$ and a Cartan subalgebra
$(W,S)$ and a Cartan subalgebra ![]() $V$ of the corresponding affine Lie algebra. If the coefficient field of
$V$ of the corresponding affine Lie algebra. If the coefficient field of ![]() $V$ has characteristic zero, then
$V$ has characteristic zero, then ![]() $V$ is reflection faithful. However if the characteristic is positive, then this is not reflection faithful. So he used a lifting to characteristic zero and used the theory of Soergel bimodules over a characteristic-zero field.
$V$ is reflection faithful. However if the characteristic is positive, then this is not reflection faithful. So he used a lifting to characteristic zero and used the theory of Soergel bimodules over a characteristic-zero field.
However, it is of course more natural to use positive-characteristic objects directly. Elias and Williamson gave an alternative category of the category of Soergel bimodules which works well even with a non-reflection-faithful representation [Reference Elias and WilliamsonEW16]. Riche and Williamson [Reference Riche and WilliamsonRW18] gave a conjecture which claims that this category describes the category of algebraic representations of an algebraic group over any field of positive characteristic. As an application, this description gives a character formula of tilting modules in terms of the ![]() $p$-canonical basis defined using the category of Elias–Williamson. Recently this character formula was proved by Achar, Makisumi, Riche and Williamson [Reference Achar, Makisumi, Riche and WilliamsonAMRW19] for the principal block when
$p$-canonical basis defined using the category of Elias–Williamson. Recently this character formula was proved by Achar, Makisumi, Riche and Williamson [Reference Achar, Makisumi, Riche and WilliamsonAMRW19] for the principal block when ![]() $p$ is greater than the Coxeter number.
$p$ is greater than the Coxeter number.
Elias and Williamson gave the definition of their category as a certain diagrammatic category with generators and relations. Such generators and relations appeared in a study of Soergel bimodules; however, the definition seems completely different from the original definition of Soergel bimodules. The aim of this paper is to give a ‘bimodule-theoretic’ definition of this category, that is, we define a new category and prove that the new category is equivalent to that of Elias and Williamson.
We first recall the category of Soergel bimodules. Let ![]() $R = S(V)$ be the symmetric algebra of
$R = S(V)$ be the symmetric algebra of ![]() $V$ and, for
$V$ and, for ![]() $s\in S$, let
$s\in S$, let ![]() $R^{s}$ be the subalgebra of
$R^{s}$ be the subalgebra of ![]() $s$-invariants. Let
$s$-invariants. Let ![]() $(n)$ be a shift of grading defined by
$(n)$ be a shift of grading defined by ![]() $M(n)^{i} = M^{i + n}$ for
$M(n)^{i} = M^{i + n}$ for ![]() $n\in \mathbb {Z}$, where
$n\in \mathbb {Z}$, where ![]() $M = {\bigoplus} _i\, M^{i}$ is a graded module. Then a Soergel bimodule is a graded
$M = {\bigoplus} _i\, M^{i}$ is a graded module. Then a Soergel bimodule is a graded ![]() $R$-bimodule which is a direct summand of a direct sum of modules of the form
$R$-bimodule which is a direct summand of a direct sum of modules of the form
for ![]() $s_1,\ldots ,s_l\in S$ and
$s_1,\ldots ,s_l\in S$ and ![]() $n\in \mathbb {Z}$. Let
$n\in \mathbb {Z}$. Let ![]() $\mathcal {S}\mathrm {Bimod}$ be the category of Soergel bimodules and
$\mathcal {S}\mathrm {Bimod}$ be the category of Soergel bimodules and ![]() $[\mathcal {S}\mathrm {Bimod}]$ the split Grothendieck group of
$[\mathcal {S}\mathrm {Bimod}]$ the split Grothendieck group of ![]() $\mathcal {S}\mathrm {Bimod}$. Then Soergel [Reference SoergelSoe07] proved the following result which we call Soergel's categorification theorem.
$\mathcal {S}\mathrm {Bimod}$. Then Soergel [Reference SoergelSoe07] proved the following result which we call Soergel's categorification theorem.
(1) For each
 $w\in W$, there exists a unique indecomposable module
$w\in W$, there exists a unique indecomposable module  $B(w)\in \mathcal {S}\mathrm {Bimod}$ which satisfies the following properties.
$B(w)\in \mathcal {S}\mathrm {Bimod}$ which satisfies the following properties.
(a) For a reduced expression
 $w = s_1\cdots s_l$,
$w = s_1\cdots s_l$,  $B(w)$ appears as a direct summand of
$B(w)$ appears as a direct summand of  $R\otimes _{R^{s_1}}\cdots \otimes _{R^{s_l}}R(l)$ with multiplicity one and the module
$R\otimes _{R^{s_1}}\cdots \otimes _{R^{s_l}}R(l)$ with multiplicity one and the module  $R\otimes _{R^{s_1}}\cdots \otimes _{R^{s_l}}R(l)$ is a direct sum of
$R\otimes _{R^{s_1}}\cdots \otimes _{R^{s_l}}R(l)$ is a direct sum of  $B(v)(l)$ where
$B(v)(l)$ where  $v < w$ and
$v < w$ and  $l\in \mathbb {Z}$.
$l\in \mathbb {Z}$.(b) Any object in
 $\mathcal {S}\mathrm {Bimod}$ is a direct sum of modules
$\mathcal {S}\mathrm {Bimod}$ is a direct sum of modules  $B(w)(n)$ (
$B(w)(n)$ ( $w\in W$,
$w\in W$,  $n\in \mathbb {Z}$).
$n\in \mathbb {Z}$).
(2) The algebra
 $[\mathcal {S}\mathrm {Bimod}]$ is isomorphic to the Hecke algebra attached to
$[\mathcal {S}\mathrm {Bimod}]$ is isomorphic to the Hecke algebra attached to  $(W,S)$.
$(W,S)$.
We prove the generalization of this theorem to ![]() $V$ which is not reflection faithful in this paper.
$V$ which is not reflection faithful in this paper.
1.1 A representation  $V$ and our category
$V$ and our category
Let ![]() $V$ be a finite-dimensional representation of
$V$ be a finite-dimensional representation of ![]() $W$ over a field
$W$ over a field ![]() $\mathbb {K}$. We assume that there exist
$\mathbb {K}$. We assume that there exist ![]() $\alpha _s\in V$ and
$\alpha _s\in V$ and ![]() $\alpha _s^{\vee }\in V^{*}$ (where
$\alpha _s^{\vee }\in V^{*}$ (where ![]() $V^{*}$ is the dual of
$V^{*}$ is the dual of ![]() $V$) for each
$V$) for each ![]() $s\in S$ such that:
$s\in S$ such that:
(1)
 $\langle \alpha ^{\vee }_s,\alpha _s\rangle = 2$ for any
$\langle \alpha ^{\vee }_s,\alpha _s\rangle = 2$ for any  $s\in S$;
$s\in S$;(2)
 $s(v) = v - \langle \alpha _s^{\vee },v\rangle \alpha _s$ for any
$s(v) = v - \langle \alpha _s^{\vee },v\rangle \alpha _s$ for any  $s\in S$ and
$s\in S$ and  $v\in V$;
$v\in V$;(3)
 $\alpha _s\ne 0$ and
$\alpha _s\ne 0$ and  $\alpha _s^{\vee }\ne 0$.
$\alpha _s^{\vee }\ne 0$.
The data ![]() $(V,\{\alpha _s\}_{s\in S},\{\alpha _s^{\vee }\}_{s\in S})$ is called a realization in [Reference Elias and WilliamsonEW16, Definition 3.1] if it satisfies a technical condition. To prove our categorification theorem, we need one more assumption. In this introduction, we make the following assumption for simplicity. See § 3.2 for details.
$(V,\{\alpha _s\}_{s\in S},\{\alpha _s^{\vee }\}_{s\in S})$ is called a realization in [Reference Elias and WilliamsonEW16, Definition 3.1] if it satisfies a technical condition. To prove our categorification theorem, we need one more assumption. In this introduction, we make the following assumption for simplicity. See § 3.2 for details.
(4) For each
 $s,t\in S$ such that the order of
$s,t\in S$ such that the order of  $st$ is finite, the representation of
$st$ is finite, the representation of  $V$ restricted to the group generated by
$V$ restricted to the group generated by  $\{s,t\}$ is reflection faithful.
$\{s,t\}$ is reflection faithful.
Under these assumptions, we consider the following category. Set ![]() $R = S(V)$ and let
$R = S(V)$ and let ![]() $Q$ be the fraction field of
$Q$ be the fraction field of ![]() $R$. We consider the following category: the objects of the category are
$R$. We consider the following category: the objects of the category are ![]() $(M,(M_Q^{w})_{w\in W},\xi _M)$ which satisfy the following condition.
$(M,(M_Q^{w})_{w\in W},\xi _M)$ which satisfy the following condition.
![]() $M$ is a graded
$M$ is a graded ![]() $R$-bimodule,
$R$-bimodule, ![]() $M_Q^{w}$ is an
$M_Q^{w}$ is an ![]() $(R,Q)$-bimodule and
$(R,Q)$-bimodule and ![]() $\xi _M\colon M\otimes _{R}Q\xrightarrow {\sim }{\bigoplus} _{w\in W}\, M_Q^{w}$ is an
$\xi _M\colon M\otimes _{R}Q\xrightarrow {\sim }{\bigoplus} _{w\in W}\, M_Q^{w}$ is an ![]() $(R,Q)$-isomorphism such that
$(R,Q)$-isomorphism such that ![]() $f\in R$ and
$f\in R$ and ![]() $m\in M_Q^{w}$ we have
$m\in M_Q^{w}$ we have ![]() $mf = w(f)m$.
$mf = w(f)m$.
The morphisms we consider are degree-zero homomorphisms as ![]() $R$-bimodules which upon tensoring with
$R$-bimodules which upon tensoring with ![]() $Q$ are compatible with isomorphisms
$Q$ are compatible with isomorphisms ![]() $\xi _M$. It is easy to see that the
$\xi _M$. It is easy to see that the ![]() $R$-bimodule (1.1) naturally has such a decomposition, and we say that
$R$-bimodule (1.1) naturally has such a decomposition, and we say that ![]() $M$ is a Soergel bimodule if it appears as a direct summand of a sum of modules of this type. We now state the main theorem of this paper.
$M$ is a Soergel bimodule if it appears as a direct summand of a sum of modules of this type. We now state the main theorem of this paper.
Theorem 1.1
(1) For this category we have Soergel's categorification theorem.
(2) This category is equivalent to the category of Elias and Williamson.
1.2 Sheaves on moment graphs
As mentioned above, Fiebig used sheaves on moment graphs to give an alternative proof of Lusztig's conjecture [Reference FiebigFie11] for sufficiently large primes. In this paper we prove the following result.
Theorem 1.2 Assume that the Goresky–Kottwitz–MacPherson (GKM) condition (see § 5.1) holds. Our category is equivalent to a certain full subcategory of ![]() $\mathcal {Z}$-modules (see § 5.1 for the precise definition) where
$\mathcal {Z}$-modules (see § 5.1 for the precise definition) where ![]() $\mathcal {Z}$ is the structure algebra of the moment graph attached to
$\mathcal {Z}$ is the structure algebra of the moment graph attached to ![]() $(W,S)$.
$(W,S)$.
As a corollary, the category of Elias and Williamson is equivalent to the full subcategory of ![]() $\mathcal {Z}$-modules. If
$\mathcal {Z}$-modules. If ![]() $(W,S,V)$ comes from a Kac–Moody group, this is proved using parity sheaves by combining works of Fiebig and Williamson [Reference Fiebig and WilliamsonFW14] and Riche and Williamson [Reference Riche and WilliamsonRW18].
$(W,S,V)$ comes from a Kac–Moody group, this is proved using parity sheaves by combining works of Fiebig and Williamson [Reference Fiebig and WilliamsonFW14] and Riche and Williamson [Reference Riche and WilliamsonRW18].
1.3 Proof
Even though the definitions and theorems are similar to that of Soergel [Reference SoergelSoe07], it seems difficult to follow his argument in our setting. For example, he proved that after a suitable localization, the modules decompose into modules attached to rank one [Reference SoergelSoe07, Lemma 6.10]. However, this does not hold in our case. Fiebig used similar arguments in his study of moment graphs. To use this argument, he assumed the GKM condition on the moment graph. This condition does not follow from our assumptions on ![]() $V$.
$V$.
There is another point in Soergel's argument which we cannot apply to our case. He considered the ‘standard module’ ![]() $\Delta _x$ for each
$\Delta _x$ for each ![]() $x\in W$ and proved that there exists an extension between
$x\in W$ and proved that there exists an extension between ![]() $\Delta _x$ and
$\Delta _x$ and ![]() $\Delta _y$ only when
$\Delta _y$ only when ![]() $x^{-1}y$ is a reflection (a conjugation of an element in
$x^{-1}y$ is a reflection (a conjugation of an element in ![]() $S$). Therefore the category
$S$). Therefore the category ![]() $\mathcal {F}_\Delta$ consisting of the objects which admit a ‘standard flag’ behaves well. In our case, however, there are more extensions and the analogue of the category
$\mathcal {F}_\Delta$ consisting of the objects which admit a ‘standard flag’ behaves well. In our case, however, there are more extensions and the analogue of the category ![]() $\mathcal {F}_\Delta$ does not seem to behave well.
$\mathcal {F}_\Delta$ does not seem to behave well.
We analyze the modules in (1.1) directly using light leaves introduced by Libedinsky [Reference LibedinskyLib08]. Using Soergel's theorem, Libedinsky proved that the light leaves give a basis of a certain space of homomorphisms. In this paper, we prove Libedinsky's result directly and use it to prove Soergel's categorification theorem. The argument is new even for the original case.
1.4 Application
Let ![]() $G$ be a connected reductive group defined over an algebraically closed field of positive characteristic and
$G$ be a connected reductive group defined over an algebraically closed field of positive characteristic and ![]() $T$ a maximal torus. Then we give an action of our category (or equivalently, the category of Elias and Williamson) attached to the affine Weyl group of
$T$ a maximal torus. Then we give an action of our category (or equivalently, the category of Elias and Williamson) attached to the affine Weyl group of ![]() $G$ on a regular block of
$G$ on a regular block of ![]() $G_1T$-modules where
$G_1T$-modules where ![]() $G_1$ is the Frobenius kernel [Reference AbeAbe19]. This is a
$G_1$ is the Frobenius kernel [Reference AbeAbe19]. This is a ![]() $G_1T$-version of a conjecture of Riche and Williamson [Reference Riche and WilliamsonRW18].
$G_1T$-version of a conjecture of Riche and Williamson [Reference Riche and WilliamsonRW18].
1.5 Organization of the paper
In the next section we introduce our category and give basic properties of it. We also introduce the notation on Hecke algebras. In § 3 we recall the definition of light leaves. Using the light leaves, we prove freeness of certain modules and calculate the graded ranks. In § 4 we prove the categorification theorem based on the theorems in § 3. In the final section we compare our category with the other categories.
2. The category
We construct the main category in this paper and prove some basic properties. We follow the notation in [Reference Elias and WilliamsonEW16].
2.1 A representation
Throughout this paper let ![]() $(W,S)$ be a Coxeter system such that
$(W,S)$ be a Coxeter system such that ![]() $\#S < \infty$, and let
$\#S < \infty$, and let ![]() $\mathbb {K}$ be a Noetherian integral domain. The length function
$\mathbb {K}$ be a Noetherian integral domain. The length function ![]() $W\to \mathbb {Z}_{\ge 0}$ of
$W\to \mathbb {Z}_{\ge 0}$ of ![]() $W$ is denoted by
$W$ is denoted by ![]() $\ell$ and the Bruhat order on
$\ell$ and the Bruhat order on ![]() $W$ is denoted by
$W$ is denoted by ![]() $\le$.
$\le$.
Let ![]() $(V,\{\alpha _s\}_{s\in S},\{\alpha _s^{\vee }\}_{s\in S})$ be a triple such that:
$(V,\{\alpha _s\}_{s\in S},\{\alpha _s^{\vee }\}_{s\in S})$ be a triple such that:
•
 $V$ is a free
$V$ is a free  $\mathbb {K}$-module of finite rank with a
$\mathbb {K}$-module of finite rank with a  $\mathbb {K}$-linear action of
$\mathbb {K}$-linear action of  $W$;
$W$;•
 $\alpha _s\in V$,
$\alpha _s\in V$,  $\alpha _s^{\vee }\in V^{*}$ where
$\alpha _s^{\vee }\in V^{*}$ where  $V^{*} = \operatorname {Hom}_{\mathbb {K}}(V,\mathbb {K})$.
$V^{*} = \operatorname {Hom}_{\mathbb {K}}(V,\mathbb {K})$.
We assume that this satisfies:
(1)
 $\langle \alpha _s^{\vee },\alpha _s\rangle = 2$ for each
$\langle \alpha _s^{\vee },\alpha _s\rangle = 2$ for each  $s\in S$;
$s\in S$;(2)
 $s(v) = v - \langle \alpha _s^{\vee },v\rangle \alpha _s$ for
$s(v) = v - \langle \alpha _s^{\vee },v\rangle \alpha _s$ for  $s\in S$ and
$s\in S$ and  $v\in V$;
$v\in V$;(3)
 $\alpha _s^{\vee }\colon V\to \mathbb {K}$ is surjective and
$\alpha _s^{\vee }\colon V\to \mathbb {K}$ is surjective and  $\alpha _s\ne 0$ for any
$\alpha _s\ne 0$ for any  $s\in S$.
$s\in S$.
Note that the third condition follows from the first condition if ![]() $2\in \mathbb {K}^{\times }$. Later we will add one more assumption (Assumption 3.2).
$2\in \mathbb {K}^{\times }$. Later we will add one more assumption (Assumption 3.2).
A triple which satisfies conditions (1) and (2) is called a realization if it satisfies one more technical condition in [Reference Elias and WilliamsonEW16, Definition 3.1]. Condition (3) is a part of the condition called Demazure surjectivity [Reference Elias and WilliamsonEW16, Assumption 3.9].
Set ![]() $R = S(V)$ and let
$R = S(V)$ and let ![]() $Q$ be the fraction field of
$Q$ be the fraction field of ![]() $R$. We regard
$R$. We regard ![]() $R$ as a graded algebra via
$R$ as a graded algebra via ![]() $\deg (V) = 2$. The action of the group
$\deg (V) = 2$. The action of the group ![]() $W$ on
$W$ on ![]() $V$ extends uniquely on
$V$ extends uniquely on ![]() $R$ by automorphisms of algebras. We remark that
$R$ by automorphisms of algebras. We remark that ![]() $R$ is a Noetherian integral domain.
$R$ is a Noetherian integral domain.
We call ![]() $t\in W$ a reflection if it is conjugate to an element in
$t\in W$ a reflection if it is conjugate to an element in ![]() $S$. Let
$S$. Let ![]() $t = wsw^{-1}$ be a reflection where
$t = wsw^{-1}$ be a reflection where ![]() $s\in S$ and
$s\in S$ and ![]() $w\in W$. Set
$w\in W$. Set ![]() $\alpha _t = w(\alpha _s)$. This depends on the choice of
$\alpha _t = w(\alpha _s)$. This depends on the choice of ![]() $s,w$ in general, so we fix such
$s,w$ in general, so we fix such ![]() $s,w$ to define
$s,w$ to define ![]() $\alpha _t$. By the following lemma,
$\alpha _t$. By the following lemma, ![]() $\mathbb {K}^{\times } \alpha _t$ does not depend on the choice of
$\mathbb {K}^{\times } \alpha _t$ does not depend on the choice of ![]() $s,w$.
$s,w$.
Lemma 2.1 If ![]() $wsw^{-1} = s'$ where
$wsw^{-1} = s'$ where ![]() $s,s'\in S$ and
$s,s'\in S$ and ![]() $w\in W$, then
$w\in W$, then ![]() $\alpha _{s'}\in \mathbb {K}^{\times } w(\alpha _s)$.
$\alpha _{s'}\in \mathbb {K}^{\times } w(\alpha _s)$.
Proof. Take ![]() $\delta \in V$ such that
$\delta \in V$ such that ![]() $\langle \alpha _s^{\vee },\delta \rangle = 1$. Then we have
$\langle \alpha _s^{\vee },\delta \rangle = 1$. Then we have ![]() $s(\delta ) = \delta - \alpha _s$. Hence
$s(\delta ) = \delta - \alpha _s$. Hence ![]() $s'(w(\delta )) = ws(\delta ) = w(\delta ) - w(\alpha _s)$. On the other hand, we have
$s'(w(\delta )) = ws(\delta ) = w(\delta ) - w(\alpha _s)$. On the other hand, we have ![]() $s'(w(\delta )) = w(\delta ) - r\alpha _{s'}$ where
$s'(w(\delta )) = w(\delta ) - r\alpha _{s'}$ where ![]() $r = \langle \alpha _{s'}^{\vee },w(\delta )\rangle \in \mathbb {K}$. Hence
$r = \langle \alpha _{s'}^{\vee },w(\delta )\rangle \in \mathbb {K}$. Hence ![]() $w(\alpha _s) = r\alpha _{s'}$. Replacing
$w(\alpha _s) = r\alpha _{s'}$. Replacing ![]() $s,w,s'$ with
$s,w,s'$ with ![]() $s',w^{-1},s$ respectively, there exists
$s',w^{-1},s$ respectively, there exists ![]() $r'$ such that
$r'$ such that ![]() $w^{-1}(\alpha _{s'}) = r'\alpha _s$. Therefore
$w^{-1}(\alpha _{s'}) = r'\alpha _s$. Therefore ![]() $w(\alpha _s) = r\alpha _{s'} = rr'w(\alpha _s)$. Since
$w(\alpha _s) = r\alpha _{s'} = rr'w(\alpha _s)$. Since ![]() $V$ is free,
$V$ is free, ![]() $\mathbb {K}$ is an integral domain and
$\mathbb {K}$ is an integral domain and ![]() $w(\alpha _s)\ne 0$, we have
$w(\alpha _s)\ne 0$, we have ![]() $rr' = 1$. Therefore
$rr' = 1$. Therefore ![]() $r,r'\in \mathbb {K}^{\times }$.
$r,r'\in \mathbb {K}^{\times }$.
2.2 The category
First we define the category ![]() $\mathcal {C}'$ as follows. The objects of
$\mathcal {C}'$ as follows. The objects of ![]() $\mathcal {C}'$ are
$\mathcal {C}'$ are ![]() $(M,(M_Q^{w})_{w\in W},\xi _M)$ where
$(M,(M_Q^{w})_{w\in W},\xi _M)$ where ![]() $M$ is a graded
$M$ is a graded ![]() $R$-bimodule,
$R$-bimodule, ![]() $M_Q^{w}$ is an
$M_Q^{w}$ is an ![]() $(R,Q)$-bimodule for each
$(R,Q)$-bimodule for each ![]() $w\in W$ and
$w\in W$ and ![]() $\xi _M$ is an isomorphism
$\xi _M$ is an isomorphism ![]() $\xi _M\colon M\otimes _{R}Q\xrightarrow {\sim } {\bigoplus} _{w\in W}\, M_Q^{w}$ as
$\xi _M\colon M\otimes _{R}Q\xrightarrow {\sim } {\bigoplus} _{w\in W}\, M_Q^{w}$ as ![]() $(R,Q)$-bimodules such that:
$(R,Q)$-bimodules such that:
•
 $M_Q^{w} \ne 0$ only for finite
$M_Q^{w} \ne 0$ only for finite  $w$;
$w$;• for
 $f\in R$ and
$f\in R$ and  $m\in M_Q^{w}$, we have
$m\in M_Q^{w}$, we have  $mf = w(f)m$.
$mf = w(f)m$.
A morphism ![]() $\varphi \colon (M,(M_Q^{w})_{w\in W},\xi _M)\to (N,(N_Q^{w})_{w\in W},\xi _N)$ in
$\varphi \colon (M,(M_Q^{w})_{w\in W},\xi _M)\to (N,(N_Q^{w})_{w\in W},\xi _N)$ in ![]() $\mathcal {C}'$ is a degree-zero
$\mathcal {C}'$ is a degree-zero ![]() $R$-bimodule homomorphism
$R$-bimodule homomorphism ![]() $\varphi \colon M\to N$ such that
$\varphi \colon M\to N$ such that ![]() $\xi _N\circ \varphi _Q\circ \xi _M^{-1}(M_Q^{w})\subset N_Q^{w}$ for any
$\xi _N\circ \varphi _Q\circ \xi _M^{-1}(M_Q^{w})\subset N_Q^{w}$ for any ![]() $w\in W$ where
$w\in W$ where ![]() $\varphi _Q\colon M\otimes _{R}Q\to N\otimes _{R}Q$ is the induced homomorphism. We often omit
$\varphi _Q\colon M\otimes _{R}Q\to N\otimes _{R}Q$ is the induced homomorphism. We often omit ![]() $M_Q^{w}$ and
$M_Q^{w}$ and ![]() $\xi _M$ from the notation. So we just say
$\xi _M$ from the notation. So we just say ![]() $M\in \mathcal {C}'$.
$M\in \mathcal {C}'$.
Remark 2.2 By the second condition, the left action of ![]() $f\in R\setminus \{0\}$ on
$f\in R\setminus \{0\}$ on ![]() $M_Q^{w}$ is invertible. Therefore it is also invertible on
$M_Q^{w}$ is invertible. Therefore it is also invertible on ![]() $M\otimes _R Q$, and therefore
$M\otimes _R Q$, and therefore ![]() $M\otimes _R Q$ is a
$M\otimes _R Q$ is a ![]() $Q$-bimodule. The isomorphism
$Q$-bimodule. The isomorphism ![]() $\xi _M\colon M\otimes _R Q \simeq {\bigoplus} _{w\in W}\, M_Q^{w}$ is an isomorphism as
$\xi _M\colon M\otimes _R Q \simeq {\bigoplus} _{w\in W}\, M_Q^{w}$ is an isomorphism as ![]() $Q$-bimodules.
$Q$-bimodules.
Remark 2.3 If ![]() $V$ is a faithful
$V$ is a faithful ![]() $W$-representation, then, for any
$W$-representation, then, for any ![]() $(M,(M_Q^{w})_{w\in W},\xi _M)\in \mathcal {C}'$ and
$(M,(M_Q^{w})_{w\in W},\xi _M)\in \mathcal {C}'$ and ![]() $(N,(N_Q^{w})_{w\in W},\xi _N)\in \mathcal {C}'$, an
$(N,(N_Q^{w})_{w\in W},\xi _N)\in \mathcal {C}'$, an ![]() $R$-bimodule homomorphism
$R$-bimodule homomorphism ![]() $M\to N$ is automatically a morphism in
$M\to N$ is automatically a morphism in ![]() $\mathcal {C}'$. Therefore the functor
$\mathcal {C}'$. Therefore the functor ![]() $(M,(M_Q^{w})_{w\in W},\xi _M)\mapsto M$ is a fully faithful functor from
$(M,(M_Q^{w})_{w\in W},\xi _M)\mapsto M$ is a fully faithful functor from ![]() $\mathcal {C}'$ to the category of graded
$\mathcal {C}'$ to the category of graded ![]() $R$-bimodules. Hence the category
$R$-bimodules. Hence the category ![]() $\mathcal {C}'$ is equivalent to a full subcategory of the category of graded
$\mathcal {C}'$ is equivalent to a full subcategory of the category of graded ![]() $R$-bimodules.
$R$-bimodules.
We also define the full subcategory ![]() $\mathcal {C}$ of
$\mathcal {C}$ of ![]() $\mathcal {C}'$ as follows. For
$\mathcal {C}'$ as follows. For ![]() $M\in \mathcal {C}'$,
$M\in \mathcal {C}'$, ![]() $M\in \mathcal {C}$ if and only if
$M\in \mathcal {C}$ if and only if ![]() $M$ is finitely generated as an
$M$ is finitely generated as an ![]() $R$-bimodule and flat as a right
$R$-bimodule and flat as a right ![]() $R$-module. Let
$R$-module. Let ![]() $M\in \mathcal {C}$. Since
$M\in \mathcal {C}$. Since ![]() $M$ is flat as a right
$M$ is flat as a right ![]() $R$-module, it is torsion-free. Hence we have
$R$-module, it is torsion-free. Hence we have ![]() $M\hookrightarrow M\otimes _R Q = {\bigoplus} _{w\in W}\, M_Q^{w}$. In particular,
$M\hookrightarrow M\otimes _R Q = {\bigoplus} _{w\in W}\, M_Q^{w}$. In particular, ![]() $M$ is torsion-free as a left
$M$ is torsion-free as a left ![]() $R$-module. As in Remark 2.2,
$R$-module. As in Remark 2.2, ![]() $f\notin R\setminus \{0\}$ acts invertibly from the left on
$f\notin R\setminus \{0\}$ acts invertibly from the left on ![]() $M\otimes _R Q$. Hence we have a homomorphism
$M\otimes _R Q$. Hence we have a homomorphism ![]() $Q\otimes _R M\hookrightarrow M\otimes _R Q$. It is not difficult to see that this is an isomorphism.
$Q\otimes _R M\hookrightarrow M\otimes _R Q$. It is not difficult to see that this is an isomorphism.
For ![]() $w\in W$, let
$w\in W$, let ![]() $R_w$ be an object of
$R_w$ be an object of ![]() $\mathcal {C}$ defined as follows. As a left
$\mathcal {C}$ defined as follows. As a left ![]() $R$-module,
$R$-module, ![]() $R_w = R$ and the bimodule structure is given by
$R_w = R$ and the bimodule structure is given by ![]() $mf = w(f)m$ for
$mf = w(f)m$ for ![]() $m\in R_w$ and
$m\in R_w$ and ![]() $f\in R$. The module
$f\in R$. The module ![]() $(R_w)_Q^{x}$ is given by
$(R_w)_Q^{x}$ is given by
 \[ (R_w)_Q^{x} = \begin{cases} Q & (x = w),\\ 0 & (x\ne w). \end{cases} \]
\[ (R_w)_Q^{x} = \begin{cases} Q & (x = w),\\ 0 & (x\ne w). \end{cases} \]
We denote ![]() $Q_w = R_w\otimes _R Q$ which is a
$Q_w = R_w\otimes _R Q$ which is a ![]() $Q$-bimodule.
$Q$-bimodule.
Let ![]() $M\in \mathcal {C}$.
$M\in \mathcal {C}$.
• For
 $m\in M$, let
$m\in M$, let  $m_w$ be the image of
$m_w$ be the image of  $m$ under
$m$ under  $M\to {\bigoplus} _{w\in W}\, M_Q^{w}\twoheadrightarrow M_Q^{w}$.
$M\to {\bigoplus} _{w\in W}\, M_Q^{w}\twoheadrightarrow M_Q^{w}$.• We set
 $M_Q = M\otimes _R Q$.
$M_Q = M\otimes _R Q$.• For
 $I\subset W$, let
$I\subset W$, let  $M_I$ (respectively,
$M_I$ (respectively,  $M^{I}$) be the inverse image of
$M^{I}$) be the inverse image of  ${\bigoplus} _{w\in I}\, M_Q^{w}$ in
${\bigoplus} _{w\in I}\, M_Q^{w}$ in  $M$ (respectively, the image of
$M$ (respectively, the image of  $M$ in
$M$ in  ${\bigoplus} _{w\in I}\, M_Q^{w}$). We regard
${\bigoplus} _{w\in I}\, M_Q^{w}$). We regard  $M_I\subset M^{I}\subset {\bigoplus} _{w\in I}\, M_Q^{w}$.
$M_I\subset M^{I}\subset {\bigoplus} _{w\in I}\, M_Q^{w}$.• For
 $w\in W$, we write
$w\in W$, we write  $M_w$ (respectively,
$M_w$ (respectively,  $M^{w}$) for
$M^{w}$) for  $M_{\{w\}}$ (respectively,
$M_{\{w\}}$ (respectively,  $M^{\{w\}}$).
$M^{\{w\}}$).• We write
 $\operatorname {supp}_W(M) = \{w\in W\mid M_Q^{w}\ne 0\}$ and
$\operatorname {supp}_W(M) = \{w\in W\mid M_Q^{w}\ne 0\}$ and  $\operatorname {supp}_W(m) = \{w\in W\mid m_w \ne 0\}$ for
$\operatorname {supp}_W(m) = \{w\in W\mid m_w \ne 0\}$ for  $m\in M$.
$m\in M$.
We have ![]() $M_I = \{m\in M\mid \operatorname {supp}_W(m)\subset I\}$.
$M_I = \{m\in M\mid \operatorname {supp}_W(m)\subset I\}$.
Lemma 2.4 The modules ![]() $M_I$ and
$M_I$ and ![]() $M^{I}$ are both objects in
$M^{I}$ are both objects in ![]() $\mathcal {C}'$ such that
$\mathcal {C}'$ such that ![]() $(M_I)_Q \simeq (M^{I})_Q \simeq {\bigoplus} _{w\in I}\, M_Q^{w}$.
$(M_I)_Q \simeq (M^{I})_Q \simeq {\bigoplus} _{w\in I}\, M_Q^{w}$.
Proof. Since ![]() $M_I\hookrightarrow M^{I}\subset {\bigoplus} _{w\in I}\, M_Q^{w}$, we have
$M_I\hookrightarrow M^{I}\subset {\bigoplus} _{w\in I}\, M_Q^{w}$, we have ![]() $M_I\otimes Q\hookrightarrow M^{I}\otimes Q\subset {\bigoplus} _{w\in I}\, M_Q^{w}$. Hence it is sufficient to prove that
$M_I\otimes Q\hookrightarrow M^{I}\otimes Q\subset {\bigoplus} _{w\in I}\, M_Q^{w}$. Hence it is sufficient to prove that ![]() $M_I\otimes Q\hookrightarrow {\bigoplus} _{w\in I}\, M_Q^{w}$ is surjective. Let
$M_I\otimes Q\hookrightarrow {\bigoplus} _{w\in I}\, M_Q^{w}$ is surjective. Let ![]() $m\in {\bigoplus} _{w\in I}\, M_Q^{w} \subset M_Q$ and take
$m\in {\bigoplus} _{w\in I}\, M_Q^{w} \subset M_Q$ and take ![]() $0\ne f\in R$ such that
$0\ne f\in R$ such that ![]() $fm \in M$. Then we have
$fm \in M$. Then we have ![]() $fm_w = (fm)_w = 0$ for any
$fm_w = (fm)_w = 0$ for any ![]() $w\in W\setminus I$. Since
$w\in W\setminus I$. Since ![]() $M_Q^{w}$ is torsion-free,
$M_Q^{w}$ is torsion-free, ![]() $m_w = 0$. Therefore
$m_w = 0$. Therefore ![]() $m\in (M_I)_Q$.
$m\in (M_I)_Q$.
The following lemma is clear from the definitions.
Lemma 2.5 Let ![]() $I\subset W$ and
$I\subset W$ and ![]() $M,N\in \mathcal {C}$ such that
$M,N\in \mathcal {C}$ such that ![]() $\operatorname {supp}_W(N)\subset I$. Then we have
$\operatorname {supp}_W(N)\subset I$. Then we have ![]() $\operatorname {Hom}_{\mathcal {C}'}(M,N)\simeq \operatorname {Hom}_{\mathcal {C}'}(M^{I},N)$ and
$\operatorname {Hom}_{\mathcal {C}'}(M,N)\simeq \operatorname {Hom}_{\mathcal {C}'}(M^{I},N)$ and ![]() $\operatorname {Hom}_{\mathcal {C}'}(N,M)\simeq \operatorname {Hom}_{\mathcal {C}'}(N,M_I)$.
$\operatorname {Hom}_{\mathcal {C}'}(N,M)\simeq \operatorname {Hom}_{\mathcal {C}'}(N,M_I)$.
Lemma 2.6 Any ![]() $M\in \mathcal {C}$ is finitely generated as a left (respectively, right)
$M\in \mathcal {C}$ is finitely generated as a left (respectively, right) ![]() $R$-module.
$R$-module.
Proof. We only prove that ![]() $M$ is finitely generated as a left
$M$ is finitely generated as a left ![]() $R$-module. Since
$R$-module. Since ![]() $M^{w}$ is a quotient of
$M^{w}$ is a quotient of ![]() $M$, this is also a finitely generated
$M$, this is also a finitely generated ![]() $R$-bimodule. The formula
$R$-bimodule. The formula ![]() $mf = w(f)m$ for
$mf = w(f)m$ for ![]() $f\in R$,
$f\in R$, ![]() $m\in M^{w}$ says that
$m\in M^{w}$ says that ![]() $M^{w}$ is also finitely generated as a left
$M^{w}$ is also finitely generated as a left ![]() $R$-module. Since
$R$-module. Since ![]() $M\hookrightarrow {\bigoplus} _{w\in W}\, M^{w}$ and
$M\hookrightarrow {\bigoplus} _{w\in W}\, M^{w}$ and ![]() $M^{w} \ne 0$ only for finite
$M^{w} \ne 0$ only for finite ![]() $w$,
$w$, ![]() $M$ is a finitely generated left
$M$ is a finitely generated left ![]() $R$-module.
$R$-module.
We define a tensor product ![]() $M\otimes N$ of
$M\otimes N$ of ![]() $M = (M,(M_Q^{w})_{w\in W},\xi _M),(N,(N_Q^{w})_{w\in W},\xi _N)\in \mathcal {C}$ as follows. As an
$M = (M,(M_Q^{w})_{w\in W},\xi _M),(N,(N_Q^{w})_{w\in W},\xi _N)\in \mathcal {C}$ as follows. As an ![]() $R$-bimodule,
$R$-bimodule, ![]() $M\otimes N = M\otimes _R N$; put
$M\otimes N = M\otimes _R N$; put ![]() $(M\otimes N)_Q^{w} = {\bigoplus} _{xy = w}\, M_Q^{x}\otimes _Q N_Q^{y}$. An isomorphism
$(M\otimes N)_Q^{w} = {\bigoplus} _{xy = w}\, M_Q^{x}\otimes _Q N_Q^{y}$. An isomorphism ![]() $\xi _{M\otimes N}\colon (M\otimes _{R} N)_Q\simeq {\bigoplus} _{w\in W}\, (M\otimes N)_Q^{w}$ is naturally defined as
$\xi _{M\otimes N}\colon (M\otimes _{R} N)_Q\simeq {\bigoplus} _{w\in W}\, (M\otimes N)_Q^{w}$ is naturally defined as ![]() $M\otimes _{R} N\otimes _{R}Q \simeq M\otimes _{R}Q\otimes _{Q}N\otimes _{R}Q \simeq M_Q\otimes _{Q}N_Q \simeq {\bigoplus} _{x,y\in W}\, M_Q^{x}\otimes _{Q} N_Q^{y}$
$M\otimes _{R} N\otimes _{R}Q \simeq M\otimes _{R}Q\otimes _{Q}N\otimes _{R}Q \simeq M_Q\otimes _{Q}N_Q \simeq {\bigoplus} _{x,y\in W}\, M_Q^{x}\otimes _{Q} N_Q^{y}$ ![]() ${\bigoplus} _{w\in W}\,(M\otimes N)_Q^{w}$ where we used the fact that
${\bigoplus} _{w\in W}\,(M\otimes N)_Q^{w}$ where we used the fact that ![]() $N_Q$ is a
$N_Q$ is a ![]() $Q$-bimodule. This gives a monoidal category structure on
$Q$-bimodule. This gives a monoidal category structure on ![]() $\mathcal {C}$. The unit object is
$\mathcal {C}$. The unit object is ![]() $R_e$ where
$R_e$ where ![]() $e$ is the unit element of
$e$ is the unit element of ![]() $W$. The following result is obvious from the definition.
$W$. The following result is obvious from the definition.
Lemma 2.7 We have ![]() $\operatorname {supp}_W(M\otimes N) = \{xy \mid x\in \operatorname {supp}_W(M),y\in \operatorname {supp}_W(N)\}$.
$\operatorname {supp}_W(M\otimes N) = \{xy \mid x\in \operatorname {supp}_W(M),y\in \operatorname {supp}_W(N)\}$.
2.3 Notes on gradings
Let ![]() $M = {\bigoplus} _{i\in \mathbb {Z}}\,M^{i}$ be a graded left
$M = {\bigoplus} _{i\in \mathbb {Z}}\,M^{i}$ be a graded left ![]() $R$-module, right
$R$-module, right ![]() $R$-module or
$R$-module or ![]() $R$-bimodule. The grading shift
$R$-bimodule. The grading shift ![]() $M(1)$ is defined as
$M(1)$ is defined as ![]() $M(1)^{i} = M^{i + 1}$. Therefore, for an element
$M(1)^{i} = M^{i + 1}$. Therefore, for an element ![]() $f\in R$ of degree
$f\in R$ of degree ![]() $k$, the multiplication
$k$, the multiplication ![]() $m\mapsto fm$ gives a degree-zero homomorphism
$m\mapsto fm$ gives a degree-zero homomorphism ![]() $M\to M(k)$ and the submodule
$M\to M(k)$ and the submodule ![]() $fR$ is isomorphic to
$fR$ is isomorphic to ![]() $R(-k)$. If
$R(-k)$. If ![]() $M$ is a graded free left
$M$ is a graded free left ![]() $R$-module, namely
$R$-module, namely ![]() $M\simeq {\bigoplus} _i\, R(n_i)$ for
$M\simeq {\bigoplus} _i\, R(n_i)$ for ![]() $n_i\in \mathbb {Z}$, we define its graded rank
$n_i\in \mathbb {Z}$, we define its graded rank ![]() $\operatorname {grk}(M)$ by
$\operatorname {grk}(M)$ by ![]() $\operatorname {grk}(M) = \sum _i v^{n_i}$ where
$\operatorname {grk}(M) = \sum _i v^{n_i}$ where ![]() $v$ is an indeterminate. Obviously we have
$v$ is an indeterminate. Obviously we have ![]() $\operatorname {grk}(M_1\oplus M_2) = \operatorname {grk}(M_1) + \operatorname {grk}(M_2)$ and
$\operatorname {grk}(M_1\oplus M_2) = \operatorname {grk}(M_1) + \operatorname {grk}(M_2)$ and ![]() $\operatorname {grk}(M(1)) = v\operatorname {grk}(M)$. If
$\operatorname {grk}(M(1)) = v\operatorname {grk}(M)$. If ![]() $M$ has a basis
$M$ has a basis ![]() $\{m_i\}$, then
$\{m_i\}$, then ![]() $\operatorname {grk}(M) = \sum _i v^{-\deg (m_i)}$.
$\operatorname {grk}(M) = \sum _i v^{-\deg (m_i)}$.
Lemma 2.8 Let ![]() $M\in \mathcal {C}$,
$M\in \mathcal {C}$, ![]() $w\in W$ and assume that
$w\in W$ and assume that ![]() $M^{w}$ is a graded free left
$M^{w}$ is a graded free left ![]() $R$-module. Then
$R$-module. Then ![]() $M^{w}\simeq {\bigoplus} _i\, R_w(n_i)$ for some
$M^{w}\simeq {\bigoplus} _i\, R_w(n_i)$ for some ![]() $n_i\in \mathbb {Z}$ as an object in
$n_i\in \mathbb {Z}$ as an object in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. The assumption says that we have an isomorphism ![]() $M^{w}\simeq {\bigoplus} _i\, R_w(n_i)$ as left
$M^{w}\simeq {\bigoplus} _i\, R_w(n_i)$ as left ![]() $R$-modules for some
$R$-modules for some ![]() $n_i\in \mathbb {Z}$. Since the right action of
$n_i\in \mathbb {Z}$. Since the right action of ![]() $f\in R$ is equal to the left action of
$f\in R$ is equal to the left action of ![]() $w(f)$ on both sides, this is an isomorphism as
$w(f)$ on both sides, this is an isomorphism as ![]() $R$-bimodules.
$R$-bimodules.
Lemma 2.9 Assume that ![]() $\mathbb {K}$ is a field. Let
$\mathbb {K}$ is a field. Let ![]() $M$ be a finitely generated graded free left
$M$ be a finitely generated graded free left ![]() $R$-module with the graded rank
$R$-module with the graded rank ![]() $p$ and
$p$ and ![]() $0 = M_0\subset M_1\subset M_2\subset \cdots \subset M_r = M$ be a filtration as graded left
$0 = M_0\subset M_1\subset M_2\subset \cdots \subset M_r = M$ be a filtration as graded left ![]() $R$-modules. Assume that there exists a graded free left
$R$-modules. Assume that there exists a graded free left ![]() $R$-submodule
$R$-submodule ![]() $N_i\subset M_i/M_{i - 1}$ with the graded rank
$N_i\subset M_i/M_{i - 1}$ with the graded rank ![]() $q^{(i)}$ such that
$q^{(i)}$ such that ![]() $\sum _i q^{(i)} = p$. Then we have
$\sum _i q^{(i)} = p$. Then we have ![]() $N_i = M_i/M_{i - 1}$.
$N_i = M_i/M_{i - 1}$.
Proof. Let ![]() $N_i^{l}$ (respectively,
$N_i^{l}$ (respectively, ![]() $M_i^{l}$,
$M_i^{l}$, ![]() $M^{l}$) be the
$M^{l}$) be the ![]() $l$th graded piece of
$l$th graded piece of ![]() $N_i$. Then we have
$N_i$. Then we have ![]() $\sum _i\dim N_i^{l} = \dim M^{l}$ by the assumption and we have
$\sum _i\dim N_i^{l} = \dim M^{l}$ by the assumption and we have ![]() $\dim M^{l} = \sum \dim (M_i/M_{i - 1})^{l}$. Hence
$\dim M^{l} = \sum \dim (M_i/M_{i - 1})^{l}$. Hence ![]() $N_i^{l} = (M_i/M_{i - 1})^{l}$ for any
$N_i^{l} = (M_i/M_{i - 1})^{l}$ for any ![]() $l$. Therefore we have
$l$. Therefore we have ![]() $N_i = M_i/M_{i - 1}$.
$N_i = M_i/M_{i - 1}$.
For ![]() $M,N\in \mathcal {C}'$, we put
$M,N\in \mathcal {C}'$, we put ![]() $\operatorname {Hom}_{\mathcal {C}'}^{\bullet }(M,N) = {\bigoplus} _{n\in \mathbb {Z}}\,\operatorname {Hom}_{\mathcal {C}'}(M,N(n))$. This has a natural structure of a graded
$\operatorname {Hom}_{\mathcal {C}'}^{\bullet }(M,N) = {\bigoplus} _{n\in \mathbb {Z}}\,\operatorname {Hom}_{\mathcal {C}'}(M,N(n))$. This has a natural structure of a graded ![]() $R$-bimodule defined by
$R$-bimodule defined by ![]() $(afb)(m) = af(bm)$ where
$(afb)(m) = af(bm)$ where ![]() $a,b\in R$,
$a,b\in R$, ![]() $f\in \operatorname {Hom}_{\mathcal {C}'}^{\bullet }(M,N)$ and
$f\in \operatorname {Hom}_{\mathcal {C}'}^{\bullet }(M,N)$ and ![]() $m\in M$. We also use a similar notation for other situations like the category of graded left
$m\in M$. We also use a similar notation for other situations like the category of graded left ![]() $R$-modules.
$R$-modules.
2.4 Soergel bimodules
Let ![]() $s\in S$ and set
$s\in S$ and set ![]() $R^{s} = \{f\in R\mid s(f) = f\}$. We define
$R^{s} = \{f\in R\mid s(f) = f\}$. We define ![]() $B_s\in \mathcal {C}$ by
$B_s\in \mathcal {C}$ by ![]() $B_s = R\otimes _{R^{s}}R(1)$. A structure as an object in
$B_s = R\otimes _{R^{s}}R(1)$. A structure as an object in ![]() $\mathcal {C}$ (namely,
$\mathcal {C}$ (namely, ![]() $Q$-bimodules
$Q$-bimodules ![]() $(B_s)_Q^{w}$ and
$(B_s)_Q^{w}$ and ![]() $\xi _{B_s}$) is determined by the condition
$\xi _{B_s}$) is determined by the condition ![]() $\operatorname {supp}_W(B_s) = \{e,s\}$ up to isomorphisms. Fix
$\operatorname {supp}_W(B_s) = \{e,s\}$ up to isomorphisms. Fix ![]() $\delta _s\in V$ such that
$\delta _s\in V$ such that ![]() $\langle \alpha _s^{\vee },\delta _s\rangle = 1$. Then an explicit description of the
$\langle \alpha _s^{\vee },\delta _s\rangle = 1$. Then an explicit description of the ![]() $Q$-bimodule
$Q$-bimodule ![]() $(B_s)_Q^{w}$ is
$(B_s)_Q^{w}$ is
 \begin{equation} \begin{aligned} (B_s)_Q^{e} & = Q(\delta_s \otimes 1 - 1 \otimes s(\delta_s))\simeq Q_e,\\ (B_s)_Q^{s} & = Q(\delta_s \otimes 1 - 1 \otimes \delta_s)\simeq Q_s. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} (B_s)_Q^{e} & = Q(\delta_s \otimes 1 - 1 \otimes s(\delta_s))\simeq Q_e,\\ (B_s)_Q^{s} & = Q(\delta_s \otimes 1 - 1 \otimes \delta_s)\simeq Q_s. \end{aligned} \end{equation}
The projection ![]() $B_s\to (B_s)_Q^{e}$ (respectively,
$B_s\to (B_s)_Q^{e}$ (respectively, ![]() $B_s\to (B_s)_Q^{s}$) is given by
$B_s\to (B_s)_Q^{s}$) is given by ![]() $f\otimes g\mapsto fg$ (respectively,
$f\otimes g\mapsto fg$ (respectively, ![]() $f\otimes g\mapsto fs(g)$). To prove this description is straightforward using the following lemma.
$f\otimes g\mapsto fs(g)$). To prove this description is straightforward using the following lemma.
Lemma 2.10 [Reference Elias and WilliamsonEW16, Claim 3.11]
We have ![]() $R = R^{s}\oplus \delta _s R^{s}$. Therefore
$R = R^{s}\oplus \delta _s R^{s}$. Therefore ![]() $B_s \simeq R(1)\oplus R(-1)$ as left or right
$B_s \simeq R(1)\oplus R(-1)$ as left or right ![]() $R$-modules.
$R$-modules.
Let ![]() $M\in \mathcal {C}$. Then we have
$M\in \mathcal {C}$. Then we have ![]() $B_s\otimes M\in \mathcal {C}$. We have
$B_s\otimes M\in \mathcal {C}$. We have ![]() $(B_s\otimes M)_Q^{w} = {\bigoplus} _{xy = w}\,(B_s)_Q^{x}\otimes M_Q^{y} = Q_e\otimes _Q M_Q^{w}\oplus Q_s\otimes _Q M_Q^{sw}$. We have
$(B_s\otimes M)_Q^{w} = {\bigoplus} _{xy = w}\,(B_s)_Q^{x}\otimes M_Q^{y} = Q_e\otimes _Q M_Q^{w}\oplus Q_s\otimes _Q M_Q^{sw}$. We have ![]() $Q_e\otimes M_Q^{w}\simeq M_Q^{w}$ and
$Q_e\otimes M_Q^{w}\simeq M_Q^{w}$ and ![]() $Q_s\otimes M_Q^{sw}\simeq M_Q^{sw}$ as right
$Q_s\otimes M_Q^{sw}\simeq M_Q^{sw}$ as right ![]() $Q$-modules. As left
$Q$-modules. As left ![]() $Q$-modules, we have
$Q$-modules, we have ![]() $Q_e\otimes M_Q^{w}\simeq M_Q^{w}$ but
$Q_e\otimes M_Q^{w}\simeq M_Q^{w}$ but ![]() $Q_s\otimes M_Q^{sw}$ is not isomorphic to
$Q_s\otimes M_Q^{sw}$ is not isomorphic to ![]() $M_Q^{sw}$. The action on the left-hand side is twisted by
$M_Q^{sw}$. The action on the left-hand side is twisted by ![]() $s$, that is, the action of
$s$, that is, the action of ![]() $f\in R$ on
$f\in R$ on ![]() $Q_s\otimes M_Q^{sw}$ is equal to the action of
$Q_s\otimes M_Q^{sw}$ is equal to the action of ![]() $s(f)$ on
$s(f)$ on ![]() $M_Q^{sw}$.
$M_Q^{sw}$.
As ![]() $R$-bimodules,
$R$-bimodules, ![]() $B_s\otimes M = R\otimes _{R^{s}}M$. In terms of this description,
$B_s\otimes M = R\otimes _{R^{s}}M$. In terms of this description, ![]() $(B_s\otimes M)_Q^{w}$ is given as follows.
$(B_s\otimes M)_Q^{w}$ is given as follows.
Lemma 2.11 Let ![]() $s\in S$ and
$s\in S$ and ![]() $M\in \mathcal {C}$.
$M\in \mathcal {C}$.
(1) The projection
 $R\otimes _{R^{s}}M = B_s\otimes M\to (B_s\otimes M)_Q^{w} = M_Q^{w}\oplus M_Q^{sw}$ is given by
$R\otimes _{R^{s}}M = B_s\otimes M\to (B_s\otimes M)_Q^{w} = M_Q^{w}\oplus M_Q^{sw}$ is given by  $f\otimes m\mapsto (fm_w,s(f)m_{sw})$.
$f\otimes m\mapsto (fm_w,s(f)m_{sw})$.(2) We have
 \begin{align*} (B_s\otimes M)_Q^{w} = \{(\delta _s\otimes m - 1\otimes s(\delta _s)m) + (\delta _s\otimes m' - 1\otimes \delta _s m')\mid m\in M_Q^{w},m'\in M_Q^{sw}\}. \end{align*}
\begin{align*} (B_s\otimes M)_Q^{w} = \{(\delta _s\otimes m - 1\otimes s(\delta _s)m) + (\delta _s\otimes m' - 1\otimes \delta _s m')\mid m\in M_Q^{w},m'\in M_Q^{sw}\}. \end{align*}
The following result is straightforward, for example from the above lemma.
Lemma 2.12 Let ![]() $s\in S$ and
$s\in S$ and ![]() $M\in \mathcal {C}$. We have
$M\in \mathcal {C}$. We have ![]() $(B_s\otimes M)_{Q}^{w} + (B_s\otimes M)_{Q}^{sw} = B_s\otimes _R M_Q^{w} + B_s\otimes _R M_Q^{sw}$.
$(B_s\otimes M)_{Q}^{w} + (B_s\otimes M)_{Q}^{sw} = B_s\otimes _R M_Q^{w} + B_s\otimes _R M_Q^{sw}$.
Let ![]() $\mathcal {BS}$ be the full subcategory of
$\mathcal {BS}$ be the full subcategory of ![]() $\mathcal {C}$ such that the objects are
$\mathcal {C}$ such that the objects are ![]() $\{B_{s_1}\otimes \cdots \otimes B_{s_l}(n)\mid s_1,\ldots ,s_l\in S,n\in \mathbb {Z}\}$ and the category
$\{B_{s_1}\otimes \cdots \otimes B_{s_l}(n)\mid s_1,\ldots ,s_l\in S,n\in \mathbb {Z}\}$ and the category ![]() $\mathcal {S}\mathrm {Bimod}$ is defined as a full subcategory of
$\mathcal {S}\mathrm {Bimod}$ is defined as a full subcategory of ![]() $\mathcal {C}$ whose objects are direct summands of objects in the category
$\mathcal {C}$ whose objects are direct summands of objects in the category ![]() $\mathcal {BS}$. Obviously these categories are stable under the tensor products.
$\mathcal {BS}$. Obviously these categories are stable under the tensor products.
For ![]() $\underline {x} = (s_1,\ldots ,s_l)\in S^{l}$, we put
$\underline {x} = (s_1,\ldots ,s_l)\in S^{l}$, we put ![]() $B_{\underline {x}} = B_{s_1}\otimes \cdots \otimes B_{s_l}$. By Lemma 2.7, we get the following result.
$B_{\underline {x}} = B_{s_1}\otimes \cdots \otimes B_{s_l}$. By Lemma 2.7, we get the following result.
Lemma 2.13 We have ![]() $\operatorname {supp}_W(B_{\underline {x}}) = \{s_1^{e_1}\cdots s_l^{e_l}\mid e_i \in \{0,1\}\}$. In particular, if
$\operatorname {supp}_W(B_{\underline {x}}) = \{s_1^{e_1}\cdots s_l^{e_l}\mid e_i \in \{0,1\}\}$. In particular, if ![]() $\underline {x}$ is a reduced expression for
$\underline {x}$ is a reduced expression for ![]() $x\in W$, then
$x\in W$, then ![]() $\operatorname {supp}_W(B_{\underline {x}}) = \{y\in W\mid y\le x\}$.
$\operatorname {supp}_W(B_{\underline {x}}) = \{y\in W\mid y\le x\}$.
Since ![]() $B_s\otimes M \simeq M(-1) \oplus M(1)$ (respectively,
$B_s\otimes M \simeq M(-1) \oplus M(1)$ (respectively, ![]() $M\otimes B_s\simeq M(-1)\oplus M(1)$) as a right (respectively, left)
$M\otimes B_s\simeq M(-1)\oplus M(1)$) as a right (respectively, left) ![]() $R$-module, we get the following result.
$R$-module, we get the following result.
Lemma 2.14 The module ![]() $B_{\underline {x}}$ is graded free as a left (respectively, right)
$B_{\underline {x}}$ is graded free as a left (respectively, right) ![]() $R$-module and its graded rank is
$R$-module and its graded rank is ![]() $(v + v^{-1})^{l}$.
$(v + v^{-1})^{l}$.
Lemma 2.15 Let ![]() $M,N\in \mathcal {C}$ and
$M,N\in \mathcal {C}$ and ![]() $s\in S$. Then
$s\in S$. Then ![]() $\operatorname {Hom}_{\mathcal {C}}(B_s\otimes M,N)\simeq \operatorname {Hom}_{\mathcal {C}}(M,B_s\otimes N)$.
$\operatorname {Hom}_{\mathcal {C}}(B_s\otimes M,N)\simeq \operatorname {Hom}_{\mathcal {C}}(M,B_s\otimes N)$.
Proof. We regard ![]() $B_s\otimes M = R\otimes _{R^{s}}M(1)$ and
$B_s\otimes M = R\otimes _{R^{s}}M(1)$ and ![]() $B_s\otimes N = R\otimes _{R^{s}}N(1)$. Take
$B_s\otimes N = R\otimes _{R^{s}}N(1)$. Take ![]() $\delta \in V$ such that
$\delta \in V$ such that ![]() $\langle \alpha _s^{\vee },\delta \rangle = 1$. Let
$\langle \alpha _s^{\vee },\delta \rangle = 1$. Let ![]() $\varphi \colon B_s\otimes M\to N$ and define
$\varphi \colon B_s\otimes M\to N$ and define ![]() $\psi \colon M\to B_s\otimes N$ by
$\psi \colon M\to B_s\otimes N$ by ![]() $\psi (m) = 1\otimes \varphi (1\otimes \delta m) - s(\delta )\otimes \varphi (1\otimes m)$. Then, as in [Reference LibedinskyLib08, Lemma 3.3],
$\psi (m) = 1\otimes \varphi (1\otimes \delta m) - s(\delta )\otimes \varphi (1\otimes m)$. Then, as in [Reference LibedinskyLib08, Lemma 3.3], ![]() $\psi$ is an
$\psi$ is an ![]() $R$-bimodule homomorphism and this correspondence gives an isomorphism between the space of
$R$-bimodule homomorphism and this correspondence gives an isomorphism between the space of ![]() $R$-bimodule homomorphisms. We prove that this correspondence preserves homomorphisms in
$R$-bimodule homomorphisms. We prove that this correspondence preserves homomorphisms in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Let ![]() $a(m) = 1\otimes \delta m - s(\delta )\otimes m$ and
$a(m) = 1\otimes \delta m - s(\delta )\otimes m$ and ![]() $b(m) = 1\otimes \delta m - \delta \otimes m$. We have
$b(m) = 1\otimes \delta m - \delta \otimes m$. We have ![]() $a(m) = (\delta - (\delta + s(\delta )))\otimes m + 1\otimes \delta m $
$a(m) = (\delta - (\delta + s(\delta )))\otimes m + 1\otimes \delta m $ ![]() $= \delta \otimes m - 1\otimes (\delta + s(\delta ))m + 1\otimes \delta m = \delta \otimes m - 1\otimes s(\delta )m$. Hence
$= \delta \otimes m - 1\otimes (\delta + s(\delta ))m + 1\otimes \delta m = \delta \otimes m - 1\otimes s(\delta )m$. Hence ![]() $(B_s \otimes M)_Q^{w} = a(M_Q^{w}) + b(M_Q^{sw})$ by Lemma 2.11. By the definition of
$(B_s \otimes M)_Q^{w} = a(M_Q^{w}) + b(M_Q^{sw})$ by Lemma 2.11. By the definition of ![]() $\psi$ and Lemma 2.11, the image of
$\psi$ and Lemma 2.11, the image of ![]() $\psi (m)$ in
$\psi (m)$ in ![]() $(B_s\otimes N)_Q^{w}$ is
$(B_s\otimes N)_Q^{w}$ is ![]() $(\varphi (a(m))_w,\varphi (b(m))_{sw})$. Therefore
$(\varphi (a(m))_w,\varphi (b(m))_{sw})$. Therefore ![]() $\psi (m)$ is a homomorphism in
$\psi (m)$ is a homomorphism in ![]() $\mathcal {C}$ if and only if
$\mathcal {C}$ if and only if ![]() $\varphi (a(M_Q^{w}))_{y} = 0$ and
$\varphi (a(M_Q^{w}))_{y} = 0$ and ![]() $\varphi (b(M_Q^{w}))_{sy} = 0$ for any
$\varphi (b(M_Q^{w}))_{sy} = 0$ for any ![]() $w,y\in W$ such that
$w,y\in W$ such that ![]() $y\ne w$, if and only if
$y\ne w$, if and only if ![]() $\varphi (a(M_Q^{w}))\subset N_Q^{w}$ and
$\varphi (a(M_Q^{w}))\subset N_Q^{w}$ and ![]() $\varphi (b(M_Q^{sw}))\subset N_Q^{w}$ for any
$\varphi (b(M_Q^{sw}))\subset N_Q^{w}$ for any ![]() $w\in W$, if and only if
$w\in W$, if and only if ![]() $\varphi$ is a homomorphism in
$\varphi$ is a homomorphism in ![]() $\mathcal {C}$.
$\mathcal {C}$.
2.5 The Hecke algebra
In this paper we use the following definition of the Hecke algebra. Let ![]() $v$ be an indeterminate. The
$v$ be an indeterminate. The ![]() $\mathbb {Z}[v^{\pm 1}]$-algebra
$\mathbb {Z}[v^{\pm 1}]$-algebra ![]() $\mathcal {H}$ is generated by
$\mathcal {H}$ is generated by ![]() $\{H_w\mid w\in W\}$ and defined by the following relations.
$\{H_w\mid w\in W\}$ and defined by the following relations.
•
 $(H_s - v^{-1})(H_s + v) = 0$ for any
$(H_s - v^{-1})(H_s + v) = 0$ for any  $s\in S$.
$s\in S$.• If
 $\ell (w_1) + \ell (w_2) = \ell (w_1w_2)$ for
$\ell (w_1) + \ell (w_2) = \ell (w_1w_2)$ for  $w_1,w_2\in W$, we have
$w_1,w_2\in W$, we have  $H_{w_1w_2} = H_{w_1}H_{w_2}$.
$H_{w_1w_2} = H_{w_1}H_{w_2}$.
For ![]() $s\in S$, we put
$s\in S$, we put ![]() $\underline {H}_s = H_s + v$, and for
$\underline {H}_s = H_s + v$, and for ![]() $\underline {x} = (s_1,\ldots ,s_l)\in S^{l}$, we put
$\underline {x} = (s_1,\ldots ,s_l)\in S^{l}$, we put ![]() $\underline {H}_{\underline {x}} = \underline {H}_{s_1}\cdots \underline {H}_{s_l}$.
$\underline {H}_{\underline {x}} = \underline {H}_{s_1}\cdots \underline {H}_{s_l}$.
It is known that ![]() $\{H_w\mid w\in W\}$ is a basis of the
$\{H_w\mid w\in W\}$ is a basis of the ![]() $\mathbb {Z}[v^{\pm 1}]$-module
$\mathbb {Z}[v^{\pm 1}]$-module ![]() $\mathcal {H}$. We define
$\mathcal {H}$. We define ![]() $p_{\underline {x}}^{w}\in \mathbb {Z}[v^{\pm 1}]$ by
$p_{\underline {x}}^{w}\in \mathbb {Z}[v^{\pm 1}]$ by ![]() $\underline {H}_{\underline {x}} = \sum _{w\in W}p_{\underline {x}}^{w} H_w$.
$\underline {H}_{\underline {x}} = \sum _{w\in W}p_{\underline {x}}^{w} H_w$.
Lemma 2.16 We have ![]() $\sum _{w\in W}v^{\ell (w)}p_{\underline {x}}^{w}(v^{-1}) = (v + v^{-1})^{l}$.
$\sum _{w\in W}v^{\ell (w)}p_{\underline {x}}^{w}(v^{-1}) = (v + v^{-1})^{l}$.
Proof. By the defining relations, ![]() $H_w\mapsto v^{-\ell (w)}$ gives an algebra homomorphism
$H_w\mapsto v^{-\ell (w)}$ gives an algebra homomorphism ![]() $\mathcal {H}\to \mathbb {Z}[v^{\pm 1}]$. Applying this homomorphism to
$\mathcal {H}\to \mathbb {Z}[v^{\pm 1}]$. Applying this homomorphism to ![]() $\underline {H}_{\underline {x}} = \sum _{w\in W}p_{\underline {x}}^{w} H_w$, we get
$\underline {H}_{\underline {x}} = \sum _{w\in W}p_{\underline {x}}^{w} H_w$, we get ![]() $(v + v^{-1})^{l} = \sum _{w\in W}p_{\underline {x}}^{w}(v)v^{-\ell (w)}$. Replacing
$(v + v^{-1})^{l} = \sum _{w\in W}p_{\underline {x}}^{w}(v)v^{-\ell (w)}$. Replacing ![]() $v$ with
$v$ with ![]() $v^{-1}$, we get the lemma.
$v^{-1}$, we get the lemma.
Lemma 2.17 The dimension of ![]() $B_{\underline {x}}^{w} \otimes Q$ as a
$B_{\underline {x}}^{w} \otimes Q$ as a ![]() $Q$-vector space is
$Q$-vector space is ![]() $p_{\underline {x}}^{w}(1)$.
$p_{\underline {x}}^{w}(1)$.
Proof. After specializing ![]() $v$ to
$v$ to ![]() $1$,
$1$, ![]() $\mathcal {H}$ is isomorphic to the group algebra
$\mathcal {H}$ is isomorphic to the group algebra ![]() $\mathbb {Z}[W]$ via
$\mathbb {Z}[W]$ via ![]() $\mathcal {H}\ni H_w\mapsto w\in \mathbb {Z}[W]$. Therefore we have
$\mathcal {H}\ni H_w\mapsto w\in \mathbb {Z}[W]$. Therefore we have ![]() $(s_1 + 1)\cdots (s_l + 1) = \sum _w p_{(s_1,\ldots ,s_l)}^{w}(1)w$. Hence we have
$(s_1 + 1)\cdots (s_l + 1) = \sum _w p_{(s_1,\ldots ,s_l)}^{w}(1)w$. Hence we have
On the other hand, we have ![]() $(B_s\otimes M)_Q^{w} = M_Q^{w}\oplus M_Q^{sw}$ for any
$(B_s\otimes M)_Q^{w} = M_Q^{w}\oplus M_Q^{sw}$ for any ![]() $M\in \mathcal {C}$. Hence we have
$M\in \mathcal {C}$. Hence we have ![]() $\dim _Q(B_s\otimes M)^{w}_Q = \dim _Q(M_Q^{w}) + \dim _Q (M_Q^{sw})$. Now we get the lemma by induction on the length of
$\dim _Q(B_s\otimes M)^{w}_Q = \dim _Q(M_Q^{w}) + \dim _Q (M_Q^{sw})$. Now we get the lemma by induction on the length of ![]() $\underline {x}$.
$\underline {x}$.
2.6 Duality
Let ![]() $M\in \mathcal {C}$. Define a new module
$M\in \mathcal {C}$. Define a new module ![]() $D(M)\in \mathcal {C}'$ by
$D(M)\in \mathcal {C}'$ by
 \begin{align*} D(M) & = \operatorname{Hom}^{{\bullet}}_{\text{-}R}(M,R),\\ D(M)_Q^{w} & = \operatorname{Hom}_{\text{-}Q}(M_Q^{w},Q). \end{align*}
\begin{align*} D(M) & = \operatorname{Hom}^{{\bullet}}_{\text{-}R}(M,R),\\ D(M)_Q^{w} & = \operatorname{Hom}_{\text{-}Q}(M_Q^{w},Q). \end{align*}
Here ![]() $\operatorname {Hom}^{\bullet }_{\text{-}R}$ means the space of homomorphisms as right
$\operatorname {Hom}^{\bullet }_{\text{-}R}$ means the space of homomorphisms as right ![]() $R$-modules and the
$R$-modules and the ![]() $R$-bimodule structure is given by
$R$-bimodule structure is given by ![]() $(afb)(m) = f(amb)$ for
$(afb)(m) = f(amb)$ for ![]() $f\in D(M)$,
$f\in D(M)$, ![]() $a,b\in R$ and
$a,b\in R$ and ![]() $m\in M$. Since
$m\in M$. Since ![]() $M$ is a finitely generated right
$M$ is a finitely generated right ![]() $R$-module, we have
$R$-module, we have ![]() $D(M)\otimes Q = \operatorname {Hom}_{\text{-}Q}(M_Q,Q) = {\bigoplus} _{w\in W}\, D(M)_Q^{w}$. Therefore
$D(M)\otimes Q = \operatorname {Hom}_{\text{-}Q}(M_Q,Q) = {\bigoplus} _{w\in W}\, D(M)_Q^{w}$. Therefore ![]() $D(M)\in \mathcal {C}'$. For
$D(M)\in \mathcal {C}'$. For ![]() $\varphi \in D(M)$ and
$\varphi \in D(M)$ and ![]() $w\in W$,
$w\in W$, ![]() $\varphi _w$ is the restriction of
$\varphi _w$ is the restriction of ![]() $\varphi \otimes \mathrm {Id}\colon M\otimes _{R}Q \simeq {\bigoplus} _{w\in W}\, M_Q^{w} \to Q$ to
$\varphi \otimes \mathrm {Id}\colon M\otimes _{R}Q \simeq {\bigoplus} _{w\in W}\, M_Q^{w} \to Q$ to ![]() $M_Q^{w}$.
$M_Q^{w}$.
Lemma 2.18 We have ![]() $D(M^{I})\simeq D(M)_I$ for any
$D(M^{I})\simeq D(M)_I$ for any ![]() $I\subset W$.
$I\subset W$.
Proof. Since ![]() $M^{I}$ is a quotient of
$M^{I}$ is a quotient of ![]() $M$, we have that
$M$, we have that ![]() $D(M^{I})\subset D(M)$ and
$D(M^{I})\subset D(M)$ and ![]() $\psi \in D(M)$ is in
$\psi \in D(M)$ is in ![]() $D(M^{I})$ if and only if
$D(M^{I})$ if and only if ![]() $\psi$ is zero on
$\psi$ is zero on ![]() $M_{W\setminus I}$. Since
$M_{W\setminus I}$. Since ![]() $R$ is an integral domain,
$R$ is an integral domain, ![]() $\psi$ is zero on
$\psi$ is zero on ![]() $M_{W\setminus I}$ if and only if
$M_{W\setminus I}$ if and only if ![]() $\mathrm {Id}\otimes \psi$ is zero on
$\mathrm {Id}\otimes \psi$ is zero on ![]() $M_{W\setminus I}\otimes Q = {\bigoplus} _{w\in W\setminus I}\,M_Q^{w}$. That is,
$M_{W\setminus I}\otimes Q = {\bigoplus} _{w\in W\setminus I}\,M_Q^{w}$. That is, ![]() $\psi \in D(M)_I$.
$\psi \in D(M)_I$.
Lemma 2.19 Let ![]() $M\in \mathcal {C}$ and
$M\in \mathcal {C}$ and ![]() $w\in W$ and assume that
$w\in W$ and assume that ![]() $M^{w}$ is graded free as a left
$M^{w}$ is graded free as a left ![]() $R$-module.
$R$-module.
(1) The module
 $D(M)_w$ is also a graded free left
$D(M)_w$ is also a graded free left  $R$-module and its graded rank is given by
$R$-module and its graded rank is given by  $\operatorname {grk}(D(M)_w)(v) = \operatorname {grk}(M^{w})(v^{-1})$.
$\operatorname {grk}(D(M)_w)(v) = \operatorname {grk}(M^{w})(v^{-1})$.(2) We have
 $D(D(M)_w)\simeq M^{w}$.
$D(D(M)_w)\simeq M^{w}$.
Proof. We may assume ![]() $M^{w} = R_w(n)$ for some
$M^{w} = R_w(n)$ for some ![]() $n\in \mathbb {Z}$. Then
$n\in \mathbb {Z}$. Then ![]() $D(R_w(n))\simeq R_w(-n)$. Since
$D(R_w(n))\simeq R_w(-n)$. Since ![]() $D(M^{w})\simeq D(M)_w$, we get the first part. We also have
$D(M^{w})\simeq D(M)_w$, we get the first part. We also have ![]() $D(D(M^{w}))\simeq M^{w}$. Therefore we have
$D(D(M^{w}))\simeq M^{w}$. Therefore we have ![]() $D(D(M)_w)\simeq D(D(M^{w}))\simeq M^{w}$.
$D(D(M)_w)\simeq D(D(M^{w}))\simeq M^{w}$.
Lemma 2.20 We have ![]() $D(B_s\otimes M)\simeq B_s\otimes D(M)$ for any
$D(B_s\otimes M)\simeq B_s\otimes D(M)$ for any ![]() $M\in \mathcal {C}$ and
$M\in \mathcal {C}$ and ![]() $s\in S$. In particular, we have that
$s\in S$. In particular, we have that ![]() $D(B_{\underline {x}})\simeq B_{\underline {x}}$ for any
$D(B_{\underline {x}})\simeq B_{\underline {x}}$ for any ![]() $\underline {x}\in S^{l}$ and
$\underline {x}\in S^{l}$ and ![]() $D$ preserves
$D$ preserves ![]() $\mathcal {BS}$ and
$\mathcal {BS}$ and ![]() $\mathcal {S}\mathrm {Bimod}$.
$\mathcal {S}\mathrm {Bimod}$.
Proof. We regard ![]() $B_s\otimes (\cdot ) = R\otimes _{R^{s}}(\cdot )$.
$B_s\otimes (\cdot ) = R\otimes _{R^{s}}(\cdot )$.
Take ![]() $\delta \in V$ such that
$\delta \in V$ such that ![]() $\langle \alpha _s^{\vee },\delta \rangle = 1$. For
$\langle \alpha _s^{\vee },\delta \rangle = 1$. For ![]() $\varphi \in D(B_s\otimes M)$, define
$\varphi \in D(B_s\otimes M)$, define ![]() $\varphi _1,\varphi _2\colon M\to R$ by
$\varphi _1,\varphi _2\colon M\to R$ by ![]() $\varphi _1(m) = \varphi (1\otimes m)$ and
$\varphi _1(m) = \varphi (1\otimes m)$ and ![]() $\varphi _2(m) = \varphi (\delta \otimes m)$. It is clear that these are right
$\varphi _2(m) = \varphi (\delta \otimes m)$. It is clear that these are right ![]() $R$-homomorphisms, hence define elements of
$R$-homomorphisms, hence define elements of ![]() $D(M)$. Set
$D(M)$. Set ![]() $\Phi (\varphi ) = 1\otimes \varphi _2 - s(\delta )\otimes \varphi _1\in B_s\otimes D(M)$.
$\Phi (\varphi ) = 1\otimes \varphi _2 - s(\delta )\otimes \varphi _1\in B_s\otimes D(M)$.
We prove that ![]() $\Phi \colon D(B_s\otimes M)\to B_s\otimes D(M)$ is an
$\Phi \colon D(B_s\otimes M)\to B_s\otimes D(M)$ is an ![]() $R$-bimodule homomorphism. Clearly we have
$R$-bimodule homomorphism. Clearly we have ![]() $(\varphi f)_1 = \varphi _1 f$ and
$(\varphi f)_1 = \varphi _1 f$ and ![]() $(\varphi f)_2 = \varphi _2 f$, hence
$(\varphi f)_2 = \varphi _2 f$, hence ![]() $\Phi$ is a right
$\Phi$ is a right ![]() $R$-module homomorphism. If
$R$-module homomorphism. If ![]() $f\in R^{s}$, then
$f\in R^{s}$, then ![]() $(f\varphi )_1(m) = \varphi (f\otimes m) = \varphi (1\otimes fm) = (f(\varphi )_1)(m)$. Hence
$(f\varphi )_1(m) = \varphi (f\otimes m) = \varphi (1\otimes fm) = (f(\varphi )_1)(m)$. Hence ![]() $(f\varphi )_1 = f\varphi _1$, and similarly we have
$(f\varphi )_1 = f\varphi _1$, and similarly we have ![]() $(f\varphi )_2 = f\varphi _2$. Therefore
$(f\varphi )_2 = f\varphi _2$. Therefore ![]() $\Phi (f\varphi ) = 1\otimes f\varphi _2 - s(\delta )\otimes f\varphi _1 = f(1\otimes \varphi _2 - s(\delta )\otimes \varphi _1) = f\Phi (\varphi )$. We prove
$\Phi (f\varphi ) = 1\otimes f\varphi _2 - s(\delta )\otimes f\varphi _1 = f(1\otimes \varphi _2 - s(\delta )\otimes \varphi _1) = f\Phi (\varphi )$. We prove ![]() $\Phi (\delta \varphi ) = \delta \Phi (\varphi )$. We have
$\Phi (\delta \varphi ) = \delta \Phi (\varphi )$. We have
 \begin{align*} ((\delta \varphi )_2)(m) &= \varphi (\delta ^{2}\otimes m) \!=\! \varphi (\delta (\delta + s(\delta ))\otimes m \!- \delta s(\delta )\otimes m) \!=\! \varphi (\delta \otimes (\delta \!+ s(\delta ))m) - \varphi (1\otimes \delta s(\delta )m)\\ & = \varphi _2((\delta + s(\delta ))m) - \varphi _1(\delta s(\delta )m)= ((\delta + s(\delta ))\varphi _2 - \delta s(\delta )\varphi _1)(m). \end{align*}
\begin{align*} ((\delta \varphi )_2)(m) &= \varphi (\delta ^{2}\otimes m) \!=\! \varphi (\delta (\delta + s(\delta ))\otimes m \!- \delta s(\delta )\otimes m) \!=\! \varphi (\delta \otimes (\delta \!+ s(\delta ))m) - \varphi (1\otimes \delta s(\delta )m)\\ & = \varphi _2((\delta + s(\delta ))m) - \varphi _1(\delta s(\delta )m)= ((\delta + s(\delta ))\varphi _2 - \delta s(\delta )\varphi _1)(m). \end{align*}
We also have ![]() $(\delta \varphi )_1 = \varphi _2$. Hence
$(\delta \varphi )_1 = \varphi _2$. Hence
By Lemma 2.10, ![]() $\Phi$ is a left
$\Phi$ is a left ![]() $R$-module, hence an
$R$-module, hence an ![]() $R$-bimodule homomorphism.
$R$-bimodule homomorphism.
We prove that ![]() $\Phi$ is a morphism in
$\Phi$ is a morphism in ![]() $\mathcal {C}'$. Let
$\mathcal {C}'$. Let ![]() $\varphi \in D(B_s\otimes M)_Q^{w}$. Since
$\varphi \in D(B_s\otimes M)_Q^{w}$. Since ![]() $B_s\otimes M_Q^{y}\subset (B_s\otimes M)_Q^{y} + (B_s\otimes M)_Q^{sy}$ by Lemma 2.12,
$B_s\otimes M_Q^{y}\subset (B_s\otimes M)_Q^{y} + (B_s\otimes M)_Q^{sy}$ by Lemma 2.12, ![]() $\varphi _1,\varphi _2$ is zero on
$\varphi _1,\varphi _2$ is zero on ![]() $M_Q^{y}$ if
$M_Q^{y}$ if ![]() $y\ne w,sw$. Hence
$y\ne w,sw$. Hence ![]() $\operatorname {supp}_W(\varphi _1),\operatorname {supp}_W(\varphi _2)\subset \{w,sw\}$. Therefore
$\operatorname {supp}_W(\varphi _1),\operatorname {supp}_W(\varphi _2)\subset \{w,sw\}$. Therefore ![]() $\operatorname {supp}_W(\Phi (\varphi ))\subset \{w,sw\}$.
$\operatorname {supp}_W(\Phi (\varphi ))\subset \{w,sw\}$.
The homomorphism ![]() $\varphi$ is zero on
$\varphi$ is zero on ![]() $(B_s\otimes M)^{sw}_Q$. By Lemma 2.11,
$(B_s\otimes M)^{sw}_Q$. By Lemma 2.11, ![]() $\varphi (\delta \otimes m - 1\otimes s(\delta ) m) = 0$ for
$\varphi (\delta \otimes m - 1\otimes s(\delta ) m) = 0$ for ![]() $m\in M_Q^{sw}$. That is, we have
$m\in M_Q^{sw}$. That is, we have ![]() $(\varphi _2)_{sw} = s(\delta )(\varphi _1)_{sw}$. Similarly, we have
$(\varphi _2)_{sw} = s(\delta )(\varphi _1)_{sw}$. Similarly, we have ![]() $(\varphi _2)_w = \delta (\varphi _1)_w$. The image of
$(\varphi _2)_w = \delta (\varphi _1)_w$. The image of ![]() $\Phi (\varphi )$ in
$\Phi (\varphi )$ in ![]() $(B_s\otimes D(M))_Q^{sw} = D(M)_Q^{sw}\oplus D(M)_Q^{w}$ is
$(B_s\otimes D(M))_Q^{sw} = D(M)_Q^{sw}\oplus D(M)_Q^{w}$ is ![]() $((\varphi _2)_{sw} - s(\delta )(\varphi _1)_{sw},(\varphi _2)_w - \delta (\varphi _1)_w)$ and this is zero. Therefore
$((\varphi _2)_{sw} - s(\delta )(\varphi _1)_{sw},(\varphi _2)_w - \delta (\varphi _1)_w)$ and this is zero. Therefore ![]() $\operatorname {supp}_W(\Phi (\varphi ))\subset \{w\}$.
$\operatorname {supp}_W(\Phi (\varphi ))\subset \{w\}$.
Since ![]() $B_s = 1\otimes R\oplus \delta _s\otimes R$, we have
$B_s = 1\otimes R\oplus \delta _s\otimes R$, we have ![]() $D(B_s\otimes M) = D(1\otimes M\oplus \delta _s\otimes M) = D(1\otimes M)\oplus D(\delta _s\otimes M)$. Then
$D(B_s\otimes M) = D(1\otimes M\oplus \delta _s\otimes M) = D(1\otimes M)\oplus D(\delta _s\otimes M)$. Then ![]() $\Phi$ sends
$\Phi$ sends ![]() $D(1\otimes M)$ (respectively,
$D(1\otimes M)$ (respectively, ![]() $D(\delta _s\otimes M)$) to
$D(\delta _s\otimes M)$) to ![]() $s(\delta )\otimes D(M)$ (respectively,
$s(\delta )\otimes D(M)$ (respectively, ![]() $1\otimes D(M)$). Since
$1\otimes D(M)$). Since ![]() $B_s\otimes D(M) = s(\delta )\otimes D(M)\oplus 1\otimes D(M)$, we have proved that
$B_s\otimes D(M) = s(\delta )\otimes D(M)\oplus 1\otimes D(M)$, we have proved that ![]() $\Phi$ is an isomorphism.
$\Phi$ is an isomorphism.
3. Light leaves
In this section we construct light leaves. These are certain homomorphisms between objects of the form ![]() $B_{\underline {x}}$ where
$B_{\underline {x}}$ where ![]() $\underline {x}$ is a sequence of elements in
$\underline {x}$ is a sequence of elements in ![]() $S$. They were constructed by Libedinsky [Reference LibedinskyLib08] first in the case of the original Soergel bimodules and also constructed by Elias and Williamson [Reference Elias and WilliamsonEW16] for the diagrammatic category. We follow their constructions and prove properties of such homomorphisms. In particular, we give a basis of
$S$. They were constructed by Libedinsky [Reference LibedinskyLib08] first in the case of the original Soergel bimodules and also constructed by Elias and Williamson [Reference Elias and WilliamsonEW16] for the diagrammatic category. We follow their constructions and prove properties of such homomorphisms. In particular, we give a basis of ![]() $B_{\underline {x}}^{w}$. In the next section, using this basis, we calculate the character (which will be defined in the next section) of
$B_{\underline {x}}^{w}$. In the next section, using this basis, we calculate the character (which will be defined in the next section) of ![]() $B_{\underline {x}}$. This is key to the proof of our categorification theorem.
$B_{\underline {x}}$. This is key to the proof of our categorification theorem.
3.1 Notation
Let ![]() $\underline {x} \in S^{l}$ and
$\underline {x} \in S^{l}$ and ![]() $\boldsymbol {e} = (\boldsymbol {e}_1,\ldots ,\boldsymbol {e}_l)\in \{0,1\}^{l}$. We set
$\boldsymbol {e} = (\boldsymbol {e}_1,\ldots ,\boldsymbol {e}_l)\in \{0,1\}^{l}$. We set ![]() $\underline {x}^{\boldsymbol {e}} = s_1^{\boldsymbol {e}_1}\ldots s_l^{\boldsymbol {e}_l}\in W$. Let
$\underline {x}^{\boldsymbol {e}} = s_1^{\boldsymbol {e}_1}\ldots s_l^{\boldsymbol {e}_l}\in W$. Let ![]() $x_0 = 1,x_1 = s_1^{\boldsymbol {e}_1}, x_2 = s_1^{\boldsymbol {e}_1}s_2^{\boldsymbol {e}_2},\ldots ,x_l = s_1^{\boldsymbol {e}_1}\cdots s_l^{\boldsymbol {e}_l} = \underline {x}^{\boldsymbol {e}}$. Using this sequence, we add a label to
$x_0 = 1,x_1 = s_1^{\boldsymbol {e}_1}, x_2 = s_1^{\boldsymbol {e}_1}s_2^{\boldsymbol {e}_2},\ldots ,x_l = s_1^{\boldsymbol {e}_1}\cdots s_l^{\boldsymbol {e}_l} = \underline {x}^{\boldsymbol {e}}$. Using this sequence, we add a label to ![]() $\boldsymbol {e}$ at each index. We assign
$\boldsymbol {e}$ at each index. We assign ![]() $U$ to the index
$U$ to the index ![]() $i$ if
$i$ if ![]() $x_{i - 1}s_i > x_{i - 1}$ and
$x_{i - 1}s_i > x_{i - 1}$ and ![]() $D$ otherwise. The defect
$D$ otherwise. The defect ![]() $d(\boldsymbol {e})$ of
$d(\boldsymbol {e})$ of ![]() $\boldsymbol {e}$ is defined by
$\boldsymbol {e}$ is defined by
Of course, this number depends on ![]() $\underline {x}$, not just on
$\underline {x}$, not just on ![]() $\boldsymbol {e}$.
$\boldsymbol {e}$.
Lemma 3.1 [Reference Elias and WilliamsonEW16, Lemma 2.7]
We have ![]() $p_{\underline {x}}^{w}(v) = \sum _{\underline {x}^{\boldsymbol {e}} = w}v^{d(\boldsymbol {e})}$.
$p_{\underline {x}}^{w}(v) = \sum _{\underline {x}^{\boldsymbol {e}} = w}v^{d(\boldsymbol {e})}$.
3.2 Assumption
For ![]() $\underline {x}\in S^{l}$, define
$\underline {x}\in S^{l}$, define ![]() $u_{\underline {x}}\in B_{\underline {x}}$ by
$u_{\underline {x}}\in B_{\underline {x}}$ by ![]() $u_{\underline {x}} = (1\otimes 1)\otimes (1\otimes 1)\otimes \cdots \otimes (1\otimes 1)$. To construct the light leaves, we need the following assumption.
$u_{\underline {x}} = (1\otimes 1)\otimes (1\otimes 1)\otimes \cdots \otimes (1\otimes 1)$. To construct the light leaves, we need the following assumption.
Assumption 3.2 For any ![]() $s,t\in S$ such that
$s,t\in S$ such that ![]() $s\ne t$ and the order
$s\ne t$ and the order ![]() $m$ of
$m$ of ![]() $st$ is finite, we have the following assertion. Set
$st$ is finite, we have the following assertion. Set ![]() $\underline {x} = (s,t,\ldots )\in S^{m}$ and
$\underline {x} = (s,t,\ldots )\in S^{m}$ and ![]() $\underline {y} = (t,s,\ldots )\in S^{m}$. Then there exists a degree-zero morphism
$\underline {y} = (t,s,\ldots )\in S^{m}$. Then there exists a degree-zero morphism ![]() $B_{\underline {x}}\to B_{\underline {y}}$ in
$B_{\underline {x}}\to B_{\underline {y}}$ in ![]() $\mathcal {C}$ which sends
$\mathcal {C}$ which sends ![]() $u_{\underline {x}}$ to
$u_{\underline {x}}$ to ![]() $u_{\underline {y}}$.
$u_{\underline {y}}$.
We retain this assumption throughout the rest of this paper. It seems to be difficult to check this condition directly. We have the following sufficient condition.
Lemma 3.3 If the following condition holds for any ![]() $s,t\in S$ such that
$s,t\in S$ such that ![]() $st$ is of finite order, Assumption 3.2 holds.
$st$ is of finite order, Assumption 3.2 holds.
• Let
 $T'$ be the reflections in the group
$T'$ be the reflections in the group  $\langle s,t\rangle$ generated by
$\langle s,t\rangle$ generated by  $\{s,t\}$. For any
$\{s,t\}$. For any  $t_1,t_2\in T'$ with
$t_1,t_2\in T'$ with  $t_1\ne t_2$, there exists
$t_1\ne t_2$, there exists  $v\in V$ such that
$v\in V$ such that  $\langle v,\alpha _{t_1}^{\vee } \rangle = 0$,
$\langle v,\alpha _{t_1}^{\vee } \rangle = 0$,  $\langle v,\alpha _{t_2}^{\vee }\rangle = 1$.
$\langle v,\alpha _{t_2}^{\vee }\rangle = 1$.
Assume that ![]() $\mathbb {K}$ is a field and the representation
$\mathbb {K}$ is a field and the representation ![]() $V$ restricted to
$V$ restricted to ![]() $\langle s,t\rangle$ is reflection faithful. Then Soergel's categorification theorem holds for
$\langle s,t\rangle$ is reflection faithful. Then Soergel's categorification theorem holds for ![]() $\langle s,t\rangle$. Let
$\langle s,t\rangle$. Let ![]() $w_0$ be the longest element in
$w_0$ be the longest element in ![]() $\langle s,t\rangle$. Then there exists a corresponding indecomposable object
$\langle s,t\rangle$. Then there exists a corresponding indecomposable object ![]() $B(w_0)$ which is a direct summand of
$B(w_0)$ which is a direct summand of ![]() $B_{\underline {x}}$ and
$B_{\underline {x}}$ and ![]() $B_{\underline {y}}$. Therefore we have a map
$B_{\underline {y}}$. Therefore we have a map ![]() $B_{\underline {x}}\twoheadrightarrow B(w_0)\hookrightarrow B_{\underline {y}}$, and after suitable normalization this gives the desired map of the assumption. The proof of the above lemma basically follows this argument. In the proof below, we follow Soergel's argument in [Reference SoergelSoe07].
$B_{\underline {x}}\twoheadrightarrow B(w_0)\hookrightarrow B_{\underline {y}}$, and after suitable normalization this gives the desired map of the assumption. The proof of the above lemma basically follows this argument. In the proof below, we follow Soergel's argument in [Reference SoergelSoe07].
In the rest of this subsection let ![]() $s,t\in S$ be as in the lemma and set
$s,t\in S$ be as in the lemma and set ![]() $W' = \langle s,t\rangle$. Let
$W' = \langle s,t\rangle$. Let ![]() $T'$ be the set of reflections in
$T'$ be the set of reflections in ![]() $W'$.
$W'$.
Lemma 3.4 The representation ![]() $V$ restricted to
$V$ restricted to ![]() $W'$ is faithful.
$W'$ is faithful.
Proof. Let ![]() $w\in W'$ and assume that
$w\in W'$ and assume that ![]() $w$ acts trivially on
$w$ acts trivially on ![]() $V$. Assume that the length of
$V$. Assume that the length of ![]() $w$ is odd. If
$w$ is odd. If ![]() $\ell (w) > 1$, then, for
$\ell (w) > 1$, then, for ![]() $s' = s$ or
$s' = s$ or ![]() $t$, we have
$t$, we have ![]() $\ell (s'ws') < \ell (w)$ and
$\ell (s'ws') < \ell (w)$ and ![]() $s'ws'$ is also acts trivially on
$s'ws'$ is also acts trivially on ![]() $V$. Therefore we conclude that
$V$. Therefore we conclude that ![]() $s$ or
$s$ or ![]() $t$ acts trivially. This is a contradiction to
$t$ acts trivially. This is a contradiction to ![]() $\alpha _{s'}^{\vee },\alpha _{s'}\ne 0$ for
$\alpha _{s'}^{\vee },\alpha _{s'}\ne 0$ for ![]() $s'\in \{s,t\}$. Now assume that
$s'\in \{s,t\}$. Now assume that ![]() $\ell (w)$ is even. Then there exist
$\ell (w)$ is even. Then there exist ![]() $t_1,t_2\in T'$ such that
$t_1,t_2\in T'$ such that ![]() $w = t_1t_2$. If
$w = t_1t_2$. If ![]() $w\ne 1$, then
$w\ne 1$, then ![]() $t_1\ne t_2$. Take
$t_1\ne t_2$. Take ![]() $v\in V$ as in the assumption of Lemma 3.3. Then
$v\in V$ as in the assumption of Lemma 3.3. Then ![]() $t_1(v) = v$ and
$t_1(v) = v$ and ![]() $t_2(v) = v - \alpha _{t_2}\ne v$. Therefore
$t_2(v) = v - \alpha _{t_2}\ne v$. Therefore ![]() $t_1(v)\ne t_2(v)$. Hence the action of
$t_1(v)\ne t_2(v)$. Hence the action of ![]() $w$ is not trivial.
$w$ is not trivial.
From this lemma it is sufficient to prove the existence of an ![]() $R$-bimodule homomorphism in the assumption.
$R$-bimodule homomorphism in the assumption.
We also note the following: if ![]() $t_1,t_2\in T'$ are different, then
$t_1,t_2\in T'$ are different, then ![]() $\{\alpha _{t_1}^{\vee },\alpha _{t_2}^{\vee }\}$ is linearly independent. That is,
$\{\alpha _{t_1}^{\vee },\alpha _{t_2}^{\vee }\}$ is linearly independent. That is, ![]() $\{\alpha _{t_1}^{\vee },\alpha _{t_2}^{\vee }\}$ generates the two-dimensional space over
$\{\alpha _{t_1}^{\vee },\alpha _{t_2}^{\vee }\}$ generates the two-dimensional space over ![]() $\operatorname {Frac}(\mathbb {K})$. Therefore
$\operatorname {Frac}(\mathbb {K})$. Therefore ![]() $\operatorname {Frac}(\mathbb{K})\alpha_{t_1}^{\vee} + \operatorname {Frac}(\mathbb{K})\alpha_{t_2}^{\vee} = \operatorname {Frac}(\mathbb{K})\alpha_{s}^{\vee} + \operatorname {Frac}(\mathbb{K})\alpha_{t}^{\vee}$. That is, the two-dimensional space does not depend on
$\operatorname {Frac}(\mathbb{K})\alpha_{t_1}^{\vee} + \operatorname {Frac}(\mathbb{K})\alpha_{t_2}^{\vee} = \operatorname {Frac}(\mathbb{K})\alpha_{s}^{\vee} + \operatorname {Frac}(\mathbb{K})\alpha_{t}^{\vee}$. That is, the two-dimensional space does not depend on ![]() $t_1,t_2$.
$t_1,t_2$.
For each ![]() $x\in W'$, set
$x\in W'$, set ![]() $\operatorname {Gr}(x) = \{(v,x^{-1}(v))\in V^{*}\times V^{*}\mid v\in V^{*}\}$, and for each
$\operatorname {Gr}(x) = \{(v,x^{-1}(v))\in V^{*}\times V^{*}\mid v\in V^{*}\}$, and for each ![]() $A\subset W'$, let
$A\subset W'$, let ![]() $R(A)$ be the space of regular functions on
$R(A)$ be the space of regular functions on ![]() ${\bigcup} _{x\in A}\operatorname {Gr}(x)$. In other words,
${\bigcup} _{x\in A}\operatorname {Gr}(x)$. In other words, ![]() $R(A)$ is the image of
$R(A)$ is the image of ![]() $R\otimes _{\mathbb {K}} R$ in
$R\otimes _{\mathbb {K}} R$ in ![]() $R^{A}$ under the map
$R^{A}$ under the map ![]() $f\otimes g\mapsto (fx(g))_{x\in A}$; here we use an identification
$f\otimes g\mapsto (fx(g))_{x\in A}$; here we use an identification ![]() $\operatorname {Gr}(x)\simeq V^{*}$ via
$\operatorname {Gr}(x)\simeq V^{*}$ via ![]() $(v,x^{-1}(v))\mapsto v$. The embedding is an isomorphism after tensoring
$(v,x^{-1}(v))\mapsto v$. The embedding is an isomorphism after tensoring ![]() $Q$, that is, we have
$Q$, that is, we have ![]() $R(A)\otimes Q\simeq Q^{A}$ and this decomposition gives the structure of an object of
$R(A)\otimes Q\simeq Q^{A}$ and this decomposition gives the structure of an object of ![]() $\mathcal {C}'$ to
$\mathcal {C}'$ to ![]() $R(A)$. In this subsection we consider an object of
$R(A)$. In this subsection we consider an object of ![]() $\mathcal {C}'$ as graded right
$\mathcal {C}'$ as graded right ![]() $R\otimes _{\mathbb {K}}R$-modules, rather than graded
$R\otimes _{\mathbb {K}}R$-modules, rather than graded ![]() $R$-bimodules.
$R$-bimodules.
The element ![]() $s\in S$ acts on
$s\in S$ acts on ![]() $V^{*}\times V^{*}$ by
$V^{*}\times V^{*}$ by ![]() $(v_1,v_2)\mapsto (v_1,s(v_2))$. If
$(v_1,v_2)\mapsto (v_1,s(v_2))$. If ![]() $A$ is stable under the right action of
$A$ is stable under the right action of ![]() $s$, then
$s$, then ![]() ${\bigcup} _{x\in A}\operatorname {Gr}(x)$ is stable under this action. Hence
${\bigcup} _{x\in A}\operatorname {Gr}(x)$ is stable under this action. Hence ![]() $s$ acts on
$s$ acts on ![]() $R(A)$. We also have an action of
$R(A)$. We also have an action of ![]() $s$ on
$s$ on ![]() $R\otimes _{\mathbb {K}}R$ defined by
$R\otimes _{\mathbb {K}}R$ defined by ![]() $f\otimes g\mapsto f\otimes s(g)$. Then the natural map
$f\otimes g\mapsto f\otimes s(g)$. Then the natural map ![]() $R\otimes _{\mathbb {K}}R\to R(A)$ is
$R\otimes _{\mathbb {K}}R\to R(A)$ is ![]() $s$-equivariant. Let
$s$-equivariant. Let ![]() $R(A)^{+}$ be the image of
$R(A)^{+}$ be the image of ![]() $R\otimes _{\mathbb {K}} R^{s}$ in
$R\otimes _{\mathbb {K}} R^{s}$ in ![]() $R(A)$. Then
$R(A)$. Then ![]() $R(A)^{+}$ is contained in
$R(A)^{+}$ is contained in ![]() $s$-invariants in
$s$-invariants in ![]() $R(A)$.
$R(A)$.
Lemma 3.5 Assume that ![]() $As = A$. Then
$As = A$. Then ![]() $R(A)^{+}\otimes _{R^{s}}R\to R(A)$ given by
$R(A)^{+}\otimes _{R^{s}}R\to R(A)$ given by ![]() $z\otimes f\mapsto z(1\otimes f)$ is an isomorphism.
$z\otimes f\mapsto z(1\otimes f)$ is an isomorphism.
Proof. It is obvious that the map is surjective. Therefore it is sufficient to prove that the map is injective. Take ![]() $\delta _s\in V$ such that
$\delta _s\in V$ such that ![]() $\langle \alpha _s^{\vee },\delta _s\rangle = 1$. Then we have
$\langle \alpha _s^{\vee },\delta _s\rangle = 1$. Then we have ![]() $R = R^{s}\oplus R^{s}\delta _s$. Therefore it is sufficient to prove that
$R = R^{s}\oplus R^{s}\delta _s$. Therefore it is sufficient to prove that ![]() $R(A)^{+}\cap R(A)^{+}(1\otimes \delta _s) = 0$.
$R(A)^{+}\cap R(A)^{+}(1\otimes \delta _s) = 0$.
Let ![]() $z_1,z_2\in R(A)^{+}$ and assume that
$z_1,z_2\in R(A)^{+}$ and assume that ![]() $z_1 = z_2(1\otimes \delta _s)$. Let
$z_1 = z_2(1\otimes \delta _s)$. Let ![]() $((z_i)_x)$ be the image of
$((z_i)_x)$ be the image of ![]() $z_i$ in
$z_i$ in ![]() $R^{A}$ for
$R^{A}$ for ![]() $i = 1,2$. By
$i = 1,2$. By ![]() $z_1 = z_2(1\otimes \delta _s)$, we have
$z_1 = z_2(1\otimes \delta _s)$, we have ![]() $(z_1)_x = (z_2)_{x}x(\delta _s)$. By replacing
$(z_1)_x = (z_2)_{x}x(\delta _s)$. By replacing ![]() $x$ with
$x$ with ![]() $xs$, we have
$xs$, we have ![]() $(z_1)_{xs} = (z_2)_{xs}xs(\delta _s)$. Since
$(z_1)_{xs} = (z_2)_{xs}xs(\delta _s)$. Since ![]() $z_1,z_2$ are
$z_1,z_2$ are ![]() $s$-invariant, we have
$s$-invariant, we have ![]() $(z_1)_{xs} = (z_1)_x$ and
$(z_1)_{xs} = (z_1)_x$ and ![]() $(z_2)_{xs} = (z_2)_{x}$. Therefore we get
$(z_2)_{xs} = (z_2)_{x}$. Therefore we get ![]() $(z_2)_{x}(x(\delta _s) - xs(\delta _s)) = 0$. Hence
$(z_2)_{x}(x(\delta _s) - xs(\delta _s)) = 0$. Hence ![]() $(z_2)_{x}x(\alpha _s) = 0$. We get
$(z_2)_{x}x(\alpha _s) = 0$. We get ![]() $(z_2)_{x} = 0$ for any
$(z_2)_{x} = 0$ for any ![]() $x\in A$ and this implies
$x\in A$ and this implies ![]() $z_2 = 0$.
$z_2 = 0$.
Lemma 3.6 Let ![]() $x\in W'$ and assume that
$x\in W'$ and assume that ![]() $xs > x$. Set
$xs > x$. Set ![]() $A = \{y\in W'\mid y\le x\}$. Then
$A = \{y\in W'\mid y\le x\}$. Then ![]() $R(A)\otimes _{R}B_s\simeq R(A\cup As)(1)\oplus R(A\cap As)(-1)$.
$R(A)\otimes _{R}B_s\simeq R(A\cup As)(1)\oplus R(A\cap As)(-1)$.
Proof. Since ![]() $xs > x$, we have
$xs > x$, we have ![]() $A\setminus As = \{x,xr\}$ for some
$A\setminus As = \{x,xr\}$ for some ![]() $r\in T'\setminus \{s\}$. Take
$r\in T'\setminus \{s\}$. Take ![]() $v_0\in V$ such that
$v_0\in V$ such that ![]() $\langle \alpha _r^{\vee },v_0\rangle = 0$ and
$\langle \alpha _r^{\vee },v_0\rangle = 0$ and ![]() $\langle \alpha _s^{\vee },v_0\rangle = 1$ and consider
$\langle \alpha _s^{\vee },v_0\rangle = 1$ and consider ![]() $z_0 = x(v_0)\otimes 1 - 1\otimes v_0$. Note that we have the restriction map
$z_0 = x(v_0)\otimes 1 - 1\otimes v_0$. Note that we have the restriction map ![]() $R(A)\to R(A\cap As)$.
$R(A)\to R(A\cap As)$.
Claim Let ![]() $f\in R(A)$. Then we have
$f\in R(A)$. Then we have ![]() $fz_0 = 0$ in
$fz_0 = 0$ in ![]() $R(A)$ if and only if
$R(A)$ if and only if ![]() $f = 0$ in
$f = 0$ in ![]() $R(A\cap As)$.
$R(A\cap As)$.
Recall the embedding ![]() $R(A)\to R^{A}$. Let
$R(A)\to R^{A}$. Let ![]() $(f_y)_{y\in A}$ be the image of
$(f_y)_{y\in A}$ be the image of ![]() $f$. Then the image of
$f$. Then the image of ![]() $fz_0$ is
$fz_0$ is ![]() $(f_y(x(v_0) - y(v_0)))_{y\in A}$. When
$(f_y(x(v_0) - y(v_0)))_{y\in A}$. When ![]() $y \in \{x,xr\} = A\setminus As$, it follows that
$y \in \{x,xr\} = A\setminus As$, it follows that ![]() $x(v_0) - y(v_0) = 0$ since
$x(v_0) - y(v_0) = 0$ since ![]() $r(v_0) = v_0$ from the assumption on
$r(v_0) = v_0$ from the assumption on ![]() $v_0$. Therefore if
$v_0$. Therefore if ![]() $f = 0$ in
$f = 0$ in ![]() $R(A\cap As)$, then since
$R(A\cap As)$, then since ![]() $f_y = 0$ for any
$f_y = 0$ for any ![]() $y\in A\cap As$, we have
$y\in A\cap As$, we have ![]() $f_y(x(v_0) - y(v_0)) = 0$ for any
$f_y(x(v_0) - y(v_0)) = 0$ for any ![]() $y\in A$. We get
$y\in A$. We get ![]() $fz_0 = 0$ in
$fz_0 = 0$ in ![]() $R(A)$.
$R(A)$.
We prove ![]() $x(v_0) - y(v_0) \ne 0$ for any
$x(v_0) - y(v_0) \ne 0$ for any ![]() $y\in A\cap As$. This gives the reverse implication. We assume that
$y\in A\cap As$. This gives the reverse implication. We assume that ![]() $y^{-1}x(v_0) = v_0$. Then we also have
$y^{-1}x(v_0) = v_0$. Then we also have ![]() $y^{-1}xr(v_0) = v_0$. Either
$y^{-1}xr(v_0) = v_0$. Either ![]() $y^{-1}x$ or
$y^{-1}x$ or ![]() $y^{-1}xr$ is in
$y^{-1}xr$ is in ![]() $T'$. Let
$T'$. Let ![]() $r'$ be the element in
$r'$ be the element in ![]() $T'$. Then
$T'$. Then ![]() $r(v_0) = r'(v_0) = v_0$ and since
$r(v_0) = r'(v_0) = v_0$ and since ![]() $y\ne x,rx$, we have
$y\ne x,rx$, we have ![]() $r\ne r'$. Therefore
$r\ne r'$. Therefore ![]() $\langle \alpha _r^{\vee },v_0\rangle = \langle \alpha _{r'}^{\vee },v_0\rangle = 0$. Hence
$\langle \alpha _r^{\vee },v_0\rangle = \langle \alpha _{r'}^{\vee },v_0\rangle = 0$. Hence ![]() $v_0$ is orthogonal to
$v_0$ is orthogonal to ![]() $\operatorname {Frac}(\mathbb {K})\alpha _r + \operatorname {Frac}(\mathbb {K})\alpha _{r'}$. Recall that this space does not depend on
$\operatorname {Frac}(\mathbb {K})\alpha _r + \operatorname {Frac}(\mathbb {K})\alpha _{r'}$. Recall that this space does not depend on ![]() $r,r'$. Hence
$r,r'$. Hence ![]() $v_0$ is orthogonal to
$v_0$ is orthogonal to ![]() $\operatorname {Frac}(\mathbb {K})\alpha _r + \operatorname {Frac}(\mathbb {K})\alpha _s$. This contradicts the assumption
$\operatorname {Frac}(\mathbb {K})\alpha _r + \operatorname {Frac}(\mathbb {K})\alpha _s$. This contradicts the assumption ![]() $\langle \alpha _s,v_0\rangle = 1$. We get the claim.
$\langle \alpha _s,v_0\rangle = 1$. We get the claim.
By the claim, we have an isomorphism ![]() $R(A\cap As)(-2)\simeq R(A)z_0$. Let
$R(A\cap As)(-2)\simeq R(A)z_0$. Let ![]() $M$ be the sub-
$M$ be the sub-![]() $(R,R^{s})$-module of
$(R,R^{s})$-module of ![]() $R(A)$ generated by
$R(A)$ generated by ![]() $z_0$. Then the above isomorphism implies
$z_0$. Then the above isomorphism implies ![]() $R(A\cap As)^{+} (-2)\simeq M$.
$R(A\cap As)^{+} (-2)\simeq M$.
Next consider the restriction map ![]() $R(A\cup As)\to R(A)$. The subset
$R(A\cup As)\to R(A)$. The subset ![]() $A\cup As$ is stable under the right multiplication of
$A\cup As$ is stable under the right multiplication of ![]() $s$. Let
$s$. Let ![]() $R(A\cup As)^{s = 1}$ be the
$R(A\cup As)^{s = 1}$ be the ![]() $s$-fixed part. Then
$s$-fixed part. Then ![]() $R(A\cup As)^{+}\subset R(A\cup As)^{s = 1}$ and the above restriction map gives an injective map
$R(A\cup As)^{+}\subset R(A\cup As)^{s = 1}$ and the above restriction map gives an injective map ![]() $R(A\cup As)^{s = 1}\hookrightarrow R(A)$. Let
$R(A\cup As)^{s = 1}\hookrightarrow R(A)$. Let ![]() $N$ be the image of
$N$ be the image of ![]() $R(A\cup As)^{+}\hookrightarrow R(A)$. We have
$R(A\cup As)^{+}\hookrightarrow R(A)$. We have ![]() $N\simeq R(A\cup As)^{+}$.
$N\simeq R(A\cup As)^{+}$.
To prove ![]() $R(A)\otimes _{R}B_s\simeq R(A\cup As)(1)\oplus R(A\cap As)(-1)$, it is sufficient to prove
$R(A)\otimes _{R}B_s\simeq R(A\cup As)(1)\oplus R(A\cap As)(-1)$, it is sufficient to prove ![]() $R(A) = M\oplus N$ by Lemma 3.5. The subspace
$R(A) = M\oplus N$ by Lemma 3.5. The subspace ![]() $M + N$ is the image of
$M + N$ is the image of ![]() $(R\otimes R^{s})z_0 + R\otimes R^{s}$. Since
$(R\otimes R^{s})z_0 + R\otimes R^{s}$. Since ![]() $z_0 = x(v_0)\otimes 1 + 1 \otimes v_0$, we have
$z_0 = x(v_0)\otimes 1 + 1 \otimes v_0$, we have ![]() $(R\otimes R^{s})z_0 + R\otimes R^{s} = R\otimes R^{s}v_0 + R\otimes R^{s}$. We have
$(R\otimes R^{s})z_0 + R\otimes R^{s} = R\otimes R^{s}v_0 + R\otimes R^{s}$. We have ![]() $R = R^{s} + R^{s}v_0$ since
$R = R^{s} + R^{s}v_0$ since ![]() $\langle \alpha _s^{\vee },v_0\rangle = 1$. Hence
$\langle \alpha _s^{\vee },v_0\rangle = 1$. Hence ![]() $(R\otimes R^{s})z_0 + R\otimes R^{s} = R\otimes R$. Therefore
$(R\otimes R^{s})z_0 + R\otimes R^{s} = R\otimes R$. Therefore ![]() $M + N = R(A)$.
$M + N = R(A)$.
Let ![]() $m\in M$ and
$m\in M$ and ![]() $n\in N$. We can write
$n\in N$. We can write ![]() $m = fz_0$ for some
$m = fz_0$ for some ![]() $f\in \operatorname {Im}(R\otimes R^{s}\to R(A))$. We assume
$f\in \operatorname {Im}(R\otimes R^{s}\to R(A))$. We assume ![]() $m = n$. Consider the image of
$m = n$. Consider the image of ![]() $f$ in
$f$ in ![]() $R(A\cap As)$ and let
$R(A\cap As)$ and let ![]() $(f_y)_{y\in A\cap As}$ be the image in
$(f_y)_{y\in A\cap As}$ be the image in ![]() $R^{A\cap As}$. We also denote the image of
$R^{A\cap As}$. We also denote the image of ![]() $n$ in
$n$ in ![]() $R^{A\cap As}$ by
$R^{A\cap As}$ by ![]() $(n_y)_{y\in A\cap As}$. Then, for each
$(n_y)_{y\in A\cap As}$. Then, for each ![]() $y\in A\cap As$, we have
$y\in A\cap As$, we have ![]() $f_y(x(v_0) - y(v_0)) = n_{y}$. We also have
$f_y(x(v_0) - y(v_0)) = n_{y}$. We also have ![]() $f_{ys}(x(v_0) - ys(v_0)) = n_{ys}$. Since
$f_{ys}(x(v_0) - ys(v_0)) = n_{ys}$. Since ![]() $f$ and
$f$ and ![]() $n$ are
$n$ are ![]() $s$-invariant,
$s$-invariant, ![]() $f_{ys} = f_{y}$,
$f_{ys} = f_{y}$, ![]() $n_{ys} = n_y$. Therefore
$n_{ys} = n_y$. Therefore ![]() $f_{y}(ys(v_0) - y(v_0)) = 0$. That is, we have
$f_{y}(ys(v_0) - y(v_0)) = 0$. That is, we have ![]() $f_{y}y(\alpha _s) = 0$. We get
$f_{y}y(\alpha _s) = 0$. We get ![]() $f_y = 0$ and hence
$f_y = 0$ and hence ![]() $fz_0\in M$ is zero.
$fz_0\in M$ is zero.
We have proved ![]() $R(A)\otimes _{R}B_s\simeq R(A\cup As)(1)\oplus R(A\cap As)(-1)$. For
$R(A)\otimes _{R}B_s\simeq R(A\cup As)(1)\oplus R(A\cap As)(-1)$. For ![]() $A = \{y\in W'\mid y\le x\}$ with
$A = \{y\in W'\mid y\le x\}$ with ![]() $xs > x$, we have
$xs > x$, we have ![]() $A\cup As = \{y\in W'\mid y\le xs\}$. We set
$A\cup As = \{y\in W'\mid y\le xs\}$. We set ![]() $R(\le x) = R(\{y\in W'\mid y\le x\})$ for
$R(\le x) = R(\{y\in W'\mid y\le x\})$ for ![]() $x\in W'$. Then
$x\in W'$. Then ![]() $R(\le xs)(1)$ is a direct summand of
$R(\le xs)(1)$ is a direct summand of ![]() $R(\le x)\otimes _{R}B_s$ if
$R(\le x)\otimes _{R}B_s$ if ![]() $xs > x$. Replacing
$xs > x$. Replacing ![]() $s$ with
$s$ with ![]() $t$,
$t$, ![]() $R(\le yt)(1)$ is a direct summand of
$R(\le yt)(1)$ is a direct summand of ![]() $R(\le y)\otimes _{R}B_s$ if
$R(\le y)\otimes _{R}B_s$ if ![]() $yt > y$. Therefore we have the following consequence. Let
$yt > y$. Therefore we have the following consequence. Let ![]() $\underline {w} \in \{s,t\}^{\ell (w)}$ be a reduced expression for
$\underline {w} \in \{s,t\}^{\ell (w)}$ be a reduced expression for ![]() $w\in W'$. Then
$w\in W'$. Then ![]() $B_{\underline {w}}$ has a direct summand
$B_{\underline {w}}$ has a direct summand ![]() $R(\le w)(\ell (w))$. Let
$R(\le w)(\ell (w))$. Let ![]() $w_0\in W'$ be the longest element. Then for
$w_0\in W'$ be the longest element. Then for ![]() $\underline {x}$ and
$\underline {x}$ and ![]() $\underline {y}$ as in Assumption 3.2,
$\underline {y}$ as in Assumption 3.2, ![]() $R(\le w_0)(\ell (w_0))$ is a direct summand of both
$R(\le w_0)(\ell (w_0))$ is a direct summand of both ![]() $B_{\underline {x}}$ and
$B_{\underline {x}}$ and ![]() $B_{\underline {y}}$. Therefore we get a non-zero homomorphism
$B_{\underline {y}}$. Therefore we get a non-zero homomorphism ![]() $\Phi \colon B_{\underline {x}}\twoheadrightarrow R(\le w_0)(\ell (w_0))\hookrightarrow B_{\underline {y}}$.
$\Phi \colon B_{\underline {x}}\twoheadrightarrow R(\le w_0)(\ell (w_0))\hookrightarrow B_{\underline {y}}$.
Lemma 3.7 The homomorphism ![]() $\Phi$ induces an isomorphism
$\Phi$ induces an isomorphism ![]() $B_{\underline {x}}^{w_0}\simeq B_{\underline {y}}^{w_0}$.
$B_{\underline {x}}^{w_0}\simeq B_{\underline {y}}^{w_0}$.
Proof. By induction, we can prove that ![]() $B_{\underline {w}}\simeq R(\le w)(\ell (w))\oplus M$ with
$B_{\underline {w}}\simeq R(\le w)(\ell (w))\oplus M$ with ![]() $\operatorname {supp}_{W'}(M)\subset \{y \in W'\mid y < w\}$ for any
$\operatorname {supp}_{W'}(M)\subset \{y \in W'\mid y < w\}$ for any ![]() $w\in W'$ and a reduced expression
$w\in W'$ and a reduced expression ![]() $\underline {w}$ for
$\underline {w}$ for ![]() $w$. Therefore
$w$. Therefore ![]() $B_{\underline {x}} = R(\le w_0)(\ell (w_0))\oplus M$ with
$B_{\underline {x}} = R(\le w_0)(\ell (w_0))\oplus M$ with ![]() $\operatorname {supp}_{W'}(M)\subset W'\setminus \{w_0\}$. Hence
$\operatorname {supp}_{W'}(M)\subset W'\setminus \{w_0\}$. Hence ![]() $B_{\underline {x}}^{w_0} = R(\le w_0)(\ell (w_0))^{w_0}$ since
$B_{\underline {x}}^{w_0} = R(\le w_0)(\ell (w_0))^{w_0}$ since ![]() $M^{w_0} = 0$. Therefore the projection
$M^{w_0} = 0$. Therefore the projection ![]() $B_{\underline {x}}\twoheadrightarrow R(\le w_0)(\ell (w_0))$ induces an isomorphism
$B_{\underline {x}}\twoheadrightarrow R(\le w_0)(\ell (w_0))$ induces an isomorphism ![]() $B_{\underline {x}}^{w_0}\simeq R(\le w_0)(\ell (w_0))^{w_0}$. Similarly, the embedding
$B_{\underline {x}}^{w_0}\simeq R(\le w_0)(\ell (w_0))^{w_0}$. Similarly, the embedding ![]() $R(\le w_0)(\ell (w_0))\hookrightarrow B_{\underline {y}}$ induces an isomorphism
$R(\le w_0)(\ell (w_0))\hookrightarrow B_{\underline {y}}$ induces an isomorphism ![]() $R(\le w_0)(\ell (w_0))^{w_0}\hookrightarrow B_{\underline {y}}^{w_0}$. We get the lemma by the construction of
$R(\le w_0)(\ell (w_0))^{w_0}\hookrightarrow B_{\underline {y}}^{w_0}$. We get the lemma by the construction of ![]() $\Phi$.
$\Phi$.
Define ![]() $\varphi _{\underline {x}}\colon B_{\underline {x}}\simeq R\otimes _{R^{s}}R\otimes _{R^{t}}\otimes \cdots \otimes R\to R(-\ell (w_0))$ by
$\varphi _{\underline {x}}\colon B_{\underline {x}}\simeq R\otimes _{R^{s}}R\otimes _{R^{t}}\otimes \cdots \otimes R\to R(-\ell (w_0))$ by
(Recall that ![]() $\underline {x} = (s,t,\ldots )$.) Then this satisfies
$\underline {x} = (s,t,\ldots )$.) Then this satisfies ![]() $\varphi _{\underline {x}}(uf) = \varphi _{\underline {x}}(w_0(f)u)$ for any
$\varphi _{\underline {x}}(uf) = \varphi _{\underline {x}}(w_0(f)u)$ for any ![]() $u\in B_{\underline {x}}$ and
$u\in B_{\underline {x}}$ and ![]() $f\in R$. Therefore it factors through
$f\in R$. Therefore it factors through ![]() $B_{\underline {x}}\to B_{\underline {x}}^{w_0}$. We get
$B_{\underline {x}}\to B_{\underline {x}}^{w_0}$. We get ![]() $\overline {\varphi }_{\underline {x}}\colon B_{\underline {x}}^{w_0}\to R(-\ell (w_0))$. This is surjective. On the other hand, after tensoring
$\overline {\varphi }_{\underline {x}}\colon B_{\underline {x}}^{w_0}\to R(-\ell (w_0))$. This is surjective. On the other hand, after tensoring ![]() $Q$, both are one-dimensional
$Q$, both are one-dimensional ![]() $Q$-vector spaces by Lemma 2.17. Therefore it is an isomorphism. In particular,
$Q$-vector spaces by Lemma 2.17. Therefore it is an isomorphism. In particular, ![]() $\overline {\varphi }_{\underline {x}}$ is injective, hence it is an isomorphism.
$\overline {\varphi }_{\underline {x}}$ is injective, hence it is an isomorphism.
Note that the ![]() $(-\ell (w))$th-degree part of
$(-\ell (w))$th-degree part of ![]() $B_{\underline {x}}$ (respectively,
$B_{\underline {x}}$ (respectively, ![]() $B_{\underline {y}}$) is a free
$B_{\underline {y}}$) is a free ![]() $\mathbb {K}$-module of rank one with a basis
$\mathbb {K}$-module of rank one with a basis ![]() $u_{\underline {x}}$ (respectively,
$u_{\underline {x}}$ (respectively, ![]() $u_{\underline {y}}$). Therefore
$u_{\underline {y}}$). Therefore ![]() $\Phi (u_{\underline {x}}) = cu_{\underline {y}}$ for some
$\Phi (u_{\underline {x}}) = cu_{\underline {y}}$ for some ![]() $c\in \mathbb {K}$. Let
$c\in \mathbb {K}$. Let ![]() $\bar {u}_{\underline {x}}\in B_{\underline {x}}^{w_0}$ (respectively,
$\bar {u}_{\underline {x}}\in B_{\underline {x}}^{w_0}$ (respectively, ![]() $\bar {u}_{\underline {y}}\in B_{\underline {y}}^{w_0}$) be the image of
$\bar {u}_{\underline {y}}\in B_{\underline {y}}^{w_0}$) be the image of ![]() $u_{\underline {x}}$ (respectively,
$u_{\underline {x}}$ (respectively, ![]() $u_{\underline {y}}$). Since
$u_{\underline {y}}$). Since ![]() $\varphi _{\underline {x}}(u_{\underline {x}}) = 1$, we have the following commutative diagram.
$\varphi _{\underline {x}}(u_{\underline {x}}) = 1$, we have the following commutative diagram.

We have that ![]() $c\in \mathbb {K}^{\times }$ and
$c\in \mathbb {K}^{\times }$ and ![]() $c^{-1}\Phi$ gives a desired homomorphism.
$c^{-1}\Phi$ gives a desired homomorphism.
3.3 Light leaves
We recall the definition of light leaves [Reference LibedinskyLib08] following the notation of [Reference Elias and WilliamsonEW16]. We need one more item of notation.
Let ![]() $w\in W$ and let
$w\in W$ and let ![]() $\underline {x},\underline {y}\in S^{\ell (w)}$ be two reduced expressions for
$\underline {x},\underline {y}\in S^{\ell (w)}$ be two reduced expressions for ![]() $w$. Then by a fundamental property of a Coxeter system, there exists a sequence
$w$. Then by a fundamental property of a Coxeter system, there exists a sequence ![]() $\underline {x}^{0} = \underline {x},\underline {x}^{1},\ldots ,\underline {x}^{r} = \underline {y}$ such that each
$\underline {x}^{0} = \underline {x},\underline {x}^{1},\ldots ,\underline {x}^{r} = \underline {y}$ such that each ![]() $\underline {x}^{i}$ and
$\underline {x}^{i}$ and ![]() $\underline {x}^{i + 1}$ only differ by a single braid relation. At each step, we can attach a homomorphism
$\underline {x}^{i + 1}$ only differ by a single braid relation. At each step, we can attach a homomorphism ![]() $B_{\underline {x}^{i}}\to B_{\underline {x}^{i + 1}}$ using the homomorphism in Assumption 3.2. We denote the composition of these maps by
$B_{\underline {x}^{i}}\to B_{\underline {x}^{i + 1}}$ using the homomorphism in Assumption 3.2. We denote the composition of these maps by ![]() $\mathrm {rex}$. Note that
$\mathrm {rex}$. Note that ![]() $\mathrm {rex}$ sends
$\mathrm {rex}$ sends ![]() $u_{\underline {x}}$ to
$u_{\underline {x}}$ to ![]() $u_{\underline {y}}$. Of course, this homomorphism is not unique. We fix it for any such two reduced expressions. See [Reference Elias and WilliamsonEW16, § 4.2] for details.
$u_{\underline {y}}$. Of course, this homomorphism is not unique. We fix it for any such two reduced expressions. See [Reference Elias and WilliamsonEW16, § 4.2] for details.
For the definition of light leaves, we use the following maps. Let ![]() $s\in S$. First set
$s\in S$. First set ![]() $\partial _s(f) = (f - s(f))/\alpha _s$. Put
$\partial _s(f) = (f - s(f))/\alpha _s$. Put
 \[ \begin{array}{rll} m^{s}\colon B_s\to R & f_1\otimes f_2\mapsto f_1f_2 & \text{degree }1,\\ i_0^{s}\colon B_s\otimes B_s\to B_s & f_1\otimes f_2\otimes f_3 \mapsto f_1\partial_s(f_2)\otimes f_3 & \text{degree }-1,\\ i_1^{s}\colon B_s\otimes B_s \to R & f_1\otimes f_2\otimes f_3 \mapsto f_1\partial_s(f_2)f_3 & \text{degree }0. \end{array} \]
\[ \begin{array}{rll} m^{s}\colon B_s\to R & f_1\otimes f_2\mapsto f_1f_2 & \text{degree }1,\\ i_0^{s}\colon B_s\otimes B_s\to B_s & f_1\otimes f_2\otimes f_3 \mapsto f_1\partial_s(f_2)\otimes f_3 & \text{degree }-1,\\ i_1^{s}\colon B_s\otimes B_s \to R & f_1\otimes f_2\otimes f_3 \mapsto f_1\partial_s(f_2)f_3 & \text{degree }0. \end{array} \]
Here ![]() $f_1,f_2,f_3\in R$ and, in the definition of
$f_1,f_2,f_3\in R$ and, in the definition of ![]() $i_0^{s},i_1^{s}$, we regard
$i_0^{s},i_1^{s}$, we regard ![]() $B_s\otimes B_s = R\otimes _{R^{s}}R\otimes _{R^{s}}R$. Since
$B_s\otimes B_s = R\otimes _{R^{s}}R\otimes _{R^{s}}R$. Since ![]() $V$ is a faithful
$V$ is a faithful ![]() $\{e,s\}$-representation, these are homomorphisms in
$\{e,s\}$-representation, these are homomorphisms in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Definition 3.8 Let ![]() $\underline {x} = (s_1,\ldots ,s_l)\in S^{l}$,
$\underline {x} = (s_1,\ldots ,s_l)\in S^{l}$, ![]() $\boldsymbol {e} = (\boldsymbol {e}_1,\ldots ,\boldsymbol {e}_l) \in \{0,1\}^{l}$. Then we define a light leaf
$\boldsymbol {e} = (\boldsymbol {e}_1,\ldots ,\boldsymbol {e}_l) \in \{0,1\}^{l}$. Then we define a light leaf ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}$ which is a morphism from
$\mathit {LL}_{\underline {x},\boldsymbol {e}}$ which is a morphism from ![]() $B_{\underline {x}}$ to
$B_{\underline {x}}$ to ![]() $B_{\underline {w}}$ in
$B_{\underline {w}}$ in ![]() $\mathcal {C}$ where
$\mathcal {C}$ where ![]() $\underline {w}$ is a fixed reduced expression for
$\underline {w}$ is a fixed reduced expression for ![]() $w = \underline {x}^{\boldsymbol {e}}$. Let
$w = \underline {x}^{\boldsymbol {e}}$. Let ![]() $\underline {x}_{\le k} = (s_1,\ldots ,s_k)$,
$\underline {x}_{\le k} = (s_1,\ldots ,s_k)$, ![]() $\boldsymbol {e}_{\le k} = (\boldsymbol {e}_1,\ldots ,\boldsymbol {e}_k)$ and
$\boldsymbol {e}_{\le k} = (\boldsymbol {e}_1,\ldots ,\boldsymbol {e}_k)$ and ![]() $w_k = \underline {x}_{\le k}^{\boldsymbol {e}_{\le k}}$. We fix a reduced expression
$w_k = \underline {x}_{\le k}^{\boldsymbol {e}_{\le k}}$. We fix a reduced expression ![]() $\underline {w}_k$ for
$\underline {w}_k$ for ![]() $w_k$ and define
$w_k$ and define ![]() $\mathit {LL}_k\colon B_{\underline {x}_{\le k}}\to B_{\underline {w}_k}$ inductively as follows.
$\mathit {LL}_k\colon B_{\underline {x}_{\le k}}\to B_{\underline {w}_k}$ inductively as follows.
(U0) For
 $\boldsymbol {e}_k = 0$ and
$\boldsymbol {e}_k = 0$ and  $w_{k - 1}s_k > w_{k - 1}$, we have
$w_{k - 1}s_k > w_{k - 1}$, we have
 \[ B_{\underline{x}_{\le k - 1}}\otimes B_{s_k}\xrightarrow{\mathit{LL}_{k - 1}\otimes \mathrm{Id}_{B_{s_k}}}B_{\underline{w}_{k - 1}}\otimes B_{s_k}\xrightarrow{\mathrm{Id}_{B_{\underline{w}_{k - 1}}}\otimes m^{s_k}} B_{\underline{w}_{k - 1}}. \]
\[ B_{\underline{x}_{\le k - 1}}\otimes B_{s_k}\xrightarrow{\mathit{LL}_{k - 1}\otimes \mathrm{Id}_{B_{s_k}}}B_{\underline{w}_{k - 1}}\otimes B_{s_k}\xrightarrow{\mathrm{Id}_{B_{\underline{w}_{k - 1}}}\otimes m^{s_k}} B_{\underline{w}_{k - 1}}. \](U1) For
 $\boldsymbol {e}_k = 1$ and
$\boldsymbol {e}_k = 1$ and  $w_{k - 1}s_k > w_{k - 1}$, we have
$w_{k - 1}s_k > w_{k - 1}$, we have
 \[ B_{\underline{x}_{k - 1}}\otimes B_{s_k}\xrightarrow{\mathit{LL}_{k - 1}\otimes\mathrm{Id}_{B_{s_k}}} B_{\underline{w}_{k - 1}}\otimes B_{s_k} \xrightarrow{\mathrm{rex}}B_{\underline{w}_k}. \]
\[ B_{\underline{x}_{k - 1}}\otimes B_{s_k}\xrightarrow{\mathit{LL}_{k - 1}\otimes\mathrm{Id}_{B_{s_k}}} B_{\underline{w}_{k - 1}}\otimes B_{s_k} \xrightarrow{\mathrm{rex}}B_{\underline{w}_k}. \](D0) For
 $\boldsymbol {e}_k = 0$ and
$\boldsymbol {e}_k = 0$ and  $w_{k - 1}s_k < w_{k - 1}$, let
$w_{k - 1}s_k < w_{k - 1}$, let  $(t_1,\ldots ,t_{p - 1},s_k)$ be a reduced expression for
$(t_1,\ldots ,t_{p - 1},s_k)$ be a reduced expression for  $w_{k - 1}$ ending with
$w_{k - 1}$ ending with  $s_k$. We have
$s_k$. We have
 \begin{align*} & \hskip0.25pc B_{\underline{x}_{\le k - 1}}\otimes B_{s_k}\xrightarrow{\mathit{LL}_{k - 1}\otimes \mathrm{Id}_{B_{s_k}}}B_{\underline{w}_{k - 1}}\otimes B_{s_k}\xrightarrow{\mathrm{rex}\otimes\mathrm{Id}_{B_{s_k}}}B_{(t_1,\ldots ,t_{p - 1},s_k)}\otimes B_{s_k}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \xrightarrow{\mathrm{Id}_{B_{(t_1,\ldots ,t_{p - 1})}}\otimes i_0^{s_k}}B_{(t_1,\ldots ,t_{p - 1},s_k)}\xrightarrow{\mathrm{rex}}B_{\underline{w}_k}.\end{align*}
\begin{align*} & \hskip0.25pc B_{\underline{x}_{\le k - 1}}\otimes B_{s_k}\xrightarrow{\mathit{LL}_{k - 1}\otimes \mathrm{Id}_{B_{s_k}}}B_{\underline{w}_{k - 1}}\otimes B_{s_k}\xrightarrow{\mathrm{rex}\otimes\mathrm{Id}_{B_{s_k}}}B_{(t_1,\ldots ,t_{p - 1},s_k)}\otimes B_{s_k}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \xrightarrow{\mathrm{Id}_{B_{(t_1,\ldots ,t_{p - 1})}}\otimes i_0^{s_k}}B_{(t_1,\ldots ,t_{p - 1},s_k)}\xrightarrow{\mathrm{rex}}B_{\underline{w}_k}.\end{align*}(D1) For
 $\boldsymbol {e}_k = 1$ and
$\boldsymbol {e}_k = 1$ and  $w_{k - 1}s_k < w_{k - 1}$, let
$w_{k - 1}s_k < w_{k - 1}$, let  $(t_1,\ldots ,t_{p - 1},s_k)$ be a reduced expression for
$(t_1,\ldots ,t_{p - 1},s_k)$ be a reduced expression for  $w_{k - 1}$ ending with
$w_{k - 1}$ ending with  $s_k$. We have
$s_k$. We have
 \begin{align*} &\hskip0.2pc B_{\underline{x}_{\le k - 1}}\otimes B_{s_k}\xrightarrow{\mathit{LL}_{k - 1}\otimes \mathrm{Id}_{B_{s_k}}}B_{\underline{w}_{k - 1}}\otimes B_{s_k}\xrightarrow{\mathrm{rex}\otimes \mathrm{Id}_{B_{s_k}}}B_{(t_1,\ldots, t_{p - 1},s_k)}\otimes B_{s_k}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \xrightarrow{\mathrm{Id}_{B_{(t_1,\ldots ,t_{p - 1})}}\otimes i_1^{s_k}}B_{(t_1,\ldots ,t_{p - 1})}\xrightarrow{\mathrm{rex}}B_{\underline{w}_k}.\end{align*}
\begin{align*} &\hskip0.2pc B_{\underline{x}_{\le k - 1}}\otimes B_{s_k}\xrightarrow{\mathit{LL}_{k - 1}\otimes \mathrm{Id}_{B_{s_k}}}B_{\underline{w}_{k - 1}}\otimes B_{s_k}\xrightarrow{\mathrm{rex}\otimes \mathrm{Id}_{B_{s_k}}}B_{(t_1,\ldots, t_{p - 1},s_k)}\otimes B_{s_k}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \xrightarrow{\mathrm{Id}_{B_{(t_1,\ldots ,t_{p - 1})}}\otimes i_1^{s_k}}B_{(t_1,\ldots ,t_{p - 1})}\xrightarrow{\mathrm{rex}}B_{\underline{w}_k}.\end{align*}
Finally, we put ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}} = \mathit {LL}_l$. By the construction, the degree of
$\mathit {LL}_{\underline {x},\boldsymbol {e}} = \mathit {LL}_l$. By the construction, the degree of ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}$ is
$\mathit {LL}_{\underline {x},\boldsymbol {e}}$ is ![]() $d(\boldsymbol {e})$.
$d(\boldsymbol {e})$.
We fix a sequence ![]() $\underline {x} = (s_1,\ldots ,s_l)$ in this subsection.
$\underline {x} = (s_1,\ldots ,s_l)$ in this subsection.
Lemma 3.9 Let ![]() $\boldsymbol {e},\boldsymbol {f}\in \{0,1\}^{l}$ such that
$\boldsymbol {e},\boldsymbol {f}\in \{0,1\}^{l}$ such that ![]() $\underline {x}^{\boldsymbol {e}} = \underline {x}^{\boldsymbol {f}}$. Assume that the labels of
$\underline {x}^{\boldsymbol {e}} = \underline {x}^{\boldsymbol {f}}$. Assume that the labels of ![]() $\boldsymbol {e}$ and
$\boldsymbol {e}$ and ![]() $\boldsymbol {f}$ at
$\boldsymbol {f}$ at ![]() $i$ are the same for all
$i$ are the same for all ![]() $i = 1,\ldots ,l$. Then we have
$i = 1,\ldots ,l$. Then we have ![]() $\boldsymbol {e} = \boldsymbol {f}$.
$\boldsymbol {e} = \boldsymbol {f}$.
Proof. We prove ![]() $\boldsymbol {e}_i = \boldsymbol {f}_i$ by backward induction on
$\boldsymbol {e}_i = \boldsymbol {f}_i$ by backward induction on ![]() $i$. Assume that we have
$i$. Assume that we have ![]() $\boldsymbol {e}_j = \boldsymbol {f}_j$ for any
$\boldsymbol {e}_j = \boldsymbol {f}_j$ for any ![]() $j > i$. Since
$j > i$. Since ![]() $s_1^{\boldsymbol {e}_1}\cdots s_l^{\boldsymbol {e}_l} = s_1^{\boldsymbol {f}_1}\cdots s_l^{\boldsymbol {f}_l}$ by the assumption and
$s_1^{\boldsymbol {e}_1}\cdots s_l^{\boldsymbol {e}_l} = s_1^{\boldsymbol {f}_1}\cdots s_l^{\boldsymbol {f}_l}$ by the assumption and ![]() $s_{i + 1}^{\boldsymbol {e}_{i + 1}}\cdots s_l^{\boldsymbol {e}_l} = s_{i + 1}^{\boldsymbol {f}_{i + 1}}\cdots s_l^{\boldsymbol {f}_l}$ by inductive hypothesis, we have
$s_{i + 1}^{\boldsymbol {e}_{i + 1}}\cdots s_l^{\boldsymbol {e}_l} = s_{i + 1}^{\boldsymbol {f}_{i + 1}}\cdots s_l^{\boldsymbol {f}_l}$ by inductive hypothesis, we have ![]() $s_1^{\boldsymbol {e}_1}\cdots s_i^{\boldsymbol {e}_i} = s_1^{\boldsymbol {f}_1}\cdots s_i^{\boldsymbol {f}_i}$.
$s_1^{\boldsymbol {e}_1}\cdots s_i^{\boldsymbol {e}_i} = s_1^{\boldsymbol {f}_1}\cdots s_i^{\boldsymbol {f}_i}$.
Assume that the label of ![]() $\boldsymbol {e}$ at
$\boldsymbol {e}$ at ![]() $i$ (hence that of
$i$ (hence that of ![]() $\boldsymbol {f}$ at
$\boldsymbol {f}$ at ![]() $i$) is
$i$) is ![]() $U$,
$U$, ![]() $\boldsymbol {e}_i = 1$,
$\boldsymbol {e}_i = 1$, ![]() $\boldsymbol {f}_i = 0$. Set
$\boldsymbol {f}_i = 0$. Set ![]() $w = s_1^{\boldsymbol {e}_1}\cdots s_{i - 1}^{\boldsymbol {e}_{i - 1}}$. Then
$w = s_1^{\boldsymbol {e}_1}\cdots s_{i - 1}^{\boldsymbol {e}_{i - 1}}$. Then ![]() $s_1^{\boldsymbol {f}_1}\cdots s_{i - 1}^{\boldsymbol {f}_{i - 1}} = ws_i$ since
$s_1^{\boldsymbol {f}_1}\cdots s_{i - 1}^{\boldsymbol {f}_{i - 1}} = ws_i$ since ![]() $s_1^{\boldsymbol {e}_1}\cdots s_{i}^{\boldsymbol {e}_{i}} = s_1^{\boldsymbol {f}_1}\cdots s_{i}^{\boldsymbol {f}_{i}}$. Then since the label of
$s_1^{\boldsymbol {e}_1}\cdots s_{i}^{\boldsymbol {e}_{i}} = s_1^{\boldsymbol {f}_1}\cdots s_{i}^{\boldsymbol {f}_{i}}$. Then since the label of ![]() $\boldsymbol {e}$ at
$\boldsymbol {e}$ at ![]() $i$ is
$i$ is ![]() $U$, we have
$U$, we have ![]() $ws_i > w$, and since the label of
$ws_i > w$, and since the label of ![]() $\boldsymbol {f}$ at
$\boldsymbol {f}$ at ![]() $i$ is also
$i$ is also ![]() $U$, we have
$U$, we have ![]() $(ws_i)s_i > ws_i$. This is a contradiction. We also have a contradiction for the other cases. Hence we have
$(ws_i)s_i > ws_i$. This is a contradiction. We also have a contradiction for the other cases. Hence we have ![]() $\boldsymbol {e}_i = \boldsymbol {f}_i$.
$\boldsymbol {e}_i = \boldsymbol {f}_i$.
Let ![]() $w\in W$. Using this lemma, we can define a total order
$w\in W$. Using this lemma, we can define a total order ![]() ${<_{\underline {x},w}}$ on
${<_{\underline {x},w}}$ on ![]() $\{\boldsymbol {e}\in S^{l}\mid \underline {x}^{\boldsymbol {e}} = w\}$ as follows:
$\{\boldsymbol {e}\in S^{l}\mid \underline {x}^{\boldsymbol {e}} = w\}$ as follows: ![]() $\boldsymbol {f} < \boldsymbol {e}$ if and only if there exists
$\boldsymbol {f} < \boldsymbol {e}$ if and only if there exists ![]() $i$ such that
$i$ such that
• the labels of
 $\boldsymbol {e}$ and
$\boldsymbol {e}$ and  $\boldsymbol {f}$ are the same at any
$\boldsymbol {f}$ are the same at any  $j < i$,
$j < i$,• the label of
 $\boldsymbol {e}$ is
$\boldsymbol {e}$ is  $D$ at
$D$ at  $i$,
$i$,• the label of
 $\boldsymbol {f}$ is
$\boldsymbol {f}$ is  $U$ at
$U$ at  $i$.
$i$.
We just write ![]() $<$ for
$<$ for ![]() $<_{\underline {x},w}$ if there is no risk of confusion.
$<_{\underline {x},w}$ if there is no risk of confusion.
Fix ![]() $\delta _s\in V$ such that
$\delta _s\in V$ such that ![]() $\langle \alpha _s^{\vee },\delta _s\rangle = 1$ for each
$\langle \alpha _s^{\vee },\delta _s\rangle = 1$ for each ![]() $s\in S$. For
$s\in S$. For ![]() $\boldsymbol {e} \in \{0,1\}^{l}$, we define
$\boldsymbol {e} \in \{0,1\}^{l}$, we define ![]() $b_{\underline {x},\boldsymbol {e}}\in B_{\underline {x}}$ by
$b_{\underline {x},\boldsymbol {e}}\in B_{\underline {x}}$ by ![]() $b_{\underline {x},\boldsymbol {e}} = b_1\otimes \cdots \otimes b_l$ where
$b_{\underline {x},\boldsymbol {e}} = b_1\otimes \cdots \otimes b_l$ where ![]() $b_i\in B_{s_i}$ is defined by
$b_i\in B_{s_i}$ is defined by
 \[ b_i = \begin{cases} 1\otimes 1 & (\text{the label of }\boldsymbol{e}\text{ at }i\text{ is }U),\\ \delta_{s_i} \otimes 1 & (\text{the label of }\boldsymbol{e}\text{ at }i\text{ is }D). \end{cases} \]
\[ b_i = \begin{cases} 1\otimes 1 & (\text{the label of }\boldsymbol{e}\text{ at }i\text{ is }U),\\ \delta_{s_i} \otimes 1 & (\text{the label of }\boldsymbol{e}\text{ at }i\text{ is }D). \end{cases} \]Then we have the following proposition.
Proposition 3.10 Let ![]() $w\in W$,
$w\in W$, ![]() $\boldsymbol {e},\boldsymbol {f}\in \{0,1\}^{l}$ and assume that
$\boldsymbol {e},\boldsymbol {f}\in \{0,1\}^{l}$ and assume that ![]() $\underline {x}^{\boldsymbol {e}} = \underline {x}^{\boldsymbol {f}} = w$. Fix a reduced expression
$\underline {x}^{\boldsymbol {e}} = \underline {x}^{\boldsymbol {f}} = w$. Fix a reduced expression ![]() $\underline {w}$ for
$\underline {w}$ for ![]() $w$. Then
$w$. Then
 \[ \mathit{LL}_{\underline{x},\boldsymbol{e}}(b_{\underline{x},\boldsymbol{f}}) = \begin{cases} u_{\underline{w}} & (\boldsymbol{f} = \boldsymbol{e}),\\ 0 & (\boldsymbol{f} < \boldsymbol{e}). \end{cases} \]
\[ \mathit{LL}_{\underline{x},\boldsymbol{e}}(b_{\underline{x},\boldsymbol{f}}) = \begin{cases} u_{\underline{w}} & (\boldsymbol{f} = \boldsymbol{e}),\\ 0 & (\boldsymbol{f} < \boldsymbol{e}). \end{cases} \]
In particular, ![]() $\{\mathit {LL}_{\underline {x},\boldsymbol {e}}\mid \underline {x}^{\boldsymbol {e}} = w\}$ is linearly independent.
$\{\mathit {LL}_{\underline {x},\boldsymbol {e}}\mid \underline {x}^{\boldsymbol {e}} = w\}$ is linearly independent.
Proof. Let ![]() $\underline {x}_{\le k}$,
$\underline {x}_{\le k}$, ![]() $\boldsymbol {e}_{\le k}$,
$\boldsymbol {e}_{\le k}$, ![]() $\underline {w}_k$ as in Definition 3.8 and
$\underline {w}_k$ as in Definition 3.8 and ![]() $\boldsymbol {f}_{\le k}$ similarly. We prove that if the labels of
$\boldsymbol {f}_{\le k}$ similarly. We prove that if the labels of ![]() $\boldsymbol {e}$ and
$\boldsymbol {e}$ and ![]() $\boldsymbol {f}$ are the same at
$\boldsymbol {f}$ are the same at ![]() $i \le k$, then
$i \le k$, then ![]() $\mathit {LL}_k(b_{\underline {x}_{\le k},\boldsymbol {f}_{\le k}}) = u_{\underline {w}_k}$ by induction on
$\mathit {LL}_k(b_{\underline {x}_{\le k},\boldsymbol {f}_{\le k}}) = u_{\underline {w}_k}$ by induction on ![]() $k$.
$k$.
Assume that the label of ![]() $\boldsymbol {e}$ at
$\boldsymbol {e}$ at ![]() $k$ is
$k$ is ![]() $U$. Then we have
$U$. Then we have ![]() $b_{\underline {x}_{\le k},\boldsymbol {f}_{\le k}} = b_{\underline {x}_{\le k - 1},\boldsymbol {f}_{\le k - 1}}\otimes (1\otimes 1)$.
$b_{\underline {x}_{\le k},\boldsymbol {f}_{\le k}} = b_{\underline {x}_{\le k - 1},\boldsymbol {f}_{\le k - 1}}\otimes (1\otimes 1)$.
If ![]() $\boldsymbol {e}_k = 0$, then we have
$\boldsymbol {e}_k = 0$, then we have
If ![]() $\boldsymbol {e}_k = 1$, then
$\boldsymbol {e}_k = 1$, then
Assume that the label of ![]() $\boldsymbol {e}$ at
$\boldsymbol {e}$ at ![]() $k$ is
$k$ is ![]() $D$. Then we have
$D$. Then we have ![]() $b_{\underline {x}_{\le k},\boldsymbol {f}_{\le k}} = b_{\underline {x}_{\le k - 1},\boldsymbol {f}_{\le k - 1}}\otimes (\delta _{s_k}\otimes 1)$. Let
$b_{\underline {x}_{\le k},\boldsymbol {f}_{\le k}} = b_{\underline {x}_{\le k - 1},\boldsymbol {f}_{\le k - 1}}\otimes (\delta _{s_k}\otimes 1)$. Let ![]() $(t_1,\ldots ,t_{p - 1},s_k)$ be a reduced expression for
$(t_1,\ldots ,t_{p - 1},s_k)$ be a reduced expression for ![]() $w_{k - 1}$. If
$w_{k - 1}$. If ![]() $\boldsymbol {e}_k = 0$, then we have
$\boldsymbol {e}_k = 0$, then we have
 \begin{align*} \mathit{LL}_k(b_{\underline{x}_{\le k},\boldsymbol{f}_{\le k}}) & = \mathrm{rex}((\mathrm{Id}\otimes i_0^{s_k})(\mathrm{rex}(\mathit{LL}_{k - 1}(b_{\underline{x}_{\le k - 1},\boldsymbol{f}_{\le k - 1}}))\otimes (\delta_{s_k}\otimes 1)))\\ & = \mathrm{rex}((\mathrm{Id}\otimes i_0^{s_k})(u_{(t_1,\ldots,t_{p - 1},s_k)}\otimes (\delta_{s_k}\otimes 1)))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes i_0^{s_k}(1\otimes \delta_{s_k}\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes (\partial_{s_k}(\delta_{s_k})\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1},s_k)})\\ & = u_{\underline{w}_k}. \end{align*}
\begin{align*} \mathit{LL}_k(b_{\underline{x}_{\le k},\boldsymbol{f}_{\le k}}) & = \mathrm{rex}((\mathrm{Id}\otimes i_0^{s_k})(\mathrm{rex}(\mathit{LL}_{k - 1}(b_{\underline{x}_{\le k - 1},\boldsymbol{f}_{\le k - 1}}))\otimes (\delta_{s_k}\otimes 1)))\\ & = \mathrm{rex}((\mathrm{Id}\otimes i_0^{s_k})(u_{(t_1,\ldots,t_{p - 1},s_k)}\otimes (\delta_{s_k}\otimes 1)))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes i_0^{s_k}(1\otimes \delta_{s_k}\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes (\partial_{s_k}(\delta_{s_k})\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1},s_k)})\\ & = u_{\underline{w}_k}. \end{align*} If ![]() $\boldsymbol {e}_k = 1$, then we have
$\boldsymbol {e}_k = 1$, then we have
 \begin{align*} \mathit{LL}_k(b_{\underline{x}_{\le k},\boldsymbol{f}_{\le k}}) & = \mathrm{rex}((\mathrm{Id}\otimes i_1^{s_k})(\mathrm{rex}(\mathit{LL}_{k - 1}(b_{\underline{x}_{\le k - 1},\boldsymbol{f}_{\le k - 1}}))\otimes (\delta_{s_k}\otimes 1)))\\ & = \mathrm{rex}((\mathrm{Id}\otimes i_1^{s_k})(u_{(t_1,\ldots,t_{p - 1},s_k)}\otimes (\delta_{s_k}\otimes 1)))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes i_1^{s_k}(1\otimes \delta_{s_k}\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\partial_{s_k}(\delta_{s_k}))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})})\\ & = u_{\underline{w}_{k}}. \end{align*}
\begin{align*} \mathit{LL}_k(b_{\underline{x}_{\le k},\boldsymbol{f}_{\le k}}) & = \mathrm{rex}((\mathrm{Id}\otimes i_1^{s_k})(\mathrm{rex}(\mathit{LL}_{k - 1}(b_{\underline{x}_{\le k - 1},\boldsymbol{f}_{\le k - 1}}))\otimes (\delta_{s_k}\otimes 1)))\\ & = \mathrm{rex}((\mathrm{Id}\otimes i_1^{s_k})(u_{(t_1,\ldots,t_{p - 1},s_k)}\otimes (\delta_{s_k}\otimes 1)))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes i_1^{s_k}(1\otimes \delta_{s_k}\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\partial_{s_k}(\delta_{s_k}))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})})\\ & = u_{\underline{w}_{k}}. \end{align*}
This is the end of the induction. In particular, we have ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}(b_{\underline {x},\boldsymbol {e}}) = u_{\underline {w}}$.
$\mathit {LL}_{\underline {x},\boldsymbol {e}}(b_{\underline {x},\boldsymbol {e}}) = u_{\underline {w}}$.
Assume that ![]() $\boldsymbol {f} < \boldsymbol {e}$ and take
$\boldsymbol {f} < \boldsymbol {e}$ and take ![]() $k$ such that the labels of
$k$ such that the labels of ![]() $\boldsymbol {e}$ and
$\boldsymbol {e}$ and ![]() $\boldsymbol {f}$ are the same at any
$\boldsymbol {f}$ are the same at any ![]() $i < k$ and the label of
$i < k$ and the label of ![]() $\boldsymbol {e}$ (respectively,
$\boldsymbol {e}$ (respectively, ![]() $\boldsymbol {f}$) at
$\boldsymbol {f}$) at ![]() $k$ is
$k$ is ![]() $D$ (respectively,
$D$ (respectively, ![]() $U$). Then we have
$U$). Then we have ![]() $b_{\underline {x}_{\le k},\boldsymbol {f}_{\le k}} = b_{\underline {x}_{\le k - 1},\boldsymbol {f}_{\le k - 1}}\otimes (1\otimes 1)$. Let
$b_{\underline {x}_{\le k},\boldsymbol {f}_{\le k}} = b_{\underline {x}_{\le k - 1},\boldsymbol {f}_{\le k - 1}}\otimes (1\otimes 1)$. Let ![]() $(t_1,\ldots ,t_{p - 1},s_k)$ be a reduced expression for
$(t_1,\ldots ,t_{p - 1},s_k)$ be a reduced expression for ![]() $w_{k - 1}$. If
$w_{k - 1}$. If ![]() $\boldsymbol {e}_k = 0$, then we have
$\boldsymbol {e}_k = 0$, then we have
 \begin{align*} \mathit{LL}_k(b_{\underline{x}_{\le k},\boldsymbol{f}_{\le k}}) & = \mathrm{rex}((\mathrm{Id}\otimes i_0^{s_k})(\mathrm{rex}(\mathit{LL}_{k - 1}(b_{\underline{x}_{\le k - 1},\boldsymbol{f}_{\le k - 1}}))\otimes (1\otimes 1)))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes i_0^{s_k}(1\otimes 1\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes (\partial_{s_k}(1)\otimes 1))\\ & = 0. \end{align*}
\begin{align*} \mathit{LL}_k(b_{\underline{x}_{\le k},\boldsymbol{f}_{\le k}}) & = \mathrm{rex}((\mathrm{Id}\otimes i_0^{s_k})(\mathrm{rex}(\mathit{LL}_{k - 1}(b_{\underline{x}_{\le k - 1},\boldsymbol{f}_{\le k - 1}}))\otimes (1\otimes 1)))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes i_0^{s_k}(1\otimes 1\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes (\partial_{s_k}(1)\otimes 1))\\ & = 0. \end{align*}
If ![]() $\boldsymbol {e}_k = 1$, then we have
$\boldsymbol {e}_k = 1$, then we have
 \begin{align*} \mathit{LL}_k(b_{\underline{x}_{\le k},\boldsymbol{f}_{\le k}}) & = \mathrm{rex}((\mathrm{Id}\otimes i_1^{s_k})(\mathrm{rex}(\mathit{LL}_{k - 1}(b_{\underline{x}_{\le k - 1},\boldsymbol{f}_{\le k - 1}}))\otimes (1\otimes 1)))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes i_1^{s_k}(1\otimes 1\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\partial_{s_k}(1))\\ & = 0. \end{align*}
\begin{align*} \mathit{LL}_k(b_{\underline{x}_{\le k},\boldsymbol{f}_{\le k}}) & = \mathrm{rex}((\mathrm{Id}\otimes i_1^{s_k})(\mathrm{rex}(\mathit{LL}_{k - 1}(b_{\underline{x}_{\le k - 1},\boldsymbol{f}_{\le k - 1}}))\otimes (1\otimes 1)))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\otimes i_1^{s_k}(1\otimes 1\otimes 1))\\ & = \mathrm{rex}(u_{(t_1,\ldots,t_{p - 1})}\partial_{s_k}(1))\\ & = 0. \end{align*} These calculations imply ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}(b_{\underline {x},\boldsymbol {f}}) = 0$.
$\mathit {LL}_{\underline {x},\boldsymbol {e}}(b_{\underline {x},\boldsymbol {f}}) = 0$.
Remark 3.11 Since the degree of ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}$ (respectively,
$\mathit {LL}_{\underline {x},\boldsymbol {e}}$ (respectively, ![]() $u_{\underline {w}}$) is
$u_{\underline {w}}$) is ![]() $d(\boldsymbol {e})$ (respectively,
$d(\boldsymbol {e})$ (respectively, ![]() $-\ell (w)$),
$-\ell (w)$), ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}(b_{\underline {x},\boldsymbol {e}}) = u_{\underline {w}}$ implies
$\mathit {LL}_{\underline {x},\boldsymbol {e}}(b_{\underline {x},\boldsymbol {e}}) = u_{\underline {w}}$ implies ![]() $\deg (b_{\underline {x},\boldsymbol {e}}) = -d(\boldsymbol {e})-\ell (w)$.
$\deg (b_{\underline {x},\boldsymbol {e}}) = -d(\boldsymbol {e})-\ell (w)$.
3.4 A basis of  $B_{\underline {x}}^{w}$
$B_{\underline {x}}^{w}$
Let ![]() $w\in W$ with a reduced expression
$w\in W$ with a reduced expression ![]() $\underline {w}$ and
$\underline {w}$ and ![]() $\underline {x}\in S^{l}$,
$\underline {x}\in S^{l}$, ![]() $\boldsymbol {e}\in \{0,1\}^{l}$ such that
$\boldsymbol {e}\in \{0,1\}^{l}$ such that ![]() $\underline {x}^{\boldsymbol {e}} = w$. Let
$\underline {x}^{\boldsymbol {e}} = w$. Let ![]() $b_{\underline {x},\boldsymbol {e}}^{w}$ be the image of
$b_{\underline {x},\boldsymbol {e}}^{w}$ be the image of ![]() $b_{\underline {x},\boldsymbol {e}}\in B_{\underline {x}}$ in
$b_{\underline {x},\boldsymbol {e}}\in B_{\underline {x}}$ in ![]() $B_{\underline {x}}^{w}$.
$B_{\underline {x}}^{w}$.
Let ![]() $\underline {w} = (t_1,\ldots ,t_r)$. We define a morphism
$\underline {w} = (t_1,\ldots ,t_r)$. We define a morphism ![]() $\varphi _{\underline {w}}\colon B_{\underline {w}}\to R_w$ in
$\varphi _{\underline {w}}\colon B_{\underline {w}}\to R_w$ in ![]() $\mathcal {C}$ by
$\mathcal {C}$ by ![]() $\varphi _{\underline {w}}(f_0\otimes \cdots \otimes f_r) = f_0(t_1(f_1))\cdots (t_1\cdots t_r(f_r))$ where
$\varphi _{\underline {w}}(f_0\otimes \cdots \otimes f_r) = f_0(t_1(f_1))\cdots (t_1\cdots t_r(f_r))$ where ![]() $f_0,\ldots ,f_r\in R$ and we identify
$f_0,\ldots ,f_r\in R$ and we identify ![]() $B_{\underline {w}} = R\otimes _{R^{t_1}}R\otimes _{R^{t_2}}\cdots \otimes _{R^{t_l}}R$.
$B_{\underline {w}} = R\otimes _{R^{t_1}}R\otimes _{R^{t_2}}\cdots \otimes _{R^{t_l}}R$.
Theorem 3.12 Fix ![]() $\underline {x}$,
$\underline {x}$, ![]() $w$ and
$w$ and ![]() $\underline {w}$.
$\underline {w}$.
(1) The left
 $R$-module
$R$-module  $B_{\underline {x}}^{w}$ has a basis
$B_{\underline {x}}^{w}$ has a basis  $\{b^{w}_{\underline {x},\boldsymbol {e}}\mid \underline {x}^{\boldsymbol {e}} = w\}$.
$\{b^{w}_{\underline {x},\boldsymbol {e}}\mid \underline {x}^{\boldsymbol {e}} = w\}$.(2) The left
 $R$-module
$R$-module  $B_{\underline {x}}^{w}$ is graded free and its graded rank
$B_{\underline {x}}^{w}$ is graded free and its graded rank  $\operatorname {grk}(B_{\underline {x}}^{w})$ is given by
$\operatorname {grk}(B_{\underline {x}}^{w})$ is given by  $\sum _{\underline {x}^{\boldsymbol {e}} = w}v^{d(\boldsymbol {e}) + \ell (w)} = v^{\ell (w)}p_{\underline {x}}^{w}(v)$.
$\sum _{\underline {x}^{\boldsymbol {e}} = w}v^{d(\boldsymbol {e}) + \ell (w)} = v^{\ell (w)}p_{\underline {x}}^{w}(v)$.(3) The homomorphisms
 $\{\varphi _{\underline {w}}\circ \mathit {LL}_{\underline {x},\boldsymbol {e}}\mid \underline {x}^{\boldsymbol {e}} = w\}$ are a basis of
$\{\varphi _{\underline {w}}\circ \mathit {LL}_{\underline {x},\boldsymbol {e}}\mid \underline {x}^{\boldsymbol {e}} = w\}$ are a basis of  $\operatorname {Hom}_{\mathcal {C}}^{\bullet }(B_{\underline {x}},R_w)$.
$\operatorname {Hom}_{\mathcal {C}}^{\bullet }(B_{\underline {x}},R_w)$.
Proof. By Proposition 3.10, we have
 \[ \varphi_{\underline{w}}(\mathit{LL}_{\underline{x},\boldsymbol{e}}(b_{\underline{x},\boldsymbol{f}})) = \begin{cases} 1 & (\boldsymbol{f} = \boldsymbol{e}),\\ 0 & (\boldsymbol{f} < \boldsymbol{e}). \end{cases} \]
\[ \varphi_{\underline{w}}(\mathit{LL}_{\underline{x},\boldsymbol{e}}(b_{\underline{x},\boldsymbol{f}})) = \begin{cases} 1 & (\boldsymbol{f} = \boldsymbol{e}),\\ 0 & (\boldsymbol{f} < \boldsymbol{e}). \end{cases} \]
Since ![]() $\varphi _{\underline {w}}\circ \mathit {LL}_{\underline {x},\boldsymbol {e}}\colon B_{\underline {x}}\to R_w$ is a homomorphism in
$\varphi _{\underline {w}}\circ \mathit {LL}_{\underline {x},\boldsymbol {e}}\colon B_{\underline {x}}\to R_w$ is a homomorphism in ![]() $\mathcal {C}$, it induces
$\mathcal {C}$, it induces ![]() $\psi _{\boldsymbol {e}}\colon B_{\underline {x}}^{w}\to R_w$ and we have
$\psi _{\boldsymbol {e}}\colon B_{\underline {x}}^{w}\to R_w$ and we have
 \[ \psi_{\boldsymbol{e}}(b_{\underline{x},\boldsymbol{f}}^{w}) = \begin{cases} 1 & (\boldsymbol{f} = \boldsymbol{e}),\\ 0 & (\boldsymbol{f} < \boldsymbol{e}). \end{cases} \]
\[ \psi_{\boldsymbol{e}}(b_{\underline{x},\boldsymbol{f}}^{w}) = \begin{cases} 1 & (\boldsymbol{f} = \boldsymbol{e}),\\ 0 & (\boldsymbol{f} < \boldsymbol{e}). \end{cases} \]
Inductively on ![]() $\boldsymbol {e}$, we can take
$\boldsymbol {e}$, we can take ![]() $\psi '_{\boldsymbol {e}} \in \psi _{\boldsymbol {e}} + \sum _{\boldsymbol {e}' > \boldsymbol {e}}R\psi _{\boldsymbol {e}'}$ such that
$\psi '_{\boldsymbol {e}} \in \psi _{\boldsymbol {e}} + \sum _{\boldsymbol {e}' > \boldsymbol {e}}R\psi _{\boldsymbol {e}'}$ such that ![]() $\psi '_{\boldsymbol {e}}(b_{\underline {x},\boldsymbol {f}}^{w}) = \delta _{\boldsymbol {e},\boldsymbol {f}}$ (Kronecker's delta). That is,
$\psi '_{\boldsymbol {e}}(b_{\underline {x},\boldsymbol {f}}^{w}) = \delta _{\boldsymbol {e},\boldsymbol {f}}$ (Kronecker's delta). That is, ![]() $m\mapsto \sum _{\underline {x}^{\boldsymbol {e}} = w}\psi '_{\boldsymbol {e}}(m)b_{\underline {x},\boldsymbol {e}}^{w}$ gives a splitting of the embedding
$m\mapsto \sum _{\underline {x}^{\boldsymbol {e}} = w}\psi '_{\boldsymbol {e}}(m)b_{\underline {x},\boldsymbol {e}}^{w}$ gives a splitting of the embedding ![]() ${\bigoplus} _{\underline {x}}^{\boldsymbol {e}}$
${\bigoplus} _{\underline {x}}^{\boldsymbol {e}}$ ![]() ${= w}\,Rb_{\underline {x},\boldsymbol {e}}^{w}\hookrightarrow B_{\underline {x}}^{w}$.
${= w}\,Rb_{\underline {x},\boldsymbol {e}}^{w}\hookrightarrow B_{\underline {x}}^{w}$.
Take ![]() $N$ such that
$N$ such that ![]() $B_{\underline {x}}^{w} = ({\bigoplus} _{\underline {x}^{\boldsymbol {e}} = w}\,Rb_{\underline {x},\boldsymbol {e}}^{w})\oplus N$. Then we have
$B_{\underline {x}}^{w} = ({\bigoplus} _{\underline {x}^{\boldsymbol {e}} = w}\,Rb_{\underline {x},\boldsymbol {e}}^{w})\oplus N$. Then we have ![]() $(B_{\underline {x}}^{w})_Q = ({\bigoplus} _{\underline {x}^{\boldsymbol {e}} = w}\,Qb_{\underline {x},\boldsymbol {e}}^{w})\oplus N_Q$. We have
$(B_{\underline {x}}^{w})_Q = ({\bigoplus} _{\underline {x}^{\boldsymbol {e}} = w}\,Qb_{\underline {x},\boldsymbol {e}}^{w})\oplus N_Q$. We have ![]() $\dim _Q (B_{\underline {x}}^{w})_Q = p_{\underline {x}}^{w}(1)$ by Lemma 2.17. By Lemma 3.1, we also have
$\dim _Q (B_{\underline {x}}^{w})_Q = p_{\underline {x}}^{w}(1)$ by Lemma 2.17. By Lemma 3.1, we also have ![]() $\dim _Q({\bigoplus} _{\underline {x}^{\boldsymbol {e}} = w}\,Qb_{\underline {x},\boldsymbol {e}}^{w}) = p_{\underline {x}}^{w}(1)$. Hence
$\dim _Q({\bigoplus} _{\underline {x}^{\boldsymbol {e}} = w}\,Qb_{\underline {x},\boldsymbol {e}}^{w}) = p_{\underline {x}}^{w}(1)$. Hence ![]() $N_Q = 0$. That is,
$N_Q = 0$. That is, ![]() $N$ is a torsion module. Since
$N$ is a torsion module. Since ![]() $N\subset B_{\underline {x}}^{w}\subset (B_{\underline {x}})_Q^{w}$,
$N\subset B_{\underline {x}}^{w}\subset (B_{\underline {x}})_Q^{w}$, ![]() $N$ is a torsion-free module. Hence
$N$ is a torsion-free module. Hence ![]() $N = 0$.
$N = 0$.
(2) follows from (1).
We prove (3). Since ![]() $\{b_{\underline {x},\boldsymbol {e}}^{w}\}$ is a basis of
$\{b_{\underline {x},\boldsymbol {e}}^{w}\}$ is a basis of ![]() $B_{\underline {x}}^{w}$,
$B_{\underline {x}}^{w}$, ![]() $\{\psi '_{\boldsymbol {e}}\}$ is a basis of
$\{\psi '_{\boldsymbol {e}}\}$ is a basis of ![]() $\operatorname {Hom}^{\bullet }_R(B_{\underline {x}}^{w},R)$ which is dual to
$\operatorname {Hom}^{\bullet }_R(B_{\underline {x}}^{w},R)$ which is dual to ![]() $\{b_{\underline {x},\boldsymbol {e}}\}$. By
$\{b_{\underline {x},\boldsymbol {e}}\}$. By ![]() $\psi '_{\boldsymbol {e}} \in \psi _{\boldsymbol {e}} + \sum _{\boldsymbol {e}' > \boldsymbol {e}}R\psi _{\boldsymbol {e}'}$,
$\psi '_{\boldsymbol {e}} \in \psi _{\boldsymbol {e}} + \sum _{\boldsymbol {e}' > \boldsymbol {e}}R\psi _{\boldsymbol {e}'}$, ![]() $\{\psi _{\boldsymbol {e}}\}$ is also a basis. Since
$\{\psi _{\boldsymbol {e}}\}$ is also a basis. Since ![]() $\operatorname {Hom}^{\bullet }_R(B_{\underline {x}}^{w},R)\simeq \operatorname {Hom}^{\bullet }_{\mathcal {C}}(B_{\underline {x}},R_w)$ and
$\operatorname {Hom}^{\bullet }_R(B_{\underline {x}}^{w},R)\simeq \operatorname {Hom}^{\bullet }_{\mathcal {C}}(B_{\underline {x}},R_w)$ and ![]() $\psi _{\boldsymbol {e}}$ corresponds to
$\psi _{\boldsymbol {e}}$ corresponds to ![]() $\varphi _{\underline {w}}\circ \mathit {LL}_{\underline {x},\boldsymbol {e}}$ by the definition of
$\varphi _{\underline {w}}\circ \mathit {LL}_{\underline {x},\boldsymbol {e}}$ by the definition of ![]() $\psi _{\boldsymbol {e}}$, we get (3).
$\psi _{\boldsymbol {e}}$, we get (3).
With Lemma 2.19, we have the following corollary.
Corollary 3.13 The left ![]() $R$-module
$R$-module ![]() $B_{\underline {x},w}$ is graded free and its graded rank is given by
$B_{\underline {x},w}$ is graded free and its graded rank is given by ![]() $v^{-\ell (w)}p_{\underline {x}}^{w}(v^{-1})$.
$v^{-\ell (w)}p_{\underline {x}}^{w}(v^{-1})$.
Corollary 3.14 The homomorphism ![]() $\varphi _{\underline {w}}\colon B_{\underline {w}}\to R_w(\ell (w))$ induces
$\varphi _{\underline {w}}\colon B_{\underline {w}}\to R_w(\ell (w))$ induces ![]() $B_{\underline {w}}^{w}\simeq R_w(\ell (w))$.
$B_{\underline {w}}^{w}\simeq R_w(\ell (w))$.
Proof. Since ![]() $\varphi _{\underline {w}}$ is a homomorphism in
$\varphi _{\underline {w}}$ is a homomorphism in ![]() $\mathcal {C}$, this induces
$\mathcal {C}$, this induces ![]() $B_{\underline {w}}^{w}\to R_w(\ell (w))$. This is obviously surjective. By the above theorem,
$B_{\underline {w}}^{w}\to R_w(\ell (w))$. This is obviously surjective. By the above theorem, ![]() $B_{\underline {w}}^{w}$ is free of rank one. Hence
$B_{\underline {w}}^{w}$ is free of rank one. Hence ![]() $B_{\underline {w}}^{w}\twoheadrightarrow R_w(\ell (w))$ is an isomorphism.
$B_{\underline {w}}^{w}\twoheadrightarrow R_w(\ell (w))$ is an isomorphism.
Corollary 3.15 Let ![]() $w\in W$ with a reduced expression
$w\in W$ with a reduced expression ![]() $\underline {w}$ and
$\underline {w}$ and ![]() $B\in \mathcal {S}\mathrm {Bimod}$. Then
$B\in \mathcal {S}\mathrm {Bimod}$. Then ![]() $\operatorname {Hom}^{\bullet }_{\mathcal {C}}(B,B_{\underline {w}})\to \operatorname {Hom}^{\bullet }_R(B^{w},B_{\underline {w}}^{w})$ is surjective.
$\operatorname {Hom}^{\bullet }_{\mathcal {C}}(B,B_{\underline {w}})\to \operatorname {Hom}^{\bullet }_R(B^{w},B_{\underline {w}}^{w})$ is surjective.
3.5 Elements supported on a closed subset
We call a subset ![]() $I\subset W$ closed if
$I\subset W$ closed if ![]() $w_1\in I$,
$w_1\in I$, ![]() $w_2\in W$,
$w_2\in W$, ![]() $w_2\le w_1$ implies
$w_2\le w_1$ implies ![]() $w_2\in I$.
$w_2\in I$.
Lemma 3.16 Let ![]() $I$ be a finite closed subset and
$I$ be a finite closed subset and ![]() $w\in I$ a maximal element with respect to the Bruhat order. Then there exists a enumeration
$w\in I$ a maximal element with respect to the Bruhat order. Then there exists a enumeration ![]() $w_1,w_2,\ldots$ of elements of
$w_1,w_2,\ldots$ of elements of ![]() $W$ such that
$W$ such that ![]() $\{w_1,\ldots ,w_i\}$ is closed for any
$\{w_1,\ldots ,w_i\}$ is closed for any ![]() $i$,
$i$, ![]() $w = w_{\#I}$ and
$w = w_{\#I}$ and ![]() $I = \{w_1,\ldots ,w_{\#I}\}$.
$I = \{w_1,\ldots ,w_{\#I}\}$.
Proof. Set ![]() $k = \#I$. Let
$k = \#I$. Let ![]() $w_1,\ldots ,w_{k - 1}$ be an enumeration of elements of
$w_1,\ldots ,w_{k - 1}$ be an enumeration of elements of ![]() $I\setminus \{w\}$ such that
$I\setminus \{w\}$ such that ![]() $w_i\le w_j$ implies
$w_i\le w_j$ implies ![]() $i\le j$. Let
$i\le j$. Let ![]() $w_{k + 1},\ldots$ be a similar enumeration of elements of
$w_{k + 1},\ldots$ be a similar enumeration of elements of ![]() $W\setminus I$ and put
$W\setminus I$ and put ![]() $w_k = w$. We prove that
$w_k = w$. We prove that ![]() $\{w_1,\ldots ,w_i\}$ is always closed. If
$\{w_1,\ldots ,w_i\}$ is always closed. If ![]() $i \le k$ then it is obvious. Assume that
$i \le k$ then it is obvious. Assume that ![]() $i > k$ and
$i > k$ and ![]() $w_j\le w_i$. If
$w_j\le w_i$. If ![]() $j\le k$, then we have
$j\le k$, then we have ![]() $j\le i$. If
$j\le i$. If ![]() $j > k$, then we have
$j > k$, then we have ![]() $j\le i$ by the assumption on the enumeration
$j\le i$ by the assumption on the enumeration ![]() $w_{k + 1},\ldots .$ In any case,
$w_{k + 1},\ldots .$ In any case, ![]() $w_j\in \{1,\ldots ,w_i\}$.
$w_j\in \{1,\ldots ,w_i\}$.
A light leaf ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}\colon B_{\underline {x}}\to B_{\underline {w}}$ gives a homomorphism
$\mathit {LL}_{\underline {x},\boldsymbol {e}}\colon B_{\underline {x}}\to B_{\underline {w}}$ gives a homomorphism ![]() $B_{\underline {w}}\simeq D(B_{\underline {w}})\xrightarrow {D(\mathit {LL}_{\underline {x},\boldsymbol {e}})} D(B_{\underline {x}})\simeq B_{\underline {x}}$. We denote this homomorphism by
$B_{\underline {w}}\simeq D(B_{\underline {w}})\xrightarrow {D(\mathit {LL}_{\underline {x},\boldsymbol {e}})} D(B_{\underline {x}})\simeq B_{\underline {x}}$. We denote this homomorphism by ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}$. Let
$\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}$. Let ![]() $\pi _{\underline {x}}^{w}\colon B_{\underline {x}}\to B_{\underline {x}}^{w}$ be the projection. If
$\pi _{\underline {x}}^{w}\colon B_{\underline {x}}\to B_{\underline {x}}^{w}$ be the projection. If ![]() $I\subset W$ and
$I\subset W$ and ![]() $w\in I$, then
$w\in I$, then ![]() $B_{\underline {x},I\setminus \{w\}}$ is the kernel of
$B_{\underline {x},I\setminus \{w\}}$ is the kernel of ![]() $B_{\underline {x},I}\to B_{\underline {x}}^{w}$. Therefore we also write
$B_{\underline {x},I}\to B_{\underline {x}}^{w}$. Therefore we also write ![]() $\pi _{\underline {x}}^{w}$ for the projection
$\pi _{\underline {x}}^{w}$ for the projection ![]() $B_{\underline {x},I}\to B_{\underline {x},I}/B_{\underline {x},I\setminus \{w\}}$.
$B_{\underline {x},I}\to B_{\underline {x},I}/B_{\underline {x},I\setminus \{w\}}$.
Theorem 3.17 Let ![]() $I$ be a closed subset and
$I$ be a closed subset and ![]() $w$ a maximal element in
$w$ a maximal element in ![]() $I$. Set
$I$. Set ![]() $I' = I\setminus \{w\}$. Let
$I' = I\setminus \{w\}$. Let ![]() $\underline {w}$ be a reduced expression for
$\underline {w}$ be a reduced expression for ![]() $w$ and
$w$ and ![]() $\underline {x}\in S^{l}$. Then
$\underline {x}\in S^{l}$. Then ![]() $\{\pi _{\underline {x}}^{w}(\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}}))\mid \underline {x}^{\boldsymbol {e}} = w\}$ is a basis of the left
$\{\pi _{\underline {x}}^{w}(\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}}))\mid \underline {x}^{\boldsymbol {e}} = w\}$ is a basis of the left ![]() $R$-module
$R$-module ![]() $B_{\underline {x},I}/B_{\underline {x},I'}$.
$B_{\underline {x},I}/B_{\underline {x},I'}$.
Proof. Note that since ![]() $\{y\in W\mid y\le w\}\subset I$, we have
$\{y\in W\mid y\le w\}\subset I$, we have ![]() $\operatorname {supp}_W(B_{\underline {w}})\subset I$. Hence the image of any homomorphism from
$\operatorname {supp}_W(B_{\underline {w}})\subset I$. Hence the image of any homomorphism from ![]() $B_{\underline {w}}$ to
$B_{\underline {w}}$ to ![]() $B_{\underline {x}}$ is contained in
$B_{\underline {x}}$ is contained in ![]() $B_{\underline {x},I}$. Therefore
$B_{\underline {x},I}$. Therefore ![]() $\pi _{\underline {x}}^{w}(\mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}(u_{\underline {w}}))\in B_{\underline {x},I}/B_{\underline {x},I'}$.
$\pi _{\underline {x}}^{w}(\mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}(u_{\underline {w}}))\in B_{\underline {x},I}/B_{\underline {x},I'}$.
First we prove that ![]() $\{\pi _{\underline {x}}^{w}(\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}}))\mid \underline {x}^{\boldsymbol {e}} = w\}$ is linearly independent. It is sufficient to prove that this set is linearly independent over
$\{\pi _{\underline {x}}^{w}(\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}}))\mid \underline {x}^{\boldsymbol {e}} = w\}$ is linearly independent. It is sufficient to prove that this set is linearly independent over ![]() $Q$.
$Q$.
Recall that we have homomorphisms
The set of these elements where ![]() $\boldsymbol {e}$ satisfies
$\boldsymbol {e}$ satisfies ![]() $\underline {x}^{\boldsymbol {e}} = w$ is linearly independent by Theorem 3.12. Therefore the dualized maps
$\underline {x}^{\boldsymbol {e}} = w$ is linearly independent by Theorem 3.12. Therefore the dualized maps
are also linearly independent. (Note that ![]() $B_{\underline {w},w}$ and
$B_{\underline {w},w}$ and ![]() $B_{\underline {x}}$ are both graded free as right
$B_{\underline {x}}$ are both graded free as right ![]() $R$-modules, hence
$R$-modules, hence ![]() $D(D(B_{\underline {w},w}))\simeq B_{\underline {w},w}$ and
$D(D(B_{\underline {w},w}))\simeq B_{\underline {w},w}$ and ![]() $D(D(B_{\underline {x}}))\simeq B_{\underline {x}}$.) This map factors through
$D(D(B_{\underline {x}}))\simeq B_{\underline {x}}$.) This map factors through ![]() $B_{\underline {x},w}\hookrightarrow B_{\underline {x}}$. Therefore the induced homomorphisms
$B_{\underline {x},w}\hookrightarrow B_{\underline {x}}$. Therefore the induced homomorphisms ![]() $B_{\underline {w},w}\to B_{\underline {x},w}$ are linearly independent. Since
$B_{\underline {w},w}\to B_{\underline {x},w}$ are linearly independent. Since ![]() $B_{\underline {x},w}$ is torsion free, the maps
$B_{\underline {x},w}$ is torsion free, the maps ![]() $B_{\underline {w},w}\otimes _R Q\xrightarrow {\eta _{\underline {x},\boldsymbol {e},Q}}B_{\underline {x},w}\otimes _R Q$ obtained by tensoring with
$B_{\underline {w},w}\otimes _R Q\xrightarrow {\eta _{\underline {x},\boldsymbol {e},Q}}B_{\underline {x},w}\otimes _R Q$ obtained by tensoring with ![]() $Q$ are also linearly independent.
$Q$ are also linearly independent.
The left ![]() $R$-module
$R$-module ![]() $B_{\underline {w}}^{w}$ is free of rank one by Theorem 3.12. Since
$B_{\underline {w}}^{w}$ is free of rank one by Theorem 3.12. Since ![]() $D(B_{\underline {w}}^{w})\simeq B_{\underline {w},w}$, this is also true for
$D(B_{\underline {w}}^{w})\simeq B_{\underline {w},w}$, this is also true for ![]() $B_{\underline {w},w}$. Therefore the dimension of both
$B_{\underline {w},w}$. Therefore the dimension of both ![]() $B_{\underline {w},w}\otimes _R Q$ and
$B_{\underline {w},w}\otimes _R Q$ and ![]() $B_{\underline {w}}^{w}\otimes _R Q$ is one and hence we have
$B_{\underline {w}}^{w}\otimes _R Q$ is one and hence we have ![]() $B_{\underline {w},w}\otimes _R Q\xrightarrow {\sim }B_{\underline {w}}^{w}\otimes _R Q$. Therefore, for any
$B_{\underline {w},w}\otimes _R Q\xrightarrow {\sim }B_{\underline {w}}^{w}\otimes _R Q$. Therefore, for any ![]() $0\ne q\in B_{\underline {w},w}\otimes _R Q\simeq B_{\underline {w}}^{w}\otimes _R Q$,
$0\ne q\in B_{\underline {w},w}\otimes _R Q\simeq B_{\underline {w}}^{w}\otimes _R Q$, ![]() $\{\eta _{\underline {x},\boldsymbol {e},Q}(q)\mid \underline {x}^{\boldsymbol {e}} = w\}\subset B_{\underline {x},w}\otimes _R Q$ is linearly independent. In particular, we can take
$\{\eta _{\underline {x},\boldsymbol {e},Q}(q)\mid \underline {x}^{\boldsymbol {e}} = w\}\subset B_{\underline {x},w}\otimes _R Q$ is linearly independent. In particular, we can take ![]() $q$ as the image of
$q$ as the image of ![]() $u_{\underline {w}}\in B_{\underline {w}}$. Therefore
$u_{\underline {w}}\in B_{\underline {w}}$. Therefore
is linearly independent. Observing the commutative diagram

we have that ![]() $\{\pi _{\underline {x}}^{w}(\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}}))\mid \underline {x}^{\boldsymbol {e}} = w\}$ is linearly independent over
$\{\pi _{\underline {x}}^{w}(\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}}))\mid \underline {x}^{\boldsymbol {e}} = w\}$ is linearly independent over ![]() $Q$.
$Q$.
Let ![]() $w_1,w_2,\ldots$ be an enumeration as in the previous lemma. Fix a reduced expression
$w_1,w_2,\ldots$ be an enumeration as in the previous lemma. Fix a reduced expression ![]() $\underline {w}_k$ for
$\underline {w}_k$ for ![]() $w_k$. Set
$w_k$. Set ![]() $I(k) = \{w_1,\ldots ,w_k\}$. We have a filtration
$I(k) = \{w_1,\ldots ,w_k\}$. We have a filtration ![]() $\{B_{\underline {x},I(k)}\}_k$ of
$\{B_{\underline {x},I(k)}\}_k$ of ![]() $B_{\underline {x}}$ and, as we have proved above,
$B_{\underline {x}}$ and, as we have proved above,
We prove that this is an isomorphism. First we prove that this map is an isomorphism when ![]() $\mathbb {K}$ is a field. We have
$\mathbb {K}$ is a field. We have ![]() $\deg (\mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}) = d(\boldsymbol {e})$ and
$\deg (\mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}) = d(\boldsymbol {e})$ and ![]() $\deg (u_{\underline {w}_k}) = -\ell (w_k)$. Therefore the graded rank of
$\deg (u_{\underline {w}_k}) = -\ell (w_k)$. Therefore the graded rank of ![]() ${\bigoplus} _{\underline {x}^{\boldsymbol {e}} = w_k}\, R\pi _{\underline {x}}^{w}(\mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}(u_{\underline {w}_k}))$ is
${\bigoplus} _{\underline {x}^{\boldsymbol {e}} = w_k}\, R\pi _{\underline {x}}^{w}(\mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}(u_{\underline {w}_k}))$ is ![]() $\sum _{\underline {x}^{\boldsymbol {e}} = w_k}v^{-d(\boldsymbol {e}) + \ell (w_k)} = v^{\ell (w_k)}p_{\underline {x}}^{w_k}(v^{-1})$. By Lemma 2.16, the sum
$\sum _{\underline {x}^{\boldsymbol {e}} = w_k}v^{-d(\boldsymbol {e}) + \ell (w_k)} = v^{\ell (w_k)}p_{\underline {x}}^{w_k}(v^{-1})$. By Lemma 2.16, the sum ![]() $\sum _k v^{\ell (w_k)}p_{\underline {x}}^{w_k}(v^{-1})$ is
$\sum _k v^{\ell (w_k)}p_{\underline {x}}^{w_k}(v^{-1})$ is ![]() $(v + v^{-1})^{l}$ and this is equal to the graded rank of
$(v + v^{-1})^{l}$ and this is equal to the graded rank of ![]() $B_{\underline {x}}$ by Lemma 2.14. Hence, if
$B_{\underline {x}}$ by Lemma 2.14. Hence, if ![]() $\mathbb {K}$ is a field, (3.1) is an isomorphism by Lemma 2.9.
$\mathbb {K}$ is a field, (3.1) is an isomorphism by Lemma 2.9.
Now we prove that the map (3.1) is an isomorphism for any Noetherian domain ![]() $\mathbb {K}$. Let
$\mathbb {K}$. Let ![]() $\mathfrak {m}$ be a maximal ideal of
$\mathfrak {m}$ be a maximal ideal of ![]() $\mathbb {K}$. Then in the commutative diagram
$\mathbb {K}$. Then in the commutative diagram

the horizontal map is an isomorphism. Hence the vertical map is surjective. Therefore, for any ![]() $k$,
$k$, ![]() $B_{\underline {x},I(k)}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}) \to (B_{\underline {x}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_{I(k)}$ is surjective.
$B_{\underline {x},I(k)}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}) \to (B_{\underline {x}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_{I(k)}$ is surjective.
We prove that the map (3.1) is an isomorphism by backward induction on ![]() $k$. By inductive hypothesis,
$k$. By inductive hypothesis, ![]() $B_{\underline {x},I(k')}/B_{\underline {x},I(k' - 1)}$ is graded free for any
$B_{\underline {x},I(k')}/B_{\underline {x},I(k' - 1)}$ is graded free for any ![]() $k' > k$. Hence
$k' > k$. Hence ![]() $B_{\underline {x}}/B_{\underline {x},I(k)}$ is graded free. Therefore
$B_{\underline {x}}/B_{\underline {x},I(k)}$ is graded free. Therefore ![]() $B_{\underline {x},I(k)}$ is a direct summand of
$B_{\underline {x},I(k)}$ is a direct summand of ![]() $B_{\underline {x}}$. Hence
$B_{\underline {x}}$. Hence ![]() $B_{\underline {x},I(k)}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})\to (B_{\underline {x}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_{I(k)}$ is injective, hence it is an isomorphism. By applying the five lemma to the commutative diagram with exact columns
$B_{\underline {x},I(k)}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})\to (B_{\underline {x}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_{I(k)}$ is injective, hence it is an isomorphism. By applying the five lemma to the commutative diagram with exact columns

the vertical map in (3.2) is an isomorphism.
Hence (3.1) is an isomorphism after tensoring ![]() $\mathbb {K}/\mathfrak {m}$. Note that both sides are finitely generated as
$\mathbb {K}/\mathfrak {m}$. Note that both sides are finitely generated as ![]() $R$-modules. Indeed, the left-hand side is obviously finitely generated and the right-hand side is finitely generated since it is a subquotient of finitely generated
$R$-modules. Indeed, the left-hand side is obviously finitely generated and the right-hand side is finitely generated since it is a subquotient of finitely generated ![]() $R$-module
$R$-module ![]() $B_{\underline {x}}$. Therefore each graded piece of both sides is a finitely generated
$B_{\underline {x}}$. Therefore each graded piece of both sides is a finitely generated ![]() $\mathbb {K}$-module. Therefore by applying Nakayama's lemma to each graded piece, (3.1) is surjective after localizing at
$\mathbb {K}$-module. Therefore by applying Nakayama's lemma to each graded piece, (3.1) is surjective after localizing at ![]() $\mathfrak {m}$. Hence it is an isomorphism. Since this is true for any maximal ideal, (3.1) itself is an isomorphism.
$\mathfrak {m}$. Hence it is an isomorphism. Since this is true for any maximal ideal, (3.1) itself is an isomorphism.
Remark 3.18 In the proof, we proved that ![]() $B_{\underline {x},I(k)}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})\simeq (B_{\underline {x}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_{I(k)}$. Since any closed subset can be realized as
$B_{\underline {x},I(k)}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})\simeq (B_{\underline {x}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_{I(k)}$. Since any closed subset can be realized as ![]() $I(k)$ for some
$I(k)$ for some ![]() $k$ (Lemma 3.16) and a certain sequence
$k$ (Lemma 3.16) and a certain sequence ![]() $\emptyset = I(0)\subset I(1)\subset \cdots$, it is true after replacing
$\emptyset = I(0)\subset I(1)\subset \cdots$, it is true after replacing ![]() $I(k)$ with any closed subset. Therefore. for any
$I(k)$ with any closed subset. Therefore. for any ![]() $B\in \mathcal {S}\mathrm {Bimod}$ and any closed subset
$B\in \mathcal {S}\mathrm {Bimod}$ and any closed subset ![]() $I$, the natural map
$I$, the natural map ![]() $B_I\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})\to (B\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_I$ is an isomorphism.
$B_I\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})\to (B\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_I$ is an isomorphism.
For ![]() $M\in \mathcal {C}$ and
$M\in \mathcal {C}$ and ![]() $w\in W$, we put
$w\in W$, we put ![]() $M_{\le w} = M_{\{y\in W\mid y\le w\}}$. We define
$M_{\le w} = M_{\{y\in W\mid y\le w\}}$. We define ![]() $M_{< w}$ in the obvious way.
$M_{< w}$ in the obvious way.
Corollary 3.19 Let ![]() $B\in \mathcal {S}\mathrm {Bimod}$.
$B\in \mathcal {S}\mathrm {Bimod}$.
(1) Let
 $I\subset W$ be a closed subset and
$I\subset W$ be a closed subset and  $w\in I$ a maximal element. Then we have
$w\in I$ a maximal element. Then we have  $B_{\le w}/B_{< w}\xrightarrow {\sim }B_{I}/B_{I\setminus \{w\}}$.
$B_{\le w}/B_{< w}\xrightarrow {\sim }B_{I}/B_{I\setminus \{w\}}$.(2) Let
 $\underline {w}$ be a reduced expression for
$\underline {w}$ be a reduced expression for  $w\in W$. Then the map
$w\in W$. Then the map  $\operatorname {Hom}^{\bullet }_{\mathcal {C}}(B_{\underline {w}},B)\to \operatorname {Hom}^{\bullet }_R(B_{\underline {w}}^{w},B_{\le w}/B_{< w})$ is surjective.
$\operatorname {Hom}^{\bullet }_{\mathcal {C}}(B_{\underline {w}},B)\to \operatorname {Hom}^{\bullet }_R(B_{\underline {w}}^{w},B_{\le w}/B_{< w})$ is surjective.
Proof. We may assume ![]() $B = B_{\underline {x}}$ for some
$B = B_{\underline {x}}$ for some ![]() $\underline {x}\in S^{l}$. By Theorem 3.17, any element in
$\underline {x}\in S^{l}$. By Theorem 3.17, any element in ![]() $B_{\underline {x},I}/B_{\underline {x},I\setminus \{w\}}$ has a representative of the form
$B_{\underline {x},I}/B_{\underline {x},I\setminus \{w\}}$ has a representative of the form ![]() $\sum c_{\boldsymbol {e}}\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}})$ with
$\sum c_{\boldsymbol {e}}\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}})$ with ![]() $c_{\boldsymbol {e}}\in R$. Since
$c_{\boldsymbol {e}}\in R$. Since ![]() $\operatorname {supp}_W(u_{\underline {w}})\subset \{y\in W\mid y\le w\}$,
$\operatorname {supp}_W(u_{\underline {w}})\subset \{y\in W\mid y\le w\}$, ![]() $\operatorname {supp}_W(\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}}))\subset \{y\in W\mid y\le w\}$. Hence
$\operatorname {supp}_W(\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}}))\subset \{y\in W\mid y\le w\}$. Hence ![]() $\sum c_{\boldsymbol {e}}\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}})\in B_{\underline {x},\le w}$. We get (1).
$\sum c_{\boldsymbol {e}}\mathit {LL}_{\underline {x},\boldsymbol {e}}^{*}(u_{\underline {w}})\in B_{\underline {x},\le w}$. We get (1).
We prove (2). The ![]() $R$-module
$R$-module ![]() $B_{\underline {w}}^{w}$ is free and
$B_{\underline {w}}^{w}$ is free and ![]() $\pi _{\underline {w}}^{w}(u_{\underline {w}})$ is a basis of this module. Hence
$\pi _{\underline {w}}^{w}(u_{\underline {w}})$ is a basis of this module. Hence ![]() $\operatorname {Hom}^{\bullet }_R(B_{\underline {w}}^{w},B_{\underline {x},\le w}/B_{\underline {x},< w})\simeq B_{\underline {x},\le w}/B_{\underline {x},< w}$ by
$\operatorname {Hom}^{\bullet }_R(B_{\underline {w}}^{w},B_{\underline {x},\le w}/B_{\underline {x},< w})\simeq B_{\underline {x},\le w}/B_{\underline {x},< w}$ by ![]() $\psi \mapsto \psi (\pi _{\underline {w}}^{w}(u_{\underline {w}}))$ By the functionality of
$\psi \mapsto \psi (\pi _{\underline {w}}^{w}(u_{\underline {w}}))$ By the functionality of ![]() $B\to B^{w}$ for
$B\to B^{w}$ for ![]() $B\in \mathcal {C}$, we have
$B\in \mathcal {C}$, we have ![]() $\psi (\pi _{\underline {w}}^{w}(u_{\underline {w}})) = \pi _{\underline {x}}^{w}(\psi (u_{\underline {w}}))$. Therefore it is sufficient to prove that
$\psi (\pi _{\underline {w}}^{w}(u_{\underline {w}})) = \pi _{\underline {x}}^{w}(\psi (u_{\underline {w}}))$. Therefore it is sufficient to prove that ![]() $\operatorname {Hom}^{\bullet }_{\mathcal {C}}(B_{\underline {w}},B_{\underline {x}})\to B_{\underline {x},\le w}/B_{\underline {x},< w}$ defined by
$\operatorname {Hom}^{\bullet }_{\mathcal {C}}(B_{\underline {w}},B_{\underline {x}})\to B_{\underline {x},\le w}/B_{\underline {x},< w}$ defined by ![]() $\varphi \mapsto \pi _{\underline {x}}^{w}(\varphi (u_{\underline {w}}))$ is surjective. This is clear from Theorem 3.17.
$\varphi \mapsto \pi _{\underline {x}}^{w}(\varphi (u_{\underline {w}}))$ is surjective. This is clear from Theorem 3.17.
The following proposition is a generalization of [Reference SoergelSoe07, Satz 6.6].
Proposition 3.20 Let ![]() $B\in \mathcal {S}\mathrm {Bimod}$ and
$B\in \mathcal {S}\mathrm {Bimod}$ and ![]() $w\in W$. Consider the element
$w\in W$. Consider the element ![]() $\prod _{tw < w}\alpha _t\in R$ where
$\prod _{tw < w}\alpha _t\in R$ where ![]() $t$ runs through reflections in
$t$ runs through reflections in ![]() $W$. Then we have
$W$. Then we have ![]() $B_w\xrightarrow {\sim }(\prod _{tw < w}\alpha _t)(B_{\le w}/B_{< w})$.
$B_w\xrightarrow {\sim }(\prod _{tw < w}\alpha _t)(B_{\le w}/B_{< w})$.
Proof. We may assume ![]() $B = B_{\underline {x}}$. It is well known that
$B = B_{\underline {x}}$. It is well known that ![]() $\#\{t\mid tw < w\} = \ell (w)$. Therefore
$\#\{t\mid tw < w\} = \ell (w)$. Therefore ![]() $\deg (\prod _{tw < w}\alpha _t) = 2\ell (w)$. Hence by Corollary 3.13 and Theorem 3.17, both sides are graded free with the same graded rank.
$\deg (\prod _{tw < w}\alpha _t) = 2\ell (w)$. Hence by Corollary 3.13 and Theorem 3.17, both sides are graded free with the same graded rank.
First we assume that ![]() $\underline {x}$ is a reduced expression for
$\underline {x}$ is a reduced expression for ![]() $w$. We denote
$w$. We denote ![]() $\underline {x}$ by
$\underline {x}$ by ![]() $\underline {w}$. We prove
$\underline {w}$. We prove ![]() $B_{\underline {w},\le w}/B_{\underline {w},< w}\simeq B_{\underline {w}}^{w}$ by induction on
$B_{\underline {w},\le w}/B_{\underline {w},< w}\simeq B_{\underline {w}}^{w}$ by induction on ![]() $\ell (w)$.
$\ell (w)$.
Let ![]() $\underline {w} = (s_1,\ldots ,s_l)$ and set
$\underline {w} = (s_1,\ldots ,s_l)$ and set ![]() $s = s_1$,
$s = s_1$, ![]() $\underline {sw} = (s_2,\ldots ,s_l)$. Then
$\underline {sw} = (s_2,\ldots ,s_l)$. Then ![]() $\underline {sw}$ is a reduced expression for
$\underline {sw}$ is a reduced expression for ![]() $sw$. Let
$sw$. Let ![]() $\delta _s\in V$ such that
$\delta _s\in V$ such that ![]() $\langle \alpha _s^{\vee },\delta _s\rangle = 1$. Take
$\langle \alpha _s^{\vee },\delta _s\rangle = 1$. Take ![]() $1\otimes m + \delta _s\otimes m'\in R\otimes _{R^{s}}B_{\underline {sw}} = B_{\underline {w}}$ and assume that
$1\otimes m + \delta _s\otimes m'\in R\otimes _{R^{s}}B_{\underline {sw}} = B_{\underline {w}}$ and assume that ![]() $1\otimes m + \delta _s\otimes m'\in B_{\underline {w},w}$. By Lemma 2.12,
$1\otimes m + \delta _s\otimes m'\in B_{\underline {w},w}$. By Lemma 2.12, ![]() $\operatorname {supp}_W(m')\in \{w,sw\}$. We also have
$\operatorname {supp}_W(m')\in \{w,sw\}$. We also have ![]() $m'_w = 0$ since
$m'_w = 0$ since ![]() $B_{\underline {sw}}^{w} = 0$. Therefore
$B_{\underline {sw}}^{w} = 0$. Therefore ![]() $m'\in B_{\underline {sw},sw}$. By inductive hypothesis, we have
$m'\in B_{\underline {sw},sw}$. By inductive hypothesis, we have ![]() $m'\in (\prod _{tsw < sw}\alpha _t)B_{\underline {sw}}^{sw}$.
$m'\in (\prod _{tsw < sw}\alpha _t)B_{\underline {sw}}^{sw}$.
Since ![]() $1\otimes m + \delta _s\otimes m'\in B_{\underline {w},w}$,
$1\otimes m + \delta _s\otimes m'\in B_{\underline {w},w}$, ![]() $(1\otimes m + \delta _s\otimes m')_{sw} = 0$. Hence we have
$(1\otimes m + \delta _s\otimes m')_{sw} = 0$. Hence we have ![]() $m_{sw} + \delta _s m'_{sw} = 0$. Therefore
$m_{sw} + \delta _s m'_{sw} = 0$. Therefore ![]() $m_{sw} + s(\delta _s) m'_{sw} = (-\delta _s + s(\delta _s))m'_{sw} = -\alpha _s m'_{sw}\in \alpha _s (\prod _{tsw < sw}\alpha _t)B_{\underline {sw}}^{sw}$. It is well known that
$m_{sw} + s(\delta _s) m'_{sw} = (-\delta _s + s(\delta _s))m'_{sw} = -\alpha _s m'_{sw}\in \alpha _s (\prod _{tsw < sw}\alpha _t)B_{\underline {sw}}^{sw}$. It is well known that ![]() $\{t\mid tw < w\} = \{s\}\cup \{sts^{-1}\mid tsw < sw\}$. Hence
$\{t\mid tw < w\} = \{s\}\cup \{sts^{-1}\mid tsw < sw\}$. Hence ![]() $\prod _{tw < w}\alpha _t = \alpha _s s(\prod _{tsw < sw}\alpha _t) = s(-\alpha _s\prod _{tsw < sw}\alpha _t)$. Therefore
$\prod _{tw < w}\alpha _t = \alpha _s s(\prod _{tsw < sw}\alpha _t) = s(-\alpha _s\prod _{tsw < sw}\alpha _t)$. Therefore ![]() $m_{sw} + s(\delta _s) m'_{sw}\in s(\prod _{tw < w}\alpha _t)B_{\underline {sw}}^{sw}$. Take
$m_{sw} + s(\delta _s) m'_{sw}\in s(\prod _{tw < w}\alpha _t)B_{\underline {sw}}^{sw}$. Take ![]() $n\in B_{\underline {sw}}$ such that
$n\in B_{\underline {sw}}$ such that ![]() $m_{sw} + s(\delta _s) m'_{sw} = s(\prod _{tw < w}\alpha _t)n_{sw}$. Now we have
$m_{sw} + s(\delta _s) m'_{sw} = s(\prod _{tw < w}\alpha _t)n_{sw}$. Now we have ![]() $(1\otimes m + \delta _s\otimes m')_w = (m_w + \delta _s m'_w,m_{sw} + s(\delta _s)m'_{sw})$ and, since
$(1\otimes m + \delta _s\otimes m')_w = (m_w + \delta _s m'_w,m_{sw} + s(\delta _s)m'_{sw})$ and, since ![]() $m_w,m'_w\in B_{\underline {sw}}^{w} = 0$, we get
$m_w,m'_w\in B_{\underline {sw}}^{w} = 0$, we get ![]() $(1\otimes m + \delta _s\otimes m')_w = (0,s(\prod _{tw < w}\alpha _t)n_{sw}) = (\prod _{tw < w}\alpha _t)(0,n_{sw})$. (Recall that the left action of
$(1\otimes m + \delta _s\otimes m')_w = (0,s(\prod _{tw < w}\alpha _t)n_{sw}) = (\prod _{tw < w}\alpha _t)(0,n_{sw})$. (Recall that the left action of ![]() $R$ on the second factor of
$R$ on the second factor of ![]() $(B_s\otimes B_{\underline {sw}})_Q^{w} = (B_{\underline {sw}})_Q^{w}\oplus (B_{\underline {sw}})_Q^{sw}$ is twisted by
$(B_s\otimes B_{\underline {sw}})_Q^{w} = (B_{\underline {sw}})_Q^{w}\oplus (B_{\underline {sw}})_Q^{sw}$ is twisted by ![]() $s$.) Again using
$s$.) Again using ![]() $n_{w}\in B_{\underline {sw}}^{w} = 0$, we have
$n_{w}\in B_{\underline {sw}}^{w} = 0$, we have ![]() $(\prod _{tw < w}\alpha _t)(0,n_{sw}) = (\prod _{tw < w}\alpha _t)(n_w,n_{sw}) = (\prod _{tw < w}\alpha _t)(1\otimes n)_w\in (\prod _{tw < w}\alpha _t)B_ {\underline {w}}^{w}$.
$(\prod _{tw < w}\alpha _t)(0,n_{sw}) = (\prod _{tw < w}\alpha _t)(n_w,n_{sw}) = (\prod _{tw < w}\alpha _t)(1\otimes n)_w\in (\prod _{tw < w}\alpha _t)B_ {\underline {w}}^{w}$.
To finish the proof for ![]() $\underline {x} = \underline {w}$, we prove that
$\underline {x} = \underline {w}$, we prove that ![]() $B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ is surjective using an argument in the proof of Theorem 3.17. Since both sides has the same graded rank, this is surjective if
$B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ is surjective using an argument in the proof of Theorem 3.17. Since both sides has the same graded rank, this is surjective if ![]() $\mathbb {K}$ is a field. Let
$\mathbb {K}$ is a field. Let ![]() $\mathfrak {m}\subset \mathbb {K}$ be a maximal ideal. The natural surjective map
$\mathfrak {m}\subset \mathbb {K}$ be a maximal ideal. The natural surjective map ![]() $B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})\to B_{\underline {w}}^{w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$ induces a surjective map
$B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})\to B_{\underline {w}}^{w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$ induces a surjective map ![]() $(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))^{w}\to B_{\underline {w}}^{w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$. Both sides are graded free with graded rank
$(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))^{w}\to B_{\underline {w}}^{w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$. Both sides are graded free with graded rank ![]() $v^{\ell (w)}$ (by Theorem 3.12, for instance). Therefore it is an isomorphism. Take the dual of this isomorphism. By Lemma 2.18, we have
$v^{\ell (w)}$ (by Theorem 3.12, for instance). Therefore it is an isomorphism. Take the dual of this isomorphism. By Lemma 2.18, we have ![]() $D((B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))^{w})\simeq D(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_w$. Since
$D((B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))^{w})\simeq D(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_w$. Since ![]() $B_{\underline {w}}$ is free as a right
$B_{\underline {w}}$ is free as a right ![]() $R$-module, we have
$R$-module, we have ![]() $D(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))\simeq D(B_{\underline {w}})\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$. By Lemma 2.20, we have
$D(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))\simeq D(B_{\underline {w}})\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$. By Lemma 2.20, we have ![]() $D(B_{\underline {w}})\simeq B_{\underline {w}}$. Since
$D(B_{\underline {w}})\simeq B_{\underline {w}}$. Since ![]() $B_{\underline {w}}^{w}$ is also free, with Lemmas 2.18 and 2.20, we also have
$B_{\underline {w}}^{w}$ is also free, with Lemmas 2.18 and 2.20, we also have ![]() $D(B_{\underline {w}}^{w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))\simeq B_{\underline {w},w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$. Hence
$D(B_{\underline {w}}^{w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))\simeq B_{\underline {w},w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$. Hence ![]() $(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_w\simeq B_{\underline {w},w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$. Therefore, by tensoring
$(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_w\simeq B_{\underline {w},w}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m})$. Therefore, by tensoring ![]() $\mathbb {K}/\mathfrak {m}$, the map
$\mathbb {K}/\mathfrak {m}$, the map ![]() $B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ becomes
$B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ becomes ![]() $(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_w\hookrightarrow (\prod _{tw < w}\alpha _t)(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))^{w}$. Since the map
$(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_w\hookrightarrow (\prod _{tw < w}\alpha _t)(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))^{w}$. Since the map ![]() $B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ is surjective if
$B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ is surjective if ![]() $\mathbb {K}$ is a field,
$\mathbb {K}$ is a field, ![]() $(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_w\hookrightarrow (\prod _{tw < w}\alpha _t)(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))^{w}$ is surjective. Therefore by Nakayama's lemma,
$(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))_w\hookrightarrow (\prod _{tw < w}\alpha _t)(B_{\underline {w}}\otimes _{\mathbb {K}}(\mathbb {K}/\mathfrak {m}))^{w}$ is surjective. Therefore by Nakayama's lemma, ![]() $B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ is surjective after localizing at
$B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ is surjective after localizing at ![]() $\mathfrak {m}$. Since this is true for any maximal ideal
$\mathfrak {m}$. Since this is true for any maximal ideal ![]() $\mathfrak {m}$,
$\mathfrak {m}$, ![]() $B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ is surjective.
$B_{\underline {w},w}\hookrightarrow (\prod _{tw < w}\alpha _t)B_{\underline {w}}^{w}$ is surjective.
We prove the proposition for ![]() $B = B_{\underline {x}}$ with
$B = B_{\underline {x}}$ with ![]() $\underline {x}\in S^{l}$. By an argument above using localization at maximal ideals and Remark 3.18, it is sufficient to prove that
$\underline {x}\in S^{l}$. By an argument above using localization at maximal ideals and Remark 3.18, it is sufficient to prove that ![]() $(\prod _{tw < w}\alpha _t)B_{\underline {x},\le w}/B_{\underline {x},< w}\subset B_{\underline {x},w}$. Set
$(\prod _{tw < w}\alpha _t)B_{\underline {x},\le w}/B_{\underline {x},< w}\subset B_{\underline {x},w}$. Set ![]() $f = \prod _{tw < w}\alpha _t$ and let
$f = \prod _{tw < w}\alpha _t$ and let ![]() $fm$ be an element of the left-hand side. Then we may assume
$fm$ be an element of the left-hand side. Then we may assume ![]() $m = \mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}(\pi _{\underline {w}}^{w}(u_{\underline {w}}))$ by Theorem 3.17. Since we have proved the proposition for
$m = \mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}(\pi _{\underline {w}}^{w}(u_{\underline {w}}))$ by Theorem 3.17. Since we have proved the proposition for ![]() $B = B_{\underline {w}}$,
$B = B_{\underline {w}}$, ![]() $f\pi _{\underline {w}}^{w}(u_{\underline {w}})\in B_{\underline {w},w}$. Hence
$f\pi _{\underline {w}}^{w}(u_{\underline {w}})\in B_{\underline {w},w}$. Hence ![]() $fm = \mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}(f\pi _{\underline {w}}^{w}(u_{\underline {w}}))\in B_{\underline {x},w}$.
$fm = \mathit {LL}^{*}_{\underline {x},\boldsymbol {e}}(f\pi _{\underline {w}}^{w}(u_{\underline {w}}))\in B_{\underline {x},w}$.
4. The categorification theorem
In this section we assume that ![]() $\mathbb {K}$ is a complete local ring. Therefore a direct summand of a graded free
$\mathbb {K}$ is a complete local ring. Therefore a direct summand of a graded free ![]() $R$-module is again graded free.
$R$-module is again graded free.
4.1 The classification of indecomposable objects
Theorem 4.1
(1) For each
 $w\in W$, there exists an indecomposable object
$w\in W$, there exists an indecomposable object  $B(w)\in \mathcal {S}\mathrm {Bimod}$ such that
$B(w)\in \mathcal {S}\mathrm {Bimod}$ such that  $\operatorname {supp}_W(B(w))\subset \{x\in W\mid x\le w\}$ and
$\operatorname {supp}_W(B(w))\subset \{x\in W\mid x\le w\}$ and  $B(w)^{w}\simeq R_w(\ell (w))$. Moreover,
$B(w)^{w}\simeq R_w(\ell (w))$. Moreover,  $B(w)$ is unique up to isomorphism.
$B(w)$ is unique up to isomorphism.(2) For any indecomposable object
 $B\in \mathcal {S}\mathrm {Bimod}$, there exists a unique
$B\in \mathcal {S}\mathrm {Bimod}$, there exists a unique  $(w,n)\in W\times \mathbb {Z}$ such that
$(w,n)\in W\times \mathbb {Z}$ such that  $B\simeq B(w)(n)$.
$B\simeq B(w)(n)$.(3) We have
 $D(B(w))\simeq B(w)$.
$D(B(w))\simeq B(w)$.(4) For a reduced expression
 $\underline {w}$ for
$\underline {w}$ for  $w\in W$, we have
$w\in W$, we have  $B_{\underline {w}} = B(w)\oplus {\bigoplus} _{y < w,n\in \mathbb {Z}}\, B(y)(n)^{m_{n,y}}$ for some
$B_{\underline {w}} = B(w)\oplus {\bigoplus} _{y < w,n\in \mathbb {Z}}\, B(y)(n)^{m_{n,y}}$ for some  $m_{n,y}\in \mathbb {Z}_{\ge 0}$.
$m_{n,y}\in \mathbb {Z}_{\ge 0}$.
Proof. Fix a reduced expression ![]() $\underline {w}$ for
$\underline {w}$ for ![]() $w$. Then we have
$w$. Then we have ![]() $B_{\underline {w}}^{w}\simeq R_w(\ell (w))$. Therefore there exists a unique indecomposable direct summand
$B_{\underline {w}}^{w}\simeq R_w(\ell (w))$. Therefore there exists a unique indecomposable direct summand ![]() $B(w)$ of
$B(w)$ of ![]() $B_{\underline {w}}$ such that
$B_{\underline {w}}$ such that ![]() $B(w)^{w} = B_{\underline {w}}^{w}(\ell (w))$. This satisfies the condition of (1) and, since
$B(w)^{w} = B_{\underline {w}}^{w}(\ell (w))$. This satisfies the condition of (1) and, since ![]() $D(B_{\underline {w}})\simeq B_{\underline {w}}$, we have
$D(B_{\underline {w}})\simeq B_{\underline {w}}$, we have ![]() $D(B(w))\simeq B(w)$.
$D(B(w))\simeq B(w)$.
It only remains to show that any object in ![]() $\mathcal {S}\mathrm {Bimod}$ is a direct sum of
$\mathcal {S}\mathrm {Bimod}$ is a direct sum of ![]() $B(w)(n)$. Let
$B(w)(n)$. Let ![]() $B\in \mathcal {S}\mathrm {Bimod}$. Take
$B\in \mathcal {S}\mathrm {Bimod}$. Take ![]() $w\in W$ such that
$w\in W$ such that ![]() $B^{w}\ne 0$ and
$B^{w}\ne 0$ and ![]() $\ell (w)$ is maximal with respect to this condition. Set
$\ell (w)$ is maximal with respect to this condition. Set ![]() $I = \{y\in W\mid \ell (y)\le \ell (w)\}$. This is a closed subset of
$I = \{y\in W\mid \ell (y)\le \ell (w)\}$. This is a closed subset of ![]() $W$. The condition of
$W$. The condition of ![]() $w$ and the definition of
$w$ and the definition of ![]() $I$ says that
$I$ says that ![]() $B_{I} = B$. Hence
$B_{I} = B$. Hence ![]() $B_I/B_{I\setminus \{w\}} = B^{w}$.
$B_I/B_{I\setminus \{w\}} = B^{w}$.
Since ![]() $B^{w}$ is graded free and
$B^{w}$ is graded free and ![]() $B_{\underline {w}}^{w}\simeq R_w(\ell (w))$, there exists
$B_{\underline {w}}^{w}\simeq R_w(\ell (w))$, there exists ![]() $n\in \mathbb {Z}$ such that
$n\in \mathbb {Z}$ such that ![]() $B_{\underline {w}}(n)^{w}$ is a direct summand of
$B_{\underline {w}}(n)^{w}$ is a direct summand of ![]() $B^{w}$. Let
$B^{w}$. Let ![]() $i\colon B_{\underline {w}}(n)^{w}\hookrightarrow B^{w}$ and
$i\colon B_{\underline {w}}(n)^{w}\hookrightarrow B^{w}$ and ![]() $p\colon B^{w}\twoheadrightarrow B_{\underline {w}}(n)^{w}$ be the embeddings from and the projection to the direct summand. Then by Corollaries 3.15 and 3.19(2), there exist
$p\colon B^{w}\twoheadrightarrow B_{\underline {w}}(n)^{w}$ be the embeddings from and the projection to the direct summand. Then by Corollaries 3.15 and 3.19(2), there exist ![]() $B_{\underline {w}}(n)\to B$ and
$B_{\underline {w}}(n)\to B$ and ![]() $B\to B_{\underline {w}}(n)$ which are lifts of
$B\to B_{\underline {w}}(n)$ which are lifts of ![]() $i$ and
$i$ and ![]() $p$, respectively. Since
$p$, respectively. Since ![]() $B(w)(n)$ is a direct summand such that
$B(w)(n)$ is a direct summand such that ![]() $B(w)(n)^{w} = B_{\underline {w}}(n)^{w}$, composing the embedding from or the projection to
$B(w)(n)^{w} = B_{\underline {w}}(n)^{w}$, composing the embedding from or the projection to ![]() $B(w)(n)$, we get lifts
$B(w)(n)$, we get lifts ![]() $\tilde {\imath }\colon B(w)(n)\to B$ and
$\tilde {\imath }\colon B(w)(n)\to B$ and ![]() $\tilde {p}\colon B\to B(w)(n)$. The composition
$\tilde {p}\colon B\to B(w)(n)$. The composition ![]() $\tilde {p}\circ \tilde {\imath }$ is identity on
$\tilde {p}\circ \tilde {\imath }$ is identity on ![]() $B(w)(n)^{w}$, hence
$B(w)(n)^{w}$, hence ![]() $\tilde {p}\circ \tilde {\imath }\in \operatorname {End}(B(w)(n))$ is not nilpotent. Since
$\tilde {p}\circ \tilde {\imath }\in \operatorname {End}(B(w)(n))$ is not nilpotent. Since ![]() $B(w)(n)$ is indecomposable,
$B(w)(n)$ is indecomposable, ![]() $\operatorname {End}(B(w)(n))$ is local. Hence
$\operatorname {End}(B(w)(n))$ is local. Hence ![]() $\tilde {p}\circ \tilde {\imath }$ is an isomorphism. Therefore
$\tilde {p}\circ \tilde {\imath }$ is an isomorphism. Therefore ![]() $B(w)(n)$ is a direct summand of
$B(w)(n)$ is a direct summand of ![]() $B$. The last statement follows from the argument with supports.
$B$. The last statement follows from the argument with supports.
It is easy to see that ![]() $B(s) = B_s$ for any
$B(s) = B_s$ for any ![]() $s\in S$.
$s\in S$.
4.2 The categorification
Let ![]() $[\mathcal {S}\mathrm {Bimod}]$ be the split Grothendieck group of the category
$[\mathcal {S}\mathrm {Bimod}]$ be the split Grothendieck group of the category ![]() $\mathcal {S}\mathrm {Bimod}$. Then this has a structure of
$\mathcal {S}\mathrm {Bimod}$. Then this has a structure of ![]() $\mathbb {Z}[v^{\pm 1}]$-algebra via
$\mathbb {Z}[v^{\pm 1}]$-algebra via ![]() $v[B] = [B(1)]$ and
$v[B] = [B(1)]$ and ![]() $[B_1][B_2] = [B_1\otimes B_2]$ where
$[B_1][B_2] = [B_1\otimes B_2]$ where ![]() $[B]$ is the image of
$[B]$ is the image of ![]() $B\in \mathcal {S}\mathrm {Bimod}$ in
$B\in \mathcal {S}\mathrm {Bimod}$ in ![]() $[\mathcal {S}\mathrm {Bimod}]$. By Theorem 4.1,
$[\mathcal {S}\mathrm {Bimod}]$. By Theorem 4.1, ![]() $\{[B(w)]\mid w\in W\}$ is a
$\{[B(w)]\mid w\in W\}$ is a ![]() $\mathbb {Z}[v^{\pm 1}]$-basis of
$\mathbb {Z}[v^{\pm 1}]$-basis of ![]() $[\mathcal {S}\mathrm {Bimod}]$. By Theorem 4.1(4),
$[\mathcal {S}\mathrm {Bimod}]$. By Theorem 4.1(4), ![]() $\{[B_{\underline {w}}]\mid w\in W\}$ is also a
$\{[B_{\underline {w}}]\mid w\in W\}$ is also a ![]() $\mathbb {Z}[v^{\pm 1}]$-basis of
$\mathbb {Z}[v^{\pm 1}]$-basis of ![]() $[\mathcal {S}\mathrm {Bimod}]$, here we fix a reduced expression
$[\mathcal {S}\mathrm {Bimod}]$, here we fix a reduced expression ![]() $\underline {w}$ for each
$\underline {w}$ for each ![]() $w\in W$. In particular,
$w\in W$. In particular, ![]() $\{[B_{\underline {x}}]\mid \underline {x}\in S^{l},l\in \mathbb {Z}_{\ge 0}\}$ generates
$\{[B_{\underline {x}}]\mid \underline {x}\in S^{l},l\in \mathbb {Z}_{\ge 0}\}$ generates ![]() $[\mathcal {S}\mathrm {Bimod}]$
$[\mathcal {S}\mathrm {Bimod}]$
By Theorem 3.12, the ![]() $R$-module
$R$-module ![]() $B_{\underline {x}}^{w}$ is graded free. Therefore the
$B_{\underline {x}}^{w}$ is graded free. Therefore the ![]() $R$-module
$R$-module ![]() $B^{w}$ for any
$B^{w}$ for any ![]() $B\in \mathcal {S}\mathrm {Bimod}$ is graded free. We define the character map
$B\in \mathcal {S}\mathrm {Bimod}$ is graded free. We define the character map ![]() $\operatorname {ch}\colon [\mathcal {S}\mathrm {Bimod}]\to \mathcal {H}$ by
$\operatorname {ch}\colon [\mathcal {S}\mathrm {Bimod}]\to \mathcal {H}$ by
Proposition 4.2 ![]() $\operatorname {ch}(B_{\underline {x}}) = \underline {H}_{\underline {x}}$.
$\operatorname {ch}(B_{\underline {x}}) = \underline {H}_{\underline {x}}$.
Proof. Clear from Theorem 3.12.
In particular, ![]() $\operatorname {ch}$ is an algebra homomorphism on
$\operatorname {ch}$ is an algebra homomorphism on ![]() $\sum _{\underline {x}\in S^{l},l\in \mathbb {Z}_{\ge 0}}\mathbb {Z}[v^{\pm 1}][B_{\underline {x}}]$. Since
$\sum _{\underline {x}\in S^{l},l\in \mathbb {Z}_{\ge 0}}\mathbb {Z}[v^{\pm 1}][B_{\underline {x}}]$. Since ![]() $\{[B_{\underline {x}}]\mid \underline {x}\in S^{l},l\in \mathbb {Z}_{\ge 0}\}$ generates
$\{[B_{\underline {x}}]\mid \underline {x}\in S^{l},l\in \mathbb {Z}_{\ge 0}\}$ generates ![]() $[\mathcal {S}\mathrm {Bimod}]$,
$[\mathcal {S}\mathrm {Bimod}]$, ![]() $\operatorname {ch}$ is an algebra homomorphism from
$\operatorname {ch}$ is an algebra homomorphism from ![]() $[\mathcal {S}\mathrm {Bimod}]$ to
$[\mathcal {S}\mathrm {Bimod}]$ to ![]() $\mathcal {H}$.
$\mathcal {H}$.
For a reduced expression ![]() $\underline {w}$ for each
$\underline {w}$ for each ![]() $w\in W$, we have
$w\in W$, we have ![]() $\underline {H}_{\underline {w}}\in H_w + \sum _{y < w}\mathbb {Z}[v^{\pm 1}]H_y$. Hence
$\underline {H}_{\underline {w}}\in H_w + \sum _{y < w}\mathbb {Z}[v^{\pm 1}]H_y$. Hence ![]() $\{\underline {H}_{\underline {w}}\mid w\in W\}$ is a basis of
$\{\underline {H}_{\underline {w}}\mid w\in W\}$ is a basis of ![]() $\mathcal {H}$. Since
$\mathcal {H}$. Since ![]() $\operatorname {ch}$ sends a basis
$\operatorname {ch}$ sends a basis ![]() $\{[B_{\underline {w}}]\mid w\in W\}$ to a basis
$\{[B_{\underline {w}}]\mid w\in W\}$ to a basis ![]() $\{\underline {H}_{\underline {w}}\mid w\in W\}$, we get the following categorification theorem.
$\{\underline {H}_{\underline {w}}\mid w\in W\}$, we get the following categorification theorem.
Theorem 4.3 The algebra homomorphism ![]() $\operatorname {ch}$ is an isomorphism
$\operatorname {ch}$ is an isomorphism ![]() $[\mathcal {S}\mathrm {Bimod}]\simeq \mathcal {H}$.
$[\mathcal {S}\mathrm {Bimod}]\simeq \mathcal {H}$.
4.3 A formula for homomorphisms
We define:
• an involution
 $h\mapsto \bar {h}$ on
$h\mapsto \bar {h}$ on  $\mathcal {H}$ by
$\mathcal {H}$ by  $\overline {\sum _{w\in W}a_w(v)H_w} = \sum _{w\in W}a_w(v^{-1})H_{w^{-1}}^{-1}$;
$\overline {\sum _{w\in W}a_w(v)H_w} = \sum _{w\in W}a_w(v^{-1})H_{w^{-1}}^{-1}$;• an anti-involution
 $\omega \colon \mathcal {H}\to \mathcal {H}$ by
$\omega \colon \mathcal {H}\to \mathcal {H}$ by  $\omega (\sum _{w\in W}a_w(v)H_w) = \sum _{w\in W}a_w(v^{-1})H_w^{-1}$;
$\omega (\sum _{w\in W}a_w(v)H_w) = \sum _{w\in W}a_w(v^{-1})H_w^{-1}$;• a
 $\mathbb {Z}[v^{\pm 1}]$-linear map
$\mathbb {Z}[v^{\pm 1}]$-linear map  $\varepsilon \colon \mathcal {H}\to \mathbb {Z}[v^{\pm 1}]$ by
$\varepsilon \colon \mathcal {H}\to \mathbb {Z}[v^{\pm 1}]$ by  $\varepsilon (\sum _{w\in W}a_wH_w) = a_e$. We also put
$\varepsilon (\sum _{w\in W}a_wH_w) = a_e$. We also put  $\overline {\varepsilon }(h) = \overline {\varepsilon (\overline {h})}$.
$\overline {\varepsilon }(h) = \overline {\varepsilon (\overline {h})}$.
The following lemma follows from a straightforward calculation.
Lemma 4.4 The linear map ![]() $\varepsilon$ is a trace, that is, it satisfies
$\varepsilon$ is a trace, that is, it satisfies ![]() $\varepsilon (hh') = \varepsilon (h'h)$ for any
$\varepsilon (hh') = \varepsilon (h'h)$ for any ![]() $h,h'\in \mathcal {H}$. The linear map
$h,h'\in \mathcal {H}$. The linear map ![]() $\overline {\varepsilon }$ is also a trace.
$\overline {\varepsilon }$ is also a trace.
Lemma 4.5 Let ![]() $s_1,\ldots ,s_l\in S$.
$s_1,\ldots ,s_l\in S$.
(1) We have
 $\omega (\underline {H}_{(s_1,\ldots ,s_l)}) = \underline {H}_{(s_l,\ldots ,s_1)}$ and
$\omega (\underline {H}_{(s_1,\ldots ,s_l)}) = \underline {H}_{(s_l,\ldots ,s_1)}$ and  $\overline {\underline {H}_{(s_1,\ldots ,s_l)}} = \underline {H}_{(s_1,\ldots ,s_l)}$.
$\overline {\underline {H}_{(s_1,\ldots ,s_l)}} = \underline {H}_{(s_1,\ldots ,s_l)}$.(2) We have
 $p_{(s_l,\ldots ,s_1)}^{w^{-1}} = p_{(s_1,\ldots ,s_l)}^{w}$ for any
$p_{(s_l,\ldots ,s_1)}^{w^{-1}} = p_{(s_1,\ldots ,s_l)}^{w}$ for any  $w\in W$.
$w\in W$.
Proof. A direct calculation shows that ![]() $\overline {\underline {H}_s} = \underline {H}_s$ and
$\overline {\underline {H}_s} = \underline {H}_s$ and ![]() $\omega (\underline {H}_s) = \underline {H}_s$. Part (1) follows from this. For (2), we have
$\omega (\underline {H}_s) = \underline {H}_s$. Part (1) follows from this. For (2), we have
 \begin{align*} \sum_{w\in W}p_{(s_l,\ldots,s_1)}^{w^{{-}1}}(v)H_{w} & = \sum_{w\in W}p_{(s_l,\ldots,s_1)}^{w}(v)H_{w^{{-}1}}\\ & = \overline{\omega\biggl(\sum_{w\in W}p_{(s_l,\ldots,s_1)}^{w}(v)H_w\biggr)}\\ & = \overline{\omega(H_{(s_l,\ldots,s_1)})}\\ & = H_{(s_1,\ldots,s_l)}\\ & = \sum_{w\in W}p_{(s_1,\ldots,s_l)}^{w}H_w. \end{align*}
\begin{align*} \sum_{w\in W}p_{(s_l,\ldots,s_1)}^{w^{{-}1}}(v)H_{w} & = \sum_{w\in W}p_{(s_l,\ldots,s_1)}^{w}(v)H_{w^{{-}1}}\\ & = \overline{\omega\biggl(\sum_{w\in W}p_{(s_l,\ldots,s_1)}^{w}(v)H_w\biggr)}\\ & = \overline{\omega(H_{(s_l,\ldots,s_1)})}\\ & = H_{(s_1,\ldots,s_l)}\\ & = \sum_{w\in W}p_{(s_1,\ldots,s_l)}^{w}H_w. \end{align*}
Comparing the coefficient of ![]() $H_w$, we get the lemma.
$H_w$, we get the lemma.
Theorem 4.6 Let ![]() $B_1,B_2\in \mathcal {S}\mathrm {Bimod}$. Then
$B_1,B_2\in \mathcal {S}\mathrm {Bimod}$. Then ![]() $\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_1,B_2)$ is graded free as a left
$\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_1,B_2)$ is graded free as a left ![]() $R$-module and its graded rank is given by
$R$-module and its graded rank is given by
Proof. For ![]() $B_1 = B_{(s_1,\ldots ,s_l)}$ and
$B_1 = B_{(s_1,\ldots ,s_l)}$ and ![]() $B_2 = B_{(t_1,\ldots ,t_r)}$, by Lemma 2.15, we have
$B_2 = B_{(t_1,\ldots ,t_r)}$, by Lemma 2.15, we have
and this is a graded free left ![]() $R$-module by Corollary 3.13. Therefore
$R$-module by Corollary 3.13. Therefore ![]() $\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_1,B_2)$ is graded free for any
$\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_1,B_2)$ is graded free for any ![]() $B_1,B_2\in \mathcal {S}\mathrm {Bimod}$.
$B_1,B_2\in \mathcal {S}\mathrm {Bimod}$.
The map ![]() $(B_1,B_2)\mapsto \operatorname {grk}(\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_1,B_2)) - \overline {\varepsilon }(\omega (\operatorname {ch}(B_1))\operatorname {ch}(B_2))$ defines a bilinear form on the
$(B_1,B_2)\mapsto \operatorname {grk}(\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_1,B_2)) - \overline {\varepsilon }(\omega (\operatorname {ch}(B_1))\operatorname {ch}(B_2))$ defines a bilinear form on the ![]() $\mathbb {Z}$-module
$\mathbb {Z}$-module ![]() $[\mathcal {S}\mathrm {Bimod}]\simeq \mathcal {H}$ which we denote by
$[\mathcal {S}\mathrm {Bimod}]\simeq \mathcal {H}$ which we denote by ![]() $f$. The following properties follow from a straightforward calculation:
$f$. The following properties follow from a straightforward calculation:
If ![]() $B_1 = R_e$ and
$B_1 = R_e$ and ![]() $B_2 = B_{\underline {x}}$, then
$B_2 = B_{\underline {x}}$, then ![]() $\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_1,B_2) = (B_{\underline {x}})_e$ has graded rank
$\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_1,B_2) = (B_{\underline {x}})_e$ has graded rank ![]() $p_{\underline {x}}^{e}(v^{-1})$ by Corollary 3.13. By Proposition 4.2 and
$p_{\underline {x}}^{e}(v^{-1})$ by Corollary 3.13. By Proposition 4.2 and ![]() $\overline {\underline {H}_{\underline {x}}} = \underline {H}_{\underline {x}}$,
$\overline {\underline {H}_{\underline {x}}} = \underline {H}_{\underline {x}}$, ![]() $\overline {\varepsilon }(\omega (\operatorname {ch}(R_e))\operatorname {ch}(B_{\underline {x}})) = \overline {\varepsilon (\overline {\underline {H}_{\underline {x}}})} = \overline {\varepsilon (\underline {H}_{\underline {x}})} = \overline {p_{\underline {x}}^{e}(v)} = p_{\underline {x}}^{e}(v^{-1})$. Hence
$\overline {\varepsilon }(\omega (\operatorname {ch}(R_e))\operatorname {ch}(B_{\underline {x}})) = \overline {\varepsilon (\overline {\underline {H}_{\underline {x}}})} = \overline {\varepsilon (\underline {H}_{\underline {x}})} = \overline {p_{\underline {x}}^{e}(v)} = p_{\underline {x}}^{e}(v^{-1})$. Hence ![]() $f(1,\underline {H}_{\underline {x}}) = 0$. Therefore by (4.3), we have
$f(1,\underline {H}_{\underline {x}}) = 0$. Therefore by (4.3), we have ![]() $f(\underline {H}_{(s_1,\ldots ,s_l)},\underline {H}_{(t_1,\ldots ,t_r)}) = f(1,\underline {H}_{(s_l,\ldots ,s_1,t_1,\ldots ,t_r)}) = 0$. Since
$f(\underline {H}_{(s_1,\ldots ,s_l)},\underline {H}_{(t_1,\ldots ,t_r)}) = f(1,\underline {H}_{(s_l,\ldots ,s_1,t_1,\ldots ,t_r)}) = 0$. Since ![]() $\{\underline {H}_{\underline {x}}\}$ spans
$\{\underline {H}_{\underline {x}}\}$ spans ![]() $\mathcal {H}$ as a
$\mathcal {H}$ as a ![]() $\mathbb {Z}[v^{\pm 1}]$-module, by (4.2),
$\mathbb {Z}[v^{\pm 1}]$-module, by (4.2), ![]() $f = 0$ on
$f = 0$ on ![]() $\mathcal {H}\times \mathcal {H}$.
$\mathcal {H}\times \mathcal {H}$.
Corollary 4.7 The graded rank of ![]() $\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_{\underline {x}},B_{\underline {y}})$ is
$\operatorname {Hom}^{\bullet }_{\mathcal {S}\mathrm {Bimod}}(B_{\underline {x}},B_{\underline {y}})$ is ![]() $\sum _{w\in W}p_{\underline {x}}^{w}(v^{-1})p_{\underline {y}}^{w}(v^{-1})$.
$\sum _{w\in W}p_{\underline {x}}^{w}(v^{-1})p_{\underline {y}}^{w}(v^{-1})$.
Proof. Let ![]() $\underline {x} = (s_1,\ldots ,s_l)$ and set
$\underline {x} = (s_1,\ldots ,s_l)$ and set ![]() $\underline {x'} = (s_l,\ldots ,s_1)$. Then we have
$\underline {x'} = (s_l,\ldots ,s_1)$. Then we have ![]() $\omega (\underline {H}_{\underline {x}}) = \underline {H}_{\underline {x'}}$. Hence
$\omega (\underline {H}_{\underline {x}}) = \underline {H}_{\underline {x'}}$. Hence ![]() $\overline {\varepsilon }(\omega (\underline {H}_{\underline {x}})\underline {H}_{\underline {y}}) = \overline {\varepsilon }(\underline {H}_{\underline {x'}}\underline {H}_{\underline {y}})$. Since
$\overline {\varepsilon }(\omega (\underline {H}_{\underline {x}})\underline {H}_{\underline {y}}) = \overline {\varepsilon }(\underline {H}_{\underline {x'}}\underline {H}_{\underline {y}})$. Since ![]() $\overline {\underline {H}_{\underline {x'}}} = \underline {H}_{\underline {x'}}$ and
$\overline {\underline {H}_{\underline {x'}}} = \underline {H}_{\underline {x'}}$ and ![]() $\overline {\underline {H}_{\underline {y}}} = \underline {H}_{\underline {y}}$, we have
$\overline {\underline {H}_{\underline {y}}} = \underline {H}_{\underline {y}}$, we have ![]() $\overline {\varepsilon }(\underline {H}_{\underline {x'}}\underline {H}_{\underline {y}}) = \overline {\varepsilon (\underline {H}_{\underline {x'}}\underline {H}_{\underline {y}})}$. We have
$\overline {\varepsilon }(\underline {H}_{\underline {x'}}\underline {H}_{\underline {y}}) = \overline {\varepsilon (\underline {H}_{\underline {x'}}\underline {H}_{\underline {y}})}$. We have
 \begin{align*} \varepsilon(\underline{H}_{\underline{x'}}\underline{H}_{\underline{y}}) & = \varepsilon\biggl(\biggl(\sum_{w_1\in W}p_{\underline{x'}}^{w_1}H_{w_1}\biggr)\biggl(\sum_{w_2\in W}p_{\underline{y}}^{w_2}H_{w_2}\biggr)\biggr)\\ & = \sum_{w_1,w_2\in W}p_{\underline{x'}}^{w_1}p_{\underline{y}}^{w_2}\varepsilon(H_{w_1}H_{w_2}). \end{align*}
\begin{align*} \varepsilon(\underline{H}_{\underline{x'}}\underline{H}_{\underline{y}}) & = \varepsilon\biggl(\biggl(\sum_{w_1\in W}p_{\underline{x'}}^{w_1}H_{w_1}\biggr)\biggl(\sum_{w_2\in W}p_{\underline{y}}^{w_2}H_{w_2}\biggr)\biggr)\\ & = \sum_{w_1,w_2\in W}p_{\underline{x'}}^{w_1}p_{\underline{y}}^{w_2}\varepsilon(H_{w_1}H_{w_2}). \end{align*}
We have ![]() $\varepsilon (H_{w_1}H_{w_2}) = \delta _{w_1^{-1},w_2}$ [Reference LibedinskyLib08, (4.3)]. Since
$\varepsilon (H_{w_1}H_{w_2}) = \delta _{w_1^{-1},w_2}$ [Reference LibedinskyLib08, (4.3)]. Since ![]() $p_{\underline {x'}}^{w_1} = p_{\underline {x}}^{w_1^{-1}}$ by Lemma 4.5, we get the corollary.
$p_{\underline {x'}}^{w_1} = p_{\underline {x}}^{w_1^{-1}}$ by Lemma 4.5, we get the corollary.
5. Relations with other categories
5.1 Sheaves on moment graphs
Define an algebra ![]() $\mathcal {Z}$ by
$\mathcal {Z}$ by
 \[ \mathcal{Z} = \biggl\{(z_w)\in \prod_{w\in W}R\,{\bigg|}\,z_{tw}\equiv z_w\!\!\!\!\pmod{\alpha_t}\text{ for any }w\in W\text{ and any reflection }t\biggr\}. \]
\[ \mathcal{Z} = \biggl\{(z_w)\in \prod_{w\in W}R\,{\bigg|}\,z_{tw}\equiv z_w\!\!\!\!\pmod{\alpha_t}\text{ for any }w\in W\text{ and any reflection }t\biggr\}. \]
This is an ![]() $R$-algebra via
$R$-algebra via ![]() $f(z_w) = (fz_w)$ for
$f(z_w) = (fz_w)$ for ![]() $f\in R$ and
$f\in R$ and ![]() $(z_w)\in \mathcal {Z}$. This is the structure algebra of the moment graph attached to
$(z_w)\in \mathcal {Z}$. This is the structure algebra of the moment graph attached to ![]() $(W,S)$. Fiebig developed the theory of sheaves on moment graphs; see [Reference FiebigFie08a, Reference FiebigFie08b]. In particular, he proved that the category of Soergel bimodules in the original sense is equivalent to a certain full subcategory of
$(W,S)$. Fiebig developed the theory of sheaves on moment graphs; see [Reference FiebigFie08a, Reference FiebigFie08b]. In particular, he proved that the category of Soergel bimodules in the original sense is equivalent to a certain full subcategory of ![]() $\mathcal {Z}$-modules when the representation
$\mathcal {Z}$-modules when the representation ![]() $V$ is reflection faithful. We generalize it.
$V$ is reflection faithful. We generalize it.
If ![]() $f\in R$, then
$f\in R$, then ![]() $(w(f))_{w\in W}\in \mathcal {Z}$. For any graded
$(w(f))_{w\in W}\in \mathcal {Z}$. For any graded ![]() $\mathcal {Z}$-module
$\mathcal {Z}$-module ![]() $M$, we define a right action of
$M$, we define a right action of ![]() $f$ as the action of
$f$ as the action of ![]() $(w(f))_{w\in W}\in \mathcal {Z}$. Hence
$(w(f))_{w\in W}\in \mathcal {Z}$. Hence ![]() $M$ is an
$M$ is an ![]() $R$-bimodule. To make a graded
$R$-bimodule. To make a graded ![]() $\mathcal {Z}$-module
$\mathcal {Z}$-module ![]() $M$ into an object of
$M$ into an object of ![]() $\mathcal {C}'$, we need a finiteness assumption on
$\mathcal {C}'$, we need a finiteness assumption on ![]() $M$.
$M$.
For a subset ![]() $I\subset W$, set
$I\subset W$, set
 \[ \mathcal{Z}^{I} = \biggl\{(z_w)\in \prod_{w\in I}R\,\bigg|\kern-3.5pt\begin{array}{l} z_{tw}\equiv z_w\pmod{\alpha_t}\text{ for any }w\in I\\ \text{and any reflection }t\in W\text{ such that }tw\in I \end{array}\!\!\!\!\biggr\}. \]
\[ \mathcal{Z}^{I} = \biggl\{(z_w)\in \prod_{w\in I}R\,\bigg|\kern-3.5pt\begin{array}{l} z_{tw}\equiv z_w\pmod{\alpha_t}\text{ for any }w\in I\\ \text{and any reflection }t\in W\text{ such that }tw\in I \end{array}\!\!\!\!\biggr\}. \]
We have a canonical homomorphism ![]() $\mathcal {Z}\to \mathcal {Z}^{I}$. Let
$\mathcal {Z}\to \mathcal {Z}^{I}$. Let ![]() ${\mathcal {Z}}\textrm {-Mod}^{f}$ be the full subcategory of the category of graded
${\mathcal {Z}}\textrm {-Mod}^{f}$ be the full subcategory of the category of graded ![]() $\mathcal {Z}$-modules which consists of modules such that the action of
$\mathcal {Z}$-modules which consists of modules such that the action of ![]() $\mathcal {Z}$ factors through
$\mathcal {Z}$ factors through ![]() $\mathcal {Z}\to \mathcal {Z}^{I}$ for some finite
$\mathcal {Z}\to \mathcal {Z}^{I}$ for some finite ![]() $I\subset W$.
$I\subset W$.
For a ![]() $\mathcal {Z}$-module
$\mathcal {Z}$-module ![]() $M$, let
$M$, let ![]() $M_Q = Q\otimes _R M$ and set
$M_Q = Q\otimes _R M$ and set
Then if ![]() $M\in {\mathcal {Z}}\textrm {-Mod}^{f}$, we have
$M\in {\mathcal {Z}}\textrm {-Mod}^{f}$, we have ![]() $M_Q = {\bigoplus} _{x\in W}\, M_Q^{x}$ [Reference FiebigFie08a, § 3.2]. It is easy to see that this defines an object of
$M_Q = {\bigoplus} _{x\in W}\, M_Q^{x}$ [Reference FiebigFie08a, § 3.2]. It is easy to see that this defines an object of ![]() $\mathcal {C}'$. Hence this gives a functor
$\mathcal {C}'$. Hence this gives a functor ![]() $F\colon {\mathcal {Z}}\textrm {-Mod}^{f}\to \mathcal {C}'$.
$F\colon {\mathcal {Z}}\textrm {-Mod}^{f}\to \mathcal {C}'$.
Proposition 5.1 Let ![]() $M,N\in {\mathcal {Z}}\textrm {-Mod}^{f}$ and assume that
$M,N\in {\mathcal {Z}}\textrm {-Mod}^{f}$ and assume that ![]() $N$ is torsion-free as an
$N$ is torsion-free as an ![]() $R$-module. Then we have
$R$-module. Then we have ![]() $\operatorname {Hom}_{{\mathcal {Z}}\textrm {-Mod}^{f}}(M,N)\xrightarrow {\sim }\operatorname {Hom}_{\mathcal {C}'}(F(M),F(N))$.
$\operatorname {Hom}_{{\mathcal {Z}}\textrm {-Mod}^{f}}(M,N)\xrightarrow {\sim }\operatorname {Hom}_{\mathcal {C}'}(F(M),F(N))$.
Proof. Let ![]() $\varphi \colon F(M)\to F(N)$ be a homomorphism in
$\varphi \colon F(M)\to F(N)$ be a homomorphism in ![]() $\mathcal {C}'$. Then
$\mathcal {C}'$. Then ![]() $\varphi$ induces a map
$\varphi$ induces a map ![]() $\varphi _w\colon M_Q^{w} \to N_Q^{w}$. For
$\varphi _w\colon M_Q^{w} \to N_Q^{w}$. For ![]() $m\in M$,
$m\in M$, ![]() $z = (z_w)\in \mathcal {Z}$ and
$z = (z_w)\in \mathcal {Z}$ and ![]() $w\in W$, we have
$w\in W$, we have ![]() $\varphi (zm)_w = \varphi _w((zm)_w) = \varphi _w(z_wm_w) = z_w\varphi _w(m_w) = z_w(\varphi (m)_w) = (z\varphi (m))_w$. Since the map
$\varphi (zm)_w = \varphi _w((zm)_w) = \varphi _w(z_wm_w) = z_w\varphi _w(m_w) = z_w(\varphi (m)_w) = (z\varphi (m))_w$. Since the map ![]() $N\to N_Q = {\bigoplus} _{w\in W}\,N_Q^{w}$ is injective by the assumption, we have
$N\to N_Q = {\bigoplus} _{w\in W}\,N_Q^{w}$ is injective by the assumption, we have ![]() $\varphi (zm) = z\varphi (m)$.
$\varphi (zm) = z\varphi (m)$.
Let ![]() $s\in S$ and define
$s\in S$ and define ![]() $\mathcal {Z}^{s} = \{(z_w)\in \mathcal {Z}\mid z_{ws} = z_w\}$. This is a subalgebra of
$\mathcal {Z}^{s} = \{(z_w)\in \mathcal {Z}\mid z_{ws} = z_w\}$. This is a subalgebra of ![]() $\mathcal {Z}$. We say that
$\mathcal {Z}$. We say that ![]() $V$ satisfies the GKM condition if
$V$ satisfies the GKM condition if ![]() $\{\alpha _{t_1},\alpha _{t_2}\}$ is linearly independent for any reflections
$\{\alpha _{t_1},\alpha _{t_2}\}$ is linearly independent for any reflections ![]() $t_1\ne t_2$.
$t_1\ne t_2$.
Lemma 5.2 Assume that ![]() $V$ satisfies GKM condition. Let
$V$ satisfies GKM condition. Let ![]() $s\in S$ and
$s\in S$ and ![]() $\delta \in V$ such that
$\delta \in V$ such that ![]() $\langle \alpha _s^{\vee },\delta \rangle = 1$. Then we have
$\langle \alpha _s^{\vee },\delta \rangle = 1$. Then we have ![]() $\mathcal {Z} = \mathcal {Z}^{s}\oplus (w(\delta ))_{w\in W}\mathcal {Z}^{s}$.
$\mathcal {Z} = \mathcal {Z}^{s}\oplus (w(\delta ))_{w\in W}\mathcal {Z}^{s}$.
Proof. Let ![]() $z = (z_w)_{w\in W}$. For each
$z = (z_w)_{w\in W}$. For each ![]() $w\in W$, there exists
$w\in W$, there exists ![]() $y_w\in R$ such that
$y_w\in R$ such that ![]() $z_{w} - z_{ws} = w(\alpha _s)y_w$. Let
$z_{w} - z_{ws} = w(\alpha _s)y_w$. Let ![]() $t\ne wsw^{-1}$ be a reflection. Then
$t\ne wsw^{-1}$ be a reflection. Then ![]() $tw(\alpha _s)\equiv w(\alpha _s)\pmod {\alpha _t}$. Hence
$tw(\alpha _s)\equiv w(\alpha _s)\pmod {\alpha _t}$. Hence ![]() $w(\alpha _s)(y_w - y_{tw})\equiv w(\alpha _s)y_w - tw(\alpha _s)y_{tw}$
$w(\alpha _s)(y_w - y_{tw})\equiv w(\alpha _s)y_w - tw(\alpha _s)y_{tw}$ ![]() $= (z_w - z_{tw}) - (z_{ws} - z_{tws})\equiv 0\pmod {\alpha _t}$. By the GKM condition,
$= (z_w - z_{tw}) - (z_{ws} - z_{tws})\equiv 0\pmod {\alpha _t}$. By the GKM condition, ![]() $\alpha _t$ and
$\alpha _t$ and ![]() $w(\alpha _s)$ are linearly independent. Hence
$w(\alpha _s)$ are linearly independent. Hence ![]() $y_w\equiv y_{tw}\pmod {\alpha _t}$. On the other hand, for
$y_w\equiv y_{tw}\pmod {\alpha _t}$. On the other hand, for ![]() $t = wsw^{-1}$, we have
$t = wsw^{-1}$, we have ![]() $y_{tw} = y_{ws} = y_w$ by the definition of
$y_{tw} = y_{ws} = y_w$ by the definition of ![]() $y_w$. Hence
$y_w$. Hence ![]() $y = (y_w)_{w\in W}\in \mathcal {Z}^{s}$. We also set
$y = (y_w)_{w\in W}\in \mathcal {Z}^{s}$. We also set ![]() $x_w = z_w - w(\delta )y_w$. Then we have
$x_w = z_w - w(\delta )y_w$. Then we have ![]() $x_{ws} = z_{ws} - ws(\delta )y_w = z_w - w(\alpha _s)y_w - ws(\delta )y_w$
$x_{ws} = z_{ws} - ws(\delta )y_w = z_w - w(\alpha _s)y_w - ws(\delta )y_w$ ![]() $= z_w - w(\alpha _s)y_w - (w(\delta ) - w(\alpha _s))y_w = z_w - w(\delta )y_w = x_w$. Hence
$= z_w - w(\alpha _s)y_w - (w(\delta ) - w(\alpha _s))y_w = z_w - w(\delta )y_w = x_w$. Hence ![]() $x = (x_w)_{w\in W}\in \mathcal {Z}^{s}$ and we have
$x = (x_w)_{w\in W}\in \mathcal {Z}^{s}$ and we have ![]() $z = x + (w(\delta ))_{w\in W}y$. Reversing this argument, we can get the uniqueness of
$z = x + (w(\delta ))_{w\in W}y$. Reversing this argument, we can get the uniqueness of ![]() $x,y$.
$x,y$.
Proposition 5.3 Assume that ![]() $V$ satisfies GKM condition. Let
$V$ satisfies GKM condition. Let ![]() $M\in {Z}\textrm {-Mod}^{f}$. Then
$M\in {Z}\textrm {-Mod}^{f}$. Then ![]() $F(\mathcal {Z}\otimes _{\mathcal {Z}^{s}}M)\simeq F(M)\otimes _R B_s$.
$F(\mathcal {Z}\otimes _{\mathcal {Z}^{s}}M)\simeq F(M)\otimes _R B_s$.
Proof. Take ![]() $\delta \in V$ such that
$\delta \in V$ such that ![]() $\langle \alpha _s^{\vee },\delta \rangle = 1$. Define
$\langle \alpha _s^{\vee },\delta \rangle = 1$. Define ![]() $F(M)\otimes _R B_s = F(M)\otimes _{R^{s}}R\to \mathcal {Z}\otimes _{\mathcal {Z}^{s}}M$ by
$F(M)\otimes _R B_s = F(M)\otimes _{R^{s}}R\to \mathcal {Z}\otimes _{\mathcal {Z}^{s}}M$ by ![]() $m\otimes f\mapsto (w(f))_{w\in W}\otimes m$. Since
$m\otimes f\mapsto (w(f))_{w\in W}\otimes m$. Since ![]() $F(M)\otimes _{R^{s}}R = F(M)\otimes 1\oplus F(M)\otimes \delta$ and
$F(M)\otimes _{R^{s}}R = F(M)\otimes 1\oplus F(M)\otimes \delta$ and ![]() $\mathcal {Z}\otimes _{\mathcal {Z}^{s}}M = 1\otimes M\oplus (w(\delta ))_{w\in W}\otimes M$, this homomorphism is an isomorphism.
$\mathcal {Z}\otimes _{\mathcal {Z}^{s}}M = 1\otimes M\oplus (w(\delta ))_{w\in W}\otimes M$, this homomorphism is an isomorphism.
Define a ![]() $\mathcal {Z}$-module structure on
$\mathcal {Z}$-module structure on ![]() $R$ by
$R$ by ![]() $(z_w)_{w\in W}f = z_ef$ for
$(z_w)_{w\in W}f = z_ef$ for ![]() $(z_w)_{w\in W}\in \mathcal {Z}$ and
$(z_w)_{w\in W}\in \mathcal {Z}$ and ![]() $f\in R$ and denote this
$f\in R$ and denote this ![]() $\mathcal {Z}$-module by
$\mathcal {Z}$-module by ![]() $R(e)$. Then
$R(e)$. Then ![]() $F(R(e)) = R_e$. Let
$F(R(e)) = R_e$. Let ![]() ${\mathcal {Z}}\textrm {-Mod}^{\textrm {S}}$ be the full subcategory of
${\mathcal {Z}}\textrm {-Mod}^{\textrm {S}}$ be the full subcategory of ![]() ${\mathcal {Z}}\textrm {-Mod}^{f}$ consisting of the direct summands of direct sums of
${\mathcal {Z}}\textrm {-Mod}^{f}$ consisting of the direct summands of direct sums of ![]() $\{\mathcal {Z}\otimes _{\mathcal {Z}^{s_1}}\cdots \otimes _{\mathcal {Z}^{s_l}}R(e)(n)\mid s_1,\ldots ,s_l\in S,n\in \mathbb {Z}\}$. The following theorem follows from the above argument.
$\{\mathcal {Z}\otimes _{\mathcal {Z}^{s_1}}\cdots \otimes _{\mathcal {Z}^{s_l}}R(e)(n)\mid s_1,\ldots ,s_l\in S,n\in \mathbb {Z}\}$. The following theorem follows from the above argument.
Theorem 5.4 Assume that ![]() $V$ satisfies GKM condition. The functor
$V$ satisfies GKM condition. The functor ![]() $F$ induces an equivalence
$F$ induces an equivalence ![]() ${\mathcal {Z}}\textrm {-Mod}^{\mathrm {S}}\to \mathcal {S}\mathrm {Bimod}$.
${\mathcal {Z}}\textrm {-Mod}^{\mathrm {S}}\to \mathcal {S}\mathrm {Bimod}$.
5.2 Double leaves
Let ![]() $\underline {x}\in S^{l}$,
$\underline {x}\in S^{l}$, ![]() $\underline {y}\in S^{l'}$,
$\underline {y}\in S^{l'}$, ![]() $\boldsymbol {e}\in \{0,1\}^{l}$ and
$\boldsymbol {e}\in \{0,1\}^{l}$ and ![]() $\boldsymbol {f}\in \{0,1\}^{l'}$ such that
$\boldsymbol {f}\in \{0,1\}^{l'}$ such that ![]() $\underline {x}^{\boldsymbol {e}} = \underline {y}^{\boldsymbol {f}}$. Set
$\underline {x}^{\boldsymbol {e}} = \underline {y}^{\boldsymbol {f}}$. Set ![]() $w = \underline {x}^{\boldsymbol {e}}$ and fix its reduced expression
$w = \underline {x}^{\boldsymbol {e}}$ and fix its reduced expression ![]() $\underline {w}$. Then we have
$\underline {w}$. Then we have ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}\colon B_{\underline {x}}\to B_{\underline {w}}$ and
$\mathit {LL}_{\underline {x},\boldsymbol {e}}\colon B_{\underline {x}}\to B_{\underline {w}}$ and ![]() $\mathit {LL}^{*}_{\underline {y},\boldsymbol {f}}\colon B_{\underline {w}}\to B_{\underline {y}}$. We put
$\mathit {LL}^{*}_{\underline {y},\boldsymbol {f}}\colon B_{\underline {w}}\to B_{\underline {y}}$. We put ![]() $\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}} = \mathit {LL}^{*}_{\underline {y},\boldsymbol {f}}\circ \mathit {LL}_{\underline {x},\boldsymbol {e}}\colon B_{\underline {x}}\to B_{\underline {y}}$ which we call a double leaf.
$\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}} = \mathit {LL}^{*}_{\underline {y},\boldsymbol {f}}\circ \mathit {LL}_{\underline {x},\boldsymbol {e}}\colon B_{\underline {x}}\to B_{\underline {y}}$ which we call a double leaf.
Theorem 5.5 The set of double leaves ![]() $\{\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}}\mid \underline {x}^{\boldsymbol {e}} = \underline {y}^{\boldsymbol {f}}\}$ is a basis of
$\{\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}}\mid \underline {x}^{\boldsymbol {e}} = \underline {y}^{\boldsymbol {f}}\}$ is a basis of ![]() $\operatorname {Hom}^{\bullet }_{\mathcal {BS}}(B_{\underline {x}},B_{\underline {y}})$.
$\operatorname {Hom}^{\bullet }_{\mathcal {BS}}(B_{\underline {x}},B_{\underline {y}})$.
Proof. The degree of ![]() $\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}}$ is
$\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}}$ is ![]() $d(\boldsymbol {e}) + d(\boldsymbol {f})$. Therefore we have
$d(\boldsymbol {e}) + d(\boldsymbol {f})$. Therefore we have ![]() $\sum _{\underline {x}^{\boldsymbol {e}} = \underline {y}^{\boldsymbol {f}}}v^{-\deg (\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}})} = \sum _{w\in W}\sum _{\underline {x}^{\boldsymbol {e}} = w}v^{-d(\boldsymbol {e})}\sum _{\underline {x}^{\boldsymbol {f}} = w}v^{-d(\boldsymbol {f})} = \sum _{w\in W}p_{\underline {x}}^{w}(v^{-1})p_{\underline {y}}^{w}(v^{-1})$. This is equal to the graded rank of
$\sum _{\underline {x}^{\boldsymbol {e}} = \underline {y}^{\boldsymbol {f}}}v^{-\deg (\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}})} = \sum _{w\in W}\sum _{\underline {x}^{\boldsymbol {e}} = w}v^{-d(\boldsymbol {e})}\sum _{\underline {x}^{\boldsymbol {f}} = w}v^{-d(\boldsymbol {f})} = \sum _{w\in W}p_{\underline {x}}^{w}(v^{-1})p_{\underline {y}}^{w}(v^{-1})$. This is equal to the graded rank of ![]() $\operatorname {Hom}^{\bullet }_{\mathcal {BS}}(B_{\underline {x}},B_{\underline {y}})$ by Corollary 4.7. Therefore it is sufficient to prove that the set of double leaves is linearly independent.
$\operatorname {Hom}^{\bullet }_{\mathcal {BS}}(B_{\underline {x}},B_{\underline {y}})$ by Corollary 4.7. Therefore it is sufficient to prove that the set of double leaves is linearly independent.
Assume that ![]() $\sum c_{\boldsymbol {e},\boldsymbol {f}}\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}} = 0$. Set
$\sum c_{\boldsymbol {e},\boldsymbol {f}}\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}} = 0$. Set ![]() $I = \{\underline {x}^{\boldsymbol {e}}\mid \underline {x}^{\boldsymbol {e}} = \underline {y}^{\boldsymbol {f}},c_{\boldsymbol {e},\boldsymbol {f}}\ne 0\}$ and assume that
$I = \{\underline {x}^{\boldsymbol {e}}\mid \underline {x}^{\boldsymbol {e}} = \underline {y}^{\boldsymbol {f}},c_{\boldsymbol {e},\boldsymbol {f}}\ne 0\}$ and assume that ![]() $I$ is not empty. Let
$I$ is not empty. Let ![]() $w\in I$ be an element with maximal length. Let
$w\in I$ be an element with maximal length. Let ![]() $\bar {I} = \{x\in W\mid \text{ there exists } y\in I$
$\bar {I} = \{x\in W\mid \text{ there exists } y\in I$ ![]() $\bar {I} = \{x\in W\mid \text{ there exists } y\in I$. Then
$\bar {I} = \{x\in W\mid \text{ there exists } y\in I$. Then ![]() $w$ is also has maximal length in
$w$ is also has maximal length in ![]() $\bar {I}$ and
$\bar {I}$ and ![]() $\bar {I}$ is closed. Set
$\bar {I}$ is closed. Set ![]() $\bar {I}' = \bar {I}\setminus \{w\}$. Then
$\bar {I}' = \bar {I}\setminus \{w\}$. Then ![]() $c_{\boldsymbol {e},\boldsymbol {f}}\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}}$ factors through
$c_{\boldsymbol {e},\boldsymbol {f}}\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}}$ factors through ![]() $B_{\underline {y},\bar {I}}\hookrightarrow B_{\underline {y}}$. Since
$B_{\underline {y},\bar {I}}\hookrightarrow B_{\underline {y}}$. Since ![]() $\bar {I}'\supset I\setminus \{w\}$, we have
$\bar {I}'\supset I\setminus \{w\}$, we have ![]() $\pi _{\underline {y}}^{w}\circ (c_{\boldsymbol {e},\boldsymbol {f}}\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}}) = 0$ unless
$\pi _{\underline {y}}^{w}\circ (c_{\boldsymbol {e},\boldsymbol {f}}\mathbb {LL}_{\boldsymbol {e},\boldsymbol {f}}) = 0$ unless ![]() $\underline {x}^{\boldsymbol {e}} = w$.
$\underline {x}^{\boldsymbol {e}} = w$.
Set ![]() $E = \{\boldsymbol {e}\mid c_{\boldsymbol {e},\boldsymbol {f}}\ne 0, \underline {x}^{\boldsymbol {e}} = w\}$. Recall that we have a total order
$E = \{\boldsymbol {e}\mid c_{\boldsymbol {e},\boldsymbol {f}}\ne 0, \underline {x}^{\boldsymbol {e}} = w\}$. Recall that we have a total order ![]() ${<} = {<_{\underline {x},w}}$ on this set. Let
${<} = {<_{\underline {x},w}}$ on this set. Let ![]() $\boldsymbol {e}'\in E$ be the minimal element. Then, for
$\boldsymbol {e}'\in E$ be the minimal element. Then, for ![]() $\boldsymbol {e}\in E$, we have
$\boldsymbol {e}\in E$, we have ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}}(b_{\underline {x},\boldsymbol {e}'}) = 0$ unless
$\mathit {LL}_{\underline {x},\boldsymbol {e}}(b_{\underline {x},\boldsymbol {e}'}) = 0$ unless ![]() $\boldsymbol {e} = \boldsymbol {e}'$ by Proposition 3.10. Therefore we have
$\boldsymbol {e} = \boldsymbol {e}'$ by Proposition 3.10. Therefore we have ![]() $\sum _{\underline {y}^{\boldsymbol {f}} = w}c_{\boldsymbol {e}',\boldsymbol {f}}(\pi _{\underline {y}}^{w}(\mathbb {LL}_{\boldsymbol {e}',\boldsymbol {f}}(b_{\underline {x},\boldsymbol {e}'}))) = 0$. Since
$\sum _{\underline {y}^{\boldsymbol {f}} = w}c_{\boldsymbol {e}',\boldsymbol {f}}(\pi _{\underline {y}}^{w}(\mathbb {LL}_{\boldsymbol {e}',\boldsymbol {f}}(b_{\underline {x},\boldsymbol {e}'}))) = 0$. Since ![]() $\mathit {LL}_{\underline {x},\boldsymbol {e}'}(b_{\underline {x},\boldsymbol {e}'}) = u_{\underline {w}}$ (Proposition 3.10), we have
$\mathit {LL}_{\underline {x},\boldsymbol {e}'}(b_{\underline {x},\boldsymbol {e}'}) = u_{\underline {w}}$ (Proposition 3.10), we have ![]() $\sum _{\underline {y}^{\boldsymbol {f}} = w}{c_{\boldsymbol {e}',\boldsymbol {f}}}\pi _{\underline {y}}^{w}(\mathit {LL}^{*}_{\underline {y},\boldsymbol {f}}(u_{\underline {w}})) = 0$. By Theorem 3.17,
$\sum _{\underline {y}^{\boldsymbol {f}} = w}{c_{\boldsymbol {e}',\boldsymbol {f}}}\pi _{\underline {y}}^{w}(\mathit {LL}^{*}_{\underline {y},\boldsymbol {f}}(u_{\underline {w}})) = 0$. By Theorem 3.17, ![]() $c_{\boldsymbol {e}',\boldsymbol {f}} = 0$ for any
$c_{\boldsymbol {e}',\boldsymbol {f}} = 0$ for any ![]() $\boldsymbol {f}$ such that
$\boldsymbol {f}$ such that ![]() $\underline {y}^{\boldsymbol {f}} = w$. This is a contradiction.
$\underline {y}^{\boldsymbol {f}} = w$. This is a contradiction.
5.3 The Elias–Williamson category
Let ![]() $\mathcal {D}$ be the category defined in [Reference Elias and WilliamsonEW16]. In this subsection we assume that the triple
$\mathcal {D}$ be the category defined in [Reference Elias and WilliamsonEW16]. In this subsection we assume that the triple ![]() $(V,\{\alpha _s\}_{s\in S},\{\alpha ^{\vee }_s\}_{s\in S})$ satisfies the following conditions.
$(V,\{\alpha _s\}_{s\in S},\{\alpha ^{\vee }_s\}_{s\in S})$ satisfies the following conditions.
(1) The triple
 $(V,\{\alpha _s\}_{s\in S},\{\alpha ^{\vee }_s\}_{s\in S})$ is a realization, that is, it satisfies the technical condition [Reference Elias and WilliamsonEW16, Definition 3.1]. The realization also satisfies the Demazure surjectivity, that is,
$(V,\{\alpha _s\}_{s\in S},\{\alpha ^{\vee }_s\}_{s\in S})$ is a realization, that is, it satisfies the technical condition [Reference Elias and WilliamsonEW16, Definition 3.1]. The realization also satisfies the Demazure surjectivity, that is,  $\alpha _s\colon V^{*}\to \mathbb {K}$ is surjective for any
$\alpha _s\colon V^{*}\to \mathbb {K}$ is surjective for any  $s\in S$.
$s\in S$.(2) For any
 $s,t\in S$ such that the order of
$s,t\in S$ such that the order of  $st$ is finite, we have:
$st$ is finite, we have:
• local non-degeneracy [Reference EliasEli16, Assumption 3.13];
• lesser invertibility [Reference EliasEli16, Assumption 3.14].
From the first assumption, the set of double leaves is a basis of the space of homomorphisms in ![]() $\mathcal {D}$. That is, Theorem 5.5 holds in the context of
$\mathcal {D}$. That is, Theorem 5.5 holds in the context of ![]() $\mathcal {D}$; see [Reference Elias and WilliamsonEW16, Theorem 6.12] for the detailed statement.
$\mathcal {D}$; see [Reference Elias and WilliamsonEW16, Theorem 6.12] for the detailed statement.
From the second assumption, we have a well-defined functor ![]() $\mathcal {F}$ from
$\mathcal {F}$ from ![]() $\mathcal {D}$ to the category of graded
$\mathcal {D}$ to the category of graded ![]() $R$-bimodules [Reference Elias and WilliamsonEW16, Claim 5.14]. The assumptions in [Reference Elias and WilliamsonEW16] are slightly implicit. In the proof in [Reference Elias and WilliamsonEW16], to construct the functor and to prove that the functor satisfies a part of defining relations of
$R$-bimodules [Reference Elias and WilliamsonEW16, Claim 5.14]. The assumptions in [Reference Elias and WilliamsonEW16] are slightly implicit. In the proof in [Reference Elias and WilliamsonEW16], to construct the functor and to prove that the functor satisfies a part of defining relations of ![]() $\mathcal {D}$, they use results of Elias [Reference EliasEli16]. Elias assumed the two conditions in his paper [Reference EliasEli16, Definition 6.18]. (In fact, he also assumed Demazure surjectivity, which we have already assumed.)
$\mathcal {D}$, they use results of Elias [Reference EliasEli16]. Elias assumed the two conditions in his paper [Reference EliasEli16, Definition 6.18]. (In fact, he also assumed Demazure surjectivity, which we have already assumed.)
Remark 5.6 Assume that ![]() $\mathbb {K}$ is a field. Let
$\mathbb {K}$ is a field. Let ![]() $s,t\in S$ such that the order of
$s,t\in S$ such that the order of ![]() $st$ is finite. If the restriction of
$st$ is finite. If the restriction of ![]() $V$ to
$V$ to ![]() $\langle s,t\rangle$ is finite, then the assumptions hold [Reference EliasEli16, § 3.9].
$\langle s,t\rangle$ is finite, then the assumptions hold [Reference EliasEli16, § 3.9].
Lemma 5.7 We make the above assumptions. Let ![]() $s,t\in S$ such that the order
$s,t\in S$ such that the order ![]() $m$ of
$m$ of ![]() $st$ is finite. Then the image of the
$st$ is finite. Then the image of the ![]() $2m$-valent vertex by
$2m$-valent vertex by ![]() $\mathcal {F}$ satisfies Assumption 3.2.
$\mathcal {F}$ satisfies Assumption 3.2.
Proof. We may assume ![]() $S = \{s,t\}$. Set
$S = \{s,t\}$. Set ![]() $\underline {x} = (s,t,\ldots )\in S^{m}$ and
$\underline {x} = (s,t,\ldots )\in S^{m}$ and ![]() $\underline {y} = (t,s,\ldots )\in S^{m}$. The graded rank of
$\underline {y} = (t,s,\ldots )\in S^{m}$. The graded rank of ![]() $\operatorname {grk} \operatorname {Hom}_{\mathcal {S}\mathrm {Bimod}}(B_{\underline {x}},B_{\underline {y}})$ is
$\operatorname {grk} \operatorname {Hom}_{\mathcal {S}\mathrm {Bimod}}(B_{\underline {x}},B_{\underline {y}})$ is ![]() $\overline {\varepsilon }(\omega (\operatorname {ch}(B_{\underline {x}}))\operatorname {ch}(B_{\underline {y}})) = \overline {\varepsilon (\underline {H}_{\underline {x}}\underline {H}_{\underline {y}})}$ by Theorem 4.6. The constant term of this (that is, the dimension of the space of degree-zero homomorphisms from
$\overline {\varepsilon }(\omega (\operatorname {ch}(B_{\underline {x}}))\operatorname {ch}(B_{\underline {y}})) = \overline {\varepsilon (\underline {H}_{\underline {x}}\underline {H}_{\underline {y}})}$ by Theorem 4.6. The constant term of this (that is, the dimension of the space of degree-zero homomorphisms from ![]() $B_{\underline {x}}$ to
$B_{\underline {x}}$ to ![]() $B_{\underline {y}}$) is
$B_{\underline {y}}$) is ![]() $1$ (see the proof of [Reference LibedinskyLib08, Proposition 4.3]). In particular, there exists only one morphism which satisfies Assumption 3.2. Let
$1$ (see the proof of [Reference LibedinskyLib08, Proposition 4.3]). In particular, there exists only one morphism which satisfies Assumption 3.2. Let ![]() $\psi \colon B_{\underline {x}}\to B_{\underline {y}}$ be the morphism.
$\psi \colon B_{\underline {x}}\to B_{\underline {y}}$ be the morphism.
Let ![]() $\varphi \colon \underline {x}\to \underline {y}$ be the
$\varphi \colon \underline {x}\to \underline {y}$ be the ![]() $2m$-valent vertex. Then
$2m$-valent vertex. Then ![]() $\varphi$ is homogeneous of degree zero and hence
$\varphi$ is homogeneous of degree zero and hence ![]() $\mathcal {F}(\varphi )$ is also homogeneous of degree zero. Therefore, as we have shown above,
$\mathcal {F}(\varphi )$ is also homogeneous of degree zero. Therefore, as we have shown above, ![]() $\mathcal {F}(\varphi ) = c\psi$ for some
$\mathcal {F}(\varphi ) = c\psi$ for some ![]() $c\in \mathbb {K}$.
$c\in \mathbb {K}$.
To prove ![]() $c = 1$, we use the calculation in localizations. Let
$c = 1$, we use the calculation in localizations. Let ![]() $\mathcal {S}\mathrm {Bimod}_Q$ be the full subcategory of
$\mathcal {S}\mathrm {Bimod}_Q$ be the full subcategory of ![]() $Q$-bimodules such that
$Q$-bimodules such that ![]() $X\in \mathcal {S}\mathrm {Bimod}_Q$ if and only if
$X\in \mathcal {S}\mathrm {Bimod}_Q$ if and only if ![]() $X$ is a direct sum of
$X$ is a direct sum of ![]() $Q_w$ with
$Q_w$ with ![]() $w\in W$. We fix an isomorphism
$w\in W$. We fix an isomorphism ![]() $(B_s)_Q\simeq Q_e\oplus Q_s$ as
$(B_s)_Q\simeq Q_e\oplus Q_s$ as ![]() $f\otimes g\mapsto (fg,fs(g))$. Then, by extending this, we have an isomorphism
$f\otimes g\mapsto (fg,fs(g))$. Then, by extending this, we have an isomorphism ![]() $(B_{\underline {x}})_Q \simeq {\bigoplus} _{\mathbf {e}\in \{0,1\}^{m}}\,Q_{\underline {x}^{\mathbf {e}}}$. For each
$(B_{\underline {x}})_Q \simeq {\bigoplus} _{\mathbf {e}\in \{0,1\}^{m}}\,Q_{\underline {x}^{\mathbf {e}}}$. For each ![]() $B_{\underline {x}}\in \mathcal {BS}$, by attaching
$B_{\underline {x}}\in \mathcal {BS}$, by attaching ![]() ${\bigoplus} _{\mathbf {e}\in \{0,1\}^{m}}\,Q_{\underline {x}^{\mathbf {e}}}$, we have the functor
${\bigoplus} _{\mathbf {e}\in \{0,1\}^{m}}\,Q_{\underline {x}^{\mathbf {e}}}$, we have the functor ![]() $\mathcal {G}\colon \mathcal {BS}\to \mathcal {S}\mathrm {Bimod}_Q$. Define
$\mathcal {G}\colon \mathcal {BS}\to \mathcal {S}\mathrm {Bimod}_Q$. Define ![]() $\operatorname {Kar}(\mathcal {D}_Q),\mathcal {D}_Q^{\mathrm {std}},\mathrm {S}\mathit {td}$ and
$\operatorname {Kar}(\mathcal {D}_Q),\mathcal {D}_Q^{\mathrm {std}},\mathrm {S}\mathit {td}$ and ![]() $\mathcal {F}^{\mathrm {std}}$ as in [Reference Elias and WilliamsonEW16, Definitions 5.15, 5.16, 5.22 and 4.9]. Then
$\mathcal {F}^{\mathrm {std}}$ as in [Reference Elias and WilliamsonEW16, Definitions 5.15, 5.16, 5.22 and 4.9]. Then ![]() $\mathcal {D}\xrightarrow {\mathcal {F}}\mathcal {BS}\xrightarrow {\mathcal {G}} \mathcal {S}\mathrm {Bimod}_Q$ and
$\mathcal {D}\xrightarrow {\mathcal {F}}\mathcal {BS}\xrightarrow {\mathcal {G}} \mathcal {S}\mathrm {Bimod}_Q$ and ![]() $\mathcal {D}\xrightarrow {\mathcal {S}\mathit {td}} \operatorname {Kar}(\mathcal {D}_Q)\xrightarrow {\mathcal {F}^{\mathrm {std}}}\mathcal {S}\mathrm {Bimod}_Q$ are the same (see the proof of [Reference Elias and WilliamsonEW16, Proposition 5.27]). Let
$\mathcal {D}\xrightarrow {\mathcal {S}\mathit {td}} \operatorname {Kar}(\mathcal {D}_Q)\xrightarrow {\mathcal {F}^{\mathrm {std}}}\mathcal {S}\mathrm {Bimod}_Q$ are the same (see the proof of [Reference Elias and WilliamsonEW16, Proposition 5.27]). Let ![]() $w_0$ be the longest element in
$w_0$ be the longest element in ![]() $\langle s,t\rangle$. Then
$\langle s,t\rangle$. Then ![]() $Q_{w_0}$ is a direct summand of both
$Q_{w_0}$ is a direct summand of both ![]() $\mathcal {G}(B_{\underline {x}})$ and
$\mathcal {G}(B_{\underline {x}})$ and ![]() $\mathcal {G}(B_{\underline {y}})$ with multiplicity one. We consider the composition
$\mathcal {G}(B_{\underline {y}})$ with multiplicity one. We consider the composition ![]() $Q_{w_0}\hookrightarrow \mathcal {G}(B_{\underline {x}})\xrightarrow {\eta }\mathcal {G}(B_{\underline {y}})\to Q_{w_0}$ for
$Q_{w_0}\hookrightarrow \mathcal {G}(B_{\underline {x}})\xrightarrow {\eta }\mathcal {G}(B_{\underline {y}})\to Q_{w_0}$ for ![]() $\eta = \mathcal {G}(\mathcal {F}(\varphi ))$ and
$\eta = \mathcal {G}(\mathcal {F}(\varphi ))$ and ![]() $\mathcal {G}(\psi )$. To prove
$\mathcal {G}(\psi )$. To prove ![]() $c = 1$, it is sufficient to prove that the composition is the identity for both
$c = 1$, it is sufficient to prove that the composition is the identity for both ![]() $\eta = \mathcal {G}(\mathcal {F}(\varphi ))$ and
$\eta = \mathcal {G}(\mathcal {F}(\varphi ))$ and ![]() $\eta = \mathcal {G}(\psi )$. For
$\eta = \mathcal {G}(\psi )$. For ![]() $\eta = \mathcal {G}(\mathcal {F}(\varphi ))$, it is the identity [Reference Elias and WilliamsonEW16, § 5.5]. For
$\eta = \mathcal {G}(\mathcal {F}(\varphi ))$, it is the identity [Reference Elias and WilliamsonEW16, § 5.5]. For ![]() $\eta = \mathcal {G}(\psi )$, take
$\eta = \mathcal {G}(\psi )$, take ![]() $q\in Q$ such that the composition is given by
$q\in Q$ such that the composition is given by ![]() $a\mapsto qa$. By the definition, the projection
$a\mapsto qa$. By the definition, the projection ![]() $(B_{\underline {x}})_Q\to Q_{w_0}$ is given by
$(B_{\underline {x}})_Q\to Q_{w_0}$ is given by ![]() $\varphi _{\underline {x}}$ which is defined in § 3.4. Hence the following diagram commutes.
$\varphi _{\underline {x}}$ which is defined in § 3.4. Hence the following diagram commutes.

Since ![]() $\psi$ satisfies Assumption 3.2, we have
$\psi$ satisfies Assumption 3.2, we have ![]() $\mathcal {G}(\psi )(u_{\underline {x}}) = u_{\underline {y}}$. By the definition of
$\mathcal {G}(\psi )(u_{\underline {x}}) = u_{\underline {y}}$. By the definition of ![]() $\varphi _{\underline {x}}$, we have
$\varphi _{\underline {x}}$, we have ![]() $\varphi _{\underline {x}}(u_{\underline {x}}) = 1$. Hence by considering the image of
$\varphi _{\underline {x}}(u_{\underline {x}}) = 1$. Hence by considering the image of ![]() $u_{\underline {x}}\in B_{\underline {x}}$ in the above diagram, we conclude that
$u_{\underline {x}}\in B_{\underline {x}}$ in the above diagram, we conclude that ![]() $q = 1$.
$q = 1$.
The functor ![]() $\mathcal {F}$ is defined as a functor from
$\mathcal {F}$ is defined as a functor from ![]() $\mathcal {D}$ to the category of graded
$\mathcal {D}$ to the category of graded ![]() $R$-bimodules. We can also consider it as a functor to
$R$-bimodules. We can also consider it as a functor to ![]() $\mathcal {BS}$ as follows. For
$\mathcal {BS}$ as follows. For ![]() $\underline {x}$, we put
$\underline {x}$, we put ![]() $\mathcal {F}(\underline {x}) = B_{\underline {x}}$. We have to prove that
$\mathcal {F}(\underline {x}) = B_{\underline {x}}$. We have to prove that ![]() $\mathcal {F}(\varphi )$ is a morphism in
$\mathcal {F}(\varphi )$ is a morphism in ![]() $\mathcal {BS}$ for any morphism
$\mathcal {BS}$ for any morphism ![]() $\varphi$ in
$\varphi$ in ![]() $\mathcal {D}$. The morphisms in
$\mathcal {D}$. The morphisms in ![]() $\mathcal {D}$ is generated by three types of morphisms: univalent vertices, trivalent vertices and the morphism in the previous lemma. If a morphism
$\mathcal {D}$ is generated by three types of morphisms: univalent vertices, trivalent vertices and the morphism in the previous lemma. If a morphism ![]() $\varphi$ in
$\varphi$ in ![]() $\mathcal {D}$ is a univalent or trivalent vertex then it is easy to see that
$\mathcal {D}$ is a univalent or trivalent vertex then it is easy to see that ![]() $\mathcal {F}(\varphi )$ is a morphism in
$\mathcal {F}(\varphi )$ is a morphism in ![]() $\mathcal {BS}$. By the previous lemma, if
$\mathcal {BS}$. By the previous lemma, if ![]() $\varphi$ is the morphism in that lemma,
$\varphi$ is the morphism in that lemma, ![]() $\mathcal {F}(\varphi )$ is a morphism in
$\mathcal {F}(\varphi )$ is a morphism in ![]() $\mathcal {BS}$. Therefore
$\mathcal {BS}$. Therefore ![]() $\mathcal {F}$ defines a functor
$\mathcal {F}$ defines a functor ![]() $\mathcal {D}\to \mathcal {BS}$ which we denote by the same letter
$\mathcal {D}\to \mathcal {BS}$ which we denote by the same letter ![]() $\mathcal {F}$.
$\mathcal {F}$.
By flipping the diagram upside-down, we have a contravariant functor ![]() $D'\colon \mathcal {D}\to \mathcal {D}$. Recall that we also have the functor
$D'\colon \mathcal {D}\to \mathcal {D}$. Recall that we also have the functor ![]() $D\colon \mathcal {BS}\to \mathcal {BS}$.
$D\colon \mathcal {BS}\to \mathcal {BS}$.
Lemma 5.8 We have ![]() $D\circ \mathcal {F}\simeq \mathcal {F}\circ D'$.
$D\circ \mathcal {F}\simeq \mathcal {F}\circ D'$.
Proof. We fix an isomorphism ![]() $D(B_{\underline {x}})\simeq B_{\underline {x}}$ obtained from the proof of Lemma 2.20. Then, for any
$D(B_{\underline {x}})\simeq B_{\underline {x}}$ obtained from the proof of Lemma 2.20. Then, for any ![]() $B\in \mathcal {D}$,
$B\in \mathcal {D}$, ![]() $D\circ \mathcal {F}(B)\simeq \mathcal {F}(D'(B))$ naturally. We prove
$D\circ \mathcal {F}(B)\simeq \mathcal {F}(D'(B))$ naturally. We prove ![]() $D(\mathcal {F}(\varphi )) = \mathcal {F}(D'(\varphi ))$ for any morphism
$D(\mathcal {F}(\varphi )) = \mathcal {F}(D'(\varphi ))$ for any morphism ![]() $\varphi$ in
$\varphi$ in ![]() $\mathcal {D}$. If
$\mathcal {D}$. If ![]() $\varphi$ is a univalent or trivalent vertex, it is easy to see that
$\varphi$ is a univalent or trivalent vertex, it is easy to see that ![]() $D(\mathcal {F}(\varphi )) = \mathcal {F}(D(\varphi ))$ by direct calculation. Let
$D(\mathcal {F}(\varphi )) = \mathcal {F}(D(\varphi ))$ by direct calculation. Let ![]() $m$ be the order of
$m$ be the order of ![]() $st$ with
$st$ with ![]() $s,t\in S$ and assume that
$s,t\in S$ and assume that ![]() $m < \infty$. Let
$m < \infty$. Let ![]() $\varphi$ be the
$\varphi$ be the ![]() $2m$-valent vertices. To prove
$2m$-valent vertices. To prove ![]() $D(\mathcal {F}(\varphi )) = \mathcal {F}(D'(\varphi ))$, by the previous lemma, it is sufficient to prove that the dual of the morphism satisfying Assumption 3.2 again satisfies Assumption 3.2.
$D(\mathcal {F}(\varphi )) = \mathcal {F}(D'(\varphi ))$, by the previous lemma, it is sufficient to prove that the dual of the morphism satisfying Assumption 3.2 again satisfies Assumption 3.2.
Let ![]() $\underline {x},\underline {y}$ be as in the previous lemma and
$\underline {x},\underline {y}$ be as in the previous lemma and ![]() $\psi \colon B_{\underline {x}}\to B_{\underline {y}}$ (respectively,
$\psi \colon B_{\underline {x}}\to B_{\underline {y}}$ (respectively, ![]() $\psi '\colon B_{\underline {y}}\to B_{\underline {x}}$) be the morphism satisfying Assumption 3.2. Then
$\psi '\colon B_{\underline {y}}\to B_{\underline {x}}$) be the morphism satisfying Assumption 3.2. Then ![]() $D(\psi ) \colon B_{\underline {y}}\to B_{\underline {x}}$ is homogeneous of degree zero, hence
$D(\psi ) \colon B_{\underline {y}}\to B_{\underline {x}}$ is homogeneous of degree zero, hence ![]() $D(\psi ) = c\psi '$ for some
$D(\psi ) = c\psi '$ for some ![]() $c\in \mathbb {K}$ since such degree-zero morphism is unique up to constant multiple. Let
$c\in \mathbb {K}$ since such degree-zero morphism is unique up to constant multiple. Let ![]() $w_0$ be the longest element in
$w_0$ be the longest element in ![]() $\langle s,t\rangle$. Then
$\langle s,t\rangle$. Then ![]() $Q_{w_0}$ is a direct summand of
$Q_{w_0}$ is a direct summand of ![]() $(B_{\underline {x}})_Q$ and
$(B_{\underline {x}})_Q$ and ![]() $(B_{\underline {y}})_Q$ with multiplicity one. Let
$(B_{\underline {y}})_Q$ with multiplicity one. Let ![]() $p_{\underline {x}}$ and
$p_{\underline {x}}$ and ![]() $i_{\underline {x}}$ be the projection to and the embedding from
$i_{\underline {x}}$ be the projection to and the embedding from ![]() $Q_{w_0}$, and the same for
$Q_{w_0}$, and the same for ![]() $p_{\underline {y}}$ and
$p_{\underline {y}}$ and ![]() $i_{\underline {y}}$. To prove
$i_{\underline {y}}$. To prove ![]() $c = 1$, it is sufficient to prove that
$c = 1$, it is sufficient to prove that ![]() $Q_{w_0}\xrightarrow {i_{\underline {y}}} (B_{\underline {y}})_Q\simeq D(B_{\underline {y}})_Q\xrightarrow {D(\psi )}D(B_{\underline {x}})_Q\simeq (B_{\underline {x}})_Q\xrightarrow {p_{\underline {x}}} Q_{w_0}$ is the identity since
$Q_{w_0}\xrightarrow {i_{\underline {y}}} (B_{\underline {y}})_Q\simeq D(B_{\underline {y}})_Q\xrightarrow {D(\psi )}D(B_{\underline {x}})_Q\simeq (B_{\underline {x}})_Q\xrightarrow {p_{\underline {x}}} Q_{w_0}$ is the identity since ![]() $\psi '$ satisfies this by the proof of the previous lemma. Obviously
$\psi '$ satisfies this by the proof of the previous lemma. Obviously ![]() $Q_{w_0}\xrightarrow {D(p_{\underline {y}})}D(B_{\underline {y}})\xrightarrow {D(\psi )}D(B_{\underline {x}})\xrightarrow {D(i_{\underline {x}})}Q_{w_0}$ is the identity. Hence it is sufficient to prove that
$Q_{w_0}\xrightarrow {D(p_{\underline {y}})}D(B_{\underline {y}})\xrightarrow {D(\psi )}D(B_{\underline {x}})\xrightarrow {D(i_{\underline {x}})}Q_{w_0}$ is the identity. Hence it is sufficient to prove that ![]() $D(p_{\underline {y}}) = i_{\underline {y}}$ under the fixed isomorphism
$D(p_{\underline {y}}) = i_{\underline {y}}$ under the fixed isomorphism ![]() $D(B_{\underline {y}})\simeq B_{\underline {y}}$. By the construction of
$D(B_{\underline {y}})\simeq B_{\underline {y}}$. By the construction of ![]() $p_{\underline {y}},i_{\underline {y}}$, it is sufficient to prove the same thing for
$p_{\underline {y}},i_{\underline {y}}$, it is sufficient to prove the same thing for ![]() $B_s$, namely, the dual of
$B_s$, namely, the dual of ![]() $(B_s)_Q\to Q_s$ is
$(B_s)_Q\to Q_s$ is ![]() $Q_s\hookrightarrow (B_s)_Q$. This can be checked directly.
$Q_s\hookrightarrow (B_s)_Q$. This can be checked directly.
Theorem 5.9 The category ![]() $\mathcal {D}$ is equivalent to
$\mathcal {D}$ is equivalent to ![]() $\mathcal {BS}$. Therefore the category
$\mathcal {BS}$. Therefore the category ![]() $\operatorname {Kar}(\mathcal {D})$ is equivalent to
$\operatorname {Kar}(\mathcal {D})$ is equivalent to ![]() $\mathcal {S}\mathrm {Bimod}$.
$\mathcal {S}\mathrm {Bimod}$.
Proof. It is sufficient to prove that ![]() $\mathcal {F}$ is fully faithful. By the constructions, Lemmas 5.7 and 5.8, the functor
$\mathcal {F}$ is fully faithful. By the constructions, Lemmas 5.7 and 5.8, the functor ![]() $\mathcal {F}$ sends double leaves to double leaves. Since the set of double leaves gives a basis of the space of homomorphisms in both categories, the functor
$\mathcal {F}$ sends double leaves to double leaves. Since the set of double leaves gives a basis of the space of homomorphisms in both categories, the functor ![]() $\mathcal {F}$ is fully faithful.
$\mathcal {F}$ is fully faithful.
Acknowledgements
The author was supported by JSPS KAKENHI Grant Number 18H01107. The author thanks Henning Haahr-Andersen and Masaharu Kaneda for reading the paper and giving helpful comments. The author also thanks the referee for a careful reading and giving many helpful comments.