1. INTRODUCTION
Currently, ground stations will support Mars explorer orbit determination. This navigation method is subject to navigation accuracy, real-timeliness, reliability and spreadability. It cannot fulfil the requirement of deep space exploration for high-accuracy and real-time navigation. Consequently autonomous navigation systems (Xiong et al., Reference Xiong, Wei and Liu2013), which need not communicate with ground stations, are highly attractive.
Traditional celestial navigation (Ning et al., Reference Ning, Wang, Wu and Fang2011; Reference Ning, Ma, Peng, Quan and Fang2012) is a commonly used autonomous navigation method, whose measurement is the angle subtended at the explorer between the line of sight to the star and near celestial body. Its position accuracy declines with the increase of the distance between the explorer and the near celestial body. The distance between the Mars explorer and the near celestial body is so long that the positioning accuracy of this navigation method is very low in transfer orbit. Thus, this method is not suitable for the transfer orbit of deep space exploration. Asteroid-based navigation methods (Zhang et al., Reference Zhang, Wang and Huang2009; Xu et al., Reference Xu, Cui, Cui and Liu2007) acquire navigation information by observing an asteroid when the explorer approaches the asteroid, but cannot obtain navigation information when the distance between the explorer and asteroid is very large. Therefore this method realizes high-accuracy positioning determination only for a small fraction of the whole transfer orbit.
X-ray pulsar navigation is a novel navigation method for deep space exploration. X-ray pulsars are rapidly rotating neutron stars, which can generate X-ray pulsed radiation. X-ray radiation signals can be collected by X-ray sensors placed on the explorer. After a period of observation usually lasting for several minutes, the stable X-ray pulse profile is acquired through the epoch folding (EF) procedure (Emadzadeh and Speyer, Reference Emadzadeh and Speyer2011a). A pulse time-of-arrival (TOA) can be obtained by comparing the observed pulse profile with the standard one (Liu et al., Reference Liu, Ma and Tian2010; Reference Liu, Ma, Tian, Kang and White2012). Since TOA accuracy is unrelated to the explorer's position, this navigation method can provide positioning information for the whole transfer orbit.
Many studies of X-ray pulsar navigation have assumed that the frequency of pulsar signals is known (Li and Ke, Reference Li and Ke2011; Emadzadeh and Speyer, Reference Emadzadeh and Speyer2011b; Rinauro et al., Reference Rinauro, Colonnese and Scarano2013), which is an important parameter in the epoch folding procedure. However, the Doppler effects caused by the motion of the explorer result in the distortion of integrated pulse profile of an X-ray pulsar. Consequently, the pulse TOA accuracy declines. As we know, the pulse TOA accuracy affects the position determination accuracy. Conversely, the distortion of an integrated pulse profile reflects the Doppler velocity. Thus, many scholars have estimated the explorer's velocity based on the pulse profile distortion. Golshan and Sheikh (Reference Golshan and Sheikh2008) utilized the maximum-likelihood (ML) estimation method to determine the position and velocity. And the accuracy of the ML method approaches the Cramer-Rao lower bound (CRLB) (Ashby and Golshan, Reference Ashby and Golshan2008). Zhang et al. (Reference Zhang, Xu and Xie2011) gave the conception of the profile entropy and based on this, a phase and frequency estimation method for X-ray pulsar has been proposed. Fei et al. (Reference Fei, Pan and Yao2011a; Reference Fei, Yao, Du and Sun2011b) divided pulsar signals into two parts, taking their similarity as the objective function, and estimated the Doppler velocity by minimizing this objective function. Xie et al. (Reference Xie, Xu, Zhang and Luo2012) defined a profile feature function to measure the integrated pulse profile distortion. According to the relationship between the function value and Doppler velocity, the Doppler velocity has been recognised by a search method. These Doppler velocity estimation methods’ velocity accuracies are also high.
The strategy of those methods is to estimate the spacecraft velocity by means of minimizing the distortion of the pulse profile. In a pulsar observation period, pulsar photons are collected by an X-ray sensor and simultaneously folded based on pulse period. At this time, the pulsar navigation performance will not be affected when the runtime of the EF procedure is less than a pulsar observation period. But after a pulsar observation, the measurements including the pulse TOA and the Doppler velocity must be acquired quickly. Unfortunately, those Doppler velocity estimation methods are executed after the pulsar observation. What is worse, they have a high computational cost. The reason is that in those methods, a large number of pulsar signals (in the order of 106∼107) are folded with different pulse periods, even the runtime for an EF procedure with one pulse period is too high for the pulsar navigation system. From the above analysis, we can see that multiple EF procedures must be avoided.
In this paper, to eliminate the Doppler effects with a small computational cost, we develop a novel X-ray pulsar navigation system for the Mars explorer resistant against Doppler effects, which avoids multiple EF procedures. In the pulsar signal observation period, we utilise the prior information to compensate for the Doppler effects. However, an error inevitably exists in the prior information, which leads to the pulse TOA bias that arises from the Doppler compensation. It can be found that there is a correlation between the pulsar navigation measurement bias and the state estimation error. Based on this, a novel TOA measurement model is built with respect to the state estimation error. We develop a closed-loop extended Kalman filter (EKF) using this novel TOA model, which is robust to the measurement bias caused by the Doppler compensation.
This paper is organized into six sections. After the introduction, the orbit dynamic model for the Mars explorer and pulsar signal Doppler compensation method are outlined in Section 2. The novel X-ray pulsar navigation measurement model is in Section 3. The closed-loop EKF using the measurement model with the Doppler effects (closed-loop EKF-MMDE) is described in Section 4. The simulation results in Section 5 demonstrate the real-timeliness and accuracy of the presented method and conclusions are drawn in Section 6.
2. PULSAR SIGNAL DOPPLER COMPENSATION
In order to illustrate, we define the TOA of an individual pulse as the sub-TOA, while the TOA obtained from the pulse integrated profile is defined as the pulse TOA.
To reduce the Doppler effects caused by the motion of a Mars explorer, the position, velocity and acceleration estimations obtained from the orbit dynamic model and prior knowledge can be utilised to compensate individual photon TOA from an X-ray pulsar. However an error inevitably exists in the prior information. Therefore there is a bias in the TOA measurement after the Doppler compensation.
In this section, we analyse the orbit dynamic model for the Mars explorer, and build the state predicted error model. The X-ray pulsar photon EF procedure based on Doppler compensation is then given. Finally, we show the effect of Doppler compensation on pulse TOA, and build the pulse TOA measurement bias model with respect to the Mars explorer's state estimation error.
2.1. The analysis of orbit dynamic model for Mars explorer
The Sun-centred inertial Cartesian coordinate system (J2000.0) is selected. The orbit dynamic model for the Mars explorer is given as:
$$\left\{ \matrix{\dot x = v_x \cr \dot y = v_y \cr \dot z = v_z \cr \dot v_x = - \mu _s \displaystyle{x \over {r_{\,ps}^3}} - \mu _m \left[ {\displaystyle{{x - x_1} \over {r_{\,pm}^3}} + \displaystyle{{x_1} \over {r_{sm}^3}}} \right] - \mu _e \left[ {\displaystyle{{x - x_2} \over {r_{\,pe}^3}} + \displaystyle{{x_2} \over {r_{se}^3}}} \right] + \Delta F_x \cr \dot v_y = - \mu _s \displaystyle{y \over {r_{\,ps}^3}} - \mu _m \left[ {\displaystyle{{y - y_1} \over {r_{\,pm}^3}} + \displaystyle{{y_1} \over {r_{sm}^3}}} \right] - \mu _e \left[ {\displaystyle{{y - y_2} \over {r_{\,pe}^3}} + \displaystyle{{y_2} \over {r_{se}^3}}} \right] + \Delta F_y \cr \dot v_z = - \mu _s \displaystyle{z \over {r_{\,ps}^3}} - \mu _m \left[ {\displaystyle{{z - z_1} \over {r_{\,pm}^3}} + \displaystyle{{z_1} \over {r_{sm}^3}}} \right] - \mu _e \left[ {\displaystyle{{z - z_2} \over {r_{\,pe}^3}} + \displaystyle{{z_2} \over {r_{se}^3}}} \right] + \Delta F_z } \right.$$Equation (1) can be rewritten in the general state equation as
$${\bi \dot X}(t) = f\,({\bi X},t) + {\bi \omega} (t)$$where the state vector X=[x, y, z, v x, vy, vz]T. r=[x, y, z] and v=⌊v x, vy, vz⌋ are the Mars explorer position and velocity vectors, respectively. 
${\bi \dot X}(t)$ is the derivative of X. [x 1, y 1, z 1] and [x 2, y 2, z 2] are the position vectors of Mars and the Earth, respectively. μ s, μm, μe are the gravitational constants of the Sun, Mars and Earth respectively, and their values are 1·327×1011 km3/s2, 3·986×105 km3/s2, 4·2828×104 km3/s2, respectively. 
$r_{\,ps} = \sqrt {x^2 + y^2 + z^2} $, 
$r_{\,pm} = \sqrt {(x - x_1 )^2 + (y - y_1 )^2 + (z - z_1 )^2} $, 
$r_{\,pe} = \sqrt {(x - x_2 )^2 + (y - y_2 )^2 + (z - z_2 )^2} $ are the distances from the Mars explorer to the Sun centre, the Mars centre and the Earth centre, respectively. 
$r_{sm} = \sqrt {x_1^2 + y_1^2 + z_1^2} $, 
$r_{se} = \sqrt {x_2^2 + y_2^2 + z_2^2} $ are the distances from the Sun centre to the Mars centre and the Earth centre respectively. ω=[0, 0, 0, ΔF x, ΔF y, ΔF z]T, where ΔF x, ΔF y, ΔF z are the perturbation force considering sun-press and other planets.
We can obtain the discrete form of Equation (2) as:
$${\bi X}_k = {\bi X}_{k - 1} + f\,({\bi X}_{k - 1}, k - 1)T + {\bi A}({\bi X}_k )f\,({\bi X}_{k - 1}, k - 1)\displaystyle{{T^2} \over 2} + {\bi \omega} _{k - 1} $$where
$${\bi A}({\bi X}_k ) = \left. {\displaystyle{{\partial f\,({\bi X})} \over {\partial {\bi X}}}} \right|_{{\bi X} = {\bi X}_k} = [{\bi 0}_{3 \times 3}, \;{\bi I}_{3 \times 3} ;{\kern 1pt} \;{\bi S}({\bi X}_k ),\;{\bi 0}_{3 \times 3} ]$$
$${\bi S}_k = \left. {\displaystyle{{\partial {\bi \dot v}} \over {\partial {\bi r}}}} \right|_{{\bi r} = {\bi r}_k} $$The corresponding state predicted model is as follows:
$${\bi \tilde X}_k = {\bi \tilde X}_{k - 1} + f\,({\bi \tilde X}_{k - 1}, k - 1)T + {\bi A}({\bi \tilde X}_k )f\,({\bi \tilde X}_{k - 1}, k - 1)\displaystyle{{T^2} \over 2} + {\bi \omega} _{k - 1} $$According to Equations (3) and (6), we can get the corresponding predicted error model as:
$$\delta {\bi X}_k = \delta {\bi X}_{k - 1} + {\bi A}({\bi \tilde X}_k )\delta {\bi X}_{k - 1} T = {\bi \Phi} _k \delta {\bi X}_{k - 1} $$where
$$\delta {\bi X}_k = {\bi X}_k - { {\bi \tilde X}}_k $$
$${\bi \Phi} _k = {\bi I}_{6 \times 6} + {\bi A}({\bi \tilde X}_k )$$2.2. Epoch folding method based on Doppler compensation
Since the pulsar signals are very weak, the EF method is commonly used to enhance the signal to noise ratio (SNR) of the pulse profile. The EF method (Emadzadeh and Speyer, Reference Emadzadeh and Speyer2011a; Sheikh et al., Reference Sheikh, Pines and Ray2006) is as follows:
(1) The X-ray sensor records the time-of-arrival of each individual X-ray photon with respect to the system clock. During the total observation period, a large number of photons, N, will have their arrival times recorded.
(2) This set of photons is then folded at the predicted pulse period based on the known timing model of the pulsar. A binned pulse profile is then constructed by dividing the pulse phase into M equal bins and dropping each of the N photons into the appropriate phase bin.
After the EF procedure, converting time to phase of the pulse period, the TOA is then determined by measuring the phase offset of the observed profile with respect to the high SNR standard profile template. However, due to the motion of the Mars explorer, the pulsar signals TOA is subject to Doppler effects, so we must compensate for Doppler effects.
To reduce the computation load, we compensate the TOA of each X-ray photon with the pulse base. In order to illustrate conveniently, we define the TOA of individual pulse as sub-TOA, while the TOA obtained from the pulse integrated profile is defined as pulse TOA.
Suppose that the ith pulse period is P i, the number of pulses in a pulsar observation period is N p, rend is defined as the explorer's position at the end of observation period, nj is the line-of-sight direction of the jth pulsar, which may be considered constant throughout the solar system since the pulsars are so distant from the solar system. p end is defined as the plane which passes through rend and is perpendicular to nj, the TOA of mth X-ray photon in the ith pulse period at pend and the explorer are τ mi and λ mi, respectively. Figure 1 presents the basic principle of pulsar signal Doppler compensation. As in the kth pulsar period, the Mars explorer moves (nj)TvkPk in the line-of-sight direction of the jth pulsar, the distance from the position of the Mars explorer at the ith pulse period to pend is 
$\sum\limits_{k = i + 1}^{N_p} {(({\bi n}^j )^{\rm T} {\bi v}_k P_k )} $. Thus, the relationship of τ mi and λ mi can be expressed as:
$$\tau _m^i = \lambda _m^i - \sum\limits_{k = i + 1}^{N_p} {\left( {\displaystyle{{({\bi n}^j )^{\rm T} {\bi v}_k P_k} \over c}} \right)} $$where v i is the Mars explorer velocity in the ith pulse period. c is the speed of light.
Figure 1. X-ray pulsar signal Doppler compensation.
As the pulse profile of a pulse period consists of the photons in this pulse period, the compensation adopted by the pulse sub-TOA equals to that of X-ray photon in this pulse period. Suppose that the ith pulse sub-TOAs at pend and the explorer are T i and t i, respectively. The relationship of T i and t i is
$$T_i = t_i - \sum\limits_{k = i + 1}^{N_p} {\left( {\displaystyle{{({\bi n}^j )^{\rm T} {\bi v}_k P_k} \over c}} \right)} $$ Using the orbit dynamic model, the velocity estimation and position estimation at the beginning of the pulsar observation period, we can predict the Mars explorer's velocity in the ith pulse period, 
${\bi \hat v}_i $, and compensate the pulse sub-time-of-arrival with this predicted velocity. The compensated TOA of mth X-ray photon in the ith pulse period at pend is 
$\hat \tau _m^i $:
$$\hat \tau _m^i = \lambda _m^i - \sum\limits_{k = i + 1}^{N_p} {\left( {\displaystyle{{({\bi n}^j )^{\rm T} {\bi \hat v}_k P_k} \over c}} \right)} $$Correspondingly, the ith pulse compensated sub-TOA at pend, 
$\hat T_i $ can be expressed as:
$$\hat T_i = t_i - \sum\limits_{k = i + 1}^{N_p} {\left( {\displaystyle{{({\bi n}^j )^{\rm T} {\bi \hat v}_k P_k} \over c}} \right)} $$The EF method based on Doppler compensation is summarised as follows:
(1) The sensor records the time-of-arrival of each individual X-ray photon.
(2) The time of arrival of each individual X-ray photon is corrected by Equation (12).
${\bi \hat v}_i $ in Equation (12) can be calculated by the fourth-order Runge-Kutta method and the transfer orbit dynamic model.(3) This set of photons is then folded at the predicted pulse period based on the known timing model of the pulsar. A binned pulse profile is then constructed by dividing the pulse phase into M equal bins and dropping each of the N photons into the appropriate phase bin.
2.3. TOA bias model
In the EF method based on Doppler compensation, the velocity prediction error affects sub-TOA accuracy. Next, we analyse this effect.
Suppose that the velocity error in the ith pulse period of the kth pulsar observation period, Δvi, is
$$\Delta {\bi v}_i = {\bi v}_i - {\bi \hat v}_i \approx [{\bi 0}{\kern 1pt} _{3 \times 3} \;{\kern 1pt} {\bi I}_{3 \times 3} ]({\bi I}_{6 \times 6} + {\bi A}({\bi \tilde X}_{k - 1} ) \cdot i \cdot P_0 )\delta {\bi X}_{k - 1} = [{\bi S}_{k - 1} \cdot i \cdot P_0, \;{\bi I}_{3 \times 3} ]\delta {\bi X}_{k - 1} $$Then, the pulse sub-TOA compensation error of the ith pulse period, 
$\Delta \hat T_i $, is:
$$\eqalign{\Delta T_i = & T_i - \hat T_i \cr {\kern 1pt} = & - \sum\limits_{k = i + 1}^{N_p} {\displaystyle{{({\bi n}^j )^{\rm T} \Delta {\bi v}_k} \over c}P_0} \cr {\kern 1pt} = & - \displaystyle{{P_0} \over c}({\bi n}^j )^{\rm T} \left[ {{\bi S}_{k - 1} \cdot \displaystyle{{N_p (N_p + 1) - i(i + 1)} \over 2} \cdot P_0, \;(N_p - i)\;{\bi I}_{3 \times 3}} \right]\delta {\bi X}_{k - 1}} $$As the pulsar profile is integrated with all pulses in the whole pulsar signal observation period, the pulse TOA estimation bias equals the mean of pulse time-of-arrival compensation error of all periods. The pulse TOA bias can be expressed as:
$$\beta _k^j = \displaystyle{1 \over {N_p}} \sum\limits_{i = 1}^{N_p} {\Delta \hat T_i} = - \displaystyle{{({\bi n}^j )^{\rm T}} \over c}\left[ {\displaystyle{{T^2} \over 3}{\bi S}_{_{k - 1}}, {\kern 1pt} \;\displaystyle{T \over 2}{\bi I}_{3 \times 3}} \right]\delta {\bi X}_{k - 1} $$where the observation period T=N pP 0. We can see that this bias is correlated with the velocity estimation error Δv.
Therefore Equation (16) is the pulse TOA measurement bias model with respect to the state estimation error.
3. X-RAY PULSAR NAVIGATION MEASUREMENT
An X-ray pulsar measurement is the difference between the pulse TOAs observed by the X-ray sensor at the Mars explorer and predicted by the pulse-timing model at SSB (solar system barycentre) (Liu et al., Reference Liu, Ma and Tian2010; Reference Liu, Ma, Tian, Kang and White2012). tj and t bj are the pulse TOAs of the jth pulsar at the Mars explorer and at the SSB respectively. nj is the line-of-sight direction vector of the jth pulsar, which may be considered constant throughout the solar system since the pulsars are so distant from the Solar system. r is the position vector of the Mars explorer with respect to the SSB. c is the speed of light. The offset t bj−tj reflects r's projection on nj. The offset to the first order is
$$t\hskip1 _b ^j - t\hskip1 ^j = \displaystyle{1 \over c}({\bi n}^j )^{\rm T} {\bi r}$$Considering the relativistic effects, geometric effects and TOA measurement bias, the time transfer model can be expressed as:
$$\eqalign{t_b^j - (t^j - \beta ^j ) =\, & \displaystyle{1 \over c}({\bi n}^j )^{\rm T} {\bi r} + \displaystyle{1 \over {2cD_0^j}} \left[ { - |{\bi r}|^2 + (({\bi n}^j )^{\rm T} {\bi r})^2 - 2{\bi b}^{\rm T} {\bi r} + 2({\bi b}^{\rm T} {\bi r})(({\bi n}^j )^{\rm T} {\bi r})} \right] \cr & + \displaystyle{{2\mu _{Sun}} \over {c^3}} \ln \left| {\displaystyle{{({\bi n}^j )^{\rm T} {\bi r} + |{\bi r}|} \over {({\bi n}^j )^{\rm T} {\bi b} + |{\bi b}|}} + 1} \right|} $$where D 0j is the range from the jth pulsar to the SSB, b is the position of the SSB relative to the Sun, μ Sun is the gravitational constant of the Sun. The second and third terms on the right-hand side of Equation (18) are referred to as Roemer delay. The fourth term is the Shapiro delay effect. Equation (18) can be also represented as:
$$\eqalign{c(t_b^j - t^j ) =\, & ({\bi n}^j )^{\rm T} {\bi r} + \displaystyle{1 \over {2D_0^j}} [ - |{\bi r}|^2 + (({\bi n}^j )^{\rm T} {\bi r})^2 - 2{\bi b}^{\rm T} {\bi r} + 2({\bi b}^{\rm T} {\bi r})(({\bi n}^j )^{\rm T} {\bi r})] \cr & + \displaystyle{{2\mu _{Sun}} \over {c^2}} \ln \left| {\displaystyle{{({\bi n}^j )^{\rm T} {\bi r} + |{\bi r}|} \over {({\bi n}^j )^{\rm T} {\bi b} + |{\bi b}|}} + 1} \right| - c\beta ^j} $$Suppose that the TOA measurement Yk=[c(t b1−t 1), c(t b2−t 2), …, c(t bnum−tnum)] and measurement noise ξ=[ς1, ς2, …, ςnum]T, where c(t bj−tj) and ςj are the measurement and noise of the jth pulsar respectively, num is the number of the adopted pulsars. The measurement model can be presented as:
$${\bi Y}_k = h({\bi X}_k, k) + {\bi B}_k + {\bi \xi} _k $$where the TOA bias matrix B k can be expressed as:
$$\eqalign{{\bi B}_k = & [ - c\beta _k^1, - c\beta _k^2, \ldots, - c\beta _k^{num} ] = {\bi n}^T \left[ {\displaystyle{{T^2} \over 3}{\bi S}_k, \displaystyle{T \over 2}{\bi I}} \right]\delta {\bi X}_{k - 1} \cr & = {\bi n}^T \left[ {\displaystyle{{5T^2} \over 6}{\bi S}_k, \displaystyle{T \over 2}{\bi I} + \displaystyle{{T^3} \over 3}{\bi S}_k} \right]\delta {\bi X}_{k - 1}} $$where
$${\bi n} = [{\bi n}^1, {\bi n}^2, \ldots, {\bi n}^{num} ]$$h(Xk, k)=[h 1(Xk, k), h 2(Xk, k), … hnum(Xk, k)]T, hj(Xk, k) is the measurement equation of the jth pulsar, and can be expressed as:
$$\eqalign{h^j ({\bi X}_k, k) =\, & ({\bi n}^j )^{\rm T} {\bi r} + \displaystyle{1 \over {2D_0^j}} [ - |{\bi r}|^2 + (({\bi n}^j )^{\rm T} {\bi r})^2 - 2{\bi b}^{\rm T} {\bi r} + 2({\bi b}^{\rm T} {\bi r})(({\bi n}^j )^{\rm T} {\bi r})] \cr & + \displaystyle{{2\mu _{Sun}} \over {c^2}} \ln \left| {\displaystyle{{({\bi n}^j )^{\rm T} {\bi r} + |{\bi r}|} \over {({\bi n}^j )^{\rm T} {\bi b} + |{\bi b}|}} + 1} \right|} $$where j = 1, 2, …, num.
It is important to determine the pulse TOA with an accuracy that is determined by the SNR of the profile and not by the time resolution. The method given by Taylor (Xie et al., Reference Xie, Xu, Zhang and Luo2012) is independent of time resolution, where a pulse TOA is generated by comparing an observed profile with high SNR standard template profile. The standard variance σj of ςj can be calculated as follows (Sheikh et al., Reference Sheikh, Pines and Ray2006):
$$\sigma ^j = \displaystyle{{Wc\sqrt {[B_X + F_X (1 - p_f )]d + F_X p_f}} \over {2F_X \sqrt {AT} p_f}} $$where B X is the X-ray background radiation flux, F X is the radiation photon flux from X-ray pulsar, p f is the ratio of the pulse radiation flux to the average radiation flux in a pulse period, A is the area of the X-ray sensor, T is the pulsar signals observation period, W is the width of the pulse, d is the ratio of the pulse width to the pulse period, c is the speed of light.
4. CLOSED-LOOP EKF
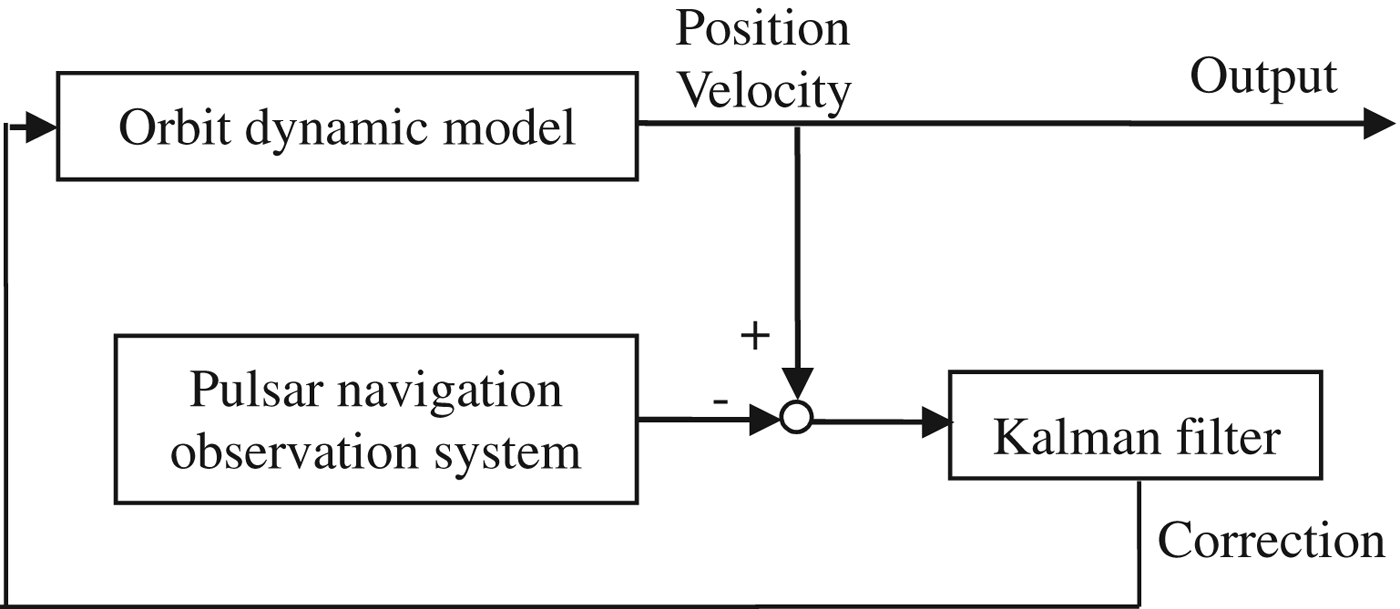
Considering the fact that the TOA measurement is related with the state error, we adopt the closed-loop EKF (Qiao et al., Reference Qiao, Liu, Zheng and Xiong2010), where the state predicted error is utilised as the novel state estimation.
Suppose that we have a system given by
$$\delta {\bi X}_k = {\bi \Phi} _k \delta {\bi X}_{k - 1} + {\bi \omega} _{k - 1} $$
$$\delta {\bi Y}_k = {\bi H}_k \delta {\bi X}_k + {\bi \delta} _k $$The error measurement considering the Doppler effects, δYk, can be expressed as:
$$\eqalign{\delta {\bi Y}_k =\, & {\bi Y}_k - h({\bi \tilde X}_k, k) \cr =\, & [{\bi n},{\kern 1pt} \;{\bi 0}_{3 \times 3} ]\delta {\bi X}_k + {\bi B} + {\bi \xi} \cr =\, & {\bi n}^{\rm T} \left[ {{\bi I}_{3 \times 3} + \displaystyle{{5T^2} \over 6}{\bi S}_{k - 1}, {\kern 1pt} \;\displaystyle{T \over 2}{\bi I}_{3 \times 3} + \displaystyle{{T^3} \over 3}{\bi S}_{k - 1}} \right]\delta {\bi X}_k + {\bi \xi} \cr =\, & {\bi H}_k \delta {\bi X}_k + {\bi \xi}} $$where
$${\bi H}_k = {\bi n}^{\rm T} \left[ {{\bi I}_{3 \times 3} + \displaystyle{{5T^2} \over 6}{\bi S}_{k - 1}, {\kern 1pt} {\kern 1pt} {\kern 1pt} \displaystyle{T \over 2}{\bi I}_{3 \times 3} + \displaystyle{{T^3} \over 3}{\bi S}_{k - 1}} \right]$$When the spacecraft is in the transfer orbit, the value of S is very large. In this condition, we can adopt the simplified measurement matrix as:
$${\bi H}_k = {\bi n}^{\rm T} \left[ {{\bi I}_{3 \times 3}, {\kern 1pt} {\kern 1pt} {\kern 1pt} \displaystyle{T \over 2}{\bi I}_{3 \times 3}} \right]$$Equation (27) is the measurement model with the Doppler effects.
The principle of the closed-loop correction filter is shown in Figure 2. The equations for the closed-loop extended Kalman filter are shown as:
$${\bi P}_k^ - = {\bi \Phi} _{k - 1} {\bi P}_{k - 1}^ + {\bi \Phi} _{k - 1}^T + {\bi Q}_{k - 1} $$
$${\bi K}_k = ({\bi P}_k^ - {\bi H}_k^{\rm T} )({\bi H}_k {\bi P}_k^ - {\bi H}_k^{\rm T} + {\bi R}_k )^{ - 1} $$
$$\delta {\bi X}_k = {\bi K}_k \delta {\bi Y}_k $$
$${\bi P}_k^ + = {\bi P}_k^ - - {\bi K}_k {\bi H}_k {\bi P}_k^ - $$
$${\bi X}_k^ + = {\bi X}_k^ - + \delta {\bi X}_k $$
Figure 2. Principle of closed-loop correction.
5. SIMULATION RESULTS
In order to demonstrate the feasibility and effectiveness of the proposed navigation system, we show the simulation results in this section. The simulation conditions are shown as follows.
We adopt two orbits: (a) The orbit of the American Mars Pathfinder, which launched on 4 December 1996 at 06:58:10·00 UT. The initial orbit elements of the American Mars Pathfinder are shown in Table 1. The simulation time is from 1 Mar 1997 00:00:00·00 UT to 2 Mar 1997 00:00:00·00 UT. (b) The orbit of the Mars satellite, whose initial orbit elements are shown in Table 2. The simulation time is 10 days. The two orbits of the Mars explorer are simulated with the Satellite Tool Kit (STK), which takes the perturbation effects into account.
Table 1. Initial orbital elements of the American Mars Pathfinder.
Table 2. Initial orbital elements of the Mars satellite.
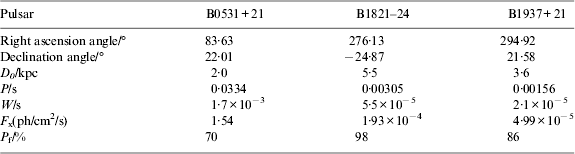
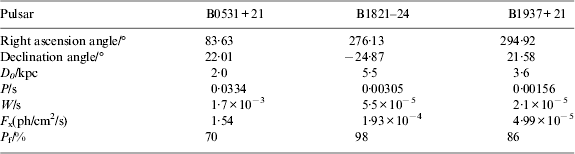
The measurement noise standard covariance of the jth pulsar can be calculated as Equation (24). The X-ray background radiation flux is assumed as 0·005 ph/cm2/s. That value was chosen based on the empirical research done at the Naval Research Laboratory (Dennis, Reference Dennis2005). The area of the X-ray sensor is 1 m2. The creation of a catalogue of pulsars is most useful for deep space navigation. In this paper, three commonly used pulsars, whose figures of merit are highest in all pulsars, are adopted, and the parameters of those pulsars are shown as Table 3.
Table 3. Parameters of pulsars.
The other parameters of the filter are shown as Table 4. The experiments were carried out on an Acer TravelMate 8572 TG Notebook with a CPU clock rate of 2·4 GHz and a memory of 2 GB.
Table 4. Parameters of navigation filter.
5.1. Mars satellite obit
We investigate the performance of closed-loop EKF-MMDE and the traditional closed-loop EKF. Figure 3 shows the performance comparison of these two navigation methods using the same simulation conditions described above. As the results in Figure 3 demonstrate, the two methods can converge very well for a Mars probe orbit, and the closed-loop EKF-MMDE performs considerably better. Table 5 shows the comparison between the traditional closed-loop EKF and the closed-loop EKF-MMDE over 100 Montè-Carlo trials. It can be seen that compared with the traditional closed-loop EKF, the closed-loop EKF-MMDE shows 64% and 62% improvement for the Mars explorer's position and velocity, respectively. The closed-loop EKF-MMDE has an approximately 11% increase in calculation time compared with the traditional one. For one step, the computation time of closed-loop EKF-MMDE increases by 11·6 us. This value is negligible compared with the filtering period of several hundred seconds. The reason is that the closed-loop EKF-MMDE uses the TOA measurement model considering the Doppler effects, and the computational load of the closed-loop EKF-MMDE is more than that of the closed-loop EKF by only one matrix S computation and two matrix accumulations. From these results, we can see that the closed-loop EKF-MMDE improves the navigation performance obviously under the condition of the Doppler effects.
Figure 3. Estimation error of the two navigation methods.
Table 5. Comparison between the traditional closed-loop EKF and the closed-loop EKF-MMDE.
Next, we investigate the impact of the X-ray sensor's area on both the closed-loop EKF-MMDE and the traditional closed-loop EKF. Figure 4 represents the simulation results with different areas of sensor over 100 Montè-Carlo trials. We can see that the performance of the two methods improves with enlarging the area of X-ray sensor, and the closed-loop EKF-MMDE method outperforms the traditional one with the same area. It is interesting to note that when the two methods reach the same accuracy, the area adopted by the closed-loop EKF-MMDE-based navigation is less than that of closed-loop EKF-based one. For instance, in order to reach 6000 m, the closed-loop EKF-MMDE-based navigation requires three X-ray sensors with 3×4000 cm2 area, while the traditional closed-loop EKF-based method needs three X-ray sensors with 3×13000 cm2. The novel closed-loop EKF-based navigation method saves 3×9000 cm2 and decreases the cost and the weight of the Mars explorer effectively.
Figure 4. Estimation error with different area of X-ray sensor.
Finally, we investigate the impact of the filtering period on both the novel closed-loop EKF-MMDE and the traditional closed-loop EKF method. Figure 5 represents the simulation results with different filtering periods over 100 Montè-Carlo trials. We can see that the accuracy of the traditional closed-loop EKF declines with the increase of filtering periods greatly, while the accuracy variation of closed-loop EKF-MMDE is very small. The closed-loop EKF-MMDE method outperforms the traditional one with the same observation period. The reason is that with the increase of observation period, the TOA bias increases, the traditional closed-loop EKF cannot resist the TOA bias, while the closed-loop EKF-MMDE is robust to the TOA bias.
Figure 5. Estimation error with different observation period.
When the X-ray sensor with small area is adopted, the number of received X-ray photons per unit time decreases greatly. In order to obtain high SNR pulsar profile, the pulsar signals observation period must be lengthened. Under this condition, the closed-loop EKF-MMDE works very well, while the closed-loop EKF does not. In brief, the closed-loop EKF-MMDE is well suited for small-area X-ray sensors.
5.2. Earth-Mars transfer obit
In this section, we investigate the performance of the closed-loop EKF and the traditional EKF in the Earth-Mars transfer orbit. When we choose Q as the state process noise covariance of the traditional EKF, the EKF cannot converge very well. The reason is that the EKF performance is affected by the correlated TOA measurement noise. Therefore, we should choose a larger Q. From a lot of simulation results, we find that when a Q of 25 is adopted, the EKF can converge very well and the estimation accuracy is high. Figure 6 shows the performance comparison of these two navigation methods using the same simulation conditions described above. As the results in Figure 6 demonstrate, the two methods can converge very well, and the closed-loop EKF-MMDE performs considerably better. Table 6 shows the comparison between the traditional EKF and the EKF-MMDE over 100 Montè-Carlo trials. It can be seen that compared with the traditional closed-loop EKF, the closed-loop EKF-MMDE shows 35% and 50% improvement for the Mars explorer's position and velocity, respectively. The closed-loop EKF-MMDE has the same calculation time as the traditional closed-loop EKF. The reason is that the closed-loop EKF-MMDE can deal with the influence of Doppler effects very well via the improvement of measurement model. In the transfer orbit, the simplified measurement model is adopted, which does not increase the computational load.
Figure 6. Estimation error of the two navigation methods.
Table 6. Comparison between the traditional EKF and the EKF-MMDE.
6. CONCLUSION
In this paper, pulsar navigation for the Mars explorer resistant against Doppler effects is proposed. In the pulsar signals observation period, the Doppler velocity predicted by the orbit dynamic model and the prior information is utilized to compensate the X-ray photon time-of-arrival. However, there is a bias caused by the Doppler compensation in the TOA estimation, and the bias is correlated with the state estimation error. To solve this problem, we build the TOA measurement model with the Doppler effects, and utilise the closed-loop EKF-MMDE as the navigation filter. Compared with the traditional closed-loop EKF, the closed-loop EKF-MMDE clearly improves the navigation performance with a negligible computational load.
This X-ray pulsar navigation system has the following virtues: (1) navigation is completely autonomous; (2) it is able to resist the Doppler effects and has high accuracy; (3) it realizes real-time Doppler compensation and state estimation; (4) it works very well with a small-area X-ray sensor. Therefore, this pulsar navigation system is suited for Mars exploration.
ACKNOWLEDGEMENTS
This work was supported by the State Key Program of National Natural Science of China (grant number 61233005), Specialized Research Fund for the Doctoral Program of Higher Education (grant number 20124219120002), Scientific Research Program Funded by Hubei Provincial Education Department (grant number Q20131110) and Natural Science Foundation of Hubei Province of China (grant number 2013CFB333).
