1. INTRODUCTION
The nonlinear interaction of high power lasers with high-density plasmas has been a subject of active research for decades due to its relevance to laser driven fusion (Kruer, Reference Kruer2000; Bruckner & Jorna, Reference Bruckner and Jorna1974). The increasing use of high power laser beams in various applications has worldwide interest in laser-plasma interaction (Borghesi et al., Reference Borghesi, KAr, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccherini, Cecchetti, Futchs, Galimberti, Gizzi, Grismayer, Lyseikina, Jung, Macchi, Mora, Osterholtz, Schiavi and Willi2007; Laska et al., Reference Laska, Jungwirth, Krasa, Krousky, Pfeifer, Rohlena, Velyhan, Ullschmied, GAmmino, Torrisi, Badziak, Parys, Rosinski, Ryc and Wolowski2008; Dromey et al., Reference Dromey, Bellei, Carroll, Clarke, Green, Kar, Kneip, Markey, Nagel, Willingale, Mckenna, Neely, Najmudin, Krushelnick, Norreys and Zepf2009) in the nonlinear regime. In collisionless plasmas, the nonlinearity arises through the ponderomotive force-induced redistribution of plasma. It is well known that various laser-plasma instabilities like, filamentation (Kaw et al., Reference Kaw, Schmidt and Wilcox1973; Young et al., Reference Young, Baldis, Drake, Campbell and Estrabrook1988; Deutsch et al., Reference Deutsch, Bret, Firpo, Gremillet, Lefebrave and Lifschitz2008), harmonic generation (Ozoki et al., Reference Ozoki, Bom Elouga, Ganeev, Kieffer, Sazuki and Kuroda2007; Baeva et al., Reference Baeva, Gordienko and Pukhov2007; Dombi et al., Reference Dombi, Racz and Bodi2009), stimulated Raman scattering (SRS) (Kline et al., Reference Kline, Montgomery, Rousseaux, Baton, Tassin, Hardin, Flippo, Johnson, Shimada, Yin, Albright, Rose and Amiranoff2009; Bers et al., Reference Bers, Shkarofsky and Shoucri2009), and stimulated Brillouin scattering (SBS) (Huller et al., Reference Huller, Masson-Laborde, Pesme, Labaune and Bandulet2008; Hasi et al., Reference Hasi, Gong, Lu, Lin, He and Fan2008; Kappe et al., Reference Kappe, Strasser and Ostermeyer2007; Wang et al., Reference Wang, Lu, He, Zheng and Zhao2009) might be generated from the interaction of laser pulses with plasmas. These instabilities affect the laser-plasma coupling efficiency and SRS can even produce energetic electrons (Estrabrook et al., Reference Estrabrook, Kruer and Lasinski1980), which can preheat the fusion fuel and change the compression ratio. Most of the theories of stimulated scattering and harmonic generation are based on the assumption of a uniform laser pump. This is contrary to almost all the experimental situations, where laser beams of finite transverse size, having non-uniform intensity distribution along their wavefront, are used. Such beams may modify the background plasma density and suffer filamentation (self-focusing). The non-uniformity in the intensity distribution of the laser also affects the scattering of a high power laser beam.
SBS is a parametric instability (Drake et al., Reference Drake, Kaw, Lee, Schmidt, Liu and Rosenbluth1974; Hüller, Reference Hüller1991) in plasma in which an electromagnetic wave (ω0, k 0) interacts with an ion acoustic wave (ω, k) to produce a scattered electromagnetic wave (ωs, k s). SBS has been a concern in inertial confinement fusion (ICF) application because it occurs up to the critical density layer of the plasma and affects the laser plasma coupling efficiency. SBS produces a significant level of backscattered light; therefore, it is important to devise techniques to suppress SBS. In plasmas of heavy ions, this could be accomplished by introducing a small fraction of light ion species that could incur heavy Landau damping in the IAW and suppresses the SBS (Baldis et al., Reference Baldis, Labaune, Moody, Jalinaud and Tikhonchuk1998; Fernandez et al., Reference Fernandez, Cobble, Failor, Dubois, Montgomery, Rose, Vu, Wilde, Wilde and Chrien1996).
Little agreement between theory (Baldis et al., Reference Baldis, Villeneuve, Fontaine, Enright, Labaune, Baton, Mounaix, Pesme, Casanova and Rozmus1993; Baton et al., Reference Baton, Rousseaux, Mounaix, Labaune, Fontaine, Pesme, Renard, Gary, Jacquet and Baldis1994) and experiments (Chirokikh et al., Reference Chirokikh, Seka, Simon, Craxton and Tikhonchuk1998) has been reported so far, in spite of intensive studies of SBS during the last two decades in both fields. Most of the earlier studies (on the discrepancy between theoretical expectations and experimental results) are focused with the saturation effects of SBS-driven IAW, such as kinetic effects, harmonic generation, and decay into sub-harmonic IAW components. But it has been shown recently (Myatt et al., Reference Myatt, Pesme, Huller, Maximov, Rozmus and Capjack2001; Fuchs et al., Reference Fuchs, Labuane, Depierreux, Baldis, Michard and James2001) that due to self-focusing, the laser pump beam looses coherence when propagating into the plasma. This incoherence could act as another potential saturation mechanism for the SBS instability. For such cases, when induced incoherence reduces SBS, the nonlinear saturation effects studied in the past may be of minor importance, because plasma waves stay at relatively low amplitudes. Recently, Huller et al. (Reference Huller, Masson-Laborde, Pesme, Labaune and Bandulet2008) did the numerical simulation in two dimensions to support this idea. The spatial incoherence in the pump laser beam due to filamentation instability (self-focusing) and non-monotonous flow, cause an inhomogeneity and the SBS decreases. In their simulation, IAW amplitudes were kept small (around 1%) so that the traditionally assumed nonlinear saturation mechanisms of SBS through nonlinear IAW can be neglected.
Giulietti et al. (Reference Giulietti, Macchi, Schifano, Biancalana, Danson, Giulietti, Gizzi and Willi1999) have measured the stimulated Brillouin back scattering from the interaction of a laser pulse with preformed, inhomogeneous plasma in conditions favorable to self-focusing. Spectral and temporal features of the reflectivity suggest a strong effect of self-focusing on back-SBS. Baton et al. (Reference Baton, Amiranoff, Malka, Modena, Salvati and Coulaud1998) have experimentally shown the dependence of the SBS reflectivity on both the focusing aperture and the incident laser intensity for millimeter size, homogeneous, stationary plasmas. Baldis et al. (Reference Baldis, Labaune, Moody, Jalinaud and Tikhonchuk1998) have given the experimental evidence of the transverse localization of SBS emission to the laser beam axis, demonstrating that only a few small regions of plasma contribute to the emission. As a consequence, SBS reflectivity of these regions is much higher than the average SBS reflectivity, by a factor of 50–100. Eliseev et al. (Reference Eliseev, Rozmus, Tikhonchuk and Capjack1996) have shown that the SBS reflectivity from a single laser hot spot is much lower than that predicted by a simple three wave coupling model because of the diffraction of the scattered light from the spatially localized IAW.
In this article, we have studied the effect of self-focusing and localization of IAW on SBS process (as a specific case, backscattering, for which k = 2k 0), using paraxial ray approximation. The nonlinear coupling between the filamented laser beam and ion acoustic wave results in the modification of the Eigen frequency of IAW; consequently, enhanced Landau damping of IAW and a modified mismatch factor in the SBS process occur. Due to enhanced Landau damping, there is a reduction in intensity of IAW, and the SBS process gets suppressed.
In our present work also, the level of IAW amplitude (after nonlinear coupling between IAW and laser beam) is around 1%. Our work goes one step ahead from the Huller et al. (Reference Huller, Masson-Laborde, Pesme, Labaune and Bandulet2008) simulation, and highlights the underlying possible physical process of this SBS saturation. This physical process involves the localization of IAW due to nonlinear coupling between pump laser beam (filamented/self-focused) and IAW due to ponderomotive nonlinearity (Sodha et al., Reference Soadha, Mishra and Mishra2009). As a consequence, the Landau damping of IAW increases and hence the SBS reflectivity is suppressed. Therefore, the present work takes into account the mechanism proposed by Huller et al. (Reference Huller, Masson-Laborde, Pesme, Labaune and Bandulet2008) in their simulation and IAW localization also for the saturation of SBS.
The article is organized as follows: In Section 2, we give the brief summary of the basic equations of the propagation of laser beam. The modified equations for the excitation of IAW are studied in the Section 3. The effect of localization of the IAW is also presented in the same section. In Section 4, we derive the basic equations that govern the dynamics of SBS process and SBS reflectivity. The important results and conclusions based on the present investigation are presented in the last section.
2. EQUATION OF LASER BEAM PROPAGATION
A high power Gaussian laser (pump) beam of frequency ω0 and the wave vector k 0 is considered to be propagating in hot collisionless and homogeneous plasma along the z axis. When a laser beam propagates through the plasma, the transverse intensity gradient generates a ponderomotive force, which modifies the plasma density profile in the transverse direction as (Sodha et al., Reference Sodha, Ghatak and Tripathi1976)
where
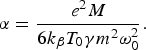
e and m are the electronic charge and mass, M and T 0 are, respectively, mass of ion and equilibrium temperature of the plasma. N 0e is the electron concentration in the presence of the laser beam, N 00 is the electron density in the absence of the beam, k β is the Boltzman's constant and γ is the ratio of the specific heats.
The wave equation for the pump laser beam has been solved using Wentzel-Kramers-Brillouin approximation and paraxial-ray approximation, and the electric field of the pump laser beam can be written as (Sodha et al., Reference Sodha, Ghatak and Tripathi1976; Akhamanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968)
![E = E_{00} \exp \left\{i\left[\omega_0 t - k_0 \left(S_0 + z\right)\right]\right\}\comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn2.gif?pub-status=live){kind=small}
where wave number and Eikonal of the beam is given as
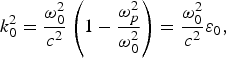
The intensity distribution of the laser beam for z > 0 may be written as (Akhamanov et al., 1968)
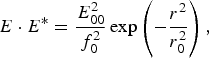
where E 00 is the axial amplitude, r 0 is the initial beam width, r refers to the cylindrical coordinate system and ε0 = (1−ωp2/ω02) is the linear part of the plasma dielectric constant. ωp is the electron plasma frequency, and f 0 is the dimensionless beam width parameter, satisfying the boundary conditions: f 0 |z =0 = 1 and df 0/dz |z=0 = 0, governed by the equation (Sodha et al., Reference Sodha, Ghatak and Tripathi1976)
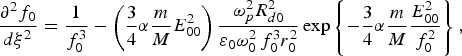
where R d0 = k 0r 02 is the diffraction length and ξ = z/R d0 is the dimensionless parameter. The density of the plasma varies through the channel due to the ponderomotive force. Therefore, the refractive index increases and the laser beam get focused in the plasma. Eq. (4) gives the intensity profile of the laser beam in the plasma, which is shown in Figure 1, using the following parameters in numerical calculation: the incident laser intensity equals α E 002 = 1.22 (laser power flux = 1016 W/cm2), r 0 = 12 µm, n/n cr = 0.1, and (T e/T i) = 10.
Fig. 1. (Color online) Variation in laser beam intensity with normalized distance (ξ = z/R d0) and radial distance (r) for laser power α E 002 = 1.22 and r 0 = 11.5 µm.
3. LOCALIZATION OF ION ACOUSTIC WAVE
Nonlinear interaction of an ion acoustic wave with the laser beam filaments leads to its excitation. To analyze this excitation process of IAW in the presence of ponderomotive nonlinearity and filamented laser beam, we use the fluid model as
The electric field E si is associated with the IAW and satisfies the Poisson's equation,
Where n es is given by
![n_{es} = n_{is} \left[1 + {k^2 \lambda_d^2 \over \lpar N_{0e}/N_{00}\rpar }\right]^{-1}. \eqno \lpar 9\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn9.gif?pub-status=live)
The Landau damping coefficient for IAW is given by (Krall & Trivelpiece, Reference Krall and Trivelpiece1973)
![\eqalignno{2\Gamma_i &= {k \over \lpar 1 + k^2 \lambda_d^2\rpar } \left({\pi k_\beta T_e \over 8M}\right)^{{{1 /2}}} \cr &\quad \times \left[\left({m \over M}\right)^{1/2} + \left({T_e \over T_i}\right)^{3/2} \exp \left(-{T_e/T_i \over \lpar 1 + k^2 \lambda_d^2\rpar }\right)\right]\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn10.gif?pub-status=live)
where T e and T i are electron and ion temperatures, V is is the ion fluid velocity, λd = (k βT 0/4π N 00e 2)1/2 is the Debye length, and v thi = (k βT i/M)1/2 is the thermal velocity of ions. Combining Eqs. (6), (7), and (9) and assuming that the plasma is cold i.e., v thi2 ≪ c s2, one obtains the general equation governing the ion density variation
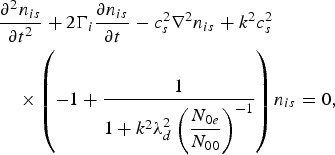
where c s = (k βT e/M)1/2 is the speed of the IAW for T e ≫ T i. The solution of the above equation can be written as
![n_{is} = n\lpar r\comma \; z\rpar \exp \left\{i\left[\omega t - k \lpar z + s\lpar r\comma \; z\rpar \rpar \right]\right\}\comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn12.gif?pub-status=live){kind=small}
here s is the Eikonal for IAW. The frequency and wave number of the IAW satisfy the following dispersion relation in the presence of laser beam
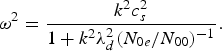
Substituting Eq. (12) into Eq. (11) and separating the real and imaginary parts, one obtains, the real part as
![\eqalignno{&2\left({\partial s \over \partial z}\right)+ \left({\partial s \over \partial r}\right)^2 = {1 \over nk^2} \left[{\partial^2 n \over \partial r^2} + {1 \over r} {\partial n \over \partial r}\right]+ {\omega^2 \over k^2 c_s^2} \cr &\quad + \left[1 - {1 \over 1 + k^2 \lambda_d^2 \lpar N_{0e}/N_{00}\rpar ^{-1}}\right]}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn14a.gif?pub-status=live)
and imaginary part as
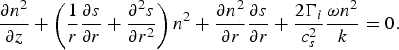
To solve the coupled Eqs. (14a) and (14b), we assume the initial radial variation of IAW density perturbation to be Gaussian, and the solution at finite z may be written as
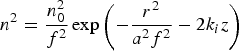
and
where k i = Γiω/kc s2, is the damping factor, f is a dimensionless beam width parameter and a is the initial beam width of the acoustic wave. We have used the following boundary conditions: df/dz = 0, f = 1 at z = 0. Using Eq. (15) in Eq. (14a) and equating the coefficients of r 2 on both sides, we obtain the following equation governing f
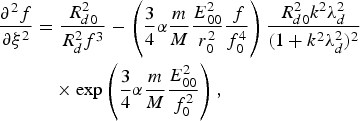
where R d = ka 2 is the diffraction length of the IAW. Eq. (16) represents the density profile of IAW in the plasma when the coupling between self-focused (filamented) laser beam and IAW is taken into account. It is interesting to compare Eq. (16) with Eq. (5) i.e., self-focusing of laser pump wave. In the absence of the coupling between the laser beam and acoustic wave, the second term in Eq. (16) is zero and the solution of Eq. (16) is given by
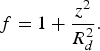
Thus propagating a distance R d, the width a is enlarged by 
and the axial amplitude of density perturbation in IAW is decreased by the same factor even in the absence of Landau damping.
We can, however, obtain an analytical solution of Eq. (16) in special case. When the laser beam has the critical power for self-focusing, the diffraction term (the first term on the right-hand-side of Eq. (5)) balances the nonlinear term in Eq. (5). Under such conditions (f 0 = 1), the main beam propagates without convergence and divergence and is generally known as the uniform waveguide mode. Therefore, the solution for f is given by
where
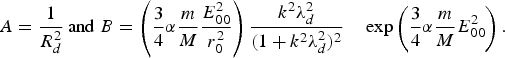
Therefore, the amplitude of IAW (given by Eq. (15a)), which depends on f will be oscillating with z due to this nonlinear coupling, hence the IAW gets localized.
When the power of laser beam is greater than the critical power for self-focusing, we have solved Eq. (15a) numerically with the help of Eq. (16) to obtain the density perturbation at finite z. The result is shown in Figure 2a, for typical laser parameters as we have used in previous section. It is evident from the figure that the IAW gets excited due to nonlinear coupling with the high power laser beam because of the ponderomotive nonlinearity. If we take the zero Landau damping of IAW, we get the structure having the amplitude varying periodically with the z coordinate as shown in Figure 2c.
Fig. 2. (Color online) Variation in IAW intensity with normalized distance (ξ = z/R d0) and radial distance (r), for a = 19 µm, (a) with Initial Landau damping (Γi/ω) = 0.0142 (b) with modified Landau damping (Γi/ω) = 0.0155 (c) with zero Landau damping.
The localization may be understood as follows: Because of the ponderomotive force exerted by the pump laser beam, the electrons are redistributed from the axial region. According to the dispersion relation ω2 = k 2c s2/(1 + k 2λd2 (N 0e/N 00)−1), the phase velocity ω/k of the acoustic wave has a minimum on the axis and is increasing away from the axis. If we consider the initial wavefront of the electrostatic wave, the secondary wavelets travel with minimum velocity along the axis and with higher velocity away from the axis. As the wavefront advances in the plasma, focusing occurs, and the amplitude of the density perturbation increases. When the size of the wave front reduces considerably, diffraction effects also become important and hence the amplitude of the density perturbation starts to decrease.
We can calculate the periodicity length L of localized structures by putting r = 0 in Eq. (15a), as shown in Figure 3. According to Figure 3, value of L comes out to be 2.62R d0. If we take the fast Fourier transform (FFT) of the structure as shown in Figure 3, we get the spectral lines in one structure at a separation of k A = 2π/L, and the value of k A is coming out to be 2.4 R d0−1. We have shown these structures in Figure 4a. These periodic localized structures are similar to the structures in a periodic potential well. This situation can be modeled by representing Eq. (11) in the form of Mathew's equation in a periodic potential well. Therefore, taking the density variation as e iωt in Eq. (11), one can write
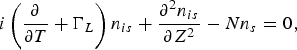
here,
where μ represents the dimensionless amplitude of the density perturbation in k-space. The normalized density of the first spectral component in Figure 4a is 5.801, which is at a distance of k A from the central component. The value of μ2 comes out to be μ2 = (N k2/N 002) = 0.0058, in which we have used the seed value of IAW(N 02/N 002) = 10−3. If n is is of the form 
, then we may write Eq. (17) in the form of Eigen value equation (Rozmus et al., Reference Rozmus, Sharma, Samson and Tighe1987)
Fig. 3. (Color online) Variation in IAW intensity with normalized distance (ξ) in real space at r = 0 corresponding to Figure 2.
Fig. 4. (Color online) Comparison of Power spectrum of IAW, for α E 002 = 1.6 (a) with Initial Landau damping (Γi/ω) = 0.0142 (b) with modified Landau damping (Γi/ω) = 0.0155.
We assume the solution of Eq. (19) in the form of Bloch wave function as
![\psi = \sum\limits_n \exp \left[i \left(k + nk_A\right)Z\right]\psi_n. \eqno \lpar 20\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn20.gif?pub-status=live){kind=small}
Substituting this solution in Eigen value Eq. (19), we obtain the equation
and
where
keeping only ψ0, ψ±1 components, we obtain (Rozmus et al., Reference Rozmus, Sharma, Samson and Tighe1987) for Λ = Λ1 + iΛ2,
where the effective damping 
is
and mismatch factor has the form
Eqs. (22) and (23) give the expression for modified frequency and enhanced Landau damping of the IAW, respectively. The value of the enhanced Landau damping is 0.0155, whereas the initial damping value was 0.0142. Therefore, we have approximately 10% increment in Landau damping of IAW, and the mismatch factor in Eigen frequency is coming out to be 0.0338. It is obvious that Landau damping governs the intensity of the IAW, and due to localization of IAW, the effective damping of the acoustic wave increases, therefore, as a result, the intensity of IAW reduces accordingly, as shown in Figure 2b. The enhanced Landau damping effect is also observable in the modified spectra of the IAW, as shown in Figure 4b.
4. STIMULATED BRILLOUIN SCATTERING
The high frequency electric field E T, satisfies the wave equation
where J T is the total current density vector in the presence of the high frequency electric field E T and it is given by
E T may be written as the sum of the electric field E of the pump laser beam and of the electric field E S of the scattered wave, i.e.,
Substituting Eqs. (26) and (27) into Eq. (25), and separating the equation for pump and scattered field
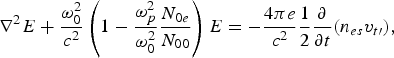
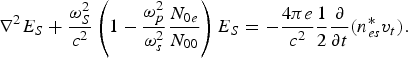
In solving Eq. (28b), the term ∇(∇×E T) may be neglected in the comparison to the ∇2E S term, assuming that the scale length of variation of the dielectric constant in the radial distance is much larger than the wavelength of the pump wave. Substituting 
in Eq. (28b), one obtains
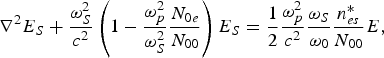
let the solution of Eq. (29) be
where 
and k s1 and ωs satisfy the matching conditions
Using Eq. (30) in Eq. (29), one gets
![\eqalignno{&-k_{S0}^2 E_{S0} + 2ik_{S0} {\partial E_{S0} \over \partial z} + \left({\partial \over \partial r^2} + {1 \over r} {\partial \over \partial r}\right)E_{S0} \cr &\quad + {\omega_S^2 \over c^2} \left[\varepsilon_{S0} + {\omega_p^2 \over \omega_S^2} \left(1 - {N_{0e} \over N_{00}}\right)\right]E_{S0} = 0\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn31.gif?pub-status=live)
![\eqalignno{&- k_{S1}^2 E_{S1} + \lpar \!-\!2ik_{S1}\rpar {\partial E_{S1} \over \partial z} + \left({\partial \over \partial r^2} + {1 \over r} {\partial \over \partial r}\right)E_{S1} \cr &\quad + {\omega_S^2 \over c^2} \left[\varepsilon_{S0} + {\omega_p^2 \over \omega_S^2} \left(1 - {N_{0e} \over N_{00}}\right)\right]E_{S1} \cr &\quad ={1 \over 2} {\omega_p^2 \over c^2} {\omega_S \over \omega_0} {n_{es}^{\ast} \over N_{00}} E_0 \exp \lpar \!- \!ik_0 s_0\rpar \comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn32.gif?pub-status=live)
to a good approximation, the solution of Eq. (32) may be written as
substituting this into Eq. (32), one obtains
![E_{S1}^{\prime} = - {1 \over 2} {\omega_p^2 \over c^2} {n^{\ast} \over N_0} {\omega_S \over \omega_0} {E_0 \over \left[k_{S1}^2 - k_{S0}^2 - \displaystyle{{\omega_p^2 \over c^2}} \left(1 - \displaystyle{{N_{0e} \over N_0}}\right)\right]}. \eqno \lpar 34\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn34.gif?pub-status=live)
Simplifying Eq. (31) and substituting E S0 = E S00e ik S0S c, one obtains after separating the real and imaginary parts
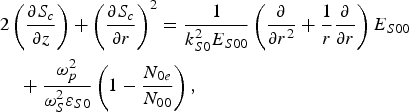
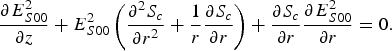
The solution of these equations may again be written as
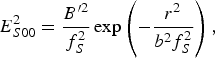
where b is the initial beam width of the scattered wave. Substituting the above solution in Eq. (35a) and equating the coefficients of r 2 on both sides, we get the equation of the spot size of scattered wave as
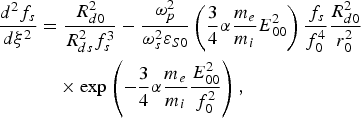
where R dS = k S0b 2 is the diffraction length of the scattered radiation.
It is easy to see from Eq. (15) that the IAW is damped, as it propagates along the z-axis. Consequently, the scattered wave amplitude should also decrease with increasing z. Therefore, expressions for B′ and b may be obtained on applying suitable boundary conditions E S = E S0exp(ik S0z) + E S1exp(−ik S1z) = 0 at z = z c; here z c is the point at which the amplitude of the scattered wave is zero. This immediately yields
![\eqalignno{B^{\prime} &= -{1 \over 2} {\omega_p^2 \over c^2} {\omega_S \over \omega_0} {n_0 \over N_{00}} {E_{00} f_S \lpar z_c\rpar \over f\lpar z_c\rpar f_0 \lpar z_c\rpar } \cr &\quad \times {\exp \lpar \!-k_i z_c\rpar \over \left[k_{S1}^2 - k_{S0}^2 - \displaystyle{{\omega_p^2 \over c^2}} \left(1 - \displaystyle{{N_{0e} \over N_{00}}}\right)\right]} \cr &\quad \times {\exp \left[-i\lpar k_{S1} z_c \! + \! k_0 S_0\rpar \right]\over \exp \left[i\lpar k_{S0} S_c \! + \! k_{S0} z_c\rpar \right]}\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021105655057-0884:S026303460999036X_eqn38.gif?pub-status=live)
with condition
The reflectivity is defined as the ratio of scattered flux and incident flux, R = (|E S|2/|E 00|2). By using Eqs. (30), (33), (34), (36), and (38), we get E SE S* = E S0E S0* + E S0E S1*exp[i(k S0 + k S1)z] + E S1E S0* exp[−i(k S0 + k S1)z] + E S1E S1* and
![\eqalignno{R &= {1 \over 4}\left({\omega_p^2 \over c^2}\right)^2 \left({\omega_s \over \omega_0}\right)^2 \left({n_0 \over N_{00}}\right)^2 \cr &\quad \times {1 \over \left[k_{s1}^2 - k_{s0}^2 - \displaystyle{{\omega_p^2 \over c^2}} \left(1 - \displaystyle{{N_{0e} \over N_{00}}}\right)\right]^2} \cr &\quad \times \left[\matrix{\displaystyle{{\,f_S^2 \lpar z_c\rpar \over f^2 \lpar z_c\rpar f_0^2 \lpar z_c\rpar }}\, \displaystyle{{1 \over f_S^2}} \exp \left(-2k_i z_c - \displaystyle{{r^2 \over b^2 f_s^2}}\right)\hfill\cr +\, \displaystyle{{1 \over f^2 f_0^2}} \exp \left(-\displaystyle{{r^2 \over a^2 f^2}} - \displaystyle{{r^2 \over b^2 f_0^2}} - 2k_i z\right)\hfill\cr +\, \displaystyle{{1 \over 2}} \,\,\displaystyle{{1 \over ff_0 f_s}} \,\,\displaystyle{{\,f_s \lpar z_c\rpar \over f\lpar z_c\rpar f_0 \lpar z_c\rpar }}\hfill\cr \times \exp \left(- \, \displaystyle{{r^2 \over 2b^2 f_s^2}} - \displaystyle{{r^2 \over 2a^2 f^2}} - \displaystyle{{r^2 \over 2b^2 f_0^2}}\right)\hfill\cr \cdot \exp \left\{-k_i \lpar z + z_c\rpar \right\}\cos \left\{\lpar k_{S0} + k_{S1}\rpar \lpar z - z_c\rpar \right\}\hfill\cr}\right].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary-alt:20160629050024-60144-mediumThumb-S026303460999036X_eqn39.jpg?pub-status=live)
It is apparent from the above equation that the reflectivity is dependant on the intensity of IAW and damping factor. To observe the effect of localization of IAW on SBS reflectivity, we have included the expression of modified Eigen frequency, (Eq. (22)) and effective damping, (Eq. (23)) in the above equation. It is clearly evident from Figure 5 that the SBS reflectivity gets reduced in the presence of the new Eigen frequency and damping values by almost the same factor as the intensity of the IAW decreases. In Figure 5, the solid red line (online only) shows the reflectivity with initial damping value and the dashed blue line (online only) shows the reflectivity including the effective enhanced Landau damping. If we calculate the integrated SBS reflectivity in two cases: namely (1) with initial damping of IAW and (2) with modified enhanced damping of IAW, we find that the reduction in SBS reflectivity comes out to be approximately 10%.
Fig. 5. (Color online) Variation in normalized back scattered reflectivity of SBS, |E s|2/|E 00|2 with normalized distance, (i) when (Γi/ω) = 0.0142 (solid red line) and (ii) when (Γi/ω) = 0.0155 (blue dashed line).
5. CONCLUSION
In the present article, we studied the filamentation of the laser beam in paraxial regime considering ponderomotive nonlinearity in hot collisionless plasma. It is evident from the results that the IAW gets excited due to nonlinear coupling with the high power filamented laser beam, and due to Landau damping, it gets damped as it propagates. The coupling is so strong that the IAW becomes highly localized and produces periodic structures. Further we discussed the effect of localization of IAW, this resulted in the modification of the Eigen frequency of IAW; consequently, an enhanced Landau damping of the IAW and a modified mismatch factor in the SBS process occurred. Solving the Eigen value problem we obtained an enhanced Landau damping, which resulted in a reduction in the intensity of the IAW. As a consequence, the back-reflectivity of the SBS process is suppressed by a factor of approximately 10%. These results should find applications in the laser induced fusion scheme where a reduction in SBS will improve the laser plasma coupling efficiency.
ACKNOWLEDGMENTS
This work was partially supported by DST, Government of India. One of the authors (Prerana Sharma) is grateful to AICTE India for providing financial assistance. One of the authors (Shivani) is grateful to Dr. R. Uma for useful discussions.
