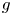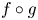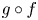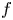1. Introduction and main results
Parrondo's paradox is a well-known paradox in game theory that affirms that a combination of losing strategies can become a winning strategy, see [Reference Harmer and Abbott9, Reference Parrondo11]. The paradox can be used to describe many situations away from game theory. In this work, we study the stability of fixed points and we shall establish the following analogy: attracting or repelling fixed points correspond to winning or losing strategies, respectively. Then, the question is the following: a fixed point that is attracting for 
$f$ and 
$g$, can it be repelling for 
$f \circ g$? If so, we say the dynamical Parrondo's paradox arises.
Let us give a more precise definition. First, a word of caution, throughout this note we use the term attracting (or attractor) and repelling (or repeller) as a synonym of asymptotically stable for a map and its inverse, respectively. For a fixed class of maps 
$\mathcal {C},$ from 
$\mathbb {R}^{k}$ into itself, we will say that a pair of maps 
$f,g\in \mathcal {C}$ exhibit a dynamical Parrondo's paradox if they have a common fixed point at which the maps are locally invertible and the fixed point is locally asymptotically stable for 
$f$ and 
$g$ but it is a repeller for the composite maps 
$g\circ f$ and 
$f\circ g.$ Note that, 
$g\circ f$ and 
$f\circ g$ are conjugate near the fixed point because, locally, 
$f\circ g= g^{-1}\circ g\circ f \circ g.$
A concrete example in which the dynamical Parrondo's paradox appears for 
$k = 2$ and 
$\mathcal {C}$ the class of polynomial maps was given in [Reference Cima, Gasull and Mañosa5, example 7]:
\begin{align*} f(x,y)&=\big({-}y+2{x}^{2}+6xy,x-3{x}^{2}+2xy+3{y}^{2}\big),\\ g(x,y)&=\big({x}/{2}-{\sqrt{3}}y/{2}-x\,(x^{2}+y^{2}), {\sqrt{3}}x/{2}+{y}/{2}-y\,(x^{2}+y^{2})\big). \end{align*}
It can be proved that the origin is a locally asymptotic stable fixed point for 
$f$ and 
$g$ and the origin is a repelling fixed point for 
$g\circ f$ by computing the so-called Birkhoff stability constants for the three maps. Note that the dynamics near the fixed points is of rotation type. Taking the product of these maps with themselves we trivially obtain examples for all even 
$k$.
As shown in [Reference Cima, Gasull and Mañosa5], the paradox does not arise when 
$k = 1$ and 
$\mathcal {C}$ is the class of analytic maps. Note also that the paradox is also impossible for any 
$k$ when 
$\mathcal {C}$ is the class of 
$C^{1}$ maps that are hyperbolic at a point 
$\textbf {x}$. Indeed, given two 
$k\times k$ matrices with all their eigenvalues with modulus smaller than 1, 
$A$ and 
$B$, it holds that 
$|\mathrm {det}(A)|<1$, 
$|\mathrm {det}(B)|<1$ and hence 
$|\mathrm {det}(A B)|<1$. As a consequence, if 
$\textbf {x}$ is asymptotically stable for 
$f$ and 
$g$, then for the composite maps 
$\textbf {x}$ is either locally asymptotically stable or of saddle type, but never repelling. Examples of saddle type points for 
$g\circ f,$ when 
$f$ and 
$g$ are linear maps, are given in [Reference Blondel, Theys, Tsitsiklis, Blondel and Megretski3] and [Reference Jungers10, p. 8].
It is worth to mention that in [Reference Cánovas, Linero and Peralta-Salas4] a different type of dynamical Parrondo's paradox is considered. The authors combine periodically two one-dimensional maps 
$f$ and 
$g$ to give rise to chaos or order.
The main goal of this paper is to give examples of the dynamical Parrondo's paradox when 
$\mathcal {C}$ is the class of homoeomorphisms and to fill the lack of examples in odd dimension. We prove that for all 
$k\ge 2$ there are pairs of maps that realize the dynamical Parrondo's paradox. Although the approach of [Reference Cima, Gasull and Mañosa5] is mainly analytic, our point of view is more qualitative. Moreover, the behaviour of our maps near the fixed point is not of rotation type and there does not seem to be a clear path to make them smooth or analytic.
Theorem 1.1 For any 
$k\ge 2$, there are pairs of homoeomorphisms from 
$\mathbb {R}^{k}$ to itself that exhibit the dynamical Parrondo's paradox. However, for 
$k=1$ the paradox never arises.
It is interesting to remark that theorem 1.1, and in consequence, the dynamical Parrondo's paradox is also relevant from the point of view of 2-periodic discrete dynamical systems. In particular, these systems are good models for describing the dynamics of biological systems under periodic fluctuations due either to external disturbances or effects of seasonality, see [Reference Elaydi and Sacker6–Reference Franke and Selgrade8, Reference Selgrade and Roberds12, Reference Selgrade and Roberds13] and the references therein.
As a byproduct of our construction of the two-dimensional example of dynamical Parrondo's paradox we will also prove that, almost surely, every orbit of the iterated function system generated by 
$f$ and 
$g$ is repelled from the origin, where 
$f$ and 
$g$ are essentially the maps constructed in theorem 1.1 and appear with certain respective probabilities 
$p$ and 
$1-p$. The result carries onto higher dimensions as well. To be more precise, consider the space 
$\{0, 1\}^{\mathbb {N}}$ equipped with the probability measure 
$\mu$ defined as the product of the Bernoulli probability measures, 
$\mu _B,$ in each factor. Recall that for the Bernoulli distribution 
$\operatorname {B}(p),$ 
$\mu _B(1)=p$ and 
$\mu _B(0)=q=1-p,$ for some 
$p\in [0,1].$ We prove:
Theorem 1.2 For any 
$k \ge 2$ and 
$0< p<1,$ there exist homoeomorphisms 
$f_0$ and 
$f_1$ from 
$\mathbb {R}^{k}$ into itself such that:
• The origin
$\mathbf {0}$ is fixed and globally asymptotically stable for $f_0$ and $f_1$.• For
$\mu$-almost all $(a_n) \in \{0,1\}^{\mathbb {N}}$ every orbit $\{F_{a_n, \cdots , a_1, a_0}(\textbf {x}) = f_{a_n} \circ \cdots \circ f_{a_1} \circ f_{a_0}(\mathbf {x})\}_{n \ge 0}$ starting at a point $\mathbf {x} \neq \mathbf {0}$ is repelled from the origin.
As we will see in the proof, for any 
$0< p<1,$ each homoeomorphism 
$f_0$ and 
$f_1$ will have a region where the radial component of the points increases and another one where it decreases. The largest of these variations corresponds to the increasing region, which is in turn considerably bigger in size than the decreasing region. Their difference becomes larger and tends to infinity when 
$p$ approaches 0 or 1.
2. Definition of $f$ and $g$ and proof of theorem 1.1
We will split the proof in three cases: 
$k=1,$ 
$k=2$ and 
$k>2.$
2.1 Proof of theorem 1.1 for $k=1$
Let us proceed by contradiction. Suppose that 
$f$ and 
$g$ are homoeomorphisms of 
$\mathbb {R}$, 
$0$ is a locally attracting fixed point for 
$f$ and 
$g$ and a locally repelling fixed point for 
$f \circ g$ and 
$g \circ f$. Assume further, for simplicity, that 
$f$ and 
$g$ reverse orientation, the other cases are handled similarly. Then:
(i)
$g$ is monotone decreasing, so if $y < x < 0$ then $0 < g(x) < g(y)$.(ii) Since
$0$ is locally attracting for $f$ and $g$, for any $y < 0 < x$ close to $0$ we have that
\[ {y < f \circ f(y) < 0 < g \circ g(x) < x.}\](iii) Since
$0$ is locally repelling for $f \circ g$ and $g \circ f$, for any $x,y > 0$ close to $0$ we have that
\[{x < f \circ g(x) \quad and \quad y < g \circ f(y).}\]
These properties put together yield a contradiction because for small positive 
$u > 0$:
\[ { u < f \circ g(u) < g \circ f(f\circ g(u)) = g(f \circ f(g(u)) < g(g(u)) < u }\]where the first two inequalities are consequence of (iii) and the last two inequalities are consequences.
However, note that it is possible to construct an example in which the origin is semistable for 
$f \circ g$ (and also for 
$g \circ f$) while it is asymptotically stable for 
$f$ and 
$g$:
\begin{align*} f(x) &= \begin{cases} -2x & \text{if }x \le 0, \\ -x/3 & \text{if } x \ge 0, \end{cases}\\ g(x) &= \begin{cases} -x/3 & \text{if }x \le 0, \\ -2x & \text{if } x \ge 0. \end{cases} \quad \quad\Rightarrow\quad\quad f \circ g(x) = \begin{cases} x/9 & \text{if }x \le 0, \\ 4x & \text{if } x \ge 0. \end{cases} \end{align*}2.2 Proof of theorem 1.1 for $k=2$
In our example the maps 
$f$ and 
$g$ are conjugate. We first focus on the definition of 
$f$, expressed in polar coordinates. The first elements of a typical orbit under 
$f$ will drift away from the origin (the radial coordinate increases) until it reaches a trapping sector in which the orbit remains forever and is slowly attracted to the origin (the radial coordinate steadily decreases). The dynamics of the angular coordinate is independent from the values of the radial coordinate and forces every orbit to be eventually contained in the trapping sector. Note that, globally, 
$f$ looks mostly expanding because the size of this sector and the speed of convergence to the origin therein are relatively small.
Let us write out the details. We use the coordinates 
$(r, \theta )$ in 
$\mathbb {R}^{2} \setminus \{\textbf {0}\}$, where 
$(e^{r}, 2\pi \theta )$ are the standard polar coordinates in the plane. Thus, 
$\theta$ takes values in 
$\mathbb {R}/\mathbb {Z}$ and 
$r$ takes values in 
$\mathbb {R}$ and the limit 
$r \to -\infty$ corresponds to the origin. We use these coordinates to simplify later definitions and computations. Let 
$I \subset \mathbb {R} / \mathbb {Z}$ be an interval centred at 
$\bar {0}$ (here 
$\bar {0}$ is used to denote the neutral element in 
$\mathbb {R} / \mathbb {Z}$) and such that 
$I \cap (I + \overline {1/2}) = \emptyset$. Let 
$f$ be a homoeomorphism of the plane that fixes the origin and satisfies the following properties (we use the notation 
$f(r, \theta ) = (r', \theta ')$):
(i)
$\Delta _r = r' - r$ and $\Delta _{\theta } = \theta ' - \theta$ only depend on $\theta$.(ii)
$\Delta _r = 4$ if $\theta \notin I$ and $\Delta _r$ is smaller than $4$ if $\theta \in I$; $\Delta _r \in [-1, 0)$ if $\theta$ belongs to an interval $J \subset I$, $\bar {0} \in J$ and equals $-1$ if $\theta = \bar {0}$, see figure 1.(iii)
$\Delta _{\theta }$ is non-negative, $\Delta _{\theta } \le \mathrm {dist}(I, I+\overline {1/2})$ and $\Delta _{\theta } = 0$ if and only if $\theta = \bar {0}$.
Figure 1. Graphs of 
$\Delta _r$ (left) and 
$\theta '$ (right) as a function of 
$\theta$ in the definition of 
$f.$
Note that (i) implies that 
$\Delta _r$ is uniformly bounded and, in particular, there is no issue concerning continuity of 
$f$ or its inverse at the origin. Property (iii) controls the one-dimensional dynamics in the angular coordinate: every orbit tends to 
$\theta = \bar {0}$. By (ii) the radial coordinate decreases indefinitely once the orbit remains close to 
$\theta = \bar {0}$.
The angular interval 
$J$ determines an infinite sector 
$\widehat J$ in 
$\mathbb {R}^{2} \setminus \{\textbf {0}\}$ in which the radial coordinate of a point decreases after applying 
$f$. Inside 
$\widehat J$ we find the trapping sector that has been previously mentioned, see figure 2. Note also that the speed of attraction (
$\Delta _r \in [-1,0$)) in the trapping sector is weaker than the speed of repulsion (
$\Delta _r = 4$) outside the sector 
$\widehat I$ determined by 
$I$.
Figure 2. Action of 
$f$ on a circle 
$r = c$ (inner circle) represented schematically by arrows, sectors 
$\widehat I$ (light) and 
$\widehat J$ (dark) are shadowed, the attracting 
$f$-invariant ray (
$\theta = \bar {0}$) is depicted vertical.
The map 
$g$ is merely a copy of 
$f$ shifted in the angular coordinate. Let 
$\tau (r, \theta ) = (r, \theta + \overline {1/2})$ be the half-turn rotation in the plane and let 
$g = \tau ^{-1} \circ f \circ \tau = \tau \circ f \circ \tau$. Being a conjugate of 
$f$, 
$g$ satisfies the same properties as 
$f$ if we replace 
$\theta$ by 
$\theta + \overline {1/2}$ in the statements. The key observation is that by the second item in (iii), 
$f(\widehat I) \cap \tau (\widehat I) = \{\textbf {0}\}$ and 
$g(\tau (\widehat I)) \cap \widehat I = \{\textbf {0}\}$. This means that the radial coordinate cannot decrease under the action of 
$f$ and then immediately decrease under the action of 
$g$, or vice versa. In fact, by (ii) the radial coordinate increases after applying 
$g \circ f$ or 
$f \circ g$.
Let us finally prove that 
$f$ and 
$g$ exhibit the dynamical Parrondo's paradox.
The origin is a globally attracting fixed point for 
$f$ and 
$g$. Let 
$\{(r_n, \theta _n)\}_{n \ge 1}$ be the orbit under 
$f$ of a point 
$(r, \theta )$. We study separately the angular coordinate 
$\{\theta _n\}$ because its evolution is independent from the values of the radial coordinate. If 
$\theta = \bar {0}$ then 
$\theta _n = \bar {0}$ for every 
$n \ge 1$, otherwise the sequence 
$\{\theta _n\}$ is increasing and converges to the unique value 
$\theta _0$ which is fixed under the one-dimensional angular dynamics, namely 
$\theta _0 = \bar {0}$. Thus, 
$\theta _n \to \bar {0}$ so 
$\theta _n \in J$ for sufficiently large 
$n$, say 
$n \ge n_0$. This implies that 
$r_{n+1} < r_n$ for every 
$n \ge n_0$ and, additionally, that 
$r_{n+1} - r_n \to -1$ as 
$n \to +\infty$ because the orbit converges towards the half-ray 
$\theta = \bar {0}$. As a consequence, 
$r_n \to -\infty$ and the orbit tends to the origin.
From the previous discussion we can deduce that the number of iterations that any orbit stays outside the sector defined by 
$J$ is bounded uniformly for all the orbits. A bound can be defined by the number 
$N$ of iterates needed for 
$J$ to cover 
$S^{1}$ under the action of the dynamics in the angular coordinate. For a given 
$r$, if we denote 
$D_r$ the disk of radius 
$r$ centred at the origin, the set
\[ U_r = \bigcup_{n \ge 0} f^{n}(D_r) \]
is a positively invariant neighbourhood of the origin that, in view of the bound 
$\Delta _r \le 4$ and the argument above, is contained inside 
$D_{r + 4N}$. Thus, 
$\{U_r\}_{r < 0}$ is a basis of positively invariant neighbourhoods of 
$\mathbf {0}$.
The same conclusion holds for 
$g$ because it is conjugate to 
$f$.
The origin is a globally repelling fixed point for 
$f \circ g$ and 
$g \circ f$. Recall that 
$f \circ g = f \circ \tau \circ f \circ \tau$ is conjugate to 
$g \circ f = \tau \circ f \circ \tau \circ f$ (note that 
$\tau ^{2} = \mathrm {id}$) so it is enough to prove the statement for the latter composition. By (ii) the radial coordinate of a point outside 
$\widehat {I}$ increases by 4 under the action of 
$f$. Thus, if 
$(r', \theta ') = g \circ f (r, \theta )$ we have that 
$r' - r \ge 3$ if 
$\theta \notin I$. The same inequality is true in the case 
$f(r, \theta )$ does not belong to 
$\tau (\widehat {I})$. Since 
$\widehat {I} \cap f^{-1}(\tau (\widehat {I})) = \{\textbf {0}\}$ we conclude that the radial coordinate of every point increases at least by 3 after applying 
$g \circ f$. Evidently, the origin is a global repeller for 
$g \circ f$ and the proof of theorem 1.1 follows for 
$k=2.$
2.3 Proof of theorem 1.1 for $k>2$
First, let us modify slightly the planar dynamics introduced in the previous subsection in order to make it symmetric with respect to the vertical axis. Define 
$h(r, \theta ) = f(r, 2\theta )$ if 
$\theta \in [\bar {0},\overline {1/2}]$ and 
$h(r, \theta ) = f(r, 1 - 2\theta )$ if 
$\theta \in [\overline {1/2}, \bar {1}]$. There are now two invariant rays for 
$h$, 
$\theta = \bar {0}$, which acts as a repeller in the dynamics in the angular coordinate, and 
$\theta = \overline {1/2}$, which acts as an attractor. The dynamics of 
$h$ within each half-plane reproduces the dynamics of 
$f$ except from the fact that both 
$h$-invariant rays correspond to the unique invariant ray 
$\{\theta = \bar {0}\}$ for 
$f$.
Now, it is straightforward to move into higher dimensions. Consider spherical coordinates 
$(r, \theta , \varphi _1, \ldots , \varphi _{k-2})$ in 
$\mathbb {R}^{k}$ and define a map 
$h_k \colon \mathbb {R}^{k} \to \mathbb {R}^{k}$ by the transformation that applies 
$h$ to the radial and polar coordinate, 
$(r', \theta ') = h(r, \theta )$, and leaves the azimuthal coordinates unchanged, 
$(\varphi '_1, \ldots , \varphi '_{k-2}) = (\varphi _1, \ldots , \varphi _{k-2})$. The dynamics of 
$h_k$ leaves invariant the two rays that form the vertical axis (north-south direction, suppose that north corresponds to 
$\theta = \bar {0}$). Points are attracted to the origin in those rays. Moreover, the radial coordinate of any point increases significantly after applying 
$h_k$ unless the point belongs to a thin double cone 
$C$ around the axis (whose size can be traced back to the size of 
$I$). Nevertheless, since every orbit either belongs to the ray pointing to the north or eventually enters the cone around the ray that points to the south and remains in it, we conclude that the origin is a globally attracting fixed point for 
$h_k$. The stability of 
$\mathbf {0}$ may be addressed in the same fashion as in the case 
$k = 2$.
An analogous construction for the second map as in the case 
$k=2$ works here as well. Let 
$\tau _k$ be a 
$90^{\circ }$ rotation in 
$\mathbb {R}^{k}$ and define 
$j_k = \tau _k^{-1} \circ h_k \circ \tau _k$. Note that
\[ { ({\star}) \quad \quad h_k(C) \cap \tau_k(C) = \{\textbf{0}\} \quad and \quad j_k(\tau_k(C)) \cap C = \{\textbf{0}\} }\]
It is straightforward to check that the origin is a globally attracting fixed point for 
$j_k$ (again by conjugation) and that the radial coordinate of every point increases under the action of 
$j_k \circ h_k$ and 
$h_k \circ j_k$ (by (
$\star$)) and the origin is a globally repelling fixed point for the composite maps.
3. Iterated function system: proof of theorem 1.2
The idea is to take as 
$f_0$ and 
$f_1$ a slight modification of the maps 
$f$ and 
$g$ defined in the proof of theorem 1.1. For the sake of clarity, we only discuss the case 
$k = 2$, the proof for 
$k > 2$ is a straightforward generalization of the argument using the maps 
$h_k$ and 
$j_k$.
Let us start with the proof of theorem 1.2 for 
$k=2$. We need to slightly modify the definition of 
$f$ and 
$g$ in § 2.2 in order to increase the rate of radial repulsion far from the invariant rays to account for the effect of the probability 
$p$. The only change in the definition of the new 
$f$, which we shall denote in the following by 
$f_0$, is that we replace property (ii) by
(ii)
$\Delta _r = a-1,$ for some fixed $a>4$ to be determined later, if $\theta \notin I$, and is smaller than $a-1$ if $\theta \in I$; $\Delta _r \in [-1, 0)$ if $\theta$ belongs to an interval $J \subset I$, $\bar {0} \in J$ and $\Delta _r = -1$ if $\theta = \bar {0}$.
Then, the new 
$g$, which shall be henceforth denoted 
$f_1$, is constructed from the new 
$f$ as in the previous section, 
$f_1 = \tau ^{-1} \circ f_0 \circ \tau$. Note that the original 
$f$ and 
$g$ considered in § 2.2 correspond to 
$a=5.$ The value 
$a$ will be fixed later, in terms of 
$p.$
Take an arbitrary point 
$\textbf {x}$ in the plane, different from the origin, and apply 
$f_0$ and 
$f_1$ randomly as in the statement, that is, apply 
$f_0$ with probability 
$p$ and 
$f_1$ with probability 
$q = 1-p.$ We claim that the orbit of 
$\textbf {x}$ is repelled from the origin almost surely, that is, with probability 1.
Take a random sequence 
$(a_n) \in \{0,1\}^{\mathbb {N}}$ with respect to the probability 
$\mu$, that is, 
$a_n$ takes the value 0 with probability 
$p$ and 
$1$ with probability 
$q = 1-p$. Then, consider the planar dynamics defined by applying sequentially the maps 
$f_{a_n}$, 
$n \ge 0$. We claim that for 
$\mu$-almost all 
$(a_n)$ the change in the radial coordinate in every orbit except from 
$\mathbf {0}$ is positive and, as a consequence, every orbit is repelled from the origin.
The proof of the claim follows from two remarks. The first one concerns the four maps 
$f_0 \circ f_0, f_0 \circ f_1, f_1 \circ f_0, f_1 \circ f_1$. Their radial coordinate change is bounded by:
\[ \Delta_r^{f_0 \circ f_0} \ge -2,\quad \Delta_r^{f_0 \circ f_1} \ge a-2,\quad \Delta_r^{f_1 \circ f_0} \ge a-2\quad \mbox{and}\quad \Delta_r^{f_1 \circ f_1} \ge -2. \]
Moreover, the map 
$f_0\circ f_0$ appears with probability 
$p^{2},$ the map 
$f_1 \circ f_1$ with probability 
$q^{2},$ while each of the maps 
$f_0\circ f_1$ and 
$f_1\circ f_0$ appears with probability 
$pq.$ Let us start giving conditions on 
$a$ that imply that the expected value of the change in radial coordinate is positive. More precisely, if 
$R^{n} \colon \{0,1\}^{n} \to \mathbb {R}$ denotes the random variable that measures the minimum of the variation of the radial coordinate between a point (different from the origin) and its image under 
$F_{a_n,\cdots , a_1, a_0}$, i.e.
\[ { R^{n}(a_0, a_1, \ldots, a_n) = \min\{r_n - r_0: (r_n,\theta_n) = F_{a_0,\ldots,a_n}(r_0, \theta_0) \}, }\]we have that
\begin{align*} E[R^{2m+2}] &\ge E[R^{2m}] + p^{2}\min\Delta_r^{f_0 \circ f_0} + pq\min\Delta_r^{f_0 \circ f_1}\\ &\quad + pq\min\Delta_r^{f_1 \circ f_0} + q^{2}\min\Delta_r^{f_1 \circ f_1}\\ &\ge E[R^{2m}]+2(a-2)pq -2(p^{2}+q^{2})=E[R^{2m}]+2\big(ap(1-p)-1\big). \end{align*}
Hence, if we take any 
$a$ such that 
$ap(1-p)-1>0$ we have that 
$E[R^{2m+2}]\ge E[R^{2m}]+ K,$ for 
$K=2(ap(1-p)-1)>0,$ and as a consequence we conclude that 
$E[R^{2m}] \ge 2K m$, that is, the expected value of 
$R^{n}$ grows linearly with 
$n$. This computation shows that in average random iteration repels points from the origin by increasing (linearly!) its radial coordinate. We need to extend this conclusion to a subset of binary sequences of full probability. Note incidentally that 
$a>1/ (p(1-p))\ge 4.$
Given a binary sequence 
$(a_n)$ we can bound the value of 
$R^{2m}$ in the following fashion:
\begin{align*} R^{2m} &\ge \min\Delta_r^{f_{a_1}\circ f_{a_0}} + \min\Delta_r^{f_{a_3}\circ f_{a_2}} + \cdots + \min\Delta_r^{f_{a_{2m}}\circ f_{a_{2m-1}}}\\ &\ge (a-2)k_m - 2(m-k_m) = ak_m-2m, \end{align*}
where 
$k_n$ denotes the number of maps among 
$f_{a_1} \circ f_{a_0}, f_{a_3} \circ f_{a_2}, \ldots , f_{a_{2n}} \circ f_{a_{2n-1}}$ that are equal to 
$f_1 \circ f_0$ or 
$f_0 \circ f_1$. Note that 
$k_n$ is the sum of 
$n$ independent Bernoulli distributions 
$\operatorname {B}(2pq),$ because 
$2pq$ is the probability of appearance of 
$f_1 \circ f_0$ or 
$f_0 \circ f_1$. Thus, if 
$\liminf _{n \to +\infty } k_n/n = \ell > 2/a$, the asymptotic growth of 
$R^{2n}$ is bounded from below by 
$(\ell - 2/a)n$. In particular, 
$R^{2n} \to +\infty$ so every point is repelled from the origin by the iterated action of the maps 
$f_{a_n}, n \ge 0$.
It only remains to prove that the subset of 
$(a_n)$ such that 
$\liminf k_n/n > 2/a$ has full probability. In fact, the Strong Law of Large Numbers [Reference Ash1, Reference Billingsley2] gives much more: for a full probability set, the previous 
$\liminf$ is indeed a limit and it coincides with the expected value of the random variable 
$\operatorname {B}(2pq),$ that is 
$2pq.$ Hence, for 
$\mu$-almost all binary sequences,
\[ \ell=\liminf_{n \to +\infty}\frac {k_n}n=\lim_{n \to +\infty}\frac {k_n}n=2pq=2p(1-p). \]For those sequences we have that,
\[ \ell-\frac 2a =2p(1-p)-\frac 2a=\frac{2\big(ap(1-p)-1\big)}{a}>0, \]as we wanted to prove, and the theorem follows.
Acknowledgements
The authors thank the anonymous referee for her/his valuable comments. This study has received funding from the Ministerio de Ciencia e Innovación (PGC2018-098321-B-I00 and PID2019-104658GB-I00 grants), the Agència de Gestió d'Ajuts Universitaris i de Recerca (2017 SGR 1617 grant).
