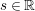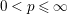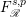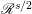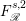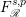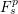1 Introduction
Let
![]() $\mathbb{C}^{n}$
be the complex
$\mathbb{C}^{n}$
be the complex
![]() $n$
-space and
$n$
-space and
![]() $dV$
be the ordinary volume measure on
$dV$
be the ordinary volume measure on
![]() $\mathbb{C}^{n}$
. If
$\mathbb{C}^{n}$
. If
![]() $z=(z_{1},\ldots ,z_{n})$
and
$z=(z_{1},\ldots ,z_{n})$
and
![]() $w=(w_{1},\ldots ,w_{n})$
are points in
$w=(w_{1},\ldots ,w_{n})$
are points in
![]() $\mathbb{C}^{n}$
, we write
$\mathbb{C}^{n}$
, we write
For any
![]() $0<p\leqslant \infty$
we let
$0<p\leqslant \infty$
we let
![]() $L_{G}^{p}$
denote the space of Lebesgue measurable functions
$L_{G}^{p}$
denote the space of Lebesgue measurable functions
![]() $f$
on
$f$
on
![]() $\mathbb{C}^{n}$
such that the function
$\mathbb{C}^{n}$
such that the function
![]() $f(z)e^{-(1/2)|z|^{2}}$
is in
$f(z)e^{-(1/2)|z|^{2}}$
is in
![]() $L^{p}(\mathbb{C}^{n},dV)$
. When
$L^{p}(\mathbb{C}^{n},dV)$
. When
![]() $0<p<\infty$
, it is clear that
$0<p<\infty$
, it is clear that
We define
For
![]() $p=\infty$
the norm in
$p=\infty$
the norm in
![]() $L_{G}^{\infty }$
is defined by
$L_{G}^{\infty }$
is defined by
Let
![]() $F^{p}$
denote the space of entire functions in
$F^{p}$
denote the space of entire functions in
![]() $L_{G}^{p}$
. Then
$L_{G}^{p}$
. Then
![]() $F^{2}$
is a closed subspace of the Hilbert space
$F^{2}$
is a closed subspace of the Hilbert space
![]() $L_{G}^{2}$
(see [Reference Zhu15]) with inner product
$L_{G}^{2}$
(see [Reference Zhu15]) with inner product
To give a motivation for our study of Fock–Sobolev spaces, recall that the annihilation operator
![]() $A_{j}$
and the creation operator
$A_{j}$
and the creation operator
![]() $A_{j}^{\ast }$
from the quantum theory are defined by the commutation relation
$A_{j}^{\ast }$
from the quantum theory are defined by the commutation relation
![]() $[A_{j},A_{k}^{\ast }]=\unicode[STIX]{x1D6FF}_{jk}I$
, where
$[A_{j},A_{k}^{\ast }]=\unicode[STIX]{x1D6FF}_{jk}I$
, where
![]() $I$
is the identity operator. A natural representation of these operators is achieved on the Fock space
$I$
is the identity operator. A natural representation of these operators is achieved on the Fock space
![]() $F^{2}$
, namely,
$F^{2}$
, namely,
Both
![]() $A_{j}$
and
$A_{j}$
and
![]() $A_{j}^{\ast }$
, as defined above, are densely defined linear operators on
$A_{j}^{\ast }$
, as defined above, are densely defined linear operators on
![]() $F^{2}$
(unbounded though) and satisfy the commutation relation
$F^{2}$
(unbounded though) and satisfy the commutation relation
![]() $[A_{j},A_{k}^{\ast }]=\unicode[STIX]{x1D6FF}_{jk}I$
. Therefore, it is important to study the operator of multiplication by
$[A_{j},A_{k}^{\ast }]=\unicode[STIX]{x1D6FF}_{jk}I$
. Therefore, it is important to study the operator of multiplication by
![]() $z_{j}$
and the operator of differentiation on the Fock space
$z_{j}$
and the operator of differentiation on the Fock space
![]() $F^{2}$
.
$F^{2}$
.
We define the radial derivative
![]() $\mathscr{R}$
by
$\mathscr{R}$
by
and the Fock–Sobolev space
![]() $F_{\mathscr{R}}^{s,p}$
of fractional order
$F_{\mathscr{R}}^{s,p}$
of fractional order
![]() $s$
for which
$s$
for which
![]() $\mathscr{R}^{s/2}f$
is given by an
$\mathscr{R}^{s/2}f$
is given by an
![]() $F^{p}$
function. Then
$F^{p}$
function. Then
![]() $F_{\mathscr{R}}^{s,2}$
is a Hilbert space with inner product
$F_{\mathscr{R}}^{s,2}$
is a Hilbert space with inner product
for
![]() $f,g\in F_{\mathscr{R}}^{s,2}$
. Each point evaluation is a bounded linear functional on
$f,g\in F_{\mathscr{R}}^{s,2}$
. Each point evaluation is a bounded linear functional on
![]() $F_{\mathscr{R}}^{s,2}$
. So, to each
$F_{\mathscr{R}}^{s,2}$
. So, to each
![]() $z\in \mathbb{C}^{n}$
there corresponds the reproducing kernel
$z\in \mathbb{C}^{n}$
there corresponds the reproducing kernel
![]() $K_{z}^{s}$
such that
$K_{z}^{s}$
such that
for
![]() $f\in F_{\mathscr{R}}^{s,2}$
. Let
$f\in F_{\mathscr{R}}^{s,2}$
. Let
![]() $K_{s}(z,w):=K_{w}^{s}(z)$
. Defining
$K_{s}(z,w):=K_{w}^{s}(z)$
. Defining
![]() $\unicode[STIX]{x1D6EC}(z,w)$
by
$\unicode[STIX]{x1D6EC}(z,w)$
by
we have the following estimates of the reproducing kernel
![]() $K_{s}(z,w)$
for
$K_{s}(z,w)$
for
![]() $F_{\mathscr{R}}^{s,2}$
.
$F_{\mathscr{R}}^{s,2}$
.
Theorem 1.1. Let
![]() $s\in \mathbb{R}$
. Then
$s\in \mathbb{R}$
. Then
and there are positive constants
![]() $C=C(s)>0$
such that
$C=C(s)>0$
such that
for
![]() $z,w\in \mathbb{C}^{n}$
.
$z,w\in \mathbb{C}^{n}$
.
It will turn out that polynomially growing/decaying weights quite naturally come into play in the study of our fractional Fock–Sobolev spaces. So, we first introduce such weighted Fock spaces. Given
![]() $s$
real we introduce the following norm on
$s$
real we introduce the following norm on
![]() $F_{s}^{p}$
when
$F_{s}^{p}$
when
![]() $0<p<\infty$
:
$0<p<\infty$
:
where
![]() $\unicode[STIX]{x1D714}_{n,s,p}$
is a normalizing constant so that the constant function
$\unicode[STIX]{x1D714}_{n,s,p}$
is a normalizing constant so that the constant function
![]() $1$
has norm
$1$
has norm
![]() $1$
in
$1$
in
![]() $F_{s}^{p}$
. When
$F_{s}^{p}$
. When
![]() $p=\infty$
, we define
$p=\infty$
, we define
where
![]() $\unicode[STIX]{x1D714}_{s}$
is a normalizing constant so that the constant function
$\unicode[STIX]{x1D714}_{s}$
is a normalizing constant so that the constant function
![]() $1$
has norm
$1$
has norm
![]() $1$
in
$1$
in
![]() $F_{s}^{\infty }$
. Let
$F_{s}^{\infty }$
. Let
![]() $L_{G,s}^{p}$
denote the space of Lebesgue measurable functions
$L_{G,s}^{p}$
denote the space of Lebesgue measurable functions
![]() $f$
on
$f$
on
![]() $\mathbb{C}^{n}$
such that the function
$\mathbb{C}^{n}$
such that the function
![]() $(1+|z|)^{s}f(z)$
is in
$(1+|z|)^{s}f(z)$
is in
![]() $L_{G}^{p}$
. Then
$L_{G}^{p}$
. Then
![]() $F_{s}^{p}$
is a closed subspace of
$F_{s}^{p}$
is a closed subspace of
![]() $L_{G,s}^{p}$
.
$L_{G,s}^{p}$
.
It follows that the fractional Fock–Sobolev spaces are realized as the weighted Fock spaces that do not involve derivatives as following Theorem 1.2. So, the study on the Fock–Sobolev spaces is reduced to that on the weighted Fock spaces. It is very convenient to study function theoretic and operator theoretic properties on the weighted Fock spaces instead of the Fock–Sobolev spaces (see [Reference Cho, Choe and Koo3, Reference Choe and Yang7, Reference Mengestie9–Reference Mengestie11, Reference Wang, Cao and Xia13]).
Theorem 1.2. Suppose
![]() $0<p\leqslant \infty$
and
$0<p\leqslant \infty$
and
![]() $s$
is a real number. Then
$s$
is a real number. Then
![]() $F_{\mathscr{R}}^{s,p}=F_{s}^{p}$
with equivalent norms.
$F_{\mathscr{R}}^{s,p}=F_{s}^{p}$
with equivalent norms.
Constants. In this paper we use the same letter
![]() $C$
to denote various positive constants which may vary at each occurrence but do not depend on the essential parameters. Variables indicating the dependency of constants
$C$
to denote various positive constants which may vary at each occurrence but do not depend on the essential parameters. Variables indicating the dependency of constants
![]() $C$
will be often specified in parenthesis. For nonnegative quantities
$C$
will be often specified in parenthesis. For nonnegative quantities
![]() $X$
and
$X$
and
![]() $Y$
the notation
$Y$
the notation
![]() $X\lesssim Y$
or
$X\lesssim Y$
or
![]() $Y\gtrsim X$
means
$Y\gtrsim X$
means
![]() $X\leqslant CY$
for some inessential constant
$X\leqslant CY$
for some inessential constant
![]() $C$
. Similarly, we write
$C$
. Similarly, we write
![]() $X\approx Y$
if both
$X\approx Y$
if both
![]() $X\lesssim Y$
and
$X\lesssim Y$
and
![]() $Y\lesssim X$
hold.
$Y\lesssim X$
hold.
2 Fractional radial derivatives
We note that
It is easy to see that
![]() $\mathscr{R}$
is unbounded, positive, self-adjoint, and invertible on
$\mathscr{R}$
is unbounded, positive, self-adjoint, and invertible on
![]() $F^{2}$
. In fact,
$F^{2}$
. In fact,
![]() $\mathscr{R}^{-1}$
is a compact operator.
$\mathscr{R}^{-1}$
is a compact operator.
Example 2.1. Let
Then
![]() $f\in F^{2}$
, but
$f\in F^{2}$
, but
![]() $\mathscr{R}f\notin F^{2}$
.
$\mathscr{R}f\notin F^{2}$
.
For
![]() $f\in F^{2}$
let
$f\in F^{2}$
let
be the orthonormal decomposition of
![]() $f$
, where
$f$
, where
![]() $e_{\unicode[STIX]{x1D6FC}}(z)=z^{\unicode[STIX]{x1D6FC}}/\Vert z^{\unicode[STIX]{x1D6FC}}\Vert _{2}.$
Associated with the operator
$e_{\unicode[STIX]{x1D6FC}}(z)=z^{\unicode[STIX]{x1D6FC}}/\Vert z^{\unicode[STIX]{x1D6FC}}\Vert _{2}.$
Associated with the operator
![]() $\mathscr{R}$
is a semigroup
$\mathscr{R}$
is a semigroup
![]() $\{{B_{t}\}}_{t\geqslant 0}$
defined by the expansion
$\{{B_{t}\}}_{t\geqslant 0}$
defined by the expansion
We can check that
![]() $u(z,t):=B_{t}f(z)$
is the solution of the heat-type equation:
$u(z,t):=B_{t}f(z)$
is the solution of the heat-type equation:
It is easy to see that
Thus
![]() $B_{t}$
is contractive. Moreover, we can see that
$B_{t}$
is contractive. Moreover, we can see that
![]() $-\mathscr{R}$
is the infinitesimal generator of
$-\mathscr{R}$
is the infinitesimal generator of
![]() $\{{B_{t}\}}_{t\geqslant 0}$
. That is,
$\{{B_{t}\}}_{t\geqslant 0}$
. That is,
See [Reference Cho, Choi and Lee5] for more properties concerning the heat semigroup as well as the spectral property of the operator
![]() $\mathscr{R}$
.
$\mathscr{R}$
.
Since
![]() $\mathscr{R}$
has discrete spectrum
$\mathscr{R}$
has discrete spectrum
![]() $\{2|\unicode[STIX]{x1D6FC}|+n:\unicode[STIX]{x1D6FC}\in \mathbb{N}_{0}^{n}\}$
, by using the spectral theorem, we define the fractional radial derivative
$\{2|\unicode[STIX]{x1D6FC}|+n:\unicode[STIX]{x1D6FC}\in \mathbb{N}_{0}^{n}\}$
, by using the spectral theorem, we define the fractional radial derivative
![]() $\mathscr{R}^{s}$
for
$\mathscr{R}^{s}$
for
![]() $s\in \mathbb{R}$
as following:
$s\in \mathbb{R}$
as following:
Definition 2.2. Let
![]() $s\in \mathbb{R}$
. For
$s\in \mathbb{R}$
. For
![]() $f\in F^{2}$
let
$f\in F^{2}$
let
be the orthonormal decomposition of
![]() $f$
. By the spectral theorem,
$f$
. By the spectral theorem,
![]() $\mathscr{R}^{s}$
is given by
$\mathscr{R}^{s}$
is given by
Definition 2.3. Let
![]() $s$
be a real number. The Fock–Sobolev space
$s$
be a real number. The Fock–Sobolev space
![]() $F_{\mathscr{R}}^{s,p}$
of fractional order
$F_{\mathscr{R}}^{s,p}$
of fractional order
![]() $s$
is the space of all entire functions for which
$s$
is the space of all entire functions for which
![]() $\mathscr{R}^{s/2}f$
is given by an
$\mathscr{R}^{s/2}f$
is given by an
![]() $F^{p}$
function. The Fock–Sobolev norm of
$F^{p}$
function. The Fock–Sobolev norm of
![]() $f$
of fractional order
$f$
of fractional order
![]() $s$
is defined accordingly,
$s$
is defined accordingly,
By using the semigroup, we have the integral representations for the fractional radial derivatives as following. See [Reference Bongioanni and Torrea2] for analogues in the context of other type of Sobolev spaces.
Proposition 2.4. Let
![]() $f\in F^{2}$
and
$f\in F^{2}$
and
![]() $z\in \mathbb{C}^{n}$
. Then the following identities hold:
$z\in \mathbb{C}^{n}$
. Then the following identities hold:
(i) For
 $0<s<1$
we have where
$0<s<1$
we have where $$\begin{eqnarray}\mathscr{R}^{s}f(z)=\frac{1}{\unicode[STIX]{x1D6E4}(-s)}\int _{0}^{\infty }\frac{[e^{-t\mathscr{R}}f(z)-f(z)]}{t^{s}}\,\frac{dt}{t},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{R}^{s}f(z)=\frac{1}{\unicode[STIX]{x1D6E4}(-s)}\int _{0}^{\infty }\frac{[e^{-t\mathscr{R}}f(z)-f(z)]}{t^{s}}\,\frac{dt}{t},\end{eqnarray}$$
 $\unicode[STIX]{x1D6E4}(-s)$
is the gamma function to negative numbers defined by choosing
$\unicode[STIX]{x1D6E4}(-s)$
is the gamma function to negative numbers defined by choosing $$\begin{eqnarray}\unicode[STIX]{x1D6E4}(-s)=\frac{\unicode[STIX]{x1D6E4}(-s+n)}{(-s)(-s+1)\cdots (-s+n-1)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}(-s)=\frac{\unicode[STIX]{x1D6E4}(-s+n)}{(-s)(-s+1)\cdots (-s+n-1)}\end{eqnarray}$$
 $n$
such that
$n$
such that
 $-s+n$
is positive.
$-s+n$
is positive.(ii) For
 $s>0$
we have
$s>0$
we have  $$\begin{eqnarray}\mathscr{R}^{-s}f(z)=\frac{1}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{\infty }t^{s}e^{-t\mathscr{R}}f(z)\,\frac{dt}{t}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{R}^{-s}f(z)=\frac{1}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{\infty }t^{s}e^{-t\mathscr{R}}f(z)\,\frac{dt}{t}.\end{eqnarray}$$
Proof. We prove (i); the proof for (ii) is simpler.
In [Reference Cho, Choe and Koo4, Proposition 2.2], we calculated the size of Taylor coefficients as following:
for a given multi-index
![]() $\unicode[STIX]{x1D6FC}$
where
$\unicode[STIX]{x1D6FC}$
where
![]() $\unicode[STIX]{x1D6FC}_{j}^{-\unicode[STIX]{x1D6FC}_{j}/2}$
is understood to be
$\unicode[STIX]{x1D6FC}_{j}^{-\unicode[STIX]{x1D6FC}_{j}/2}$
is understood to be
![]() $1$
when
$1$
when
![]() $\unicode[STIX]{x1D6FC}_{j}=0$
.
$\unicode[STIX]{x1D6FC}_{j}=0$
.
For
![]() $f\in F^{2}$
let
$f\in F^{2}$
let
be the orthonormal decomposition of
![]() $f$
, where
$f$
, where
![]() $c_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}f(0)/\sqrt{\unicode[STIX]{x1D6FC}!}$
and
$c_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}f(0)/\sqrt{\unicode[STIX]{x1D6FC}!}$
and
![]() $e_{\unicode[STIX]{x1D6FC}}(z)=z^{\unicode[STIX]{x1D6FC}}/\sqrt{\unicode[STIX]{x1D6FC}!}$
. Note that
$e_{\unicode[STIX]{x1D6FC}}(z)=z^{\unicode[STIX]{x1D6FC}}/\sqrt{\unicode[STIX]{x1D6FC}!}$
. Note that
By (2.1) and (2.2), it follows that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}|c_{\unicode[STIX]{x1D6FC}}||e_{\unicode[STIX]{x1D6FC}}(z)|\int _{0}^{\infty }|e^{-(2|\unicode[STIX]{x1D6FC}|+n)t}-1|\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|c_{\unicode[STIX]{x1D6FC}}||e_{\unicode[STIX]{x1D6FC}}(z)|\,(2|\unicode[STIX]{x1D6FC}|+n)^{s}|\unicode[STIX]{x1D6E4}(-s)|\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}}e^{|\unicode[STIX]{x1D6FC}|/2}\biggl(\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6FC}_{j}^{-\unicode[STIX]{x1D6FC}_{j}/2}\biggr)(2|\unicode[STIX]{x1D6FC}|+n)^{s}|z^{\unicode[STIX]{x1D6FC}}|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}|c_{\unicode[STIX]{x1D6FC}}||e_{\unicode[STIX]{x1D6FC}}(z)|\int _{0}^{\infty }|e^{-(2|\unicode[STIX]{x1D6FC}|+n)t}-1|\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|c_{\unicode[STIX]{x1D6FC}}||e_{\unicode[STIX]{x1D6FC}}(z)|\,(2|\unicode[STIX]{x1D6FC}|+n)^{s}|\unicode[STIX]{x1D6E4}(-s)|\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}}e^{|\unicode[STIX]{x1D6FC}|/2}\biggl(\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6FC}_{j}^{-\unicode[STIX]{x1D6FC}_{j}/2}\biggr)(2|\unicode[STIX]{x1D6FC}|+n)^{s}|z^{\unicode[STIX]{x1D6FC}}|.\nonumber\end{eqnarray}$$
We note that the power series on the right side of the inequality above is convergent for every
![]() $z\in \mathbb{C}^{n}$
. By the dominated convergence theorem, we have
$z\in \mathbb{C}^{n}$
. By the dominated convergence theorem, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(-s)\mathscr{R}^{s}f(z) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}c_{\unicode[STIX]{x1D6FC}}e_{\unicode[STIX]{x1D6FC}}(z)\,(2|\unicode[STIX]{x1D6FC}|+n)^{s}\unicode[STIX]{x1D6E4}(-s)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}c_{\unicode[STIX]{x1D6FC}}e_{\unicode[STIX]{x1D6FC}}(z)\int _{0}^{\infty }(e^{-(2|\unicode[STIX]{x1D6FC}|+n)t}-1)\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D6FC}}c_{\unicode[STIX]{x1D6FC}}e_{\unicode[STIX]{x1D6FC}}(z)(e^{-(2|\unicode[STIX]{x1D6FC}|+n)t}-1)\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\frac{[e^{-t\mathscr{R}}f(z)-f(z)]}{t^{s}}\,\frac{dt}{t}.\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(-s)\mathscr{R}^{s}f(z) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}c_{\unicode[STIX]{x1D6FC}}e_{\unicode[STIX]{x1D6FC}}(z)\,(2|\unicode[STIX]{x1D6FC}|+n)^{s}\unicode[STIX]{x1D6E4}(-s)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}c_{\unicode[STIX]{x1D6FC}}e_{\unicode[STIX]{x1D6FC}}(z)\int _{0}^{\infty }(e^{-(2|\unicode[STIX]{x1D6FC}|+n)t}-1)\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D6FC}}c_{\unicode[STIX]{x1D6FC}}e_{\unicode[STIX]{x1D6FC}}(z)(e^{-(2|\unicode[STIX]{x1D6FC}|+n)t}-1)\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\frac{[e^{-t\mathscr{R}}f(z)-f(z)]}{t^{s}}\,\frac{dt}{t}.\square\nonumber\end{eqnarray}$$
Remark 2.5. We refer to [Reference Cho, Choe and Koo4] for another fractional derivatives. In [Reference Cho, Choe and Koo4], the following derivative
![]() ${\mathcal{D}}^{s}f$
is given by
${\mathcal{D}}^{s}f$
is given by
We remark that our definition of
![]() $\mathscr{R}^{s}f$
is slightly different from
$\mathscr{R}^{s}f$
is slightly different from
![]() ${\mathcal{D}}^{s}f$
, but they are asymptotically the same in the sense that
${\mathcal{D}}^{s}f$
, but they are asymptotically the same in the sense that
![]() $\unicode[STIX]{x1D6E4}(n+s+|\unicode[STIX]{x1D6FC}|)/\unicode[STIX]{x1D6E4}(n+|\unicode[STIX]{x1D6FC}|)\approx (2|\unicode[STIX]{x1D6FC}|+n)^{s}$
as
$\unicode[STIX]{x1D6E4}(n+s+|\unicode[STIX]{x1D6FC}|)/\unicode[STIX]{x1D6E4}(n+|\unicode[STIX]{x1D6FC}|)\approx (2|\unicode[STIX]{x1D6FC}|+n)^{s}$
as
![]() $|\unicode[STIX]{x1D6FC}|\rightarrow \infty$
by Stirling’s formula.
$|\unicode[STIX]{x1D6FC}|\rightarrow \infty$
by Stirling’s formula.
3 Estimates of the reproducing kernel for
 $F_{\mathscr{R}}^{s,2}$
$F_{\mathscr{R}}^{s,2}$
In what follows we use the conventional multi-index notation. Thus for an
![]() $n$
-tuple
$n$
-tuple
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
of nonnegative integers we write
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
of nonnegative integers we write
where
![]() $\unicode[STIX]{x2202}_{j}$
denotes partial differentiation with respect to the
$\unicode[STIX]{x2202}_{j}$
denotes partial differentiation with respect to the
![]() $j$
th component. If
$j$
th component. If
![]() $z=(z_{1},\ldots ,z_{n})$
, then
$z=(z_{1},\ldots ,z_{n})$
, then
![]() $z^{\unicode[STIX]{x1D6FC}}=z_{1}^{\unicode[STIX]{x1D6FC}_{1}}\cdots z_{n}^{\unicode[STIX]{x1D6FC}_{n}}$
.
$z^{\unicode[STIX]{x1D6FC}}=z_{1}^{\unicode[STIX]{x1D6FC}_{1}}\cdots z_{n}^{\unicode[STIX]{x1D6FC}_{n}}$
.
First we get pointwise size estimates for the fractional radial derivatives of the Fock kernel as following.
Theorem 3.1. Given
![]() $s$
real, there are positive constants
$s$
real, there are positive constants
![]() $C=C(s)>0$
such that
$C=C(s)>0$
such that
for
![]() $z,w\in \mathbb{C}^{n}$
.
$z,w\in \mathbb{C}^{n}$
.
Proof. Since
the cases
![]() $s=0,1$
are trivial.
$s=0,1$
are trivial.
Let
![]() $0<s<1$
. By (i) of Proposition 2.4, we have
$0<s<1$
. By (i) of Proposition 2.4, we have
Now
 $$\begin{eqnarray}\displaystyle e^{-t\mathscr{R}}(e^{z\cdot \overline{w}}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}\frac{z^{\unicode[STIX]{x1D6FC}}\overline{w}^{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}!}e^{-(2|\unicode[STIX]{x1D6FC}|+n)t}\nonumber\\ \displaystyle & = & \displaystyle \exp (e^{-2t}z\cdot \overline{w})e^{-nt}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e^{-t\mathscr{R}}(e^{z\cdot \overline{w}}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}\frac{z^{\unicode[STIX]{x1D6FC}}\overline{w}^{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}!}e^{-(2|\unicode[STIX]{x1D6FC}|+n)t}\nonumber\\ \displaystyle & = & \displaystyle \exp (e^{-2t}z\cdot \overline{w})e^{-nt}.\nonumber\end{eqnarray}$$
Thus
We write the integral on the right-hand side of (3.1) as the sum of two pieces
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
defined by
$I_{2}$
defined by
and
Given
![]() $z,w\in \mathbb{C}^{n}$
, put
$z,w\in \mathbb{C}^{n}$
, put
![]() $x=\text{Re}(z\cdot \overline{w})$
for short. Then
$x=\text{Re}(z\cdot \overline{w})$
for short. Then
 $$\begin{eqnarray}\displaystyle |I_{2}| & {\lesssim} & \displaystyle \int _{1}^{\infty }[\exp (e^{-2t}x)e^{-nt}+e^{x}]\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \left\{\begin{array}{@{}ll@{}}1 & \text{if }x\leqslant 1,\\ e^{x} & \text{if }x>1.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |I_{2}| & {\lesssim} & \displaystyle \int _{1}^{\infty }[\exp (e^{-2t}x)e^{-nt}+e^{x}]\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \left\{\begin{array}{@{}ll@{}}1 & \text{if }x\leqslant 1,\\ e^{x} & \text{if }x>1.\end{array}\right.\nonumber\end{eqnarray}$$
Also,
 $$\begin{eqnarray}\displaystyle |I_{1}| & {\lesssim} & \displaystyle e^{x}\int _{0}^{1}|\text{exp}(-(1-e^{-2t})z\cdot \overline{w}-nt)-1|\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & = & \displaystyle e^{x}\int _{0}^{1}|E_{1}(-(1-e^{-2t})z\cdot \overline{w}-nt)|\,\frac{dt}{t^{1+s}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |I_{1}| & {\lesssim} & \displaystyle e^{x}\int _{0}^{1}|\text{exp}(-(1-e^{-2t})z\cdot \overline{w}-nt)-1|\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & = & \displaystyle e^{x}\int _{0}^{1}|E_{1}(-(1-e^{-2t})z\cdot \overline{w}-nt)|\,\frac{dt}{t^{1+s}}.\nonumber\end{eqnarray}$$
Here
![]() $E_{s}(x)$
is the truncated exponential function (see Definition A.1 in Appendix A). Note that (see (A1))
$E_{s}(x)$
is the truncated exponential function (see Definition A.1 in Appendix A). Note that (see (A1))
Then
Hence we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}|E_{1}(-(1-e^{-2t})z\cdot \overline{w}-nt)|\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,\int _{0}^{1}|(1-e^{-2t})z\cdot \overline{w}+nt|\int _{0}^{1}e^{-\unicode[STIX]{x1D70C}\{(1-e^{-2t})x+nt\}}\,d\unicode[STIX]{x1D70C}\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{1}\biggl|\frac{1-e^{-2t}}{t}z\cdot \overline{w}+n\biggr|\int _{0}^{1}e^{-\unicode[STIX]{x1D70C}\{(1-e^{-2t})x+nt\}}\,d\unicode[STIX]{x1D70C}\,\frac{dt}{t^{s}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}|E_{1}(-(1-e^{-2t})z\cdot \overline{w}-nt)|\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,\int _{0}^{1}|(1-e^{-2t})z\cdot \overline{w}+nt|\int _{0}^{1}e^{-\unicode[STIX]{x1D70C}\{(1-e^{-2t})x+nt\}}\,d\unicode[STIX]{x1D70C}\,\frac{dt}{t^{1+s}}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{1}\biggl|\frac{1-e^{-2t}}{t}z\cdot \overline{w}+n\biggr|\int _{0}^{1}e^{-\unicode[STIX]{x1D70C}\{(1-e^{-2t})x+nt\}}\,d\unicode[STIX]{x1D70C}\,\frac{dt}{t^{s}}.\nonumber\end{eqnarray}$$
Since
there exist
![]() $c>0$
such that
$c>0$
such that
If
![]() $x\leqslant 1$
, then
$x\leqslant 1$
, then
So, in case
![]() $x\leqslant 1$
, we have
$x\leqslant 1$
, we have
 $$\begin{eqnarray}\displaystyle |\mathscr{R}^{s}(e^{z\cdot \overline{w}})| & {\lesssim} & \displaystyle 1+|z\cdot \overline{w}|\nonumber\\ \displaystyle & {\lesssim} & \displaystyle (1+|z\cdot \overline{w}|)^{s}e^{(1/2)|z||w|}\frac{(1+|z\cdot \overline{w}|)^{1-s}}{e^{(1/2)|z||w|}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle (1+|z\cdot \overline{w}|)^{s}e^{(1/2)|z||w|}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle (1+|z\cdot \overline{w}|)^{s}e^{(1/2)|z|^{2}+(1/2)|w|^{2}-(1/8)|z-w|^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathscr{R}^{s}(e^{z\cdot \overline{w}})| & {\lesssim} & \displaystyle 1+|z\cdot \overline{w}|\nonumber\\ \displaystyle & {\lesssim} & \displaystyle (1+|z\cdot \overline{w}|)^{s}e^{(1/2)|z||w|}\frac{(1+|z\cdot \overline{w}|)^{1-s}}{e^{(1/2)|z||w|}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle (1+|z\cdot \overline{w}|)^{s}e^{(1/2)|z||w|}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle (1+|z\cdot \overline{w}|)^{s}e^{(1/2)|z|^{2}+(1/2)|w|^{2}-(1/8)|z-w|^{2}}.\end{eqnarray}$$
Here we used the following inequality
If
![]() $x>1$
, by Fubini’s theorem, it follows that
$x>1$
, by Fubini’s theorem, it follows that
 $$\begin{eqnarray}\displaystyle \int _{0}^{1}\int _{0}^{1}e^{-c\unicode[STIX]{x1D70C}tx}\,d\unicode[STIX]{x1D70C}\,\frac{dt}{t^{s}} & = & \displaystyle \int _{0}^{1}\int _{0}^{1}e^{-c\unicode[STIX]{x1D70C}tx}t^{-s}\,dt\,d\unicode[STIX]{x1D70C}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle x^{s-1}\unicode[STIX]{x1D6E4}(1-s)\int _{0}^{1}\unicode[STIX]{x1D70C}^{s-1}\,d\unicode[STIX]{x1D70C}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle x^{s-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{1}\int _{0}^{1}e^{-c\unicode[STIX]{x1D70C}tx}\,d\unicode[STIX]{x1D70C}\,\frac{dt}{t^{s}} & = & \displaystyle \int _{0}^{1}\int _{0}^{1}e^{-c\unicode[STIX]{x1D70C}tx}t^{-s}\,dt\,d\unicode[STIX]{x1D70C}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle x^{s-1}\unicode[STIX]{x1D6E4}(1-s)\int _{0}^{1}\unicode[STIX]{x1D70C}^{s-1}\,d\unicode[STIX]{x1D70C}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle x^{s-1}.\nonumber\end{eqnarray}$$
Hence, in case
![]() $x>1$
, we have
$x>1$
, we have
For the case
![]() $x=\text{Re}(z\cdot \overline{w})>1$
, we write
$x=\text{Re}(z\cdot \overline{w})>1$
, we write
![]() $\text{Re}(z\cdot \overline{w})=|z||w|\cos \unicode[STIX]{x1D703}$
, where
$\text{Re}(z\cdot \overline{w})=|z||w|\cos \unicode[STIX]{x1D703}$
, where
![]() $\unicode[STIX]{x1D703}$
is the angle between
$\unicode[STIX]{x1D703}$
is the angle between
![]() $z$
and
$z$
and
![]() $w$
identified as real vectors in
$w$
identified as real vectors in
![]() $\mathbb{R}^{2n}$
, and
$\mathbb{R}^{2n}$
, and
![]() $\unicode[STIX]{x1D6FF}=\cos ^{-1}(\frac{1}{4})$
. If
$\unicode[STIX]{x1D6FF}=\cos ^{-1}(\frac{1}{4})$
. If
![]() $|\unicode[STIX]{x1D703}|\leqslant \unicode[STIX]{x1D6FF}$
, then
$|\unicode[STIX]{x1D703}|\leqslant \unicode[STIX]{x1D6FF}$
, then
Hence we have
If
![]() $\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}/2$
, then
$\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}/2$
, then
Hence
 $$\begin{eqnarray}\displaystyle e^{x}|z\cdot \overline{w}|x^{s-1} & {\leqslant} & \displaystyle e^{(1/2)|z||w|}|z\cdot \overline{w}|^{s}\frac{|z\cdot \overline{w}|^{1-s}}{x^{1-s}e^{(1/4)|z\cdot \overline{w}|}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle e^{(1/2)|z|^{2}+(1/2)|w|^{2}-(1/8)|z-w|^{2}}|z\cdot \overline{w}|^{s}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e^{x}|z\cdot \overline{w}|x^{s-1} & {\leqslant} & \displaystyle e^{(1/2)|z||w|}|z\cdot \overline{w}|^{s}\frac{|z\cdot \overline{w}|^{1-s}}{x^{1-s}e^{(1/4)|z\cdot \overline{w}|}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle e^{(1/2)|z|^{2}+(1/2)|w|^{2}-(1/8)|z-w|^{2}}|z\cdot \overline{w}|^{s}.\end{eqnarray}$$
This, together with (3.2), yields the asserted estimate for
![]() $0<s<1$
.
$0<s<1$
.
Now, assume
![]() $s>1$
. Let
$s>1$
. Let
![]() $m$
be the greatest nonnegative integer less than
$m$
be the greatest nonnegative integer less than
![]() $s$
. Then
$s$
. Then
 $$\begin{eqnarray}\displaystyle \mathscr{R}^{s}(e^{z\cdot \overline{w}}) & = & \displaystyle \mathscr{R}^{s-m}\mathscr{R}^{m}(e^{z\cdot \overline{w}})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(m-s)}\int _{0}^{\infty }[\mathscr{R}^{m}\exp \big(e^{-2t}z\cdot \overline{w}\big)e^{-nt}-\mathscr{R}^{m}e^{z\cdot \overline{w}}]\,\frac{dt}{t^{1+s-m}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{R}^{s}(e^{z\cdot \overline{w}}) & = & \displaystyle \mathscr{R}^{s-m}\mathscr{R}^{m}(e^{z\cdot \overline{w}})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(m-s)}\int _{0}^{\infty }[\mathscr{R}^{m}\exp \big(e^{-2t}z\cdot \overline{w}\big)e^{-nt}-\mathscr{R}^{m}e^{z\cdot \overline{w}}]\,\frac{dt}{t^{1+s-m}}.\nonumber\end{eqnarray}$$
Note that
and
for some nonnegative integers
![]() $\ell _{j}$
. Thus
$\ell _{j}$
. Thus
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathscr{R}^{s}(e^{z\cdot \overline{w}})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{\unicode[STIX]{x1D6E4}(m-s)}\mathop{\sum }_{j=0}^{m}\ell _{j}(z\cdot \overline{w})^{j}\int _{0}^{\infty }[\exp (e^{-2t}z\cdot \overline{w})e^{-(2j+n)t}-e^{z\cdot \overline{w}}]\,\frac{dt}{t^{1+s-m}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathscr{R}^{s}(e^{z\cdot \overline{w}})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{\unicode[STIX]{x1D6E4}(m-s)}\mathop{\sum }_{j=0}^{m}\ell _{j}(z\cdot \overline{w})^{j}\int _{0}^{\infty }[\exp (e^{-2t}z\cdot \overline{w})e^{-(2j+n)t}-e^{z\cdot \overline{w}}]\,\frac{dt}{t^{1+s-m}}.\nonumber\end{eqnarray}$$
We write the integral on the right-hand side of the above equation as the sum of two pieces
![]() $J_{1}$
and
$J_{1}$
and
![]() $J_{2}$
defined by
$J_{2}$
defined by
and
Then
and
 $$\begin{eqnarray}\displaystyle |J_{1}| & {\lesssim} & \displaystyle e^{x}\int _{0}^{1}|E_{1}(-(1-e^{-2t})z\cdot \overline{w}-(2j+n)t)|\,\frac{dt}{t^{1+s-m}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle e^{x}|z\cdot \overline{w}|\int _{0}^{1}\int _{0}^{1}e^{-c\unicode[STIX]{x1D70C}tx}\,d\unicode[STIX]{x1D70C}\,\frac{dt}{t^{s-m}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |J_{1}| & {\lesssim} & \displaystyle e^{x}\int _{0}^{1}|E_{1}(-(1-e^{-2t})z\cdot \overline{w}-(2j+n)t)|\,\frac{dt}{t^{1+s-m}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle e^{x}|z\cdot \overline{w}|\int _{0}^{1}\int _{0}^{1}e^{-c\unicode[STIX]{x1D70C}tx}\,d\unicode[STIX]{x1D70C}\,\frac{dt}{t^{s-m}}.\nonumber\end{eqnarray}$$
These yield the asserted estimate for
![]() $s>1$
.
$s>1$
.
Now for
![]() $s>0$
, by (ii) of Proposition 2.4, we have
$s>0$
, by (ii) of Proposition 2.4, we have
 $$\begin{eqnarray}\displaystyle \mathscr{R}^{-s}(e^{z\cdot \overline{w}}) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{\infty }e^{-t\mathscr{R}}(e^{z\cdot \overline{w}})\,\frac{dt}{t^{1-s}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{\infty }\exp (e^{-2t}z\cdot \overline{w})e^{-nt}\,\frac{dt}{t^{1-s}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{R}^{-s}(e^{z\cdot \overline{w}}) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{\infty }e^{-t\mathscr{R}}(e^{z\cdot \overline{w}})\,\frac{dt}{t^{1-s}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{\infty }\exp (e^{-2t}z\cdot \overline{w})e^{-nt}\,\frac{dt}{t^{1-s}}.\nonumber\end{eqnarray}$$
Hence
If
![]() $x=\text{Re}(z\cdot \overline{w})\leqslant 1$
, then
$x=\text{Re}(z\cdot \overline{w})\leqslant 1$
, then
Now we assume that
![]() $x=\text{Re}(z\cdot \overline{w})>1$
. Then
$x=\text{Re}(z\cdot \overline{w})>1$
. Then
 $$\begin{eqnarray}\displaystyle |\mathscr{R}^{-s}(e^{z\cdot \overline{w}})| & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\mathop{\sum }_{k=0}^{\infty }\int _{0}^{\infty }\frac{(e^{-2t}x)^{k}}{k!}e^{-nt}\,\frac{dt}{t^{1-s}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k}}{k!}\frac{1}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{\infty }e^{-(2k+n)t}\,\frac{dt}{t^{1-s}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k}}{(2k+n)^{s}k!}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathscr{R}^{-s}(e^{z\cdot \overline{w}})| & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\mathop{\sum }_{k=0}^{\infty }\int _{0}^{\infty }\frac{(e^{-2t}x)^{k}}{k!}e^{-nt}\,\frac{dt}{t^{1-s}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k}}{k!}\frac{1}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{\infty }e^{-(2k+n)t}\,\frac{dt}{t^{1-s}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k}}{(2k+n)^{s}k!}.\nonumber\end{eqnarray}$$
By Stirling’s formula, it follows that
Hence, by Corollary A.4, we have
 $$\begin{eqnarray}\displaystyle |\mathscr{R}^{-s}(e^{z\cdot \overline{w}})| & {\lesssim} & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k+s}}{\unicode[STIX]{x1D6E4}(k+1+s)}x^{-s}\nonumber\\ \displaystyle & = & \displaystyle E_{s}(x)x^{-s}\nonumber\\ \displaystyle & {\approx} & \displaystyle e^{x}x^{-s},\quad x>1.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathscr{R}^{-s}(e^{z\cdot \overline{w}})| & {\lesssim} & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k+s}}{\unicode[STIX]{x1D6E4}(k+1+s)}x^{-s}\nonumber\\ \displaystyle & = & \displaystyle E_{s}(x)x^{-s}\nonumber\\ \displaystyle & {\approx} & \displaystyle e^{x}x^{-s},\quad x>1.\end{eqnarray}$$
For the case
![]() $x=\text{Re}(z\cdot \overline{w})>1$
, we write
$x=\text{Re}(z\cdot \overline{w})>1$
, we write
![]() $\text{Re}(z\cdot \overline{w})=|z||w|\cos \unicode[STIX]{x1D703}$
, where
$\text{Re}(z\cdot \overline{w})=|z||w|\cos \unicode[STIX]{x1D703}$
, where
![]() $\unicode[STIX]{x1D703}$
is the angle between
$\unicode[STIX]{x1D703}$
is the angle between
![]() $z$
and
$z$
and
![]() $w$
identified as real vectors in
$w$
identified as real vectors in
![]() $\mathbb{R}^{2n}$
, and
$\mathbb{R}^{2n}$
, and
![]() $\unicode[STIX]{x1D6FF}=\cos ^{-1}(\frac{1}{4})$
. It is easily seen from (3.5) that the required estimate holds when
$\unicode[STIX]{x1D6FF}=\cos ^{-1}(\frac{1}{4})$
. It is easily seen from (3.5) that the required estimate holds when
![]() $|\unicode[STIX]{x1D703}|\leqslant \unicode[STIX]{x1D6FF}$
, because
$|\unicode[STIX]{x1D703}|\leqslant \unicode[STIX]{x1D6FF}$
, because
![]() $x\approx |z||w|$
for such
$x\approx |z||w|$
for such
![]() $z$
and
$z$
and
![]() $w$
. So, assume
$w$
. So, assume
![]() $\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}/2$
. Note
$\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}/2$
. Note
![]() $x<\frac{1}{4}|z||w|$
for such
$x<\frac{1}{4}|z||w|$
for such
![]() $z$
and
$z$
and
![]() $w$
. We thus have by our choice of
$w$
. We thus have by our choice of
![]() $\unicode[STIX]{x1D6FF}$
$\unicode[STIX]{x1D6FF}$
 $$\begin{eqnarray}\displaystyle \frac{e^{x}}{x^{s}} & {\leqslant} & \displaystyle \frac{e^{(1/4)|z||w|}}{x^{s}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle e^{(1/4)|z||w|}\nonumber\\ \displaystyle & = & \displaystyle \frac{e^{(1/2)|z||w|}}{(|z||w|)^{s}}\frac{(|z||w|)^{s}}{e^{(1/4)|z||w|}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \frac{e^{(1/2)|z||w|}}{(|z||w|)^{s}},\quad x>1.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{e^{x}}{x^{s}} & {\leqslant} & \displaystyle \frac{e^{(1/4)|z||w|}}{x^{s}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle e^{(1/4)|z||w|}\nonumber\\ \displaystyle & = & \displaystyle \frac{e^{(1/2)|z||w|}}{(|z||w|)^{s}}\frac{(|z||w|)^{s}}{e^{(1/4)|z||w|}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \frac{e^{(1/2)|z||w|}}{(|z||w|)^{s}},\quad x>1.\end{eqnarray}$$
This, together with (3.5), yields the asserted estimate for
![]() $x>1$
. This completes the proof.◻
$x>1$
. This completes the proof.◻
It is the well-known formula [Reference Aronszajn1] that
where
![]() $\{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\}$
is any orthonormal basis for
$\{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\}$
is any orthonormal basis for
![]() $F_{\mathscr{R}}^{s,2}$
.
$F_{\mathscr{R}}^{s,2}$
.
Lemma 3.2. Let
![]() $s$
be real and
$s$
be real and
![]() $\unicode[STIX]{x1D6FC}$
be a multi-index of nonnegative integers. Then
$\unicode[STIX]{x1D6FC}$
be a multi-index of nonnegative integers. Then
Proof. Since
![]() $\mathscr{R}^{s/2}z^{\unicode[STIX]{x1D6FC}}=(2|\unicode[STIX]{x1D6FC}|+n)^{s/2}z^{\unicode[STIX]{x1D6FC}}$
, we have
$\mathscr{R}^{s/2}z^{\unicode[STIX]{x1D6FC}}=(2|\unicode[STIX]{x1D6FC}|+n)^{s/2}z^{\unicode[STIX]{x1D6FC}}$
, we have
Theorem 3.3. Let
![]() $s\in \mathbb{R}$
. Then
$s\in \mathbb{R}$
. Then
and there are positive constants
![]() $C=C(s)>0$
such that
$C=C(s)>0$
such that
for
![]() $z,w\in \mathbb{C}^{n}$
.
$z,w\in \mathbb{C}^{n}$
.
Proof. By Lemma 3.2, we get
 $$\begin{eqnarray}\displaystyle K_{s}(z,w) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \mathbb{N}_{0}^{n}}\frac{z^{\unicode[STIX]{x1D6FC}}\overline{w}^{\unicode[STIX]{x1D6FC}}}{\Vert z^{\unicode[STIX]{x1D6FC}}\Vert _{F_{\mathscr{R}}^{s,2}}^{2}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}\frac{z^{\unicode[STIX]{x1D6FC}}\overline{w}^{\unicode[STIX]{x1D6FC}}}{(2|\unicode[STIX]{x1D6FC}|+n)^{s}\unicode[STIX]{x1D6FC}!}\nonumber\\ \displaystyle & = & \displaystyle \mathscr{R}_{z}^{-s}(e^{z\cdot \overline{w}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{s}(z,w) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \mathbb{N}_{0}^{n}}\frac{z^{\unicode[STIX]{x1D6FC}}\overline{w}^{\unicode[STIX]{x1D6FC}}}{\Vert z^{\unicode[STIX]{x1D6FC}}\Vert _{F_{\mathscr{R}}^{s,2}}^{2}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}}\frac{z^{\unicode[STIX]{x1D6FC}}\overline{w}^{\unicode[STIX]{x1D6FC}}}{(2|\unicode[STIX]{x1D6FC}|+n)^{s}\unicode[STIX]{x1D6FC}!}\nonumber\\ \displaystyle & = & \displaystyle \mathscr{R}_{z}^{-s}(e^{z\cdot \overline{w}}).\nonumber\end{eqnarray}$$
Hence the size estimates of
![]() $K_{s}(z,w)$
follow from Theorem 3.1.◻
$K_{s}(z,w)$
follow from Theorem 3.1.◻
4 Auxiliary integral estimates
It follows that the fractional Fock–Sobolev spaces are realized as the weighted Fock spaces that do not involve derivatives. To prove the results we introduce an auxiliary integral estimate for
![]() $\unicode[STIX]{x1D6EC}$
defined by
$\unicode[STIX]{x1D6EC}$
defined by
To handle the case
![]() $1\leqslant p<\infty$
and for other purposes later, we introduce an integral operator induced by
$1\leqslant p<\infty$
and for other purposes later, we introduce an integral operator induced by
![]() $\unicode[STIX]{x1D6EC}$
. Given
$\unicode[STIX]{x1D6EC}$
. Given
![]() $s$
real, we consider an integral operator
$s$
real, we consider an integral operator
![]() $L_{s}$
defined by
$L_{s}$
defined by
for
![]() $\unicode[STIX]{x1D713}$
which makes the above integral well-defined.
$\unicode[STIX]{x1D713}$
which makes the above integral well-defined.
Lemma 4.1. [Reference Cho, Choe and Koo4]
Given
![]() $s$
real, the operator
$s$
real, the operator
![]() $L_{s}$
is bounded on
$L_{s}$
is bounded on
![]() $L_{G}^{p}$
for any
$L_{G}^{p}$
for any
![]() $1\leqslant p\leqslant \infty$
.
$1\leqslant p\leqslant \infty$
.
The following Jensen-type inequality is needed to handle the case
![]() $0<p\leqslant 1$
.
$0<p\leqslant 1$
.
Lemma 4.2. [Reference Cho, Choe and Koo4]
Given
![]() $0<p\leqslant 1$
,
$0<p\leqslant 1$
,
![]() $a>0$
and
$a>0$
and
![]() $s$
real, there is a constant
$s$
real, there is a constant
![]() $C=C(p,a,s)>0$
such that
$C=C(p,a,s)>0$
such that
for
![]() $f\in H(\mathbb{C}^{n})$
.
$f\in H(\mathbb{C}^{n})$
.
Lemma 4.3. [Reference Cho, Choe and Koo4]
Let
![]() $0<p<\infty$
and
$0<p<\infty$
and
![]() $\unicode[STIX]{x1D6FC}$
be an arbitrary real number. Then there is
$\unicode[STIX]{x1D6FC}$
be an arbitrary real number. Then there is
![]() $C=C(p,\unicode[STIX]{x1D6FC})>0$
such that
$C=C(p,\unicode[STIX]{x1D6FC})>0$
such that
5 Fourier type characterization
Cho and Zhu [Reference Cho and Zhu6] studied Fock–Sobolev spaces of positive integer order. For any positive integer
![]() $m$
and
$m$
and
![]() $0<p\leqslant \infty$
we consider the space
$0<p\leqslant \infty$
we consider the space
![]() $F^{m,p}$
consisting of entire functions
$F^{m,p}$
consisting of entire functions
![]() $f$
on
$f$
on
![]() $\mathbb{C}^{n}$
such that
$\mathbb{C}^{n}$
such that
where
![]() $\Vert ~\Vert _{p}$
is the norm in
$\Vert ~\Vert _{p}$
is the norm in
![]() $F^{p}$
. See [Reference Hall and Lewkeeratiyutkul8, Reference Radha and Thangavelu12] for other similar Sobolev spaces. Cho and Zhu [Reference Cho and Zhu6] proved a useful Fourier type characterization of the Fock–Sobolev space of integer order as following.
$F^{p}$
. See [Reference Hall and Lewkeeratiyutkul8, Reference Radha and Thangavelu12] for other similar Sobolev spaces. Cho and Zhu [Reference Cho and Zhu6] proved a useful Fourier type characterization of the Fock–Sobolev space of integer order as following.
Theorem 5.1. [Reference Cho and Zhu6]
Suppose
![]() $0<p\leqslant \infty$
,
$0<p\leqslant \infty$
,
![]() $m$
is a nonnegative integer, and
$m$
is a nonnegative integer, and
![]() $f$
is an entire function on
$f$
is an entire function on
![]() $\mathbb{C}^{n}$
. Then
$\mathbb{C}^{n}$
. Then
![]() $f\in F^{m,p}$
if and only if the function
$f\in F^{m,p}$
if and only if the function
![]() $z^{\unicode[STIX]{x1D6FC}}f(z)$
is in
$z^{\unicode[STIX]{x1D6FC}}f(z)$
is in
![]() $F^{p}$
for all multi-indices
$F^{p}$
for all multi-indices
![]() $\unicode[STIX]{x1D6FC}$
with
$\unicode[STIX]{x1D6FC}$
with
![]() $|\unicode[STIX]{x1D6FC}|=m$
. Moreover,
$|\unicode[STIX]{x1D6FC}|=m$
. Moreover,
![]() $\Vert f\Vert _{F^{m,p}}$
is comparable to the norm of the function
$\Vert f\Vert _{F^{m,p}}$
is comparable to the norm of the function
![]() $|z|^{m}f(z)$
in
$|z|^{m}f(z)$
in
![]() $L_{G}^{p}$
.
$L_{G}^{p}$
.
The purpose of the current paper is to extend the notion of the Fock–Sobolev spaces to the case of fractional orders allowed to be any real number.
Theorem 5.2. Let
![]() $s\in \mathbb{R}$
and
$s\in \mathbb{R}$
and
![]() $0<p\leqslant \infty$
. There is a constant
$0<p\leqslant \infty$
. There is a constant
![]() $C=C(s,p)>0$
such that
$C=C(s,p)>0$
such that
Proof. We now consider the cases
![]() $0<p<1$
and
$0<p<1$
and
![]() $1\leqslant p\leqslant \infty$
separately.
$1\leqslant p\leqslant \infty$
separately.
Assume
![]() $1\leqslant p\leqslant \infty$
. If the function
$1\leqslant p\leqslant \infty$
. If the function
![]() $(1+|w|)^{s}f(w)$
is in
$(1+|w|)^{s}f(w)$
is in
![]() $L_{G}^{p}$
, then
$L_{G}^{p}$
, then
Thus we obtain
The convergence of the integrals above follows from pointwise estimates for functions in Fock spaces. Hence it follows that
 $$\begin{eqnarray}\displaystyle |\mathscr{R}^{s/2}f(z)| & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70B}^{n}}\int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}(e^{z\cdot \overline{w}})||f(w)|e^{-|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|f(w)|(1+|w|)^{s}\biggl(\frac{1+|z|}{1+|w|}\biggr)^{s/2}\unicode[STIX]{x1D6EC}(z,w)e^{-|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & = & \displaystyle L_{s}((1+|w|)^{s}|f|)(z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathscr{R}^{s/2}f(z)| & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70B}^{n}}\int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}(e^{z\cdot \overline{w}})||f(w)|e^{-|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|f(w)|(1+|w|)^{s}\biggl(\frac{1+|z|}{1+|w|}\biggr)^{s/2}\unicode[STIX]{x1D6EC}(z,w)e^{-|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & = & \displaystyle L_{s}((1+|w|)^{s}|f|)(z).\nonumber\end{eqnarray}$$
By Lemma 4.1, we have
Now let
![]() $0<p<1$
. Then, by Lemma 4.2 and Theorem 3.1,
$0<p<1$
. Then, by Lemma 4.2 and Theorem 3.1,
 $$\begin{eqnarray}\displaystyle |\mathscr{R}^{s/2}f(z)|^{p} & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}(e^{z\cdot \overline{w}})|^{p}|f(w)|^{p}e^{-p|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|f(w)|^{p}(1+|w|)^{sp/2}(1+|z|)^{sp/2}\unicode[STIX]{x1D6EC}(z,w)^{p}e^{-p|w|^{2}}\,dV(w)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathscr{R}^{s/2}f(z)|^{p} & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}(e^{z\cdot \overline{w}})|^{p}|f(w)|^{p}e^{-p|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|f(w)|^{p}(1+|w|)^{sp/2}(1+|z|)^{sp/2}\unicode[STIX]{x1D6EC}(z,w)^{p}e^{-p|w|^{2}}\,dV(w)\nonumber\end{eqnarray}$$
or
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(z)|^{p}e^{-(p/2)|z|^{2}}\,dV(z)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \,\int _{\mathbb{C}^{n}}|f(w)|^{p}(1+|w|)^{sp/2}e^{-p|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\mathbb{C}^{n}}(1+|z|)^{sp/2}\unicode[STIX]{x1D6EC}(z,w)^{p}e^{-(p/2)|z|^{2}}\,dV(z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(z)|^{p}e^{-(p/2)|z|^{2}}\,dV(z)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \,\int _{\mathbb{C}^{n}}|f(w)|^{p}(1+|w|)^{sp/2}e^{-p|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\mathbb{C}^{n}}(1+|z|)^{sp/2}\unicode[STIX]{x1D6EC}(z,w)^{p}e^{-(p/2)|z|^{2}}\,dV(z).\nonumber\end{eqnarray}$$
Now, by Lemma 4.3, it follows that
Hence
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(z)|^{p}e^{-(p/2)|z|^{2}}\,dV(z)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \int _{\mathbb{C}^{n}}|f(w)|^{p}(1+|w|)^{sp}e^{-(p/2)|w|^{2}}\,dV(w).\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(z)|^{p}e^{-(p/2)|z|^{2}}\,dV(z)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \int _{\mathbb{C}^{n}}|f(w)|^{p}(1+|w|)^{sp}e^{-(p/2)|w|^{2}}\,dV(w).\square\nonumber\end{eqnarray}$$
Theorem 5.3. Suppose
![]() $0<p\leqslant \infty$
and
$0<p\leqslant \infty$
and
![]() $s$
is a real number. Then there is a constant
$s$
is a real number. Then there is a constant
![]() $C=C(s,p)>0$
such that
$C=C(s,p)>0$
such that
for all
![]() $f\in F_{\mathscr{R}}^{s,p}$
.
$f\in F_{\mathscr{R}}^{s,p}$
.
Proof. Let
![]() $1\leqslant p\leqslant \infty$
. From the reproducing formula for
$1\leqslant p\leqslant \infty$
. From the reproducing formula for
![]() $\mathscr{R}^{s/2}f$
we obtain
$\mathscr{R}^{s/2}f$
we obtain
This together with Theorem 3.1 shows that
 $$\begin{eqnarray}\displaystyle (1+|z|)^{s}|f(z)| & {\lesssim} & \displaystyle (1+|z|)^{s}\int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(w)||\mathscr{R}^{-s/2}(e^{z\cdot \overline{w}})|e^{-|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(w)|\biggl(\frac{1+|z|}{1+|w|}\biggr)^{s/2}\unicode[STIX]{x1D6EC}(z,w)e^{-|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & = & \displaystyle L_{s}(|\mathscr{R}^{s/2}f|)(z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (1+|z|)^{s}|f(z)| & {\lesssim} & \displaystyle (1+|z|)^{s}\int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(w)||\mathscr{R}^{-s/2}(e^{z\cdot \overline{w}})|e^{-|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(w)|\biggl(\frac{1+|z|}{1+|w|}\biggr)^{s/2}\unicode[STIX]{x1D6EC}(z,w)e^{-|w|^{2}}\,dV(w)\nonumber\\ \displaystyle & = & \displaystyle L_{s}(|\mathscr{R}^{s/2}f|)(z).\nonumber\end{eqnarray}$$
By Lemma 4.1, we have
When
![]() $0<p<1$
, it follows from Lemma 4.2 and Theorem 3.1 that
$0<p<1$
, it follows from Lemma 4.2 and Theorem 3.1 that
 $$\begin{eqnarray}\displaystyle |f(z)|^{p} & {\lesssim} & \displaystyle \biggl|\int _{\mathbb{C}^{n}}\mathscr{R}^{s/2}f(w)\mathscr{R}^{-s/2}(e^{z\cdot \overline{w}})e^{-|w|^{2}}\,dV(w)\biggr|^{p}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(w)\mathscr{R}^{-s/2}(e^{z\cdot \overline{w}})e^{-|w|^{2}}|^{p}\,dV(w)\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(w)|^{p}\frac{e^{(p/2)|z|^{2}-(p/2)|w|^{2}-(p/8)|z-w|^{2}}}{(1+|z|)^{sp/2}(1+|w|)^{sp/2}}\,dV(w).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |f(z)|^{p} & {\lesssim} & \displaystyle \biggl|\int _{\mathbb{C}^{n}}\mathscr{R}^{s/2}f(w)\mathscr{R}^{-s/2}(e^{z\cdot \overline{w}})e^{-|w|^{2}}\,dV(w)\biggr|^{p}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(w)\mathscr{R}^{-s/2}(e^{z\cdot \overline{w}})e^{-|w|^{2}}|^{p}\,dV(w)\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \int _{\mathbb{C}^{n}}|\mathscr{R}^{s/2}f(w)|^{p}\frac{e^{(p/2)|z|^{2}-(p/2)|w|^{2}-(p/8)|z-w|^{2}}}{(1+|z|)^{sp/2}(1+|w|)^{sp/2}}\,dV(w).\nonumber\end{eqnarray}$$
Fubini’s theorem shows that the integral
satisfies the following estimates:
Note that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{C}^{n}}\biggl(\frac{1+|z|}{1+|w|}\biggr)^{sp/2}e^{-(p/8)|z-w|^{2}}\,dV(z)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \,\int _{\mathbb{C}^{n}}(1+|z-w|)^{sp/2}e^{-(p/8)|z-w|^{2}}\,dV(z)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \,1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{C}^{n}}\biggl(\frac{1+|z|}{1+|w|}\biggr)^{sp/2}e^{-(p/8)|z-w|^{2}}\,dV(z)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \,\int _{\mathbb{C}^{n}}(1+|z-w|)^{sp/2}e^{-(p/8)|z-w|^{2}}\,dV(z)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \,1.\nonumber\end{eqnarray}$$
The proof is complete. ◻
Appendix. Truncated exponential functions
Let
![]() $m$
be a positive integer. We consider the left truncated exponential function of integer order
$m$
be a positive integer. We consider the left truncated exponential function of integer order
![]() $m$
,
$m$
,
![]() $E_{m}(\unicode[STIX]{x1D706})$
, defined by
$E_{m}(\unicode[STIX]{x1D706})$
, defined by
 $$\begin{eqnarray}\displaystyle E_{m}(\unicode[STIX]{x1D706}) & = & \displaystyle e^{\unicode[STIX]{x1D706}}-1-\unicode[STIX]{x1D706}-\frac{\unicode[STIX]{x1D706}^{2}}{2!}-\cdots -\frac{\unicode[STIX]{x1D706}^{m-1}}{(m-1)!}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D706}^{k+m}}{\unicode[STIX]{x1D6E4}(k+1+m)},\quad \unicode[STIX]{x1D706}\in \mathbb{C},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{m}(\unicode[STIX]{x1D706}) & = & \displaystyle e^{\unicode[STIX]{x1D706}}-1-\unicode[STIX]{x1D706}-\frac{\unicode[STIX]{x1D706}^{2}}{2!}-\cdots -\frac{\unicode[STIX]{x1D706}^{m-1}}{(m-1)!}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D706}^{k+m}}{\unicode[STIX]{x1D6E4}(k+1+m)},\quad \unicode[STIX]{x1D706}\in \mathbb{C},\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}$
is the classical gamma function.
$\unicode[STIX]{x1D6E4}$
is the classical gamma function.
It is easy to check that
which immediately yields a useful inequality
Now we consider the truncated exponential function of fractional order.
Definition A.1. Let
![]() $s\in \mathbb{R}$
. We define the generalized exponential function of fractional order
$s\in \mathbb{R}$
. We define the generalized exponential function of fractional order
![]() $s$
,
$s$
,
![]() $E_{s}(x)$
, by
$E_{s}(x)$
, by
We have the following integral representation of
![]() $E_{s}(x)$
:
$E_{s}(x)$
:
Proposition A.2. Let
![]() $s>0$
. Then
$s>0$
. Then
Proof. Note that the following well-known property of gamma functions
Thus
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k+s}}{\unicode[STIX]{x1D6E4}(k+1+s)} & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k+s}}{\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D6E4}(k+1)}\int _{0}^{1}(1-t)^{s-1}t^{k}\,dt\nonumber\\ \displaystyle & = & \displaystyle \frac{x^{s}}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{1}(1-t)^{s-1}e^{tx}\,dt\nonumber\\ \displaystyle & = & \displaystyle \frac{e^{x}}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{x}t^{s-1}e^{-t}\,dt.\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k+s}}{\unicode[STIX]{x1D6E4}(k+1+s)} & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k+s}}{\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D6E4}(k+1)}\int _{0}^{1}(1-t)^{s-1}t^{k}\,dt\nonumber\\ \displaystyle & = & \displaystyle \frac{x^{s}}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{1}(1-t)^{s-1}e^{tx}\,dt\nonumber\\ \displaystyle & = & \displaystyle \frac{e^{x}}{\unicode[STIX]{x1D6E4}(s)}\int _{0}^{x}t^{s-1}e^{-t}\,dt.\square\nonumber\end{eqnarray}$$
Proposition A.3. Let
![]() $s=m+r$
where
$s=m+r$
where
![]() $m$
is a nonnegative integer and
$m$
is a nonnegative integer and
![]() $0\leqslant r<1$
. Then
$0\leqslant r<1$
. Then
Proof. We have
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)} & = & \displaystyle \mathop{\sum }_{k=m+1}^{\infty }\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)}+\mathop{\sum }_{k=0}^{m}\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k+1-r}}{\unicode[STIX]{x1D6E4}(k+2-r)}+\mathop{\sum }_{k=0}^{m}\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)}\nonumber\\ \displaystyle & = & \displaystyle \frac{e^{x}}{\unicode[STIX]{x1D6E4}(1-r)}\int _{0}^{x}t^{-r}e^{-t}\,dt+\mathop{\sum }_{k=0}^{m}\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)}.\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)} & = & \displaystyle \mathop{\sum }_{k=m+1}^{\infty }\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)}+\mathop{\sum }_{k=0}^{m}\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{\infty }\frac{x^{k+1-r}}{\unicode[STIX]{x1D6E4}(k+2-r)}+\mathop{\sum }_{k=0}^{m}\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)}\nonumber\\ \displaystyle & = & \displaystyle \frac{e^{x}}{\unicode[STIX]{x1D6E4}(1-r)}\int _{0}^{x}t^{-r}e^{-t}\,dt+\mathop{\sum }_{k=0}^{m}\frac{x^{k-s}}{\unicode[STIX]{x1D6E4}(k+1-s)}.\square\nonumber\end{eqnarray}$$
By Propositions A.2 and A.3, we have the following.
Corollary A.4. Let
![]() $s\in \mathbb{R}$
. Then
$s\in \mathbb{R}$
. Then