Introduction
Intense laser beam interaction with solid surfaces leads to the formation of plasma associated with the production of particles emission (Gamaly et al., Reference Gamaly, Madsen, Duering, Rode and Luther-Davies2005; Trusso et al., Reference Trusso, Barletta, Barreca and Fazio2005; Alti and Khare, Reference Alti and Khare2006; Torrisi et al., Reference Torrisi, Ceccio, Restuccia, Messina, Gucciardi and Cutroneo2017; Zhang et al., Reference Zhang, Shen, Ye, Wu, Zhu and Hu2017). This phenomenon is used in the preparation of nanometer materials as well as the investigation of formation dynamics of nanoscale structures (Wang et al., Reference Wang, Xu, Zhou, Chu and Fu2007; Batani et al., Reference Batani, Vinci and Bleiner2014; Singh et al., Reference Singh, Khare and Sharma2017; Anastassiya et al., Reference Anastassiya, Ahmed and Ahmed2018; Shaheen et al., Reference Shaheen, Gagnon and Fryer2019).
Nanometer materials consisting of various nanoscale structures, such as nanoparticle (NP), nanotube, nanorod, and nanowire, which have been applied widely in a lot of fields, for example, photovoltaic (Cho et al., Reference Cho, Park, Hao, Song, Conibeer, Park and Green2008), light-emitting diode (Maier-Flaig et al., Reference Maier-Flaig, Rinck, Stephan, Bocksrocker, Bruns, Kübel, Powell, Ozin and Lemmer2013), lithium-ion battery (Zhu et al., Reference Zhu, Jin, Tan, Zong, Hu, Chen, Chen, Zhang and Zhu2015), memory cell (El-Atab et al., Reference El-Atab, Ozcan, Alkis, Okyay and Nayfeh2014, Reference El-Atab, Ozcan, Alkis, Okyay and Nayfeh2015), laser (Wang et al., Reference Wang, Zhang, Zeng, Zhou W, Ma, Wang, Zhou, Hu, Zhang, Lu and Wu2018), catalyst (Peng et al., Reference Peng, Wang, Ge, He, Cao, He, Ma and Sun2013), and fluorescence imaging (Gu et al., Reference Gu, David, Qin, Anglin, Joo, Mooney, Howell and Sailor2013). Nowadays, more and more researchers tend to the preparation, characterization and application of nanometer materials, especially those with new nanoscale structures (Li et al., Reference Li, Guan, Xu, Zhao, Sun, Wu and Xu2016; Zhao et al., Reference Zhao, Li and Wang2016; Anoop et al., Reference Anoop, Verma, Joy, Harilal and Philip2018; Sarfraz et al., Reference Sarfraz, Bashir and Mahmood2019), whereas fewer attention is paid on the formation dynamics of nanoscale structures, although it is the earliest and longest-duration research topic in nanofield. However, the formation dynamics is crucial to the number- and size-controllable preparation of the nanostructures, which impacts the characteristics and application of the nanometer materials. As already known, during the formation of nanoscale structures, nucleation and growth are always two conclusive processes that we can not parry (Morales and Lieber, Reference Morales and Lieber1998; Yan et al., Reference Yan, Cingarapu, Klabunde, Chakrabarti and Sorensen2009; Batani et al., Reference Batani, Vinci and Bleiner2014). It is the nucleation and growth that, respectively, determine the number and size of nanoscale structures. Therefore, the nucleation probability and growth duration become the critical parameters in the investigation on the formation dynamics of nanoscale structures (Satoh et al., Reference Satoh, Itoh, Kawashima and Washio2017; Carlos et al., Reference Carlos, Alejandro, Nair and Basilio2018; Hijazi et al., Reference Hijazi, Dubrovskii and Monier2018).
For the past several decades, as the crucial materials, the Si-based nanometer materials composed of silicon nanoparticles (Si-NPs) have been investigated extensively due to their unique applications in solar cell, bioengineering, optoelectronic, and microelectronic devices. Experimentally, some methods have been successfully used to prepare Si-NPs, such as arc discharge (Yu et al., Reference Yu, Xue, Huang, Liu, Yu, Sun, Dong, Cao and Jung2014; Shah and Cui, Reference Shah and Cui2015), chemical vapor deposition (Sukkaew et al., Reference Sukkaew, Kalered, Erik, Kordina, Örjan and Lars2018), magnetron sputtering (Guo et al., Reference Guo, Ye, Wang, Yang and Zhang2017a, Reference Guo, Ye, Wang, Yang and Zhang2017b; Liu et al., Reference Liu, Zheng, Liu, Luo and Wu2018), electron beam evaporation (Karakiz et al., Reference Karakiz, Toydemir, Unal and Colakerol2014; Il'ves et al., Reference Il'ves, Zuev, Sokovnin and Murzakaev2015), and pulsed laser ablation (PLA) (Sobhani and Mahdieh, Reference Sobhani and Mahdieh2013; Myungjoon et al., Reference Myungjoon, Saho, Taesung, Hidenori and Takafumi2016; Zehra et al., Reference Zehra, Bashir, Hassan, Ahmed, Akram and Hayat2017; Qi et al., Reference Qi, Zhang, Yu and Zhang2018). It is worth mentioning that PLA has become the most popular method for fundamental research and industrial application due to the unique virtues of rapid thermogenic speed, small surface contamination, and high particles concentration. Using PLA, researchers try to obtain the NPs with the area number density and size that they want by altering the technological parameters, for example, laser pulse repetition rate (Wang et al., Reference Wang, Xu, Zhou, Chu and Fu2007), laser wavelength or fluence (Polek and Hassanein, Reference Polek and Hassanein2016; Chen and Bi, Reference Chen and Bi2017), background gas kind or pressure (Wang et al., Reference Wang, Deng, Fu, ZhouY and Peng2006; Akram et al., Reference Akram, Bashir, Hayat, Mahmood, Ahmad and Khaleeq-U-Rahaman2014; Zehra et al., Reference Zehra, Bashir, Hassan, Ahmed, Akram and Hayat2017), and substrate temperature (Heimburger et al., Reference Heimburger, Deßmann, Teubner, Schramm, Boeck and Fornari2012). In fact, both the area number density and size are altered by thermodynamic parameters, that is, the density and temperature of ablated particles, which can be determined by the above technological parameters. According to the results of Morales and Lieber (Reference Morales and Lieber1998) and Fu et al. (Reference Fu, Wang, Chu, Zhou, Yu, Han and Peng2005), only if the conditions related to the density and temperature of ablated particles are satisfied simultaneously, the NP can form and grow in the so-called “nucleation region”. The formed NPs and the ablated particles are transported onto the substrate and form the film. It is difficult to accurately measure the number and size of NPs in the nucleation region, even if the precision photoelectric techniques, such as enhanced charge-coupled device (CCD) (Ikurou et al., Reference Ikurou, Yusuke, Hiroshi, Naomichi, Tamao and Akira2016), are used due to the confinement of spatiotemporal resolution. More conveniently, the area number density and the mean size of NPs on the substrate can be obtained by scanning electron microscopy (SEM) and Raman spectrometer (Raman). The number density and size distribution of NPs in the nucleation region are obtained by the transportation dynamics of the formed NPs based on the results of SEM and Raman in many previous works.
In general, there are two typical options for the orientation of substrates in PLA, parallel or vertical to the target surface. The substrates parallel to the target surface, as a baffle, can exacerbate collisions among ablated particles because of the stronger second sputtering and oscillatory waves (Zhang et al., Reference Zhang, Chen, Wang, Wang, Sui, Ke, Li, Jiang and Jin2018; Zohar et al., Reference Zohar, Shalom and Erez2019), thus, complicate the process of formation and transportation of NPs. For the substrate vertical to the target surface under the ablated plume axis, the formed NPs at different spatial locations in the “nucleation region” can directly be deposited on the substrates at different positions by the projectile motion, which simplifies the transportation process of ablated particles and formed NPs (Wang et al., Reference Wang, Chen, Ding, Chu, Deng, Liang, Chen and Fu2011), being convenient for us to derive the spatial location in the “nucleation region” corresponding to NPs deposited on substrates at different positions.
Understandably, the dependence of the area number density and the mean size of NPs in the formed films on the technological parameters during PLA can not only determine the number- and size-controllable preparation of NPs experimentally but also help to understand the recognition for the nucleation and growth of NPs in the “nucleation region” theoretically. In our previous work (Wang et al., Reference Wang, Xu, Zhou, Chu and Fu2007), using the substrates parallel to the target surface, the influence of pulse repetition rate on the mean size of Si-NPs, and, the nonlinear dynamics of the laser-ablative deposition was investigated, providing much information about the nucleation and growth for explaining the experiment results. In the above experiment, the substrate holder acted as a baffle, which may cover the essence of nucleation and growth.
In this article, using the substrates vertical to the target surface under the ablated plume axis, nanocrystalline Si films are prepared by PLA in high-purity argon (Ar) gas with a constant pressure at room temperature, under different pulse repetition rates, using a nanosecond laser. SEM, Raman, and Langmuir probe are carried to characterize the area number density/mean size of NPs on the substrates and density/temperature of ablated particles in the “nucleation region”. Coupled with the nucleation probability, growth/aggregation duration of NPs in the “nucleation region”, and the effect of the baffle, the influence of pulse repetition rate on the formation of NPs is addressed.
Experimental details
A schematic sketch of the experimental setup is given in Figure 1. For producing plasma to form NPs, 308 nm (wavelength) and 15 ns [full-width at half-maximum (FWHM)] pulses from an XeCl excimer laser were used. The chamber was pumped using a turbo molecular pump after the base pressure was 2 × 10−4 Pa, pure Ar gas (99.999%) was inflated into the chamber and maintained at 10 Pa. The single-crystal Si (111) target was rotated by a stepping motor at a speed of 6 rpm for uniform ablation. A laser beam was focused onto the target surface through a convex lens and the focus area was 2 mm2, the incident angle of the laser was 45° off from the normal direction of the target, and the laser fluence was maintained at 4 J/cm2. Substrates were parallel to the plume axis, and the vertical distance to the focus was 2 cm, the lateral intervals to the target surface were 2.5, 3.0, and 3.5 cm. Laser pulse repetition rates were 1–40 Hz, the total number of pulses were 720 for each repetition rate. A Langmuir probe made of a tungsten material was used to measure plasma characteristics. The probe tip was 10 mm in length and 0.15 mm in diameter, which was coaxial with ablation plume and the interval distance between the probe tip and the target surface was 2–3 cm. In this work, the delay time for the signal acquisition was 12 µs after pulsed laser-off, the voltage of the probe changed from −30 to 50 V. Both the density and temperature of the ablated ions obtained through fitting and analyzing the I–V curves.

Fig. 1. Schematic sketch of PLA apparatus without the baffle.
It should be noted that the sketch (substrate orientation vertical to the target surface) in this experiment is different from that (substrate orientation parallel to the target surface) in our previous work (Wang et al., Reference Wang, Xu, Zhou, Chu and Fu2007), as shown in Figures 1 and 2. The round tray holding the substrate in Figure 2 acts as a baffle to block the ablated particles. Additionally, compared with our other previous work (Wang et al., Reference Wang, Chen, Ding, Chu, Deng, Liang, Chen and Fu2011), this work removes the external electric field in order to simplify the dynamical formation process of NPs.

Fig. 2. Schematic sketch of PLA apparatus with the baffle.
The samples were analyzed by scanning electron microscopy (SEM; JSM-7500F) and Raman spectrometer (Raman; MKI-2000) to characterize the surface morphology and crystalline state, respectively.
Experimental results
The SEM images and the Raman spectra of the films prepared under different pulse repetition rates for the lateral distances of 2.5, 3.0, and 3.5 cm are investigated systematically. As a typical example, the SEM images of the samples located at 3.0 cm are shown in Figure 3, in which Figure 3a–3g correspond to pulse repetition rates of 1, 3, 5, 10, 20, 30, and 40 Hz, respectively. Obvious grains can be observed on the surfaces of the samples from Figure 3a–3g, and it is found that both their size and area number density strongly dependent on the laser repetition rate. Figure 4 represents the corresponding Raman spectra of the typical samples, whose main peaks are located, respectively, at 517.01, 515.53, 515.04, 514.05, 511.1, 513.56, and 511.6 cm−1 for the pulse repetition rates from 1 to 40 Hz. These peaks are near to the characteristic peak, 520.73 cm−1, of single-crystal Si. The FWHM of these spectra are bigger than that of single-crystal Si, which is reasonable since the crystallinity of NPs is not as good as single-crystal Si. Additionally, the left- or right-shifts of the peaks indicate the influence of pulse repetition rate on the mean size of the NPs.

Fig. 3. SEM graphs of samples under different laser pulse repetition rates: (a) 1 Hz, (b) 3 Hz, (c) 5 Hz, (d) 10 Hz, (e) 20 Hz, (f) 30 Hz, and (g) 40 Hz.

Fig. 4. Raman shift of samples with different laser pulse repetition rates.
Based on the statistic operation on more than one hundred of NPs in each sample deposited at different locations, the mean size and the area number density under different pulse repetition rates are shown in Figures 5 and 6, respectively. The squares, circles, and triangles, respectively, depict the data for 2.5, 3.0, and 3.5 cm. Obviously, for a fixed pulse repetition rate, the mean size decreases, while the area number density increases, with the addition of lateral distance from substrates to the target surface, demonstrating the consistent tendency with our previous work (Wang et al., Reference Wang, Chen, Ding, Chu, Deng, Liang, Chen and Fu2011). More importantly, when the lateral distance is fixed, the mean size decreases from 1 to 20 Hz at first, and then increases until 30 Hz, with the increase of repetition rate, and it decreases again. Compared with the change curve of the mean size, the area number density demonstrates the inverse change tendency.

Fig. 5. Mean size of NPs with different laser pulse repetition rates.
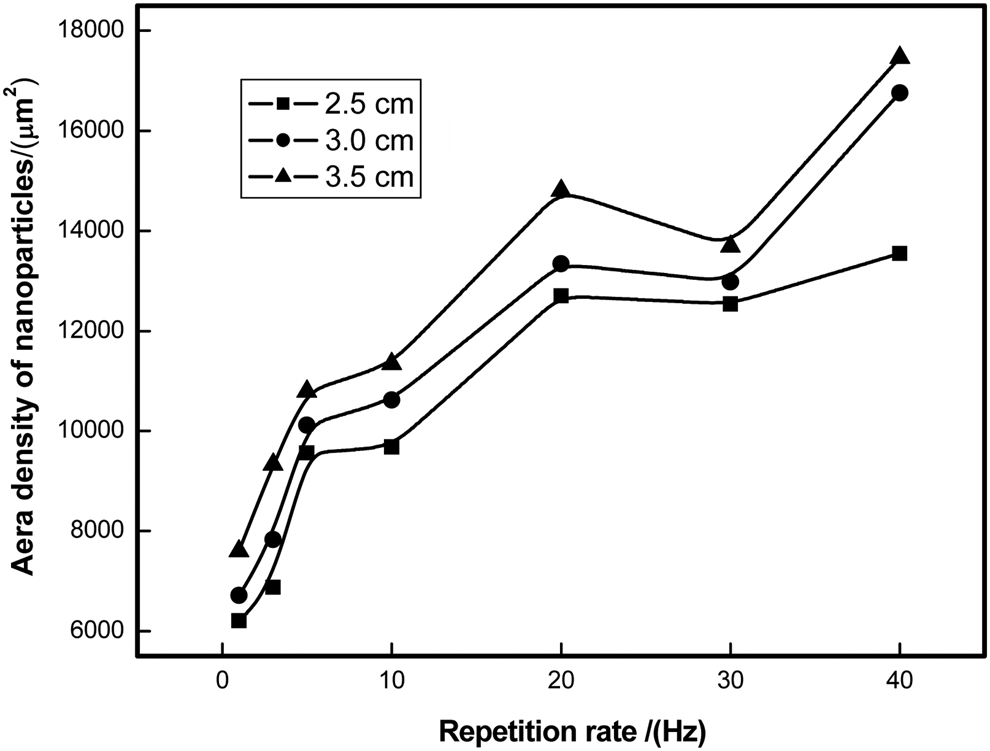
Fig. 6. Area number density of NPs with different laser pulse repetition rates.
Langmuir probe is used to measure the temperature and density of ablated ions under different laser pulse repetition rates. It is found that no obvious change of temperature induced by the repetition rate. On the other hand, the repetition rate strongly affects the density of ablated ions, as exhibited in Figure 7. The representative data acquired by probe located at 2.5 cm to the target surface. It is evident that the ablated ions density monotonically increases with augment of the repetition rate.

Fig. 7. Ablated Si ions density with different laser pulse repetition rates.
Discussion
The investigation on the nucleation and growth of Si-NP in our previous work (Wang et al., Reference Wang, Xu, Zhou, Chu and Fu2007), which based on Morales's nanowire formation model (Morales and Lieber, Reference Morales and Lieber1998), indicated that the nucleation occurs due to hot vapor condensation as the ablated particles (atoms and ions) cool down through collisions with the background gas, and the growth begins when the temperature and number density get to their critical values and maintains until these conditions can not be met (Morales and Lieber, Reference Morales and Lieber1998; Fu et al., Reference Fu, Wang, Chu, Zhou, Yu, Han and Peng2005). In other words, the NPs are always formed by the growth on the basis of nucleation, and more importantly, both the beginning and maintaining of nucleation and growth have to require the appropriate range of two thermodynamics parameters, that is, the number density of the ablated particles higher than the supersaturation value, and temperature window (Wang et al., Reference Wang, Qin, Chu, Deng, Ding and Guan2017). For a constant laser fluence for each rate used in this work, the ratio of ablated ions and ablated particles is constant for each pulse, which indicates the temperature/density of ablated ions can represent the temperature/density of the ablated particles when the characteristics of temperature and density is investigated. Thus, the temperature of the ablated particles almost keeps invariant under different repetition rates, which is also confirmed for the ablated ions in our Langmuir probe data. Spontaneously, the number density of the ablated particles becomes the only crucial factor impacting the beginning and maintaining of nucleation and growth in this article, corresponding to the location of the “nucleation region” proposed in our previous work (Fu et al., Reference Fu, Wang, Chu, Zhou, Yu, Han and Peng2005; Wang et al., Reference Wang, Chen, Ding, Chu, Deng, Liang, Chen and Fu2011).
As all known, the nucleation and the growth in the microscopic process determine the area number density and the mean size of NPs in the prepared film separately. In fact, Figure 6 demonstrates the number of nuclei formed in the “nucleation region” under different repetition rates. For this substrate, the nucleus number is the product of the nucleation probability and the number of ablated particles in the corresponding “nucleation region”. In Figure 6, with increasing the pulse repetition rate from 1 to 40 Hz, the nucleus number first increases to its maximum at 20 Hz, then decreases until 30 Hz, and then increases after 30 Hz. Figure 7 shows that the number density of ablated ions, also denoted as the number density of ablated particles, increases monotonously with the increase of repetition rate. For a specific repetition rate, the nucleation probability of ablated particles can be roughly calculated by dividing the value in Figure 6 by that in Figure 7, as demonstrated in Figure 8. This indicates that the nucleation probability of ablated particles in the “nucleation region” nearly increases monotonically with increasing of repetition rate between 1–40 Hz except for ~30 Hz, which may be contributed to the impact intensity between the ablated particles.

Fig. 8. Nucleation probability of ablated particles under different laser pulse repetition rates.
When the two thermodynamics parameters can sustain the nucleation and growth of the NPs, their mean size depends on the growth duration. Namely, the time interval surviving in the “nucleation region” for a nucleus after nucleation determines the size of the formed NP (Fu et al., Reference Fu, Wang, Chu, Zhou, Yu, Han and Peng2005). The growth duration corresponding to different repetition rates is also shown in Figure 5.
For one formed nucleon in the dynamical process, there are two follow-up choices, that is, growth by the stronger bonding with the circumambient ablated particles, aggregation by the weaker bonding with other nucleons. The successive mode of the formed nucleon depends on the comparison of energy (Wang et al., Reference Wang, Deng, Chu, Fu and Peng2009; Zeng et al., Reference Zeng, Yu and Lu2010; Sun et al., Reference Sun, Zeng, Yu and Kevin2013). Naturally, both the two modes induce the increase of the NP's size. However, the total number of NPs decreases for aggregation, while stays the same for growth.
Based on the above analysis, the influence of pulse repetition rate on the mean size and area number density of NPs, which obtained from the experiment for nanosecond pulsed laser-ablated deposition, can be understood by the nucleation and growth of NPs. With the increase of repetition rate, both the number density and nucleation probability of the ablated particles in the ambient gas increase (Figs 7 and 8), so that the nucleation times increase, leading to the increase of the NP's area number density (Fig. 6). On the other hand, the increase of number density of the ablated particles exacerbates the collision among particles, hampers the growth process of NPs, due to the decrease of its growth duration, resulting in the decrease of the NP size (Fig. 5). After 20 Hz, the number density of the ablated particles continues to increase with a smaller rate (Fig. 7), while the nucleation probability decreases (Fig. 8). Therefore, the nucleation times decrease, accompanying with the decrease of the NP's area number density (Fig. 6) since aggregation among small NPs becomes dominant due to the shorter distance among the formed nucleons, further increasing the NP's mean size accordingly (Fig. 5). For the repetition rate from 30 to 40 Hz, both the area number density (Fig. 7) and nucleation probability (Fig. 8) increase distinctly, thus the nucleation times increase, leading to the increase of the NP's area number density (Fig. 6). At the same time, the decrease of the NP's mean size (Fig. 5) can be contributed to the decrease of the NP's growth duration.
It is interesting and necessary to investigate the difference of the results in this article with those in our previous work about the influence of laser repetition rate on the mean size of NPs (Wang et al., Reference Wang, Xu, Zhou, Chu and Fu2007), due to the baffle effect, as shown in Figures 1 and 2.
Firstly, corresponding to the total pulse number of 600 in our previous experiment with a baffle (Wang et al., Reference Wang, Xu, Zhou, Chu and Fu2007), 720 pulses of laser retained in this work. The baffle facing the target forces more particles to participate in the collision; however, more pulses of laser are necessary for the preparation system without the baffle to obtain the obvious measure results.
Secondly, the previous work indicated, as shown by the squares of Figure 9, with increasing pulse repetition rate, the mean size of the NPs in the film first decreases and reaches its minimum at 20 Hz, and then increases, which may be attributed to the nonlinear dynamics of the laser-ablative deposition. Compared with this tendency, in this article, interestingly, the increase of size after the repetition rate of 20 Hz is slowed down obviously, and the size starts to decrease again after 30 Hz. It is the baffle that induces the difference. The reflection of the baffle on the ablated particles enhances the density of ablated particles between the target and the substrate, therefore, exacerbates the aggregation between 20 and 30 Hz, and forces the growth after 30 Hz to become the aggregation. In other words, the aggregation duration of the nucleus is prolonged distinctly, and the increase ramp of the size is much larger than that without the baffle after 20 Hz. The higher repetition rate can result in the bigger increase ramp in NP's size. Therefore, baffle plays an important role to accelerate the increase process of size with increasing repetition rate, especially for repetition rate higher than 20 Hz.

Fig. 9. Size and area number density of NPs under different laser pulse repetition rates with the baffle.
Lastly, the area number density of NPs versus repetition rate is demonstrated with the solid circles in Figure 9. In this article, for the mean size or the area number density of NPs, both 20 and 30 Hz corresponding to the transformation rates, that is, pulse repetition rates at which increase and decrease are inter-transformed. Surprisingly, for the area number density of NPs, Figure 9 demonstrates the transformation rate of 10 Hz, departing from that of 20 Hz for the mean size of NPs. The baffle enhances the number density of the ablated particles and exacerbates the collision among particles, thus a smaller repetition rate is enough for the decrease of the area number density of NPs due to the aggregation among small NPs. It should be noted that 10–20 Hz is the rate range in which the aggregation and the growth coexist. In this range, the NP size decreases with the increase of repetition rate because the decrease of growth duration plays a bigger role than that of the increase of aggregation duration.
Conclusion
Using the substrates with the different orientation from that of the conventional PLA method, in the situation without the baffle, Si-NPs are deposited in the argon atmosphere of 10 Pa. The mean size and area number density of NPs, the density and the temperature of the ablated ions are achieved by the results of SEM, Raman, and Langmuir probe under different pulse repetition rates between 1 and 40 Hz. Moreover, according to the “nucleation region” model and transportation dynamics, the nucleation probability of ablated particles, the growth/aggregation duration of NPs in the “nucleation region”, versus the pulse repetition rate, are investigated. It is found that the transformation rates are the same for both the area number density and the mean size of Si-NPs without the baffle; however, the transformation rates are different with the baffle. And there are less transformation rates with the baffle than without the baffle. Moreover, the two growth modes, that is, growth and aggregation, are distinguished in different ranges of pulse repetition rate. These may pave a way for effectively understanding the nucleation/growth/aggregation, and thus investigating the formation dynamics for nanostructures of Si as well as other materials formed in the gas phase.
Acknowledgments
The authors express their thanks to B.T. Liu for many useful discussions. This work was supported by the NSFC (41504127) and the NSF of Hebei Province (A2018201249, D2018201035), China. The anonymous referee's critical suggestions are acknowledged.











