No CrossRef data available.
Published online by Cambridge University Press: 25 October 2005
Recent emphasis has been placed on exploring behavioral aspects of individual agents in explaining macroeconomic phenomena. Of particular interest is augmenting New Keynesian models to produce costly disinflation, as empirics and consensus suggest. We presume a fraction of agents using rule-of-thumb behavior in price setting in an otherwise standard New Keynesian model. Our findings suggest that relatively small amounts of rule-of-thumb behavior are required to offset the net effects of Ball's disinflationary boom. Moderate levels of rule-of-thumb behavior can produce delayed recessions consistent with some VAR evidence. However, high proportions of rule-of-thumb behavior are needed to produce immediate reductions in output following implementation.
One of the widely held fundamentals in the field of macroeconomics is the belief that disinflations are costly. Much empirical evidence exists to corroborate this view; see, for example, Ball (1994a). To this end, the more debatable issue is how costly disinflations really are. At one extreme, purely autoregressive Phillips curves suggest very large costs to disinflation, whereas purely forward-looking Phillips curves have been shown to imply that disinflation need not be costly. Underlying the debate of costs to disinflation is which metric of inflation dynamics is correct.
New Keynesian models assume some amount of nominal rigidity, which imparts persistence in prices. With infrequent price changes, the perception is that price-level inertia translates to inflation inertia, and therefore makes it more difficult for monetary policymakers to engineer a relatively painless disinflation. However, even if firms exhibit staggered prices, this does not necessarily result in inflation inertia: Changes in the price level are quite distinct from the rate of change of the price level.
As a result, the apparent lack of inflation inertia common in New Keynesian models of sticky prices have provided the basis for recent criticism due to their lack in producing models that impart costs to disinflation. Under the assumptions of rational expectations and a credible central bank, an announced disinflation allows agents to fully adjust to a disinflation policy of any size, implying zero costs to the disinflation. Even more confounding is the result of Ball (1994b), which shows that with staggered price setting, disinflations cannot only be costless, but can cause a boom rather than a recession. This result, of course, stands in stark contrast to empirical evidence. In a follow up to that paper, Ball (1995) shows that if the central bank is not fully credible in its announced disinflation, then the expected result of negative real output effects can occur.
Several more recent papers have attempted to amend the New Keynesian theory to support the costly disinflation result. Jackson (2004) and Ascari and Rankin (2002) show that under two different versions of a purely forward-looking New Keynesian model, allowing for an interest-rate channel for monetary policy yields costly disinflations. Those results, however, can yield implausibly large initial responses to output, and do not match very well the implied dynamics of VARs. Mankiw and Reis (2002) explore the role that information dissemination plays in the disinflation process. Mankiw and Reis set up a model in which agents have access to information that disseminates slowly through price-setting agents. As a result, even though agents may be reacting rationally, the price-setting decisions made by some agents could be based on outdated information.1
See Carroll (2003) for an excellent exposition of how the sticky information model can be derived from microfoundations.
Our priors suggest that with theoretically zero costs (or a boom) under disinflation in a purely forward-looking model, and “large” costs to output under a backward-looking Phillips curve, the empirical costs and dynamics consistent with disinflation could be obtained with some appropriate deviation from full rationality.
This paper investigates the extent to which the presence of rule-of-thumb agents can impart negative real effects from a disinflationary program, even if the monetary authority is credible. Rational agents are assumed to have a deep understanding of the modeled economy and are able to provide complex predictions about the path of prices or other variables of interest. A growing body of literature concerning the bounded rationality of agents has sought to temper the strong assumptions imposed by full rationality. The early compilation from Frydman and Phelps (1983) was one of the first comprehensive critical evaluations of full rationality. The recent emergence of the learning literature, highlighted by Evans and Honkapohja (2001) provides a formal methodology for deviations from rational expectations. In the learning literature, agents are often assumed to act like econometricians, and under certain conditions can eventually learn the rational expectations equilibrium.
The approach we take is motivated by the results of Gali and Gertler (1999), who estimate a theoretically implied Phillips curve, assuming some fraction of agents use a rule of thumb in choosing prices. Depending on the specification used, Gali and Gertler estimate this rule-of-thumb behavior to be anywhere from about one-fourth to one-half of price-setting agents. They conclude that adaptive behavior, though statistically significant, is relatively unimportant to inflation dynamics, and that purely forward-looking models of inflation dynamics match actual inflation fairly well. That conclusion is still subject to the costless disinflation criticism (or the Ball boom property), which leads one to wonder how important adaptive behavior is on aggregate dynamics. Gali and Gertler do not explicitly address the issue of costs to disinflation with adaptive agents. This paper bridges the gap between the motivation that Gali and Gertler provide and the actual implementation of a disinflation under such an environment.
This paper continues in the spirit of the learning literature and bounded rationality by allowing for the possibility that some agents do not behave in a fully rational manner. More to the point, the presence of adaptive agents is designed to capture transitory human error and the barriers of imperfect information in decision making. The justification for the inclusion of adaptive behavior presumes that some agents may have a finite capacity for either gathering or processing the information necessary to obtain the rational solution. Alternatively, it could be that agents have access to the rational predictors, but that the costs of acquiring these predictors are too high to justify the acquisition. Interestingly, however, Branch (2004) finds that the costs of obtaining rational predictors may be lower than less sophisticated predictors, such as an adaptive predictor. He concludes that agents may have an inherent predisposition to using one predictor over another, but if the forecast errors become sufficiently large relative to the costs of acquisition, agents will switch predictors.
Several recent empirical papers have endeavored to identify the importance and magnitude of including less-than-rational agents. Empirical estimates from Baak (1999) shows evidence of less-than-rational behavior in pricing decisions. Specifically, Baak uses data on U.S. cattle market prices from 1900 to 1990 and estimates approximately 33% of participants to be boundedly rational.2
Baak assumes that boundedly rational agents use an AR(1) forecast to determine the one-step-ahead expected price.
Branch defines the adaptive inflation predictor equal to what agents predicted inflation to be for last period, adjusted by a fraction of the predictor error from last period. The naive predictor presumes inflation will be what it was last period.
We frame our results borrowing from the theoretical framework of Ball (1994b) primarily for two reasons. First, the extreme result that disinflation causes a boom in that model makes it a natural candidate to consider alternative assumptions that could reconcile the framework with empirics. Ball extends the model to include noncredible policy that can produce costly disinflation; however, there is no consensus among economists that this explanation is sufficient. Certainly, keeping as close to Ball's framework for comparison purposes is imperative. Second, the model's simplicity and transparency lends itself well to exploring alternative assumptions.
The results of the current paper indicate that rule-of-thumb behavior can indeed have a significant impact on the path of output, leading in most cases to a recession after an initial boom. However, the detailed implications for the output effects of disinflation are mixed, depending on the precise features one is attempting to match. Under our preferred parameterizations, a relatively low amount of rule-of-thumb behavior is enough to turn Ball's boom into a net recession. Furthermore, moderate proportions of rule-of-thumb agents, consistent with the empirical evidence just presented, are sufficient to mimic estimates of impulse responses from contractionary monetary policy. One the other hand, relatively high proportions of rule-of-thumb behavior are required to essentially eliminate the initial boom, and also to closely match empirical estimates of sacrifice ratios.
After a (credible) disinflation announcement by the central bank, rational agents react immediately to the announcement by slowing the growth of prices so that individual firms' prices are in line with the money supply and aggregate price level. For most parameterizations, allowing for adaptive behavior results in the price path eventually overshooting the money supply, leading to periods of boom and bust. For sufficient proportions of adaptive agents, we show that over time the net effects on output can become negative. For a given proportion of adaptive agents, allowing for stronger adaptive behavior produces more volatile paths for output and larger costs to disinflation. After presenting these results, we examine the question of appropriate monetary policy. It is argued that for a small fraction of rule-of-thumb behavior, a gradualist disinflation policy is optimal, whereas for large fractions of rule-of-thumb behavior, a “cold-turkey” disinflation is best.
The rest of this paper is organized as follows. Section 2 outlines the theoretical framework, borrowing from the theory of Ball (1994b, 1995). Section 3 presents results of the baseline model. Section 4 considers some alternative specifications such as an adaptive rule to forecast the path of money, a rule requiring adaptive agents to forecast output, and a generalization of the adaptive expectations approach which nests the baseline model as a special case. In Section 5, we consider the effects that rule-of-thumb agents have on the sacrifice ratio. Section 6 investigates the policy implications of longer disinflations on output. Concluding remarks are contained in Section 7.
Agents in the economy are assumed to be yeoman farmers producing a differentiated good. We assume initially that all agents are rational, yielding the results of Ball (1994b). Each agent owns a corresponding monopolistically competitive firm indexed by
, and makes choices on how much to consume, work, and charge for their differentiated product. Utility is increasing in consumption, and decreasing in labor; see Ball and Romer (1989) for a more complete description. Individuals consume goods across the spectrum of differentiated products using a constant elasticity of substitution aggregator. Individual utility maximization results in an isoelastic firm demand curve increasing in aggregate output and decreasing in relative (log) price:
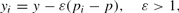
where
is the elasticity of demand for goods. Given the demand the firm faces, each firm's profit-maximizing relative price
is increasing in aggregate output:
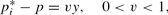
where y is aggregate output, v is an appropriately chosen coefficient,4
In fact,
, where
is the firm's log marginal cost, assumed constant. See Ball (1990) for greater detail.
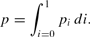
Money enters the economy through a transactions demand for money,
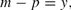
where m is the nominal money stock. From (2) and (4) the individual firm's instantaneous profit-maximizing price is chosen as a convex combination of the nominal money stock and the aggregate price level,
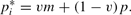
If firms were allowed to continuously update prices, profit maximization would yield
, and output would remain constant at
.
Following Ball (1994b), we assume that prices are adjusted once per one-period length of time. As a normalization, we assume that one period is equivalent to one year.5
Evidence from Blinder (1994) indicates that firm prices are changed infrequently, usually once every three to four quarters; however, more recent evidence suggests firms may update prices more frequently. Future research should explore how the length of contract will affect the results of this paper.
General arguments for infrequent price changes have been made by Ball et al. (1988). The most frequent explanations include menu costs or implicit contracts as a primary source of rigidity. Ball and Cecchetti (1988) argue that infrequent price changes are a result of price setters' having imperfect information about the state of the economy. Thus, price setters choose to delay setting prices until seeing the prices of others. Not only does this produce infrequent price changes, but it also results in uniform staggering (as opposed to synchronization). A similar argument is proposed by Caballero (1989) which suggests that the costly gathering of pricing information produces staggering. Ball and Romer (1989) also make arguments for staggered price setting on the grounds that firm-specific shocks produces staggering among firms.
,7
The subscript here is dropped because all firms who reset at time t will choose the same price; hence, there is no need to distinguish among firms.
. Letting the loss function of the firm be denoted as
, we have
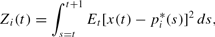
where
is the rational expectations operator, the mathematical expectation conditioned on all information up to and including time t. Dynamic minimization of (6) shows that firms will choose a price that is the average of the firms' expected profit-maximizing price over the following unit interval:
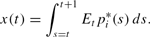
Substitution of (5) into (7) yields
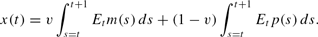
One can think of (8) as the index of newly set prices. From the definition of the price aggregator (3) and the staggering of pricing decisions among firms, the aggregate price path can be written
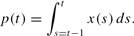
Thus, the aggregate price level is the average of all prices set over the previous period.
The monetary authority is assumed to have full credibility with respect to announced policy actions. We assume initially that all agents are rational, and agents will take the prescribed disinflation announcement as the actual path of money. As a normalization, it is assumed that the money supply grows linearly at rate 1 over time. At time
, the central bank announces a disinflation program (not known in advance) in which it will reduce the growth rate of the money supply linearly over one period until time
, at which point money growth is zero. Thus,
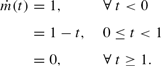
The path of the money stock can be written as
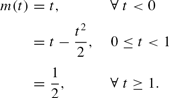
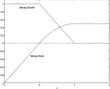
Figure 1 shows the money stock and growth rate of money over time. For any
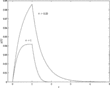
, the announced disinflation causes an immediate boom, and real output never falls below zero.8
This is Ball's (1994b) suprising result of a “disinflationary boom.” For a proof that output is never negative, see Ball (1990).
, and for the limiting case of
.

Money stock and money growth.

Ball's result.
We use the term adaptive in the sense that agents are backward-looking, rather than adaptive in the learning sense. In specifying an adaptive contingent, the following considerations were used: (i) Adaptive behavior should be consistent with rational behavior in a steady state, (ii) adaptive behavior should be simple to formulate, and (iii) the solution should produce a unique rational expectations equilibrium path for prices. We start with the assumption that adaptive agents behave exactly as rational agents do in every respect except for the way in which future prices are forecasted. Because of the complex computations required to solve the rational expectations solution, we assume adaptive agents choose a price based on an expected rule-of-thumb price path denoted
, using information known at time t. Since prices are in logs, we specify the rule

At any given time t, adaptive agents expect the price path one period advanced to be simply what the price level is now, adjusted for trend inflation over the previous one-period interval.9
The assumption that adaptive agents know the current aggregate price level is one of convenience. Realistically, given the lag in publication of economic statistics, (adaptive) price setters may not know the actual aggregate price level for weeks or months. If we assume a lag in the availability of information of one quarter, then (12) becomes
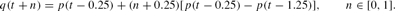
Assuming a one-quarter lag in information makes the results of this paper stronger by increasing the inertia present.
We assume initially that adaptive agents lend the same credibility and have the same access to monetary policy information as rational agents, hence the expected money path is symmetric with respect to the two types of agents. Later this assumption is relaxed.

Adaptive price-setting behavior.
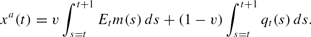
Note the superscript a refers to the pricing decisions by adaptive agents, and from now on, a superscript r denotes their rational counterparts.
Letting
denote the fraction of adaptive price setters, the index of reset prices is given by
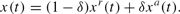
Finally, by substituting (14) into (9), we can write the aggregate price path as
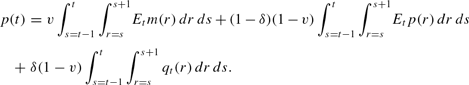
The case in which
gives the aggregate price path for Ball's (1994b) result. We assume throughout the paper that
.
To solve for the aggregate price path, we assume that the price path converges to the long-run equilibrium
after 50 periods. Assuming convergence longer than 50 periods does not affect the convergence process. In fact, for most settings the price path converges before 20 periods. As in Ball (1994b), we choose an initial price path, integrate (15) numerically, and iteratively substitute until the price path converges to a rational expectations equilibrium.11
Technically, we assume convergence of the price path vector if the sum of the squared difference between the previous and next price vector iterations is less than
.
and
. For
, (15) can be shown to satisfy both the monotonicity and discounting assumptions of Blackwell's theorem [see Stokey and Lucas (1989, p. 54)] and therefore is a contraction mapping. It follows by the contraction mapping theorem [Stokey and Lucas (1989, p. 50)] that (15) has a unique equilibrium price path.
With the introduction of adaptive behavior, the adjustment of the price path is considerably slower. This inertia in price setting in most cases leads the price path eventually to overshoot the money stock, leading the initial boom to be followed by recession. Figure 4 shows output paths for
under proportions of adaptive agents of
, 0.05, 0.1, and 0.2. Using a similar model, Ball et al. (1988) argue that their baseline parameterization,
, is consistent with the common view that relative prices vary little in response to aggregate fluctuations, and considers settings ranging from
to near 0.3.12
Following King et al. (1988) and assuming an elasticity of marginal utility of leisure with respect to leisure of −10 yields
. Measures of the elasticity of substitution are varied: Woodford (1996) assumes
, implying
. Assuming
yields
. King and Wolman (1996) use
, implying
; Sbordone (2002) uses
, implying
. Finally, Chari et al. (2000) use
, resulting in
.
. Results for the settings
, 0.25, and 0.75 are provided in the tables.

Output paths: v=0.1.
As one can see, output in all four cases increases initially as the path of money overshoots the aggregate price level, due to an initial rise in real money balances. In all cases where
is positive, inflation inertia is large enough such that as money growth slows, the price level eventually overcomes money, resulting in negative real output growth. For
, the deepest part of the recession shows trend GDP falling by more than 15% from the steady state. Under all four parameterizations, output converges close to trend after approximately four periods, with output under the larger proportion of adaptive agents rising again above trend before settling down. For any value of v, as the proportion of adaptive agents increases beyond
, the path of output becomes more volatile and convergence takes more time. The major result of the paper is clearly shown in Figure 4: Even minor deviations from full rationality are enough to overturn Ball's boom. The stark quantitative predictions of the output effects generated by the simulations are partially a result of the choice of parameterization of v. The output paths are somewhat sensitive to the settings of v: as v becomes larger, the fluctuations in output become smaller, and in particular, the severity of recessions is lessened.13
We remind the reader of the previous discussion of the choice for v and note that there is a “trade-off” in the quantitative results on the path of output and the sacrifice ratio. In particular, matching empirical sacrifice ratios prefers a lower setting for v, while mimicking quantitative fluctuations in output paths is better with a higher setting for v, such as
. Regardless of the choice of v, the qualitative feature that the Ball boom disappears holds, which is the major contribution of this paper.
It is quite apparent from Figure 4 that as the percentage of adaptive agents rises, the initial booms created become smaller and the eventual recessions become larger. As more rule-of-thumb agents are introduced, the inertia in the price path following disinflation implementation squeezes the aggregate price path closer to the path of money, mitigating the Ball boom. Net output, as measured by the total area under the output path, generally decreases as
rises. Table 1 shows net output for specified values of
and v.14
The reported values do not discount future output. Using discount rates of
and
did not significantly affect the results, and therefore are not reported here.
, net output turns negative for
greater than approximately 9%, and for
becomes negative at approximately
.

For larger v, agents choose prices closer to the path of money, and therefore output fluctuations are much smaller. As a result, for larger v, a larger proportion of adaptive agents is required to produce zero net output. Figure 5 (dashed line) shows the critical proportion of rule-of-thumb agents required to produce a net output loss, as a function of the parameter v. For
pairs in the northwest quadrant, net output is negative, whereas pairs in the lower right quadrant produce positive net effects. Although the amount of rule-of-thumb behavior necessary to yield a net output loss can be minimal (on the order of 10%), these results do not necessarily support rule-of-thumb behavior as a channel to explaining costly disinflation. As seen in Figure 4, even with a 20% presence of rule-of-thumb behavior, a small boom still occurs before output becomes negative, a tenuous feature considering the ultimate goal of the paper is to potentially remove the Ball boom. We discuss in the next section some of the VAR evidence concerning monetary shocks and their dynamic effects.

Critical values of δ, baseline model.
Following a contractionary monetary shock, the general consensus among most of the VAR literature is that output follows a hump-shaped dynamic, with the maximum (negative) effect on output occurring with some delay, around one to two years. There is some precedent in the VAR literature for output rising before falling after a contractionary policy. Leeper et al. (1996) use a four-variable system15
The four variables are the CPI, real GDP, fed funds rate, and the level of M1.
Comparing the paths of output for our simulations to those of the impulse responses described above give quite similar pictures. For
, output rises temporarily, followed by a sustained decline in output, resulting in recession after approximately one-half of a period (six months) and the trough of the recession occurring almost a full two periods (years) later. The three VAR simulations described earlier yield approximately the same timing dynamics.
Christiano et al. (1999) point out that the output boom that occurs initially can be eliminated by excluding current prices from the information set. In a similar exercise, we assume that there is a one-quarter period delay in the availability of pricing information, and find that with
, the initial boom is essentially eliminated.
In the absence of any consensus of the exact timing of recession following disinflation, we calculate the proportion of rule-of-thumb agents required to yield a recession after a given amount of time. Figure 5 shows the loci of points that, for a given
combination, result in recession after three months, one month, one week, and immediately following a disinflation policy. For our setting
, recession after three months occurs with approximately one-third proportion of rule-of-thumb agents. For recession to occur after one month, approximately 63% of rule-of-thumb agents are needed. Recessions generated in one week or sooner are not feasible in this model, for
.
The conclusion drawn from our simulations and comparisons to the VAR literature indicates that rule-of-thumb behavior can be important to explaining output dynamics; however, timing is of critical importance. If one believes that recession should follow immediately after disinflation implementation, then the simulation results suggest that an implausibly high amount of rule-of-thumb behavior is needed. However, for recessions occurring two to three months after implementation, estimates of the proportion of rule-of-thumb agents fall in line with estimates of previous studies [e.g., Gali and Gertler (1999), Branch (2004)], and these simulations roughly mimic those of their VAR counterparts described above.
Results from Section 3 indicate that inflation inertia through the behavior of adaptive agents is quite important to the effects of output. As
increases, inflation inertia becomes stronger and the effects on output become more pronounced. This section investigates how additional assumptions on the behavior of adaptive agents changes the effects on output paths. In particular, assumptions are introduced that require adaptive agents to forecast the money path in a similar methodology to that of the price path, as well as an assumption requiring adaptive agents to forecast output. The first assumption introduces additional inflation inertia, which reinforces the results of the paper; the second assumption yields results very similar to the first assumption. We also expand the analysis of Section 3.1 to encompass a broader family of adaptive expectations rules, of which the baseline rule of thumb used is a special case of this broader family.
This section investigates the consequences of rational agents having more information, in terms of monetary policy actions, than adaptive agents. More precisely, we again assume that rational agents have perfect foresight. However, adaptive agents are not aware of the disinflation policy because of informational asymmetries. The approach we take here can be thought of as being both complementary to and distinct from the introduction of noncredibility by Ball (1995). Ball assumes a homogeneous population of agents, who collectively assert a constant probability that the Fed will renege. For the current paper, we assume a heterogeneous sophistication of agents: a fraction of the population
has perfect foresight, and hence gives the Fed full credibility, while the remaining fraction
employs an adaptive rule to project the money path. We stop short of relying on the notion of credibility to explain the use of the adaptive money rule. Rather, as the theme of this paper suggests, a lack of sophistication on the part of some agents either in the ability to access information, or use that information, is the motivating factor.16
Note that under the current assumptions, the agents who use rule-of-thumb pricing will also employ the adaptive money rule.
In the case of Ball's (1995) credibility model, once the Fed does renege on its disinflation policy, money growth remains constant at the rate that prevails at the moment the Fed reneges. Eventually, the expectation of the path of money characterized by the adaptive money rule as in (16) will converge to the actual path of money with the passage of time in Ball (1995). In general, however, the mechanisms by which the future path of money is projected differ across this paper and in Ball (1995).
Starting from (13), adaptive agents choose the adaptive money rule
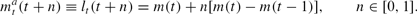
Again, adaptive agents forecast the future money stock as the current money stock, adjusted for the previous period's money growth rate. By substitution, we have the index of prices set by adaptive agents as
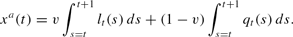
From (14) and (9), the aggregate price path using an adaptive money rule can be rewritten as
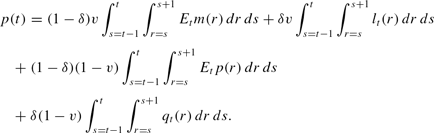
Figures 6A and 6B contrast the aggregate output paths for the baseline model, and the model in which adaptive agents use the money forecasting rule. Not surprisingly, the additional inertia imparted by the adaptive money rule makes adjustment of relative prices sluggish, resulting in a deeper recession and shallower initial boom. With 5% adaptive agents, the peak boom results in output approximately 7% above trend, while the ensuing recession bottoms out close to 0.5% below trend output. These results are quite similar to the baseline model, though the output path for the baseline model lies slightly above the money rule output path. Increasing the proportion of adaptive agents to 20% significantly changes the results. In the baseline model, output jumps close to 2%, falls nearly 16% below trend, and overshoots into a slight boom before converging. Under the adaptive money rule, the initial boom is closer to 1%, followed by a deep recession of more than 18% before overshooting to convergence.

Output paths, alternative specifications: v=0.1, δ=0.05.

Output paths, alternative specifications: v=0.1, δ=0.2.
The reinforcing feature of agents using the adaptive money rule results in less adaptive behavior required to push the economy into negative net output. As evidenced by Figure 7, for most values of v, less than 10% of adaptive agents are needed to result in zero net output for the prescribed disinflation program.

Critical δ values for zero net output, alternative specifications.
Here we assume that each firm knows the demand curve it faces; thus, (2) is known. However, suppose that adaptive agents do not know the inner workings of the economy, and hence do not know the aggregate demand equation (4). Adaptive agents will then set prices according to (2), requiring them to determine expected future output (essentially estimating expected aggregate demand). Because detrended data by definition have no trend, it would not make sense to use a rule similar to (16).18
In fact, if such a rule were specified, the aggregate price path would be identical to that of the case requiring agents to use a money rule.
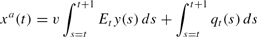
can be written as
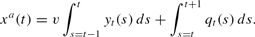
Again, from (14) and (9), the aggregate price path can be written
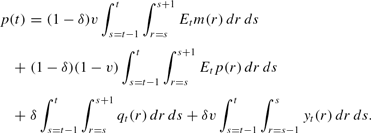
From Table 2, one can see that the net output effects are nearly identical to those under the adaptive money rule. Additionally, the dynamics of the price path are nearly identical between the two cases. As stated in note 18, if one were to forecast output in a way similar to how the money stock is forecasted, the aggregate price path would be exactly identical. Interestingly, the implication is that even if adaptive agents have no knowledge of the process governing the determination of aggregate output, in the end the aggregate effects will be much the same.

Here we consider a more general way of expressing the rule-of-thumb pricing scheme as a special case of a family of broader adaptive rules.19
I thank the associate editor for suggesting this approach.
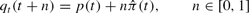
where
is the adaptive expectations forecast of the inflation rate, which evolves according to
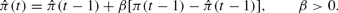
Here,
is the adjustment parameter that governs how quickly adaptive agents adjust to changes in the actual inflation rate. Note that the baseline rule-of-thumb behavior is nested as a special case of (23) where
. Essentially, agents update their expectation of inflation based on what their expectation of inflation was last period, adjusted by a fraction of the error. As
becomes smaller, agents respond less to errors. In the extreme case of
, expectations are completely static; that is, they do not respond at all to changes in the inflation rate. Hence, expected inflation is always equal to 1 (by assumption). Figure 8 shows the effect of varying values for
. Clearly, as
decreases, the effect of any given proportion of rule-of-thumb behavior becomes much more pronounced. An alternative interpretation is that less rule-of-thumb behavior is necessary to achieve a particular output effect, essentially because the degree of nonrationality for any given proportion of rule-of-thumb agents is larger.

Output paths for varying β: v=0.1, δ=0.2.
Two important questions often debated with regard to disinflation policy are (i) does the size of disinflation matter, and (ii) what is the sacrifice ratio? In the context of the model outlined above, the size of disinflation does not matter. Effects on the level of output will be smaller for smaller disinflations; however, one can show that, whether the Fed engineers a 1% or a 100% disinflation, the size of the sacrifice ratio will still be the same under either program. Very simply, the scaling factor reducing the size of the disinflation also scales output by the exact same amount, therefore leaving the overall sacrifice ratio the same. In practice, this feature seems a bit optimistic. Higher average inflation rates are usually accompanied by a higher frequency of price adjustment. Even if large adjustments to prices (and price growth) are required, more frequent price adjustments allow agents to keep prices closer to the relative profit-maximizing prices, thus lowering the costs to disinflation. Ball (1994a) uses data to estimate sacrifice ratios for selected OECD countries, and finds mixed evidence on whether the initial level of inflation influences the sacrifice ratio.
Comparing previous estimates of the sacrifice ratio to the predictions of this model allows one to gauge the importance that rule-of-thumb behavior has on the economy. Ball's (1994a) study indicates that for the United States, sacrifice ratio estimates of particular disinflation episodes using annual data range from approximately 1.6 to 3.3 percentage points of output given up per percentage point reduction in the rate of inflation, with an average of 2.3. Using quarterly data, estimates range from 1.8 to 2.9, with an average of 2.4. Across all the selected OECD countries, the estimates average 0.8 for annual data, and 1.4 for quarterly data. These estimates are in line with recent episode-specific sacrifice ratio estimates. Mankiw (2000), calculates a sacrifice ratio for the Volcker disinflation as 2.8. Using similar methodology to Ball's (1994a), Schelde-Anderson (1992) finds a Volcker sacrifice ratio of 1.4. Figure 9 shows the (
) loci that yield sacrifice ratios of 0, 1, and 2. In this paper, a natural definition of the sacrifice ratio, denoted
is

Critical δ's for sacrifice ratios of 0, 1 and 2.
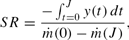
where J is chosen sufficiently far in advance to ensure convergence to trend output.20
The natural choice of J is 50 periods, since it is assumed that the system converges after 50 periods. This interpretation of the sacrifice ratio is the same as Ball's (1995).
For
, approximately 45% of rule-of-thumb agents would be required to produce a unit sacrifice ratio, and 74% rule-of-thumb agents would be needed to invoke a sacrifice ratio of 2. For
, all agents in the economy would need to use rule-of-thumb behavior to produce close to a unit sacrifice ratio. Even under the OECD average estimate of 0.8, relatively large numbers of backward-looking agents would be needed to produce that sacrifice ratio. For
, less rule-of-thumb behavior is necessary to produce given sacrifice ratios. For
values of 0.28 and 0.44, the sacrifice ratio estimates are 1 and 2, respectively. The lower level of v makes the firm's chosen price more dependent on expectations; the greater volatility in the price path results in higher costs to disinflate.
One of the long-debated questions of inflation management is whether a disinflation should be conducted quickly—the “cold-turkey” approach—or more gradually. A cold-turkey proponent would argue that quicker disinflations may cause short-term losses because price setters are unable to adjust prices quickly enough such that relative prices are close to profit-maximizing levels. However, long-term losses are reduced because price setters are forced to make large price adjustments in a short period of time, allowing price setters to choose a relative price closer to the long-term profit-maximizing level. A gradualist would argue the exact opposite: slow downward adjustment of the inflation rate allows price setters to sustain relative prices closer to profit-maximizing levels, resulting in smaller short-term losses. Over an extended time, these short-term losses will not be as costly as a quick disinflation. The answer to which approach is most appropriate lies in which school has the lowest overall costs, weighing both near-term and long-term net costs. This section intends to investigate which approach is best in the context of this model.
Again, we assume rational agents behave as before, and adaptive agents behave as in the baseline model described above. At time
, the central bank announces a linear disinflation spanning two periods rather than one.21
Again, we assume the announcement is fully credible and that the disinflation program is not known in advance.
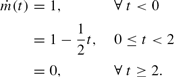
We can normalize the path of money as
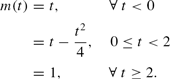
From Table 2, it is apparent that a disinflation of two periods greatly reduces the costs to disinflation. Indeed, for all values of
, net output is unambiguously higher relative to the baseline model. With a steeper (cold-turkey) money growth slowdown, inflation inertia squeezes the aggregate price path closer to the path of money, producing a smaller boom and larger subsequent recession. With a two-period disinflation, inflation inertia is less problematic: relative prices are closer to the profit-maximizing level if firms were allowed to continuously reset. As a result, welfare overall is higher under the gradualist disinflation.
Comparison of the paths of output in Figures 6A and 6B reinforces the result. Under
, output peaks near 15% and never fall into recession. With the higher proportion of adaptive agents,
, output peaks are close to 3% and then fall to near
9% before converging. Clearly, the longer disinflation policy reduces the volatility of pricing behavior, thus reducing aggregate fluctuations in output relative to the baseline case.
Because the costs to a longer disinflation are decreased, a higher proportion of adaptive agents are required to produce zero net output over time. Reflecting this feature is Figure 7, which shows the break-even net output locus significantly skewed to the upper left quadrant relative to the baseline model.
Though the results above would support a gradualist policy, overall the results depend in a relative sense on the degree of nonrationality. As the length of the disinflation increases to three periods, for very large
, output actually decreases. Figure 10 shows the optimal disinflation length for various proportions of nonrational agents ranging from
to 1.22
Not shown are the results for full rationality,
. Here, the optimal disinflation length is greater than 30 periods. For aesthetic purposes, this result was not included.
.23
Formally, we cannot prove that these are the maximizing values, however extensive numerical calculations imply the result.
and disinflation length are displayed above the bars. It is quite apparent that as the degree of rationality increases (
becomes smaller), the optimal disinflation length becomes larger, and the maximum achievable net output increases. The most striking feature of Figure 10 lies in the results on output. If 30% of the population are nonrational (
), the best option for a disinflation policy is to disinflate over seven periods, and even at that, net output still falls 38%. With
, the optimal policy of the Fed is to disinflate over 10 periods, resulting in near break-even net output. For
, the results are even more discouraging. Though the optimal disinflation length decreases, the maximum achievable net output decreases substantially. It is noteworthy to remind the reader that the results in Figure 10 assume a 100% disinflation. For smaller disinflations, the qualitative results still hold; however, the scale of the output effects are smaller.

Optimal disinflation lengths for given δ: v=0.1 (net output above bars).
The results from Figure 10 indicate that for large
, the best disinflation policy argues for cold-turkey, whereas for small
, a gradualist policy maximizes output. On one extreme, with
, a disinflation of any size will have large negative effects on output. Extending the length of the disinflation over a protracted period of time builds up losses in output because the aggregate price path is too slow to adjust to the disinflation. If the Fed chooses a shorter recession (say two periods) the up-front costs in terms of output loss are large, but the price path and output path adjust to a steady-state equilibrium more quickly, overall allowing for a less costly disinflation. At the other extreme, if
the predominantly rational contingent determines the price path. A disinflation over a shorter period yields a large boom in a relatively short period of time. Alternatively, a longer disinflation squeezes the aggregate price path closer to the path of money, yielding smaller gains at any moment in time. The combined smaller gains over a protracted period of time increase net output more than a quick disinflation.
Note that the above results do not deal with credibility problems that the central bank would likely face with longer disinflations. In particular, for relatively high proportions of rationality, it is optimistic to assume that rational agents will believe the central bank in announcing, say, a 17-year-long disinflation policy. More practically, the loss of credibility by the central bank will greatly reduce both the maximum achievable net output, and the optimal disinflation length. The qualitative result that cold turkey is best for large proportions of nonrational agents, whereas gradualist is best for near rationality may not hold if credibility is introduced.
Ball (1995) shows that under a similar model, the loss of credibility imparts significant costs to disinflation. However, Ball does not investigate the effects nonrationality has on aggregate dynamics in the context of a less-than-fully credible Fed. Mankiw (2001) posits that, in essence, all disinflations are credible, and therefore credibility should not be a consideration. To verify the above assertion of the qualitative features, one would have to specify various probabilities, or hazard rates of reneging as in Ball (1995) across different announced disinflation lengths and for any particular degree of nonrationality. Of course, the results will depend upon the amount of the disinflation, and the (subjective) importance that credibility plays in the firm-level decision-making process.
Most economists agree that disinflations are costly in terms of output. Ball (1994b) shows that staggered pricing models with rational agents can produce a disinflationary boom. Some recent attempts to amend the Ball results include noncredible monetary policies, accounting for interest rate effects, and behavioral macroeconomic considerations, such as Mankiw and Reis' (2002) “inattentive agents” framework. Following the behavioral macroeconomics literature, we argue that by introducing nonrational behavior by some agents, the model can be consistent with empirical evidence.
With the introduction of rule-of-thumb behavior, even small proportions of nonrational agents eventually produce a recession. As important, relatively small proportions of rule-of-thumb behavior can produce zero or negative net output over time, as evidenced by Figure 5. As the proportions of adaptive agents rise, for a given disinflation the eventual recession becomes larger and more pronounced. If adaptive agents are required to forecast output or money in an adaptive way, aggregate fluctuations in output are even more apparent. Certainly, to give added robustness to these results advocating the rule-of-thumb approach, alternative New Keynesian models should be examined, which we leave open for future research.
The model's implications for matching the empirical estimates of the sacrifice ratio suggest that high concentrations of nonrationality are required. Under the staggered pricing model outlined in this paper, a longer disinflation is preferable to a cold-turkey disinflation for a mostly rational population of agents. As the proportion of nonrationality increases, it becomes more preferable for the central bank to disinflate more quickly, as measured by maximizing net output.
Though the results presented in this paper rely on a specific form of nonrationality, the rule-of-thumb devised by Gali and Gertler (1999), we do not necessarily advocate this specific rule as a cure-all to explain monetary phenomena. Not unlike how rational expectations are viewed as a focal point for aggregate behavior, here we split aggregate behavior into two subsegments: that which can be explained by (rational) agents with superior information and/or intellectual capabilities; and those agents who, either by choice or by birthright, are compelled to use methods that are simple to use and understand. In that respect, rational expectations can be thought of as a focal point for the “supersmart,” while rule-of-thumb behavior is a focal point for nonrational behavior.
Critics of this approach may contend that this opens up the opportunity for markets to exploit information. Indeed, if nonrational agents are not charging the profit-maximizing price, then there exists the opportunity to sell pricing information to improve the firms profitability. However, we point out two factors that may inhibit this process. First, given the scope and scale of the real economy, it may be difficult for information sellers to identify information buyers, and vice versa. In other words, those who use adaptive pricing schemes may not know where to get this information, or that it even exists. Second, even if the buyers and sellers of rational predictors are identified, we assert that the costs to obtaining them, either monetary, time, or otherwise, outweigh any benefits in terms of recovered profits, thus it is reasonable to assume that nonrationally inclined agents will use some method of approximation to get close to the rational target.24
As a stylized example, any industry where an estimate for work is a binding contract between two parties may be a candidate for some form of rule-of-thumb pricing. An excellent example is the construction industry, where firms oftentimes must make educated guesses about raw materials and labor costs months or even years before a project is to be built, with little or no recourse if their estimates are too low (or too high). Given the complex factors that determine commodity prices (and hence construction raw materials), it is oftentimes exceedingly prohibitive to determine the optimal price to charge.
The rule-of-thumb predictor is one of many possible choices to consider in an economy of heterogeneous agents. With an ever-expanding emphasis on behavioral macroeconomics, future researchers will, without a doubt, pay particular attention to the decision-making processes of individual agents and firms.
This paper has benefited immensely from the insightful suggestions and comments by George W. Evans. I would also like to thank William Branch for his feedback on earlier versions of this paper, as well as anonymous referees and an associate editor. Any remaining errors or omissions are my own.
Money stock and money growth.
Ball's result.

Adaptive price-setting behavior.
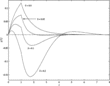
Output paths: v=0.1.

Net output for selected parameter values
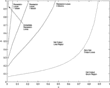
Critical values of δ, baseline model.
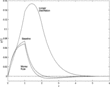
Output paths, alternative specifications: v=0.1, δ=0.05.
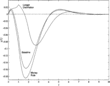
Output paths, alternative specifications: v=0.1, δ=0.2.
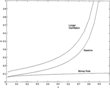
Critical δ values for zero net output, alternative specifications.

Net output for selected parameter values, alternative specifications
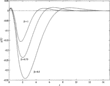
Output paths for varying β: v=0.1, δ=0.2.
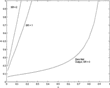
Critical δ's for sacrifice ratios of 0, 1 and 2.
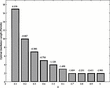
Optimal disinflation lengths for given δ: v=0.1 (net output above bars).