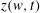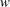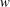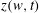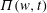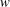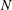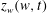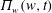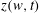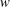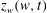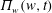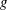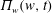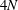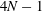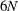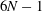1 Introduction and basic equations

Figure 1. Shaded area represents the domain occupied by fluid in the physical plane $z=x+\text{i}y$ (a) and the same domain in $w=u+\text{i}v$ plane (b). Thick solid lines correspond to the fluid’s free surface.

We consider two-dimensional potential motion of an ideal incompressible fluid with a free surface of infinite depth. Fluid occupies the infinite region $-\infty <x<\infty$ in the horizontal direction $x$ and extends down to $y\rightarrow -\infty$ in the vertical direction $y$ , as schematically shown in figure 1(a). We assume that fluid is unperturbed both at $x\rightarrow \pm \infty$ and $y\rightarrow -\infty$ .

We use a time-dependent conformal mapping

(1.1) $$\begin{eqnarray}\displaystyle z(w,t)=x(w,t)+\text{i}y(w,t) & & \displaystyle\end{eqnarray}$$

of the lower complex half-plane $\mathbb{C}^{-}$ of the auxiliary complex variable $w\equiv u+\text{i}v$ , $-\infty <u<\infty$ , into the area in the $(x,y)$ plane occupied by the fluid. Here the real line $v=0$ is mapped into the fluid free surface (see figure 1) and $\mathbb{C}^{-}$ is defined by the condition $-\infty <v\leqslant 0$ . Then the time-dependent fluid free surface is represented in parametric form as

(1.2a,b ) $$\begin{eqnarray}\displaystyle x=x(u,t),\quad y=y(u,t). & & \displaystyle\end{eqnarray}$$

A decay of perturbation of fluid beyond flat surface at $x(u,t)\rightarrow \pm \infty$ and/or $y\rightarrow -\infty$ requires that

(1.3) $$\begin{eqnarray}\displaystyle z(w,t)\rightarrow w\quad \text{for }|w|\rightarrow \infty ,w\in \mathbb{C}^{-}. & & \displaystyle\end{eqnarray}$$

The conformal mapping (1.1) implies that $z(w,t)$ is an analytic function of $w\in \mathbb{C}^{-}$ and

(1.4) $$\begin{eqnarray}\displaystyle z_{w}\neq 0\quad \text{for any }w\in \mathbb{C}^{-}. & & \displaystyle\end{eqnarray}$$

Potential motion means that the velocity $\boldsymbol{v}$ of fluid is determined by a velocity potential $\unicode[STIX]{x1D6F7}(\boldsymbol{r},t)$ as $\boldsymbol{v}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}$ with $\unicode[STIX]{x1D735}\equiv (\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)$ . The incompressibility condition $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0$ implies the Laplace equation

(1.5) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D6F7}=0 & & \displaystyle\end{eqnarray}$$

inside the fluid, i.e.  $\unicode[STIX]{x1D6F7}$ is a harmonic function inside the fluid. Equation (1.5) is supplemented with a decaying boundary condition (BC) at infinity,

(1.6) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}\rightarrow 0\quad \text{for }|x|\rightarrow \infty \text{or }y\rightarrow -\infty . & & \displaystyle\end{eqnarray}$$

The harmonic conjugate of $\unicode[STIX]{x1D6F7}$ is a streamfunction $\unicode[STIX]{x1D6E9}$ defined by

(1.7a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{x}=-\unicode[STIX]{x1D6F7}_{y}\quad \text{and}\quad \unicode[STIX]{x1D6E9}_{y}=\unicode[STIX]{x1D6F7}_{x}. & & \displaystyle\end{eqnarray}$$

Similar to (1.6), we set without loss of generality a zero Dirichlet BC for $\unicode[STIX]{x1D6E9}$ as

(1.8) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}\rightarrow 0\quad \text{for }|x|\rightarrow \infty \text{or }y\rightarrow -\infty . & & \displaystyle\end{eqnarray}$$

We define a complex velocity potential $\unicode[STIX]{x1D6F1}(z,t)$  as

(1.9) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F7}+\text{i}\unicode[STIX]{x1D6E9}. & & \displaystyle\end{eqnarray}$$

Then equations (1.7) turn into Cauchy–Riemann equations ensuring the analyticity of $\unicode[STIX]{x1D6F1}(z,t)$ in the domain of $z$ plane occupied by the fluid. A physical velocity with the components $v_{x}$ and $v_{y}$ (in the $x$ and $y$ directions, respectively) is obtained from $\unicode[STIX]{x1D6F1}$ as $\text{d}\unicode[STIX]{x1D6F1}/\text{d}z=v_{x}-\text{i}v_{y}$ . The conformal mapping (1.1) ensures that the function $\unicode[STIX]{x1D6F1}(z,t)$ (1.9) transforms into $\unicode[STIX]{x1D6F1}(w,t)$ which is an analytic function of $w$ for $w\in \mathbb{C}^{-}$ (in the bulk of the fluid). Here and below we abuse the notation and use the same symbols for functions of either $w$ or $z$ (in other words, we assume that e.g. $\tilde{\unicode[STIX]{x1D6F1}}(w,t)=\unicode[STIX]{x1D6F1}(z(w,t),t)$ and remove the $\tilde{}$ sign). The conformal transformation (1.1) also ensures the Cauchy–Riemann equations hold $\unicode[STIX]{x1D6E9}_{u}=-\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D6E9}_{v}=\unicode[STIX]{x1D6F7}_{u}$ in $w$ plane.

BCs at the free surface are time dependent and consist of kinematic and dynamic BCs. A kinematic BC ensures that the free surface moves with a normal velocity component $v_{n}$ of fluid particles at the free surface. Motion of the free surface is determined by the time derivative of the parameterization (1.2) while the kinematic BC is given by a projection into the normal direction as

(1.10) $$\begin{eqnarray}\displaystyle \boldsymbol{n}\boldsymbol{\cdot }(x_{t},y_{t})=v_{n}\equiv \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}|_{x=x(u,t),y=y(u,t)}, & & \displaystyle\end{eqnarray}$$

where $\boldsymbol{n}=(-y_{u},x_{u})/(x_{u}^{2}+y_{u}^{2})^{1/2}$ is the outward unit normal vector to the free surface and use of subscripts here and below means partial derivatives, $x_{t}\equiv \unicode[STIX]{x2202}x(u,t)/\unicode[STIX]{x2202}t$ etc.

Equation (1.10) results in a compact expression

(1.11) $$\begin{eqnarray}\displaystyle y_{t}x_{u}-x_{t}y_{u}=-{\hat{H}}\unicode[STIX]{x1D713}_{u} & & \displaystyle\end{eqnarray}$$

for the kinematic BC as was found in Dyachenko et al. (Reference Dyachenko, Kuznetsov, Spector and Zakharov1996), see also Dyachenko, Lushnikov & Zakharov (Reference Dyachenko, Lushnikov and Zakharov2019) for more details. Here

(1.12) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(u,t)\equiv \unicode[STIX]{x1D6F7}(u,v,t)|_{v=0} & & \displaystyle\end{eqnarray}$$

is the Dirichlet BC for $\unicode[STIX]{x1D6F7}$ at the free surface and

(1.13) $$\begin{eqnarray}\displaystyle {\hat{H}}f(u)=\frac{1}{\unicode[STIX]{x03C0}}\text{p.v.}\int _{-\infty }^{+\infty }\frac{f(u^{\prime })}{u^{\prime }-u}\,\text{d}u^{\prime } & & \displaystyle\end{eqnarray}$$

is the Hilbert transform with $\text{p.v.}$ meaning a Cauchy principal value of the integral. Real and imaginary parts of both $z$ and $\unicode[STIX]{x1D6F1}$ at $v=0$ are related through ${\hat{H}}$ as follows:

(1.14a,b ) $$\begin{eqnarray}\displaystyle \tilde{x}\equiv x-u=-{\hat{H}}y,\quad {\hat{H}}x=y & & \displaystyle\end{eqnarray}$$

and

(1.15a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}|_{w=u}={\hat{H}}\unicode[STIX]{x1D713},\quad \unicode[STIX]{x1D713}=-{\hat{H}}\unicode[STIX]{x1D6E9}|_{w=u}, & & \displaystyle\end{eqnarray}$$

see e.g. appendix A of Dyachenko et al. (Reference Dyachenko, Lushnikov and Zakharov2019). Thus it is sufficient to find $y(u,t)$ and $\unicode[STIX]{x1D713}(u,t)$ while $x(u,t)$ and $\unicode[STIX]{x1D6E9}(u,t)$ can be recovered from equations (1.14) and (1.15).

A dynamic BC is given by the time-dependent Bernoulli equation (see e.g. Landau & Lifshitz (Reference Landau and Lifshitz1989)) at the free surface,

(1.16) $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F7}_{t}+{\textstyle \frac{1}{2}}(\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7})^{2}+gy)|_{x=x(u,t),y=y(u,t)}=-P_{\unicode[STIX]{x1D6FC}}, & & \displaystyle\end{eqnarray}$$

where $g$ is the acceleration due to gravity and $P_{\unicode[STIX]{x1D6FC}}=-(\unicode[STIX]{x1D6FC}(x_{u}y_{uu}-x_{uu}y_{u})/(x_{u}^{2}+y_{u})^{3/2})$ is the pressure jump at the free surface due to the surface tension coefficient $\unicode[STIX]{x1D6FC}$ . Here without loss of generality we assumed that pressure is zero above the free surface (i.e. in vacuum). All results below apply both to the surface gravity wave case ( $g>0$ ) and the Rayleigh–Taylor problem $(g<0)$ . We also consider a particular case $g=0$ where inertia forces well exceed gravity force.

Equation (1.16) can be transformed into

(1.17) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}y_{u}-\unicode[STIX]{x1D713}_{u}y_{t}+gyy_{u}=-{\hat{H}}(\unicode[STIX]{x1D713}_{t}x_{u}-\unicode[STIX]{x1D713}_{u}x_{t}+gyx_{u})-\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{x_{u}}{|z_{u}|}+\unicode[STIX]{x1D6FC}{\hat{H}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{y_{u}}{|z_{u}|}, & & \displaystyle\end{eqnarray}$$

thus representing the dynamic BC in the conformal variables; see Dyachenko et al. (Reference Dyachenko, Lushnikov and Zakharov2019) for details of such a transformation.

Equations (1.11), (1.14) and (1.17) form a closed set of equations which is equivalent to the Euler equations for the dynamics of an ideal fluid with a free surface. The idea of using a time-dependent conformal transformation like (1.1) to address systems equivalent/similar to equations (1.11), (1.14) and (1.17) was exploited by several authors including Ovsyannikov (Reference Ovsyannikov1973), Meison, Orzag & Izraely (Reference Meison, Orzag and Izraely1981), Tanveer (Reference Tanveer1991, Reference Tanveer1993), Dyachenko et al. (Reference Dyachenko, Kuznetsov, Spector and Zakharov1996), Chalikov & Sheinin (Reference Chalikov and Sheinin1998, Reference Chalikov and Sheinin2005), Chalikov (Reference Chalikov2016), Zakharov, Dyachenko & Vasiliev (Reference Zakharov, Dyachenko and Vasiliev2002). We follow the analysis of Zakharov & Dyachenko (Reference Zakharov and Dyachenko2012), Dyachenko et al. (Reference Dyachenko, Lushnikov and Zakharov2019) which found that equations (1.11), (1.14) and (1.17) can be explicitly solved for the time derivatives $y_{t},\unicode[STIX]{x1D713}_{t}$ and rewritten in the non-canonical Hamiltonian form

(1.18) $$\begin{eqnarray}\displaystyle \boldsymbol{Q}_{t}=\hat{R}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\boldsymbol{Q}},\quad \boldsymbol{Q}\equiv \left(\begin{array}{@{}c@{}}y\\ \unicode[STIX]{x1D713}\end{array}\right) & & \displaystyle\end{eqnarray}$$

for the Hamiltonian variables $y(u,t)$ and $\unicode[STIX]{x1D713}(u,t),$ where $\hat{R}=\hat{\unicode[STIX]{x1D6FA}}^{-1}=\big(\!\begin{smallmatrix}0 & \hat{R}_{12}\\ \hat{R}_{21} & \hat{R}_{22}\end{smallmatrix}\!\big)$ is a $2\times 2$ skew-symmetric matrix operator with the components

(1.19) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \hat{R}_{11}q=0,\quad \hat{R}_{12}q=\frac{x_{u}}{J}q-y_{u}{\hat{H}}\left(\frac{q}{J}\right),\\ \displaystyle \hat{R}_{21}q=-\frac{x_{u}}{J}q-\frac{1}{J}{\hat{H}}(y_{u}q),\quad \hat{R}_{21}^{\dagger }=-\hat{R}_{12},\\ \displaystyle \hat{R}_{22}q=-\unicode[STIX]{x1D713}_{u}{\hat{H}}\left(\frac{q}{J}\right)-\frac{1}{J}{\hat{H}}(\unicode[STIX]{x1D713}_{u}q),\quad \hat{R}_{11}^{\dagger }=-\hat{R}_{11}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

We call $\hat{R}=\hat{\unicode[STIX]{x1D6FA}}^{-1}$ by the ‘implectic’ operator (sometimes this type of inverse of the symplectic operator is also called by the co-symplectic operator, see e.g. Weinstein (Reference Weinstein1983)). Here the Hamiltonian $H$ is the total energy of the fluid (kinetic plus potential energy in the gravitational field and surface tension energy) which is written in terms of the Hamiltonian variables as

(1.20) $$\begin{eqnarray}\displaystyle H & = & \displaystyle -\frac{1}{2}\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}{\hat{H}}\unicode[STIX]{x1D713}_{u}\,\text{d}u+\frac{g}{2}\int _{-\infty }^{\infty }y^{2}(1-{\hat{H}}y_{u})\,\text{d}u\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}\int _{-\infty }^{\infty }\left(\sqrt{(1-{\hat{H}}y_{u})^{2}+y_{u}^{2}}-1+{\hat{H}}y_{u}\right)\,\text{d}u.\end{eqnarray}$$

Equations (1.18) allow us to define the Poisson bracket (see Dyachenko et al. (Reference Dyachenko, Lushnikov and Zakharov2019))

(1.21) $$\begin{eqnarray}\displaystyle \{F,G\}=\int _{-\infty }^{\infty }\,\text{d}u\left(\frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}y}\hat{R}_{12}\frac{\unicode[STIX]{x1D6FF}G}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}+\frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\hat{R}_{21}\frac{\unicode[STIX]{x1D6FF}G}{\unicode[STIX]{x1D6FF}y}+\frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\hat{R}_{22}\frac{\unicode[STIX]{x1D6FF}G}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right), & & \displaystyle\end{eqnarray}$$

and to rewrite equation (1.18) in terms of Poisson mechanics as

(1.22) $$\begin{eqnarray}\displaystyle \boldsymbol{Q}_{t}=\{\boldsymbol{Q},H\}. & & \displaystyle\end{eqnarray}$$

Thus a functional $F$ is a constant of motion of equation (1.22) provided $\{F,H\}=0$ .

The Hamiltonian system (1.18)–(1.22) is the generalization of the results of Zakharov (Reference Zakharov1968). It was conjectured in Dyachenko & Zakharov (Reference Dyachenko and Zakharov1994) that the system (1.14), (1.11) and (1.17) is completely integrable at least for the case of the zero surface tension. Since then the arguments pro and contra were presented, see e.g. Dyachenko, Kachulin & Zakharov (Reference Dyachenko, Kachulin and Zakharov2013a ). Thus this question is still open.

The system (1.11), (1.14) and (1.17) has an infinite number of degrees of freedom. The most important feature of integrable systems is the existence of ‘additional’ constants of motion which are different from ‘natural’ motion constants (integrals) (see Zakharov & Faddeev Reference Zakharov and Faddeev1971; Novikov et al. Reference Novikov, Manakov, Pitaevskii and Zakharov1984; Arnold Reference Arnold1989). For the system (1.11), (1.14) and (1.17), the natural integrals are the energy $H$ (1.20), the total mass of fluid and the horizontal component of the momentum. For $g=0,$ the vertical component of momentum is also an integral of motion. See Dyachenko et al. (Reference Dyachenko, Lushnikov and Zakharov2019) for the explicit expressions for these natural integrals.

In this paper we show that the system (1.11), (1.14) and (1.17) has a number of additional constants of motion. We cannot so far determine/estimate the total number of these constants. Instead we show examples of initial data such that the system has almost obvious, very simply constructed additional constants. We must stress that the number of known additional constants depends so far on the choice of initial data and can be made arbitrarily large for the specific choices of initial data. Some of these new integrals of motion are functional of $y$ only. It follows from equation (1.21) that any functionals $F$ and $G,$ which depend only on $y$ , commute with each other, i.e. $\{F,G\}=0$ . We suggest that the existence of such commuting integrals of motion might be a sign of the Hamiltonian integrability of the free surface hydrodynamics. Such a conjecture is in agreement with the history of the discovery of the Hamiltonian integrability of the Korteweg de Vries equation, nonlinear Schrödinger and many other partial differential equations, see Gardner et al. (Reference Gardner, Greene, Kruskal and Miura1967), Zakharov & Faddeev (Reference Zakharov and Faddeev1971), Zakharov & Shabat (Reference Zakharov and Shabat1972), Novikov et al. (Reference Novikov, Manakov, Pitaevskii and Zakharov1984), Arnold (Reference Arnold1989)).

The plan of the paper is the following. In § 2 we introduce the dynamic equations in complex form for unknowns $R$ and $V$ and consider an analytical continuation of the solution in the upper complex half-plane. Section 3 discusses the non-persistence of pole solutions in both the $R$ and $V$ variables within arbitrarily small time while addressing the fact that power law branch points are persistent. New constants of motion for the gravity case but with zero surface tension are found in § 4 for solutions of the full hydrodynamic equations with simple complex poles in the original variables $z_{w}$ and $\unicode[STIX]{x1D6F1}_{w}$ . Section 5 provides another view of the new motion constants. Section 6 identifies new constants of motion for non-zero surface tension and second-order poles. Section 7 discusses a global analysis for analytical continuation into multi-sheet Riemann surfaces and introduces a Kelvin theorem for phantom hydrodynamics. Section 8 provides a brief description of our numerical methods for the simulation of free surface dynamics by a spectrally accurate adaptive mesh refinement approach and a procedure for recovering of the structure of the complex singularities above the fluid’s surface. Section 9 is devoted to the numerical results on free surface hydrodynamic simulations which provides a detailed verification of the results of all other sections. Section 10 gives a summary of the obtained results and a discussion of future directions.

2 Dynamic equations in the complex form and analytical continuation of the solution into the upper complex half-plane

Dynamical equations (1.11), (1.14) and (1.17) are defined on the real line $w=u$ with the analyticity of $z(w,t)$ and $\unicode[STIX]{x1D6F1}(w,t)$ in $w\in \mathbb{C}^{-}$ taken into account through the Hilbert operator ${\hat{H}}$ . In this paper we consider also the analytical continuation of these functions into the upper complex half-plane $w\in \mathbb{C}^{+}$ . Both $z(w,t)$ and $\unicode[STIX]{x1D6F1}(w,t)$ have time-dependent complex singularities for $w\in \mathbb{C}^{+}$ .

Using the Hilbert operator ${\hat{H}}$ (1.13), we introduce the operators

(2.1a,b ) $$\begin{eqnarray}\displaystyle \hat{P}^{-}={\textstyle \frac{1}{2}}(1+\text{i}{\hat{H}})\quad \text{and}\quad \hat{P}^{+}={\textstyle \frac{1}{2}}(1-\text{i}{\hat{H}}), & & \displaystyle\end{eqnarray}$$

which are the projector operators of a function $q(u)$ defined at the real line $w=u$ into functions $q^{+}(u)$ and $q^{-}(u)$ analytic in $w\in \mathbb{C}^{-}$ and $w\in \mathbb{C}^{+}$ , respectively, such that

(2.2) $$\begin{eqnarray}\displaystyle q=q^{+}+q^{-}. & & \displaystyle\end{eqnarray}$$

Here we assume that $q(u)\rightarrow 0$ for $u\rightarrow \pm \infty$ . Equations (2.1) imply that

(2.3a,b ) $$\begin{eqnarray}\displaystyle \hat{P}^{+}(q^{+}+q^{-})=q^{+}\quad \text{and}\quad \hat{P}^{-}(q^{+}+q^{-})=q^{-}, & & \displaystyle\end{eqnarray}$$

see more discussion of the operators (2.1) in Dyachenko et al. (Reference Dyachenko, Lushnikov and Zakharov2019).

Using equations (1.9), (1.14), (1.15) and (2.1) we obtain that

(2.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D713}+\text{i}{\hat{H}}\unicode[STIX]{x1D713}=2\hat{P}^{-}\unicode[STIX]{x1D713} & & \displaystyle\end{eqnarray}$$

and

(2.5) $$\begin{eqnarray}\displaystyle z-u=-{\hat{H}}y+\text{i}y=2\text{i}\hat{P}^{-}y. & & \displaystyle\end{eqnarray}$$

Analytical continuation of equations (2.4) and (2.5) into the complex plane $w\in \mathbb{C}$ amounts to a straightforward replacing of $u$ by $w$ in the integral representation of $\hat{P}^{+}q(w)$ and $\hat{P}^{-}q(w)$ as detailed in Dyachenko et al. (Reference Dyachenko, Lushnikov and Zakharov2019).

Applying the projector $\hat{P}^{-}$ and using equations (2.4), (2.5), one can rewrite (see Dyachenko et al. Reference Dyachenko, Lushnikov and Zakharov2019) the dynamical equations (1.18), (1.19) in complex form

(2.6) $$\begin{eqnarray}\displaystyle & \displaystyle z_{t}=\text{i}Uz_{u}, & \displaystyle\end{eqnarray}$$

(2.7) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{t}=\text{i}U\unicode[STIX]{x1D6F1}_{u}-B-{\mathcal{P}}, & \displaystyle\end{eqnarray}$$

where

(2.8) $$\begin{eqnarray}\displaystyle U\equiv \hat{P}^{-}(R\bar{V}+\bar{R}V) & & \displaystyle\end{eqnarray}$$

is the complex transport velocity with

(2.9) $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{P}}=-\text{i}g(z-w)-2\text{i}\unicode[STIX]{x1D6FC}\hat{P}^{-}(Q_{u}\bar{Q}-Q\bar{Q}_{u}), & \displaystyle\end{eqnarray}$$

(2.10) $$\begin{eqnarray}\displaystyle & \displaystyle Q\equiv \frac{1}{\sqrt{z_{u}}}=\sqrt{R} & \displaystyle\end{eqnarray}$$

and

(2.11) $$\begin{eqnarray}\displaystyle B\equiv \hat{P}^{-}(|V|^{2}). & & \displaystyle\end{eqnarray}$$

A complex conjugation $\bar{f}(w)$ of $f(w)$ in equations (2.8), (2.9), (2.11) and throughout this paper is understood as applied with the assumption that $f(w)$ is the complex-valued function of the real argument $w$ even if $w$ takes the complex values so that

(2.12) $$\begin{eqnarray}\displaystyle \bar{f}(w)\equiv \overline{f(\bar{w})}. & & \displaystyle\end{eqnarray}$$

This definition ensures the analytical continuation of $f(w)$ from the real axis $w=u$ into the complex plane of $w\in \mathbb{C}$ .

Another equivalent complex form of the dynamical equations (1.18), (1.19) is given by the ‘Dyachenko’ equations (Dyachenko Reference Dyachenko2001)

(2.13) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}=\text{i}(UR_{u}-RU_{u}), & \displaystyle\end{eqnarray}$$

(2.14) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}=\text{i}[UV_{u}-RB_{u}]+g(R-1)-2\unicode[STIX]{x1D6FC}R\hat{P}^{-}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}(Q_{u}\bar{Q}-Q\bar{Q}_{u}), & \displaystyle\end{eqnarray}$$

where

(2.15) $$\begin{eqnarray}\displaystyle & \displaystyle R=\frac{1}{z_{u}}, & \displaystyle\end{eqnarray}$$

(2.16) $$\begin{eqnarray}\displaystyle & \displaystyle V=\text{i}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F1}}{\unicode[STIX]{x2202}z}=\text{i}R\unicode[STIX]{x1D6F1}_{u} & \displaystyle\end{eqnarray}$$

are the new unknowns first introduced in Dyachenko (Reference Dyachenko2001). Equations (2.13) and (2.14) can be obtained by differentiating equations (2.6), (2.7) over $u$ and using the definitions (2.15) and (2.16), see also Dyachenko et al. (Reference Dyachenko, Lushnikov and Zakharov2019) for more details.

3 Local analysis: non-persistence of poles in $R$ and $V$ variables and persistence of power law branch points

All four functions $R$ , $V$ , $U$ and $B$ of equations (2.8), (2.11), (2.13) and (2.14) must have singularities in the upper half-plane $w\in \mathbb{C}^{+}$ while being analytic for $w\in \mathbb{C}^{-}$ (a trivial case of the singularity at the complex infinity only is also possible). At the initial time $t=0,$ any singularity for $w\in \mathbb{C}^{+}$ is allowed including poles, branch points, etc. We are interested in singularities that keep their nature in the course of evolution for at least a finite duration of time. This ‘persistence’ requirement is very restrictive. It would be extremely attractive to find solutions containing only pole-type singularities such that $R$ , $V$ , $U$ and $B$ would be rational functions of $w$ . There are examples of different reductions/models of free surface hydrodynamics which allow such rational solutions. They include a free surface dynamics for the quantum Kelvin–Helmholtz instability between two components of superfluid Helium (Lushnikov & Zubarev Reference Lushnikov and Zubarev2018); an interface dynamic between an ideal fluid and a light highly viscous fluid Lushnikov (Reference Lushnikov2004) and motion of a dielectric fluid with a charged and ideally conducting free surface in a vertical electric field (Zubarev Reference Zubarev2000, Reference Zubarev2002, Reference Zubarev2008).

However, for the Dyachenko equations (2.8), (2.11), (2.13) and (2.14) without surface tension, which take the form

(3.1) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}=\text{i}(UR_{u}-RU_{u}), & & \displaystyle\end{eqnarray}$$

(3.2a,b ) $$\begin{eqnarray}\displaystyle U=\hat{P}^{-}(R\bar{V}+\bar{R}V),\quad B=\hat{P}^{-}(|V|^{2}), & & \displaystyle\end{eqnarray}$$

(3.3) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}=\text{i}[UV_{u}-RB_{u}]+g(R-1), & & \displaystyle\end{eqnarray}$$

rational solutions are not known and we conjecture that they cannot be constructed to satisfy $R(w)\neq 0$ and $|R(w)|<\infty$ for all $w\in \mathbb{C}^{-}$ (as required by the conformal mapping (1.1) with the condition (1.4)). The only known exception is the trivial case

(3.4a-c ) $$\begin{eqnarray}\displaystyle g=0,\quad \frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}\equiv 0,\quad \text{and}\quad V\equiv 0, & & \displaystyle\end{eqnarray}$$

i.e. a stationary solution of a fluid at rest without gravity. In that case any singularities (including rational solutions) are allowed in $R(w)$ for $w\in \mathbb{C}^{+}$ and these singularities remain constant in time. We note that in equations (3.1)–(3.3) and throughout this paper we use the partial derivatives over $w$ and $u$ interchangeably by assuming analyticity in $w$ .

In this section we provide the local analysis of the existence versus non-existence of persistent pole singularities in equations (3.1)–(3.3). The analysis is local because we use the Laurent series of solutions of free surface hydrodynamics at any moving point $w=a(t)$ , $\text{Im}(a)>0$ . This means that we are not restricted to rational solutions because such a local analysis does not exclude the existence of branch points for $w\neq a(t),w\in \mathbb{C}^{+}$ .

We note that the conformal map (1.1) and the definition (2.15) imply that $R(w)\neq 0$ for $w\in \mathbb{C}^{-}$ and, respectively,

(3.5) $$\begin{eqnarray}\displaystyle \bar{R}(w)\neq 0\quad \text{for }w\in \mathbb{C}^{+}. & & \displaystyle\end{eqnarray}$$

We stress that this is a fact of essential importance. Here and below we often omit the second argument $t$ when we focus on analytical properties in $w$ .

We prove Theorem 1 ‘ad absurdum’. Simple poles imply that $V(w)$ and $R(w)$ at $w=a\in \mathbb{C}^{+}$ can be written as

(3.6) $$\begin{eqnarray}\displaystyle & \displaystyle V=\frac{V_{-1}}{w-a}+V_{reg}, & \displaystyle\end{eqnarray}$$

(3.7) $$\begin{eqnarray}\displaystyle & \displaystyle R=\frac{R_{-1}}{w-a}+R_{reg}, & \displaystyle\end{eqnarray}$$

where

(3.8) $$\begin{eqnarray}\displaystyle V_{reg}=\mathop{\sum }_{j=0}^{\infty }V_{j}(w-a)^{j} & & \displaystyle\end{eqnarray}$$

and

(3.9) $$\begin{eqnarray}\displaystyle R_{reg}=\mathop{\sum }_{j=0}^{\infty }R_{j}(w-a)^{j} & & \displaystyle\end{eqnarray}$$

are the regular parts of $V$ and $R$ (these regular parts are analytic functions at $w=a$ ). The coefficients $R_{j},V_{j},j=-1,0,\ldots$ and $a$ in equations (3.6)–(3.9) are assumed to be functions of $t$ only. In a similar way, below we designate by the subscript ‘ $reg$ ’ the non-singular part of all functions at $w=a.$ The functions $U(w)$ and $B(w)$ (3.2) generally also have simple poles at $w=a$ , so that we write them as

(3.10a,b ) $$\begin{eqnarray}\displaystyle U=\frac{U_{-1}}{w-a}+U_{reg},\quad U_{reg}=\mathop{\sum }_{j=0}^{\infty }U_{j}(w-a)^{j}, & & \displaystyle\end{eqnarray}$$

(3.11a,b ) $$\begin{eqnarray}\displaystyle B=\frac{B_{-1}}{w-a}+B_{reg},\quad B_{reg}=\mathop{\sum }_{j=0}^{\infty }B_{j}(w-a)^{j}. & & \displaystyle\end{eqnarray}$$

To understand the validity of these equations and find $U_{-1}$ and $B_{-1}$ we note that using equations (2.1)–(2.3) we can rewrite the definitions (3.2) as

(3.12) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle U=R\bar{V}+\bar{R}V-\hat{P}^{+}(R\bar{V}+\bar{R}V),\\ \displaystyle B=V\bar{V}-\hat{P}^{+}(V\bar{V}).\end{array}\right\} & & \displaystyle\end{eqnarray}$$

The functions $\hat{P}^{+}(R\bar{V}+\bar{R}V)$ and $\hat{P}^{+}(V\bar{V})$ are analytic at $w=a\in \mathbb{C}^{+}$ thus they only contribute to $U_{reg}$ and $B_{reg}$ , respectively. The functions $\bar{R}$ and $\bar{V}$ are also analytic at $w=a$ with Taylor series representations

(3.13) $$\begin{eqnarray}\displaystyle \bar{R}(w)\equiv R_{c}+\mathop{\sum }_{j=1}^{\infty }R_{c,j}(w-a)^{j}, & & \displaystyle\end{eqnarray}$$

and

(3.14) $$\begin{eqnarray}\displaystyle \bar{V}(w)\equiv V_{c}+\mathop{\sum }_{j=1}^{\infty }V_{c,j}(w-a)^{j}, & & \displaystyle\end{eqnarray}$$

where $R_{c}\equiv \bar{R}(a)$ and $V_{c}\equiv \bar{V}(a)$ are zero-order terms and $R_{c,j}$ , $V_{c,j}$ are the coefficients of the higher-order terms of the respective power series.

Equations (3.12)–(3.14) imply that generally $U$ and $B$ have the same types of singularities as $R$ and $V$ except for special cases where the poles of either $R$ or $V$ are cancelled out. Calculating residues of $R\bar{V}+\bar{R}V$ and $|V|^{2}$ at $w=a$ we obtain that

(3.15) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle U_{-1}=R_{c}V_{-1}+V_{c}R_{-1},\\ \displaystyle B_{-1}=V_{c}V_{-1,}\\ \displaystyle R_{c}\equiv \bar{R}(a)\neq 0,\quad V_{c}\equiv \bar{V}(a),\end{array}\right\} & & \displaystyle\end{eqnarray}$$

where we used equations (3.6)–(3.11), (3.13) and (3.14). Also $R_{c}=\bar{R}(a)\neq 0$ follows from the general condition (3.5).

According to Theorem 1’s assumption, $V_{-1}\neq 0$ . Calculating the partial derivative of equation (3.6),

(3.16) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}=\frac{a_{t}V_{-1}}{(w-a)^{2}}+\frac{(V_{-1})_{t}}{w-a}+(V_{reg})_{t}, & & \displaystyle\end{eqnarray}$$

we see that the left-hand side of equation (3.3) has at most (if $a_{t}\neq 0$ ) the second-order pole. At the same time, the right-hand side of equation (3.3) has the third-order pole $-\text{i}R_{c}V_{-1}^{2}/(w-a)^{3}$ because $R_{c}\neq 0,$ where we used equations (3.15). This implies that $V_{-1}=0$ is required to match left-hand side and right-hand side of equation (3.3) which contradicts the initial assumption, thus completing the proof of Theorem 1.

Consider now a more difficult case $R_{-1}\neq 0$ and $V_{-1}=0.$ Equations (3.6)–(3.11) and (3.11)–(3.15) imply that $V(w)$ and $B(w)$ are regular functions at $w=a$ . If $V_{c}\neq 0$ then $U(w)$ has a pole according to equations (3.10) and (3.15). This leads to the formation of a second-order pole in equation (3.1) which is cancelled out provided

(3.17) $$\begin{eqnarray}\displaystyle a_{t}=\text{i}[R_{0}V_{c}-U_{0}], & & \displaystyle\end{eqnarray}$$

where $U_{0}$ cannot be obtained from the local analysis of this section because it requires us to evaluate the projector in equation (3.12) which needs global information about $V$ and $R$ in the complex plane $w\in \mathbb{C}$ .

At the next order, $(w-a)^{-1}$ , we obtain that

(3.18) $$\begin{eqnarray}\displaystyle (R_{-1})_{t}=-2\text{i}R_{-1}(U_{1}-R_{1}V_{c}), & & \displaystyle\end{eqnarray}$$

and

(3.19) $$\begin{eqnarray}\displaystyle B_{1}=-\text{i}g+V_{1}V_{c}, & & \displaystyle\end{eqnarray}$$

where again $U_{1}$ and $B_{1}$ can be found only if $V$ and $R$ are known globally in the complex plane $w\in \mathbb{C}$ . The conditions (3.17)–(3.19) must be satisfied during evolution. Similar conditions can be obtained from terms of orders $(w-a)^{0},(w-a)^{1},\ldots$ to give equations for the time derivatives of the coefficients of the series of the regular parts of  $R$ and $V$ (e.g. the order $(w-a)^{0}$ provides the explicit expressions for $(R_{0})_{t}$ and $(V_{0})_{t}$ etc.).

We conclude that the local analysis does not exclude the possibility of the existence of the persistent-in-time solution with $R_{-1}\neq 0$ and $V_{-1}=0$ . The exceptional case, when global information is not needed, is $V\equiv 0$ (meaning that $U\equiv 0$ and $B\equiv 0$ ) which implies that equation (3.19) cannot be satisfied for $g\neq 0$ . Then by contradiction we conclude that

(3.20) $$\begin{eqnarray}\displaystyle R_{-1}=0,\quad \text{for }V\equiv 0\text{ and }g\neq 0, & & \displaystyle\end{eqnarray}$$

i.e. no persistent poles exist in that case even for the pole only in $R$ with $V$ analytic at that point.

Theorem 1 can be generalized to prove non-persistence of the same higher-order poles $R$ with $V$ . The analysis of that case is beyond the scope of this paper.

We note that the analysis of Tanveer (Reference Tanveer1993) assumed that both $\unicode[STIX]{x1D6F1}_{u}$ and $z_{u}$ are analytic in the entire complex plane $w\in \mathbb{C}$ at $t=0$ (Tanveer (Reference Tanveer1993) actually considered periodic solutions with an additional symmetry in the horizontal direction with the fluid domain mapped to the unit disk, but we can adjust results of this case to our conformal map). In terms of $R$ and $V$ , this means that poles are possible only if $z_{u}$ has a regular $n$ th-order zero at $w=a$ with $n=1,2,\ldots .$ Tanveer (Reference Tanveer1993) assumed $z_{u}(w=a,t=0)=0$ and $z_{uu}(w=a,t=0)\neq 0$ , i.e. $n=1.$ Two cases were considered in Tanveer (Reference Tanveer1993) for $a\in \mathbb{C}^{+}$ : (i)  $\unicode[STIX]{x1D6F1}_{u}(w=a,t)\neq 0$ and (ii)  $\unicode[STIX]{x1D6F1}_{u}(w,t)\equiv 0$ in $\mathbb{C}$ . The case (i) implies that $V_{-1}(w=a,t=0)\neq 0$ and $R_{-1}(w=a,t=0)\neq 0$ . Then our Theorem 1 above proves that such an initial condition cannot lead to persistent pole solutions. This agrees with the asymptotic result of Tanveer (Reference Tanveer1993) that a couple of branch points are formed from those initial conditions during an infinitely small duration of time. The case (ii) of Tanveer (Reference Tanveer1993) means that $V\equiv 0$ for $t=0$ which has no poles as proven in equation (3.20). Kuznetsov, Spector & Zakharov (Reference Kuznetsov, Spector and Zakharov1993, Reference Kuznetsov, Spector and Zakharov1994) considered a related case $R\equiv 1$ and a pole in $V$ at $t=0$ which results in the formation of a couple of branch points in an infinitely small duration of time. That result is again consistent with Theorem 1. Thus our results on the non-existence of persistent poles are in full agreement with the particular conditions of Kuznetsov et al. (Reference Kuznetsov, Spector and Zakharov1993, Reference Kuznetsov, Spector and Zakharov1994), Tanveer (Reference Tanveer1993).

We also note that taking into account a non-zero surface tension, i.e. working with equations (2.8), (2.11), (2.13) and (2.14) instead of equations (3.1)–(3.3), immediately shows that the pole singularity both for $R$ and $V$ is non-persistent because the dependence of the surface tension terms of $Q=\sqrt{R}$ introduces the square root singularity into equation (2.14) which cannot be compensated by other terms with poles.

Contrary to the poles analysed above, power law branch points of power $\unicode[STIX]{x1D6FE}$ are persistent in time for free surface dynamics which can be shown by a local analysis that is qualitatively similar to the pole analysis above. The detailed analysis of the persistence of power branch points is however beyond the scope of this paper. The most common type of branch point observed in our numerical experiments is $\unicode[STIX]{x1D6FE}=\frac{1}{2}$ which is consistent with the results of Grant (Reference Grant1973), Tanveer (Reference Tanveer1991, Reference Tanveer1993), Kuznetsov et al. (Reference Kuznetsov, Spector and Zakharov1993, Reference Kuznetsov, Spector and Zakharov1994). Square root singularities have been also intensively studied based on the representation of a vortex sheet in Moore (Reference Moore1979), Baker, Meiron & Orszag (Reference Baker, Meiron and Orszag1982), Meiron, Baker & Orszag (Reference Meiron, Baker and Orszag1982), Krasny (Reference Krasny1986), Caflisch & Orellana (Reference Caflisch and Orellana1989), Baker & Shelley (Reference Baker and Shelley1990), Caflisch, Orellana & Siegel (Reference Caflisch, Orellana and Siegel1990), Shelley (Reference Shelley1992), Baker, Caflisch & Siegel (Reference Baker, Caflisch and Siegel1993), Caflisch et al. (Reference Caflisch, Ercolani, Hou and Landis1993), Cowley, Baker & Tanveer (Reference Cowley, Baker and Tanveer1999), Baker & Xie (Reference Baker and Xie2011), Karabut & Zhuravleva (Reference Karabut and Zhuravleva2014), Zubarev & Kuznetsov (Reference Zubarev and Kuznetsov2014), Zubarev & Karabut (Reference Zubarev and Karabut2018).

A particular solution of equations (3.1)–(3.3) is the Stokes wave, which is a nonlinear periodic gravity wave propagating with constant velocity  (Stokes Reference Stokes1847, Reference Stokes1880). In the generic situation, when the singularity of the Stokes wave is away from the real axis (non-limiting Stokes wave), the only allowed singularity in $\mathbb{C}$ is $\unicode[STIX]{x1D6FE}=1/2$ , as was proven in Tanveer (Reference Tanveer1991) for the first (physical) sheet of the Riemann surface and in Lushnikov (Reference Lushnikov2016) for an infinite number of other (non-physical) sheets of the Riemann surface. Dyachenko, Lushnikov & Korotkevich (Reference Dyachenko, Lushnikov and Korotkevich2013b , Reference Dyachenko, Lushnikov and Korotkevich2016), Lushnikov, Dyachenko & Silantyev (Reference Lushnikov, Dyachenko and Silantyev2017) provided detailed numerical verification of these singularities. The limiting Stokes wave is the special case $\unicode[STIX]{x1D6FE}=1/3$ with $a=\text{i}\text{Im}(a)$ . Also Tanveer (Reference Tanveer1993) suggested the possibility in exceptional cases of the existence of $\unicode[STIX]{x1D6FE}=1/n$ singularities with $n$ being any positive integer as well as singularities involving logarithms.

4 New constants of motion for the gravity case but with zero surface tension

Assume that both functions $R$ and $V$ are analytic on a Riemann surface $\unicode[STIX]{x1D6E4}$ . The complex plane of $w$ is the first sheet of this surface, which we assume to contain a finite number of branch points $w=w_{m},m=1,2,\ldots ,M$ .

We now address the question of whether $R$ could have isolated zeros at some other points of $\mathbb{C}^{+}$ . (We remind the reader that $R(w)\neq 0$ for $w\in \mathbb{C}^{-}$ because the mapping (1.1) is conformal.) Assume that $R$ has a simple zero at $w=a(t)$ , i.e. $R(a)=0$ and $R_{u}(a)\neq 0$ . We assume that the functions $R$ and $V$ are analytic at that point which implies, through equation (3.12), that the functions $U$ and $B$  (3.2) are also analytic at that point with the Taylor series

(4.1) $$\begin{eqnarray}\displaystyle & \displaystyle R=R_{1}(w-a)+R_{2}(w-a)^{2}+\cdots \,,R_{1}\neq 0, & \displaystyle\end{eqnarray}$$

(4.2) $$\begin{eqnarray}\displaystyle & \displaystyle V=V_{0}+V_{1}(w-a)+V_{2}(w-a)^{2}+\cdots \,, & \displaystyle\end{eqnarray}$$

and

(4.3) $$\begin{eqnarray}\displaystyle & \displaystyle U=U_{0}+U_{1}(w-a)+U_{2}(w-a)^{2}+\cdots \,, & \displaystyle\end{eqnarray}$$

(4.4) $$\begin{eqnarray}\displaystyle & \displaystyle B=B_{0}+B_{1}(w-a)+B_{2}(w-a)^{2}+\cdots \,. & \displaystyle\end{eqnarray}$$

Similar to § 3, by plugging equations (4.1)–(4.4) into equations (3.1) and (3.3) and collecting terms of the same order as $(w-a)^{j}$ we obtain for $j=0$ that

(4.5) $$\begin{eqnarray}\displaystyle a_{t}=-\text{i}U_{0} & & \displaystyle\end{eqnarray}$$

and

(4.6) $$\begin{eqnarray}\displaystyle (V_{0})_{t}=-g. & & \displaystyle\end{eqnarray}$$

The order $j=1$ results in

(4.7) $$\begin{eqnarray}\displaystyle (R_{1})_{t}=0 & & \displaystyle\end{eqnarray}$$

and

(4.8) $$\begin{eqnarray}\displaystyle (V_{1})_{t}=gR_{1}+\text{i}(U_{1}V_{1}-B_{1}R_{1}). & & \displaystyle\end{eqnarray}$$

Equations (4.6) and (4.7) are of fundamental importance. Equation (4.7) states that both in the absence and in the presence of gravity

(4.9) $$\begin{eqnarray}\displaystyle R_{1}=\text{const.}\equiv \frac{1}{c_{1}^{(1)}}, & & \displaystyle\end{eqnarray}$$

where $c_{1}^{(1)}$ is a complex time-independent constant. Equation (4.10) results in a trivial dependence on time,

(4.10) $$\begin{eqnarray}\displaystyle V_{0}(t)=-gt+e_{1}^{(1)}, & & \displaystyle\end{eqnarray}$$

where $e_{1}^{(1)}$ is a complex constant defined by the initial condition, $e_{1}^{(1)}=V_{0}(t=0).$ Here the subscript ‘ $1$ ’ stands for the first order of zeros of $R$ in equation (4.1). We conclude that each simple zero of function $R$ generates four additional real integrals of motion. Two of them are the real and imaginary parts of $c_{1}^{(1)}=1/R_{1}.$ The two others are the real and imaginary parts of $e_{1}^{(1)}=V_{0}(t)+gt.$ In addition, $V_{0}(t)$ either obeys the trivial linear dependence on time for non-zero gravity $g\neq 0$ or coincides with $e_{1}^{(1)}$ for $g=0$ . Equation (4.5) provides another important relation showing that $-\text{i}U_{0}$ is ‘the transport velocity’ which governs the propagation of the zeros of the function $R$ in the complex plane of $w$ .

Taking into account all $N$ isolated simple zeros of $R$ at $w=a^{(j)},j=1,\ldots ,N$ and designating by the superscript ‘ $(j)$ ’ the corresponding $j$ th zero, we obtain from equations (4.9) and (4.10) that $R_{1}^{(n)}=\text{const.}\equiv 1/c_{1}^{(n)}$ and $V_{0}^{(n)}(t)=-gt+e_{1}^{(n)}$ . Then we notice that any difference $e_{1}^{(j)}-e_{1}^{(n)},j,n=1,\ldots N,j\neq n,$ is the true integral of motion even for $g\neq 0.$

We conclude that $N$ simple isolated zeros of $R,$ separated from branch points, imply for $g\neq 0$ the existence of $4N-1$ independent new constants of motion $\text{Re}(c_{1}^{(n)})$ , $\text{Im}(c_{1}^{(n)}),n=1,\ldots ,N$ , $\text{Re}(e_{1}^{(n)}-e_{1}^{(N)})$ , $\text{Im}(e_{1}^{(n)}-e_{1}^{(N)}),n=1,\ldots ,N-1$ and $\text{Im}(e_{1}^{(N)})$ as well as one linear function of time $\text{Re}(V_{0}^{(N)})=-gt+\text{Re}(e_{1}^{(N)})$ . For zero gravity $g=0$ we have $4N$ independent new constants of motion $\text{Re}(c_{1}^{(n)})$ , $\text{Im}(c_{1}^{(n)}),\text{Re}(e_{1}^{(n)})$ , $\text{Im}(e_{1}^{(n)}),n=1,\ldots ,N$ .

Section 9 below demonstrates, in a number of particular cases, the independence of these motion constants on time in full nonlinear simulations of equations (3.1)–(3.3).

Using definitions (2.15) and (2.16), we obtain from equations (4.1) and (4.2) that

(4.11) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle z_{w}=\frac{1}{R_{1}(w-a)}+(z_{w})_{reg},\\ \displaystyle \unicode[STIX]{x1D6F1}_{w}=\frac{-\text{i}V_{0}}{R_{1}(w-a)}+(\unicode[STIX]{x1D6F1}_{w})_{reg}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

Equations (4.9)–(4.11) imply that the residues (i.e. the coefficients of $(w-a)^{-1}$ of the Laurent series),

(4.12) $$\begin{eqnarray}\displaystyle \underset{w=a}{\text{Res}}(z_{w})=\frac{1}{R_{1}}=c_{1}^{(1)}=\text{const.} & & \displaystyle\end{eqnarray}$$

and $\underset{w=a}{\text{Res}}(\unicode[STIX]{x1D6F1}_{w})=-\text{i}V_{0}/R_{1}=-\text{i}c_{1}^{(1)}e_{1}^{(1)}=\text{const.}$ , of both $z_{w}$ and $\unicode[STIX]{x1D6F1}_{w}$ are constants of motion for $g=0$ . For $g\neq 0$ , $\underset{w=a}{\text{Res}}(z_{w})$ remains the integral of motion while

(4.13) $$\begin{eqnarray}\displaystyle \underset{w=a}{\text{Res}}(\unicode[STIX]{x1D6F1}_{w})=-\text{i}c_{1}^{(1)}[-gt+e_{1}^{(n)}], & & \displaystyle\end{eqnarray}$$

i.e. it has a linear dependence on time. Section 5 provides another way to straightforwardly derive that these residues are constants of motion.

A Poisson bracket (1.21) between any motion constant is a motion constant itself (see e.g. Arnold Reference Arnold1989). Together such motion constants form a Lie algebra. We conjecture that this Lie algebra is commutative. However, in this paper we are able to prove only the weaker statement that

(4.14) $$\begin{eqnarray}\displaystyle \{c_{1}^{(n)},c_{1}^{(k)}\}=0 & & \displaystyle\end{eqnarray}$$

for any $n,k=1,\ldots ,N.$ The proof is almost trivial and relies on the fact that all $c_{1}^{(n)}$ integrals are determined by the shape of the free surface $z(u,t)$ , i.e. they are functionals of $z$ only. Hence

(4.15) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}c_{1}^{(n)}}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}=0,\quad n=1,\ldots ,N, & & \displaystyle\end{eqnarray}$$

and equation (4.14) immediately follows from the Poisson bracket definition (1.21). The question about the explicit calculation of Poisson brackets $\{c_{1}^{(n)},e_{1}^{(k)}\}$ and $\{e_{1}^{(n)},e_{1}^{(k)}\}$ , $n,k=1,\ldots ,N,$ remains open.

We note that the existence of an arbitrary number of integrals of motion was not addressed in Tanveer (Reference Tanveer1993) because it focused on the particular case of analytic initial data in the entire complex plane $w\in \mathbb{C}$ .

5 Another view of the new motion constants

In this section we use the dynamical equations (2.6), (2.7) with $\unicode[STIX]{x1D6FC}=0$ . It is useful to introduce new functions

(5.1a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}\equiv z_{u}=\frac{1}{R}\quad \text{and}\quad W\equiv \unicode[STIX]{x1D6F1}_{u}=-\text{i}\frac{V}{R}. & & \displaystyle\end{eqnarray}$$

Then differentiating equations (2.6) and (2.7) over $u$ together with the definitions (5.1) implies that

(5.2) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{t}=\text{i}(U\unicode[STIX]{x1D70C})_{u},\\ W_{t}=\text{i}(UW)_{u}-B_{u}+\text{i}g(\unicode[STIX]{x1D70C}-1).\end{array}\right\} & & \displaystyle\end{eqnarray}$$

Let us address a question about possible singularities of the functions $\unicode[STIX]{x1D70C}$ and $W$ . We assume that the functions $R$ and $V$ (2.15), (2.16) have only a finite number of branch points for $w\in C^{+}.$ Apparently, $\unicode[STIX]{x1D70C}$ and $W$ generally inherit these branch points (with the only exception being the possible cancellation of some branch points because $W=-\text{i}V/R$ ) but they cannot have any additional branch point. In other words, if a branch point appears in $\unicode[STIX]{x1D70C}$ and $W$ at some moment of time, then it immediately implies a branch point creation in both $R$ and $V$ .

However, $\unicode[STIX]{x1D70C}$ and $W$ can have poles in the domains of the regularity of $R$ and $V$ . Indeed, assume that $R$ has a regular pole of order $m$ at $w=a$ while $V$ is regular and non-zero at $w=a$ . This means that at $w=a$ both $R$ and $V$ can be represented by Taylor series

(5.3) $$\begin{eqnarray}\displaystyle & \displaystyle R=R_{m}(w-a)^{m}+\cdots \,,R_{m}\neq 0, & \displaystyle\end{eqnarray}$$

(5.4) $$\begin{eqnarray}\displaystyle & \displaystyle V=V_{0}+V_{1}(w-a)+V_{2}(w-a)^{2}+\cdots \,. & \displaystyle\end{eqnarray}$$

Then equations (5.1), (5.3) and (5.4) imply the Laurent series

(5.5) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D70C}=\mathop{\sum }_{j=-m}^{\infty }(w-a)^{j}\unicode[STIX]{x1D70C}_{j},\\ \displaystyle W=\mathop{\sum }_{j=-m}^{\infty }(w-a)^{j}W_{j}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

Here $\unicode[STIX]{x1D70C}_{-1}$ and $W_{-1}$ are the residues of $\unicode[STIX]{x1D70C}$ and $W$ at $w=a$ which can be represented by the contour integrals

(5.6) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{-1}=\frac{1}{2\unicode[STIX]{x03C0}\text{i}}\oint _{C}\unicode[STIX]{x1D70C}\,\text{d}w=\frac{1}{2\unicode[STIX]{x03C0}\text{i}}\oint _{C}\frac{\text{d}w}{R}, & & \displaystyle\end{eqnarray}$$

and

(5.7) $$\begin{eqnarray}\displaystyle W_{-1}=\frac{1}{2\unicode[STIX]{x03C0}\text{i}}\oint _{C}W\,\text{d}w=-\frac{1}{2\unicode[STIX]{x03C0}}\oint _{C}\frac{V\text{d}w}{R}, & & \displaystyle\end{eqnarray}$$

where $C$ is the counterclockwise closed contour around $w=0$ which is taken to be small enough to avoid including any branch point in the interior.

A direct integration of equations (5.2) over the contour $C$ implies, together with equations (5.6) and (5.7), that

(5.8) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D70C}_{-1}=0, & \displaystyle\end{eqnarray}$$

(5.9) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}W_{-1}=\text{i}g\unicode[STIX]{x1D70C}_{-1}, & \displaystyle\end{eqnarray}$$

which is another way to recover the results of § 4 ((4.12) and (4.13)) in terms of $\unicode[STIX]{x1D70C}$ and $W$ . In particular, equation (5.8) means that $\unicode[STIX]{x1D70C}_{-1}$ is a constant of motion and $W_{-1}$ is a motion constant only for $g=0$ while generally

(5.10) $$\begin{eqnarray}\displaystyle W_{-1}=W_{-1}^{(0)}+\text{i}g\unicode[STIX]{x1D70C}_{-1}t, & & \displaystyle\end{eqnarray}$$

with $W_{-1}^{(0)}$ being the complex constant.

Thus poles in $\unicode[STIX]{x1D70C}$ and $W$ are persistent in time (at least during a finite time while $w=a$ remains a regular point of both $\unicode[STIX]{x1D70C}$ and $W$ ) which suggests the following decomposition

(5.11) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{rational}+\unicode[STIX]{x1D70C}_{b},\\ W=W_{rational}+W_{b},\end{array}\right\} & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D70C}_{rational}$ and $W_{rational}$ are rational functions of $w$ while $\unicode[STIX]{x1D70C}_{b}$ and $W_{b}$ generally have branch points.

Assume that at the initial time $t=0$ , both $\unicode[STIX]{x1D70C}$ and $W$ are purely rational, i.e. $\unicode[STIX]{x1D70C}_{b}|_{t=0}=W_{b}|_{t=0}\equiv 0$ . As a simple particular case one can assume that these rational functions have only simple poles with residues $\unicode[STIX]{x1D70C}_{-1}^{(k)}$ and $W_{-1}^{(k)}$ at $N$ points $w=a_{k},\text{Im}(a_{k})>0,k=1,2,\ldots ,N$ as follows:

(5.12a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}|_{t=0}=1+\mathop{\sum }_{k=1}^{N}\frac{\unicode[STIX]{x1D70C}_{-1}^{(k)}}{w-a_{k}},\quad W|_{t=0}=\mathop{\sum }_{k=1}^{N}\frac{W_{-1}^{(k)}}{w-a_{k}}, & & \displaystyle\end{eqnarray}$$

where the 1 on the right-hand side of the first equation ensures the correct limit (1.3). Generally these points might be different for $\unicode[STIX]{x1D70C}$ and $W$ but our particular choice of the same points corresponds to the common poles originating from the zeros of $R$ in equations (5.1). This type of initial condition is studied numerically in § 9. Note that the initial conditions (5.12) imply logarithmic singularities at $w=a_{k},k=1,2,\ldots ,N$ in both $z$ and $\unicode[STIX]{x1D6F1}$ through the definitions (5.1) provided $\unicode[STIX]{x1D70C}_{-1}^{(k)}\neq 0$ and $W_{-1}^{(k)}\neq 0$ .

Bringing equations (5.12) to the common denominator, we immediately conclude that $\unicode[STIX]{x1D70C}|_{t=0}$ has $N$ zeros (counting according to their algebraic multiplicity) at some points $w=b_{k},k=1,2,\ldots ,N$ . Equation (1.4) requires that $\text{Im}(b_{k})>0$ for all $k=1,2,\ldots ,N$ which must be taken into account in choosing initial conditions (5.12) for the simulations.

At a general position $W|_{w=b_{k}}\neq 0$ . Assume that $w=b_{k}$ is an $m$ th-order zero of $\unicode[STIX]{x1D70C}|_{t=0}$ . Then equations (5.1) imply that the Laurent series of both $R$ and $V$ have poles of order $m$ . According to § 3 such poles are not persistent in time, meaning that in an arbitrarily small time they turn into branch points.

The branch point at $w=b_{k}$ is generally moving with time, i.e. $b_{k}=b_{k}(t)$ . At the initial time $t=0$ , the point $w=b_{k}$ is separated from all poles $w=a_{j},j=1,2,.\ldots ,N$ in equations (5.12). This means that at least during a finite time $w=b_{k}$ will remain separated from poles $w=a_{j}(t),j=1,2,\ldots ,N$ which move according to equation (4.5) (this equation is also valid for arbitrary $m$ as shown in § 6 below for $m=2$ , equation (6.5)). During that finite time one can write a decomposition (5.11) as

(5.13) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D70C}=1+\mathop{\sum }_{j=1}^{m}\mathop{\sum }_{k=1}^{N}\frac{\unicode[STIX]{x1D70C}_{-j}^{(k)}}{(w-a_{k}(t))^{j}}+\unicode[STIX]{x1D70C}_{b},\\ \displaystyle W=\mathop{\sum }_{j=1}^{m}\mathop{\sum }_{k=1}^{N}\frac{W_{-j}^{(k)}(t)}{(w-a_{k}(t))^{j}}+W_{b},\end{array}\right\} & & \displaystyle\end{eqnarray}$$

where the ‘non-rational’ terms $\unicode[STIX]{x1D70C}_{b}$ and $W_{b}$ are identically zero at $t=0$ . Here $\unicode[STIX]{x1D70C}_{-1}^{(k)}$ is the motion constant and $W_{-1}^{(k)}(t)$ is a linear function of time according to equations (5.8) and (5.10). Results of the numerical experiment of § 9 support this decomposition scenario completely.

6 New constants of motion for non-zero surface tension and second-order poles in $z_{w}$ and $\unicode[STIX]{x1D6F1}_{w}$

On taking into account non-zero surface tension, $\unicode[STIX]{x1D6FC}\neq 0,$ then instead of equations (3.1)–(3.3) we have to consider the more general equations (2.8), (2.11), (2.13) and (2.14). Expressing $Q=\sqrt{R}$ through $R$ we obtain from equation (2.14) that

(6.1) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}=\text{i}\left[UV_{u}-R\hat{P}^{-}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}(|V|^{2})\right]+g(R-1)-\unicode[STIX]{x1D6FC}R\hat{P}^{-}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\left(\frac{R_{u}\sqrt{\bar{R}}}{\sqrt{R}}-\frac{\bar{R}_{u}\sqrt{R}}{\sqrt{\bar{R}}}\right). & & \displaystyle\end{eqnarray}$$

Assume that initially $R$ and $V$ satisfy equations (4.1)–(4.2). Plugging them into the right-hand side of equation (6.1), one obtains at the leading power of $w-a$ that

(6.2) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}\propto \frac{1}{\sqrt{w-a}}, & & \displaystyle\end{eqnarray}$$

i.e. a square root singularity appears in $V$ in an infinitely small time. Thus the analysis of § 4 fails for non-zero surface tension. However, we can now consider the double zero in $R$ , i.e. equation (4.1) is replaced by

(6.3) $$\begin{eqnarray}\displaystyle & \displaystyle R=R_{2}(w-a)^{2}+\cdots \,,R_{2}\neq 0, & \displaystyle\end{eqnarray}$$

(6.4) $$\begin{eqnarray}\displaystyle & \displaystyle V=V_{0}+V_{1}(w-a)+V_{2}(w-a)^{2}+\cdots \,, & \displaystyle\end{eqnarray}$$

and, respectively, the square root disappears in $\sqrt{R}$ .

Plugging equations (4.3), (4.4), (6.3) and (6.4) into equations (3.1) and (6.1), and collecting terms of the same order $(w-a)^{j}$ we obtain, similar to § 4, at order $j=0$ that

(6.5) $$\begin{eqnarray}\displaystyle a_{t}=-\text{i}U_{0}, & & \displaystyle\end{eqnarray}$$

and

(6.6) $$\begin{eqnarray}\displaystyle (V_{0})_{t}=-g, & & \displaystyle\end{eqnarray}$$

which are exactly the same as equations (4.5) and (4.6) and which implies that equation (4.10) is now trivially replaced by

(6.7) $$\begin{eqnarray}\displaystyle V_{0}(t)=-gt+e_{2}^{(1)}, & & \displaystyle\end{eqnarray}$$

where $e_{2}^{(1)}$ is the constant defined by the initial condition, $e_{2}^{(1)}=V_{0}(t=0)$ . Here the subscript ‘ $2$ ’ stands for the second order of zero of $R$ in equation (6.3).

The orders $j=1$ and $j=2$ result in

(6.8) $$\begin{eqnarray}\displaystyle (R_{2})_{t}=\text{i}R_{2}U_{1}, & & \displaystyle\end{eqnarray}$$

and

(6.9) $$\begin{eqnarray}\displaystyle (V_{1})_{t}=\text{i}V_{1}U_{1}, & & \displaystyle\end{eqnarray}$$

where we do not show an explicit expression for $(V_{2})_{t}$ which appears not to be very useful.

Excluding $U_{1}$ from equations (6.8) and (6.9) we obtain the constant of motion

(6.10) $$\begin{eqnarray}\displaystyle \frac{V_{1}}{R_{2}}=\text{const.}\equiv f_{2}^{(1)}. & & \displaystyle\end{eqnarray}$$

We note that the surface tension coefficient $\unicode[STIX]{x1D6FC}$ does not contribute to equations (6.7) and (6.10) ( $\unicode[STIX]{x1D6FC}$ contributes only to the expression for $(V_{2})_{t}$ and higher orders in powers of $w-a$ ). Thus equation (6.10) is valid for arbitrary $g$ and $\unicode[STIX]{x1D6FC}$ .

Equations (2.15), (2.16), (5.3) and (5.4) imply that equation (4.11) is replaced by the Laurent series

(6.11) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle z_{w}=\frac{1}{R_{2}(w-a)^{2}}-\frac{R_{3}}{R_{2}^{2}(w-a)}+O((w-a)^{0}),\\ \displaystyle \unicode[STIX]{x1D6F1}_{w}=\frac{-\text{i}V_{0}}{R_{2}(w-a)^{2}}+\frac{\text{i}(R_{3}V_{0}-R_{2}V_{1})}{R_{2}^{2}(w-a)}+O((w-a)^{0}).\end{array}\right\} & & \displaystyle\end{eqnarray}$$

However, equations (6.6) and (6.10) do not exhaust all integrals of motion for the case of the second-order pole of this section. For this we note that the results of § 5 on time independence of $\unicode[STIX]{x1D70C}_{-1}=\underset{w=a}{\text{Res}}(z_{w})$ and linear dependence of $W_{-1}=\underset{w=a}{\text{Res}}(\unicode[STIX]{x1D6F1}_{w})$ on time (see equations (5.8) and (5.9)) are true for the second-order pole and they remain valid for $\unicode[STIX]{x1D6FC}\neq 0$ . We note that it is possible to derive equations (5.8) and (5.9) by direct computations in the $R$ and $V$ variables, similar to the derivation of equation (6.10), but we do not provide it here because the analysis of § 5 is much more elegant for these residues. Thus equation (5.8) implies that it is natural to replace the definition of the motion constant $c_{1}^{(1)}$ from equation (4.12) of § 4 for the first-order pole by

(6.12) $$\begin{eqnarray}\displaystyle \underset{w=a}{\text{Res}}(z_{w})\equiv c_{2}^{(1)}=\text{const.} & & \displaystyle\end{eqnarray}$$

for the second-order pole, where the subscript ‘2’ means ‘second order’. Using equation (6.7), one can also rewrite equation (5.10) as follows

(6.13) $$\begin{eqnarray}\displaystyle \underset{w=a}{\text{Res}}(\unicode[STIX]{x1D6F1}_{w})+\text{i}\underset{w=a}{\text{Res}}(z_{w})V_{0}=\text{const}. & & \displaystyle\end{eqnarray}$$

The explicit expressions for $\underset{w=a}{\text{Res}}(z_{w})$ and $\underset{w=a}{\text{Res}}(\unicode[STIX]{x1D6F1}_{w})$ immediately follow from equation (6.11) giving

(6.14a,b ) $$\begin{eqnarray}\displaystyle \underset{w=a}{\text{Res}}(z_{w})=\frac{-R_{3}}{R_{2}^{2}},\quad \underset{w=a}{\text{Res}}(\unicode[STIX]{x1D6F1}_{w})=-\text{i}\underset{w=a}{\text{Res}}(z_{w})V_{0}-\frac{\text{i}V_{1}}{R_{2}}. & & \displaystyle\end{eqnarray}$$

Equations (6.10) and (6.14) also imply that equation (6.13) is not an independent integral of motion.

We now generalize the statement of § 4 on the number of motion constants to the second-order pole case of this section. Taking into account all $N$ isolated zeros of the second order of $R$ at $w=a^{(j)},j=1,\ldots ,N$ and designating by the superscript ‘ $(j)$ ’ the corresponding $j$ th zero, we obtain $2N$ real independent integrals of motion $\text{Re}(f_{2}^{(j)}),\text{Im}(f_{2}^{(j)}),j=1,\ldots ,N$ from equation (6.10); $2N-1$ real independent integrals of motion $\text{Re}(e_{2}^{(j)}-e_{2}^{(N)}),\text{Im}(e_{2}^{(j)}-e_{2}^{(N)}),j=1,\ldots N-1,$ $\text{Im}(e_{2}^{(N)})$ as well as one linear function of time $\text{Re}(V_{0}^{(N)})=-gt+\text{Re}(e_{2}^{(N)})$ (similar to § 4, the number of integrals turns into $2N$ for $g=0$ by adding $\text{Re}(e_{2}^{(N)})$ ) from equation (6.7); and $2N$ real independent integrals of motion $\text{Re}(c_{2}^{(j)}),\text{Im}(c_{2}^{(j)}),j=1,\ldots ,N$ from equation (6.12). Thus the total number of independent complex integrals of motion is either $6N-1$ for $g\neq 0$ or $6N$ for $g=0$ . All these results for the motion constants are valid for non-zero surface tension $\unicode[STIX]{x1D6FC}\neq 0.$ We note that if we look at the poles of an order higher than two, the number of independent integrals of motion is increasing (with $\unicode[STIX]{x1D6FC}\neq 0$ allowed for all even orders). However, such a general case of third- and higher-order poles is beyond the scope of this paper.

One can easily generalize the results of both this section and § 4 by allowing a mixture of the terms with the highest first- and the second-order poles (corresponding to equations (4.1) and (6.3), respectively) at each of the $N$ points of zero of $R$ . The corresponding number of independent integrals of motion can be easily recalculated for that more general case.

The constants of motion $c_{2}^{(j)},j=1,\ldots ,N$ (6.12) are functionals of $z$ only, similar to $c_{1}^{(j)},j=1,\ldots ,N$ of § 4. This implies an immediate generalization of equations (4.14) and (4.15) to

(6.15) $$\begin{eqnarray}\displaystyle \{c_{m_{1}}^{(n)},c_{m_{2}}^{(k)}\}=0, & & \displaystyle\end{eqnarray}$$

and

(6.16) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}c_{m}^{(n)}}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}=0, & & \displaystyle\end{eqnarray}$$

for any $n,k=1,\ldots ,N$ and any $1\leqslant m,m_{1},m_{2}\leqslant 2$ .

7 Kelvin theorem for phantom hydrodynamics and global analysis

In this section we return to the analysis of the free surface hydrodynamics in terms of the functions $R$  (2.15) and $V$ (2.16) which satisfy the Dyachenko equations (2.8), (2.10), (2.11), (2.13) and (2.14). Similar to § 5, we assume that both $R$ and $V$ have a finite number of branch points and pole singularities for $w\in \mathbb{C}^{+}$ . As discussed in § 3, equations (3.12)–(3.14) imply that generally the functions $U$ and $B$ have the same types of singularities as $R$ and $V$ excepting the special cases of cancellation of the singularities. Moreover, both $U$ and $B$ can have singularities only at points were $R$ and $V$ also have singularities. Also all four functions $R$ , $V$ , $U$ and $B$ are analytic for $w\in \mathbb{C}^{-}$ . We note that beyond the branch point our analysis cannot fully exclude the appearance of essential singularities. However, all our numerical simulations of § 9 indicate only the formation of branch points, which is also consistent with the assumption of this section that the only possible singularities of are poles and branch points. See also Lushnikov (Reference Lushnikov2016) for similar discussion in the particular case of the Stokes wave.

We stress that the main task of the theory is to address the analytic properties of $R$ and $V$ in the entire complex plane $w\in \mathbb{C}$ . Moreover, we consider an analytical continuation of these functions into the Riemann surfaces which we call $\unicode[STIX]{x1D6E4}_{R}(w)$ and $\unicode[STIX]{x1D6E4}_{V}(w)$ , respectively. This means that we need a global analysis beyond the local analysis of §§ 3–5. Little is known about these surfaces. If either $R$ or $V$ is a purely rational function, then the corresponding Riemann surface would have a genus zero (see e.g. Dubrovin, Fomenko & Novikov Reference Dubrovin, Fomenko and Novikov1985). However, the results of § 3 suggest that such rational solutions are unlikely to exist for any finite duration of time. The local analysis of § 3 suggests that a branch point in $V$ implies that $R$ also has a branch point of the same type at that point. Then we expect that a covering map exists from $\unicode[STIX]{x1D6E4}_{R}(w)$ onto $\unicode[STIX]{x1D6E4}_{V}(w).$ Then from equation (3.12) we conclude that $U$ has the same Riemann surface as $\unicode[STIX]{x1D6E4}_{R}(w)$ while $B$ has the same Riemann surface as $\unicode[STIX]{x1D6E4}_{V}(w).$ We conjecture that in the general case, branch points of $\unicode[STIX]{x1D6E4}_{R}(w)$ and $\unicode[STIX]{x1D6E4}_{V}(w)$ are of square root type, i.e. their genera are non-zero. We also conjecture, based on the results of § 3, that $V(w)$ generally has no poles for $w\in \mathbb{C}$ with the same valid for $B(w)$ . We conjecture that at a general position $\unicode[STIX]{x1D6E4}_{R}(w)$ and $\unicode[STIX]{x1D6E4}_{V}(w)$ are non-compact surfaces with the unknown total number of sheets. Our experience with the Stokes wave (Lushnikov Reference Lushnikov2016) suggests that generally the number of sheets is infinite. Some exceptional cases such as those found in Karabut & Zhuravleva (Reference Karabut and Zhuravleva2014), Zubarev & Karabut (Reference Zubarev and Karabut2018) have only a finite number of sheets of the Riemann surface (these solutions however have diverging values of $V$ and $R$ at $w\rightarrow \infty$ ). We suggest that the detailed study of such many and infinite sheet Riemann surfaces is one of the most urgent goals in free surface hydrodynamics. This topic is however beyond the scope of this paper.

Both Riemann surfaces $\unicode[STIX]{x1D6E4}_{V}(w)$ and $\unicode[STIX]{x1D6E4}_{R}(w)$ appear after we define the conformal mapping (1.1). There is another Riemann surface, which we call $G(z),$ appearing before the conformal mapping. Indeed, we can look at the complex velocity $V$ inside the fluid in the complex $z$ plane using the definition (2.16). An analytical continuation of $V(z,t)$ outside of the fluid defines $G(z)$ . For stationary waves such a continuation had been considered since the 19th century, see e.g. Lamb (Reference Lamb1945). Here, $\unicode[STIX]{x1D6E4}_{V}(w)$ is the composition of $G(z)$ and $z(w)$ as $\unicode[STIX]{x1D6E4}(w)=G(z(w))$ . The analytical continuation of the time-dependent Bernoulli equation (1.16) also allows us to recover the fluid pressure in the $z$ plane.

The analytically continued function $V(z,t)$ describes the flow of an imaginary (fictional) fluid on the Riemann surface $G(z)$ . We call the corresponding theory ‘the phantom hydrodynamics’. We introduce this new concept in effort to find a physical interpretation of the new motion integrals found in §§ 4–5. The idea of using the circulation over a complex contour in the domain of analyticity of the analytical extension as the integral of motion was also introduced by Crowdy (Reference Crowdy2002) in the quite different physical settings of the rotating Hele-Shaw problem and the viscous sintering problem. For the Hele-Shaw problem (in the approximation of the Laplace growth equation) an infinite number of integrals of motion were also discovered in Richardson (Reference Richardson1972) and later used in Mineev-Weinstein, Wiegmann & Zabrodin (Reference Mineev-Weinstein, Wiegmann and Zabrodin2000) to show the integrability of that equation in the sense of the existence of an infinite number of integrals of motion and its relation to the dispersionless limit of the integrable Toda hierarchy.

Hereafter, we assume that the non-persistence of poles is valid for any order of pole both in $V$ and $R$ (as was proved for more restricted cases in Theorem 1 of § 3 (it also means that we fully exclude a trivial case given by equation (3.4)). Then $R$ can be analytically continued to the same surface as $\unicode[STIX]{x1D6E4}_{V}$ without the introduction of additional singularities, i.e. $\unicode[STIX]{x1D6E4}_{R}=\unicode[STIX]{x1D6E4}_{V}$ . Respectively, one can consider both equations (5.6) and (5.7) on the whole surface $\unicode[STIX]{x1D6E4}_{V}$ beyond just $w\in \mathbb{C}$ . Now $C$ in equations (5.6) and (5.7) is any closed and small enough contour on $\unicode[STIX]{x1D6E4}_{V}$ , which moves together with the surface. This means that the poles of both $\unicode[STIX]{x1D70C}$ and $W$ on other sheets of $\unicode[STIX]{x1D6E4}_{V}$ generate integrals of motion and the total number of these integrals is unknown. One can consider these integrals on the physical surface $G$ . As far as $\text{d}w/R=\text{d}z$ , one can rewrite the right-hand side of equation (5.7) as $-(1/2\unicode[STIX]{x03C0})\oint _{}V\text{d}z$ and interpret a conservation of $W_{-1}$ at $g=0$ as a ‘generalized Kelvin theorem’ valid for the phantom hydrodynamics (see e.g. Landau & Lifshitz (Reference Landau and Lifshitz1989) for the Kelvin theorem of the usual hydrodynamics). Notice however, that this generalized Kelvin theorem can be formulated only after the conformal mapping of the surface $G$ to the surface $\unicode[STIX]{x1D6E4}_{V}$ .

8 Numerical simulations of free surface hydrodynamics through additional time-dependent conformal mapping

8.1 Basic equations for simulations and spectrally accurate adaptive mesh refinement

We performed simulations of the Dyachenko equations (2.8), (2.10), (2.11), (2.13) and (2.14) using a pseudo-spectral numerical method based on a fast Fourier transform (FFT) coupled with an additional conformal mapping (Lushnikov et al. Reference Lushnikov, Dyachenko and Silantyev2017)

(8.1) $$\begin{eqnarray}\displaystyle q=q^{\ast }+2\,\text{arctan}\left[\frac{1}{L}\tan \frac{w-w^{\ast }}{2}\right]. & & \displaystyle\end{eqnarray}$$

Equation (8.1) provides the mapping from our standard conformal variable $w=u~Iv$ into the new conformal variable $q$ . Here $L,q^{\ast },w^{\ast }\in \mathbb{R}$ are the parameters of that additional conformal mapping. The details of the numerical method are provided in Lushnikov et al. (Reference Lushnikov, Dyachenko and Silantyev2017). Here and below we assume without loss of generality that both $R$ and $V$ are periodic functions of $w$ with period $2\unicode[STIX]{x03C0}$ (if the period is different then one can rescale independent variables $w$ and $t$ as well as $g$ and $\unicode[STIX]{x1D6FC}$ to ensure $2\unicode[STIX]{x03C0}$ periodicity while keeping the same form of equations (2.8), (2.11), (2.13) and (2.14)). To recover the limit of the decaying solution at $|u|\rightarrow \infty$ considered in the previous sections, we take the limit of a large spatial period (before rescaling to $2\unicode[STIX]{x03C0}$ ). In terms of rescaled variables, this means that the distance of the complex singularities of interest to the real line $u=w$ must be much smaller than $2\unicode[STIX]{x03C0}$ . However, the analytical results of previous sections are valid for the periodic case also. See also Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016) for a detailed discussion of the periodic case compared with the decaying case. We also note that the conformal map (8.1) conserves the $2\unicode[STIX]{x03C0}$ periodicity of both $R$ and $V$ .

The goal of our simulations was to reach a high and a well-controlled numerical precision while maintaining the analytical properties in the complex plane. The reason for using the new conformal variable (8.1) for the simulations is that a straightforward representation of $R$ and $V$ by Fourier series (while ensuring the analyticity of both $R$ and $V$ for $w\in \mathbb{R}$ ) would be much less efficient as the lowest complex singularity at $w=w_{c}\equiv u_{c}+\text{i}v_{c}$ of $R$ or/and $V$ approaches the real line during the dynamics. Such an approach would imply a slow decay of the Fourier coefficients as

(8.2) $$\begin{eqnarray}\displaystyle \propto \text{e}^{-v_{c}|k|}\quad \text{for }k\gg 1, & & \displaystyle\end{eqnarray}$$

where $k$ is the Fourier wavenumber. It was found in Lushnikov et al. (Reference Lushnikov, Dyachenko and Silantyev2017) that the conformal mapping (8.1) allows us to move the singularity $w=w_{c}$ significantly away from the real line. It was shown there that the optimal choice of the parameter $L$ is

(8.3) $$\begin{eqnarray}\displaystyle L=L_{optimal}\simeq \left(\frac{v_{c}}{2}\right)^{1/2}, & & \displaystyle\end{eqnarray}$$

which ensures a mapping of $w=w_{c}$ into $q=q_{c},$ $\text{Im}(q_{c})\approx (2v_{c})^{1/2}\gg v_{c}$ for $v_{c}\ll 1$ and the fastest possible convergence of Fourier modes in the $q$ variable as

(8.4) $$\begin{eqnarray}\displaystyle \propto \text{e}^{-(2v_{c})^{1/2}|k|}\quad \text{for }k\gg 1. & & \displaystyle\end{eqnarray}$$

The parameters $u^{\ast }$ and $q^{\ast }$ of equation (8.1) are $u^{\ast }=u_{c}$ and $q^{\ast }=2\arctan [L\tan (u^{\ast }/2)]$ . The introduction of these parameters is a modification of the results of Lushnikov et al. (Reference Lushnikov, Dyachenko and Silantyev2017) to account for the motion of complex singularities in the horizontal direction. The scaling (8.4) is greatly beneficial compared with the scaling (8.2) for $v_{c}\ll 1$ because to reach the same numerical precision one needs to take into account a factor ${\sim}(v_{c}/2)^{1/2}$ less Fourier modes. For example, Lushnikov et al. (Reference Lushnikov, Dyachenko and Silantyev2017) demonstrated a ${\sim}10^{6}$ fold speed up of simulations of a Stokes wave with $v_{c}\simeq 10^{-11}$ . In our time-dependent simulations described below we routinely reached down as low as $v_{c}\simeq 10^{-6}$ . It is definitely possible to extend our simulations for significantly smaller $v_{c}$ , which is however beyond the scope of this paper which is focused on numerical verifications of the analytical results of the above sections.

Our simulation method is based on the representation of $R$ and $V$ in Fourier series in the $q$ variable as $R(q,t)=\sum _{k=0}^{-\infty }R_{k}(t)\text{e}^{\text{i}kq}$ and $V(q)=\sum _{k=0}^{-\infty }V_{k}(t)\text{e}^{\text{i}kq}$ , where $R_{k}(t)$ and $V_{k}(t)$ are Fourier modes for the integer wavenumber $k$ . These modes are set to zero for $k>0$ which ensures analyticity of $R$ and $V$ for $w\in \mathbb{C}^{-}$ . For the simulations we truncated Fourier series to the finite sums $R(q,t)=\sum _{k=0}^{-N}R_{k}(t)\text{e}^{\text{i}kq}$ and $V(q)=\sum _{k=0}^{-N}V_{k}(t)\text{e}^{\text{i}kq}$ , where the integer $N$ is a time dependent and chosen large enough at each $t$ to ensure approximately round-off double precision ${\sim}10^{-16}$ . Equations (2.8), (2.11), (2.13) and (2.14) were rewritten in the $q$ variable with the main difficulty being to numerically calculate the projector $\hat{P}^{-}$ (defined by equation (2.1) in the $u$ variable but which must be numerically calculated in the $q$ variable) which we did based on Lushnikov et al. (Reference Lushnikov, Dyachenko and Silantyev2017). We used a uniform grid in $q$ (it is needed for the FFT), which we call the computational domain. In the $u$ variable such a case implies a highly non-uniform grid which focuses on the domain closest to the lowest complex singularity, see Lushnikov et al. (Reference Lushnikov, Dyachenko and Silantyev2017) for details. In other words, our numerical method provides a spectrally accurate adaptive mesh refinement.

During the dynamics we fixed $N$ , $u^{\ast }$ and $L$ for a finite period of time during which the Fourier spectrum was resolved up to a prescribed tolerance (typically we chose that tolerance to be ${\sim}10^{-13}$ for the double precision simulations). Advance in time was achieved by the sixth-order Runge–Kutta method with an adaptive time step to both maintain the numerical precision and satisfy the numerical stability. The de-aliasing (see e.g. Boyd Reference Boyd2001) was not required because after each time step we set all positive Fourier modes to zero to ensure analyticity for $w\in \mathbb{C}^{-}.$ If the Fourier spectrum at some moment of time became too wide to meet the tolerance (this occurs due to the motion of the lowest singularity $w_{c}$ in $\mathbb{C}^{+}$ ) then we first attempted to adjust $u^{\ast }$ and $L$ to make the spectrum narrower to meet the tolerance. This was achieved through the approximation of $u_{c}=u^{\ast }$ by the location of the maximum of the Jacobian $|z_{u}|^{2}$ at the real line $w=u$ while the updated value of $L$ was obtained by decreasing $L$ by a factor $2^{1/2}.$ An alternative procedure to find more accurate values of $v_{c}$ (and respectively more accurate values of  $L$ through equation (8.1)) is to either use the asymptotic of the Fourier series as in Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2013b , Reference Dyachenko, Lushnikov and Korotkevich2016) or to perform a least-square-based rational approximation of the solution (described below) to find an updated value of $w_{c}$ and, respectively to update $u^{\ast }$ and $L$ . After finding new values of $u^{\ast }$ and $L$ , the spectral interpolation was performed on the new grid with the updated values $u^{\ast }$ and $L$ . That step cannot be performed with FFT because the change of $u^{\ast }$ and $L$ causes a nonlinear distortion of the uniform grid compared with the previous value of $L$ . Instead, straightforward evaluations of the Fourier series at each new value of $q$ were performed requiring ${\sim}N^{2}$ flops (while FFT requires only ${\sim}N\log N$ flops). However, such a change of $L$ and/or $u^{\ast }$ was required typically once every few hundred or even many thousands of time steps so the added numerical cost from the $N^{2}$ flops step was moderate. If such a first attempt to update $u^{\ast }$ and $L$ was not sufficient to meet the tolerance, $N$ was also additionally increased by the spectral interpolation to the new grid in $q$ by adding extra Fourier modes of zero amplitude (i.e. increasing $N$ ) and calculating numerical values on the new grid through FFT.

8.2 Recovering the motion of the singularities for $w\in \mathbb{C}^{+}$ by the least-squares rational approximation

The simulation approaches of § 8.1 result in numerical approximations of $R$ and $V$ on the real line $w=u$ for each $t$ . To recover the structure of the complex singularities of $R$ and $V$ for $w\in \mathbb{C}^{+}$ for each $t$ we used the least-squares rational approximation based on the Alpert–Greengard–Hagstrom (AGH) algorithm Alpert, Greengard & Hagstrom (Reference Alpert, Greengard and Hagstrom2000) adapted to water wave simulations in Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016). Contrary to the analytical continuation of a Fourier series (see e.g. Dyachenko et al. Reference Dyachenko, Lushnikov and Korotkevich2013b , Reference Dyachenko, Lushnikov and Korotkevich2016), the AGH algorithm allows for analytical continuation from the real line $w=u$ into $w\in \mathbb{C}^{+}$ well above the lowest singularity $w=w_{c}.$ The AGH algorithm is based on an approximation of the function $f(u)$ with the function values given on the real line $w=u$ by the rational function in the least-squares sense. The rational approximant is then straightforward to analytically continue to the complex plane by replacing $u$ by $w$ . The AGH algorithm overcomes numerical instabilities typical for the Padé approximation (see e.g. Baker & Graves-Morris Reference Baker and Graves-Morris1996) which is based on a value of function and its derivative at a single point, see Gonnet, Pachon & Trefethen (Reference Gonnet, Pachon and Trefethen2011), Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016) for more discussion. The AGH algorithm robustly recovers poles in the solution while branch cuts are approximated by a set of poles as follows:

(8.5) $$\begin{eqnarray}\displaystyle g(\unicode[STIX]{x1D701})=\frac{1}{2\unicode[STIX]{x03C0}}\int _{C}\frac{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D701}^{\prime })\,\text{d}\unicode[STIX]{x1D701}^{\prime }}{\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}^{\prime }}\simeq \mathop{\sum }_{n=1}^{N}\frac{\unicode[STIX]{x1D70E}_{n}}{\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{n}}, & & \displaystyle\end{eqnarray}$$

where the function $g(\unicode[STIX]{x1D701})$ has a single branch cut along the contour $C$ in the complex plane of $\unicode[STIX]{x1D701}$ with $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D701})$ being a jump of $g(\unicode[STIX]{x1D701})$ at the branch cut. The right-hand side of equation (8.5) approximates $g(\unicode[STIX]{x1D701})$ by simple poles located at $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{n}\in C,n=1,\ldots ,N$ with the residues $\unicode[STIX]{x1D70E}_{n},n=1,\ldots ,N$ . A generalization to multiple branch cuts is straightforward. Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016) demonstrated for the particular case of a Stokes wave that $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D701})$ can be robustly recovered from $\unicode[STIX]{x1D701}_{n}$ and $\unicode[STIX]{x1D70E}_{n}$ by increasing $N$ with an increase of the numerical precision. For fixed $N$ , the right-hand side of equation (8.5) approximates $g(\unicode[STIX]{x1D701})$ with high precision for all points $\unicode[STIX]{x1D701}\in \mathbb{C}$ located away from $C$ by a distance several times exceeding the distance between neighbouring $\unicode[STIX]{x1D701}_{n}.$ In the numerical examples below we distinguish actual poles of $g(w)$ from the artificial poles which occur in the approximation of branch cuts, as in equation (8.5), by changing the numerical precision (the actual poles remain the same while the number of poles in approximation (8.5) increases with the increase of the numerical precision). An alternative way is to look at the dynamics of the poles: while actual poles move continuously with time and their residues either remain constant or change gradually in time (in accordance with the analysis of §§ 4–6), the poles approximating branch cuts quickly change both their positions and residues with their number $N$ also changing, as seen in the numerical examples of § 9 below.

To take into account the $2\unicode[STIX]{x03C0}$ periodicity of our simulation in the $w$ variable we define an auxiliary conformal transformation

(8.6) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}=\tan \frac{w}{2}, & & \displaystyle\end{eqnarray}$$

which maps the stripe $-\unicode[STIX]{x03C0}<\text{Re}(w)<\unicode[STIX]{x03C0}$ into the complex $\unicode[STIX]{x1D701}$ plane. Also $w\in \mathbb{C}^{+}(\mathbb{C}^{-})$ imply that $\unicode[STIX]{x1D701}\in \mathbb{C}^{+}(\mathbb{C}^{-})$ , see also Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016) for more details of the mapping (8.6). The $\unicode[STIX]{x1D701}$ variable is convenient to use in the AGH algorithm (Dyachenko et al. Reference Dyachenko, Lushnikov and Korotkevich2016) which is assumed below.

While the simulations of the dynamics were performed in double precision arithmetic, the AGH algorithm was performed in variable precision (typically we used 512 bits, i.e. approximately 128 digits). It is also possible to use a variable precision for the dynamics (as was done in Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016) for a Stokes wave) to improve the numerical approximation of the branch cuts, which is however beyond the scope of this paper.

9 Recovering the motion of the singularities from simulations and comparison with analytical results

The initial data for $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ (which immediately implies the initial data for $R$ and $V$ through the definitions (2.15) and (2.16)) were chosen in the rational form for the variable $\unicode[STIX]{x1D701}$ (8.6) which ensures $2\unicode[STIX]{x03C0}$ periodicity in $w$ variable. Below we count the number poles per period, i.e. inside a single stripe $-\unicode[STIX]{x03C0}<\text{Re}(w)<\unicode[STIX]{x03C0}$ which is the same number as in the complex plane of $\unicode[STIX]{x1D701}$ .

9.1 A pair of simple poles in the initial conditions and the formation of an oblique jet

Consider an initial condition in the form of a pair of simple poles at $w=a_{1}(0)$ and $w=a_{2}(0)$ both for $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ as follows

(9.1) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}z_{u} & = & \displaystyle 1-q\left[\cot \left(\frac{w-a_{1}(0)}{2}\right)-\cot \left(\frac{w-a_{2}(0)}{2}\right)\right]\\ & = & \displaystyle 1-q\left[\frac{1+\unicode[STIX]{x1D701}\tan \displaystyle \frac{a_{1}(0)}{2}}{\unicode[STIX]{x1D701}-\tan \displaystyle \frac{a_{1}(0)}{2}}-\frac{1+\unicode[STIX]{x1D701}\tan \displaystyle \frac{a_{2}(0)}{2}}{\unicode[STIX]{x1D701}-\tan \displaystyle \frac{a_{2}(0)}{2}}\right],\\ \unicode[STIX]{x1D6F1}_{u} & = & \text{i}c(1-z_{u}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$

where $a_{1}(0),a_{2}(0)\in \mathbb{C}^{+}$ , $c,q\in \mathbb{C}$ are constants and we used the trigonometric identity

(9.2) $$\begin{eqnarray}\displaystyle \cot (a-b)=\frac{1+\tan a\tan b}{\tan a-\tan b}. & & \displaystyle\end{eqnarray}$$

Equations (9.1) and (2.15) and (2.16) imply that $R=1/z_{u}$ is analytic and has simple zeros at $w=a_{1}$ and $w=a_{2}$ while $V$ is analytic and non-zero at these points provided $q\neq 0$ and $c\neq 0$ which corresponds to the case of equations (4.1) and (4.2).

The conformal map (1.1) requires that $z_{u}\neq 0$ for $w\in \mathbb{C}^{-}$ . Solving for $z_{u}=0$ in the first equation of (9.1) results in

(9.3) $$\begin{eqnarray}\displaystyle w_{\pm } & = & \displaystyle 2\arctan \left[\frac{A_{1}+A_{2}\pm \sqrt{(1-4q^{2})(A_{2}-A_{1})^{2}+4q(A_{1}A_{2}+1)(A_{1}-A_{2})}}{2(1-q[A_{1}-A_{2}])}\right],\nonumber\\ \displaystyle & & \displaystyle A_{1}\equiv \tan \frac{a_{1}(0)}{2},\quad A_{2}\equiv \tan \frac{a_{2}(0)}{2},\end{eqnarray}$$

which provides a restriction on the allowed numerical values of $q,a_{1}(0)$ and $a_{2}(0)$ to ensure that $w_{\pm }\in \mathbb{C}^{+}$ .

We choose

(9.4a-d ) $$\begin{eqnarray}\displaystyle a_{1}(0)=0.3\text{i},\quad a_{2}(0)=0.6\text{i},\quad c=0.64/q\quad \text{and}\quad q=0.4\exp \left(\frac{3\unicode[STIX]{x03C0}}{5}\text{i}\right).\quad & & \displaystyle\end{eqnarray}$$

Equations (9.3) and (9.4) result in

(9.5a,b ) $$\begin{eqnarray}\displaystyle w_{+}=0.465388\ldots +\text{i}\,0.532846\ldots \quad \text{and}\quad w_{-}=-0.465388\ldots +\text{i}\,0.367154\ldots , & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

i.e. $w_{\pm }\in \mathbb{C}^{+}$ in this case as required. Taylor series expansions of $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ (9.1) at $w=w_{\pm }\in \mathbb{C}^{+}$ and $t=0$ reproduce equations (3.6) and (3.7) in the variables $R$ and $V$ with $R_{-1}\neq 0$ and $V_{-1}\neq 0$ . Then Theorem 1 of § 3 proves that solutions (3.6) and (3.7) are not persistent in time. Generally, we expect the formation of a pair of square root branch points from $w=w_{\pm }$ at arbitrarily small time $t>0$ which is also consistent with Kuznetsov et al. (Reference Kuznetsov, Spector and Zakharov1993, Reference Kuznetsov, Spector and Zakharov1994), Tanveer (Reference Tanveer1993). The initial poles at $w=a_{1}(0)$ and $w=a_{2}(0)$ are expected to be persistent for at least a finite time duration according to the results of § 4.

Figure 2(a) shows profiles of the free surface at various times obtained from simulations of the Dyachenko equations (2.8), (2.10), (2.11), (2.13) and (2.14) with the initial conditions (9.1), (9.4) and $g=\unicode[STIX]{x1D6FC}=0$ . Figure 2(b–d) demonstrates both a persistence in time of the poles originating from $w=a_{1}(0),w=a_{2}(0)$ and the formation of branch cuts at $w=w_{\pm }$ . Figure 2(b) shows the positions of complex singularities of $z_{u}$ in the complex plane $w\in \mathbb{C}$ at small times when the branch cuts originating from $w=w_{\pm }$ have small lengths. Figure 2(d) shows these positions at larger times when the lengths of these branch cuts increase up to ${\sim}1$ . Figure 2(c) provides a zoom-in of the left branch cut of figure 2(b). The motion of two poles originating at $w=a_{1}(0)$ and $w=a_{2}(0)$ is shown by thick dots in these figures. Branch cuts are numerically approximated in the AGH algorithm by a set of poles according to equation (8.5) with neighbouring poles connected by solid lines in figure 2(d). An increase of the numerical precision results in an increase of number of these artificial poles approximating the branch cuts. There are several ways to determine the type of a branch point, see e.g. Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2013b , Reference Dyachenko, Lushnikov and Korotkevich2016). Such a detailed study of the branch point type is however outside the scope of this paper. We only demonstrate that a square root branch point exists in figure 5(a) by a direct fit of the free surface profile. We also note from simulations that at larger times the poles start absorbing into branch cuts, which is consistent with the assumption of § 4 that the conservation of the residues is guaranteed only at small enough times. The study of such absorption is beyond the scope of this paper.

Figure 2. Simulations with the initial conditions (9.1), (9.4) and $g=\unicode[STIX]{x1D6FC}=0$ . (a) Profiles of free surface at different times. (b) Complex singularities of $z_{u}$ recovered by the AGH algorithm at small times including the initial time $t=0$ . Two persistent poles recovered by the AGH algorithm are shown by thick dots of different style moving near the imaginary axis. It is seen that these two poles, originating from the initial conditions (their initial positions are exactly at the imaginary axis according to equation (9.4)), only slightly move away from the initial positions at these early times. Two initial zeros of $z_{u}$ located at $w=w_{\pm }$ according to equation (9.5) turn into two short branch cuts at arbitrarily short times. Each branch cut connects two branch points. These branch cuts are revealed in the AGH algorithm by a dense set of poles located near $w=w_{\pm }$ with the number of these poles growing with time. (c) The schematic zoom into a small area around $w=w_{-}$ (in (b) that area is shown by the rectangular frame around the left branch cut) to display the extension of branch cut with time. The small filled square shows the point $w=w_{-}$ . The length of each branch cut grows approximately linearly with time. (d) The same as in (b) but at larger times when the length of the branch cuts reaches ${\sim}1$ . Poles approximating branch cuts are connected by solid lines.

Figures 3(a) and 3(b) demonstrate that the residues of both $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ are the integrals of motions for $g=0$ fully confirming the analytical results of equations (4.12) and (4.13). Figure 3(c) zooms into the trajectories of motion of poles $w=a_{1}(t)$ and $w=a_{2}(t)$ in the $w$ plane. Figure 3(d) shows a time dependence of the pole positions $w=a_{1}(t)$ and $w=a_{2}(t)$ and compares it with the result of the time integration of equation (4.5). The difference between the analytical curves and numerical ones is nearly visually indistinguishable. For that comparison $U$ was calculated numerically at each moment of time from $R$ and $V$ by using the definition (2.8) and applying the AGH algorithm to recover $U_{0}(t)$ ( $U_{0}$ is defined in equation (4.3)). Only at larger times, when the distance from the branch cuts to either $a_{1}$ or $a_{2}$ becomes comparable with the spacing between the poles approximating the branch cut in the AGH algorithm, does the difference between the analytical and numerical values become noticeable, as expected from the discussion of § 8.2.

Figure 3. (a) The residues of $z_{u}$ at $w=a_{1}(t)$ and $w=a_{2}(t)$ as functions of $t$ compared with equation (4.12). (b) The residues of $\unicode[STIX]{x1D6F1}_{u}$ at $w=a_{1}(t)$ and $w=a_{2}(t)$ compared with equation (4.13). (c) Trajectories of $w=a_{1}(t)$ and $w=a_{2}(t)$ in the $w$ plane compared with the result of the integration of the analytical expression (4.5). (d) Dependence of real and imaginary parts of $a_{1}$ and $a_{2}$ on $t$ for the same data as in (b). (a–d) Show the same simulation as in figure 2 (with $g=0$ ). (e,f) Show the same type of plots as (a,b) except a non-zero gravity $g=0.04$ is added to the simulation with all other parameters the same as in the simulations of figure 2.

Assuming $g=0.04$ with all other numerical parameters as above, we obtain simulation results similar to those shown in figure 2 because the simulation time remains relatively small so that the effect of non-zero $g$ is small for free surface profiles. However, the residue of $\unicode[STIX]{x1D6F1}_{u}$ is not constant any more but attains a linear dependence on time as follows from equation (4.13). Then figures 3(a) and 3(b) (the case $g=0$ ) are replaced by the new figures 3(e) and 3(f) (the case $g=0.04$ ). There is again excellent agreement between the simulations and the theoretical curves given by equations (4.12) and (4.13).

Figure 4. Simulations with the initial conditions (9.1), (9.6) and $\unicode[STIX]{x1D6FC}=0.$ (a,b) Profiles of free surface at different times for $g=0$ and $g=0.005$ , respectively. (c) Positions of two persistent poles (originate at $w=a_{1}(0)$ and $w=a_{2}(0)$ , shown by small open circles, triangles and rhombi) and branch cuts (thick dots and triangles connected by solid lines) are shown at different $t$ for simulation with $g=0$ . These poles and branch cuts determine the mushroom type shape of (a). There are other branch cuts well above (not shown) which determine only the background of the free surface height outside of the mushroom. (d) Vertical positions for both poles (solid and dashed lines) for $g=0$ and $g=0.005$ versus $t$ in log scale. The exponential dependence $\propto \text{e}^{-\unicode[STIX]{x1D6FD}t}$ , $\unicode[STIX]{x1D6FD}\simeq 0.578329$ is also shown for comparison. (e) The residues of $z_{u}$ at $w=a_{1}(t)$ and $w=a_{2}(t)$ extracted from the simulations are constant in time both for $g=0$ and $g=0.005$ in agreement with equation (4.12). (f) The residues of $\unicode[STIX]{x1D6F1}_{u}$ at $w=a_{1}(t)$ and $w=a_{2}(t)$ are either constant or a linear function of $t$ depending on $g$ and are visually indistinguishable from equation (4.13).

We now consider the initial conditions (9.1) for another set of numerical values

(9.6a-d ) $$\begin{eqnarray}\displaystyle a_{1}(0)=0.0050\,\text{i},\quad a_{2}(0)=0.0075\,\text{i},\quad q=1.25\text{i},\quad c=0.02. & & \displaystyle\end{eqnarray}$$

Equations (9.3) and (9.6) result in $w_{+}=0.0790677\cdots +\text{i}\,0.00625\ldots \text{and }w_{-}=-0.0790677\cdots +\text{i}\,0.00625\ldots ,$ i.e. $w_{\pm }\in \mathbb{C}^{+}$ in this case as required. Similar to the previous simulations’ description of this section, Taylor series expansion of $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ (9.1) at $w=w_{\pm }\in \mathbb{C}^{+}$ and $t=0$ reproduces equations (3.6) and (3.7) in the variables $R$ and $V$ with $R_{-1}\neq 0$ and $V_{-1}\neq 0$ . Then Theorem 1 of § 3 proves that solutions (3.6) and (3.7) are not persistent in time. At $w=w_{\pm }$ we again expect the formation of a pair of square root branch points at arbitrarily small time $t>0$ . The initial poles at $w=a_{1}(0)$ and $w=a_{2}(0)$ are expected to be persistent for at least a finite time duration according to the results of § 4.

Figure 4(a) shows profiles of the free surface at various times obtained from simulations of the Dyachenko equations (2.8), (2.10), (2.11), (2.13) and (2.14) with the initial conditions (9.1), (9.6) and $g=\unicode[STIX]{x1D6FC}=0$ . Figure 4(b) shows a simulation with the same parameters except $g=0.005$ and $\unicode[STIX]{x1D6FC}=0$ . It is seen in figures 4(a) and 4(b) that the initial free surface has the form of a disk standing on a nearly flat surface. Then this disk moves upwards with almost constant velocity (for $g=0$ ) forming a mushroom with a narrow neck (stipe). For $g=0.005$ that upward motion is quickly suppressed by the non-zero gravity. Figure 4(c) demonstrates both a persistence in time of the two poles originating from $w=a_{1}(0),w=a_{2}(0)$ and a self-similar dynamics of the branch cuts originating from $w=w_{\pm }$ . Figure 4(d) shows a time dependence of the position of two poles moving strictly in the vertical direction. Contrary to the previous numerical example, both poles are never absorbed into a branch cut and they are persistent at all times. Figures 4(e) and 4(f) demonstrate that the dynamics of the residues of both $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ is in full agreement with equations (4.12) and (4.13) both for $g=0$ and $g\neq 0.$ Log–linear scaling of Figure 4(c) also demonstrates that at large time and $g=0$ both poles and surrounding branch cuts evolve in a self-similar way (if we rescale with time both $u$ and $v$ ) approaching the real line with a spatial scaling $\propto \text{e}^{-\unicode[STIX]{x1D6FD}t}$ , where $\unicode[STIX]{x1D6FD}\simeq 0.578329$ is obtained from the numerical fit of the curves of figure 4(d).

Figure 5. Simulations of the initial conditions (9.1), (9.7),  $g=\unicode[STIX]{x1D6FC}=0$ and either (9.8) (a,c,e) or (9.9) (b,d,f). (a,b) The shape of the surface. Dotted line in (a) shows a fit of the overturning portion of the wave to the square root dependence $z=q\,(w-w_{c})^{1/2}+z_{0}$ , where fitting parameters are $z_{0}=0.0923+0.0961\,\text{i}$ and $q=0.595329+4.48567\,\text{i}$ while $w_{c}=-0.02348+3.2923\times 10^{-6}\,\text{i}$ is recovered from the AGH algorithm as the position of the lowest end of the branch cut. (c,d) The motion of the poles (small open circles and triangles) and branch cuts (filled circles and triangles connected by solid lines) in the $w$ plane. The small filled squares show the point $w=w_{\pm }$ from equation (9.3). (e,f) Residues of $z_{u}$ extracted from simulations are constant in time in agreement with equation (4.12). A similar statement is true for the residues of $\unicode[STIX]{x1D6F1}_{u}$ in accordance with equation (4.13) (not shown).

Two more sets of the initial conditions (9.1) have initial poles away from the imaginary axis and are given by

(9.7a-c ) $$\begin{eqnarray}\displaystyle a_{1}(0)=0.004\,\text{i},\quad a_{2}(0)=0.016+0.020\,\text{i},\quad q=0.025\text{e}^{\text{i}0.71\unicode[STIX]{x03C0}}, & & \displaystyle\end{eqnarray}$$

with either

(9.8) $$\begin{eqnarray}\displaystyle c=0.03-0.02\text{i} & & \displaystyle\end{eqnarray}$$

or

(9.9) $$\begin{eqnarray}\displaystyle c=0.02. & & \displaystyle\end{eqnarray}$$

Equations (9.3) and (9.7) result in $w_{+}=0.0415052\cdots +\text{i}\,0.0117937\ldots \text{and }w_{-}=-0.0255052\cdots +\text{i}\,0.0122063\ldots ,$ i.e. $w_{\pm }\in \mathbb{C}^{+}$ in these cases as required. Figure 5(a,b) shows jets propelled in the direction oblique to the imaginary axis which are more pronounced in the case (9.8) (figure 5 a). The initial poles at $w=a_{1}(0)$ and $w=a_{2}(0)$ are again persistent in time with residues obeying equations (4.12) and (4.13) as shown in figures 5(c,d) and 5(e,f). Also a fit to the square root dependence, shown on figure 5(a) by the dotted line, corresponds to the square root branch point at the lowest end of the left branch cut as seen in figure 5(c).

9.2 Simulations with second-order poles

Consider an initial condition in the form of the second-order pole at $w=a(0)$ both in $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ as follows:

(9.10) $$\begin{eqnarray}\displaystyle & \displaystyle z_{u}=1+\frac{q}{\cos (w-a(0))-1}=1-\frac{q(\unicode[STIX]{x1D701}^{2}+1)}{2\cos ^{2}\displaystyle \frac{a}{2}\left(\unicode[STIX]{x1D701}-\tan \displaystyle \frac{a}{2}\right)^{2}}, & \displaystyle\end{eqnarray}$$

(9.11) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{u}=\text{i}c(1-z_{u}), & \displaystyle\end{eqnarray}$$

where $a(0)\in \mathbb{C}^{+}$ , $c\neq 0,q\neq 0\in \mathbb{C}$ are the constants and we used the identity (9.2).

The initial conditions (9.10) and (9.11) together with equations (2.15) and (2.16) imply that both $R$ and $V$ are analytic at $w=a(0)$ for $t=0$ with their Taylor series coefficients satisfying

(9.12) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle R_{0}(0)=R_{1}(0)=R_{3}(0)=0,\quad R_{2}(0)=-\frac{1}{2q}\neq 0,\quad V_{0}(0)=c\neq 0,\quad V_{1}(0)=0,\\ \displaystyle V_{2}(0)=\frac{c}{2q}\quad \text{at }w=a\end{array}\right\} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

for $t=0.$ Thus $R$ has a second-order zero while $V$ is non-zero at $w=a(0)$ provided $q\neq 0$ and $c\neq 0$ which corresponds to the case of equations (6.3) and (6.4). Then the analytical results of § 6 predict a persistence of second-order poles at $w=a(t)$ of both $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ for at least a finite duration of time for arbitrary values of $g$ and $\unicode[STIX]{x1D6FC}$ . We study four separate cases $g=\unicode[STIX]{x1D6FC}=0;g=0,\unicode[STIX]{x1D6FC}\neq 0;g\neq 0,\unicode[STIX]{x1D6FC}=0;g\neq 0,\unicode[STIX]{x1D6FC}\neq 0.$

The conformal map (1.1) requires that $z_{u}\neq 0$ for $w\in \mathbb{C}^{-}$ . Solving for $z_{u}=0$ in equation (9.10) results in

(9.13) $$\begin{eqnarray}\displaystyle w_{\pm }=2\arctan \left[\frac{2A\pm (1+A^{2})\sqrt{q(2-q)}}{2-q[A^{2}+1]}\right],\quad A\equiv \tan \frac{a(0)}{2}, & & \displaystyle\end{eqnarray}$$

which provides a restriction on the allowed numerical values of $q$ and $a(0)$ to ensure that $w_{\pm }\in \mathbb{C}^{+}$ .

We choose numerical values

(9.14a-c ) $$\begin{eqnarray}\displaystyle c=0.5,\quad q=0.25\quad \text{and}\quad a(0)=0.5\text{i} & & \displaystyle\end{eqnarray}$$

for all four cases. Equations (9.13) and (9.14) result in

(9.15a,b ) $$\begin{eqnarray}\displaystyle w_{+}=0.722734\ldots +\text{i}\,0.5\quad \text{and}\quad w_{-}=-0.722734\ldots +\text{i}\,0.5, & & \displaystyle\end{eqnarray}$$

i.e. $w_{\pm }\in \mathbb{C}^{+}$ in this case as required. Taylor series expansion of $z_{u}$ and $\unicode[STIX]{x1D6F1}_{u}$ (9.1) at $w=w_{\pm }\in \mathbb{C}^{+}$ and $t=0$ reproduces equations (3.6) and (3.7) in the variables $R$ and $V$ with $R_{-1}\neq 0$ and $V_{-1}\neq 0$ . Then Theorem 1 of § 3 proves that solutions (3.6) and (3.7) are not persistent in time. Similar to the discussion of § 9.1, we expect the formation of a pair of square root branch points at an arbitrary small time $t>0$ .

Figure 6. (a) Free surface profiles resulting from simulations for the cases (A), (B), (C) and (D) of equation (9.16) at $t=0.25$ compared with the initial profile at $t=0.$ (b) $|V|^{2}$ at the free surface for the same cases.

Figures 6(a) and 6(b) shows profiles of the free surface and $|V|^{2}$ obtained from simulations of the Dyachenko equations (2.8), (2.10), (2.11), (2.13) and (2.14) with the initial conditions (9.10), (9.11), (9.14) and four particular cases

(9.16) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}(\text{A})\;g=\unicode[STIX]{x1D6FC}=0;\quad (\text{B})\;g=0,\quad \unicode[STIX]{x1D6FC}=0.04;\\ (\text{C})\;g=0.05,\quad \unicode[STIX]{x1D6FC}=0;\quad \text{and}\quad (\text{D})\;g=0.05,\quad \unicode[STIX]{x1D6FC}=0.04.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

Figures 7(a,b) and 7(c,d) shows time dependencies of the position of the second-order pole of both $z_{w}(w,t)$ and $\unicode[STIX]{x1D6F1}_{w}(w,t)$ at $w=a(t)$ as well as the coefficient $R_{2}(t)$ of Taylor series (6.3) (also entering into equations (6.11)) compared with the time integration of equations (6.5) and (6.8). It confirms a persistence in time of second-order poles originating from $w=a(0)$ for the initial conditions (9.10) and (9.11). We also recovered $V_{1}(t)$ from simulations (not shown in figures) which together with $R_{2}(t)$ allowed us to confirm the integral of motion (6.10).

Figure 7(e,f) shows the positions of complex singularities of $z$ in the complex plane $w\in \mathbb{C}$ . The branch cuts form at arbitrarily small time $t>0$ from the points $w=w_{\pm }$  (9.15). It is seen that the non-zero surface tension on figure 7(f) results in a significantly faster extension of these branch cuts compared with the zero surface tension case on the left panel. This is consistent with the results of Dyachenko & Newell (Reference Dyachenko and Newell2016) that the addition of surface tension results in the quick approach of singularities to the real line. Similar to simulations of § 9.1, at larger times the poles start absorbing into branch cuts. The deviation between analytical and numerical results in figures 7(b) and 7(d) at later times is due to the faster approach of branch cuts to the pole position for $\unicode[STIX]{x1D6FC}\neq 0$ thus resulting in the AGH algorithm losing numerical precision as expected from the discussion of § 8.2. We also note that our use of $z$ (instead of using $z_{u}$ in § 9.1) to obtain figure 7(a–f) is due to the convenience of recovering simple poles in the AGH algorithm compared with the second-order poles. Indeed, $z$ has the first-order pole at $w=a$ as obtained from the integration of equation (6.11) over $w$ . Generally such integration produces also a logarithmic branch point $w=a$ from the simple pole in equation (6.11) which would imply the formation of multiple poles approximating that branch point by the AGH algorithm in figure 7(e,f). However, the particular initial conditions (9.10) and (9.11) imply through equations (6.10), (6.12)–(6.14), (9.12) that $V_{1}(t)=R_{3}(t)=0,$ i.e. $\underset{w=a}{\text{Res}}(\unicode[STIX]{x1D6F1}_{w})=\underset{w=a}{\text{Res}}(z_{w})=0$ thus removing a logarithmic branch point $w=a.$ The absence a logarithmic branch point $w=a$ in figure 7(e,f) also provides another confirmation of the persistence of the second-order pole in $z_{u}$ at $w=a$ and the validity of the motion integrals (6.10) and (6.12)–(6.14).

Figure 7. Data extracted from simulations for the cases (A) (a,c,e) and (B) (b,d,f) of equation (9.16). (a,b) The dependence of $\text{Im}(a)$ on $t$ in equation (6.11) compared with the result of the integration of the analytical expression (6.5) ( $a$ is purely imaginary in these cases). For each moment of time the location of $w=a=\text{i}\,\text{Im}(a)$ was found as the solution of $R(w)=0$ by Newton’s method. (c,d) The dependence of $R_{2}$ on $t$ in equation (6.11) compared with the result of the integration of the analytical expression (6.8).  $R_{2}$ is purely real in these cases. In (a,b) and (c,d) $U_{0}(t)$ and $U_{1}(t)$ were obtained from the AGH algorithm similar to § 9.1. (e,f) Motion of the pole (small open circle and triangles) and branch cuts (filled triangles connected by solid lines) in the $w$ plane for $z(w,t)$ . The small filled squares show the points $w=w_{\pm }$ from equation (9.15).

Figure 8. Similar results to figures 7(a,b) and 7(c,d) but for the cases (C) (a,c) and (D) (b,d) of equation (9.16).

Figure 8 shows results similar to figures 7(a,b) and 7(c,d) but with $g\neq 0$ . The positions of complex singularities are not shown because they are nearly the same as in figure 7(e,f).

We conclude that in this section we verified with a high numerical precision the conservation of both complex integrals of motion of § 4 and all three independent complex integrals of motions for the second-order pole case of § 6.

10 Conclusion and discussion

The main result of this paper is the existence of new integrals of motion in free surface hydrodynamics. These integrals are closely tied to the existence of solutions with poles of the first and second orders in both $z_{w}$ and $\unicode[STIX]{x1D6F1}_{w}.$ The residues of $z_{w}$ are the integral of motion while residues of $\unicode[STIX]{x1D6F1}_{w}$ are a linear function of time for non-zero gravity turning into the integrals of motion for zero gravity. The residues of $z_{w}$ at different points commute with each other in the sense of the underlying non-canonical Hamiltonian dynamics. This provides an argument in support of the conjecture of complete integrability of free surface hydrodynamics in deep water. We also suggested treating the analytical continuation of the free surface dynamics outside of the physical fluid as phantom hydrodynamics on the multi-sheet Riemann surface. This phantom hydrodynamics allows for a generalized Kelvin theorem. We expect that generally a number of sheets will be infinite with generic solutions involving poles and square root branch points in multiple sheets.

For future work we suggest an extension to the general case of poles of arbitrary order in $z_{w}$ and $\unicode[STIX]{x1D6F1}_{w}$ to count the total number of independent integrals of motion. We propose also to study the expected pole solutions in other (non-physical) sheets of a Riemann surface. The commutativity properties between different integrals of motion need to be studied in the general case.