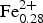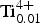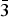Introduction
Fluoro-tremolite is the fluorine-analogue of tremolite, the composition at the root of amphibole compositional space in all classification schemes used to date.
According to the IMA list of minerals, (Pasero, 2018) the name tremolite was introduced to the mineralogical literature in 1789 (Höpfner, Reference Höpfner1789) and the name has been grandfathered into all nomenclature schemes. The structure of tremolite was solved by Warren (Reference Warren1929). Structural data were first provided by Papike et al. (Reference Papike, Ross and Clark1969) on tremolite from the Gouverneur mining district, NewYork. However, due to the extensive presence of inclusions and exolution, these data should be considered with some caution. The structural reference data to date were provided by Hawthorne and Grundy (Reference Hawthorne and Grundy1976) for a sample that has ![]() ${\rm F}_{{\rm 0}{\rm. 66}}^{\rm -} $ per formula unit (pfu). Because F– occurs at the O(3) site, which is coordinated by the cations occurring at the M(l) and M(3) sites, these authors observed a significant shortening of the <M(l)–O> and <M(3)–O> distances.
${\rm F}_{{\rm 0}{\rm. 66}}^{\rm -} $ per formula unit (pfu). Because F– occurs at the O(3) site, which is coordinated by the cations occurring at the M(l) and M(3) sites, these authors observed a significant shortening of the <M(l)–O> and <M(3)–O> distances.
Despite the frequent use of the term ‘fluoro-tremolite’ (and its spelling variants: ‘fluorotremolite and ‘fluortremolite’) in the mineralogical literature (e.g. Valley et al., Reference Valley, Petersen, Essene and Bowman1982; Petersen et al., Reference Petersen, Essene, Peacor and Valley1982; Dachs et al., Reference Dachs, Baumgartner, Bertoldi, Benisek, Tippelt and Maresch2010), this still has remained a named amphibole (Burke and Leake, Reference Burke and Leake2004) and lacked a complete mineralogical description.
Structural data of natural and synthetic tremolite crystals started being reported in the 1970s; structural data for synthetic fluoro-tremolite were first reported by Cameron and Gibbs (Reference Cameron and Gibbs1973), who showed that the substitution of F– for (OH)– significantly reduces the size of the strip of octahedra and hence the a and b cell parameters. The higher thermal stability of fluoro-tremolite was explained both by the higher bond-strength of the Mg–F bonds, and by the loss of local electroneutrality due to the thermal instability of the O–H bond and the subsequent H loss at high temperature, which cannot be balanced by oxidation of divalent cations at the M(l) and M(3) sites.
In this paper, we provide a complete mineral description of fluoro-tremolite from the Limecrest-Southdown quarry, Sparta, New Jersey, USA, which was kindly provided by the Franklin Mineral Museum. We also provide new structure and crystal-chemical data for synthetic fluoro-tremolite (code 751 in the amphibole database of the CNR-IGG in Pavia, Italy) and tremolite from the type locality of Val Tremola (code 361 in the amphibole database of the CNR-IGG).
Mineral data
Occurrence and type material
The sample comes from the skarns at the Limecrest-Southdown quarry, Sparta, New Jersey, USA. It was provided by John Cianciulli, the former curator of the Franklin Mineral Museum (32 Evans Street, Franklin, 07416 New Jersey, USA) and is labelled G409. Co-existing phases in the holotype are: calcite, chondrodite and pyrrhotite. The refined and analysed crystal of this work was assigned code 1082 in the amphibole database of the CNR-IGG.
The new mineral and its name have been approved by Commission on New Minerals, Nomenclature and Classification of the International Mineralogical Association (IMA2016-018). Holotype material has been deposited at the Franklin Mineral Museum under the catalogue number 7710.
Appearance, physical and optical properties
Fluoro-tremolite occurs as prismatic light-greenish to colourless crystals forming grey to whitish green aggregates. It has a grey streak and vitreous lustre; the crystals are transparent and do not fluoresce under ultraviolet illumination. Based on the unit-cell parameters and the empirical formula, the calculated density is 3.044 g cm–3.
Fluoro-tremolite is biaxial (+), with α = 1.5987(5), β = 1.6102(5), γ = 1.6257(5) (589 nm) 2Vz(meas.) = 85(1)° and 2Vz(calc.) = 82°. Refractive indexes were determined by the double-variation method (Su et al., 1987, Gunter et al., Reference Gunter, Downs, Bartelmehs, Evans, Pommier, Grow, Sanchez and Bloss2005) using standard Cargille liquids.
Crystallography
For holotype fluoro-tremolite and for the other crystals reported in this work, single-crystal diffraction data were collected in the θ range 2–30° with a Philips PW1100 diffractometer working with graphite monochromatized MoKα X-radiation (λ = 0.7107 Å). Unit-cell parameters were calculated by a least-squares procedure using the d* values measured for reflections belonging to 60 selected rows of reciprocal space and occurring in the θ range –30 to +30°.
Two sets of monoclinic equivalents (hkl and h–kl) were collected. Intensities were corrected for Lorentz and polarization effects and for absorption and then merged. The reflections with Io > 3σ(I) were considered as observed during unweighted full-matrix least-squares refinement on F. Scattering curves for fully ionized chemical species were used at sites where chemical substitutions occur; neutral versus ionized scattering curves were refined for the T and anion sites [except O(3)] in the full-matrix least-squares refinement on I > 3σ(I). The relevant crystallographic details are reported in Table 1. Atom coordinates, site-scattering values and anisotropic-displacement parameters resulting from the structure refinement are given in Table 2, and selected interatomic distances and angles are given in Table 3. The crystallographic information files with embedded structure factors are available as supplementary material (see below).
Table 1. Unit-cell parameters and crystallographic details for holotype fluoro-tremolite (1082)*, new refinements of synthetic fluoro-tremolite (751) and tremolite (361) provided in this work, and a comparison with those reported by Hawthorne and Grundy (Reference Hawthorne and Grundy1976) for A(Na0.192K0.118)B(Na0.191Ca1.809)C(Mg5)T(Al0.228Si7.767)O22W(OH1.337F0.660Cl0.012).

n.r. = not reported;
* Specimen numbers in the amphibole database of CNR-IGG;
**H&G = Hawthorne and Grundy (1976).
Table 2. Refined site-scattering values (ss, electrons per formula unit), fractional atom coordinates and atom-displacement parameters (B eq, Å2; βij x 104) for holotype fluoro-tremolite (crystal 1082) and the other samples described in this work.

Table 3. Selected interatomic distances (Å) and angles (o) in holotype fluoro-tremolite 1082 and in the other crystals of this work.

Powder X-ray diffraction data (CuKα,λ = 1.54178 Å) for holotype fluoro-tremolite were obtained using the XPREP utility of SAINT (Bruker, Reference Bruker2003), which generates a 2D powder diffractogram (Debye-Scherrer technique) starting from the F obs collected on a second single-crystal and taking into account solely the information concerning the unit-cell parameters (ucp) and the Laue symmetry. No Lorentz and polarization corrections were applied. Powder X-ray-diffraction data are given in Table 4. In order to check its composition, diffraction data for the second crystal were collected in the diffraction lab of the CrisDi (University of Torino) with an Oxford Gemini R Ultra diffractometer equipped with a CCD area detector and working with graphite-monochromatized MoKα radiation (λ = 0.7107 Å). The unit-cell parameters are: a = 9.8423(4) Å, b = 18.0613(5) Å, c = 5.2737(2) Å, β = 104.693(4)° and V = 906.81(6) Å3, and the structure refinement is almost indistinguishable from that of the analysed crystal 1082 (and therefore is not reported in the following tables).
Table 4. Calculated powder X-ray data for holotype fluoro-tremolite.

The strongest ten reflections are in bold.
Empirical formula
Chemical analyses (3 analytical points) were obtained for crystal 1082 using a Cameca SX50 at Istituto di Geologia Ambientale e Geoingegneria (IGAG), Università di Roma “La Sapienza”. Analytical conditions were 15 kV accelerating voltage and 15 nA beam current, with a 5 µm beam diameter. Counting time was 20 s on both peak and background. Analytical errors are 1% rel. except for fluorine which is estimated to be 3% rel. Standards, spectral lines, and crystals used were: wollastonite (SiKα, CaKα, PET), rutile (TiKα, LIF), corundum (AlKα, TAP), magnetite (FeKα, LIF), Mn metal (MnKα, LIF), Zn metal (ZnKα, LIF), Cr metal (CrKα, PET), periclase (MgKα, TAP), jadeite (NaKα, TAP), orthoclase (KKα, PET), synthetic fluor-phlogopite (FKα, TAP) and sylvite (ClKα, PET). Data reduction was done by the PAP method (Pouchou and Pichoir, Reference Pouchou, Pichoir and Armstrong1985). The H2O content was calculated by stoichiometry (F+OH+Cl = 2 atoms per formula unit (apfu)), taking into account the total number of cations obtained by structure refinement. Analytical data are given in Table 5. The empirical formula (based on 24 anions pfu) is A(Na0.28K0.02)Σ0.30 B(Ca1.99Na0.01)Σ2.00 C(Mg4.70![]() ${\rm Fe}_{{\rm 0}{\rm. 28}}^{{\rm 2 +}} $Zn0.01
${\rm Fe}_{{\rm 0}{\rm. 28}}^{{\rm 2 +}} $Zn0.01![]() ${\rm Ti}_{{\rm 0}{\rm. 01}}^{{\rm 4 +}} $)Σ5.00 T(Si7.68Al0.32)Σ8.00 O22 W(F1.16OH0.84)Σ2.00. The ideal formula for end-member fluoro-tremolite (Hawthorne et al., Reference Hawthorne, Oberti, Harlow, Maresch, Martin, Schumacher and Welch2012) is A□ BCa2 CMg5 TSi8 O22 WF2, which requires SiO2 58.88, MgO 24.68, CaO 13.74, F 4.65, –F=O –1.95, total 100.00 wt.%.
${\rm Ti}_{{\rm 0}{\rm. 01}}^{{\rm 4 +}} $)Σ5.00 T(Si7.68Al0.32)Σ8.00 O22 W(F1.16OH0.84)Σ2.00. The ideal formula for end-member fluoro-tremolite (Hawthorne et al., Reference Hawthorne, Oberti, Harlow, Maresch, Martin, Schumacher and Welch2012) is A□ BCa2 CMg5 TSi8 O22 WF2, which requires SiO2 58.88, MgO 24.68, CaO 13.74, F 4.65, –F=O –1.95, total 100.00 wt.%.
Table 5. Chemical composition and unit formula (atoms per formula unit, apfu) calculated based on 24 (O, OH, F) apfu for holotype fluoro-tremolite (crystal 1082) and in the other crystals of this work.

* calculated based on single-crystal structure-refinement results and with the constraints of non-negative Fe2+ values and W(OH, F, Cl) = 2 apfu.
The compatibility index [1 – (Kp/Kc); Mandarino, Reference Mandarino1981] is 0.010 (superior).
Fourier-transform infrared spectroscopy
The powder Fourier-transform infrared (FTIR) spectra were collected at the Dipartimento di Scienze, Università Roma Tre on a Nicolet Magna 760 FTIR spectrometer equipped with a DTGS detector and a KBr beamsplitter; the nominal resolution was 4 cm–1 and 64 scans were averaged for each sample and for the background. The spectra were collected from KBr disks with ~7 mg of sample in 150 mg of KBr for the 3600–3720 cm–1 region, and 3.5 mg of sample in 150 mg of KBr for the 550–2000 cm–1 region. The FTIR spectrum in the OH-stretching region (Fig. 1a) shows only two well-resolved peak at 3672 cm–1 and 3658 cm–1 and one broad and very weak band at 3643 cm–1. The spectral range from 1200 to 400 cm–1, typical of lattice vibrations, can be divided in three regions, which are characterized by the occurrence of three multicomponent absorptions (Fig. 1b and Table 6). Region 1 (1200–800 cm–1) shows ten strong bands or shoulders, region 2 (800–630 cm–1) shows five weaker absorptions, and region 3 (600–550 cm–1) shows one very strong absorption at 509 cm–1 with a pronounced shoulder at 544 cm–1.

Fig. 1. FTIR spectra of fluoro-tremolite: (a) region of the absorptions due to OH-stretching, (b) region of the absorptions due to structural vibrations.
Table 6. Position (cm–1) and assignments of the bands in the FTIR spectra of fluoro-tremolite.

* Assignments and letters for the absorptions in regions 1, 2 and 3 from Ishida et al. (Reference Ishida, Jenkins and Hawthorne2008).
p: resolved peak; sh: shoulder; n.r.: not resolved.
Discussion and concluding remarks
Site populations for crystal 1082 were derived from the unit-formula and the results of the structure refinement. They are reported in Table 7.
Table 7. Site population for fluoro-tremolite 1082. There is a good agreement between the refined values of site-scattering (ss, electrons per formula unit) and mean bond-lengths (mbl, Å) and those calculated based on the proposed site populations.

As expected from the current knowledge of amphibole crystal-chemistry (cf. the review of Oberti et al., Reference Oberti, Hawthorne, Cannillo, Cámara, Hawthorne, Oberti, Della Ventura and Mottana2007), CFe2+ has the following (weak) site preference: M(2)>M(1)>M(3). As expected for a fluorine-rich amphibole, the A cations preferentially order at the A(m) subsite where Coulombic interactions with F– are stronger.
Contrary to what is expected as a result of the presence of F− at the O(3) site, the M(1)–O(3) distance for fluoro-tremolite 1082 is the longest in the M(1) octahedron, whereas the M(3)–O(3) distance is the shortest in the M(3) octahedron (and much shorter than expected), suggesting a relaxation pattern peculiar to this composition. This pattern is more evident if individual M(1,3)–O distances are compared as a function of F– content (Fig. 2). In fact, although the M(1)–O(3) distance is the longest of the M(1) polyhedron in tremolite 361 and in fluoro-tremolite 1082, it is the shortest in synthetic fluoro-tremolite 751, where it is 2.054(1) Å (Table 3). Therefore, complete O(3)![]() ${\rm (OH)}_{\rm -1}\!$O(3)
${\rm (OH)}_{\rm -1}\!$O(3)![]() ${\rm F}_{\rm 1}^{\rm \ndash} $ substitution appears to result in a reduction of this distance of 0.028 Å, i.e. ~1.4%, half of what is expected based on the ionic radii for (OH)– and F– in 4-coordination (1.35 and 1.31 Å, respectively; Shannon, Reference Shannon1976). A somewhat stronger shortening is observed for the M(3)–O(3) distance (Δ = –0.040 Å, ≈ 1.9%). Sample 1082 plots slightly above the line in Fig. 2 because of its small Fe2+ content. The significant contraction observed for the M(1)–O(2) and M(3)–O(1) bond distances deserves comment: although the O(1) and O(2) sites are not involved in the O(3)
${\rm F}_{\rm 1}^{\rm \ndash} $ substitution appears to result in a reduction of this distance of 0.028 Å, i.e. ~1.4%, half of what is expected based on the ionic radii for (OH)– and F– in 4-coordination (1.35 and 1.31 Å, respectively; Shannon, Reference Shannon1976). A somewhat stronger shortening is observed for the M(3)–O(3) distance (Δ = –0.040 Å, ≈ 1.9%). Sample 1082 plots slightly above the line in Fig. 2 because of its small Fe2+ content. The significant contraction observed for the M(1)–O(2) and M(3)–O(1) bond distances deserves comment: although the O(1) and O(2) sites are not involved in the O(3)![]() ${\rm (OH)}_{\rm -1}$O(3)
${\rm (OH)}_{\rm -1}$O(3)![]() ${\rm F}_{\rm 1}^{\rm \ndash} $ exchange, complete substitution of (OH)– by F– produces a decrease of 0.017 Å and 0.013 Å for the M(1)–O(2) and M(3)–O(1) bond distances, respectively. This shortening must be related to a general contraction of the O-layer due to the presence of F– at the O(3) site, as shown in Fig. 3. With complete O(3)
${\rm F}_{\rm 1}^{\rm \ndash} $ exchange, complete substitution of (OH)– by F– produces a decrease of 0.017 Å and 0.013 Å for the M(1)–O(2) and M(3)–O(1) bond distances, respectively. This shortening must be related to a general contraction of the O-layer due to the presence of F– at the O(3) site, as shown in Fig. 3. With complete O(3)![]() ${\rm (OH)}_{\rm -1}$O(3)
${\rm (OH)}_{\rm -1}$O(3)![]() ${\rm F}_{\rm 1}^{\rm \ndash} $ substitution, the O(3)–O(1) and O(3)–O(2) distances shorten by 0.068 Å and 0.018 Å, respectively, and this change is coupled to a small but significant increase of the rotation of the double chain of tetrahedra (the angle T(1)–O(7)–T(1) shrinks by 1.3°). Interestingly, at the M(2) site, complete O(3)
${\rm F}_{\rm 1}^{\rm \ndash} $ substitution, the O(3)–O(1) and O(3)–O(2) distances shorten by 0.068 Å and 0.018 Å, respectively, and this change is coupled to a small but significant increase of the rotation of the double chain of tetrahedra (the angle T(1)–O(7)–T(1) shrinks by 1.3°). Interestingly, at the M(2) site, complete O(3)![]() ${\rm (OH)}_{\rm -1}$O(3)
${\rm (OH)}_{\rm -1}$O(3)![]() ${\rm F}_{\rm 1}^{\rm \ndash} $ substitution produces a significant increase of the M(2)–O(1) distance (by 0.012 Å).
${\rm F}_{\rm 1}^{\rm \ndash} $ substitution produces a significant increase of the M(2)–O(1) distance (by 0.012 Å).

Fig. 2. Changes in the individual M(1,3)–O bond distances as a function of the F content in the samples studied. Errors are within symbol size. Equations give the slopes of the lines joining the geometries of the end-member compositions. Sample 1082 plots above the lines due its low but significant Fe2+ content, which enlarges the M(1) and M(3) polyhedra.

Fig. 3. The local environment of the O(3) site: the arrows show the shortening of the O(3)–O(1) (white) and O(3)–O(2) edges (green) and of the M(1,3)–O(3) bond distances (yellow) passing from tremolite 361 to synthetic fluoro-tremolite 751 (i.e. for complete O(3)![]() ${\rm (OH)}_{\rm -1}$O(3)
${\rm (OH)}_{\rm -1}$O(3)![]() ${\rm F}_{\rm 1}^{\rm \ndash} $ substitution).
${\rm F}_{\rm 1}^{\rm \ndash} $ substitution).
The FTIR spectrum of fluoro-tremolite 1082 is quite similar to that reported for synthetic fluoro-tremolite (1.9 F– apfu) by Ishida et al. (Reference Ishida, Jenkins and Hawthorne2008). Differences can be related to the more complex composition of the mineral. In the region of the OH-stretching vibrations, the band at 3672 cm–1 can be assigned to the local arrangement MgMgMg–OH–A□:SiSi characteristic of end-member tremolite. Its position was 3675 cm–1 in the tremolite with 0.66 F– apfu studied by Hawthorne et al. (Reference Hawthorne, Welch, Della Ventura, Liu, Robert and Jenkins2000). The other absorptions at 3658 cm–1 and 3643 cm–1 might be assigned, respectively, to the arrangements MgMgFe–OH–A□:SiSi and MgFeFe–OH–A□:SiSi (Burns and Strens, Reference Burns and Strens1966; Hawthorne et al., Reference Hawthorne, Della Ventura, Hawthorne, Oberti, Della Ventura and Mottana2007). However, considering the low Fe2+ content at the M(1) and M(3) sites and the presence of 0.32 apfu of Al at the T(1) site (Table 7), these assignments may not be correct. In fact, the substitution of Al for Si lowers the frequency of the OH absorption (~25 cm–1), so that the weak band at 3643 cm–1 can be better assigned to the MgMgMg-OH-A□:AlSi arrangement (Hawthorne et al., Reference Hawthorne, Della Ventura and Robert1996, Reference Hawthorne, Welch, Della Ventura, Liu, Robert and Jenkins2000).
Another interesting feature is the lack of absorptions at frequencies higher than 3672 cm–1, typical of A-site-filled arrangements, notwithstanding the presence of 0.30 apfu of A cations. The low band intensity, which is due to the presence of only 0.84 (OH)– apfu is not a satisfactory explanation. We infer complete local coupling of A cations with O(3)F–, as confirmed by the shape of the electron density, which is consistent with their order at the A(m) subsite closer to O(3) (cf. Hawthorne et al., Reference Hawthorne, Della Ventura and Robert1996). A further consideration may be applied to the band at 3658 cm–1. A downward shift of the OH-band by 15–18 cm–1 due to the O(3)![]() ${\rm (OH)}_{\rm -1}$O(3)
${\rm (OH)}_{\rm -1}$O(3)![]() ${\rm F}_{\rm 1}^{\rm \ndash} $ exchange has been observed and discussed in other amphibole compositions by Robert et al. (Reference Robert, Della Ventura and Hawthorne1999, Reference Robert, Della Ventura, Welch and Hawthorne2000) and Della Ventura et al. (Reference Della Ventura, Bellatreccia, Cámara and Oberti2014), who interpreted this shift on the basis of the presence of the O(3)OH–ANa–O(3)F local arrangement. In tremolite, the local arrangement MgMgMg–OH–A□:SiSi (the band occurring at 3672 cm–1) could also generate a band at 3658 cm–1 due to O(3)OH–ANa–O(3)F local order.
${\rm F}_{\rm 1}^{\rm \ndash} $ exchange has been observed and discussed in other amphibole compositions by Robert et al. (Reference Robert, Della Ventura and Hawthorne1999, Reference Robert, Della Ventura, Welch and Hawthorne2000) and Della Ventura et al. (Reference Della Ventura, Bellatreccia, Cámara and Oberti2014), who interpreted this shift on the basis of the presence of the O(3)OH–ANa–O(3)F local arrangement. In tremolite, the local arrangement MgMgMg–OH–A□:SiSi (the band occurring at 3672 cm–1) could also generate a band at 3658 cm–1 due to O(3)OH–ANa–O(3)F local order.
The FTIR spectrum of fluoro-tremolite in the range from 1200 to 400 cm–1 is very similar to the spectrum of synthetic fluoro-tremolite described in Ishida et al. (Reference Ishida, Jenkins and Hawthorne2008), who ascribed region 1 to Si–O stretching vibrations, and region 2 mainly to Si–O–Si and O–Si–O deformation, except for the band at 687 cm–1 that can be assigned to the O–H libration. The strong band at 509 cm–1 and its pronounced shoulder at 544 cm–1 are due to M–O (M = Mg, Ca, Na, Si and Al) deformations (Lazarev, Reference Lazarev1972; Strens, Reference Strens and Farmer1974; Ishida, Reference Ishida1990; Andrut et al., Reference Andrut, Gottschalk, Melzer and Najorka2000; Ishida et al., Reference Ishida, Jenkins and Hawthorne2008).
Acknowledgements
The authors are grateful to Frank Hawthorne and Andrew Locock, who provided careful reviews of the manuscript.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/minmag.2017.081.029