1. INTRODUCTION
There are several promising concepts how to ignite in practice inertial confinement fusion (ICF) target. One of them, shock ignition (SI) concept, suggests to heat a pre-compressed core by means of a converging shock wave driven by a high-intensity laser pulse (Scherbakov, Reference Scherbakov1983; Betti et al., Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov2007; Ribeyre et al., Reference Ribeyre, Schurtz, Lafon, Galera and Weber2009). Interaction of such laser pulse with the plasma is strongly affected by non-collisional absorption mechanisms leading to a generation of fast (super-thermal) electrons. Therefore, the effects of the fast electron energy transport on the ablation pressure produced the shock wave generation and on the target compression belong to the most important problems in SI concept. In addition, the fast electron energy transfer may lead to a preheating of the target, which results in a decreased target compression.
From a point of view of practical realization of SI, the essential questions related to the fast electron energy transport can be divided into two groups. The first one is the preheating of the target due to the direct fast electron energy transport into the compressed matter. The second one concerns the influence of the fast electron energy transfer in the evaporated part of the target on the ablation pressure generation and the energy coupling to the shock wave. The latter were intensively studied during several experimental sessions at Prague Asterix Laser System (PALS). In the paper (Gus'kov et al., Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowski, Renenr, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014), such investigations were carried out in the frame of experiments where the planar Al or Cu targets were irradiated by one beam of the PALS iodine laser. This work was a direct continuation of our earlier experimental studies (Gus'kov et al., Reference Gus'kov, Borodziuk, Kalal, Kasperczuk, Kralikova, Krousky, Limpouch, Masek, Pisarczyk, Pisarczyk, Pfeifer, Rohlena, Skala and Ullschmied2004, Reference Gus'kov, Kasperczuk, Pisarczyk, Borodziuk, Kalal, Limpouch, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2006), which have demonstrated the increasing contribution of fast electrons to energy transfer to shock wave with growth of intensity and wavelength of laser radiation. Bearing in mind the PALS laser pulse duration of 250 ps, it is worth mentioning that for the intensity range of 1–10 PW/cm2 the target irradiation conditions differed from those characteristic for the SI laser spike only due to the application of the single laser beam acting directly on a solid target surface. According to the SI concept, the igniting shock wave is generated by the action of the laser spike on the extended low-density plasma produced by the first nanosecond part of the laser pulse in the stage of the preliminary compression of the ICF target. This difference in the energy deposition conditions could relate to the different mechanisms of the fast electrons generation. In a larger scale, pre-plasma fast electrons are predominantly generated due to stimulated parametric processes in lower density plasma (Theobald et al., Reference Theobald, Betti, Stoeckl, Aanderson, Delettrez, Glebov, Goncharov, Marshall, Maywar, Mccrory, Meyerhofer, Radha, Sangster, Seka, Shvarts, Smalyuk, Solodov, Yaakobi, Zhou, Frenje, Li, Siguin, Petrasso and Perkins2008, Reference Theobald, Nora, Lafon, Casner, Ribeyre, Anderson, Betti, Delettrez, Frenje, Glebov, Gotchev, Hohenberger, Hu, Marshall, Meyerhofer, Sangster, Schurtz, Seka, Smalyuk, Stoeckl and Yaakobi2012; Batani et al., Reference Batani, Koenig, Baton, Perez, Gizzi, Koester, Labate, Honrubia, Antonelli, Morace, Volpe, Santos, Schurtz, Hulin, Ribeyre, Fourment, Nicolai, Vauzour, Gremillet, Nazarov, Pasley, Richetta, Lancaster, Spindloe, Tolley, Neely, Kozlová, Nejdl, Rus, Wolowski, Badziak and Dorchies2011; Jacquemot et al., Reference Jacquemot, Amiranoff, Baton, Chanteloup, Labaune, Koenig, Michel, Perez, Schlenvoigt, Canaud, Cherfils Clérouin, Debras, Depierreux, Ebrardt, Juraszek, Lafitte, Loiseau, Miquel, Philippe, Rousseaux, Blanchot, Edwards, Norreys, Atzeni, Schiavi, Breil, Feugeas, Hallo, Lafon, Ribeyre, Santos, Schurtz, Tikhonchuk, Debayle and Honrubia2011; Klimo et al., Reference Klimo, Tikhonchuk, Rebeyre, Schurtz, Riconda, Weber and Limpouch2011; LLE Review, 2012). Nevertheless, the average energy of fast electrons in the PALS experiment was close to that measured in the OMEGA laser experiments (Theobald et al., Reference Theobald, Betti, Stoeckl, Aanderson, Delettrez, Glebov, Goncharov, Marshall, Maywar, Mccrory, Meyerhofer, Radha, Sangster, Seka, Shvarts, Smalyuk, Solodov, Yaakobi, Zhou, Frenje, Li, Siguin, Petrasso and Perkins2008, Reference Theobald, Nora, Lafon, Casner, Ribeyre, Anderson, Betti, Delettrez, Frenje, Glebov, Gotchev, Hohenberger, Hu, Marshall, Meyerhofer, Sangster, Schurtz, Seka, Smalyuk, Stoeckl and Yaakobi2012) and also to the values anticipated for the SI conditions (Klimo et al., Reference Klimo, Tikhonchuk, Rebeyre, Schurtz, Riconda, Weber and Limpouch2011).
Efficiency of the laser radiation energy transport into the shock wave generated in layered planar targets (consisting of massive Cu coated by thin CH layer) was investigated in the paper by Pisarczyk et al. (Reference Pisarczyk, Gus'kov, Kalinowska, Badziak, Batani, Antonelli, Folpini, Maheut, Baffigi, Borodziuk, Chodukowski, Cristoforetti, Demchenko, Gizzi, Kasperczuk, Koester, Krousky, Labate, Parys, Pfeifer, Renner, Smid, Rosinski, Skala, Dudzak, Ullschmied and Pisarczyk2014). The targets were irradiated using two laser pulses. The ω pulse with the energy of ~50 J produced a pre-plasma, imitating the corona of the pre-compressed ICF target. The second main pulse used the 1ω or 3ω laser harmonics with the energy of ~200 J. The influence of the pre-plasma on parameters of the shock wave was determined from the crater volume measurements and from the electron density distribution measured by three-frame interferometry. The experimental results show that the energy transport by fast electrons provides a contribution to the dynamics of the ablative process, to the shock wave generation, and to the ablation pressure in dependence on the target irradiation conditions. A strong influence of the pre-plasma on the investigated process was observed in the 1ω case. Our theoretical analysis supports the explanation of experimental results.
One of the essential problems appearing in SI experiments is the possibility of generation of high pressures. It was shown (Batani et al., Reference Batani, Antonelli, Atzeni, Badziak, Baffigi, Chodukowski, Consoli, Cristoforetti, Deangelis, Dudzak, Folpini, Giuffrida, Gizzi, Kalinowska, Koester, Krousky, Krus, Labate, Levato, Maheut, Malka, Margarone, Marocchino, Nejdl, Nicolai, O'Dell, Pisarczyk, Renner, Rhee, Ribeyre, Richetta, Rosinski, Sawicka, Schiavi, Skala, Smid, Spindloe, Ullschmied, Velyhan and Vinci2014a, Reference Batani, Baton, Casner, Depierreux, Hohenberger, Klimo, Koenig, Labaune, Ribeyre, Rousseaux, Schurtz, Theobald and Tikhonchukb) that one can couple a laser beam to a payload and generate a rather strong shock (90 Mbar) even in the presence of an extended plasma corona.
Another interesting remark appearing at that work is connected with relations between effectiveness of SI and the wavelength at which ignition experiments are being attempted. Authors suggest that unlike the case of pellet compression, where one must use short wavelengths in order to reduce target preheating (due to both electrons and X-rays) and increase hydrodynamic efficiency (i.e., maximize the mass ablation rate and shock pressure generation), the target preheating is not such a severe issue in SI because hot electrons are generated at the end of the compression. This may re-open the way to the use of longer wavelength lasers, maybe even lasers working at 1ω (at least for the final laser spike).
The properties of plasmas formed by sequential action of two laser beams on a flat target were investigated (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015) to simulate the conditions of the shock-ignited ICF target exposure. Those experiments were performed using planar targets with the same construction as in our previous papers (Koester et al., Reference Koester, Antonelli, Atzeni, Badziak, Baffigi, Batani, Cecchetti, Chodukowski, Consoli, Cristoforetti, Deangelis, Folpini, Gizzi, Kalinowska, Krousky, Kucharik, Labate, Levato, Liska, Malka, Maheut, Marocchino, O'Dell, Parys, Pisarczyk, Raczka, Renner, Rhee, Ribeyre, Richetta, Rosinski, Ryc, Skala, Schiavi, Schurtz, Smid, Spindloe, Ullschmied, Wolowski and Zaras2013; Batani et al., Reference Batani, Antonelli, Atzeni, Badziak, Baffigi, Chodukowski, Consoli, Cristoforetti, Deangelis, Dudzak, Folpini, Giuffrida, Gizzi, Kalinowska, Koester, Krousky, Krus, Labate, Levato, Maheut, Malka, Margarone, Marocchino, Nejdl, Nicolai, O'Dell, Pisarczyk, Renner, Rhee, Ribeyre, Richetta, Rosinski, Sawicka, Schiavi, Skala, Smid, Spindloe, Ullschmied, Velyhan and Vinci2014a, Reference Batani, Baton, Casner, Depierreux, Hohenberger, Klimo, Koenig, Labaune, Ribeyre, Rousseaux, Schurtz, Theobald and Tikhonchukb; Pisarczyk et al., Reference Pisarczyk, Gus'kov, Kalinowska, Badziak, Batani, Antonelli, Folpini, Maheut, Baffigi, Borodziuk, Chodukowski, Cristoforetti, Demchenko, Gizzi, Kasperczuk, Koester, Krousky, Labate, Parys, Pfeifer, Renner, Smid, Rosinski, Skala, Dudzak, Ullschmied and Pisarczyk2014; Badziak et al., Reference Badziak, Antonelli, Baffigi, Batani, Chodukowski, Cristoforetti, Dudzak, Gizzi, Folpini, Hall, Kalinowska, Koester, Krousky, Kucharik, Labate, Liska, Malka, Maheut, Parys, Pfeifer, Pisarczyk, Renner, Rosiński, Ryc, Skala, Smid, Spindloe, Ullschmied and Zaraś-Szydłowska2015), which were irradiated by the 1ω PALS laser beam (λ = 1.315 µm) at the energy of 250 J. To investigate the influence of the pre-plasma on efficiency of the laser radiation energy transport to a shock wave and the fast electron emission, our research was based on application of the multi-frame interferometry and of a unique set of X-ray and ion diagnostics. The femtosecond interferometry turned out to be especially useful to determine the changes of the electron density gradients during the laser pulse interaction with a target, which definitively confirmed an occurrence of the resonant absorption in the case of 1ω main beam and its influence on the laser radiation energy transport to a shock wave. The general conclusion is that the fraction of the main laser beam energy deposited in a massive Cu target at two-beam irradiation decreases in comparison with the case of the target irradiation at the absence of the pre-plasma. The reason is that the pre-formed and expanding plasma deteriorates the efficiency of the energy transfer from the main laser pulse to a solid part of the targets by means of the fast electrons and the wave of an electron thermal conductivity.
The present paper is a continuation of our previous paper with the use of the femtosecond interferometry (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015). It concerns the role of pre-plasma on the transport of laser radiation energy and formation of shock wave pressure ablation experiments simulating the conditions of the SI. The investigation presented in this paper uses 3ω iodine laser light to create the igniting shockwave. One of the most important points of these studies was the influence of the laser intensity changing by means of focal spot radius variation on plasma expansion, efficiency of the laser energy transfer to the shock wave and fast electron emission.
The paper is structured as follows. In Section 2, the experimental setup is described. The results concerning investigation of efficiency of laser energy transfer to a solid target via interferometry and crater measurements are presented in Section 3. In Section 4, the measurements of the fast electrons and ions emission are presented. Section 5 brings the results of numerical simulations. Finally, Section 6 summarizes the obtained results.
2. EXPERIMENTAL SETUP
To simulate the SI conditions two beams experiments with use of two-layer targets (Fig. 1) consisting of a planar massive part with Cu, covered by 25 µm layer of polyethylene were carried out on PALS.

Fig. 1. The target construction and the way of its irradiation in the experiment.
In these experiments, the three-harmonic (λ3 = 438 nm) iodine laser was applied, as the main laser beam, producing a shock wave with the intensity of the radiation in the range of 1–20 PW/cm2 corresponding to changes of parameter Iλ32: 2 × 1014 – 4 × 1015 Wμm2/cm2. The desired intensity of the main beam was achieved at constant laser energy at a level of about of 200 J by changing the focal spot radius of the laser beam on the target in range of R L = 50–200 µm.
The pre-plasma, which simulates the pre-compressed plasma in real inertial fusion experiment, was created by means of the one-harmonic laser beam with energy of about 40 J, which was defocused to the focal spot radius of R L = 300 µm. Analogously as in the previous experiments (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Kalinowska, Badziak, Batani, Antonelli, Folpini, Maheut, Baffigi, Borodziuk, Chodukowski, Cristoforetti, Demchenko, Gizzi, Kasperczuk, Koester, Krousky, Labate, Parys, Pfeifer, Renner, Smid, Rosinski, Skala, Dudzak, Ullschmied and Pisarczyk2014, Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015), 3ω main pulse was delayed by 1.2 ns relative to the pulse creating the pre-plasma.
The influence of the pre-plasma on the laser energy transport to the shock wave and the fast electron emission were carried out using the following diagnostic sets:
• The three-frame interferometer with the delay line irradiated by femtosecond Ti:Sa laser(t = 40 fs and λ = 808 nm), to measure the electron density distributions of the ablative plasma;
• Two-dimensional (2D) imaging of the emission of Cu K α line using spectrograph with a spherical crystal type (211) to determine the distribution of fast electrons population and their energy; and
• The grid collectors to measure the angular distributions of the ion emission, as a source of information about the ablative plasma electron temperature, the average energy of fast electrons and the geometry of the ablative plasma expansion.
Apart from the above-mentioned diagnostics, crater volume measurements were carried out as a routine diagnostics in PALS experiments which were used to evaluate the efficiency of the laser energy transfer to the shock wave generated in the massive part of the two-layer targets. The location of the diagnostics used in the PALS experiment is shown in Figure 2.

Fig. 2. Diagnostics used in the experiment and their placement in the experimental chamber.
As the fundamental option of measurements, two-beam experiments for different irradiation conditions of the targets depending on the focal spot radius were realized. To better characterize of the pre-plasma influence on the laser energy transport to the massive part of the target and the fast electron emission parameters, the results of two beams experiments have been compared with the single-beam experiments (without pre-plasma) for the same irradiation condition as in the case of two-beam experiments when the pre-plasma was created. Additionally, to determine the fast electron energy, the 2D imaging of the K α line, experiments with use of two-layer targets, covered by the polyethylene layers of different thickness : Δpl = 15, 25, 50, and 100 µm were performed.
The 2D numerical simulations (2DS) based on application of the ALANT-HE code that includes resonant absorption of laser radiation has been used to support the experimental data.
3. INVESTIGATION OF THE ABLATIVE PLASMA EXPANSION AND THE LASER ENERGY TRANSPORT EFFICIENCY AT PRE-PLASMA PRESENE
3.1. The space–time electron density distributions measurements in ablative plasma
To obtain information about the space–time electron density distributions of the ablative plasma, created by 3ω main beam (λ3 = 438 nm), the interferometric measurements were carried out using a three-frame interferometer, which was irradiated by means of the fundamental harmonic (λ = 808 nm) of the femtosecond PALS Ti:Sa laser with the pulse duration about of 40 fs. Such a short diagnostic pulse ensured obtaining interferograms with a high time resolution, which is sufficient to see the temporal changes of the electron density during the laser pulse interaction with a target. Such as in our previous paper (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015), determining the information about the temporal changes of the density scalelength (L) and the maximal density gradient (dn e/dz) were the main aim of these investigations.
To know the electron density of the ablative plasma in the period which included the main pulse interaction with a target, three-frames were recorded successively with the time distance of 400 ps and the first frame was recorded before the main laser pulse in the range of −400 to 200 ps relative to the maximum intensity of the main laser beam. Tens of interferograms were obtained for different conditions of irradiation of two-layer targets. To determine the electron density distributions in the ablative plasma, the way of the quantitative analysis of the interferograms described in our previous papers (Gus'kov et al., Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowski, Renenr, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014; Pisarczyk et al., Reference Pisarczyk, Gus'kov, Kalinowska, Badziak, Batani, Antonelli, Folpini, Maheut, Baffigi, Borodziuk, Chodukowski, Cristoforetti, Demchenko, Gizzi, Kasperczuk, Koester, Krousky, Labate, Parys, Pfeifer, Renner, Smid, Rosinski, Skala, Dudzak, Ullschmied and Pisarczyk2014; Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015) was applied.
The comparison of the electron density distribution of the ablative plasma obtained under the absence and the presence of the pre-plasma at different focal spot radii and for different time of the plasma stream expansion is presented in Figure 3. The time delays between each individual frame relate to the maximal intensity of the main pulse.

Fig. 3. Comparison of the electron density distributions of ablative plasma obtained in the case of: (a) the absence and (b) presence of pre-plasma at different focal spot radii and for different times of the plasma stream expansion.
Similarly as for the 1ω main laser beam (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015), in the case without the pre-plasma, Figure 3a, the electron density distributions demonstrate the hemi-spherical character of plasma expansion, with a characteristic minimum of density on the axis, which is particularly visible for small focal spot radii. In the case of the pre-plasma presence, Figure 3b, the electron density distributions indicate that the light plasma of higher pressure, being generated from the thin plastic layer by 1ω auxiliary beam, limits the radial expansion of the central plasma created by the 3ω main laser beam. The radial limitation favors the axial character of plasma expansion particularly in the case of larger focal spot radii. These change in the character of the ablative plasma expansion (from hemi-spherical to axial), caused by the pre-plasma presence and increasing focal spot radius, are clearly demonstrated by the axial density profiles shown in Figure 4.

Fig. 4. Comparison of the axial density profiles and scalelength values in the ablative plasma obtained in the case of: (a) the absence and (b) presence of the pre-plasma at different focal spot radii and for different plasma expansion times.
These axial density profiles were the starting point for obtaining information about the electron density scalelength and the maximal density gradient for selected expansion times of the ablative plasma created at different laser focal spot radii.
To obtain information about the density gradient and scalelength, exponential fitting of the experimental axial density profiles has been applied: n e(z) = n 0e −z/L. The parameters of this function determine the maximum electron density gradient in the opacity zone: (dn e/dz)z = 0 = n o/L, where L is the scalelength of the electron density and n 0 is the maximum electron density. The changes of the axial density profiles and the density scalelength (L) of the ablative plasma caused by increasing focal spot radius in the case of the pre-plasma absence are demonstrated in Figure 4a, while these changes in the case of the pre-plasma presence are illustrated in Figure 4b.
A detailed comparison of the ablative plasma expansion in the case of absence and presence of pre-plasma is presented in Figure 5. This figure shows the maximal density gradient and the scalelength for three characteristic times of expansion: 0, 300, and 600 ps in relation to the maximum intensity of the main laser beam. Single values corresponding to the chosen expansion times and focal spot radii have been determined by interpolation of the experimental data. From Figure 5a it results that in the case without the pre-plasma the highest density gradient values corresponds to the maximum laser pulse intensity (t = 0). Its maximum value is about 5 × 1022 cm−4 for the focal spot radius equal to R L = 100 µm and corresponds to the minimal scalelength L = 100 µm. Such a value of the scalelength is approximately the same in the whole range of the changes of the focal spot radius. For later times of plasma expansion, the density gradient decreases rapidly, reaching a value by five times smaller (at t = 600 ps) in comparison with the maximum value, while the scalelength increases to the value about L = 300 µm at the same expansion time of the ablative plasma.

Fig. 5. Comparison of the maximal density gradient and the scalelength following from interferometric fitting obtained in the case of: (a) the absence and (b) presence of the pre-plasma.
An increase of the focal spot radius above R L = 100 µm leads to a decrease of the density gradient and small changes in the scalelength. Further increasing the focal spot radius (above R = 150 µm) increases the density gradient, reducing little the scalelength, which is the result of the increasing role of one-dimensional (1D) expansion of the ablative plasma for larger focal spot radii (Gus'kov et al., Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowski, Renenr, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014; Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015).
However, the presence of the pre-plasma (Figure 5b) does not degenerate, both the maximal density gradient neither the scalelength of electron density, such as in the case of the first harmonicas the main beam-generating igniting shock wave (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015). As it results from Figure 5b, the strong limitation of the radial expansion of the 3ω ablative plasma by the external light plastic pre-plasma which is created by means of the 1ω auxiliary laser beam, leads to an increase in the electron density on the axis, and consequently to increase the density gradient. The largest density gradient occurs during the intensity peak of the main laser beam (t = 0), for smallest focal spot radius (R L = 50 µm) and its value is about 7 × 1022 cm−4, which is even a bit higher than in the absence of the pre-plasma. However, this gradient drops rapidly, both as a function of the expansion time and focal spot radius. It should also be noted that the plasma stream formed in the presence of the pre-plasma is characterized by a greater scalelength than in the absence of the pre-plasma. As it results from Figure 5b, the smallest density scalelength, L = 220 µm, corresponds to the maximum laser pulse intensity (t = 0) and minimal focus spot radius. With the increase in focal spot radius, the scalelength increases monotonously, reaching a value of one and a half time greater (about L = 340 µm) than in the case without pre-plasma. For later times of ablative plasma expansion, the changes of scalelength as a function of focal spot radius are very similar to those for the initial phase of expansion. This proves the stabilizing influence of the pre-plasma on the central plasma created by 3ω main beam.
In previous experiments carried out with the first-harmonic main pulse (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015), the significant effect of energy transfer by fast electrons on the formation of plasma density and temperature distributions was found and, as a result, also on the formation of ablation pressure and laser energy transfer to shock wave. In the absence of the pre-plasma, the fast electron energy transport deep into the corona at high laser intensity (small radii of laser beam) was more effective than the electron thermal conductivity and led to a significant increase in the ablation density in comparison with low critical plasma density corresponding to the first-harmonic radiation. This explains the measured sufficiently high values of the electron density gradient of about 1022 cm−4 at the small beam radii. The generation of fast electrons was due to a significant contribution of resonant mechanism of laser light absorption. The presence of pre-plasma significantly worsened both the conditions for the generation of fast electrons and the effectiveness of the energy transfer by them, that was manifested by a significant decrease (two to four times) of the density gradient.
The results of the experiments presented here with the third-harmonic main pulse do not reveal the influence of energy transfer by fast electrons to plasma formation. The non-monotonic behavior of the gradient density with a laser beam radius in both the presence and absence of the pre-plasma is determined by the competition of the processes of plasma motion and electron heat conduction in the conditions of 1D and 2D expansions at large and small values of the beam radius, respectively. The total significant excess of the density gradient in the case of the third-harmonic main pulse in comparison with the first-harmonic one is due to ninefold excess of the critical plasma density.
3.2. Crater volume measurements
The crater volume measurements are applied in the PALS experiments as a routine diagnostic to evaluate the efficiency of the transfer of laser energy, absorbed by the ablative plasma, to the shock wave generated in a massive planar target. The diagnostic with the interferometric measurements enabled us to determine the N/V cr parameter (where N is the total electron number in the plasma plume, and V cr is the crater volume), defined in previous papers (Gus'kov et al., Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowski, Renenr, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014; Pisarczyk et al., Reference Pisarczyk, Gus'kov, Kalinowska, Badziak, Batani, Antonelli, Folpini, Maheut, Baffigi, Borodziuk, Chodukowski, Cristoforetti, Demchenko, Gizzi, Kasperczuk, Koester, Krousky, Labate, Parys, Pfeifer, Renner, Smid, Rosinski, Skala, Dudzak, Ullschmied and Pisarczyk2014, Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015) and which creates possibilities to obtain essential information regarding the mechanisms of absorption of laser radiation depending on the target irradiation conditions. This parameter determines a number of thermal electrons participating in the creation of crater volume unit (1 cm3).
For measuring the crater volumes, a digital microscope (HIROX-KH-8700 model) from the Institute of Optoelectronics of MUT, Warsaw was used. This microscope enables the determination of both the crater parameters in the selected cross-sections with the micron accuracy and their visualization. Using this instrument, the volume and dimensions of craters have been measured for all laser shots taken during the PALS measurement session. Examples of the visualization of the craters by means of the HIROX microscope, obtained in the case of the absence and presence of the pre-plasma, corresponding to different irradiation conditions (depending on the focal spot radius of the laser beam), are shown in Figure 6.

Fig. 6. Visualization of craters done by HIROX microscope, showing the craters obtained in the two-layer targets in the case of: (a) without and (b) in the presence of pre-plasma for two different focal spot radii of the laser beam.
The N/V cr parameter was evaluated only for expansion time: t = 600 ps, that is, after the end of main laser pulse, when both the ablation process and processes related to the absorption of laser radiation were completed. The results of calculations of the crater volumes V cr, the total electron number N, and the N/V cr parameter for different options of irradiation of the two-layer targets are shown in Figure 7.

Fig. 7. Comparison of the crater volumes V cr, total electron number N, and N/V cr parameter obtained in the case of: (a) the absence and (b) presence of the pre-plasma.
First of all, it should be noted that in comparison with the results of 1ω main pulse experiments (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015), in the 3ω case the crater volume increases significantly weaker with decreasing radius in the region of its low value, R L < 100 µm. This indicates that in the case of the 3ω radiation the strong effect of energy transfer by fast electrons deep into a dense plasma observed in the case of the 1ω is absent. As a result, there is only one transport mechanism, that caused by the electron thermal conductivity, which leads to just a weak growth in the crater volume with increasing the laser intensity with decreasing the beam radius. Furthermore, the crater volume in the case of the third-harmonic main pulse is six to eight times larger in comparison with the case of the 1ω main pulse. This is due to a more efficient energy transfer to shock wave associated with a larger ablation pressure due to a significantly (ninefold) higher the critical plasma density in the case of the third-harmonic radiation. The presence of pre-plasma, which increases the corona mass and therefore the number of electrons N, slightly reduces crater volume by reducing the efficiency of energy transfer by electron conductivity. At the same time, the decrease in the ratio N/V cr in both the cases of the absence and presence of the pre-plasma shows that in the absence of fast electron energy transfer, when electron conductivity is the dominant mechanism of energy transfer, the most favorable conditions for the energy transfer to shock wave correspond to the plane expansion of the plasma at the large values of the beam radius (Gus'kov et al., Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowski, Renenr, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014; Pisarczyk et al., Reference Pisarczyk, Gus'kov, Kalinowska, Badziak, Batani, Antonelli, Folpini, Maheut, Baffigi, Borodziuk, Chodukowski, Cristoforetti, Demchenko, Gizzi, Kasperczuk, Koester, Krousky, Labate, Parys, Pfeifer, Renner, Smid, Rosinski, Skala, Dudzak, Ullschmied and Pisarczyk2014).
4. PRE-PLASMA EFFECT ON FAST ELECTRON PRODUCTION AND ION EMISSION
4.1. The 2D imaging of the Cu K α line emission
To characterize in more detail the impact of the pre-plasma on the laser energy transport and the formation of ablation pressure, the interferometry and crater volume measurements were complemented by quasi-monochromatic X-ray imaging of K α line emission from near-surface Cu layers. The aim of this study was to investigate the generation of fast electrons, their energy and conversion efficiency of the laser radiation into supra-thermal electron population at different irradiation conditions of two-layer targets, in particular, under the presence and absence of the pre-plasma.
The research was carried out using the 3ω radiation of the main laser beam with the energy at the level of 200 J, its intensity was varied by changing the focal spot radius on the target within the range of R L = 50–200 µm. To determine the energy of the fast electrons, two-layer targets with different thicknesses of the plastic coating (Δpl = 15, 25, 50, and 100 µm) were used.
The imaging setup was the same as in previous experiments (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015). The detected signal was integrated over the full Cu K α image produced by fast electrons in a relatively cold, dense Cu plasma (Smid et al., Reference Smid, Antonelli and Renner2013).The X-ray images were recorded using a spherically bent crystal of quartz (422), which was set up as an imaging mode monochromator (with the Bragg angle θ = 88.2° and magnification of 1.73) to provide a distribution of the 2D spatially resolved Cu K α emission along the target surface. The time-integrated K α signals attenuated by the transmission through filters consisting of 10 µm of Cu, 20 µm of Al, and 40 µm of mylar were registered with the Kodak AA400 X-ray film. The recorded images were digitized with a calibrated table-top scanner, recalculated to optical densities and intensities of the impinging radiation using the characteristic curve of the film.
The 2D-resolved records contain information on the emitting area and intensity of the K α emission generated in Cu by fast electrons. The quantitative evaluation of these data was based on assumption of the Maxwellian energy distribution of supra-thermal electrons impacting on the double-layer target and an exponential decay of the photon emission I with the increasing thickness x of the plastic layer I(x) = A·exp (−x/L), where L is an attenuation coefficient. The experimental data were interpreted using Monte Carlo simulations of the electron and photon transport performed with the PENELOPE code [F. Salvat, J.M. Fernandez-Varea, and J. Sempau. Penelope-2008: A Code System for Monte Carlo Simulation of Electron and Photon Transport. 2009. ISBN 978-92-64-99066-1]. Assuming characteristic temperature T HE of Maxwellian hot electron distribution, the trajectories of electrons propagating into the target were calculated both in the plastic and Cu layers, the generation of K α emission inside the Cu layer and its propagation and absorption in the target was taken into account. A set of simulations was performed for different T HE values and various plastic thicknesses. Each simulation calculated the probability dp/dΩ(ψ) that one electron produces an K α photon escaping the target in an unit solid angle Ω at the given polar angle ψ. These probabilities were further used in interpretation of the experimental data and in derivation of sought interaction characteristics, for example, the exponential attenuation of the fast-electron-generated photon emission due to different-thickness surface plastic layers. The calculated dependence of the attenuation coefficient L on the supra-thermal electron energy is shown in Figure 8.

Fig. 8. The attenuation coefficient L as a function of the fast electron energy.
The final experimental results were obtained via fitting the photon fluxes spatially integrated over 2D-resolved images with simulations. To determine the energy of fast electrons E, the Cu K α emission was measured at targets with different thickness plastic layers. Results of these measurements are shown in Figure 9 in dependence on the thickness of the surface plastic layer Δpl and under the absence and presence of the pre-plasma. All these data were taken when irradiating the target by the 3ω beam focused to the focal spot with radius of R L = 50 µm. In addition to the useful K α signal and film noise, the recorded images captured a non-negligible amount of the continuum radiation emitted primarily by the plastic layer covering the Cu substrate. This radiation has independently been measured using self-supporting plastic foils and subtracted from the recorded images, but the uncertainty estimate has significantly increased due to the fluctuation of the background signal. Consequently, the error bars indicate mainly uncertainties in the background subtraction. The number of incident photons refers to photon fluxes impinging on the filmpack, that is, when processing the recorded images, the filters covering the film were already taken into account, but not the transmission function of the crystal imager (Smid et al., Reference Smid, Antonelli and Renner2013). Dependences plotted in Figure 9a and b demonstrate the variation of the Cu K α photon fluxes with the increasing thickness of plastic and a significant increase of the emission in the presence of the pre-plasma (Fig. 9b).The best-fit values of the attenuation coefficient L and the hot electron energy E are also indicated in Figure 9.

Fig. 9. Photon fluxes spatially integrated over 2D-resolved Cu K α images. The signal attenuation due to different thickness Δpl of plastic layers is plotted for cases of the absent (a) and present (b) pre-plasma.
Their uncertainties were defined to keep the sum of squares of the fitting residuals within 5% from its minimum value. These uncertainties are caused mainly by the shot-to-shot fluctuations of the relatively weak signals: After subtracting the film noise and the above-discussed continuum radiation, the weakest useful spatially integrated K α signals measured at the Cu substrates coated with 100-μm-thick plastic layers were at the level of 350 and 700 photons for the pre-plasma absence and presence, that is, by a factor of 2 and 3.5 above the resulting standard deviation following from the Poisson distribution of the incident radiation, respectively. The continuous line represents the best fit; the thin dashed lines correspond to the indicated extreme values of L. The main conclusion following from the interpretation of experimental data presented in Figure 9 is the dependence of the hot electron energy on the plasma scalelength. The average energy E = 37 keV of the fast electrons produced in the case of the single-beam irradiation of the targets (Fig. 9a) is almost two times smaller than that observed in the presence of the pre-plasma (Fig. 9b).
The effect of the pre-plasma on the total number of detected Cu K α photons in dependence on the laser intensity, that is, on the focal spot radius, is shown in Figure 10. All these data fitted with the second degree polynomial was measured at the Cu targets coated with 25 µm of plastic. While the number of detected Cu K α photons (and consequently also the production of hot electrons) increases only slightly with the focal spot radius at the pre-plasma absence, the presence of the pre-plasma results in a distinct growth of the fast electron population peaking at R L ≈ 150 µm. Obviously the increased scalelength of the ablative plasma under the presence of the pre-plasma increases both the production and energy of the fast electrons.

Fig. 10. Integrated photon fluxes from2D-resolved Cu Kα images as a function of the laser focal spot radius under the absence (a) and presence (b) of the pre-plasma.
To estimate the conversion of the laser energy into the fast electrons, the number of detected photons N Kα was related to the number of hot electrons N HE propagating through the target using the expression
where r = 8.3 × 10−7 is the ray-tracing constant relating the fraction of photons impinging on the detector to the number of photons isotropically emitted from the cold Cu into the full solid angle 4π within the Cu K α1,2 profile. This assumption is well justified for Cu targets coated with 25 µm of plastic where the frequency-shifted satellite emission generated by fast electrons in the heated Cu can be neglected. By taking into account the average energies E presented in Figure 9, and the found values of N HE were further related to the conversion efficiency η of the laser energy into hot electrons.
In the current experiment, the typical numbers of fast electrons N HE propagating through the target were within the range of 1–5 × 1012. The conversion efficiencies calculated as the ratio of the total energy carried by fast electrons entering the target to the energy of the main 3ω laser beam under the presence/absence of the pre-plasma are shown in Figure 11. The conversion efficiencies are grouped near four laser intensities 1 × 1016, 2.5 × 1015, 1 × 1015, and 6 × 1014 W/cm2 corresponding to focal spot radii of 50, 100, 150, and 200 µm, respectively. The found values of η are considerably scattered and do not display a distinct dependence on the laser intensity. On the other hand, the presence of the pre-plasma unambiguously increases their average values (1.2 × 10−4 at the pre-plasma absence and 3.5 × 10−4 at its presence) by a factor of approximately 2.9.

Fig. 11. Conversion efficiency of the 3ω beam energy into hot electrons as a function of the laser intensity.
At given conditions of the target irradiation, the observed laser energy conversion to fast electrons is rather small in both cases of the pre-plasma presence and absence. This conversion is too small to fast electrons can have any noticeable impact on the laser-produced plasma evolution as well as on the processes of the laser energy deposition and pressure formation at the 3ω main pulse PALS experiments.
4.2. Ion emission measurements
The ion diagnostics applied in the PALS experiment consisted of several ion collectors installed at different angles (from 0° to 60°) at the distance of 40 cm from the target. The collected ion current was emitted from two-layer targets (see Fig. 1). Some of the selected results provided by this diagnostic system are presented in Figures 12 and 13. In the left column, there are the results obtained without application of pre-pulse and in the right column – those obtained with it. The parameters of the 3ω laser beam were at the same level for all the presented measurements (about 200 J in the main beam and about 40 J in the pre-pulse).

Fig. 12. Oscillograms illustrating the ion collector signals measured at different angles (with respect to the laser beam) and at various focal spot radii of the main laser beam in the case of the pre-plasma absence (a) and presence (b).

Fig. 13. The angular distribution of the ion charge density for different focal spot radii in the case of pre-plasma absence (a) and presence (b).
Figure 12 shows the ion collector signals for different angles and focal spot radii. All the signals for both the cases of pre-plasma absence and presence correspond to thermal ions only and do not contain any response related to fast ions. It is in contrast to the results of our previous experiments carried out with the 1ω main beam, where strong signals related to fast ions were measured for the case of pre-plasma absence at high main beam intensities of (0.5–2) × 1016 W/cm2 (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015).
It should be also noted that in the case of the 1ω beam the collector signals referring to thermal ions were more than twice less compared with the 3ω beam both for case of the pre-plasma absence and presence. It means that in the case of 3ω beam the absorption of laser light is significantly higher than that for the 1ω beam. According to the results of numerical simulations presented in the next paragraph, the absorption efficiency for 3ω is 0.7–0.8, while for 1ω (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015) it was 0.4–0.5.
Other conclusions deduced from the ion collector measurements (Fig. 12) may be summarized in several points:
• The number of thermal ions in the case of pre-plasma presence is approximately 1.2–1.5 times larger than that observed in the case of pre-plasma absence for all focal spot radii.
• The signal of fast ions is not measurable that confirms the results of previous paragraphs about the negligible effect of the fast electron generation.
• The thermal ion signals peak practically at the same time for both the case of pre-plasma presence and absence, at about 0.5 µs, which is by a factor of 1.4–1.6 smaller in comparison with the case of 1ω-main pulse (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015). It means that the temperature of plasma produced by 3ω beam is higher than that generated by the 1ω beam. This correlates well with the increase of absorption efficiency for the shorter wavelengths revealed by numerical simulations.
• The ion collector data, non-separated with respect to the ion types, give a possibility to determine only the scales of temperature of the plasma plume and average energy of fast electrons. Taking the time of the second peak as 0.5 µs, the average velocity of thermal ions as (3T/2m p)1/2 (in the A/Z = 2 approximation) and the distance between the target and the collector equal to 40 cm, we obtain that the value of plasma temperature, averaged in space and time, is approximately equal to 3–4 keV.
Figure 13 shows the plots of charge distributions for each experimental series, calculated on the basis of integration of the charge of thermal ions (for the time-of-flight ranging from 50 to 500 ns). It can be seen that in the case of the pre-plasma presence, the ion charge density on the axis is higher compared with the case when the pre-plasma is absent.
5. NUMERICAL SIMULATIONS AND DISCUSSION
Such as in our previous paper (Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015), 2DS were carried out using the 2D hydrodynamic code ATLANT-HE (Lebo et al., Reference Lebo, Demchenko, Iskakov, Limpouch, Rozanov and Tishkin2004; Gus'kov et al., Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowski, Renenr, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014), which includes modeling of the laser radiation refraction in the plasma, inverse bremsstrahlung and resonance absorption of laser radiation, generation of fast electrons due to resonance absorption, and the fast electron energy transfer via ionization losses. The aim of the simulations was obtaining information about:
• The temporal evolution of 2D spatial distributions of the density as well as electron and ion temperatures of the laser-produced plasma;
• The fractions of laser energy absorbed in a plasma by resonant and inverse bremsstrahlung mechanisms; and
• The energy of fast electrons.
To model the experimental conditions, the computations were performed for the 3ω radiation of the main laser beam with the energy of 200 J and three values of the focal spot radius: 50, 100, and 200 µm. In the case of the two-beam experiment, the pre-plasma was created by an auxiliary 1ω laser beam of energy of 40 J, focused to a focal spot radius R L of 300 µm, and preceding the main laser pulse by 1.2 ns.
For the case of the pre-plasma absence, the 2D calculations of the density and temperature corresponding to the maximum laser intensity are presented in Figure 14.

Fig. 14. The density (a) and temperature distribution (b) of the ablative plasma created by the 3ω main laser beam at the time of its intensity maximum.
The increase of focal spot radius leads to the increase of transverse size and decrease of axial size of expanding plasma. In consequence, the angles between the directions of density gradient and the normal to the target surface will decrease and the geometry of expansion will be close to the plane one.
A satisfactory agreement of calculations with the experiment was obtained in the case of laser beam interaction with a target in the presence of pre-plasma, as illustrated by the electron density distributions shown below.
The 2D distributions of the density and temperature characterizing the process of the interaction of the main beam with the pre-plasma created by the auxiliary laser beam are presented in Figure 15. Analogously, as in the case of the experimental data, to obtain the information about the density scalelength (L), exponential fitting of numerical data have been applied: n e(z) = n 0e −z/L.

Fig. 15. The density (a) and temperature distribution (b) characterizing the laser interaction with the pre-plasma at the time delay of t = 1.2 ns between the auxiliary and the 3ω main laser beam.
A comparison of the axial density profiles and L in the ablative plasma, both in the case of the pre-plasma absence and presence, is shown in Figure 16.

Fig. 16. Comparison of the axial density profiles and the scalelength obtained in the case of: (a) the absence and (b) presence of the pre-plasma.
Compared with the situation when the pre-plasma is not created, the scalelength of the ablative plasma in the case of the pre-plasma presence is considerably larger. A more detailed comparison of the experimental data with the 2DS is presented in Tables 1 and 2.
Table 1. Comparison of the experimental L with the 2DS in the case of presence and absence of pre-plasma
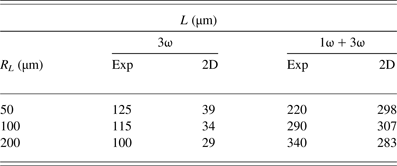
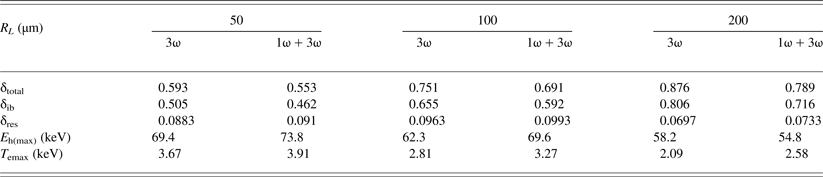
Table 2. Comparison of numerical simulations of the total (δtotal), resonant (δres), and inverse bremsstrahlung δib absorption coefficients in the cases of pre-plasma absence and presence

This comparison has been performed in the range of the electron density smaller than 1020 cm−3 as determined from the femtosecond interferometry. Table 1 indicates that there is a satisfactory agreement between the experimental and numerical data in the case of the pre-plasma presence. In the case of the pre-plasma absence, the qualitative character is the same, but the observed and simulated L values differ considerably. The large values of experimental L result from the action of the temporally extended beam profile, which is characteristic for the PALS laser and contributes to the creation of the low-density plasma even in the case of the pre-pulse absence. A long pedestal (even about 1 ns long) of the pulse is not taken into account in numerical simulations. In the case of the pre-plasma presence, the contribution of the pre-pulse is significantly smaller compared with the pre-plasma itself. This is why the experimental and numerical values of L agree well in the case of the pre-plasma presence.
Table 2 clearly indicates that in the case of the absence of pre-plasma, the total absorption increases with the increasing focal spot radius from the values 0.593 to 0.876. In contrast, the fraction of resonant absorption decreases from 0.0883 to 0.0697 staying small. The average energy of fast electrons E h(max)/2 is about 30–35 keV for both the with and without pre-plasma cases. The average fast electron energy is close to the experimental values, obtained from Cu K α line measurements in the experiment without the pre-plasma. The pre-pulse has a small effect on these quantities and does not alter their dependence on the radius of the main beam. These results differ significantly from the case of the 1ω main pulse, which was presented in (Table 3 in Pisarczyk et al., Reference Pisarczyk, Gus'kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal, Badziak, Batani, Volpe, Krousky, Dudzak, Ullschmied, Turcicova, Hrebickj, Medrik, Pfeifer, Skala, Zaras-Szydlowska, Antonelli, Maheut, Borodziuk, Kasperczuk and Pisarczyk2015). It should be noted, that the contribution of resonant absorption depends on the parameter:
where k 0 is the wave number of the laser light, L c is a size of the plasma inhomogeneities of density near the surface with critical density, θ0 is the angle of incidence of the laser light. The value of τ ≈ 0.7 is optimal for resonant absorption. The increase of focal spot radius leads to a decrease of the laser light intensity and an increase of size of the plasma inhomogeneities L c, since this size is determined by the action of the ponderomotive force. From other side, as it was noted above, the increase of focal spot radius leads to the decrease of the angle of incidence θ0, since the expansion becomes more close to a plane one. By these reasons, as it follows from the data of Table 2, the dependence of the fraction of resonant absorption on the focal spot radius is not strong.
It should be noted that the difference of the average energy of fast electrons from the maximum value due to various factors. The most obvious of these is the temporal dependence of the laser pulse intensity. Scale of fast electron energy is the energy of electron oscillations in a resonant field, where the strength square is proportional to the incident laser radiation intensity. If approximate temporal pulse shape of a triangle, the average intensity is half the maximum. This fact was taken into account in the above presented evaluation of the average energy of fast electrons. Another factor is the spatial distribution of the resonance field strength along the surface of plasma with critical density. Resonant field is concentrated in a narrow region adjacent to the surface of critical density. In the above evaluation of the fast electron average energy, the square of electric field strength in this narrow region is considered as a constant.
6. CONCLUSIONS
The reported investigations performed at the PALS facility show that by using the third-harmonic main pulse the laser energy conversion into the energy of fast electrons is very small – the fraction of fast electron energy does not exceed a few tenths of a percent of laser energy both in the absence and in presence of the pre-plasma. This conclusion deduced from K α emission measurements and numerical simulations is confirmed by the measurements of ion yield and volumes of laser-produced craters, which characterizes the amount of energy transferred to shock waves. Measurements of the ion signal show virtually no contribution of the fast ion component. The crater volume measurements in combination with femtosecond interferometry both in the case of the pre-plasma presence and absence show that the target ablation and laser-produced plasma evolution are determined by electron conductivity energy transfer in conditions of 1D or 2D matter expansion without any appreciable effect of energy transfer by fast electrons. Both the maximal volume of the crater (the maximum energy of the shock wave) and the minimal N/V cr parameter corresponds to the greatest radius of the focal spot at which the negative effect of 2D-expansion of the plasma is minimal and, as a result, the ablation pressure is maximal (Gus'kov et al., Reference Gus'kov, Borodziuk, Kalal, Kasperczuk, Kralikova, Krousky, Limpouch, Masek, Pisarczyk, Pisarczyk, Pfeifer, Rohlena, Skala and Ullschmied2004, Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowski, Renenr, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014). This result holds for both the experiments in the absence and presence of the pre-plasma. With the decrease of focal spot radius the negative effect of 2D-plasma expansion increases, and the crater volume decreases. This is in contrast with experiments with the first-harmonic main pulse, in which increasing the intensity of long-wavelength radiation leads to such a significant generation of fast electron by the resonance mechanism and to such a strong effect of the fast electron energy transfer in the target depth that its contribution to the shock generation is significant and the crater volume strongly increases with decreasing the focal spot radius (Gus'kov et al., Reference Gus'kov, Borodziuk, Kalal, Kasperczuk, Kralikova, Krousky, Limpouch, Masek, Pisarczyk, Pisarczyk, Pfeifer, Rohlena, Skala and Ullschmied2004, Reference Gus'kov, Kasperczuk, Pisarczyk, Borodziuk, Kalal, Limpouch, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2006, Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowski, Renenr, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014).
ACKNOWLEDGMENTS
This paper was supported in part by the Access to Research Infrastructure activity in the 7th Framework Program of the EU Contract No. 284464, Laserlab Europe III, by the Czech Republic's Ministry of Education, Youth and Sports under PALS RI-LM 2010014 and by the ToIFE Project of the EUROfusion Consortium and by the French-Polish bilateral collaboration program POLONIUM and of the COST Action MP1208 “Developing the physics and the Scientific Community for Inertial Fusion by Russian Foundation for Basic Research (Projects Nos 14-02-00010 and 13-02-00295). It was also supported in part by National Centre for Science (NCN), Poland, under Grant No. 2012/04/M/ST2/00452. The project P205-11-P712 supported by the Grant Agency of the Czech Republic is also gratefully acknowledged.”