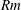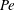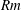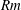1 Introduction
The generation of magnetic fields by a turbulent flow of a conducting fluid is a fundamental problem which has a number of applications in astrophysics, geophysics, planetary physics and laboratory experiments (see, e.g. Moffatt Reference Moffatt1978; Parker Reference Parker1979; Krause & Rädler Reference Krause and Rädler1980; Zeldovich, Ruzmaikin & Sokolov Reference Zeldovich, Ruzmaikin and Sokolov1983; Ruzmaikin, Shukurov & Sokoloff Reference Ruzmaikin, Shukurov and Sokoloff1988; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Rüdiger, Kitchatinov & Hollerbach Reference Rüdiger, Kitchatinov and Hollerbach2013). Two types of turbulent dynamos are usually considered: large-scale and small-scale dynamos. Magnetic field generation on scales much smaller and much larger than the integral scale of turbulence are described as small-scale dynamos and large-scale dynamos, respectively.
The theory of large-scale dynamos is based on a mean-field approach (Moffatt Reference Moffatt1978; Krause & Rädler Reference Krause and Rädler1980) in which the magnetic and velocity fields are decomposed into mean and fluctuating parts. Assuming that the averages obey the Reynolds rules, it follows that the fluctuating parts have zero mean values. Let us furthermore assume that there exists a separation of scales, i.e. the maximum scale of turbulent motions (the turbulent integral scale) is much smaller than the characteristic scales of inhomogeneity of the mean fields. In the framework of the mean-field approach, turbulence effects are described in terms of the mean electromotive force,
![]() $\overline{\boldsymbol{{\mathcal{E}}}}=\overline{\boldsymbol{u}\times \boldsymbol{b}}$
as a function of the large-scale magnetic field
$\overline{\boldsymbol{{\mathcal{E}}}}=\overline{\boldsymbol{u}\times \boldsymbol{b}}$
as a function of the large-scale magnetic field
![]() $\overline{\boldsymbol{B}}$
, where
$\overline{\boldsymbol{B}}$
, where
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\boldsymbol{b}$
are fluctuations of velocity and magnetic field.
$\boldsymbol{b}$
are fluctuations of velocity and magnetic field.
For a number of astrophysical applications, the nonlinear dependence of the function
![]() $\overline{\boldsymbol{{\mathcal{E}}}}(\overline{\boldsymbol{B}})$
has been determined analytically for flows that are incompressible, i.e. div
$\overline{\boldsymbol{{\mathcal{E}}}}(\overline{\boldsymbol{B}})$
has been determined analytically for flows that are incompressible, i.e. div
![]() $\boldsymbol{U}=0$
(see, e.g. Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2000, Reference Rogachevskii and Kleeorin2001, Reference Rogachevskii and Kleeorin2004; Rogachevskii et al.
Reference Rogachevskii, Kleeorin, Brandenburg and Eichler2012; Rüdiger et al.
Reference Rüdiger, Kitchatinov and Hollerbach2013; Rogachevskii et al.
Reference Rogachevskii, Ruchayskiy, Boyarsky, Fröhlich, Kleeorin, Brandenburg and Schober2017), or for low Mach number density-stratified flows in the anelastic approximation,
$\boldsymbol{U}=0$
(see, e.g. Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2000, Reference Rogachevskii and Kleeorin2001, Reference Rogachevskii and Kleeorin2004; Rogachevskii et al.
Reference Rogachevskii, Kleeorin, Brandenburg and Eichler2012; Rüdiger et al.
Reference Rüdiger, Kitchatinov and Hollerbach2013; Rogachevskii et al.
Reference Rogachevskii, Ruchayskiy, Boyarsky, Fröhlich, Kleeorin, Brandenburg and Schober2017), or for low Mach number density-stratified flows in the anelastic approximation,
![]() $\text{div}\,(\unicode[STIX]{x1D70C}\,\boldsymbol{U})=0$
(see, e.g. Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2003; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2006), where
$\text{div}\,(\unicode[STIX]{x1D70C}\,\boldsymbol{U})=0$
(see, e.g. Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2003; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2006), where
![]() $\unicode[STIX]{x1D70C}$
is the fluid density. However, in many astrophysical flows, the Mach number is not small and compressibility effects on the mean electromotive force can be important.
$\unicode[STIX]{x1D70C}$
is the fluid density. However, in many astrophysical flows, the Mach number is not small and compressibility effects on the mean electromotive force can be important.
Similar questions associated with compressibility effects arise in turbulent transport of passive scalars, where the mean-field approach allows us to determine the large-scale dynamics of passive scalars in small-scale turbulence (McComb Reference McComb1990; Zeldovich, Ruzmaikin & Sokoloff Reference Zeldovich, Ruzmaikin and Sokoloff1990; Frisch Reference Frisch1995; Zaichik, Alipchenkov & Sinaiski Reference Zaichik, Alipchenkov and Sinaiski2008; Monin & Yaglom Reference Monin and Yaglom2013). The effects of turbulence on passive scalar transport are described by means of a turbulent flux of passive scalar concentration or particle number density
![]() $\boldsymbol{F}=\overline{n\,\boldsymbol{u}}$
, where
$\boldsymbol{F}=\overline{n\,\boldsymbol{u}}$
, where
![]() $n$
is the fluctuation of the particle number density (Csanady Reference Csanady1980; Balachandar & Eaton Reference Balachandar and Eaton2010; Crowe et al.
Reference Crowe, Schwarzkopf, Sommerfeld and Tsuji2011; Piterbarg & Ostrovskii Reference Piterbarg and Ostrovskii2013). Compressibility effects play a crucial role in particle transport, for example they can cause the formation of spatially inhomogeneous distributions of particles, known as particle clusters. These effects are very important in a range of astrophysical and planetary science applications, where turbulence can be temperature stratified at finite Mach numbers (Priest Reference Priest1982; Ruzmaikin et al.
Reference Ruzmaikin, Shukurov and Sokoloff1988; Armitage Reference Armitage2010).
$n$
is the fluctuation of the particle number density (Csanady Reference Csanady1980; Balachandar & Eaton Reference Balachandar and Eaton2010; Crowe et al.
Reference Crowe, Schwarzkopf, Sommerfeld and Tsuji2011; Piterbarg & Ostrovskii Reference Piterbarg and Ostrovskii2013). Compressibility effects play a crucial role in particle transport, for example they can cause the formation of spatially inhomogeneous distributions of particles, known as particle clusters. These effects are very important in a range of astrophysical and planetary science applications, where turbulence can be temperature stratified at finite Mach numbers (Priest Reference Priest1982; Ruzmaikin et al.
Reference Ruzmaikin, Shukurov and Sokoloff1988; Armitage Reference Armitage2010).
For temperature-stratified turbulence, large-scale particle clusters (on scales much larger than the integral scale of the turbulence) are formed due to turbulent thermal diffusion (Elperin, Kleeorin & Rogachevskii Reference Elperin, Kleeorin and Rogachevskii1996, Reference Elperin, Kleeorin and Rogachevskii1997). The effects related to compressibility of the turbulent flow or the particle velocity field, result in a pumping effect of particles in regions of minimum mean fluid temperature. In particular, turbulent thermal diffusion causes a turbulent non-diffusive flux of particles in the direction of the turbulent heat flux, so that particles are accumulated in the vicinity of the mean temperature minimum. The phenomenon of turbulent thermal diffusion has been studied theoretically (Elperin et al. Reference Elperin, Kleeorin, Rogachevskii and Sokoloff2000, Reference Elperin, Kleeorin, Rogachevskii and Sokoloff2001; Amir et al. Reference Amir, Bar, Eidelman, Elperin, Kleeorin and Rogachevskii2017), detected in direct numerical simulations (Haugen et al. Reference Haugen, Kleeorin, Rogachevskii and Brandenburg2012), different laboratory experiments (Buchholz et al. Reference Buchholz, Eidelman, Elperin, Grünefeld, Kleeorin, Krein and Rogachevskii2004; Eidelman et al. Reference Eidelman, Elperin, Kleeorin, Rogachevskii and Sapir-Katiraie2006, Reference Eidelman, Elperin, Kleeorin, Melnik and Rogachevskii2010; Amir et al. Reference Amir, Bar, Eidelman, Elperin, Kleeorin and Rogachevskii2017) and atmospheric turbulence with temperature inversions (Sofiev et al. Reference Sofiev, Sofieva, Elperin, Kleeorin, Rogachevskii and Zilitinkevich2009). It was also shown to be important for concentrating dust in protoplanetary discs (Hubbard Reference Hubbard2015).
A suppression of turbulent magnetic diffusivity by the compressibility of a random homogeneous flow using the quasi-linear approach (the second-order correlation approximation) was demonstrated by Krause & Rädler (Reference Krause and Rädler1980). In particular, Krause & Rädler (Reference Krause and Rädler1980) derived an equation for the turbulent magnetic diffusivity,
![]() $\unicode[STIX]{x1D702}_{\text{t}}$
, for small magnetic Reynolds numbers:
$\unicode[STIX]{x1D702}_{\text{t}}$
, for small magnetic Reynolds numbers:
![]() $\unicode[STIX]{x1D702}_{\text{t}}=(\overline{\unicode[STIX]{x1D74D}^{2}}-\overline{\unicode[STIX]{x1D719}^{2}})/3\unicode[STIX]{x1D702}$
, where
$\unicode[STIX]{x1D702}_{\text{t}}=(\overline{\unicode[STIX]{x1D74D}^{2}}-\overline{\unicode[STIX]{x1D719}^{2}})/3\unicode[STIX]{x1D702}$
, where
![]() $\unicode[STIX]{x1D702}$
is the microscopic magnetic diffusivity and the velocity fluctuations are represented as the sum of vortical and potential parts,
$\unicode[STIX]{x1D702}$
is the microscopic magnetic diffusivity and the velocity fluctuations are represented as the sum of vortical and potential parts,
![]() $\boldsymbol{u}=\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D74D}+\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
. Later, Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011) determined mean-field diffusivities both for passive scalars and magnetic fields for an irrotational homogeneous deterministic flow, using the quasi-linear approach and the test-field method in direct numerical simulations. They showed that the expression for the turbulent diffusivity of a passive scalar coincides with that of
$\boldsymbol{u}=\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D74D}+\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
. Later, Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011) determined mean-field diffusivities both for passive scalars and magnetic fields for an irrotational homogeneous deterministic flow, using the quasi-linear approach and the test-field method in direct numerical simulations. They showed that the expression for the turbulent diffusivity of a passive scalar coincides with that of
![]() $\unicode[STIX]{x1D702}_{\text{t}}$
for small magnetic Reynolds and Péclet numbers after replacing
$\unicode[STIX]{x1D702}_{\text{t}}$
for small magnetic Reynolds and Péclet numbers after replacing
![]() $\unicode[STIX]{x1D702}$
by the molecular diffusion coefficient for the passive scalar. They also found that the total mean-field diffusivity in irrotational flows may well be smaller than the molecular diffusivity.
$\unicode[STIX]{x1D702}$
by the molecular diffusion coefficient for the passive scalar. They also found that the total mean-field diffusivity in irrotational flows may well be smaller than the molecular diffusivity.
In the present study, a mean-field theory of compressibility effects in turbulent magnetohydrodynamics (MHD) and passive scalar transport is developed for inhomogeneous density-stratified turbulent flows at arbitrary Mach number. We also consider helical turbulence with uniform kinetic helicity. We use the quasi-linear approach, which is valid for small magnetic Reynolds and Péclet numbers, and the spectral
![]() $\unicode[STIX]{x1D70F}$
approach, which is applicable to large magnetic Reynolds and Péclet numbers in fully developed turbulence. This allows us to determine the mean electromotive force and the turbulent flux of particles in compressible density-stratified inhomogeneous turbulence.
$\unicode[STIX]{x1D70F}$
approach, which is applicable to large magnetic Reynolds and Péclet numbers in fully developed turbulence. This allows us to determine the mean electromotive force and the turbulent flux of particles in compressible density-stratified inhomogeneous turbulence.
2 Turbulent transport of magnetic field
In this section we study turbulent transport of a magnetic field in compressible helical inhomogeneous turbulence for small and large magnetic Reynolds numbers.
2.1 Governing equations
The magnetic field
![]() $\boldsymbol{B}(\boldsymbol{x},t)$
is governed by the induction equation:
$\boldsymbol{B}(\boldsymbol{x},t)$
is governed by the induction equation:
where
![]() $\unicode[STIX]{x1D702}$
is the magnetic diffusivity due to the electrical conductivity of the fluid, and fluid velocity
$\unicode[STIX]{x1D702}$
is the magnetic diffusivity due to the electrical conductivity of the fluid, and fluid velocity
![]() $\boldsymbol{U}(\boldsymbol{x},t)$
is determined by the Navier–Stokes equation,
$\boldsymbol{U}(\boldsymbol{x},t)$
is determined by the Navier–Stokes equation,
where
![]() $P(\boldsymbol{x},t)$
is the fluid pressure,
$P(\boldsymbol{x},t)$
is the fluid pressure,
![]() $\unicode[STIX]{x1D61A}_{ij}^{(\text{U})}=1/2(U_{i,j}+U_{j,i})-1/3\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{U}$
are the components of the traceless rate-of-strain tensor
$\unicode[STIX]{x1D61A}_{ij}^{(\text{U})}=1/2(U_{i,j}+U_{j,i})-1/3\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{U}$
are the components of the traceless rate-of-strain tensor
![]() $\unicode[STIX]{x1D64E}^{(\text{U})}$
, commas denote partial differentiation and
$\unicode[STIX]{x1D64E}^{(\text{U})}$
, commas denote partial differentiation and
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity.
$\unicode[STIX]{x1D708}$
is the kinematic viscosity.
We apply a mean-field approach and use Reynolds averaging (Krause & Rädler Reference Krause and Rädler1980). In the framework of this approach, velocity and magnetic fields, fluid density and pressure are decomposed into mean (denoted by overbars) and fluctuating parts (lowercase symbols). Ensemble averaging of (2.1) yields an equation for the mean magnetic field
![]() $\overline{\boldsymbol{B}}(\boldsymbol{x},t)$
:
$\overline{\boldsymbol{B}}(\boldsymbol{x},t)$
:
where
![]() $\overline{\boldsymbol{U}}(\boldsymbol{x},t)$
is the mean velocity and
$\overline{\boldsymbol{U}}(\boldsymbol{x},t)$
is the mean velocity and
![]() $\overline{\boldsymbol{{\mathcal{E}}}}=\overline{\boldsymbol{u}\times \boldsymbol{b}}$
is the mean electromotive force. For simplicity, we consider in this study the case
$\overline{\boldsymbol{{\mathcal{E}}}}=\overline{\boldsymbol{u}\times \boldsymbol{b}}$
is the mean electromotive force. For simplicity, we consider in this study the case
![]() $\overline{\boldsymbol{U}}=\mathbf{0}$
. We determine
$\overline{\boldsymbol{U}}=\mathbf{0}$
. We determine
![]() $\overline{\boldsymbol{{\mathcal{E}}}}$
for compressible inhomogeneous and helical turbulence. The procedure of the derivation of the equation for the mean electromotive force is as follows. The momentum and induction equations for fluctuations are given by
$\overline{\boldsymbol{{\mathcal{E}}}}$
for compressible inhomogeneous and helical turbulence. The procedure of the derivation of the equation for the mean electromotive force is as follows. The momentum and induction equations for fluctuations are given by
where
![]() $\boldsymbol{u}(\boldsymbol{x},t)$
and
$\boldsymbol{u}(\boldsymbol{x},t)$
and
![]() $\boldsymbol{b}(\boldsymbol{x},t)$
are the fluctuations of velocity and magnetic fields,
$\boldsymbol{b}(\boldsymbol{x},t)$
are the fluctuations of velocity and magnetic fields,
![]() $\boldsymbol{u}^{(\text{N})}$
and
$\boldsymbol{u}^{(\text{N})}$
and
![]() $\boldsymbol{b}^{(\text{N})}$
are terms that are nonlinear in the fluctuations,
$\boldsymbol{b}^{(\text{N})}$
are terms that are nonlinear in the fluctuations,
![]() $p_{\text{tot}}=p+\unicode[STIX]{x1D707}_{0}^{-1}(\overline{\boldsymbol{B}}\boldsymbol{\cdot }\boldsymbol{b})$
are the fluctuations of the total pressure,
$p_{\text{tot}}=p+\unicode[STIX]{x1D707}_{0}^{-1}(\overline{\boldsymbol{B}}\boldsymbol{\cdot }\boldsymbol{b})$
are the fluctuations of the total pressure,
![]() $\unicode[STIX]{x1D64E}^{\text{(u)}}\equiv \unicode[STIX]{x1D61A}_{ij}^{\text{(u)}}=1/2(u_{i,j}+u_{j,i})-1/3\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$
, and
$\unicode[STIX]{x1D64E}^{\text{(u)}}\equiv \unicode[STIX]{x1D61A}_{ij}^{\text{(u)}}=1/2(u_{i,j}+u_{j,i})-1/3\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$
, and
![]() $p(\boldsymbol{x},t)$
is the fluctuation of the fluid pressure. We rewrite (2.4) and (2.5) in
$p(\boldsymbol{x},t)$
is the fluctuation of the fluid pressure. We rewrite (2.4) and (2.5) in
![]() $\boldsymbol{k}$
space. In the following, we derive equations for the mean electromotive force for small and large magnetic Reynolds numbers.
$\boldsymbol{k}$
space. In the following, we derive equations for the mean electromotive force for small and large magnetic Reynolds numbers.
2.2 Small magnetic Reynolds numbers
We use a quasi-linear approach (also known in the literature as ‘first-order smoothing’ or ‘second-order correlation approximation’), which is valid for small hydrodynamic and magnetic Reynolds numbers,
![]() $Re=\ell _{0}\sqrt{\overline{\boldsymbol{u}^{2}}}/\unicode[STIX]{x1D708}\ll 1$
and
$Re=\ell _{0}\sqrt{\overline{\boldsymbol{u}^{2}}}/\unicode[STIX]{x1D708}\ll 1$
and
![]() $Rm=\ell _{0}\sqrt{\overline{\boldsymbol{u}^{2}}}/\unicode[STIX]{x1D702}\ll 1$
, respectively. Here
$Rm=\ell _{0}\sqrt{\overline{\boldsymbol{u}^{2}}}/\unicode[STIX]{x1D702}\ll 1$
, respectively. Here
![]() $\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the characteristic turbulent velocity in the integral turbulent scale
$\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the characteristic turbulent velocity in the integral turbulent scale
![]() $\ell _{0}$
. In the high conductivity limit (very small microscopic magnetic diffusivity
$\ell _{0}$
. In the high conductivity limit (very small microscopic magnetic diffusivity
![]() $\unicode[STIX]{x1D702}$
), the quasi-linear approach is only valid for small Strouhal numbers, which is defined as the ratio of turbulent correlation time,
$\unicode[STIX]{x1D702}$
), the quasi-linear approach is only valid for small Strouhal numbers, which is defined as the ratio of turbulent correlation time,
![]() $\unicode[STIX]{x1D70F}_{0}$
, to turnover time,
$\unicode[STIX]{x1D70F}_{0}$
, to turnover time,
![]() $\ell _{0}/\sqrt{\overline{\boldsymbol{u}^{2}}}$
. This implies that the quasi-linear approach in this limit is only valid for very short turbulent correlation times. Often (see, e.g. Krause & Rädler Reference Krause and Rädler1980) the quasi-linear approach is applied only to the induction equation and the origin of the velocity field is not discussed. In this case the evolution of the magnetic field is considered for a prescribed velocity field, and formally the validity of the quasi-linear approach only requires small magnetic Reynolds numbers.
$\ell _{0}/\sqrt{\overline{\boldsymbol{u}^{2}}}$
. This implies that the quasi-linear approach in this limit is only valid for very short turbulent correlation times. Often (see, e.g. Krause & Rädler Reference Krause and Rädler1980) the quasi-linear approach is applied only to the induction equation and the origin of the velocity field is not discussed. In this case the evolution of the magnetic field is considered for a prescribed velocity field, and formally the validity of the quasi-linear approach only requires small magnetic Reynolds numbers.
2.2.1 Multi-scale approach
To determine the mean electromotive force, which is a one-point correlation function, and to take into account small-scale properties of the turbulence, e.g. the turbulent spectrum, one must use two-point correlation functions. For fully developed turbulence, scalings for the turbulent correlation time and energy spectrum are related via the Kolmogorov scalings (McComb Reference McComb1990; Frisch Reference Frisch1995; Monin & Yaglom Reference Monin and Yaglom2013). This is the reason why for calculations of the mean electromotive force in fully developed turbulence, we use instantaneous two-point correlation functions. On the other hand, for a random flow with small
![]() $Re$
and
$Re$
and
![]() $Rm$
, there are no universal scalings for the correlation time and energy spectrum. This is the reason why we have to use non-instantaneous two-point correlation functions in this case.
$Rm$
, there are no universal scalings for the correlation time and energy spectrum. This is the reason why we have to use non-instantaneous two-point correlation functions in this case.
In the framework of the mean-field approach, we assume that there is a separation of spatial and temporal scales, i.e.
![]() $\ell _{0}\ll L_{B}$
and
$\ell _{0}\ll L_{B}$
and
![]() $\unicode[STIX]{x1D70F}_{0}\ll t_{B}$
, where
$\unicode[STIX]{x1D70F}_{0}\ll t_{B}$
, where
![]() $L_{B}$
and
$L_{B}$
and
![]() $t_{B}$
are the characteristic spatial and temporal scales characterizing the variations of the mean magnetic field. The mean fields depend on ‘slow’ variables, while fluctuations depend on ‘fast’ variables. Separation into slow and fast variables is widely used in theoretical physics, and all calculations are reduced to Taylor expansions of all functions using small parameters
$t_{B}$
are the characteristic spatial and temporal scales characterizing the variations of the mean magnetic field. The mean fields depend on ‘slow’ variables, while fluctuations depend on ‘fast’ variables. Separation into slow and fast variables is widely used in theoretical physics, and all calculations are reduced to Taylor expansions of all functions using small parameters
![]() $\ell _{0}/L_{B}$
and
$\ell _{0}/L_{B}$
and
![]() $\unicode[STIX]{x1D70F}_{0}/t_{B}$
. The findings are further truncated to leading-order terms.
$\unicode[STIX]{x1D70F}_{0}/t_{B}$
. The findings are further truncated to leading-order terms.
Separation to slow and fast variables is performed by means of a standard multi-scale approach (Roberts & Soward Reference Roberts and Soward1975). In the framework of this approach, the non-instantaneous two-point second-order correlation function of
![]() $\boldsymbol{b}$
and
$\boldsymbol{b}$
and
![]() $\boldsymbol{u}$
is written as follows:
$\boldsymbol{u}$
is written as follows:
 $$\begin{eqnarray}\displaystyle \overline{b_{i}(\boldsymbol{x},t_{1})u_{j}(\boldsymbol{y},t_{2})} & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}_{1}\,\text{d}\unicode[STIX]{x1D714}_{2}\,\text{d}\boldsymbol{k}_{1}\,\text{d}\boldsymbol{k}_{2}\,\overline{b_{i}(\boldsymbol{k}_{1},\unicode[STIX]{x1D714}_{1})u_{j}(\boldsymbol{k}_{2},\unicode[STIX]{x1D714}_{2})}\exp [\text{i}(\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{x}+\boldsymbol{k}_{2}\boldsymbol{\cdot }\boldsymbol{y})\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}(\unicode[STIX]{x1D714}_{1}t_{1}+\unicode[STIX]{x1D714}_{2}t_{2})]=\int g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},t,\boldsymbol{R})\exp [\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}+\text{i}\unicode[STIX]{x1D714}\,\tilde{\unicode[STIX]{x1D70F}}]\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\boldsymbol{k},\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{b_{i}(\boldsymbol{x},t_{1})u_{j}(\boldsymbol{y},t_{2})} & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}_{1}\,\text{d}\unicode[STIX]{x1D714}_{2}\,\text{d}\boldsymbol{k}_{1}\,\text{d}\boldsymbol{k}_{2}\,\overline{b_{i}(\boldsymbol{k}_{1},\unicode[STIX]{x1D714}_{1})u_{j}(\boldsymbol{k}_{2},\unicode[STIX]{x1D714}_{2})}\exp [\text{i}(\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{x}+\boldsymbol{k}_{2}\boldsymbol{\cdot }\boldsymbol{y})\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}(\unicode[STIX]{x1D714}_{1}t_{1}+\unicode[STIX]{x1D714}_{2}t_{2})]=\int g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},t,\boldsymbol{R})\exp [\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}+\text{i}\unicode[STIX]{x1D714}\,\tilde{\unicode[STIX]{x1D70F}}]\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\boldsymbol{k},\qquad\end{eqnarray}$$
where
Here we introduced large-scale variables:
![]() $\boldsymbol{R}=(\boldsymbol{x}+\boldsymbol{y})/2$
,
$\boldsymbol{R}=(\boldsymbol{x}+\boldsymbol{y})/2$
,
![]() $\boldsymbol{K}=\boldsymbol{k}_{1}+\boldsymbol{k}_{2}$
,
$\boldsymbol{K}=\boldsymbol{k}_{1}+\boldsymbol{k}_{2}$
,
![]() $t=(t_{1}+t_{2})/2$
,
$t=(t_{1}+t_{2})/2$
,
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D714}_{2}$
, and small-scale variables:
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D714}_{2}$
, and small-scale variables:
![]() $\boldsymbol{r}=\boldsymbol{x}-\boldsymbol{y}$
,
$\boldsymbol{r}=\boldsymbol{x}-\boldsymbol{y}$
,
![]() $\boldsymbol{k}=(\boldsymbol{k}_{1}-\boldsymbol{k}_{2})/2$
,
$\boldsymbol{k}=(\boldsymbol{k}_{1}-\boldsymbol{k}_{2})/2$
,
![]() $\tilde{\unicode[STIX]{x1D70F}}=t_{1}-t_{2}$
,
$\tilde{\unicode[STIX]{x1D70F}}=t_{1}-t_{2}$
,
![]() $\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D714}_{1}-\unicode[STIX]{x1D714}_{2})/2$
. This implies that
$\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D714}_{1}-\unicode[STIX]{x1D714}_{2})/2$
. This implies that
![]() $\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FA}/2$
,
$\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FA}/2$
,
![]() $\unicode[STIX]{x1D714}_{2}=-\unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FA}/2$
,
$\unicode[STIX]{x1D714}_{2}=-\unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FA}/2$
,
![]() $\boldsymbol{k}_{1}=\boldsymbol{k}+\boldsymbol{K}/2$
and
$\boldsymbol{k}_{1}=\boldsymbol{k}+\boldsymbol{K}/2$
and
![]() $\boldsymbol{k}_{2}=-\boldsymbol{k}+\boldsymbol{K}/2$
. Mean fields depend on the large-scale variables, while fluctuations depend on the small-scale variables. We have used here the Fourier transformation:
$\boldsymbol{k}_{2}=-\boldsymbol{k}+\boldsymbol{K}/2$
. Mean fields depend on the large-scale variables, while fluctuations depend on the small-scale variables. We have used here the Fourier transformation:
Similarly to (2.6)–(2.7), we obtain
After separation into slow and fast variables and calculating the function
![]() $g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
, expression (2.6) allows us to determine the cross-helicity tensor in physical space and to calculate the limit of
$g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
, expression (2.6) allows us to determine the cross-helicity tensor in physical space and to calculate the limit of
![]() $\boldsymbol{r}\rightarrow \mathbf{0}$
and
$\boldsymbol{r}\rightarrow \mathbf{0}$
and
![]() $\tilde{\unicode[STIX]{x1D70F}}\rightarrow 0$
, which yields
$\tilde{\unicode[STIX]{x1D70F}}\rightarrow 0$
, which yields
For brevity of notations we omit below the large-scale variables
![]() $t$
and
$t$
and
![]() $\boldsymbol{R}$
in the correlation functions
$\boldsymbol{R}$
in the correlation functions
![]() $f_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
and
$f_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
and
![]() $g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
.
$g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
.
2.2.2 Cross-helicity tensor
In the framework of the quasi-linear approach, we neglect nonlinear terms, but keep molecular dissipative terms in (2.5) for the magnetic fluctuations. This allows us to obtain the solution of (2.5) in the limit of small magnetic Reynolds number. Using this solution, we derive the equation for the correlation function
![]() $g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714})$
:
$g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714})$
:
 $$\begin{eqnarray}\displaystyle g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714}) & = & \displaystyle G_{\unicode[STIX]{x1D702}}\left\{\overline{B}_{p}\left[\text{i}k_{p}f_{ij}+\frac{1}{2}\unicode[STIX]{x1D735}_{p}f_{ij}-\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}\unicode[STIX]{x1D735}_{s}f_{ij}\right]\right.\nonumber\\ \displaystyle & & \displaystyle -\,\overline{B}_{i}\left[\text{i}k_{p}f_{pj}+\frac{1}{2}\unicode[STIX]{x1D735}_{p}f_{pj}-\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}\unicode[STIX]{x1D735}_{s}f_{pj}\right]-(\unicode[STIX]{x1D735}_{s}\overline{B}_{p})\left[\frac{1}{2}k_{p}\frac{\unicode[STIX]{x2202}f_{ij}}{\unicode[STIX]{x2202}k_{s}}+\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}f_{ij}\right]\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}(\unicode[STIX]{x1D735}_{s}\overline{B}_{i})\left[-f_{sj}+k_{p}\frac{\unicode[STIX]{x2202}f_{pj}}{\unicode[STIX]{x2202}k_{s}}+2\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}f_{pj}\right]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714}) & = & \displaystyle G_{\unicode[STIX]{x1D702}}\left\{\overline{B}_{p}\left[\text{i}k_{p}f_{ij}+\frac{1}{2}\unicode[STIX]{x1D735}_{p}f_{ij}-\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}\unicode[STIX]{x1D735}_{s}f_{ij}\right]\right.\nonumber\\ \displaystyle & & \displaystyle -\,\overline{B}_{i}\left[\text{i}k_{p}f_{pj}+\frac{1}{2}\unicode[STIX]{x1D735}_{p}f_{pj}-\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}\unicode[STIX]{x1D735}_{s}f_{pj}\right]-(\unicode[STIX]{x1D735}_{s}\overline{B}_{p})\left[\frac{1}{2}k_{p}\frac{\unicode[STIX]{x2202}f_{ij}}{\unicode[STIX]{x2202}k_{s}}+\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}f_{ij}\right]\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}(\unicode[STIX]{x1D735}_{s}\overline{B}_{i})\left[-f_{sj}+k_{p}\frac{\unicode[STIX]{x2202}f_{pj}}{\unicode[STIX]{x2202}k_{s}}+2\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}f_{pj}\right]\right\},\end{eqnarray}$$
where
![]() $k_{ij}=k_{i}\,k_{j}/k^{2}$
and
$k_{ij}=k_{i}\,k_{j}/k^{2}$
and
![]() $G_{\unicode[STIX]{x1D702}}\equiv G_{\unicode[STIX]{x1D702}}(\boldsymbol{k},\unicode[STIX]{x1D714})=(\unicode[STIX]{x1D702}\boldsymbol{k}^{2}+\text{i}\unicode[STIX]{x1D714})^{-1}$
. The derivation of (2.11) is given in appendix A. Here, for brevity of notation, we omit the large-scale variables
$G_{\unicode[STIX]{x1D702}}\equiv G_{\unicode[STIX]{x1D702}}(\boldsymbol{k},\unicode[STIX]{x1D714})=(\unicode[STIX]{x1D702}\boldsymbol{k}^{2}+\text{i}\unicode[STIX]{x1D714})^{-1}$
. The derivation of (2.11) is given in appendix A. Here, for brevity of notation, we omit the large-scale variables
![]() $\boldsymbol{R}$
and
$\boldsymbol{R}$
and
![]() $t$
in the mean magnetic field
$t$
in the mean magnetic field
![]() $\overline{B}_{p}$
and correlation functions
$\overline{B}_{p}$
and correlation functions
![]() $g_{ij}$
and
$g_{ij}$
and
![]() $f_{ij}$
. When
$f_{ij}$
. When
![]() $\overline{\boldsymbol{B}}^{2}/4\unicode[STIX]{x03C0}\ll \overline{\unicode[STIX]{x1D70C}}\overline{\boldsymbol{u}^{2}}$
, the correlation function
$\overline{\boldsymbol{B}}^{2}/4\unicode[STIX]{x03C0}\ll \overline{\unicode[STIX]{x1D70C}}\overline{\boldsymbol{u}^{2}}$
, the correlation function
![]() $f_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714})$
in (2.11) should be replaced by the correlation function
$f_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714})$
in (2.11) should be replaced by the correlation function
![]() $f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714})$
given below by (2.12) for the random flow with a zero mean magnetic field, called background flow.
$f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714})$
given below by (2.12) for the random flow with a zero mean magnetic field, called background flow.
2.2.3 A model for the background random flow for
 $Re\ll 1$
$Re\ll 1$
In the next step of the derivation, we need a model for the background random flow with a zero mean magnetic field. We consider a random, statistically stationary, density-stratified, inhomogeneous, compressible and helical background flow, which is determined by the following correlation function in Fourier space:
 $$\begin{eqnarray}\displaystyle f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R}) & = & \displaystyle \frac{\unicode[STIX]{x1D6F7}_{u}(\unicode[STIX]{x1D714})E(k)}{8\unicode[STIX]{x03C0}\,k^{2}(1+\unicode[STIX]{x1D70E}_{c})}\left\{\left[\unicode[STIX]{x1D6FF}_{ij}-k_{ij}+\frac{\text{i}}{k^{2}}(k_{j}\unicode[STIX]{x1D706}_{i}-k_{i}\unicode[STIX]{x1D706}_{j})+2\unicode[STIX]{x1D70E}_{c}\,k_{ij}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.(1+2\unicode[STIX]{x1D70E}_{c})\frac{\text{i}}{2k^{2}}(k_{i}\unicode[STIX]{x1D735}_{j}-k_{j}\unicode[STIX]{x1D735}_{i})\right]\overline{\boldsymbol{u}^{2}}-\frac{\text{i}}{k^{2}}\,\unicode[STIX]{x1D700}_{ijp}\,k_{p}\unicode[STIX]{x1D712}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R}) & = & \displaystyle \frac{\unicode[STIX]{x1D6F7}_{u}(\unicode[STIX]{x1D714})E(k)}{8\unicode[STIX]{x03C0}\,k^{2}(1+\unicode[STIX]{x1D70E}_{c})}\left\{\left[\unicode[STIX]{x1D6FF}_{ij}-k_{ij}+\frac{\text{i}}{k^{2}}(k_{j}\unicode[STIX]{x1D706}_{i}-k_{i}\unicode[STIX]{x1D706}_{j})+2\unicode[STIX]{x1D70E}_{c}\,k_{ij}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.(1+2\unicode[STIX]{x1D70E}_{c})\frac{\text{i}}{2k^{2}}(k_{i}\unicode[STIX]{x1D735}_{j}-k_{j}\unicode[STIX]{x1D735}_{i})\right]\overline{\boldsymbol{u}^{2}}-\frac{\text{i}}{k^{2}}\,\unicode[STIX]{x1D700}_{ijp}\,k_{p}\unicode[STIX]{x1D712}\right\}.\end{eqnarray}$$
Here
![]() $\unicode[STIX]{x1D740}=-\unicode[STIX]{x1D735}\ln \overline{\unicode[STIX]{x1D70C}}$
characterizes the fluid density stratification,
$\unicode[STIX]{x1D740}=-\unicode[STIX]{x1D735}\ln \overline{\unicode[STIX]{x1D70C}}$
characterizes the fluid density stratification,
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker tensor,
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker tensor,
![]() $\unicode[STIX]{x1D700}_{ijn}$
is the fully antisymmetric Levi-Civita tensor,
$\unicode[STIX]{x1D700}_{ijn}$
is the fully antisymmetric Levi-Civita tensor,
![]() $\unicode[STIX]{x1D712}=\overline{\boldsymbol{u}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{u})}$
is the kinetic helicity and the parameter
$\unicode[STIX]{x1D712}=\overline{\boldsymbol{u}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{u})}$
is the kinetic helicity and the parameter
is the degree of compressibility of the turbulent velocity field. In (2.12), we neglect higher-order effects
![]() ${\sim}O(\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D6FB}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{i}\overline{\boldsymbol{u}^{2}})$
, i.e. we assume that
${\sim}O(\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D6FB}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{i}\overline{\boldsymbol{u}^{2}})$
, i.e. we assume that
![]() $\ell _{0}\ll H$
and
$\ell _{0}\ll H$
and
![]() $\ell _{0}\ll L_{B}$
, where
$\ell _{0}\ll L_{B}$
, where
![]() $\ell _{0}$
is the maximum scale of random motions,
$\ell _{0}$
is the maximum scale of random motions,
![]() $H=|\unicode[STIX]{x1D740}|^{-1}$
is the mean density variation scale, which is assumed to be constant. This means that in (2.12) we only take into account leading effects, which are linear in stratification (
$H=|\unicode[STIX]{x1D740}|^{-1}$
is the mean density variation scale, which is assumed to be constant. This means that in (2.12) we only take into account leading effects, which are linear in stratification (
![]() $\propto \ell _{0}/H$
) and inhomogeneity of turbulence (
$\propto \ell _{0}/H$
) and inhomogeneity of turbulence (
![]() $\propto \ell _{0}/L_{B}$
). Generally, stratification also contributes to div
$\propto \ell _{0}/L_{B}$
). Generally, stratification also contributes to div
![]() $\boldsymbol{u}$
, and therefore it contributes to the parameter
$\boldsymbol{u}$
, and therefore it contributes to the parameter
![]() $\unicode[STIX]{x1D70E}_{c}$
. However, this contribution is small [
$\unicode[STIX]{x1D70E}_{c}$
. However, this contribution is small [
![]() ${\sim}O(\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}})$
], and neglected in (2.12). This implies that we separate effects of the arbitrary Mach number, characterized by the parameter
${\sim}O(\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}})$
], and neglected in (2.12). This implies that we separate effects of the arbitrary Mach number, characterized by the parameter
![]() $\unicode[STIX]{x1D70E}_{c}$
, and density stratification, described by
$\unicode[STIX]{x1D70E}_{c}$
, and density stratification, described by
![]() $\unicode[STIX]{x1D740}$
. Note that the degree of compressibility,
$\unicode[STIX]{x1D740}$
. Note that the degree of compressibility,
![]() $\unicode[STIX]{x1D70E}_{c}$
, depends on the Mach number, but this dependence is not known for arbitrary Mach numbers and has to be determined in direct numerical simulations.
$\unicode[STIX]{x1D70E}_{c}$
, depends on the Mach number, but this dependence is not known for arbitrary Mach numbers and has to be determined in direct numerical simulations.
We also do not consider here effects related to the non-uniformity of kinetic helicity (
![]() $\propto \unicode[STIX]{x1D735}\unicode[STIX]{x1D712}$
) or the combined effect of stratification and kinetic helicity (
$\propto \unicode[STIX]{x1D735}\unicode[STIX]{x1D712}$
) or the combined effect of stratification and kinetic helicity (
![]() $\propto \unicode[STIX]{x1D740}\unicode[STIX]{x1D712}$
), because their contributions to the mean electromotive force are much smaller in comparison with the standard contributions to the mean electromotive force caused by the turbulent motions (they are of the order of the terms we neglected in the present study). The non-uniformity of kinetic helicity (Yokoi & Yoshizawa Reference Yokoi and Yoshizawa1993; Yokoi & Brandenburg Reference Yokoi and Brandenburg2016; Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2018) or the combined effect of stratification and kinetic helicity (Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2018) contribute to the generation of large-scale vorticity or large-scale shear motions.
$\propto \unicode[STIX]{x1D740}\unicode[STIX]{x1D712}$
), because their contributions to the mean electromotive force are much smaller in comparison with the standard contributions to the mean electromotive force caused by the turbulent motions (they are of the order of the terms we neglected in the present study). The non-uniformity of kinetic helicity (Yokoi & Yoshizawa Reference Yokoi and Yoshizawa1993; Yokoi & Brandenburg Reference Yokoi and Brandenburg2016; Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2018) or the combined effect of stratification and kinetic helicity (Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2018) contribute to the generation of large-scale vorticity or large-scale shear motions.
In (2.12), we assume that helical and non-helical parts of random flow have the same power-law spectrum
![]() $E(k)=k_{0}^{-1}(q-1)(k/k_{0})^{-q}$
for the wavenumber range
$E(k)=k_{0}^{-1}(q-1)(k/k_{0})^{-q}$
for the wavenumber range
![]() $k_{0}<k<k_{\unicode[STIX]{x1D708}}$
, where
$k_{0}<k<k_{\unicode[STIX]{x1D708}}$
, where
![]() $k_{\unicode[STIX]{x1D708}}=1/\ell _{\unicode[STIX]{x1D708}}$
is the wavenumber based on the viscous scale
$k_{\unicode[STIX]{x1D708}}=1/\ell _{\unicode[STIX]{x1D708}}$
is the wavenumber based on the viscous scale
![]() $\ell _{\unicode[STIX]{x1D708}}$
, and
$\ell _{\unicode[STIX]{x1D708}}$
, and
![]() $k_{0}=1/\ell _{0}\ll k_{\unicode[STIX]{x1D708}}$
. We assume that there are no random motions for
$k_{0}=1/\ell _{0}\ll k_{\unicode[STIX]{x1D708}}$
. We assume that there are no random motions for
![]() $k<k_{0}$
. This implies that
$k<k_{0}$
. This implies that
![]() $\ell _{0}$
is the maximum scale of random motions, and
$\ell _{0}$
is the maximum scale of random motions, and
![]() $E(k)=0$
for
$E(k)=0$
for
![]() $k<k_{0}$
. For simplicity we also assume that compressible and incompressible parts of the random flow have the same spectra. We consider the frequency function
$k<k_{0}$
. For simplicity we also assume that compressible and incompressible parts of the random flow have the same spectra. We consider the frequency function
![]() $\unicode[STIX]{x1D6F7}_{u}(\unicode[STIX]{x1D714})$
in the form of a Lorentz profile:
$\unicode[STIX]{x1D6F7}_{u}(\unicode[STIX]{x1D714})$
in the form of a Lorentz profile:
![]() $\unicode[STIX]{x1D6F7}_{u}(\unicode[STIX]{x1D714})=[\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{0}(\unicode[STIX]{x1D714}^{2}+\unicode[STIX]{x1D70F}_{0}^{-2})]^{-1}$
, where
$\unicode[STIX]{x1D6F7}_{u}(\unicode[STIX]{x1D714})=[\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{0}(\unicode[STIX]{x1D714}^{2}+\unicode[STIX]{x1D70F}_{0}^{-2})]^{-1}$
, where
![]() $\unicode[STIX]{x1D70F}_{0}=\ell _{0}/\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the correlation time and
$\unicode[STIX]{x1D70F}_{0}=\ell _{0}/\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the correlation time and
![]() $\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the characteristic turbulent velocity at scale
$\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the characteristic turbulent velocity at scale
![]() $\ell _{0}$
. This model for the frequency function corresponds to the correlation function
$\ell _{0}$
. This model for the frequency function corresponds to the correlation function
We take into account that for small magnetic Reynolds numbers,
![]() $\unicode[STIX]{x1D70F}_{0}\gg (\unicode[STIX]{x1D702}k^{2})^{-1}$
for all turbulent scales.
$\unicode[STIX]{x1D70F}_{0}\gg (\unicode[STIX]{x1D702}k^{2})^{-1}$
for all turbulent scales.
In spite of the large-scale effects caused by stratification
![]() $\unicode[STIX]{x1D740}$
and inhomogeneous turbulence
$\unicode[STIX]{x1D740}$
and inhomogeneous turbulence
![]() $\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, the model (2.12) describes a weakly anisotropic approximation. Indeed, the contributions of these effects to
$\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, the model (2.12) describes a weakly anisotropic approximation. Indeed, the contributions of these effects to
![]() $f_{ij}^{(0)}$
are small because
$f_{ij}^{(0)}$
are small because
![]() $\ell _{0}\ll H$
and
$\ell _{0}\ll H$
and
![]() $\ell _{0}\ll L_{B}$
. Since we consider only linear effects in
$\ell _{0}\ll L_{B}$
. Since we consider only linear effects in
![]() $\unicode[STIX]{x1D740}$
and
$\unicode[STIX]{x1D740}$
and
![]() $\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, the second rank tensor
$\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, the second rank tensor
![]() $f_{ij}^{(0)}$
is constructed as a linear combination of symmetric tensors with respect to the indexes
$f_{ij}^{(0)}$
is constructed as a linear combination of symmetric tensors with respect to the indexes
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
![]() $\unicode[STIX]{x1D6FF}_{ij}$
,
$\unicode[STIX]{x1D6FF}_{ij}$
,
![]() $k_{ij}$
, non-symmetric tensors:
$k_{ij}$
, non-symmetric tensors:
![]() $k_{i}\unicode[STIX]{x1D706}_{j}$
,
$k_{i}\unicode[STIX]{x1D706}_{j}$
,
![]() $k_{j}\unicode[STIX]{x1D706}_{i}$
,
$k_{j}\unicode[STIX]{x1D706}_{i}$
,
![]() $k_{i}\unicode[STIX]{x1D735}_{j}\overline{\boldsymbol{u}^{2}}$
,
$k_{i}\unicode[STIX]{x1D735}_{j}\overline{\boldsymbol{u}^{2}}$
,
![]() $k_{j}\unicode[STIX]{x1D735}_{i}\overline{\boldsymbol{u}^{2}}$
and fully antisymmetric tensor
$k_{j}\unicode[STIX]{x1D735}_{i}\overline{\boldsymbol{u}^{2}}$
and fully antisymmetric tensor
![]() $\unicode[STIX]{x1D700}_{ijp}\,k_{p}$
. To determine unknown coefficients multiplying by these tensors, we use the following conditions in the derivation of (2.12):
$\unicode[STIX]{x1D700}_{ijp}\,k_{p}$
. To determine unknown coefficients multiplying by these tensors, we use the following conditions in the derivation of (2.12):
(i)
 $\int f_{ii}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\boldsymbol{K}=\overline{\boldsymbol{u}^{2}}$
;
$\int f_{ii}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\boldsymbol{K}=\overline{\boldsymbol{u}^{2}}$
;(ii)
 $i\unicode[STIX]{x1D700}_{ipj}\int (-k_{p}+K_{p}/2)f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\boldsymbol{K}=\unicode[STIX]{x1D712}$
;
$i\unicode[STIX]{x1D700}_{ipj}\int (-k_{p}+K_{p}/2)f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\boldsymbol{K}=\unicode[STIX]{x1D712}$
;(iii)
 $f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})=f_{ji}^{\ast (0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})=f_{ji}^{(0)}(-\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})$
.
$f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})=f_{ji}^{\ast (0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})=f_{ji}^{(0)}(-\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})$
.(iv)
 $\int (k_{i}+K_{i}/2)(k_{j}-K_{j}/2)f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\boldsymbol{K}=\overline{(\text{div}\,\boldsymbol{u})^{2}}$
;
$\int (k_{i}+K_{i}/2)(k_{j}-K_{j}/2)f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\boldsymbol{K}=\overline{(\text{div}\,\boldsymbol{u})^{2}}$
;(v) for very low Mach number and when the parameter
 $\unicode[STIX]{x1D70E}_{c}$
is very small, the continuity equation can be written in the anelastic approximation,
$\unicode[STIX]{x1D70E}_{c}$
is very small, the continuity equation can be written in the anelastic approximation,
 $\text{div}(\overline{\unicode[STIX]{x1D70C}}\,\boldsymbol{u})=0$
, which implies that
$\text{div}(\overline{\unicode[STIX]{x1D70C}}\,\boldsymbol{u})=0$
, which implies that
 $(\text{i}k_{i}+\text{i}K_{i}/2-\unicode[STIX]{x1D706}_{i})f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})=0$
and
$(\text{i}k_{i}+\text{i}K_{i}/2-\unicode[STIX]{x1D706}_{i})f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})=0$
and
 $(-\text{i}k_{j}+\text{i}K_{j}/2-\unicode[STIX]{x1D706}_{j})f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})=0$
.
$(-\text{i}k_{j}+\text{i}K_{j}/2-\unicode[STIX]{x1D706}_{j})f_{ij}^{(0)}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{K})=0$
.
Different contributions to (2.12) have been discussed by Batchelor (Reference Batchelor1953), Elperin, Kleeorin & Rogachevskii (Reference Elperin, Kleeorin and Rogachevskii1995), Rädler, Kleeorin & Rogachevskii (Reference Rädler, Kleeorin and Rogachevskii2003), Rogachevskii & Kleeorin (Reference Rogachevskii and Kleeorin2018) and Kleeorin & Rogachevskii (Reference Kleeorin and Rogachevskii2018). Note that for a purely potential flow, equation (2.12) for the background turbulence is used in the limit
![]() $\unicode[STIX]{x1D70E}_{c}\rightarrow \infty$
, which yields
$\unicode[STIX]{x1D70E}_{c}\rightarrow \infty$
, which yields
2.2.4 Mean electromotive force for
 $Rm\ll 1$
$Rm\ll 1$
The mean electromotive force is given by
Integrating in
![]() $\unicode[STIX]{x1D714}$
space and
$\unicode[STIX]{x1D714}$
space and
![]() $\boldsymbol{k}$
space in (2.16) and neglecting higher-order effects
$\boldsymbol{k}$
space in (2.16) and neglecting higher-order effects
![]() ${\sim}O(\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D6FB}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{i}\overline{\boldsymbol{u}^{2}})$
, we arrive at an equation for the mean electromotive force,
${\sim}O(\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D6FB}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{i}\overline{\boldsymbol{u}^{2}})$
, we arrive at an equation for the mean electromotive force,
![]() $\overline{\boldsymbol{{\mathcal{E}}}}=\overline{\boldsymbol{u}\times \boldsymbol{b}}$
, for compressible, density-stratified, inhomogeneous and helical background turbulence:
$\overline{\boldsymbol{{\mathcal{E}}}}=\overline{\boldsymbol{u}\times \boldsymbol{b}}$
, for compressible, density-stratified, inhomogeneous and helical background turbulence:
where the
![]() $\unicode[STIX]{x1D6FC}$
effect, the turbulent magnetic diffusivity
$\unicode[STIX]{x1D6FC}$
effect, the turbulent magnetic diffusivity
![]() $\unicode[STIX]{x1D702}_{\text{t}}$
, and the pumping velocity
$\unicode[STIX]{x1D702}_{\text{t}}$
, and the pumping velocity
![]() $\unicode[STIX]{x1D738}$
for
$\unicode[STIX]{x1D738}$
for
![]() $Rm\ll 1$
are given by
$Rm\ll 1$
are given by
and
![]() $\unicode[STIX]{x1D70F}_{0}=\ell _{0}/\sqrt{\overline{\boldsymbol{u}^{2}}}$
. Let us analyse the obtained results. Since
$\unicode[STIX]{x1D70F}_{0}=\ell _{0}/\sqrt{\overline{\boldsymbol{u}^{2}}}$
. Let us analyse the obtained results. Since
![]() $\unicode[STIX]{x1D70F}_{0}\,Rm=\ell _{0}^{2}/\unicode[STIX]{x1D702}$
, the turbulent transport coefficients given by (2.18)–(2.20) are determined only by the resistive time scale,
$\unicode[STIX]{x1D70F}_{0}\,Rm=\ell _{0}^{2}/\unicode[STIX]{x1D702}$
, the turbulent transport coefficients given by (2.18)–(2.20) are determined only by the resistive time scale,
![]() $\ell _{0}^{2}/\unicode[STIX]{x1D702}$
. The effective pumping velocity
$\ell _{0}^{2}/\unicode[STIX]{x1D702}$
. The effective pumping velocity
![]() $\unicode[STIX]{x1D738}$
of the large-scale magnetic field is independent of
$\unicode[STIX]{x1D738}$
of the large-scale magnetic field is independent of
![]() $\unicode[STIX]{x1D740}$
(see detailed derivation of (2.20) and discussion in appendix B). We also have shown that there are no contributions of
$\unicode[STIX]{x1D740}$
(see detailed derivation of (2.20) and discussion in appendix B). We also have shown that there are no contributions of
![]() $\unicode[STIX]{x1D740}$
to the effective pumping velocity even for strong stratifications (see appendix B).
$\unicode[STIX]{x1D740}$
to the effective pumping velocity even for strong stratifications (see appendix B).
Equations (2.18)–(2.20) imply that for small magnetic Reynolds numbers, compressibility effects characterized by the parameter
![]() $\unicode[STIX]{x1D70E}_{c}$
decrease the
$\unicode[STIX]{x1D70E}_{c}$
decrease the
![]() $\unicode[STIX]{x1D6FC}$
effect, turbulent magnetic diffusion, and the effective pumping velocity. However, the total magnetic diffusivity,
$\unicode[STIX]{x1D6FC}$
effect, turbulent magnetic diffusion, and the effective pumping velocity. However, the total magnetic diffusivity,
![]() $\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}_{\text{t}}$
, cannot be negative, because for
$\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}_{\text{t}}$
, cannot be negative, because for
![]() $Rm\ll 1$
the magnetic diffusivity,
$Rm\ll 1$
the magnetic diffusivity,
![]() $\unicode[STIX]{x1D702}$
, is much larger than the turbulent value, i.e.
$\unicode[STIX]{x1D702}$
, is much larger than the turbulent value, i.e.
![]() $\unicode[STIX]{x1D702}\gg |\unicode[STIX]{x1D702}_{\text{t}}|$
. The decrease of turbulent magnetic diffusivity by compressible flows is consistent with the results obtained by Krause & Rädler (Reference Krause and Rädler1980) and Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011) for homogeneous random flow at small magnetic Reynolds numbers. Detailed comparison with these results is discussed in § 4.
$\unicode[STIX]{x1D702}\gg |\unicode[STIX]{x1D702}_{\text{t}}|$
. The decrease of turbulent magnetic diffusivity by compressible flows is consistent with the results obtained by Krause & Rädler (Reference Krause and Rädler1980) and Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011) for homogeneous random flow at small magnetic Reynolds numbers. Detailed comparison with these results is discussed in § 4.
As follows from (2.17)–(2.19), the resulting mean electromotive force
![]() $\overline{{\mathcal{E}}}_{i}$
is determined by the isotropic
$\overline{{\mathcal{E}}}_{i}$
is determined by the isotropic
![]() $\unicode[STIX]{x1D6FC}$
effect and turbulent diffusivity. The reason for that is as follows. (i) We consider the case of weak mean magnetic field, i.e. the energy of the mean magnetic field is much smaller than the turbulent kinetic energy. For large mean magnetic field, when the energy of the mean magnetic field is of the order of the turbulent kinetic energy, the
$\unicode[STIX]{x1D6FC}$
effect and turbulent diffusivity. The reason for that is as follows. (i) We consider the case of weak mean magnetic field, i.e. the energy of the mean magnetic field is much smaller than the turbulent kinetic energy. For large mean magnetic field, when the energy of the mean magnetic field is of the order of the turbulent kinetic energy, the
![]() $\unicode[STIX]{x1D6FC}$
tensor and turbulent diffusivity are anisotropic (Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2000, Reference Rogachevskii and Kleeorin2001). (ii) We do not consider the effects of uniform rotation or large-scale shear. In the case of rotating turbulence (Rädler et al.
Reference Rädler, Kleeorin and Rogachevskii2003; Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2003) or turbulence with large-scale shear (Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2003, Reference Rogachevskii and Kleeorin2004), the
$\unicode[STIX]{x1D6FC}$
tensor and turbulent diffusivity are anisotropic (Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2000, Reference Rogachevskii and Kleeorin2001). (ii) We do not consider the effects of uniform rotation or large-scale shear. In the case of rotating turbulence (Rädler et al.
Reference Rädler, Kleeorin and Rogachevskii2003; Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2003) or turbulence with large-scale shear (Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2003, Reference Rogachevskii and Kleeorin2004), the
![]() $\unicode[STIX]{x1D6FC}$
tensor and turbulent diffusivity are anisotropic. (iii) For anisotropic background turbulence, e.g. for turbulent convection (Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2003), or for magnetically driven turbulence with relativistic particles (Rogachevskii et al.
Reference Rogachevskii, Kleeorin, Brandenburg and Eichler2012, Reference Rogachevskii, Ruchayskiy, Boyarsky, Fröhlich, Kleeorin, Brandenburg and Schober2017), the
$\unicode[STIX]{x1D6FC}$
tensor and turbulent diffusivity are anisotropic. (iii) For anisotropic background turbulence, e.g. for turbulent convection (Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2003), or for magnetically driven turbulence with relativistic particles (Rogachevskii et al.
Reference Rogachevskii, Kleeorin, Brandenburg and Eichler2012, Reference Rogachevskii, Ruchayskiy, Boyarsky, Fröhlich, Kleeorin, Brandenburg and Schober2017), the
![]() $\unicode[STIX]{x1D6FC}$
tensor and turbulent diffusivity are also anisotropic. (iv) The model (2.12) of background random flow is weakly anisotropic, because
$\unicode[STIX]{x1D6FC}$
tensor and turbulent diffusivity are also anisotropic. (iv) The model (2.12) of background random flow is weakly anisotropic, because
![]() $\ell _{0}\ll H$
and
$\ell _{0}\ll H$
and
![]() $\ell _{0}\ll L_{B}$
.
$\ell _{0}\ll L_{B}$
.
2.3 Large fluid and magnetic Reynolds numbers
In this section we consider the case of large fluid and magnetic Reynolds numbers, so that turbulence is fully developed, the Strouhal number is of the order of unity, and the turbulent correlation time is scale dependent, as in Kolmogorov type turbulence (see, e.g. McComb Reference McComb1990; Frisch Reference Frisch1995; Monin & Yaglom Reference Monin and Yaglom2013). In this case, we perform the Fourier transformation only in
![]() $\boldsymbol{k}$
space (but not in
$\boldsymbol{k}$
space (but not in
![]() $\unicode[STIX]{x1D714}$
space), as is usually done in studies of turbulent transport in a fully developed Kolmogorov-type turbulence. We take into account the nonlinear terms in (2.4) and (2.5) for velocity and magnetic fluctuations and apply the
$\unicode[STIX]{x1D714}$
space), as is usually done in studies of turbulent transport in a fully developed Kolmogorov-type turbulence. We take into account the nonlinear terms in (2.4) and (2.5) for velocity and magnetic fluctuations and apply the
![]() $\unicode[STIX]{x1D70F}$
approach.
$\unicode[STIX]{x1D70F}$
approach.
The
![]() $\unicode[STIX]{x1D70F}$
approach is a universal tool in turbulent transport for strongly nonlinear systems that allow us to obtain closed results and compare them with the results of laboratory experiments, observations and numerical simulations (see, e.g. Orszag Reference Orszag1970; Pouquet, Frisch & Léorat Reference Pouquet, Frisch and Léorat1976; Kleeorin, Rogachevskii & Ruzmaikin Reference Kleeorin, Rogachevskii and Ruzmaikin1990; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2004; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2007; Rogachevskii et al.
Reference Rogachevskii, Kleeorin, Käpylä and Brandenburg2011). The
$\unicode[STIX]{x1D70F}$
approach is a universal tool in turbulent transport for strongly nonlinear systems that allow us to obtain closed results and compare them with the results of laboratory experiments, observations and numerical simulations (see, e.g. Orszag Reference Orszag1970; Pouquet, Frisch & Léorat Reference Pouquet, Frisch and Léorat1976; Kleeorin, Rogachevskii & Ruzmaikin Reference Kleeorin, Rogachevskii and Ruzmaikin1990; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2004; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2007; Rogachevskii et al.
Reference Rogachevskii, Kleeorin, Käpylä and Brandenburg2011). The
![]() $\unicode[STIX]{x1D70F}$
approximation reproduces many well-known phenomena found by other methods in turbulent transport of particles (see, e.g. Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1996, Reference Elperin, Kleeorin and Rogachevskii1997; Pandya & Mashayek Reference Pandya and Mashayek2002; Blackman & Field Reference Blackman and Field2003; Reeks Reference Reeks2005; Sofiev et al.
Reference Sofiev, Sofieva, Elperin, Kleeorin, Rogachevskii and Zilitinkevich2009) and magnetic fields, in turbulent convection (see, e.g. Elperin et al.
Reference Elperin, Kleeorin, Rogachevskii and Zilitinkevich2002, Reference Elperin, Kleeorin, Rogachevskii and Zilitinkevich2006) and stably stratified turbulent flows (see, e.g. Elperin et al.
Reference Elperin, Kleeorin, Rogachevskii and Zilitinkevich2002; Zilitinkevich et al.
Reference Zilitinkevich, Elperin, Kleeorin, Lvov and Rogachevskii2009, Reference Zilitinkevich, Elperin, Kleeorin, Rogachevskii and Esau2013) for large fluid and magnetic Reynolds and Péclet numbers. This approach is different from the quasi-linear approach applied in the high-conductivity limit. The latter approach is only valid for small Strouhal numbers, i.e. for very short correlation time. Therefore, the final results found with this approach are different from those obtained using the
$\unicode[STIX]{x1D70F}$
approximation reproduces many well-known phenomena found by other methods in turbulent transport of particles (see, e.g. Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1996, Reference Elperin, Kleeorin and Rogachevskii1997; Pandya & Mashayek Reference Pandya and Mashayek2002; Blackman & Field Reference Blackman and Field2003; Reeks Reference Reeks2005; Sofiev et al.
Reference Sofiev, Sofieva, Elperin, Kleeorin, Rogachevskii and Zilitinkevich2009) and magnetic fields, in turbulent convection (see, e.g. Elperin et al.
Reference Elperin, Kleeorin, Rogachevskii and Zilitinkevich2002, Reference Elperin, Kleeorin, Rogachevskii and Zilitinkevich2006) and stably stratified turbulent flows (see, e.g. Elperin et al.
Reference Elperin, Kleeorin, Rogachevskii and Zilitinkevich2002; Zilitinkevich et al.
Reference Zilitinkevich, Elperin, Kleeorin, Lvov and Rogachevskii2009, Reference Zilitinkevich, Elperin, Kleeorin, Rogachevskii and Esau2013) for large fluid and magnetic Reynolds and Péclet numbers. This approach is different from the quasi-linear approach applied in the high-conductivity limit. The latter approach is only valid for small Strouhal numbers, i.e. for very short correlation time. Therefore, the final results found with this approach are different from those obtained using the
![]() $\unicode[STIX]{x1D70F}$
approach.
$\unicode[STIX]{x1D70F}$
approach.
Using (2.5) for the magnetic fluctuations
![]() $\boldsymbol{b}$
and the Navier–Stokes equation (2.4) for the velocity fluctuations
$\boldsymbol{b}$
and the Navier–Stokes equation (2.4) for the velocity fluctuations
![]() $\boldsymbol{u}$
in Fourier space, we derive an evolution equation for the cross-helicity tensor,
$\boldsymbol{u}$
in Fourier space, we derive an evolution equation for the cross-helicity tensor,
which depends on the velocity correlation function:
The evolution equation for the cross-helicity tensor reads:
where, for brevity of notation, we omit the large-scale variables
![]() $t$
and
$t$
and
![]() $\boldsymbol{R}$
in the functions
$\boldsymbol{R}$
in the functions
![]() $f_{ij}(\boldsymbol{k},\boldsymbol{R},t)$
,
$f_{ij}(\boldsymbol{k},\boldsymbol{R},t)$
,
![]() $g_{ij}(\boldsymbol{k},\boldsymbol{R},t)$
,
$g_{ij}(\boldsymbol{k},\boldsymbol{R},t)$
,
![]() $g_{ij}^{(\text{N})}(\boldsymbol{k},\boldsymbol{R},t)$
and
$g_{ij}^{(\text{N})}(\boldsymbol{k},\boldsymbol{R},t)$
and
![]() $\overline{\boldsymbol{B}}(\boldsymbol{R},t)$
. Here the term
$\overline{\boldsymbol{B}}(\boldsymbol{R},t)$
. Here the term
![]() $g_{ij}^{(\text{N})}$
$g_{ij}^{(\text{N})}$
is determined by the third-order moments appearing due to the nonlinear terms. Note that since the Navier–Stokes equation is nonlinear, it appears only in the third-order moments
![]() $g_{ij}^{(\text{N})}$
. Here we took into account that the fluid pressure is nonlinear in the fluctuations. For large magnetic and fluid Reynolds numbers, the dissipative terms caused by the kinematic viscosity
$g_{ij}^{(\text{N})}$
. Here we took into account that the fluid pressure is nonlinear in the fluctuations. For large magnetic and fluid Reynolds numbers, the dissipative terms caused by the kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
and magnetic diffusivity
$\unicode[STIX]{x1D708}$
and magnetic diffusivity
![]() $\unicode[STIX]{x1D702}$
in (2.23) are negligibly small in comparison with the nonlinear terms. The term,
$\unicode[STIX]{x1D702}$
in (2.23) are negligibly small in comparison with the nonlinear terms. The term,
![]() $I_{ij}$
, which contains the large-scale spatial derivatives of both, the mean magnetic field and the turbulent intensity, is given by
$I_{ij}$
, which contains the large-scale spatial derivatives of both, the mean magnetic field and the turbulent intensity, is given by
This term determines the turbulent magnetic diffusivity and effects of inhomogeneous turbulence. The derivation of (2.23) is given in appendix C. We consider the case of weak mean magnetic fields, i.e. the energy of the mean magnetic field is much less than the turbulent kinetic energy. This implies that in the present study we do not investigate quenching of the turbulent transport coefficients. Therefore, we do not need evolution equations for the second moments of velocity,
![]() $\langle u_{i}u_{j}\rangle$
, and magnetic field,
$\langle u_{i}u_{j}\rangle$
, and magnetic field,
![]() $\langle b_{i}b_{j}\rangle$
(see, e.g. Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2000, Reference Rogachevskii and Kleeorin2001, Reference Rogachevskii and Kleeorin2004). This implies that we consider linear effects in the mean magnetic field. The nonlinear mean-field theory for the mean electromotive force in a turbulent compressible fluid flow is the subject of a separate ongoing study.
$\langle b_{i}b_{j}\rangle$
(see, e.g. Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2000, Reference Rogachevskii and Kleeorin2001, Reference Rogachevskii and Kleeorin2004). This implies that we consider linear effects in the mean magnetic field. The nonlinear mean-field theory for the mean electromotive force in a turbulent compressible fluid flow is the subject of a separate ongoing study.
2.3.1 The
 $\unicode[STIX]{x1D70F}$
approach
$\unicode[STIX]{x1D70F}$
approach
Equation (2.23) for the second moment includes first-order spatial differential operators
![]() $\hat{{\mathcal{M}}}$
applied to the third-order moments
$\hat{{\mathcal{M}}}$
applied to the third-order moments
![]() $F^{(\text{III})}$
. The problem arises in how to close (2.23), i.e. how to express the third-order term
$F^{(\text{III})}$
. The problem arises in how to close (2.23), i.e. how to express the third-order term
![]() $\hat{{\mathcal{M}}}F^{(\text{III})}$
through the lower moments
$\hat{{\mathcal{M}}}F^{(\text{III})}$
through the lower moments
![]() $F^{(\text{II})}$
(McComb Reference McComb1990; Monin & Yaglom Reference Monin and Yaglom2013). We use the spectral
$F^{(\text{II})}$
(McComb Reference McComb1990; Monin & Yaglom Reference Monin and Yaglom2013). We use the spectral
![]() $\unicode[STIX]{x1D70F}$
approximation which postulates that the deviations of the third moment terms,
$\unicode[STIX]{x1D70F}$
approximation which postulates that the deviations of the third moment terms,
![]() $\hat{{\mathcal{M}}}F^{(\text{III})}(\boldsymbol{k})$
, from the contributions to these terms afforded by the background turbulence,
$\hat{{\mathcal{M}}}F^{(\text{III})}(\boldsymbol{k})$
, from the contributions to these terms afforded by the background turbulence,
![]() $\hat{{\mathcal{M}}}F^{(\text{III},0)}(\boldsymbol{k})$
, can be expressed through similar deviations of the second moments,
$\hat{{\mathcal{M}}}F^{(\text{III},0)}(\boldsymbol{k})$
, can be expressed through similar deviations of the second moments,
![]() $F^{(\text{II})}(\boldsymbol{k})-F^{(\text{II},0)}(\boldsymbol{k})$
:
$F^{(\text{II})}(\boldsymbol{k})-F^{(\text{II},0)}(\boldsymbol{k})$
:
where
![]() $\unicode[STIX]{x1D70F}_{r}(k)$
is the scale-dependent relaxation time, which can be identified with the correlation time
$\unicode[STIX]{x1D70F}_{r}(k)$
is the scale-dependent relaxation time, which can be identified with the correlation time
![]() $\unicode[STIX]{x1D70F}(k)$
of the turbulent velocity field for large fluid and magnetic Reynolds numbers (Orszag Reference Orszag1970; Pouquet et al.
Reference Pouquet, Frisch and Léorat1976; Kleeorin et al.
Reference Kleeorin, Rogachevskii and Ruzmaikin1990; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2004). The functions with the superscript
$\unicode[STIX]{x1D70F}(k)$
of the turbulent velocity field for large fluid and magnetic Reynolds numbers (Orszag Reference Orszag1970; Pouquet et al.
Reference Pouquet, Frisch and Léorat1976; Kleeorin et al.
Reference Kleeorin, Rogachevskii and Ruzmaikin1990; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2004). The functions with the superscript
![]() $(0)$
correspond to the background turbulence with zero mean magnetic field. We take into account that
$(0)$
correspond to the background turbulence with zero mean magnetic field. We take into account that
![]() $g_{ij}^{(0)}=0$
, because when the mean magnetic field is zero, the electromotive force vanishes. We do not take into account magnetic fluctuations caused by a small-scale dynamo (i.e. a dynamo with zero mean magnetic field). Therefore, equation (2.26) for
$g_{ij}^{(0)}=0$
, because when the mean magnetic field is zero, the electromotive force vanishes. We do not take into account magnetic fluctuations caused by a small-scale dynamo (i.e. a dynamo with zero mean magnetic field). Therefore, equation (2.26) for
![]() $g_{ij}(\boldsymbol{k})$
reduces to
$g_{ij}(\boldsymbol{k})$
reduces to
![]() $\hat{{\mathcal{M}}}F_{i}^{(\text{III})}(\boldsymbol{k})=-F_{i}(\boldsymbol{k})/\unicode[STIX]{x1D70F}(k)$
. Validation of the
$\hat{{\mathcal{M}}}F_{i}^{(\text{III})}(\boldsymbol{k})=-F_{i}(\boldsymbol{k})/\unicode[STIX]{x1D70F}(k)$
. Validation of the
![]() $\unicode[STIX]{x1D70F}$
approximation for different situations has been performed in various numerical simulations and analytical studies (Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2007; Rogachevskii et al.
Reference Rogachevskii, Kleeorin, Käpylä and Brandenburg2011, Reference Rogachevskii, Kleeorin, Brandenburg and Eichler2012; Brandenburg et al.
Reference Brandenburg, Gressel, Käpylä, Kleeorin, Mantere and Rogachevskii2012a
; Käpylä et al.
Reference Käpylä, Brandenburg, Kleeorin, Mantere and Rogachevskii2012).
$\unicode[STIX]{x1D70F}$
approximation for different situations has been performed in various numerical simulations and analytical studies (Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2007; Rogachevskii et al.
Reference Rogachevskii, Kleeorin, Käpylä and Brandenburg2011, Reference Rogachevskii, Kleeorin, Brandenburg and Eichler2012; Brandenburg et al.
Reference Brandenburg, Gressel, Käpylä, Kleeorin, Mantere and Rogachevskii2012a
; Käpylä et al.
Reference Käpylä, Brandenburg, Kleeorin, Mantere and Rogachevskii2012).
2.3.2 Model of background turbulence for
 $Re\gg 1$
$Re\gg 1$
In the next step of the derivation we need a model for the background turbulence. We use statistically stationary, density-stratified, inhomogeneous, compressible and helical background turbulence, which is determined by the following correlation function in
![]() $\boldsymbol{k}$
space:
$\boldsymbol{k}$
space:
 $$\begin{eqnarray}\displaystyle f_{ij}^{(0)}(\boldsymbol{k}) & = & \displaystyle \frac{E(k)}{8\unicode[STIX]{x03C0}\,k^{2}(1+\unicode[STIX]{x1D70E}_{c})}\left\{\left[\unicode[STIX]{x1D6FF}_{ij}-k_{ij}+\frac{\text{i}}{k^{2}}(k_{j}\unicode[STIX]{x1D706}_{i}-k_{i}\unicode[STIX]{x1D706}_{j})+2\unicode[STIX]{x1D70E}_{c}\,k_{ij}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.(1+2\unicode[STIX]{x1D70E}_{c})\frac{\text{i}}{2k^{2}}(k_{i}\unicode[STIX]{x1D735}_{j}-k_{j}\unicode[STIX]{x1D735}_{i})\right]\overline{\boldsymbol{u}^{2}}-\frac{\text{i}}{k^{2}}\,\unicode[STIX]{x1D700}_{ijp}\,k_{p}\unicode[STIX]{x1D712}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{ij}^{(0)}(\boldsymbol{k}) & = & \displaystyle \frac{E(k)}{8\unicode[STIX]{x03C0}\,k^{2}(1+\unicode[STIX]{x1D70E}_{c})}\left\{\left[\unicode[STIX]{x1D6FF}_{ij}-k_{ij}+\frac{\text{i}}{k^{2}}(k_{j}\unicode[STIX]{x1D706}_{i}-k_{i}\unicode[STIX]{x1D706}_{j})+2\unicode[STIX]{x1D70E}_{c}\,k_{ij}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.(1+2\unicode[STIX]{x1D70E}_{c})\frac{\text{i}}{2k^{2}}(k_{i}\unicode[STIX]{x1D735}_{j}-k_{j}\unicode[STIX]{x1D735}_{i})\right]\overline{\boldsymbol{u}^{2}}-\frac{\text{i}}{k^{2}}\,\unicode[STIX]{x1D700}_{ijp}\,k_{p}\unicode[STIX]{x1D712}\right\}.\end{eqnarray}$$
Note that most statements and conditions used for the derivation of the tensorial structure of (2.12) are also valid for (2.27). We assume here that the background turbulence is of Kolmogorov type with constant fluxes of energy and kinetic helicity over the spectrum, i.e. the kinetic energy spectrum for the range of wavenumbers
![]() $k_{0}<k<k_{\unicode[STIX]{x1D708}}$
is
$k_{0}<k<k_{\unicode[STIX]{x1D708}}$
is
![]() $E(k)=-\text{d}\bar{\unicode[STIX]{x1D70F}}(k)/\text{d}k$
, the function
$E(k)=-\text{d}\bar{\unicode[STIX]{x1D70F}}(k)/\text{d}k$
, the function
![]() $\bar{\unicode[STIX]{x1D70F}}(k)=(k/k_{0})^{1-q}$
with
$\bar{\unicode[STIX]{x1D70F}}(k)=(k/k_{0})^{1-q}$
with
![]() $1<q<3$
being the exponent of the kinetic energy spectrum (
$1<q<3$
being the exponent of the kinetic energy spectrum (
![]() $q=5/3$
for a Kolmogorov spectrum). The condition
$q=5/3$
for a Kolmogorov spectrum). The condition
![]() $q>1$
corresponds to finite kinetic energy for very large fluid Reynolds numbers, while
$q>1$
corresponds to finite kinetic energy for very large fluid Reynolds numbers, while
![]() $q<3$
corresponds to finite dissipation of the turbulent kinetic energy at the viscous scale (see, e.g. McComb Reference McComb1990; Frisch Reference Frisch1995; Monin & Yaglom Reference Monin and Yaglom2013). The turbulent correlation time in
$q<3$
corresponds to finite dissipation of the turbulent kinetic energy at the viscous scale (see, e.g. McComb Reference McComb1990; Frisch Reference Frisch1995; Monin & Yaglom Reference Monin and Yaglom2013). The turbulent correlation time in
![]() $\boldsymbol{k}$
space is
$\boldsymbol{k}$
space is
![]() $\unicode[STIX]{x1D70F}(k)=2\unicode[STIX]{x1D70F}_{0}\,\bar{\unicode[STIX]{x1D70F}}(k)$
, where
$\unicode[STIX]{x1D70F}(k)=2\unicode[STIX]{x1D70F}_{0}\,\bar{\unicode[STIX]{x1D70F}}(k)$
, where
![]() $\unicode[STIX]{x1D70F}_{0}=\ell _{0}/\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the turbulent correlation time in physical space, and
$\unicode[STIX]{x1D70F}_{0}=\ell _{0}/\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the turbulent correlation time in physical space, and
![]() $\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the characteristic turbulent velocity at scale
$\sqrt{\overline{\boldsymbol{u}^{2}}}$
is the characteristic turbulent velocity at scale
![]() $\ell _{0}$
. Note that for fully developed Kolmogorov like turbulence,
$\ell _{0}$
. Note that for fully developed Kolmogorov like turbulence,
![]() $\unicode[STIX]{x1D70E}_{c}<1$
(Chassaing et al.
Reference Chassaing, Antonia, Anselmet, Joly and Sarkar2013).
$\unicode[STIX]{x1D70E}_{c}<1$
(Chassaing et al.
Reference Chassaing, Antonia, Anselmet, Joly and Sarkar2013).
2.3.3 Mean electromotive force for
 $Rm\gg 1$
$Rm\gg 1$
We use the spectral
![]() $\unicode[STIX]{x1D70F}$
approach and assume that the characteristic time of variation of the mean magnetic field
$\unicode[STIX]{x1D70F}$
approach and assume that the characteristic time of variation of the mean magnetic field
![]() $\overline{\boldsymbol{B}}$
is substantially larger than the correlation time
$\overline{\boldsymbol{B}}$
is substantially larger than the correlation time
![]() $\unicode[STIX]{x1D70F}(k)$
for all turbulence scales. This allows us to get a stationary solution of (2.23). We consider linear effects in the mean magnetic field, so that the function
$\unicode[STIX]{x1D70F}(k)$
for all turbulence scales. This allows us to get a stationary solution of (2.23). We consider linear effects in the mean magnetic field, so that the function
![]() $f_{ij}(\boldsymbol{k})$
in (2.23) and (2.25) should be replaced by
$f_{ij}(\boldsymbol{k})$
in (2.23) and (2.25) should be replaced by
![]() $f_{ij}^{(0)}(\boldsymbol{k})$
. The mean electromotive force is determined by
$f_{ij}^{(0)}(\boldsymbol{k})$
. The mean electromotive force is determined by
![]() $\overline{{\mathcal{E}}}_{i}=\unicode[STIX]{x1D700}_{inm}\int g_{mn}(\boldsymbol{k})\,\text{d}\boldsymbol{k}$
. We take into account that the terms with symmetric tensors with respect to the indexes
$\overline{{\mathcal{E}}}_{i}=\unicode[STIX]{x1D700}_{inm}\int g_{mn}(\boldsymbol{k})\,\text{d}\boldsymbol{k}$
. We take into account that the terms with symmetric tensors with respect to the indexes
![]() $m$
and
$m$
and
![]() $n$
in
$n$
in
![]() $g_{mn}(\boldsymbol{k})$
do not contribute to the mean electromotive force. Therefore, the equation for the mean electromotive force is given by
$g_{mn}(\boldsymbol{k})$
do not contribute to the mean electromotive force. Therefore, the equation for the mean electromotive force is given by
 $$\begin{eqnarray}\displaystyle \overline{{\mathcal{E}}}_{m} & = & \displaystyle \unicode[STIX]{x1D700}_{mji}\int \unicode[STIX]{x1D70F}(k)\left\{\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\overline{\boldsymbol{B}})f_{ij}^{(0)}-\overline{B}_{i}\left(\text{i}k_{n}\,f_{nj}^{(0)}+\frac{1}{2}\unicode[STIX]{x1D735}_{n}f_{nj}^{(0)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\left[f_{nj}^{(0)}+\frac{k}{2}\left(\frac{\text{d}\ln \unicode[STIX]{x1D70F}}{\text{d}k}\right)k_{np}\,f_{pj}^{(0)}\right]\unicode[STIX]{x1D735}_{n}\overline{B}_{i}\right\}\,\text{d}\boldsymbol{k}.\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{{\mathcal{E}}}_{m} & = & \displaystyle \unicode[STIX]{x1D700}_{mji}\int \unicode[STIX]{x1D70F}(k)\left\{\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\overline{\boldsymbol{B}})f_{ij}^{(0)}-\overline{B}_{i}\left(\text{i}k_{n}\,f_{nj}^{(0)}+\frac{1}{2}\unicode[STIX]{x1D735}_{n}f_{nj}^{(0)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\left[f_{nj}^{(0)}+\frac{k}{2}\left(\frac{\text{d}\ln \unicode[STIX]{x1D70F}}{\text{d}k}\right)k_{np}\,f_{pj}^{(0)}\right]\unicode[STIX]{x1D735}_{n}\overline{B}_{i}\right\}\,\text{d}\boldsymbol{k}.\quad\end{eqnarray}$$
Using the model of background turbulence given by (2.27) and integrating in
![]() $\boldsymbol{k}$
-space (2.28), we arrive at equation for the mean electromotive force (2.17), where the
$\boldsymbol{k}$
-space (2.28), we arrive at equation for the mean electromotive force (2.17), where the
![]() $\unicode[STIX]{x1D6FC}$
effect, the turbulent magnetic diffusivity
$\unicode[STIX]{x1D6FC}$
effect, the turbulent magnetic diffusivity
![]() $\unicode[STIX]{x1D702}_{\text{t}}$
and the pumping velocity
$\unicode[STIX]{x1D702}_{\text{t}}$
and the pumping velocity
![]() $\unicode[STIX]{x1D738}$
for large magnetic Reynolds numbers
$\unicode[STIX]{x1D738}$
for large magnetic Reynolds numbers
![]() $(Rm\gg 1)$
are given by
$(Rm\gg 1)$
are given by
Equations (2.29) and (2.30) imply that for large magnetic Reynolds numbers, compressibility decreases both the
![]() $\unicode[STIX]{x1D6FC}$
effect and turbulent magnetic diffusivity. Since
$\unicode[STIX]{x1D6FC}$
effect and turbulent magnetic diffusivity. Since
![]() $1<q<3$
, the turbulent magnetic diffusivity is always positive for
$1<q<3$
, the turbulent magnetic diffusivity is always positive for
![]() $Rm\gg 1$
, even for very large compressibility,
$Rm\gg 1$
, even for very large compressibility,
![]() $\unicode[STIX]{x1D70E}_{c}\gg 1$
(e.g. for irrotational flows). Note that for an incompressible flow the turbulent magnetic diffusivity is independent of
$\unicode[STIX]{x1D70E}_{c}\gg 1$
(e.g. for irrotational flows). Note that for an incompressible flow the turbulent magnetic diffusivity is independent of
![]() $q$
. On the other hand, compressibility of fluid flow does not affect the pumping velocity
$q$
. On the other hand, compressibility of fluid flow does not affect the pumping velocity
![]() $\unicode[STIX]{x1D738}$
of the mean magnetic field for
$\unicode[STIX]{x1D738}$
of the mean magnetic field for
![]() $Rm\gg 1$
, similarly to the case of
$Rm\gg 1$
, similarly to the case of
![]() $Rm\ll 1$
.
$Rm\ll 1$
.
In the framework of mean-field dynamo theory, the threshold for the generation of a mean magnetic field is formulated in terms of the dynamo number. In the case of an
![]() $\unicode[STIX]{x1D6FC}^{2}$
dynamo, the dynamo number is given by
$\unicode[STIX]{x1D6FC}^{2}$
dynamo, the dynamo number is given by
![]() $R_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FC}L_{B}/\unicode[STIX]{x1D702}_{\text{t}}$
. Using (2.29) and (2.30), we find that, for a compressible flow,
$R_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FC}L_{B}/\unicode[STIX]{x1D702}_{\text{t}}$
. Using (2.29) and (2.30), we find that, for a compressible flow,
![]() $R_{\unicode[STIX]{x1D6FC}}$
is given by
$R_{\unicode[STIX]{x1D6FC}}$
is given by
where
![]() $R_{\unicode[STIX]{x1D6FC}}^{(\text{in})}$
applies to the corresponding incompressible flow. This implies that compressibility decreases the dynamo number.
$R_{\unicode[STIX]{x1D6FC}}^{(\text{in})}$
applies to the corresponding incompressible flow. This implies that compressibility decreases the dynamo number.
3 Turbulent transport of particles
In this section we consider non-inertial particles or gaseous admixtures in a compressible fluid flow. Equation for the particle number density,
![]() $n^{(\text{p})}(\boldsymbol{x},t)$
, reads (Chandrasekhar Reference Chandrasekhar1943; Akhiezer & Peletminskii Reference Akhiezer and Peletminskii1981):
$n^{(\text{p})}(\boldsymbol{x},t)$
, reads (Chandrasekhar Reference Chandrasekhar1943; Akhiezer & Peletminskii Reference Akhiezer and Peletminskii1981):
where
![]() $D$
is the microphysical diffusivity describing Brownian diffusion of particles and
$D$
is the microphysical diffusivity describing Brownian diffusion of particles and
![]() $\boldsymbol{U}$
is a fluid velocity. Equation (3.1) implies conservation of the total number of particles in a closed volume. We consider one way coupling, i.e. we take into account the effect of turbulence on particle transport, but neglect the effect of particles on the turbulence. This corresponds to turbulent transport of a passive scalar.
$\boldsymbol{U}$
is a fluid velocity. Equation (3.1) implies conservation of the total number of particles in a closed volume. We consider one way coupling, i.e. we take into account the effect of turbulence on particle transport, but neglect the effect of particles on the turbulence. This corresponds to turbulent transport of a passive scalar.
To determine the turbulent flux of particles, we use a mean-field approach in which the number density of particles and fluid velocity are decomposed into mean and fluctuating parts, where the fluctuating parts have zero mean values. Averaging (3.1) over an ensemble, we arrive at an equation for the mean number density,
![]() $N(\boldsymbol{x},t)\equiv \overline{n^{(\text{p})}}$
:
$N(\boldsymbol{x},t)\equiv \overline{n^{(\text{p})}}$
:
where
![]() $\boldsymbol{F}=\overline{n(\boldsymbol{x},t)\boldsymbol{u}(\boldsymbol{x},t)}$
is the turbulent flux of particles and we consider the case of a zero mean fluid velocity,
$\boldsymbol{F}=\overline{n(\boldsymbol{x},t)\boldsymbol{u}(\boldsymbol{x},t)}$
is the turbulent flux of particles and we consider the case of a zero mean fluid velocity,
![]() $\overline{\text{U}}=0$
.
$\overline{\text{U}}=0$
.
To determine the turbulent flux of particles we use the equation for the fluctuations of the particle number density,
![]() $n(\boldsymbol{x},t)=n^{(\text{p})}-N$
, which follows from (3.1) and (3.2):
$n(\boldsymbol{x},t)=n^{(\text{p})}-N$
, which follows from (3.1) and (3.2):
where
![]() ${\mathcal{Q}}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n\boldsymbol{u}-\overline{n\boldsymbol{u}})$
are nonlinear terms and
${\mathcal{Q}}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n\boldsymbol{u}-\overline{n\boldsymbol{u}})$
are nonlinear terms and
![]() $I=-N\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}-(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})N$
is the source term of particle number density fluctuations. The ratio of the nonlinear terms to the diffusion term is the Péclet number, that is estimated as
$I=-N\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}-(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})N$
is the source term of particle number density fluctuations. The ratio of the nonlinear terms to the diffusion term is the Péclet number, that is estimated as
![]() $Pe=u_{0}\,\ell _{0}/D$
. In the next subsections we derive equations for the turbulent transport coefficients of particles for small and large Péclet numbers.
$Pe=u_{0}\,\ell _{0}/D$
. In the next subsections we derive equations for the turbulent transport coefficients of particles for small and large Péclet numbers.
3.1 Turbulent transport coefficients for
 $Pe\ll 1$
$Pe\ll 1$
We derive an equation for the turbulent flux of particles,
for small Péclet numbers using a quasi-linear approach, where
For brevity of notations we omit below the large-scale variables
![]() $t$
and
$t$
and
![]() $\boldsymbol{R}$
in
$\boldsymbol{R}$
in
![]() $F_{j}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
and
$F_{j}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
and
![]() $N(\boldsymbol{R},t)$
. We neglect the nonlinear term
$N(\boldsymbol{R},t)$
. We neglect the nonlinear term
![]() $\boldsymbol{{\mathcal{Q}}}$
, but keep the molecular diffusion term in (3.3). We rewrite (3.3) in Fourier space and find the solution of this equation (see (A 20) in appendix A). Here we apply the same approach that was used in § 2.2, i.e. we assume that there is a separation of spatial and time scales,
$\boldsymbol{{\mathcal{Q}}}$
, but keep the molecular diffusion term in (3.3). We rewrite (3.3) in Fourier space and find the solution of this equation (see (A 20) in appendix A). Here we apply the same approach that was used in § 2.2, i.e. we assume that there is a separation of spatial and time scales,
![]() $\ell _{0}\ll L_{N}$
and
$\ell _{0}\ll L_{N}$
and
![]() $\unicode[STIX]{x1D70F}_{0}\ll t_{N}$
, where
$\unicode[STIX]{x1D70F}_{0}\ll t_{N}$
, where
![]() $L_{N}$
and
$L_{N}$
and
![]() $t_{N}$
are the characteristic spatial and time scales of the mean particle number density variations. We perform calculations presented in appendix A, so that equation for the turbulent flux of particles is given by
$t_{N}$
are the characteristic spatial and time scales of the mean particle number density variations. We perform calculations presented in appendix A, so that equation for the turbulent flux of particles is given by
 $$\begin{eqnarray}\displaystyle F_{j} & = & \displaystyle -\int G_{D}\left[N\left(\text{i}k_{i}f_{ij}+\frac{1}{2}\unicode[STIX]{x1D735}_{i}f_{ij}-Dk^{2}G_{D}k_{im}\unicode[STIX]{x1D735}_{m}f_{ij}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\left(f_{mj}-k_{i}\frac{\unicode[STIX]{x2202}f_{ij}}{\unicode[STIX]{x2202}k_{m}}-2Dk^{2}G_{D}\,k_{im}f_{ij}\right)\unicode[STIX]{x1D735}_{m}N\right]\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{j} & = & \displaystyle -\int G_{D}\left[N\left(\text{i}k_{i}f_{ij}+\frac{1}{2}\unicode[STIX]{x1D735}_{i}f_{ij}-Dk^{2}G_{D}k_{im}\unicode[STIX]{x1D735}_{m}f_{ij}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\left(f_{mj}-k_{i}\frac{\unicode[STIX]{x2202}f_{ij}}{\unicode[STIX]{x2202}k_{m}}-2Dk^{2}G_{D}\,k_{im}f_{ij}\right)\unicode[STIX]{x1D735}_{m}N\right]\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
where
![]() $G_{D}\equiv G_{D}(\boldsymbol{k},\unicode[STIX]{x1D714})=(D\boldsymbol{k}^{2}+\text{i}\unicode[STIX]{x1D714})^{-1}$
and
$G_{D}\equiv G_{D}(\boldsymbol{k},\unicode[STIX]{x1D714})=(D\boldsymbol{k}^{2}+\text{i}\unicode[STIX]{x1D714})^{-1}$
and
![]() $f_{ij}=f_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
. Since we consider one way coupling, the correlation function
$f_{ij}=f_{ij}(\boldsymbol{k},\unicode[STIX]{x1D714},\boldsymbol{R},t)$
. Since we consider one way coupling, the correlation function
![]() $f_{ij}$
in (3.6) should be replaced by
$f_{ij}$
in (3.6) should be replaced by
![]() $f_{ij}^{(0)}$
for the background random flow with zero turbulent flux of particles. Using the model of background random flow given by (2.12) with zero kinetic helicity, and integrating in
$f_{ij}^{(0)}$
for the background random flow with zero turbulent flux of particles. Using the model of background random flow given by (2.12) with zero kinetic helicity, and integrating in
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $\boldsymbol{k}$
-space, we arrive at an equation for the turbulent flux of particles:
$\boldsymbol{k}$
-space, we arrive at an equation for the turbulent flux of particles:
where for small Péclet numbers
![]() $(Pe\ll 1)$
, the turbulent diffusivity
$(Pe\ll 1)$
, the turbulent diffusivity
![]() $D_{\text{t}}$
and the effective pumping velocity
$D_{\text{t}}$
and the effective pumping velocity
![]() $\boldsymbol{V}^{\text{eff}}$
are given by
$\boldsymbol{V}^{\text{eff}}$
are given by
Since
![]() $\unicode[STIX]{x1D70F}_{0}\,Pe=\ell _{0}^{2}/D$
, the turbulent transport coefficients given by (3.8) and (3.9) are determined only by the microphysical diffusion time scale,
$\unicode[STIX]{x1D70F}_{0}\,Pe=\ell _{0}^{2}/D$
, the turbulent transport coefficients given by (3.8) and (3.9) are determined only by the microphysical diffusion time scale,
![]() $\ell _{0}^{2}/D$
. Remarkably, equation (3.8) for the turbulent diffusivity of passive scalars
$\ell _{0}^{2}/D$
. Remarkably, equation (3.8) for the turbulent diffusivity of passive scalars
![]() $D_{\text{t}}$
coincides with (2.19) for the turbulent magnetic diffusivity
$D_{\text{t}}$
coincides with (2.19) for the turbulent magnetic diffusivity
![]() $\unicode[STIX]{x1D702}_{\text{t}}$
after replacing
$\unicode[STIX]{x1D702}_{\text{t}}$
after replacing
![]() $Pe$
by
$Pe$
by
![]() $Rm$
.
$Rm$
.
Equation (3.8) implies that for small Péclet numbers, compressibility effects decrease the turbulent diffusivity. However, the total (effective) diffusivity,
![]() $D+D_{\text{t}}$
, cannot be negative, because for
$D+D_{\text{t}}$
, cannot be negative, because for
![]() $Pe\ll 1$
, the molecular diffusivity is much larger than the turbulent one,
$Pe\ll 1$
, the molecular diffusivity is much larger than the turbulent one,
![]() $D\gg |D_{\text{t}}|$
. This result is consistent with that of Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011), where it has been demonstrated that the total mean-field diffusivity for passive scalar transport in irrotational flows is smaller than the molecular diffusivity (see § 4 for a detailed comparison).
$D\gg |D_{\text{t}}|$
. This result is consistent with that of Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011), where it has been demonstrated that the total mean-field diffusivity for passive scalar transport in irrotational flows is smaller than the molecular diffusivity (see § 4 for a detailed comparison).
The physics related to different terms in (3.9) will be discussed in the next section. In the present study of turbulent transport of passive scalar and non-inertial particles, we consider non-helical turbulence, because there is no effect of the kinetic helicity on the particle flux – at least in the system investigated here (without rotation, the large-scale shear and neglecting effects
![]() ${\sim}O(\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D6FB}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{j}\overline{\boldsymbol{u}^{2}})$
).
${\sim}O(\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D6FB}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{j}\overline{\boldsymbol{u}^{2}})$
).
By means of the equation of state for a perfect gas,
![]() $\unicode[STIX]{x1D735}\ln \overline{p}=\unicode[STIX]{x1D735}\ln \overline{\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D735}\ln \overline{T}$
, we rewrite (3.9) for the effective pumping velocity as:
$\unicode[STIX]{x1D735}\ln \overline{p}=\unicode[STIX]{x1D735}\ln \overline{\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D735}\ln \overline{T}$
, we rewrite (3.9) for the effective pumping velocity as:
where
![]() $\overline{T}$
and
$\overline{T}$
and
![]() $\overline{p}$
are the mean temperature and the mean pressure, respectively. Note that, since the density–temperature correlation
$\overline{p}$
are the mean temperature and the mean pressure, respectively. Note that, since the density–temperature correlation
![]() $\overline{\unicode[STIX]{x1D70C}^{\prime }\unicode[STIX]{x1D717}}$
is much smaller than
$\overline{\unicode[STIX]{x1D70C}^{\prime }\unicode[STIX]{x1D717}}$
is much smaller than
![]() $\overline{\unicode[STIX]{x1D70C}}\,\overline{T}$
(Chassaing et al.
Reference Chassaing, Antonia, Anselmet, Joly and Sarkar2013), the equation of state for perfect gas is also valid for the mean quantities, where
$\overline{\unicode[STIX]{x1D70C}}\,\overline{T}$
(Chassaing et al.
Reference Chassaing, Antonia, Anselmet, Joly and Sarkar2013), the equation of state for perfect gas is also valid for the mean quantities, where
![]() $\unicode[STIX]{x1D70C}^{\prime }$
and
$\unicode[STIX]{x1D70C}^{\prime }$
and
![]() $\unicode[STIX]{x1D717}$
are fluctuations of the fluid density and temperature.
$\unicode[STIX]{x1D717}$
are fluctuations of the fluid density and temperature.
3.2 Turbulent transport coefficients for
 $Pe\gg 1$
$Pe\gg 1$
In this section we determine the turbulent flux of particles for large Péclet and Reynolds numbers. Similar to the study performed in § 2.3, we consider fully developed turbulence, where the Strouhal number is of the order of unity and the turbulent correlation time is scale dependent, so we apply the Fourier transformation only in
![]() $\boldsymbol{k}$
space. Using (3.3) for the fluctuations
$\boldsymbol{k}$
space. Using (3.3) for the fluctuations
![]() $n$
and the Navier–Stokes equation for the velocity
$n$
and the Navier–Stokes equation for the velocity
![]() $\boldsymbol{u}$
written in Fourier space, we derive an equation for the instantaneous two-point correlation function
$\boldsymbol{u}$
written in Fourier space, we derive an equation for the instantaneous two-point correlation function
For brevity of notation we omit the large-scale variables
![]() $t$
and
$t$
and
![]() $\boldsymbol{R}$
in the function
$\boldsymbol{R}$
in the function
![]() $F_{j}(\boldsymbol{k},\boldsymbol{R},t)$
and the mean number density
$F_{j}(\boldsymbol{k},\boldsymbol{R},t)$
and the mean number density
![]() $N(\boldsymbol{R},t)$
. To derive an evolution equation for
$N(\boldsymbol{R},t)$
. To derive an evolution equation for
![]() $F_{j}(\boldsymbol{k})$
, we perform the calculations presented in appendix C, which yields
$F_{j}(\boldsymbol{k})$
, we perform the calculations presented in appendix C, which yields
where
are the third-order moment terms in
![]() $\boldsymbol{k}$
space appearing due to the nonlinear terms.
$\boldsymbol{k}$
space appearing due to the nonlinear terms.
We use the spectral
![]() $\unicode[STIX]{x1D70F}$
approximation (2.26), where functions with superscript
$\unicode[STIX]{x1D70F}$
approximation (2.26), where functions with superscript
![]() $(0)$
correspond to background turbulence with zero turbulent particle flux. Therefore, equation (2.26) reduces to
$(0)$
correspond to background turbulence with zero turbulent particle flux. Therefore, equation (2.26) reduces to
![]() $\hat{{\mathcal{M}}}F_{i}^{(\text{III})}(\boldsymbol{k})=-F_{i}(\boldsymbol{k})/\unicode[STIX]{x1D70F}(k)$
. We also assume that the characteristic time of variation of the second moment
$\hat{{\mathcal{M}}}F_{i}^{(\text{III})}(\boldsymbol{k})=-F_{i}(\boldsymbol{k})/\unicode[STIX]{x1D70F}(k)$
. We also assume that the characteristic time of variation of the second moment
![]() $F_{i}(\boldsymbol{k})$
is substantially larger than the correlation time
$F_{i}(\boldsymbol{k})$
is substantially larger than the correlation time
![]() $\unicode[STIX]{x1D70F}(k)$
on all turbulence scales. Therefore, the particle flux is given by
$\unicode[STIX]{x1D70F}(k)$
on all turbulence scales. Therefore, the particle flux is given by
Using the model of background turbulence for
![]() $f_{ij}^{(0)}$
given by (2.27) with a zero kinetic helicity, and integrating (3.14) in
$f_{ij}^{(0)}$
given by (2.27) with a zero kinetic helicity, and integrating (3.14) in
![]() $\boldsymbol{k}$
-space, we obtain the turbulent flux of particles (3.7), where the turbulent diffusivity
$\boldsymbol{k}$
-space, we obtain the turbulent flux of particles (3.7), where the turbulent diffusivity
![]() $D_{\text{t}}$
and the effective pumping velocity
$D_{\text{t}}$
and the effective pumping velocity
![]() $\boldsymbol{V}^{\text{eff}}$
of non-inertial particles for
$\boldsymbol{V}^{\text{eff}}$
of non-inertial particles for
![]() $Pe\gg 1$
are given by
$Pe\gg 1$
are given by
Equation (3.15) for the turbulent diffusivity of particles
![]() $D_{\text{t}}$
coincides with (2.30) for the turbulent magnetic diffusivity
$D_{\text{t}}$
coincides with (2.30) for the turbulent magnetic diffusivity
![]() $\unicode[STIX]{x1D702}_{\text{t}}$
after replacing
$\unicode[STIX]{x1D702}_{\text{t}}$
after replacing
![]() $Pe$
by
$Pe$
by
![]() $Rm$
. Equation (3.15) implies that for large Péclet numbers, compressibility decreases the turbulent diffusivity of particles. Since
$Rm$
. Equation (3.15) implies that for large Péclet numbers, compressibility decreases the turbulent diffusivity of particles. Since
![]() $1<q<3$
, the turbulent diffusivity is always positive when
$1<q<3$
, the turbulent diffusivity is always positive when
![]() $Pe\gg 1$
, even for very strong compressibility,
$Pe\gg 1$
, even for very strong compressibility,
![]() $\unicode[STIX]{x1D70E}_{c}\gg 1$
.
$\unicode[STIX]{x1D70E}_{c}\gg 1$
.

Figure 1. Dependence of
![]() $V^{\text{eff}}$
(dotted line) and
$V^{\text{eff}}$
(dotted line) and
![]() $\unicode[STIX]{x1D6FE}$
(dashed line) (here in the
$\unicode[STIX]{x1D6FE}$
(dashed line) (here in the
![]() $z$
direction) as a function of the inverse scale height
$z$
direction) as a function of the inverse scale height
![]() $H$
, normalized by the wavenumber
$H$
, normalized by the wavenumber
![]() $k_{\text{f}}$
of the energy-carrying eddies. The turbulent pumping velocity
$k_{\text{f}}$
of the energy-carrying eddies. The turbulent pumping velocity
![]() $\unicode[STIX]{x1D6FE}$
caused by the non-uniformity of the turbulent r.m.s. velocity (solid line) in a non-stratified turbulence. Here the symbol
$\unicode[STIX]{x1D6FE}$
caused by the non-uniformity of the turbulent r.m.s. velocity (solid line) in a non-stratified turbulence. Here the symbol
![]() $H$
is used either for the density scale height,
$H$
is used either for the density scale height,
![]() $H=\unicode[STIX]{x1D706}^{-1}$
, or for the characteristic scale of the non-uniformity of the turbulent r.m.s. velocity,
$H=\unicode[STIX]{x1D706}^{-1}$
, or for the characteristic scale of the non-uniformity of the turbulent r.m.s. velocity,
![]() $H^{-1}=\unicode[STIX]{x1D735}u_{\text{rms}}/u_{\text{rms}}$
.
$H^{-1}=\unicode[STIX]{x1D735}u_{\text{rms}}/u_{\text{rms}}$
.
Equation (3.16) determines effective pumping velocity,
![]() $\boldsymbol{V}^{\text{eff}}$
, of passive scalars and non-inertial particles. The first term in (3.16), and likewise in (3.9) for
$\boldsymbol{V}^{\text{eff}}$
, of passive scalars and non-inertial particles. The first term in (3.16), and likewise in (3.9) for
![]() $Pe\ll 1$
, describes pumping of passive scalars caused by density stratification. This effect for low Mach numbers has been studied theoretically using various analytical approaches (Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1995, Reference Elperin, Kleeorin and Rogachevskii1996, Reference Elperin, Kleeorin and Rogachevskii1997, Reference Elperin, Kleeorin, Rogachevskii and Sokoloff2000, Reference Elperin, Kleeorin, Rogachevskii and Sokoloff2001; Pandya & Mashayek Reference Pandya and Mashayek2002; Reeks Reference Reeks2005; Amir et al.
Reference Amir, Bar, Eidelman, Elperin, Kleeorin and Rogachevskii2017). It has also been detected in the direct numerical simulations of Brandenburg, Rädler & Kemel (Reference Brandenburg, Rädler and Kemel2012b
), where the density stratification was caused by gravity. Their result is reproduced in figure 1 and compared with the corresponding turbulent pumping velocities of mean magnetic field, which is close to zero. This demonstrates very clearly the different natures of pumping of particles and magnetic fields in one and the same simulation. Here, the relevant components of the effective pumping velocities of particles,
$Pe\ll 1$
, describes pumping of passive scalars caused by density stratification. This effect for low Mach numbers has been studied theoretically using various analytical approaches (Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1995, Reference Elperin, Kleeorin and Rogachevskii1996, Reference Elperin, Kleeorin and Rogachevskii1997, Reference Elperin, Kleeorin, Rogachevskii and Sokoloff2000, Reference Elperin, Kleeorin, Rogachevskii and Sokoloff2001; Pandya & Mashayek Reference Pandya and Mashayek2002; Reeks Reference Reeks2005; Amir et al.
Reference Amir, Bar, Eidelman, Elperin, Kleeorin and Rogachevskii2017). It has also been detected in the direct numerical simulations of Brandenburg, Rädler & Kemel (Reference Brandenburg, Rädler and Kemel2012b
), where the density stratification was caused by gravity. Their result is reproduced in figure 1 and compared with the corresponding turbulent pumping velocities of mean magnetic field, which is close to zero. This demonstrates very clearly the different natures of pumping of particles and magnetic fields in one and the same simulation. Here, the relevant components of the effective pumping velocities of particles,
![]() $\boldsymbol{V}^{\text{eff}}$
, and magnetic field,
$\boldsymbol{V}^{\text{eff}}$
, and magnetic field,
![]() $\unicode[STIX]{x1D738}$
, have been determined using the test-field method for axisymmetric turbulence described in Brandenburg et al. (Reference Brandenburg, Rädler and Kemel2012b
). The simulations have been carried out for approximately 200 turnover times, for
$\unicode[STIX]{x1D738}$
, have been determined using the test-field method for axisymmetric turbulence described in Brandenburg et al. (Reference Brandenburg, Rädler and Kemel2012b
). The simulations have been carried out for approximately 200 turnover times, for
![]() $Pe=Re=u_{\text{rms}}/\unicode[STIX]{x1D708}k_{\text{f}}=22$
and
$Pe=Re=u_{\text{rms}}/\unicode[STIX]{x1D708}k_{\text{f}}=22$
and
![]() $k_{\text{f}}/k_{1}=5$
, where
$k_{\text{f}}/k_{1}=5$
, where
![]() $k_{1}$
is the wavenumber based on the size of the computational domain and
$k_{1}$
is the wavenumber based on the size of the computational domain and
![]() $k_{\text{f}}$
is the forcing scale of turbulence. Error bars have been determined using any one third of the full time series of the instantaneous, but spatially averaged mean values of
$k_{\text{f}}$
is the forcing scale of turbulence. Error bars have been determined using any one third of the full time series of the instantaneous, but spatially averaged mean values of
![]() $\boldsymbol{V}^{\text{eff}}$
and
$\boldsymbol{V}^{\text{eff}}$
and
![]() $\unicode[STIX]{x1D738}$
. Within error bars, the result for
$\unicode[STIX]{x1D738}$
. Within error bars, the result for
![]() $\unicode[STIX]{x1D738}$
is not quite compatible with zero, but this is entirely explicable as a consequence of a small upward increase in the root-mean-square (r.m.s.) velocity with height and thus a small positive gradient. Also, the deviation of the theoretical from the numerical results for larger
$\unicode[STIX]{x1D738}$
is not quite compatible with zero, but this is entirely explicable as a consequence of a small upward increase in the root-mean-square (r.m.s.) velocity with height and thus a small positive gradient. Also, the deviation of the theoretical from the numerical results for larger
![]() $(k_{\text{f}}H)^{-1}$
is caused by the fact that the parameter
$(k_{\text{f}}H)^{-1}$
is caused by the fact that the parameter
![]() $\ell _{0}/H$
is no longer very small, as was assumed in the theory. The effective pumping velocity of particles
$\ell _{0}/H$
is no longer very small, as was assumed in the theory. The effective pumping velocity of particles
![]() $\boldsymbol{V}^{\text{eff}}$
for arbitrary stratifications has been determined analytically by Amir et al. (Reference Amir, Bar, Eidelman, Elperin, Kleeorin and Rogachevskii2017). They have shown that there is a quenching of the pumping velocity caused by the strong stratification. This tendency is already seen in figure 1 (dotted line) for larger density stratifications.
$\boldsymbol{V}^{\text{eff}}$
for arbitrary stratifications has been determined analytically by Amir et al. (Reference Amir, Bar, Eidelman, Elperin, Kleeorin and Rogachevskii2017). They have shown that there is a quenching of the pumping velocity caused by the strong stratification. This tendency is already seen in figure 1 (dotted line) for larger density stratifications.
Let us discuss the physics related to the first term in the right-hand side of (3.16) caused by the fluid density stratification, considering density-stratified homogeneous turbulence. Substituting (3.7) into (3.2), we obtain the equation for the mean number density,
![]() $N$
:
$N$
:
The steady-state solution of (3.17) for the mean number density of non-inertial particles is given by
![]() $N/N_{0}=[\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{0}]^{D_{\text{t}}/(D+D_{\text{t}})}$
, where subscripts
$N/N_{0}=[\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{0}]^{D_{\text{t}}/(D+D_{\text{t}})}$
, where subscripts
![]() $0$
represent the values in the region with homogeneous fluid density. Here we used (3.8) and (3.9) or (3.15) and (3.16) for homogeneous turbulence. This solution implies that small particles are accumulated in the vicinity of the maximum of the fluid density, because the non-diffusive flux of particles,
$0$
represent the values in the region with homogeneous fluid density. Here we used (3.8) and (3.9) or (3.15) and (3.16) for homogeneous turbulence. This solution implies that small particles are accumulated in the vicinity of the maximum of the fluid density, because the non-diffusive flux of particles,
![]() $N\,\boldsymbol{V}^{\text{eff}}$
, is directed toward the maximum of the fluid density.
$N\,\boldsymbol{V}^{\text{eff}}$
, is directed toward the maximum of the fluid density.
The accumulation of non-inertial particles in the vicinity of the maximum of the mean fluid density can be explained as follows (Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1995, Reference Elperin, Kleeorin and Rogachevskii1997; Haugen et al.
Reference Haugen, Kleeorin, Rogachevskii and Brandenburg2012). Let us assume that the mean fluid density is inhomogeneous along the
![]() $x$
axis, and the mean density
$x$
axis, and the mean density
![]() $\overline{\unicode[STIX]{x1D70C}}_{2}$
at point
$\overline{\unicode[STIX]{x1D70C}}_{2}$
at point
![]() $2$
is larger than the mean density
$2$
is larger than the mean density
![]() $\overline{\unicode[STIX]{x1D70C}}_{1}$
at point
$\overline{\unicode[STIX]{x1D70C}}_{1}$
at point
![]() $1$
. Consider two small control volumes ‘
$1$
. Consider two small control volumes ‘
![]() $\mathsf{a}$
’ and ‘
$\mathsf{a}$
’ and ‘
![]() $\mathsf{b}$
’ located between these two points, and let the direction of the local turbulent velocity in volume ‘
$\mathsf{b}$
’ located between these two points, and let the direction of the local turbulent velocity in volume ‘
![]() $\mathsf{a}$
’ at some instant be the same as the direction of the mean fluid density gradient
$\mathsf{a}$
’ at some instant be the same as the direction of the mean fluid density gradient
![]() $\unicode[STIX]{x1D735}\,\overline{\unicode[STIX]{x1D70C}}$
(e.g. along the
$\unicode[STIX]{x1D735}\,\overline{\unicode[STIX]{x1D70C}}$
(e.g. along the
![]() $x$
axis toward point 2). Let the local turbulent velocity in volume ‘
$x$
axis toward point 2). Let the local turbulent velocity in volume ‘
![]() $\mathsf{b}$
’ at this instant be directed opposite to the mean fluid density gradient (i.e. toward point 1). In a fluid flow with an imposed mean fluid density gradient, one of the sources of particle number density fluctuations,
$\mathsf{b}$
’ at this instant be directed opposite to the mean fluid density gradient (i.e. toward point 1). In a fluid flow with an imposed mean fluid density gradient, one of the sources of particle number density fluctuations,
![]() $n\propto -\unicode[STIX]{x1D70F}_{0}\,N(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})$
, is caused by a non-zero
$n\propto -\unicode[STIX]{x1D70F}_{0}\,N(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})$
, is caused by a non-zero
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}\approx -\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln \overline{\unicode[STIX]{x1D70C}}\not =0$
(see the first term on the right-hand side of (3.3)). Since fluctuations of the fluid velocity
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}\approx -\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln \overline{\unicode[STIX]{x1D70C}}\not =0$
(see the first term on the right-hand side of (3.3)). Since fluctuations of the fluid velocity
![]() $u_{x}$
are positive in volume ‘
$u_{x}$
are positive in volume ‘
![]() $\mathsf{a}$
’ and negative in volume ‘
$\mathsf{a}$
’ and negative in volume ‘
![]() $\mathsf{b}$
’,
$\mathsf{b}$
’,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}<0$
in volume ‘
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}<0$
in volume ‘
![]() $\mathsf{a}$
’ and
$\mathsf{a}$
’ and
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}>0$
in volume ‘
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}>0$
in volume ‘
![]() $\mathsf{b}$
’. Therefore, the fluctuations of the particle number density
$\mathsf{b}$
’. Therefore, the fluctuations of the particle number density
![]() $n\propto -\unicode[STIX]{x1D70F}_{0}\,N(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})$
are positive in volume ‘
$n\propto -\unicode[STIX]{x1D70F}_{0}\,N(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})$
are positive in volume ‘
![]() $\mathsf{a}$
’ and negative in volume ‘
$\mathsf{a}$
’ and negative in volume ‘
![]() $\mathsf{b}$
’. However, the flux of particles
$\mathsf{b}$
’. However, the flux of particles
![]() $n\,u_{x}$
is positive in volume ‘
$n\,u_{x}$
is positive in volume ‘
![]() $\mathsf{a}$
’ (i.e. it is directed toward point 2), and it is also positive in volume ‘
$\mathsf{a}$
’ (i.e. it is directed toward point 2), and it is also positive in volume ‘
![]() $\mathsf{b}$
’ (because both fluctuations of fluid velocity and number density of particles are negative in volume ‘
$\mathsf{b}$
’ (because both fluctuations of fluid velocity and number density of particles are negative in volume ‘
![]() $\mathsf{b}$
’). Therefore, the mean flux of particles
$\mathsf{b}$
’). Therefore, the mean flux of particles
![]() $\overline{n\,\boldsymbol{u}}$
is directed, as is the mean fluid density gradient
$\overline{n\,\boldsymbol{u}}$
is directed, as is the mean fluid density gradient
![]() $\unicode[STIX]{x1D735}\,\overline{\unicode[STIX]{x1D70C}}$
, toward point 2. This forms large-scale heterogeneous structures of non-inertial particles in regions with a mean fluid density maximum.
$\unicode[STIX]{x1D735}\,\overline{\unicode[STIX]{x1D70C}}$
, toward point 2. This forms large-scale heterogeneous structures of non-inertial particles in regions with a mean fluid density maximum.
Indirect manifestations of the pumping effect caused by the density stratification through an observed increase of small-scale clustering of particles can be identified in the direct numerical simulations of van Aartrijk & Clercx (Reference van Aartrijk and Clercx2008), who studied the evolution of inertial particles in stably stratified turbulence. This pumping effect increases the small-scale clustering of inertial particles by forming inhomogeneous distributions of the mean particle number density. Note also that tangling of the mean particle number density,
![]() $N$
, by compressible velocity fluctuations (described by the source term
$N$
, by compressible velocity fluctuations (described by the source term
![]() $-N\,\text{div}\,\boldsymbol{u}$
in (3.3)), can increase the level of particle number density fluctuations,
$-N\,\text{div}\,\boldsymbol{u}$
in (3.3)), can increase the level of particle number density fluctuations,
![]() $n$
, when the source term
$n$
, when the source term
![]() $-N\,\text{div}\,\boldsymbol{u}>0$
. In this case
$-N\,\text{div}\,\boldsymbol{u}>0$
. In this case
![]() $\unicode[STIX]{x2202}n/\unicode[STIX]{x2202}t>0$
, see (3.3). This can amplify the particle clustering (Eidelman et al.
Reference Eidelman, Elperin, Kleeorin, Melnik and Rogachevskii2010; Elperin et al.
Reference Elperin, Kleeorin, Liberman and Rogachevskii2013).
$\unicode[STIX]{x2202}n/\unicode[STIX]{x2202}t>0$
, see (3.3). This can amplify the particle clustering (Eidelman et al.
Reference Eidelman, Elperin, Kleeorin, Melnik and Rogachevskii2010; Elperin et al.
Reference Elperin, Kleeorin, Liberman and Rogachevskii2013).
Using the equation of state for a perfect gas, we rewrite (3.16) for the pumping effective velocity in the form
The first term on the right-hand side of (3.18) describes turbulent barodiffusion (Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1997), while the second term characterizes the phenomenon of turbulent thermal diffusion (Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1996, Reference Elperin, Kleeorin, Rogachevskii and Sokoloff2000; Amir et al.
Reference Amir, Bar, Eidelman, Elperin, Kleeorin and Rogachevskii2017). The last term in (3.18),
![]() $\propto \unicode[STIX]{x1D70E}_{c}\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, describes the compressible turbophoresis for non-inertial particles.
$\propto \unicode[STIX]{x1D70E}_{c}\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, describes the compressible turbophoresis for non-inertial particles.
The classical turbophoresis (Caporaloni et al.
Reference Caporaloni, Tampieri, Trombetti and Vittori1975; Reeks Reference Reeks1983, Reference Reeks1992; Elperin, Kleeorin & Rogachevskii Reference Elperin, Kleeorin and Rogachevskii1998a
; Mitra, Haugen & Rogachevskii Reference Mitra, Haugen and Rogachevskii2018) exists only for inertial particles and causes an additional mean particle velocity that is proportional to
![]() $-\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, where
$-\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, where
![]() $\unicode[STIX]{x1D70F}_{s}=m_{p}/6\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}\,\unicode[STIX]{x1D708}a_{p}$
is the particle Stokes time, i.e. the characteristic time of coupling between small spherical particles (of radius
$\unicode[STIX]{x1D70F}_{s}=m_{p}/6\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}\,\unicode[STIX]{x1D708}a_{p}$
is the particle Stokes time, i.e. the characteristic time of coupling between small spherical particles (of radius
![]() $a_{p}$
and mass
$a_{p}$
and mass
![]() $m_{p}$
) and surrounding fluid. To illustrate the classical turbophoresis effect, let us consider small inertial particles in an isotropic incompressible turbulence and use equation of motion for a particle:
$m_{p}$
) and surrounding fluid. To illustrate the classical turbophoresis effect, let us consider small inertial particles in an isotropic incompressible turbulence and use equation of motion for a particle:
![]() $\text{d}\boldsymbol{v}^{(\text{p})}/\text{d}t=-(\boldsymbol{v}^{(\text{p})}-\boldsymbol{u})/\unicode[STIX]{x1D70F}_{s}$
, where
$\text{d}\boldsymbol{v}^{(\text{p})}/\text{d}t=-(\boldsymbol{v}^{(\text{p})}-\boldsymbol{u})/\unicode[STIX]{x1D70F}_{s}$
, where
![]() $\boldsymbol{v}^{(\text{p})}$
is the particle velocity. This equation represents a balance of particle inertia with the fluid drag force produced by the motion of the particle relative to the surrounding fluid. Solution of this equation for small Stokes time is given by:
$\boldsymbol{v}^{(\text{p})}$
is the particle velocity. This equation represents a balance of particle inertia with the fluid drag force produced by the motion of the particle relative to the surrounding fluid. Solution of this equation for small Stokes time is given by:
![]() $\boldsymbol{v}^{(\text{p})}=\boldsymbol{u}-\unicode[STIX]{x1D70F}_{s}[\unicode[STIX]{x2202}\boldsymbol{u}/\unicode[STIX]{x2202}t+(\boldsymbol{u}\cdot \unicode[STIX]{x1D735})\boldsymbol{u}]+O(\unicode[STIX]{x1D70F}_{s}^{2})$
(Maxey Reference Maxey1987). Averaging this equation over statistics of fluid velocity fluctuations, we determine the mean particle velocity:
$\boldsymbol{v}^{(\text{p})}=\boldsymbol{u}-\unicode[STIX]{x1D70F}_{s}[\unicode[STIX]{x2202}\boldsymbol{u}/\unicode[STIX]{x2202}t+(\boldsymbol{u}\cdot \unicode[STIX]{x1D735})\boldsymbol{u}]+O(\unicode[STIX]{x1D70F}_{s}^{2})$
(Maxey Reference Maxey1987). Averaging this equation over statistics of fluid velocity fluctuations, we determine the mean particle velocity:
![]() $\overline{v}_{j}^{(\text{p})}=-\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D735}_{j}\overline{u_{i}u_{j}}$
. We take into account that for isotropic turbulence
$\overline{v}_{j}^{(\text{p})}=-\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D735}_{j}\overline{u_{i}u_{j}}$
. We take into account that for isotropic turbulence
![]() $\overline{u_{i}u_{j}}=(1/3)\overline{\boldsymbol{u}^{2}}\unicode[STIX]{x1D6FF}_{ij}$
. Therefore, the mean particle velocity is
$\overline{u_{i}u_{j}}=(1/3)\overline{\boldsymbol{u}^{2}}\unicode[STIX]{x1D6FF}_{ij}$
. Therefore, the mean particle velocity is
![]() $\overline{\boldsymbol{v}}^{(\text{p})}=-(\unicode[STIX]{x1D70F}_{s}/3)\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
(for details, see Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1998a
). This turbophoresis effect results in the formation of large-scale clusters of inertial particles at local minima of the mean-squared turbulent velocity. Note that the compressible turbophoresis for non-inertial particles originates from the turbulent particle flux
$\overline{\boldsymbol{v}}^{(\text{p})}=-(\unicode[STIX]{x1D70F}_{s}/3)\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
(for details, see Elperin et al.
Reference Elperin, Kleeorin and Rogachevskii1998a
). This turbophoresis effect results in the formation of large-scale clusters of inertial particles at local minima of the mean-squared turbulent velocity. Note that the compressible turbophoresis for non-inertial particles originates from the turbulent particle flux
![]() $\overline{n\,\boldsymbol{u}}$
, i.e. it describes a collective statistical phenomenon, while classical turbophoresis is not related to the correlations between velocity and number density fluctuations and is obtained from the expression for the mean velocity of inertial particles.
$\overline{n\,\boldsymbol{u}}$
, i.e. it describes a collective statistical phenomenon, while classical turbophoresis is not related to the correlations between velocity and number density fluctuations and is obtained from the expression for the mean velocity of inertial particles.
In the case of rapidly rotating turbulence, another pumping effect of inertial particles arises which can accumulate particles (Hodgson & Brandenburg Reference Hodgson and Brandenburg1998; Elperin, Kleeorin & Rogachevskii Reference Elperin, Kleeorin and Rogachevskii1998b ). This effect can be related to the combined action of particle inertia and non-zero mean kinetic helicity in rotating turbulence.
4 Comparison with Krause & Rädler (Reference Krause and Rädler1980) and Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011)
In this section we compare our results with those obtained previously by Krause & Rädler (Reference Krause and Rädler1980) and Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011). Let us consider non-stratified, isotropic, homogeneous and non-helical random flow. In this case (2.12) reads:
where the first two terms,
![]() $\unicode[STIX]{x1D6FF}_{ij}-k_{ij}$
, in the squared brackets describes the vortical part of the turbulent flow, while the last term,
$\unicode[STIX]{x1D6FF}_{ij}-k_{ij}$
, in the squared brackets describes the vortical part of the turbulent flow, while the last term,
![]() $2\unicode[STIX]{x1D70E}_{c}\,k_{ij}$
determines the potential part of the flow. Representing the velocity fluctuations as the sum of vortical and potential parts,
$2\unicode[STIX]{x1D70E}_{c}\,k_{ij}$
determines the potential part of the flow. Representing the velocity fluctuations as the sum of vortical and potential parts,
we can construct the correlation function,
![]() $f_{ij}^{(0)}(\boldsymbol{k})=\overline{u_{i}(\boldsymbol{k})u_{j}(-\boldsymbol{k})}$
, of the velocity field in
$f_{ij}^{(0)}(\boldsymbol{k})=\overline{u_{i}(\boldsymbol{k})u_{j}(-\boldsymbol{k})}$
, of the velocity field in
![]() $\boldsymbol{k}$
space for non-stratified, isotropic, homogeneous and non-helical random background flow as
$\boldsymbol{k}$
space for non-stratified, isotropic, homogeneous and non-helical random background flow as
where
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D74D}=0$
, and we also assumed that compressible and incompressible parts of the random velocity field have the same spectra,
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D74D}=0$
, and we also assumed that compressible and incompressible parts of the random velocity field have the same spectra,
![]() $E(k)$
. It follows from (4.1) and (4.3) that the degree of compressibility is
$E(k)$
. It follows from (4.1) and (4.3) that the degree of compressibility is
![]() $\unicode[STIX]{x1D70E}_{c}=\overline{\unicode[STIX]{x1D719}^{2}}/\overline{\unicode[STIX]{x1D74D}^{2}}$
. For simplicity, we consider here the instantaneous correlation function.
$\unicode[STIX]{x1D70E}_{c}=\overline{\unicode[STIX]{x1D719}^{2}}/\overline{\unicode[STIX]{x1D74D}^{2}}$
. For simplicity, we consider here the instantaneous correlation function.
To derive (4.3), we rewrite (4.2) in
![]() $\boldsymbol{k}$
space:
$\boldsymbol{k}$
space:
![]() $u_{i}(\boldsymbol{k})=\text{i}k_{m}\unicode[STIX]{x1D700}_{imn}\unicode[STIX]{x1D713}_{n}(\boldsymbol{k})+\text{i}k_{i}\unicode[STIX]{x1D719}(\boldsymbol{k})$
, and assume that the vortical and potential parts are not correlated. This allows us to obtain the following expression for
$u_{i}(\boldsymbol{k})=\text{i}k_{m}\unicode[STIX]{x1D700}_{imn}\unicode[STIX]{x1D713}_{n}(\boldsymbol{k})+\text{i}k_{i}\unicode[STIX]{x1D719}(\boldsymbol{k})$
, and assume that the vortical and potential parts are not correlated. This allows us to obtain the following expression for
![]() $f_{ij}^{(0)}(\boldsymbol{k})$
:
$f_{ij}^{(0)}(\boldsymbol{k})$
:
where
Taking into account that for the vortical field
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D74D}=0$
, the correlation function is of the form
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D74D}=0$
, the correlation function is of the form
![]() $\overline{\unicode[STIX]{x1D713}_{i}(\boldsymbol{k})\unicode[STIX]{x1D713}_{j}(-\boldsymbol{k})}\propto \unicode[STIX]{x1D6FF}_{ij}-k_{ij}$
, and using (4.5) we obtain
$\overline{\unicode[STIX]{x1D713}_{i}(\boldsymbol{k})\unicode[STIX]{x1D713}_{j}(-\boldsymbol{k})}\propto \unicode[STIX]{x1D6FF}_{ij}-k_{ij}$
, and using (4.5) we obtain
Substituting (4.6)–(4.7) into (4.4), we arrive at (4.3).
4.1 Small magnetic Reynolds numbers
Substituting (4.3) into (2.16) and using (2.11), we find that the turbulent magnetic diffusivity for small magnetic Reynolds numbers reads:
This result agrees with that of Krause & Rädler (Reference Krause and Rädler1980). Substituting (4.3) into (3.6), we find that the turbulent diffusion coefficient for passive scalars at small Péclet numbers is given by:
This result also agrees with that of Rädler et al. (Reference Rädler, Brandenburg, Del Sordo and Rheinhardt2011).
4.2 Large magnetic Reynolds numbers
In the case of large magnetic Reynolds numbers, substituting (4.3) into (2.28), we find for the turbulent magnetic diffusivity
This result is in good agreement with (2.30) for
![]() $\unicode[STIX]{x1D702}_{\text{t}}$
and with (3.15) for
$\unicode[STIX]{x1D702}_{\text{t}}$
and with (3.15) for
![]() $D_{\text{t}}$
.
$D_{\text{t}}$
.
5 Conclusions
A mean-field theory for the compressibility effects in the mean electromotive force in turbulent magnetohydrodynamics and in the turbulent flux of passive scalars or particles has been developed. This study is based on the quasi-linear approach applied for small magnetic Reynolds and Péclet numbers, and on the spectral
![]() $\unicode[STIX]{x1D70F}$
-approach for large fluid (
$\unicode[STIX]{x1D70F}$
-approach for large fluid (
![]() $Re$
) and magnetic (
$Re$
) and magnetic (
![]() $Rm$
) Reynolds numbers and large Péclet numbers (
$Rm$
) Reynolds numbers and large Péclet numbers (
![]() $Pe$
). Compressibility is found to cause a depletion of the
$Pe$
). Compressibility is found to cause a depletion of the
![]() $\unicode[STIX]{x1D6FC}$
effect and turbulent magnetic diffusion for small and large
$\unicode[STIX]{x1D6FC}$
effect and turbulent magnetic diffusion for small and large
![]() $Rm$
. It also decreases the turbulent diffusivity of passive scalars for small and large
$Rm$
. It also decreases the turbulent diffusivity of passive scalars for small and large
![]() $Pe$
. Indeed, the expressions for the turbulent magnetic diffusivity and the turbulent diffusivity of passive scalars coincide after replacing
$Pe$
. Indeed, the expressions for the turbulent magnetic diffusivity and the turbulent diffusivity of passive scalars coincide after replacing
![]() $Rm$
by
$Rm$
by
![]() $Pe$
, and vice versa. Compressibility does not change the effective pumping velocity of the magnetic field for
$Pe$
, and vice versa. Compressibility does not change the effective pumping velocity of the magnetic field for
![]() $Rm\gg 1$
, but decreases it for
$Rm\gg 1$
, but decreases it for
![]() $Rm\ll 1$
. In addition, compressibility causes a pumping of particles in regions with higher turbulent intensity for small and large Péclet numbers. This new effect is interpreted in terms of compressible turbophoresis for non-inertial particles. This effect is completely different from classical turbophoresis, which only affects inertial particles and results in pumping of inertial particles to regions of lower turbulent intensity. Compressible turbophoresis for non-inertial particles is a collective statistical phenomenon originating from the turbulent particle flux. On the other hand, classical turbophoresis originates directly from the expression for the mean velocity of inertial particles. For small Mach numbers, compressibility effects are only determined by the density stratification through the
$Rm\ll 1$
. In addition, compressibility causes a pumping of particles in regions with higher turbulent intensity for small and large Péclet numbers. This new effect is interpreted in terms of compressible turbophoresis for non-inertial particles. This effect is completely different from classical turbophoresis, which only affects inertial particles and results in pumping of inertial particles to regions of lower turbulent intensity. Compressible turbophoresis for non-inertial particles is a collective statistical phenomenon originating from the turbulent particle flux. On the other hand, classical turbophoresis originates directly from the expression for the mean velocity of inertial particles. For small Mach numbers, compressibility effects are only determined by the density stratification through the
![]() $\unicode[STIX]{x1D706}$
terms in (2.12) and (2.27). We find that the density stratification does not affect the magnetic field, although it causes a turbulent pumping of particles to regions of maximum mean fluid density.
$\unicode[STIX]{x1D706}$
terms in (2.12) and (2.27). We find that the density stratification does not affect the magnetic field, although it causes a turbulent pumping of particles to regions of maximum mean fluid density.
The mean-field theory developed for compressibility effects in turbulent magnetohydrodynamics and turbulent transport of passive scalars and particles needs to be verified in direct numerical simulations and large-eddy simulations using the test-field and test-scalar methods (see, e.g. Schrinner et al. Reference Schrinner, Rädler, Schmitt, Rheinhardt and Christensen2005, Reference Schrinner, Rädler, Schmitt, Rheinhardt and Christensen2007; Brandenburg et al. Reference Brandenburg, Rädler, Rheinhardt and Käpylä2008, Reference Brandenburg, Rädler and Kemel2012b ), which is the subject of a separate study. Furthermore, in view of astrophysical and geophysical applications, it is important to consider the additional effects of rotation, turbulent convection and the presence of stably stratified turbulence with large-scale temperature gradients (see, e.g. Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2003; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2006, Reference Rogachevskii and Kleeorin2007; Brandenburg et al. Reference Brandenburg, Rädler and Kemel2012b ).
Acknowledgements
We thank M. Rheinhardt for his many questions and suggestions which have significantly improved the clarity of the presentation. This work was supported in part by the Research Council of Norway under the FRINATEK (grant no. 231444), the Israel Science Foundation governed by the Israeli Academy of Sciences (grant no. 1210/15), the National Science Foundation under grants no. NSF PHY-1748958 and AAG-1615100 and the University of Colorado through its support of the George Ellery Hale visiting faculty appointment. I.R. acknowledges the hospitality of Nordita, the Laboratory for Atmospheric and Space Physics of the University of Colorado, the Kavli Institute for Theoretical Physics in Santa Barbara and the École Polytechnique Fédérale de Lausanne.
Appendix A. Derivation of (2.11) for
 $Rm\ll 1$
, and (3.6) for
$Rm\ll 1$
, and (3.6) for
 $Pe\ll 1$
$Pe\ll 1$
In the limit of small magnetic Reynolds number, we neglect in (2.5) nonlinear terms, but keep molecular dissipative terms of the magnetic fluctuations. The solution of (2.5) reads:
where
![]() $G_{\unicode[STIX]{x1D702}}(\boldsymbol{k},\unicode[STIX]{x1D714})=(\unicode[STIX]{x1D702}\boldsymbol{k}^{2}+\text{i}\unicode[STIX]{x1D714})^{-1}$
. To derive (A 1), we consider the source term in the induction equation for the magnetic fluctuations,
$G_{\unicode[STIX]{x1D702}}(\boldsymbol{k},\unicode[STIX]{x1D714})=(\unicode[STIX]{x1D702}\boldsymbol{k}^{2}+\text{i}\unicode[STIX]{x1D714})^{-1}$
. To derive (A 1), we consider the source term in the induction equation for the magnetic fluctuations,
![]() $(\overline{\boldsymbol{B}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}$
, which can be rewritten using Fourier transformation as
$(\overline{\boldsymbol{B}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}$
, which can be rewritten using Fourier transformation as
For brevity of notation we omit hereafter the arguments
![]() $t$
and
$t$
and
![]() $\boldsymbol{x}$
in the functions
$\boldsymbol{x}$
in the functions
![]() $\overline{\boldsymbol{B}}(\boldsymbol{x},t)$
and
$\overline{\boldsymbol{B}}(\boldsymbol{x},t)$
and
![]() $\boldsymbol{u}(\boldsymbol{x},t)$
, and also the variable
$\boldsymbol{u}(\boldsymbol{x},t)$
, and also the variable
![]() $t$
in the functions
$t$
in the functions
![]() $\overline{B}_{p}(\boldsymbol{Q},t)$
and
$\overline{B}_{p}(\boldsymbol{Q},t)$
and
![]() $u_{i}(\boldsymbol{k},t)$
. We introduce a new variable
$u_{i}(\boldsymbol{k},t)$
. We introduce a new variable
![]() $\boldsymbol{k}=\boldsymbol{k}^{\prime }+\boldsymbol{Q}$
and take into account that
$\boldsymbol{k}=\boldsymbol{k}^{\prime }+\boldsymbol{Q}$
and take into account that
![]() $Q_{p}\,\overline{B}_{p}(\boldsymbol{Q})=0$
, which yields
$Q_{p}\,\overline{B}_{p}(\boldsymbol{Q})=0$
, which yields
 $$\begin{eqnarray}\displaystyle (\overline{\boldsymbol{B}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})u_{i} & = & \displaystyle \int \left(\text{i}k_{p}\int \overline{B}_{p}(\boldsymbol{Q})u_{i}(\boldsymbol{k}-\boldsymbol{Q})\,\text{d}\boldsymbol{Q}\right)\exp (\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & \equiv & \displaystyle \int \left[(\overline{\boldsymbol{B}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})u_{i}\right]_{\boldsymbol{k}}\exp (\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})\,\text{d}\boldsymbol{k},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\overline{\boldsymbol{B}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})u_{i} & = & \displaystyle \int \left(\text{i}k_{p}\int \overline{B}_{p}(\boldsymbol{Q})u_{i}(\boldsymbol{k}-\boldsymbol{Q})\,\text{d}\boldsymbol{Q}\right)\exp (\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})\,\text{d}\boldsymbol{k}\nonumber\\ \displaystyle & \equiv & \displaystyle \int \left[(\overline{\boldsymbol{B}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})u_{i}\right]_{\boldsymbol{k}}\exp (\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})\,\text{d}\boldsymbol{k},\end{eqnarray}$$
where
![]() $[\cdots \,]_{\boldsymbol{k}}$
denotes the Fourier transform. Therefore,
$[\cdots \,]_{\boldsymbol{k}}$
denotes the Fourier transform. Therefore,
Similar derivations are used for the other terms in the induction equation:
which yield (A 1).
To derive (2.11), we use (2.7) and (A 1) which yield
where
 $$\begin{eqnarray}\displaystyle J_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)G_{\unicode[STIX]{x1D702}}(\boldsymbol{k}+\boldsymbol{K}/2)\overline{u_{p}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{B}_{i}(\boldsymbol{Q})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)G_{\unicode[STIX]{x1D702}}(\boldsymbol{k}+\boldsymbol{K}/2)\overline{u_{p}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{B}_{i}(\boldsymbol{Q})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle J_{ij}^{(2)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)G_{\unicode[STIX]{x1D702}}(\boldsymbol{k}+\boldsymbol{K}/2)\overline{u_{i}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{B}_{p}(\boldsymbol{Q})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{ij}^{(2)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)G_{\unicode[STIX]{x1D702}}(\boldsymbol{k}+\boldsymbol{K}/2)\overline{u_{i}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{B}_{p}(\boldsymbol{Q})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q},\end{eqnarray}$$
and the functions
![]() $J_{ij}^{(1)}$
,
$J_{ij}^{(1)}$
,
![]() $J_{ij}^{(2)}$
,
$J_{ij}^{(2)}$
,
![]() $G_{\unicode[STIX]{x1D702}}$
and
$G_{\unicode[STIX]{x1D702}}$
and
![]() $u_{i}$
depend also on
$u_{i}$
depend also on
![]() $\unicode[STIX]{x1D714}$
. To simplify the notation, we do not show this dependence in the following calculations. First we determine the function
$\unicode[STIX]{x1D714}$
. To simplify the notation, we do not show this dependence in the following calculations. First we determine the function
![]() $J_{ij}^{(1)}$
, using new variables:
$J_{ij}^{(1)}$
, using new variables:
Therefore,
 $$\begin{eqnarray}\displaystyle J_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)f_{pj}(\boldsymbol{k}-\boldsymbol{Q}/2,\boldsymbol{K}-\boldsymbol{Q})G_{\unicode[STIX]{x1D702}}(\boldsymbol{k}+\boldsymbol{K}/2)\overline{B}_{i}(\boldsymbol{Q})\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)f_{pj}(\boldsymbol{k}-\boldsymbol{Q}/2,\boldsymbol{K}-\boldsymbol{Q})G_{\unicode[STIX]{x1D702}}(\boldsymbol{k}+\boldsymbol{K}/2)\overline{B}_{i}(\boldsymbol{Q})\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q}.\end{eqnarray}$$
Since
![]() $|\boldsymbol{Q}|\ll |\boldsymbol{k}|$
and
$|\boldsymbol{Q}|\ll |\boldsymbol{k}|$
and
![]() $|\boldsymbol{K}|\ll |\boldsymbol{k}|$
, we use the Taylor expansion
$|\boldsymbol{K}|\ll |\boldsymbol{k}|$
, we use the Taylor expansion
Substituting (A 12) and (A 13) into (A 11), we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle J_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R})=\text{i}G_{\unicode[STIX]{x1D702}}(\boldsymbol{k})\int \left[\left(k_{p}-\unicode[STIX]{x1D702}G_{\unicode[STIX]{x1D702}}(\boldsymbol{k})k_{p}k_{s}K_{s}+\frac{1}{2}K_{p}\right)\left(\int f_{pj}(\boldsymbol{k},\boldsymbol{K}-\boldsymbol{Q})\overline{B}_{i}(\boldsymbol{Q})\,\text{d}\boldsymbol{Q}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \quad -\left.\frac{1}{2}k_{p}\left(\int Q_{s}\overline{B}_{i}(\boldsymbol{Q})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k_{s}}f_{pj}(\boldsymbol{k},\boldsymbol{K}-\boldsymbol{Q})\,\text{d}\boldsymbol{Q}\right)\right]\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}+O(\boldsymbol{K}^{2},\boldsymbol{Q}^{2},K_{p}Q_{s}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle J_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R})=\text{i}G_{\unicode[STIX]{x1D702}}(\boldsymbol{k})\int \left[\left(k_{p}-\unicode[STIX]{x1D702}G_{\unicode[STIX]{x1D702}}(\boldsymbol{k})k_{p}k_{s}K_{s}+\frac{1}{2}K_{p}\right)\left(\int f_{pj}(\boldsymbol{k},\boldsymbol{K}-\boldsymbol{Q})\overline{B}_{i}(\boldsymbol{Q})\,\text{d}\boldsymbol{Q}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \quad -\left.\frac{1}{2}k_{p}\left(\int Q_{s}\overline{B}_{i}(\boldsymbol{Q})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k_{s}}f_{pj}(\boldsymbol{k},\boldsymbol{K}-\boldsymbol{Q})\,\text{d}\boldsymbol{Q}\right)\right]\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}+O(\boldsymbol{K}^{2},\boldsymbol{Q}^{2},K_{p}Q_{s}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
We use the following identity:
where
Similarly,
Therefore, (A 14)–(A 17) yield
 $$\begin{eqnarray}\displaystyle J_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle G_{\unicode[STIX]{x1D702}}\left\{\left[\text{i}k_{p}\left(1+\text{i}\unicode[STIX]{x1D702}\,G_{\unicode[STIX]{x1D702}}k_{s}\unicode[STIX]{x1D735}_{s}\right)\left(\overline{B}_{i}\,f_{pj}\right)+\overline{B}_{i}\frac{1}{2}\unicode[STIX]{x1D735}_{p}f_{pj}\right]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\left(f_{pj}-k_{m}\frac{\unicode[STIX]{x2202}f_{mj}}{\unicode[STIX]{x2202}k_{p}}\right)(\unicode[STIX]{x1D735}_{p}\overline{B}_{i})\right\}+O(\unicode[STIX]{x1D6FB}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle G_{\unicode[STIX]{x1D702}}\left\{\left[\text{i}k_{p}\left(1+\text{i}\unicode[STIX]{x1D702}\,G_{\unicode[STIX]{x1D702}}k_{s}\unicode[STIX]{x1D735}_{s}\right)\left(\overline{B}_{i}\,f_{pj}\right)+\overline{B}_{i}\frac{1}{2}\unicode[STIX]{x1D735}_{p}f_{pj}\right]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\left(f_{pj}-k_{m}\frac{\unicode[STIX]{x2202}f_{mj}}{\unicode[STIX]{x2202}k_{p}}\right)(\unicode[STIX]{x1D735}_{p}\overline{B}_{i})\right\}+O(\unicode[STIX]{x1D6FB}^{2}).\end{eqnarray}$$
A similar derivation is also performed for
![]() $J_{ij}^{(2)}$
, which yields
$J_{ij}^{(2)}$
, which yields
 $$\begin{eqnarray}\displaystyle J_{ij}^{(2)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle G_{\unicode[STIX]{x1D702}}\left\{\overline{B}_{p}\left[\text{i}k_{p}f_{ij}+\frac{1}{2}\unicode[STIX]{x1D735}_{p}f_{ij}-\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}\unicode[STIX]{x1D735}_{s}f_{ij}\right]\right.\nonumber\\ \displaystyle & & \displaystyle -\left.(\unicode[STIX]{x1D735}_{s}\overline{B}_{p})\left[\frac{1}{2}k_{p}\frac{\unicode[STIX]{x2202}f_{ij}}{\unicode[STIX]{x2202}k_{s}}+\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}f_{ij}\right]\right\}+O(\unicode[STIX]{x1D6FB}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{ij}^{(2)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle G_{\unicode[STIX]{x1D702}}\left\{\overline{B}_{p}\left[\text{i}k_{p}f_{ij}+\frac{1}{2}\unicode[STIX]{x1D735}_{p}f_{ij}-\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}\unicode[STIX]{x1D735}_{s}f_{ij}\right]\right.\nonumber\\ \displaystyle & & \displaystyle -\left.(\unicode[STIX]{x1D735}_{s}\overline{B}_{p})\left[\frac{1}{2}k_{p}\frac{\unicode[STIX]{x2202}f_{ij}}{\unicode[STIX]{x2202}k_{s}}+\unicode[STIX]{x1D702}k^{2}G_{\unicode[STIX]{x1D702}}\,k_{sp}f_{ij}\right]\right\}+O(\unicode[STIX]{x1D6FB}^{2}).\end{eqnarray}$$
Therefore, (A 18) and (A 19) yield (2.11).
To determine the turbulent flux of particles for small Péclet numbers, we rewrite (3.3) in Fourier space using an equation similar to (A 4), and find the solution of (3.3) as
where
![]() $G_{D}(\boldsymbol{k},\unicode[STIX]{x1D714})=(D\boldsymbol{k}^{2}+\text{i}\unicode[STIX]{x1D714})^{-1}$
. The function
$G_{D}(\boldsymbol{k},\unicode[STIX]{x1D714})=(D\boldsymbol{k}^{2}+\text{i}\unicode[STIX]{x1D714})^{-1}$
. The function
![]() $F_{j}(\boldsymbol{k},\boldsymbol{R})$
, defined by (3.5), is
$F_{j}(\boldsymbol{k},\boldsymbol{R})$
, defined by (3.5), is
 $$\begin{eqnarray}\displaystyle F_{j}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle -\text{i}\int (k_{p}+K_{p}/2)\overline{u_{p}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,G_{D}(\boldsymbol{k}+\boldsymbol{K}/2)N(\boldsymbol{Q})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{j}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle -\text{i}\int (k_{p}+K_{p}/2)\overline{u_{p}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,G_{D}(\boldsymbol{k}+\boldsymbol{K}/2)N(\boldsymbol{Q})\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q},\end{eqnarray}$$
where the functions
![]() $F_{j}$
,
$F_{j}$
,
![]() $G_{D}$
and
$G_{D}$
and
![]() $u_{i}$
depend also on
$u_{i}$
depend also on
![]() $\unicode[STIX]{x1D714}$
, and
$\unicode[STIX]{x1D714}$
, and
![]() $N$
depends on
$N$
depends on
![]() $t$
as well. To simplify the notation, we do not show this dependence here. We perform calculations similar to those in (A 8)–(A 18). In particular, after the Taylor expansion for
$t$
as well. To simplify the notation, we do not show this dependence here. We perform calculations similar to those in (A 8)–(A 18). In particular, after the Taylor expansion for
![]() $|\boldsymbol{Q}|\ll |\boldsymbol{k}|$
and
$|\boldsymbol{Q}|\ll |\boldsymbol{k}|$
and
![]() $|\boldsymbol{K}|\ll |\boldsymbol{k}|$
, we arrive at expression (3.6) for the turbulent flux of particles in Fourier space for small Péclet numbers.
$|\boldsymbol{K}|\ll |\boldsymbol{k}|$
, we arrive at expression (3.6) for the turbulent flux of particles in Fourier space for small Péclet numbers.
Appendix B. Derivation of (2.20) for
 $Rm\ll 1$
$Rm\ll 1$
The effective pumping velocity
![]() $\unicode[STIX]{x1D738}$
of the large-scale magnetic field is independent of
$\unicode[STIX]{x1D738}$
of the large-scale magnetic field is independent of
![]() $\unicode[STIX]{x1D740}$
for
$\unicode[STIX]{x1D740}$
for
![]() $Rm\ll 1$
. Indeed, the contribution of
$Rm\ll 1$
. Indeed, the contribution of
![]() $\unicode[STIX]{x1D740}$
to the effective pumping velocity
$\unicode[STIX]{x1D740}$
to the effective pumping velocity
![]() $\unicode[STIX]{x1D738}$
can only arise from the term
$\unicode[STIX]{x1D738}$
can only arise from the term
Integration over solid angles in
![]() $\boldsymbol{k}$
space in
$\boldsymbol{k}$
space in
![]() $g_{ij}^{(1)}=\int g_{ij}^{(1)}(\boldsymbol{k},\unicode[STIX]{x1D714})\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714}$
yields
$g_{ij}^{(1)}=\int g_{ij}^{(1)}(\boldsymbol{k},\unicode[STIX]{x1D714})\,\text{d}\boldsymbol{k}\,\text{d}\unicode[STIX]{x1D714}$
yields
which is a symmetric tensor with respect to the indexes
![]() $i$
and
$i$
and
![]() $j$
. Therefore, it cannot contribute to the mean electromotive force nor to
$j$
. Therefore, it cannot contribute to the mean electromotive force nor to
![]() $\unicode[STIX]{x1D738}$
. For integration over solid angles in
$\unicode[STIX]{x1D738}$
. For integration over solid angles in
![]() $\boldsymbol{k}$
space in the expression for
$\boldsymbol{k}$
space in the expression for
![]() $g_{ij}^{(1)}$
, we take into account that
$g_{ij}^{(1)}$
, we take into account that
![]() $\int k_{ij}\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D711}=(4\unicode[STIX]{x03C0}/3)\unicode[STIX]{x1D6FF}_{ij}$
, where we use spherical coordinates
$\int k_{ij}\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D711}=(4\unicode[STIX]{x03C0}/3)\unicode[STIX]{x1D6FF}_{ij}$
, where we use spherical coordinates
![]() $(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
in
$(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
in
![]() $\boldsymbol{k}$
space.
$\boldsymbol{k}$
space.
The remaining contribution, which is proportional to the mean magnetic field, is
Since we neglect effects
![]() ${\sim}O(\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{i}\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D6FB}^{2}\,\overline{\boldsymbol{u}^{2}})$
, the term
${\sim}O(\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{i}\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D706}^{2}\,\overline{\boldsymbol{u}^{2}},\unicode[STIX]{x1D6FB}^{2}\,\overline{\boldsymbol{u}^{2}})$
, the term
![]() $g_{ij}^{(2)}(\boldsymbol{k},\unicode[STIX]{x1D714})$
describes only the contribution to
$g_{ij}^{(2)}(\boldsymbol{k},\unicode[STIX]{x1D714})$
describes only the contribution to
![]() $\unicode[STIX]{x1D738}$
caused by
$\unicode[STIX]{x1D738}$
caused by
![]() $\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, i.e. the effect of inhomogeneity of turbulence, rather than the effect of stratification on
$\unicode[STIX]{x1D735}\overline{\boldsymbol{u}^{2}}$
, i.e. the effect of inhomogeneity of turbulence, rather than the effect of stratification on
![]() $\unicode[STIX]{x1D738}$
. A non-zero contribution to
$\unicode[STIX]{x1D738}$
. A non-zero contribution to
![]() $g_{ij}^{(2)}$
(and to the mean electromotive force) is only from the last two terms in (B 3), which are proportional to
$g_{ij}^{(2)}$
(and to the mean electromotive force) is only from the last two terms in (B 3), which are proportional to
![]() $f_{sj}$
, where
$f_{sj}$
, where
![]() $f_{sj}\propto (\unicode[STIX]{x1D6FF}_{sj}-k_{sj}+2\unicode[STIX]{x1D70E}_{c}\,k_{sj})\overline{\boldsymbol{u}^{2}}$
. Indeed, the first two terms
$f_{sj}\propto (\unicode[STIX]{x1D6FF}_{sj}-k_{sj}+2\unicode[STIX]{x1D70E}_{c}\,k_{sj})\overline{\boldsymbol{u}^{2}}$
. Indeed, the first two terms
![]() $\propto f_{ij}$
in (B 3) (which is a symmetric tensor with respect to the indexes
$\propto f_{ij}$
in (B 3) (which is a symmetric tensor with respect to the indexes
![]() $i$
and
$i$
and
![]() $j$
) cannot contribute to the electromotive force. Here we also took into account that
$j$
) cannot contribute to the electromotive force. Here we also took into account that
![]() $\int k_{i}\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D711}=0$
. After integration in
$\int k_{i}\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D711}=0$
. After integration in
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\unicode[STIX]{x1D714}$
space we arrive at (2.20) for the effective pumping velocity
$\unicode[STIX]{x1D714}$
space we arrive at (2.20) for the effective pumping velocity
![]() $\unicode[STIX]{x1D738}$
for
$\unicode[STIX]{x1D738}$
for
![]() $Rm\ll 1$
. For integration over
$Rm\ll 1$
. For integration over
![]() $\unicode[STIX]{x1D714}$
, we use the following integrals
$\unicode[STIX]{x1D714}$
, we use the following integrals
![]() $\unicode[STIX]{x1D70F}_{0}\gg (\unicode[STIX]{x1D702}k^{2})^{-1}$
:
$\unicode[STIX]{x1D70F}_{0}\gg (\unicode[STIX]{x1D702}k^{2})^{-1}$
:
Applying the turbulence model of Amir et al. (Reference Amir, Bar, Eidelman, Elperin, Kleeorin and Rogachevskii2017) for arbitrary stratification (see also Elperin et al. Reference Elperin, Kleeorin and Rogachevskii1995),
we show that there are no contributions of
![]() $\unicode[STIX]{x1D740}$
to the effective pumping velocity
$\unicode[STIX]{x1D740}$
to the effective pumping velocity
![]() $\unicode[STIX]{x1D738}$
of the large-scale magnetic field – even for strong stratifications. In particular, we substitute (B 6) into (B 2), taking into account that
$\unicode[STIX]{x1D738}$
of the large-scale magnetic field – even for strong stratifications. In particular, we substitute (B 6) into (B 2), taking into account that
![]() $\int k_{p}\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D711}=0$
. Note also that a cross-effect of stratification and inhomogeneity of turbulence,
$\int k_{p}\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D711}=0$
. Note also that a cross-effect of stratification and inhomogeneity of turbulence,
![]() $(\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{j}-\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D735}_{i})\overline{\boldsymbol{u}^{2}}$
, in the model of the background turbulence does not contribute to the effective pumping velocity
$(\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D735}_{j}-\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D735}_{i})\overline{\boldsymbol{u}^{2}}$
, in the model of the background turbulence does not contribute to the effective pumping velocity
![]() $\boldsymbol{\unicode[STIX]{x1D6FE}}$
for the same reasons.
$\boldsymbol{\unicode[STIX]{x1D6FE}}$
for the same reasons.
Appendix C. Derivation of (2.23) for
 $Rm\gg 1$
and (3.12) for
$Rm\gg 1$
and (3.12) for
 $Pe\gg 1$
$Pe\gg 1$
For the derivation of (2.23), we perform the following calculation. We use the identity:
We rewrite the induction equation (2.5) for magnetic fluctuations in
![]() $\boldsymbol{k}$
space:
$\boldsymbol{k}$
space:
using (A 4)–(A 6). Here
![]() $b_{i}^{(\text{N})}(\boldsymbol{k})$
includes the nonlinear terms. For brevity of notation we omit below the variable
$b_{i}^{(\text{N})}(\boldsymbol{k})$
includes the nonlinear terms. For brevity of notation we omit below the variable
![]() $t$
in the functions
$t$
in the functions
![]() $\overline{B}_{i}(\boldsymbol{Q},t)$
,
$\overline{B}_{i}(\boldsymbol{Q},t)$
,
![]() $b_{i}(\boldsymbol{k},t)$
,
$b_{i}(\boldsymbol{k},t)$
,
![]() $b_{i}^{(\text{N})}(\boldsymbol{k},t)$
and
$b_{i}^{(\text{N})}(\boldsymbol{k},t)$
and
![]() $u_{i}(\boldsymbol{k},t)$
. To derive (2.23), we use (C 1) and (C 2) which yields
$u_{i}(\boldsymbol{k},t)$
. To derive (2.23), we use (C 1) and (C 2) which yields
where
 $$\begin{eqnarray}\displaystyle \tilde{J}_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)\overline{B}_{p}(\boldsymbol{Q})\overline{u_{i}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{J}_{ij}^{(1)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)\overline{B}_{p}(\boldsymbol{Q})\overline{u_{i}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \tilde{J}_{ij}^{(2)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)\overline{B}_{i}(\boldsymbol{Q})\overline{u_{p}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{J}_{ij}^{(2)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle \text{i}\int (k_{p}+K_{p}/2)\overline{B}_{i}(\boldsymbol{Q})\overline{u_{p}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q}.\end{eqnarray}$$
Next, we perform calculations that are similar to (A 10)–(A 12) and (A 14)–(A 18). In particular, we introduce new variables:
![]() $\tilde{\boldsymbol{k}}=(\tilde{\boldsymbol{k}}_{1}-\tilde{\boldsymbol{k}}_{2})/2=\boldsymbol{k}-\boldsymbol{Q}/2$
and
$\tilde{\boldsymbol{k}}=(\tilde{\boldsymbol{k}}_{1}-\tilde{\boldsymbol{k}}_{2})/2=\boldsymbol{k}-\boldsymbol{Q}/2$
and
![]() $\tilde{\boldsymbol{K}}=\tilde{\boldsymbol{k}}_{1}+\tilde{\boldsymbol{k}}_{2}=\boldsymbol{K}-\boldsymbol{Q}$
, and use the Taylor expansions for
$\tilde{\boldsymbol{K}}=\tilde{\boldsymbol{k}}_{1}+\tilde{\boldsymbol{k}}_{2}=\boldsymbol{K}-\boldsymbol{Q}$
, and use the Taylor expansions for
![]() $|\boldsymbol{Q}|\ll |\boldsymbol{k}|$
and
$|\boldsymbol{Q}|\ll |\boldsymbol{k}|$
and
![]() $|\boldsymbol{K}|\ll |\boldsymbol{k}|$
, which yield
$|\boldsymbol{K}|\ll |\boldsymbol{k}|$
, which yield
Therefore, (C 2)–(C 7) yield (2.23) for
![]() $Rm\gg 1$
.
$Rm\gg 1$
.
For the derivation of (3.12), we perform the following calculation. We use the identity:
We rewrite (3.3) for fluctuations of the particle number density, in
![]() $\boldsymbol{k}$
space:
$\boldsymbol{k}$
space:
using (A 4). Here
![]() $n^{(\text{N})}(\boldsymbol{k})$
includes the nonlinear terms. For brevity of notation we omit below the variable
$n^{(\text{N})}(\boldsymbol{k})$
includes the nonlinear terms. For brevity of notation we omit below the variable
![]() $t$
in the functions
$t$
in the functions
![]() $N(\boldsymbol{Q},t)$
,
$N(\boldsymbol{Q},t)$
,
![]() $n(\boldsymbol{k},t)$
,
$n(\boldsymbol{k},t)$
,
![]() $n^{(\text{N})}(\boldsymbol{k},t)$
and
$n^{(\text{N})}(\boldsymbol{k},t)$
and
![]() $u_{i}(\boldsymbol{k},t)$
. To derive (3.12), we use (C 8) and (C 9) which yields
$u_{i}(\boldsymbol{k},t)$
. To derive (3.12), we use (C 8) and (C 9) which yields
where
 $$\begin{eqnarray}\displaystyle \tilde{J}_{j}^{(3)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle -\text{i}\int (\boldsymbol{k}_{p}+K_{p}/2)N(\boldsymbol{Q})\overline{u_{p}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{J}_{j}^{(3)}(\boldsymbol{k},\boldsymbol{R}) & = & \displaystyle -\text{i}\int (\boldsymbol{k}_{p}+K_{p}/2)N(\boldsymbol{Q})\overline{u_{p}(\boldsymbol{k}+\boldsymbol{K}/2-\boldsymbol{Q})u_{j}(-\boldsymbol{k}+\boldsymbol{K}/2)}\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R})\,\text{d}\boldsymbol{K}\,\text{d}\boldsymbol{Q}.\end{eqnarray}$$
We perform calculations that are similar to (A 10)–(A 12) and (A 14)–(A 18), which yield