1. Why conventional rationality requirements are insufficient

In the joke above, John appears to act irrationally. The apparent reason for this is that he prefers strawberry to chocolate and chocolate to strawberry. There are some potential explanations for why John behaves irrationally available in the literature on rational choice and normative theory. In this section, I discuss three possible explanations and dismiss all of these on the grounds that they fail to recognize the importance of individuating alternatives appropriately. The first explanation refers to how the better than relation that reflects John’s judgements does not seem to be asymmetric. The second explanation refers to how John’s decision method violates basic contraction consistency. The third explanation refers to how John’s decision method violates normative invariance. I explain in further detail what these terms mean below.

First, it might be said that John expresses a better than relation that is not asymmetric. A relation, R, is asymmetric if and only if for all elements that it applies to, if it holds between two elements, a and b, it does not hold between b and a. Consider two examples: greater than as it applies to the set of real numbers and more creative as it applies to the set of composers. If one real number is greater than another, the latter is not greater than the former. If Mozart was a more creative composer than Salieri, then Salieri was not a more creative composer than Mozart. It seems obvious that also better than is a relation that is asymmetric. If a is better than b, then b is not better than a. John, however, expresses the view that strawberry is better than chocolate, but he also seems to express the view that chocolate is better than strawberry. If the better than relation that reflects John’s judgements was asymmetric, strawberry and chocolate could not bear these relations to each other. If strawberry is better than chocolate, then by asymmetry chocolate cannot be better than strawberry, and vice versa. It seems nonsensical and irrational to hold judgements that are reflected by non-asymmetric better than relations and, to my knowledge, no one has ever suggested that the better than relation is not asymmetric. Thereby, John is irrational.

Second, his decision method might be said to violate basic contraction consistency (sometimes called alpha or the Chernoff condition, cf. Chernoff Reference Chernoff1954; Sen Reference Sen1970, Reference Sen1993; Fleurbaey et al. Reference Fleurbaey, Tungodden and Vallentyne2009; Temkin Reference Temkin2012; Voorhoeve Reference Voorhoeve2014; Herlitz Reference Herlitz2019):

This condition has significant intuitive appeal and some take it to be a basic requirement of rationality (cf. Chernoff Reference Chernoff1954; Sen Reference Sen1970; Fleurbaey et al. Reference Fleurbaey, Tungodden and Vallentyne2009). Amartya Sen, for example, has (in his early work) suggested that this is the condition that ensures that if the best athlete in the world is a Pakistani, then she must also be the best athlete in Pakistan (Sen Reference Sen1970).

Since, by definition, all sets are subsets of themselves, basic contraction consistency seems to be violated by John. He prefers strawberry in the set {strawberry, chocolate}, while he prefers chocolate in the subset {strawberry, chocolate}. Accepting decision methods that violate basic contraction consistency is irrational, and thereby John is irrational.Footnote ¹

Third, consider what Krister Bykvist (accrediting Wlodek Rabinowicz with the term) calls ‘normative invariance’ (cf. Carlson Reference Carlson1995; Bykvist Reference Bykvist2007a, Reference Bykvist2007b, Reference Bykvist, Hirose and Reisner2015; Arrhenius and Rabinowicz Reference Arrhenius, Rabinowicz, I. and Olson2014):

We might make a small adjustment to this condition so that it addresses outcomes rather than actions:

John’s decision method seems to ascribe normative statuses in a way that violates normative invariance*. Although this condition is not generally accepted as a basic requirement of rationality, and Bykvist dismisses its general relevance, one could use it (or some variation of it) to argue that John acts irrationally (Bykvist Reference Bykvist2007a). I will, however, not attempt to modify the condition in order to narrow it down to a version that might be generally relevant. I introduce it in order to illustrate a way of thinking about rationality, but I think that it faces the same significant flaw as the lines of arguments that invoke asymmetry of the better than relation and basic contraction consistency.

These three explanations are not satisfactory. John does not necessarily express a non-asymmetric better than relation and he does not necessarily violate either basic contraction consistency or normative invariance*. Sometimes, the act of choice in combination with a certain decision method or a certain normative theory give us reason to believe that apparent expressions of a non-asymmetric better than relation and apparent violations of basic contraction consistency and normative invariance* in fact should be explained in other ways. Consider, for instance, the possibility that John uses a decision method that states that he should always change his mind. With such a decision method, John does not express a non-asymmetric better than relation and his decision method does not violate basic contraction consistency or normative invariance*, because when he makes a choice some relevant features of the choice situation change, and so do the options that he faces. Strawberry and chocolate are not always strawberry and chocolate, as Sen has repeatedly stressed (cf. Sen Reference Sen1993, Reference Sen1997).

A common explanation of why certain theories seem to violate basic contraction consistency while they in fact do not refers to how one should sometimes individuate alternatives in a way that takes context into account (cf. Sugden Reference Sugden1985; Broome Reference Broome1991; Sen Reference Sen1993, Reference Sen1997; Kamm Reference Kamm1996; Arrhenius Reference Arrhenius, M. A. and D. T.2009; Voorhoeve Reference Voorhoeve2014; Herlitz Reference Herlitz2019). The decision method that someone is using, or the normative theory that one is examining, might imply that there is a significant difference between alternatives depending on context, for example before and after a choice has been made. If John uses a decision method that implies that there is a difference between strawberry before and after a choice has been made and/or between chocolate before and after a choice has been made, the alternatives should, according to this decision method, be individuated differently depending on whether a choice has been made. One could, for example, describe the alternatives in the following way: S and C before a choice has been made and S* and C* after a choice has been made. A relation, R, that can be shown to hold such that S R C and C* R S* has not been shown to not be asymmetric. And a theory that implies that S is permissible in {S, C} and that S* is not permissible in {S*, C*} does not violate basic contraction consistency. Similarly, normative invariance* is not violated because the normative status of S has not changed when S* is considered worse than C*. Therefore, John’s irrationality cannot be explained with reference to either non-asymmetric better than relations, basic contraction consistency or normative invariance*.

To summarize this section, agents who express a better than relation that is not asymmetric and agents who use decision methods that violate either basic contraction consistency or normative invariance* might well be accused of being irrational. However, none of these conditions can be invoked to show that John is necessarily irrational when he steps into the ice-cream parlour and expresses his preferences. This must be explained in some other way.

2. The stability condition

We should hold John to be irrational, but this is not because he expresses non-asymmetric better than relations or because his decision method violates basic contraction consistency or normative invariance*. In this section, I will suggest that an appropriate explanation of why John is irrational is that his decision method violates what I will call the stability condition.

In order to introduce the stability condition, let me first define what I will call transmutation_X :

As we saw in the previous sections, decision methods and normative theories sometimes imply that alternatives that seem identical should be individuated differently depending on context. One context that could be relevant according to a decision method is whether a choice has been made or not. On some normative views, certain positive and negative values are actualized by certain choices. These must then be dispersed across the alternatives in order for the individuations to appropriately correspond to the normative theory. The alternatives are thereby transmuted. Transmutation_X describes the particular kind of transmutation that is implied by a decision method or normative theory when a particular choice, X, has been made.

Transmutation_X describes the relevant implications for how alternatives ought to be individuated that follow making a particular choice. In order for a choice to be explicable in terms of the decision method/normative theory that is used, alternatives must be individuated so that the characteristics that in light of the decision method/normative theory are considered pertinent grounds for the choice are included (Broome Reference Broome1991; Voorhoeve Reference Voorhoeve2014; Herlitz Reference Herlitz2019). If a normative theory states, for instance, that utility should be maximized, alternatives should be individuated so that the amount of utility produced by choosing them is reflected in the individuations. Some decision methods and normative theories imply that making a choice changes the pertinent grounds for making a choice. These changes of what the pertinent grounds for making a choice are should thus be reflected in the individuations of the alternatives. Transmutation_X describes the changes of what the pertinent grounds for making a choice are that occur in a set of alternatives when a choice is made. In other words, transmutation_X describes the implications for how alternatives ought to be individuated according to a decision method/normative theory of making a choice. Dispersing the ‘negative and positive values associated with choosing X’ means that the characteristics that according to the decision method/normative theory have possible implications for the normative statuses of the different alternatives when a choice is made are incorporated in the new individuations of the alternatives. Importantly, thus, in a transmutation_X, all features of the alternatives that are unrelated to whether X is chosen or not are held constant. For instance, John’s subjective valuation of eating strawberry ice-cream is held constant when strawberry is transmuted_X as it is chosen.

Furthermore, transmutations_X do not take into account effects that can be said to be external to the choice itself, for example satisfaction and aggregative effects. If John first orders strawberry ice-cream, gets an opportunity to order a second ice-cream and then picks chocolate over strawberry, the alternatives have plausibly been transmuted by the fact that he already has one strawberry ice-cream (perhaps he values variation, or perhaps he wants to give the second ice-cream to his friend who prefers chocolate). Similarly, the fact that someone has already donated one million dollars to a particular charity has implications for whether or not it makes sense to donate another million dollars to that charity (perhaps she feels invested in the cause and sees even more reason to support it, or perhaps she values spreading her donations). Clearly, external effects of the choice like these imply that the alternatives must be individuated differently. However, by transmutation_X I only have in mind the implications for how alternatives ought to be individuated that follow the act of choosing a particular alternative, X, itself, not these external effects.Footnote ²

Having defined transmutation_X, the kind of transmutation that relates to whether or not a choice has been made, the stability condition can be introduced:

A different way of thinking about this condition is this. Let A_A and B_A describe options A and B respectively after A, which was initially maximal, has been chosen and the values associated with this choice has been dispersed across A and B so that these are transformed into A_A and B_A (i.e. they are the transmutations_A of A and B respectively). The stability condition states that the negative and positive values that are associated with choosing a maximal option, A, cannot be of such magnitude so that they alter the valence of the alternatives so significantly so that an option that was maximal (i.e. not worse than any alternative) prior to the choice no longer is maximal after it has been chosen.

It is common that making a choice is associated with some value, and this might also change the comparative relation between two alternatives. For instance, if moving to New York City and moving to Los Angeles are equally good (or even incomparable) alternatives and an agent decides to move to Los Angeles, this choice might entail that moving to Los Angeles is in fact better than moving to New York City (cf. Bricker Reference Bricker1980: 397–398). The choice itself means that the agent has reasons to favour Los Angeles over New York City. The transmutations_LA of New York City and Los Angeles that is associated with choosing Los Angeles (New York City_LA and Los Angeles_LA) have in this case changed the valence. New York City and Los Angeles are equally good. Yet New York City_LA is worse than Los Angeles_LA. It is important to note that the stability condition is not violated by a decision method or normative theory with such implications. The stability condition only rules out changes in the comparative relations of a certain kind, i.e. changes that make a maximal alternative non-maximal when it is chosen. If moving to New York City and moving to Los Angeles are equally good they are both maximal, and if New York City_LA is worse than Los Angeles_LA then the choice of a maximal alternative has entailed that the transmuted_X alternative is better than the other; it is still maximal. By contrast, decision methods that entail that if an agent decides to move to Los Angeles, then Los Angeles_LA is worse than New York City_LA violate the stability condition. In that case, choosing a maximal alternative entails that the transmuted_X version of this is no longer maximal.

John’s decision method violates the stability condition. According to John’s decision method, S is a maximal alternative in the set of alternatives {S, C}, but S* is not a maximal alternative in the set of alternatives {S*; C*}. The only difference between {S, C} and {S*, C*} is that in {S*, C*} the negative and positive values associated with choosing S have been dispersed across the alternatives S and C. Hence, S* and C* are nothing but the transmutations_S of S and C. John’s decision method thus implies that it is sometimes false that if an option, S, that according to the decision method is maximal in a set of alternatives, {S, C}, is chosen, then the transmutation_S of S, S_S , is also maximal according to the decision method in the set of transmuted_S alternatives, {S_S, C_S}.

Besides the intuitive appeal of the stability condition and its appealing result when applied to John and his decision method, there are at least three other reasons to accept it. Firstly, the reasons that support normative invariance and its relevance in certain contexts support also the stability condition. Bykvist argues that we should reject a theory that violates normative invariance when ‘the way it violates [normative invariance] makes the theory a poor guide to action’ (Bykvist Reference Bykvist2007a: 99). Bykvist recognizes several ways in which a theory can be a poor guide to action. The most relevant of these in this context is when a theory is not satisfiable, i.e. it is not possible to comply with:

In so far as we assume the general – and, I take it, uncontroversial – view that one conforms to a normative theory by choosing alternatives that are maximal according to the theory, theories that violate the stability condition are obviously not satisfiable. In the situations in which the choice of an alternative that according to the theory is maximal implies that the transmuted_X alternative is not maximal according to the theory choosing a maximal alternative implies a failure to conform to the theory.

Secondly, and related to the first point, agents who use decision methods and normative theories that violate the stability conditions use decision methods/normative theories that are not always aligned with available justifications. It is typically true of decision methods/normative theories that once a choice that conforms to the theory has been made, the agent can justify this choice with reference to how it is supported by her decision method/normative theory. This is not true for decision methods/normative theories that violate the stability condition. Agents who use such decision methods/normative theories will sometimes find themselves in the peculiar situation of having to accept that the choices they made cannot be justified with the decision method/normative theory that supported the choice. This undesirable misalignment of decision methods/normative theories that violate the stability condition and available justifications gives us reason to accept the stability condition.

Thirdly, at least some of the approaches that the stability condition disqualifies imply that agents using them can be money-pumped. This gives support to the stability condition since decision methods/normative theories the use of which exposes decision makers to money-pumping are undesirable. Consider John in the ice-cream parlour. As John chooses strawberry, the vendor might ask him whether he is really sure, or whether he would not rather have chocolate. Since John prefers chocolate to strawberry after he has chosen strawberry he is not only willing to change his mind, but also prepared to pay a small fee for this. Yet when this transaction is done, the vendor might again ask John if he is really sure, and offer him to change back to strawberry for a small fee. Since John now prefers strawberry, he will happily pay to change his mind. This process can go on till John has no money left. The feature of John’s decision method that implies that John is exposed to money pumps like this is an undesirable feature of any decision method/normative theory. The stability condition rules out at least some theories with this feature.

It is possible that the stability condition is an instance of a more general principle that states that principles that imply certain kinds of changes of the normative status from what one might call a ‘positive’ status to a ‘negative’ status when a choice is made are unreasonable. I have focused on views according to which the comparative relation between different alternatives changes and presented the stability condition within a framework where maximality is a central concept. The stability condition can be formulated also within other frameworks. For instance, a version of the stability condition states that a theory that implies that an alternative that was permissible before a choice is made is impermissible after it is chosen is unreasonable. Similarly, one can formulate a stability condition that disqualifies theories that imply changes of the normative status of a chosen alternative from virtuous to vicious, or from right to wrong. In light of the quite significant terminological differences between different normative frameworks it is hard to present a generalized version of the stability condition that fits all frameworks. But it seems to me plausible that the stability condition I have introduced above has parallels in most other normative frameworks, and that it thereby is an instance of a more general principle.

The stability condition can help us explain why John is acting irrationally. I suggest that the condition also has significant intuitive support, and contend that it furthermore is supported by some of the underlying reasons to accept normative invariance and its relevance in certain contexts, that it should be accepted because it rules out theories that are misaligned with available justifications, and that it is appealing because it rules out some decision methods and normative theories that imply that agents using them can be money-pumped. Thus, I suggest that the stability condition should be generally accepted and used to evaluate how reasonable different decision methods and normative theories are. By only ruling out changes in the comparative relations that render maximal alternatives that are chosen non-maximal it is weak enough to allow for the act of choice to have some implications for how alternatives relate to each other. This is important in order to allow for, for example, commitments to provide positive value to that which one commits to, something which does not seem at all irrational (cf. Chang Reference Chang2013). However, the condition does rule out as irrational theories that allow for the utter nonsense that John expresses, where the act of choice makes the chosen alternative impermissible.

3. Distributive theories and the stability condition

There is of course no serious theory in normative theory that defends a decision method that so bluntly violates the stability condition as John’s decision method does. However, on scrutiny, several distributive theories that have been promoted do violate the stability condition. In particular, this seems to be a risk that can be associated with theories that ascribe importance to what the status quo is. In this section, I illustrate how at least one version of the so-called ‘severity approach’ in health economics and a particular understanding of prioritarianism violate the stability condition and briefly discuss how this is likely the case of many other distributive theories that ascribe particular importance to the status quo.

Consider how the severity approach, developed by health economist Erik Nord, suggests that we should value different health benefits:

Health improvements are ascribed a value that reflects both the size of the benefit and the severity of the patient’s initial condition. On one (non-literal) reading of this, the severity approach merely suggests that one compresses the value of different people’s health states after they have received their health benefits with something like a prioritarian weighting function (cf. Adler Reference Adler2012). However, on a different (literal) reading, the health implications that are evaluated are weighted with reference to the recipient’s condition if nothing is done, i.e. ‘the patient’s initial condition’. Nord is explicit that this is one way that he thinks that one can plausibly operationalize the severity approach: the severity approach can be operationalized in numerical valuation models ‘by multiplying utility gains in the conventional QALY model by weights reflecting the severity of the start point’ (Nord Reference Nord2005: 258).

The view that the value of different benefits should be weighted with weights that reflect how well off recipients are if nothing is done is also expressed by certain prioritarians who write on how to allocate health-related resources. For instance, when describing Lifetime QALY prioritarianism, according to which health benefits to the worse off matter more, Tryggve Ottersen defines the worse off as ‘those with the fewer QALYs given all interventions currently implemented’ (Ottersen Reference Ottersen2013: 175). On this view, a benefit is valued higher the worse off the recipient is in the status quo, i.e. under the interventions currently implemented. The view that what qualifies the value of benefits is what happens if there is no intervention is even more clearly expressed when Ottersen, together with Ottar Maested and Ole Fritjof Norheim, describe the ‘worse off principle’: ‘resources should be directed toward the intervention benefitting those initially worse off, i.e., those worse off without intervention’ (Ottersen et al. Reference Ottersen, Maestad and Norheim2014: 1). Similarly, when Tyler M. John, Joseph Millum and David Wasserman write that they favour a prioritarian view according to which the value of a benefit is a function of the size of the benefit and the ‘degree of disadvantage of the beneficiaries, so that a benefit is given greater weight the more disadvantaged the beneficiary would otherwise be’ (John et al. Reference John, Millum and Wasserman2017: 177), it is natural to interpret this as a commitment to weight benefits with reference to status quo, i.e. with reference to what ‘would otherwise be’.

Although this understanding of prioritarianism might seem unconventional, it is defended also by prominent moral philosophers. In a recent book, Fred Feldman argues that reference to starting points in the status quo that ground the weights ascribed to different new benefits and burdens reflects the best understanding of Derek Parfit’s canonical description of prioritarianism: ‘Benefitting people matters more the worse off these people are’ (Parfit Reference Parfit1991: 19). As Feldman puts it:

According to Feldman, what Parfit had in mind when he presented prioritarianism is thus the following view:

Views that qualify the value of different benefits with reference to how well off recipients are at the start point/baseline/if nothing is done violate the stability condition. To see this, consider what these views say about how we should evaluate the following outcomes (I am using real numbers to describe the amounts of lifetime benefits each individual has in the different outcomes; how benefits are specified (e.g. health, welfare, opportunities) is irrelevant to the argument):

According to views that weight benefits with reference to the start point/baseline, the status quo is incredibly important. It is the severity of the start point, how well off recipients are at baseline, if nothing is done, that grounds how much weight one should ascribe to different benefits. To make things simple, I have assumed that the individuals are equally well off in status quo. Since they are equally well off, the views that ascribe extra weights to benefits to the worse off would be indifferent to Outcomes X and Y. One individual receives more benefits than the other in both outcomes, but the amounts and the distributions are the same regardless of what outcome one chooses, and the benefits matter equally much because the individuals are equally well off in status quo. Both Outcome X and Outcome Y are thus maximal alternatives; neither is worse than the other.

Imagine now that one actually makes a choice, and chooses a maximal alternative: Outcome X. This means that Outcome X is status quo; it reflects the severity of the start point, it is the new baseline, the state of the world if nothing is done:

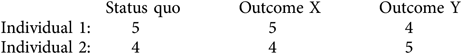
Yet, when Outcome X is status quo, the views that use weights based on how well off individuals are at the start point/baseline/if nothing is done will no longer hold the two outcomes to be equally good. In fact, when Outcome X is status quo this is worse than Outcome Y according to these views. Individual 2 is worse off (has less lifetime benefits) than Individual 1 in the new status quo. This means that benefitting Individual 2 with 1 outweighs the negative value of imposing a loss amounting to 1 on Individual 1. When Outcome X is the status quo, Outcome Y is better than Outcome X. The reverse is of course also true. When Outcome Y has been chosen, this is no longer maximal because Outcome Y is then worse than Outcome X. Thus, according to these views it will sometimes be the case that when a maximal alternative is chosen, this alternative is no longer maximal.

The views that qualify the value of different benefits with reference to how well off recipients are at the start point/baseline/if nothing is done violate the stability condition. Explained in the terms introduced in the previous section, the stability condition is violated because X is maximal in the set {X, Y}, but X_X is not maximal in the set {X_X, Y_X}, where the latter set is the transmutation_X of the alternatives in the former set that reflects the dispersion of negative and positive values associated with choosing X. These views of how to give priority to the worse off are as unreasonable as John’s decision method.

The reason these views violate the stability condition is that they ascribe particular importance to what the status quo is, and ground parts of the value of the different benefits (and losses) in this. Since the act of choosing an alternative changes the status quo, the valuation of benefits (and losses) changes, and this sometimes means that an option that is maximal before a choice is made ceases to be maximal once it is chosen.

The views mentioned above are not the only normative views that ascribe importance to the status quo in this way. For instance, Jacob M. Nebel has recently defended the normative relevance of status quo and my impression is that his version of prioritarianism also risks violating the stability condition since also he seems to qualify the value of different benefits and losses with reference to status quo (Nebel Reference Nebel2015, Reference Nebel2017). Furthermore, this is a feature also of certain theories that promote need satisfaction (cf. Herlitz and Horan Reference Herlitz and Horan2016). Needs are commonly conceptualized as a function of capacity to benefit and how badly off individuals are (Williams Reference Williams1973; Elster Reference Elster, Altham and Harrison1995; Herlitz and Horan Reference Herlitz and Horan2016; Herlitz Reference Herlitz2017). The greater the capacity to benefit, the greater the need, and the worse off an individual is, the greater the need. If one establishes how badly off individuals are with reference to the status quo, theories that promote need satisfaction face the same problem as the views discussed above. The same will be true for all theories that in some way promote priority to the worse off and establish how well off individuals are with reference to their status prior to receipt of benefit. If the stability condition is as appealing as I think it is, we should be sceptical of all normative theories that ascribe importance to the status quo in this way.