Published online by Cambridge University Press: 01 February 2005
I study the bias of actuarially fair measures commonly used to evaluate the impact of a social security system on the well-being of individuals. I investigate how the magnitude of this bias is affected by different features of a pay-as-you-go social security system. Social security affects an individual's welfare in ways other than through its direct effect on her lifetime income. It influences labor and savings decisions and hence factor prices, affecting labor income and the return to savings. Although social security can provide insurance against risk, it can also push borrowing-constrained individuals further away from their optimal consumption paths. I show that, by ignoring these features, actuarially fair measures can grossly misevaluate the impact of social security on the well-being of an individual.
The U.S. social security system is mostly financed on a pay-as-you-go basis with payroll taxes levied on current generations of workers, financing the payment of benefits to retirees. It can therefore be viewed as a schedule that transfers income from workers to retirees.
Individual equity under this system is generally equated with actuarial fairness, and most evaluations of social security are based on this idea. When evaluating how individuals fare under the social security system, the actuarial fairness approach compares (explicitly or implicitly) the return that contributors receive from the system with the returns that they could have earned by investing in bonds or in the U.S. stock market.
This approach has been commonly used in the public economics literature to evaluate how agents fare under social security. Many studies have examined how individuals fare under social security by computing the expected net present value of social security benefits, or a comparable measure, for households with different characteristics and earnings levels. These studies include Nichols and Schreitmueller (1978), Outslay and Wheeler (1982), Pellechio and Goodfellow (1983), Hurd and Shoven (1985), Boskin et al. (1987), Feldstein and Samwick (1992), Steuerle and Bakija (1997), and Diamond and Grueber (1999). More recently, Coronado et al. (1999) have studied how postwar Americans are being treated. They consider the dispersion of all potential outcomes using PSID data to compute the net social security transfers for individuals.
Feldstein and Samwick (1998) use a micro simulation model [the Social Security Simulation Model (SSSIM)] to evaluate how individuals fare under alternative privatization paths by computing actuarial present values.
Similarly, Caldwell et al. (1999) and Gokhale and Kotlikoff (1999) developed a simulation model that combines a dynamic micro simulation model and a detailed social security benefit calculator to compute actuarially fair measures that are then used to evaluate how postwar Americans will fare under the current system and with alternative adjustments to the system.
In this paper, I take a closer look at several features of a pay-as-you-go social security system and examine the bias they generate in commonly used actuarially fair measures. I show that, because they do not account for these features, actuarially fair measures can grossly misevaluate the impact of social security on individuals. By extricating the net direct social security transfers from a measure of the full impact of social security on agents' welfare, the methodology developed in this paper also allows us to clarify and understand the implications of various aspects of a pay-as-you-go social security system on the well-being of individuals.
Even though actuarially fair measurements might be an accurate way of comparing alternative private investments, they may be seriously misleading when applied to a public program such as social security. Social security is not an individual choice; it is a public policy that affects the behavior of all individuals in the economy. It distorts their savings and labor supply decisions and affects the aggregate level of capital and the supply of labor in the economy. Through its impact on the capital stock and on the effective labor supply, social security also affects the interest rate and wages, changing individuals' labor income and the return to their savings. Cooley and Soares (1999) found that, even though the net present value of benefits is negative for a majority of the population, the effects of social security on the rate of return to private savings and on wages are so important that social security is implemented and sustained as a political equilibrium in a majority voting process.
Even when social security does not affect factor prices, its impact on the individual decisions cannot be ignored when evaluating the welfare repercussions of this policy. Because in the presence of a social security system a tax rate is levied on an individual's labor income, social security distorts labor leisure decisions. Even when all benefits are earnings-dependent, this effect is not negligible.
More importantly, social security can partially insure individuals against different types of risk when asset markets are incomplete. Until recently, much of the literature on social security has ignored the insurance features of these policies. Hubbard (1987), Huggett and Ventura (1999), and Conesa and Krueger (1999), among others, find that social security might play an important role as insurance against idiosyncratic risks such as lifetime and labor income uncertainty. Hubbard (1987) shows that when individuals face uncertainty over the lengths of their lives and there is a market failure in the private provision of annuities, there might be large welfare gains associated with the public provision of annuities through social security.
Finally, in the presence of borrowing constraints, individuals are not able to reallocate resources optimally across their lives. In such an environment, an individual's well-being depends not only on the net value of the resources available over her lifetime but, more importantly, on the time at which these resources are made available. As discussed by Hubbard and Judd (1987), social security taxes labor income when it is more likely that the borrowing constraint is binding. Also, social security benefits cannot be optimally reallocated across time when agents' borrowing is restricted. Hence, an increase in social security benefits and taxation might make agents worse off even if it increases their lifetime resources.
Moreover, actuarially fair measures are used in policy analysis to study how individuals fare under alternative systems and also to compare how different individuals fare relative to each other under a given social security system. Because all the factors not accounted for by actuarially fair measures affect individuals differently, actuarially fair measures also misevaluate the redistributive properties of social security policies in terms of their impact on different agents' welfare.
The distortionary effect of social security is shown to be significant while its impact on factor prices has a much larger effect on individuals' well-being. I also show that the biases of actuarially fair measures for not accounting for borrowing constraints or the insurance value of social security are extremely large. More importantly, because poorer individuals are more affected by borrowing constraints and risk, the bias extends to the redistributional impact of this policy when measured using actuarially fair measures.
In sum, this paper looks closely at different aspects of social security and shows how they generate biases in commonly used actuarially fair measures. It illustrates that, to accurately evaluate how a social security system affects the well-being of individuals, we need to use a general equilibrium framework with an explicit specification of individuals' preferences where we can account for all relevant repercussions of social security. Using measures that ignore these features is misleading and can lead to erroneous evaluations of social security and policies to reform the current system.
There is an extensive literature that studies the impact of social security on individuals' welfare using general equilibrium overlapping generations models, for instance, Auerbach and Kotlikoff (1987), Hubbard and Judd (1987), Imrohoroglu et al. (1995), and Huggett and Ventura (1999). The study presented in this paper is distinct in several aspects.
In the first place, the aim of this paper is to compare the commonly used actuarially fair measures with measures that account for the full impact of social security on the well-being of individuals, a comparison that even if it is implicit in the findings of some of those papers has not been the object of a clear and direct analyzes.
In the second place, by running different experiments, I am able to isolate the impact of each of several features of a social security system on the well-being of an agent and on the bias of actuarially fair measures.
Finally, most of the literature focuses on comparisons across steady states. That is, they take an individual from the reference steady state and compare her utility with the one she would have in the steady state with a given social security system. As shown in this paper, even though such a comparison is informative, it does not accurately measure the value that social security has to an individual. To evaluate the impact of social security on an individual's well-being, we need to compare how the individual fares in the path that the economy takes in the presence of social security with how she fares in the path that the economy follows in the absence of social security.
I study the social security system using an overlapping generations economy where a large number of heterogenous agents are “born” each period and live for a maximum of T periods. The population in this economy grows at a constant rate and individuals supply labor endogenously for the first N periods of their lives and retire during the last T−N periods before dying.
With a pay-as-you-go social security system, the government levies a constant tax on labor income and uses the revenue to fund the benefits of the retirees. I assume that benefits are proportional to the average labor income per worker.
I compute equilibrium paths for these economies and evaluate the impact of social security on individuals' welfare. To assess how different individuals fare under a social security system, I construct a measure of the welfare gains from social security based on the Hicks compensation principle. I show the relation between the different channels through which social security might affect an individual's well-being and the biases of the actuarially fair measures.
I quantify the findings by calibrating the parameters of the economy and solving numerically for its equilibrium.
I study an economy where, in each period, a large number of heterogeneous agents with a maximum lifetime of T periods are born.1
The model economy described is a version of the well-known A-K model presented in the seminal work of Auerbach and Kotlikoff (1987).
,
is constant over time and
, with
. Within each generation, there are J types of agents; the share of type j agents in the population,
, is constant.
Agents in each generation maximize their discounted lifetime utility: For a type j agent born in period t, the lifetime utility is given by
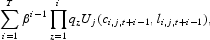
where β is the discount factor, ci,j,t+i−1 is consumption, and li,j,t+i−1 is leisure of an age i, type j individual in period t+i−1.
The “momentary” utility function is assumed to take the constant relative risk aversion form of a Cobb-Douglas consumption-leisure index,
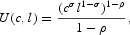
where ρ is the inverse of the intertemporal elasticity of substitution and σ is the coefficient of consumption on the Cobb-Douglas index.
Agents in this economy accumulate claims on real capital, used in production by firms, to help smooth consumption across time. The budget constraint facing a type j individual of age i can be written as
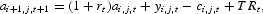
where yi,j,t is the real net labor income plus social security transfers of a type j, age i individual; ai,j,t denotes the asset holdings of a type j, age i individual at the beginning of the period t; and rt denotes the rate of return on these assets. TRt is a lump-sum transfer.
I assume that agents may work the first Tw periods of their lives, but must retire afterward. Before their mandatory retirement, age i, type j workers endogenously supply hi,j hours of labor and have different productivity levels represented by
, an efficiency index that quantifies the productivity of an hour of work supplied by a type j agent of age i. After retirement, the noncapital income of a retiree is just the social security benefit, bt. For a more realistic representation of the U.S. social security system, I should assume that the level of benefits has two components: one proportional to past contributions and another independent of past contributions. The first component of benefits would be proportional to the average labor income of the retiree while the second one would be proportional to the income of agents currently employed:
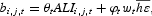
where
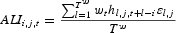
gives us the average earnings of an age i, type j retiree at time t and
is the weighted average earnings of the working generations.
In the benchmark economy, I maintain the standard schedule, where the level of benefits is independent of past earnings and is proportional to the income of agents currently employed. This system is more distortionary and it allows us to obtain an upper bound for the bias of actuarially fair measures associated with the distortionary effect of social security taxes. Moreover, it is computationally more tractable. Later, in a separate experiment, I analyze the impact of linking individual earnings to benefits on the bias of the actuarially fair measures and I compare the results with the ones obtained in the benchmark economy.
Under these assumptions, the net labor income of an individual is given by
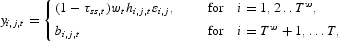
where
is the social security tax rate on labor income.
The production technology of the economy is described by a constant-returns-to-scale function,

where
is the labor share of output, Yt, and Kt and Lt are the capital and labor inputs, respectively. I allow for exogenous growth in labor productivity at a constant rate g. The capital stock is equal to the aggregate asset holdings of agents in the economy. It depreciates at a constant rate
and evolves according to the law of motion
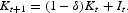
There is a government in this economy that implements the pay-as-you-go social insurance system. The government must impose taxes on labor income so that its budget is balanced each period:

where B is the level of total benefits paid to current retirees. I also assume that the government distributes any accidental bequests among all agents in equal amounts as lump-sum transfers.
In this paper, I do not take into account the remaining activities of the government. In particular, I do not allow for government debt and I do not include taxes other than social security ones. Because tax distortions increase more than proportionally with the tax rate, excluding other taxes significantly decreases the distortions associated with social security taxation. However, to introduce other taxes, I would also need to make assumptions on the government expenditures financed by these taxes and how they respond to changes in the economic environment. Hence, even though these are also factors that need to be taken into account when analyzing the impact of social security on the welfare of agents, I chose not to take a stance on issues that are debatable and would call for an extensive analysis that goes beyond the scope of this paper.
Given a sequence of social security taxes, the economic problem of an age i, type j individual is to choose a sequence of consumption, leisure, and asset holdings that maximizes the expected discounted lifetime utility subject to her budget constraints. I write this as
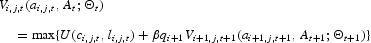
s.t.
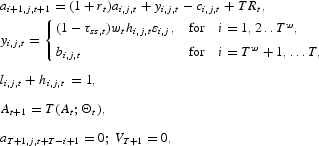
given
,
Here, At represents the distribution of capital across agents and
is the law of motion of the distribution of capital.
is a given sequence of taxes that describes the social security policy in each period.
A set of decision functions
,
,
, a law of motion
, and value functions
are obtained.
In this economy, competitive firms maximize profits, which are equal to Yt−wtLt−rtKt, taking the wage rate and interest rate as given. The first-order conditions for the firm's problem determine the following functions for the net real return to capital and the real wage rate:
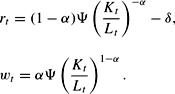
DEFINITION 1. An equilibrium is a set of value functions,
; decision rules for consumption; individual labor supply and asset holding
,
,
,
i, j; a law of motion for the distribution of capital
; a sequence of relative factor price functions
; functions for the level of capital per capita
and for the effective labor supply per capita
such that these functions satisfy
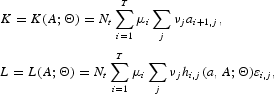
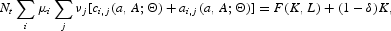
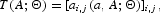
For a small open economy, I have
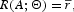
where
is the exogenously given international interest rate. Aggregate capital (K) is such that the first-order conditions for the firm's problem are satisfied. In this case,
, where
is the net level of domestic capital owned by foreign resident and
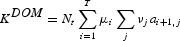
is the level of capital owned by domestic residents.
Most discussions of social security programs evaluate this policy using measures based on the concept of actuarial fairness. The approach commonly used is to construct tax and benefit streams and compare the tax cost of the coverage to the level of benefits by computing either the present value of net benefits (PVNB) or the internal rate of return. The expected PVNB is computed using a market real interest rate. The internal rate of return is the rate of discount that equates the expected present value of benefits with the expected present value of taxes. So, these welfare measures compare the return on funds contributed to the system with the returns that would have been earned had the funds been invested in alternative applications such as bonds or the stock market.
The PVNB for an age i, type j agent at time t is given by
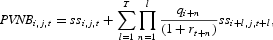
where
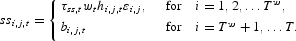
This measure corresponds to the difference between the present value of lifetime resources of the agent with social security and without social security when everything else remains constant.
To evaluate the impact of the social security policy on the well-being of individuals, we need to compare the utility of individuals in the economy with social security to their utility in the economy without social security.
I assume that the economy is in a steady state without social security and I compute the path for the economy when a social security system is implemented. Unless otherwise specified, I assume that a social security system described by a constant tax rate on labor income,
, is introduced. The revenues generated are equally distributed as benefits among the retirees. I then compare the utility of agents in the economy without the system with the utility they attain when the system is implemented.
To assess how different individuals fare under a social security system, I construct an equivalent variation measure (EVM). I compute the level of transfers required to make each individual able to attain the same level of lifetime utility in the economy without social security as in the economy with the social security system. The transfer is optimally allocated by the individual to consumption and savings and allows her to attain the reference level of utility.
The compensation to be given to a type j, age i agent endowed with a level of assets ai,j in an economy without social security and an aggregate state described by A, is xi,j such that
, where
is the lifetime utility level of that agent in the environment we want to evaluate. The measure of welfare is then
, where r is the real interest rate in the reference steady state.
To solve this model numerically, I calibrate the steady state of the economy with social security. Agents in this model are assumed to be born at age 21 when they become full-time workers, working 45 years
and then retiring for a maximum of 15 years (T=60).
I set the coefficient of risk aversion, ρ, to 2 and choose the value for the discount factor,
, so that the equilibrium interest rate is approximately 6%. I take the coefficient of consumption in the utility function,
, so that, on average, agents in the labor force allocate around 31% of their time to market activities.
Following Cooley and Prescott (1995), I set the share of labor in the production function to 0.6 and I set the depreciation rate so that the steady-state annual investment/capital ratio for this economy is 0.076.
The age-specific endowments of efficiency units for the economies with heterogeneous agents are taken from Hansen (1993).
Finally, I set the exogenous growth rate to be 1.83%.
In the economy with lifetime uncertainty, I set the probabilities of surviving using the values from Faber (1982).
I match the annual population growth rate for the model to the average population growth rate in the U.S. economy in the past decades, 0.0124 (Citibase Data, 1946–1993).
The social security tax rate is set exogenously to 12.8%. The total social security payroll tax including hospital and disability insurances (HI and DI) is 14.7%; the OASI tax rate is about 9.9%, HI payroll tax is about 2.9%, and DI tax is about 1.9%. Whereas HI can be modeled as a transfer to agents of age 65 and over, DI benefits would be a transfer to agents below age 65. So, I set the social security tax rate in the model to 12.8% [see Altig et al. (2001)].
I use this procedure to calibrate several economies first with intragenerational homogeneity and then with intragenerational heterogeneity: the benchmark economy where all agents live for T periods, an economy where social security benefits are proportional to retirees' contributions, one with lifetime uncertainty, and another where agents cannot borrow against future income.
The parameter choices for these economies are summarized in Table 1.

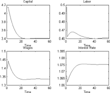
Figure 1 shows the evolution of equilibrium capital stock K, the effective labor supply L, the interest rate r, and the wage rate w along the transition path resulting from introducing a social security system (
%
) in a steady state without social security (
).

Transition dynamics.
Social security is an economywide policy (as opposed to an individual choice) that affects the behavior of all individuals in the economy. It distorts their savings and labor supply decisions and affects the aggregate level of capital and the supply of labor in the economy. Older generations have a larger marginal propensity to consume than younger ones. That is, older individuals consume a higher share of any additional income than do younger ones. The introduction of social security implies a redistribution of resources away from the young and toward older generations, which leads to an increase in the aggregate consumption level, a decrease in savings, and a corresponding decrease in the accumulation of physical capital. Furthermore, the increase in the taxation of labor income and in retirement benefits lowers the incentives of individuals to work and save. This leads to a decline of the capital stock and the effective labor supply, affecting the interest rate and wages, as can be seen in Figure 1. Hence, social security also changes individuals' labor income and the returns to their savings.
Notice also the immediate response of the factor prices to the implementation of the social security system due to the decrease in the labor supply. There is an instant increase in wages, which benefits the young, and a decline in the interest rate, which is detrimental to old workers and retirees who get a higher share of their income from capital. Following the initial period, capital decreases while labor supply has an initial surge and drops again. This generates a drop in the wage rate and a rise in the interest rate while the economy converges to a steady state with a lower capital level.
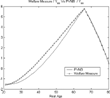
The values, as a fraction of per capita output, of the equivalent variation measure (EVM) and of the PVNB for each type of agents as a function of age are shown in Figure 2.

Benchmark calibration—PVNB and welfare measure.
An important attribute of the equilibrium is that both the PVNB and the EVM are negative for the youngest generations (below 40–45 years old) and positive for the remaining ones, peaking for the youngest retirees.
However, the welfare loss of the young generated by the social security system is lower than what is implied by the PVNB while the welfare gains of the middle-aged are higher than those implied by the actuarially fair measure. This disparity becomes clear in Figure 4 where the difference between these two measures is represented, ranging from around 70% of the steady-state output per capita to about −10% of output.
In a small open economy, where factor prices remain unchanged, both measures are slightly different (see Figure 3). The difference between the two measures follows the evolution of the present value of agents' lifetime labor income, and it represents the welfare impact of the distortionary tax levied on labor income. Besides the income effect of social security, measured in this case by the actuarially fair measure, the introduction of the social security tax rate distorts the price of leisure relative to consumption.

Benchmark calibration—small open economy.
The significance of the impact of the tax distortion on welfare also shows that linking social security contributions to benefits can have some impact on welfare because it might reduce the distortionary effect of social security taxation. Furthermore, because the distortionary effect increases more than proportionally with the tax rate, the mismeasurement of actuarially fair measures will increase with the predicted future increase in the social security tax rate.
In a closed economy, the negative distortionary effect of taxation is more than offset by the impact of social security on factor prices (see Figure 4).

Benchmark calibration—closed economy.
Older agents are affected by the initial decrease in interest rates, wherease younger retirees have time to benefit from the future increase in interest rates. The middle-aged, with most of their working life behind them and with significant assets, benefit from the initial increase in wages and the future increase in interest rates without being significantly affected by future decreases in wage rates. Younger agents are hurt by the future decrease in wages, and their lower income does not allow them to accumulate many assets and take advantage of the future increase in interest rates.
The size of the disparity between the two measures illustrates that the general equilibrium effect of social security on the utility of agents, through its impact on the levels of capital, effective labor supply, and on factor prices is important.
In Table 2, I compare the bias of the actuarial fair measure for short-run and long-run evaluations of the impact of social security on an age-1 individual. For the small open economy, there is no difference, but for the closed economy, the difference is significant. The bias more than quadruples from the short run to the long run. The general equilibrium effects of social security are much more pronounced in the long run, as we can see in Figure 1. The equilibrium levels of capital as well as the labor supply decrease dramatically with the introduction of a pay-as-you-go social security system. The real rate of return on private savings increases while the wage rate decreases.

More importantly, when the objective of the analysis is to evaluate the impact of social security on an individual, comparisons across steady states can be even more misleading than the use of actuarial fair measures. We need to compare the utility of agents when there is no social security to the one they would get if social security were to be implemented.
Because the distortionary tax and the general equilibrium effects might affect heterogeneous individuals diversely, I study, in this section, the sensitivity of the bias of the actuarially fair measures to heterogeneity. I focus on two sources of intragenerational heterogeneity, allowing agents to differ in their efficiency levels,
, in one experiment, and in their discount factors,
, in another experiment.
I start by differentiating agents according to their efficiency levels,
. I use the same calibrations as Altig et al. (2001), ordering 12 different agent types from the less efficient and poorer (type 1) to the more efficient and richer (type 12).
The graphs (Figures 5 and 6) show the bias of the PVNB relative to the welfare measure across ages for different types of agents. It has the same configuration across ages as in the economy with homogeneous agents. It is clear that this bias varies across types and is related to the differences in agents' “labor effectiveness.”

Heterogeneous labor efficiency—small open economy.

Heterogeneous labor efficiency—closed economy.
In the small open economy (Figure 5), the bias is generated by the distortionary tax on labor income and as expected agents with higher effective labor supply are more hurt by tax distortions.
In the closed economy (Figure 6), more efficient agents benefit more from the initial increase of the wage rate and are more hurt by decreases in future wage rates. Because they also accumulate more assets, they gain more from future increases in interest rates while being more affected by the current decrease in the interest rate.
So, the bias associated with the PVNB measure depends not only on the age of individuals but also on the type. Consequently, the relative impact of social security on different types of individuals is also mismeasured when using an actuarially fair approach.
In Table 3, I compare the bias of the actuarially fair measure for short-run and long-run evaluations. Again, in a small open economy, there is no distinction, but in a closed economy the difference is significant. In fact, in a closed economy, less effective age-1 agents benefit from social security by more than the PVNB measure indicates, but all agents born in the steady state of the economy with social security are much worse off than what the actuarially fair measure shows.

Carroll and Samwick (1997) show that much of the variation in wealth accumulation over the life cycle can be related to the values of agents' discount rates. Krusell and Smith (1998) establish that heterogeneity in the discount factor can significantly improve the ability of their model to match the U.S. wealth distribution. Following these results, I differentiate agents according to their discount factors,
, and analyze the bias of actuarially fair measures, given this source of heterogeneity. As in Samwick (1998), I assume that there are seven types of agents in each cohort. I then set the values of the parameters so that the model matches the targeted values described in the calibration section while the percent deviation from the mean of the discount factors and the population shares of each type of agents are consistent with the distribution of households' rates of time preference estimated by Samwick. Keep in mind that the aim of the experiment is to construct a model with some illustrative value and not an attempt to match the earnings or wealth inequality observed in the U.S. economy. I set the average discount factor to 0.971 and the coefficient of consumption in the utility function to 0.3; the values for β and
are described in Table 4.

The bias of the actuarially fair measure for different types of agents across ages is represented in Figures 7 and 8. For many agent types, the bias has a similar configuration across ages as in the economy with homogeneous agents. But, unlike in the previous case, the bias does not seem to change monotonically with the differences in the discount factor and it is clearer that the PVNB does not capture the intragenerational impact of social security. In the small open economy (Figure 5), the bias is once again related to the distortionary effect of social security. This effect increases with the effective labor supply. Agents with a lower discount factor care more about current leisure and supply less labor in the earlier periods of their lives while accumulating negative levels of assets in order to finance consumption; hence, the impact of tax distortions on their utility is relatively small. However, as they get older, they work more to finance consumption and pay back their loans. The distortionary effect of social security is then higher relative to that for other agents from the same cohort. Conversely, younger agents with higher
allocate more of their time to work and are more affected by the tax distortion. As they grow old, they can finance consumption with their accumulated wealth and decrease their supply of labor to enjoy more leisure. They are then less affected by the distortionary tax.

Heterogeneous discount factors—small open economy.

Heterogeneous discount factors—closed economy.
However, the distortionary effect of social security seems also to be low for the younger agents with the highest levels of
. Whereas young agents' labor supply increases with the discount factor, the elasticity of labor supply decreases. For the higher levels of
, the labor supply elasticity is very low and labor supply becomes less responsive. Even though agents allocate most of their time to labor, the tax rate becomes less distortionary.
As in the preceding section, in the closed economy (Figure 8), the tax distortion becomes almost irrelevant. Agents with a lower discount rate borrow and do not work in their early years. Because the rate of interest increases and the wage rate decreases later in the transition, when they supply more labor and are in debt, they are worse off than what is indicated by the PVNB measure. Older agents enjoy the initial increase in wages when they are supplying more labor, but they also have accumulated debt and are going to face significantly higher interest payments. Agents with a higher discount rate supply more labor initially, benefiting from the early increase in the wage rate and save more, accumulating more wealth. Hence, they gain from the future increase in the interest rate.
In Table 5, we can see that, in the closed economy, the results from the preceding section are reversed. In this case, the three wealthiest agent types benefit from social security by more than indicated by the actuarially fair measures. The remaining agents would be much worse off than what is indicated by the actuarially fair measure. Furthermore, whereas the PVNB decreases with the agent type, the reverse happens for the welfare measure, which becomes positive for the wealthiest agents, indicating that they would be better off if they would be born in the steady state of the economy with social security.

The U.S. social security system has two components: one proportional to past contributions and another independent of past contributions. These components have distinct implications in terms of the redistributional impact of a social security system. Whereas the latter implies some redistribution from high to low earners, with high earners contributing significantly more than low earners and receiving the same benefits, the first does not imply any direct intergenerational redistribution.
Even though the comparison between these components tends to orbit around the redistributional impact of social security, a considerable role has also been given to the reduction in the distortionary effect of social security taxation provided when benefits are linked to past contributions. Auerbach and Kotlikoff (1987) show that there might be large efficiency gains from establishing a link between an agent's contributions and benefits. In this section, I analyze the impact of linking individual earnings to benefits on the bias of the actuarially fair measures by assuming that all social security benefits are proportional to the average labor income of the retiree:
and
. I then compare the results with the ones obtained for the benchmark economy.2
In this environment, another state variable needs to be included in problem (10):
, the average earnings of type j, age i individual at time t and its aggregate counterpart.
I compute the steady-state value of the replacement rate,
, such that the social security budget is balanced for a tax rate of 12.8%. I then compute the transition path resulting from implementing the social security system described by that replacement rate in a steady state without social security. I further assume that along the transition the social security tax rate is set to maintain a balanced government budget.
In Figure 9, we can see the bias of the actuarially fair measure in a small open economy. As expected, the introduction of a social security system in which benefits depend on earnings decreases the distortionary impact of social security taxation on the supply of labor relatively to the benchmark case. Furthermore, the coefficient of consumption in the utility function required to target the average time allocated to labor observed for the U.S. economy in this economy is lower than in the benchmark case. Agents with a lower coefficient of consumption in the utility function care more about leisure and have a higher labor supply elasticity. Their labor decisions respond more to the social security tax rate but they also supply less labor. The overall impact of tax distortions on utility is relatively small.

Earnings-dependent benefits—small open economy.
However, the amplitude of the bias in the closed economy is significantly higher (see Figure 10) than in the benchmark economy. We notice that the bias peaks for middle-aged agents at a much higher level and reaches more negative values for some of the current retirees but it is also less negative for younger agents.

Earnings-dependent benefits—closed economy.
The link between labor income and social security benefits increases the incentives to supply labor. This effect is partially offset by the decrease in the coefficient of consumption. A lower level of this parameter implies a higher elasticity of labor supply and hence a higher response of labor supply. The higher decrease in labor supply in response to the introduction of social security leads to a significantly higher rise in initial wages and drop in interest rates.
Furthermore, the earnings dependency of benefits also results in a bigger decrease in savings. Because the impact on capital is relatively higher than the one on labor supply, the future decrease of wages and increase of interest rates are also higher than in the benchmark case. The middle-aged have more to gain from the initial increase in wages and the future increase in interest rates. Younger agents benefit more from the initial increase of the wage rate, and are more affected by future decreases in wage rates. As agents accumulate more wealth than in the benchmark case, they gain from increases in future interest rates, while being more affected by the current decrease of the interest rate. Hence, the stronger response of the price factors to the introduction of social security results in a higher bias of the actuarially fair measures.
In Table 6, the results from the benchmark economy are confirmed. The difference between the short and the long run in the small open economy case is a result of the higher tax rates needed to finance social security benefits in the short run.

I now look at the bias of the actuarially fair measures when agents differ according to their efficiency levels,
.
Even though a system with earnings-dependent benefits has different redistributional implications than a universal system, these differences are captured by the actuarially fair measures. As can be seen by comparing Figures 11 and 12 with Figures 5 and 4 (in the Benchmark section) the intragenerational bias of the actuarially fair measures is hardly affected by this aspect of the system.

Earnings-dependent benefits—heterogeneous labor efficiency, small open economy.

Earnings-dependent benefits—heterogeneous labor efficiency, closed economy.
In this section, I study the value of social security as insurance against risk in an economy with incomplete asset markets. As in Hubbard (1987), uncertainty appears in the model as a positive probability of agents dying in any given period along their lives. I assume that, upon an agent's death, the government fully taxes her bequests and distributes the revenue equally among all surviving agents. Although social security plays an important insurance role against other types of risk, this straightforward way of introducing lifetime uncertainty allows me to show how the presence of risk can affect the evaluation of social security by individuals and increase the margin of error of actuarially fair measures, while avoiding intragenerational heterogeneity as a by-product. Therefore, even though this type of uncertainty could be at least partially insured against through private annuity markets, I assume that there is a market failure in the private provision of annuities. I do not make the absence of annuity markets endogenous to the model, referring the reader to Rothschild and Stiglitz (1976) and Eckstein et al. (1985) for possible explanations. When individuals face uncertain lifetimes and cannot resort to private annuities to insure for the possibility of living longer than expected, they resort to precautionary savings. Because of the inability to purchase annuities, agents have to save more than enough to finance their expected lifetime consumption if they want to avoid very low levels of consumption when they live longer than expected. Hence, even though individuals also discount the future more heavily, this type of uncertainty tends to increase capital accumulation.
As Hubbard and Judd (1987) show, when individuals face uncertainty over the lengths of their lives and there is a market failure in the private provision of annuities, there are large welfare gains associated with the public provision of annuities through social security. Therefore, an evaluation of social security that looks only at the net present value of transfers associated with this policy is erroneous because it does not account for the insurance value of social security.3
Some actuarial fairness analyses recognize that social security contains an insurance component and use risk-adjusted returns in the calculations. If assets that provide the same insurance as social security are available in the economy, their returns can be used to compute actuarial fair measures. However, as it happens with factor prices in our benchmark economy, risk premia are endogenous and are affected by the implementation of social security, particularly when this policy provides the same coverage. If social security provides insurance for risks not covered by existing assets, the available rates of return contain information on the value of different types of coverage and misevaluate the insurance value of social security.

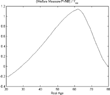
Uncertain lifetime—small open economy.
Notice that for the youngest generations, the bias of the actuarially fair measure is negative. On the one hand, they receive significantly fewer transfers because of the reduction in involuntary bequests. On the other hand, they have a very low probability of dying, and they heavily discount future periods when the insurance role of social security is more important. Therefore, they do not positively value the insurance scheme provided by the social security system.
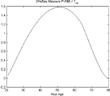
In addition, in the closed economy (Figure 14), social security has the general equilibrium effects described in the previous sections and it will further decrease capital because individuals do not need to save as much to finance consumption if, after retirement, they live longer than expected.

Uncertain lifetime—closed economy.
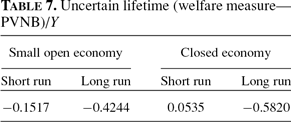
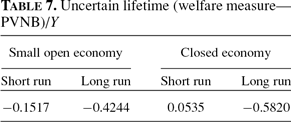
For both the small open economy and the closed economy, the difference in the bias of the actuarially fair measure between the short run and the long run is significant (see Table 7). In the open economy the difference is because agents born before the implementation of social security have accumulated a level of assets different from the levels amassed had they been born under the new policy. This implies that the levels of accidental bequests received by young agents in the short run are different from the long-run ones.
In this section, I study the bias of the actuarially fair measures across heterogeneous agents by allowing agents to differ in their efficiency levels,
.
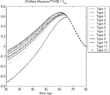
There is some difference in the bias of the actuarially fair measure across types. While losses from the decrease in accidental bequests are identical for all agents, the insurance value of social security is lower for high-earnings agents. Their contributions are much higher than average but their annuities are the same (Figure 15).

Uncertain lifetime and heterogeneous labor efficiency—small open economy.
In the closed economy (Figure 16), the difference is mitigated by the benefits of a higher return to savings (increase in interest rate).

Uncertain lifetime and heterogeneous labor efficiency—closed economy.
In Table 8, I compare the bias of the actuarial fair measure for short-run and long-run evaluations. Again, for both the small open economy and the closed economy, the difference is significant and it is higher for the poorer agents who benefit from higher levels of redistribution through involuntary bequests in the short run.

However, to better evaluate the redistributive impact of social security and the bias of the PVNB measure in an environment with uncertainty, we should also consider that different types of individuals incur different levels of risk and have access to different instruments to insure against risk. For instance, typically, low-income agents face higher probabilities of death or health problems than high-earnings ones. Wealthier agents also have access to a wider variety of financial instruments that allow them to better insure against risk. The redistributive impact of social security would change in an environment with such features and this would also not be captured by the PVNB measure.
Implicit to actuarially fair measures is the assumption that agents can reallocate resources across their lives optimally. Consequently, if individuals' ability to do so is impeded, it results in another source of misevaluation of the welfare implications of a social security policy that reallocates resources across agents lives.
To study this type of bias, I analyze the value of social security in an economy with borrowing constraints. In this model economy, individuals cannot anticipate future incomes—labor income or social security benefits—for current consumption by accumulating negative net assets. That is,
.
In a life-cycle economy, consumption-smoothing individuals wish to borrow during the early periods of their lives when their income is insufficient to cover their desired consumption. In the presence of borrowing constraints, they are not able to borrow from future earnings and they consume the totality of their after-tax labor income, below their optimal consumption levels. Since social security is financed through a tax on labor income, social security taxes depress consumption when the liquidity constraints are binding and make it more likely that they become binding. An increase in social security benefits and therefore on taxation might make agents worse off even if it increases their lifetime resources as asset market imperfections limit the extent to which agents can allocate their resources optimally over their lifetimes. Actuarially fair measures cannot account for the implications of the liquidity constraints faced by individuals.
This is evident in a small open economy. In Figure 17, we clearly see the bias of the actuarially fair measure becoming very large for agents for whom the borrowing constraint is active. Whereas in the absence of these constraints the bias was almost flat for young agents (see Figure 3), now it is initially very high with the actuarially fair measure grossly overestimating the cost of social security for these agents.

Borrowing constraints—small open economy.
This result might seem surprising because we could think that, to compute the welfare implications of this policy, we would have to subtract the utility cost of taxing constrained agents from the net present value of benefits. The welfare measure would therefore be lower than the actuarially fair measure. Because
, a borrowing-constrained agent's valuation of current resources relative to future resources is different from the market real interest rate and the difference increases exponentially with the number of periods an agent is constrained. That is, the discount rate used to compute the actuarially fair measures is not an accurate measure of a constrained agent's evaluation of future resources. When an agent cannot borrow, she values current resources much more than resources that are only made available to her in the future. In the case of social security, she values highly the negative impact of current taxation and she strongly discounts future payments and benefits. So, to correctly measure the value of social security for an agent, much more weight has to be given to the impact of the social security taxes that she has to pay in the initial periods of her life than to future transfers.
Furthermore, because the agent cannot borrow, her initial consumption is very low and her marginal utility very high and any small transfer has a significant impact on her utility. Hence, even though social security can have a much higher impact on the utility of a liquidity-constrained individual than on the utility of an individual that is not constrained, the absolute value of the current welfare measure can be much lower for the former than for the latter. Furthermore, the absolute value of this welfare measure is much lower than the actuarially fair measure for agents for whom the borrowing constraint is active. Consequently, the use of the current welfare measure to evaluate the impact of social security across agents can be misleading.
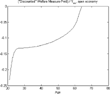
Therefore, I construct a measure that circumvents this problem and allows a straightforward comparison of the welfare impact of social security on heterogeneous individuals. As before, I compute the current value of the additional amount of goods to be given to an individual to make her able to attain the same level of lifetime utility in the economy with social security as in the economy without the social security system. Now, however, I delay the transfer to a period in time when the individual is no longer borrowing constrained; moreover, I also delay any negative transfers that make the constraint binding. I then compute the present value of the transfer using the equilibrium real interest rate as the discount rate. Hence forth, I call the resulting measure the “discounted” welfare measure.
Figure 18 shows the bias of the actuarially fair measure relative to the “discounted” welfare measure. We observe that the bias is very large for agents for whom the borrowing constraint is active. Whereas this bias was flat for young agents in the absence of liquidity constraints, now it is very high, with the actuarially fair measure grossly underestimating the cost of social security for these agents. The increase in the bias (in absolute value) is due to the high cost of social security taxation for borrowing-constrained individuals. To make those individuals as well off as with social security, we need to give them an amount equal to the net present value of benefits, and take away from them an amount that accounts for the negative impact of having to pay social security taxes when they are liquidity constrained.

Borrowing constraints—small open economy.
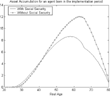
In a closed economy, the bias curve (see Figure 19) is not significantly different from the one in the benchmark economy (see Figure 4). Even though the negative impact of social security taxation on borrowing-constrained individuals is still present, it is mitigated by the impact of social security on factor prices. Upon the introduction of a pay-as-you-go social security system, agents' lifetime income decreases, future wages decrease while current real wage rate increases dramatically (see Figure 1). The decrease in lifetime income implies a higher decrease in current consumption. The increase in current wages and the decrease in future wages means that labor income profiles are smoother and the need to reallocate resources intertemporally by borrowing is lower. Hence, the borrowing constraint is less binding than in an open economy. Whereas before the implementation of social security, agents only started accumulating assets after age 29, upon the implementation of the system they start at age 26 with a significant reduction in the burden of the constraints, as can be seen in Figure 20, where I represent the lifetime asset accumulation of an agent in the steady state of the economy without social security and along the path of the economy once social security is implemented. Therefore, the impact of social security on borrowing-constrained agents is significantly less dramatic than in the previous case when factor prices were unchanged, and it can even be positive. The effect of the change in factor prices on borrowing-constrained individuals seems to be overlooked in the literature. For instance, Hubbard and Judd (1987), describe in some detail the importance of borrowing constraints in evaluating the welfare impact of social security but they do not mention this feature, which is also not uncovered by Conesa and Krueger (1999) where it combines with the effects of lifetime uncertainty and intragenerational heterogeneity.

Borrowing constraints—closed economy.

Borrowing constraints—closed economy.
As usual, the bias more than doubles from the short run to the long run in the closed economy (see Table 9). Furthermore, for the small open economy there is a dramatic increase in the bias relative to the benchmark economy case (see Table 2)—the size of the bias doubles—whereas for the closed economy, the difference is significant but not as dramatic, which reinforces the findings from the short-run analysis.

Once again, I differentiate agents according to their efficiency levels,
, to see how the bias differs across different types of agents.
The graphs (Figures 21 and 24) show the bias of the PVNB relative to the welfare measure for different types of agents across ages. It is again clear that this bias differs across types.

Borrowing constraints and heterogeneous labor efficiency—small open economy.
In the small open economy (Figure 21), for high-earnings agents, the age-profile of the actuarially fair measure bias is very similar to the one computed for the economy without borrowing constraints. However, agents with lower efficiency levels are relatively more hurt by the social security system than the PVNB measure indicates because their welfare levels are also affected by the impossibility of borrowing against future income. This not only occurs in the initial periods of their lives, but, as we can see in Figure 21, it becomes more important for the poorer middle-aged who would like to borrow against future retirement benefits, namely agents of types 1, 2, and 3. The actuarially fair measure grossly misestimates the impact of social security on these agents' well-being. Even though social security redistributes resources from the wealthy to the poor, as captured by the PVNB measure, it taxes the poor when they work and, because of the borrowing constraint, cannot anticipate their future benefits to attain higher levels of consumption prior to retirement.
In Figure 22, I show the asset accumulation of agents who are 50 years old when social security is implemented. I represent the asset accumulation profiles for the poorest types in the borrowing-constrained economy and in the unconstrained one (the benchmark economy). We can see that the poorest agents would like to borrow against their future income when they are young. When social security is implemented, they are 50 years old and start consuming out of their assets. They dissave and wish to borrow against their social security benefits.

Borrowing constraints and heterogeneous labor efficiency—small open economy.
In Figure 23, I show the asset accumulation of agents who are born in the implementation period. Again, I represent the asset accumulation profiles for the poorest types in the borrowing-constrained economy and in the unconstrained one (the benchmark economy). We can see that the two poorest agent types would like to be in debt for the duration of their lives, borrowing against their labor income and social security payments. Other, less poor agents wish to borrow against their labor income initially and, by the time they are middle-aged, have a positive net asset position. They would then dissave and borrow against their social security benefits. The actual response of the liquidity-constrained agents to the implementation of social security is clearly different from what would be optimal, and this is not accounted for by the actuarially fair measures.

Borrowing constraints and heterogeneous labor efficiency—small open economy.
In the closed economy (Figure 24) as in the case with intragenerational homogeneity, the biases are very similar to the ones in the benchmark economy. The only significant differences are for the poorest workers in the economy who would like to borrow against their social security benefits and, as in the previous cases, the actuarially fair measure does not take into account that they cannot do so.

Borrowing constraints and heterogeneous labor efficiency—closed economy.
In Table 10, I compare the bias of the actuarially fair measure for short-run and long-run evaluations. Again, for the small open economy, there is no change in the bias from the short run to the long run, but for the closed economy the difference is significant. Furthermore, while some of the less effective agents born in the implementation period benefit from social security (the ones that benefit from the redistribution of resources but are not heavily penalized by the borrowing constraint), agents born in the steady state of the economy without social security are better off than the ones born in the steady state of the economy with social security, independently of their types.

Most current analyses of social security still rely on measures based on the concept of actuarial fairness to evaluate this policy. These measures compare the expected tax cost of the coverage to the expected social security benefits. The findings of this paper suggest that such approach is incomplete and misleading. The general equilibrium effects of social security as well as its distortionary effects are ignored. I show that even though the social security tax rate might not generate very significant distortions, the general equilibrium effects induced by this policy have a strong impact on the well-being of individuals because there is a sizeable effect on the wage level and the rate of return to private savings. More importantly, social security plays an insurance role that is also not accounted for by these measures. The value of social security as insurance for uncertain lifetime is extremely high in an economy with a market failure in the private provision of annuities. Finally, in an economy with borrowing constraints, social security can significantly worsen the well-being of individuals as credit constraints limit the extent to which agents can reallocate its incidences optimally over their lifetimes. In the presence of borrowing constraints, agents cannot anticipate the transfers they will receive from social security while their labor income is taxed when they need it the most. Even when they receive positive net benefits they might be worse off.
It is also important to notice that there is a significant difference between the “along the transition path” (short-run) and the “across steady states” (long-run) comparisons. When evaluating the impact of social security on an individual's well-being, we need to evaluate how this individual fares in the economy with social security and how she would fare without social security. This entails comparing the path that the economy follows from its current state if social security is implemented or maintained to the path it follows absent social security.
The analysis in this paper abstracts from many important issues that might affect the bias of actuarially fair measures. In particular, I do not allow for other sources of uncertainty not insured by the existing contingent claims markets [for a discussion of different types of risk sharing that can be accomplished through a social security system, see Shiller (1999)]]. Even though I look at the role of social security as insurance against lifetime uncertainty, I ignore the insurance role of social security against, for instance, idiosyncractic earnings risk and aggregate intergenerational risk. I also do not address endogenous retirement decisions and abstract from altruism, endogenous fertility and investment in human capital. Moreover, I exclude any other government policies that might be affected by social security; for instance, Glomm and Kaganovich (2003) and Soares (2002) show that social security can have important interactions with public education policies.
The inclusion of these factors would add to the results of the analysis in important ways because none of these features are accounted for by the actuarially fair measures. However, the current results do underline the importance of evaluating the impact of fiscal policies on individuals' well-being in a general equilibrium framework with an explicit specification of individuals' preferences. Fiscal policies have a considerable impact on many variables in the economy that affect the welfare of individuals. More importantly, however, most fiscal policies are implemented to correct some market imperfection. Ignoring such factors by focusing solely on their direct effect on an individual's net income can only lead to erroneous evaluations of the impact of these policies on the individuals' well-being.
This appendix briefly describes the numerical procedure used for solving the equilibria for the overlapping generations economies described in this paper. The simulations were conducted using a program written in Matlab that implements a very simple algorithm.
As discussed in the paper, I assume that, initially, the economy is in a steady state without social security. I then compute the path from that steady state once social security is implemented. Hence, in my computations, I start by computing the initial steady state and then the transition path from that steady state.
— I start by choosing arbitrary initial levels of assets and labor supply for the individuals living in the initial economy. I can then compute the aggregate capital stock and effective labor supply. I use these values to calculate factor prices in the closed economy (for the open economy, we do not need to iterate on factor prices because they are assumed to be fixed) and the level of social security benefits if they depend on the aggregate variables.
— Given factor prices and social security benefits, I can use the optimality conditions of the household problems (first-order conditions and budget constraints) to calculate household savings and labor supply. I resort to Matlab's nonlinear equation solver to find the solution to the optimality conditions.
— I use these results to update my initial guess, until the desired convergence is attained.
— Once I solve for the initial and final steady states, I use the corresponding levels of individual asset accumulation and labor supply to formulate an initial guess for the behavior of these variables along the path. I then calculate the corresponding path for the capital stock and effective labor supply. As before, I use these values to compute the path for factor prices and social security benefits.
— Given the path for factor prices and social security benefits, I can solve the optimality conditions of the household problems, which yields time paths of individuals' assets and labor supply.
— I use these results to update my initial guess, and repeat the computations until the desired convergence is attained.
In the absence of borrowing constraints, this approach can also be used to solve for the equilibrium paths when benefits are earnings dependent. We just need to account for the impact of current labor supply decisions on lifetime utility, via its impact of social security benefits. The Euler equations corresponding to the asset accumulation decisions can be used to make this relation a function of current marginal utility and the future path of wages and interest rates.
To solve for the model with borrowing constraints, we just need to incorporate these constraints in our iterations, namely, in the individuals' optimality condition. However, this procedure might not be suitable for solving for an economy in which all the features described in this paper are introduced simultaneously. For instance, because the Euler equations do not have to hold in the presence of borrowing constraints, I can no longer use them to simplify the computations to solve for the equilibrium when benefits are earning dependent. Nevertheless, I chose to use this approach because the resulting calculations of the welfare measure, the focus of the paper, were significantly more accurate than the ones I obtained when I extended the procedure used by Conesa and Krueger (1999).
I am grateful to two anonymous referees for their helpful comments and suggestions. All remaining errors are my responsibility.

Calibration
Transition dynamics.
Benchmark calibration—PVNB and welfare measure.
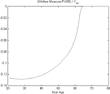
Benchmark calibration—small open economy.
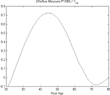
Benchmark calibration—closed economy.

Benchmark calibration (welfare measure—PVNB)/Y
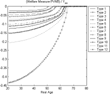
Heterogeneous labor efficiency—small open economy.

Heterogeneous labor efficiency—closed economy.

Heterogeneous labor efficiency (welfare measure—PVNB)/Y

Heterogeneous discount factors
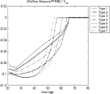
Heterogeneous discount factors—small open economy.
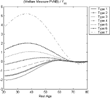
Heterogeneous discount factors—closed economy.

Heterogeneous discount factor (welfare measure—PVNB)/Y

Earnings-dependent benefits—small open economy.
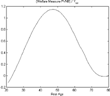
Earnings-dependent benefits—closed economy.

Earning-dependent benefits (welfare measure—PVNB)/Y
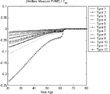
Earnings-dependent benefits—heterogeneous labor efficiency, small open economy.
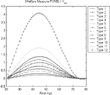
Earnings-dependent benefits—heterogeneous labor efficiency, closed economy.
Uncertain lifetime—small open economy.
Uncertain lifetime—closed economy.
Uncertain lifetime (welfare measure—PVNB)/Y
Uncertain lifetime and heterogeneous labor efficiency—small open economy.
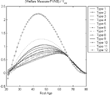
Uncertain lifetime and heterogeneous labor efficiency—closed economy.

Uncertain lifetime and heterogeneous labor efficiency (welfare measure—PVNB)/Y
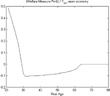
Borrowing constraints—small open economy.
Borrowing constraints—small open economy.

Borrowing constraints—closed economy.
Borrowing constraints—closed economy.

Borrowing constraints (“discounted” welfare measure—PVNB)/Y
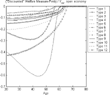
Borrowing constraints and heterogeneous labor efficiency—small open economy.
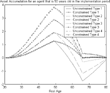
Borrowing constraints and heterogeneous labor efficiency—small open economy.
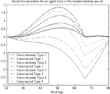
Borrowing constraints and heterogeneous labor efficiency—small open economy.
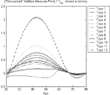
Borrowing constraints and heterogeneous labor efficiency—closed economy.

Borrowing constraints and heterogeneous labor efficiency (“discounted” welfare measure—PVNB)/Y