I. INTRODUCTION
The story begins with Adam Smith’s macrodynamic conception of wage determination. According to Samuel Hollander (1973, p. 157):
The characteristic feature of Smith’s analysis is the role accorded to the rate of capital accumulation as an ‘independent’ variable governing the demand for labour, upon which depends the (long-run or secular) real wage rate and the growth of population; to each growth rate of labour demand there corresponds a long-run real wage rate which assures an equivalent rate of growth of population, and therefore the work force.
In attempting to formalize this account (Waterman Reference Waterman2009), I became aware of a problem: Smith’s analysis as reported by Hollander rests upon a key assumption: that the division of labor to be expected as the economy grows will not produce increasing returns to scale (IRS). For if it did, then labor productivity and the real wage would rise continually.Footnote 1
Now Smith’s price theory requires determinate “natural prices” of the factors of production. Smith maintained that the natural price of labor would depend on whether the economy were growing, stationary, or declining. The passage from Hollander quoted above is the rationale of this belief. But if there is growth, the extent of the market may increase; further division of labor would then take place; “the productive powers of labour” (WN I.i.1) would be enhanced; and the real wage would rise. Hence Smith’s wage theory is undermined: there can be no determinate natural wage associated with any particular growth rate—unless any consequent division of labor is without effect on the average productivity of labor.
Paul Samuelson (Reference Samuelson1977) recognized this, and in his elegant and sophisticated attempt to formalize Smith’s price theory explicitly assumed constant returns to scale (CRS). He also incorporated the central feature of his “canonical classical model” (Samuelson Reference Samuelson1978): diminishing returns to variable labor-cum-capital with fixed land, and so allowed his dynamic model to subside to the stationary state—in which the natural price of labor is simply the “subsistence” (or zero population-growth) real wage.
In subsequent work on Smithian growth theory (Waterman Reference Waterman2012; Reference Waterman2013), it became increasingly clear to me that we ought not to sweep the division of labor under the rug—even though virtually all theorists had done so for a century and a half after Wealth of Nations. Despite my great respect and admiration for Samuelson, therefore,Footnote 2 I was forced to re-examine his assumption that we can ignore the effect of the division of labor upon returns to scale in a growing economy.
If we assume instead—as most commentators seem willing to do—that Smith’s conception of the division of labor does indeed imply IRS at the macroeconomic level, then “the productive powers of labour” must rise for as long as economic growth enlarges the size of the market. The growth rate will accelerate, capital (which determines the demand for labor) will continue to outstrip labor supply, and therefore wages will rise. The correspondence of some particular “natural wage” with any given rate of accumulation in steady stateFootnote 3 will disappear. Indeed, save only in the special case of stationarity, steady state itself disappears and the “natural wage” becomes unknowable. There would thus seem to be an irreconcilable contradiction between Smith’s exposition of the division of labor in Book I, chapters 1 to 3, and his price theory as set out in Book I, chapters 6 to 9.
If I am right, this is a much more serious “Adam Smith Problem” than the traditional, “so-called ‘Adam Smith Problem’ . . . based on ignorance and misunderstanding” (Raphael and Macfie 1976; see also Tribe Reference Tribe2008). But because there may be some who agree with Samuelson that the division of labor need not imply IRS—or more strongly, that it need not increase the average product of labor—I have written my title in interrogative form.
In what follows, I shall first explicate what I perceive to be the problem; next, review some of the literature on the division of labor in WN that might conceivably bear on that problem; and then take a careful and critical look at the few important formal reconstructions of what we now think of as the “growth theory” and the “price theory” in WN Books I and II. Finally, I report my conclusions. An appendix contains mathematical and graphical treatment that closely parallels the exposition in part II below for the benefit of those averse to “the laborious literary working over of essentially simple mathematical concepts” (Samuelson Reference Samuelson1947, p. 6) and who want a short cut to the bottom line.
II. THE PROBLEM EXPLICATED
(a) Price Theory
When the price of any commodity is neither more nor less than what is sufficient to pay the rent of the land, the wages of the labour, and the profits of the stock employed in raising, preparing, and bringing it to market, according to their natural rates, the commodity is then sold for what may be called its natural price. (WN I.vii.4; my italics)
That is to say, Smith tells us, “The commodity is then sold precisely for what it is worth, or for what it really costs the person who brings it to market” since unless the master makes “the ordinary rate of profit” on his stock, “he is evidently a loser by the trade” (WN I.vii.5).
The market price of a commodity is governed by the relation between “the quantity which is actually brought to the market, and the demand of those who are willing to pay the natural price.” If these differ, the market price will change: either it will be bid up by some unsatisfied customers or bid down by sellers obliged to part with unsold goods. “Competition of the different dealers” ensures that the “quantity of every commodity brought to market naturally suits itself to the effectual demand” and hence that the “natural price . . . is . . . the central price, to which the prices of all the commodities are continually gravitating” (WN I.vii.8, 9, 10, 11, 12, 15).
It is evident from this account that the natural prices of land, labor, and capital are an essential part of the price theory of WN. Smith argued that in these cases, too, the market rates will adjust to the natural rates as quantities supplied adjust to the effectual demand (WN I.vii.13). We must therefore examine that mechanism carefully, for elsewhere in this chapter Smith tells us that the natural prices of labor and capital are “regulated” by “the advancing, stationary or declining condition” of society (WN I.vii.1, 33–36; see also I.viii.41, 43, 52; ix.1); and in chapter I.viii, he provided a detailed analysis of the determination of wages by the rate of economic growth. Since Smith claimed that the “rise and fall of the profits of stock depend upon the same causes with the rise and fall in the wages of labour” except that the “increase of stock, which raises wages, tends to lower profits” (WN I.ix.1, 2), we may attend solely to wages in explicating the problem.
(b) The Natural Wage
I have previously considered Smith’s wage theory in some detail, and in particular as it relates to Robert Malthus’s (Waterman Reference Waterman2012). For the latter, Smith’s recipe for high wages would be defeated by diminishing returns; and the best remedy for that would be “moral restraint.” But though Samuelson (Reference Samuelson1978) believed that diminishing returns may be detected in WN, and though there are a few signs in that work that Smith realized that the subsistence wage was socially determined, neither plays any analytical part in his wage theory.
Smith constructed his account of wage determination upon a fundamental ecological assumption, later identified as “Malthusian” but which was actually commonplace among all eighteenth-century economic thinkers (e.g., Cantillon Reference Cantillon and Higgs1931, p. 82): “Every species of animal multiplies in proportion to the means of their subsistence, and no species can ever multiply beyond it” (WN I.viii.39). Since wage earners were assumed to have no other means of subsistence than their wages, and their “maintenance” to be “advanced” to them “from the stock of a master,” their numbers must eventually depend upon “the funds which are destined for the payment of wages” (WN I.viii.5–10, 7, 18). Therefore, “the demand for men, like that for any other commodity, necessarily regulates the production of men” (WN I.viii.40).
The demand for those who live by wages . . . necessarily increases with the increase in the revenue and stock of every country, and cannot possibly increase without it. The increase of revenue and stock is the increase of national wealth. The demand for those who live by wages, therefore, naturally increases with the increase of national wealth. . . . (WN I.viii.21)
How then does “the advancing, stationary or declining condition” of society “regulate” the natural wage? If the demand for labor is “continually increasing,”
the reward of labour must necessarily encourage in such a manner the marriage and multiplication of labourers, as may enable them to supply that continually increasing demand by a continually increasing population. If the reward should at any time be less than what was requisite for this purpose, the deficiency of hands would soon raise it; and if it should at any time be more, their excessive multiplication would soon lower it to this necessary rate. (WN I.viii.40)
In other words, Smith assumed—as is now customary in formalizing Malthusian models mathematically—that any particular rate of “continually increasing population” is determined by some particular “reward of labour” [see appendix (b), equation (2)]. Hence, if as a result of “the advancing” condition of society, there is a “continually increasing demand” for labor, the wage rate will be bid up to that level at which the population growth rate becomes equal to the rate of “the increase of national wealth.”
Evidently there is a wage rate at which population would be stationary: “the lowest rate which is consistent with common humanity,” which Smith illustrated by his account of the stagnant Chinese economy of his day (WN I.viii.24). And “where the funds destined for the maintenance of labour were sensibly decaying,” wages would fall even below this rate “to the most miserable and scanty subsistence of the labourer,” and “Want, famine and mortality would immediately prevail . . . till the number of the inhabitants in the country was reduced to what could easily be maintained by the revenue and stock which remained in it” (WN I.viii.26).
It seems clear from WN I.viii as summarized above that in Smith’s thinking, the natural wage is determined by the rate of growth of the “national wealth.” When the market wage has adjusted to that rate at which population is growing (or declining) at the same rate as the increase (or decrease) of the national “revenue and stock,” there is balanced growth (or decay). Population, work force, capital stock, and national income all grow (or decline) at the same exponential rate. If there is what we should now call “steady state”—i.e., the rate of balanced growth remains constant—the consequent market real wage is the natural wage. A stationary state may exist at which steady-state growth is zero and the natural wage is the Malthusian “subsistence” (or ZPG) wage. But this is a special case. Smith seems to suppose that growth is normal, at least in those countries that have not yet “acquired that full complement of riches which the nature of its laws and institutions permits it to acquire” (WN I.viii.24); that stationarity is infrequent; and that decay, if not rare, is at any rate pathological.
Two crucial questions are therefore raised by this account: what determines the growth of national wealth, and what grounds are there for supposing steady-state growth to be normal? Smith’s explanation of the natural wage—and therefore his entire price theory—requires a satisfactory answer to the second of these questions.
(c) Parsimony
Notwithstanding the effects of the division of labor described in WN I.i, “Parsimony, and not industry, is the immediate cause of the increase of capital” (WN II.iii.16; my italics).
It is not too much to say first, that parsimony is a crucial analytical concept in WN, and secondly, that it has been almost entirely neglected by all subsequent analysts, beginning with Malthus and Ricardo. Among modern students of Smith, unable or unwilling to work with his distinction between “productive” and “unproductive” labor, only Walter Eltis (1976; Reference Eltis2000) has attempted to specify a Smithian growth model in which this distinction is essential [see part IV below]. I have discussed Smith’s concept of parsimony at some length in (Waterman Reference Waterman2013).
By “parsimony,” Smith meant the psychological propensity of masters to spend some portion of their “revenue” on the employment of “productive” labor, “which adds to the value of the subjects upon which it is bestowed,” rather than on “menial servants” and luxury goods (WN II.iii.15, 1). Parsimony is driven by “the desire of bettering our condition, a desire . . . which comes with us from the womb, and never leaves us till we go into the grave” (WN II.iii.28). Smith has in mind an economy of small masters (farmers, manufacturers, merchants, master artisans) who advance “provisions, materials and finished work” to their “labourers” at the beginning of each production period (notionally one year), and at the end of that period receive the whole proceeds of the sale of finished goods. If the value of the latter exceeds that of advances, there has been profit (WN II.iii.4). After the master has replaced his capital (supposing he chooses to do so), he may spend all his profits on unproductive labor, or he may “save” some to add to his capital (WN II.iii.15). In the latter case, he will employ more productive laborers and produce more goods in the current than in the previous period. If all masters have a similar propensity to add to their capital, which Smith seems to have assumed, their parsimony,
by increasing the fund which is destined for the maintenance of productive hands, tends to increase the number of those hands whose labour adds to the value of the subjects upon which it is bestowed. It tends therefore to increase the exchangeable value of the annual produce of the land and labour of the country. It puts into motion an additional quantity of industry, which gives an additional value to the annual produce. (WN II.iii.17)
If we think of parsimony as the fraction of their total revenue from the last production period that masters destine for productive employment in the current period, then it is evident that a particular value of this fraction will exactly suffice, given the average productivity of the ‘labor-cum-capital’ composite (Samuelson Reference Samuelson1978), to maintain production constant. If instead we think of parsimony, as did Smith himself, as a fraction of profits, then a zero value would maintain constant production. But since Smith sometimes envisages the erosion of capital by “prodigality and misconduct” (WN II.iii.14), which would imply a negative value of the parsimony fraction, I prefer the more tractable definition. It makes no difference to the analysis [see appendix (c)].
(d) The Accumulation of Capital
We now have the ingredients of a ‘Smithian’ theory of economic growth. If the average productivity of labor-cum-capital remains constant, a given degree of parsimony will cause “the annual produce” to grow (decay, remain constant) at a constant exponential rate, provided that the supply of labor can keep pace. And provided that capital grows (declines, remains stationary) at a constant rate for long enough, that will be brought about by means of the “Malthusian” mechanism explained in WN I.viii. When the dynamic system has settled down, there will be balanced growth (decay, stationarity) in steady state [see appendix (d)].
(e) Dynamic Equilibrium
Adam Smith’s macrodynamic conception of the natural wage (Waterman Reference Waterman2009) is now apparent. Given the possibility of steady-state balanced growth, we appear to have a coherent account of the natural wage, and therefore of a necessary element in Smith’s price theory [see appendix (e)]. What then is our “Problem”?
In present-day jargon, it is that one of the “parameters” of the growth model we can reconstruct from Smith’s text is the average product of labor-cum-capital. And Smith explicitly recognizes that this will not remain constant if the economy grows.
(f) Division of Labor
“The greatest improvement in the productive powers of labour, and the greater part of the skill, dexterity, and judgment with which it is any where directed, or applied, seem to have been the effects of the division of labour” (WN I.i.1). And the “division of labour . . . so far as it can be introduced, occasions, in every art, a proportionable increase in the productive powers of labour” (WN I.i.4; my italics). What determines how far the division of labor can be introduced?
The “propensity to truck, barter and exchange one thing for another” (WN I.ii.1) is a necessary condition of any division of labor. But “the extent of this division must always be limited . . . by the extent of the market.” For “when the market is very small, no person can have any encouragement to dedicate himself entirely to one employment” (WN I.iii.1). But in large markets created by “water-carriage,” for example, as on sea coasts and along navigable rivers, “industry of every kind naturally begins to subdivide and improve itself,” and soon such “improvements extend themselves to the inland parts of the country” (WN I.iii.3). However, though most of WN I.iii merely illustrates the geographical determinants of the division of labor, a crucial (though almost buried) passage reveals that Smith understood that economic growth of itself may extend the market: “The inland parts of the country can for a long time have no other market . . . but the country which lies round about them. . . The extent of their market, therefore, must for a long time be in proportion to the riches and population of that country . . . ”(WN I.iii.4; my italics). This view is strongly confirmed by Smith’s the treatment of the division of labor in the Introduction to Book II:
As the accumulation of stock must . . . be previous to the division of labour, so labour can be more and more subdivided only as stock is previously more and more accumulated. . . . As the accumulation of stock is previously necessary for carrying on this great improvement in the productive powers of labour, so that accumulation naturally leads to this improvement. (WN II.Intro.3.4; my italics)
There seems no reason to doubt, therefore, that Smith believed that in general an increase in “the riches and population of a country”—that is, the economic growth he analyzes in WN I.viii and II.iii taken together—if it is sustained, will extend the market even in geographic isolation, and will cause the necessary accumulation of stock; and therefore that the process of growth will be accompanied by a continuing “proportionable increase in the productive powers of labour.”
The average product of the labor-cum-capital composite, that is to say, will no longer be a parameter of the growth process but will become a variable. So long as growth is positive, the market grows, capital accumulates, the division of labor becomes ever greater, and productivity rises continually [see appendix (f)].
(g) Price Theory Contradicted by the Division of Labor
Now if labor productivity increases with constant parsimony, the growth rate will accelerate if there is no offsetting impediment to growth (such as land scarcity), since the employment of a given fraction of productive labor will now afford ever-increasing output. But the acceleration of output and accumulation will accelerate the demand for labor, and wages will rise. So long as the growth rate rises, so will wages, as capital (i.e., labor demand) continually outstrips labor supply. Thanks to an increasing division of labor resulting from the ever-widening extent of the market produced by economic growth, steady state is no longer possible. The rates of capital accumulation and population growth must accelerate, and wages must rise continually. There is and can be no determinate “natural wage” [see appendix (g)].
There would seem, therefore, to be a fundamental incoherence in Wealth of Nations. Either the price theory of WN I.vii, which depends on a determinate natural wage, must be maintained, and the treatment of the division of labor in WN I.i-iii ignored as irrelevant; or division of labor must be regarded as Smith’s valid contribution to our understanding of economic growth, and his price theory dismissed as confused and wrong.
Where does this leave Smith’s growth theory? Provided it is not invoked to explain the natural wage—for which we should have to assume not only no division of labor but also free land, zero technical progress, and constant capital intensity (Waterman Reference Waterman2009)—it remains intact. And, indeed, the effect of the division of labor actually strengthens the growth theory and makes it more realistic. For though—as noted above—Smith maintained that “Parsimony, and not industry, is the immediate cause of the increase of capital,” once enough stock has accumulated and growth gets under way, “industry,” by extending the market and increasing productivity, will accelerate accumulation and set wages rising at any given level of parsimony. To be sure, parsimony is both necessary and sufficient for economic growth. But though Smith virtually ignored “industry” in WN II.iii, his all too brief, almost parenthetical remarks in WN I.iii.4 and II.iii.16, taken together with WN II.Intro, leave no doubt that given the necessary condition of parsimony, the division of labor will play an increasingly important part in the growth of output and capital.
III. THE DIVISION OF LABOR IN SOME SUBSEQUENT LITERATURE
In Wealth of Nations itself, there is very little mention of the division of labor after the Introduction to Book II. The chief exception is a detailed and illuminating example of the division of labor in WN III.i, “Of the natural Progress of Opulence,” which describes and discusses the standard eighteenth-century, two-sector general equilibrium model of the interdependence of “town” and “country” (Waterman Reference Waterman1996; Reference Waterman, Forget and Peart2001). The demand of each sector for the output of the other extends the market for both, which stimulates the specialization of many different kinds of “artificers”—“smiths, carpenters, wheel-wrights . . . bricklayers, tanners, shoemakers,” etc., soon joined by Smith’s favorite trio, “the butcher, the brewer and the baker” (WN III.i.1, 2, 4). None of this, however, bears in any way on the theory of economic growth or the determination of the natural wage.
For whatever reason, Smith’s immediate successors in the English School virtually ignored the division of labor and the increasing returns to scale (IRS) it may produce. There are a few scattered references to division of labor in Malthus’s Principles (1989b), but he makes no analytical use of the concept, and, in his testimony to the Parliamentary Select Committee on Artizans and Machinery, he expressed reservations about the principle (Malthus 1989b I, p. li). Among the “classical” economists, only Karl Marx may be thought to have made use of IRS, in his account of the “Historical Tendency of Capitalist Accumulation” (Capital, vol. I, ch. 32), in which, in accordance with “the immanent laws of capitalist production itself,” capital is centralized and “one capitalist always kills many.” However Marx, like David Ricardo, was not interested in Smith’s price theory because he thought he had a better one.
The advent of what we now call “neo-classical” economics in the work of Stanley Jevons (Reference Jevons1866, Reference Jevons1871), Léon Walras (Reference Walras1874), and Carl Menger (Reference Menger1871) removed the division of labor and IRS from the theoretical agenda, and also the study of economic growth so characteristic of classical economics. None of the pioneers of mathematical economics made any attempt to analyze dynamic processes by the use of dated variables. Save in a merely notional, Marshallian way, neo-classical theory abstracted from time. Analytical attention shifted away from growth and development in a more or less explicitly macro-dynamic framework to the performance of interdependent markets under perfect competition, and to the hypothetical behavior of rational agents conceived to determine that performance. Hence price theory became a technically refined, strictly static development of the supply-and-demand analysis pioneered by Smith and Malthus.
Moreover, as it came to be realized that IRS are incompatible with general competitive equilibrium, these had to be assumed away. From the 1870s to the culmination of neo-classical economics in the work of Kenneth Arrow and Gérard Debreu (1954), constant returns to scale (CRS) at the industry level were implicitly or explicitly assumed. Each identical firm, having exhausted all possible economies of scale, operates at the bottom of its long-period, U-shaped, average-cost curve; each industry grows or declines by the entrance or exit of identical firms in response to changing demand; and there is no scope for any further division of labor.
It is therefore no surprise that with a very few exceptions, commentators in this period and for a while thereafter paid virtually no attention to the division of labor and IRS, and none at all to the possible relation between these and Adam Smith’s price theory. It need hardly be said that no textbook of the history of economic thought until Takashi Negishi (Reference Negishi1989) has ever attempted to capture Smith’s exposition in WN II.iii and I.viii, or to address the relation between that and the price theory of WN I.vii.
The most important exceptions to this general neglect of the division of labor in the high neoclassical period were by Piero Sraffa and Allyn Young (Reference Young1928). Sraffa (1926, pp. 536, 537–538) noted the “dark spot” in contemporary value theory: “consideration of that . . . internal division of labour, which is rendered possible by an increase in the dimensions of an individual firm, [has been] entirely abandoned, as it was seen to be incompatible with competitive conditions.” Young’s celebrated article “Increasing Returns and Economic Progress” analyzed the relation between the division of labor and economies of scale, and generalized Smith’s treatment. But Young paid no heed to the relation between this and price theory.
Nicholas Kaldor (Reference Kaldor1972) gives an extended commentary on Young (Reference Young1928), arguing that Smith’s price theory in WN I.iv–vii rests on the assumption of competitive equilibrium and CRS, and hence is contradicted by his analysis of division of labor in WN I.i–iii. Although this is not the incompatibility I have identified as the “Problem,” it is closely related to it. However, G. B. Richardson (1976) suggested that Smith did not believe that IRS need seriously weaken competition. Other belated responses to Young (Reference Young1928) include that of West (Reference West1964), who argued that Smith’s view of the advantages of the division of labor in WN I is contradicted by his account of its disadvantages in WN V, and Rosenberg (Reference Rosenberg1965), which was a critique of West. Though several of the contributors to Skinner and Wilson (Reference Skinner and Wilson1975) discussed the division of labor and increasing returns in WN, none considered price theory.
During the decade of the 1980s, there was a convergence of separate research problems, “all of which resort to generalized increasing returns as a common feature” (Buchanan and Yoon Reference Buchanan and Yoon1994, p. 4). James Buchanan and Yong Yoon themselves sought to show that “‘generalized increasing returns’ may be incorporated into the neoclassical model without undermining the distributional validity of Euler’s theorem” and “without damage to the existence proofs for general competitive equilibrium” (Buchanan and Yoon Reference Buchanan and Yoon1999, p. 517). However, even if their analysis were proffered as an interpretation of WN rather than an adaptation of it—in order to explain how competition could survive in the analytical framework of WN as well as in the economy as envisaged by Buchanan and Yoo, when the extent of the market grows—it would have no relevance for the “Problem” I have identified. For that problem is simply a consequence of the fact that the “productive powers of labour” are increased by the division of labor in either a Smithian or a neoclassical framework.
Post-war interest in the theory of economic growth arising out of the pioneering work of R. F. Harrod (Reference Harrod1939), Evsey Domar (Reference Domar1946), Robert Solow (Reference Solow1956), and T. W. Swan (Reference Swan1956) directed the attention of historians of economic thought for the first time to what W. J. Baumol (1951) called the “magnificent dynamics” to be discovered in WN and in the thought of Smith’s classical successors. Both Solow and Swan had shown that endogenous population growth can be incorporated in the neoclassical growth model; and Swan had analyzed, with explicit reference to classical growth theory, the effect of assuming a third factor, land, in fixed supply.
There were various attempts to model Smith’s growth theory informally in this period, the earliest of which, by Adolf Lowe (Reference Lowe1954), was literary. William O. Thweatt (Reference Thweatt1957) provided a diagrammatical exposition of Lowe’s model. J. J. Spengler’s (Reference Spengler1959) two-part treatment of “Adam Smith’s Theory of Economic Growth” briefly considered Thweatt’s diagram. Robert Heilbroner (Reference Heilbroner1973) followed Lowe’s account of Smith’s growth theory. But none connected economic growth, with or without IRS, with Smith’s price theory in any way.
Hollander’s authoritative treatise, The Economics of Adam Smith (1973), is in many ways the definitive account of the “economic analysis” we may discover in WN when we look at it—as I have tried to do in this article—through our own, present-day theoretical spectacles. It recognizes the macrodynamic element in Smith’s thinking; and the passage I have quoted above perfectly elucidates the relation in WN I.viii between economic growth and the (dynamic) equilibrium level of wages. But there is no recognition of a possible conflict between this picture and one in which wages must rise continually when increasing division of labor produced by economic growth causes that growth to accelerate and wages to rise continually. Hollander eschewed explicit mathematical formulation of analytical relations. But rightly used, a mathematical model may serve as an observational instrument, allowing the historian to behold with greater acuity the distant prospect of eighteenth-century political œconomy. Only with the beginning of mathematical modeling of classical growth theory did our putative “Problem” gradually come into view.
IV. FORMAL ANALYSIS
In the earliest formal model, by Lief Johansen (Reference Johansen and Feinstein1967) captured many of the features of Smith’s own analysis, including the joint determination of the rates of capital accumulation and population growth, and the determination of a dynamic-equilibrium wage rate in steady state. He also incorporated technical progress, and what he confusingly called “decreasing returns to scale,” by which he meant diminishing returns to labor and capital with scarce land. But he ignored division of labor and IRS; he understood the natural wage, as did Ricardo, to be the ZPG rate; and he was not interested in Smith’s price theory.
Haim Barkai (Reference Barkai1969), who wrote in ignorance of Johansen, did incorporate the effect of IRS in the aggregate production function. But he made no mention of population growth, and provided no explicit dynamic analysis of accumulation and no account of the determination of the natural wage. Like Johansen, he was not interested in Smith’s price theory. But Gideon Rosenbluth (1969, p. 314) was; and showed that however “Smith's account of the adjustment mechanism is interpreted, his major conclusion that in the long-run the level of the real wage depends on the rate of growth or decline remains valid.” But he took no account of IRS in his analysis.
In many ways, Walter Eltis (1976, Reference Eltis2000) was the most faithful to Smith’s text. Above all, he captured the characteristically Smithian idea that accumulation (of circulating capital) is motivated not by the rate of profit as other commentators have assumed, but by the parsimony of the masters (Eltis Reference Eltis2000, pp. 93–94, equation 3.9). The level of wages measured in corn, but not measured in manufactured goods, will be consistent with population growth driven by accumulation provided there is no impediment to population growth (Eltis Reference Eltis2000, pp. 87–89; cf. WN I.viii.22, 23; IV.v.a.12) and there are no IRS. But since “returns to scale play a crucial role in Wealth of Nations,” Eltis allowed for this in his production function (Eltis Reference Eltis2000, p. 91, equation 3.1). Hence, circulating capital may grow faster than the productive workforce. As a result, Eltis was forced to conclude that Smith expected that both population and the wage rate would continually rise with capital accumulation when the division of labor produces IRS (Eltis Reference Eltis2000, pp. 91–93, equations 3.5–3.8). He was therefore unable to explain the determination, or even the existence, of the natural wage. But this was of no concern to him, since his object was to capture Smith’s growth theory in WN I.viii and II.iii, and not in any way to connect this with the price theory of WN I.vii.
By far the most powerful and sophisticated attempt to model the economic analysis we may discover in Books I and II of WN is Paul Samuelson’s (Reference Samuelson1977) “A Modern Theorist’s Vindication of Adam Smith” from the “criticisms of Ricardo and Marx and from the general supercilious discounting of Smith as an unoriginal theorist who is logically fuzzy and eclectically empty” (Samuelson Reference Samuelson1977, p. 42). Like Gideon Rosenbluth (Reference Rosenbluth1969) and Hollander (Reference Hollander1973), Samuelson accepted Smith’s assumption that the natural prices of labor and capital are determined in steady state of a dynamic model. But because Smith explicitly included rental costs as a component of natural commodity prices, Samuelson was obliged to assume that economic growth produces land scarcity; that diminishing returns to fixed land afford rents; and that eventually the steady-state equilibrium is driven to stationary state—as in his famous “Canonical Classical Model” (Samuelson Reference Samuelson1978). The natural wage is thus the ZPG rate, and rents are determinate (and maximal). Given the constancy in stationary state of wages, rents, and profits, it was then a straightforward though technically brilliant matter requiring non-linear programming, to demonstrate that:
1) Smith's value-added accounting was shown to be correct by Leontief-Sraffa modeling.
2) His pluralistic supply-and-demand analysis in terms of all three components of wages, rents, and profits is a valid and valuable anticipation of general equilibrium modeling.
3) His vision of transient growth from invention and capital accumulation, which is brought to an equilibrium end with a low rate of profit and a high total of land rent, is isomorphic with the model of Malthus, Ricardo, and Marx (Samuelson Reference Samuelson1977, p. 42).
However, it must appear from the material above that Samuelson’s achievement is problematic. For though he considered that “by the division of labor or otherwise” (Samuelson Reference Samuelson1977, p. 46) capital and population may begin to grow, he abstracted from the consequent IRS, which would work against the effect of diminishing returns and make any outcome indeterminate. Indeed, among “Smith’s Assumptions,” Samuelson listed: “(v) Perfect competition prevails. . . . Free entry and constant returns to scale prevail . . .” (my italics). Moreover, as Hollander (Reference Hollander1980) has pointed out, land scarcity and diminishing returns, though sometimes visible in the text of WN, are not integrated into its analysis. Samuelson did indeed note the case of free land in which there can be “golden age” growth. But unlike Smith himself, who, in much of the discussion in WN I.viii, appears to be assuming free land save in exceptions like China, and who judged that even in slow-growing Britain, wages “in the present times” were above subsistence (WN I.viii.28), Samuelson (1977, p. 49) treated balanced exponential growth and high wages as “transient.”
Takashi Negishi (Reference Negishi1989) provided a simpler, linear-programming, version of Samuelson’s model, and noted two deficiencies in the latter: “Samuelson did not discuss the behaviour of wages and profits in a growing economy” and he “considered only what the modern mathematical programming technique can do better with the basic assumption of convexity” (Negishi Reference Negishi1989, p. 82)—i.e., he ignored the possibility of IRS. Negishi attempted to remedy the former by constructing a Neumann-type growth model of a steadily growing economy in which the wage rate is higher than in stationary state (Negishi Reference Negishi1989, pp. 83–88). But either free land must then be assumed and IRS taken to be absent; or, with scarce land and diminishing returns, IRS must be assumed exactly to offset the latter (Negishi Reference Negishi1989, p. 88n10). Thus IRS are not essentially incorporated in the growth model, but are merely a dispensable, ad hoc assumption. Negishi (1989, pp. 89–102) therefore provided a detailed verbal discussion of the division of labor and IRS, both in relation to the possibility of maintaining competition and to the accumulation of capital. But although he acknowledged that the marginal product of labor would be increased by IRS (implying a rising wage rate), there is no consideration of this possibility and its implications either in his verbal discussion or in his mathematical model.
The exchange between Cigdem Kurdas (Reference Kurdas1988) and Samuelson (Reference Samuelson1988) on the difficulty created for the “Canonical Classical Model” by the division of labor ignores the effect of the latter on the “natural wage.” In subsequent correspondence (letter to Donald Winch, 29 May 1997), Samuelson conceded that IRS must vitiate Smith’s theory of competitive prices and lead to a “Chamberlain-Robinson world of imperfect competition” (cf. Kaldor Reference Kaldor1972, noted above).
In the last two or three decades, there has been much analytical treatment of the “Smithian” themes in Young (Reference Young1928) and their relation to contemporary theories of endogenous growth. Two recent surveys, one highly technical (Yang Reference Yang2003), the other popular and journalistic (Warsh Reference Warsh2006), appear to be comprehensive. But none of the literature they report takes any note of the issue considered here. This is almost certainly because the “Problem” identified in this article arises from Smith’s unique and eccentric macrodynamic conception of the “regulation” of the natural wage, applicable only—even if then—to a long-departed, eighteenth-century world in which population and work force respond passively to the investment decisions of the masters.
V. CONCLUSION
Smith’s price theory requires a determinate natural wage. Smith conceived the latter to be “regulated” by the rate of economic growth. But a growing economy fosters the division of labor, which produces “a proportionable increase in the productive powers of labour.” Hence economic growth will normally be accompanied by rising wages. There can be no determinate natural wage, and therefore Smith’s price theory is incoherent. At the root of this incoherence is an assumption that Smith shared with his predecessors in seventeenth- and eighteenth-century political œconomy: that population and work force respond passively to the investment decisions of masters—an assumption strongly challenged by Malthus and all his successors in the English School (Waterman Reference Waterman2012).
It seems at present, therefore, that the “Problem”—that of a seeming inconsistency between the division of labor and other important elements in Adam Smith’s economic analysis—remains unsolved and may well be insoluble. This need neither surprise nor disappoint historians of economic thought. We have been properly warned by Quentin Skinner (Reference Skinner1969) against what he called “the mythology of coherence.” Attempts to show that Smith really was coherent after all may simply be bad history.
(a) Price theory
Smith’s implicit price theory is elucidated—for the first time ever—in the “Mathematical Appendix” to Samuelson (Reference Samuelson1977) in which “Smith’s value-added accounting is shown to be correct by Sraffa-Leontief modeling,” provided there is a determinate natural wage. Smith’s “complete system” is summarized in equations (25a, b, c, d, e) and (27). But Samuelson’s result requires scarce land, diminishing returns, the absence of any offsetting improvement in “the productive powers of labour” resulting from the division of labor, and hence a determinate (zero-population-growth) equilibrium wage in stationary state.
(b) The natural wage
Let the population and workforce (assumed to be the same) “naturally” multiply “in proportion to the means of their subsistence” (WN I.viii.39) such that
$${N_{t + 1}} = {N_t}[1 + m({w_t} - s)],\quad m > 0,$$or, in continuous terms, since [(N t+1/Nt) – 1] = m(w t– s)],
$$gN = m(w - s)$$for small differences, where the operator g is interpreted in general such that gY(t) ≡ d/dt(lnY) when Y(t) is any continuous, differentiable function of time, t. Alternatively,
$$w = s + {{gN} \mathord{\left/ {\vphantom {{gN} m}} \right. \kern-\nulldelimiterspace} m},$$where w is the real market wage rate and s is the socially determined ‘subsistence,’ or zero-population-growth, wage. The parameter s is behavioral, but it might become endogenous if workers learned to expect higher living standards after a prolonged period of rapid growth. The parameter m measures the speed of population response to above-subsistence per capita income. Since the degree of parsimony π measures the fraction of productive labor in the total workforce [see appendix (c) below], then gN = gN p for any given π.
When gN + gK = g* and there is steady state, the balanced rate of growth [see appendix (d) below] determines the natural wage by equation (3).
(c) Parsimony
Smith conceived the act of parsimony as the expenditure by masters of a fraction of their profit (“annual gains”) on the employment of productive labor (WN II.iii.15). Let the capital stock in the last period, consisting wholly of circulating capital, be K t–1 and revenue from sale of last period’s production be F t –1, both measured in units of “foodstuff.” Then, since K t–1 is the only cost of production, the profit P t realized as a result of last period’s production and sales is the excess of revenue over the replacement of their capital, K t–1:
$${P_t} = {F_{t - 1}} - {K_{t - 1}}$$Let Smith’s conception of parsimony be captured by the index p, where either 0 ≤ p ≤ 1, which is the normal case; or p ≤ 0, which is the case where “the prodigal . . . encroaches upon his capital” (WN II.iii.20). Then the total expenditure by masters on productive labor in the current period is their replacement of capital augmented by the share of profits plowed back: K t–1 + p(F t –1 – K t–1). Therefore, when the wage rate is w, this will employ a total of productive workers in period t,
$$N_t^p = {{\left[ {\left( {1 - p} \right){K_{t - 1}} + p.{F_{t - 1}}} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {1 - p} \right){K_{t - 1}} + p.{F_{t - 1}}} \right]} w}} \right. \kern-\nulldelimiterspace} w}$$Since total employment, N t = F t –1 /w, we may conceive parsimony as the fraction of last period’s total revenue from production and sales that masters “destine” for the employment of productive labor. Let that fraction be defined as the degree of parsimony, π where 0 ≤ π ≤ 1, as used in previous modeling of Smith’s growth theory (Waterman Reference Waterman2009, Reference Waterman2012, Reference Waterman2013; see also Eltis Reference Eltis2000, p. 94, equation 3.9). Then from (5),
$$\displaylines{ \pi = {{N_t^p} \mathord{\left/ {\vphantom {{N_t^p} {{N_t}}}} \right. \kern-\nulldelimiterspace} {{N_t}}} \cr = {{\left( {1 - p} \right){K_{t - 1}}} \mathord{\left/ {\vphantom {{\left( {1 - p} \right){K_{t - 1}}} {{F_{t - 1}} + p}}} \right. \kern-\nulldelimiterspace} {{F_{t - 1}} + p}}. \cr}$$ And since 
${K_{t - 1}} = w.N_{t - 1}^p\;and\;{F_{t - 1}} = \alpha .N_{t - 1}^p$ where α is the average product of labor, the relation between Smith’s conception of “parsimony” and that used in this article is therefore
$$\pi = {w \mathord{\left/ {\vphantom {w \alpha }} \right. \kern-\nulldelimiterspace} \alpha } + p\left( {1 - {w \mathord{\left/ {\vphantom {w \alpha }} \right. \kern-\nulldelimiterspace} \alpha }} \right).$$This more tractable formulation of the concept of parsimony makes no difference to the analysis.
(d) The accumulation of capital
Let the capital stock in period t, consisting wholly of circulating capital, be
$${K_t} = \pi .{F_{t - 1}}.$$Let production in current period be
$${F_t} = \alpha N_t^p,$$where the average product of labor, α, is a technical parameter and N p is the population of productive workers, fully employed at all times. Note that
$$N_t^p = {{{K_t}} \mathord{\left/ {\vphantom {{{K_t}} {{w_t}}}} \right. \kern-\nulldelimiterspace} {{w_t}}}.$$Then by (10) into (9), and (9) into (8), the annual growth-rate of capital,
$${{\left( {{K_t} - {K_{t - 1}}} \right)} \mathord{\left/ {\vphantom {{\left( {{K_t} - {K_{t - 1}}} \right)} {{K_{t - 1}}}}} \right. \kern-\nulldelimiterspace} {{K_{t - 1}}}} = {{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } {w - 1}}} \right. \kern-\nulldelimiterspace} {w - 1}},$$which for small differences we may regard as a discrete approximation to the logarithmic growth-rate [cf. (1) and (2) above]. Then
$$gK = \left[ {({{{K_t}} \mathord{\left/ {\vphantom {{{K_t}} {{K_{t - 1}}}}} \right. \kern-\nulldelimiterspace} {{K_{t - 1}}}}) - 1} \right] = {{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } {w - 1}}} \right. \kern-\nulldelimiterspace} {w - 1}};$$or alternatively,
$$w = {{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } {(1 + gK)}}} \right. \kern-\nulldelimiterspace} {(1 + gK)}}.$$If the degree of parsimony π is greater than the ratio of the real wage to average product, the economy will grow and vice versa. If π = w/α the entire per-period surplus (1 – π )F t –1 is spent on unproductive labor, therefore per-period production and the end-of-period capital stock remain stationary.
(e) Dynamic equilibrium
If (3) and (13) are graphed in (w, g) space, the negatively sloped w(gK) locus intersects with the positively sloped w(gN) locus to determine a balanced growth rate g* for capital, population, and productive employment, and a natural wage rate w*.
However, because the w(gK) function is a rectangular hyperbola, there will exist a second point of intersection with the w(gN) function in the third quadrant. Since negative wage rates are not economically meaningful, this may be ignored. Moreover, because the vertical asymptote of the w(gK) function is g = –1, and the curve approaches the horizontal axis as g → +∞, the function may be approximated for graphical purposes as a straight line over that narrow range of values of g in the first quadrant, say from – 0.1 to + 0.1, for which the analysis is intended to apply. From (13), the slope of the w(gK) function in general is
$${{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial gK}}} \right. \kern-\nulldelimiterspace} {\partial gK}} = {{ - \alpha \pi } \mathord{\left/ {\vphantom {{ - \alpha \pi } {{{(1 + gK)}^2}}}} \right. \kern-\nulldelimiterspace} {{{(1 + gK)}^2}}},$$which is – απ in the special case when gK = 0, that is to say on the vertical axis. A linear approximation to (13) may therefore be written, and graphed in figure 1, as:
$$w = \alpha \pi - \alpha \pi .gK.$$
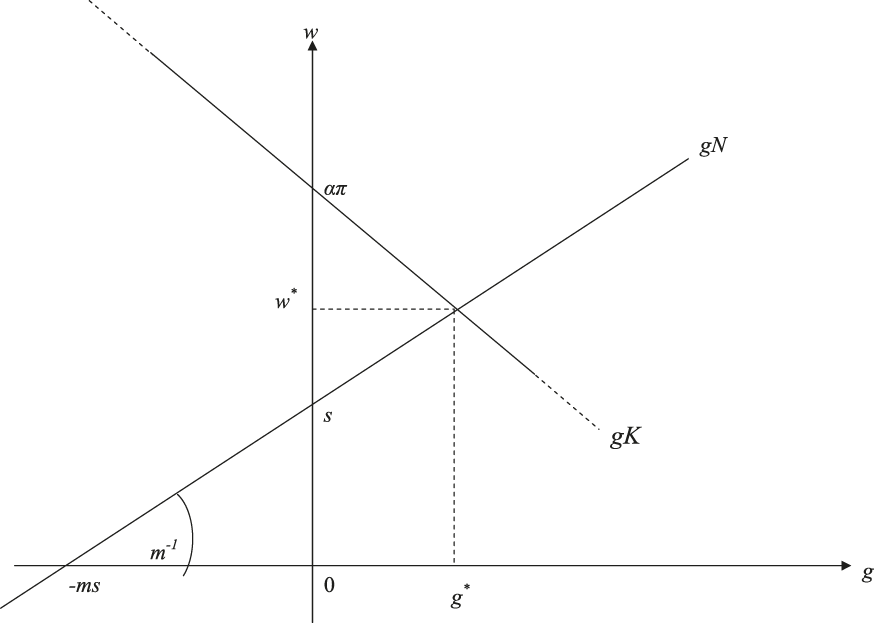
Figure 1. Mutual Determination of the Rate of Accumulation and the Natural Wage
Figure 1 bears a family resemblance to diagrams used by Hollander (1984, Reference Hollander1997) and Eltis (2000, ch. 4) to analyze the growth theories of Malthus and Ricardo.
Because the balanced-growth rate of accumulation is (gK = gN = g*) when the balanced-growth wage rate is w = w*, a pair of simultaneous, linear equations,
$$w* = \alpha \pi - \alpha \pi .g*.$$
$$w* = s + {{g*} \mathord{\left/ {\vphantom {{g*} m}} \right. \kern-\nulldelimiterspace} m},$$determines the graphical solutions:
$$w* = {{\alpha \pi (1 + ms)} \mathord{\left/ {\vphantom {{\alpha \pi (1 + ms)} {(1 + \alpha \pi m)}}} \right. \kern-\nulldelimiterspace} {(1 + \alpha \pi m)}}$$
$$g* = {{m(\alpha \pi - s)} \mathord{\left/ {\vphantom {{m(\alpha \pi - s)} {(1 + \alpha \pi m)}}} \right. \kern-\nulldelimiterspace} {(1 + \alpha \pi m)}}.$$That the market wage rate w will “gravitate” to the natural wage rate w*, for reasons similar to those that Smith considered for product prices in WN I.vii.7–15, is easily seen. For when w < w*, capital accumulation is faster than growth in the workforce, hence demand for labor will rise in relation to supply and force up the market wage—and vice versa. We can investigate local stability in the first quadrant by using linearized (13) for gN. Let the out-of-steady-state rate of wage adjustment be
$${{dw} \mathord{\left/ {\vphantom {{dw} {dt}}} \right. \kern-\nulldelimiterspace} {dt}} = H[gK - gN] = H[(1 - {w \mathord{\left/ {\vphantom {w {\alpha \pi }}} \right. \kern-\nulldelimiterspace} {\alpha \pi }}) - m(w - s)];\;H' > 0.$$Then
$${d \mathord{\left/ {\vphantom {d {dw}}} \right. \kern-\nulldelimiterspace} {dw}}({{dw} \mathord{\left/ {\vphantom {{dw} {dt}}} \right. \kern-\nulldelimiterspace} {dt}}) = - H'(m + {1 \mathord{\left/ {\vphantom {1 {\alpha \pi }}} \right. \kern-\nulldelimiterspace} {\alpha \pi }}) < 0,$$which is sufficient for convergence of w upon w*.
With the stability of balanced growth assured, we may proceed to comparative dynamics. The effect upon w* and g* of a once-for-all change in each of the four parameters (α, π, m, and s) may be seen from figure 1 below. An increase in α or π shifts the w(gK) curve upwards; an increase in s shifts the w(gN) curve upwards; and an increase in m causes the w(gN) curve to rotate clockwise about its vertical intercept. The outcomes of these shifts may be verified by partial differentiation of the balanced-growth equations, which it is preferable to use in their general, quadratic forms obtained from (3) and (13) by substitution, setting gK = gN = g*, which implies that w = w*:
$$m{w^{*2}} + (1 - ms)w* = \alpha \pi$$
$${g^{*2}} + (1 + ms)g* = m\left( {\alpha \pi - s} \right)$$Equations (8), (9), (10), and (1) imply a second-order difference equation in N(t):
$${N_{t + 1}} - (1 - ms){N_t} - m\pi \alpha {N_{t - 1}} = 0.$$For the equivalence of the discrete system with the continuous analysis employed in this article, see Waterman (2009, Appendix 1).
(f) Division of labor
If there is free land, constant capital intensity, zero technical progress, and no division of labor, α is a parameter and the positive root of (22) defines Adam Smith’s natural wage.
But if there is increasing division of labor as the extent of the market (proxied by N) increases, then 
$\alpha = \alpha (N),\;\alpha ' > 0$: “the productive powers of labour” will increase as population grows unless this effect is offset by diminishing returns. Therefore, by partial differentiation of (22) and (23) with respect to N, we obtain:
$${{\partial w*} \mathord{\left/ {\vphantom {{\partial w*} {\partial N}}} \right. \kern-\nulldelimiterspace} {\partial N}} = \alpha '\pi {\left[ {1 + m(2w* - s)} \right]^{ - 1}} > 0,$$and
$${{\partial g*} \mathord{\left/ {\vphantom {{\partial g*} {\partial N}}} \right. \kern-\nulldelimiterspace} {\partial N}} = \alpha 'm\pi {\left( {1 + ms + 2g*} \right)^{ - 1}} > 0.$$Both the market equilibrium wage rate and the balanced rate of growth will increase continually as population, capital, and the extent of the market grow. As noted above, this is what Eltis (2000, pp. 91–93) concluded from his own reconstruction of Smith’s argument.
(g) Price theory contradicted by the division of labor
However, if there is scarce land and diminishing returns, and if the effect of these on the average product of labor dominates that of the division of labor, 
$\alpha = \alpha (N),\;\alpha ' < 0$. In this case, the signs of the partial derivatives in (25) and (26) will be negative.
Hence if g* > 0, gK and gN will decline to zero, at which w = απ = s, the “subsistence” wage. Since this is what Samuelson (Reference Samuelson1977) assumes, he takes the natural wage, as did Ricardo, to be s. Given that assumption, his “Vindication” of Smith’s price theory holds.
However, as appendix (f) shows, this result can be obtained only by denying that the division of labor has any effect in increasing α, the measure of “the productive powers of labour,” as K t and N t grow and the extent of the market is continually enlarged.
This conclusion, the analysis of appendix (e) above, and the analyses of Rosenbluth, Hollander, Eltis, Samuelson, and Negishi reported in part IV above, may be illustrated diagrammatically.
In figure 1, growth functions of (variable) capital (gK) and population/workforce (gN) are plotted with the wage rate (w) on the vertical axis and growth rates (g) on the horizontal. Population growth is an increasing function of the wage rate as in equation (2). The rate of capital accumulation is a decreasing function of wage rate as in equation (12) linearized as (15).
Where the two curves intersect, an equilibrium wage and rate of balanced growth are determined. This illustrates the analysis in Rosenbluth (Reference Rosenbluth1969) and the quotation from Hollander (1973, p. 157) above. Hollander himself uses this diagram as figure 1 in chapter 1 of his (1997), and something quite like it makes its first appearance as figure 1 in Johansen (Reference Johansen and Feinstein1967).
Suppose that when 
$\left( {g* = gK = gN} \right) > 0$ division of labor increases as growing K and N enlarge the extent of the market. The parameter α increases (as Negishi recognized) and the gK curve shifts vertically upward. Both the wage rate and the growth rate increase, and do so without bound. Other things being equal, the division of labor accelerates growth and causes ever-rising wages (as Eltis concluded). There can be no determinate “natural wage.”
If, when 
$\left( {g* = gK = gN} \right) > 0$, there are diminishing returns but no increase in the division of labor (which is what Samuelson assumed), α decreases and the gK curve shifts vertically downward until it intersects gN on the vertical axis and stationary state is obtained. The “natural wage” is determined at the “subsistence” or ZPG rate, s. Samuelson (Reference Samuelson1977) is justified.
If, when 
$\left( {g* = gK = gN} \right) > 0$, there are diminishing returns and exactly offsetting effects from increasing division of labor, α remains constant, steady state is therefore possible at that g*, and there is a determinate w (Negishi’s ad hoc conjecture.)
