1. INTRODUCTION
Moral cognitivists take moral judgements to be beliefs. Some (possibly most) moral cognitivists take moral beliefs – just like non-moral beliefs – to come in degrees that ought (for a rational agent) to obey the probability axioms. Indeed, over the last decade issues of decision-making under conditions of moral uncertainty have begun to receive much attention in the literature.
Cases in which an agent is in a state of moral uncertainty are to be distinguished from cases in which the agent is in a state of uncertainty regarding a descriptive issue with moral implications. For example, a doctor might be uncertain whether she ought to perform some medical procedure because she is uncertain how to morally compare the benefits and disadvantages the procedure might bring to the patient (a case of moral uncertainty), but she might also be uncertain whether she ought to perform the procedure because she is uncertain about the consequences of performing it (a case of morally relevant descriptive uncertainty).
As many real-life choice situations involve both kinds of uncertainty, it seems to me that any account of decision-making under conditions of moral uncertainty must handle the question of the relation between these two types of uncertainty. However, not much attention has been given to this question in the literature. In this paper I will argue that giving this question proper attention undermines a central claim shared by virtually everyone discussing choice under conditions of moral uncertainty.
This claim is the following one. When a morally motivated rational agent is in a state of moral uncertainty he ought to maximize expected moral value relative to his moral uncertainty. In some cases, a weaker version of this thesis is assumed. According to the weaker version of the thesis, when choosing under conditions of moral uncertainty, a morally motivated rational agent ought to take into account not only his degrees of belief in different moral theories, but also the degrees of moral value these theories assign to the acts he can choose from. In the literature (see, e.g. Lockhart Reference Lockhart2000; Sepielli Reference Sepielli2009, Reference Sepielli2012) the term 'moral hedging' is sometimes used to describe this thesis.Footnote 1
As will become clear as the argument proceeds (and after I will formally characterize the two theses) assuming that the agent is rational, the only difference between the weaker thesis and the stronger one is that the latter assumes risk neutrality with regard to moral value, while the former allows for risk aversion or risk seeking in this regard. Here is a typical example of such reasoning:
Suppose, for example, that an agent is uncertain between two views about the morality of eating meat. In one view, eating meat is tantamount to murder; it is much, much worse, then, to eat meat than to abstain from it. In another view, it is ever so slightly better to eat meat than to abstain – better, perhaps, for reasons of health or pleasure. In the most plausible views of rationality under moral uncertainty, it is rational to avoid eating meat, even if one's belief in the second view is slightly higher. One view of rationality that yields this result is the view that it is rational to do the action with the highest expected moral value. An action's expected moral value is the probability-weighted sum of its moral values according to the various moral views or theories. But this is far from the only view of rationality that has this implication. Almost any plausible theory of rationality under uncertainty about the moral will care about how the moral 'stakes' according to one moral theory compare to the moral stakes according to the others. (Sepielli Reference Sepielli2012)
I will argue that the reasoning described in the given quotation, as intuitively compelling as it might be, is flawed. To be clear, the argument is not that it can be misleading to use this kind of reasoning in some cases, or that it is easy to exploit this line of reasoning or that it is pragmatically impossible to use it in a constructive way. Rather, the argument is that moral hedging is not a demand of either rationality or morality. Its intuitive appeal, I will argue, is misleading.
The general structure of the argument is as follows. I start by making a conceptual distinction between a morally motivated rational agent's attitude toward risk and a moral theory's attitude toward risk. I then consider the possibility of a morally motivated rational agent assigning positive credence to at least one moral theory with an attitude toward risk which is different from the agent's own.
The argument, then, takes the form of a dilemma.Footnote 2 The first horn of the dilemma involves arguing that such cases are impossible: a rational agent must assign positive credence only to moral theories that have the same attitude toward risk as the agent's own. I show that by choosing this horn one must either conclude that the moral hedging thesis does not constrain choice under conditions of moral uncertainty in any way, or else understand the term 'moral value' in a way that makes this thesis meaningless.
The second horn of the dilemma involves allowing for cases in which the agent assigns positive credence to at least one theory with an attitude toward risk which is different from the agent's own. I show that by choosing this horn, the hedger must, in some cases, violate dominance, i.e. there are cases in which hedging leads to preferring one act, c, to another act, l, even though there is a partition of the set of states of the world such that given any one of the events in the partition, l is preferred to c.
The rest of the paper is organized in the following way. In section 1 I discuss some necessary background issues and present the first horn of the dilemma. In section 2 I present the second horn of the dilemma and offer an explanation for the failure of the moral hedging thesis, namely that it is based on the false assumption that inter-theoretical comparisons of moral value are meaningful.
2. THE MORAL HEDGING THESIS AND ATTITUDES TO RISK INVOLVING MORAL VALUE
In the philosophical literature that discusses choice under conditions of moral uncertainty, different types of propositions are assumed to be the object of the uncertainty. In some cases these are propositions that express comparative moral judgements (i.e. propositions of the form 'a is morally superior to b', when ‘a’ and ‘b’ are either acts or states of affairs). In other cases the writers refer to 'moral theories' and it seems that what they have in mind are actual theories that can be found in the philosophical literature. In yet other cases the relevant class of propositions are those that assign a specific degree of moral value to some act or outcome.
In any case, in order to obey the moral hedging thesis, one must be able to assign a specific degree of moral value to each of the acts available to one, conditional on each of the possible objects of uncertainty obtaining. For example, if one is uncertain whether act a is morally superior to act b, then in order to follow the moral hedging thesis, one must assign specific levels of moral value to both a and b, whether a is superior to b or b is superior to a.
Moreover, one must also assume that these values are comparable across the different moral hypotheses to which one assigns a positive probability. For example, one must be able to compare the value of a when a is morally superior to b to the value of a when b is morally superior to a.
From the perspective of the moral hedging thesis, then, when it comes to choice, the type of moral uncertainty in question (i.e. the type of propositions which are the objects of the uncertainty) is insignificant. What a morally motivated rational agent ought to do when faced with any kind of moral uncertainty is the following. He ought to translate the uncertainty he is faced with into uncertainty regarding all possible combinations of assignments of degrees of moral value to each one of the acts available to him that he thinks might be true, and then maximize the expected moral value relative to this uncertainty (using some method of inter-theoretical comparison of moral value). In other words, the agent ought to translate the moral uncertainty he is faced with into uncertainty regarding the question of which of several possible moral value functions is the true one.
It is important to emphasize again that, since agents are also faced with descriptive uncertainty in most real-life moral decisions, these value functions must assign degrees of moral value not only to acts with definite consequences, but also to lotteries, i.e. to acts with uncertain consequences (where the uncertainty in question is descriptive).
Now, it is usually assumed in the literature – and I will follow this assumption – that a rational agent assigns a positive probability only to rational theories.Footnote 3 This demand can be explicated in the following way.Footnote 4
Each value function ranks the different acts available to the agent (and other hypothetical acts) according to how valuable they are. An act is ranked higher than another act iff its value, according to the given value function, is higher than the value of the other act. A value function is rational iff the ranking it leads to obey the VNM axioms. We can call a ranking that obeys the VNM axioms 'a rational ranking'.
Now, each rational ranking can be represented as resulting from a maximization of many value functions. Some of these value functions have an expectational form, i.e. the value of each act is its expected value, when the expectation is calculated relative to the probabilities of the different (descriptive) states. In fact, it is possible to represent each rational ranking as resulting from a maximization of expected value for some value function which is unique up to affine transformation (i.e. if V is such a value function, so is U = dV + e, for any ‘d’ and ‘e’). However, not all value functions the maximization of which leads to a given ranking have an expectational form. Each ranking can be represented both as resulting from a maximization of a value function that has an expectational form and as resulting from a maximization of a value function that does not have an expectational form (see Weymark Reference Weymark, Elster and Roemer1991 for a good discussion of this point).
To say that a moral value function has an expectational form is to say that this moral value function is risk-neutral with respect to moral value, but rationality does not require risk-neutrality with respect to any value, and specifically with respect to moral value.
Does morality require risk neutrality with respect to moral value? In other words, is it the case that the moral value of any act with uncertain consequences is its expected moral value? John Broome (Reference Broome1991a) discussed an analogous questionFootnote 5 in chapter 6 of his Weighing Goods. Broome argued – and I agree – that the answer to this question depends on the way one chooses to understand the term 'moral value'. It is possible to understand this term in a way that makes the requirement that the moral value of any act is its expected moral value 'an implausible restriction' (Broome Reference Broome1991b: fn 2), but it is also possible to understand the term in a way that makes this requirement a conceptual truth.
The way to understand the term 'moral value' in which the requirement is implausible is, I take it, the following one. We start the discussion with a primitive notion of 'moral value'. Although we may be uncertain about the truth values of propositions that assign particular degrees of moral value to acts and outcomes, we do not aim to explain how these truth values are constituted. Specifically, we do not assume that their truth values are constituted by their relative place in the correct moral ranking (i.e. the facts about which acts are morally superior to which).
In this approach, to assume that morality is always risk neutral is to rule out the possibility that there is some intrinsic moral value in the way one handles descriptive uncertainty while making moral decisions – that is, that in some cases there are morally better or worse ways to handle descriptive uncertainty.
An example might help here. Consider the following two options:
1. One person is certain to die (in a particular situation).
2. There is a probability of 0.01 that 100 people will die and a probability of 0.99 that nobody will die (in the same situation).
To argue that morality is risk-neutral regarding these two options is to argue that if the value of 100 lives is equal to 100 times the value of one life, then options 1 and 2 have the same moral value. It might be argued, however, that this is wrong. It might be argued that even if moral value is linear with respect to the number of lives (i.e. the value of 100 lives is equal to 100 times the value of one life), option 1 has greater moral value than option 2, due to the fact that it guarantees that 99 people will not die.
I do not know whether this claim is correct. In fact I am uncertain of the truth of this claim and I believe many others feel like me. For my purposes here, I do not need to take a position in this debate, but I do need to assume that (under the first understanding of the term 'moral value') a morally motivated rational agent can be uncertain about whether morality is risk-neutral.
More generally, I have to assume that a morally motivated rational agent can be uncertain about the true moral theory's attitude to risk. I need to assume, that is, that a morally motivated rational agent can ascribe positive credence to at least two moral theories that assign exactly the same values to all sure outcomes, but different values to some lotteries among these sure outcomes.
What can be a plausible ground for ruling out this kind of case (e.g. ruling out the possibility that an agent can be uncertain of whether option 1 and 2 in the example above are equally valuable, although he does not face any uncertainty regarding the value of sure lives)? One way to go is to argue that there is no truth of the matter regarding the 'right' moral attitude toward risk. Moral theories, one might argue, assign values only to sure outcomes, and when choosing under condition of uncertainty (of any kind) the agent uses his own risk attitudes.Footnote 6
However, if one takes this route, one must conclude that the moral hedging thesis does not constrain choices under moral uncertainty in any way. Rationality does not demand that the agent adopt any particular attitude toward risk, and any choice under moral uncertainty can be justified by adopting one or another attitude toward risk. Thus, if there is no 'right' attitude toward risk to adopt when making moral choices (if it is not 'immoral' to adopt any attitude toward risk with respect to moral value), nothing constrains the set of permissible choices given the agent's uncertainty. The moral hedging thesis turns out to be empty under this approach.
The other way to go is to argue that there is a truth of the matter regarding the question of the 'right' moral attitude toward risk. If this is true, then a rational agent might be uncertain what this truth is. The demand not to be uncertain regarding this question is clearly not a demand of rationality in the same way that the demand not to be uncertain regarding whether it will rain tomorrow is not a demand of rationality. Thus, I conclude, if we choose the first way of understanding the term 'moral value', according to which the truth of propositions that assign particular moral value to acts or outcomes is not constituted by the 'real' moral ranking, we must allow for cases in which a morally motivated rational agent assigns positive credence to at least one moral theory with a risk attitude which is different from his own.
This brings us to the second way of understanding the term 'moral value', in which the claim that morality is risk-neutral is a conceptual truth. Instead of taking the objects of the uncertainty to be moral value functions, we take them to be rational rankings of the available acts and some other hypothetical ones. In the interpretation, these rankings are the moral rankings of the acts according to each one of the possible 'moral hypotheses' or 'moral theories' to which the agent assigns positive credence.
As explained, if the probability of the different descriptive states is given, we can represent each of the moral rankings as resulting from a maximization of expected value for some value function which is unique up to affine transformation. We can then call this function, for which the maximization of expectation leads to a given ranking, the 'moral value function' of the theory associated with the given ranking.
Under this approach (which I favour), the risk-neutrality of morality becomes a conceptual truth, as the moral value function was constructed under the assumption that the agent maximizes expected moral value.
This second explication has one philosophical advantage and one philosophical disadvantage compared with the first one. The advantage of the second explication is the following. It seems to many scholars (and I am among them) that the simple assumptions we used in the second explication (i.e. the VNM axioms) are intuitively compelling as principles of rationality in a way that the demand to maximize the expectation of some value relative to one's descriptive uncertainty is not (we are now discussing the rationality of each one of the ‘moral hypotheses’ the agent believes might be true, not the rationality of his choices, given his moral uncertainty).
When an agent faces a choice situation in which he has no value uncertainty, but does have some descriptive uncertainty, there are many alternative decision methods he can adopt. For example, he can choose the alternative that guarantees the maximal amount of value gained (i.e. use the maximin choice rule), or he can choose the one which is the most likely to be better than all the others in terms of the value gained, or he can maximize a weighted expectation of some value, etc. Why, one might wonder, is maximizing the expected value the only rational thing to do?
The representation theorems of decision-theory provide an answer to this question in terms of the second explication presented: if the agent's comparative value judgements obey the intuitive axioms of rationality, it will always be possible to describe the agent as maximizing the expectation of some value, in the sense that the agent will always judge one act to be more valuable than another if the expected value of the former act is greater than that of the latter. Now, so the argument goes, when we talk about the value the agent attaches to the various outcomes, we are talking about the value revealed through the agent's consistent comparative judgements. Thus, under this interpretation of the term 'value' and under the assumption that the comparative value judgements are consistent, the claim that the value of an act is its expected value becomes a conceptual truth.
It is important to emphasize that it does not follow from accepting this latter claim that the moral hedging thesis is correct. Maximizing expected value relative to descriptive uncertainty is different from maximizing expected moral value relative to uncertainty regarding the value function itself.
This is true in two different senses. First, in the same way that a moral theory may have different attitudes toward risk, a morally motivated rational agent facing moral uncertainty may have different attitudes toward risk relative to the moral uncertainty he is facing. If the agent is not risk-neutral, he will not obey the moral hedging thesis under its stronger interpretation, i.e. he will not maximize expected moral value relative to the moral uncertainty he is facing. However, he may still obey the moral hedging thesis under its weak interpretation, i.e. he may still maximize the expectation of some function which is increasing in moral value (but not linearly increasing).
An analogy might help here. Consider the value of money, for example. Clearly, the claim that a rational agent should always maximize his expected money payoffs is false. If the agent is risk-averse with respect to money, he should not maximize expected money payoffs. It is still true that if his choices are consistent, then he must be maximizing the expectation of some value, but this value is not the money value of the outcomes of the acts. It is a different value, which (neo-classical) economists call 'utility'.
In the same way, if a morally motivated rational agent is risk-averse with respect to well-being (which is just a different way of saying that the agent is a prioritarian or that he morally values assigning units of well-being to people to a lesser extent, the more well-being they enjoy) he should not maximize the expected sum of well-being in his moral choices. Rather, he should maximize the expectation of some other value, which some philosophers tend to call 'moral value'.
Now, in the same way that an agent who is risk-averse with respect to money does not maximize expected money payoffs in his choices, and a morally motivated agent who is a prioritarian does not maximize expected social well-being, it might be the case that an agent who is risk-averse with respect to moral value should not maximize expected moral value. Although such an agent does not obey the moral hedging thesis in its stronger sense, he can still obey it in its weaker sense.
It is important to emphasize again a point that was already mentioned and that will reappear later in the discussion. The type of risk attitude just discussed – that of an agent facing moral uncertainty – is independent of the risk attitudes of the moral theories to which the agent assigns positive credence. An agent facing uncertainty can be risk-neutral (or risk-seeking or risk-averse) with respect to moral value, while assigning positive credence to several theories with different attitudes toward risk.
This is true in the same way that a morally motivated rational agent's attitude toward risk with respect to social well-being when faced with the decision of how to distribute goods among members of some society is independent of the attitudes toward this risk held by the individuals themselves. Although each member of the society can be, for example, risk-averse with respect to his own well-being (e.g. prefer x units of well-being to an act that offers 2x units of well-being with probability 0.5 and 0 units with probability 0.5), the distributor might be risk-neutral with respect to social well-being.
I have dedicated a lot of space to discussing the risk attitudes of moral theories and morally motivated agents, as well as the relations between them, since clarity about these issues is important for the argument presented in the next section. However, this discussion is not part of my argument. My argument against the moral hedging thesis, I want to emphasize, is against the thesis in its weaker form (and thus against the thesis in its stronger form as well). It is an argument against the claim that the degrees of moral value the different moral theories assign to available acts must play some role in the decision procedure a morally motivated rational agent employs when faced with moral uncertainty.
This leads us to the disadvantage of the second way to understand the term 'moral value', which involves the limitation on the uniqueness of the value function that the representation theorems give us. Since the value functions are unique only up to affine transformation, neither the size of the units in which the value is measured (the ‘d's) nor the zero point (the ‘e's), are morally significant. Since an agent who wants to obey the moral hedging thesis needs to compare the values assigned by each of the possible theories to the available acts on a single scale and since, according to the second explication, the truth values of propositions that assign certain moral values to acts are constituted in a way that is insensitive to scale, the moral hedging thesis becomes meaningless.Footnote 7
Thus, the price I – and anybody like me who chooses to understand the term 'moral value' in such a way – must pay is to give up on the idea of maximization of expected moral value relative to the moral uncertainty the agent faces. More generally, we must reject any decision rule for choice under conditions of moral uncertainty that makes use of inter-theoretical comparisons of moral value. We must pay this price because we are committed to a semantics of moral propositions (which assign moral value to acts) according to which inter-theoretical comparisons of moral value are meaningless.
Those who prefer the first approach do not, however, have to pay this price. Since they are not committing themselves to any specific semantics for moral value propositions, they can still hold the position that inter-theoretical comparisons of moral value are meaningful. Indeed, much of the discussion in the literature about moral uncertainty is dedicated to the issue of such comparisons. As my aim in this paper is to question the plausibility of the moral hedging thesis, I will start by assuming – contrary to what I actually believe – that inter-theoretical comparisons of moral value are not only meaningful but also possible. Even under these assumptions, the conclusion will be that moral hedging is not a principle of either rationality or morality.
The conclusion so far is the following one. A commitment to the risk-neutrality of moral value makes sense only when one understands the term 'moral value' in such a way that makes this risk-neutrality a conceptual truth. However, if this is the right way to understand the term 'moral value', then inter-theoretical comparisons of moral value are meaningless and so is the moral hedging thesis.
Those who wish to keep the moral hedging thesis must assume that inter-theoretical comparisons of moral value are meaningful, and thus must understand the term 'moral value' differently. However they choose to understand it, they must admit that the moral theories to which a morally motivated rational agent assigns positive credence can differ in their attitudes toward risk. As we will see in the next section, this will lead them into a dilemma.
3. THE MORAL HEDGING THESIS CONFLICTS WITH DOMINANCE
In this section I will show that in some cases in which an agent assigns a positive credence to two moral theories that differ in their attitudes to risk, a conflict arises between the moral hedging thesis and two compelling dominance principles:
1. The 'Moral Dominance Assumption' (MDA): if according to all theories to which an agent assigns positive credence, one act, x, is more morally valuable than another act, y, then x should be morally preferred to y.
2. Standard Dominance: if an agent who suffers from descriptive uncertainty morally prefers one act, x, to another act, y, in all possible descriptive states, he should prefer x to y.
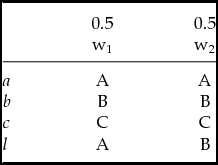
Consider the simple choice situation illustrated in Table 1.
Table 1. Basic decision problem.
A morally motivated rational agent, let us call him Bob, has a choice between four possible acts. Act a leads to outcome A (x dollars goes to charity A) in every state of the world, act b leads to outcome B (x dollars goes to charity B) in every state of the world, act c leads to outcome C (x dollars goes to charity C) in every state of the world and finally act l (lottery) leads to outcome A in one state of the world, w 1, and outcome B in another state of the world, w 2.
Assume Bob divides his credence equally between w 1 and w 2. Assume also that Bob divides his credence equally between two moral theories, T1 and T2. T2 is the theory that assigns a moral value of 1 to B, 0 to A, and 0.6 to C, and is risk-neutral with respect to the moral value of A and B – i.e. according to T2 the value of a lottery that leads to B with probability p and to A with probability (1-p) is p.
T1 is the theory that assigns a moral value of 1 to A, 0 to B, and 0.3 to C, and a moral value of p 2 to every lottery that gives A with probability p and B with probability (1-p) – i.e. T1 is a risk-seeking moral theory.
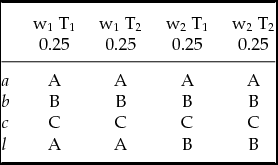
Finally, assume that Bob's moral beliefs are probabilistically independent of his descriptive beliefs, i.e. Bob's degree of belief in T1 conditional on w1 being the real state of the world is equal to his unconditional degree of belief in T1 and thus equals 0.5. The same, of course, goes for T2 (the independence assumption is not necessary, as a similar example can be constructed for the case in which Bob's descriptive beliefs are probabilistically dependent on his normative beliefs). Table 2 shows the decision problem Bob faces, taking under consideration both his moral uncertainty and his descriptive uncertainty.
Table 2. Decision problem with moral uncertainty.

Now, if Bob wants to follow the moral hedging thesis, he must assign moral values to the various outcomes. How should this be done? It is tempting to argue that the moral value Bob ought to attach to an outcome in every state in which a given theory holds must be equal to the moral value the theory assigns to this outcome.Footnote 8 I believe that all the philosophers who have argued for the moral hedging thesis have implicitly assumed that this is the case, and so I will also adopt this assumption. To be clear, however, this condition does not follow from what we stipulated about T1 and T2. Although T1, for example, assigns a value 0.3 to the outcome 'x dollars goes to C', it might assign a different value to the outcome 'x dollars goes to C and T1 is true'.
It might be interesting to further explore moral theories that make such distinctions, i.e. that take their own truth value to be morally significant, but I do not think such an exploration would lead to any conclusions relevant to the discussion here. In any case, if the moral hedging thesis is correct, it surely must also be correct for the case of an agent who assigns positive credence only to theories that avoid making such distinctions. Thus, in the rest of the paper I will assume that the agent assigns moral values to the various outcomes in the way just described, i.e. the moral value the agent attaches to an outcome in every state in which a given theory holds is equal to the moral value the theory assigns to this outcome.
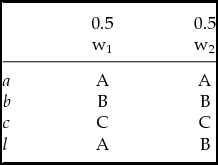
Table 3 illustrates the way Bob's decision problem would look like under this suggestion.
Table 3. Decision problem with moral uncertainty and values.

What is the moral value of act l according to the two theories? In the general case there seem to be two possible answers to this question. According to the first answer, the value of l according to Ti should be calculated using the moral value function according to Ti, VTi and the agent's actual degrees of belief. According the second answer the value of l according to Ti should be calculated using the moral value function according to Ti, VTi and the agent's degrees of belief, under the assumption that Ti is true.
When the agent's degrees of belief in normative propositions are probabilistically dependent on his degrees of belief in descriptive propositions, the two answers are not equivalent. However, in our case, Bob's normative degrees of belief are probabilistically independent of his descriptive degrees of belief, and so the two answers are equivalent. Here is the calculation.
VT1(l) = VT1('probability 0.5 for A and probability 0.5 for B') = 0.52 = 0.25
VT2(l) = VT2('probability 0.5 for A and probability 0.5 for B') = 0.5
Now, since the value of c according to T1 is 0.3 and according to T2 is 0.6, if the moral hedging thesis is correct then irrespectively of Bob's attitude toward risk, Bob must morally prefer act c to act l (this, it should be noted, follows directly from the MDA).
However, it is straightforward to see that, for a large family of possible risk attitudes with respect to moral value that Bob might adopt, and specifically for the case in which Bob is risk-neutral with respect to moral value, rationality dictates preferring l to c. Let us demonstrate this for the case of risk neutrality:
Let Vwi(.) be the agent's value function after learning that the actual descriptive state is wi.
If w1 is true, act l brings outcome A for sure, thus:
However,
 \begin{eqnarray*}
{\rm V}_{{w1}} {\rm (c)}&= &{\rm 0}{\rm .5V}_{{\rm T1}} {\rm (C)}\;{\rm + }\;{\rm 0}{\rm .5V}_{{\rm T2}} {\rm (C)}\;{\rm = }\;{\rm 0}{\rm .5}\;{\rm \times }\;{\rm 0}{\rm .3}\;{\rm + }\;{\rm 0}{\rm .5}\;{\rm \times }\;{\rm 0}{\rm .6}\;{\rm = }\;{\rm 0}{\rm .45}\;{\rm < }\;{\rm 0}{\rm .5}\nonumber\\
&=&{\rm V}_{{w1}} {\rm (l)}
\end{eqnarray*}
\begin{eqnarray*}
{\rm V}_{{w1}} {\rm (c)}&= &{\rm 0}{\rm .5V}_{{\rm T1}} {\rm (C)}\;{\rm + }\;{\rm 0}{\rm .5V}_{{\rm T2}} {\rm (C)}\;{\rm = }\;{\rm 0}{\rm .5}\;{\rm \times }\;{\rm 0}{\rm .3}\;{\rm + }\;{\rm 0}{\rm .5}\;{\rm \times }\;{\rm 0}{\rm .6}\;{\rm = }\;{\rm 0}{\rm .45}\;{\rm < }\;{\rm 0}{\rm .5}\nonumber\\
&=&{\rm V}_{{w1}} {\rm (l)}
\end{eqnarray*}
if w2 is true, act l brings outcome B for sure, thus,
However,
 \begin{eqnarray*}
{\rm V}_{{w2}} {\rm (c)}\;&=& \;{\rm 0}{\rm .5V}_{{\rm T1}} {\rm (C)}\;{\rm + }\;{\rm 0}{\rm .5V}_{{\rm T2}} {\rm (C)}\;{\rm = }\;{\rm 0}{\rm .5}\;{\rm \times }\;{\rm 0}{\rm .3}\;{\rm + }\;{\rm 0}{\rm .5}\;{\rm \times }\;{\rm 0}{\rm .6}\nonumber\\
\;&{\rm = }&\;{\rm 0}{\rm .45}\;{\rm < }\;{\rm 0}{\rm .5}\;{\rm = }\;{\rm V}_{{w2}} {(l)}
\end{eqnarray*}
\begin{eqnarray*}
{\rm V}_{{w2}} {\rm (c)}\;&=& \;{\rm 0}{\rm .5V}_{{\rm T1}} {\rm (C)}\;{\rm + }\;{\rm 0}{\rm .5V}_{{\rm T2}} {\rm (C)}\;{\rm = }\;{\rm 0}{\rm .5}\;{\rm \times }\;{\rm 0}{\rm .3}\;{\rm + }\;{\rm 0}{\rm .5}\;{\rm \times }\;{\rm 0}{\rm .6}\nonumber\\
\;&{\rm = }&\;{\rm 0}{\rm .45}\;{\rm < }\;{\rm 0}{\rm .5}\;{\rm = }\;{\rm V}_{{w2}} {(l)}
\end{eqnarray*}
Thus, l strongly dominates c and must be preferred to it.
In other words, in our example a rational agent who is risk-neutral with respect to moral value cannot obey the moral hedging thesis.
The problem is clear. There is a conflict between the two different dominance principles introduced above, dominance over the 'moral partition' and dominance over the 'descriptive partition'.Footnote 9 Obeying the former dominance principle is consistent with moral hedging, but violates a standard rationality condition. Obeying the latter is consistent with standard rationality conditions, but violates what seems to be a highly intuitive principle for choice under conditions of moral uncertainty, i.e. the MDA. Which one of these principles should Bob follow?
Here is one way to look at it. The initial plausibility of the moral hedging thesis seems to come from its being an instance of the more general thesis of maximizing expected value (MEV). The latter is the claim that, under conditions of uncertainty, given a value function that truly represents a rational agent's goals, the agent must choose the act(s) that maximizes expected value. The former is just the application of the MEV thesis to the case in which the uncertainty is about which value function the agent should use.
This explains the intuitive force of the moral hedging thesis. As the MEV thesis follows from the standard rationality assumptions and the moral hedging thesis is just an instance of it, the moral hedging thesis seems to be dictated by rationality, or so the argument might go. However, here we see that by obeying the moral hedging thesis, Bob must choose irrationally! Thus, something in the intuitive reasoning that has led many philosophers to adopt the moral hedging thesis must be wrong. What is it?
Well, if inter-theoretical comparisons of moral value are meaningful, then the moral hedging thesis is indeed just an instance of the MEV thesis, and thus must be dictated by rationality (at least to the same extent to which the MEV thesis is dictated by rationality). Since the example clearly shows that an agent cannot be both rational (in the standard sense) and obey the moral hedging thesis, the conclusion must be, then, that inter-theoretical comparisons of moral value are meaningless.
This conclusion gets further support from a consideration of the mathematical mechanism responsible for the conflict between the two principles of dominance in our example. The conflict arises (and can only arise) as a result of allowing Bob's risk attitude to differ from the risk attitude of at least one of the theories to which he assigns positive credence (in our case T1).Footnote 10
When the risk attitudes of all the theories to which an agent assigns positive credence are the same, and are identical to the agent's own risk attitude with respect to moral value, the conflict never arises. This is so since in such cases the choice of the partition over which one applies the dominance principle does not matter: however one chooses to cut the space of possible states, one calculates the moral value of the different prospects in the same way (i.e. using the same risk attitude).
What made the conflict possible in our example is that Bob used T1's risk attitudes when considering the value of act l under the assumption that T1 is true, even though these attitudes are different from both those of T2 and Bob's own attitude.
Thus, by assuming that the agent can only assign positive credence to risk-neutral theories,Footnote 11 we can get rid of our dilemma. However, as discussed in the previous section, assuming the risk-neutrality of moral theories (i.e. assuming that the agent cannot be uncertain about the right attitude toward risk with respect to moral value) makes sense only if we understand the term 'moral value' in such a way that risk-neutrality with respect to it becomes a conceptual truth and, under such an understanding of the term, inter-theoretical comparisons of moral value are meaningless and so is the moral hedging thesis.
It might be revealing, in light of our discussion so far, to investigate the claim – made in the previous section – regarding the implausibility of a commitment to the risk-neutrality of moral theories if inter-theoretical comparisons of moral value are meaningful. Our example, as we just saw, depends on Bob's risk attitude being different from that of at least one of the theories to which Bob assigns a positive probability. It is clear that if we want to rule out this kind of case we must argue that Bob cannot be uncertain about the 'right' attitude toward risk with respect to moral value, i.e. Bob must assign positive credence only to theories that share the same attitude toward risk with respect to moral value. If Bob assigns positive credence to at least two theories with different attitudes to risk, his own risk attitude must be different from that of least one of these theories.
As explained, there is one natural way to justify this assumption, namely to understand the term 'moral value' in a way that makes the restriction a conceptual truth. However, this way of understanding the term 'moral value' also makes the moral hedging thesis meaningless.
Might there be another way to justify the restriction, which does not assume a semantics of moral propositions that makes inter-theoretical comparisons of moral value meaningless? I obviously cannot present an argument against all possible justifications. What I can do is to show why, on the assumption that inter-theoretical comparisons of moral value are meaningful, ruling out uncertainty regarding the right attitude to risks involving moral value, seems implausible. I will try to do this now.
As mentioned, John Broome, for example, argued that the claim that the correct moral value function is risk-neutral is 'very implausible'. Broome did not argue that this claim is false (nor did he argue that it is true), but only that it is implausible. Thus, I take it that Broome was uncertain about whether the claim is true. So there is at least one person – arguably a person who is a good candidate to be a morally motivated rational agent – who has been uncertain at least at one point in his life about the 'correct' moral attitude toward risk.
To be sure, we can stipulate that rational agents cannot be faced with such uncertainty, but if we want our concept of rationality not to be too detached from our pre-theoretical intuitions about it (and intuitively it seems that even if Broome was not a morally motivated rational agent at the time he wrote chapter 6 of 'Weighing Goods', it was not due to his uncertainty about the 'correct' moral attitude toward risk), we must provide a justification for this stipulation.
What I am saying is that restricting the moral hedging thesis to cases with no uncertainty about attitudes to risk makes the thesis irrelevant to many cases in which people face moral uncertainty. Again, we can stipulate that these people are irrational, but this does not solve the problem of offering them a decision rule they can use for making a choice in the situation they are confronted with.
The point here is not merely pragmatic, however. If we really take moral value to be a primitive concept, if we really believe that there is a way to understand this concept that does not involve a definition in terms of a representation of moral rankings (e.g. if we believe that there are real quantities of moral value out there), then the claim that morality is risk-neutral does not follow from either standard principles of rationality (just in the same way that risk-neutrality with respect to money value does not follow from standard principles of rationality) or any uncontroversial principle of morality. Thus, uncertainty regarding the right attitude to risk involving moral value must be possible (even if, as a matter of fact, morality is risk-neutral).
We face, then, the following trilemma. We must choose one of the following alternatives:
1. Insist that inter-theoretical comparisons of moral value are meaningful, accept the moral hedging thesis and argue that the standard dominance principle does not hold under conditions of moral uncertainty.
2. Insist that inter-theoretical comparisons of moral value are meaningful and that the standard rationality assumptions hold even under conditions of moral uncertainty, but reject the moral hedging thesis.
3. Accept that inter-theoretical comparisons of moral value are meaningless and thus reject the moral hedging thesis.
I tend to prefer the third option. My main reason is that I cannot think of any plausible alternative to the 'representation of moral rankings' explication of the term 'moral value', and under this explication inter-theoretical comparisons of moral value are indeed meaningless. Accepting the third option, however, leaves the question of choice under conditions of moral uncertainty unanswered. Elsewhere (Nissan-Rozen Reference Nissan-Rozen2012) I suggested an answer to this question. Here I do not want to argue for any alternative decision rule. My aim in this paper is only to argue against the moral hedging thesis.
The example above constitutes an argument against the moral hedging thesis in two ways. First, as mentioned above, the example shows that – contrary to what I believe is an implicit assumption of most supporters of the moral hedging thesis – the thesis is neither dictated by standard principles of rationality nor consistent with them. Thus, if the thesis is justified, it is not in virtue of it being a rationality thesis. Moreover, any justification for the thesis should also explain why the standard principles of rationality do not hold in cases of moral uncertainty. I do not see what such a justification might look like.
Second, it seems obvious to me that, if inter-theoretical comparisons of moral value are meaningful, act l in our example should be morally preferable to act c – i.e. the moral hedging thesis gives the wrong recommendation. This claim is supported by two different considerations. First, the expected moral value of act l, when the expectation is calculated using Bob's joint probability distribution, is higher than that of act c. The only reason the DMA dictates that c is preferable to l is that, according to T1, an outcome with a sure moral value of 0.3 is more valuable than a prospect that gives an outcome with a moral value of 1 with probability 0.5 and an outcome with a moral value of 0 with probability 0.5. However, Bob's own risk attitude is different from that of T1. Specifically, we assumed that Bob (like T2) is risk-neutral with respect to moral value and thus must consider an outcome with a sure moral value of 0.3 to be less valuable than a prospect that gives an outcome with a moral value of 1 with probability 0.5 and an outcome with a moral value of 0 with probability 0.5.
Second, while preferring c to l necessarily involves a violation of an intuitive reflection principle, preferring l to c does not necessarily involve such a violation. In the example, we can assume that Bob is certain that at some point in time he will learn whether w1 or w2 is the actual state of the world (we can think of the state of the world as determined by a coin toss, for example). Thus, preferring c to l necessarily makes Bob dynamically inconsistent and Bob is certain that this is the case.
Bob is uncertain, however, whether (and – we can stipulate – even certain that it is not the case that), the moral uncertainty he faces will be dissolved at some point. For all Bob knows, he will always remain uncertain as to whether T1 or T2 is the true moral theory. Thus, there is no necessary violation of dynamic consistency involved in preferring l to c.
Thus even those who insist that inter-theoretical comparisons of moral value are meaningful should reject the claim that Bob should obey the moral hedging thesis, and so this thesis cannot be a requirement of either rationality or morality. However, if inter-theoretical comparisons of moral value are meaningful, it seems that the moral hedging thesis is a requirement of rationality. Thus, I believe, we have no alternative but to deny that inter-theoretical comparisons of moral value are meaningful.
The argument presented in this section shows that when (1) an agent is faced with both descriptive uncertainty and moral uncertainty, and (2) faces moral uncertainty about the right attitude toward risk with respect to moral value, moral hedging is irrational. I have already justified the claim that if (1) is true, we should not rule out cases in which (2) is also true. However, some might claim that my argument does not show that in cases in which an agent faces moral uncertainty, but not descriptive uncertainty, moral hedging is still irrational.
Perhaps, one might claim that moral hedging is a principle of rationality when the agent does not face any descriptive uncertainty, but is not a principle of rationality when the agent does face descriptive uncertainty.
I do not find this objection very worrying. First, if my diagnosis for the failure of the moral hedging thesis – namely, that it is based on the false assumption that inter-theoretical comparisons of moral value are meaningful – is correct, then the moral hedging thesis is meaningless, and this is true regardless of whether descriptive uncertainty is involved.
Second, even those who insist on holding the position that inter-theoretical comparisons of moral value are meaningful should not be satisfied with the mere claim that the moral hedging thesis applies only to cases in which no descriptive uncertainty is involved. As it is, this claim is no more than an ad-hoc qualification of the thesis designed to deal with my counterexample. To make it plausible, one must offer an explanation for why the thesis only applies to cases in which no descriptive uncertainty is involved.
However, we already have such an explanation. We already know why the thesis fails when descriptive uncertainty is involved: it is because in such cases the agent might be uncertain regarding the right attitude toward risk with respect to moral value, and this leads to a conflict with the standard dominance principle. Thus, the correct explanation for the thesis’ failure when descriptive uncertainty is involved is due to the fact that inter-theoretical comparisons of moral value allow for uncertainty regarding the right attitude toward risk.
Third, certainty about descriptive matters is usually (some may argue, always) an idealization. In some choice situations, it might be a useful idealization, i.e. one that is unlikely to lead to choice recommendations that significantly differ from those that one would otherwise reach. However, the argument presented here shows that when an agent is faced with moral uncertainty, then idealizing in such a way and using the moral hedging thesis might lead to a violation of the standard dominance principle. Thus, even if one adopts the claim that the moral hedging thesis applies only to situations in which no descriptive uncertainty is involved, the thesis would be true only for a very limited set of choice situations, i.e. situations in which descriptive certainty is not an idealization.
Thus I think my argument applies equally well (or almost equally well) to cases where no descriptive uncertainty is involved. If this is so, however, then the counter-example presented is only a symptom of a deeper problem with the moral hedging thesis. This problem, I have argued, is its reliance on the false assumption that inter-theoretical comparisons of moral value are meaningful. I have not, however, presented an independent argument against the meaningfulness of inter-theoretical comparisons of moral value. Such arguments are not hard to come by, as good discussions of them can easily be found in the literature (see Lockhart Reference Lockhart2000 for an overview).
Interestingly, I am not aware of any argument for the meaningfulness of inter-theoretical comparisons of moral value which is independent of the moral hedging thesis: Since the moral hedging thesis seems to many philosophers to be highly plausible, and since inter-theoretical comparisons of moral value are necessary to make it meaningful, these philosophers have concluded that inter-theoretical comparisons of moral value must be meaningful. This is the only argument I am aware of for the meaningfulness of inter-theoretical comparisons of moral value. There is, of course, a lively discussion regarding the issue of how these comparisons should be made (see Lockhart Reference Lockhart2000; Sepielli Reference Sepielli2012), but the discussion is based on the assumption that they are meaningful.
The main contribution of this paper, I believe, is that it shows that even if inter-theoretical comparisons of moral value are meaningful, a morally motivated rational agent should not obey the moral hedging thesis. Thus, both the motivation for and the main reason to believe that inter-theoretical comparisons of moral value are meaningful are undermined.
Acknowledgements
This research was supported by the Israel Science Foundation (grant 0341643). Earlier versions of this paper were presented in the Van-Leer Epistemology group and in the Law and Philosophy workshop at the Hebrew University. I thank David Enoch, Ron Aboodi, Richard Bradley and three anonymous referees for helpful comments.