1. INTRODUCTION
The last decades have witnessed a considerable effort among political philosophers to analyse the problem of distributive justice. A central impetus for this should be attributed to John Rawls’s theory (e.g. Rawls Reference Rawls1971), probably the most influential endorsement of egalitarianism in the 20th century. Roughly speaking, Rawls argued that in an ‘original position’, before knowing what our talents, wealth or education are, we would agree on basic principles about justice and the distribution of the fruits of collaboration in society. Rawls then concluded that justice thus defined depends entirely on the pattern or end-state distribution at any moment in time. Rawls’s conclusion, the so-called Difference Principle, is that social and economic inequalities are to be arranged so that they are to the greatest benefit of the least advantaged.
Prompted by Rawls’s theory, Robert Nozick presented another (polar) theory of distributive justice (e.g. Nozick Reference Nozick1973, Reference Nozick1974). The theory is grounded on self-ownership, one of the fundamental axioms of liberal political philosophy, represented classically by John Locke (e.g. Locke Reference Locke and Laslett1988). Self-ownership, which is taken to a different level in Nozick’s theory, is a widely accepted postulate (albeit denied by Rawls himself and other influential political philosophers, such as Ronald Dworkin) declaring some rights to derive from superior skills. Nozick’s theory questions Rawls’ focus on the end-state distribution in assessing distributive justice. The core of his argument is that, if the initial distribution of property rights is just (i.e. property does not derive from exploitation or theft), and the exchanges that follow this initial situation are voluntary (i.e. there is no coercion), then the resulting distribution, no matter how unequal, would also be just. Nozick argues that justice consists of respecting individuals’ rights, particularly the right to self-ownership and the freedom to decide how to use one’s property. This means that economic inequalities need not be considered unjust nor be rectified to the benefit of the disadvantaged. Nozick stresses that justice corresponds to the respect of individual rights, which are more important than an agreement reached in Rawls’ original position (which is just a thought experiment). Thus, if attaining end-state equity requires violating property rights, this cannot be just.
More precisely, the following quote from Nozick (Reference Nozick1973: 47) nicely summarizes the core position regarding his liberal theory of private ownership:
If the world were wholly just, the following inductive definition would exhaustively cover the subject of justice in holdings:
1. A person who acquires a holding in accordance with the principle of justice in acquisition is entitled to that holding.
2. A person who acquires a holding in accordance with the principle of justice in transfer, from someone else entitled to the holding, is entitled to the holding.
3. No one is entitled to a holding except by repeated applications of (1) and (2).
Our aim in this paper is to show that, in a stylized framework for the allocation of goods in joint ventures, Nozick’s and Rawls’ approaches can be seen as complementary.
To wit, we consider a model formalizing three different levels of fairness for the allocation of goods in joint ventures:
1. Fairness in the allocation of rights.
2. Fairness in the transaction of rights.
3. Fairness of the end-state allocation.
The formalization of the first two levels will be inspired by Nozick’s procedural approach. More precisely, we shall focus on a family of rules allocating goods in two stages. The first stage (rights assignment) determines an allocation of rights. The second stage (exchange) determines a final allocation from such an allocation.
We formulate self-ownership as an axiom for the first stage of rights assignment inspired by Nozick’s principle of justice in acquisition. In our model, we assume the existence of individual claims that represent the (objective and verifiable) amounts of goods the person can obtain through her self-ownership, when it does not conflict with the self-ownership of anyone else. Thus, in an economy with abundant social endowment for fully satisfying all individual claims, self-ownership guarantees that all claims are granted.
Nozick’s procedural approach can also provide a useful guideline for the second stage of exchange. More precisely, the second stage implements Nozick’s principle of just transfer by imposing the application of a voluntary exchange rule, i.e. a rule guaranteeing that agents only exchange when they improve from their endowments.
The formalization of the third level will rely on the notion of no-envy, probably the concept with the longest tradition in the theory of fair allocation (e.g. Tinbergen Reference Tinbergen1953; Foley Reference Foley1967).Footnote 1 No-envy is satisfied if no agent prefers the consumption by anyone else to her own. The same comparative notion of fairness, defined through interpersonal comparisons of net consumptions (consumptions net of ‘claims’), gives rise to the notion of net-no-envy, which we shall also consider here.Footnote 2
No-envy conceptualizes the impartial spectator’s point of view, à la Adam Smith, by requiring that agents place themselves in the situation of other agents. A different, yet related, conceptualization of the impartial spectator is the contractarian construct of veil of ignorance by John Harsanyi (Reference Harsanyi1953, Reference Harsanyi1955) and John Rawls (1971), behind which the decision maker evaluates the outcome through the individual standards of well-being.Footnote 3 The main advantage of no-envy, in comparison with the mentioned contractarian theories, is that it does not rely on cardinal preferences; it is based purely on ordinal preferences.
Our results show that the combination of a rights-assignment rule, satisfying self-ownership, with a voluntary exchange rule, may lead to end-state fairness, as formalized by the no-envy axioms described above, as well as to (Pareto) efficiency. Conversely, we show that the two focal (and polar) rules, known as constrained equal awards and constrained equal net-awards are the unique solidaristic ones that lead to fair end-state allocations.Footnote 4 The two rules have a long tradition of use, which can be traced back to Maimonides (e.g. Thomson Reference Thomson2003). Although they assign rights in quite different ways, they both achieve equality with different perspectives; namely, equality of the absolute or net amounts.
Therefore, our investigation provides an instance where a principle of end-state fairness can facilitate the search of appropriate procedural principles of justice (in particular, principles of just acquisition), which constitute Nozick’s procedural (or historical) theory of justice. Conversely, Nozick’s theory can be used to implement a principle of end-state fairness through informationally simple and voluntary procedures. This is why we claim that Nozick’s procedural approach, at least in our framework, is complementary to the (Rawlsian) end-state approach.
We stress that, in our model, the rights resolution is not based on preferences. This makes the procedure informationally simple. Now, one might argue that this assumption renders some of our requirements for the rights resolution not entirely appealing, as they use the objective standards of comparison, instead of the subjective standard of well-being. We believe that this is, actually, a merit instead of a shortcoming of our approach. This parsimony may be problematic if it would lead to incompatibility with other important preference-related requirements. But, as we shall see, our results are mostly constructive.
Our contribution in this paper can also be viewed as an alternative way of extending Locke’s theory (at least in a highly stylized framework of joint ventures). Following a similar line of investigation, Roemer (Reference Roemer1988, Reference Roemer1989), Moulin (Reference Moulin1987, Reference Moulin1990) and Roemer and Silvestre (Reference Roemer and Silvestre1993) propose generalizations of Locke’s theory in the framework of common resources under a decreasing returns to scale technology, which gives rise to the so-called tragedy of the commons. The allocation rules proposed in these works respect Locke’s thesis based on self-ownership: that is, they coincide with the unlimited appropriation outcome in the case of a constant returns to scale technology, the case satisfying the Lockean proviso.Footnote 5 Nevertheless, unlike Nozick’s radical generalization, they all have egalitarian features. It turns out that some of the rules highlighted in this literature are similar to the rules derived here.
Somewhat related, Gibbard (Reference Gibbard1976) and Grunebaum (Reference Grunebaum1987) propose ‘equal rights’ or ‘public ownership’ of unowned properties to be the baseline upon which the appropriation should be judged.Footnote 6 Moulin and Roemer (Reference Roemer1989), in a production economy model, investigate implications of the baseline of public ownership without denying the thesis of self-ownership.Footnote 7 Their axiomatic approach shows that the axioms for public ownership and self-ownership, together with other standard axioms, imply a unique welfare-egalitarian outcome, which disregards any difference in individual talents. Hence slightly strengthening their axiom of self-ownership to rule out the welfare-egalitarian outcomes and admit only less extreme ones will break the coherency of the set of axioms. All their axioms are for end-state rules and they do not deal with the assignment of ownership rights. The egalitarian rules we support here exhibit their egalitarian features only in the assignment of property rights and so diverse end-state allocations may arise through the exchange of the property rights.
Moulin and Roemer (Reference Roemer1989) assume a single representative utility function and, due to this feature, their axiom of self-ownership, which is essentially an order preservation property for rights-assignment rules, coincides with no-envy. We do not impose from the outset an order-preservation property because it is implied by other basic axioms. The solidarity axiom we consider (for rights-assignment rules) may be compared to their axiom of public ownership, called ‘technology monotonicity’. However, our axioms are merely requirements in the rights-assignment stage. They are not requirements for end-state rules as in Moulin and Roemer (Reference Roemer1989). Hence, it could be argued that our axioms are in a certain sense weaker than theirs; in fact, they are extremely mild allowing for a rich spectrum of rules. In our approach, the baseline of public ownership and the thesis of self-ownership can be met jointly without putting too much restriction on the choice of rules. End-state fairness plays a critical role to pin down a unique egalitarian rule.
Using no-envy as both procedural and end-state principles of fairness, Kolm (Reference Kolm1972), Feldman and Kirman (Reference Feldman and Kirman1974), Goldman and Sussangkarn (Reference Goldman and Sussangkarn1980) and Thomson (Reference Thomson1982), among others, investigate whether procedural fairness induces end-state fairness. The results are negative. The combination of envy-free initial allocation (equal division) and a sequence of envy-free trades may lead to a core allocation with envy. Our results impose different versions of no-envy as the principle of end-state fairness and obtain no-envy, ‘with some constraints’, of the initial allocation as an implication. We do not impose no-envy as a procedural requirement. Nevertheless, other axioms are used as procedural requirements such as self-ownership for rights assignment rules and voluntary exchange for exchange rules.Footnote 8
In standard exchange economies, Thomson (Reference Thomson1983) is also concerned with the three levels of justice: fair initial position (endowment), fair trade (or exchange), and end-state fairness. In his approach, the principle of fair trade plays a central role and the principle of fair initial position is formulated through the possibility of changing the initial positions of agents (as in the definition of no-envy) and their objections based on the principle of fair trade from any reshuffled position. Thus, the key idea of no-envy is behind his notion of fair initial position. He shows that no-envy is the unique end-state fairness concept that is obtained from his procedural approach using voluntary exchange as the principle of fair trade (Proposition 1). His main result is that Walrasian trade and the principle of fair initial position defined via Walrasian trade give rise to the same outcomes as the Walrasian rule from equal division (Proposition 2). In a sense, this result says that if one accepts Walrasian trade to be a fair rule of trade, and one also accepts the possibility of changing initial positions among agents, then the only fair initial position is equal division. Our Theorem 1 can be viewed as reinforcing this conclusion in our extended framework, when adopting Nozick’s normative perspective. Our approach is informationally simple and guarantees freedom of choice. It is also representative of actual institutions. The first stage of rights assignment allows us to use the findings in the vast literature on rights problems.Footnote 9 The second exchange stage is assumed to meet voluntary exchange; so not only the Walrasian (perfectly competitive market) trade but also non-Walrasian (imperfectly competitive market) trades are covered. Unlike Thomson (1983), we use no-envy as the end-state fairness axiom and characterize egalitarian rights-assignment rules for the first stage.
2. A MODEL OF JOINT VENTURES
Consider a society N of agents, who share common resources for producing ℓ privately appropriable and infinitely divisible goods. Each agent i ∈ N is endowed with specific capabilities that would allow her to produce certain amounts of the ℓ goods with exclusive access to the common resources. We shall refer to the resulting profile of those amounts, denoted by c i, as the claim of agent i. We assume that claims are objective and verifiable. The classical Lockean ‘thesis of self-ownership’ (e.g. Locke Reference Locke and Laslett1988), to which Nozick (Reference Nozick1974) adheres, would state in this context that, in the society consisting of a single person, she is the only one with access to the common resources and, thus, her claim can be granted. We assume that all agents in society collaborate in a joint venture, which allows them to use the common resources cooperatively to produce a social endowment Ω of the ℓ goods.Footnote 10 When the joint production technology exhibits decreasing returns to scale, the sum of claims exceeds the social endowment, i.e. ∑i ∈ Nc i≧Ω.Footnote 11 When the technology exhibits increasing returns to scale, the sum of claims does not reach the social endowment, i.e. ∑i ∈ Nc i≦Ω.
We thus consider the problem of allocating the social endowment among the agents based on their claims. Formally, an economy e ≡ (N, Ω, c, R) is defined by the set of agents, a social endowment Ω, a profile of individual claims c ≡ (c i)i ∈ N and a profile of preferences R ≡ (R i)i ∈ N. Let 
$\mathcal {E}$ denote the set of all economies. Throughout the paper, we will assume ‘private goods’ economies where each agent is not concerned with how much others consume. Hence agent i’s preferences R i, namely the binary orderings of her well-being, can be defined over her consumption bundles. Given any pair of consumption bundles 
$x,y\in \mathbb {R}_{+}^{\ell }$, we write xR iy when agent i is at least as well off with consuming x as with consuming y; we write xP iy when agent i is better off with consuming x than with consuming y.Footnote 12
An allocation for an economy is a profile of individual consumption bundles, denoted by z ≡ (z i)i ∈ N, which is feasible in the sense that the total consumption of each good equals the total endowment, i.e. ∑i ∈ Nz i = Ω. It is Pareto efficient if there is no other allocation that makes a person better off without making anyone else worse off.
The following examples fit the stylized model just described.
Example 1. Property rights disputes (Ju and Moreno-Ternero Reference Ju and Moreno-Ternero2017). Consider a society in which each person has initial property rights (claims). Due to an unexpected misfortune, for which no one is responsible, the initial property rights cannot be fully respected; the society does not have enough resources to satisfy all of them. That is, denoting the available social endowment by Ω, and claims as (ci)i ∈ N, ∑i ∈ Nci≧Ω.
Example 2. Surplus sharing. Consider the alternative case to the previous one in which society not only has enough resources to satisfy all individual property rights, but also has a surplus to be shared among all members of society. That is, ∑i ∈ Nci≦Ω.
Example 3. Simple joint production economy. Consider a production economy with a common capital good (land) that can be used for producing a good in each period. There are ℓ different periods and the good produced at period l is referred to as good l. Each agent has a skill to produce each good. Let si ≡ (sil)ℓl = 1 be i’s skill vector. All agents supply the same unit labour for the joint production and thus effective labour is identified with skill. The production technology for each good l is represented by a production function 
$f_{l}:\mathbb {R}_{+}\rightarrow \mathbb {R}_{+}$mapping the total effective labour ∑ i ∈ Nsil into the amount of output for good l. Thus, when agent i uses the land alone, she can produce fl(sil) units of each good l = 1, . . ., ℓ. Let ci ≡ (fl(sil))l = 1, . . ., ℓ be i’s claim vector. When the production technology is subadditive,Footnote 13 the joint production is below the sum of claims.Footnote 14 When the production technology is superadditive,Footnote 15 the joint production is above the sum of claims.
An allocation rule associates with each economy a non-empty set of end-state allocations. We shall be mostly interested in allocation rules that are defined by the following two stages: First, a rights-assignment stage to deal with the assignment of rights, mapping the non-preference information into a profile of individual endowments, and second, an exchange stage determining final allocations for the exchange economy resulting from such a profile of individual endowments obtained in the first stage. In doing so, we shall be able to scrutinize the relationship between principles of procedural justice (imposed in each of these two stages) and principles of end-state justice (imposed on the final allocations determined by allocation rules).
2.1. Rights assignment
A rights problem is defined by a set of persons N, a social endowment Ω, and a profile of individual claims c. Let 
$\mathcal {C}$ denote the set of all rights problems (N, Ω, c). Good l is in deficit if the endowment of good l is not large enough to honour all claims, that is, ∑i ∈ Nc il ⩾ Ωl. It is in surplus if the endowment is more than sufficient to satisfy all claims, that is, ∑i ∈ Nc il ⩽ Ωl. A rights problem may involve both a deficit in one good and a surplus in some other good.
A rights-assignment rule φ associates with each rights problem (N, Ω, c) individual property rights over the social endowment, specified by an allocation of individual endowments φ(N, Ω, c) ≡ (ωi)i ∈ N (with the feasibility, ∑i ∈ Nωi = Ω) to be traded in the exchange stage.
We impose from the outset the following mild requirement on rights-assignment rules that models the thesis of self-ownership. It is that each person be assigned ownership rights that fully respect her claim, if allowing her ownership of the claimed resources leaves (as stated in the Lockean proviso) ‘enough and as good left in common for others’ (Locke Reference Locke and Laslett1988: 27). As her claim represents her own capabilities, the assigned rights in this case fully respect her self-ownership (the ownership of her own capabilities).
Self-Ownership. For each 
$(N,\Omega ,c)\in \mathcal {C}$ and i ∈ N, if Ω − c i≧∑j ∈ N\{i}c j, then φi(N, Ω, c)≧c i.
Then, by the resource constraint in the definition of a rights-assignment rule, whenever the sum of individual claims equals the social endowment (∑i ∈ Nc i = Ω), the rights-assignment should be determined by the claims (φ(N, Ω, c) = c). Self-ownership concerns problems where a person’s claimed ownership leaves enough of the social endowment to fully honour all the remaining claims. If this requirement is not met, private appropriation of socially endowed goods needs to be restricted.
Additionally, we consider a solidarity axiom, which says that the arrival of immigrants, whether or not accompanied by changes in the available endowment, should affect all original agents in the same direction: either all gain or all lose.Footnote 16 Formally,
Solidarity. Let (N, Ω, c) and 
$(N^{\prime },\Omega ^{\prime },c^{\prime })\in \mathcal {C}$ be such that N⊆N′ and, for each i ∈ N, c′i = ci. Then, one of the following statements hold:
$$\begin{equation*}
\varphi _{i}(N,\Omega ,c)\le \varphi _{i}(N^{\prime },\Omega ^{\prime },c^{\prime })\text{ for each }i\in N,
\end{equation*}$$
$$\begin{equation*}
\varphi _{i}(N,\Omega ,c)\ge \varphi _{i}(N^{\prime },\Omega ^{\prime },c^{\prime })\text{ for each }i\in N.
\end{equation*}$$
Two focal rights-assignment rules, each obeying the axioms just presented, are defined next.
The constrained equal awards rule φCEA splits the social endowment as equally as possible, provided no agent is awarded more than his claim, in the case of a social deficit, and less than her claim, in the case of a social surplus. Formally, for each 
$(N,\Omega ,c)\in \mathcal {C}$, each i ∈ N, and each l ∈ {1, . . ., ℓ},
$$\begin{equation*}
\varphi _{il}^{CEA}(N,\Omega ,c)=\left\lbrace \begin{array}{@{}l@{\quad }l@{}}\min \lbrace c_{il},\lambda \rbrace , & \text{if }\sum _{i\in N}c_{il}\ge \Omega _{l},\\
\max \lbrace c_{il},\mu \rbrace , & \text{if }\sum _{i\in N}c_{il}\le \Omega _{l}, \end{array}\right.
\end{equation*}$$
where λ and μ guarantee that the feasibility conditions ∑i ∈ Nmin{c il, λ} = Ωl and ∑i ∈ Nmax{c il, μ} = Ωl are met. In particular, if for each i ∈ N, c il is larger than equal division of good l, or c il is smaller than equal division of good l, the constrained equal awards rule divides good l equally (i.e. φCEAil(N, Ω, c) = Ωl/n, where n denotes the number of agents in N).
The constrained equal net-awards rule φCEN allocates the social endowment so that both agents end up having as equal net awards as possible, provided no agent gets a negative amount. Formally, for each 
$(N,\Omega ,c)\in \mathcal {C}$, each i ∈ N, and each l ∈ {1, . . ., ℓ},
$$\begin{equation*}
\varphi _{il}^{CEN}(N,\Omega ,c)=\max \left\lbrace c_{il}-\nu ,0\right\rbrace ,
\end{equation*}$$
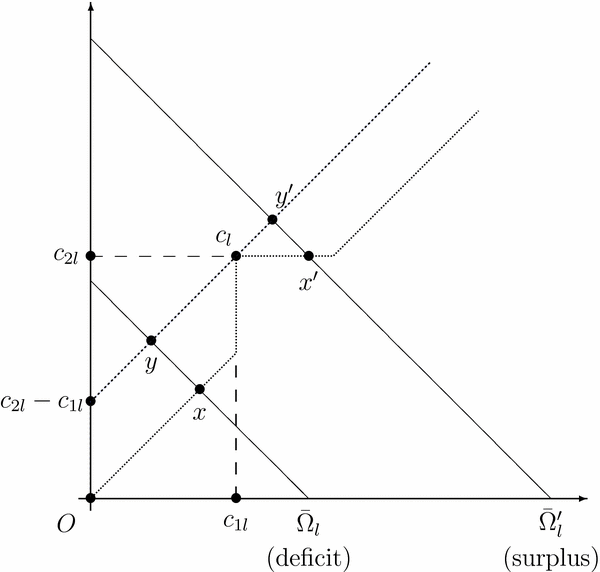
where ν guarantees the feasibility condition ∑i ∈ Nmax{c il − ν, 0} = Ωl. In particular, if, for each i ∈ N, c il is larger than the equal net awards of good l, the constrained equal net-awards rule divides the total net-awards of good l equally (i.e. cil − φCENil(N, Ω, c) = cjl − φCENjl(N, Ω, c) = (∑i ∈ Ncil − Ωl)/n). These two rules are illustrated in Figure 1 for the case of two agents.
Figure 1. Rules in the two-agent case. This figure illustrates the ‘paths of awards’ (the locus of the awards vector chosen by a rule as the endowment Ωl varies from 0 to ∞) of the constrained equal awards rule and the constrained equal net-awards rule for N = {1, 2} and 
$c_l\in \mathbb {R}_{+}^{N}$ with c 1l < c 2l. The path of awards of the constrained equal awards rule (dotted) follows the 45o line until agent 1 obtains her whole claim. Then, it is vertical until it reaches the vector of claims. For endowments above the aggregate claim (i.e. the surplus case), the path is horizontal until agent 1 obtains c 2l. From there on it follows again the 45o line. As for the constrained equal net-awards, its path of awards (dashed) is vertical until the average loss coincides with the lowest claim, i.e. until the endowment reaches Ωl = c 2l − c 1l. After that, it becomes the line of slope 1 (thus crossing the vector of claims, when moving to the surplus case). In the specific deficit case illustrated in the figure (for endowment 
$\bar{\Omega }_{l}<c_{1l}+c_{2l}$), the allocation proposed by the constrained equal awards rule is at the intersection x with the 45o line, whereas the allocation proposed by the constrained equal net-awards rule is at the intersection y with the parallel line emanating from (0, c 2l − c 1l). In the specific surplus case illustrated in the figure (for endowment 
$\bar{\Omega }_{l}^{\prime }>c_{1l}+c_{2l}$) the allocation proposed by the constrained equal awards rule is at the intersection x′ with the horizontal line from c l, whereas the allocation proposed by the constrained equal net-awards rule is also at the point of intersection y′ with the line of slope 1 emanating from (0, c 2l − c 1l).
The next property, which is a useful implication of the combination of self-ownership and solidarity (as shown in Lemma 1 in the Appendix), indicates that in a deficit situation all agents are rationed, whereas in a surplus situation no one is.
Claims Boundedness.
• For each
$(N,\Omega ,c)\in \mathcal {C}$ and each l, if ∑i ∈ Nc il ⩾ Ωl, for each i ∈ N, then φil(N, Ω, c) ⩽ c il.• For each
$(N,\Omega ,c)\in \mathcal {C}$ and each l, if ∑i ∈ Nc il ⩽ Ωl, for each i ∈ N, then φil(N, Ω, c) ⩾ c il.
It is evident that the two focal rights-assignment rules satisfy claims boundedness. The two rules are egalitarian, one equalizing awards and the other equalizing net awards, unless equalizing awards or net awards violate claims boundedness.
2.2. Exchange
A rights-assignment rule converts each economy into an ordinary exchange economy with individual property rights (individual endowments) compatible with the social endowment. Formally, an exchange economy is a triple (N, ω, R), where ω denotes the profile of individual endowments (adding up to the social endowment Ω). Let 
$\bar{\mathcal {E}}$ denote the set of exchange economies. An exchange rule F associates with each exchange economy a non-empty set of allocations. Exchange rules are studied extensively in the literature. The best known one is the so-called Walrasian (exchange) rule, F W, which associates with each exchange economy its set of Walrasian equilibrium allocations.Footnote 17 We shall also consider other rules that are not Walrasian, yet satisfy the following basic condition of voluntary exchange, which can be seen as the natural way of implementing Nozick’s principle of just transfer. In words, voluntary exchange requires that the outcome of the exchange process determined by the exchange rule does not leave any agent within the group worse off (according to the agent’s preferences) than in the initial situation, where they were all in possession of their endowments.Footnote 18 That is, everyone ends up at least as well off as she initially was. Formally,
Voluntary exchange. For each 
$(N,\omega ,R)\in \bar{\mathcal {E}}$, z ∈ F(N, ω, R), and i ∈ N,
$$\begin{equation*}
z_{i}\,R_{i}\,\omega _{i}.
\end{equation*}$$
Note that the so-called no-trade exchange rule, which recommends the initial profile of endowments as the outcome of the exchange process, is a well-defined exchange rule satisfying voluntary exchange. The Walrasian rule also does.Footnote 19 An important distinction between the two is that the former does not guarantee Pareto efficiency of the final outcome, whereas the latter does so, by virtue of the First Fundamental Theorem of Welfare Economics (see, for instance, Mas-Colell et al. Reference Mas-Colell, Whinston and Green1995: 549). Another example is the Core rule selecting the allocations upon which no coalition of agents can improve through the exchange of endowments among coalition members excluding non-members. The Core rule also guarantees Pareto efficiency and contains all Walrasian equilibrium allocations (e.g. Mas-Colell et al. Reference Mas-Colell, Whinston and Green1995: 654).
2.3. End-state fairness
An allocation rule S associates with each economy a non-empty set of allocations. We model end-state fairness by means of some classical fairness axioms for allocation rules. One of the fundamental notions in the theory of fair allocation is envy-freeness, which can be traced back to Tinbergen (Reference Tinbergen1953) and Foley (Reference Foley1967). The concept has come to play a central role in the theory of fair allocation.Footnote 20 An allocation satisfies no-envy, or is said to be envy-free, if no agent prefers the consumption of another agent. An allocation rule S satisfies no-envy if it only selects envy-free allocations. Formally,
No-Envy. For each 
$e\equiv \left(N,\Omega ,c,R\right)\in \mathcal {E}$, and each z ∈ S(e), there is no pair of agents i, j ∈ N such that z jP iz i.
The above notion does not use information on claims to establish envy comparisons. The following one does so. For each allocation and each agent, we can describe an agent’s net awards at the allocation as the vector of differences between the agent’s claim of each good and the corresponding awarded amount. An allocation satisfies net-no-envy, or is said to be net-envy-free, if no agent prefers the net awards of anyone else to her own net awards. An allocation rule S satisfies net-no-envy if it only selects net-envy-free allocations. Formally,
Net-No-Envy. For each 
$e\equiv \left(N,\Omega ,c,R\right)\in \mathcal {E}$, and each z ∈ S(e), there is no pair of agents i, j ∈ N, such that (c i − (c j − z j))P iz i.Footnote 21
Net-no-envy is the analogue to the notion of fair net trades for exchange economies (e.g. Schmeidler and Vind Reference Schmeidler and Vind1972), in which the no-envy requirement is formalized for agents’ net trades, i.e. the differences between their allocations and their endowments.
2.4. Market-based allocation rules
The composition of a rights-assignment rule and an exchange rule gives rise to an allocation rule. If the rights-assignment rule satisfies self-ownership and the exchange rule satisfies voluntary exchange, we say that the resulting allocation rule is market-based.
Market-based allocation rules. There exist a rights-assignment rule φ, satisfying self-ownership, and an exchange rule F, satisfying voluntary exchange, such that S ≡ F○φ, i.e. for each 
$e\equiv \left(N,\Omega ,c,R\right)\in \mathcal {E}$, S(e) = F(N, φ(N, Ω, c), R).
As trivial examples, each rights-assignment rule satisfying self-ownership yields a market-based allocation rule, when combined with the no-trade exchange rule. Focal market-based allocation rules arise when combining a rights-assignment rule satisfying self-ownership (such as the two presented above) with Walrasian exchange.
Figure 2. Market-based allocation rules. A market-based allocation rule S is the result of applying a rights-assignment rule φ, satisfying the self-ownership thesis (and, possibly, solidarity), and an exchange rule F satisfying voluntary exchange. For each 
$e\equiv \left(N,\Omega ,c,R\right)\in \mathcal {E}$, S(e) = F(N, φ(N, Ω, c), R).
3. THE RESULTS
Our first results exhibit how, in our stylized context, Nozick’s theory can indeed be seen as a way of obtaining end-state fairness. More precisely, we show that there exist market-based allocation rules that yield no-envy in each of the two forms described above.
We consider first end-state fairness expressed as no-envy, whose scope needs to be limited. This is because of claims-boundedness, a consequence of the combination of self-ownership and solidarity. More precisely, an unequal choice of endowments, inevitable when equal division violates claims-boundedness, and any voluntary exchange from these endowments can cause an agent with a small claim (and hence with a small endowment) envy an agent with a large claim (and hence with a large endowment). To rule out such cases, we restrict our attention to the domain of economies where equal division satisfies claims boundedness.
The first result says that there exist market-based allocation rules that yield efficient and envy-free allocations at any economy within such a domain. In other words, self-ownership followed by voluntary exchange (formalizing Nozick’s principles of just acquisition and just transfer) guarantee end-estate fairness of no-envy together with efficiency.
Proposition 1. There exist market-based allocation rules satisfying efficiency and no-envy (on the domain of economies where equal division satisfies claims boundedness).
Proof. We consider the (market-based) allocation rule arising when combining the constrained equal awards rights-assignment rule with Walrasian exchange. Such a rule guarantees equal allocation of initial rights for the domain of economies where equal division satisfies claims boundedness. The Walrasian exchange from equal endowments guarantees no-envy and efficiency. The former follows because individual budget sets are identical across agents and, thus, each one selects her optimal bundle within such a budget set. The latter follows by the First Fundamental Theorem of Welfare Economics. 
$\Box$
We now switch to net-no-envy, whose scope needs to be limited too. Note that, when agents have sufficiently disparate claims (e.g. an agent with claims larger than the social endowment, and the others with negligible claims), it may not be possible to satisfy net-no-envy. Thus, we restrict our attention to economies without disparate claims. More precisely, we focus on the domain of economies for which equal net division is feasible. The next result states that there exist market-based allocation rules that yield efficient and net-envy-free allocations at any economy within such a domain. Again, self-ownership, followed by voluntary exchange can also guarantee end-state fairness, formalized as net-no-envy.
Proposition 2. There exist market-based allocation rules satisfying efficiency and net-no-envy (on the domain of economies where equal net division is feasible).
Proof. We consider the (market-based) allocation rule arising when combining the constrained equal net-awards rights-assignment rule with Walrasian exchange. Such a rule guarantees equal net awards among agents at the allocation of initial rights for the domain of economies where equal net division is feasible. As the Walrasian budget sets provide equal opportunities of trades across agents, when the endowment is chosen at the allocation with equal net awards, they provide equal opportunities for final net awards across agents (note that the final net award of each agent results from the sum of the equal net award at the endowment and her Walrasian trade). Therefore, all equilibrium allocations satisfy net-no-envy. Furthermore, Walrasian exchange guarantees efficiency of the final outcomes, by virtue of the First Fundamental Theorem of Welfare Economics. 
$\Box$
The previous results have illustrated how self-ownership, followed by voluntary exchange, can be invoked to guarantee end-state fairness. In what follows, we focus on the opposite implication, i.e. we search for rights-assignment rules that lead to market-based allocation rules yielding (end-state) fair outcomes. For such an implication, the notion of solidarity introduced above becomes relevant. More precisely, we show that the only way to derive end-state fairness, under solidaristic market-based allocation rules (composing a rights-assignment rule satisfying self-ownership and solidarity, and a voluntary exchange rule), is to use an egalitarian rights-assignment rule.
As we show in the next result, if one focuses on solidaristic market-based allocation rules satisfying no-envy (on the domain of economies where equal division satisfies claims boundedness) only one rights-assignment rule survives.
Theorem 1. A market-based allocation rule, generated by a solidaristic rights-assignment rule, satisfies no-envy (on the domain of economies where equal division satisfies claims boundedness) only if the rights-assignment rule is the constrained equal awards rule.
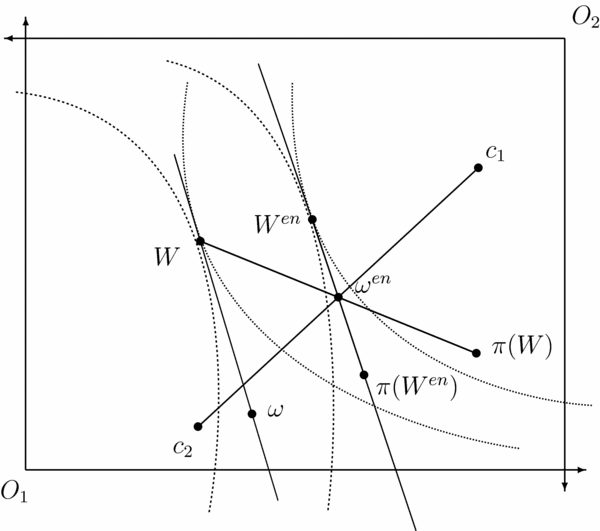
The proof of this result can be found in the appendix. The intuition goes as follows. Suppose first, by contradiction, that the rights-assignment rule does not yield the same outcome (equal division) as the constrained equal awards rule (such as allocation ω in Figure 3). If so, an economy can be constructed for which an agent is poorer than another after the rights-assignment (this cannot happen with the equal division, as all agents have the same endowment; everyone is equally rich) and, at the end of the market exchange, the poorer agent’s consumption is so restricted by her low budget that she ends up preferring the other’s consumption to her own. This shows that any market-based allocation rule, arising from such a rights-assignment rule, produces envy. An illustration for the case of two agents and two goods, assuming the Walrasian exchange for the exchange procedure, is provided in Figure 3.Footnote 22 Thus, if we want to obtain no-envy of the market-based allocation rule, we are forced to allocate initial rights as equally as possible, bounded by claims, for all the corresponding rights problems.
Figure 3. No-Envy in the Edgeworth box. Let ωed ≡ φCEA(N, Ω, c) be equal division and W ed ≡ F W(N, ωed, R) the Walrasian equilibrium from equal division. Let π(W ed) be the allocation obtained by swapping the two bundles at W ed. Note that for each i, W edR iπ(W ed). Thus, W ed satisfies no-envy. Consider any rights-assignment rule φ( ·) that yields ω ≡ φ(N, c, Ω) ≠ ωed. Let W ≡ F W(N, ω, R). Let π(W) be the allocation obtained by swapping the two bundles at W. Under the above preferences, π(W)P 1W, that is, agent 1 prefers 2’s bundle to her own. Thus, W violates no-envy.
A parallel result is obtained for net-no-envy and the constrained equal net-awards rule.
Theorem 2 A market-based allocation rule, generated by a solidaristic rights-assignment rule, satisfies net-no-envy (on the domain of economies where equal net division is feasible) only if the rights-assignment rule is the constrained equal net-awards rule.
The proof of this result can also be found in the appendix. Its intuition goes parallel to that of the previous one. More precisely, suppose first, by contradiction, that the rights-assignment rule does not yield the same outcome as the constrained equal net-awards rule. If so, an economy can be constructed for which any market-based allocation rule, arising from such a rights-assignment rule, produces net-envy. Thus, if we want to obtain net-no-envy of the market-based allocation rule, we are forced to allocate net-awards as equally as possible, bounded by claims, for all the corresponding rights problems. An illustration for the case of two agents and two goods, assuming the Walrasian exchange for the exchange procedure, appears in Figure 4.
Figure 4. Net-No-Envy in the Edgeworth box. Let ωen ≡ φCEN(N, Ω, c) be the equal net division and W en ≡ F W(N, ωen, R) the Walrasian equilibrium from the equal net division. Let π(W en) be the allocation obtained by swapping the two bundles at W en. Note that, for each i, W enR iπ(W en). Thus, W en satisfies net-no-envy. Consider any rights-assignment rule φ(·) that yields ω ≡ φ(N, c, Ω) ≠ ωen. Let W ≡ F W(N, ω, R). Let π(W) be the allocation obtained by swapping the two net awards in W. Under the above preferences, π(W)P 1W, that is, agent 1 prefers agent 2’s net awards instead of her own. Thus, W violates net-no-envy.
4. DISCUSSION
We have revisited Nozick’s entitlement theory of justice in a stylized context for the allocation of goods in joint ventures. We have considered a general model of exchange economies that accommodate the three levels in which fairness can be scrutinized in this context; namely, fairness in the allocation of rights on the social endowment, fairness in the transaction of allocated rights, and fairness of the end-state allocation. We have focused, in such a context, on what we dubbed market-based allocation rules, which arise after the combination of rights-assignment rules satisfying self-ownership and voluntary exchange rules.
Self-ownership (and, therefore, Nozick’s extension of Locke’s theory) is too weak to provide a useful guideline for the resolution of problems such as the ones modelled in this paper. In particular, it gives a green light to any resolution satisfying some minimal respect of the claims. For the case of joint ventures exemplified in our stylized model, Nozick’s principle of just acquisition is, consequently, not only modelled by self-ownership, but by the rights-assignment rules we consider. We also keep Nozick’s principle of just transfers (voluntary exchange) and show that end-state fairness (formalized by the no-envy conditions we consider) is obtained as a result of combining both principles. More importantly, we show that the only way to derive end-state fairness when composing a solidaristic rights-assignment rule, and a voluntary exchange rule, is to consider an egalitarian rights-assignment rule.
Our approach also resembles Dworkin’s insurance mechanism (e.g. Dworkin Reference Dworkin1981). Dworkin wished to hold persons responsible for their risk preferences, but not for each person’s talent. Thus, behind the veil of ignorance he constructed, the soul representing a person knows its person’s utility function, but does not know its person’s talent. Behind the veil, the souls purchase insurance against bad luck in the birth lottery. Equality enters importantly into Dworkin’s view, as he assumes that the souls have equal purchasing power for insurance. This means that the only way to purchase insurance for indemnity in one state is to sell insurance for the other’s indemnity in the other state.Footnote 23 In our setting, if claims are interpreted as individuals’ purchasing power, then equality is not imposed from the outset. Nevertheless, we obtain equality (in one of the two focal forms considered) of the end-state allocations via the market-based allocation rules. Likewise, we derive equality of the allocation of rights as a necessary condition for the end-state fairness of market-based allocation rules.
Finally, we elaborate further on the connection between our work and the theory of exploitation. Most philosophers agree that exploitation should be understood as taking advantage of another person in a way that is unfair or degrading. Classical liberals distinguish between exploitation that is harmful, and exploitation that is mutually advantageous (e.g. Wertheimer and Zwolinski Reference Wertheimer, Zwolinski and Zalta2015). Both Nozick’s procedural approach and ours preclude harmful exploitation. Mutually advantageous exploitation occurs when parties come away from a transaction better off than they would have been without it, but one party considers the distribution of the benefits as unfair. In the parlance of our approach, and if we define unfairness (of the end-state allocations) as envy (in one of the two forms defined in our model), this is equivalent to saying that, once the allocation of initial property rights has been addressed, voluntary exchange might not preclude the existence of envy (in the end-state allocations). The theoretical implications of our formal approach convey that a just allocation is an allocation without mutually advantageous exploitation. In other words, we have shown that there exist market-based allocation rules that yield allocations without mutually advantageous exploitation. Furthermore, we have also shown that, under a solidaristic assignment of initial rights, just allocations exist only if such an assignment is egalitarian.
Acknowledgements
We thank Roberto Veneziani, as well as the remaining participants of the 2015 QMUL Exploitation Workshop for helpful comments and suggestions. We are also grateful to Michael Ash, Hun Chung, Hyunseop Kim, William Thomson, Naoki Yoshihara, Richard Bradley (editor of this journal), and two anonymous referees for their insightful comments to revise the paper. Financial support from the National Research Foundation of Korea Grant funded by the Korean Government (NRF-2016S1A3A2924944), from the Center for Distributive Justice, Institute of Economic Research at Seoul National University, and from the Spanish Ministry of Economics and Competitiveness (ECO2014-57413-P) is gratefully acknowledged.
5. APPENDIX
We collect in this appendix most of the technical parts of our analysis, as well as some auxiliary results.
First, we show some implications of our axioms for our analysis.
The solidarity axiom implies the axiom of resource monotonicity, which says that when there is more to be divided, other things being equal, nobody should lose.Footnote 24 Formally,
Resource Monotonicity. For each pair (N, Ω, c) and 
$(N,\Omega ^{\prime },c)\in \mathcal {C}$, such that Ω≦Ω′, φ(N, Ω, c)≦φ(N, Ω′, c).
Resource monotonicity captures the idea that if the social endowment increases, no one’s property rights decrease.
Resource monotonicity allows us to assign rights good by good. More precisely, for each pair of rights problems with identical claims, if the endowment of one good is the same in both problems, then the rights-assignment for such a good should be the same. Formally,
Decomposability. For each pair (N, Ω, c) and 
$(N,\Omega ^{\prime },c)\in \mathcal {C}$, and each l ∈ {1, . . ., ℓ} such that Ωl = Ω′l, (φil(N, Ω, c))i ∈ N = (φil(N, Ω′, c))i ∈ N.
We first show that the combination of self-ownership and resource monotonicity implies claims boundedness: hence, in a deficit situation all agents are rationed, whereas in a surplus situation no one is.
Lemma 1. Self-ownership and resource monotonicity together imply claims boundedness.
Proof. Let φ be a rights-assignment rule satisfying self-ownership and resource monotonicity. Let 
$(N,\Omega ,c)\in \mathcal {C}$. Let Ω[0] ≡ ∑i ∈ Nc i. Consider good 1. Let Ω[1] be such that Ω[1]1 ≡ Ω1 and, for each l ≠ 1, Ω[1]l ≡ Ωl[0].
Suppose ∑i ∈ Nc i1 ⩾ Ω1. By self-ownership and feasibility, φ(N, Ω[0], c) = c. Then, by resource monotonicity, for each i ∈ N, φi1(N, Ω[1], c) ⩽ φi1(N, Ω[0], c) = c i1 and, by decomposability, φi1(N, Ω, c) = φi1(N, Ω[1], c). Therefore,
$$\begin{equation*}
\varphi _{i1}(N,\Omega ,c)\le c_{i1}.
\end{equation*}$$
The inequality is reversed when ∑i ∈ Nc i1 ⩽ Ω1.
The same argument applies for all other goods k = 2, . . ., ℓ. 
$\Box$
Solidarity also requires that the application of a rule to each subproblem derived by imagining that some agents leave with their corresponding awards in the original problem, and reassessing the situation from the viewpoint of the remaining agents, produces precisely the allocation that the subgroup obtained in the original problem. This is normally known in the literature as the axiom of consistency, which has played a crucial role in axiomatic work (e.g. Thomson 2012). Formally,
Consistency. For each 
$(N,\Omega ,c)\in \mathcal {C}$, each M⊂N, each j ∈ N\M, and each l ∈ {1, . . ., ℓ},
$$\begin{equation*}
\varphi _{jl}(N\backslash M,\sum _{k\in N\backslash M}\varphi _{k}(N,\Omega ,c),c_{N\backslash M})=\varphi _{jl}(N,\Omega ,c).
\end{equation*}$$
The last property we consider is the converse to the previous one. It allows us to deduce the desirability of a proposed awards vector for a given problem from the desirability of its restriction to each two-agent subgroup for the reduced problem obtained by imagining the departure of the members of the complementary subgroup with their awards. The property says that if an awards vector is such that for each problem and each two-agent subgroup, the rule chooses the corresponding awards of the vector to this subgroup for the reduced problem it faces, then the rule should choose the awards vector for the initial problem. Formally, for each 
$(N,\Omega ,c)\in \mathcal {C}$ and each rule φ, let cv.cs(N, Ω, c; φ) ≡ {ω : ∑i ∈ Nωi = Ω and, for each M⊂N with|M| = 2, ωM = φ(M, ∑i ∈ Mωi, c M)}.
Converse Consistency. For each 
$(N,\Omega ,c)\in \mathcal {C}$, there is ω such that {ω} = cv.cs(N, Ω, c; φ) and ω = φ(N, Ω, c).
For (unidimensional) rights problems with deficit, resource monotonicity and consistency imply converse consistency. The same result holds in our model.Footnote 25 Thus, a rule satisfying solidarity also satisfies converse consistency. This is the case for the two rules introduced above.
The previous implication has important consequences. As stated by the so-called Elevator Lemma (e.g. Thomson Reference Thomson2017a), if a conversely consistent rule coincides with a consistent rule in the two-agent case, coincidence holds in general. Thus, it suffices to characterize the constrained equal awards rule and the constrained equal net-awards rule in the two-agent case, to derive characterizations in the general case appealing to consistency.
Finally, we introduce additional notation. Let 
$\mathcal {E}^{0}$ denote the domain of economies in which equal division satisfies claims boundedness. Formally, 
$\mathcal {E}^{0}\equiv \lbrace (N,\Omega ,c,R)\in \mathcal {E}\!:$ for each l = 1, . . ., ℓ, either, for each i ∈ N,Ωl/n ⩽ c il, or for each i ∈ N,Ωl/n ⩾ c il}. Let 
$\mathcal {C}^{0}$ be the corresponding domain of claims problems.
We are now ready to prove Theorem 1.
Proof of Theorem 1. Let φ be a rights-assignment rule satisfying self-ownership and solidarity, F be an exchange rule satisfying voluntary exchange, and S ≡ F○φ be the corresponding market-based allocation rule satisfying no-envy on 
$\mathcal {E}^{0}$. We will prove that φ = φCEA on the class of 2-person problems. Then, the coincidence extends to all other problems with more than 2 persons by the Elevator Lemma. In what follows, and without loss of generality, we fix the set of 2 persons to be N ≡ {1, 2}. We skip N from the notation.
For each l = 0, . . ., ℓ, we define the set of problems 
$\mathcal {C}^{0}(l)\equiv \lbrace (\Omega ,c)\in \mathcal {C}:\text{ for each }k\ge l+1,$ either c ik ⩾ Ωk/2 for each i = 1, 2, or c ik ⩽ Ωk/2 for each i = 1, 2.}. Note that 
$\mathcal {C}^{0}(0)=\mathcal {C}^{0}$ and 
$\mathcal {C}^{0}(\ell )=\mathcal {C}$. We show that φ coincides with φCEA on each of those sets by induction.
We show first that φ = φCEA on 
$\mathcal {C}^{0}(0)$. Consider any problem 
$(\Omega ,c)\in \mathcal {C}^{0}(0)$. Suppose, by contradiction, that φ(Ω, c) ≠ (Ω/2, Ω/2). Then, there is an economy (Ω, c, R) such that ω ≡ φ(Ω, c) is the only efficient allocation satisfying voluntary exchange, from the endowment ω, and such that one of the two agents envies the other at ω.Footnote 26 Then, the market-based allocation rule necessarily chooses ω and no-envy is violated.
Suppose, as our induction basis, that φ coincides with φCEA on 
$\mathcal {C}^{0}(k)$ for each k ⩽ l − 1. We now prove that φ coincides with φCEA on 
$\mathcal {C}^{0}(l)$. Let 
$(\Omega ,c)\in \mathcal {C}^{0}(l)\backslash \mathcal {C}^{0}(l-1)$.
Case 1: c 1l + c 2l ⩾ Ωl. Without loss of generality, suppose c 1l < c 2l. Then c 1l < Ωl/2 ⩽ c 2l and, for each k ⩾ l + 1, either for each i = 1, 2, c ik ⩾ Ωk/2 or for each i = 1, 2, c ik ⩽ Ωk/2. Thus, φCEAl(Ω, c) = (c 1l, Ωl − c 1l). Let ω ≡ φ(Ω, c). Let Ω′ be such that Ω′l ≡ 2c 1l and for each k ≠ l, Ω′k ≡ Ωk. Then, 
$(\Omega ^{\prime },c)\in \mathcal {C}^{0}(l-1)$ and, by the induction hypothesis,
$$\begin{equation}
\varphi (\Omega ^{\prime },c)=\varphi ^{CEA}(\Omega ^{\prime },c).
\end{equation}$$
In particular, φl(Ω′, c) = (Ω′l/2, Ω′l/2) = (c 1l, c 1l). As Ω′≦Ω, then, by resource monotonicity, ω = φ(Ω, c)≧φ(Ω′, c). By claims boundedness, ω1l = c 1l. Then, ω2l = Ωl − c 1l. Therefore, φl(Ω, c) = φCEAl(Ω, c). As Ω′k = Ωk for each k ≠ l, then by decomposability of both φ and φCEA, φk(Ω′, c) = φk(Ω, c) and φCEAk(Ω′, c) = φkCEA(Ω, c). Hence, using (1), we conclude the proof.
Case 2: c 1l + c 2l < Ωl. Without loss of generality, suppose c 1l < c 2l. Then c 1l < Ωl/2 ⩽ c 2l and, for each k ⩾ l + 1, either for each i = 1, 2, c ik ⩾ Ωk/2 or for each i = 1, 2, c ik ⩽ Ωk/2. Thus, φCEAl(Ω, c) = (Ωl − c 2l, c 2l). Let ω ≡ φ(Ω, c). Let Ω′ be such that Ω′l ≡ 2c 2l and, for each k ≠ l, Ω′k ≡ Ωk. Then 
$(\Omega ^{\prime },c)\in \mathcal {C}^{0}(l-1)$ and, by the induction hypothesis, (1) holds here too.
In particular, φl(Ω′, c) = (Ω′l/2, Ω′l/2) = (c 2l, c 2l). As Ω′≧Ω, then, by resource monotonicity, ω = φ(Ω, c)≦φ(Ω′, c). By claims boundedness, ω2l = c 2l. Then, ω1l = Ωl − c 2l. Therefore, φl(Ω, c) = φCEAl(Ω, c). As Ω′k = Ωk for each k ≠ l, then, by decomposability of both φ and φCEA, φk(Ω′, c) = φk(Ω, c) and φCEAk(Ω′, c) = φkCEA(Ω, c). Hence, using (1), we conclude the proof. 
$\Box$
For the proof of Theorem 2, we need additional notation. Let 
$\mathcal {E}^{*}$ denote the domain of economies in which equal net division is feasible. Formally, 
$\mathcal {E}^{*}\equiv \lbrace e=(N,\Omega ,c,R)\in \mathcal {E}\!: \text{ for each }i\in N\text{, } 0\leqq c_{i}-(\sum _{j\in N}c_{j}-\Omega )/n \rbrace$. Let 
$\mathcal {C}^{*}$ be the corresponding domain of claims problems.
Proof of Theorem 2. Let φ be a rights-assignment mechanism satisfying self-ownership and solidarity, F be an exchange rule satisfying voluntary exchange, and S ≡ F○φ be the corresponding market-based allocation rule satisfying net-no-envy on 
$\mathcal {E}^{*}$. We will prove that φ = φCEN on the class of 2-person problems. Then the coincidence extends to all other problems with more than 2 persons by the Elevator Lemma. In what follows, and without loss of generality, we set N ≡ {1, 2} and skip N from the notation.
For each l = 0, . . ., ℓ, we define the set of problems 
$\mathcal {C}^{*}(l)\equiv \lbrace (\Omega ,c)\in \mathcal {C}\!:\text{ for each } k\ge l+1,\text{ and for each } i=1,2,\mbox{ }(c_{1k}+c_{2k}-\Omega _{k})/2\le c_{ik}\rbrace$. Note that 
$\mathcal {C}^{*}(0)\equiv \mathcal {C}^{*}$ (the domain of claims problems for which equal net division is feasible) and 
$\mathcal {C}^{\ast }(\ell )=\mathcal {C}$. We show that φ coincides with φCEN on each of those sets using induction.
We first show that φ = φCEN on 
$\mathcal {C}^{*}(0)$. Let 
$(\Omega ,c)\in \mathcal {C}^{*}(0)$. Suppose, by contradiction, that φ(Ω, c) = ω ≠ φCEN(Ω, c). Then, there is an economy for which ω is the only efficient allocation satisfying voluntary exchange (from endowment ω) and therein one of the two agents envies the net consumption of the other. Then, the market-based allocation rule necessarily chooses ω and net-no-envy is violated.
Let l ∈ {1, . . ., ℓ}. Suppose, by induction, that φ = φCEN on 
$\mathcal {C}^{*}(k)$ for each k ⩽ l − 1. We now prove that φ = φCEN on 
$\mathcal {C}^{*}(l)$. Let 
$(\Omega ,c)\in \mathcal {C}^{*}(l)\backslash \mathcal {C}^{*}(l-1)$. Without loss of generality, suppose c 1l ⩽ c 2l. Then, since 
$(\Omega ,c)\notin \mathcal {C}^{*}(l-1)$, (c 1l + c 2l − Ωl)/2 > c 1l (i.e. c 2l − c 1l > Ωl). Hence, φCENl(Ω, c)=(0, Ωl) and φCENl(Ω, c) ⩽ (0, c 2l − c 1l). Let Ω′l ≡ c 2l − c 1l and, for each k ≠ l, Ω′k = Ωk. Then 
$(\Omega ^{\prime },c)\in \mathcal {C}^{*}(l-1)$ and, by the induction hypothesis,
$$\begin{equation}
\varphi (\Omega ^{\prime },c)=\varphi ^{CEN}(\Omega ^{\prime },c).
\end{equation}$$
Note that φCENl(Ω′, c) = (0, c 2l − c 1l). Since Ω≦Ω′, by resource monotonicity and non-negativity, φ1l(Ω, c) = 0, which implies φ2l(Ω, c) = Ωl. Therefore, φl(Ω, c) = φCENl(Ω, c). As Ω′k = Ωk for each k ≠ l, then applying resource monotonicity to both φ and φCEN, we have φk(Ω, c) = φk(Ω′, c) and φCENk(Ω′, c) = φkCEN(Ω, c). Hence, using (2), φk(Ω, c) = φCENk(Ω, c). 
$\Box$
