2. INITIAL MOTIVATION FOR THE TECHNIQUE OF BEAM SMOOTHING

Optical self-focusing (or filamentation) of laser beams in plasmas was discussed since the self-focusing phenomenon was observed in condensed materials in liquids and solids, where the threshold of a laser power P* was characteristic. This was first derived by Chiao et al. (1964) and was based on the nonlinear extension of the dielectric constant of condensed materials. For Plasmas, the first theory of this self-focusing threshold (Hora, 1969b)—after self-focusing had been measured (Korobkin & Alcock, 1968)—was derived from the fact that the laser beam expels plasma from its center by the radial gradient of the time averaged electric field E of the beam

where E_o is the amplitude of the optical field oscillating with a radian frequency ω and where n is the complex refractive index in the plasma with an electron density n_e determined by Langmuir's plasma frequency ω_p

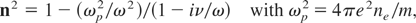
e is the charge, m is the mass of the electron, and ν is the electron ion collision frequency in the plasma, which causes the damping of the electromagnetic wave similar to the metal optics. The theory of self-focusing in plasma (Hora, 1969b) included the compensation of nonlinear or ponderomotive force (1), by the force of the gas dynamic pressure acting against the expelling of the plasma from the laser beam. Further, the condition of total reflection of the beamlets by the radically varying refractive index, due to the variation of plasma density, and further the condition of self diffraction of the laser beam had to be added to arrive at the threshold P* (in Watts), of self-focusing in the plasma including the Rayleigh factor of 1.22 for a beam instead of a factor of 1 for a slit (Hora, 1969b), depending on the plasma temperature T (in eV), and the electron density given by the plasma frequency ω_p, Eq. (2) as

Since the laser produced plasmas have temperatures at least of several eV, the self-focusing begins from laser powers of about MW.

This megawatt threshold P* has a crucial importance of laser interaction with plasmas. Below P*, the interaction works fully classically with generation, and heating of the plasma to temperatures of a few eV with classical hydrodynamic motion of the plasma, and emitting electrons according to space charge limitation and ions with energies of a few eV. Above P*, it was observed that the emitted ions had energies (Linlor, 1963) up to 10 keV, and electron emission current density was more than 1000 times higher (Honig, 1963) than permitted by space charge limitation. These observations were the first unexpected anomalies which were confusing the whole field of high intensity interaction of lasers with materials producing plasma indicating the nonlinear physics.

It turned out (Hora, 1969b) that the self-focusing is the reason causing a shrinking of the laser beam to such diameter (for P = 10 MW measured of 3 to 5 μm, see Korobkin & Alcock, 1968), such that the laser intensity exceeds about 10¹³/λ² W/cm² (laser wave length λ in μm) where the nonlinear electro-dynamic (ponderomotive) forces in the plasma dominate against the thermo-kinetic forces. The laser forces accelerated the electron cloud and the ions follow separated by the charge number Z of the ions as observed from the linear Z-dependence of the ion energy. This all could be based on the general formulation of the force density in plasmas (Hora, 1969a, 1985a or 1985b) f = f_th + f_NL consisting in the thermo-kinetic force f_th = −∇P given by the gas dynamic pressure P and the general nonlinear force

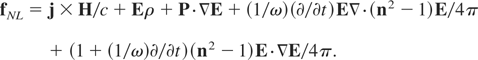
Here one recognizes on the right-hand side, the first Lorentz term f_Lorentz = j × H/c with the plasma current density j, and the vacuum velocity of light c, then the Coulomb term Eρ with the electric charge density ρ, and as the third term, the Kelvin ponderomotive term (Hora, 2000, Eq. (1)) using the polarization vector P = (n² − 1)E/(4π)

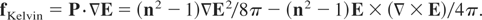
The remaining terms in Eq. (4) are new nonlinear terms which were derived for the general equation of motion in plasmas from the studies of laser interaction (Hora, 1969b, 1985a or 1985b, 2000). The proof for the final generality of Eq. (4) was given by momentum conservation for the non-transient case (Hora, 1969a) (∂/∂t = 0) and for the transient case by symmetry of the terms (Hora, 1985a or 1985b) and from gauge and Lorentz invariance (Rowlands, 1990).

For the correct interpretation, it is necessary to mention that Kelvin's ponderomotive force is identical with the nonlinear Schlüter (1950) term (see Hora, 1969b, 2000)

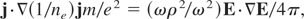
remembering the definition of the electric polarization P and Eq. (2) without collisions

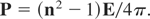
From Kelvin's ponderomotive force, Eq. (5) follows formally as an expression of the “field gradient force” (1), that led to the common expression of “ponderomotive force” for Eq. (1). As is known, for (plane wave) perpendicular incidence of laser radiation on plasma (Hora, 2000), the Schlüter (1950) term is then zero. Nevertheless, there is a force of the form of Eq. (1). In this case, however, the nonlinear force f_NL is the result of the Lorentz term in Eq. (4). This confusion of the definitions is avoided if one uses the general expression of the nonlinear force (4) for the electro-dynamic part of the force density in plasma.

If a laser beam has local intensity maxima, the so-called hot spots, which are produced by dielectric nonlinearities, especially in solid state laser amplifiers or optical glass components, even if single mode laser oscillators are used, then it is necessary to avoid this nonuniform irradiation for special cases as for laser fusion. This was the motivation to invent the smoothing techniques.

3. BEAM SMOOTHING TECHNIQUES

Very curious phenomena were observed at high intensity laser irradiation of solid targets, as seen from high energy Z-separated ion emission, and very high current densities also of electron emission (Linlor, 1963; Honig, 1963), from X-ray emission spectra indicating a number of temperatures, and from back scattered spectra of the fundamental laser frequency, or of its harmonics (Hora, 1991). Some reduction of these anomalies was first observed by the experiments of Deng and Wenyan (1984), when laser irradiation had a broad spectrum, just using the backscattered light as source of irradiation. This motivated Deng and Wenyan (1984) to use a fly-eye smoothing where a plate with an array of a large number of little lenses was put into the laser beam before irradiation of the target. A reduction of the anomalies was observed. It should be noted that Sklizkov (1964, private communication), even in his early Kalmar laser system had used a kind of a phase correction plate as discussed in view of an earlier patent (Hora, 1965), which may have led to some reduction of the anomalies

The convincing break through for smoothing came with the random phase plate (RPP) (Kato et al., 1984) and the induced spatial incoherence (ISI) (Lehmberg & Obenschain, 1983; Obenschain et al., 1989). The random phase plate consists in a glass plate where there is some roster or pattern with evaporated plane parallel dielectric material of different thickness for each part. This causes the laser beam to split into a large number of beamlets, each of which is phase shifted against the neighboring beamlet. The plate is introduced into the laser beam at the end, just before being focused on the target. The ISI requires that the laser oscillator receives a temporal incoherence, e.g., of 2 ps at the beginning of the beam chain before going to the amplifier system.

The results are seen from an example comparing the laser intensity across a diameter with no smoothing, with RPP and ISI before the application to a target (Giulietti et al., 1991), Figure 1. It should be noted that the RPP case may not have resulted in the best achievement. Varying the roster finesse may have arrived at a different result. An example of a different roster structure was shown in the work by Labaune et al. (1992). Despite the possible non-optimized RPP, the effect caused by the smoothing is exceedingly significant as shown in Figure 2, with the reduction of the backscattered 3/2th harmonics down to nearly one thousandths (!) of the unsmoothed case.

Intensity of a laser beam measured (Giulietti et al., 1991) along a diameter using smoothing by ISI (a), RPP (b), and without smoothing (c).

Measured (Giulietti et al., 1991) backscattering per incident laser power of the 3/2th harmonics for various neodymium glass laser intensities without smoothing (coherent) and with smoothing using RPP or ISI.

It is the standard assumption that the 3/2th harmonics emitted from a laser produced plasma is due to parametric instabilities, the stimulated Raman scattering SRS, and the stimulated Brillouin scattering (SBS). When all the above mentioned extreme anomalies of laser-plasma interaction appeared, most attention was given to the suggestion that this were due to the parametric instabilities (Hora, 1991, Sec. 9.5), and whole libraries were filled with speculations and comparison about unexplained experiments. One of the possible alternatives was an explanation by electric double layers as result of the genuine two-fluid model computations (Eliezer & Hora, 1989; Hora, 1991). There is indeed a generation of higher harmonics (Hora & Ghatak, 1985; Goldsworthy et al., 1990), causing a resonance in the super critical range of the plasma density even at perpendicular incidence (contrary to the Försterling-Denisov resonance absorption, see Hora, 1991, Chap. 11.2). Furthermore, the second harmonics generation measured by Aleksandrova et al. (1985; Hora, 1991, pp. 25, 203), even at very low plasma densities, could be explained by this alternative theory and not by the parametric instabilities which are restricted to certain specific densities only.

It should be mentioned that further smoothing schemes, e.g., by the combination of RPP and ISI have been developed (Skupsky & Lee, 1983). The generation of a broad band spectrum from the otherwise very narrow band of the coherent laser beam is an essential result of ISI, and was developed also as “broad band smoothing” (Bibeau et al., 2000). The smoothing in the Omega laser (Soures et al., 1996) was based on polarization smoothing using refracting crystals.

Another observation was important by using the smoothing. It was observed, Figure 3, that irradiation of the target with (unsmoothed) coherent laser light produced a stochastic pulsation of the 3/2 harmonics emission (Giulietti et al., 1991), with a duration of few tens of a picosecond. When using the smoothing, the 3/2 emission was not pulsating and was nearly continuously constant. This kind of few tens of a ps pulsation was also seen from the Rogowski coil diagnostics of the emitted plasma, at nearly constant unsmoothed laser irradiation (see Eliezer & Hora, 1989, Fig. 26). The same experiment was not performed with smoothing.

Time resolved 3/2 harmonics spectrum from an Al target at a 600 ps second harmonics neodymium glass laser irradiation of 6 ×1014 W/cm2 with a preheating (Giulietti et al., 1991).

4. PULSATION BY SELF-GENERATED VON-LAUE-GRATINGS AND THEIR SUPPRESSION BY LASER BEAM SMOOTHING

On top of the mentioned complications of laser-plasma interaction

• with generation of ions with charge numbers of Z = 58 and energies up to the GeV range (Haseroth & Hora, 1996)
• with anomalously high current densities, with ponderomotive (Hora, 1969b) and relativistic (Hora, 1975a; Häuser et al., 1992; Osman et al., 1999) self focusing and
• with suppression of higher harmonics by smoothing (Fig. 2) up to a factor 1000, there seems to be another phenomenon of key importance. This is the stochastic pulsation with a sequence in the few to dozens of a ps range as shown in Figure 3. It's incidentally observed suppression by smoothing may have nothing to do with instabilities, but may be a process of self generating von-Laue gratings, and their thermal washing out followed by another grating generation and again washing out etc. The suppression of this pulsating (stuttering) interaction could be performed with laser beam smoothing. This increased the laser driven plasma compression and the direct drive laser fusion gain by more than a factor 10 using the random phase plate (Azechi et al., 1991) (Fig. 4).

Measured laser compression of deuterated polyethylene of 1 g/cc solid state density with tritium content depending on the thickness of the laser irradiated spherical shell of different target diameter with and without random phase plate smoothing (Azechi et al., 1991) showing an increase of compression by more than a factor 10 to 2000 times the solid state density.

The first indication of these mechanisms was seen in numerical studies (Hora, 1975b, Sec. 7.5). It all began with the computation of the plane geometry interaction of laser radiation with plasmas including the nonlinear force, where the optical properties were carefully taken into account based on the usual optical absorption, and on the correct (contrary to the Silin-Max approximation) nonlinear optical constants, and the Maxwellian exact wave field with appropriate use of the “local reflection” (see Hora, 1991, Sec. 7). Irradiation of a 2 × 10¹⁴ W/cm² neodymium glass laser intensity on a linearly increasing ramp of deuterium plasma of 50 μm thickness at the first stage A, Figure 5, resulted in a penetration of the laser light to the critical density where this was reflected as a mirror reflection, similar to the case of a metal within the skin depth, and (due to absorption) in the generation of a partial standing wave pattern. 2 ps later, however, when the fully coherently assumed laser intensity has grown to 2 × 10¹⁶ W/cm² (B in Fig. 5), the light entered into the very low plasma density but reached the critical density after fading down to less than one hundredth of the initial intensity. What has happened? The partial standing wave field had pushed the plasma toward the nodes of the standing wave and produced a density ripple which acted as an ideally, self produced von-Laue-Bragg grating for a nearly 98% phase reflection of the light, even at the very low peripheral plasma density. One may say that such a von-Laue process is a Brillouin process, but we carefully have to avoid the word Brillouin since it is used in laser plasma interaction for the basically different (not hydrodynamic!) microscopic instability process, where laser radiation is converted into acoustic waves determined by wave vector relations.

(a) A laser beam incident from the right hand side on plasma of initial temperature of 100 eV and linear density increasing from zero at x = 50 μm to the cut-off density at x = 0 (where ωp = ω) and the increasing more rapidly. The exact stationary time dependent solution without retardation of the Maxwellian equations with the nonlinear refractive index, based on the intensity dependent collision frequency, results in an oscillation of the electromagnetic energy density (E2 + H2)/8π due to the partial standing wave and dielectric swelling of the amplitude (curve A). At a later time (2 ps) the laser intensity is 2 × 1016 W/cm2 (curve B), where the relative swelling remains, but the intensity at x = 0 is attenuated by more than a factor 100 due to the phase reflection of the electromagnetic wave by the then density ripple given by the straight line in the upper part of (b) which was produced by the nonlinear force pushing the plasma into the nodes of the partial standing wave while slowly moving hydrodynamically to lower density of the dashed line initial density. The electron and ion temperatures are increased following the ripple by dynamic compression at conditions identical to curve B.

This change from mirror to phase reflection was seen by Lubin in 1974 from measuring the time resolved reflection of a laser produced plasma. At the mentioned intensities, first the reflectivity was few percent for few picoseconds, growing then to more than 90% for several picoseconds, jumped then for few ps again to less than 10%, and after further few ps again above 90% etc. The duration of the long high reflecting periods was stochastically changing between some picoseconds and few tens of ps similar to stochastic pulsation later seen (Fig. 3), and Eliezer and Hora (1989, Fig. 26), or with the nonlinear force produced anomalous double layers (Hora et al., 1984). Also, the “question mark experiment” (Pant et al. 1976; Jackel et al., 1976) showed the phase reflection with the reflected question mark pattern standing upside down. If this experiment would have been done with few ps time resolution and with detection of very low reflectivity, there would have been upright faint question marks between the strong upside-down cases stochastically changing within the mentioned several ps intervals.

This very complicated interaction process can be understood as seen numerically first in the cases of Figure 5 (see more in the initial reference Hora, 1975b, Sec. 7.5; Hora, 1991, Figs. 10.10 and 10.11). When, however, the phase reflection is cutting the optical penetration through the plasma corona, it happens that the density rippled plasma there is then gas dynamic relaxing and disappearing of the density ripple within several ps such that then the laser light can penetrate again to the critical density, and produce mirror reflection there. But then again the density ripple of the plasma corona occurs again with phase reflection etc. This has been reproduced numerically by Hora and Aydin (1992, 1999). It shows also that the plasma corona as a whole block is getting a non linear force acceleration to the well known velocities above 10⁷ cm/s, which acceleration ends each after few ps because of the mentioned density ripple and phase reflection until the thermal relaxation of the ripple, when another hit of the plasma corona produces the mentioned velocities as seen form Figure 6, lower part. The plasma corona is pushed to the velocity of about 10⁷ cm/s within the first few ps, while the velocity ripple shows the motion of the plasma to the nodes of the standing wave field as seen in the energy density profile (upper part of Fig. 6). While the plasma then moved initially, shifting the critical density to the plasma interior (blue shift, see Fig. 3), the generated density ripple relaxes until about 20 ps when again the laser penetrates along the then monotonous and unrippled density profile to the critical density for mirror reflection, generating again a partial standing wave with pushing the plasma to the nodes as seen from the rippled velocity profiles, and stopping the interaction after having given another push to the plasma corona by an additional 10⁷ cm/s velocity.

Computation for neodymium glass laser irradiation with 1015 W/cm2 intensity on a plasma slab of 20 μm thickness and initially density growing linearly from 0 .5 to 1.3 times critical density and 100 eV temperature. The time development in steps of one ps of the electromagnetic energy density of the laser field ε = (E2 + H2)/8π (a) and of the ion velocity vi shows the pulsation of penetration or stopping of the laser energy synchronous with ion motion whose net value increases in blocks after each electromagnetic interaction with the corona (Hora & Aydin, 1992, 1999; Boreham et al., 1997; Miley et al., 2005).

This stochastically stuttering interaction was measured—after seen by Giulietti et al. (1991), see Figure 3—by Maddever et al. (1990) by observing the ps pulsation of the acceleration of the plasma at laser irradiation see Maddever et al. (1990, Fig. 4.14c), while the pulsating acceleration of each plasma group to each about 10⁷cm/s was seen form the fully modulated spectrum at a narrow angle measured with glass fibers (Maddever, 1988, Fig. 3.7).

This experiment provides the key answer together with the theory (Hora & Aydin, 1992, Fig. 6) why direct drive for laser fusion was very difficulty during the preceding 20 years. This was showing also that not the instabilities were the reason for this dilemma, but the 10 ps stochastic pulsation (stuttering) process. The computations of the stuttering (Hora & Aydin, 1992, 1999) interaction (Fig. 6) were extended to use a wide band laser irradiation, e.g., of 0.5% frequency width. It was then seen (Azechi et al., 1991) that this washes out the coherent density ripple and immediately results in a suppression of stuttering, and an ideal high transfer of the laser radiation at low reflectivity to the plasma corona as needed for direct drive laser fusion. This was seen before experimentally by using the intuitively suggested laser beam smoothing techniques with wide band laser radiation with more than ten times increase of plasma compression and fusion gain.

5. EXPERIMENTAL EVIDENCE OF PULSATION AND SUPPRESSION BY SMOOTHING

Another experiment for a detailed proof that the smoothing is not only suppressing the filamentation—as expected from the beginning—but is suppressing the much more important stochastic pulsation, was published by Labaune et al. (1992), (Fig. 7). When the random phase plate for a 9 cm diameter laser beam had dielectric 2 mm squares for 180° phase change, the pictures of spatially and temporally resolved plasma still showed an unsmooth result with beam parallel filament structures (Fig. 7a, left-hand side). On top of this, the picture also showed structures perpendicular to the laser beam in about 40 ps distance clearly indicating the stochastic pulsation. But when using a random phase plate with 1 mm squares a rather smooth plasma was shown (Fig. 7b, right hand side) where both the filamentation and the pulsation had disappeared. For wave optics, the squares would have led to a focal spot diameter of 132 μm and 265 μm for the 2 mm, respectively, 1 mm squares. It is remarkable that in this case, ray optics may be applicable where the filaments are squeezed into the 65 μm focal diameter of interaction. The beamlets of the squares are then about two wave lengths for the 2 mm and about one wave length for the 1 mm squares. This is just what we expect from our density ripple calculations. As soon as neighbor filaments are out of phase within a wave length distance or less, the washing out of any density ripple happens due to lateral interaction. For two wave length distance, the effect of washing out is too little. Indeed the addition of broad band as used by SSD (Giulietti et al., 1991; Skupsky & Lee, 1983) may better lead at the necessary low reflectivity, non-pulsating, instability-suppressed, and filament less interaction as needed for the ideal direct drive laser fusion. This was considered in the past to be possible only with the third harmonics of the laser beam. The use of the fundamental wave length should work similarly applying some modifications for the different conditions compared with the third harmonics. For the applied random phase plate, a condition may be that the width w of the squares should be determined by the laser wave length λ

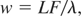
where L is the diameter of the lens equal to the laser beam or the random phase plate, and F is the focus diameter of the laser beam at the plasma interaction.

Time dependence of the transmitted laser light through a 1.5 × 1015 W/cm2 neodymium glass laser irradiated layer from Labaune et al. (1992) In the case a), the random phase plate had cells of 2 mm width where the filamentation (horizontal structures) and also pulsation (vertical structures) can be seen. Using the random phase plate with 1mm width, the structures all had gone case b) as expected from the numerical results (Hora & Aydin, 1992).