1. Introduction
Inertial waves arise in rotating fluids due to the presence of Coriolis-type restoring forces (Greenspan Reference Greenspan1968). In the inviscid limit, the equations of motion for an infinitesimal disturbance to a background solid-body rotation reduce to a linear partial differential equation of hyperbolic type, provided that the disturbance frequency is less than twice the background rotation frequency in an inertial reference frame. A set of eigenmodes with associated frequencies was first shown by Kelvin (Reference Kelvin1880) to provide an orthogonal basis for the inviscid inertial waves in a rotating cylinder, and such modes now bear his name. In contained bodies of either inviscid or viscous rotating fluid, inertial waves may also arise, though the associated frequencies and eigenmodes must then be tuned to satisfy boundary conditions at walls. When Reynolds numbers are high enough, one may expect that Kelvin modes provide good approximations to the viscous eigenmodes, and it is found experimentally that a rotating flow may readily be excited near the frequencies predicted by Kelvin’s theory (Fultz Reference Fultz1959). Experiments since the 1960s have revealed a rich variety of nonlinear phenomena such as recurrent collapses and catastrophic transitions in rapidly rotating cylinder flows that were excited in various different ways, including boundary perturbations and axial precession (e.g. McEwan Reference McEwan1970; Manasseh Reference Manasseh1992).
McEwan (Reference McEwan1970) first suggested that a triadic-resonance model might help to explain these phenomena. The concept of triadic interactions of modes resulting from the quadratic nonlinearity in the Euler equations of motion, leading to resonant growth, is well accepted in other applications (e.g. Craik Reference Craik1988). Mahalov (Reference Mahalov1993) developed the idea of triadic resonances of Kelvin modes in a precessing cylinder of unbounded axial extent. Kerswell (Reference Kerswell1999) developed a stability model for triadic resonances in a rotating cylinder of finite length. Although the focus was on elliptic instabilities where the forced flow has azimuthal wavenumber
$m=2$
, he also pointed out that much the same mechanism applies in precessing cylinders where the forced flow has
$m=1$
(Kerswell Reference Kerswell2002). More recently, Lagrange et al. (Reference Lagrange, Meunier, Nadal and Eloy2011) produced a weakly nonlinear Kelvin-triad-interaction theory to predict the growth and saturation of instabilities in precessing cylinder flows, and provided experimental results in support.
Successful comparison of resonant triad theory with experiment in a precessing cylinder (Lagrange et al. Reference Lagrange, Eloy, Nadal and Meunier2008; Meunier et al. Reference Meunier, Eloy, Lagrange and Nadal2008; Lagrange et al. Reference Lagrange, Meunier, Nadal and Eloy2011) involved a cylinder of aspect ratio precisely ‘tuned’ to make one triad exact. While the theory can accommodate detuning from exact resonances, isolation of exact triads in finite cylinders and calculation of predicted growth rates is non-trivial and requires careful consideration, as we outline in § 2. The theory was challenged in a recent numerical study of precessing cylinder flow by Kong et al. (Reference Kong, Cui, Liao and Zhang2015), which attempted to examine the triadic-resonance mechanism, and concluded that it did not explain the observed nonlinearities. Instead, it was suggested that the energy contained in the precessionally forced mode is primarily transferred, through nonlinear effects in the viscous boundary layers, to a geostrophic flow. Our principal objective here is to demonstrate that weakly nonlinear models based on a triadic-resonance approximation are indeed a robust descriptor of the flow in rapidly rotating precessing cylinders, valid for a variety of both well and imperfectly tuned cases.
2. Background
2.1. Problem definition
A rotating and precessing cylinder flow is shown schematically in figure 1(a). An incompressible fluid with kinematic viscosity
${\it\nu}$
is contained in a cylinder of radius
$R$
and height
$H$
, mounted on a turntable via a gimbal that allows the cylinder axis to be tilted through nutation angle
${\it\alpha}$
. The cylinder rotates with an angular velocity
${\it\bf\Omega}_{1}$
that precesses at angular velocity
${\it\bf\Omega}_{2}$
with respect to the turntable axis
$\hat{\boldsymbol{z}}$
. Without loss of generality, we take
${\it\Omega}_{1}={\it\bf\Omega}_{1}\boldsymbol{\cdot }\hat{\boldsymbol{z}}>0$
. Precession may be prograde (
${\it\Omega}_{2}={\it\bf\Omega}_{2}\boldsymbol{\cdot }\hat{\boldsymbol{z}}>0$
) or retrograde (
${\it\Omega}_{2}<0$
) with respect to
${\it\bf\Omega}_{1}$
. The total angular rotation in an inertial reference frame is
${\it\bf\Omega}_{1}+{\it\bf\Omega}_{2}$
. The flow is governed by the incompressible Navier–Stokes equations with no-slip boundary conditions on the cylinder walls. Using
$R$
as the length scale and
${\it\Omega}_{1}^{-1}$
as the time scale, the non-dimensional governing equations in a rotating reference frame are
$$\begin{eqnarray}\partial \boldsymbol{v}/\partial t+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}+2{\it\bf\Omega}\times \boldsymbol{v}+(\text{d}{\it\bf\Omega}/\text{d}t)\times \boldsymbol{r}=-\boldsymbol{{\rm\nabla}}p+Re^{-1}{\rm\nabla}^{2}\boldsymbol{v},\quad \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0,\end{eqnarray}$$
where
$\boldsymbol{v}$
and
$\boldsymbol{r}$
are velocity and position vectors and the Reynolds number
$Re={\it\Omega}_{1}R^{2}/{\it\nu}$
. The non-dimensional rotation vector
${\it\bf\Omega}=({\it\bf\Omega}_{1}+{\it\bf\Omega}_{2})/{\it\Omega}_{1}$
can be written in an inertial reference frame
$(\hat{\boldsymbol{x}},\hat{\boldsymbol{y}},\hat{\boldsymbol{z}})$
as
$(\sin {\it\alpha}\cos (Po\,t),\sin {\it\alpha}\sin (Po\,t),Po+\cos {\it\alpha})$
, with the Poincaré number
$Po={\it\Omega}_{2}/{\it\Omega}_{1}$
. The term
$(\text{d}{\it\bf\Omega}/\text{d}t)\times \boldsymbol{r}$
allows for changes in direction and/or magnitude of the rotation vector. Body forces (e.g. centrifugal force) that can be written as gradients of a scalar are included in the non-dimensional reduced pressure
$p$
. Four independent non-dimensional governing parameters are the cylinder aspect ratio
${\it\Gamma}=H/R$
, Reynolds number
$Re$
, Poincaré number
$Po$
and nutation angle
${\it\alpha}$
. We note that
$Re$
time units is the viscous diffusion time scale for the system. It is convenient to introduce the projection of the non-dimensional rotation vector
${\it\bf\Omega}$
in the inertial frame onto the cylinder axis,
${\it\Omega}=1+Po\cos {\it\alpha}$
. In the problem considered, initially the nutation angle
${\it\alpha}=0$
and the cylinder of fluid is in solid-body rotation;
${\it\alpha}$
is then increased over a short time interval to a subsequently fixed value.
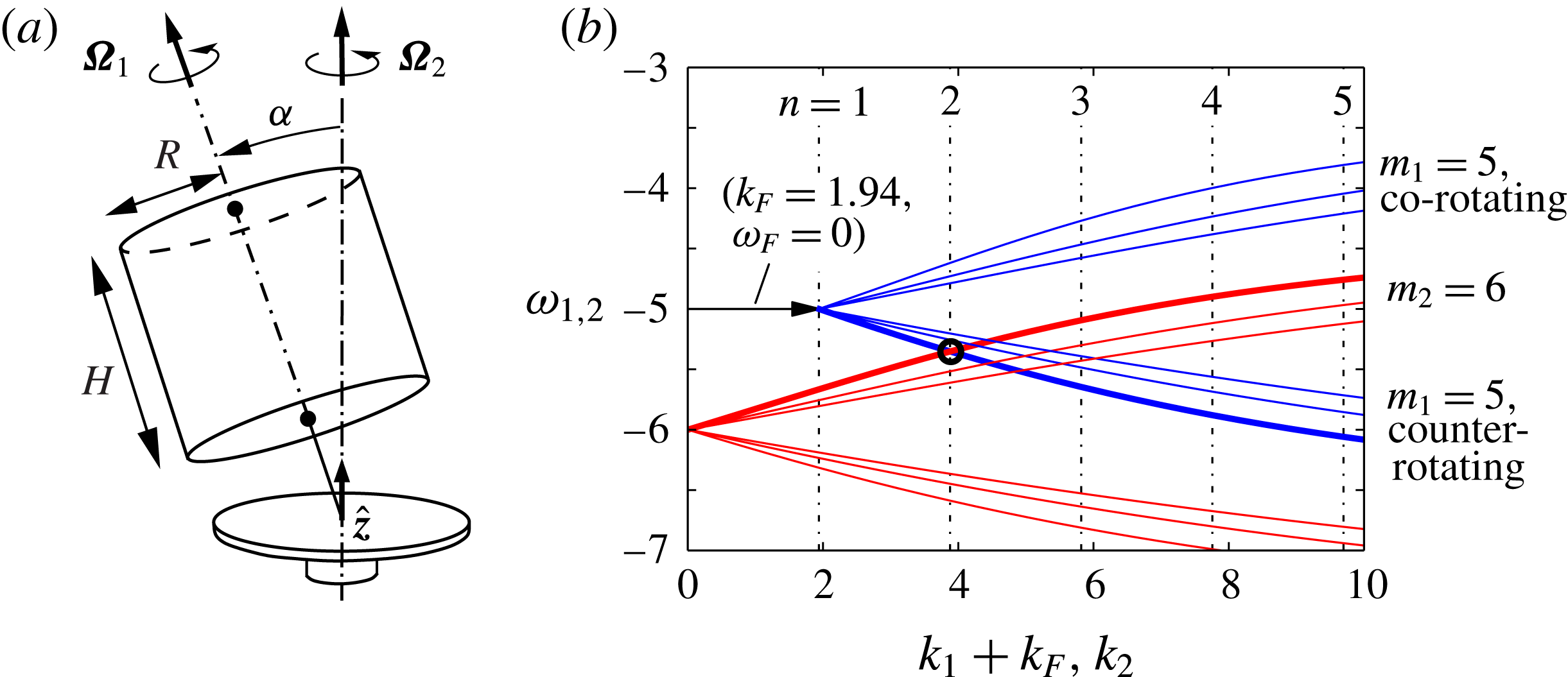
Figure 1. (a) Schematic of the precessing flow. (b) The dispersion relations (2.2a
) between the temporal frequencies
${\it\omega}$
and the axial wavenumbers
$k$
of two parasitic Kelvin modes for azimuthal wavenumbers
$m_{1}=5$
(blue lines) and
$m_{2}=6$
(red lines) in the gimbal frame of reference, where the frequency of the forced mode
${\it\omega}_{F}=0$
. In each set, upper/lower branches are for modes that co/counter-rotate with the cylinder in the cylinder frame, and the lines successively represent
$l=1,2,\dots ,$
which label the roots of (2.2a
). An exact resonant triad with the
$(1,1,1)$
mode is indicated by the circle: the frequency of the
$-(n_{1}=1,l_{1}=1,m_{1}=5)$
Kelvin mode is equal to the frequency of the
$(n_{2}=2,l_{2}=1,m_{2}=6)$
Kelvin mode, and their axial wavenumbers differ by that of the forced mode, as indicated by the arrow. In the gimbal frame, the two parasitic modes counter-rotate.
2.2. Precessional forcing of Kelvin modes
For vanishing forcing amplitude and rapid rotation, we approach the linear inviscid limit considered by Kelvin (Reference Kelvin1880) of small deviations from solid-body rotation. Kelvin mode velocity and pressure fields are given by products of Bessel functions in the radial direction with trigonometric functions
$\exp (\text{i}kz+\text{i}m{\it\phi}+\text{i}{\it\omega}t)+\text{c.c.}$
, where
$k$
and
$m$
are the axial and azimuthal wavenumbers and
${\it\omega}$
is the dimensionless frequency of the mode (Greenspan Reference Greenspan1968). In the gimbal frame of reference, i.e. a frame aligned with the cylinder axis and in which the cylinder rotates, radial and axial no-penetration boundary conditions are satisfied respectively by dispersion relations
$$\begin{eqnarray}\displaystyle \frac{{\it\omega}+m}{{\it\Omega}}{\it\lambda}_{nlm}J_{m}^{\prime }({\it\lambda}_{nlm})+2mJ_{m}({\it\lambda}_{nlm})=0,\quad \left(\frac{2{\it\Omega}}{{\it\omega}+m}\right)^{2}=1+\left(\frac{{\it\lambda}_{nlm}{\it\Gamma}}{n{\rm\pi}}\right)^{2}, & & \displaystyle\end{eqnarray}$$
where
$J_{m}^{\prime }$
is the derivative of Bessel function
$J_{m}$
, the radial wavenumber
${\it\lambda}_{nlm}$
is the
$l$
th root of (2.2a
) and
$n=k{\it\Gamma}/{\rm\pi}$
is the number of axial half-wavelengths. Each mode is characterized by three integer indices
$(n,l,m)$
corresponding to axial, radial and azimuthal directions respectively.
In a precessing cylinder, precession forces an azimuthal wavenumber
$m=1$
flow that is fixed in the gimbal frame of reference (i.e. at a frequency
${\it\omega}=0$
). This forcing can excite a Kelvin mode if
${\it\Omega}$
is sufficiently close to a value
${\it\Omega}_{nlm}$
that satisfies both dispersion relations of (2.2) with
$m=1$
and
${\it\omega}=0$
. For each
$(n,l,m)$
combination, there are two values
${\it\Omega}_{nlm}$
, with
${\it\Omega}_{nlm}>0$
and
${<}0$
corresponding to eigenmodes rotating in the same or opposite sense to the cylinder in the cylinder frame. Each of the pair of eigenmodes has distinct radial structure. Modes for
${\it\Omega}<0$
will be denoted
$-(n,l,m)$
. When
${\it\Omega}$
(which is tuned by adjusting
$Po$
and
${\it\alpha}$
) is close to a resonant value
${\it\Omega}_{nlm}$
, a forced Kelvin mode can be strongly amplified even by weak precessional forcing (small
$|Po\sin {\it\alpha}|$
). Viscosity limits the resonant growth to amplitudes of order
$Re^{1/2}$
(Gans Reference Gans1970; Meunier et al.
Reference Meunier, Eloy, Lagrange and Nadal2008). For the cases examined herein,
${\it\Omega}$
is chosen such that the
$(1,1,1)$
mode resonance provides the largest contribution to the initial forced response, and is referred to as the ‘forced mode’. However, other Kelvin modes also satisfy the dispersion relations (2.2), and by appropriate choice of
${\it\Gamma}$
, two such modes may form a resonant triad with the forced mode.
2.3. Resonant triad principles
Quadratic nonlinearity in the equations of motion may couple a pair of modes to a third mode. If one mode in the triad were forced, the other two would grow and ‘parasitically’ extract energy from it. In the weakly nonlinear model, the perturbation velocity field is assumed to be an infinite sum of all the Kelvin modes, with each mode multiplied by an arbitrarily time-varying amplitude. This sum is substituted either into the Euler equations (Manasseh Reference Manasseh1996) or into the order-above-leading order in an asymptotic expansion (Lagrange et al. Reference Lagrange, Meunier, Nadal and Eloy2011). An energy inner product exploits orthogonality of Kelvin eigenmodes to isolate evolution equations for the amplitude of a given mode.
Since Kelvin modes are sinusoidal in the axial and azimuthal directions and sinusoidal in time, the inner-product integrals of the axial and azimuthal factors reduce to products of Dirac delta functions, giving the triad conditions
$$\begin{eqnarray}n_{F}=|\!\pm n_{1}\pm n_{2}|,\quad m_{F}=|\!\pm m_{1}\pm m_{2}|\quad \text{and}\quad {\it\omega}_{F}=|\!\pm {\it\omega}_{1}\pm {\it\omega}_{2}|,\end{eqnarray}$$
where
$n$
is the number of axial half-wavelengths,
$m$
is the azimuthal wavenumber and
${\it\omega}$
is the dimensionless temporal frequency. Subscripts 1 and 2 denote the two parasitic modes nonlinearly interacting with the forced mode, denoted by subscript
$F$
. For a Kelvin mode triadic resonance to occur in a finite precessing cylinder, the modes must satisfy the dispersion relations (2.2) in addition to the triad conditions (2.3).
Lagrange et al. (Reference Lagrange, Eloy, Nadal and Meunier2008) first showed that it is possible to find a triadic-resonance instability of Kelvin modes provided that
${\it\Gamma}$
and
$Po$
are carefully tuned, the latter requirement due to the frequency constraints implied by the final relationship in (2.3). This resonance, for the aspect ratio
${\it\Gamma}=1.62$
they used, is depicted in figure 1(b), where the dispersion relationships (2.2a
) in the gimbal frame of reference are shown for parasitic modes with
$m_{1}=5$
(blue lines) and
$m_{2}=6$
(red lines), with thick lines showing their first radial branch (i.e.
$l=1$
). In the cylinder frame of reference, all solid lines would start at the origin, and the upper (lower) branches would have positive (negative) frequencies. However, in the gimbal frame, solid lines are translated vertically by
$-m_{1,2}$
. One parasitic mode is also translated horizontally by
$k_{F}=n_{F}{\rm\pi}/{\it\Gamma}$
. This ensures that any crossing of the two parasitic modes satisfies the resonance condition, i.e. their frequencies are equal, and their axial wavenumbers add up to
$n_{F}$
according to (2.3). Vertical dashed lines are spaced by
$n_{F}$
and show axial wavenumbers for which a Kelvin mode fits inside the cylinder, thus satisfying (2.2b
). If a crossing falls on such a vertical line, a tuned resonant triad of Kelvin modes exists (the black circle in figure 1
b, where
${\it\omega}_{1,2}=5.325$
).
Initial analysis and experiments (Lagrange et al.
Reference Lagrange, Eloy, Nadal and Meunier2008) focused on the resonance shown in figure 1(b), with
$m_{1}=5$
and
$m_{2}=6$
. The range of resonances was later expanded, and it was shown theoretically that this combination of azimuthal wavenumbers is the easiest to excite for
${\it\Gamma}\gtrsim 1.3$
(Lagrange et al.
Reference Lagrange, Meunier, Nadal and Eloy2011, figure 9).
2.4. Weakly nonlinear stability model
By deriving amplitude evolution equations in an asymptotic framework (Lagrange et al.
Reference Lagrange, Meunier, Nadal and Eloy2011), the linear stability of the forced mode with respect to the parasitic modes can be assessed by taking the time dependence to be of form
$\exp ({\it\sigma}t)$
, leading to
$$\begin{eqnarray}{\it\Omega}^{-2}[{\it\sigma}+{\it\Omega}{\it\beta}_{1}][{\it\sigma}+{\it\Omega}{\it\beta}_{2}]=|{\it\varepsilon}|^{2}C_{1}C_{2},\end{eqnarray}$$
where
${\it\beta}_{1,2}$
account for viscous and detuning effects on the parasitic modes,
${\it\varepsilon}$
represents the magnitude of the forced mode and
$C_{1,2}$
account for the nonlinear couplings between the parasitic modes; they are given in detail by the right-hand sides of (4.14), (3.12) and (B1,2) respectively in Lagrange et al. (Reference Lagrange, Meunier, Nadal and Eloy2011). The real part of
${\it\sigma}$
gives the initial growth rates of various pairs of candidate parasitic modes that may participate in a triadic instability of the forced mode.
3. Numerical method
A nodal spectral element–Fourier direct numerical simulation (DNS) code was used to solve (2.1) in a reference frame rotating at angular velocity
${\it\bf\Omega}$
using cylindrical coordinates
$(r,{\it\phi},z)$
. The meshes are time invariant, advection and frame acceleration terms were evaluated pseudo-spectrally, and time integration was second-order semi-implicit. Blackburn & Sherwin (Reference Blackburn and Sherwin2004) provide details regarding the treatment of the axial coordinate singularity, the convergence properties of the method and the time integration scheme.
The initial state is solid-body rotation and the tilt-over of the cylinder occurs smoothly over one-tenth of a cylinder rotation period, mimicking the experimental procedure in Lagrange et al. (Reference Lagrange, Eloy, Nadal and Meunier2008). This is much shorter than the time required for equilibration through nonlinear and viscous interactions, and one may expect that the details of the tilt-over motion are not dynamically significant in the longer term. The components of
${\it\bf\Omega}$
may be chosen in either the gimbal frame of reference (where the cylinder walls move with respect to the reference frame, and where
$\text{d}{\it\bf\Omega}/\text{d}t\rightarrow 0$
as
${\it\alpha}\rightarrow \text{const.}$
) or the cylinder frame of reference (where the walls are fixed and
$\text{d}{\it\bf\Omega}/\text{d}t\neq 0$
always). Both implementations give the same flow dynamics, modulo a solid-body rotation.
Our baseline case had 192 spectral elements at polynomial degree
$N_{P}=6$
in each of the
$(r,z)$
directions and 64 azimuthal Fourier modes. Using 2048 time steps per cylinder revolution, the run-time to integrate over 1000 time units with 16 processors was approximately 20 h. A grid resolution study showed that the growth rates of the Fourier mode energy reduce by 2 % (0.1 %) when using half (twice) the resolution in all dimensions. Doubling the temporal resolution reduced the growth rates by 0.1 %.
4. Results
In the following, azimuthal Fourier modal energies
$E_{m}$
represent contributions to the domain-integral kinetic energy per unit mass, as measured in the cylinder frame of reference (i.e.
$E_{0}$
contains no contribution from solid-body rotation):
$$\begin{eqnarray}E_{m}=\frac{1}{2A}\int _{A}\widehat{\boldsymbol{u}}_{m}\boldsymbol{\cdot }\widehat{\boldsymbol{u}}_{m}^{\ast }r\,\text{d}A,\end{eqnarray}$$
where
$A={\it\Gamma}R^{2}$
is the area of the meridional semi-plane and
$\widehat{\boldsymbol{u}}_{m}$
is azimuthal mode
$m$
of the Fourier transform of the velocity field in the cylinder frame of reference.
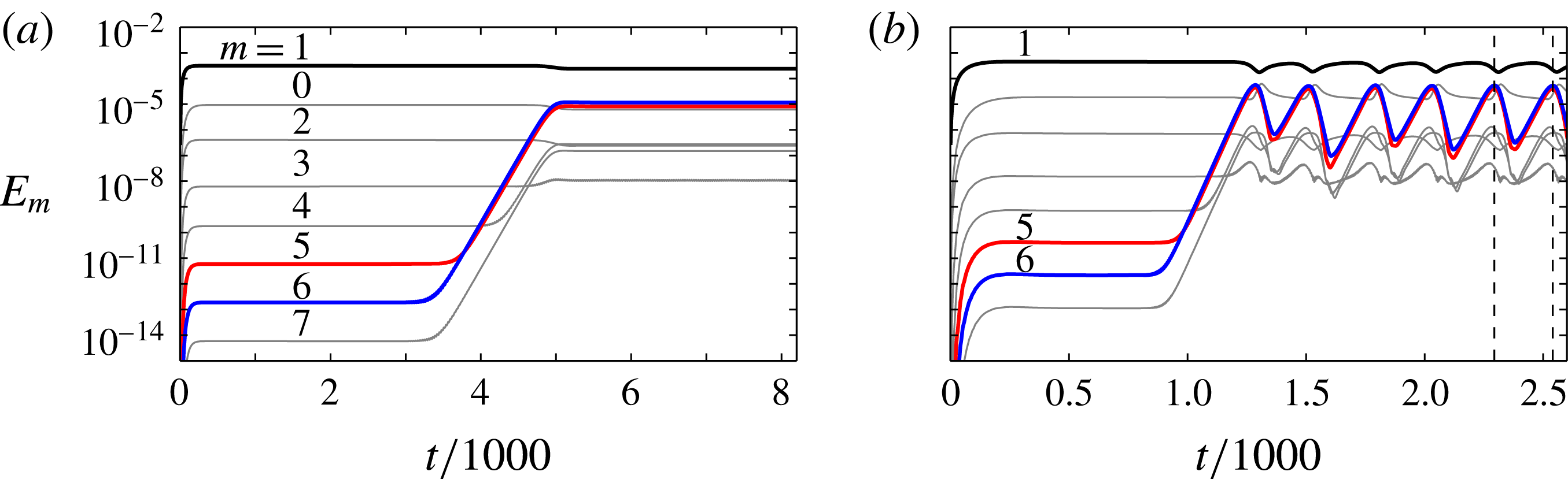
Figure 2. Time series of modal kinetic energies in the first eight azimuthal Fourier modes for
${\it\Gamma}=1.62$
,
${\it\alpha}=1^{\circ }$
and
$Po=-0.153$
with (a)
$Re=5310$
, showing triadic resonance of modes 1, 5 and 6 saturating to a periodic limit cycle state, and (b)
$Re=7670$
, showing the quasi-periodic saturated state with a low-frequency oscillation of period
$T_{DNS}\approx 250$
. An animation of the recurrent long-time-scale behaviour over the interval indicated in (b) is provided as supplementary movie 1, which shows isosurfaces of helicity in physical space.
4.1. Modal dynamics and structure of a baseline case
The parameters of the initial DNS match those of Lagrange et al. (Reference Lagrange, Eloy, Nadal and Meunier2008):
${\it\Gamma}=1.62$
,
${\it\alpha}=1^{\circ }$
,
$Po=-0.153$
and various
$Re$
. It should be noted that they used
${\it\Omega}$
rather than
${\it\Omega}_{1}$
to define
$Re$
; here we have converted their values of
$Re={\it\Omega}R^{2}/{\it\nu}$
to our definition,
$Re={\it\Omega}_{1}R^{2}/{\it\nu}$
. These frequencies and aspect ratio match the case shown in figure 1(b), and so theory predicts a resonant triad with
$(n_{F}=1,l_{F}=1,m_{F}=1)$
as the forced mode and
$-(1,1,5)$
and
$(2,1,6)$
as the parasitic modes.
Figure 2 shows the evolution of Fourier modal energies for
$Re=5310$
and
$Re=7670$
. For both
$Re$
, an energy plateau is rapidly established in
$m=1$
, and energies in all higher Fourier modes represent harmonics of the flow in
$m=1$
. This basic state is directly forced by the precession. As indicated by the level of
$E_{0}$
(lower than
$E_{1}$
by a factor of approximately 30), steady streaming flow also forms a significant component of the basic state, a point we will revisit in § 5. After a time of order
$Re$
, exponential growth above the levels of the basic state is observed for Fourier modes
$m=5$
and 6, and this growth nonlinearly feeds through to other Fourier modes. Following a period of exponential growth during which there is no perceptible decrease in energy at
$m=1$
, the energy in the parasitic modes saturates with an observable decrease in
$E_{1}$
. For
$Re=5310$
(figure 2
a), the saturated state has modal energies with (unobservable) small-amplitude periodic oscillations. The associated frequency
$5.328$
is very close to that predicted by the triadic resonance shown in figure 1(b),
${\it\omega}_{1,2}\approx 5.325$
. At
$Re=7670$
(figure 2
b), the saturated flow settles to a quasi-periodic state with both the
${\it\omega}_{1,2}=5.328$
oscillation and a well-defined low-frequency oscillation of period
$T_{DNS}\approx 250$
. Theory developed in Lagrange et al. (Reference Lagrange, Meunier, Nadal and Eloy2011) predicts that at the larger Reynolds number there would be a low-frequency oscillation with period
$T=295$
. In experiments (Lagrange et al.
Reference Lagrange, Eloy, Nadal and Meunier2008), this period was determined to be in the range 243–342.
An examination of the spatial structure at the cylinder mid-height,
$z=0$
, at a time when three-dimensional features were most evident, was presented by Lagrange et al. (Reference Lagrange, Eloy, Nadal and Meunier2008). Their data were obtained via particle image velocimetry (PIV), using a laser sheet in a plane normal to the turntable axis at
$z=0$
. The background solid-body rotation was subtracted from their data prior to post-processing to obtain the relative axial vorticity, reproduced in figure 3(a). Due to practical restrictions, they were unable to resolve the boundary layer structure. The relative axial vorticity from DNS at
$z=0$
and at
$t=2140$
(i.e. corresponding to the energy peaks for
$m=5$
and 6 in figure 2
b) is shown in figure 3(b). At this axial location, both the experiment and DNS show significant structure in the Fourier mode
$m=6$
. This matches the predictions of the resonant triad theory: as outlined in § 2.3, theory predicts parasitic modes
$-(1,1,5)$
and
$(2,1,6)$
, and at this axial location, relative axial vorticity should only appear for the modes with even axial wavenumbers
$n$
. For comparison, the axial vorticity for the
$(2,1,6)$
Kelvin mode at
$z=0$
is shown in figure 3(c).
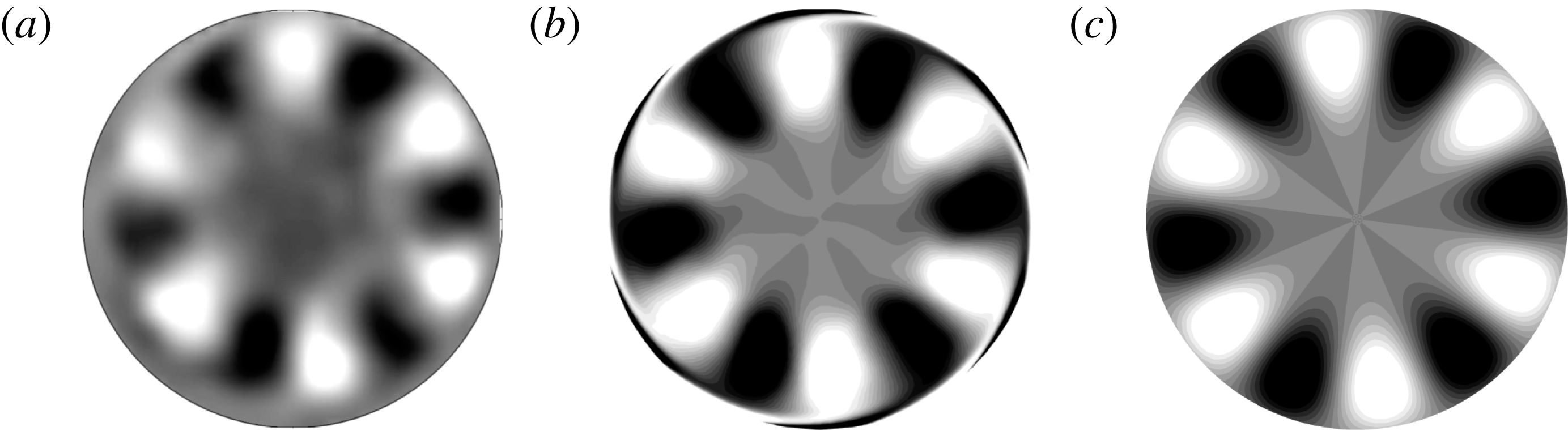
Figure 3. Contours of relative axial vorticity at
$z=0$
for
${\it\Gamma}=1.62$
,
${\it\alpha}=1^{\circ }$
,
$Po=-0.153$
and
$Re=7670$
from (a) PIV measurements (Lagrange et al.
Reference Lagrange, Eloy, Nadal and Meunier2008), (b) DNS at
$t=2140$
and (c) the Kelvin mode
$(2,1,6)$
.
Direct numerical simulation allows examination of axial structure not easily obtained in physical experiments. Figure 4(a,b) shows the axial velocity of the Fourier modes
$m=5$
and 6 for the case in figure 3(b). The axial shapes are dominated by
$n=1$
for
$m=5$
and
$n=2$
for
$m=6$
, in accord with the resonant triad prediction of parasitic modes
$-(1,1,5)$
and
$(2,1,6)$
(§ 2.4):
$|n_{2}-n_{1}|=n_{F}=1$
. The axial mode shapes of the corresponding Kelvin modes are similar, as shown in figure 4(c,d).
Figure 4. Contours of the axial velocity for the same parameters as in figure 3, at the meridional semi-plane of maximum amplitude, showing (a) the Fourier component
$m=5$
and (b) the Fourier component
$m=6$
, both from DNS; (c) the Kelvin mode
$-(1,1,5)$
and (d) the Kelvin mode
$(2,1,6)$
.
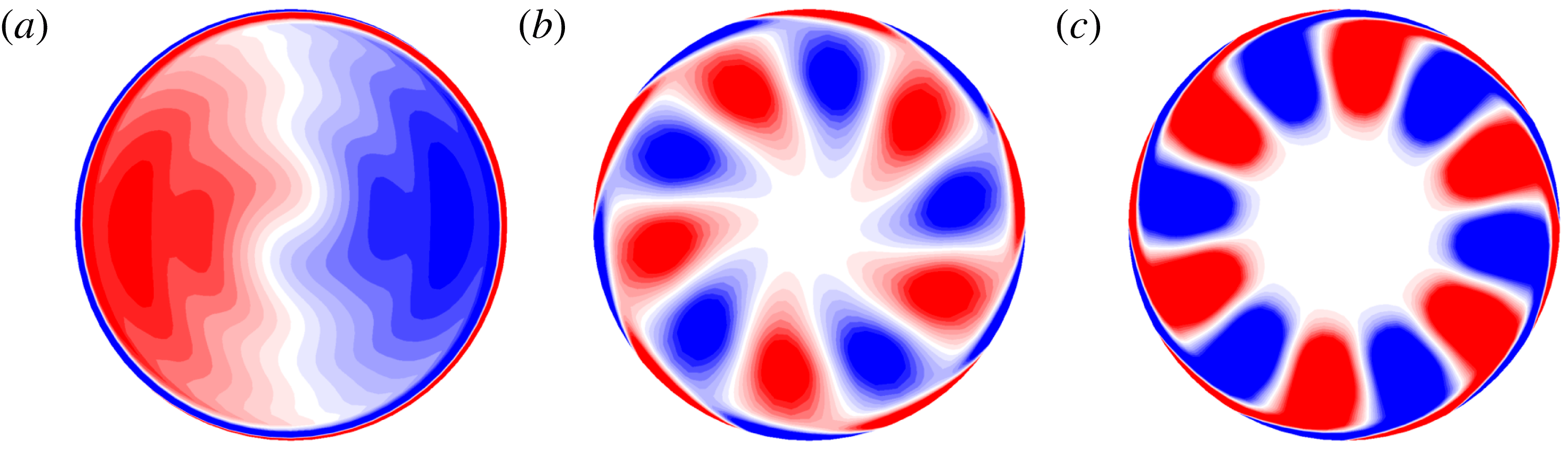
Figure 5. Contours of axial vorticity for parameters corresponding to figure 3, showing (a) the Fourier component
$m=1$
at
$z=-0.25{\it\Gamma}$
, (b) the Fourier component
$m=5$
at
$z=-0.25{\it\Gamma}$
and (c) the Fourier component
$m=6$
at
$z=0$
. In the cylinder frame of reference, the mode
$m=1$
rotates at the precession frequency while the parasitic modes
$m=5$
and
$m=6$
counter-rotate, whereas in the gimbal frame of reference the mode
$m=1$
is fixed while modes
$m=5$
and 6 co-rotate (see supplementary movies 2 and 3).
Theory (§§ 2.2 and 2.3, figure 1
b) predicts that the two parasitic modes involved in the present resonant triad should counter-rotate in the cylinder frame of reference. Animations of vorticity components filtered to azimuthal wavenumbers
$m=1$
, 5 and 6 have been prepared as supplementary movies shown in http://dx.doi.org/10.1017/jfm.2015.377, and show the anticipated behaviour. One frame of such an animation is shown in figure 5. Animations in the cylinder frame of reference clearly show the
$-(1,1,5)$
mode rotating in the opposite sense to the
$(2,1,6)$
mode, as expected, such that their product rotates at the same speed and sense as the driving
$(1,1,1)$
mode, exactly as required for a resonant triad.
If energies are computed from the projection of velocity fields onto Kelvin modes instead of Fourier modes, the temporal behaviour and energy levels of the leading Kelvin modes with
$m>0$
are generally similar to what may be observed in figure 2. For example, energies in
$m=5$
and
$m=6$
are dominated by contributions from the
$-(1,1,5)$
and
$(2,1,6)$
Kelvin modes. However, there is rather less energy in the
$(1,1,1)$
Kelvin mode than in the Fourier mode
$m=1$
, as might be anticipated from the axial vorticity observed in figure 5(a), which has a richer structure than that of the
$(1,1,1)$
Kelvin mode.
4.2. Modal dynamics and growth rates for other aspect ratios and at small
${\it\alpha}$
Further DNS were carried out for
${\it\Gamma}=1.620$
(as in § 4.1) and four other values of
${\it\Gamma}$
, with
$Po$
set to excite the forced
$(1,1,1)$
mode at its first resonance, and fixed
${\it\Omega}R^{2}/{\it\nu}=6500$
, for variable
${\it\alpha}$
. Two aspect ratios (
${\it\Gamma}=3.600$
and 0.758) were chosen to provide exact triads according to the dispersion relation analysis, while the other two (
${\it\Gamma}=2.667$
and 0.923) were not so tuned. Triadic-resonance instability, similar to that shown in figure 2, was observed for all cases when the nutation angle
${\it\alpha}$
was sufficiently large. In figure 6, the growth rates of the triadic resonances extracted from the DNS during the exponential growth phase are compared with those predicted by (2.4). It is clear that the growth rates from the DNS match the theoretical values well, particularly close to the stability threshold in
${\it\alpha}$
. Away from the threshold, theory continues to capture the trend.
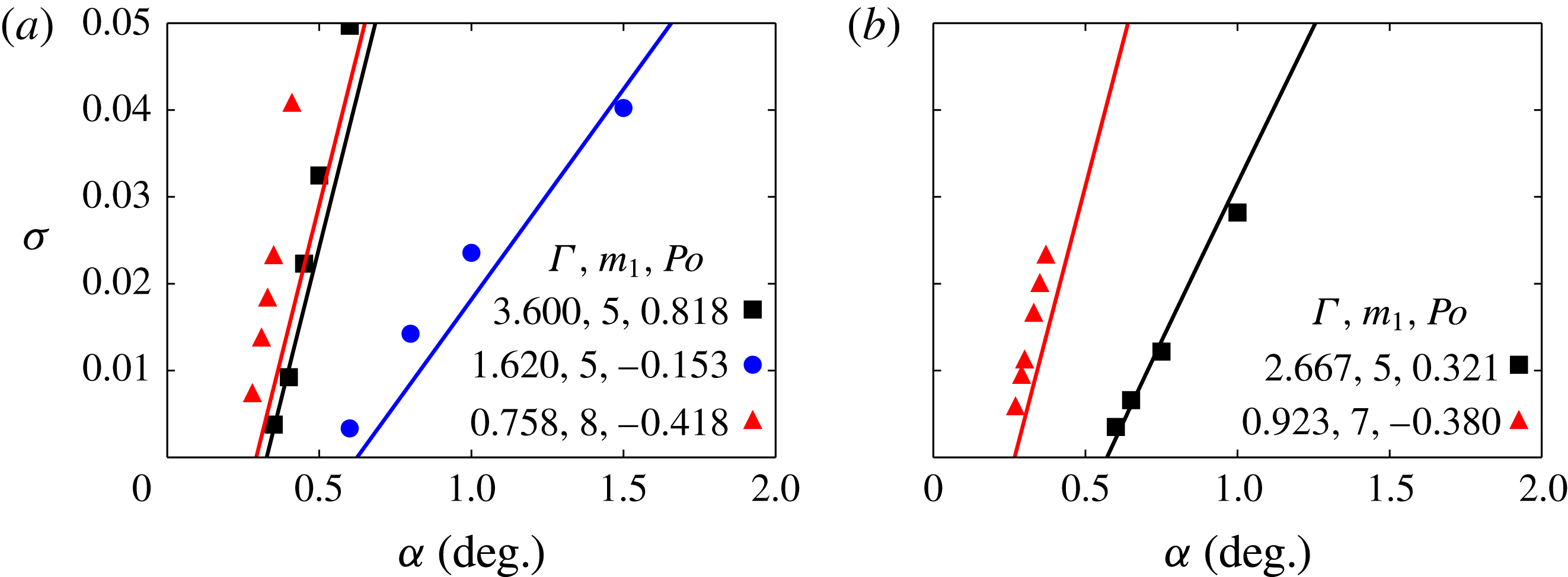
Figure 6. Growth rates for (a) tuned and (b) untuned aspect ratios
${\it\Gamma}$
obtained from theory ((2.4), lines) and DNS (symbols), with
${\it\alpha}$
as a parameter at
${\it\Omega}R^{2}/{\it\nu}=6500$
.
For
${\it\Gamma}=2.667$
and
$Po=0.321$
(investigated at
${\it\alpha}=1^{\circ }$
in Manasseh Reference Manasseh1992, for which the instabilities were described as ‘Type B and C collapses’), a dispersion relation analysis equivalent to figure 1(b) shows that the triad
$(1,1,1)$
,
$-(1,1,5)$
,
$(2,1,6)$
is the closest to an exact resonance, and this set is found in the modal dynamics. Visualizations equivalent to figure 3 also show the
$m=6$
mode, as expected. Furthermore, at
${\it\alpha}=1^{\circ }$
, this case exhibits long-time-scale quasi-periodic behaviour (cf. figure 2
b), suggestive of a Type C resonant collapse. For the other untuned aspect ratio,
${\it\Gamma}=0.923$
at
${\it\alpha}=0.27^{\circ }$
and
$Po=-0.380$
, the DNS visualization shows
$m=8$
. This case is between two exact resonances (
${\it\Gamma}=1.09$
for modes
$m=6$
and 7 and
${\it\Gamma}=0.886$
for modes
$m=7$
and 8, cf. table 1 in Lagrange et al.
Reference Lagrange, Meunier, Nadal and Eloy2011). The dominant modes are
$m=1$
, 7 and 8, suggesting a triadic resonance despite this untuned aspect ratio. We have found that the same is true for the untuned aspect ratio
${\it\Gamma}=1.297$
,
${\it\alpha}=0.36^{\circ }$
and
$Po=-0.270$
(not represented in figure 6), where we expect, and observe,
$m=6$
and 7.
4.3. Resonant triad behaviour for a ‘spherical-like’ aspect ratio and
${\it\alpha}=45^{\circ }$
In searching for a triadic resonance at
${\it\alpha}=45^{\circ }$
for an aspect ratio of
${\it\Gamma}=H/R=1.990$
(i.e.
$H/(2R)=1.005$
) and an Ekman number of
${\it\nu}/{\it\Omega}_{1}H^{2}=10^{-4}$
, which corresponds to
$Re={\it\Omega}_{1}R^{2}/{\it\nu}=2482$
, Kong et al. (Reference Kong, Cui, Liao and Zhang2015) varied
$Po$
over a range
$Po\in [0.001,0.1]$
. This aspect ratio has the resonance of the
$(1,1,1)$
Kelvin mode at vanishing Poincaré number (or at
${\it\alpha}\rightarrow 90^{\circ }$
), as in the case of a sphere (hence the classification ‘spherical-like’). They concluded that despite a large effort, the forced
$m=1$
flow was not unstable with respect to a triadic resonance. Their
$Po\leqslant 0.01$
cases had the forced
$m=1$
state saturate, whereas their
$Po=0.1$
case became nonlinearly complicated through sidewall interactions. They expected the flow to equilibrate in a spin-up time of order
$Re^{1/2}$
. However, near onset an instability may take much longer to be manifested. At
$Re=2482$
and for
$Po=0.01$
, theory predicts a slightly positive growth rate of
${\it\sigma}=1.90\times 10^{-4}$
for a triadic resonance involving the
$(1,1,1)$
,
$-(1,1,5)$
and
$(2,1,6)$
Kelvin modes, suggesting that in DNS it might take approximately
$6\times 10^{4}$
time units (approximately 25 viscous times) for the disturbance energy to grow from the double precision noise level,
$O(10^{-30})$
, to significant values of
$O(10^{-6})$
.
We re-examined this case (
${\it\Gamma}=1.990$
,
$Re=2482$
,
$Po=0.01$
,
${\it\alpha}=45^{\circ }$
), evolving our DNS for considerably longer than Kong et al. (Reference Kong, Cui, Liao and Zhang2015).
Figure 7(a) shows the time series of the leading modal kinetic energies; they appear to have quickly saturated to the forced (
$m=1$
) flow, with the streaming (
$m=0$
) component and the harmonics of the
$m=1$
component essentially constant after a spin-up time of
$t\approx 140$
. More than two viscous times later, the modes
$m=5$
and 6 grow at
${\it\sigma}=2.04\times 10^{-3}$
until they saturate, accompanied by a small decline in
$E_{1}$
(not observable in the figure). It is clear that at this
$Re$
, the system is very close to the triad-resonance-induced instability of the forced
$m=1$
flow.
For larger
$Re=3475$
, theory predicts instability with a growth rate of
${\it\sigma}=2.85\times 10^{-2}$
. Direct numerical simulation at this
$Re$
(see figure 7
b) shows that the parasitic modes now grow at a faster rate and become visible earlier, by
$t\sim 600$
, but this is still an order of magnitude longer than the viscous spin-up time
$Re^{1/2}=59$
. It should be noted that the initial transient from solid-body rotation with
${\it\alpha}=0$
at
$t=0$
does spin up to the
$m=1$
forced flow on the
$Re^{1/2}$
time scale, but the subsequent instability of the forced flow is manifested on the slow time scale. The
$m=5$
and 6 modes become energetic and quasi-periodic, and oscillate with a long-time-scale period of
$133.5\pm 4$
. At this larger Reynolds number, the theoretical and observed growth rates differ by only 6.6 %, clearly showing that the theory incorporating detuning and viscous effects works very well in predicting the correct dynamics.
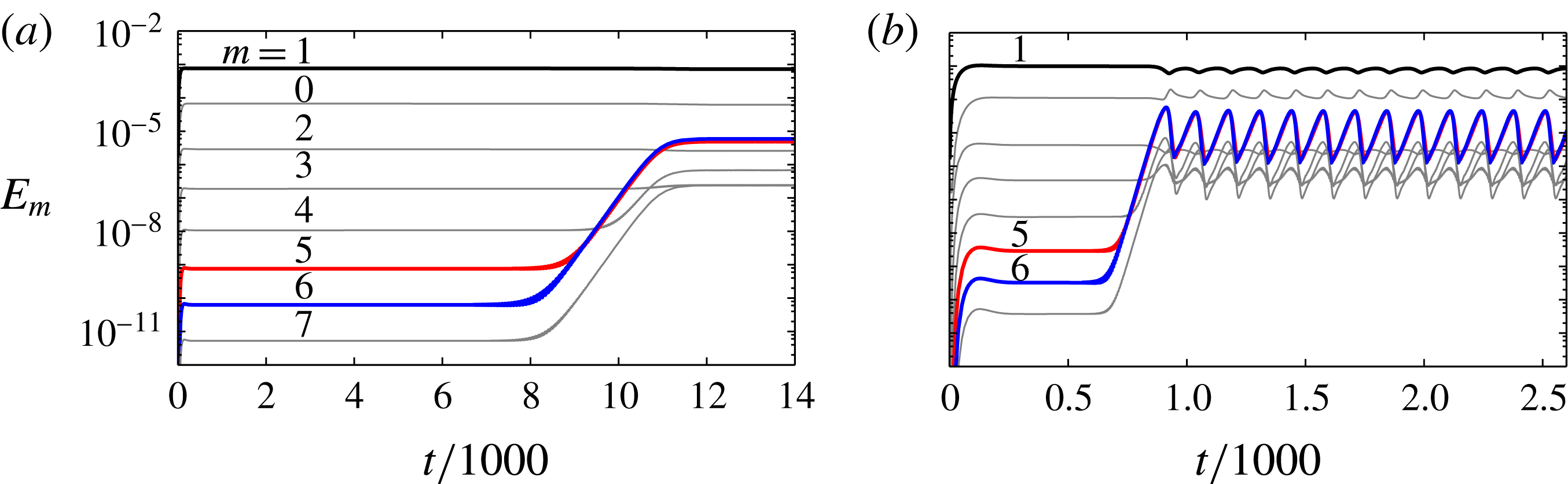
Figure 7. Time series of modal kinetic energies in the first eight azimuthal Fourier modes for
${\it\Gamma}=1.990$
,
${\it\alpha}=45^{\circ }$
and
$Po=0.01$
, with (a)
$Re=2482$
, as considered by Kong et al. (Reference Kong, Cui, Liao and Zhang2015), and (b)
$Re=3475$
.
5. Conclusions
Our study of triadic-resonance instability in precessing cylinders with small nutation angle suggests that the reduced weakly nonlinear model based on Kelvin modes presented by Lagrange et al. (Reference Lagrange, Meunier, Nadal and Eloy2011) works very well for a precisely tuned case, providing good agreement with observed rotational frequencies, modal structure, onset of instability, growth rates, and, for quasi-periodic saturated states, a reasonable estimate of the long-cycle oscillation period. The dispersion relation analysis identifies potential triadic resonances, while the stability analysis predicts the growth rates of the parasitic modes. The methodology is not restricted to precisely tuned cases. In the absence of exact triadic resonance, detuning terms are included in the model (Lagrange et al. Reference Lagrange, Meunier, Nadal and Eloy2011). Detuning decreases the inviscid growth rates, and for growth to occur the amplitude of the forced Kelvin mode has to be large enough in order to compensate the viscous damping.
The details of the model (Lagrange et al.
Reference Lagrange, Meunier, Nadal and Eloy2011) incorporate estimates of the streaming (
$m=0$
) flows associated with the parasitic Kelvin modes as parameters for nonlinear coupling. However, our results clearly show that the largest streaming flow present in the system is directly coupled to the precessionally driven flow, since the energy in the axisymmetric flow component (
$E_{0}$
) becomes large as soon as the driven flow (
$E_{1}$
) is established. This may help to explain some of the small discrepancies between the growth rates predicted by the reduced model and those observed from DNS of the full Navier–Stokes equations.
We have simulated an additional case from the literature (Kong et al.
Reference Kong, Cui, Liao and Zhang2015), which has small Poincaré number but large nutation angle (
${\it\alpha}=45^{\circ }$
), as opposed to small angle and larger Poincaré number; either combination provides weak precessional forcing suitable for the triadic-resonance model. At the Reynolds number used by Kong et al., the model suggests marginally unstable behaviour, and DNS also indicates instability occurring through triadic resonance. A long time (of the order of several viscous time scales) elapses before the energy of the parasitic modes grows to an appreciable level.
Finally, the quasi-periodic saturated states predicted by the model and observed in the DNS are consistent with reported experiments (Manasseh Reference Manasseh1992, Reference Manasseh1994, Reference Manasseh1996; Lagrange et al. Reference Lagrange, Eloy, Nadal and Meunier2008; Meunier et al. Reference Meunier, Eloy, Lagrange and Nadal2008; Lagrange et al. Reference Lagrange, Meunier, Nadal and Eloy2011).
Acknowledgements
We are grateful for financial support provided by Australian Research Council Discovery grant DP130101744 and US National Science Foundation grant CBET-1336410, and for resources provided by the Australian National Computational Infrastructure (NCI).
Supplementary movies
Supplementary movies are available at http://dx.doi.org/10.1017/jfm.2015.377.
