Structure of the monopulse comparator

As shown in Fig. 1, the monopulse comparator consists of an interconnection of four 90°, 3 dB hybrid couplers along with four 90° phase shifters. A schematic of a monopulse comparator and signal designations at the eight ports and the interconnections are also indicated in Fig. 2. As shown, port 2 is considered as a phase reference. Cascading of two 90° phase shifters was used to achieve a 180° phase shift. Ports 1, 2, 3, and 4 are feeding inputs to the antenna and port 5 is the SUM channel, port 6 is the DELTA1 channel in the azimuth, port 7 is the DELTA2 channel in the elevation, and port 8 is the isolated channel.

Fig. 2. Schematic of a monopulse comparator with signal flow.

The broad-band phase shifter

The Schiffman phase shifter [Reference Schiffman5, Reference Quirarte and Starski6] is a broadband differential phase shifter where the desired phase shift is obtained as a subtraction of the phase response of a coupled section with that of an adjacent uncoupled C-shaped line named a reference line. Figure 3 shows the structure of a standard 90° Schiffman phase shifter. In this configuration, K denotes the ratio of the length of a uniform transmission line to that of the coupled line.

Fig. 3. Standard Schiffman 90° phase shifter (K = 3).

The standard Schiffman phase shifter is based on stripline technology, where the phase velocity of the odd and even modes, propagating along the coupled lines, are equal. While the phase velocities in the microstrip lines are unequal, indeed a limited coupling ratio will be loaded to microstrip coupled lines [Reference Guo, Zhang and Ong7]. This limitation shrinks the realizable frequency bandwidth. In [Reference Guo, Zhang and Ong7], a patterned ground plane is used to improve the bandwidth, while this idea in antenna array design leads to unwanted spurious radiation and high side lobe level.

To obtain a minimum phase deviation and return loss, we slightly changed the standard 90° Schiffman phase shifter as reported in [Reference Mohammadpour-Aghdam, Komjani, Vandenbosch and De Raedt8] and is shown in Fig. 4. In order to broaden the operating bandwidth, another coupled line beside the main coupled line has been used and by optimizing the initially obtained design parameters by a commercially available full wave simulator, we have obtained phase deviation of better than 1° and return loss better than 17 dB in the frequency range of 14.2–18.6 GHz. To obtain initial values for optimization, the equations of standard Schiffman phase shifter are used.

Fig. 4. Optimized structure of a modified Schiffman phase shifter.

The required phase shift of a standard Schiffman phase shifter, Δφ, was derived, as [Reference Quirarte and Starski6]:

(1)$$\Delta \varphi = k\theta - \cos ^{ - 1}\left( {\displaystyle{{\rho - {\tan} ^2\theta} \over {\rho + {\tan} ^2\theta}}} \right),$$

where θ is the electrical length of the coupled section and ρ is the even to odd mode characteristics impedance ratio. An expression for the maximum phase shift as a function of ρ is as below [Reference Quirarte and Starski6]:

(2)$$\Delta \varphi _{\max} = k\tan ^{ - 1}\sqrt {\displaystyle{{k\rho - 2\sqrt \rho} \over {2\sqrt \rho - k}}} - \cos ^{ - 1}\left( {\displaystyle{{\rho + 1 - k\sqrt \rho} \over {\rho - 1}}} \right).$$

Considering the above equations, we obtain a design curve which is shown in Fig. 5. For a Schiffman phase shifter with ±1 phase deviation, ρ should be equal to 2.47. Consequently, the even and odd impedances of the coupled line could be determined as $Z_{oe} = 100\sqrt {2.47} = 157.26\,\Omega $ and $Z_{0o} = 100/\sqrt {2.47} = 63.59\,$. To achieve such even and odd mode impedances and 90° phase shift, the width of coupled line (W), the spacing (S), and the length (L) are determined and are shown in Fig. 4 on Rogers-RO4003 substrate, having a thickness of 0.508 mm and dielectric constant of 3.55. The phase deviation of 90° phase shifter is shown in Fig. 6. As can be seen from this figure, a 90° phase shift with ±1° phase deviation has been obtained in the 15.5–19 GHz frequency range.

Fig. 5. Simulated design curve for impedance ratio, ρ, versus required phase deviation.

Fig. 6. Simulated result of an optimized phase shifter.

A hybrid coupler

The branch-line hybrid couplers are recognized directional couplers with a 3-dB coupling value. Typical branch-line couplers have narrow frequency bandwidth. An efficient method to increase the bandwidth is adding additional parts to the vertical sections of the coupler, as shown in Fig. 7. However because of limitation in the obtainable impedance range in microstrip lines, it is difficult to achieve more than four branch lines in hybrid couplers [Reference Muraguchi, Yukitake and Naito9]. To obtain better phase deviation, a half wavelength stub has been connected to the conventional four branch-line coupler as shown in Fig. 7. If the proposed coupler is assumed as a lossless reciprocal four-port coupler, then the square summation of return losses, couplings, and isolation shall be equal to 1 while for an ideal hybrid coupler, return loss and isolation is equal to zero. By the aid of a circuit modeling computer program, we defined a cost function and obtained initial values for the design parameters. Finally, the parameters are optimized in a full-wave simulator and are shown in Fig. 7.

Fig. 7. Optimized 90° hybrid coupler.

As this comparator is designed to be used in a monopulse antenna array where its feeding network ends with lines with a characteristic impedance of 100 Ω, all embodiments of the comparator were dimensioned for the connection line with a characteristic impedance of 100 Ω. Due to this fact, the hybrid coupler is designed for the connection line with a characteristic impedance of 100 Ω. The simulated S-parameters and phase deviation (phase(S ₂₁) − phase(S ₃₁)) of the proposed hybrid coupler are shown in Figs 8 and 9, respectively.

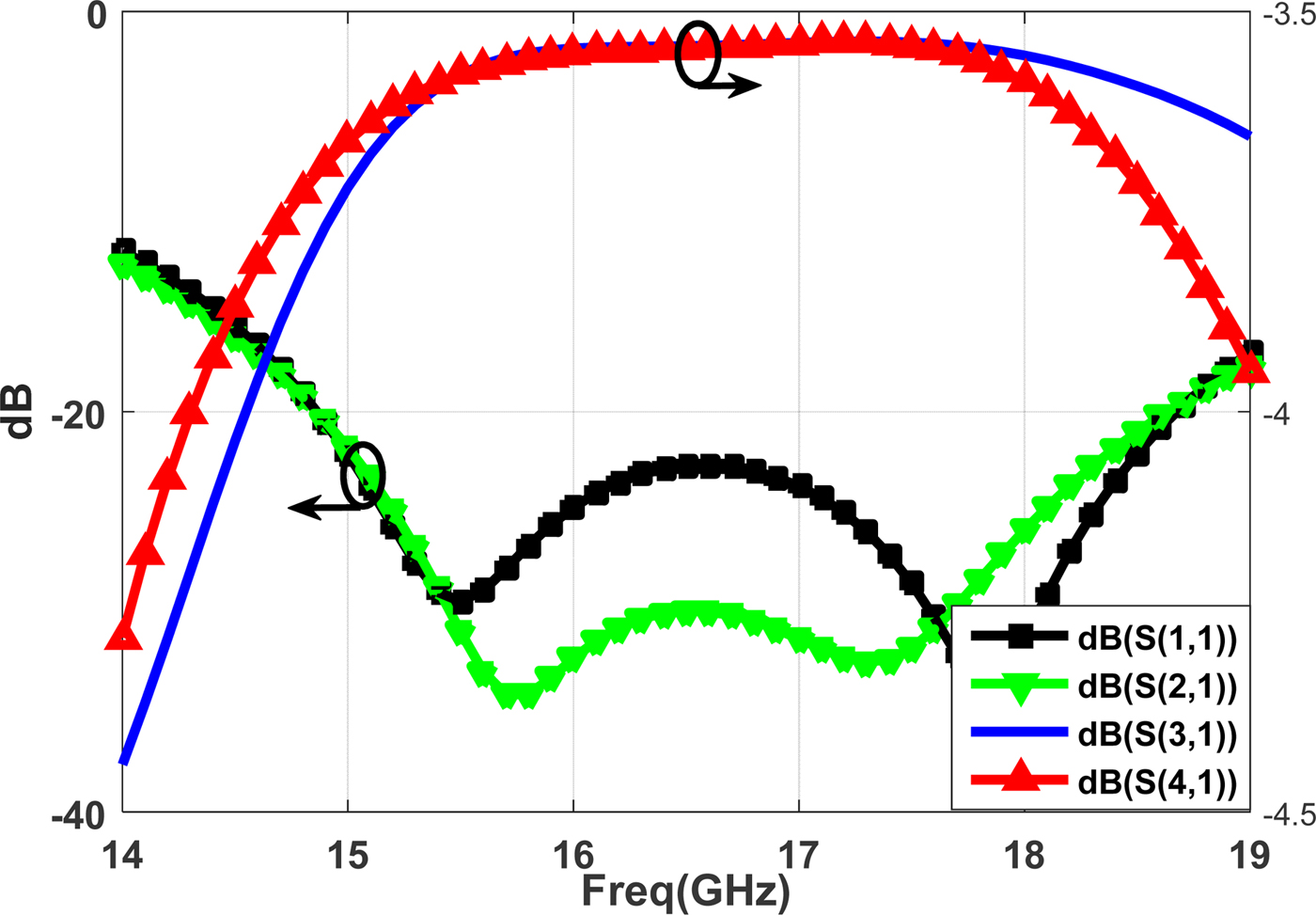
Fig. 8. Simulated S-parameters of an optimized 3-dB, 90° hybrid coupler.

Fig. 9. Simulated phase deviation of an optimized 3-dB, 90° hybrid coupler.

As shown, the amplitude imbalance of ±0.05 dB and phase deviation of ±1° was achieved in the desired pass band. In addition, the input port isolation is almost better than 30 dB.

Implementation and measurement results

The proposed monopulse comparator whose layout is shown in Fig. 2 has been implemented via single layer standard PCB technology. Figure 10 shows a photograph of the fabricated monopulse comparator. It consists of four identical hybrids directly interconnected using 100 Ω microstrip lines. In order to match the output of the comparator to 50 Ω SubMiniature version A connector, optimum Klopfenstein's tapering profile was used as in [Reference Aghdam, Faraji-Dana and Rashed-Mohassel10]. The overall circuit dimensions without a Klopfenstein matching taper are approximately 7 cm × 4 cm.

Fig. 10. Photograph of the fabricated monopulse comparator.

Overall, 16 two-port measurements were made using a vector network analyzer, without any circuit tuning. For each two-port measurement, the other six ports were terminated in 50 Ω load. Measured amplitude imbalance and phase deviation of four input ports to the antenna in the SUM port is shown in Figs 11 and 12, respectively. The summation of S-parameters is considered as the reference line.

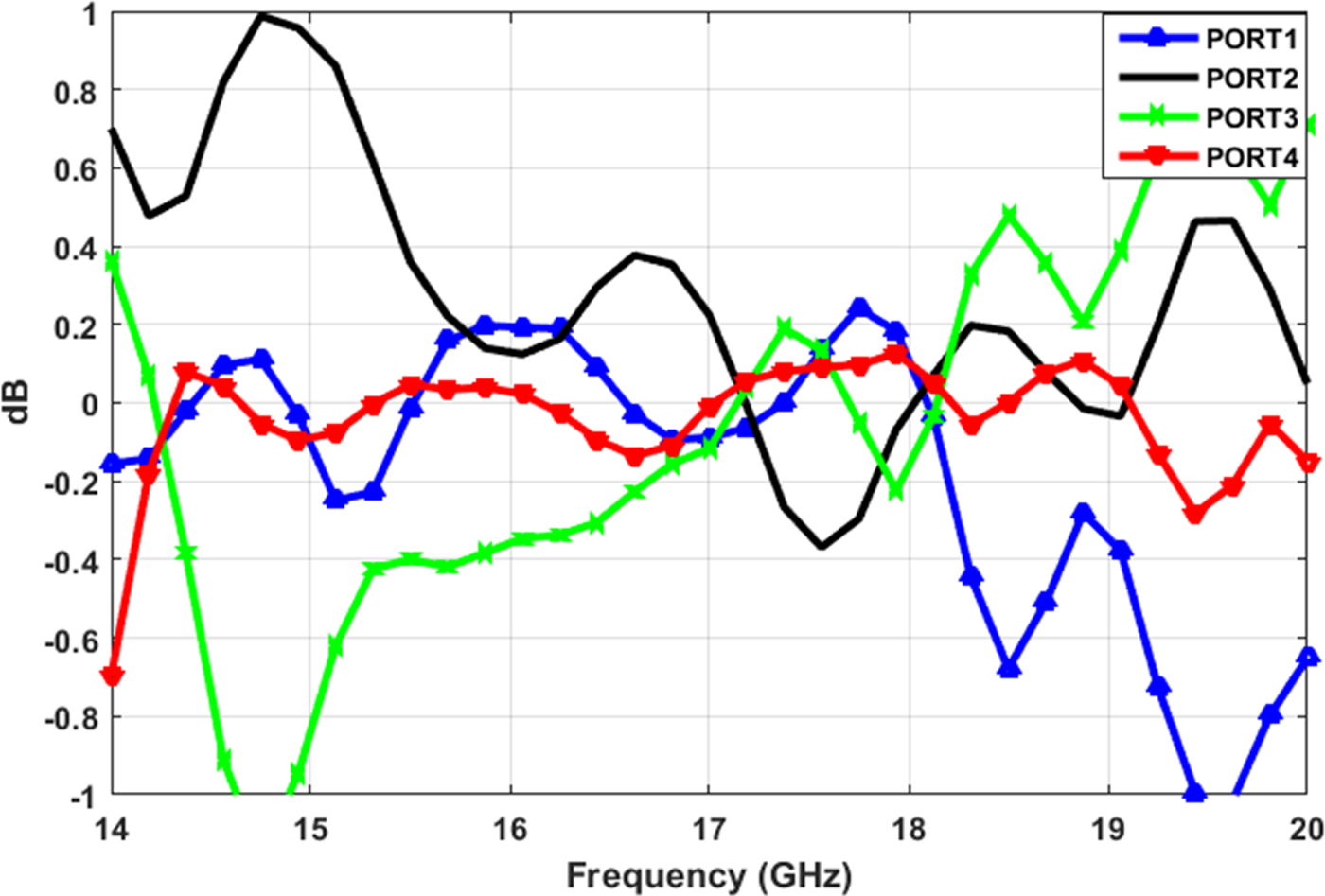
Fig. 11. Measured amplitude imbalance of antenna inputs in the SUM port.

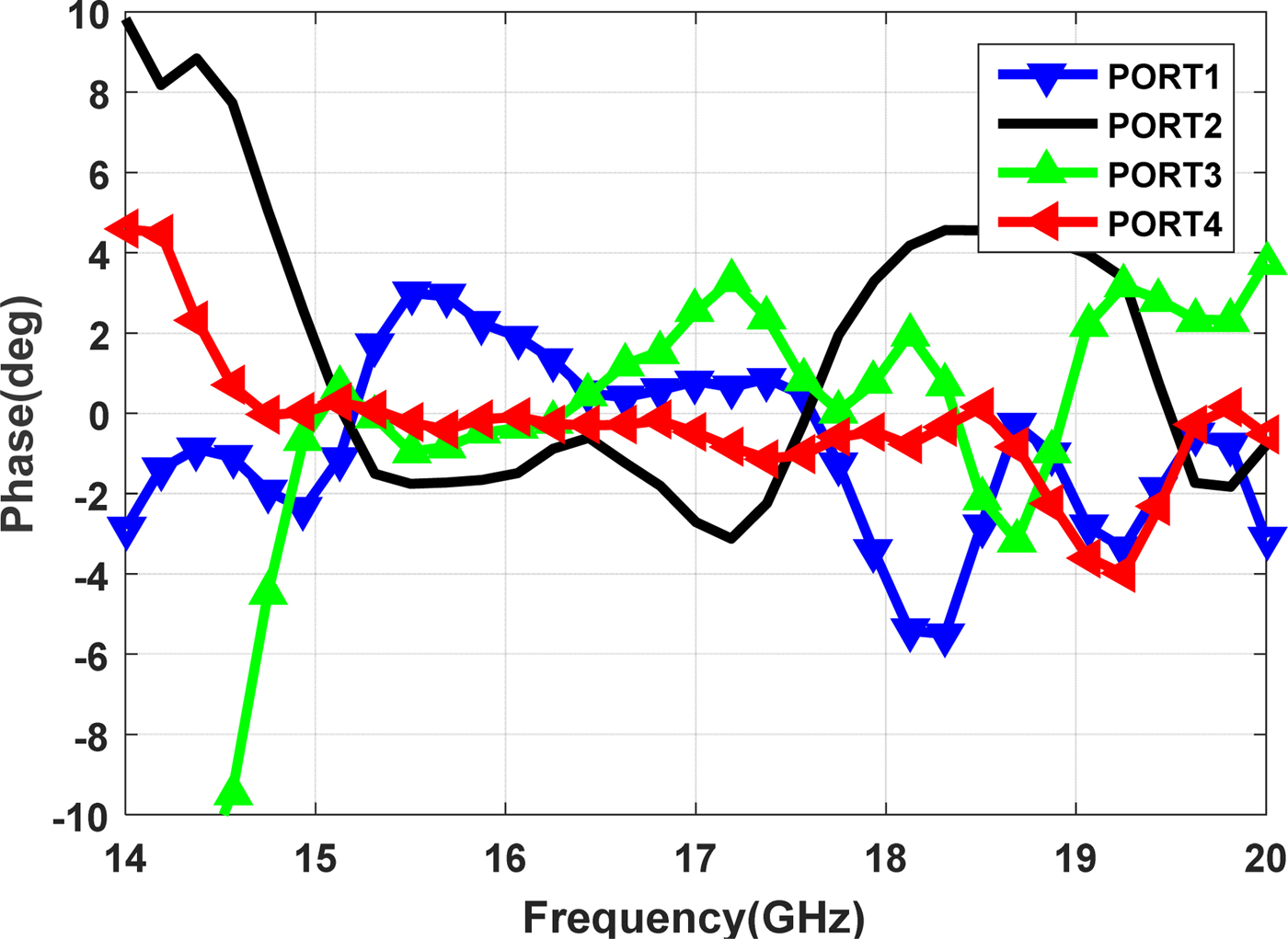
Fig. 12. Measured phase deviation of antenna inputs in the SUM port.

To evaluate the nulling performance of the monopulse comparator, S-parameter files were used. The null depth at both DELTA1 and DELTA2 could be calculated as [Reference Wang, Fang and Chen4]:

(3)$${\rm DELTA}1 = 20\log \left( {\displaystyle{{S_{61} + S_{62} + S_{63} + S_{64}} \over {S_{51} + S_{52} + S_{53} + S_{54}}}} \right).$$

In order to calculate the null depth for port 7, one can easily replace port 6 with 7 in Eq. (3), and in the SUM channel we have:

(4)$${\rm SUM} = 20\log \left( {{\textstyle{1 \over 4}}\left( {S_{51} + S_{52} + S_{53} + S_{54}} \right)} \right) + 6\,[{\rm dB}].$$

Figure 13 shows the measured results for the S-parameters of the SUM and DELTA channels. The SUM channel exhibits a wide band-pass response from 14 to 19 GHz. The insertion loss is within −1.5 to −2.5 dB in the SUM channel pass-band. The null depth of better than 30 dB was achieved in both DELTA1 and DELTA2 channels in the 14.8–18.2 GHz frequency range, which are in good agreement with simulation results. Figure 14 shows that the measured voltage standing wave ratio (VSWR) of all eight ports are better than 1.8:1 for all ports.

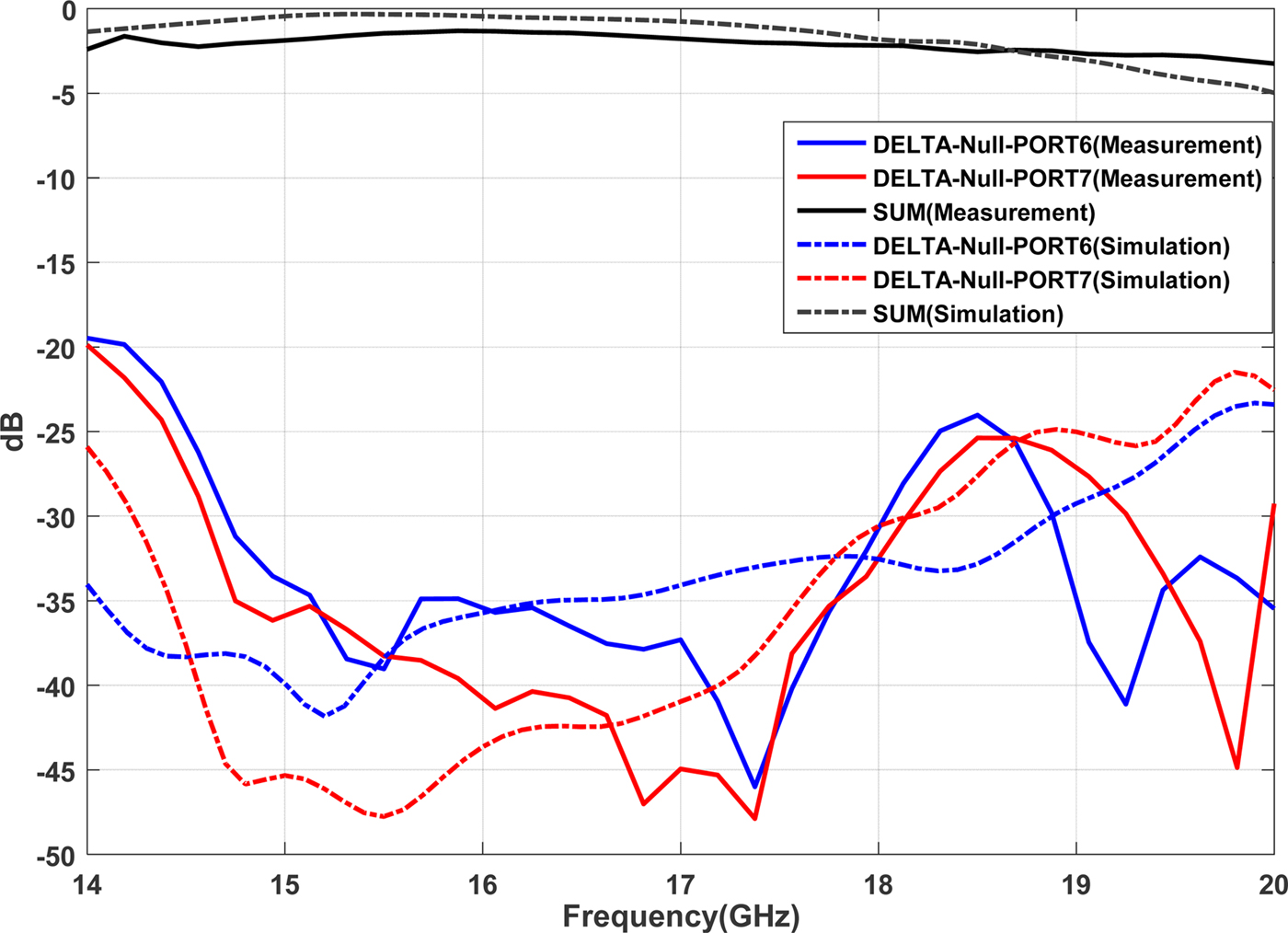
Fig. 13. S-parameters of the SUM and DELTA channels obtained.

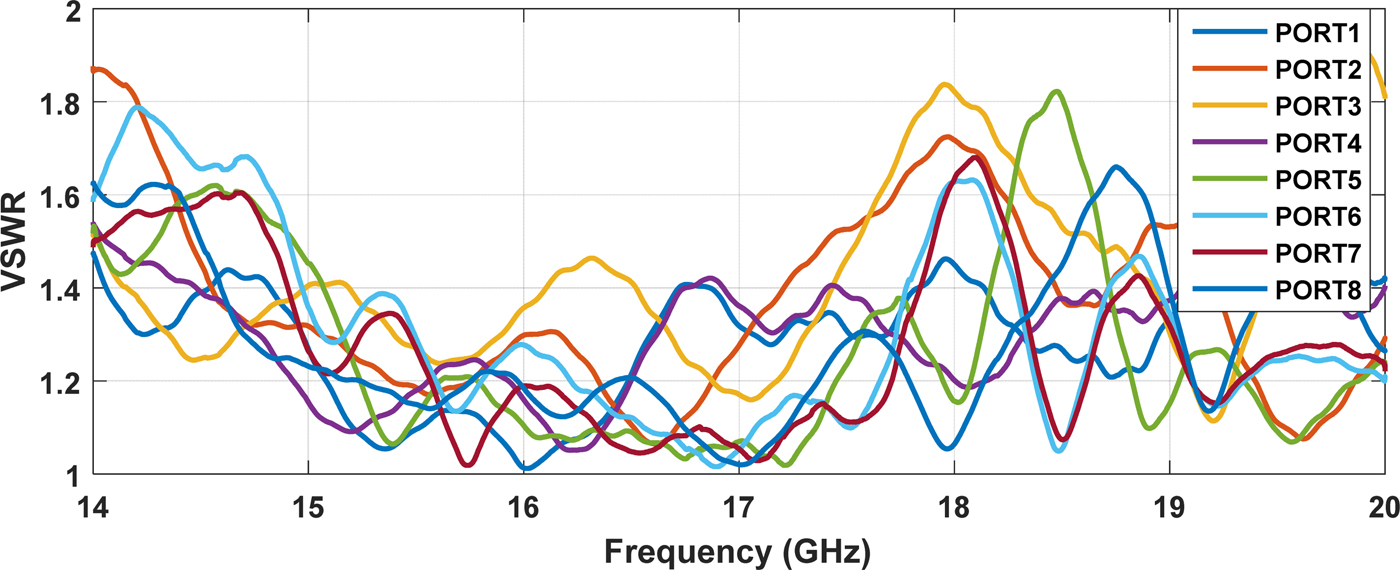
Fig. 14. VSWR of all ports.