In 1859, with Piedmont inspiring insurrections in Austria’s Italian provinces, the Austrians demanded the demobilization of the Piedmontese. A compromise proposal was floated according to which the Austrians would pull their troops back from the boarder in return for Piedmontese disarmament. The Austrians rejected the compromise, insisting on disarmament without an Austrian withdrawal. With only these two options on the table, the Austrian decision not to compromise conveyed information about the conditions under which Austria would go to war. Observing the Austrian stance communicated through private diplomatic channels, the British ambassador to Austria, Lord Loftus, concluded: ‘I have not the smallest hope that the Austrian Government will agree to any such [compromise]’.Footnote 1 Loftus may have drawn this inference because he believed that Austria, having made the threat, would not have wanted to be caught in a bluff, but this could be said of every threat and statesmen sometimes believe that threats lack credibility.Footnote 2 Although a range of factors certainly affected Loftus’ conclusion, he likely made the following simple inference: in demanding more, Austria had given up the opportunity to achieve a compromise solution that Austria knew Piedmont was much more likely to have conceded without fighting; therefore, Austria is resolved to fight for the more substantial demand. Through this mechanism, the scope of state demands commonly conveys information about resolve to adversaries in international politics.
Despite literature in international relations that argues the contrary, such simple inferences are often quite rational in diplomatic relations. In this article, I analyze a model similar to Fearon (Reference Fearon1995) in order to demonstrate that higher demands can increase perceptions of a state’s resolve to fight for more favorable outcomes when two conditions hold. First, both sides must share in the bargaining surplus from avoiding war. This tends to occur when goods are only partially divisible or when settling on a negotiated solution is the outcome of a bargaining process in which both sides take part, rather than a take-it-or-leave-it offer from one side. Second, higher demands must be less likely to be accepted even when the associated threat is credible. This condition can hold as a result of player preferences, such as in cases where, for the most resolved types on each side of a dispute, no negotiated solution exists that both prefer to conflict. The heart of the analysis below makes this simplifying assumption. I also show, however, that essentially similar signaling dynamics result when both sides know that there exists a negotiated solution that both prefer, but both also understand that bargaining dynamics are such that this mutually preferred solution may not be reached.
These two signaling conditions imply that less resolved signalers do not necessarily have incentive to imitate the signals sent by more resolved signalers. The first signaling condition ensures that a compromise has value to types that prefer the compromise to war. Since a credible, high demand will not necessarily be accepted according to the second condition, the two conditions imply that equilibria exist in which less resolved types must weigh an intuitive tradeoff: demanding more holds the possibility of receiving a larger concession from an adversary, but also implies a lower probability of receiving somewhat less without having to fight for it. Thus, when states do make large demands, they run a risk, and since states would not be willing to run this risk unless a large concession (rather than an intermediate compromise) were sufficiently important, these threats convey information.
The mechanism by which resolve is signaled to an adversary is therefore different from the mechanism in most other models in the literature. In other models, it is often a state’s willingness to risk war that conveys resolve. Here, the signaler decides whether to initiate a conflict and never directly risks conflict. The least resolved signaler is never forced to go to war but nevertheless may be unwilling to imitate the signaling behavior of more resolved signalers. The reason is that less resolved signalers are unwilling to risk getting less from the negotiation even if they will not choose war if the negotiations do not go their way.Footnote 3 Further, when one side believes the other is sufficiently unlikely to make a full concession, then demanding a full concession allows the other side to be certain that the demanding state will fight unless such a concession is offered. This contrasts with most cheap talk models in the literature in which demands never or rarely convey certain information about a state’s willingness to fight.
The models also allow us to understand when offers of compromise will be made even though they signal a measure of weakness by increasing an adversary’s perception that the compromising state would be willing to make an even greater concession.Footnote 4 This occurs only when an adversary is believed unlikely to accede to maximalist demands. In such cases, states that are unwilling to fight if they are offered no concession and those states that would choose not to fight if they are offered just a moderate concession both send the same signal while only states that are willing to fight unless they receive a large concession send that signal. The less resolved states accept the appearance of weakness because they understand that making a maximalist demand runs a substantial risk of receiving no concession at all whereas making a moderate demand implies a higher likelihood of a moderate concession. Thus, the model explains why states are sometimes willing to make offers that signal a form of weakness. If, on the other hand, an adversary is believed likely to make a maximalist concession, offers of compromise either will not be made, or if they are, they will not lead to the inference that the conceding state is more likely to be willing to make further concessions. The reason is that, in this context, states that are unwilling to fight if they are offered no concession nevertheless make maximalist demands; if offers of compromise are made at all, and they may not be, such offers will be made only by a state that is willing to fight unless it receives some measure of compromise. An adversary will be able to conclude following a moderate demand, therefore, that a moderate concession is required to avoid conflict.
Inferences based on the scope of threats
A debate continues over how and whether adversaries learn from diplomatic conversations that occur away from the public eye, and more generally, whether these encounters play an important role in constructing the international environment of states. Intuition suggests that adversaries will not take each other’s statements at face value, but, in one model meant to represent international bargaining, Fearon (Reference Fearon1995) showed additionally that the scope of costless demands would convey nothing whatsoever to an adversary. The analysis below illuminates the assumptions on which this conclusions rests and demonstrates a simple rationalist mechanism through which the scope of costless demands is likely to convey information in many international contexts.
The models described and analyzed in this article follow in the tradition begun in the seminal paper by Crawford and Sobel (Reference Crawford and Sobel1982). They showed that actions that in themselves have no effect whatever on player utilities and options can nevertheless have substantial effect on the equilibria of game theoretic models. These ‘costless signals’ affect equilibrium behavior by conveying information. These models have been thought to represent talking well, since speech often appears to have substantial effects on outcomes without directly affecting material contexts, or actor preferences or options. The effects that speech has on the course of events is usually the result of how other actors respond to it rather than a direct effect of the speech itself.
Most of the literature in economics and political science takes a different approach, modeling talk as costly in some fashion. By far the largest literature of this variety uses variants of alternating offer Rubinstein (Reference Rubinstein1982) models. These articles have examined how player preferences over bargaining failure affect the results of bargaining, whether resolve can be signaled through delay in reaching agreements, the conditions under which bargaining outcomes will be efficient and other topics. In international relations scholarship, models that follow this approach include Powell (Reference Powell1988, 2002, Reference Powell2004a, Reference Powellb, 2006), Slantchev (Reference Slantchev2003), and Leventoglu and Tarar (Reference Leventoglu and Tarar2008). I do not follow this approach for several reasons. The most important is that these models are not designed to address questions related to when talking conveys information and effects the course of events as a result. On the contrary, these models assume that talking does so and therefore cannot pose the question.Footnote 5
The question of how the scope of demands might convey information, the central question addressed here, has, however, been addressed in this literature. One answer is that higher demands can convey resolve because such demands signal a willingness to accept delay in reaching a negotiated solution or even risk reaching a solution at all.Footnote 6 Because this literature assumes that demands inherently affect actor payoffs and the choices available to actors later on, it has not addressed the conditions under which higher demands convey information in this fashion. Below, I describe such conditions. I also give conditions under which higher demands may actually decrease adversaries’ estimates of resolve. The current approach does not rely on a discount factor to generate a cost to making a risky offer that is unlikely to be accepted. As such, the costless signaling models are able to explain how the scope of demands can convey information even when there is no direct cost to sending a misleading signal. Following the costless signaling tradition, the models presented in this article assist in understanding when relations are too adversarial to allow for communication and when, despite appearances, they are not.Footnote 7
The models that bear the most similarity to the models described below are Farrell and Gibbons (Reference Farrell and Gibbons1989), Ramsay (Reference Ramsay2011), Sartori (Reference Sartori2005), Kurizaki (Reference Kurizaki2007), and Trager (Reference Trager2011). Unlike the first two, the approach used here does not rely on multiple equilibria in the game without costless signals to demonstrate that costless signals can affect equilibrium behavior. Instead of modeling international negotiation as a double auction from the economics literature, I employ a standard crisis bargaining framework often used to analyze credibility in international relations. Unlike Sartori (Reference Sartori2005) and Kurizaki (Reference Kurizaki2007), the models below allow costless demands to have scope rather than considering only a choice to threaten or not. In all of these works, signaling occurs through entirely different mechanisms.Footnote 8
Finally, unlike Trager (Reference Trager2011), the model below applies to cases where the players know how the other ranks settlement options along a single issue dimension. This appears a reasonable representation of many cases in international politics where acceptance of a high demand necessarily implies acceptance of lesser demands as well. If a state demands the cession of a territory on its border, for instance, it may be impractical for the threatened state to offer to cede half the territory that does not border on the threatening state but keep half the territory that does border on the threatening state. The amount of territory demanded is therefore a question of degree. The threatened state will then want to know whether the threatening state would settle for a compromise: perhaps the half of the territory nearest to the threatening state would be a sufficient concession to avoid war. In such cases, the model described below appears to be a good representation of international negotiation. On the other hand, if players may have strong or weak preferences over multiple issue dimensions, the model described in Trager (Reference Trager2011) may be more appropriate.Footnote 9
A striking example of the signaling context analyzed below comes from the negotiations prior to the first Gulf War. In February of 1991, the United States promised to begin a ground offensive unless Iraq withdrew from Kuwait City in two days and from Kuwait in seven. The US demand consisted of two essential parts: the requirement to leave Kuwait and the specific timetable for withdrawal. Iraq had already offered to leave Kuwait in 21 days and Kuwait City in 4. The importance of the second US demand for a shorter timetable was that Iraq would not be able to unwind its positions and leave with its equipment in the shorter time-frame. By this point in the conflict, a key US goal was to degrade the ability of the Iraqi army to threaten its neighbors. The Iraqi regime accepted the first US demand, but not the accelerated timetable.Footnote 10 The US–Iraqi negotiations, conducted through Soviet mediation, concerned questions of degree: Iraq could not agree to the timetable, but refuse to leave Kuwait. Iraq was largely convinced by this stage that the United States would fight to restore Kuwaiti independence, but Iraqi leaders and analysts did not know whether the United States would go to war rather than accept the Iraqi timetable for withdrawal (See Woods (Reference Woods2008, chap. 8)). On February 23rd, the United States bluntly informed the Soviets in a private exchange that the United States would not accept the Iraqi timetable. The Soviets promptly communicated to the Iraqis that the United States would invade unless Iraq agreed to a more accelerated timetable for withdrawal.Footnote 11
I will show below that costless statements in such contexts can convey information even when previously described mechanisms are unavailable. Signaling is likely to be particularly effective when the signaling state is believed to be highly resolved to fight at least for a partial concession from the second state, and the second state is believed sufficiently likely to be resolved to fight rather than make a full concession to the signaling state. The claim is not, however, that in such cases states are likely to reach a compromise, which would be unsurprising. It is rather the quite different claim that in this context, attempts at communication will change the threatened states beliefs about the threatening states intentions. In fact, in such cases, when the threatening state demands a full concession, the threatened state will know for sure that the threat is credible even though it did not believe the threatening state would fight for sure for a full concession before the threat was made.
To understand the intuition for the signaling dynamics described below, consider what the Iraqi government could have learned from the scope of the US demand. First, note that Iraq was itself very unlikely to comply with a demand that involved such a significant degrading of its military capability. Second, with the United States insisting on the accelerated time table, the Iraqi government would be hesitant to unilaterally remove its troops from Kuwait at the slower timetable because Iraqi forces leaving their chosen and prepared positions would have been the more vulnerable to US attack. Thus, by insisting on the greater Iraqi concession of the accelerated time table, the United States ensured that no partial Iraqi concession would be forthcoming. Suppose, by contrast, that the US government insisted only on the slower Iraqi withdrawal. This, the Iraqis were clearly much more likely to do. From the point of view of the US government, it only made sense to insist on the accelerated time table if the accelerated time table were of sufficient importance to US policy makers. Put in this way, it is obvious that Iraqi decision makers could conclude from US statements that US resolve not to make a concession was high. In diplomatic crises, similar dynamics to these recur. Of course, governments are always confronted with a range of signals and indices; this is but one.Footnote 12
A bargaining model with a discrete set of compromise outcomes
In order to most closely relate the discussion to previous literature on these topics, the first model I shall describe is identical to the well-known model of cheap talk communication in Fearon (Reference Fearon1995), except in these three respects: (1) states have a discrete set of compromise solutions available, (2) both sides are uncertain about the other’s resolve and (3) states are uncertain about each others utilities over compromise outcomes rather than over each other’s costs of war.Footnote 13 These modifications in the model often better fit the facts of international politics. Negotiations often center on a few discrete options, and this is sometimes because only a discrete set of options are practical without linking discussions to other issue areas. I shall consider a divisible issue space in the next section. Second, no statesman could claim to have certain knowledge of how adversaries weigh proposed compromise solutions against one another and this is precisely what diplomats often strive to communicate.Footnote 14
As in Fearon (Reference Fearon1995), the game described here has two players, a ‘Signaler’ and a ‘Target’ indexed by 
$$i\in I\,\equiv\,\{ s,t\} $$
, and four stages. In the first stage, Nature draws utility functions 
$$u_{i}^{z} (x)$$
for each player 
$$i$$
over outcomes in the bargaining space X ≡ [0,1] (with generic element x) according to the independent, commonly known, discrete distribution functions 
$$h_{i} (u_{i}^{z} )$$
. For each player, there are three possible utility functions, so 
$$h_{i} (u_{i}^{z} )$$
has support 
$$\{ u_{i}^{l} ,u_{i}^{m} ,u_{i}^{h} \} $$
. The superscripts l, m, and h will be used in several places in the model and can be interpreted as ‘low’, ‘medium’, and ‘high’. In reference to the utility functions, the superscripts indicate the level of resolve of the player in a sense described below. The players have directly opposed preferences over the set of compromise outcomes so that, for all z, 
$$u_{s}^{z} (x)$$
is strictly increasing in x, while 
$$u_{t}^{z} (x)$$
is strictly decreasing in x. Player utility functions are the private information of each player.
In the second stage, the Signaler has the opportunity to send a message y∈M to the Target from a large but finite set of messages. Assume that m, h∈M s.t. m≠h. After the message is sent, the Target chooses one of three settlement outcomes 
$$\{ x_{l} ,x_{m} ,x_{h} \} $$
, where 
$$0 \, \lt \, x_{l} \, \lt \, x_{m} \, \lt \, x_{h} \, \lt \, 1$$
.Footnote 15 In the final stage, the Signaler chooses r∈R ≡ {0,1}, where r=1 indicates a decision to initiate a war and r=0 indicates peace, and then the game ends. If war occurs, the Signaler wins with probability 
$$p$$
, the Target wins with probability 1−p, and the victorious player attains its most preferred outcome in X, 1 for the Signaler and 0 for the Target. Players have commonly known costs of fighting 
$$c_{i} $$
. 
$$\mu (u_{s}^{z} \,\mid\,y)$$
represents the Target’s updated beliefs about the Signaler’s type 
$$u_{s}^{z} $$
given signal y in a particular perfect Bayesian equilibrium (PBE). The game is represented in Figure 1. To highlight the elements of the game most clearly, only one of the branches at the Signaler’s messaging node and the Target’s response nodes are shown. The superscripts on player utility functions at peaceful outcomes and the initial move by Nature are also suppressed.
Figure 1 The Signaling game.
In order to most closely relate this model to other models in the literature, I shall assume that uncertainty about preferences relates only to player preferences over the compromise outcomes rather than to the extreme outcomes. Thus, we can set 
$$u_{s}^{z} (0)=u_{t}^{z} (1)=0$$
and 
$$u_{s}^{z} (1)=u_{t}^{z} (0)=1$$
for all z. This implies that expected utilities for war are 
$$w_{s} =p{\minus}c_{s} $$
for the Signaler and 
$$w_{t} =1{\minus}p{\minus}c_{t} $$
for the Target.
I also make several assumptions about player preferences. First, players prefer war to their least preferred outcome in X (formally, 
$$w_{i} \,\gt\,0\,\forall i$$
) and prefer at least one of the three possible negotiated outcomes in the interior of X to war (formally, 
$$u_{s}^{z} (x_{h} ) \, \gt \, w_{s} $$
and 
$$u_{t}^{z} (x_{l} ) \, \gt \, w_{t} \,\forall z$$
). Second, each player is uncertain whether the other will or will not fight if offered anything but its most preferred compromise outcome. In other words, both sides are uncertain whether the other would be willing to fight rather than accept any but its most preferred of the three compromise solutions. Formally, for the Signaler, this implies 
$$u_{s}^{l} (x_{l} ) \, \gt \, w_{s} $$
, 
$$u_{s}^{m} (x_{m} ) \, \gt \, w_{s} \, \gt \, u_{s}^{m} (x_{l} )$$
, and 
$$w_{s} \, \gt \, u_{s}^{h} (x_{m} )$$
. For the Target, this implies 
$$u_{t}^{l} (x_{h} ) \, \gt \, w_{t} $$
, 
$$u_{t}^{m} (x_{m} ) \, \gt \, w_{t} \, \gt \, u_{t}^{m} (x_{h} )$$
, and 
$$w_{t} \, \gt \, u_{t}^{h} (x_{m} )$$
. Figure 2 is an example of Signaler-type utility functions that satisfy these assumptions.
Figure 2 An example of Signaler utilities.
This sort of uncertainty implies the possibility that there may be no negotiated solution that both sides prefer to war ex ante. This implication is controversial because it is often supposed that preferences should be modeled with weakly risk averse utility functions, which imply that a mutually preferred negotiated solution must exist when the good in contention is divisible. I nevertheless assume the sort of uncertainty described above because it represents what we see in cases. When Britain and Germany negotiated over Czechoslovakia before the Second World War, for instance, neither side knew whether the other would accept a negotiated solution in which Germany annexed only the Sudetenland. In fact, the essence of compromises is often an agreement that neither side knew the other would accept at the start of negotiations. Compromise generally involves both sides giving up something that each had claimed to be unwilling to give up. To model this sort of uncertainty in the conventional way requires assuming that there are types that will agree to such compromises and types that will not. This directly implies, however, that there is a possibility that a negotiated solution may not exist to which both sides are willing to agree. Why this sort of uncertainty exists, and how it should be reconciled with traditional modeling approaches, are difficult questions. That such uncertainties exist and should be accounted for in models of international politics is certain, and justifies the structure of uncertainty assumed here.Footnote 16
The first proposition gives sufficient conditions for an equilibrium to exist in which the Target’s beliefs are affected by the Signaler’s cheap talk message. So long as both sides are sufficiently unlikely to be the least resolved type (the type unwilling to fight even if it is offered its least preferred of the three settlement outcomes), an equilibrium exists in which the least resolved and middle resolved Signalers claim they will fight unless the Target offers at least x m and only the most resolved Signaler’s claim to be willing to fight unless they are offered the maximal concession x h. Thus, when the Signaler says it will fight unless it is offered a maximal concession, the Target knows for sure that this is true. When the Signaler admits that it will settle for x m, the Target revises upwards its belief that, in fact, the Signaler would not go to war if it were offered only x l.
In this equilibrium, when the least resolved Target type, 
$$u_{t}^{l} $$
, observes the Signaler claim to be the most resolved type (y=h), this Target type offers the maximalist concession x h because the Target knows that any other offer results in war. Other Target types are not willing to accept such a poor outcome, however, and refuse to compromise at all. In response to the message h, the two more resolved Target types offer x l, knowing that this will result in war. This implies that the expected utility of sending the strong signal, h, is 
$$h_{t} (u_{t}^{l} )u_{s}^{l} (x_{h} ){\plus}[1{\minus}h_{t} (u_{t}^{l} )]u_{s}^{l} (x_{l} )$$
for the least resolved Signaler type, 
$$u_{s}^{l} $$
, because that type is not willing to go to war under any circumstances. The expected utility of sending h for the Signaler type whose resolve is in the middle range, 
$$u_{s}^{m} $$
, is 
$$h_{t} (u_{t}^{l} )u_{s}^{m} (x_{h} ){\plus}[1{\minus}h_{t} (u_{t}^{l} )]w_{s} $$
because that type prefers to go to war rather than accept x l.
How will the Target respond when it observes the signal m? The Target knows that the Signaler will accept x m rather than fight, but the Target also understands that the Signaler may be willing to accept x l as well. However, as long as the probability that the Signaler is the least resolved type, 
$$u_{s}^{l} $$
, is not too high and as long as the Target is not the most resolved type, the Target will settle for x m. If the Target is the most resolved type, it risks war by offering x l. This implies that the expected utility of sending the signal m is 
$$(h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} ))u_{s}^{l} (x_{m} ){\plus}[1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} )]u_{s}^{l} (x_{l} )$$
for the least resolved Signaler type and 
$$(h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} ))u_{s}^{l} (x_{m} ){\plus}[1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} )]w_{s} $$
for the moderately resolved Signaler type.
In this context, would the less resolved Signaler types be willing to admit that they are not the most resolved type, as the equilibrium requires? They would if their expected utilities for sending the signal m are greater than their expected utilities for claiming to be the most resolved type by sending the signal h. The expected utilities just stated imply that the least resolved Signaler type prefers to send the signal m when,
$$\openup 6pt\eqalign{[h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} )]u_{s}^{l} (x_{m} ){\plus}[1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} )]u_{s}^{l} (x_{l} ) \cr \quad \ges h_{t} (u_{t}^{l} )u_{s}^{l} (x_{h} ){\plus}[1{\minus}h_{t} (u_{t}^{l} )]u_{s}^{l} (x_{l} )$$
Moderately resolved Signalers also prefer to send the signal m when,
$$\openup 6pt\eqalign{Eu_{s} (m\,\mid\,u_{s}^{m} )=[h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} )]u_{s}^{m} (x_{m} ){\plus}[1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} )]w_{s} \cr \quad\ges h_{t} (u_{t}^{l} )u_{s}^{m} (x_{h} ){\plus}[1{\minus}h_{t} (u_{t}^{l} )]w_{s}$$
Notice that both conditions are satisfied as long as the probability that the Target is the least resolved type, 
$$h_{t} (u_{t}^{l} )$$
, is not too high. If it is, then the prospect of achieving the very favorable deal, x h, is too tempting, causing the less resolved Signaler types to misrepresent their levels of resolve, and signaling equilibria of this form become impossible. Proposition 1, proved in the Appendix, formally describes the properties of this equilibrium and gives the sufficient condition for its existence: the probability that the players are the least resolved types cannot be too low.
Proposition 1: If 
$$h_{i} (u_{i}^{l} )$$
is sufficiently low for all i, a perfect Bayesian equilibrium exists in which the signals m and h are sent with positive probability and,
$$\mu (u_{s}^{h} \,\mid\,h)=1\,\&\,\mu (u_{s}^{h} \,\mid\,y)=0 \, \forall y\,\ne\,h \eqno (1)$$
$$\mu (u_{s}^{m} \,\mid\,m)={{h_{s} (u_{s}^{m} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}} \, \lt \, 1\,\&\,1 \, \gt \, \mu (u_{s}^{l} \,\mid\,m)={{h_{s} (u_{s}^{l} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}} \, \gt \, h_{s} (u_{s}^{l} ) \eqno(2)$$
$$\mu (u_{s}^{l} \,\mid\,y)=1\,\forall y\,\ne\,m,h \eqno (3)$$
The assumption that there is a positive probability that player utilities are risk loving, which is an implication of the structure of uncertainty, is not necessary for signaling of this sort. If there is no Target type 
$$u_{t}^{h} $$
, but the remaining two Target types satisfy the assumptions made above, then the assumptions are consistent with risk averse utility functions for all types of all players. In this modified game, Proposition 1 still holds.Footnote 17 This result is stated as Corollary 1. Notice, however, that because the issue space is not divisible, there is still a positive probability that no negotiated solution exists that both sides prefer to war. I shall discuss related issues further below.
Corollary 1: Proposition 1 holds in a modified game in which the 
$$u_{t}^{h} $$
type does not exist and in which players have risk averse utilities over outcomes in X.
When the Signaler is less convinced that the Target is not the least resolved type, an equilibrium with informative signals but different properties from those described in Proposition 1 can also exist.Footnote 18 Here, the least resolved and most resolved Signaler’s send the same signal, while Signaler’s that would fight unless they are offered at least x m send a unique signal. Thus, in this case, admitting a willingness to compromise on x m does not increase the Target’s belief that the Signaler would accept x l over war as well. Rather, the Target knows for sure following such a signal that an offer of x m will be accepted and avoid war while an offer of only x l will not. Proposition 2 gives sufficient conditions for an equilibrium of this type.
Proposition 2: If 
$$h_{s} (u_{s}^{l} )$$
is sufficiently low and 
$$h_{t} (u_{t}^{l} )\in \left({{h_{t} (u_{t}^{m} )[u_{s}^{l} (x_{m} ){\minus}u_{s}^{l} (x_{l} )]} \over {u_{s}^{l} (x_{h} ){\minus}u_{s}^{l} (x_{m} )}},$$
$$ {{h_{t} (u_{t}^{m} )[u_{s}^{m} (x_{m} ){\minus}w_{s} ]} \over {u_{s}^{m} (x_{h} ){\minus}u_{s}^{m} (x_{m} )}}\Big)$$
, a perfect Bayesian equilibrium exists in which the signals m and h are sent with positive probability and,
$$\mu (u_{s}^{h} \,\mid\,h)={{h_{s} (u_{s}^{h} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{h} )}}\,\&\,\mu (u_{s}^{h} \,\mid\,y)=0\,\forall y\,\ne\,h \eqno(1)$$
$$\mu (u_{s}^{m} \,\mid\,m)=1\,\&\,\mu (u_{s}^{l} \,\mid\,m)=0\eqno(2)$$
$$\mu (u_{s}^{l} \,\mid\,y)=1\,\forall y\,\ne\,m,h \eqno(3)$$
Thus, when the Signaler believes the Target is somewhat more likely to accept the Signaler’s most preferred negotiated solution, the signaling dynamics may change to those described in Proposition 2. This will not necessarily be the case, however, because the parameters of the model may be such that no range of the sort specified in the proposition for 
$$h_{t} (u_{t}^{l} )$$
exists. In fact, it is reasonable to doubt whether equilibria of this sort closely track many situations in international politics. The reason is that in these equilibria, the least resolved Signaler’s must prefer to gamble that they will get their most preferred outcome (by sending the same signal as the most resolved types) rather than achieve x m for sure, while Signalers that are somewhat more resolved would prefer x m for sure rather than take a similar gamble. Why should states that are willing to fight for a better deal be less willing to take such risks? There is no reason to expect this to be the case in general. Nevertheless, Corollary 2 suggests a way to understand when we might expect to observe equilibria of this sort: when 
$$u_{s}^{l} $$
and 
$$u_{s}^{m} $$
are equivalent at x m and x h and the Signaler is not too likely to be the least resolved type, then an equilibrium of the type described in Proposition 2 exists when the likelihood that the Target is the least resolved type is in a middle range.
Corollary 2: If 
$$u_{s}^{l} (x_{m} )=u_{s}^{m} (x_{m} )$$
and 
$$u_{s}^{l} (x_{h} )=u_{s}^{m} (x_{h} )$$
and 
$$h_{s} (u_{s}^{l} )$$
is sufficiently low, then a range of values of 
$$h_{t} (u_{t}^{l} )$$
exists such that an equilibrium of the type described in Proposition 2 exists.
Proposition 3 demonstrates that whenever the Target is believed sufficiently unlikely to make the maximalist concession x h, any separating or semi-separating equilibrium will have the properties described in Proposition 1. This means that the model gives us a strong empirical expectation: when there is reason to believe that the states involved are each unlikely to accept their least preferred among the three settlement outcomes, signaling will have the properties described in Proposition 1.
Proposition 3: For 
$$h_{t} (u_{t}^{l} )$$
sufficiently low, any pure strategy PBE in which Signalers do not pool on a single message has the properties described in Proposition 1.
In cheap talk models of this sort, so long as the probability that the Signaler is the least resolved type is sufficiently low, the possibility of communication never increases the probability of war and sometimes, communication makes war less likely. This result is proved as Proposition 4. Note that this is in contrast to models of signaling based on reputation and other models in the literature (Sartori (Reference Sartori2005); Slantchev (Reference Slantchev2010a, 136–141).
Proposition 4: For 
$$h_{s} (u_{s}^{l} )$$
sufficiently low, no pure strategy PBE of the game with the cheap talk stage has a higher probability of war than the same game without communication.
Robustness: divisible issue spaces and risk aversion
A principle effect of the partial issue indivisibility in the previous model is to ensure that the Target does not capture all the gains from agreeing on a negotiated solution that both prefer to war. Many bargaining contexts will result in outcomes in which the gains from agreement are shared between the parties, however. As long as the gains from agreement are shared among the players and uncertainty is the sort characterized above, the results related to costless signaling described above will hold. The dynamics will be essentially the same as those described in the partially divisible good case.
To see this, consider a model in which the issue space can be infinitely divided and which is identical to the one described above, except in these respects. Following the Signaler’s message, the players simultaneously announce a compromise position a i∈X. If the players announce different positions, the status quo position x l remains, where x l satisfies the conditions on x l from the previous model. If the players announce the same position, this agreement becomes the new status quo. Following the announcements, paralleling the previous model, the Signaler decides whether or not to go to war.
The simple protocol of announcing a point of agreement is a sensible representation of bargaining if both sides must cooperate to implement or work out a compromise agreement. The result, as the formal analysis in the appendix demonstrates, is that equilibria exist in which both sides share in a potential bargaining surplus. And the result of that is that costless signaling is possible. Many other bargaining protocols besides simply agreeing on an announcement would yield similar results. For instance, Rubinstein models and Nash Bargaining also produce outcomes where both sides share in the bargaining surplus.Footnote 19
Thus, in this modified model, although the issue space is infinitely divisible, costless signaling is possible. As in the case of discrete options, the players will have ideas about what particular bargaining outcomes are likely under different courses of action. Whether these outcomes are exogenously given discrete choices or arrived at through bargaining does not greatly affect the signaling dynamics as long as both sides are expected to share in the bargaining surplus. As before, so long as the Target is not overly likely to be the least resolved type, informative signaling of the sort described in Proposition 1 is possible. This result, which is proved as Proposition 5, shows that the results are robust to cases where the issue space is divisible.Footnote 20
Proposition 5: Proposition 1 holds in the modified game.
As in Proposition 1, the signaling dynamics represented in Proposition 5 do not depend on risk averse preferences of the players. An analogous result to Corollary 1 applies to Proposition 5. Thus, costless signaling can still occur if utility functions are certain to be risk averse, the good in question is divisible, and therefore a negotiated solution exists that both sides prefer to conflict. In this case, however, the bargaining must take a particular form. In any equilibrium with the properties described in Proposition 5, the unique signal sent by the most resolved types cannot be certain to lead to an agreement that the most resolved types of each player prefer to war. If it did, then less resolved types would represent themselves as highly resolved and the signaling equilibrium constructed in the proposition would cease to exist. In the Proposition 5 equilibrium, after the most resolved Signaler type sends a unique signal to the Target, this type presses for a favorable settlement by making an announcement that the 
$$u_{t}^{l} $$
Target type would accept, but the 
$$u_{t}^{m} $$
type would not. Thus, the Signaler’s high demand is associated with a risk of a lesser negotiated outcome than the middle range demand. Many other models of bargaining also involve similar risks. Unlike in other models, however, non-agreement does not directly mean war. Non-agreement means only that the status quo outcome obtains unless the Signaler decides to go to war. Less resolved Signaler types that prefer the status quo to war do not risk war by representing themselves as highly resolved.
Discussion
The bargaining equilibria analyzed in the previous sections have two key properties that are necessary for costless signals to convey information. First, admitting a willingness to compromise cannot result in all the benefits to avoiding conflict being captured by the other side. If requesting a compromise makes a state indifferent between the compromise and going to war whereas making a maximalist demand yields the possibility of a more favorable outcome, states willing to compromise will make maximalist demands. Second, increasing the scope of the demand must decrease the probability that the demand is accepted. If a maximalist demand yields both the possibility of a maximal concession and a higher likelihood of it, clearly, all states would make maximalist demands. Thus, when either of these conditions does not hold, states willing to make a compromise have nothing to lose by overstating their resolve and therefore signaling is impossible.Footnote 21
In these models, communication is possible between adversaries because some Signaler types admit that they’re not the most resolved of the possible Signaler types. These types are willing to reveal this information, in spite of the fact that they also have incentive to misrepresent themselves as more resolved than they are in order to achieve a more favorable bargain, because demanding more sometimes also entails a risk such types are unwilling to run. The risk is that an increased demand will be declined whereas a more moderate demand would not be, resulting in a worse bargaining outcome over which the signaler may or may not choose to fight. This form of signaling, which does not directly risk war, can only occur in contexts in which the scope of demands is an issue, that is, when more than two non-conflict outcomes are possible. If the only choice of the Signaler is to threaten or not threaten and the only choice of the Target is to back down or not, in the signaling context analyzed here, no communication of resolve will be possible because demanding more carries no risk of getting even less at the bargaining table and therefore the incentives to misrepresent imply that no semi-separating equilibria exist.
Unlike in many other models of diplomatic signaling, therefore, it is not through risking conflict that information is conveyed.Footnote 22 In the Proposition 1 equilibrium, when the most resolved Signaler types send a signal that other types are unwilling to send, the probability that war occurs decreases. This is because only the Signaler has the option to initiate conflict and when resolved Signalers send such a signal, they are more likely to get a better offer and therefore less likely to initiate a conflict. Further, for most parameterizations of the model that seem reasonable, the existence of signaling mechanisms of the type described here either does not increase the likelihood of conflict or actually causes the probability of war to decline.Footnote 23
An example of the effect of communication on the probability of conflict is shown in Figure 3. On the left of the figure, communication strictly decreases the probability of war. As it becomes more likely that the Signaler is the most resolved type, the benefit of communication increases up to a point and then the probability of conflict in the equilibrium without communication falls discontinuously to be equal to the likelihood of conflict in the cheap talk equilibrium. The reason for this is that, as the Target becomes more convinced that the Signaler is the most resolved type, the Target becomes less willing to risk conflict even without a credible signal of resolve. On the right of the figure, as the Target becomes still more convinced that the Signaler is the most resolved type, the Target becomes less convinced that the Signaler’s resolve is in a middle range. Therefore, the Target becomes less likely to be willing to offer a middle range compromise in response to a less than maximalist demand by the Signaler. The result is that the Signaler becomes unwilling to make less than maximalist demands, the communication equilibrium breaks down and the probability of conflict increases dramatically.Footnote 24
Figure 3 The probability of war.
There are two primary reasons these results are different from those presented in Fearon (Reference Fearon1995). The first is the fact that in the Fearon model, the Target captures all of the benefit from avoiding war. The Target’s disproportionate share of the benefits of peace results from (1) the take-it-or-leave-it aspect of the model and (2) the infinitely divisible issue space. This is because, in that model, when the Target of a threat knows the Signaler’s type, its take-it-or-leave-it equilibrium offer leaves the Signaler indifferent between choosing war or peace. As a result, the Signaler has no incentive to reveal information: although peace may result, the nature of the peace is such that the Signaler finds war an equally compelling alternative. If either of these two assumptions are relaxed, the Target need not capture all of the gains from a negotiated solution, the Signaler can therefore have an incentive to reveal its type, and the scope of a costless demand can – if other conditions hold – convey information to the Target.
While the take-it-or-leave-it model with an infinitely divisible issue space is interesting to study, it is likely that in most bargaining contexts, the players expect the benefits of peace to be spread more evenly among the players.Footnote 25 When states are highly resolved and willing to go to war over a particular set of issues, they still often have a strong preference for getting their way through the threat rather than the costly use of force. For this reason, resolved states are thought to have an incentive to reveal their types. In the Fearon model, by contrast, not only unresolved, but also resolved states have no incentive to reveal their types. If they do, they end up with their war payoff and if they are not able to, they still get their war payoff. Thus, what prevents costless signals from conveying information is not merely that unresolved types have an incentive to misrepresent themselves as resolved (that is true in the model analyzed above), but also that both resolved and unresolved types have no incentive to make their signals credible.
In many real-world crises, a model in which even successful, highly resolved signalers receive no benefit from success does not appear to correspond actors’ understandings of the situation. In the Cuban Missile Crisis, for instance, the Kennedy administration signaled a willingness to compromise through a non-invasion pledge and the removal of the Jupiter missiles from Turkey. Although the administration was willing to initiate conflict with the Soviet Union through an air strike on Cuba, members of the administration were very glad to have forced the removal of the missiles without having to do so. That US policy makers were so relieved at the resolution of the crisis indicates that the Soviets were unable to capture all of the gains from peace in this case, as Targets are in the majority of crisis bargaining encounters.
One reason the gains from cooperation are shared in real-world cases is that no continuously divisible issue space exists in many instances or, for complex reasons outside of the questions considered here, in practice, actors do not consider the issue space divisible. Fearon (Reference Fearon1995, 389–390) and Powell (Reference Powell2006) note that mechanisms, such as randomization devices or alternating possession of the good, exist to make the issue space divisible, and that therefore indivisibility is generally not by itself a rationalist explanation for war. They also emphasize, however, that for complex reasons, states often act as if issues are indivisible. This may result from the construction of the conflict Goddard (Reference Goddard2006), from inherent features of the issues involved,Footnote 26 from the logic of commitment problems Powell (Reference Powell2006), from the positions of other powers that limit the options of the two states,Footnote 27 or because the set of potential issues of contention in particular cases is not large enough.Footnote 28 Yet another reason issues may be indivisible in practice has to do with bargaining reputation. As Schelling has pointed out, the United States would have a hard time offering to give up California and then establishing a credible commitment to give up no additional territory. It is the unavailability of other salient lines that leads to a sort of indivisibility of the initial grouping of territory Schelling (Reference Schelling1966, chap. 2). Still another reason for indivisibility relates to what moral codes allow leaders to offer and demand of each other. Hitler could demand the Sudetenland, and even that the West stand aside while he occupied Czechoslovakia in the name of protecting Germans in the Sudetenland, but he could not demand ‘three quarters of Czechoslovakia’. At the Munich conference and in the diplomatic negotiations that preceded it, neither side considered such demands and offers.
Besides issue indivisibility, another reason Targets often are not expected to garner all gains from cooperation is that bargaining outcomes that are preferable to conflict to both sides often require actions to be taken by both sides. Each side may be willing to withdraw its troops from a border, but only if the other side also does so. Saddam Hussein may have been willing to withdraw his forces from Kuwait on a particular timetable, but only in return for a public guarantee of their safety from the United States. If neither side can achieve the preferred compromise outcomes unilaterally, we should expect that the sides negotiate and – if they reach agreement – that they share the bargaining surplus between them.
A second driver of the signaling dynamics in the model described in Propositions 1–4 is the assumption that both sides are uncertain whether the other would or would not be willing to fight rather than accept any but its most preferred of the three compromise solutions. As a result, when the Target believes the Signaler is a type that would be unwilling to make a compromise that the Target would accept, the Target no longer has any interest in making concessions to the Signaler. This gives less resolved Signalers a disincentive to misrepresent themselves as more resolved than they are. This also ensures that if the Signaler convinces its adversary that the Signaler is highly resolved, this does not necessarily lead to a better outcome for the Signaler because the Target is sometimes unwilling to give the Signaler what it wants even if the Target knows that the Signaler will go to war if the Target doesn’t.
The assumption that both sides are uncertain whether the other would accept any but its most preferred compromise appears uncontroversial in that it faithfully represents the subjective states of international actors in crises. However, the implication of the assumption is that it is possible that no compromise exists that both sides prefer to conflict. Put in this way, the assumption appears controversial. Nevertheless, since in the Sudentenland crisis, discussed above, and many others, actors clearly had this sort of uncertainty, models should not rule it out. We can also think of this assumption as merely a simplification of a more complex strategic process that is not modeled explicitly. To see this, note that virtually all crisis bargaining models share the following property: for some combinations of player types, war occurs with certainty.Footnote 29 In many models, war would not occur between these types under complete information, whereas in the model of Propositions 1–4, incomplete information is not required to produce war between the most resolved types. Nevertheless, whether war between such types results from an explicitly modeled strategic context or directly from the preferences of actors is not the focus of the present inquiry. Thus, the assumption that player preferences can result in war might be justified by embedding many prominent crisis bargaining models from the literature in the game presented here. This would substantially complicate the analysis, of course, as well as obscure the dynamics of the current framework, which is why the simpler strategy was adopted above.
The model of Proposition 5 further shows that even if we assume that the issue space is fully divisible and that players have risk averse utility functions so that a negotiated solution preferred by both sides must exist, signaling is still possible. In addition to the bargaining surplus from avoiding war being divided between the sides, such a communication equilibrium must also have the property that increasing the scope of demands decreases the probability that the demand is accepted. We have seen that this is possible if a highly resolved Signaler presses for such a favorable division that the Target may not be willing to go along (Proposition 5). In an online appendix, I confirm that these two properties drive the different result in the Fearon (Reference Fearon1995) model by showing that a slight modification of that model that allows equilibria to have these properties is sufficient to enable informative signaling.Footnote 30
These two signaling conditions therefore imply a restricted set of cases in which the logic of Fearon’s divisible, take-it-or-leave-it model might be expected to operate: (1) when the Target of a threat can unilaterally choose from a set of options that approximate a divisible issue space and when the Signaler has few options short of conflict or acquiescence, or (2) when, given that a threat is credible, a higher demand is not expected to increase the likelihood that the demand is rejected. In such cases, costless signals will not convey information through the mechanisms described here. One might suspect, however, that such cases are not the norm in international politics because, in practice, inherent indivisibilities exist or compromise outcomes preferable to conflict require the give and take agreement of both sides, and maximalist demands often run a risk of rejection, even when the rejecting state believes that conflict will be the result. Of course, signals may nevertheless convey little to adversaries for other reasons. A claim to be willing to fight for a large concession, for instance, will likely signal little to the adversary when all sides believe that the state making the claim believes that the adversary is likely to be willing make the large concession. Such threats may be effective even when they do not influence adversary calculations.Footnote 31
The analysis here also demonstrates why states would make compromises even though doing so will often result in the perception that they would accept outcomes involving even greater concessions – thereby encouraging an adversary to demand these additional concessions. In the informative equilibria characterized in Propositions 1 and 5, when the Target sees the Signaler send the signal that the middle range compromise is acceptable, the Target knows the Signaler is less likely to go to war if the Target makes no concession at all to the Signaler. Nevertheless, the Signaler sometimes still prefers to send the signal that it would settle for the compromise position. The reason is that by demanding too much, that which the Target is relatively unlikely to give up, the Signaler risks getting nothing at all. By demanding only the compromise, the Signaler increases its chances of getting something. Alongside Proposition 1, Proposition 3 demonstrates that this dynamic will be associated with any offer of compromise when the players are each believed, before the diplomatic signal, to be sufficiently unlikely to be willing to settle for their least preferred compromise outcome. If this condition does not hold, the Signaler types that are unwilling to fight for any concession, those that are in this sense least resolved, will represent themselves as willing to fight for a maximalist concession. Thus, signaling may not be possible at all in such a case because of the incentive of less resolved types to represent themselves as maximally resolved. If signaling can occur, only the moderately resolved type makes the middle range demand, with the result that the Target knows for sure that a middle range concession is both necessary and sufficient to avoid war.
Diplomatic documents provide many examples of conclusions being drawn from the scope of threats. High demands are perceived as risking that no agreement is reached and in many of these instances, diplomats explicitly conclude that the willingness to risk non-agreement demonstrates the resolve of the demanding state. In 1912, for instance, the British noted Austria’s ‘irreconcilable attitude with regard to a Servian port on the Adriatic, even when [various compromises had been proposed]’. The British concluded, therefore, that Austria might be ‘wishing to satisfy her amour propre’ (Gooch and Temperley Reference Gooch and Temperley1979, v. 9, part 2, p. 217). Several times in the course of negotiations over Morocco in 1906, the intractability of one or other of the powers was seen as risking an agreement and therefore as conveying information. In one instance, German insistence that France relinquish control of the Moroccan police force lead the British and Russians to conclude that because Germany was unwilling to pursue negotiating for an intermediate compromise, Germany was more likely to insist on the full concessions it was demanding. All understood that through insisting on terms, Germany risked the breakup of the conference of powers that had been convened to adjudicate differences, and that Germany would consider this a poor outcome (Gooch and Temperley Reference Gooch and Temperley1979, v. 3, p. 274). Similarly, concessions were often made specifically in order to avoid the failure of negotiations. Thus, when the Germans did make concessions on the Moroccan police force, it was understood that this was done in order to ensure that the conference of the powers would remain in session.Footnote 32
Finally, concessions have often been seen as an indication of willingness to make additional concessions. During the Franco–Prussian war in 1870, for instance, following the capture of Napoleon III by Prussian forces but long before the end of the war, the French requested that the representatives of several foreign powers initiate peace negotiations with Prussia. The French specified a willingness to make a range of concessions, but the British ambassador to France concluded that in fact France would ‘yield almost anything that may be demanded, provided the integrity of the territory be preserved’. The ambassador’s judgments were a direct reaction to the private communications from the French government. Thus, the dire military situation of France provided the context in which such a judgment was possible, but the French statements convinced the British that France preferred making further substantial concessions to continuing to fight (Bourne and Watt Reference Bourne and Watt1987, part I, series F, v. 32, p. 80).
The British understanding of Russian actions in the Balkans in the years before the First World War provides other examples. In 1912, the British ambassador to Austria noted that Austria had ‘modified’ its views with respect to the Sanjak of Novibazar. Using this as evidence, the ambassador concluded that Austria would go even further: ‘I am inclined to think that... Austria [would] barter her claims and right in the Sanjak’ (Gooch and Temperley Reference Gooch and Temperley1979, v. 9, part 2, p. 123). The British drew a similar conclusion in 1913 when Russia urged the session of the fortress of Silistra from Bulgaria to Romania. The British view was that Russia urged this on its nominal ally, Bulgaria, because Russia wished to prevent a broader European war ‘almost at any price’ (Gooch and Temperley Reference Gooch and Temperley1979, v. 9, part 2, p. 508). Thus, as the models predict, the scope of demands is often understood to convey information about state intentions.
Conclusion
The models demonstrate that leaders can often learn a great deal about the intentions of other leaders from the scope of the demands other leaders make. The scope of a demand conveys information because of the negotiating risks involved in larger demands. The demanding state may end up worse off than if it had asked only for a compromise outcome that is more likely to be forthcoming. International bargaining is particularly likely to have these properties when compromise outcomes require the give and take agreement of both sides or the issue space consists of discrete alternatives and when adversaries each believe the other relatively unlikely to accept the negotiated outcome that each most prefers. In such cases, compromises will be offered even though these compromises increase the perception that the compromiser would be willing to settle for even less than the compromise offered. This appears to be a commonly used and intuitive signaling mechanism in international politics.
Acknowledgements
I am grateful to Robert Jervis, Andrew Kydd, Dov Levin, Chad Nelson, Barry O’Neill, Bob Pape and seminar participants at UCLA and the University of Chicago for trenchant comments and advice. Any missteps are mine.
Appendix
Proof of Proposition 1: I will show that for 
$$h_{i} (u_{i}^{l} )$$
sufficiently low for all i, the following strategies and beliefs constitute a perfect Bayesian equilibrium. The Signaler’s strategy is: for 
$$u_{s}^{l} $$
, send m and choose r=0; for 
$$u_{s}^{m} $$
, send m and choose r=1 following x l and r=0 otherwise; for 
$$u_{s}^{h} $$
, send 
$$h$$
and choose r=1 following x l and x m and r=0 otherwise. The Target’s strategy is: for 
$$u_{t}^{l} $$
, choose x l following 
$$y\ \forall y\,\ne\,m,h$$
, x m following m, and x n following h; for 
$$u_{t}^{m} $$
, choose x l following 
$$y\ \forall y\,\ne\,m,h$$
, 
$$x_{m} $$
following m, and x 1 following h; for 
$$u_{t}^{h} $$
, choose x 1 following y ∀y. The Target’s updated beliefs are: 
$$\mu (u_{s}^{l} \,\mid\,y)=1$$
, 
$$\mu (u_{s}^{m} \,\mid\,y)=\mu (u_{s}^{h} \,\mid\,y)=0$$
$$\forall y\,\ne\,m,h$$
; 
$$\mu (u_{s}^{l} \,\mid\,m)={{h_{s} (u_{s}^{l} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}}$$
, 
$$\mu (u_{s}^{m} \,\mid\,m)={{h_{s} (u_{s}^{m} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}}$$
, 
$$\mu (u_{s}^{h} \,\mid\,m)=0$$
; 
$$\mu (u_{s}^{l} \,\mid\,h)=\mu (u_{s}^{m} \,\mid\,h)=0$$
, and 
$$\mu (u_{s}^{h} \,\mid\,h)=1$$
. We need not specify the Signaler’s updated beliefs except to say that they must accord with Bayes’ rule.
Note that beliefs following signals m and h follow directly from Bayes’ rule and the Signaler’s strategy, and that the Target’s beliefs at other information sets are unconstrained in a PBE. Also note that these beliefs imply the properties described in the proposition. Optimality of the Signaler’s strategy at the nodes following the Target’s action follows from a direct comparison of the payoffs.
To see that the Signaler’s action at the signaling stage is optimal, first note that no Signaler-type can do better by deviating to a signal other than m or h because this guarantees the action 
$$x_{l} $$
on the part of the Target. Second, note that 
$$u_{s}^{h} $$
Signaler-types certainly cannot do better by deviating. Given the Target’s strategy and beliefs and the other components of the Signaler’s strategy, this leaves two conditions that must be satisfied for the Signaler’s strategy to be optimal:
$$Eu_{s} (m\,\mid\,u_{s}^{l} )=[h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} )]u_{s}^{l} (x_{m} ){\plus}[1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} )]u_{s}^{l} (x_{l} ) $$
$$\ges \,Eu_{s} (h\,\mid\,u_{s}^{l} )=h_{t} (u_{t}^{l} )u_{s}^{l} (x_{h} ){\plus}[1{\minus}h_{t} (u_{t}^{l} )]u_{s}^{l} (x_{l} )$$
$$Eu_{s} (m\,\mid\,u_{s}^{m} )=[h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} )]u_{s}^{m} (x_{m} ){\plus}[1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} )]w_{s} $$
$$\ges \,Eu_{s} (h\,\mid\,u_{s}^{m} )=h_{t} (u_{t}^{l} )u_{s}^{m} (x_{h} ){\plus}[1{\minus}h_{t} (u_{t}^{l} )]w_{s} $$
Both conditions hold for sufficiently low 
$$h_{t} (u_{t}^{l} )$$
.
To see that the Target’s strategy is optimal, note that 
$$x_{l} $$
is clearly an optimal choice for 
$$u_{t}^{h} $$
following any signal and that x l is optimal for any Target type, given the Target’s beliefs, following any signal other than m or h. For Target type 
$$u_{t}^{l} $$
, following m, x m gives utility 
$$u_{t}^{l} (x_{m} )$$
with certainty, so this Target type never chooses x h following m. Thus, the Target’s strategy is optimal in the information set following m if the following condition holds:
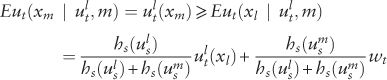$$Eu_{t} (x_{m} \,\mid\,u_{t}^{l} ,m)=u_{t}^{l} (x_{m} )\, \ges \,Eu_{t} (x_{l} \,\mid\,u_{t}^{l} ,m)={{h_{s} (u_{s}^{l} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}}u_{t}^{l} (x_{l} ){\plus}{{h_{s} (u_{s}^{m} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}}w_{t} $$
Target type 
$$u_{t}^{l} $$
’s strategy is optimal following h because, given the Target’s beliefs, any other choice results in war, which is a worse outcome for this type. For Target type 
$$u_{t}^{m} $$
, its strategy following h is optimal because a different choice produces either 
$$u_{t}^{m} (x_{h} ) \, \lt \, w_{t} $$
or w t, which is the same as the utility that results from its equilibrium strategy. For this Target type, following m, x h is clearly not preferred to h since the latter is certain to be accepted by the Signaler. Thus, the strategy ascribed to the Target is optimal for 
$$u_{t}^{m} $$
if the following condition holds:
$$Eu_{t} (x_{m} \,\mid\,u_{t}^{m} ,m)=u_{t}^{m} (x_{m} )^{3} \,\ges \,Eu_{t} (x_{l} \,\mid\,u_{t}^{m} ,m)={{h_{s} (u_{s}^{l} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}}u_{t}^{m} (x_{l} ){\plus}{{h_{s} (u_{s}^{m} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}}w_{t} $$
Conditions (3) and (4) are both satisfied for sufficiently low 
$$h_{s} (u_{s}^{l} )$$
.
The proof of Proposition 2 follows the form of the proof of Proposition 1 closely and is therefore omitted.
Lemma 1: No fully separating equilibria exist in the model with discrete compromise options and only two semi-separating equibiliria are possible: where 
$$u_{s}^{l} $$
pools with 
$$u_{s}^{m} $$
but not 
$$u_{s}^{h} $$
, and where 
$$u_{s}^{l} $$
pools with 
$$u_{s}^{h} $$
but not 
$$u_{s}^{m} $$
.
Proof: Note that in any PBE, the Signaler type 
$$u_{s}^{l} $$
never sends a signal that neither of the other two types send. In such an equilibrium, whether the other two types pool or send unique signals, it will always be optimal, for any set of Target beliefs consistent with Bayes’ rule, for Target-type 
$$u_{t}^{l} $$
to offer more than x l in response to the signal or signals sent by Signaler types 
$$u_{s}^{m} $$
and 
$$u_{s}^{h} $$
and no Target-types can offer less than x l. Since in equilibrium all Target types must respond with x l following a unique signal sent by 
$$u_{s}^{l} $$
, Signaler-type 
$$u_{s}^{l} $$
would prefer to deviate to the message assigned to one of the other Signaler types, which means that no such equilibrium exists. Thus, no fully separating equilibria exist and only the two semi-separating equilibria described in the Lemma are possible.
Proof of Proposition 3: The proof of Proposition 1 demonstrates that equilibria of the first type described in Lemma 1 have the properties described in the proposition. Thus, by Lemma 1, we need only show that, for sufficiently low 
$$h_{t} (u_{t}^{l} )$$
, an equilibrium does not exist in which 
$$u_{s}^{l} $$
pools with 
$$u_{s}^{h} $$
.
In any such equilibrium, since Bayes’ rule implies that the Target believes it is facing a 
$$u_{s}^{m} $$
type Signaler following that type’s unique signal m, 
$$u_{t}^{l} $$
and 
$$u_{t}^{m} $$
type Targets must choose x m following m and 
$$u_{t}^{h} $$
must choose x l (since other offers would be accepted and result in lower utility for this type than conflict). This implies that 
$$Eu_{s} (m\,\mid\,u_{s}^{l} )=(h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} ))u_{s}^{l} (x_{m} ){\plus}$$
$$ (1{\minus}h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} ))u_{s}^{l} (x_{l} )$$
.
Following the common signal sent by 
$$u_{s}^{l} $$
and 
$$u_{s}^{h} $$
, 
$$u_{t}^{h} $$
types must choose x l because there is a positive probability of either of the other offers being accepted, which leads to lower expected utility than conflict for this Target type. Note that no Target type offers x m following h because an offer of x l yields the same probability of war and is preferable if accepted. Thus, following h, 
$$u_{t}^{m} $$
must choose x l because a choice of x h will be accepted in any PBE, leading to a strictly lower payoff. This implies that 
$$Eu_{s} (h\,\mid\,u_{s}^{l} )\,\poundsh \,\les \,h_{t} (u_{t}^{l} )u_{s}^{l} (x_{h} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ))u_{s}^{l} (x_{l} )$$
, which implies that the equilibrium condition, 
$$Eu_{s} (h\,\mid\,u_{s}^{l} )\ges Eu_{s} (m\,\mid\,u_{s}^{l} )$$
, cannot hold for sufficiently low 
$$h_{t} (u_{t}^{l} )$$
.
Proof of Proposition 4: By Lemma 1, the only equilibria in which cheap talk affects the outcome are (1) those in which the 
$$u_{s}^{l} $$
type sends the same signal as the 
$$u_{s}^{m} $$
type, while the 
$$u_{s}^{h} $$
type sends a different signal and (2) those in which the 
$$u_{s}^{l} $$
type sends the same signal as the 
$$u_{s}^{h} $$
type, while the 
$$u_{s}^{m} $$
type sends a different signal.
Consider the first form of signaling equilibrium. In any such equilibrium, following the signal sent by the 
$$u_{s}^{l} $$
and 
$$u_{s}^{m} $$
types (m without loss of generality), 
$$u_{t}^{m} $$
Target type must choose x m because if such Target’s choose x l, then 
$$u_{s}^{m} $$
strictly prefer to deviate from their equilibrium strategy to the signal sent by 
$$u_{s}^{h} $$
types (h). Further, for 
$$h_{s} (u_{s}^{l} )$$
sufficiently low, the Target prefers 
$$x_{m} $$
to 
$$x_{l} $$
following m. In any PBE, 
$$u_{t}^{h} $$
must choose x l following m. Following h, 
$$u_{t}^{m} $$
and 
$$u_{t}^{h} $$
certainly cannot offer x h given beliefs consistent with Bayes’ rule. These considerations imply that the probability of war in such cases is 
$$h_{s} (u_{s}^{h} )(h_{t} (u_{t}^{m} ){\plus}h_{t} (u_{t}^{h} )){\plus}h_{s} (u_{s}^{m} )h_{t} (u_{t}^{h} )$$
.
In a PBE of a world without communication, clearly no Target type can make an offer that if likes less than going to war because there is a positive probability that the offer will be accepted. Thus, the equilibrium probability of war is at least 
$$h_{s} (u_{s}^{h} )(h_{t} (u_{t}^{m} ){\plus}h_{t} (u_{t}^{h} )){\plus}h_{s} (u_{s}^{m} )h_{t} (u_{t}^{h} )$$
, which is the probability of war in the PBE with communication for sufficiently low 
$$h_{s} (u_{s}^{l} )$$
.
Now consider the second form of signaling equilibrium. In any equilibrium of this type, the Target type 
$$u_{t}^{h} $$
must choose x l following the signal sent by 
$$u_{s}^{m} $$
, and then 
$$u_{s}^{m} $$
must choose war in a PBE. Following the signal sent by 
$$u_{s}^{l} $$
and 
$$u_{s}^{h} $$
, Target types 
$$u_{t}^{m} $$
and 
$$u_{t}^{h} $$
must choose x l (no other feasible x that is preferred by these Target types to war has a higher chance of being accepted by the Signaler). Since Signaler types 
$$u_{s}^{l} $$
never elect to fight, these considerations imply that the probability of war in this equilibrium is equal to 
$$h_{t} (u_{s}^{m} )h_{t} (u_{t}^{h} ){\plus}h_{s} (u_{s}^{h} )(h_{t} (u_{t}^{h} ){\plus}h_{t} (u_{t}^{m} ))$$
, which equals the minimum probability of war in the game without cheap talk communication.
Proof of Proposition 5: Take the Signaler’s strategy to be: for 
$$u_{s}^{l} $$
, send m, announce 
$$a_{s} ={{u_{s}^{{m{\minus}1}} (w_{s} ){\plus}u_{t}^{{m{\minus}1}} (w_{t} )} \over 2}\,\equiv\,\chi _{m} $$
following 
$$m,a_{s} ={{\max \{ u_{s}^{{h{\minus}1}} (w_{s} ),u_{t}^{{m{\minus}1}} (w_{t} )\} {\plus}u_{t}^{{l{\minus}1}} (w_{t} )} \over 2}\,\equiv\,\chi _{h} $$
following h, 
$$a_{s} =u_{s}^{{l{\minus}1}} (w_{s} )\,\equiv\,\chi _{l} $$
following any signal other than y=m,h, where the −1 superscripts represent the inverse of the functions, and choose r=0; for 
$$u_{s}^{m} $$
, send 
$$m$$
, announce 
$$a_{s} =\chi _{m} $$
following 
$$m$$
, 
$$a_{s} =\chi _{h} $$
following 
$$h$$
, 
$$a_{s} =\chi _{l} $$
following any signal other than y=m,h, and choose r=1 iff either 
$$a_{t} \,\ne\,a_{s} $$
or 
$$a_{t} \, \lt \, u_{s}^{{m{\minus}1}} (w_{s} )$$
; for 
$$u_{s}^{h} $$
, send h, announce 
$$\chi _{h} $$
following 
$$h$$
, 
$$a_{s} =\chi _{m} $$
following 
$$m$$
, 
$$a_{s} =\chi _{l} $$
following any signal other than y=m,h, and choose r=1 iff either 
$$a_{t} \,\ne\,a_{s} $$
or 
$$a_{t} \, \lt \, u_{s}^{{h{\minus}1}} (w_{s} )$$
.
Take the Target’s strategy to be: for 
$$u_{t}^{l} $$
, announce 
$$a_{t} =\chi _{m} $$
following m, 
$$a_{t} =\chi _{h} $$
following 
$$h$$
, 
$$a_{t} = \chi _{l} $$
following any signal other than y=m,h; for 
$$u_{t}^{m} $$
, announce 
$$a_{t} =\chi _{m} $$
following m, 
$$a_{t} =\chi _{l} $$
following any signal other than y=m; for 
$$u_{t}^{h} $$
, announce 
$$a_{t} =\chi _{l} $$
following any signal.
The Target’s updated beliefs following the signal are: for all 
$$y\,\ne\,m,h$$
, 
$$m(u_{s}^{l} \,\mid\,y)=1$$
, 
$$\mu (u_{s}^{m} \,\mid\,y)=\mu (u_{s}^{h} \,\mid\,y)=0$$
; 
$$\mu (u_{s}^{l} \,\mid\,m)={{h_{s} (u_{s}^{l} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}}$$
, 
$$\mu (u_{s}^{m} \,\mid\,m)={{h_{s} (u_{s}^{m} )} \over {h_{s} (u_{s}^{l} ){\plus}h_{s} (u_{s}^{m} )}}$$
, 
$$\mu (u_{s}^{h} \,\mid\,m)=0$$
; 
$$\mu (u_{s}^{l} \,\mid\,h)=\mu (u_{s}^{m} \,\mid\,h)=0$$
, and 
$$\mu (u_{s}^{h} \,\mid\,h)=1$$
. Note that these beliefs are consistent with Bayes’ rule and the Signaler’s strategy. We need not specify the Signaler’s updated beliefs at its final move except to say that these beliefs must also accord with Bayes’ rule.
The sequential rationality of the Signaler’s war choice follows directly from the Signaler’s payoffs. Consider the optimality of the Signaler’s strategy at information sets at the announcement stage. For type 
$$u_{s}^{l} $$
, at the information set following 
$$m$$
, the Signaler’s strategy results in an expected utility of 
$$(h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} ))u_{s}^{l} (\chi _{m} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} ))u_{s}^{l} (\chi _{l} )$$
given the players’ strategies and beliefs, whereas any other announcement results in 
$$u_{s}^{l} (\chi _{l} )$$
for sure. Similarly, following m ≠ m,h, matching the Target’s announcement of χ l yields the same outcome and payoff as any other announcement. Following y=h, the Signaler’s equilibrium strategy yields an expected payoff of 
$$h_{t} (u_{t}^{l} )u_{s}^{l} (\chi _{h} ){\plus}(1{\minus}h_{t} (u_{t}^{l} )u_{s}^{l} (\chi _{l} )$$
whereas any other announcement yields 
$$u_{s}^{l} (\chi _{l} )$$
for sure.
For type 
$$u_{s}^{m} $$
, at the information set following m, the Signaler’s strategy results in an expected utility of 
$$(h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{l} ))u_{s}^{m} (\chi _{m} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{l} ))w_{s} $$
given the players’ strategies and beliefs, whereas any other announcement results in χ l for sure as the status quo and thus the payoff of w s in the game because the Signaler’s strategy implies that it chooses war in the next stage. Following m≠m,h, matching the Target’s announcement of χ l yields χ l as the status quo and again the war payoff in the game, which is the same result as any other announcement the Signaler might make. Following y=h, the action assigned by the Signaler’s equilibrium strategy yields an expected payoff of 
$$h_{t} (u_{t}^{l} )u_{s}^{m} (\chi _{h} ){\plus}(1{\minus}h_{t} (u_{t}^{l} )w_{s} $$
whereas any other announcement again yields w s for sure.
For type 
$$u_{s}^{h} $$
, at the information sets following m≠h, the Signaler’s assigned action is again optimal because doing so results in w s, the same expected utility as any other announcement in such an information set. Following y=h, the Signaler’s equilibrium strategy yields an expected payoff of 
$$h_{t} (u_{t}^{l} )u_{s}^{h} (\chi _{h} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ))w_{s} $$
whereas any other announcement yields w s for sure.
I now turn to the sequential rationality of the message component of the Signaler’s strategy given the players’ strategies and beliefs in the equilibrium. For type 
$$u_{s}^{h} $$
, the Signaler’s strategy yields an expected utility of 
$$h_{t} (u_{t}^{l} )u_{s}^{h} (\chi _{h} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ))w_{s} $$
whereas any other message m yields w s for sure. For type 
$$u_{s}^{m} $$
, the Signaler’s expected utility from m is 
$$(h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} ))u_{s}^{m} (\chi _{m} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} ))w_{s} $$
whereas it’s expected utility from h is 
$$h_{t} (u_{t}^{l} )u_{s}^{m} (\chi _{h} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ))w_{s} $$
and w s for sure for any other message. For type 
$$u_{s}^{l} $$
, the Signaler’s strategy yields expected utility 
$$(h_{t} (u_{t}^{l} ){\plus}h_{t} (u_{t}^{m} ))u_{s}^{l} (\chi _{m} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ){\minus}h_{t} (u_{t}^{m} ))u_{s}^{l} (\chi _{l} )$$
whereas it’s utility from h is 
$$h_{t} (u_{t}^{l} )u_{s}^{l} (\chi _{h} ){\plus}(1{\minus}h_{t} (u_{t}^{l} ))u_{s}^{l} (\chi _{l} )$$
and 
$$u_{s}^{l} (\chi _{l} )$$
for sure for any other message. Thus, for types 
$$u_{s}^{l} $$
and 
$$u_{s}^{m} $$
, the Signaler’s actions at these information sets are optimal for 
$$h_{t} (u_{t}^{l} )$$
sufficiently low.
Now consider the Target’s strategy given the Target’s beliefs and the Signaler’s strategy. Following h, the Target’s strategy is optimal for the 
$$u_{t}^{l} $$
type because it yields an expected utility of 
$$u_{t}^{l} (\chi _{h} )$$
and any other announcement yields an expected utility of w t. The Target’s strategy for types 
$$u_{t}^{m} $$
and 
$$u_{t}^{h} $$
of announcing χ l is optimal because these types prefer war to χ n and any announcement other than χ n is expected to result in war given the other components of the equilibrium. Following m, the Target’s strategy for the 
$$u_{t}^{l} $$
type yields 
$$u_{t}^{l} (\chi _{m} )$$
whereas any other announcement yields expected utility 
$$h_{s} (u_{s}^{l} )u_{t}^{l} (\chi _{l} ){\plus}(1{\minus}h_{s} (u_{s}^{l} ))w_{t} $$
. Similarly, the Target’s strategy for the 
$$u_{t}^{m} $$
type yields 
$$u_{t}^{m} (\chi _{m} )$$
and any other action for this type yields 
$$h_{s} (u_{s}^{l} )u_{t}^{m} (\chi ^{l} ){\plus}(1{\minus}h_{s} (u_{s}^{l} ))w_{t} $$
. Thus, the Target’s strategy is optimal for 
$$u_{t}^{l} $$
and 
$$u_{t}^{m} $$
for sufficiently low 
$$h_{s} (u_{s}^{l} )$$
. For the 
$$u_{t}^{h} $$
, the Target’s strategy yields 
$$h_{s} (u_{s}^{l} )u_{t}^{h} (\chi _{l} ){\plus}(1{\minus}h_{s} (u_{s}^{l} ))w_{t} \, \gt \, u_{t}^{h} (\chi _{m} )$$
, and any other choice at that information set yields the same or 
$$u_{t}^{h} (\chi _{m} )$$
. Following a signal other than 
$$m$$
or 
$$h$$
, the Target’s strategy yields expected utility 
$$u_{t}^{z} (\chi ^{l} )\, \forall z$$
and any other choice is expected to yield the same.
