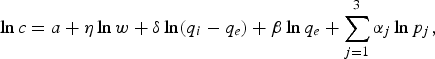1. Introduction
Industrialization is one of the major goals of many developing countries; however, its negative externality problems arise due to ignorance and undervaluation of the environment, which there is no appropriate regulation and/or instrument to control. Government regulations have always played a critical role in protecting environmental media from further deterioration. To protect the environment and to reach a concordant economic, social and environmental development, the Malaysian government enacted the Environmental Quality Act (EQA) and has implemented a set of principles and policies since 1974. Employing various instruments such as market-based instruments (MBI) and a command-and-control (CAC) approach, the Department of Environment (DOE) forces industries to comply with the EQA. However, the number of clean rivers, for instance, decreased from 94 to 79 during 2007–2008 (see table 1). Consequently, there was a significant increase in the number of slightly polluted rivers in 2008 compared with 2007, from 37 to 46. The number of polluted river basins increased from 12 in 2007 to 18 in 2008.
Table 1. Water quality of river basins based on the BOD
Source: DOE (2008).
Based on the Water Quality Index (WQI), in 2006 the number of polluted river basins was seven, which did not decrease during 2007 and 2008. Of these seven polluted river basins, five (or 72 per cent) were located in the states of Selangor and Johor. In 2008, this percentage rose to 85 per cent. The Environmental Quality Report of the DOE shows that there are 54 polluted rivers in Malaysia, six of which are in Selangor and 20 in Johor. In total, 26 (49 per cent) of the polluted rivers are in these states (table 2). Nearly all of these rivers are in Class 3, meaning that extensive treatment is required before effluents can be discharged into the rivers. Also, these two states were reported as the major polluted areas in Malaysia by the DOE (2006). Based on the DOE reports, palm oil mills (POMs) are one of the water polluting sources in Malaysia. POMs are usually located near to rivers in order to use water for their operations and they discharge treated or partially treated wastewater back into the rivers. While there is a special section in the EQA to regulate POMs, they create far greater water pollution problems compared to rubber, textile and paper factories.
The seriousness of the effluent discharge from the POMs is measured in terms of population-equivalent. The population-equivalent load of the raw effluent discharged by a single average-sized POM is as much as the untreated sewage of a city with 300,000 people.
When POM effluent, which is under natural decomposition, is discharged into a water body, the dissolved oxygen of the water body is rapidly depleted as a result of natural biochemical processes. The consequent exhaustion of the dissolved oxygen leads to anaerobic conditions in which foul-smelling gases are created. Other negative impacts include the destruction of aquatic life and the deterioration of river ecosystems.
In order to investigate and improve the environmental policies set for Malaysian industries, the palm oil industry – which is a significant industry in Malaysia – was surveyed. Naturally, examining the effectiveness of the existing tools would be of high interest as it is the very first step in preventing environmental damages and the social costs associated with them.
Theoretically, a polluting firm treats its pollution at a point where the effluent charge equals the marginal cost of abatement. Simply put, firms will not comply if the charge is not greater than the marginal cost of abatement at the standard level (in other words, a polluter will comply when the charge is higher than the marginal cost of abatement at that standard). Thus, the charge should be high enough that a polluter prefers to comply with the standard. Even when the standard level has been achieved, it would be necessary for firms to pay effluent-related fees so that they are encouraged to approach the ultimate goal of zero pollution. Our data collection reveals that almost all of the surveyed POMs use the old pond systems. Hence, imposition of high effluent-related fees would encourage mills to utilize newer technologies to treat their pollution even beyond the standard level. In addition, effluent-related fees and the effluent charge should be modified annually to take inflation into account. However, based on the EQA, effluent-related fees and the effluent charge have not been revised during the last two decades. To our knowledge, there has not been any study to determine them in Malaysia. Therefore, the following questions need to be explored:
• What is the amount of the marginal and total costs of pollution abatement?
• What should the effluent-related fees and effluent charge be at the standard level?
• Why do firms pay the effluent charges instead of complying with the standard?
To answer these questions, the marginal cost function for water pollution abatement should first be estimated. Subsequently, by substituting the value of the standard level into this function, it becomes possible to determine the abatement cost corresponding to the standard level. Firms have to abate if the effluent charge is higher than the marginal cost corresponding to the standard level. Also, setting the effluent-related fee equal to (or above) the marginal cost of abatement encourages firms to employ new technologies and treat their pollution even beyond the standard level (as an ideal goal).
2. The environmental quality regulations for POMs
The crude palm oil industry was considered to be the largest industrial source of organic pollution in comparison with the major pollution sources by industry sectors at this time. It was consequently decided that environmental control of this industry justified a licensed approach that would enable intimate control of mills. The Environmental Quality Regulations 1977 for crude palm oil, promulgated under the enabling powers of Section 51 of the EQA, which are the governing regulations, contain the effluent discharge standards and other regulatory requirements to be imposed on individual POMs through conditions of license. Violating mills have to pay RM 100 per ton for BOD loads exceeding the standard level. In addition, a firm must pay a license renewal fee of RM 100. Based on Malaysian environmental regulations, pollution loads of less than or equal to 15 tons are subject to an effluent fee of RM 150. For pollution loads beyond 15 tons, an additional effluent fee of RM 10 per ton is charged. The effluent-related fees for mills with watercourse and land disposal methods respectively are as follows:
$$\lcub \lsqb \hbox{BOD concentration \lpar mg/1\rpar } \times \hbox{wastewater volume} \lpar {\rm m}^3 \rpar \rsqb /10\hat{}6\rcub \times {\rm RM 10}$$
$$\lcub \lsqb \hbox{BOD concentration \lpar mg/1\rpar } \times \hbox{wastewater volume} \lpar {\rm m}^3 \rpar \rsqb /10\hat{}9\rcub \times {\rm RM 50}$$The standard level of BOD concentration is 100 mg/l and 5,000 mg/l, for watercourse and land disposal methods, respectively. For instance, the fee calculated based on 100 mg/l BOD concentration in 156, 000 m3 wastewater volume for a representative POM is:
$$\lsqb \lpar 100 \times 156\comma \; 000\rpar /10^{\wedge} 6\rsqb \times 10 = \hbox{RM} 156$$Moreover, the firm has a total abatement cost which is computed by the area under the marginal abatement cost (MAC). Figure 1 indicates the present effluent fee and cost of abatement at the standard level of watercourse disposal method.
Figure 1. Current effluent fees
On the other hand, if the firm pollutes beyond the standard, say 120 mg/l, it is charged 100 RM per ton BOD by the DOE. For example, the charges computed for a supplementary 20 mg/l BOD are as follows:
$$\lsqb \lpar 20\times 156000\rpar /10^{\wedge} 6\rsqb \times 100= \hbox{RM } 312$$Therefore, this mill has to pay RM 312 + RM 156 in total.
3. Water pollution abatement cost in previous studies
According to the literature, various types of functional forms have been used for the abatement cost function. Some of them are evaluated herein:
$$\ln c =a+\alpha \ln w+\beta \ln \lsqb q_{i} /q_{e} \rsqb +\sum {b_{j} \ln p_{j}}$$
$$\ln c =a+\alpha \ln w+\beta \ln q_{i} +\gamma \ln q_{e} +\sum {b_{j} \ln p_{j}}$$where c is cost of abatement, w is the volume of wastewater discharged by a firm, q i and q e are concentration levels of pollutant before and after treatment, respectively, and p j is the price of the j th input. Some researchers (see James and Murty, Reference James and Murty1996), have used equation (1), while some others like Roy and Ganguli (Reference Roy and Ganguli1997), Pandey (Reference Pandey1998) and Goldar and Pandey (Reference Goldar and Pandey2001) employed equation (2), which is not as restrictive as equation (1), since the former permits different coefficients for q i and q e. However, both of them have the same shortcoming when q i equals q e, namely neither equation yields a zero cost when there is no pollution abatement. In fact, the cost estimated can even be well above zero in such a case. The two equations above overestimate abatement cost which obviously detracts from the quality of the estimated values. Also, in the economic literature on environment protection, the MAC is a function of pollutant concentration and treatment level of pollutant, but abatement level is neglected in equations (1) and (2).
Some other studies have considered cost function based on the proportion of pollutant treated, leading to the equation below:
$$c=bw^{\eta}\lsqb \lpar q_{i} -q_{e}\rpar /q_{i}\rsqb ^{\delta}\Pi p_{j}^{\beta_{j}}.$$This functional form has two disadvantages. First, the cost of abatement is not only a function of the proportion of pollutant treated but also of the pollutant concentration in the effluent. The latter, however, is neglected in equation (3). Second, after estimation of the model, the value of δ will be less than unity; thus the second-order partial derivative of c with respect to q e will be negative. Hence, the MAC curve cannot have the expected shape, i.e., it has a maximum instead of a minimum.
Some studies excluded the price of inputs in the abatement cost function (e.g., Mehta et al., Reference Mehta, Mundle and Sankar1993). In a study by Hartman et al. (Reference Hartman, Wheeler and Singh1994), the authors specified the abatement cost function as:
$$c=b+\sum \alpha_{j} a_{j} + \sum \beta_{j} a_{j}^{2}$$where a j is the level of abatement for the j th pollutant. In this case, MACs are separately calculated for various pollutants. In this functional form, the economies of scale are not available. Basically, the MAC rises with an increase in the level of abatement implying the positivity of βj, meaning that the MAC does not change inversely with the treated volume of wastewater.
4. Water pollution abatement cost function
4.1. Theoretical specification
According to the existing literature, output of abatement activity could be seen most appropriately as a service. Essentially, a firm reduces pollutants in wastewater. Hence, output of abatement activity is measured by the amount of pollutant reduction achieved for a certain volume of wastewater treated (Goldar et al., Reference Goldar, Misra and Mukherji2001). In this study, the abatement cost function will be estimated based on the abatement in pollutant. Since in Malaysia the standard has been coded in terms of pollutant concentration, in this study pollutant concentration will be used in the model to estimate water pollution abatement cost. Also, the authors were motivated to include wastewater volume in the abatement cost function because the effluent fee and effluent charge are load-based in Malaysia. Inclusion of both pollutant concentration and wastewater volume permits computation of MAC based on the pollution load treated at a specific concentration such as the standard level.
The output of water pollution abatement could be expressed as follows (Goldar et al., Reference Goldar, Misra and Mukherji2001):
$$y = w \lpar q_{i} - q_{e}\rpar \quad \partial y/\partial q_{e} \lt 0.$$The output of pollution abatement could be interpreted as follows. If q i and q e denote BOD concentrations in influent and effluent respectively, then (q i – q e) represents the abatement in BOD per liter of the wastewater treated so that output y represents the reduction in the pollution load. The smaller the q e, the bigger is y. To achieve a higher amount of output, a higher amount of input is required. Hence, the pollutant concentration after treatment, q e, could be written as:
$$q_{e} = f \lpar w\comma \; q_{\rm i}\comma \; X\rpar$$where w is volume of wastewater, q i is pollutant concentration in waste-water before treatment and X is the vector of inputs.
Assuming minimized costs for abatement activities and existence of a competitive market for inputs, the cost function of abatement could be derived as:
$$c = g \lpar p\comma \; y\rpar$$where c denotes abatement cost and p is the vector of input prices. Substituting equation (5) into equation (7), the cost function would be obtained as:
$$c = g \lsqb p\comma \; w\comma \; \lpar q_{i} - q_{e}\rpar \rsqb.$$But q i =(q i − q e) + q e. Thus, equation (8) could be written as:
$$c = g \lsqb p\comma \; w\comma \; \lpar q_{i} - q_{e}\rpar \comma \; q_{e}\rsqb .$$Simultaneous presence of (q i – q e) and q e in the model could be tested after the empirical model has been specified. The abatement cost function could be represented in Cobb–Douglas functional form as:
$$c=bw^{\eta}\lpar q_{i} -q_{e}\rpar ^{\delta} \lpar q_{e}\rpar ^{\beta} \Pi p_{j}^{\alpha_{j}}.$$4.2. Empirical specification
The Cobb–Douglas functional form is popular and useful, and many studies have applied it to estimate cost function of abatement (e.g., Goldar et al., Reference Goldar, Misra and Mukherji2001). In comparison with the Translog function, the Cobb–Douglas is much easier to estimate and has fewer coefficients. Hence, the results of the Cobb–Douglas model will be more significant, especially for samples of relatively small size (like ours). Some previous studies such as Dasgupta et al. (Reference Dasgupta, Huq, Wheeler and Zhang2001) and Khalid (Reference Khalid1993) employed the Cobb–Douglas functional form in their studies. In this study, the Cobb–Douglas cost function for abatement is written as:
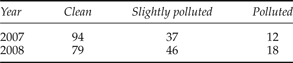
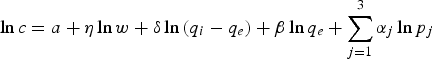$$\ln c=a+\eta \ln w+\delta \ln\, \lpar q_{i} -q_{e} \rpar +\beta \ln q_{e} +\sum_{j=1}^3 \alpha_{j} \ln p_{j}$$where w is the volume of wastewater discharged by a firm, q i and q e are concentration levels of pollutant before and after treatment, respectively, and p j is the price of the j th input (labor, capital and electricity). The estimated values for the parameter αj must be positive and sum to unity.
4.3. Data and variables
The panel data set was used to estimate the abatement cost function for the years 2006–2008. Panel data, with its two-dimensionality, has the advantage of allowing us not only to cross from one firm to another but to observe the time trends and dynamics of changes in short periods of time (Gujarati and Porter, Reference Gujarati and Porter2009).
The sample was chosen based on careful consideration of several factors: mandatory standard level set by DOE, systems of treatment, and types of pollutants which vary from one industry to another. For these reasons, and also noting the level of pollution, POMs were selected as the industry of interest in this study.
The states we chose for our study were Selangor and Johor where there are 88 POMs. These two states were selected due to their high level of pollution compared to other states. Using a self-distribution method (visiting mills) to fill out the questionnaires resulted in a high response rate of 51 per cent. Also, by so doing, we prevented ‘pattern answering’ which might be straight down the page or diagonally across the questions (Brace, Reference Brace2004). Primary data were collected from 45 POMs in these two states using structured questionnaires.
The study utilizes a three-input model. Labor is taken as one input, while capital and electricity are the others. Cost of abatement is obtained as the sum total of costs corresponding to these three inputs. To estimate the abatement cost function, prices of inputs are required. The price of labor is gained from the wage bill of the firms (RM/worker). The price of electricity is calculated based on the price of one kilowatt hour which was recorded in the firms' documents. Adding the costs of repair and replacement to that of investment in treatment systems yields the cost of capital. The price of capital is obtained from the following equation:
$$p_{\rm k} = p_{\rm i}\, \lpar r + d\rpar$$where p k denotes the price of capital, p i the price index of capital goods, d stands for depreciation rate and r represents rate of return on capital. The machinery price index used to obtain the price index of capital goods p i was obtained from the Malaysian Yearbook of Statistics, 2006–2008. Stock of capital goods was computed based on the price in 2006. To measure the rate of return on capital r for each mill, the following formula was employed:
$$\eqalign{r &= \hbox{\lpar total revenue of mill - summing input costs except capital cost\rpar /} \cr & \quad \quad \hbox{total value of assets}}$$All inputs' prices were deflated by the producer price index. Thus, input costs are in real values. The results for all inputs were then summed to yield the total cost which was naturally in real values.
In this study, the data are collected from firms on concentration levels of BOD and wastewater volume in terms of mg/l and cubic meter, respectively. Including BOD and COD simultaneously leads to a multicollinearity problem in the model (James and Murty, Reference James and Murty1996).
4.4. Estimation of the model
Choosing the proper type of panel data is the first step in employing the panel data set in empirical studies. Breusch and Pagan (Reference Breusch and Pagan1980) developed a Lagrange Multiplier test to choose between random effects and pooled OLS models. The result of the test shows that the pooled OLS model is rejected for the panel data model.
To select one of the two types of panel data, the model was checked using the Hausman (Reference Hausman1978) test. The random effects model is rejected in favor of the fixed effects model. In most empirical studies, the reason for employing the fixed effect model is to permit the unobserved firm effects to be correlated with the explanatory variables. Hence, it is a useful tool to estimate unobserved firm effects (Wooldridge, Reference Wooldridge2009). Also, ‘in some applications of panel data methods, we cannot treat our sample as a random sample from a large population, especially when the unit of observation is a large geographical unit such as a state. Thus, it often makes sense to think of each unobserved effect as a separate intercept to do the estimation for each cross-sectional unit. In this case, we use fixed effect method’ (Wooldridge, Reference Wooldridge2009: 493). In our cost model, input prices could be related to unobserved firm effects not because they interact with each other but because the model consists of a series of effects that influence input choice and cost in production decisions (Baltagi, Reference Baltagi2008). Therefore, the fixed effect model seems to be more appropriate for estimating abatement cost.
Inter-firm and inter-temporal standard deviations are employed to choose between one- or two-way fixed effects models. Expectedly, for most of the variables, the standard deviations across units are larger than those within each unit. Hence, the one-way fixed effect model (between cross-sectional units) was chosen as the most appropriate one. The model was estimated by OLS. However, there was a problem with the estimated model, namely the sum of the price coefficients exceeding unity. In other words, it did not meet the linear homogeneity condition of cost functions. Therefore, we imposed the restriction of linear homogeneity and re-estimated the model. The results are reported in table 3. All of the obtained coefficients are statistically significant. Since the results of the restricted model meet the condition of linear homogeneity, they will be employed to compute MAC.
Table 3. Results for water pollution abatement cost after imposing the linear homogenous restriction
Notes: ***, statistical significance at the level of 1%.
As the R-squared suggests, the model satisfactorily fits through the data. The sign of partial derivatives of cost function with respect to every explanatory variable was checked in order to interpret the results and verify that all coefficients are of the signs anticipated. The coefficient of w which indicates the elasticity of cost with respect to wastewater volume was estimated to be less than unity, indicating the existence of economies of scale in abatement activity. The coefficient of (q i − q e) which indicates the level of abatement of BOD is positive, implying that the greater the abatement, the higher is its cost. The estimated coefficient of q e, the BOD concentration in effluent, was found to be negative. This suggests that the lower the BOD concentration in the effluent, the greater will be the abatement cost. The coefficient of factor prices was found to be positive, that is a rise in factor prices increases the abatement cost.
Pollutant concentrations in effluent q e, and abatement in pollutant (q i − q e) are included in the model simultaneously. One may choose to test if (q i − q e) could be omitted from the model. However, if the models are found to be nested models, it could be concluded that (q i − q e) could not be omitted from the analysis. To test the null hypothesis α3 = 0 (α3 is coefficient of (q i − q e)), F-statistics were used. This test was conducted and the related null hypothesis was rejected at the 1 per cent level of significance. It followed that these two models are nested, and the cost function depends on BOD concentration in effluent and abating level in BOD.
4.5. Marginal abatement cost
Table 4 presents the estimated marginal costs of abatement at various levels of BOD concentration in the effluents (on the basis of marginal cost of abatement obtained from the cost function estimated). These estimates are based on the mean values of all variables except q e.Footnote 1 The marginal cost of abatement varies inversely with BOD concentration in the effluent.
Table 4. Marginal abatement cost for various levels of pollutant concentration and load
In Malaysia POMs use two methods of discharge, namely watercourse and land disposals. Computed effluent fees for both are presented in table 4. At the standard level set by DOE (100 mg/l) for watercourse disposal, the corresponding MAC is found to be RM 33.44 (RM1 = US$0.33, August 2010). Since the effluent fee is load based in Malaysia, to investigate whether the effluent fee is effective, the MAC per ton BOD of 100 mg/l and 5,000 mg/l concentrations must be computed. Table 5 indicates that MAC for one ton of BOD with 100 mg/l concentration is RM 213.22. It can be observed in table 6 that the MAC for treating 1 ton of BOD with 5,000 mg/l concentration (which is the standard level set by DOE for the land disposal method) is RM 3.80. The MAC is much lower for the land disposal method than for the watercourse disposal method. This, in our opinion, may increase pollution in groundwater.
Table 5. MAC and effluent-related fees at the standard level for a mill with watercourse disposal method
Table 6. MAC and effluent-related fees at the standard level for a mill with land disposal method
It can be seen in table 4 that, at a BOD concentration of 50 mg/l (which is less than the standard level determined by DOE), the MAC is found to be RM 68.24 per 1 mg/l of BOD. Table 7 shows that the MAC for treating 1 ton of BOD with 50 mg/l concentration is RM 435.11. Should policy makers choose to improve the current standards, they may find the above results useful. However, our findings show that the POMs are using the old ponding system to treat their water pollution and bear a high cost of abatement. Setting a new standard may increase their abatement cost and reduce their profit, and this could lead to a decrease in their competitive power. New technologies should be employed by firms to reduce their cost of abatement before changing the current standard.
Table 7. Marginal abatement cost for a new standard (50 mg/l)
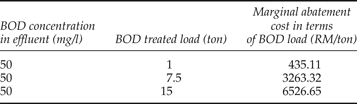
Table 5 presents various levels of BOD load which could be compared with effluent fees at the standard level. The effluent fee is less than the MAC for 1 ton of BOD. With an annual average wastewater discharge of 156, 848 m3, a POM could produce 15.68 tons of BOD with a concentration of 100 mg/l. However, according to table 5, the MAC for the 15th ton of BOD is RM 3198.3, while the effluent fee is only RM 150. The MAC for the 20th ton of BOD is RM 4264.4, while the effluent fee is only RM 200. It can be concluded that the effluent fee is not sufficiently high to encourage firms to approach the ideal goal of zero pollution.
This conclusion holds for the land disposal method where the MAC is very much higher than the effluent fee at the standard level (see table 6). At 5,000 mg/l BOD concentration, effluent fees do not exceed the MAC for various BOD loads. With an annual average wastewater discharge of 156, 848 m3, a POM could produce 785 tons of BOD with a concentration of 5,000 mg/l. However, according to table 6, the MAC for the 785th ton of BOD is RM 2,983, while the effluent fee is only RM 39.25. This result is consistent for the 1st and the 1,000th ton of BOD load, meaning that the MAC is above the effluent fees. In other words, the effluent fee for the land disposal method is not sufficiently high to encourage firms to approach the ultimate target of abatement activity, namely treating pollution perfectly. With an annual average wastewater discharge of 156, 848 m3, a POM could produce 7.5 tons of BOD with a concentration of 50 mg/l. According to table 7, the MAC for the 7.5th ton of BOD is RM 3,263.32. The MAC was RM 6,526.65 for the 15th ton of BOD with a concentration of 50 mg/l, while it was only RM 3,198.3 for the 15th ton of BOD with 100 mg/l concentration. It could be deduced that, if the standard is changed to 50 mg/l, firms will bear a higher cost.
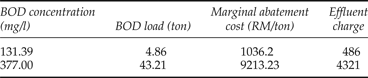
Based on the completed questionnaires, some of the POMs had not met the standard set by DOE. Our collected data revealed that 38 mills, i.e., 83 per cent of the whole sample, violated the standard. This percentage was 80 per cent and 86 per cent for Selangor and Johor, respectively. According to the Environmental Quality for Crude Palm Oil Regulation 1977, the mills violating the standard level are required to pay an effluent charge of RM 100 per ton of BOD. In our sample, the annual average concentrations of BOD (in the wastewater after treatment) were 131.39 mg/l for the watercourse disposal method. Therefore, on average, every POM exceeds the BOD standard for 31 mg/l annually. With an annual average wastewater discharge of 156, 848 m3, a POM could produce 4.86 tons of BOD beyond the standard. They gain economic surplus from current charges. This problem has probably arisen as a result of low effluent charges. The MAC for treating this load of BOD is RM 1,036.08, while the effluent charge is only RM 486. Effluent charges should, consequently, be increased to a level preventing the mills from further polluting. The efficient level should be equal to the MAC or a higher number. The most polluting mill with a BOD concentration of 377 mg/l at the same wastewater volume produces 43.21 tons of BOD load beyond the standard. The MAC to treat this load is RM 9,213.23 (see table 8). For mills which use the land disposal method, our results reveal that the effluent charge is higher than the MAC.
Table 8. Comparing marginal abatement cost and effluent charge for violating mills
5. Conclusion and policy implications
We explored the influence of economic instruments through testing whether effluent fees are sufficiently high to encourage Malaysian POMs to approach the ultimate goal of abatement activities, which is that of treating pollution perfectly. Our study also analyzed whether effluent charges are sufficiently high to force Malaysian POMs to meet the mandatory standard. The results show:
(1) The effluent fees, for watercourse and land disposal methods, are much lower than the MAC of the firms.
(2) The effluent charge is lower than the MAC for firms which use the watercourse disposal method. This causes firms not to abate to the standard level, leading to more polluted surface water resources. Thus, it is recommended here that effluent-related fees be increased to an effective level equaling the firm's marginal costs.
(3) The land disposal method has been less valued in comparison to the watercourse method. In fact, the latitude to which the standard level (100 mg/l in contrast to 5,000 mg/l for the watercourse disposal method) entitles the firms has led to extensive pollution of the land and groundwater resources. From an economic standpoint, pollution raises the community's costs and affects social welfare in the long run. Thus, it is recommended that effluent fees be increased to an effective level equaling and/or exceeding firms' marginal costs.
(4) Thanks to the existence of economies of scale in abatement activities, the standard level for BOD can be increased to 50 mg/l.
(5) In view of the low charge and high abatement costs, firms are benefiting from paying the low charges from polluting, rather than paying the high costs of abating.
The policy prescription is as follows:
Considering the marginal benefit of firms is essential in improving the standards. In fact, if the standards are improved disregarding the incurred costs, the competitiveness of firms – especially that of the smaller ones – will be affected. A two-stage program is recommended. In the first stage, charges should be increased to the marginal cost associated with the present standard level. Doing so takes from the firms their extra surplus. In the second stage, new standards should be introduced (but not compulsorily), and the income resulting from the increased charges should be granted to the firms accepting the standards, in the form of long-term loans with negligible interests so that they can make use of new technologies and reduce their abatement costs. Once a considerable number of firms have adopted the standard, the standard must be enforced so that the remaining firms will join the program too. It is noteworthy that this program should be executed for all firms simultaneously so that a significant earning could be made from the increase in the charges.
