A. Synthesis

A sample of Ag₆GeO₃ was synthesized via the cation exchange method (Pugh, Reference Pugh1926; Ouyang et al., Reference Ouyang, Kikugawa, Zou and Ye2009). We first prepared the precursor Na₂GeO₃ from stoichiometric amounts of reagent-grade chemicals Na₂CO₃ (99.5%) and GeO₂ (99.99%). They were well mixed and heated at 1173 K for 12 h, followed by quenching in air. The obtained Na₂GeO₃ sample was subsequently mixed with AgNO₃ chemical (99.8%) in molar ratios of [Na₂GeO₃:AgNO₃]=[1:4] and heated at 483 K for 40 h. The product was washed by distilled water to remove excess AgNO₃ and by-product NaNO₃. Finally, the resulting sample was dried at 343 K for 8 h to obtain the powder specimen, which was mainly consisting of Ag₂GeO₃ together with small amounts of Ag metal and Na₂GeO₃ .

B. Data collection

A diffractometer (X’Pert PRO Alpha-1, PANalytical B.V., Almelo, The Netherlands), equipped with an incident-beam Ge(111) Johansson monochromator to obtain Cu Kα ₁ radiation and a high-speed detector, was used in the Bragg-Brentano geometry. The X-ray generator was operated at 45 kV and 40 mA. A variable divergence slit was used to keep a

Figure 1. (Color online) (Color online) Comparison of the observed diffraction pattern of Ag₂GeO₃, Ag, and Na₂GeO₃ (symbol: +) with the corresponding calculated pattern (upper solid line). The difference curve is shown in the lower part of the diagram. Vertical bars indicate the positions of possible Bragg reflections for Ag₂GeO₃, Ag, and Na₂GeO₃.

constant illuminated length of 5 mm on the specimen surface. Other experimental conditions were the following: continuous scan, experimental 2θ range from 6.0039° to 148.9353° (an accuracy of ±0.0001° 2θ), 17 107 total data points, and 17.5 h total experimental time. The structure data were standardized according to the rules formulated by Gelato and Parthé (Parthé and Gelato, Reference Parthé and Gelato1984) using the computer program STRUCTURE TIDY (Gelato and Parthé, Reference Gelato and Parthé1987). The crystal-structure models were visualized with the computer program VESTA (Momma and Izumi, Reference Momma and Izumi2008).

A. Crystal structure refinement

The XRPD pattern in Figure 1 showed the presence of weak diffraction intensities peculiar to Ag and Na₂GeO₃; hence we carefully determined the peak positions with Ag₂GeO₃ by finding minima in the second derivatives using the computer program PowderX (Dong, Reference Dong1999). The 2θ values of 26 observed peak positions were then used as input data to the automatic indexing computer program TREOR90 (Werner et al., Reference Werner, Eriksson and Westdahl1985). One orthorhombic unit cell was found with satisfactory figures of merit: M26/F26=37/37 (0.006 174, 115) (de Wolff, Reference de Wolff1968; Smith and Snyder, Reference Smith and Snyder1979). The derived unit-cell parameters of a=0.463 10(6) nm, b=0.713 90(6) nm, and c=1.041 01(8) nmcould index all reflections with Ag₂GeO₃ in the observed diffraction pattern. The observed diffraction peaks were examined to confirm the presence or absence of reflections. There was no systematic absence for hkl, 0kl, h0l, nor hk0 reflections, which implied that one of the possible space groups was P2₁2₁2₁. This space group and the derived unit-cell dimensions were in accord with those of Ag₂SiO₃ [space group P2₁2₁2₁ and unit-cell dimensions a=0.4527(1) nm, b=0.7108(1) nm, and c=0.9959(1) nm], which strongly suggests that Ag₂GeO₃ and Ag₂SiO₃ are isotypic.

The initial structural parameters of Ag₂GeO₃ were taken from those of Ag₂SiO₃ (Jansen et al., Reference Jansen, Heidebrecht, Matthes and Eysel1991). There are six independent sites (i.e., two Ag site, one Ge site, and three O sites) with the Wyckoff position 4a in the unit cell. The structural parameters of all atoms were refined by the Rietveld method (Rietveld, Reference Rietveld1967) using the computer program RIETAN-FP (Izumi and Momma, Reference Izumi and Momma2007) with the profile-intensity data in the 2θ range of 13.0059° to 148.9353° (Figure 1). The structural model of Ag metal (Becherer and Ifland, Reference Becherer and Ifland1954) and that of Na₂GeO₃ (Cruickshank et al., Reference Cruickshank, Kalman and Stephens1978) were included in the refinement as coexisting phases. A Legendre polynomial with 12 adjustable parameters was fitted to background intensities. The split Pearson VII function (Toraya, Reference Toraya1990) was used to fit the peak profiles. The preferred-orientation parameter of March-Dollase function (Dollase, Reference Dollase1986), r, was refined to be r=0.972(2)with the preferred-orientation vector [001], suggesting that the crystal grains were slightly fractured along the cleavage planes parallel to (001). Isotropic displacement (B) parameters were assigned to all atoms. All of the B parameters of oxygen atoms were constrained to have the same value. Reliability indices (Young, Reference Young and Young1993) for a final result were R_wp=5.58%, S(=R_wp/R_e)=1.26, and R_p=4.20% (R_B=0.67% and R_F=0.35% for Ag₂GeO₃). Crystal data are given in Table I

TABLE I. Crystal data for Ag₂GeO₃.

TABLE II. Structural parameters for Ag₂GeO₃.

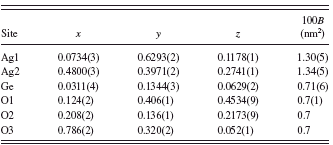
and the final atomic positional and B parameters are listed in Table II.

Quantitative X-ray analysis with correction for microabsorption according to Brindley’s procedure (Brindley, Reference Brindley1949) was implemented in the program RIETAN-FP. The phase composition was found to be 96.5 mass % Ag₂GeO₃, 1.2 mass % Ag, and 2.3 mass % Na₂GeO₃. These values are in accord with those of the potocatalyst specimen (92.6 mass % Ag₂GeO₃, 3.4 mass % Ag, and 4.0 mass % Na₂GeO₃) that was prepared in a previous study (Ouyang et al., Reference Ouyang, Kikugawa, Zou and Ye2009).

B. Structure description

Figure 2 shows the refined structural model of Ag₂GeO₃. The structure is isomorphous with Ag₂SiO₃. Selected interatomic distances and bond angles, together with their standard deviations, are listed in Table III). There are two crystallographically independent silver atoms, Ag1 and Ag2. Each Ag1 atom is coordinated by three O atoms and each Ag2 atom is almost linearly coordinated by two O atoms. These Ag atoms aggregate to form a layered structure (Figure 3, in analogy with Ag₂SiO₃. Individual silver layers are stacked along the [001] direction, and they are interconnected via infinite single chains of [Ge₂O₆] to form a three-dimensional structure.

The chains of [Ge₂O₆] are running parallel to [100], with two tetrahedra per identity. The mean Ge-O bond length of 0.176 nm in the GeO₄tetrahedra is in good agreement with

Figure 2. (Color online) (Color online) Perspective a-axis projection of Ag₂GeO₃. Numbering of silver atoms corresponds to those given in Table II.

TABLE III. Bond lengths (nm) and angles (deg) for Ag₂GeO₃.

^a Symmetry transformations used to generate equivalent atoms: −x+1/2, −y, z+1/2.

^b Symmetry transformations used to generate equivalent atoms: −x, y+1/2, −z+1/2.

^c Symmetry transformations used to generate equivalent atoms: x+1/2, −y+1/2, −z.

that expected from the bond valence sum (0.1748 nm). The O-Ge-O angles (the mean value=109.5°) are more distorted from the regular tetrahedral value than the O-Si-O angles in Ag₂SiO₃. These mean values are in good agreement with those found in other metagermanates Na₂GeO₃ (Cruickshank

Figure 3. (Color online) (Color online) Arrangement of silver atoms in Ag₂GeO₃. Numbering of atoms corresponds to those given in Table II.

et al., Reference Cruickshank, Kalman and Stephens1978), CoGeO₃ (Peacor, Reference Peacor1968), and MnGeO₃ (Fang et al., Reference Fang, Townes and Robinson1969). As is common for germanates and silicates, the Ge-O (bridging)-Ge angle (129.5°) in Ag₂GeO₃ is smaller than the Si-O-Si angle (131.4°) in Ag₂SiO₃. The polyhedral volume of [GeO₄] (0.002 798 nm³) is larger than that of [SiO₄] (0.002 230 nm³) . Because the tetrahedral chains lie between the silver layers, the interlayer spacings are larger for Ag₂GeO₃ than for Ag₂SiO₃.

It was reported that the bonding Ag(I)-Ag(I) interactions usually range from 0.289 to 0.340 nm (Jansen, Reference Jansen1980, Reference Jansen1987). The silver-silver distances within individual silver layers satisfy this requirement for both Ag₂GeO₃ and Ag₂SiO₃; they are 0.2992(2) to 0.3390(2) nm for the former (Table III) and 0.2933(1) to 0.3352(1) nm for the latter. This implies that the attractive interaction between silver atoms would be actually operative and indispensable for the stabilization of the silver substructure. On the other hand, between the silver layers, the Ag(I)-Ag(I) interaction is not expected for Ag₂GeO₃ but anticipated for Ag₂SiO₃ because the nearest silver-silver distances between adjacent layers are 0.3591(2) (>0.340) nm for the former and 0.3359(1) (<0.340) nm for the latter. Consequently, the Ag₂GeO₃ structure can be characterized by the absence of attractive interaction between the silver layers, although the two silver compounds are isotypic.