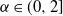1 Introduction
Strong ergodicity of Markov processes is an important topic in ergodic theory for stochastic processes. Lyapunov (drift) criteria have been used to provide sufficient conditions for strong ergodicity of Markov processes; see, e.g., [Reference Chen2, Reference Chen3, Reference Chen and Wang4, Reference Down, Meyn and Tweedie5, Reference Meyn and Tweedie10, Reference Wang16]. In principle some of these results also provide necessary conditions, but to apply them to establish absence of strong ergodicity requires showing that no suitable Lyapunov function exists, which is usually impractical. Thus the aim of this paper is to provide applicable sufficient (Lyapunov) conditions for non-strong ergodicity.
It is well known that for a right continuous, strongly ergodic Markov process, expectations of hitting times of non-negligible sets are uniformly bounded. Our main results exploit this observation, via application of some martingale ideas, in two different, but related, forms.
First, we extend some Lyapunov function ideas for establishing non-integrability of passage times; see, e.g., [Reference Fayolle6] for null recurrence of Markov chains, and [Reference Stramer and Tweedie14] for general Markov processes. We extend the method to non-strong ergodicity. Second, we take properties of the Green function to motivate development of a sufficient condition in terms of a sequence of Lyapunov functions. We show that one or other of these criteria can be used to obtain sharp results in the case of some simple one-dimensional birth–death or diffusion processes (Section 1), some diffusions on Riemannian manifolds (Section 3), and multidimensional Ornstein–Uhlenbeck processes driven by 
$\alpha$-stable noises (Section 4).
Let 
$(X_t)_{t\geqslant 0}$ be a Markov process on a Polish space 
$(E,\mathscr{E})$ with transition function 
$P_t(x,\cdot)$. A 
$\sigma$-finite measure 
$\pi$ on 
$(E,\mathscr{E})$ is called an invariant measure for 
$(X_t)_{t\geqslant 0}$ if, for all 
$t>0$ and 
$A\in \mathscr{E}$, 
$\pi(A)=\int_{E}P_t(x,A)\pi(\mathrm{d} x)$. The process is called ergodic if there exists a unique invariant probability measure 
$\pi$ such that, for all 
$x \in E$, 
$\lim\limits_{t\rightarrow\infty}\|P_t(x,\cdot)-\pi(\cdot)\|_{\mathrm{Var}}=0,$ where 
$\|\cdot\|_{\mathrm{Var}} $ denotes total variation distance.
In this paper we are interested in strong ergodicity. 
$(X_t)_{t\geqslant 0}$ is said to be strongly ergodic (or uniformly ergodic) if there exist 
$\varepsilon>0$, a constant 
$C>0$, and a (unique) invariant probability measure 
$\pi$ such that, for all 
$t\geqslant 0$,
\begin{equation*}\sup\limits_{x\in E}\|P_t(x,\cdot)-\pi(\cdot)\|_{\mathrm{Var}}\leqslant C \mathrm{e}^{-\varepsilon t}.\end{equation*}
From now on, we suppose that 
$(X_t)_{t\geqslant 0}$ is a time-homogeneous right continuous Markov process and evolves on a probability space 
$(\Omega, \mathscr{F}, (\mathscr{F}_t)_{t\geqslant0},\mathbb{P})$ with natural filtration 
$(\mathscr{F}_t)_{t\geqslant0}$. Assume that 
$(X_t)_{t\geqslant 0}$ is progressively measurable, so that for any 
$A\in \mathscr{E}$ its hitting time 
$\tau_{A}\,:{=}\break\inf\{t\geqslant 0\,:\, X_t\in A\}$ is a stopping time with respect to 
$(\mathscr{F}_t)_{t\geqslant0}$.
We recall several notions that we are going to use in our main results. Let 
$\{E_n\}_{n=1}^{\infty}\subset \mathscr{E}$ be a sequence of bounded open sets such that 
$E_n\uparrow E$, which means that
\begin{equation*} E_1 \subseteq E_2 \subseteq \cdots , \qquad \bigcup_nE_n=E.\end{equation*}
Denote 
$\zeta=\lim\limits_{n\rightarrow\infty}\tau_{E_n^{\rm c}}$. The process 
$(X_t)_{t\geqslant 0}$ is called non-explosive if 
$\mathbb{P}_x[\zeta=\infty]=1$ for all 
$x\in E$.
Let L be the infinitesimal generator of the process 
$(X_t)_{t\geqslant 0}$ whose domain D(L) is given by
\begin{equation*}\begin{split}D(L)\,:{=}\,\bigg\{&f \,:\, (E, \mathscr{E})\rightarrow (\mathbb{R},\mathscr{B} )\ \text{is measurable:}\ \lim_{h\rightarrow0}\frac{\mathbb{E}_x[\,f(X_h)]-f(x)}{h}\ \text{exists pointwise,} \\&\text{and satisfies } \lim\limits_{h\rightarrow0}\mathbb{E}_x[L\kern2pt f(X_h)]=L{\kern2pt}f(x)\bigg\}.\\\end{split}\end{equation*}
Following [Reference Down, Meyn and Tweedie5], we use an enlarged domain of L as follows:
\begin{equation*}\begin{split}D_w(L)\,:{=}\,\bigg\{&f \,:\, (E, \mathscr{E})\rightarrow (\mathbb{R},\mathscr{B} )\ \text{is measurable, } \text{such that}\, f(X_t)-f(X_0)- \!\! \int_{0}^{t} \!\!\! L{\kern2pt}f(X_s)\mathrm{d} s\\& \text{is a local martingale}\bigg\}.\\\end{split}\end{equation*}
We say 
$(L,D_w(L))$ is the extended generator of 
$(X_t)_{t\geqslant 0}$. According to [Reference Meyn and Tweedie11, p. 522], 
$D(L)\cap\{\,f\,:\,L{\kern2pt}f \ \text{is locally bounded}\}\subset D_w(L)$.
A measurable function 
$f\,:\,E\rightarrow\mathbb{R}_+$ is called a norm-like function (or compact function) if, for some sequence of bounded open sets 
$E_n \uparrow E$, 
$\lim_{n\rightarrow\infty}\inf_{x\notin E_n}f(x)=\infty$, which means that for each 
$r>0$, the level sets 
$L_r(\,f)\,:\!= \{x\,:\,f(x)\leqslant r\}$ are precompact and satisfy 
$L_r(\,f)\neq E$; see [Reference Meyn and Tweedie11, p. 522].
Note that the last condition, 
$L_r(\,f)\neq E$, is indispensable. For example, if E is a compact space, then the level sets 
$L_r(\,f)$ are always precompact for any measurable function f even if it is bounded. In fact, a non-explosive Markov process on compact space is strongly ergodic. We will also find that in Theorem 1, for this process the test function u does not exist.
Now we state the main results of this paper. The proofs will be presented in Section 2.
Theorem 1. Assume that 
$(X_t)_{t\geqslant 0}$ is non-explosive and ergodic. Let 
$H\subset E$ be closed and bounded, with 
$\pi(H)>0$. If there exist non-negative norm-like functions 
$u,v\in D_w(L)$ such that
(a) u is locally bounded, and for all
$x\notin H$, $Lu(x)\geqslant -1$;-
(b) there exists a constant
$d > 0$ such that $Lv(x)\leqslant d \textbf{1}_H(x) $; -
(c) for some sequence of bounded open sets
$E_n \uparrow E$, $\lim\limits_{n\rightarrow\infty}\sup\limits_{x\notin E_n}u(x)/v(x)=0,$
then 
$(X_t)_{t\geqslant 0}$ is non-strongly ergodic.
(1) In fact, the test function u is closely connected with the first moment of hitting time of H; see (2.6) in the proof of Theorem 1. So, if E is a compact space, then u which satisfies condition (a) cannot be a norm-like function.
-
(2) In particular, let E be a countable state space, H be a non-empty finite subset of E, and
$(X_t)_{t\geqslant 0}$ be a Q-process with an irreducible regular Q-matrix $Q=(q_{ij})_{i,j\in E}$, its generator L being defined as $(L{\kern2pt}f)_i=\sum_{j\in E'}q_{ij}f_j$ for $f=(\,f_i)_{i\in E'}$. According to [Reference Meyn and Tweedie11], any finite-valued function on E is included in $D_w(L)$.Applying Theorem 1 to this Q-process, we have that if there exist u, v such that
(a)
$\text{for all } i\notin H, \sum_{j\in\mathbb{Z}_+}q_{ij}u_j\geqslant -1$ and $\sum_{j\in\mathbb{Z}_+}q_{ij}v_j\leqslant 0 $;-
(b)
$\varlimsup\limits_{i\rightarrow\infty}u_i=\varlimsup\limits_{i\rightarrow\infty}v_i=\infty$ and $\varlimsup\limits_{i\rightarrow\infty}u_i/v_i=0$,
then this Q-process is non-strongly ergodic.
(3) A different criterion for non-strong ergodicity of a Markov chain is obtained in [Reference Menshikov and Petritis9, Theorem 1.15(2)] (they call non-strong ergodicity ‘implosion does not occur’). The criterion is proved by a semimartingale approach for the Markov chain (see [Reference Menshikov and Petritis9, p.2396]) and the idea is different from our method. For Markov chains, these two methods are both applicable.
Next, we use a Green-function idea to study expected hitting times. Let D be a domain with 
$\pi(D^{\rm c})>0$, and define 
$P_t^D(x, A)\,:{=}\,\mathbb{P}_x[X_t\in A,\tau_{D^{\rm c}}>t]$. Assume that 
$P_t^D(x, \cdot)$ has a density 
$p_t^D(x, y)$ with respect to invariant measure 
$\pi(\mathrm{d} y)$. Then we define the Green function on D as 
$G_D(x,y)=\int_{0}^{\infty}p_t^D(x, y)\mathrm{d} t$. If 
$\mathbb{E}_x \tau_{D^{\rm c}}<\infty$ (the condition is ensured by ergodicity and 
$\pi(D^{\rm c})>0$), then
\begin{align*} u_D(x) &\,:{=}\, \int_DG_D(x,y)\pi(\mathrm{d} y)=\int_D \int_{0}^{\infty}p_t^D(x, y)\mathrm{d} t \, \pi(\mathrm{d} y) \\[3pt] &= \int_{0}^{\infty}\mathbb{P}_x(\tau_{D^{\rm c}}>t)\mathrm{d} t=\mathbb{E}_x\tau_{D^{\rm c}}.\end{align*}
Let H and 
$\{E_n\}_{n=1}^{\infty}\subset \mathscr{E}$ be as in Theorem 1. Assume that 
$(X_t)_{t\geqslant 0}$ is ergodic; then, the Poisson equation
\begin{align}\begin{cases}
Lu_n(x)= -1, \quad & \text{in}\ E_n\setminus H, \\
u_n(x)=0, & \text{in} \ E_n^{\rm c}\cup H,
\end{cases}\end{align}
has finite solution 
$u_n(x)=\mathbb{E}_x[\tau_H\wedge \tau_{E_n^{\rm c}}]=\int_{E_n\setminus H}G_{E_n\setminus H}(x,y)\pi(\mathrm{d} y)$. Hence, the solution of the Poisson equation (1.1) could be represented by a Green function. If 
$\sup\limits_{x\notin H}\varlimsup\limits_{n\rightarrow\infty}u_n(x)=\infty$, then
\begin{equation*}\sup\limits_{x\notin H}\mathbb{E}_x\tau_H=\sup\limits_{x\notin H}\varlimsup\limits_{n\rightarrow\infty}\mathbb{E}_x[\tau_H\wedge \tau_{E_n^{\rm c}}]=\sup\limits_{x\notin H}\varlimsup\limits_{n\rightarrow\infty}u_n(x)=\infty,\end{equation*}
and therefore, by [Reference Mao7, Lemma 2.1], the process is non-strongly ergodic.
Motivated by this fact, we have the following result (the proof will be presented in Section 2).
Theorem 2. Assume that 
$(X_t)_{t\geqslant 0}$ is non-explosive and ergodic. Let H and 
$\{E_n\}_{n=1}^{\infty}\subset \mathscr{E}$ be as in Theorem 1. If, for each 
$n\geqslant1$, there exists a non-negative function 
$u_n(x)\in D_w(L)$ such that
(a)
$\text{for all } x\in E_n\setminus H$, $Lu_n(x)\geqslant -1$;-
(b)
$u_n(x)=0$ in $ E_n^{\rm c}\cup H$, and $u_n$ is bounded in $E_n\setminus H$; -
(c)
$\sup\limits_{x\notin H}\varlimsup\limits_{n\rightarrow\infty}u_n(x)=\infty,$
then 
$(X_t)_{t\geqslant 0}$ is non-strongly ergodic.
As the first step of our applications, let us check three simple examples. The following three corollaries are known, and our new methodology is applied to reproduce these results as motivation.
Corollary 1. (Diffusion process on haLf-line.) Let 
$L=a(x)\frac{\mathrm{d}^2}{\mathrm{d}x^2}+b(x)\frac{\mathrm{d}}{\mathrm{d}x}$, 
$a(x)>0$, and a,b continuous on 
$(0,\infty)$. Define 
$C(x)=\int_{1}^{x}(b(y)/a(y))\mathrm{d}y$ and 
$m(\mathrm{d} x)={a(x)}^{-1}\mathrm{e}^{C(x)}\mathrm{d} x$. Suppose the L-diffusion process 
$(X_t)_{t\geqslant 0}$ on 
$[0,\infty)$ with reflecting boundary at 0 is non-explosive and ergodic, i.e.
\begin{equation*}\int_{0}^{\infty}\mathrm{e}^{-C(y)}\left(\int_{0}^{y}\frac{\mathrm{e}^{C(z)}}{a(z)}\mathrm{d}z\right)\mathrm{d}y=\infty, \qquad m([0,\infty))<\infty.\end{equation*}
According to [Reference Mao7, Theorem 2.1], the process is strongly ergodic if and only if
\begin{equation*}\delta\,:{=}\,\int_{0}^{\infty}\mathrm{e}^{-C(y)}\left(\int_{y}^{\infty}\frac{\mathrm{e}^{C(z)}}{a(z)}\mathrm{d}z\right)\mathrm{d}y<\infty.\end{equation*}
Proof. Here we only consider the necessity, i.e. if 
$\delta=\infty$, then the process is non-strongly ergodic.
In order to apply Theorem 1, let 
$u(x)=\int_{0}^{x}\mathrm{e}^{-C(y)}\left(\int_{y}^{\infty}{a(z)}^{-1}\mathrm{e}^{C(z)}\mathrm{d}z\right)\mathrm{d}y$ and 
$v(x)=\int_{0}^{x}\mathrm{e}^{-C(y)}\mathrm{d} y$; then, 
$Lu=-1$ and 
$Lv=0$. Since 
$\delta=\infty$, 
$\lim\limits_{x\rightarrow\infty}u(x)=\delta=\infty$. Because the process is ergodic, it is recurrent, so 
$\int_{0}^{\infty}\mathrm{e}^{-C(y)}\mathrm{d} y=\infty$. Therefore, 
$\lim\limits_{x\rightarrow\infty}v(x)=\infty$. Thus, by L’Hôspital’s rule and ergodicity,
\begin{equation*}\lim\limits_{x\rightarrow\infty}\frac{u(x)}{v(x)}=\lim\limits_{x\rightarrow\infty}\int_{x}^{\infty}\frac{\mathrm{e}^{C(y)}}{a(y)}\mathrm{d}y=0.\end{equation*}
By Theorem 1, we see that the process is non-strongly ergodic.
Now we apply Theorem 2. Let 
$E_n=(0,n)$, 
$H=(0,1)$. For 
$n\geqslant2$ and 
$1\leqslant x,y\leqslant n$, the Green function on 
$E_n\setminus H$ can be represented as
\begin{equation*}G_{1,n}(x,y)=\frac{(s(n)-s(x\vee y))(s(x\wedge y)-s(1))}{s(n)-s(1)},\end{equation*}
where 
$s(x)=\int_{1}^{x}\mathrm{e}^{-C(y)} \mathrm{d} y$ satisfies 
$\lim\limits_{n\rightarrow\infty}s(n)=\infty$. Let 
$u_n(x)=\int_{1}^{n}G_{1,n}(x,y)m(\mathrm{d} y)$. For 
$x>1$,
\begin{equation*}\begin{split}\lim\limits_{n\rightarrow\infty}u_n(x)&=\int_{1}^{x}\mathrm{e}^{-C(t)}\left[\int_{t}^{x}\frac{1}{a(l)}\mathrm{e}^{C(l)}\mathrm{d} l\right]\mathrm{d} t+(s(x)-s(1))\int_{x}^{\infty}\frac{1}{a(l)}\mathrm{e}^{C(l)}\mathrm{d} l\\[3pt] &=\int_{1}^{x}\mathrm{e}^{-C(t)}\left[\int_{t}^{\infty}\frac{1}{a(l)}\mathrm{e}^{C(l)}\mathrm{d} l\right]\mathrm{d} t.\end{split}\end{equation*}
Hence, when 
$\delta=\infty$, according to Theorem 2, the process is non-strongly ergodic.
Corollary 2. (Single-birth processes.) Let 
$Q=(q_{ij})_{i,j\in\mathbb{Z}_+}$ be a single-birth Q-matrix, i.e. 
$q_{i,i+1}>0$, 
$q_{i,i+j}=0$ for 
$i\in \mathbb{Z}_+$, 
$j\geqslant2$. Assume that Q is totally stable and conservative: 
$q_i\,:\!=-q_{ii}=\sum_{j\neq i}q_{ij}<\infty$. Define
\begin{align*}q_n^{(k)}=\sum_{j=0}^{k}q_{nj}, \quad F_n^{(n)}=1, \quad F_n^{(i)}=\frac{1}{q_{n,n+1}}\sum_{k=i}^{n-1}q_n^{(k)}F_k^{(i)}, \qquad 0\leqslant i<n,\\[3pt] d_0=1, \quad d_n=\frac{1}{q_{n,n+1}}\left(1+\sum_{k=0}^{n-1}q_n^{(k)}d_k\right), \quad n\geqslant 1, \qquad d\,:{=}\,\sup_{k\in\mathbb{Z}_+}\frac{\sum_{n=0}^{k}d_n}{\sum_{n=0}^{k}F_n^{(0)}}.\end{align*}
Assume that the Q-process is ergodic, i.e. 
$d<\infty$. According to [Reference Zhang17, Theorem 1.1], the Q-process is strongly ergodic if and only if 
$\sup_{k\geqslant 0}\sum_{n=0}^{k}(F_n^{(0)}d-d_n)<\infty$.
Proof. Here we only consider the necessity. Let 
$H=\{0\}$ and 
$u_k=\sum_{n=0}^{k-1}(F_n^{(0)}d-d_n)$, 
$v_k=\sum_{n=0}^{k-1}F_n^{(0)}$. It is well known that if 
$d<\infty$, then u, v satisfy 
$\sum_{j\geqslant 0}q_{ij}u_j=-1, \ \sum_{j\geqslant 0}q_{ij}v_j=0$, for 
$i\notin H$. By [Reference Zhang17, Remarks 2.3(ii)], 
$\lim\limits_{k\rightarrow\infty}{d_k}/{F_k^{(0)}}=d$, and hence 
$\lim\limits_{k\rightarrow\infty}u_k/v_k=0$. Therefore, the non-strong ergodicity follows from Remark 1(2).
Corollary 3. Let 
$Q=(q_{ij})_{i,j\geqslant 0}$ be a birth–death Q-matrix with
\begin{equation}q_{ij}=\left\{\begin{split}&p_i, & \ j=i+1;\\&q_i,& \ j=i-1;\\&q_0,& \ j=i=0;\\&0,& \ \text{otherwise}.\\\end{split}\right.\end{equation}
(1) If
$p_i=q_i=i^{\alpha}$ with $\alpha>1$, then the process is ergodic; furthermore, if $\alpha\leqslant2$, then the process is not strongly ergodic.-
(2) If
$p_i\equiv p>0$, $q_i\equiv q>p$, then the process is ergodic but not strongly ergodic. -
(3) If
$p_i\equiv p$, $q_i=i^\alpha$ with $\alpha\in (0,1]$, then the process is non-strongly ergodic.
Proof.
(1) If
$p_i=q_i=i^{\alpha}$, then the invariant measure $\mu=\sum_{i=1}^{\infty}p_0i^{-\alpha}$, and hence it is ergodic if and only if $\alpha>1$. Furthermore, it is strongly ergodic if and only if $S\,:{=}\,\sum_{i=0}^{\infty}\sum_{j=i+1}^{\infty}j^{-\alpha}<\infty$, i.e. $\alpha>2$ (see [7, Theorem 3.1]). In particular, we can use Theorem 1 to check the non-strong ergodicity. Let $u_i=\log(i+1)$ and $v_i=i$. Then $\lim\limits_{k\rightarrow\infty}u_k/v_k=0$, and
If
\begin{equation*}(Lv)_i=\sum_{j\geqslant 0}q_{ij}v_j=0, \qquad (Lu)_i=\sum_{j\geqslant 0}q_{ij}u_j=i^\alpha\log[1-1/(i+1)^2].\end{equation*}
$\alpha\leqslant 2$, then we can choose N large enough such that, for $i>N$, $(Lu)_i\geqslant-1$. Thus the condition in Remark 1(2) is satisfied, and the process is non-strongly ergodic.
-
(2) If
$p_i\equiv p$, $q_i\equiv q>p$, then the invariant measure $\mu=q^{-1}p_0\sum_{i=1}^{\infty}\left({p}/{q}\right)^{i-1}<\infty$, and hence it is ergodic. Let $H=\{0\}$, $u_i=\log(i+1)$, and $v_i=i$. Then $\lim\limits_{k\rightarrow\infty}u_k/v_k=0$, $(Lv)_i=\sum_{j\geqslant 0}q_{ij}v_j=p-q<0$, and
Thus, the condition in Remark 1(2) is satisfied, and the process is non-strongly ergodic.
\begin{equation*} (Lu)_i=\sum_{j\geqslant 0}q_{ij}u_j=p\log\left(\frac{i+2}{i+1}\right)-q\log\left(\frac{i+1}{i}\right)\geqslant-q\log 2, \quad \text{for all} \ i\notin H.\end{equation*}
-
(3) Let
$u_i=\log(i+1)$, $v_i=i$, and $H=\{0,\ldots, p^{1/\alpha}\vee 1\}$. Then $\lim\limits_{k\rightarrow\infty}u_k/v_k=0$, and for $i\notin H$, $(Lv)_i=\sum_{j\geqslant 0}q_{ij}v_j=p-i^\alpha<0$ and
So the condition in Remark 1(2) is satisfied: the process is non-strongly ergodic.
\begin{equation*} (Lu)_i=\sum_{j\geqslant 0}q_{ij}u_j=p\log\left(\frac{i+2}{i+1}\right)-i^{\alpha}\log\left(\frac{i+1}{i}\right)\geqslant-i^{\alpha-1}\geqslant-1.\end{equation*}
The remainder of this paper is organized as follows. In Section 2 we give proofs of Theorems 1 and 2. In Section 3 we present a new sufficient condition for non-strong ergodicity of diffusion process on a Riemannian manifold and give some examples. In Section 4 we prove the non-strong ergodicity of Ornstein–Uhlenbeck processes driven by symmetric 
$\alpha$-stable noise.
2. General criteria for non-strong ergodicity
In this section we prove Theorems 1 and 2. For this, we need the following result.
Lemma 1. [7, Lemma 2.1] Let 
$(X_t)_{t\geqslant 0}$ be a right continuous Markov process on 
$(E,\mathscr{E})$. If 
$(X_t)_{t\geqslant 0}$ is strongly ergodic, then we have 
$\sup\limits_{x\in E}\mathbb{E}_x\tau_A<\infty$ for any closed set 
$A\subset E$ with 
$\pi(A)>0$.
Proof of Theorem 1. First, fix 
$n\in\mathbb{N}$. According to conditions (a) and (b), we have that, for 
$t\geqslant 0$ and 
$x\in E_n\setminus H$,
\begin{equation}\mathbb{E}_x[u(X_{ t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}})]-u(x)=\mathbb{E}_x\left[\int_{0}^{t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}}Lu(X_s)\mathrm{d} s\right]\geqslant -\mathbb{E}_x[ t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}] \end{equation}
and
\begin{equation*}\mathbb{E}_x[v(X_{ t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}})]-v(x)=\mathbb{E}_x\left[\int_{0}^{t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}}Lv(X_s)\mathrm{d} s\right]\leqslant 0.\end{equation*}
According to Fatou’s lemma, ergodicity, and the fact that 
$\pi(H) > 0$, 
$\mathbb{P}_x(\tau_H < \infty) = 1$ for all 
$x\in E$, we have, for 
$x\in E_n\setminus H$,
\begin{equation}\mathbb{E}_x[v(X_{\tau_{H}\wedge \tau_{E_n^{\rm c}}})]\leqslant \varliminf_{t\rightarrow\infty}\mathbb{E}_x[v(X_{t\wedge \tau_{H}\wedge \tau_{E_n^{\rm c}}})]\leqslant v(x).\end{equation}
Next, note that on 
$\{t<\tau_{H}\wedge \tau_{E_n^{\rm c}}\}$, 
$X_t\in E_n\setminus H$, and hence, by the local boundedness of u, 
$u(X_t)\textbf{1}_{\{t<\tau_{H}\wedge \tau_{E_n^{\rm c}}\}}\leqslant \sup_{x\in {E_n\setminus H}}u(x)\,{=}:\,M_n<\infty$. Thus, by ergodicity,
\begin{equation*}0\leqslant\lim_{t\rightarrow\infty}\mathbb{E}_x[u(X_t)\textbf{1}_{\{t<\tau_{H}\wedge \tau_{E_n^{\rm c}}\}}]\leqslant M_n \lim_{t\rightarrow\infty}\mathbb{P}_x[\tau_{H}\wedge \tau_{E_n^{\rm c}}>t]=0.\end{equation*}
Therefore,
\begin{align}\varlimsup_{t\rightarrow\infty} \! \mathbb{E}_x[u(X_{ t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}})]&= \! \varlimsup_{t\rightarrow\infty} \! \mathbb{E}_x[u(X_{ \tau_{H}\wedge \tau_{E_n^{\rm c}}})\textbf{1}_{\{t\geqslant\tau_{H}\wedge \tau_{E_n^{\rm c}}\}}]+ \! \lim_{t\rightarrow\infty} \! \mathbb{E}_x[u(X_t)\textbf{1}_{\{t<\tau_{H}\wedge \tau_{E_n^{\rm c}}\}}] \nonumber \\[3pt] & \leqslant\mathbb{E}_x[u(X_{ \tau_{H}\wedge \tau_{E_n^{\rm c}}})]. \end{align}
Now, by combining (2.1) and (2.3), according to the dominated convergence theorem, we have
\begin{equation}\mathbb{E}_x[\tau_{H}\wedge \tau_{E_n^{\rm c}}]\geqslant u(x)-\mathbb{E}_x[u(X_{ \tau_{H}\wedge \tau_{E_n^{\rm c}}})].\end{equation}
Since 
$\mathbb{E}_x[u(X_{\tau_{H}\wedge \tau_{E_n^{\rm c}}})]=\mathbb{E}_x[u(X_{\tau_{H}})\textbf{1}_{\{\tau_{H}<\tau_{E_n^{\rm c}}\}}]+\mathbb{E}_x[u(X_{\tau_{E_n^{\rm c}}})\textbf{1}_{\{\tau_{H}>\tau_{E_n^{\rm c}}\}}]$, and, by (2.2),
\begin{equation}\mathbb{E}_x[v(X_{\tau_{E_n^{\rm c}}})\textbf{1}_{\{\tau_{H}>\tau_{E_n^{\rm c}}\}}]\leqslant v(x),\end{equation}
it follows from (2.4), (2.5), and the fact that 
$v \geqslant 0 $ that
\begin{equation*}\begin{split} \mathbb{E}_x[\tau_{H}\wedge \tau_{E_n^{\rm c}}]&\geqslant u(x)-\mathbb{E}_x[u(X_{\tau_{H}})]-\mathbb{E}_x\left[\frac{u(X_{\tau_{E_n^{\rm c}}})}{v(X_{\tau_{E_n^{\rm c}}})}v(X_{\tau_{E_n^{\rm c}}})\textbf{1}_{\{\tau_{H}>\tau_{E_n^{\rm c}}\}}\right]\\[3pt]&\geqslant u(x)-\mathbb{E}_x[u(X_{\tau_{H}})]-\left(\sup_{x\notin E_n}\frac{u(x)}{v(x)}\right)v(x).\\\end{split}\end{equation*}
Let 
$n\rightarrow\infty$; by condition (c), the fact that u is a norm-like function, and 
$\tau_{E_n^{\rm c}}\uparrow\infty$, we get that
\begin{equation}\sup\limits_{x\notin H}\mathbb{E}_x[\tau_{H}]\geqslant \sup\limits_{x\notin H}u(x)-\sup\limits_{x\in H}u(x)=\infty.\end{equation}
Therefore, the process is non-strongly ergodic.
Proof of Theorem 2. First, fix 
$n\in\mathbb{N}$. According to the condition (a) in Theorem 2, for 
$t\geqslant 0$ and 
$x\in E_n\setminus H$,
\begin{equation*}\mathbb{E}_x[u_n(X_{ t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}})]-u_n(x)=\mathbb{E}_x\left[\int_{0}^{t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}}Lu_n(X_s)\mathrm{d} s\right]\geqslant -\mathbb{E}_x[ t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}].\end{equation*}
By a similar argument to the proof of Theorem 1, we get
\begin{align*}\varlimsup_{t\rightarrow\infty}\mathbb{E}_x[u_n(X_{ t\wedge\tau_{H}\wedge \tau_{E_n^{\rm c}}})]&\leqslant\mathbb{E}_x[u_n(X_{ \tau_{H}\wedge \tau_{E_n^{\rm c}}})]+\lim_{t\rightarrow\infty}\mathbb{E}_x[u_n(X_t)\textbf{1}_{\{t<\tau_{H}\wedge \tau_{E_n^{\rm c}}\}}] \\ & \leqslant\mathbb{E}_x[u_n(X_{ \tau_{H}\wedge \tau_{E_n^{\rm c}}})]=0,\end{align*}
where we use condition (b) in the last term. So, for 
$x\in E_n\setminus H$, 
$\mathbb{E}_x[\tau_{H}\wedge \tau_{E_n^{\rm c}}]\geqslant u_n(x)$. Next, by letting 
$n\rightarrow\infty$, according to condition (c) we have, for all 
$x\notin H$, 
$\mathbb{E}_x[\tau_{H}]\geqslant \varlimsup\limits_{n\rightarrow\infty}u_n(x)$. Therefore, 
$\sup_{x\notin H}\mathbb{E}_x[\tau_{H}]\geqslant \sup_{x\notin H}\varlimsup_{n\rightarrow\infty}u_n(x)=\infty$. This proves that 
$(X_t)_{t\geqslant 0}$ is non-strongly ergodic.
3. Diffusion processes
Let M be a d-dimensional complete connected Riemannian manifold, and 
$(X_t)_{t\geqslant 0}$ be a non-explosive and ergodic diffusion process on M with generator 
$L=\Delta+Z$, where Z is a 
$C^1$ vector field. Assume that the generalized martingale problem for L is well posed, i.e. for 
$f\in C^2(M)$ and Lf locally bounded, 
$f(X_t)-f(X_0)-\int_{0}^{t}L{\kern2pt}f(X_s)\mathrm{d} s $ is a local martingale with respect to 
$\mathbb{P}_x$, for any 
$ x\in M$. On a proper local chart of M, the generator L has the form
\begin{equation}L=\sum_{i,j=1}^{d}a_{ij}(x)\frac{\partial^2}{\partial x_i\partial x_j}+\sum_{i=1}^{d}b_i(x)\frac{\partial}{\partial x_i}.\end{equation}
Specially, if 
$M=\mathbb{R}^d$, then the form (3.1) is a global representation. If a is positive definite and symmetric, and a, b are locally bounded, then the martingale problem for L is well posed (see [Reference Pinsky Ross12, Theorem 1.13.1]).
Let 
$\rho\in C^2(M\times M)$ be a distance which need not be a Riemannian metric. Fix 
$o\in M$, let 
$\rho(x)=\rho(x,o)$, and let 
$B_r\,:{=}\,\{x\in M\,:\,\rho(x)\leqslant r\}$ be the geodesic ball. Assume that 
$\sup_x \rho(x)=\infty$.
For 
$\xi,\eta \in C^2(M)$, define 
$\Gamma(\xi,\eta)=\frac{1}{2}\left(L(\xi\eta)-\xi L\eta-\eta L\xi\right)$. If 
$\rho$ is the Riemannian distance on M, then 
$\Gamma(\rho,\rho)(x)\equiv 1$. When 
$M=\mathbb{R}^d$, 
$\rho$ is the Euclidean distance and L has the form (3.1) satisfying that a(x) is positive definite, we have 
$\Gamma(\rho,\rho)=\frac{1}{|x|^2}\sum_{i,j=1}^{d}a_{ij}(x)x_ix_j>0$.
In this section we always assume that the distance function 
$\rho$ satisfies 
$\Gamma(\rho,\rho)>0$.
Define 
$\mathscr{F}=\{\,f\in C^2[0, D]\,:\,f\big|_{(0,D)}>0, f'\big|_{(0,D)}\geqslant 0\}$. For 
$f\in \mathscr{F}$, 
$L{\kern2pt}f\circ\rho(x)=\Gamma(\rho,\rho)(x)f''\break[\rho(x)]+ L\rho(x)f'[\rho(x)]$.
Next, fix 
$p>0$ and choose the functions as follows: for 
$r\geqslant p$,
\begin{alignat*}{2}\overline{\alpha}(r) & \geqslant\sup_{\rho(x)=r}\Gamma(\rho,\rho)(x), \qquad & \underline{\alpha}(r) & \leqslant\inf_{\rho(x)=r}\Gamma(\rho,\rho)(x); \\[3pt]\overline{\beta}(r) & \geqslant\sup_{\rho(x)=r}L\rho(x), & \underline{\beta}(r) & \leqslant \inf_{\rho(x)=r}L\rho(x); \\[3pt]\overline{C}(r) & = \int_{p}^{r}\frac{\overline{\beta}(s)}{\underline{\alpha}(s)}\mathrm{d} s, & \underline{C}(r) & =\int_{p}^{r}\frac{\underline{\beta}(s)}{\overline{\alpha}(s)}\mathrm{d} s.\end{alignat*}
By comparing 
$(X_t)_{t\geqslant 0}$ with its radial process and applying Foster–Lyapunov criteria (see [Reference Down, Meyn and Tweedie5, Theorem 5.2(c)]) and Theorem 2, we obtain the explicit conditions for the strong ergodicity and the non-strong ergodicity of diffusion processes on manifolds.
(1) If
then the process
\begin{equation*} \overline{\delta}_p(\rho)\,:{=}\,\int_ {p}^{\infty}\mathrm{e}^{-\overline{C}(y)}\left(\int_ {y}^{\infty}\frac{\mathrm{e}^{\overline{C}(z)}}{\underline{\alpha}(z)}\mathrm{d} z\right)\mathrm{d} y<\infty,\end{equation*}
$(X_t)_{t\geqslant 0}$ is strongly ergodic.
-
(2) If
(3.2)then the process
\begin{equation}\underline{\delta}_p(\rho)\,:{=}\,\int_ {p}^{\infty}\mathrm{e}^{-\underline{C}(y)}\left(\int_ {y}^{\infty}\frac{\mathrm{e}^{\underline{C}(z)}\mathrm{d} z}{\overline{\alpha}(z)}\right)\mathrm{d} y=\infty,\end{equation}
$(X_t)_{t\geqslant 0}$ is non-strongly ergodic.
To prove Theorem 3, we need the following lemma.
Lemma 2. Assume the diffusion 
$(X_t)_{t\geqslant 0}$ is non-explosive. If 
$s(\infty)\,:{=}\,\int_{1}^{\infty}\mathrm{e}^{-\underline{C}(l)}\mathrm{d} l<\infty$, then 
$(X_t)_{t\geqslant 0}$ is transient.
Proof. For 
$r\geqslant 1$, define 
$s(r)\,:{=}\,\int_{1}^{r}\mathrm{e}^{-\underline{C}(l)}\mathrm{d} l$; then, for 
$r\geqslant 1$, 
$\overline{\alpha}(r)s''(r)+\underline{\beta}(r)s'(r)=0$, i.e. 
$s''(r)+\frac{\underline{\beta}(r)}{\overline{\alpha}(r)}s'(r)=0$. Thus, for 
$x\in E$ with 
$\rho(x)=r$,
\begin{equation*} Ls\circ\rho(x)=A(x)\left(s''[\rho(x)]+\frac{B(x)}{A(x)}s'[\rho(x)]\right)\geqslant A(x)\left(s''(r)+\frac{\underline{\beta}(r)}{\overline{\alpha}(r)}s'(r)\right)=0.\end{equation*}
Since the martingale problem for L is well posed, for 
$1\leqslant R<\infty$,
\begin{equation}\mathbb{E}_x[s\circ\rho(X_{t\wedge \tau_{B_{1}}\wedge \tau_{B_{R}^{\rm c}}})]-s\circ\rho(x)\geqslant \mathbb{E}_x\left[\int_{0}^{t\wedge\tau_{B_1}\wedge \tau_{B_{R}^{\rm c}}}Ls\circ\rho(X_s)\mathrm{d} s\right]\geqslant0.\end{equation}
Now, we first calculate 
$\varlimsup\limits_{t\rightarrow\infty}\mathbb{E}_x[s\circ\rho(X_{t\wedge \tau_{B_{1}}\wedge \tau_{B_{R}^{\rm c}}})].$ Note that on 
$\{t<\tau_{B_{1}}\wedge \tau_{B_{R}^{\rm c}}\}$, 
$|X_t|\in (1,R]$; hence, by the local boundedness and monotonicity of s, we have 
$s\circ\rho(X_t)\textbf{1}_{\{t<\tau_{B_1}\wedge \tau_{B_{R}^{\rm c}}\}}\leqslant s(R)<\infty$. Thus, by recurrence (if not, then Lemma 2 has been proved),
\begin{equation*}0\leqslant\lim_{t\rightarrow\infty}\mathbb{E}_x[s\circ\rho(X_t)\textbf{1}_{\{t<\tau_{B_{1}}\wedge \tau_{B_{R}^{\rm c}}\}}]\leqslant s(R) \lim_{t\rightarrow\infty}\mathbb{P}_x[\tau_{H}\wedge \tau_{E_n^{\rm c}}>t]=0.\end{equation*}
Therefore, by a similar argument to (2.3),
\begin{equation}\varlimsup_{t\rightarrow\infty}\mathbb{E}_x[s\circ\rho(X_{ t\wedge\tau_{B_{1}}\wedge \tau_{B_{R}^{\rm c}}})]\leqslant\mathbb{E}_x[s\circ\rho(X_{\tau_{B_{1}}\wedge \tau_{B_{R}^{\rm c}}})],\end{equation}
Now, by combining (3.3) and (3.4),
\begin{align*}s\circ\rho(x)&\leqslant\mathbb{E}_x[s\circ\rho(X_{ \tau_{B_{1}}\wedge \tau_{B_{R}^{\rm c}}})]=\mathbb{P}_x[\tau_{B_1}<\tau_{B_{R}^{\rm c}}]s(1)+\mathbb{P}_x[\tau_{B_1}\geqslant\tau_{B_{R}^{\rm c}}]s(R)\\ &=(1-\mathbb{P}_x[\tau_{B_1}<\tau_{B_{R}^{\rm c}}])s(R).\end{align*}
So,
\begin{equation*}\mathbb{P}_x[\tau_{B_1}<\tau_{B_{R}^{\rm c}}]\leqslant \frac{s(R)-s(\rho(x))}{s(R)}, \qquad \text{for}\ 1\leqslant\rho(x)\leqslant R.\end{equation*}
Because 
$(X_t)_{t\geqslant 0}$ is non-explosive, let 
$R\rightarrow \infty$ to get, for 
$x\in E$ with 
$\rho(x)\geqslant 1$,
\begin{equation*}\qquad\qquad\qquad\qquad\qquad\qquad\mathbb{P}_x[\tau_{B_1}<\infty]\leqslant \frac{s(\infty)-s(\rho(x))}{s(\infty)}<1.\qquad\qquad\qquad\qquad\qquad\qed\end{equation*}
Therefore 
$(X_t)_{t\geqslant 0}$ is transient.
Proof of Theorem 3.
(1) For all
$r\geqslant p$, define
then,
\begin{equation*} f_1(r)=\int_{p}^{r}\mathrm{e}^{-\overline{C}(y)}\left(\int_ {y}^{\infty}\frac{\mathrm{e}^{\overline{C}(z)}}{\underline{\alpha}(z)}\mathrm{d} z\right)\mathrm{d} y ; \end{equation*}
$f_1$ satisfies $\underline{\alpha}(r)f_1^{\prime\prime}(r)+\overline{\beta}(r)f_1^{\prime}(r)=-1$. Hence, for $x\in M$ with $\rho(x)=r$,
If
\begin{align*}L{\kern2pt}f_1\circ\rho(x)&=\Gamma(\rho,\rho)(x)\left(\,f_1^{\prime\prime}[\rho(x)]+\frac{L\rho(x)}{\Gamma(\rho,\rho)(x)}f_1^{\prime}[\rho(x)]\right)\\&\leqslant \underline{\alpha}(r)f_1^{\prime\prime}(r)+\overline{\beta}(r)f_1^{\prime}(r)=-1.\end{align*}
$\overline{\delta}_p(\rho)<\infty$, then by letting $V(x)=f_1\circ\rho(x)$ and $C=\overline{B_p}$ in [5, Theorem 5.2(c)], we obtain that the process is strongly ergodic.
-
(2) For any
$ n\geqslant1$, let $E_n=B_{n+p}$ and $u_n(x)=\psi_n\circ\rho(x)$ be defined by
where
\begin{equation*} \psi_n(r)=\int_ {p}^{p+n}G(r,l)\frac{1}{\overline{\alpha}(l)}\mathrm{e}^{\underline{C}(l)}\mathrm{d} l, \qquad p\leqslant r\leqslant p+n,\end{equation*}
Obviously, for all
\begin{equation*}G(r,l)\,:{=}\, \begin{cases}\dfrac{[s(r)-s(p)][s(n+p)-s(l)]}{s(n+p)-s(p)} & r<l , \\ \\[-6pt] \dfrac{[s(l)-s(p)][s(n+p)-s(r)]}{s(n+p)-s(p)} & r\geqslant l . \\\end{cases}\end{equation*}
$x\in E_n\setminus H$, $Lu_n(x)\geqslant -1$ and $u_n\big|_{E_n\cup \partial H}=0$. Rewrite $u_n(r)$ as
\begin{align*}\psi_n(r) & = \int_{p}^{r}\frac{[s(l)-s(p)][s(n+p)-s(r)]}{s(n+p)-s(p)}\frac{\mathrm{e}^{\underline{C}(l)}}{\overline{\alpha}(l)}\mathrm{d} l \\ \\[-5pt] & \quad + \int_{r}^{p+n}\frac{[s(r)-s(p)][s(n+p)-s(l)]}{s(n+p)-s(p)}\frac{\mathrm{e}^{\underline{C}(l)}}{\overline{\alpha}(l)}\mathrm{d} l.\end{align*}
If 
$\lim\limits_{R\rightarrow \infty}s(R)<\infty$, then by Lemma 2 we know that 
$(X_t)_{t\geqslant 0}$ is transient. So, we assume that 
$\lim\limits_{R\rightarrow \infty}s(R)=\infty$. Therefore,
\begin{align*}\lim_{n\rightarrow \infty}\psi_n(r) & = \int_{p}^{r}\left[\int_{p}^{l}\mathrm{e}^{-\underline{C}(t)}\mathrm{d} t\right]\frac{\mathrm{e}^{\underline{C}(l)}}{\overline{\alpha}(l)}\mathrm{d} l+\int_{p}^{r}\mathrm{e}^{-\underline{C}(t)}\mathrm{d} t\int_{r}^{\infty}\frac{\mathrm{e}^{\underline{C}(l)}}{\overline{\alpha}(l)}\mathrm{d} l \\[3pt] & = \int_{p}^{r}\mathrm{e}^{-\underline{C}(t)}\left[\int_{t}^{r}\frac{\mathrm{e}^{\underline{C}(l)}}{\overline{\alpha}(l)}\mathrm{d} l\right]\mathrm{d} t+\int_{p}^{r}\mathrm{e}^{-\underline{C}(t)}\left[\int_{r}^{\infty}\frac{\mathrm{e}^{\underline{C}(l)}}{\overline{\alpha}(l)}\mathrm{d} l\right]\mathrm{d} t \\[3pt] & = \int_{p}^{r}\mathrm{e}^{-\underline{C}(t)}\left[\int_{t}^{\infty}\frac{\mathrm{e}^{\underline{C}(l)}}{\overline{\alpha}(l)}\mathrm{d} l\right]\mathrm{d} t.\end{align*}
Then, (3.2) yields that 
$\sup\limits_{x\notin H}\lim\limits_{n\rightarrow \infty}u_n(x)=\sup\limits_{r\geqslant p}\lim\limits_{n\rightarrow \infty}\psi_n(r)=\infty.$ It follows from Theorem 1 that 
$(X_t)_{t\geqslant 0}$ is non-strongly ergodic.
We use Theorem 3 to check some examples such as a radial process.
Corollary 4. [8, Example 3.6] Consider a d-dimensional ergodic diffusion process 
$(X_t)_{t\geqslant 0}$ with generator 
$L=\Delta+\nabla V\cdot\nabla$, where 
$V(x)=-|x|^{c}$, 
$c>0$. Then 
$(X_t)_{t\geqslant 0}$ is strongly ergodic if and only if 
$c>2$. In particular, the classical Ornstein–Uhlenbeck process (
$c=2$) is non-strongly ergodic.
Proof. Let 
$\rho(x)=|x|$. By Theorem 3, we know 
$(X_t)_{t\geqslant 0}$ is strongly ergodic if and only if
\begin{equation*} \int_ {1}^{\infty}y^{1-d}\mathrm{e}^{y^{c}}\left(\int_ {y}^{\infty}z^{d-1}\mathrm{e}^{-z^{c}}\mathrm{d} z\right)\mathrm{d} y
< \infty.\end{equation*}
By using integration by parts, we obtain that there exist 
$C_1,C_2>0$ such that
\begin{equation}C_1 y^{d-c}\mathrm{e}^{-y^{c}}\leqslant\int_ {y}^{\infty}z^{d-1}\mathrm{e}^{-z^{c}}\mathrm{d} z\leqslant C_2 y^{d-c}\mathrm{e}^{-y^{c}}.\end{equation}
Hence, 
$(X_t)_{t\geqslant 0}$ is strongly ergodic if and only if
\begin{equation*}\infty>\int_ {1}^{\infty}y^{1-d}\mathrm{e}^{y^{c}}y^{d-c}\mathrm{e}^{-y^{c}}\mathrm{d} y = \int_ {1}^{\infty}y^{1-c}\mathrm{d} y,\end{equation*}
which is equivalent to 
$ c>2$.
On the other hand, we can also use a Lyapunov function for strong ergodicity and Theorem 1.
For 
$0<c\leqslant 2$, we choose 
$u(x)=\log (|x|+1)$, 
$v(x)=|x|$. Then
\begin{equation*}Lu\geqslant\frac{d-2}{(|x|+1)^2}-\frac{1}{|x|(|x|+1)^2}-c|x|^{c-2}, \qquad Lv=\frac{d-1-c|x|^{c}}{|x|}.\end{equation*}
Let 
$r=\left(d-1/c\right)^{1/c}$, 
$H=\overline{B_r}$, and 
$E_n=B_{r+n}$. When 
$x\notin H$,
\begin{equation*}Lv(x)\leqslant 0, \qquad Lu(x)\geqslant-\left(\frac{d-1}{c}\right)^{-\frac{3}{c}}-c\left(\frac{d-1}{c}\right)^{\frac{c-2}{c}}.\end{equation*}
It is easy to check that u,v satisfy the condition in Theorem 1, so 
$(X_t)_{t\geqslant 0}$ is non-strongly ergodic.
When 
$c>2$, let 
$w(x)=1-{\log(|x|+1)}^{-1}$. This satisfies the Lyapunov condition for strong ergodicity (see [5, Theorem 5.2(c)]), and therefore we have that 
$(X_t)_{t\geqslant 0}$ is strongly ergodic.
Now we remark that for Theorem 3 it is somewhat difficult to get the strong ergodicity for some non-radial processes. To use Theorem 3, we need to choose a distance function 
$\rho$ to compare 
$(X_t)_{t\geqslant 0}$ with its radial process. However, for some processes, choosing the (smooth) distance function (such as the Riemannian metric) makes it difficult to get the strong ergodicity. However, Theorem 1 can still be valid.
Corollary 5. Let 
$(X_t)_{t\geqslant 0}$ be a diffusion process on 
$\mathbb{R}^2$ with generator 
$L=\frac{\partial^2}{\partial x_1^2}+\frac{\partial^2}{\partial x_2^2}-x_1\frac{\partial}{\partial x_1}-x_2^2\frac{\partial}{\partial x_2}$. Then 
$(X_t)_{t\geqslant 0}$ is non-strongly ergodic.
Proof. Let 
$\rho(x)=|x|$ be the Euclid metric. For 
$r>0$ large enough, we choose
\begin{equation*}\overline{\alpha}(r)=\underline{\alpha}(r)=1, \quad \overline{\beta}(r)=\frac{1+r^3}{r}, \quad \underline{\beta}(r)=\frac{1-r^3}{r}\end{equation*}
and
\begin{equation*}\overline{C}(r)=\log r+\frac{r^3-1}{3}, \qquad \underline{C}(r)=\log r-\frac{r^3-1}{3}.\end{equation*}
For 
$p>0$ large enough, on the one hand,
\begin{equation*}\overline{\delta}_p(\rho)=\int_ {p}^{\infty}y^{-1}\mathrm{e}^{-y^3/3}\left(\int_ {y}^{\infty}z\mathrm{e}^{z^3/3}\mathrm{d} z\right)\mathrm{d} y\geqslant \int_ {p}^{\infty}y^{-1}\left(\int_ {y}^{\infty}z \mathrm{d} z\right) \mathrm{d} y = \infty;\end{equation*}
but on the other hand, 
$\underline{\delta}_p(\rho)<\infty$ according to (3.5). Thus, Theorem 3 is invalid for checking the strong ergodicity.
Now we apply Theorem 1. We choose the functions 
$u(x)=\log (x_1^2+1)$, 
$v(x)=x_1^2+1$, 
$E_n=\{x\,:\,|x_1|< n, |x_2|< n\}$ for 
$n\geqslant 2$, and 
$H=\overline{E_1}$. For 
$ x\notin H$,
\begin{equation*}Lu=\frac{2(1-x_1^2)}{(1+x_1^2)^2}-\frac{2x_1^2}{1+x_1^2}\geqslant-\frac{5}{2}, \quad Lv=2-2x_1^2\leqslant 0, \quad \lim\limits_{n\rightarrow\infty}\frac{u(x)}{v(x)}=0.\end{equation*}
Thus, the process is non-strongly ergodic.
4. Ornstein–Uhlenbeck processes driven by $\alpha$-stable noise
Let 
$(Z_t)_{t\geqslant 0}$ be a d-dimensional symmetric 
$\alpha$-stable process with generator 
$-({-}\Delta)^{\alpha/2}$ (
$0<\alpha<2$), which has the following expression:
\begin{equation*}-({-}\Delta)^{\alpha/2}f(x)\,:{=}\,\int_{\mathbb{R}^d\setminus\{0\}}\left(\,f(x+z)-f(x)-\nabla f(x)\cdot z\textbf{1}_{\{|z|\leqslant 1\}}\right)\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z.\end{equation*}
Here, 
$C_{d,\alpha}=\frac{\alpha2^{\alpha-1}\Gamma((d+\alpha)/2)}{\pi^{d/2}\Gamma(1-\alpha/2)}$ is the normalizing constant such that, for 
$u\in D(L)$, the Fourier transform of 
$-({-}\Delta)^{\alpha/2}u$ is 
$-|\xi|^{\alpha}\hat{u}(\xi)$, where 
$\hat{u}$ is the Fourier transform of u.
Consider the following stochastic differential equation (SDE) driven by 
$\alpha$-stable noise on 
$\mathbb{R}^d$:
\begin{equation*}\mathrm{d} X_t = AX_t \mathrm{d} t + \mathrm{d} Z_t, \qquad X_0 = x,\end{equation*}
where A is a real 
$d \times d$ matrix. It is well known that the SDE has the unique strong solution 
$(X_t)_{t\geqslant 0}$ which is (strong) Feller and Lebesgue irreducible (see, e.g., [Reference Wang16]). We call 
$(X_t)_{t\geqslant 0}$ a d-dimensional Ornstein–Uhlenbeck process driven by symmetric 
$\alpha$-stable noise. The generator L is represented for any 
$f\in D_w(L)$ as
\begin{equation*}L{\kern2pt}f(x)=\int_{\mathbb{R}^d\setminus\{0\}}\left(\,f(x+z)-f(x)-\nabla f(x)\cdot z\textbf{1}_{\{|z|\leqslant 1\}}\right)\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z+\langle Ax,\nabla f(x)\rangle,\end{equation*}
and
\begin{equation*}\left\{ f \in C^2(\mathbb{R}^d)\,:\,\int_{\{|z|>1\}}[\,f(x+z)-f(x)]\frac{1}{|z|^{d+\alpha}}\mathrm{d} z<\infty, \ \text{for} \ x\in \mathbb{R}^d \right\}\subset D_w(L).\end{equation*}
By [Reference Wang15, Theorem 3], if the real parts of all the eigenvalues of A are negative, then the process is exponentially ergodic, i.e. there exist a constant 
$\lambda_1>0$ and 
$C(x)<\infty$ such that 
$\|P_t(x,\cdot)-\pi(\cdot)\|_{\mathrm{Var}}\leqslant C(x) \mathrm{e}^{-\lambda_1 t}$. We will prove the non-strong ergodicity by Theorem 1.
Theorem 4. The Ornstein–Uhlenbeck process 
$(X_t)_{t\geqslant 0}$ driven by symmetric 
$\alpha$-stable noise is not strongly ergodic.
Proof. Since the process is ergodic, we can apply Theorem 1 to check the non-strong ergodicity.
Let 
$u(x)=\log (|x|+1)$ and 
$v(x)=|x|^{\theta}$, where 
$\theta\in (0,1\wedge \alpha)$. It is easy to check that 
$u(x), v(x)\in D_w(L)$ and 
$\lim\limits_{|x|\rightarrow\infty}{u(x)}/{v(x)}=0$. Moreover, there exists 
$r_0>0$ such that 
$Lv(x)\leqslant\textbf{1}_{B(0,r_0)}$ (see [Reference Wang16]).
To apply Theorem 1, we need only prove that there exists 
$C(d,\alpha)$ depending only on d and 
$\alpha$ such that 
$Lu(x)\geqslant -C(d,\alpha)$ for 
$|x|$ large enough.
First, we estimate the drift coefficient:
\begin{equation}\langle\nabla u(x),Ax\rangle=\frac{\langle x,Ax\rangle}{|x|(|x|+1)}\geqslant -\left(\sum_{i,j=1}^{d}a_{ij}^2\right)^{\frac{1}{2}}.\end{equation}
Next, we turn to estimating the fractional Laplacian for large enough 
$|x|$:
\begin{align*}-({-}\Delta)^{\alpha/2}u(x) & = \int_{\mathbb{R}^d\setminus\{0\}}\left(u(x+z)-u(x)-\nabla u(x)\cdot z\textbf{1}_{\{|z|\leqslant 1\}}\right)\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & \geqslant \int_{\{|z|\leqslant 1\}}\left(u(x+z)-u(x)-\nabla u(x)\cdot z\right)\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & \quad + \int_{\{|z|>1 \}}(u(x+z)-u(x))\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z\\[3pt] & \,{=}:\, A(x)+B(x).\end{align*}
For 
$|x|> 1,$
\begin{align*}A(x) & = \frac{1}{2}\int_{\{|z|\leqslant 1\}}\left[z^\top \mathrm{Hess}(u(x+\theta z))z\right]\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt]& \geqslant \frac{1}{2} C_{d,\alpha}\left(\frac{1}{(|x|+2)(|x|+1)}-\frac{2}{(|x|-1)^2}-\frac{1}{(|x|-1)^3}\right)\int_{\{|z|\leqslant 1\}}\frac{1}{|z|^{d+\alpha-2}}\mathrm{d} z\\[3pt]& \rightarrow 0 \ \text{as} \ |x|\rightarrow\infty.\end{align*}
The calculation of B(x) is complicated, and is divided in three cases: 
$\alpha\in (1,2)$, 
$\alpha=1$, and 
$\alpha\in (0,1)$.
For 
$\alpha\in (1,2)$, using Taylor’s formula for u(x) we have
\begin{align*}B(x) & = \int_{\{|z|\geqslant1 \}}(u(x+z)-u(x))\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & = \int_{\{|z|\geqslant1 \}}\frac{\langle x+\theta z,z\rangle}{(|x+\theta z|+1)(|x+\theta z|)}\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & \geqslant {-} \int_{\{|z|\geqslant1 \}}\frac{1}{|x+\theta z|+1}\frac{C_{d,\alpha}}{|z|^{d+\alpha-1}} \mathrm{d} z\\[3pt] & \geqslant - C(d)\int_{1}^{\infty}\frac{1}{r^{\alpha}}\mathrm{d} r=-\frac{C(d)}{\alpha-1}.\end{align*}
So, there exists a large enough 
$R_1$ such that 
$-({-}\Delta)^{\alpha/2}u(x)\geqslant-\frac{2C(d)}{\alpha-1} \ \text{for}\ |x|>R_1$.
For 
$\alpha=1$, using integration by parts,
\begin{align*}B(x) & = \int_{\{1<|z|<|x| \}}(u(x+z)-u(x))\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z+\int_{\{|z|\geqslant|x| \}}(u(x+z)-u(x))\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & = C(d)\int_1^{|x|}\log\left(1-\frac{r}{|x|+1}\right)\frac{1}{r^2} \mathrm{d} r+C(d)\int_{|x|}^{\infty}\log\left(\frac{(r-|x|+1)}{|x|+1}\right)\frac{1}{r^2} \mathrm{d} r \\[3pt] & = C(d)\left[\frac{1}{|x|}\log|x|-\frac{2\log|x|}{|x|+1}-\frac{1}{|x|}\log|x|+\frac{\log|x|}{|x|-1}\right] \\[3pt] & \rightarrow 0 \ \text{as}\ |x|\rightarrow\infty.\end{align*}
Thus, there exists a large enough 
$R_2$ such that 
$-({-}\Delta)^{\alpha/2}u(x)\geqslant-1$, 
$\text{for}\ |x|>R_2$.
For 
$\alpha\in (0,1)$, we divide B(x) into three parts:
\begin{align*}B(x) & = \int_{\{1<|z|<|x|-1 \}}(u(x+z)-u(x))\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & \quad + \int_{\{|x|-1\leqslant|z|\leqslant|x|+1 \}}(u(x+z)-u(x))\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & \quad + \int_{\{|z|>|x|+1 \}}(u(x+z)-u(x))\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & \,{=}:\, I_1(x)+I_2(x)+I_3(x).\end{align*}
We estimate 
$I_1$, 
$I_2$, and 
$I_3$ one by one. First, we have
\begin{align*}I_1 & = \int_{\{1<|z|\leqslant |x|-1\}}\big(\log(|x+z|+1)-\log(|x|+1)\big)\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & \geqslant \int_{\{1<|z|\leqslant |x|-1\}}\log\left(\frac{(|x|-|z|+1)}{|x|+1}\right)\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & = C(d)\int_1^{|x|-1}\log\left(1-\frac{r}{|x|+1}\right)\frac{1}{r^{1+\alpha}} \mathrm{d} r \\[3pt] & \geqslant \frac{C(d)}{\alpha}\left[\log\left(\frac{|x|}{|x|+1}\right)-\frac{1}{(|x|-1)^{\alpha}}\log\left(\frac{2}{|x|+1}\right)-\int_0^{|x|-1}\frac{1}{r^{\alpha}}\frac{1}{|x|+1-r}\mathrm{d} r\right].\end{align*}
To estimate the last integral above, we use the integral representation of the Gauss hypergeometric function F(a, b, c, z) (see [Reference Abramowitz and Stegun1, 15.3.1]):
\begin{equation*} F(a,\ b,\ c,\ z)=\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\int_{0}^{1}t^{b-1}(1-t)^{c-b-1}(1-tz)^{-a}\mathrm{d} t, \qquad \mathrm{Re}(c)>\mathrm{Re}(b)>0.\end{equation*}
Using this formula, we have
\begin{align*}-\!\int_0^{|x|-1}\!\!\frac{1}{r^{\alpha}}\frac{1}{|x|+1-r}\mathrm{d} r & = - \frac{1}{(1-\alpha)(|x|-1)^{\alpha-1}(|x|+1)}F\left(1,1-\alpha,2-\alpha,\frac{|x|-1}{1+|x|}\right) \\[3pt] & \,{=}:\, J_1(x).\end{align*}
Similarly,
\begin{align*}I_3(x) & = \int_{\{|z|\geqslant |x|+1\}}\big(\log(|x+z|+1)-\log(|x|+1)\big)\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & \geqslant \int_{\{|z|\geqslant |x|+1\}}\log\left(\frac{(|z|-|x|+1)}{|x|+1}\right)\frac{C_{d,\alpha}}{|z|^{d+\alpha}} \mathrm{d} z \\[3pt] & = C(d)\int_{|x|+1}^{\infty}\log\left(\frac{(r-|x|+1)}{|x|+1}\right)\frac{1}{r^{1+\alpha}} \mathrm{d} r \\[3pt] & = \frac{C(d)}{\alpha(|x|+1)^{\alpha}}\log\left(\frac{2}{|x|+1}\right)+\frac{C(d)}{\alpha}\int_{|x|+1}^{\infty}\frac{1}{r^{\alpha}}\frac{1}{1-|x|+r}\mathrm{d} r\end{align*}
and
\begin{equation*}\int_{|x|+1}^{\infty}\frac{1}{r^{\alpha}}\frac{1}{1-|x|+r}\mathrm{d} r = \frac{1}{\alpha(|x|+1)^{\alpha}}F\left(1,\alpha,1+\alpha,\frac{|x|-1}{|x|+1}\right)\,{=}:\,J_2(x).\end{equation*}
Next, we calculate
\begin{align*}J_1(x)+J_2(x) & = \frac{F\left(1,1-\alpha,2-\alpha,\frac{|x|-1}{1+|x|}\right)}{(\alpha-1)(|x|-1)^{\alpha-1}(|x|+1)}+\frac{F\left(1,\alpha,1+\alpha,\frac{|x|-1}{|x|+1}\right)}{\alpha(|x|+1)^{\alpha}} \\[3pt] & = \left[\frac{F\left(1,1-\alpha,2-\alpha,\frac{|x|-1}{1+|x|}\right)}{(\alpha-1)(|x|-1)^{\alpha-1}(|x|+1)}-\frac{F\left(1,1-\alpha,2-\alpha,\frac{|x|-1}{1+|x|}\right)}{(\alpha-1)(|x|+1)^{\alpha}}\right] \\[3pt] & \quad + \left[\frac{F\left(1,1-\alpha,2-\alpha,\frac{|x|-1}{1+|x|}\right)}{(\alpha-1)(|x|+1)^{\alpha}}+\frac{F\left(1,\alpha,1+\alpha,\frac{|x|-1}{|x|+1}\right)}{\alpha(|x|+1)^{\alpha}}\right] \\[3pt] & \,{=}:\, K_1(x)+K_2(x).\end{align*}
According to [Reference Sandrić13, (3.18)–(3.21)], 
$\lim\limits_{|x|\rightarrow\infty}(1+|x|)^{\alpha}(K_1(x)+K_2(x))=\pi \cot \left(\pi\alpha/2\right)$. Hence,
\begin{align*}I_1(x)+I_3(x) & \geqslant \frac{C(d)}{\alpha}\left[\log\left(\frac{|x|}{|x|+1}\right)+\frac{1}{(|x|-1)^{\alpha}}\log\left(\frac{2}{|x|+1}\right)\right] \\[3pt] & \quad + \frac{C(d)}{\alpha(|x|+1)^{\alpha}}\log\left(\frac{2}{|x|+1}\right)+\frac{C(d)}{\alpha}(K_1(x)+K_2(x)) \\[3pt] & \rightarrow 0 \ \text{as}\ |x|\rightarrow\infty.\end{align*}
Next, we consider 
$I_2(x)$. Since
\begin{align*}\int_{|x|-1}^{|x|+1}\log\left(\frac{|r-|x||+1}{|x|+1}\right)\frac{1}{r^{1+\alpha}} \mathrm{d} r & \geqslant \frac{\log(|x|+1)}{\alpha}\left[\frac{1}{(|x|+1)^{\alpha}}-\frac{1}{(|x|-1)^{\alpha}}\right] \\[3pt] & \rightarrow 0 \ \text{as}\ |x|\rightarrow\infty,\end{align*}
we have 
$\lim\limits_{|x|\rightarrow\infty}I_2(x)=0$. Thus, for 
$\alpha\in (0,1)$,
\begin{equation*}\lim\limits_{|x|\rightarrow\infty}-({-}\Delta)^{\alpha/2}u(x)\geqslant \lim\limits_{|x|\rightarrow\infty}(I_1(x)+I_2(x)+I_3(x))=0.\end{equation*}
Therefore, we choose 
$R_3>1$ large enough that 
$-({-}\Delta)^{\alpha/2}u(x)\geqslant-1$ for any 
$|x|>R_3.$
Finally, we obtain that, for each 
$\alpha\in (0,2)$, there exists a large enough positive number 
$R_3$ such that 
$-({-}\Delta)^{\alpha/2}u(x)\geqslant-c$, where c is a positive number.
Therefore, by combining (4.1) and the above three cases for 
$\alpha$, we prove that there exists 
$C(d,\alpha)$ depending only on d and 
$\alpha$ such that 
$Lu(x)\geqslant -C(d,\alpha)$ for 
$|x|$ large enough.
Corollary 6. Consider the following SDE driven by 
$\alpha$-stable noise on 
$\mathbb{R}^d$:
\begin{equation*}\mathrm{d} X_t = b(X_t) \mathrm{d} t + \mathrm{d} Z_t, \qquad X_0 = x_0,\end{equation*}
where 
$b(x)=-x|x|^{\delta}$, 
$\delta\geqslant 0$. If 
$\delta>0$, [Reference Wang16, Example 1.2] has proved the process is strongly ergodic. If 
$\delta=0$, then by Theorem 4 the process is non-strongly ergodic. Thus, the process is strongly ergodic if and only if 
$\delta>0$.
Remark 2. According to Corollary 6 and Example 4, we know that for an SDE driven by a symmetric 
$\alpha$-stable process (
$\alpha\in (0,2]$) with polynomial drift 
$b(x)=-x|x|^{\delta}$, the strong ergodicity is independent of 
$\alpha$.
Acknowledgements
The authors thank the reviewers for their valuable comments and helpful references on the first version of the paper. The authors would also like to thank Professor Mu-Fa Chen for his valuable suggestions. This work is supported in part by the National Natural Science Foundation of China (Grant Nos. 11771046 and 11771047), a project from the Ministry of Education in China.
