2. FORMULATION

Consider two-color linearly polarized laser pulses, represented by the vector potential ${{\vec A}_{\rm L}} = \hat y{A_1}(x,t)\cos ({k_1}x - {{\rm \omega} _1}t) \,+{\hat z}{A_2}(x,t)\cos ({k_2}x - {{\rm \omega} _2}t)$, where A _j(x, t),  k _j and ω_j are, respectively, the amplitude, propagation constant, and frequency of the first (j = 1) and second (j = 2) laser pulse. The two-laser pulses copropagate through homogeneous plasma along the positive x-direction. It may be noted here that the laser pulse having ω₁ frequency is polarized along the y-direction while the other pulse, having ω₂(<ω₁) frequency, is polarized along the z-direction. The plasma, assumed to be cold and underdense, is magnetized by applying static magnetic field (B ₀) along the z-direction. The external magnetic field confines the propagation of the first laser pulse, polarized along the y-direction, in the extraordinary mode; and for the other pulse, polarized along the z-direction, in the ordinary mode. The equations governing the interaction of the laser pulses with the magnetized plasma are the Lorentz force, continuity and Poisson's equations respectively given by,

(1)$$\displaystyle{{\partial \left({\rm \gamma} {\vec v} \,\right)} \over {\partial t}} + \left({{\vec v} . {\vec \nabla} }\right)\left({{\rm \gamma} {\vec v}}\right) = - \displaystyle{e \over m}\left({{\vec E} + \displaystyle{{\vec v} \over c} \times \left({{\vec B} + {\vec B}_{0}}\right)}\right),$$

(2)$$\displaystyle{{\partial {n_{\rm e}}} \over {\partial t}} + {\vec \nabla}. \left( {{n_{\rm e}}{\vec v}} \,\right) = 0,$$

and

(3)$${\nabla ^2}{\rm \phi} = - 4{\rm \pi} e\left( {{n_0} - {n_{\rm e}}} \right),$$

where γ( = (1 − v ²/c ²)^−1/2) is the relativistic factor, while ${\vec v}$ and n _e represent the velocity and density of plasma electrons, respectively, φ is the scalar potential. Interaction of laser pulses with the plasma leads to plasma electron oscillations at the laser frequency (fast oscillations) as well as at the plasma frequency (slow oscillations). In the present study, ${\vec E}\,( = \!-{\vec \nabla} {\rm \phi} - \partial {{\vec A}}/c\partial t)$ and $\vec B\,( = \!{\vec \nabla} \times {{\vec A}}$, where ${\vec A}$ is the vector potential) represent the fast as well as the slow electric and magnetic fields.

The fast components of the transverse and longitudinal, relativistic plasma electron velocities are respectively obtained from the Lorentz force Eq. (1) as,

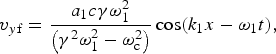(4a)$${v_{y{\rm f}}} = \displaystyle{{{a_1}c{\rm \gamma} {\rm \omega} _1^2 {\rm }} \over {\left( {{{\rm \gamma}^2}{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 } \right)}}\cos ({k_1}x - {{\rm \omega} _1}t),$$

(4b)$${v_{z{\rm f}}} = \displaystyle{{c{a_2}} \over {\rm \gamma}} \cos ({k_1}x - {{\rm \omega} _1}t),$$

and

(4c)$${v_{x{\rm f}}} = \displaystyle{{{a_1}c{{\rm \omega} _1}{{\rm \omega} _{\rm c}}{\rm }} \over {\left( {{{\rm \gamma} ^2}{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 } \right)}}\sin \, ({k_1}x - {{\rm \omega} _1}t),$$

where a _j(=eA _j/mc ²) is the amplitude of the normalized vector potential of the laser pulses for j = 1,  2, and ω_c(= eB ₀/mc) is the electron cyclotron frequency. It may be noted that the transverse velocity along the z-direction remains unaffected by the static field leading to ordinary mode propagation of the laser pulse polarized along the z-direction. The fast longitudinal velocity along the propagation direction of the laser pulses arises due to the presence of the static magnetic field. The equations, governing the evolution of the transverse and longitudinal slow plasma electron velocities, may be obtained from Eq. (1) as,

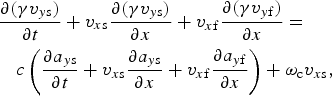(5a)$$\eqalign{& \displaystyle{{\partial ({\rm \gamma} {v_{y{\rm s}}})} \over {\partial t}} + {v_{x{\rm s}}}\displaystyle{{\partial ({\rm \gamma} {v_{y{\rm s}}})} \over {\partial x}} + {v_{x{\rm f}}}\displaystyle{{\partial ({\rm \gamma} {v_{y{\rm f}}})} \over {\partial x}} = \cr & \quad c\left( {\displaystyle{{\partial {a_{y{\rm s}}}} \over {\partial t}} + {v_{x{\rm s}}}\displaystyle{{\partial {a_{y{\rm s}}}} \over {\partial x}} + {v_{x{\rm f}}}\displaystyle{{\partial {a_{y{\rm f}}}} \over {\partial x}}} \right) + {{\rm \omega} _{\rm c}}{v_{x{\rm s}}},}$$

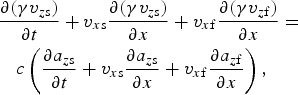(5b)$$\eqalign{& \displaystyle{{\partial ({\rm \gamma} {v_{z{\rm s}}})} \over {\partial t}} + {v_{x{\rm s}}}\displaystyle{{\partial ({\rm \gamma} {v_{z{\rm s}}})} \over {\partial x}} + {v_{x{\rm f}}}\displaystyle{{\partial ({\rm \gamma} {v_{z{\rm f}}})} \over {\partial x}} = \cr & \quad c\left( {\displaystyle{{\partial {a_{z{\rm s}}}} \over {\partial t}} + {v_{x{\rm s}}}\displaystyle{{\partial {a_{z{\rm s}}}} \over {\partial x}} + {v_{x{\rm f}}}\displaystyle{{\partial {a_{z{\rm f}}}} \over {\partial x}}} \right),}$$

and

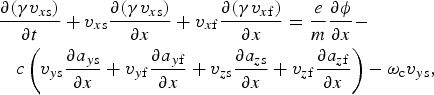(5c)$$\eqalign{& \displaystyle{{\partial ({\rm \gamma} {v_{x{\rm s}}})} \over {\partial t}} + {v_{x{\rm s}}}\displaystyle{{\partial ({\rm \gamma} {v_{x{\rm s}}})} \over {\partial x}} + {v_{x{\rm f}}}\displaystyle{{\partial ({\rm \gamma} {v_{x{\rm f}}})} \over {\partial x}} = \displaystyle{e \over m}\displaystyle{{\partial {\rm \phi}} \over {\partial x}} - \cr & \quad c\left( {{v_{y{\rm s}}}\displaystyle{{\partial {a_{y{\rm s}}}} \over {\partial x}} + {v_{y{\rm f}}}\displaystyle{{\partial {a_{y{\rm f}}}} \over {\partial x}} + {v_{z{\rm s}}}\displaystyle{{\partial {a_{z{\rm s}}}} \over {\partial x}} + {v_{z{\rm f}}}\displaystyle{{\partial {a_{z{\rm f}}}} \over {\partial x}}} \right) - {{\rm \omega} _{\rm c}}{v_{y{\rm s}}},}$$

where v _(x,y,z)s and a _(y,z)s represent respectively the slowly varying velocities and amplitudes of the generated fields along the respective directions.

On substituting the fast velocity [Eq. 4(b)] in Eq. 5(b), the third terms on both the sides of this equation cancel each other and no other driving term is present. Therefore, the generation of slow transverse velocity along the z-direction is zero. However, it may be noted that the fast velocity along the z-direction, arising due to the propagation of the second laser pulse along with the first pulse in the magnetized plasma, leads to the occurrence of an additional driving term, which enhances the longitudinal slow velocity [in Eq. 5(c)]. Substitution of this velocity using Eq. 5(c) into Eq. 5(a) shows that the ${\vec v} \times {\vec B_0}$ force, arising due to the presence of external magnetic field, leads to the coupling between the enhanced axial and transverse slow velocities. This points toward the possibility of generation of a slow transverse wave of enhanced amplitude along the direction of polarization of the laser pulse propagating in the extraordinary mode. When the second laser pulse propagating in the ordinary mode is switched off, Eqs. 5(a)–(c) transform to the set of equations obtained for a single laser pulse propagating in the magnetized plasma (Jha & Verma, Reference Jha and Verma2014).

3. NUMERICAL ANALYSIS FOR THz GENERATION

The slow components of the axial as well as transvers velocities [Eq. (5)] and the continuity and Poisson's Eqs. [(2) and (3)] are transformed in terms of independent variables ξ = x − ct and τ = t. The quasi-static approximation (QSA) is applied to the set of transformed equations. Under QSA, it is assumed that the laser pulses do not evolve significantly as they transit a plasma electron. Therefore, variations with respect to τ have been neglected. The transformed 1D equations are thus given by,

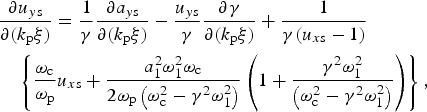(6a)$$\eqalign{& \displaystyle{{\partial {u_{y{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} = \displaystyle{1 \over {\rm \gamma} }\displaystyle{{\partial {a_{y{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} - \displaystyle{{{u_{y{\rm s}}}} \over {\rm \gamma} }\displaystyle{{\partial {\rm \gamma} } \over {\partial ({k_{\rm p}}{\rm \xi} )}} + \displaystyle{1 \over {{\rm \gamma} ({u_{x{\rm s}}} - 1)}} \cr & \quad \left\{ {\displaystyle{{{{\rm \omega} _{\rm c}}} \over {{{\rm \omega} _{\rm p}}}}{u_{x{\rm s}}} + \displaystyle{{a_1^2 {\rm \omega} _1^2 {{\rm \omega} _{\rm c}}} \over {2{{\rm \omega} _{\rm p}}\left( {{\rm \omega} _{\rm c}^2 - {{\rm \gamma} ^2}{\rm \omega} _1^2 } \right)}}\left( {1 + \displaystyle{{{{\rm \gamma} ^2}{\rm \omega} _1^2 } \over {\left( {{\rm \omega} _{\rm c}^2 - {{\rm \gamma} ^2}{\rm \omega} _1^2 } \right)}}} \right)} \right\},}$$

(6b)$$\displaystyle{{\partial ({\rm \gamma} {u_{z{\rm s}}} - {a_{z{\rm s}}})} \over {\partial ({k_{\rm p}}{\rm \xi} )}} = 0,$$

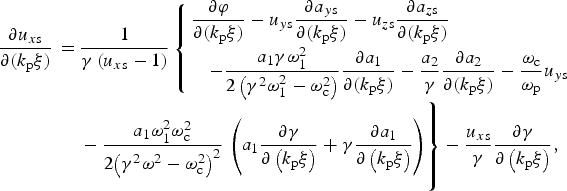(6c)$$\eqalign{\displaystyle{{\partial {u_{x{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} \,=\, & \displaystyle{1 \over {{\rm \gamma} \left( {{u_{x{\rm s}}} - 1} \right)}}\left\{ \matrix{\displaystyle{{\partial {\rm \varphi} } \over {\partial ({k_{\rm p}}{\rm \xi} )}} - {u_{y{\rm s}}}\displaystyle{{\partial {a_{y{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} - {u_{z{\rm s}}}\displaystyle{{\partial {a_{z{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} \hfill \cr \quad - \displaystyle{{{a_1}{\rm \gamma} {\rm \omega} _1^2 } \over {2\left( {{{\rm \gamma} ^2}{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 } \right)}}\displaystyle{{\partial {a_1}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} - \displaystyle{{{a_2}} \over {\rm \gamma} }\displaystyle{{\partial {a_2}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} - \displaystyle{{{{\rm \omega} _{\rm c}}} \over {{{\rm \omega} _{\rm p}}}}{u_{y{\rm s}}} \hfill} \right. \cr & \displaystyle-{{{a_1}{\rm \omega} _1^2 {\rm \omega} _{\rm c}^2 } \over {2{{\left( {{{\rm \gamma} ^2}{{\rm \omega} ^2} - {\rm \omega} _{\rm c}^2 } \right)}^2}}}{\rm }\left. \vphantom{\matrix{\displaystyle{{\partial {\rm \varphi} } \over {\partial ({k_{\rm p}}{\rm \xi} )}} - {u_{y{\rm s}}}\displaystyle{{\partial {a_{y{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} - {u_{z{\rm s}}}\displaystyle{{\partial {a_{z{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} \hfill \cr \quad - \displaystyle{{{a_1}{\rm \gamma} {\rm \omega} _1^2 } \over {2\left( {{{\rm \gamma} ^2}{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 } \right)}}\displaystyle{{\partial {a_1}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} - \displaystyle{{{a_2}} \over {\rm \gamma} }\displaystyle{{\partial {a_2}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} - \displaystyle{{{{\rm \omega} _{\rm c}}} \over {{{\rm \omega} _{\rm p}}}}{u_{y{\rm s}}} \hfill}} {\left( {{a_1}\displaystyle{{\partial {\rm \gamma} } \over {\partial \left( {{k_{\rm p}}{\rm \xi} } \right)}} + {\rm \gamma} \displaystyle{{\partial {a_1}} \over {\partial \left( {{k_{\rm p}}{\rm \xi} } \right)}}} \right)} \right\} - \displaystyle{{{u_{x{\rm s}}}} \over {\rm \gamma} }\displaystyle{{\partial {\rm \gamma} } \over {\partial \left( {{k_{\rm p}}{\rm \xi} } \right)}},{\rm }}$$

(7)$$\displaystyle{{\partial n} \over {\partial ({k_{\rm p}}{\rm \xi} )}} = \displaystyle{n \over {\left( {1 - {u_{x{\rm s}}}} \right)}}\displaystyle{{\partial {u_{x{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}},$$

and

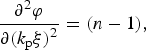(8)$$\displaystyle{{{\partial ^2}{\rm \varphi}} \over {\partial {{({k_{\rm p}}{\rm \xi} )}^2}}} = (n - 1),$$

where u _is(v _is/c, i = x, y, z) is the normalized plasma electron velocity, φ(=eφ/mc ²) is the normalized scalar potential, and n(=n _e/n ₀) is the normalized plasma electron density. While deriving Eqs. (6)–(8), the fast velocities [Eq. (4)] have been used and the harmonics of the laser frequency have been neglected.

It may be seen from Eq. (6b) that the slow velocity and hence the slow vortex currents do not arise along the z-direction. Also from Eq. (6a), it may be noted that the transverse velocity is generated along the y-direction only, and is driven by the enhanced longitudinal velocity obtained due to the presence of the second laser pulse. Therefore, the enhanced vortex current is generated in the wake of the laser pulse, leading to the generation of a transverse electromagnetic wave, oscillating at the plasma frequency $({{\rm \omega} _{\rm p}} = {(4{\rm \pi} {n_0}{e^2}/m)^{1/2}})$. The evolution of the electric field E _yTHz (normalized by e/mcω_p) of the slow transverse electromagnetic wave generated in the wake of the laser pulses is governed by,

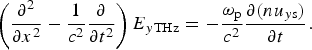(9)$$\left( {\displaystyle{{{\partial ^2}} \over {\partial {x^2}}} - \displaystyle{1 \over {{c^2}}}\displaystyle{\partial \over {\partial {t^2}}}} \right){E_{y{\rm TH}{\rm z}}} = - \displaystyle{{{{\rm \omega} _{\rm p}}} \over {{c^2}}}\displaystyle{{\partial (n{u_{y{\rm s}}})} \over {\partial t}}.$$

Since this slow wave travels with the group velocity of the laser pulse, Eq. (9) may be transformed to the laser pulse frame to give,

(10)$$n\displaystyle{{\partial {u_{y{\rm s}}}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} + {u_{y{\rm s}}}\displaystyle{{\partial n} \over {\partial ({k_{\rm p}}{\rm \xi} )}} = 0. $$

The slow transverse electric field may be evaluated by substituting Eqs. (6)–(8) into the transformed Eq. (10) to give,

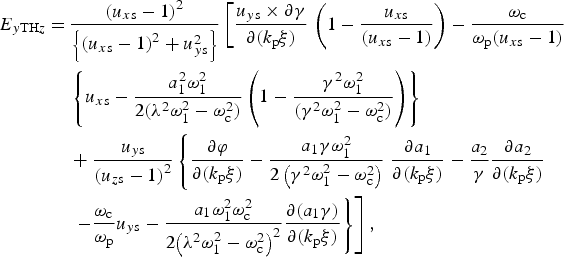(11)$$\eqalign{{E_{y{\rm TH}z}} =\, & \displaystyle{{{{({u_{x{\rm s}}} - 1)}^2}} \over {\left\{ {{{({u_{x{\rm s}}} - 1)}^2} + u_{y{\rm s}}^2 } \right\}}}\left[ {\displaystyle{{{u_{y{\rm s}}} \times \partial {\rm \gamma} } \over {\partial ({k_{\rm p}}{\rm \xi} )}}} \right.\left( {1 - \displaystyle{{{u_{x{\rm s}}}} \over {({u_{x{\rm s}}} - 1)}}} \right) - \displaystyle{{{{\rm \omega} _{\rm c}}} \over {{{\rm \omega} _{\rm p}}({u_{x{\rm s}}} - 1)}} \cr & \left\{ {{u_{x{\rm s}}} - \displaystyle{{a_1^2 {\rm \omega} _1^2 } \over {2({{\rm \lambda} ^2}{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}}\left( {1 - \displaystyle{{{{\rm \gamma} ^2}{\rm \omega} _1^2 } \over {({{\rm \gamma} ^2}{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}}} \right)} \right\} \cr &+ \displaystyle{{{u_{y{\rm s}}}} \over {{{({u_{z{\rm s}}} - 1)}^2}}}\left\{ {\displaystyle{{\partial {\rm \varphi} } \over {\partial ({k_{\rm p}}{\rm \xi} )}} - \displaystyle{{{a_1}{\rm \gamma} {\rm \omega} _1^2 } \over {2\left( {{{\rm \gamma} ^2}{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 } \right)}}} \right.\displaystyle{{\partial {a_1}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} - \displaystyle{{{a_2}} \over {\rm \gamma} }\displaystyle{{\partial {a_2}} \over {\partial ({k_{\rm p}}{\rm \xi} )}} \cr & {\rm }\left. {\left. { - \displaystyle{{{{\rm \omega} _{\rm c}}} \over {{{\rm \omega} _{\rm p}}}}{u_{y{\rm s}}} - \displaystyle{{{a_1}{\rm \omega} _1^2 {\rm \omega} _{\rm c}^2 } \over {2{{\left( {{{\rm \lambda} ^2}{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 } \right)}^2}}}\displaystyle{{\partial ({a_1}{\rm \gamma} )} \over {\partial ({k_{\rm p}}{\rm \xi} )}}} \right\}} \right],} $$

where ∂a _ys/∂(k _pξ) = E _yTHz has also been substituted.

In order to analyze the generation of the slow transverse electromagnetic waves, Eqs. (6)–(8) and (11) are solved simultaneously, for the appropriate laser and plasma parameters, using the fourth-order Runge–Kutta algorithm. For the numerical analysis, we consider two laser pulses having a sinusoidal profile of the form a _j = a _0j sin (πξ/L _j), [where a _0j and L _j are the normalized peak amplitude and length of the first (j = 1) and second (j = 2) laser pulses, respectively]. The wavelength of the two laser pulses are 800 nm (ω₁ = 2.355 × 10¹⁵radHz) and 821 nm (ω₂ = 2.296 × 10¹⁵rad Hz). The laser pulses are assumed to be copropagating in the plasma having ambient plasma density n ₀ = 1.09 × 10¹⁸/cm³ (ω_p = 5.887 × 10¹³rad Hz). The pulse length of the two-laser pulses is assumed to be 31 μm in order to satisfy the maximum wake condition L ~ λ_P. The applied magnetic field (B ₀) is considered to be 20 T.

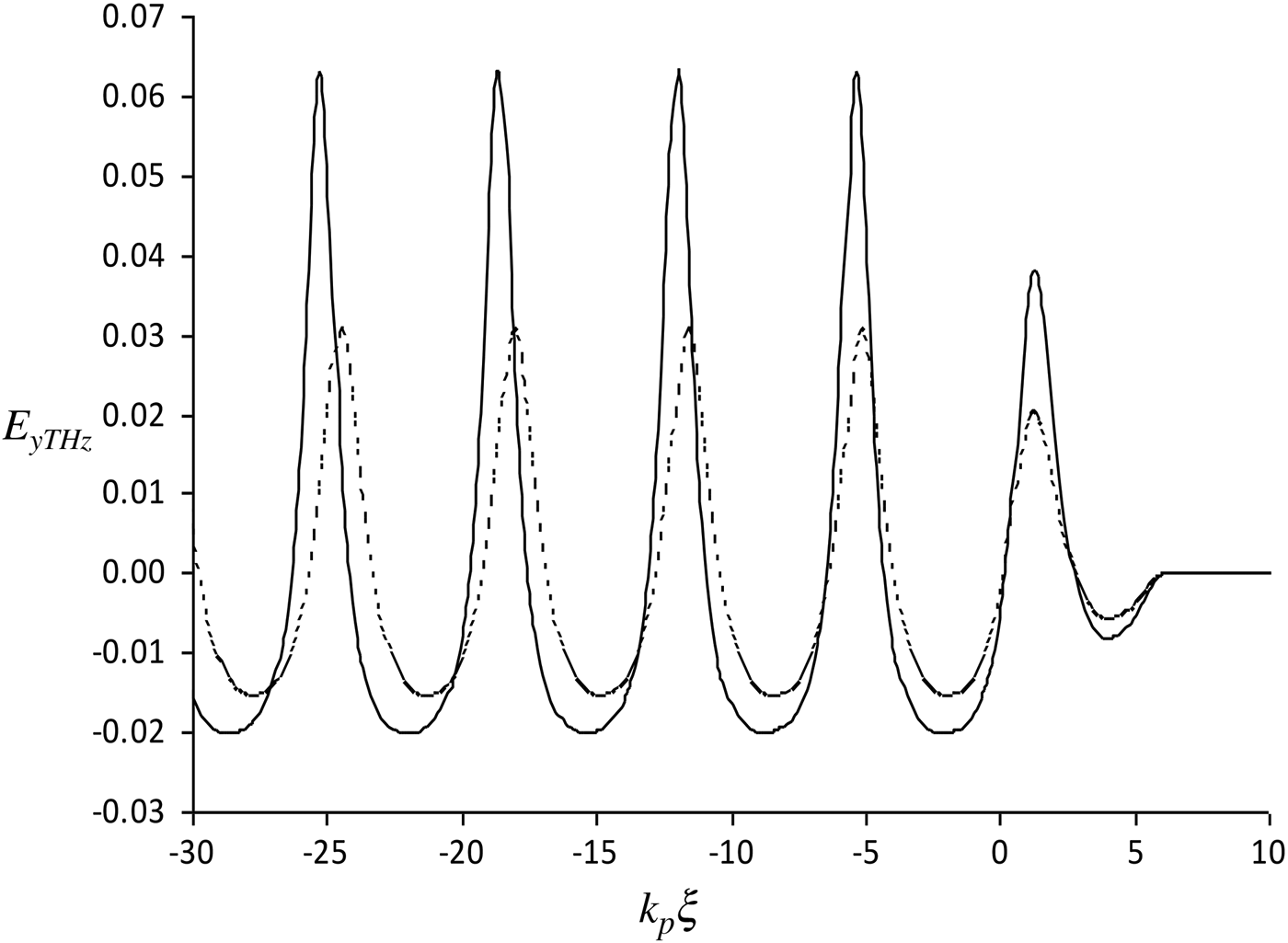
Variation of normalized amplitude of the slow transverse electric wakefield along the y-direction (E _yTHz) with respect to k _pξ is depicted in Figure 1. The dashed curve shows the variation of slow transverse field for a single laser pulse propagating in the extraordinary mode, having intensity I ₁ = 2.14 × 10¹⁸ W/cm² which corresponds to the normalized amplitude a ₀₁ = 1. The solid curve depicts the evolution of the amplitude of slow transverse field for the two-color pulse system, wherein the second laser pulse copropagates in the ordinary mode and has intensity half (I ₂ = 1.07 × 10¹⁸ W/cm²) that of the first pulse. Simultaneous transverse oscillatory magnetic fields of the same amplitude are generated along the z-direction. These transverse electric and magnetic fields generated in the wake of the laser pulses oscillate at the plasma frequency (≈9.4 THz) and having equal amplitudes constitute THz radiation. It is seen that there is an enhancement of 78% in the THz amplitude in case of two-color laser pulses (solid curve) propagating in the plasma as compared with that of a single laser pulse (dotted curve).

Fig. 1. Variation of the normalized transverse electric field, E _yTHz with k _pξ for the two-color pulse system (solid curve) for I ₁ = 2.14 × 10¹⁸ W/cm²,  I ₂ = 1.07 × 10¹⁸ W/cm² and for a single laser pulse (dotted curve) of I ₁ = 2.14 × 10¹⁸ W/cm². The externally applied magnetic field is 20 T, for both the curves.

4. 2D-PIC SIMULATION STUDY

A 2D PIC simulation study was performed using the XOOPIC code. In the simulation process, two-color laser pulses having sinusoidal profile were launched along the x-direction through homogeneous plasma. The two laser pulses were orthogonally polarized along the y- and z-directions. Application of the static magnetic field (=20 T) along the z-direction allowed the laser pulse polarized along the y-direction to propagate in the extraordinary mode, while the laser pulse polarized along the z-direction in the ordinary mode. The transverse laser spot size of the two-laser pulses has been considered to be 50 μm. The size of the simulation domain was 160 μm in the laser propagation direction (x) and 400 μm in the transverse direction (y). Half (80 μm) of the longitudinal domain was comprised of the plasma, while the remaining (80 μm) was considered to be vacuum. The domain was divided into 4096 × 512 meshes. The time step was taken to be 0.127 fs in order to satisfy the courant condition. The other laser and plasma parameters are the same as those used for the 1D numerical study.

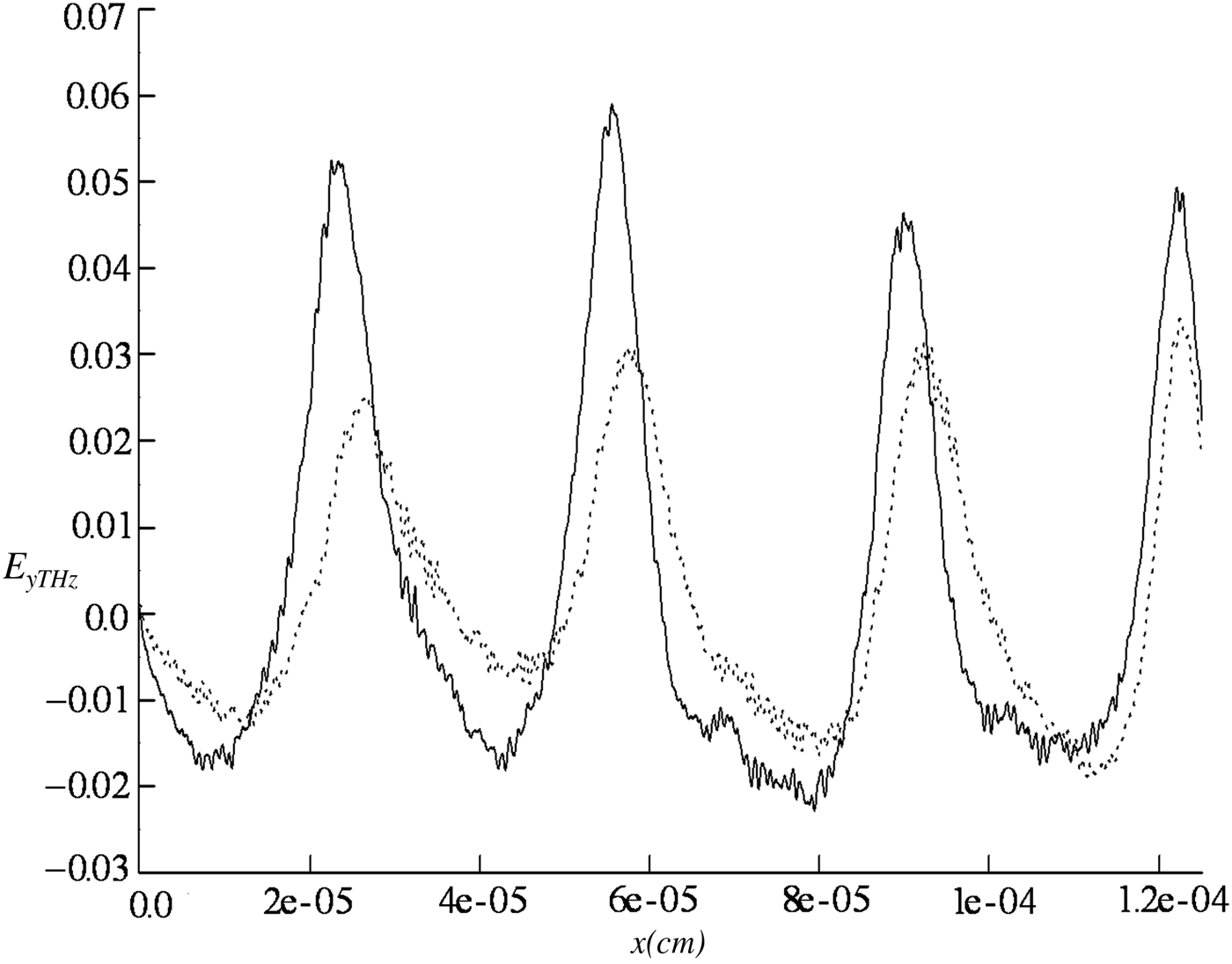
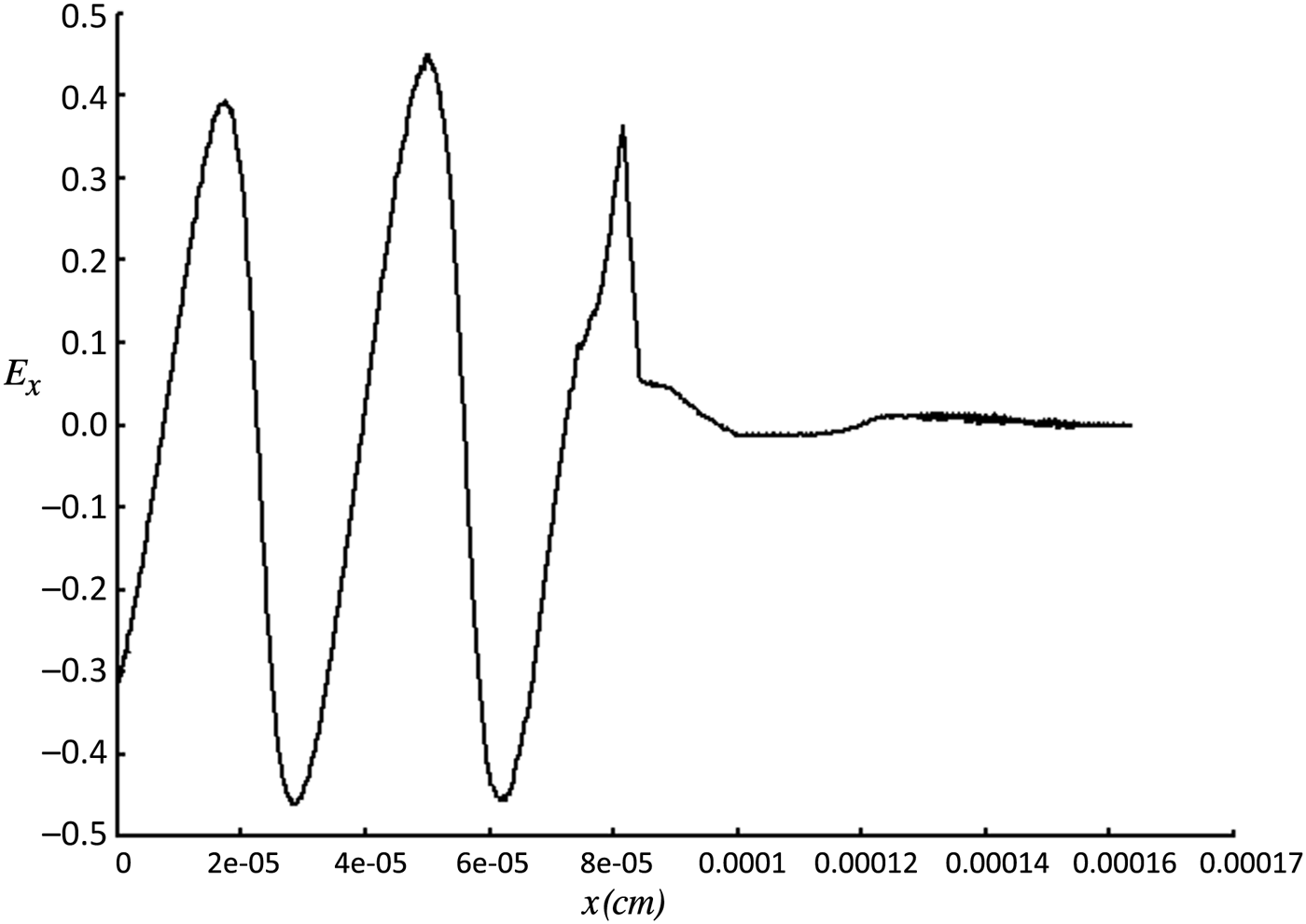
Figure 2 shows the evolution of the normalized amplitude E _yTHz along the y-direction of the transverse electric field, generated behind the laser pulse, with propagation distance x. The solid curve depicts the evolution of the amplitude of the slow transverse field for the two-color pulse system comprising of ordinary and extraordinary modes, while the dashed curve shows the variation of the slow transverse field for a single laser pulse propagating in the extraordinary mode. Simultaneously, a magnetic field of the same amplitude is generated along the z-direction. It is seen that these transverse fields can transmit into vacuum, leading to the generation of enhanced THz radiation that can propagate out of the plasma. The simulation results show the same trend in the evolution of THz radiation amplitude as obtained via 1D numerical study. A comparison of amplitude of generated THz radiation by the propagation of two-color laser pulses in the plasma (solid curve) with that of a single laser pulse (dotted curve) shows that 76% higher amplitude may be obtained in the former case. A comparison of Figure 2 with Figure 1 shows that the amplitude of the transverse electric field obtained via simulation is approximately the same as obtained from the 1D study. The normalized (by e/mcω _p) amplitude of the longitudinal wakefield generated in the plasma, for the same parameters as in Figure 2, has been shown in Figure 3. Due to electrostatic nature of the longitudinal wakefield it cannot propagate out of the plasma.

Fig. 2. Variation of the normalized transverse electric field, E _yTHz behind the laser pulse with propagation distance (x) in the plasma (from 0 to 80 μm) and in vacuum (80 to 160 μm) using the XOOPIC code. The solid curve for two-color laser pulses of intensities, I ₁ = 2.14 × 10¹⁸ W/cm², I₂ = 1.07 × 10¹⁸ W/cm² and dotted curve for a single laser pulse with I ₁ = 2.14 × 10¹⁸W/cm². The externally applied magnetic field is 20 T, for both the curves.

Fig. 3. Variation of the normalized longitudinal wakefield behind the laser pulse, with propagation distance (x) in the plasma (from 0 to 80 μm) and in vacuum (from 80 to 160 μm) using the XOOPIC code.

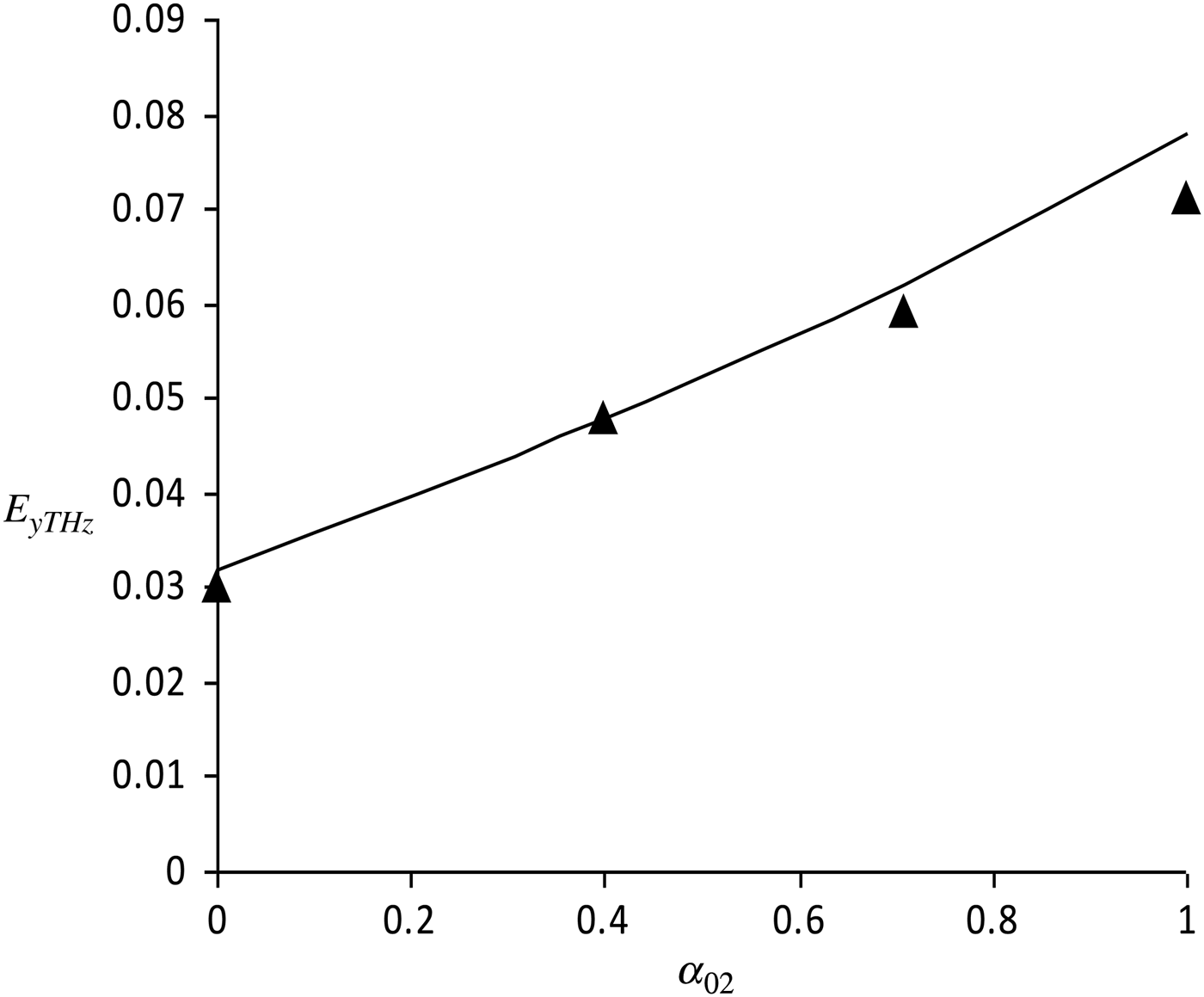
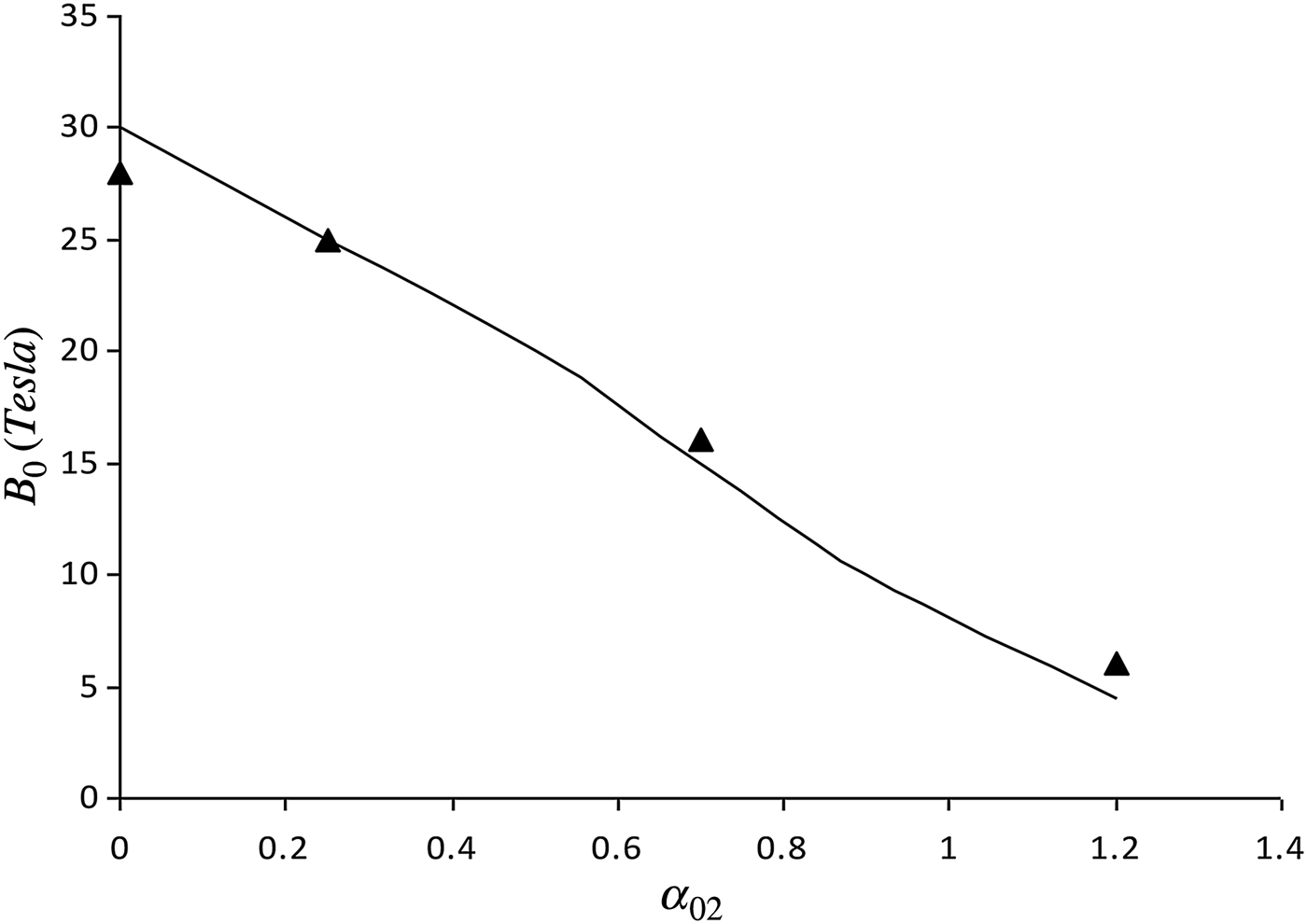
Variation of the normalized THz amplitude vs the normalized laser strength parameter of the second laser pulse with other parameters same as in Figures 1 and 2, has been shown in Figure 4. The solid line shows the results obtained from a numerical model, while the solid triangles represent the electric field amplitudes obtained via simulations. It is seen that for a given value of external magnetic field the amplitude of THz radiation increases linearly with the normalized amplitude of the second laser pulse. Figure 5 shows the variation of external magnetic field with normalized amplitude of the second laser pulse, for a generation of THz radiation of given normalized amplitude ≈5.0 × 10.⁻² The solid line depicts the results obtained from 1D numerical model, while the solid triangles represent the electric field amplitudes obtained via simulations. It is seen that the magnitude of the external field may be reduced by increasing the amplitude of the laser pulse propagating in the ordinary mode. For example, the external magnetic field may be reduced approximately to one-third by simultaneously increasing the intensity of the second laser pulse to a value equal to that of the first laser pulse propagating in the extraordinary mode.

Fig. 4. Variation of the normalized amplitude of the transverse electric field with the normalized amplitude of the second laser pulse, for ${I_1} = 2.14 \times {10^{18}}\,{\rm W/c}{{\rm m}^2}, \,{{\rm \omega} _1} = 2.355 \,\times\, {10^{15}}\,{\rm rad} {\rm Hz},\,{{\rm \omega} _2} = 2.296 \,\times\, {10^{15}}{\rm rad} {\rm Hz,} {{\rm \omega} _{\rm p}} = 5.887 \,\times\, {10^{13}}\,{\rm rad} {\rm Hz}$ and the applied magnetic field 20 T, obtained from the numerical model (solid line) and from the simulation study (solid triangles).

Fig. 5. Variation of the external magnetic field with the normalized amplitude of the second laser pulse for the generation of normalized THz amplitude ≈5.0 × 10⁻², for ${I_1} = 2.14 \times {10^{18}}\,{\rm W/c}{{\rm m}^2},{{\rm \omega} _1} = 2.355 \times {10^{15}}\,{\rm rad} {\rm Hz},\,{{\rm \omega} _2} = 2.296 \times {10^{15}}\,{\rm rad} \,{\rm Hz}\,{\rm and}\,{{\rm \omega} _{\rm p}} = 5.887 \times {10^{13}}\,{\rm rad} \,{\rm Hz},$obtained from the numerical model (solid line) and from the simulation study (solid triangles).

5. SUMMARY AND DISCUSSION

A 1D numerical model for studying the generation of enhanced THz radiation by the interaction of a two-color laser pulse system with a magnetized plasma has been presented. The direction of the external magnetic field is considered in such a way that one of the two laser pulses propagates in the extraordinary mode, while the other in the ordinary mode through homogeneous plasma. The nonlinear fluid equations governing the interaction of the laser pulse with magnetized plasma are transformed to the laser pulse frame. Further, by applying QSA the transformed equations are reduced to a time-independent form. The time-independent equations are solved numerically using fourth-order Runge–Kutta algorithm, in order to study the generation of transverse electric and magnetic fields. It is seen that the occurrence of the second laser pulse along with externally applied magnetic field enhances slow vortex currents generated along the polarization direction of the laser pulse propagating in the extraordinary mode. These slow currents further lead to the generation of transverse electromagnetic fields with enhanced amplitudes. These fields oscillate at the plasma frequency, thereby leading to the generation of enhanced THz radiation. The amplitude of THz radiation generated by mixing of ordinary and extraordinary modes of two-color laser pulses propagating in the plasma is seen to be enhanced as compared with that obtained for a single laser pulse.

Further, the results obtained from the 1D numerical model have been verified by conducting 2D PIC simulations using the XOOPIC code. The results obtained via simulation study validate those obtained from the 1D numerical model, leading to the verification of numerically predicted results. Also, the simulation studies show that the generated transverse fields can transmit into vacuum, leading to the generation of enhanced THz radiation that can propagate out of the plasma.