2.1. The General Dual-frequency Signal Model and the Linearly Combined Composite Signal

Consider the following situation: There are N signals s₁(t), s₂(t), …, s_N(t) to be multiplexed and transmitted at a carrier frequency f ₀. They can be expressed as

(1)$$s_n \!\lpar t \rpar =\sqrt {P_n} d_n \!\lpar t \rpar \sum\limits_{i=-\infty}^{+\infty} {c_n \!\lpar i \rpar p_n \!\lpar {t-iT_{c_i}} \rpar }$$

where P _n is the power of the nth signal, d _n(t) denotes the navigation message data for the data component or the secondary code for the pilot component, c _n is the spreading code, whose chip duration is $T_{c_n}$ and p _n(t) is the chip waveform, which is generally a binary waveform in a GNSS signal. Note that d _n(t) and c _n take binary values of +1 or −1. Thus, s _n(t) is a binary level signal. Without loss of generality, assuming that there are L signals s₁(t), s₂(t), …, s_L(t) in the lower sideband with a centre frequency of f ₀−f _sc, the remaining N−L signals s_L+1(t), s_L+2(t), …, s_N(t) are located in the upper sideband with a centre frequency of f ₀+f _sc.

First, we combine the signals in each sideband using an arbitrary single-frequency multiplexing technique and obtain two constant envelope signals, which are equivalent to two Phase-Shift Keying (PSK)-modulated signals and can be expressed as

(2)$$S_l \lpar t \rpar = \sqrt{P_l} e^{j\theta_l \lpar t \rpar }, S_u \lpar t \rpar = \sqrt{P_u} e^{j\theta_u \lpar t \rpar }$$

where P _l and P _u are the powers in the lower and upper sidebands. θ_l (t) can take 2^L possible values, $\theta_{l1},\theta_{l2},\cdots,\theta_{l2^{L}}$ and $\theta_{u} \!\lpar t \rpar $ can take 2^N−L possible values, $\theta_{u1},\theta_{u2},\cdots,\theta_{u2^{N-L}}$; these values are uniquely determined by the combination of signal chips in each sideband.

To transmit these two constant envelope signals through a common High-Power Amplifier (HPA), a natural approach is to modulate these two signals by their respective complex subcarriers and then add them together. This integrated signal is termed the linearly combined baseband signal and can be expressed as

(3)$$\matrix{S_{{\rm linear}} \!\lpar t \rpar =\sqrt {P_l} e^{\,j\!\lpar {-2\pi f_{sc} t+\theta_l \!\lpar t \rpar } \rpar } + \sqrt{P_u} e^{\,j\!\lpar {2\pi f_{sc} t+\theta_u \!\lpar t \rpar } \rpar } \cr =\sqrt {P_l} e^{\,j{\!\lpar {\theta_l \!\lpar t \rpar +\theta_u \!\lpar t \rpar } \rpar }/2}\!\lpar {e^{-j\!\lpar {2\pi f_{sc} t+{\!\lpar {\theta_u \!\lpar t \rpar -\theta_l \!\lpar t \rpar } \rpar } / 2} \rpar }+\alpha e^{\,j\!\lpar {2\pi f_{sc} t+{\!\lpar {\theta_u \!\lpar t \rpar -\theta_l \!\lpar t \rpar } \rpar } / 2} \rpar }} \rpar }$$

where $\alpha =\sqrt {{P_{u}}/{P_{l}}}$. The cases of α=0 and α=+∞ correspond to single-frequency multiplexing. For clarity, only the case of 0<α<∞ is considered in the following derivation. Note that our focus is the power ratio between the two sidebands rather than the absolute power value; therefore, P _l=1 is assumed in the following derivation.

The frequency difference f _sc also denotes the complex subcarrier frequency. Note that θ_l (t) and θ_u (t) are constants during the least common subchip length of the signal components. Thus, the constellation diagram of S _linear(t) is a series of ellipses for α≠1 or a series of line segments for α=1. Each combination of θ_l (t) and θ_u (t) corresponds to an ellipse or line segment. The period of each ellipse or line segment is T _sc=1/f _sc. An example for α=2 and θ_l (t), θ_u (t)∈ {(2i−1)π / 4}, with i=1, 2, 3 and 4, is shown in Figure 1, where only four possible ellipses are presented. Clearly, the envelope of S _linear(t) is not constant.

Figure 1. The constellation diagram of the linearly combined baseband signal.

2.2. The Proposed Constant Envelope Multiplexing Technique

To obtain a constant envelope composite signal, a phase-aligned method is introduced. More precisely, the phase of the constant envelope composite signal is aligned with the phase of the linearly combined baseband signal S _linear(t), but the amplitude is forced to be constant. Consequently, the constant envelope composite signal can be written as

(4)$$S_{{\rm CE}} \!\lpar t \rpar =e^{\,j\angle S_{{\rm linear}} \!\lpar t \rpar }$$

where $\angle S_{{\rm linear}} \!\lpar t \rpar $ represents the angle of S _linear(t), which is given by

(5)$$\angle S_{{\rm linear}} \!\lpar t \rpar = {\theta_l \!\lpar t \rpar +\theta_u \!\lpar t \rpar \over 2} + \hbox{atan}\ 2 \left[\matrix{\lpar {\alpha -1} \rpar \sin \!\left(2\pi f_{sc} t + {\theta_l \!\lpar t \rpar -\theta_u \!\lpar t \rpar \over 2} \right), \cr \lpar 1 + \alpha \rpar \cos \left(2\pi f_{sc} t + {\theta_u \!\lpar t \rpar - \theta_l \lpar t \rpar \over 2} \right)} \right]$$

where $\hbox{atan}\,2\!\lpar \bullet\rpar $ is the four-quadrant arctangent function.

In fact, S _CE(t) can be regarded as an amplitude modulation applied to $S_{\rm linear}(t)$ and can be expressed as

(6)$$S_{\rm CE} \!\lpar t \rpar = {S_{{\rm linear}} \!\lpar t \rpar \over \vert S_{{\rm linear} \!\lpar t \rpar } \vert } = {e^{\,j\!\lpar {-2\pi f_{sc} t+\theta_l \!\lpar t \rpar } \rpar }+\alpha e^{\,j\!\lpar {2\pi f_{sc} t+\theta_u \!\lpar t \rpar } \rpar } \over \sqrt{1 + \alpha^2 + 2\alpha \cos \lpar 4\pi f_{sc} t + \theta_u \lpar t \rpar - \theta_l \lpar t \rpar \rpar}}$$

where |•| is the modulus operator.

Supposing that the least common subchip length of the signal components is T _G, then θ_l(t) and θ_u(t) maintain constant values of θ_l(k) and θ_u(k), respectively, over any time interval t∈[kT _G, (k+1)T _G), and the constant envelope signal can be rewritten as

(7)$$\eqalign{S_{\rm CE} \!\lpar t \rpar &=\sum\limits_{k=-\infty}^{+\infty} {{e^{\,j\!\lpar {-2\pi f_{sc} t+\theta_l \!\lpar k \rpar } \rpar }+\alpha e^{\,j\!\lpar {2\pi f_{sc} t+\theta_u \!\lpar k \rpar } \rpar } \over \sqrt {1+\alpha ^2+2\alpha \cos \!\lpar {4\pi f_{sc} t+\theta_u \!\lpar k \rpar -\theta_l \!\lpar k \rpar } \rpar }}\Pi \!\lpar {t-kT_G} \rpar } \cr &=\sum\limits_{k=-\infty}^{+\infty} {\lpar {e^{\,j\!\lpar {-2\pi f_{sc} t+\theta_l \!\lpar k \rpar } \rpar }+\alpha e^{\,j\!\lpar {2\pi f_{sc} t+\theta_u \!\lpar k \rpar } \rpar }} \rpar \cdot \hbox{M}\!\left({t-{\theta_u \!\lpar k \rpar -\theta_l \!\lpar k \rpar \over 4\pi f_{sc}}} \right)\cdot \Pi \!\lpar {t-kT_G} \rpar }}$$

where M(t) is the modulation function and Π(t) is the rectangular function. These functions are defined as

(8)$$\hbox{M}\!\lpar t \rpar = {1 \over \sqrt{1+\alpha ^2+2\alpha \cos \!\lpar {4\pi f_{sc} t} \rpar }}$$

(9)$$\Pi \lpar t \rpar =\left\{\matrix{1,\hfill &0\le t \lt T_G \cr 0, \hfill &\hbox{otherwise}}\right.$$

By expanding M(t) as a Fourier series and using the delay characteristic, we can rewrite Equation (7) as follows:

(10)$$\eqalign{S_{\rm CE} \lpar t \rpar &=\sum\limits_{k=-\infty}^{+\infty} {\!\lpar {e^{\,j\!\lpar {-2\pi f_{sc} t + \theta_l \!\lpar k \rpar } \rpar } + \alpha e^{\,j\!\lpar {2\pi f_{sc} t + \theta_u \!\lpar k \rpar } \rpar }} \rpar \!\left({\sum\limits_{n=-\infty}^{+\infty} {a_n e^{\,jn\!\lpar {\theta_u \!\lpar k \rpar -\theta_l \!\lpar k \rpar } \rpar }e^{\,j4n\pi f_{sc} t}}} \right)\Pi \!\lpar {t-kT_G} \rpar } \cr &= \lpar {a_0 +a_{-1} \alpha} \rpar e^{\,j\!\lpar {-2\pi f_{sc} t+\theta_l \!\lpar t \rpar } \rpar }+\!\lpar {\alpha a_0 +a_1} \rpar e^{\,j\!\lpar {2\pi f_{sc} t+\theta_u \!\lpar t \rpar } \rpar }+\hbox{H}\!\lpar t \rpar }$$

where H(t) denotes the higher-order harmonic components of the constant envelope composite signal. The $\lcub a_{k} \vert k=0,\pm 1,\pm 2,\cdots \rcub $ are the Fourier series coefficients of M(t) and can be calculated as

(11)$$a_k = {2 \over T_{sc}} \int_0^{T_{sc}/2} {e^{-jk4\pi f_{sc} t} \over \sqrt{1 + \alpha ^2 + 2\alpha \cos \lpar 4\pi f_{sc} t \rpar }}dt$$

A comparison of Equation (10) with Equation (3) reveals that to achieve a constant envelope, some undesired higher-order harmonic components are introduced. These higher-order harmonics will cause a loss of transmission power. In addition, the average correlation outputs of the constant envelope signal with respect to the replicas of the lower sideband signal are

(12)$$\eqalign{R_{{\rm CE},l} & = {1 \over T_p} \int\limits_0^{T_p} {S_{\rm CE} \!\lpar t \rpar \!\lpar {e^{\,j\!\lpar {{\rm-}2\pi f_{sc} t+\theta_l \!\lpar t \rpar } \rpar }} \rpar ^{\rm \ast}dt}\cr &= {1 \over T_p} \int_0^{T_p} {{1+\alpha e^{\,j\!\lpar {4\pi f_{sc} t+\theta_u \!\lpar t \rpar {\rm-}\theta_l \!\lpar t \rpar } \rpar } \over \sqrt {1{\rm +}\alpha ^2{\rm +}2\alpha \cos \!\lpar {4\pi f_{sc} t+\theta_u \!\lpar t \rpar -\theta_l \!\lpar t \rpar } \rpar }}dt}}$$

where T _p represents the coherent integration time (in the derivation, we assume that T _p approaches infinity) and the superscript ‘*’ represents the conjugate operator. Generally, in the GNSS context, the code rate R _c and the subcarrier frequency f _sc are both integer multiples of the base frequency f _base=1.023 MHz, and R _c is smaller than f _sc. In the derivation, we also assume that 2f _sc/R _c is an integer. These assumptions also hold in the following derivation. Therefore, Equation (12) can be rewritten as

(13)$$R_{{\rm CE},l} = \mathop{E}\limits_{\lcub \theta_l, \theta_u \rcub } \left({2 \over T_{sc}} \int_0^{{T_{sc}}/2} {1+\alpha e^{j \lpar {4\pi f_{sc} t+\theta_u {\rm-}\theta_l} \rpar } \over \sqrt {1{\rm +}\alpha^2{\rm +}2\alpha \cos \lpar 4\pi f_{sc} t + \theta_u - \theta_l} \rpar} dt \right) = a_0 +\alpha a_{-1}$$

Similarly, the average correlation outputs of the constant envelope signal with respect to the replicas of the upper sideband signal are

(14)$$R_{{\rm CE},u} = {1 \over T_p} \int\limits_0^{T_p} {S_{\rm CE} \!\lpar t \rpar \!\lpar {e^{\,j\!\lpar {2\pi f_{sc} t+\theta_u \!\lpar t \rpar } \rpar }} \rpar ^{\rm \ast}dt} =a_1 +\alpha a_0$$

As shown in Equations (13) and (14), the cross-correlations of the composite signal with respect to the replicas of the lower sideband signal and the upper sideband signal are exactly the coefficients of the components at ±f _sc in Equation (10), which indicates that the higher-order harmonic components have no effect on the average correlation outputs for useful signal components.

Note that the function given in Equation (8) is a real even function, whose Fourier series coefficients satisfy the relationship a _−k=a _k. Therefore, hereafter, we replace all a _−k with a _k. According to Equations (13) and (14), we calculate the power ratio between the upper and lower sidebands of the modulated signal as follows:

(15)$$\alpha_{{\rm CE}}^2 ={P_{{\rm CE},u} \over P_{{\rm CE},l}} = {R_{{\rm CE},u}^2 \over R_{{\rm CE},l}^2} = \left\vert {{a_1 +a_0 \alpha \over a_0 +a_1 \alpha}} \right\vert^2$$

Consequently, we can calculate α by substituting the designed power ratio, which is $\alpha_{{\rm CE}}^{\rm 2}$, into Equation (15), and then, the desired constant envelope composite signal can be obtained by inserting α into Equation (6).

In the proposed method, the power loss consists of two main components: one is the loss caused by the single-frequency multiplexing in each sideband, and the other is caused by the higher-order harmonic components, as shown in Equation (10). Thus, the multiplexing efficiency of the proposed method can be calculated as follows:

(16)$$\eta =\vert {a_1 +a_0 \alpha} \vert ^2\cdot \eta_u +\vert {a_0 +a_1 \alpha} \vert ^2\cdot \eta_l$$

where η_u and η_l are the single-frequency multiplexing efficiencies in the upper and lower sidebands, respectively. From Equations (11) and (16), we find that the total multiplexing efficiency depends only on α, η_u and η_l.

Figure 2 shows the multiplexing efficiencies for different values of α, where the logarithm of α is used as the x axis. Three pairs of typical values for η_u and η_l are considered. The single-frequency multiplexing efficiency η_l=1 or η_u=1 represents the multiplexing of two signals in the corresponding sideband, and η_l=0.75 or η_u=0.75 represents the multiplexing of three signals with equal power in the corresponding sideband. We can obtain the following conclusions from this figure: the greater the power difference between the upper and lower sidebands, the higher the multiplexing efficiency of the proposed method. Furthermore, the minimum multiplexing efficiency occurs near α=1, and the multiplexing efficiency approaches η_u for α=+∞ and η_l for α=0.

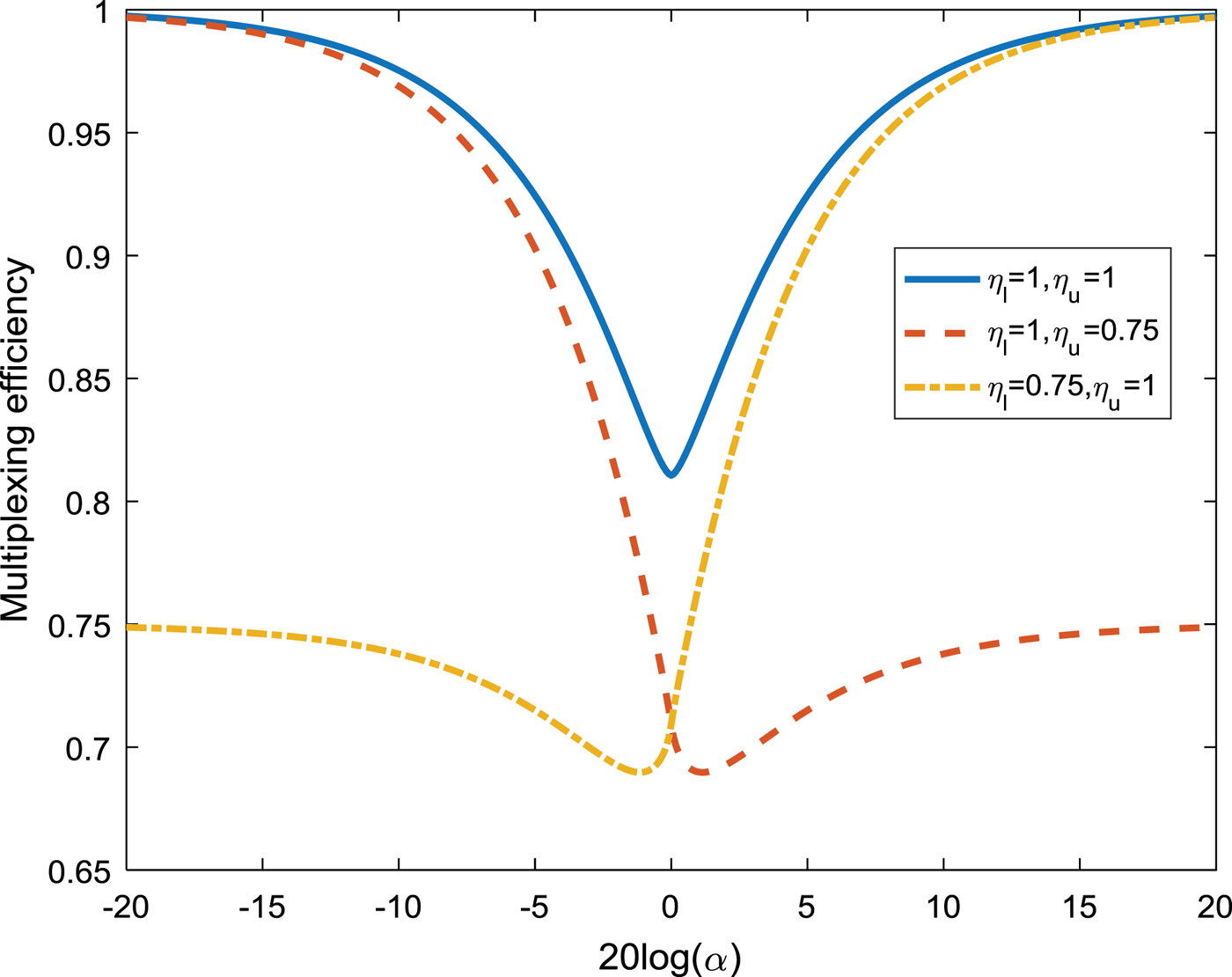
Figure 2. The multiplexing efficiency of the proposed method for different values of α.

Figure 3 shows a schematic depiction of the proposed method. The process can be described as follows: 1. Combine the signals in the lower and upper sidebands into two constant envelope signals. 2. Calculate the value of α based on the required power ratio α_CE according to Equations (11) and (15). 3. Generate the equivalent baseband signal according to Equation (3). 4. Generate the dual-frequency constant envelope composite signal according to Equations (4) or (6).

Figure 3. Schematic diagram of the proposed method.

2.3. The Special Case of α=1

Note that S _CE(t) may approach infinity when α=1, according to Equation (6). In this case, the expression for S _linear(t) can be written as

(17)$$S_{\rm linear} \lpar t \rpar = 2e^{\,j {\theta_l \!\lpar t \rpar {\rm +}\theta_u \!\lpar t \rpar \over 2}}\cos \!\left({2\pi f_{sc} t{\rm +} {\theta_u \!\lpar t \rpar \hbox{-}\theta_l \!\lpar t \rpar \over 2}} \right)$$

Its constellation diagram consists of 2^N possible line segments through the origin. According to Equation (6), the expression for S _CE(t) is

(18)$$S_{\rm CE} \lpar t \rpar = {S_{\rm linear} \lpar t \rpar \over \vert S_{\rm linear} \lpar t \rpar \vert } = e^{j {\theta_l \!\lpar t \rpar +\theta_u \!\lpar t \rpar \over 2}} sign \left({\cos \!\left({2\pi f_{sc} t+ {\theta_u \!\lpar t \rpar -\theta_l \!\lpar t \rpar \over 2}} \right)} \right)$$

where sign(x) is the sign function. Our concern here is the definition of sign(0). In this paper, we take the common definition used in communications as follows:

(19)$$\hbox{sign}\!\lpar x \rpar = \left\{\matrix{1 \hfill &x\ge 0 \hfill \cr -1 \hfill &x \lt 0} \right.$$

Consequently, each line segment in the complex plane is mapped to two phase states.

Substituting Equation (18) into Equations (12) and (13), we obtain R _CE,l=R _CE,u=2 /π. The power ratio between the upper and lower sidebands of the composite signal is still equal to 1. The multiplexing efficiency in this case is 4(η_l+η_u) /π².

4.1. Case 1 (p₁:p ₂:p ₃:p ₄=1:γ:1:γ)

In this case, more power is allocated to the pilot component to achieve improved tracking performance. The power levels in the lower and upper sidebands are equal. The signals in each sideband are combined via Quadrature Phase-Shift Keying (QPSK), and they can be expressed as

(28)$$\eqalign{S_l \lpar t \rpar &= {\sqrt{2} \over 2}\!\left({s_1 \!\lpar t \rpar +j\sqrt \gamma s_2 \!\lpar t \rpar } \right)=e^{\,j\theta_l \!\lpar t \rpar } \cr S_u \!\lpar t \rpar &= {\sqrt{2} \over 2}\!\left({s_3 \!\lpar t \rpar +j\sqrt \gamma s_4 \!\lpar t \rpar } \right)=e^{\,j\theta_u \!\lpar t \rpar }}$$

The values of θ_l and θ_u and the corresponding values of the composite signal at t=0⁺ are shown in Table 2, where β represents the value of θ_l or θ_u when s ₁ (t)=s ₂(t)=s ₃(t)=s ₄(t)=1 and thus is defined as $\beta = \tan^{-1} \left(1 /\sqrt{\gamma} \right)$. The notation exp() represents the exponential function. The constellation diagram of the baseband composite signal is shown in the last column of Table 2. These results are consistent with those of ACEBOC, which implies that the proposed method is equivalent to ACEBOC under this power allocation scheme.

Table 2. Graphical representation of the proposed modulation table (1:γ:1:γ).

Specifically, let us consider γ=1 as an example, which is the same as in the Galileo E5 signal. For this example, β=π/4, and the number of possible phases in the constellation diagram reduces to eight. Table 3 shows a graphical representation of the proposed method. From the fifth and sixth columns, we can see that θ_l and θ_u satisfy the relationship expressed in Equation (26). Therefore, an optimal subcarrier sampling rate exists and is f _s=8f _sc, according to Equation (27). This result implies that the phase of the composite signal in a single subcarrier period can be divided into eight parts, as shown in the rightmost column of Table 3. Note that Table 3 is consistent with the graphical representation of AltBOC (Lestarquit et al., Reference Lestarquit, Artaud and Issler2008), which implies that AltBOC is a special case of the proposed method.

Table 3. Graphical representation of the proposed modulation table (1:1:1:1).

4.2. Case 2 (p₁:p ₂:p ₃:p ₄=1:1:γ:γ)

In this case, more power is allocated to one sideband; such a case is also considered in generalised AltBOC. Again, QPSK modulation is used to combine the signals in each sideband, and the modulated phases θ_l and θ_u are obtained as follows:

(29)$$\eqalign{S_l \lpar t \rpar &= {\sqrt{2} \over 2} \lpar s_1 \lpar t \rpar + js_2 \lpar t \rpar \rpar = e^{\,j\theta_l \lpar t \rpar } \cr S_u \lpar t \rpar &= {\sqrt{2\gamma} \over 2} \lpar s_3 \lpar t \rpar + js_4 \lpar t \rpar \rpar e^{j\varphi} = \sqrt{\gamma} e^{j\theta_u \lpar t \rpar }}$$

Note that an additional phase difference φ between the upper and lower sidebands is introduced in Equation (29). This is because this phase difference will affect the measured power ratio and the multiplexing efficiency obtained from the LUT in this case. The power ratio and multiplexing efficiency of the continuous signal expressed in Equation (6), which are calculated by Equations (15) and (16), do not depend on the phase relationship between the upper and lower sidebands. For the example of γ=3, according to Equations (11) and (15), α=1·2144 is obtained. We can then plot the measured power ratios and multiplexing efficiencies under different phase differences as shown in Figure 4, where the additional phase difference between the upper and lower sidebands varies from 0° to 90°. The curves labelled K→∞ represent the continuous signal as shown in Equation (6). The curves labelled K=8 represent the case of a subcarrier sampling rate of f _s=8f _sc, which is also employed in generalised AltBOC. For K→∞, the power ratio and multiplexing efficiency are constant, but for K=8, they vary with the phase difference. In GNSS signal design, the power ratio is a strong constraint; we must ensure that the power ratio for K=8 is equal to the power ratio for K→∞. One of the two intersections between the two power ratio curves, as shown in Figure 4, should be chosen, and the corresponding phase difference should be used to generate the LUT.

Figure 4. The power ratios and multiplexing efficiencies under different phase differences.

Figure 5 shows the multiplexing efficiencies of the proposed method for K→∞ and K=8 and the multiplexing efficiencies of generalised AltBOC and ACEBOC. The x-axis represents the logarithm of the power ratio between the upper and lower sidebands. For K=8, the multiplexing efficiencies are obtained by generating LUTs with suitable phase differences, as analysed above. Clearly, the multiplexing efficiency for K=8 is lower than the multiplexing efficiency for K→∞, which indicates that some additional loss due to sampling is introduced in the LUT-based method. The multiplexing efficiency of ACEBOC is constant at 0.8106. The multiplexing efficiency of the proposed method with K=8 is slightly lower than that of generalised AltBOC, but both methods are significantly improved relative to ACEBOC. Nevertheless, we can further improve the multiplexing efficiency of the LUT-based method by increasing the subcarrier sampling rate. Moreover, for the proposed method and generalised AltBOC, the larger the power difference is between the two sidebands, the greater is the improvement in multiplexing efficiency. When γ=1, which is exactly case 1, these three methods are equivalent to each other and to AltBOC. When γ→0 or γ→+∞, the multiplexing efficiencies of the proposed method with K=8 and generalised AltBOC approach the same value of 94·96%, which is exactly the efficiency of single-sideband complex subcarriers with four levels.

Figure 5. The multiplexing efficiencies under different power ratios.

5.1. Proposed Method for Beidou B1 Signals

The application under consideration is the multiplexing of Beidou B1 signals. The same parameters employed in GCE-BOC (Huang et al., Reference Huang, Zhu, Tang, Gong and Ou2015) are used in this application. The details are listed in Table 4. There are four newly designed signals (namely, B1Cd, B1Cp, B1Ad and B1Ap) and one inherited signal (B1I) in the Beidou B1 band. Note that B1Ad and B1Ap are combined into one code sequence through Time-Division Data Multiplexing (TDDM); we term this combined signal B1A. Therefore, these five signal components are mapped to the four code sequences B1Cd, B1Cp, B1A and B1I, which have a power ratio of 1:3:4:2. Without loss of generality, let us assume that the power values of B1Cd, B1Cp, B1A and B1I are 1 W, 3 W, 4 W and 2 W, respectively. Note that AltBOC, ACEBOC and generalised AltBOC cannot be used for this application.

Table 4. Signal parameters in the Beidou B1 band.

First, the signals in the upper sideband are combined into a constant envelope signal using the Coherent Adaptive Subcarrier Modulation (CASM) method (Dafesh et al., Reference Dafesh, Nguyen and Lazar1999); this combined signal can be expressed as

(30)$$\eqalign{s_{u\_B1} \lpar t \rpar &=\left({\sqrt {P_{up\_I}} s_{B1Cp} \lpar t \rpar \cos \lpar m \rpar +\sqrt {P_{up\_Q}} s_{B1Cd} \lpar t \rpar \sin \lpar m \rpar } \right) \cr &\quad + j\left({\sqrt {P_{up\_Q}} s_{B1A} \lpar t \rpar \cos \lpar m \rpar -\sqrt {P_{up\_I}} s_{B1Cp} \lpar t \rpar s_{B1Cd} \lpar t \rpar s_{B1A} \lpar t \rpar \sin \lpar m \rpar } \right)}$$

where m is the modulation index, which is calculated as

(31)$$m = \tan^{-1} \sqrt{{P_{B1Cd} \over P_{B1A}}} = \tan^{-1} \left({1 \over 2} \right) = 0{\cdot}4636$$

$P_{up\_I}$ and $P_{up\_Q}$ are the powers in the in-phase and quadrature-phase channels and can be calculated as

(32)$$\eqalign{P_{up\_I} &= P_{B1Cp} /\cos^2 \lpar m \rpar = 3{\cdot}75\;\hbox{W} \cr P_{up\_Q} &= P_{B1A} /\cos^2 \lpar m \rpar = 5\;\hbox{W}}$$

Therefore, the total power of the combined signal in the upper sideband is 8·75 W.

There is only one signal in the lower sideband; thus, the combined signal in the lower sideband is

(33)$$s_{l\_B1} \lpar t \rpar = j \sqrt{P_{B1I}} s_{B1I} \lpar t \rpar $$

The desired power ratio between the upper and lower sidebands is α_CE²=8·75 / 2=4·375. Thus, a value of α=1·3496 can be calculated from Equations (11) and (15) using numerical methods. The modulated phases in the upper and lower sidebands are

(34)$$\eqalign{\theta_u \lpar t \rpar & =\hbox{atan}\,2 \lpar s_{u\_B1} \lpar t \rpar \rpar \cr \theta_l \lpar t \rpar &= \hbox{atan}\,2 \lpar s_{l\_B1} \lpar t \rpar \rpar }$$

According to Equation (6), the final composite signal is obtained as follows:

(35)$$S_{B1} \!\lpar t \rpar = {e^{\,j\!\lpar {-2\pi f_{sc\_B1} t+\theta_l \!\lpar t \rpar } \rpar }+1{\cdot}3496e^{\,j\!\lpar {2\pi f_{sc\_B1} t+\theta_u \!\lpar t \rpar } \rpar } \over \sqrt {2{\cdot}8214+2{\cdot}6992\cos \!\lpar {4\pi f_{sc\_B1} t+\theta_u \!\lpar t \rpar -\theta_l \!\lpar t \rpar } \rpar }}$$

Note that the subcarrier frequency is $f_{sc\_B1}=7f_{base}$. Figure 6 shows the multiplexing efficiencies of the proposed method and GCE-BOC for different subcarrier sampling rates. It is clear that our method offers higher multiplexing efficiency than GCE-BOC. As the subcarrier sampling rate increases, the multiplexing efficiency of the proposed method also increases and approaches 0·8148, as calculated according to Equation (16).

Figure 6. The multiplexing efficiencies of the proposed method and GCE-BOC in the Beidou B1 band.

5.2. LUT-based Implementation

For the selection of the subcarrier sampling rate, we consider two types of signal generators as follows. Note that there are a BOC(14,2) signal and a TMBOC(6,1,1/11) signal in the B1 band and an AltBOC-like signal in the B2 band; the driving clock on the satellite must have the ability to generate the subcarrier frequencies 14f _base, 6f _base and 15f _base.

1) B1 and B2 share a relatively high clock rate and use a fractional frequency to obtain their own driving clock rate. Therefore, the required minimum driving clock rate is 210f _base. The subcarrier sampling rate should be a factor of 210f _base, which implies that K must be a factor of 30, according to Equation (20). As shown in Figure 6, the multiplexing efficiency increases with increasing K, but the size of the LUT also increases. Therefore, considering the size of the LUT and the multiplexing efficiency, K=15 is chosen, which implies that the subcarrier sampling rate should be $f_{s\_B1} = 15f_{sc\_B1} = 105f_{base}$. The multiplexing efficiency under this subcarrier sampling rate is 80·20%, which is 5·14% higher than that of GCE-BOC.

2) The driving clock rate of B1 and B2 is obtained as a multiple of a relatively low fundamental clock rate. Therefore, for B1 signal generation, the required minimum driving clock rate is 42f _base. However, this minimum driving clock rate would lead to a relatively low subcarrier sampling rate of $6f_{sc\_B1}$, which would produce a significant loss in multiplexing efficiency, as shown in Figure 6. Therefore, we double this minimum driving clock rate to 82f _base to obtain a relatively large subcarrier sampling rate of $12f_{sc\_B1}$. The multiplexing efficiency under this subcarrier sampling rate is 79·49%, which is 6·92% higher than that of GCE-BOC.

In the following analysis and simulation, we consider only a signal generator with a subcarrier sampling rate of $f_{s\_B1} =15f_{sc\_B1} =105f_{base}$. Table 5 shows the phase LUT for the proposed method under this subcarrier sampling rate. Note that only half of the states are listed, considering the symmetry of the phase LUT. This symmetry implies that when all chip values are complemented, the stored phase value increases by π (Dafesh and Cahn, Reference Dafesh and Cahn2009). There are a total of 240 phase states in the LUT.

Table 5. LUT of the phase states in the Beidou B1 band for the proposed method.

According to Equations (22) and (23), the average correlations of B1A, B1C_p, B1C_d and B1I are j0·5664, 0·4906, 0·2833 and j0·4004, respectively. Thus, the useful signal components can be modelled as

(36)$$\eqalign{S_{B1}^{useful} \lpar t \rpar &=\lpar {0{\cdot}2833s_{B1Cd} \lpar t \rpar + 0{\cdot}4906s_{B1Cp} \lpar t \rpar + j0{\cdot}5664s_{B1A} \lpar t \rpar } \rpar e^{j2\pi f_{sc\_B1} t} \cr &\quad + j0{\cdot}4004s_{B1I} \lpar t \rpar e^{-j2\pi f_{sc\_B1} t}}$$

The average power ratio of the four signal components is $\vert {corr_{B1A}} \vert ^{2}{:}\vert {corr_{B1Cp}} \vert ^{2}{:}\break \vert {corr_{B1Cd}} \vert ^{2}{:}\vert {corr_{B1I}} \vert ^{2}=4{\cdot}00{:}3{\cdot}00{:}1{\cdot}00{:}2{\cdot}00$, and the phase values of the four signal components are 90°, 0°, 0° and 90°, respectively. The multiplexing efficiency is given by $\vert {corr_{B1A}} \vert ^{2} + \vert {corr_{B1Cp}} \vert ^{2}+\vert {corr_{B1Cd}} \vert ^{2}+\vert {corr_{B1I}} \vert ^{2}=80{\cdot}2\hbox{0}\% $.

5.3. Cross-correlation Functions (CCFs)

Figure 7 shows the simulation architecture for obtaining the CCFs of the B1 signal. First, four binary signal components s _B1I(t), s _B1Cd(t), s _B1Cp(t) and s _B1A(t) are generated with random spreading codes. We then generate the composite signal s _B1(t) through the LUT method. The envelope of s _B1(t) is 1. The simulated sampling rate of the complex baseband signal is 214·83 MHz. The signals in the lower sideband and upper sideband are up- or down-converted to remove the subcarrier. The converted signals are then correlated with useful signal components in the corresponding sideband to obtain the CCFs. The coherent integration time is T=1 ms.

Figure 7. The simulation architecture to obtain the CCFs of Beidou B1 signals.

The simulated CCFs for the B1 signal are shown in Figure 8. To obtain an accurate estimation, the CCFs are averaged from 100 pairs of different random PRN codes. The results show that each simulated CCF has the expected shape. The peak values of these CCFs are 0·2813, 0·4899, 0·5666 and 0·4003. The difference between the simulated values and expected values is less than 1%. The simulated CCF shapes and peaks demonstrate that the BOC(14,2), TMBOC(6,1,4/33), BOC(1,1) and BPSK-R(2) signals are combined correctly in the composite signals and that the desired power allocation is achieved.

Figure 8. The CCFs of the generated Beidou B1 signals.

5.4. Power Spectral Density (PSD)

To verify the PSD of the proposed scheme for the B1 signal, the simulated PSD is compared with the directly summed PSD of useful signal components in this subsection. The simulated PSD is obtained by generating the signals with random spreading codes and averaging the results of the periodogram algorithm through 10,000 Monte Carlo runs, and the spectrum measurement is improved by a correction factor to compensate for the sampling effect (Dafesh and Cahn, Reference Dafesh and Cahn2009); the directly summed PSD is calculated as follows:

(37)$$\eqalign{PSD_{B1}^{sum} \lpar f \rpar &=0{\cdot}2833^2G_{BOC(1,1)} \lpar {f - f_{sc}} \rpar + 0{\cdot}4906^2G_{TMBOC(6,1,4/33)} \lpar {f - f_{sc}} \rpar \cr &\quad+0{\cdot}5664^2G_{BOC(14,2)} \lpar {f - f_{sc}} \rpar + 0{\cdot}4004^2G_{BPSK(2)} \lpar {f + f_{sc}} \rpar }$$

where G(f) represents the theoretical PSD of the corresponding modulation.

Figure 9 shows the simulated PSD and the summed PSD in the Beidou B1 band. The shapes of the main lobes in the simulated PSD are essentially the same as those in the directly summed PSD. In greater detail, the main lobes of the directly summed PSD and the simulated PSD at $\pm 1{\cdot}023\;\hbox{MHz}$ are nearly the same, but the main lobes of the directly summed PSD at −7 MHz and +21 MHz are approximately 1 dB lower than those of the simulated PSD. Moreover, a marked difference between the simulated and directly summed PSDs appears at high frequencies. The directly summed PSD includes only the useful signal components, whereas the simulated PSD includes not only the useful signal components but also the higher-order harmonic components and the inter-modulation products, which are two sources of the difference between the two PSDs. In addition, the sampling also contributes to the difference between the two PSDs. In short, the locations and shapes of the main lobes in the simulated PSD demonstrate that the proposed technique can indeed modulate these useful signal components to the desired frequencies.

Figure 9. The PSDs of the generated Beidou B1 signals.