1. INTRODUCTION
Integer ambiguity resolution is able to improve positioning accuracy and reduce convergence time. Several methods have been developed for Precise Point Positioning (PPP) integer ambiguity resolution, which include the single-difference between satellites method, the integer phase clock model and the decoupled clock model. Intensive investigations have been conducted to assess the positioning accuracy improvement by integer ambiguity resolution in PPP (Collins et al., Reference Collins, Bisnath, Francois and Héroux2010; Ge et al., Reference Ge, Gendt, Rothacher, Shi and Liu2008; Geng et al., Reference Geng, Teferle, Shi, Meng, Dodson and Liu2009; Laurichesse et al., Reference Laurichesse, Mercier, Berthias and Bijac2008).
Ge et al. (Reference Ge, Gendt, Rothacher, Shi and Liu2008) showed that the PPP ambiguity-resolved positioning accuracies in east/north/height could reach 2·8/3·0/7·8 mm respectively whereas the ambiguity-float positioning accuracies were 4·1/3·1/8·3 mm based on the single-difference between satellites method and daily observations. The most significant improvement was obtained in the east component, while the height solution improvement was found less significant. Geng et al. (Reference Geng, Teferle, Shi, Meng, Dodson and Liu2009) also demonstrated the hourly positioning accuracy improvements from 3·8/1·5/2·8 to 0·5/0·5/1·4 cm in the east/north/height directions, respectively. The height accuracy improvement was again found less significant compared to the horizontal components. By using the un-differenced integer phase clock model, Laurichesse et al. (Reference Laurichesse, Mercier, Berthias and Bijac2008) demonstrated ambiguity-resolved horizontal positioning accuracy of 2 cm using a 24-hour data set from a ground geodetic receiver. However, there was not much discussion about the performance in the vertical component. Collins (Reference Collins2008) proposed another method known as the decoupled clock model, and demonstrated a daily ambiguity-resolved positioning accuracy of 0·5/0·4/1·4 cm against the ambiguity-float accuracy of 0·4/0·6/1·4 cm in latitude/longitude/height, respectively. Collins et al. (Reference Collins, Lahaye, Heroux and Bisnath2008) also evaluated the decoupled clock model with hourly observations and showed that 2 cm ambiguity-resolved horizontal accuracy could be obtained within one hour. Similar to the daily solution, the hourly ambiguity-resolved solution was not improved much for the height component, only from ∼ 8 to ∼ 6 cm. Collins et al. (Reference Collins, Henton, Mireault, Héroux, Schmidt, Dragert and Bisnath2009) further applied the decoupled clock model to a tsunami warning system located along the western coastline of Canada. The results indicated an improvement of 30·2% in the horizontal components, but again the height improvement was not promising as the ambiguity-resolved height solution even suffered a degradation of 7·5%.
Insignificant accuracy improvement for PPP ambiguity-resolved height solutions was most likely due to a strong correlation between the troposphere and the height parameters. Tregoning and Herring (Reference Tregoning and Herring2006) investigated the impact of a priori troposphere zenith delays on differential GPS zenith total delay and height estimates. Their results based on a double-difference positioning model revealed a height bias of −0·1 to 0·2 mm/hPa and annual variations up to 2 mm between solutions using real and empirical meteorological data. Unfortunately there is little work about the effect of the troposphere delay on the PPP height solution, especially the PPP ambiguity-resolved height solution. Shi and Gao (Reference Shi and Gao2012) evaluated the ambiguity-resolved troposphere solution and investigated the relationship between PPP integer ambiguities and the troposphere solution, but the relationship between the ambiguity-resolved troposphere and height solutions in PPP has not yet been studied.
This paper proposes a troposphere constraint method to improve the PPP ambiguity-resolved height solution. The effects of the troposphere delay on the PPP ambiguity-resolved height solution are first identified based on the decoupled clock model and hourly observations. Numerical results are analysed afterwards to demonstrate the accuracy improvement of the PPP ambiguity-resolved height solution by the proposed method. In the end some discussions about the selection of external troposphere corrections are presented.
2. METHODOLOGY
Shown in Figure 1 is a flowchart that describes the procedures for the determination of the PPP ambiguity-float and ambiguity-resolved solutions. For PPP integer ambiguity resolution, two types of external correction data are required. The first is the satellite orbit product that will be applied to remove the orbital error. The second type is the advanced ambiguity corrections that will be applied to recover the integer property of the phase ambiguity in PPP. The contents and forms of the ambiguity corrections depend on the utilized ambiguity resolution method. These ambiguity corrections can be the wide-lane and narrow-lane fractional cycle biases (FCBs) for the single-difference between satellites method, the wide-lane satellite bias (WSB) and the integer phase clock corrections for the integer phase clock model, or the satellite decoupled code and phase clock corrections for the decoupled clock model. The unknown parameters to be estimated include the following four types: the coordinate, the receiver clock, the troposphere delay and the ambiguity.
Figure 1. Flowchart of PPP integer ambiguity resolution with external troposphere corrections. The left and right dotted boxes represent the PPP ambiguity-float and ambiguity-resolved solutions, respectively.
The conventional approach to treat the troposphere delay is to estimate only the troposphere zenith wet delay instead of the zenith total delay. This approach requires the troposphere zenith hydrostatic delay to be calibrated in advance. Different tropospheric models, such as the Saastamoinen model, can be applied for the determination of the troposphere zenith hydrostatic delay with real meteorological data observed at the receiver site (Gérard and Luzum, Reference Gérard and Luzum2010). As indicated by Shi and Gao (Reference Shi and Gao2012), PPP integer ambiguity resolution cannot immediately lead to the convergence of the tropospheric parameter. Instead it can only speed up the troposphere convergence after the ambiguity parameters have been fixed to their integer values. The troposphere convergence is in fact dominated by the actual environment at the observation site. It is not uncommon that the troposphere convergence would require a considerable time period, for example longer than one hour. As a result, the residual troposphere delay will degrade other unknown parameters, especially the height coordinate.
A troposphere constraint method is proposed in this paper to improve the PPP ambiguity-resolved height solution. Instead of using the empirical tropospheric models, the proposed method will apply external troposphere corrections to calibrate the a priori troposphere zenith delay. Due to the high precision of the external troposphere corrections, the residual troposphere delay can therefore be constrained with a small initial standard deviation. Subsequently the ambiguity-resolved height solution in PPP can be expected to be improved because of the reduced correlation between the troposphere and height parameters.
The implementation of the proposed troposphere constraint method in this paper will be based on the decoupled clock model although it can be applied to all three PPP integer ambiguity resolution methods. The observation equations in the decoupled clock model include the following three code and phase combinations (Collins, Reference Collins2008):
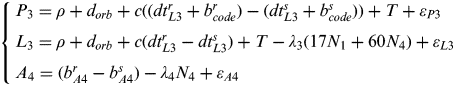$$\left\{ \matrix{P_3 = \rho + d_{orb} + c((dt_{L3}^r + b_{code}^r )- (dt_{L3}^s + b_{code}^s )) + T+ \varepsilon _{P3} \cr L_3 = \rho + d_{orb} + c(dt_{L3}^r - dt_{L3}^s ) + T - \lambda _3 (17N_1 + 60N_4 ) + \varepsilon _{L3} \cr A_4 =(b_{A4}^r - b_{A4}^s )- \lambda _4 N_4 + \varepsilon _{A4} } \right.$$where
$$P_3 = \displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}} P_1 + \displaystyle{{ - f_2^2} \over {\,f_1^2 - f_2^2}} P_2,\ L_3 = \displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}} L_1 + \displaystyle{{ - f_2^2} \over {\,f_1^2 - f_2^2}} L_2$$
$$A_4 = \left(\displaystyle{{\,f_1} \over {\,f_1 - f_2}} L_1 + \displaystyle{{ - f_2} \over {\,f_1 - f_2}} L_2 \right) - \left(\displaystyle{{\,f_1} \over {\,f_1 + f_2}} P_1 + \displaystyle{{\,f_2} \over {\,f_1 + f_2}} P_2 \right)$$with f 1=154f 0, f 2=120f 0 and f 0=10·23 MHz, ρ is the geometric distance between the satellite and the receiver, d orb is the satellite orbital error which can be corrected by precise orbit products, dt s L3, dt L3s+b codes and b A4s are three satellite decoupled clocks, dtr L3, dt L3r+b r code and b A4r are three receiver decoupled clocks, T is the residual troposphere delay, N 1 and N 4 are integer ambiguities, and ε * represents the noises. The corresponding stochastic model for the observations is
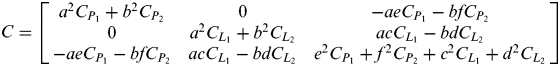$$C = \left[ {\matrix{ {a^2 C_{P_1} + b^2 C_{P_2}} & 0 & { - aeC_{P_1} - bfC_{P_2}} \cr 0 & {a^2 C_{L_1} + b^2 C_{L_2}} & {acC_{L_1} - bdC_{L_2}} \cr { - aeC_{P_1} - bfC_{P_2}} & {acC_{L_1} - bdC_{L_2}} & {e^2 C_{P_1} + f^2 C_{P_2} + c^2 C_{L_1} + d^2 C_{L_2}} \cr}} \right]$$where C P1, C P2, C L1, C L2 are the variances for code and phase observations P 1, P 2, L 1, L 2, and 
$a = \displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}}, {\rm} b = \displaystyle{{ - f_2^2} \over {\,f_1^2 - f_2^2}}, {\rm} c = \displaystyle{{\,f_1} \over {\,f_1 - f_2}}, {\rm} d = \displaystyle{{\,f_2} \over {\,f_1 - f_2}}, {\rm} e = \displaystyle{{\,f_1} \over {\,f_1 + f_2}}, {\rm} f = \displaystyle{{\,f_2} \over {\,f_1 + f_2}} $.
The vector of the unknown parameters is
$$x = [x,y,z,dt_{L3}^r, b_{code}^r, b_{A4}^r, T,N_1 ^1, \cdots, N_1 ^{n - 1}, N_4 ^1, \cdots, N_4 ^{n - 1} ]$$where x, y, z are the receiver coordinates; dtr L3, br code, b rA 4 are three receiver decoupled clock terms; T denotes the residual troposphere delay; N 11, …, N 1n−1 and N 41, …, N 4n−1 are the integer N 1and wide-lane ambiguity parameters.
The receiver coordinates in Equation (3) are estimated as random constants for static positioning applications. The three receiver decoupled clock terms and the residual troposphere delay are estimated as random walk, while both the N 1 and wide-lane ambiguities should be estimated as random constants. The initial standard deviation of the residual troposphere delay can be set to a very small value such as 10−4 m as a tight constraint when applying the proposed troposphere constraint method.
3. NUMERICAL RESULTS AND ANALYSIS
Firstly, the test data sets used for numerical calculations and analysis will be described. Secondly, they are processed using the conventional troposphere estimation method to investigate the effects of the troposphere delay on PPP ambiguity-resolved height solutions. Finally, the data sets are re-processed using the proposed troposphere constraint method to assess the improvement of the PPP ambiguity-resolved height solution.
3.1. Data Description
In order to study the relationship between the PPP ambiguity-resolved troposphere and height solutions, GPS observations were collected from a Canadian PPP-inferred near real-time precipitable water vapour system (Figure 2) on 3 March 2008. The precise satellite orbit product for that day is igs14691.sp3. The satellite decoupled clock product to facilitate integer ambiguity resolution is provided by NRCan. The test data sets from nine GPS stations are available with an observation interval of 15 seconds and an elevation angle mask of 10 degrees. Pressure and temperature data are also available at each station. The reference coordinates for each station are obtained by processing the station data over 24 hours using NRCan's online PPP service (Tétreault et al., Reference Tétreault, Kouba, Héroux and Legree2005). The absolute phase centre correction model (Schmid et al., Reference Schmid, Steigenberger, Gendt, Ge and Rothacher2007) is utilized to calibrate the antenna phase centre offset and variation. The a priori troposphere zenith delay is calculated using the Saastamoinen model with the meteorological data collected at each receiver site (Gérard and Luzum, Reference Gérard and Luzum2010). The residual troposphere zenith delay is estimated with an initial standard deviation of 10−2 m.
Figure 2. Network of the Canadian PPP-inferred near real-time precipitable water vapor system.
3.2. Troposphere Effects On PPP Ambiguity-Resolved Height Solutions
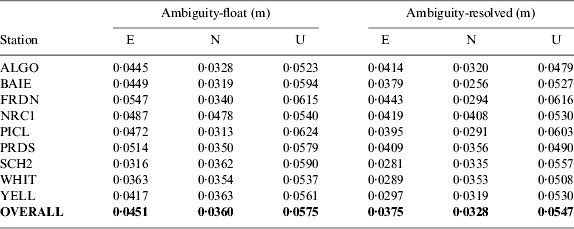
The test data sets were processed on an hourly basis using the conventional troposphere estimation method. Only the solutions with three-dimensional ambiguity-float positioning errors less than 10 cm were chosen for integer ambiguity resolution. This is a commonly used threshold for PPP integer ambiguity resolution (Collins et al., Reference Collins, Lahaye, Heroux and Bisnath2008; Geng et al., Reference Geng, Teferle, Shi, Meng, Dodson and Liu2009). The PPP ambiguity-float and ambiguity-resolved coordinate accuracies are listed in Table 1. The accuracy statistics were calculated as the root-mean-square (RMS) errors of the coordinate differences from the epoch when PPP integer ambiguity resolution was achieved to the observation period end. The overall accuracies for the nine stations in east/north/up are improved from 4·51/3·60/5·75 to 3·75/3·28/5·47 cm, corresponding to an improvement of 16·85/8·85/4·84% for the three coordinate components. It is clear that the height improvement is much less significant than the horizontal components.
Table 1. Accuracy statistics for all test stations.
We first analysed the results for station YELL as an example. Excluding the first (UTC 00:00–01:00) and last two (UTC 22:00–23:00 and 23:00–24:00) hourly observations that cannot be applied for satellite orbit interpolation, 21 hourly observations were processed. Two hourly ambiguity-float coordinate solutions with errors larger than 10 cm were excluded. 18 out of the remaining 19 solutions that can successfully resolve the integer ambiguities within one hour were classified into two groups to assess the height solution improvement by PPP integer ambiguity resolution. The first group contains the solutions with the standard deviation of estimated troposphere parameters less than 5 mm, which we define as the troposphere convergence within one hour. For example, Figure 3a shows the troposphere solution from UTC 05:00 to UTC 06:00 with troposphere converged. The ambiguity-resolved height accuracy as shown in Figure 3b is 5·23 cm. If the troposphere solution cannot converge within the observation period as shown in Figure 4a, the improvement will be less significant due to the existence of residual troposphere delays. The ambiguity-resolved height solution in Figure 4b demonstrates a diverging tendency with an accuracy of 6·45 cm.
Figure 3. Troposphere solution can converge within one hour (UTC 05:00–06:00) of 3 March 2008 at station YELL. The corresponding ambiguity-resolved height solution is 5·23 cm (18·79 % improvement over the ambiguity-float solution). The legend in Figure 3b reads RMS/STD/MEAN in m.
Figure 4. Troposphere solution cannot converge within one hour (UTC 03:00–04:00) of 3 March 2008 at station YELL. The corresponding ambiguity-resolved height solution is 6·46 cm (2·86% improvement over the ambiguity-float solution). The legend in Figure 4b reads RMS/STD/MEAN in m.
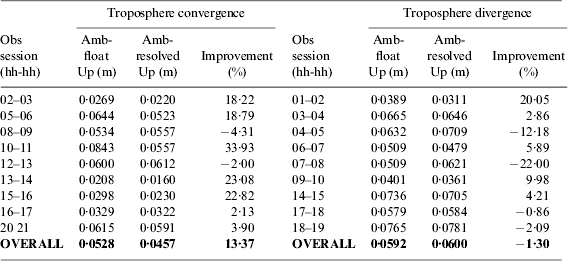
The 18 qualified solutions for station YELL are classified into two groups according to their troposphere convergence status. The first group is denoted as “Troposphere convergence” listed in the left part of Table 2, while the second group “Troposphere divergence” is presented in the right part. It can be seen that the overall ambiguity-resolved height solutions in the “Troposphere convergence” group are improved from 5·28 to 4·57 cm, i.e. an improvement of 13·37%. However, the ambiguity-resolved height solutions in the “Troposphere divergence” group suffer 1·30% degradation with the overall accuracy decreased from 5·92 to 6·00 cm.
Table 2. Height improvements for the “Troposphere convergence” and “Troposphere divergence” groups at station YELL.
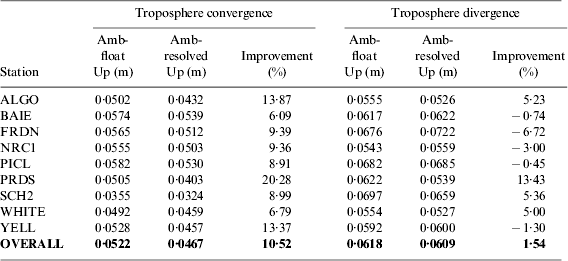
The qualified hourly solutions at other test stations are also classified in the same way and the results for all stations are summarized in Table 3. As shown in Table 3, the ambiguity-resolved height accuracy with troposphere converged can reach 4·67 cm by PPP integer ambiguity resolution, while the ambiguity-resolved height accuracy in the “Troposphere divergence” group is only improved to 6·09 cm. The histograms of the height improvements with troposphere converged and diverged are depicted in Figure 5. It can be seen that the height improvements of the solutions with troposphere converged are obviously better than those with troposphere diverged. As the result, it is concluded that the troposphere convergence is a critical factor to the improvement of the ambiguity-resolved height solution in PPP.
Figure 5. Histograms of the height improvements caused by integer ambiguity resolution for the “Troposphere convergence” and “Troposphere divergence” groups at all test stations.
Table 3. Height improvements for the “Troposphere convergence” and “Troposphere divergence” groups at all test stations.
3.3. PPP Ambiguity-Resolved Height Solution Using Troposphere Constraint Method
Since the convergence of the troposphere parameter is proven as a critical factor that affects the ambiguity-resolved height solution in PPP, the troposphere constraint method is then applied in this section to remove the troposphere effects on the height solution. Instead of using meteorological data and the Saastamoinen model to calculate the a priori troposphere zenith delay, precise troposphere corrections are used to calibrate the troposphere zenith delay. Due to the high precision of the applied troposphere corrections, the residual troposphere zenith delay can be estimated with the small initial standard deviation (for example 10−4m). In this paper the International GNSS Service (IGS) troposphere zenith path delay (ZPD) product (Byun and Bar-Sever, Reference Byun and Bar-Sever2009) was selected as the external troposphere corrections.
The two hourly observations in Figures 3 and 4 were re-processed using the proposed method. Figure 6 illustrates the results with the IGS troposphere ZPD product from UTC 05:00 to UTC 06:00. In addition to the removal of a bias between the estimated (2·3025 m in Figure 3a) and the IGS (2·2792 m in Figure 6a) ZPDs, the variation of the residual troposphere delays has also been eliminated in Figure 6a. Consequently, the ambiguity-resolved height accuracy is improved to 1·14 cm, much better than that obtained using the conventional troposphere estimation method (5·23 cm in Figure 3b). The same phenomenon can also be detected for the session when the troposphere parameter cannot converge. In Figure 7, both the bias and variations of the troposphere delay are removed by using the IGS troposphere ZPD product and the proposed troposphere constraint method. The ambiguity-resolved height accuracy is 3·83 cm (Figure 7b), which is also much better than that obtained with the conventional troposphere estimation method (6·45 cm in Figure 4b).
Figure 6. Troposphere solution can converge within one hour (UTC 05:00–06:00) of 3 March 2008 at station YELL. The corresponding ambiguity-resolved height solution with the IGS ZPD correction is 1·44 cm (34·55% improvement over the ambiguity-float solution). The legend in Figure 6b reads RMS/STD/MEAN in m.
Figure 7. Troposphere solution cannot converge within one hour (UTC 03:00–04:00) of 3 March 2008 at station YELL. The corresponding ambiguity-resolved height solution with the IGS ZPD correction is 3·83 cm (11·55% improvement over the ambiguity-float solution). The legend in Figure 7b reads RMS/STD/MEAN in m.
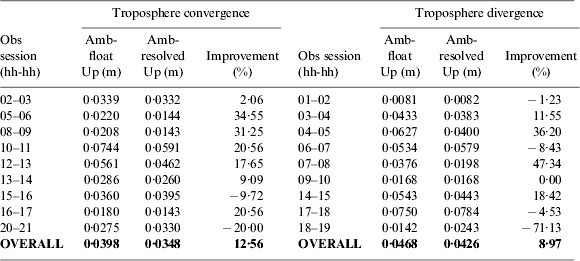
Using the IGS troposphere ZPD product, the 18 hourly data sets at station YELL are re-processed with results listed in Table 4. The overall accuracy of ambiguity-resolved height solutions in the “Troposphere convergence” group is improved from 3·98 to 3·48 cm. On the other hand, the ambiguity-resolved height accuracy in the “Troposphere divergence” group can achieve 4·26 cm. Figure 8a illustrates the PPP ambiguity-resolved height accuracies for the 18 hourly solutions at station YELL by using the proposed troposphere constraint method. The height accuracies using the conventional troposphere estimation method are also depicted in Figure 8b for comparison. The accuracy is calculated as the RMS statistics of the height accuracies for the 18 hourly solutions. It is clear that the ambiguity-float height accuracy with the IGS troposphere ZPD product is 4·32 cm, much better than that with the model-derived troposphere delays (5·59 cm). Furthermore, the PPP ambiguity-resolved height solutions with the IGS troposphere ZPD product can be improved by 27·44% over those with the model-derived troposphere delays (3·86 cm versus 5·32 cm).
Figure 8. Ambiguity-float and ambiguity-resolved height accuracies for the troposphere constraint method (a), and the troposphere estimation method (b).
Table 4. Height improvements with IGS troposphere ZPD products at station YELL.
4. CONCLUSIONS AND DISCUSSIONS
The insignificant PPP ambiguity-resolved height improvement is identified and addressed in this paper. Numerical analysis is based on the decoupled clock model and hourly GPS observations from a Canadian PPP-inferred troposphere precipitable water vapour system. Compared to 16·85/8·84 % improvements (from 4·52/3·60 to 3·76/3·28 cm) in the east/north directions, only 4·84% improvement (from 5·75 to 5·47 cm) is obtained in the height component. The effects of the troposphere delay on the PPP ambiguity-resolved height solution have been investigated and the results indicate that the troposphere convergence is a critical factor to the improvement of the ambiguity-resolved height solution in PPP.
A troposphere constraint method has been proposed to remove the effects of the troposphere delay on the PPP ambiguity-resolved height solution. The PPP ambiguity-resolved height accuracy for station YELL can be improved by 27·44% (from 5·32 to 3·86 cm) using the proposed method, which can be considered as an effective way to improve the PPP ambiguity-resolved height solution.
In this paper the external troposphere corrections are chosen as the station-based IGS troposphere ZPD product which is probably not the optimal choice in practice. Instead the regional grid-based troposphere corrections should be considered in the future so that the proposed method can be extended to any receiver located within the troposphere grid coverage. In addition, the troposphere gradients should also be taken into consideration to further improve the ambiguity-resolved horizontal accuracy along with the height accuracy.
ACKNOWLEDGMENTS
NRCan is thanked for providing satellite decoupled clock products. IGS is acknowledged for satellite precise orbit and troposphere products. This research is supported by NSERC and the Liaoning Talent Program (Grant No. LR2011007). In addition, the first author is financially supported by Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation (Grant No. PF2012–13).
Based on a paper presented to the Institute of Navigation GNSS 2012 conference, Nashville Tennessee, September 2012.
