1. Introduction
Ample evidence documents a strong relationship between birth order and health, education, and labor market outcomes. Evidence, largely from developed countries, generally finds that younger children often lag behind their older siblings in outcomes such as educational attainment, cognitive ability, and earnings.Footnote 1 However, evidence on the effects of birth order on health is mixed with the direction of the effect depending on the health outcome being examined [Black et al. (Reference Black, Devereux and Salvanes2016), Elliott (Reference Elliott1992)]. A number of mechanisms offer potential explanations for the human capital effects of birth order including biological mechanisms related to differences in health endowments at birth and/or behavioral mechanisms related to parental investment. Socio-economic circumstances may also play a role in determining the birth order effect. Indeed, characteristics related to poverty appear to magnify the birth order effect on health [De Haan et al. (Reference De Haan, Plug and Rosero2014)].Footnote 2 A better understanding of the underlying mechanisms of the birth order effect may better equip policymakers to design interventions aimed at improving human capital outcomes particularly for poor families. This is particularly important in the context of developing countries where poverty is widespread and improving human capital is a policy imperative for economic growth.
In this paper, we examine the relationship between birth order and health in a developing country context using a nationally representative sample of households in South Africa. In particular, for a sample of individuals between the ages of 1 and 18 years, we investigate the effect of birth order on height-for-age z-score (HAZ), a widely used indicator of long-term nutrition and health status among children [Strauss and Thomas (Reference Strauss, Thomas, Shultz and Strauss2008)]. Using a mother fixed-effects specification, we find an inverse relationship between birth order and HAZ. We further explore potential mechanisms underlying this finding. Specifically, we examine parental preferences, socio-economic, and biological determinants as possible explanations for the birth order effect in our data. We do not find evidence supporting mechanisms related to parental preference due to gender differences across children of different birth ranks or biology through an effect on birth health. However, in looking at income-based subsamples, we do find evidence suggesting that the socio-economic circumstances and resource constraints faced by households may play a large role in explaining our observed birth order effects. We also find that the birth order effect is partially explained by heterogeneity across households depending on the number of children they choose to have.
The rest of this paper is organized as follows: Section 2 briefly reviews existing evidence for the birth order effect and its potential explanations. In Section 3, we discuss our data. Section 4 presents our econometric model. In Section 5, we discuss our estimation results. Finally, we conclude in Section 6.
2. Birth order effects on health
Birth order effects have been studied for more than a century in economics, psychology, sociology, and epidemiology. Recently, new theories and evidence on the role of genetics, parental behavior, and household resource allocation have renewed interest in understanding the human capital effects of birth order and the mechanisms underlying them.Footnote 3 For example, research in epidemiology and the social sciences links birth order to numerous health outcomes and disease progression.Footnote 4 Higher birth order is related to increased body mass index, mortality risk and rate, and hospitalization rates due to injuries. It is also associated with early and frequent indulgence in risky behavior and worse self-reported physical and mental health [Black et al. (Reference Black, Devereux and Salvanes2016), Barclay and Kolk (Reference Barclay and Kolk2015), Bozzoli et al. (Reference Bozzoli, Deaton and Quintana-Domeque2007), Argys et al. (Reference Argys, Rees, Averett and Witoonchart2006), Modin (Reference Modin2002), Elliott (Reference Elliott1992)]. Firstborns are also found to have taller stature than their siblings at the same age at different stages of the life course, i.e., in childhood, adolescence, and adulthood [Savage et al. (Reference Savage, Derraik, Miles, Mouat, Cutfield and Hofman2013)].Footnote 5
While birth order effects are widely documented in both developed and developing countries, the mechanisms underlying these effects may be context-specific. Indeed, Modin (Reference Modin2002) argues that birth order effects tend to vary in strength over time and space. In our analysis, we are specifically concerned with understanding the birth order effect in a poor country context. Therefore, in the following discussion, we focus on research coming from either developing countries or contexts similar to the developing country setting.
While we are unaware of previous research on birth order effects in South Africa, a sizable literature relates birth order to anthropometric measures such as height and weight in developing countries. Studies in these countries find that higher birth order has a negative effect on health. Some attribute this effect to socio-economic circumstances as well as limited access to resources characteristic in poor country contexts [Hatton and Martin (Reference Hatton and Martin2010), Horton (Reference Horton1988)]. For a sample of Filipino children, Horton (Reference Horton1988) finds a strong negative effect of birth order on HAZ but only modest effects on weight-for-height. She concludes that birth order effects are not due to discrimination among siblings but rather parents’ inability to provide nutritious food to their later-born children. Similarly, Behrman (Reference Behrman1988) finds that parental investment tends to favor lower birth order children in rural India. Kebede (Reference Kebede2005) finds that older children in Ethiopia are taller than their younger siblings, but this finding was significant only up to the third child. Hatton and Martin (Reference Hatton and Martin2010) examine the birth order effects on height-for-age and body mass index using a sample of predominantly poor families in the UK during the 1930s (a sample that may more resemble some developing country contexts than others from developed countries). They find a negative effect of birth order on HAZ but not on the body mass index. Using family fixed-effects model, the authors further find that socio-economic conditions like per capita expenditure on food, hygiene, and living conditions at home are important determinants of birth order effects.
Research in economics, psychology, and epidemiology offers several theories on possible pathways through which birth order effects operate. Hence, the mechanisms behind birth order effects may differ in high- and low-income countries. Regardless, in both settings, these mechanisms can be broadly categorized into biological mechanisms, intra-family dynamics, and socio-economic factors.
2.1. Biological mechanisms
Theories on biological channels argue that later-born children are generally born to older mothers who have a higher incidence of chromosomal and congenital defects as well as a higher probability of delivering prematurely. All of these factors may negatively impact child health, giving firstborn children a health advantage at birth [Cleary-Goldman et al. (Reference Cleary-Goldman, Malone, Vidaver, Ball, Nyberg and Comstock2005)]. Conversely, later-born children may have better in-utero environment as a woman's womb becomes more effective at nurturing the fetus [Khong et al. (Reference Khong, Adema and Erwich2003)]. Thus, later-born children tend to have higher birth weight which may lead to better health at birth. Brenøe and Molitor (Reference Brenøe and Molitor2015) find that firstborn children enjoy a health advantage at birth; however, most studies find no significant difference between the birth health of firstborns and that of later-born children [De Haan et al. (Reference De Haan, Plug and Rosero2014)]. Thus, evidence supporting biological mechanisms as drivers of the birth order effect is weak.
2.2. Intrahousehold dynamics and parental preferences
Intrahousehold dynamics relating to parental behaviors offer another potential explanation for the birth order effect. Parents may favor firstborns or one gender over another. For example, the oldest son is important in funeral rites in India, so they may be favored [Horton (Reference Horton1988)]. Indeed, Jayachandran and Pande (Reference Jayachandran and Pande2017) find favoritism for eldest sons explains a large part of the birth order gradient in India. Additionally, lower birth order children become economically independent earlier, thus parents may prefer to invest more in older siblings [Ejrnæs and Pörtner (Reference Ejrnæs and Pörtner2004)]. Parents may also stop having children once the desired child (such as the desired gender) is born, resulting in favoritism toward the last-born child [Basu and De Jong (Reference Basu and De Jong2010)]. Additionally, the presence of an older or younger sibling can lead to dissimilar home environments for children within the same household. For example, earlier-born children are more likely to have childcare responsibilities for their younger siblings. This likelihood is generally greater for earlier-born female children than male children [Evans (Reference Evans2010)]. Parents may also exhibit “strategic parenting” practices by enforcing stricter disciplinary environments for earlier-born children than later born [Hotz and Pantano (Reference Hotz and Pantano2015)].
2.3. Resource dilution
Resource dilution theory points out that as the number of children increases, parents face different constraints over time causing unequal resource distribution among children. There are two competing narratives on how resource allocation affects siblings of different birth order. First, later-born children are necessarily born into a larger family. Much of the family size literature finds a negative association between family size and child human capital development indicating a potential tradeoff between the number of children and average child quality (Becker, Reference Becker1991). As family size increases, resources for per capita health investment (e.g., food, hygiene, and health expenditure) decrease resulting in lower health outcomes in later-born children [Behrman (Reference Behrman1988), Hatton and Martin (Reference Hatton and Martin2010)]. Later-born children may receive less quality time with their parents or be breastfed for a shorter time or less often [Lehmann et al. (Reference Lehmann, Nuevo-Chiquero and Vidal-Fernandez2016), Buckles and Kolka (Reference Buckles and Kolka2014), Price (Reference Price2008)]. Parenting style and focus may shift with the birth order. For example, women have also been found to be more likely to delay prenatal care and less likely to reduce their smoking or drinking for later pregnancies than earlier ones [Lehmann et al. (Reference Lehmann, Nuevo-Chiquero and Vidal-Fernandez2016)]. Later-born children are also more likely to be cared for by their older siblings (usually older sisters) than firstborns, which implies a lower quality of care [Jayachandran and Pande (Reference Jayachandran and Pande2017), Evans (Reference Evans2010)]. This practice is especially prevalent in many sub-Saharan African countries such as South Africa.
Conversely, some find that family resource dynamics may instead favor later-born children. Later-born children are born to older parents who often have more education, experience, and higher earnings, due to life cycle effects, resulting in improved health investments [Hatton and Martin (Reference Hatton and Martin2010)]. Some evidence exists showing that women have increased labor market attachment and engagement in risky behaviors during earlier pregnancies than later ones [Black et al. (Reference Black, Devereux and Salvanes2016), Brenøe and Molitor (Reference Brenøe and Molitor2015)]. De Haan et al. (Reference De Haan, Plug and Rosero2014) find that later-born children in Ecuador receive more quality time with their mothers and are breastfed for longer than their older siblings.
2.4. Heterogeneity across families of different sizes
The extent that birth order influences human capital outcomes depends on the social, cultural, and historical context of the population [Modin (Reference Modin2002)]. Existing evidence suggests that socio-economic characteristics relating to poverty and access to resources influence the magnitude of the birth order effect. For example, De Haan et al. (Reference De Haan, Plug and Rosero2014) find that birth order effects are stronger in families that are poorer, have a less educated household head, or where the mother was a teenager at her first birth. Hatton and Martin (Reference Hatton and Martin2010) find that increased family size and poor housing conditions exacerbate observed birth order effects. If poorer households with more limited access to resources are also more likely to have a greater number of children such as those residing in rural areas of developing countries, then the birth order effect may in fact be largely driven by selection bias due to systematic differences between households that select into larger versus smaller family sizes. In the following analysis, we examine each of these mechanisms as possible explanations for the birth order effects we find for this South African sample.
3. Data
To examine the birth order effect as well as its underlying mechanisms, we employ data from the National Income Dynamics Study (NIDS), which surveyed a sample of 7,300 households consisting of approximately 28,000 individuals in South Africa.Footnote 6 These nationally representative surveys currently consist of four waves covering the years 2008, 2010, 2012, and 2014 and include detailed information on numerous household and child characteristics in addition to a complete fertility history of mothers. We only use the fourth wave of NIDS in order to ensure that none of our sample children were born before 1994 when Apartheid in South Africa ended. Children born during the Apartheid era were exposed to a considerably different economic and political climate. In order to examine the birth order effect among siblings born after the apartheid era, we also limit our sample to the children who are 18 years old or younger with living biological mothers. The fourth wave consists of 7,910 children fitting this description.
For the purposes of this paper, we employ a number of exclusions common in the birth order literature for our final working sample. We drop families with only a single child since there can be no birth order effect if there are no siblings. We exclude all children whose biological mother is not alive to reduce heterogeneity due to orphans and adopted children. We further exclude families with stillbirths or infant deaths as well as with multiple births (i.e., twins or triplets) due to difficulty in assigning birth order.Footnote 7 We also exclude families with six or more children because our sample includes too few households in this category to garner precise estimates.Footnote 8 Furthermore, we lose an additional 390 children due to missing information. This leaves us with a final working sample of 4670 children born to 2,068 mothers.Footnote 9
We use child HAZ as an indicator of long-term health and nutrition status for the children in our sample. Deficits in child HAZ reflect long-term, cumulative deficiencies in health and/or nutrition resulting in a child failing to reach his or her growth potential [World Health Organization (1995)]. Low child HAZ is associated with increased morbidity and mortality as well as reduced long-term health. It is also widely associated with a wide range of socio-economic outcomes such as education, cognitive ability, and adult economic productivity [e.g., Vogl (Reference Vogle2014), Strauss and Thomas (Reference Strauss, Thomas, Shultz and Strauss2008), Victora et al. (Reference Victora, Adair, Fall, Hallal, Martorell, Richter and Sachdev2008), World Health Organization (1995)]. For these reasons, HAZ has long been used as an indicator for long-term child health in the nutrition, epidemiological, and economic literature.
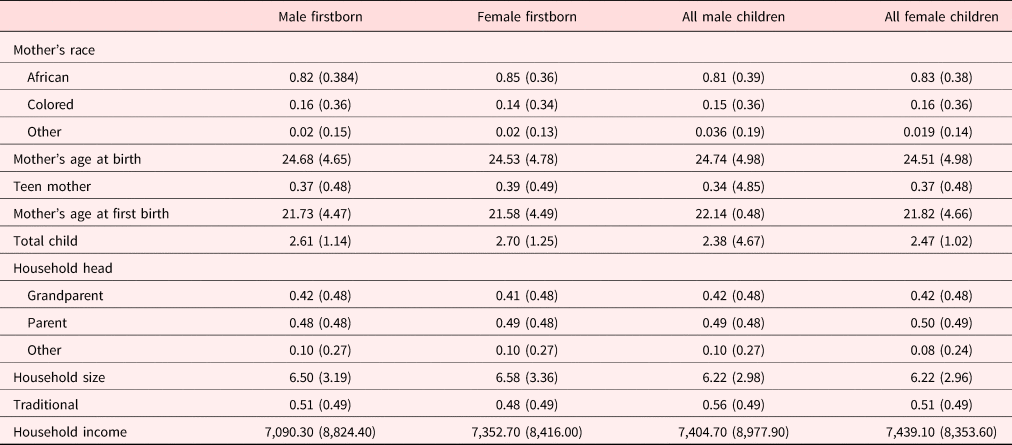
Table 1 describes child-level characteristics by birth order for the full working sample. HAZ gradually decreases with birth order with an average difference of 0.472 standard deviations between first- and fifth-born children. Average birth weight does not statistically differ across children in each birth order category. Approximately half of all first-, second-, and third-born children are male. The proportion of male children increases to approximately 60% for fourth- and fifth-born children. This could be indicative of families having additional children in the hopes of having a male child.Footnote 10
Table 1. Child characteristics by birth rank

Standard errors in parentheses.
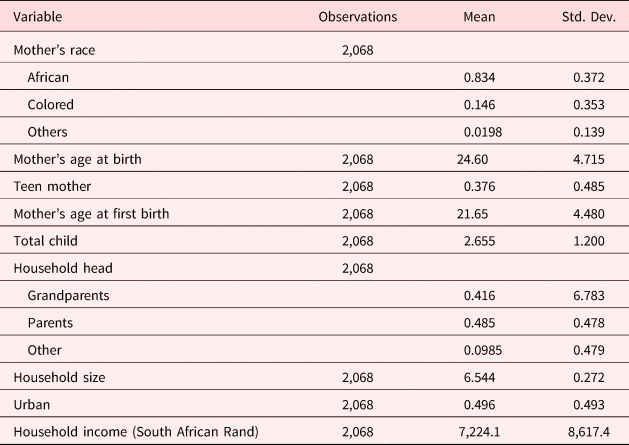
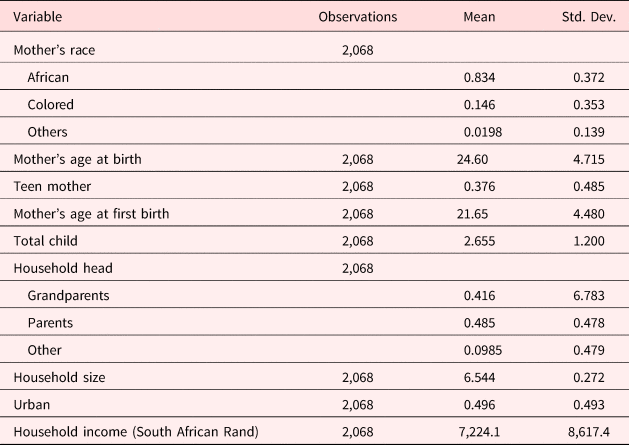
Table 2 reports descriptive statistics at the mother and household level. The majority of the mothers (83%) in our sample are Black African. Thirty-eight percent of our sample mothers were teenagers in their first pregnancy.Footnote 11 On average, our sample mothers have 2.66 children. Households in our sample are roughly evenly split between residing in urban and traditional areas. Traditional areas are administrative areas in South Africa rooted in Apartheid. They consist of commonly owned land under the jurisdiction of traditional leaders and settlements. They are generally rural and have less developed infrastructure. For the remainder of this paper, we use the terms rural areas and traditional areas interchangeably.
Table 2. Mother and household characteristics
4. Empirical strategy
We estimate the birth order effects on health status among the children aged 1–18 years using the following linear model with mother fixed effects.
where H im is the HAZ of a child i born to the mother m. λ m is a vector of mother fixed effects, and thus captures all unobserved family characteristics that do not vary across siblings (e.g., the role of genetics in determining height). The variables secondim, thirdim, fourthim, and fifthim indicate whether child i is a second, third, fourth, or fifth born, respectively. Children of birth order 1 serve as the omitted category. Thus, the coefficients on each of the birth order dummy variables can be interpreted as the average difference between the HAZ of firstborns and that of the corresponding younger sibling. X im is a vector of controls and includes the gender of the child, a quadratic of mother's age, child's age squared, household income, and household size.Footnote 12 It also includes district fixed effects to control for community-level heterogeneity and birth year fixed effects to control for cohort-specific heterogeneity. In many developing countries, children born in later years tend to be taller due to the economic growth and improved access to health and nutrition inputs. Finally, we cluster standard errors at the mother level.
5. Results
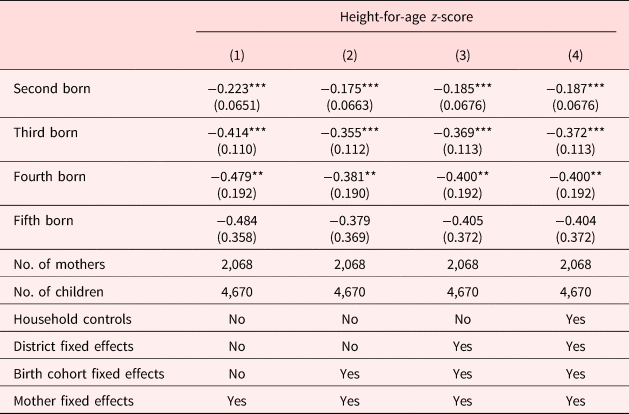
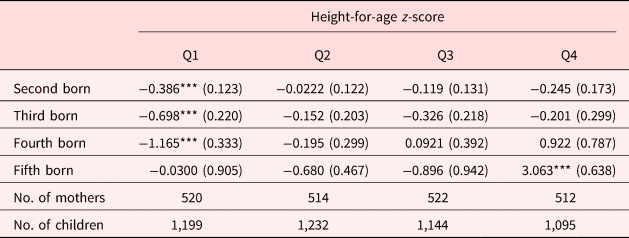
Table 3 reports the birth order effects on child HAZ estimated from equation (1). Columns (1) through (4) incrementally add controls for cohort fixed effects, district fixed effects, and household-level controls. While adding these controls marginally reduces the magnitude of the birth order effect, in each specification we see a clear pattern; we find a significant and negative association between birth order and HAZ. Relative to that of firstborns, children of a higher birth order experience reduced HAZ with the biggest change (gradient) happening after the second child. Compared with firstborns, second-born children's HAZ is approximately 0.175–0.223 standard deviations smaller on average. Similarly, third- and fourth-born children are approximately 0.355–0.414 and 0.381–0.479 standard deviations shorter, respectively, than firstborns. While the HAZ of fifth-born children is not statistically different from that of firstborns, the point estimates are similar in magnitude to those of fourth-born children. Further, there are only 23 fifth-born children in our sample. Therefore, the lack of significance may be due to a lack of precision rather than a zero effect. These results are consistent with previous findings by Hatton and Martin (Reference Hatton and Martin2010) in interwar Britain; Behrman (Reference Behrman1988) in India; Horton (Reference Horton1988) in the Philippines; and Lehmann et al. (Reference Lehmann, Nuevo-Chiquero and Vidal-Fernandez2016) in the USA. Studies examining adult height [Black et al. (Reference Black, Devereux and Salvanes2016), Myrskylä, et al. (Reference Myrskylä, Silventoinen, Jelenkovic, Tynelius and Rasmussen2013)] also find that the later-born children are shorter than the firstborns, on average.
Table 3. The birth order effects on health status
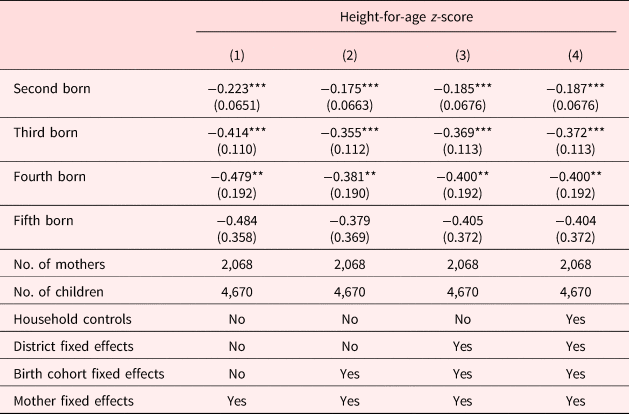
Note: Standard errors in parentheses and clustered at the mother level. All specifications include controls for gender of the child, quadratic of mother's age, and child's age squared. Controls for household characteristics include household income and household size.
*p < 0.10, **p < 0.05, ***p < 0.01.
Our findings reinforce the well-established notion that later-born children tend to be worse off in terms of height. However, the results reported in Table 3 do not indicate the mechanisms underlying this finding and are thus unable to inform policies aimed at improving human capital outcomes such as health. If the birth order effect is primarily due to biological mechanisms, then there is a little policymakers can do to improve the health outcomes of later-born children. However, HAZ is a good proxy for long-term health as well as for health inputs early in life when linear growth is especially rapid. If the birth order effect is primarily due to socio-economic characteristics or resource dilution in larger families, then there is potential for effective interventions.
The next step then is to investigate more fully some possible explanations behind the birth order effect. We previously discussed a number of potential explanations: heterogeneity across families of different sizes, biological mechanisms, parental preferences or behaviors, and resource dilution. In the following, we explore each of these explanations.
5.1. Birth order effects due to heterogeneity across families of different sizes
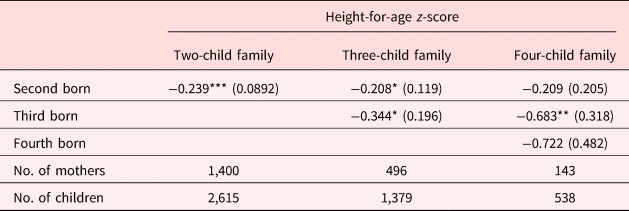
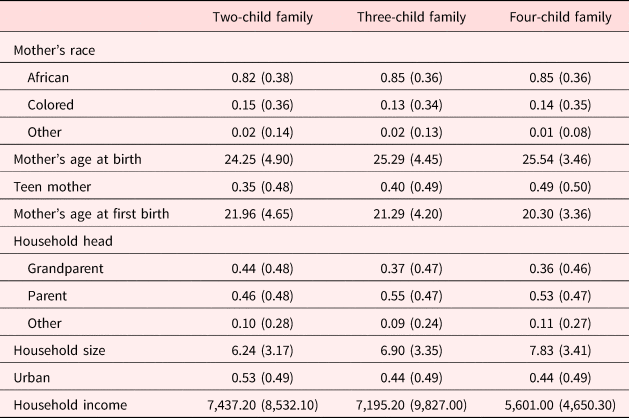
Higher birth order necessarily means that children are born into a larger family. Households that select into larger families may be systematically different in ways correlated with the health outcomes of their children [Hatton and Martin (Reference Hatton and Martin2010)]. For example, rural households tend to have more children, and have reduced access to resources often resulting in lower average economic and health outcomes [Paciorek et al. (Reference Paciorek, Stevens, Finucane and Ezzati2013)]. Although the inclusion of mother fixed-effects controls for the family size, heterogeneity across families of different sizes still may bias our findings. To explore if selection into different sized families is driving our estimated birth order effect, we estimate equation (1) separately on three subsamples of our data: families with two children only, families with three children, and families with four children. We omit the families with five children due to small sample size. Table A1 in the Appendix reports average household characteristics for families of different sizes. Here we see that households with larger families tend to be poorer and less likely to live in an urban area. Mothers in larger families also appear to be more likely to be a teen at the time of their first birth. Because later-born children, by construction, are more likely to be in larger families, then the birth order effect observed in the pooled sample may be driven by these factors resulting in a large birth order effect for children in larger families that does not exist in smaller families. If this is in fact the case, then we would expect to see the birth order effect disappear when comparing families of the same size.
Table 4 reports estimated birth order effects by family size. Results are significant and consistent with those reported for the full sample. However, some of the estimated birth order effects increase in magnitude with family size. A joint test rejects the equivalence of birth order coefficients across family size subsamples at the 1% level with a χ 2 statistic of 17.93. Specifically, the effect of being a third-born child is twice as high in a four-child family than in a three-child family. On average, a third-born child in three-child families is 0.344 standard deviations shorter than firstborns while those in four-child families are 0.683 standard deviations shorter. The increasing magnitude of the birth order effect with family size is suggestive of either resource dilution in larger families, that families of different sizes are indeed systematically different, or some combination of the two. However, the fact that the birth order effect exists in each family size subsample indicates that heterogeneity cannot fully explain the birth order effect.
Table 4. Birth order effects by family size
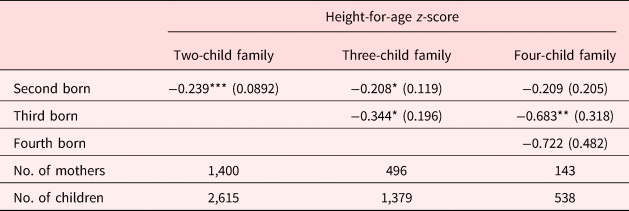
Note: Standard errors in parentheses and clustered at the mother level. Controls include gender of the child, quadratic of mother's age, child's age squared, household income, and household size. We also include mother, district, and birth cohort fixed effects.
*p < 0.10, **p < 0.05, ***p < 0.01.
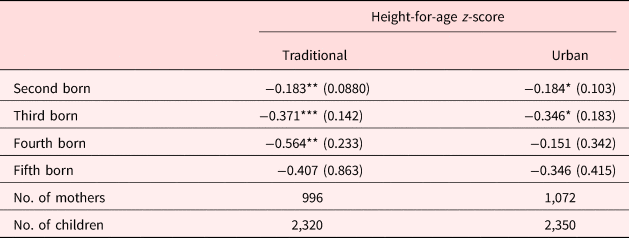
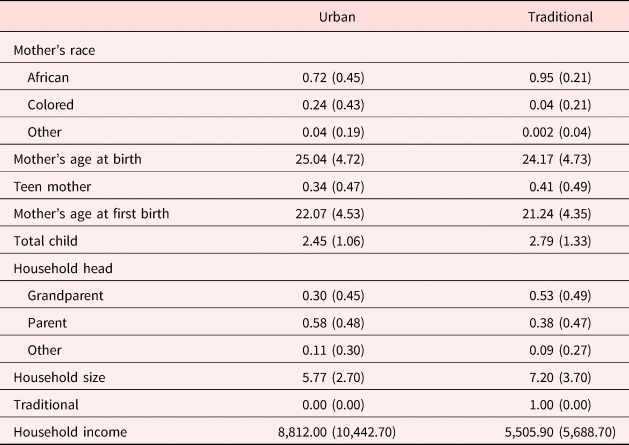
To further explore the possibility of heterogeneity across households driving our estimated birth order effects, we estimate equation (1) separately for households living in rural (traditional) and urban areas. Existing evidence demonstrates that rural areas are often disadvantaged in terms of health and access to health resources [Paciorek et al. (Reference Paciorek, Stevens, Finucane and Ezzati2013)]. Given the apartheid history of South Africa, there exists a large chasm between a traditional and urban area in terms of quality, access, and utilization of healthcare, as well as overall quality of life. Table A2 in the Appendix reports household and mother characteristics for our sample households living in rural and urban areas. Indeed, rural households tend to be poorer and live in larger households. They are also almost entirely made up of black South Africans.
Table 5 reports equation (1) estimates separately for traditional and urban households. Results indicate that a statistically significant birth order effect exists in both urban and traditional areas. The magnitude of the birth order effect of being a fourth- or fifth-born child also appears to be larger in the traditional areas. The point estimate on being a fourth-born child is over five times higher in the traditional sample than it is in the urban. This may indicate that access to health resources and systematic differences between traditional and urban households may in part explain the birth order effect. However, these estimates are imprecise and a joint test fails to reject that the coefficients are statistically different across the two samples. Regardless the birth effect remains across both families of different sizes (Table 4) and across rural and urban areas (Table 5). Thus, while heterogeneity across families and regions may play some part in explaining our results, they are unable to completely account for the birth order effect in this South African sample.
Table 5. Birth order effects across urban and traditional households

Note: Standard errors in parentheses and clustered at the mother level. Controls include gender of the child, quadratic of mother's age, child's age squared, household income, and household size. We also include mother, district, and birth cohort fixed effects.
*p < 0.10, **p < 0.05, ***p < 0.01.
5.2. Birth order effects due to biological mechanisms
To explore whether the birth order effect is due to biological channels affecting health endowments, we examine whether a birth order effect exists in health at birth, proxied by birth weight.Footnote 13 Of course, health at birth in part reflects a child's health endowment but it also reflects prenatal conditions. Unfortunately, we do not have information on maternal behaviors during pregnancy (e.g., smoking, doctor visits, employment status, etc.) nor do we have information of socioeconomic status at the time of the child's birth. Therefore, any birth order health effects we find at birth may not be solely due to a biological transmission. However, in South Africa, free healthcare is provided to pregnant woman and children under the age 6, thus heterogeneity due to pre- and post-natal care (like doctor visits, etc.) is minimal. Regardless, a lack of birth order effects at birth would make it unlikely that the birth order effects observed later in childhood are due to biological channels. Table 6 reports estimated birth order effects on the log of the child birth weight in grams. According to these results, there is no statistically significant difference in the birth weight of children of different birth orders. Moreover, the point estimates indicate that later-born children are heavier at birth than their earlier-born counterparts, suggesting that if a birth order effect does exist, it is in the opposite direction of that reported in Table 3. Therefore, the health disadvantage of later-born children appears to develop after birth and thus it is unlikely that biological mechanisms underlie this disparity in later childhood.
Table 6. Birth order effects on birth weight

Note: Standard errors in parentheses and clustered at the mother level. Controls include gender of the child, quadratic of mother's age, child's age squared, household income, and household size. We also include mother, district, and birth cohort fixed effects.
*p < 0.10, **p < 0.05, ***p < 0.01.
5.3. Birth order effects due to parental behaviors and preferences
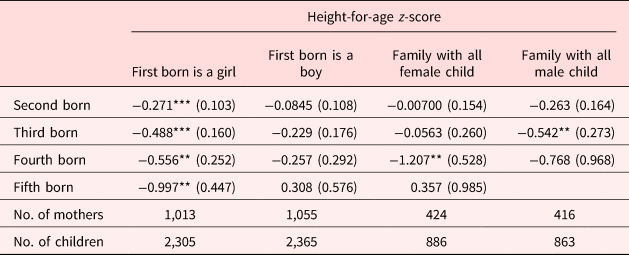
Another potential explanation underlying the birth order effects we find may relate to parental behaviors and preferential investments giving advantage to children of different birth ranks. We unfortunately do not observe parental investments for each child at the same age. We therefore cannot disentangle whether current differences in investment across children are due to difference in age or preferential treatment depending on birth order. However, we can examine whether the birth order effect we observe is driven by the gender composition of the sibling group and is thus due to parents exhibiting discrimination or preferential treatment in their investment behaviors due to the gender of the child. Gender preference in parents can result in a birth order effect through its influence on parents’ decisions on both fertility and resource allocation among their children. These gender preferences may be reflected in the birth order if parents also employ a stopping rule in which they continue to have children until they get a child of their preferred gender. For example, if male is a preferred gender and the firstborn is a girl, parents may continue to have more children until they have a male child. In that case, we may find that parents invest more in later-born children. Conversely, if earlier-born children are males, parents may divert resources away from younger siblings toward their older male children. While male preference is widely documented in East and South Asian countries, there is less evidence for it in sub-Saharan Africa. Instead, evidence in sub-Saharan Africa seems to indicate female preferences or a preference for mixed genders [Rossi and Rouanet (Reference Rossi and Rouanet2015)]. Despite this, households in our sample seem to employ a male-preference stopping rule as we see a higher proportion of males in later-born children. Approximately 50% of the first-, second-, and third-born children in our sample are male, while 60% of the fourth- and fifth-born children are male (Table 1). Evidence, mostly from developing non-African countries, observes that the gender of the first-born influences family dynamics and can drive a large part of estimated birth order effects [e.g., Jayachandran and Pande (Reference Jayachandran and Pande2017)]. To understand whether this may be a factor we estimate equation (1) separately for households whose firstborn is a girl and those whose firstborn is a boy. These results are reported in columns (1) and (2) of Table 7, respectively. We also estimate equation (1) for families with all female children (column 3 of Table 7) and those with all male children (column 4 of Table 7).Footnote 14
Table 7. Birth order effects by sibling composition
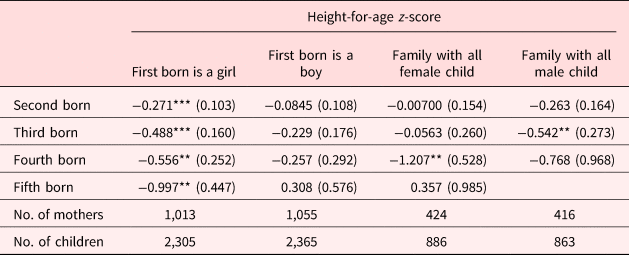
Note: Standard errors in parentheses and clustered at the mother level. Controls include gender of the child, quadratic of mother's age, child's age squared, household income, and household size. We also include mother, district, and birth cohort fixed effects.
*p < 0.10, **p < 0.05, ***p < 0.01.
Looking at columns (3) and (4) of Table 7, birth order effects appear to exist in both the all-female and all-male child samples. However, sample size is greatly reduced in these cases and thus not all of the birth order effects are estimated with precision. A joint test rejects that the coefficients across birth order ranks are equal at the 1 and 5% levels of significance for the all-female and all-male groups, respectively. If gender bias is driving our estimated birth order effects, then we would not expect to find any birth order effect in these households where gender does not vary across children.
Turning to columns (1) and (2) of Table 7, we find statistically significant birth order effects in families whose firstborn is a girl (column 1) but not in families whose firstborn is a boy (column 2). The birth order effects found for families with firstborn girls are similar in magnitude to those found for the full working sample, and coefficients are not statistically different.Footnote 15 A joint test rejects that the coefficients across birth order ranks are equal in the female firstborn sample at the 1% level. If the birth order effect was due to favoring firstborns, then we would expect to find it in both samples with female and male firstborns. Therefore, favoritism toward firstborns does not appear to be driving the effects we find. If a male bias was present, then we would expect to find significant birth order effects in families with male firstborns (i.e., these families would exhibit favoritism toward their male firstborn children). However, instead we find significant birth order effects for families with female firstborns. This may be due to the fact that female children are much more likely to be given childcare responsibilities over their younger siblings than male children. In much of sub-Saharan Africa, it is not unusual for older siblings to play significant roles in caring for younger siblings. Moreover, girls are more likely to be involved in the direct care of their siblings and spend more time in childcare activities than boys. Older boys, on the other hand, are more likely to care for younger siblings through financial support [Evans (Reference Evans2010)]. Therefore, the birth order effect may be in part due to later-born children in these households being more likely to be cared for by their older sisters resulting in less quality time with their parents than if the firstborn was male. This finding indicates that parents do invest differentially depending on the gender of their child. However, this is likely due to traditional gender roles in the household rather than an explicit gender bias. Therefore, neither biological mechanisms nor parental favoritism can fully account for birth order effects found in this sample.
5.4. Birth order effects due to resource dilution in larger families
Much of our findings at this point suggest that resource dilution, particularly in poorer households, may play a role in causing our observed birth order effects. According to the resource dilution hypothesis, available resources for human capital investment decrease as the number of children (and thus family size) increases. A higher birth order inevitably means a child has a larger sibling size. Considerable evidence demonstrates that average human capital outcomes decrease as family size increases [Hatton and Martin (Reference Hatton and Martin2010), Marteleto and de Souza (Reference Marteleto and de Souza2012), Stradford et al. (Reference Stradford, van Poppel and Lumey2017)]. Following this literature, we estimate the effect of number of children in a family on its average child HAZ. We do so using ordinary least squares method as well as by instrumenting family size with incidence of twin births. Consistent with the family size literature, we find that increasing family size by one child reduces average family child HAZ by approximately half a standard deviation. These results along with a description of how they are estimated can be found in Appendix B.
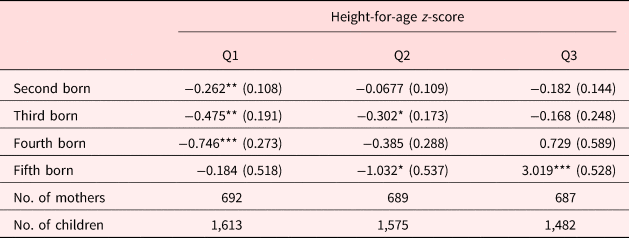
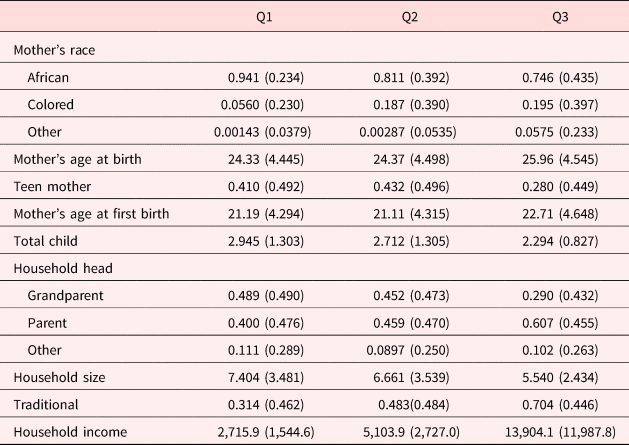
However our goal is not to estimate the family size effect, but rather to explore resource dilution as a potential mechanism underlying the birth order effect we observe in our sample. If resource dilution is in fact a major underlying factor in the birth order effect we observe, we expect it to be more prevalent in households where resource constraints are more binding. To further examine whether resource dilution in households at a lower socioeconomic status plays a role in the observed birth order effects, we split our sample into three subsamples based on income terciles and estimate equation (1) on each of these subsamples. Results are reported in Table 8. Household and mother characteristics for each of these subsamples can be found in Table A5 in the Appendix.
Table 8. Birth order effects across income terciles

Note: Standard errors in parentheses and clustered at the mother level. Controls include gender of the child, quadratic of mother's age, child's age squared, household income, and household size. We also include mother, district, and birth cohort fixed effects. Q1 represents the poorest terciles and Q3 represents the richest terciles.
*p < 0.10, **p < 0.05, ***p < 0.01.
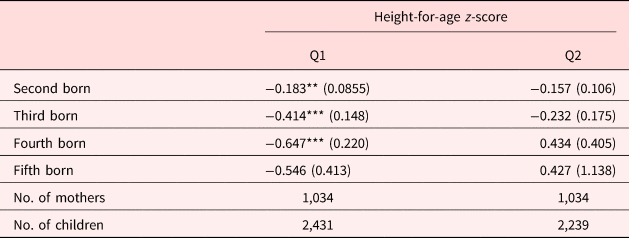
According to Table 8, the birth order effect appears strongest in both magnitude and significance in the bottom tercile with later-born children being approximately 0.26–0.75 standard deviations shorter than firstborns, on average. In the middle tercile, only the coefficients on third- and fifth-born children are statistically significant with point estimates of −0.30 and −1.03, respectively. Finally, none of the birth order effects are statistically significant in the richest tercile except that on fifth-born children. The coefficient on fifth-born children in the richest tercile is both statistically significant and positive indicating that these children are taller than firstborns on average. However, there is only one fifth-born child in the highest tercile. Therefore, there is not much we can infer from this result. A joint test rejects the equivalence of the birth order coefficients across the three income terciles at the 1% level with a χ 2 statistic of 82.27. Our results indicate that the birth order effect appears to exist in households with binding resources constraints and is mitigated and even disappears as those constraints are relaxed. We also performed the same analysis by separating the sample into two groups at median income and into four groups based on income quartiles. These results are reported in Tables A6 and A7 in the appendix and tell a similar story as those reported in Table 8. Therefore, it appears that the dilution of resources in larger families for households facing binding economic constraints is likely an important mechanism determining the birth order effect in this developing country.
6. Conclusion
In this paper, we examine the effect of birth order on health status measured in HAZ. Consistent with a large body of previous research, we find that higher birth order is associated with lower HAZ, indicating that firstborn children enjoy a health advantage over their later-born siblings. We further explore potential explanations behind the birth order effect we observe. Namely, we explore whether this effect is due to biological mechanisms, parental preferences, or resource dilution in larger families. We also investigate if this effect is simply due to systematic differences between households that select into different sized families. We find that the birth order effect does differ in magnitude across families of different sizes and that these families differ in a number of household and maternal characteristics. This indicates that heterogeneity across families of different sizes serves as a partial explanation for the birth order effect in this sample. However, it cannot fully account for the effects we observe as we find significant birth order effects in families of each observed size.
Understanding the mechanisms underlying the birth order effect can help to elucidate the potential for policies to improve child outcomes and reduce disparities within families. For example, if the primary mechanism underlying the birth order effect is biological, due to say being born to an older mother, then there is little room for policy to intervene. If instead the birth order effect is largely driven by male bias [as Jayachandran and Pande (Reference Jayachandran and Pande2017) found], then child well-being would be improved by interventions targeting female children. Finally, if the birth order effect is the result of resource dilution, then policies aimed at relaxing household resource constraints could hold promise.
We find no evidence to support that the birth order effect is due to biological mechanisms or parental favoritisms for firstborns or male children. Much of our results indicate that the birth order effect is stronger in poorer, more disadvantaged families, which is suggestive that this effect is largely driven by resource dilution in this South African sample. In Table 4, we see that the magnitude of the birth order effect increases with family size and Appendix Table A1 reports that larger families tend to be poorer and more likely to live in rural areas, which also tend to be poorer with lower access to resources than urban areas. In Table 5, we similarly see that the birth order effect appears to be larger in rural households. In Table 7, we do not find a significant birth order effect for families with male firstborns but we do for those with female firstborns, suggesting that later-born children with older sisters potentially receive less quality time with their parents. All of this is suggestive that as families increase in size, there are fewer resources per capita to invest in child health (i.e., resource dilution) and that this effect is felt more strongly by households facing tighter economic constraints. We test this explanation more explicitly in Table 8, where we find that birth order effects are stronger in significance and magnitude in the lowest tercile of our sample but are largely nonexistent in the richer terciles. Finally, we also find (reported in Appendix B) that as instrumented family size increases, average child HAZ in a family decreases.
Our results suggest that the birth order effect we observe in this South African sample is largely due to the dilution of resources in larger families (e.g., resources for health investments and parental investments including time with parents). Consequently, birth order effects resulting from resource dilution appear to be much more salient in poorer, resource-constrained households. However, the dilution of resources in larger families does not result in a significant birth order effect in richer households with less binding constraints on their resources. Thus wealthier families appear to be able to absorb increases in family size without reductions in child HAZ. Therefore, policies that relax the resource constraints faced by poor households – such as improved health infrastructure in rural areas, cash transfers, and other income generating programs – offer much promise in improving child health outcomes and reducing within household disparities.
Acknowledgements
We would like to thank anonymous reviewers for their invaluable suggestions.
Conflict of interest
All authors have no conflict of interest.
Appendix A
(see Tables A1–A7).
Table A1. Mother and household characteristics by family size
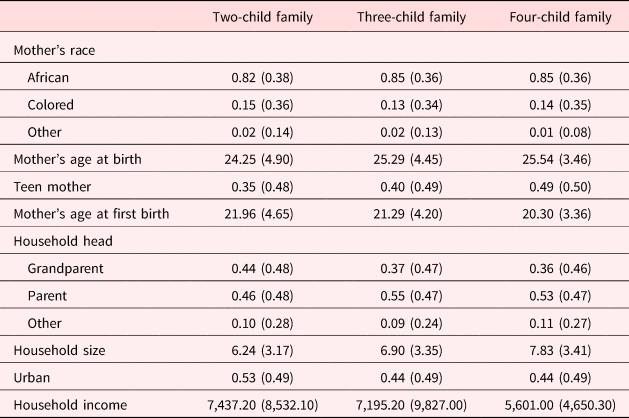
Table A2. Mother and household characteristics across urban and traditional areas
Table A3. Mother and child characteristics for birth weight sample
Table A4. Mother and household characteristics by child gender decomposition
Table A5. Mother and household characteristics across income terciles
Table A6. Birth order effects across income quartiles
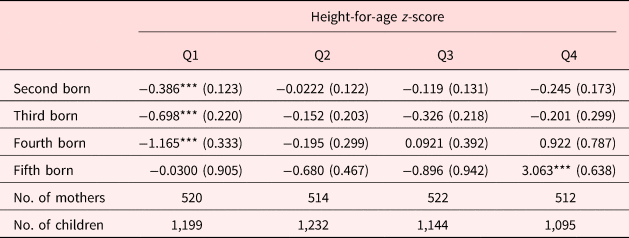
Table A7. Birth order effects across household above and below median income
Appendix B
While examining the relationship between sibling size and birth order, to test the resource dilution hypothesis, we follow the standard methodology popular in the literature. Although this sample includes the families with multiple births (twin, triplets, or more), the sample size is obviously larger than what we have in the main results. Besides using ordinary least square (OLS) estimation technique, we use instrumental variable (IV) approach to address the endogeneity problem. Endogeneity occurs if a family that chooses more children also chooses a lower quality of life, for reasons not associated with the binding resource constraint. Using incidence of twin births as an exogenous shock to family size as it is random and increases family size by two children rather than one, we estimate the following linear model.
where H m is the mean height-for-age z-score (HAZ) of the children born to the motherm. Y m is a vector of child characteristics and X m is a vector of mother and household characteristics. Finally, ε is the random error.
Table B1. Effect of total children on height-for-age z-score

In Table B1, we estimate the effect of total children born to a mother on average height-for-age z-score of the siblings. Both estimation techniques show an inverse relationship between the total number of children and the average HAZ. In fact, the first column shows that an increase in one more sibling decreases the average HAZ by 0.0414. Despite being a weak instrument (F stat = 11.02), we find a negative and significant effect to total children on HAZ. Although birth order and family size have negative effects on HAZ, family size alone cannot predict the birth order effect through resource dilution.